1. INTRODUCTION
It is well known that the interaction of an intense laser pulse with
a solid target generates hot electrons (Forslund
et al., 1977; Gibbon and
Förster, 1996; Borghesi et al.,
1999; Davies et al., 1999;
Gremillet et al., 1999; Eder et al., 2000; Batani et al., 2001; Feurer et al., 2001). These particles
propagate further into the material and can be observed to emerge on
the other side of the target. The great interest in this effect stems
from applications of these electron beams in a variety of experiments
and proposals, such as the hot igniter (Tabak et
al., 1994), generation of high-energy protons and ions
(Snavely et al., 2000; Wilks et al., 2001; Hegelich et al., 2002), ultrashort X-ray
pulses, and X-ray lasers (Rose-Petruck et
al., 1999; Fill,
2001b).
It is very important to characterize the generated electrons with
respect to their abundance, energy, and directionality. The latter
properties are a function of the mechanism of their generation.
Electron diagnostics have relied on the generated X-rays (Wilks et al., 1992; Eder et al., 2000; Pretzler et
al., 2000, 2001), backlighting with a visible pulse (Borghesi et al., 1999; Batani et al., 2001), and transition
radiation (Santos et al., 2002).
More recently a new method has been used to investigate features of the
generated electron beams, namely, recording the visible Čerenkov
radiation of the electrons emerging from the rear of the target in a
suitable medium (Brandl et al.,
2003). In this way the spatial features of the generated
electrons can be determined as well as their numbers.
In this article we demonstrate the application of the Čerenkov
method to investigate propagation of the electrons through foils. We
further study the propagation of hot electrons across narrow vacuum
gaps behind the primary target by means of X-ray diagnostics.
Čerenkov radiation is generated by particles exceeding the
velocity of light in a dielectric. The Čerenkov detector widely
used in high-energy physics is based on this effect. The classical
theory of Čerenkov radiation (laid down by Frank and Tamm
already in 1937, see Jelley, 1958) shows that
the radiation is emitted in a cone of apex half-angle
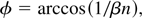
where β is the particle velocity divided by the vacuum light
velocity and n is the refractive index of the medium. The
intensity of the radiation per electron is given by the equation
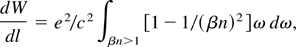
where l is the length along the path of the electron,
e the elementary charge, and ω the frequency of the
radiation. If the medium is thin enough to keep β unaltered along
the particle path, the emission is proportional to the length of the
medium. This is in contrast to optical transition radiation, which is
generated only at the boundary of a medium. Radiation is emitted only
in the visible and near UV regions of the spectrum, where n
> 1 and where there is only little absorption. For a medium thin
enough for β to be constant the number of photons emitted per
electron at a wavelength λ in the interval Δλ as derived
from Eq. (2) is given by
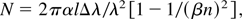
where α = 1/137 is the fine-structure constant.
Equation (3) shows that Čerenkov radiation is quite an
efficient process that may result in many photons per electron. The
spectrum emitted sharply rises towards the UV region until anomalous
dispersion and absorption eliminate the possibility of Čerenkov
emission.
In the experiments reported in this article Čerenkov radiation
is used to determine spatial features of the generated electron pulses.
From these the mechanisms generating the electrons can be deduced.
Furthermore, the radiation can be used to determine the number of
generated electrons. Note that Čerenkov diagnostics probes only
a certain window in the electron energy distribution, the lower end of
which is determined by βmin = 1/n (emission
on axis, see Eq. (1)). The upper limit of the electron energy detected
is related to the f-number of the optics used for collecting
the radiation. For electrons propagating on axis and symmetric imaging
of the Čerenkov radiation it is given by
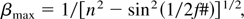
where f# is the f-number of the optics. For
n = 1.48 and f# = 2 one has a relatively small
range of βmin = 0.67 and βmax = 0.68,
corresponding to electron energies of 182 and 190 keV, respectively.
However, if an angular spread of the electrons is taken into account,
βmin is still given by 1/n, but for
βmax one obtains the expression
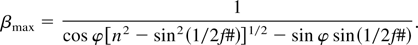
Here φ is half the angular spread of the electron beam
propagating in the Čerenkov medium. As an example, at an
intensity of 5 × 1018 W/cm2 the half
angle of emission has been determined to be 12.5° (Brandl et al., 2003) resulting in
βmax = 0.73 and a maximum energy of 236 keV.
A further interesting task of electron diagnostics is investigation
of the effect of narrow vacuum gaps on the propagation of the
electrons. In this case self-generated fields stop most of the
electrons and prevent them from reaching a medium behind the gap. We
demonstrate the effect of vacuum gaps by X-rays generated in a suitable
“fluor” behind the target. The X-ray data are in good
agreement with a simple theory treating self-fields of the
electrons.
2. EXPERIMENTAL ARRANGEMENT
The experimental setup used is shown in Figure
1. Titanium–sapphire laser pulses from the ATLAS laser of
our institute (Baumhacker et al.,
2002) are focused with an off-axis parabola to a spot 10 μm
in diameter. The pulses had an energy of up to 600 mJ and a duration of
150 fs. The maximum intensities obtained were in the range of
1019 W/cm2. Aluminum and copper foils with
thicknesses ranging from 10 to 100 μm were used as the targets. The
laser pulses were incident p-polarized at 45° to the
target.
Experimental arrangement used for X-ray and Čerenkov
diagnostics of hot electrons.
The Čerenkov medium used in the present study was a 60-μm
thin foil of polypropylene. Due to its index of refraction of 1.48 and
an insignificant fluorescence yield this material is well suited as a
Čerenkov medium. In addition, a 60-μm path length of this
low-Z substance has a negligible effect on the energy and
direction of the electrons, allowing unaltered detection of the beams
emerging from the primary target. The thin Čerenkov medium also
allows imaging of the electron pattern with a relatively high
resolution. With a thicker medium a higher emission is achieved, but at
the expense of smearing the spatial pattern.
Visible Čerenkov radiation was collected behind the target by
means of an f/2 objective and then recorded spatially
resolved by an intensified gated CCD with gate duration of 5 ns. The
CCD image thus gives a two-dimensional (2D) image of the cross section
of the electron beam as it arrives at the rear side of the target. To
block any light from the laser pulse and its harmonic, a 6-mm Schott
BG18 filter and a 3-mm VG8 filter were inserted into the beam path.
3. ELECTRONS PROPAGATING THROUGH FOILS
Spatial patterns of the radiation detected behind 100 μm of Al
foil are shown in Figure 2. The figure gives
two patterns obtained at intensities of 5 × 1018 and
1019 W/cm2. Lineouts along the horizontal
direction are also shown. It is striking that the higher intensity
results in the appearance of two distinct maxima, whereas at the lower
intensity only a dip in the pattern is discernible.
Spatially resolved Čerenkov radiation behind 100-μm
aluminum foil at intensities of 5 × 1018 and
1019 W/cm2. The two peaks resulting from
electrons propagating perpendicularly to the target surface and in line
with the laser radiation are clearly visible. Lineouts shown are along
dashed lines.
The interpretation of these results invokes two mechanisms generating
the hot electrons, namely, resonance absorption and ponderomotive
acceleration (Santala et al., 2000).
The electron population due to resonance absorption propagates
perpendicularly to the target surface, whereas the ponderomotively
accelerated electrons are in line with the laser radiation.
Semi-empirical scaling laws for the electron temperatures obtained with
the two processes were derived, yielding (Beg et
al., 1997)
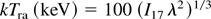
for the electrons generated by resonance absorption and (Malka & Miquel, 1996)
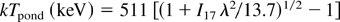
for the electrons heated by ponderomotive acceleration. Here
I17 is the intensity of the laser pulse in units of
1017 W/cm2.
Using these scaling laws for the electron temperatures, one can
evaluate the two peaks seen in the spatial Čerenkov pattern and
derive the number of electrons in each electron population. For this
evaluation it has to be taken into account that the original Boltzmann
distribution of the electrons is altered by their propagation through
the foil. We use the Bethe–Bloch formula (see, e.g., Birkhoff, 1960) to calculate the resulting electron
energy distributions. Results of such calculations are shown in Figure 3, which also gives the limits of electron
energies contributing to the Čerenkov radiation due to the
values of βmin and βmax given above. The
electron numbers and conversion efficiencies for the two populations
obtained in this way are given in Figure 4.
It is seen that the efficiencies in transferring laser energy into
hot-electron energy due to resonance absorption and ponderomotive
acceleration are quite different and depend strongly on the intensity
of the radiation. The data show that the electron numbers detected by
Čerenkov radiation are not much different for the two
populations and that the higher efficiency into ponderomotively
accelerated electrons is mainly due to the higher temperature generated
by this mechanism.
Electron energy distributions behind 100-μm Al foil, calculated
by means of the Bethe–Bloch formula. Input energies are Boltzmann
distributions with temperatures given by Eq. (4) (perpendicular
electrons). Limits of electron energies contributing to the detected
Čerenkov radiation due to βmin and
βmax as defined in the introduction are also
shown.
a: Numbers of electrons detected by Čerenkov radiation as a
function of intensity. b: Conversion efficiencies into hot electrons
derived from these data. Squares: electrons perpendicular to the target
surface (resonance absorption); circles: electrons in line with the
laser (ponderomotive acceleration). Dashed and dotted lines display
linear fits to the two sets of data.
4. ELECTRONS CROSSING VACUUM GAPS
The physics of electrons crossing thin vacuum gaps has important
implications relating to X-ray irradiation experiments and ion
acceleration. However, detailed studies of the transition of ultrashort
high-current electron beams from the conductor into a vacuum are still
lacking. Straightforward application of the Poisson equation predicts
that large electrostatic fields are generated behind the target,
slowing down the electrons or entirely preventing their propagation.
The question to be answered is how close can one approach the target
generating the radiation (henceforth called primary target) and still
separate the effects of the X rays from those of the electrons.
The experiments and the theory presented in this article help to
answer the above question. The method of investigation is to record the
emission of an X-ray “fluor” (the secondary target) in
immediate contact with the primary target and compare it with the
emission when the fluor is placed at a distance behind it.
The targets used in these experiments are shown in Figure 5. A 10-μm copper foil is the primary
target. The secondary target consists either of a 125-μm-thick
plate of molybdenum or of 10-μm nickel foil. Gaps of 50 μm up
to 500 μm were realized by means of a stainless-steel spacer
between the primary and secondary targets. Taking advantage of the fact
that the 17.4-keV Mo Kα radiation is well transmitted
through the 10-μm Cu primary target, the molybdenum experiments
used the CCD placed in front of the target. The 20-keV K-edge
of Mo is significantly above the photon energy of the copper
K-shell lines and thus the amount of photopumping is expected
to be small. For the experiments with nickel the CCD was placed behind
the target and the X rays were observed in transmission. Again,
photopumping is small, because the photon energy of Cu Kα
radiation is below the nickel K-edge.
Targets used for demonstrating the effect of self-fields of the
electrons for preventing them from crossing narrow vacuum gaps. The
primary target consists of a 10-μm copper foil. A spacer between
primary and secondary targets generates gaps of different widths. The
secondary targets (“fluors”) consist of a 10-μm nickel
foil or a 125-μm-thick molybdenum plate. For the experiments with
Ni as a fluor, the X rays were detected behind, and for Mo fluor in
front of the target.
The X rays generated by the electrons were detected by means of a
backside-illuminated, thinned X-ray CCD in the single-photon mode. In
this mode the generated charge is proportional to the energy of the
photon and can thus be used to roughly disperse the detected radiation.
The spectral resolution is improved by applying numerical event
recognition techniques, which discriminate against so-called multipixel
events in which the generated charge is distributed among many pixels
(Owens et al., 1994).
The Mo Kα photon yields for the two gap widths relative
to the yields for no gap are shown in Figure
6. The strong drop in photon yield already at the smallest gap
width of 50 μm is evident. With increasing gap width the photon
yield is further reduced but at a lesser rate. Figure 6 also shows a theoretical curve obtained by
a semi-analytical theory that combines the effect of the self-fields
(Fill, 2001a) with Monte Carlo
simulations of electron propagation through solid material. The
self-fields induce a cutoff energy of the electrons that is the higher
the larger the distance behind the target. Electrons with an initial
energy below the cutoff energy are pulled back to the target.
Mo and Ni Kα photon yield for gap widths ranging from 50
to 500 μm relative to the yield with no gap (fluor in immediate
contact with primary target). The strong reduction in X-ray yield
caused by a gap is evident. Theoretical curves obtained by an
analytical theory are also displayed in the diagram.
For an infinitely short electron pulse in one dimension the cutoff
energy can be calculated in the following way. Consider a
one-dimensional electron beam with an areal density
Na entering a vacuum from a metallic solid. At a
distance x from the solid a fraction of ξ of the electrons
has travelled beyond that distance. The quantity ξ can be
considered as a Lagrangian coordinate of the electrons. Straightforward
integration of the Poisson equation yields the field experienced by
electrons with the Lagrangian coordinate ξ as given by
E(ξ) = 4πeξNa and
thus the electrons experience a decelerating force given by
−eE(ξ). Equating the initial electron energy
U to the work done on these electrons by the decelerating
force one obtains the equation
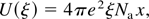
where x is the distance at which electrons with initial
energy U(ξ) are stopped. The Lagrangian coordinate
ξ(U) is calculated by integrating the electron energy
distribution f (U)dU from U to
infinity and U(ξ) is just its inverse. Solution of the
transcendental Eq. (8) yields the cutoff energy U(ξ) at a
distance x from the solid. We note that with an exponential
electron energy distribution, Eq. (8) becomes relatively simple,
because U(ξ) and its inverse ξ(U) can then be
expressed as analytical functions. This may work for an ultrathin foil.
However, for 10 μm of copper the Monte Carlo simulations show that
the electron distribution behind the primary target is considerably
altered, reflecting the fact that fewer electrons with a low energy are
transmitted. The theoretical curve is obtained by running the Monte
Carlo code (Seltzer, 1991) with the
respective cutoff energy. Two electron populations (resonance
absorption and ponderomotively scattered electrons) are separately
taken into account. A more detailed account of the theory is left to a
further publication.
The simulation results agree reasonably well with the experimental
data, the latter consistently exhibiting somewhat higher values. This
may be explained by the fact that the electron energy distribution is
shifted to lower energies upon propagation, and, owing to the higher
cross section for K-hole generation at lower energies, more X
rays are generated.
This study shows that self-fields generated by the electrons are
indeed quite effective in stopping the propagation of a large fraction
of them. However, electrons above the cutoff energy are still able to
cross relatively large distances.
5. FUTURE INVESTIGATIONS
The method of Čerenkov diagnostics allows a number of further
investigations on hot electrons to be made. The first of these relates
to the spectrum of the Čerenkov radiation. The classical theory
predicts a smooth spectrum exhibiting a monotonic rise of the emission
at shorter wavelengths (see Eq. (3)). However, the ponderomotively
scattered electrons should exhibit a component oscillating at the
second harmonic of the laser frequency. This effect has already been
observed using optical transition radiation (Baton
et al., 2003). However, the second-harmonic component
should be absent in the population generated by resonance absorption,
and thus a spatially resolved spectrum of the Čerenkov radiation
should reflect this feature in the two mechanisms generating the hot
electrons.
A further interesting aspect to be investigated by Čerenkov
diagnostics is the filamentation of the generated electron beams. The
Weibel instability (Weibel, 1959) results in
the generation of small current filaments with a diameter given
approximately by the skin depth c/ωp,
where ωp is the plasma frequency at the electron
density of the solid (Lee & Lampe, 1973;
Honda et al., 2000). This aspect is
essential for relativistic electron transport in fast ignition of
targets for inertial confinement fusion (Honda
et al., 2000). The small skin depth leads to submicron
diameters of the filaments in normal solids. However, using a
low-density target material might significantly increase the diameter
of the filaments and allow their detection by optical imaging.
A final example of using Čerenkov radiation for determining
electron beam parameters relates to the time duration of the electron
pulse. Theory shows that the emission of Čerenkov radiation is
an infinitely short process. In a practical experiment the temporal
resolution is limited by the dispersion of the medium, which results in
different propagation velocities of the generated photons and thus
spreads the emitted light flash. By observing only a limited spectral
region of the radiation this effect is minimized and the duration of
the Čerenkov radiation pulse should reflect the duration of the
electron pulse. An experiment making use of the optical Kerr effect
(Albrecht et al., 1992) could
establish a cross-correlation between the laser pulse and the
Čerenkov pulse and clarify if the generated electron pulse is as
short as the laser pulse.
Measuring the electron pulse duration is a way to determine the
duration of X-ray pulses generated by the electrons. Ultrashort hard
X-ray pulses are essential in time-resolved X-ray diffraction
experiments (Rose-Petruck et al.,
1999; Rousse et al., 2001;
Sokolowski-Tinten et al., 2003), for
testing of optics for fourth-generation light sources, and for pumping
of inner-shell X-ray lasers (Pretzler et
al., 2001).
ACKNOWLEDGMENTS
A. Böswald and H. Haas are thanked for ensuring reliable
operation of the ATLAS laser facility. We are grateful to W.
Fölsner for fabricating the targets. This work was supported in
part by the Commission of the Euratom/Max-Planck-Institut für
Plasmaphysik Association.
