Introduction
Background
Plants have evolved a variety of ways to disperse their diaspores (Tiffney Reference Soons and Bullock1986). Each dispersal mode uses biotic and/or abiotic vectors, and often comes with a suite of associated morphological characters to promote dispersal via specific pathways (Howe and Smallwood Reference Howe and Miriti1982; Van der Pijl Reference Uhl1982). Such seed dispersal syndromes are commonly still visible in fossil remains and can thus be used to infer the dominant dispersal mode in extinct plant groups (Tiffney Reference Soons and Bullock1986, Reference Tiffney2004; Eriksson et al. Reference Eriksson, Friis and Löfgren2000). During the Pennsylvanian and early Permian seeds with adaptations for wind and water dispersal (anemochory and hydrochory) appeared in several lineages (Tiffney Reference Soons and Bullock1986, Reference Tiffney2004). For instance, in early conifers (Voltziales) a variety of seed morphologies existed characteristic of wind dispersal (Rothwell et al. 2005). Some members of the walchian Voltziales produced seeds with integumentary-derived lateral or encircling wings (e.g., Otovicia hypnoides; Kerp et al. Reference Hughes, Dunlop, French, Leishman, Rice, Rodgerson and Westoby1990; Rothwell et al. 2005). Two taxa within their sister group, the voltzian Voltziales, developed larger integumentary wings positioned toward the chalazal end of the seed (Clement-Westerhof Reference Clement-Westerhof1984, Reference Clement-Westerhof1987, Reference Clement-Westerhof1988; Looy and Stevenson Reference Looy2014).
The earliest conifer known to produce seeds with large wings indicative of autorotative flight, is an early/middle Permian voltzian conifer (Kungurian–Roadian, ca. 270 Ma) from north-central Texas (DiMichele et al. Reference DiMichele, Mamay, Chaney, Hook and Nelson2001; Looy and Stevenson Reference Looy2014). These seeds, belonging to Manifera talaris, are exceptional in that they have a variable wing morphology (Fig. 1A–I). Their wing configuration ranges from two equal-sized wings, to (functionally) single-winged specimens via intermediate morphologies with various levels of underdevelopment of one of the wings (Looy and Stevenson Reference Looy2014). The variety of seed morphotypes produced by M. talaris raises the question: what is the effect of wing configuration on aerodynamics and, ultimately, dispersal potential?

Figure 1 Seeds of Manifera talaris Looy and Stevenson (Reference Looy and Stevenson2014). All images are at the same scale. A–C, Single-winged seeds. D–F, Asymmetrical double-winged seeds. G–I, Symmetrical double-winged seeds. J–L, Functionally single-winged seeds of Agathis australis. USNM numbers: A, 544043; B, 544018; C, 544015; D, 544038; E, 544008; F, 543999; G, 544624; H, 544020; I, 544035. UCMP numbers: J, 254910; K, 254911; L, 254912.
Studies of the aerodynamics of extant plants often use the actual seeds or fruits (Norberg Reference Nathan, Schurr, Spiegel, Steinitz, Trakhtenbrot and Tsoar1973; Burrows Reference Burrows1975; Sipe and Linnerooth Reference Schulz, Knopf and Stützel1985; Azuma and Okuno Reference Azuma and Okuno1987; Azuma and Yasuda Reference Azuma and Yasuda1989; Greene and Johnson Reference Greene and Johnson1990; Greene and Quesada Reference Greene and Johnson1992; Lentink et al. Reference Labandeira2009; Evangelista et al. Reference Evangelista, Hotton and Dumais2011; Varshney et al. Reference Van der Pijl2012), but reconstructed diaspore models also are known to provide close approximations. For example, paper models have been used in studies of the limits of stability in autorotation (Yasuda and Azuma Reference Willson and Traveset1997) or in analogues of turbulence (Childress et al. Reference Childress, Vandenberghe and Zhang2006). In paleobotanical studies of seed flight, Call and Dilcher (Reference Call and Dilcher1997) also used paper models to observe occurrence of rolling autorotation in Eocene members of the genus Eucommia. So far, however, no performance studies have been done on seeds with two functional wings positioned toward the chalazal end of the seed; therefore, we could only surmise their mode of descent thus far. On the basis of these previous studies, we designed a series of model tests to (1) examine the role of wing morphotype in determining flight behavior (to address the consequences of the polymorphism seen in M. talaris), (2) examine the interplay between wing morphotype and seed weight (which reflects the trade-offs between parental investment, dispersal range, and seedling establishment success), and (3) validate paper models by comparison with autorotating seeds of an extant conifer. We experimentally tested physical models to observe the mode of descent (common modes include plummeting, parachuting stable drag descents, straight-line stable gliding, stable helical gliding, long-axis rotation/rolling, autorotation, autorotation with sideslip; see four examples in Fig. 2), the frequencies of each mode, and other measures of autorotative flight performance (e.g., speed and descent time). We used models of Manifera talaris morphotypes as well as similarly shaped and sized functionally single-winged seeds of the extant kauri (Agathis australis; Fig 1K-L) and their models. The results of these paleobiomechanical simulations are used to explore the evolution and ecological implications of autorotating winged seeds.

Figure 2 Descent modes. A, Plummeting. B, Gliding with a constant yaw turn. C, Autorotation with sideslip. D, Autorotation.
Material and Methods
Geological Setting and Localities
The fossils studied here are from the lower part of the Pease River Group, which is latest Leonardian (Kungurian) to Wordian in age (Wardlaw Reference Varshney, Chang and Wang2005). Plant fossils representing the Lower Pease River Flora are preserved in mudstones of the Flowerpot Shale Member of the San Angelo Formation, at or near the contact with the overlying Blaine Formation (DiMichele et al. Reference DiMichele, Mamay, Chaney, Hook and Nelson2001). The assemblages are para-autochthonous and occur in channel facies within a coastal plain setting in the Midland Basin. The Lower Pease River Flora is known from seven localities in King, Knox, and Stonewall Counties, in north central Texas. The winged seed specimens for this paper are from the Buzzard Peak locality collections, and are listed under USNM collecting locality numbers 41391, 41395–41398 and 42103. Information on the exact locality is not recorded in this report, but is on file at the U.S. National Museum of Natural History (NMNH). More information on the Lower Pease River Flora, biostratigraphy and geological setting is provided by DiMichele et al. (Reference DiMichele, Mamay, Chaney, Hook and Nelson2001) and Looy (Reference Levin, Muller-Landau, Nathan and Chave2007).
Fossil Plant Material
The Lower Pease River Flora is dominated by gymnosperms and includes cordaites, ginkgophytes, cycadophytes, calamites, and walchian and voltzian conifers (DiMichele et al. Reference DiMichele, Mamay, Chaney, Hook and Nelson2001). The voltzian conifer that produced the winged seeds, Manifera talaris, belongs to the Majonicaceae (Looy and Stevenson Reference Looy2014), an extinct monophyletic group of tree taxa with an orthotropic branching pattern (Rothwell et al. 2005). In this study we examined 23 dispersed Manifera talaris seeds in a morphometric analysis. These specimens are housed in the Paleobotanical Collections of the U.S. National Museum of Natural History, Smithsonian Institution, Washington, D.C. Illustrated or traced specimens are stored in the Paleobotanical Type and Illustrated Collections under the following USNM catalog numbers: 543998, 543999, 544000, 544003, 544004, 544008, 544009, 544015, 544018, 544020, 544021, 544024, 544029, 544030, 544033, 544035, 544038, 544040, 544043, 544622, 544623, 544624, 544625 (also see figure captions).
The seed body of the Manifera talaris seeds is bilaterally symmetrical, rhomboid to obovate in outline. The micropylar end varies between acute and obtuse at its apex. Extensions of the integument form two wings of variable size (Fig. 1A–I) near the chalazal end of the seeds. The wings are thicker at their base, but thin distally along the wingspan. They are oriented at approximately 35–60° relative to the seed’s mediolateral axis. Wing geometries vary from irregularly oval to trapezoidal. For a more detailed description of the seeds and their ovuliferous dwarf shoots, see Looy and Stevenson (Reference Looy2014).
Seed Morphotypes
We photographed the fossil seeds using a Zeiss Stemi SV 11 with a Nikon DXM1200F digital camera or a Canon EOS 5D Mark II camera with a Canon EF 100 mm Macro lens. We screened the images for completeness of the seed outline and ability to clearly differentiate the fossils from the matrix. We used ImageJ (NIH, Bethesda, MD) to determine the morphometrics of the most intact seeds. Seed body (without wings) lengths were taken along the central axis. Seed widths were measured perpendicular to the seed axis at the junction of the integument, between the lower side of wing(s) and the seed coat. We defined wing length as the distance between the middle of the base chord of the wing to the farthest point on the wing, and its width as the maximum chord length normal to the length of the wing.
We grouped the seeds into three morphotypes based on the ratio of smallest wing area to largest wing area: (1) a functionally “single-winged,” (2) “asymmetrical double-winged”, and (3) “symmetrical double-winged.” The cutoff between the two double-wing morphotypes was made at a smallest/largest wing surface area ratio of 0.75. For geometric morphometrics shape analysis we used TPS suite software (Rohlf, http://life.bio.sunysb.edu/morph) to create a consensus shape of each morphotype based on three single-winged, fifteen asymmetrical double-winged, and five symmetrical double-winged seed types. We selected ten relatively small seeds from a mature kauri cone (Agathis australis from the University of California Botanical Garden at Berkeley; specimen number 73.0561) for the same process. The figured seeds are reposited in the Paleobotanical Collections of the University of California Museum of Paleontology (UCMP specimen numbers 254910, 254911, 254912). We chose the seeds of this species because of their similarity to the single-winged seeds of Manifera talaris. Depending on the morphotype and taxon, we used 3 or 4 landmarks and 60–135 semi-landmarks to trace the seed outlines and generate the respective consensus shapes (Fig. 3).

Figure 3 (Semi-)landmarks of size-normalized Manifera talaris and Agathis australis seeds. Original seed shapes (upper row) and resulting consensus shapes (lower row). A, Single-winged M. talaris. B, Asymmetrical double-winged M. talaris. C, Symmetrical double-winged M. talaris. D, Single-winged A. australis.
Model Construction
For our experiments, we produced three different seed morphotype models of Manifera talaris—single-winged, asymmetrical double-winged, and symmetrical double-winged seeds—each in a range of different weight classes. To validate our methods, we also produced and tested the similarly shaped seeds and models of extant Agathis australis (Mirams Reference Minami and Azuma1957; Owens et al. Reference Okubo and Levin1997).
For the construction of the models, we rescaled the Manifera talaris and Agathis australis seed consensus shapes to an average surface area of 0.80–0.82 cm2 using Adobe Illustrator (CS 6, Adobe Systems Inc.). These scaled vector tracings were used to laser cut (VLS 6.60, Universal Laser Systems, Scottsdale, Arizona) the base shape of the models from tissue paper (Spectra® Deluxe Bleeding Art Tissue™) with an area density similar to that of the wings of A. australis (1.75 and 1.80 mg cm−2, respectively) (Supplementary File S3). Whereas the weights of extant A. australis seeds are easy to determine, we lack accurate estimates for the fossil M. talaris seed weights. Comparison with similar-sized A. australis seeds suggests that M. talaris seeds may have weighed 6–7 mg. To control total weight, and because seed weight also may reflect a trade-off in parental investment, we varied seed and seed model weights over a wide range (~3.5–15.5 mg) through use of oval-shaped weights cut from an adhesive polyester film (Artist and Craftsman Supply, Berkeley; density 9.86 mg cm−2) (Supplementary File S4). We placed the weights on the seeds’ body centroids, parallel to the central axis of the seed body, and weighed each seed and model (Mettler Toledo Mx5, resolution 0.01 mg). Variation in weight was 0.5–2.5 times the mean weight of the A. australis seeds from the UCB Botanical Garden (on average 7 mg), or 20–85% of the average reported weight of seeds of this species reported in other studies (i.e., up to 18.5 mg for much larger seeds; Royal Botanic Gardens Kew Seed Information Database 2008).
Experiments
In order to reconstruct the aerodynamics of the descent of Manifera talaris seeds, we used a high-speed camera to examine the flight performance of same-scale models, dropped in a controlled environment. We used two setups: a wider camera view (70 cm away) at lower frame rate was used to establish the frequency of different descent modes, whereas a closer camera view (50 cm away) at a higher frame rate was used to measure detailed autorotation kinematics. Descents of the models and seeds were captured with a high-speed camera (HiSpec 1, Fastec Imaging, San Diego, Calif.) operated at 240 or 500 frames per second and equipped with a 25 mm f/1.4 lens (Navitar, Rochester, N.Y.) (for an example see Supplementary File S5). Lighting was provided by a pair of 150-W flood lamps. Models and seeds were held with forceps at the chalazal end, oriented parallel to the ground, and dropped 2 m above the field of capture via a ladder and a hard-mounted ring used to provide a consistent drop position. A scale, held parallel to the falling seeds’ trajectory and at the same distance from the camera, was visible in every video. The scale and the ring were several diameters of disk area away from the seed flight path to avoid aerodynamic interactions. We dropped the seeds and models in still air, shielded from ventilation within an enclosure purpose-built for studies of directed aerial descent in insects (Zeng Reference Yasuda and Azuma2013) and small vertebrates (Evangelista Reference Evangelista2013; Evangelista et al. Reference Evangelista, Cam, Huynh, Krivitskiy and Dudley2014a).
To examine descent mode, we dropped all seeds and models ten times. In all cases, the filmer noted an initial determination of descent mode. Video was retained for further detailed study for all cases in which the seed remained in focus within the viewing volume. To examine autorotation kinematics, seeds and models were dropped until five autorotational descents were captured in focus and within the viewing volume, or until five consecutive failures to capture such a descent occurred. We recorded a total of 103 specimens (78 models of M. talaris in three morphotypes and a range of different weights; ten models of A. australis and 16 A. australis seeds) in 486 separate videos comprising 100 GB of data.
Digitization and Analysis
We determined seed position in the videos by manually digitizing two points (distal wing tip, seed body center) using the MTrackJ plugin (Meijering and Smal Reference McCutchen2012) for ImageJ (NIH, Bethesda, Md.). All videos in which we observed autorotation were digitized, for a total of 60,176 points. For digitization in each video we used a sequence of frames in which at least two rotations of the seed were in focus and in the middle of the screen away from any barrel distortion and at steady state; for these sequences every frame was digitized. In addition, we partially digitized a reduced set of the descent mode videos to obtain estimates of the descent speed and of the frequency of rotations, for comparison with the autorotation data. We used the scale to convert digitized points to positions.
By using a series of custom-written scripts for Python (version 2.7.3, with Numpy version 1.8.0 and Scipy version 0.9.0) and R (version 3.0.3 [R Development Core Team 2013] with ggplot2 version 0.9.3.1 [Wickham Reference Wardlaw2009] and dplyr version 0.1.2) we were able to extract kinematics from the digitized points. From every video, we computed the vertical descent speed V, a primary measure of performance, using finite differences and taking the mean for the entire steady-state video. The inverse of the descent speed, t D=1/V, gave the descent time per meter, which we used in the discussion as an alternate measure of autorotative performance because of its particular ecological relevance as it scales with dispersal potential. In addition, we used a Fast Fourier Transform (FFT; numpy.fft.rfft) to extract the dominant frequency from seed horizontal position. In autorotative descents this corresponded to the first rotational frequency f 1R, whereas in other descent modes this corresponded to the frequency of yawing or helical motions. For every digitized frame, we calculated the angle of the seed with respect to the horizontal. The range (max-min) of this angle gave us the coning angle, β, for each video. We then coded the descent modes, kinematics, seed and model geometry information, and masses into a table for further computation and statistical analysis in R.
To facilitate comparison with other published seed and aerodynamic literature, we computed the Reynolds number (Re), a nondimensional quantity that reflects the relative contribution of inertia and viscosity; we also computed the advance ratio, J, used to examine whether the motion is dominated by the vertical descent speed or the autorotation frequency:
where l is the span, and ν=15×10−6m2 s−1 is the kinematic viscosity of air. For Re~1000, we expect inertia to dominate the flow. J appears in studies of bird and bat flight, where J>7 typically indicates forward flight, and J<5 indicates hovering; here we take these to indicate whether V or f 1R is driving the aerodynamics.
We also computed the Strouhal number, a nondimensional frequency, as St=1/J for comparisons where f 1R=0 (e.g., plummeting). For additional comparisons, we computed disk loading, tip speed, thrust coefficient C T, and effective drag and lift coefficients, C D,eff and C L,eff (using notation from Azuma and Yasuda Reference Azuma and Yasuda1989):
where m is the mass, g=9.81 m s−2 is the acceleration of gravity, ρ=1.2 kg m−3 is the density of air, S=πl2 is the disk area, S W is the wing area, and solidity ratio σ=S W/S. The span l was used in disk area calculations because the instantaneous center and radius of rotation were difficult to determine in most videos. For a wing of near-constant cross-section, the effective lift coefficient here scales as the section lift coefficient, providing a means to check the degree to which the camber (the chord-wise curvature of the wing), etc. of our fossil shapes matches those of extant autorotators. Previous studies of autorotating seeds use nondimensional coefficients drawn from studies of propellers (Azuma and Yasuda Reference Azuma and Yasuda1989; Lentink et al. Reference Labandeira2009; Norberg Reference Nathan, Schurr, Spiegel, Steinitz, Trakhtenbrot and Tsoar1973; Varshney et al. Reference Van der Pijl2012; Yasuda and Azuma Reference Willson and Traveset1997), but we include here an effective drag coefficient based on descent speed V for comparison to drag-based descent seen in pollen and small plumose seeds (Burrows Reference Burrows1975; Greene and Johnson Reference Greene and Johnson1990; Greene and Quesada Reference Greene and Johnson1992). For seed and model planforms, we also computed shape descriptors typically used in flight biomechanics, including aspect ratio (eq. 8) and second moment of area (eq. 9):
During the early to middle Permian, air density (~1.4–1.5 kg m−3) and kinematic viscosity most probably were slightly higher than at present because of elevated oxygen content (~1.5 present atmospheric level [PAL]) and CO2 levels (4–5 PAL [Berner Reference Berner2009; Bergman et al. Reference Bergman, Lenton and Watson2004; Montañez et al. Reference Mirams2007]). The higher air density would increase the aerodynamic forces (which scale with ρ) by about 25%. This potentially leads to decreasing descent velocities and increasing descent times by 5% and has been proposed to have been a factor in the evolution of flight in insects during the Carboniferous (Dudley Reference Dudley1998; Dudley and Chai Reference Dudley and Chai1996; Graham et al. Reference Givnish1995). Because the model tests were in modern atmospheres, all calculations used modern values for density and kinematic viscosity.
Results
Fossil and Extant Seed Morphometrics
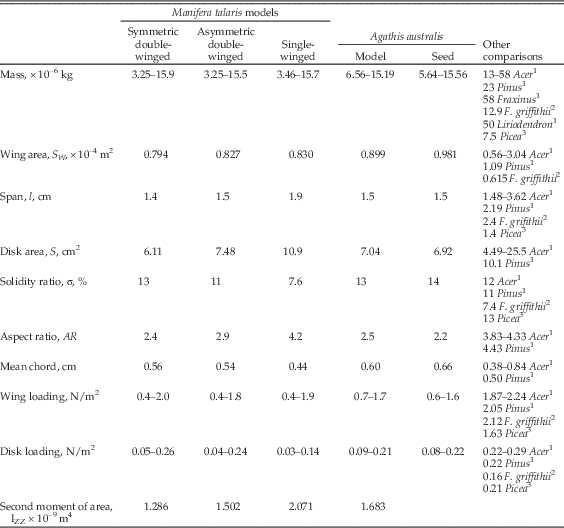
The shape and size of the seed bodies and wings of the three different Manifera talaris morphotypes show distinct differences (Table 1, Fig. 1). On average, asymmetrical double-winged seeds have a larger total area (1.15 cm2) than the symmetrical double-winged and single-winged morphotypes (respectively 0.83 and 0.99 cm2). Seed body geometries are similar in all types, but the symmetrical double-winged seed bodies are 15–20% smaller than the two other types. Wing geometries differ among all three types. Functionally single-winged seeds have long, oblong primary wings that are the longest of all the morphotypes and a secondary wing that is reduced to such an extent that it is rudimentary. Asymmetrical double-winged seeds have trapezoidal to obovate primary wings that are somewhat shorter, but the increased flaring on the lower edge of the wing results in an average area that is comparable to that of the single-winged morphotype. The secondary wing of the asymmetrical double-winged seeds is similar in shape to the obovate-to-oval wings of the symmetrical double-winged seeds. They are, however, reduced in size such that they make up less than 35% of total wing area in all samples. Both wings of the symmetrical double-winged seeds are roughly similar in size and shape. Despite the differences in wing size and morphology, the average total wing area as a proportion of the average total area differs by only 3% among the morphotypes (range of 66–69%). To maintain similar surface areas across the models of all three seed morphologies, we scaled the single-winged and asymmetrical double-winged models to 82% and 70% the size their fossil counterparts, respectively. This allowed us to compare the effect of seed shape on flight performance and kinematics independent of seed size.
Table 1 Manifera talaris seed morphotypes and Agathis australis seeds.

Seed bodies of Agathis australis are comparable in size to Manifera talaris’s symmetrical double-winged morphotype (~0.28 cm2; Table 1). The oblong wing of A. australis is shorter than the primary wing of both the single- and the asymmetrical double-winged M. talaris morphotypes, but its consistent width results in an area that is similar to both. The average total wing area as a proportion of the average total area is 70%, similar to that of the fossils. The seed body accounts for approximately 80% of the total weight of the seed.
Assuming the center of rotation in autorotative descent is approximately in the center of the seeds, the average seed lengths would give a maximum disk area approximation of 10.9 cm2, 7.48 cm2, 6.11 cm2, and 6.92 cm2 for the single, asymmetrical and symmetrical double-winged Manifera talaris models and Agathis australis seeds, respectively. The average maximum chord length of the single-winged seeds is a quarter smaller than that of the larger wing of the asymmetrical double-winged types (0.63 cm vs. 0.8 cm, respectively), but longer than that of the symmetrical double-winged seeds (0.56 and 0.55 cm). The difference in lengths and widths of the single-winged seeds and the larger wing of asymmetrical double-winged seeds results in wing areas that are approximately the same (0.66 cm2 vs. 0.65 cm2 respectively). In order to compare the effect of the different seed morphologies in the experiments, we rescaled their consensus shapes so that they had a constant area. See Table 2 for the geometric properties of the A. australis seeds and rescaled models.
Table 2 Manifera talaris and Agathis australis seed and models geometric properties for aerodynamic calculations and comparisons. Ranges given indicate the minimum and maximum values. Seed consensus shapes depicted in Figure 3. To provide equal-area comparisons, models were scaled to have constant area of about 0.8 cm2.

Sources:1 Table 1 of Azuma and Yasuda Reference Azuma and Yasuda1989;
2 Table 4 of Minami and Azuma Reference Meijering and Smal2003;
3 Norberg 1973.
Descent Mode and Frequency
Figure 2A–D illustrates representative descents for all observed modes: plummeting, gliding with a constant yaw turn, autorotation, and autorotation with sideslip. All morphotypes exhibited these modes, but the relative frequencies of each varied substantially between morphotypes (Fig. 4). In the lower weight classes (3.5–9.5 mg) the double-winged morphotypes failed to initiate autorotation in more than half of the cases, resulting in a plummeting or gliding descent. In all the weight classes combined, autorotation was the most frequently observed descent mode for the single-winged morphotype. We did not observe straight-like stable glides, parachuting stable drag descents, or rolling autorotation about the long axis in either Manifera talaris or Agathis australis.

Figure 4 Relative descent mode frequencies per mass bin of falling Manifera talaris morphotype models.
Flight Performance, Aerodynamic Parameters, and Autorotation Kinematics
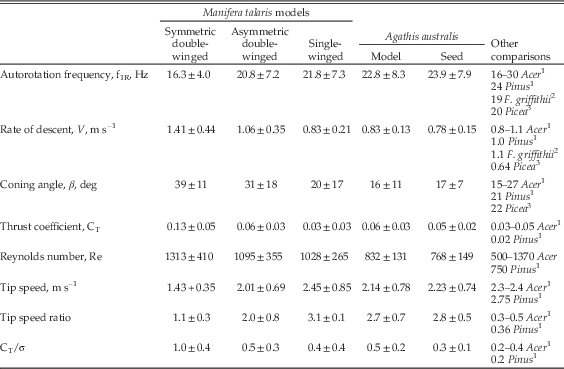
For a quantitative biomechanical comparison of falling-seed models used in our experiment and in similar studies in the literature, we have included a wide range of commonly assessed parameters and measurements related to flight performance: Table 2 compares wing geometries for the models and several extant autorotating seeds (including equations 9–10). Table 3 compares the resulting autorotation kinematics and nondimensional aerodynamic parameters for these same seeds. Autorotation kinematics are summarized in Figure 5, which shows the effect of seed mass on coning angle, autorotation frequency, and vertical descent speed. Modes and nondimensional aerodynamic parameters (eqs. 1–8) are shown in Figure 6 and Supplementary Figure S1. Descent time (s/m) at terminal velocity is shown in Figure 7.

Figure 5 Autorotation kinematics with increasing mass. All parameters are plotted against mass (mg) of Manifera talaris models and Agathis australis models and seeds. A, Descent speed (V, m/s). B, Coning angle (β, deg, see inset detail). C, Autorotation frequency (f 1R, Hz). D, Tip speed (eq. 4, m/s).

Figure 6 Nondimensional aerodynamic parameters and descent mode in Manifera talaris models and Agathis australis models and seeds. A, Advance ratio (J, eq. 2). B, Strouhal number (St=1/J). C, Drag coefficient (C D,eff, eq. 6). All plotted against Reynolds number (Re, eq. 1). Autorotation takes place at low advance ratio and high effective drag; gliding and plummeting are characterized by very high advance ratio and low effective drag. For all modes, Re~1000.

Figure 7 Wind dispersal potential. Summary diagram, combining results from the descent mode and aerodynamics experiments with Manifera talaris models and Agathis australis models and seeds, showing the relative frequency of seeds and models that plummet and glide (black bars), and autorotate with various levels of effectiveness (i.e., descent time bins at terminal velocity; gray bars). Each frequency distribution is the average of the frequency distributions of four discrete mass intervals of seeds and models: 5–8, 8–11, 11–14, and 14–17 mg. Results of even lighter models (<5 mg; shown in, for instance, Figs. 4 and 5) were not included because such small masses were not encountered in the A. australis seeds.
Table 3 Manifera talaris and Agathis australis seed and models aerodynamic properties and comparisons. Values show mean±SD and include all weight classes tested. For more detailed information see supplementary Figures 5 and S1. The variation in parameters reflects the intentional changing of model weights in the range 3.5–15 mg.

Sources: 1 Table 2 of Azuma and Yasuda Reference Azuma and Yasuda1989;
2 Table 4 of Minami and Azuma Reference Meijering and Smal2003;
In general, overall flight performance improved in going from double-winged symmetric, via double-winged asymmetric, to single-winged morphotypes. Furthermore, whereas increases in mass might be expected a priori to increase the descent speed for a case of simple drag (v~m 0.5), this appears not to be the case during autorotation. As mass increased, the coning angle decreased and rotational frequency increased in ways that kept changes in descent speed (Figs. 5 and S1) and descent time (Fig. 7) unexpectedly small.
Biomechanical Evaluation
Model Validation
Obviously, the terminal velocity of shed conifer seeds in the Paleozoic cannot be directly measured from fossils. Evaluating the performance of the range of seed morphologies produced by Manifera talaris called for an empirical approach using seed models. In the same-scale model experiments we tested the validity of our models by comparing flight characteristics of similarly made seed models of the extant Agathis australis with the real seeds the models were based on. Overall flight performance was similar between model and actual Agathis australis seeds (Fig. 7). As mass was varied, the observed autorotation kinematics (Fig. 5, right two columns) and nondimensional parameters (Fig. S1) were identical for model and actual seeds of A. australis. In addition, all observations fell within the ranges reported by others for extant autorotating seeds of similar mass (Tables 2, 3). This suggests that our same-scale model approach provided a realistic reconstruction of the flight performance of the seed of M. talaris.
Reconstructed Flight Performance
As expected, the aerodynamic characteristics of the various seed morphologies produced by Manifera talaris were quite different. The model study yielded three important observations for the three contrasting morphologies in M. talaris:
1. Initiation of autorotation failed frequently in symmetrical double-winged seeds, less frequently in asymmetrical double-winged seeds, and infrequently in single-winged seeds. Failed initiation of autorotation resulted in plummeting or gliding. Failing autorotation was most frequent in the lighter seeds.
2. Even during autorotative flight, the symmetrical double-winged seeds descended much faster on average (1.3–1.7x) than the other morphologies.
3. As symmetrical double-winged seeds increase in weight, their median descent velocity roughly increased with the square root of their weight (as predicted by scaling), even when autorotating. In contrast, the terminal descent velocity of their single-winged and asymmetrical double-winged counterparts hardly changed with increased wing loading, ranging from 6 to 29 mg/cm2. Hence, flight effectiveness during autorotation actually increased with wing loading; single-wing and asymmetrical double-winged autorotators would have been able to transport larger seeds without compromising descent performance.
Flight Kinematics as Mass and Disk Loading Change
As mass is increased within an asymmetrical double-winged or single-winged morphotype, the vertical speed and descent times can be held within a relatively constant and useful range. The changes in autorotation flight kinematics as mass changes can be understood from a free body diagram (Fig. S2, after Burrows Reference Burrows1975; Norberg Reference Nathan, Schurr, Spiegel, Steinitz, Trakhtenbrot and Tsoar1973). For an asymmetric wing with the weight of the seed placed nearest the chalazal end, the aerodynamic forces on the wing act at a point different from the center of mass. During autorotation, the seed must be inclined at some coning angle, and must be spinning, so that the vertical component of the aerodynamic forces (lift and drag) balance the weight, while the horizontal component results in the centripetal acceleration for spinning (Fig. S2A). As mass increases, reduced coning angles (Fig. 5B) balance the added weight by providing a larger vertical component of the resultant aerodynamic forces (Fig. S2B). This confirms observations in other studies of extant autorotators (Norberg Reference Nathan, Schurr, Spiegel, Steinitz, Trakhtenbrot and Tsoar1973; Azuma and Okuno Reference Azuma and Okuno1987). Aerodynamic forces scale as the square of speed, so as mass increases, speeds should increase. In autorotation, as loading increases, both autorotational frequency (f 1R) and vertical speed (V) increase (Fig. 5A,C). For single-winged Manifera talaris seed models, however, the increase in autorotational frequency is enough to increase lift to such an extent that vertical speed hardly changes despite a quadrupling of mass (Fig. 5A). This outcome also matches the results of Norberg (Reference Nathan, Schurr, Spiegel, Steinitz, Trakhtenbrot and Tsoar1973) and Azuma and Okuno (1989) and the trends correspond to what Varshney et al. (Reference Van der Pijl2012) observed when they sequentially trimmed away the wings of Acer samaras.
Because of the changes in coning angle and autorotation frequency, vertical speed during autorotation is relatively insensitive to seed mass in single-winged or asymmetrical double-winged Manifera talaris and Agathis australis. If we consider seed mass as a measure of parental investment, the ability to increase the seed mass with somewhat constant transport costs (same size and mass of wing) would be advantageous whenever long-distance dispersal improves a population’s fitness. A biomechanical limit to this could be the seed weight at which it can no longer set up stable autorotation. Experiments with non-biological cut cards and balsa models to probe this limit did not identify a weight limit (Yasuda and Azuma Reference Willson and Traveset1997) and neither did the trimming of wings of diaspores in Acer (Varshney et al. Reference Van der Pijl2012). Nor did the variation in weights—50% to 250% of extant A. australis of similar area and linear dimensions—used here. However, drop studies comparing multiple species suggest mass scaling eventually catches up (Greene and Johnson Reference Greene and Johnson1993).
Biomechanics of Manifera talaris Seeds and Extant Gliders and Autorotators
Our estimated Manifera talaris descent speeds, autorotation frequencies, and nondimensional coefficients are about the same as for previous studies of extant autorotating seeds (Azuma and Yasuda Reference Azuma and Yasuda1989; Minami and Azuma Reference Meijering and Smal2003; Norberg Reference Nathan, Schurr, Spiegel, Steinitz, Trakhtenbrot and Tsoar1973; Nathan et al. Reference Nathan, Safriel and Noy-Meir2002) (Tables 2, 3), as well as for our models versus actual seeds of A. australis (Figs. 5 and S1). This suggests that our modeling approach is valid. The thrust coefficient (Table 3) and effective lift coefficients (Fig. S1C) match extant examples, suggesting there are no unmodeled camber or wing-section effects in our physical model. Although the cross-section of the seed may be difficult to observe in compression fossils, the coefficients would suggest that details of the wing section do not substantially drive the autorotative performance seen here.
In 486 trials, the seeds never went into the rolling autorotation modes as described, for instance, for Eucommia (Call and Dilcher Reference Call and Dilcher1997) or for the tulip poplar, Liriodendron tulipifera (McCutchen Reference McCay1977). We also did not observe Magnus-effect rotational lift in Manifera talaris or Agathis australis. The seeds and models were too heavy for drag-based “parachuting” modes seen only in very light, plumed or pappose seeds (Greene and Johnson Reference Greene and Johnson1990; Greene and Quesada Reference Greene and Johnson1992; Minami and Azuma Reference Meijering and Smal2003). Long-distance straight-line stable glides as in Alsomitra macrocarpa (Azuma and Okuno Reference Azuma and Okuno1987) or other straight gliders also were not observed (Burrows Reference Burrows1975; Minami and Azuma Reference Meijering and Smal2003). We propose that the absence of straight-line glides is due to asymmetry and instability (Varshney et al. Reference Van der Pijl2012; Evangelista Reference Evangelista2013; Evangelista et al. 2014a,b). Distinct modes, with wide separation between the nondimensional aerodynamic parameters, occur because of mechanical bifurcations; i.e., small amounts of asymmetry result in instability that mechanically enforces differences in kinematics and aerodynamics and thus results in a different descent mode. In the seeds discussed here, straight-line gliding appears to require more precise control of symmetry than other modes; a small degree of asymmetry will result in turning or spinning behavior that pushes the diaspore into autorotation. This difference in sensitivity to small variations in morphology among descent modes may offer a mechanical explanation for why some modes appear more frequently in the plant world than others.
In Manifera talaris and Agathis australis, seeds were observed to plummet, stably glide in a helical pattern at high advance ratio, and autorotate at low advance ratio (Figs. 2, 6). The first mode, plummeting, happens for a heavy seed with no wing or a very small wing in relation to its weight. Plummeting is not very useful for dispersal but should be considered a reasonable assumption for an ancestral condition. As wing surfaces became more elaborate, they would have been symmetric or asymmetric. Symmetric wings appear to do best if they have a large area and glide stably, either in a classic stable glide as in Alsomitra macrocarpa, through use of phugoid mode, or through use of rolling Magnus-effect mode as in some Liriodendron tulipifera (some tulip poplar seeds have marked asymmetry; these combine rolling and autorotation). There are two constraints. First, to achieve stability, the shape of the seed must be close to symmetric (as seen in the examples of Minami and Azuma Reference Meijering and Smal2003). Empirically, even the slight left-right difference in our symmetrical double-winged M. talaris models appears enough to prevent long- distance straight-line glides (see below). Nor do our seeds have strong differences in the inertias about the principal axes (Varshney et al. Reference Van der Pijl2012) that would stably sustain rolling autorotation. The second constraint is that the static stability achievable by a flying-wing seed is limited to the moments that can be generated as the center of pressure moves forward or aft a few percent of the chord (short direction along the wing). This may limit static-stability gliding to low-wind, low-turbulence situations. Such conditions are common for the environments in which A. macrocarpa grows. This species, a liana from Malaysian and Indonesian rain forests, produces diaspores with large thin wings that are well known for their stable glide (Azuma and Okuno Reference Azuma and Okuno1987), but the Alsomitra-type winged seed is not widely distributed in regions with higher wind or turbulence.
A winged seed with even moderate asymmetry should result in two types of descent. During stable glides, the asymmetry will result in flight paths with slight, constant yaw, wasting a portion of lift on side forces, and reducing the probability of very long, straight-line glides. The helical path expected in this condition is seen in the lower weight classes of both model Manifera talaris and Agathis australis seeds and their models. As wing shapes (or the mass loading) become even more asymmetric, they are forced into autorotation, in which large effective drag coefficients are achievable owing to the squared dependence of forces on autorotation frequency. This is seen empirically here as shape changes from double-winged symmetric through double-winged asymmetric and single-winged, and also when wing loading is changed by increasing the mass of the off-center ballast of the seed (Fig. 5, Supplemental Fig. S1). During autorotation, the offset between the center of mass and the net aerodynamic center as the wing spins means that restoring moments scale with the span of the wing, making it potentially more stable than could be achieved in straight-line stable gliding. Stabilization in this manner is also seen in extant angiosperm autorotators, e.g., Buckleya joan and Tilia miqueliana (Azuma and Yasuda Reference Azuma and Yasuda1989), and in the much smaller “parachuting” seeds like Taraxacum (Greene and Johnson Reference Greene and Johnson1990). Aside from the mass distribution (Yasuda and Azuma Reference Willson and Traveset1997), countertorques generated by spinning also would stabilize the rotation (Hedrick et al. Reference Greene and Quesada2009; Varshney et al. Reference Van der Pijl2012). This is important in the face of environmental disturbances: if the parent trees are canopy trees or lianas, or stand in relatively open stands, this allows the seed to exploit higher winds (Horn et al. Reference Hedrick, Cheng and Deng2001; McCay Reference Looy and Stevenson2003). Morphologies that remain stable in turbulence (Childress et al. Reference Childress, Vandenberghe and Zhang2006; Evangelista Reference Evangelista2013; Evangelista et al. 2014b) could use this property to remain aloft or to enhance dispersal, by continuing to function when the possibility of large gusts is higher. In our results, autorotating seeds were able to maintain stability even with large horizontal translational velocities superimposed on top of the descent. Of autorotating descents, 18% had a measurable sideslip, and in a few extraordinary trials, stable sideslip velocities ranged as high as 0.96 m s−1, up to 80% of the descent speed.
Autorotation generates large forces by virtue of fast relative motion between the wing and the air, parallel to what is seen in animal flight (Norberg Reference Nathan, Schurr, Spiegel, Steinitz, Trakhtenbrot and Tsoar1973; Dudley et al. Reference Dudley, Byrnes, Yanoviak, Borrell, Brownand and McGuire2007; Evangelista Reference Evangelista2013; Evangelista et al. 2014a). Another mode of decent that might be predicted is the use of the broad surface of the diaspore as a “parachute”. However, even if Manifera talaris were to retard its descent using the maximally achievable bluff body parachuting drag, it would fall 1.4 to 2.2-times faster (v=(2mg/ρAC D)–2) than the autorotating case. The high drag parachuting strategy only works for small and tiny seeds that are able to exploit high drag at much lower Re (for Re<1, drag coefficients scale inversely with Re); these seeds experience Re~1000. A large high-drag surface would be subject to premature detachment (Schippers and Jongejans 2005; Evangelista et al. Reference Evangelista, Hotton and Dumais2011) in low winds, disadvantageous for the dispersal of viable offspring. The compressed form seen in all M. talaris morphotypes would be unstable during parachuting, and thus unable to function in high winds or high turbulence that, in the autorotation case, could carry seeds on occasional long-distance dispersal paths (Hughes et al. Reference Howe and Smallwood1994; Clark Reference Clark1998; Nathan et al. Reference Nathan, Katul, Horn, Thomas, Oren, Avissar, Pacala and Levin2008).
Paleoecological and Evolutionary Discussion
Ecological and Biogeographical Implications
The ecological implications of the autorotative seed dispersal syndrome have been discussed in several studies (Green Reference Graham, Dudley, Aguilar and Gans1980; Augspurger Reference Augspurger1986; Greene and Johnson Reference Green1989, 1992; Horn 2001). The ecological relevance of slowing down seed descent lies in the modification of seed dispersal patterns. For wind-dispersed seeds, the strongest predictor for dispersal distance is horizontal wind speed (Nathan et al. Reference Nathan and Muller-Landau2001). After that, seed release thresholds, release height, terminal velocity of the seed, and canopy structure are the most important factors (Okubo and Levin Reference Norberg1989; Nathan et al. Reference Nathan and Muller-Landau2001; Levin et al. Reference Leslie, Beaulieu, Crane and Donoghue2003; Schippers and Jongejans 2005). In order to make the most of horizontal winds, seeds have to maximize their flight time, which is a function of release height and descent velocity (Fig. 7). Maximization of descent time in a manner that is stable in turbulent, gusty wind conditions is especially advantageous for long-distance dispersal. Seeds with a morphology that makes them effective autorotators, rather than gliders or plummeters, do exactly that: they excel in longer mean descent times (Fig. 7) because aerodynamic stability allows them to keep going even when perturbed by gusts. This has profound effects on their potential dispersal distance and the geographical shape of the dispersed seed distribution. Furthermore, seeds that autorotate like Manifera talaris or Majonica alpina, growing on relatively small dwarf shoots with their large wings sticking out, likely have a larger chance of becoming dislodged as a result of gusty winds than simple wingless seeds would have. Thus, the moment of release of autorotative seeds would have had an enhanced chance of coinciding with the very conditions (horizontal and turbulent winds) they optimally exploited.
Most studies on the dispersal of autorotating seeds show a unimodal leptokurtic distribution surface, with a sharp peak close to the parent plant, and more distally a long tail (Levin et al. Reference Leslie, Beaulieu, Crane and Donoghue2003). The differential flight characteristics of the various seed morphologies produced by Manifera talaris would have added even more kurtosis to its seed distribution compared with the distributions of extant autorotating conifers, making the distribution pattern hyperleptokurtic. The plummeting (a)symmetrical double-winged seeds add to the “peakedness” in seed frequency near the parent plant, whereas the (almost) single-winged autorotators make for a longer tail, yet one that is thinner than in obligate autorotators, since only a portion of all the Manifera seeds have these flight capabilities. The long tail would result in occasional dispersal events of extremely long range, thus having a disproportionately large effect on seed-shadow size.
In 2004, Howe and Miriti listed three reasons why it may be important for seedlings that their parent plant have effective seed dispersal mechanisms: (1) to escape density-dependent mortality near the parent plant; (2) to colonize open habitats; (3) to travel to microsites required for establishment (based on Howe and Smallwood Reference Howe and Miriti1982). An increase in seed dispersal potential will affect the speed with which plant populations can shift their range during rapid climate change (e.g., Clark Reference Clark1998; Nathan et al. Reference Nathan, Safriel and Noy-Meir2002; Soons and Bullock Reference Sipe and Linnerooth2008), but also change their spatial and genetic heterogeneity. Therefore, we propose two more situations in which greater dispersal potential is important, especially on slightly longer time scales: (4) when a species living in scattered habitats of an ephemeral nature (e.g., wetlands) must escape the old locality as it disappears, and find and colonize new habitats; and (5) when migration speed is of the essence, e.g., during times of rapid climate change and the resulting fast latitudinal shift of biomes.
The last two situations, a need to find ephemeral, scattered habitats and a need for high migration rates, might have been important for early to middle Permian Euramerican plant populations. During this time period the equatorial Euramerican floral realm became increasingly arid (or rather, less wet) as a result of changes in volume of the Southern Hemisphere ice caps (Montañez et al. Reference Mirams2007). Initially, during the very beginning of the Permian, merely seasonally dry habitats extended over large, interconnected parts of the landscape, whereas the dryer “seasonally wet” habitats may have coexisted in smaller isolated patches (DiMichele et al. Reference DiMichele, Tabor, Chaney and Nelson2006). As dry seasons became progressively longer, a gradual change in the structure of the habitat landscape took place. The seasonally wet patches increased in size and started to connect, whereas the wetter seasonally dry habitats were shrinking and became fragmented. Aridification, however, progressed even further and by the end of the early Permian, seasonally wet habitats also shrank and fragmented, and corridors flanking river channels were probably among the few environments that supported rich plant life in the Midland Basin (DiMichele et al. Reference DiMichele, Tabor, Chaney and Nelson2006).
The Lower Pease River flora is one of only two fossil floras known from the Midland Basin from this particular time interval (DiMichele et al. Reference DiMichele, Mamay, Chaney, Hook and Nelson2001, 2004). The fossil flora is dominated by relatively drought-tolerant seed plants such as the voltzian conifers Manifera talaris and Lebowskia grandifolia, ginkgophytes, and cycadophytes. The assemblages are para-autochthonous and thus represent local plant communities growing near the small channels in which they were deposited and preserved. Paleosols and sedimentary patterns indicate that the environments these plants grew in were predominantly hot and dry, with a short rainy season (DiMichele et al. Reference DiMichele, Tabor, Chaney and Nelson2006). The Lower Pease River flora represents a species pool distinct from the preceding Clear Fork floras (Chaney and DiMichele Reference Chaney and DiMichele2007). The Lower Pease River Flora likely migrated in from somewhere else in the region, perhaps from areas where orographic rainfall might have differentiated this flora from that of the basinal lowlands. Winged seeds may have enabled increased migration speeds for M. talaris during the expansion phase of the early Permian seasonally wet areas, and increased the chances of reaching new habitats when habitable areas became limited and scattered over the landscape.
Evolutionary Implications
In order for their populations to maintain a high fitness, extant plant lineages adhering to various ecological strategies rely on efficient long-distance seed dispersal. Thus, it seems reasonable to assume that in the past various seed morphologies that facilitated more efficient long-range dispersal produced peaks in the fitness landscape of their producers. Accordingly, extant plants display a wide range of seed dispersal mechanisms, such as co-option of small-sized animal hosts, direct dispersal using dehiscent mechanisms, and wind dispersal utilizing drag, lift, combinations of these, or autorotation (e.g., Van der Pijl Reference Uhl1982; Tiffney and Mazer Reference Tiffney1995; Willson and Traveset Reference Wickham2000). Although the morphology and function of the autorotating voltzian conifer seeds are comparable to extant ones, the ecosystems in which they evolved were certainly not. Seed predation and dispersal by arthropods and vertebrates did not become prevalent until the Mesozoic (Tiffney Reference Soons and Bullock1986, Reference Tiffney2004; Labandeira Reference Kvaček2002; Leslie Reference Lentink, Dickson, van Leeuwen and Dickinson2011). In the absence of suitable animal vectors for seed dispersal in the Paleozoic, adaptive opportunity to improve dispersal was rather limited. Water-bound plants may have developed more-effective hydrochorous diaspore dispersal syndromes (e.g., Lepidophloios’s aquacarps [Phillips and DiMichele Reference Owens, Catalano and Aitken-Christie1992]), but for Paleozoic plants with non-hydrophytic, non-riparian lifestyles wind dispersal was the only long-range option.
The benefits of more effective wind dispersal include an increased seed-shadow size, and broader seed-shadow frequency distribution with a long tail, indicating still rare, but relatively more frequent very long-distance dispersal events. These effects allow subsequent generations to colonize new areas away from parental competition and shading, far from established populations of pathogens and the few existing predators (e.g., Nathan and Muller-Landau Reference Montañez, Tabor, Niemeier, DiMichele, Frank, Fielding, Isbell, Birgenheier and Rygel2000). Greater seed-shadow sizes and higher frequencies of very long-distance dispersal can also be achieved via production of more seeds, but this would mean a vastly expanded resource investment, as it would mainly result in higher seed densities close to the parent plant. By comparison, the enhanced dispersal performance of autorotating seeds comes at virtually no extra cost; the size investment per seed can even be increased in autorotating seeds at no cost to descent time, further enhancing successful seedling establishment. Moreover, autorotation would have allowed for adaptive flexibility in seed mass with hardly any effect on wind dispersal capability. The evolution of winged seeds in the voltzian conifers would have augmented the fitness of the populations that produced them by speeding up maximum migration rates and permitting the propagules to reach favorable microhabitats, potentially leading to attainment or maintenance of dominance within the plant community.
Winged seeds and diaspores like the ones described here seem to have evolved multiple times and independently in various conifer (Pinaceae, Cupressaceae and Araucariaceae) and numerous angiosperm lineages (e.g., Givnish Reference Farjon1980; Azuma and Yasuda Reference Azuma and Yasuda1989; Farjon Reference Farjon1990, Reference Farjon2005, Reference Farjon2010; Benkman Reference Benkman1995; Schulz et al. Reference Schippers and Jongejans2005; Eckenwalder Reference Eckenwalder2009; Leslie et al. Reference Leslie2013). In extant conifer taxa, symmetric double-winged seeds occur very rarely in Agathis species such as A. robusta and A. australis (Mirams Reference Minami and Azuma1957; Kvaček Reference Kerp, Poort, Swinkels and Verwer2002; personal observation). These double-winged seeds are vastly outnumbered by single-winged seeds produced on the same individual plant. The near absence of modern double-winged seeds in Agathis, and complete absence in other autorotating seed producing taxa, corroborates the conclusion that the more effectively dispersing single-winged morphology improves the fitness of their producers in the context of their ecological strategy.
An Imperfect Evolutionary Takeoff
Looy and Stevenson (Reference Looy2014) proposed that the lateral sporophylls of the dwarf shoot may have been predominantly responsible for the production of very asymmetric wing topologies, whereas the central sporophylls primarily produced more bilaterally symmetric ones. Moreover, they found only “left-winged” seeds on the left lateral sporophylls, whereas the right lateral sporophylls bore only “right-winged” single-winged seeds (see Fig. 8A). The only attached seed they observed with a sizable second wing was attached to a median sporophyll. For every median sporophyll there are two lateral ones, which could explain the approximately 2:1 ratio of (almost) single-winged seeds over (almost) symmetrical ones, as observed among 71 dispersed seed fossils collected at the Buzzard Peak locality in Texas (Looy and Stevenson Reference Looy2014). The oldest conifer known to produce single-winged seeds only (or seeds with a very rudimentary second wing at most) is the late Permian fellow-majonicacean Majonica alpina (Clement-Westerhof Reference Clement-Westerhof1987). Interestingly, almost all its fossilized dwarf shoots lack a median sporophyll (Fig. 8B).

Figure 8 Ovuliferous dwarf shoots, sporophyll position, and seed wing morphology. A, Ovuliferous dwarf shoot of Manifera talaris and the expected range of seed morphologies produced by the two lateral and one median sporophylls (based on fossil observations, see Looy and Stevenson Reference Looy and Stevenson2014). B, Typical Majonica alpina dwarf shoot lacking a median sporophyll and the seed morphologies it produced (Clement-Westerhof Reference Clement-Westerhof1987).
On the basis of our observations of seed morphology and the position on dwarf shoots of Manifera talaris and Majonica alpina, we hypothesize that the evolution of the autorotative seed dispersal syndrome was a discretely three-stepped evolutionary developmental process within this lineage:
1. Development of lateral integument outgrowths, giving rise to wings that increase chances of wind dispersal when the seed is released or when it is already on the ground.
2. Capacity for overdevelopment of the integument outgrowth at the chalazal end, on the side farthest from the dwarf shoot axis, thus producing a range in wing topologies as observed in Manifera talaris, depending on the position of the sporophyll on the dwarf shoot. Because this range includes the autorotative morphologies of superior functionality (in terms of wind dispersal potential), M. talaris benefited from greatly improved dispersal capacity and an increase in fitness at little extra cost.
3. Loss of the median sporophyll in winged-seed-producing voltzians (as observed in Majonica alpina); thus, an individual’s seed production investment is focused on production of the more functional single-winged autorotators only.
Because steps 2 and 3 would have required different types of genotypic adaptation, this hypothesis could explain how Manifera talaris may have persisted to produce the full range of seed morphologies, while only a portion of the seeds would have had the high dispersal capability. It is possible that step 3, the loss of the median sporophyll, was induced by developmental adaptations other than, or in addition to, the benefits of more effective seed dispersal. Within the Permian voltzian conifers there is a range in female cone structure from very open dwarf shoot- and bract-bearing fertile zones or shoots, as in Manifera’s contemporary Lebowskia grandifolia (Looy Reference Levin, Muller-Landau, Nathan and Chave2007), to condensed cones with tightly packed dwarf shoots, as in the end-Permian Pseudovoltzia liebeana (e.g., Uhl 2004). An evolutionary trend toward more- condensed, better-protected cone-like structures may also have led to reduction of dwarf shoot complexity and loss of sporophylls.
In the fossil record, only two other instances are described of conifers that produced winged seeds that routinely included symmetric double-winged forms: the Paleogene Araucariacean Doliostrobus (Kvaček Reference Kerp, Poort, Swinkels and Verwer2002) and Paleocene Agathis-like seeds (Escapa et al. Reference Escapa, Iglesias, Wilf and Cuneo2013). Interestingly, just like Manifera, these taxa represent early occurrences of autorotating seed dispersal within their lineage. Also in these separate instances of autorotative wind dispersal evolution, the exclusively autorotating dispersal syndrome seen later in these lineages may well have been the product of a similar multistep process.
Acknowledgments
We thank M. Gibson, former manager of the 6666 Ranch, for permission to work on ranch property, and J.-L. Wilde and L. Lyles for access to their property. D. Chaney and W. DiMichele are acknowledged for bringing Looy into the field and for many fruitful discussions. N. Nagalingum (Royal Botanic Gardens, Sydney) and H. Forbes (UC Botanical Garden at Berkeley) provided us with Agathis seeds. K. Calderwood and our Undergraduate Research Apprentice Program students at University of California, Berkeley (R. Ayala, A. Ayuby, M. Hao, F. Kusumo, K. Lee, and especially R. Balbin Uy) assisted with photographing, filming, and data collection. The Center for Integrative Biomechanics Education and Research (CIBER) is thanked for use of equipment. R. Dudley and Y. Zeng graciously provided additional equipment and a controlled space for drop tests. I. Duijnstee is acknowledged for discussions and help with data analysis and figure preparation. D. Contreras, S. P. Quek, D. Lentink, and two anonymous reviewers helped to improve our research project and this manuscript. This research was supported by the Hellman Fellowship, and the University of California Museum of Paleontology. This is University of California Museum of Paleontology Contribution number 2054.
Supplementary Material
Supplemental materials deposited at Dryad: doi:10.5061/dryad.h6289