Published online by Cambridge University Press: 09 February 2006
We investigate the convergence in distribution of integrals of stochastic processes satisfying a functional limit theorem. We allow a large class of continuous Gaussian processes in the limit. Depending on the continuity properties of the underlying process, local Lebesgue or Riemann integrability is required.We are grateful to the referees and Benedikt Pötscher for their helpful and constructive comments. The research of the first author was partially supported by OTKA grants T37668 and T43037 and NSF-OTKA grant INT-0223262. The research of the second author was partially supported by NATO grant PST.EAP.CLG 980599 and NSF-OTKA grant INT-0223262.
Let {xk,n,1 ≤ k ≤ n,n = 1,2,…} be a triangular array of random elements in
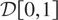
, the Skorokhod space of functions on [0,1], and assume that
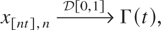
where
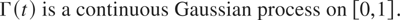
Condition (1.2) means that almost all sample paths of Γ(t) are continuous on [0,1]. In many applications one needs the relation
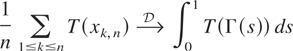
with some real-valued function T, where
denotes convergence in distribution. This paper seeks to establish (1.3) for various processes {xk,n,1 ≤ k ≤ n} under general conditions on the function T(x).
THEOREM 1.1. If T is continuous on (−∞,∞) and (1.1) and (1.2) are satisfied, then (1.3) holds.
Under the conditions of Theorem 1.1, the sample paths of T(Γ(s)), 0 ≤ s ≤ 1 are continuous with probability one, and thus the integral

exists pathwise.
In the case when Γ(t) is a Brownian motion, a short proof of Theorem 1.1 is provided by Pötscher (2004), using the continuous mapping theorem. His proof works also under (1.2). For the sake of completeness, in Section 3 we give a quick proof of Theorem 1.1 using the Skorokhod–Dudley–Wichura representation theorem.
Park and Phillips (1999), de Jong (2004), Pötscher (2004), and de Jong and Wang (2005) consider extensions of Theorem 1.1 for a larger class of functions T. The following result is due to Pötscher (2004).
THEOREM 1.2. Let Γ(t) be Brownian motion and assume that (1.1) holds and
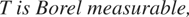
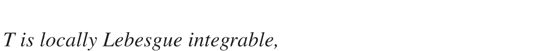

Then relation (1.3) holds.
Here the integral
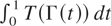
is defined pathwise; its existence is established in Karatzas and Shreve (1991, Prop. 6.27). Densities are always meant with respect to the Lebesgue measure. Local Lebesgue integrability of T means that

exists for all N in the Lebesgue sense.
In this note we investigate two extensions of Theorem 1.2. First we consider the case when the limit in (1.1) is Gaussian, but not necessarily a Brownian motion, and then we study the case when the distribution of xk,n is not necessarily smooth, i.e., (1.6) may not hold.
Assuming only (1.2), (1.4), and (1.5) we want to define
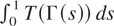
pathwise as a Lebesgue integral. Conditions (1.2) and (1.4) imply that the paths of T(Γ(s)), 0 ≤ s ≤ 1 are Borel measurable with probability one, but as the next example shows, (1.5) in general is not enough for the existence of
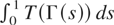
.
Let T(x) = |x|−1/2 for x ≠ 0 and T(0) = 0 and let Γ(t) = t2ξ, 0 ≤ t ≤ 1, where ξ is a standard normal random variable. (Or, alternatively, let T be as before and Γ(t) = t2W(t), 0 ≤ t ≤ 1, where W(t), 0 ≤ t ≤ 1 is a Brownian motion.) Then

does not exist.
Our first result gives a sufficient condition for the existence of
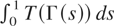
.
THEOREM 2.1. If (1.2) and (1.4) hold,
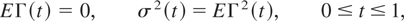

and
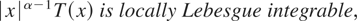
then
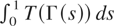
exists with probability one.
We note if Γ(t) has stationary increments, Γ(0) = 0 and
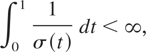
then the local time of Γ exists with probability one (cf. Geman and Horowitz, 1980, Thm. 22.1). Geman and Horowitz (1980) also point out that under conditions like (2.4) the trajectories of Γ(t) oscillate wildly. Hence (2.4) is never satisfied for smooth (e.g., differentiable) Gaussian processes.
Remark 2.1. Although Theorem 2.1 covers a very large class of functions T, from a purely mathematical point of view the question arises what happens if instead of (1.4) we assume only that T is Lebesgue measurable, i.e., the level sets {T < c} are Lebesgue measurable for any real c. (A set on the real line is called Lebesgue measurable if it is the union of a Borel set and a subset of a Borel set with measure 0. Unlike the class
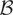
of Borel sets, the class
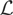
of Lebesgue measurable sets has the property that given any set

with measure 0, all subsets of A belong to
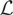
.) If instead of (1.4) we assume only that T is Lebesgue measurable, the pathwise existence of
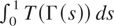
becomes a delicate problem, because the composition of a Lebesgue measurable and a continuous function is in general not Lebesgue measurable. (See Halmos, 1950, p. 83.) If Γ(t) has a continuous local time, this problem disappears because, as an argument in Pötscher (2004, p. 5) shows, in this case the integrand in (1.3) differs from a Borel-measurable function only on a set of Lebesgue measure 0, and hence it is Lebesgue measurable. However, the assumptions of Theorem 2.1 do not, in general, imply the existence of a local time for Γ, and thus the measurability of T(Γ(t)) remains open. To handle this case, let Tn be a sequence of functions such that Tn is continuous in the interval

. (Such a sequence Tn exists by Luzin's theorem (cf. Hewitt and Stromberg, 1969, Thm. 11.36).) As a trivial modification of the proof of Theorem 2.1 shows, in this case

is a Cauchy sequence of random variables in L1 norm and hence convergent in L1. Defining its limit (which is easily shown to be independent of the approximating sequence Tn) as

, all results of our paper remain valid under the Lebesgue measurability of T. Note that in this case the definition of the integral
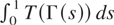
is not pathwise.
Next we show an example where Theorem 2.1 can be used to establish the existence of

.
Let T(x) = |x|−1/2, x ≠ 0, T(0) = 0, and

where W(t) is Brownian motion. Clearly, Γ(t) is differentiable and σ2(t) = t3/3. Theorem 2.1 can be used with
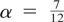
to establish the existence of
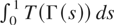
in this case.
After giving conditions for the existence of
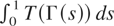
, we turn to generalizations of Theorem 1.2.
THEOREM 2.2. Assume that (1.1), (1.2), (1.4), (2.1), (2.2), and (2.3) are satisfied and there exist numbers ci,k > 0, 1 ≤ k ≤ n, n ≥ 1 such that
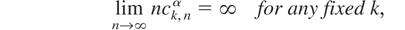
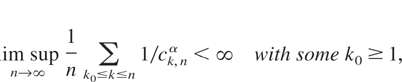
and
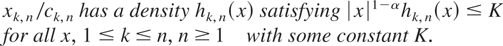
Then (1.3) holds.
We now give some applications of Theorem 2.2. Let ei, 1 ≤ i < ∞ be a stationary sequence of Gaussian random variables with Eei = 0 and r(i − j) = Eei ej such that
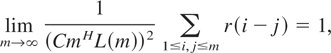
where
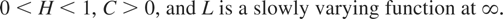
Let

for any 1 ≤ k ≤ n. According to Lemma 5.1 of Taqqu (1975),
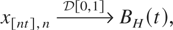
where BH(t) is a fractional Brownian motion with parameter H. This means that BH(t) is a continuous Gaussian process with EBH(t) = 0 and
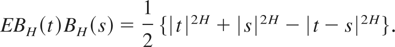
Thus conditions (1.1), (1.2), (2.1), and (2.4) are satisfied, because σ(t) = (EBH2(t))1/2 = tH, 0 ≤ t ≤ 1. Clearly xk,n /ck,n is standard normal and

By 0 < H < 1 we have for any fixed k

provided that [sum ]1≤i,j≤k r(i − j) > 0. On the other hand, if [sum ]1≤i,j≤k r(i − j) = 0, then P(xk,n = 0) = 1. By (2.8) this can happen only for finitely many k's, independently of n. Drop these 0 terms and use Theorem 2.2 for the rest of the array only. By (2.8) there is a constant k0 such that

Using the properties of slowly varying functions (cf. Bingham, Goldie, and Teugels, 1987, p. 26) we obtain

Hence (2.6) holds with α = 1, and therefore all conditions of Theorem 2.2 are established with α = 1.
The next two examples are from Taqqu (1975).
If the covariance functions satisfy

where L1(x) and L2(x) are slowly varying function at infinity, then (2.8) and (2.9) hold. For the proof we refer to Taqqu (1975).
Let {εk,−∞ < k < ∞} be a sequence of independent, identically distributed standard normal random variables and define
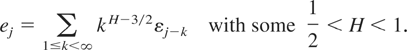
It is easy to see that {ej, 1 ≤ j < ∞} is a stationary Gaussian sequence with Eej = 0 and covariance function r satisfying
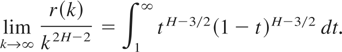
Thus (2.8) and (2.9) hold.
We note that the convergence relation (1.3) was also established by Jeganathan (2004) under the conditions of Example 2.4 assuming that T and T2 are both Lebesgue integrable on the real line. The limit in Jeganathan (2004) is given as a functional of the local time of fractional Brownian motion.
Our next example is from Horváth and Kokoszka (1997).
Consider the fractional ARIMA (p,d,q) process, which is a parametric model frequently used in modeling of long-memory time series (see, e.g., Brockwell and Davis, 1991, Sec. 13.2). Let {εk,−∞ < k < ∞} be a sequence of independent, identically distributed normal random variables with Eεk = 0 and σ2 = Eεk2 > 0. Define the polynomials
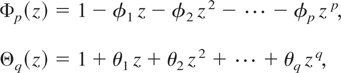
with real coefficients φj, θj. As usual, we assume that Φp and Θq have no common roots and no roots in the closed unit disk. The fractional ARIMA (p,d,q) process is defined as the unique solution {en} of the equations

where
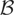
denotes the backward shift operator defined by
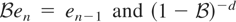
is a linear time-invariant filter defined by
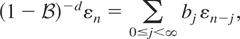
with {bj, 0 ≤ j < ∞} being the coefficients in the series expansion of (1 − z)−d, |z| < 1. If d < ½, then the infinite sum in (2.12) converges with probability one, and (2.11) has a unique moving-average solution
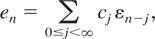
with the weights cj tending to zero at the rate jd−1.
Theorem 13.2.2 of Brockwell and Davis (1991) and Theorem 4.10.1 of Bingham et al. (1987) yield
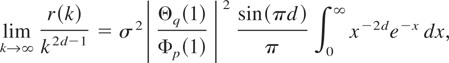
where r(k) = Eej ej+k. It is clear that (2.8) and (2.9) hold with H = d + ½ and L(x) = 1.
Let ei, −∞ < i < ∞ be defined as in Example 2.4. It is easy to see that
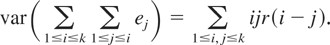
By (2.10) there is a constant c1 > 0 such that
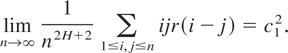
Let

and define
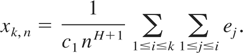
Because xk,n /ck,n is standard normal, (2.7) holds for 0 < α ≤ 1. Also,

and hence (1.1) and (1.2) are satisfied. Using the covariance of BH(s) we get

and therefore (2.2) holds for all 0 ≤ α < 1/(1 + H). By (2.13) we have (2.5) for all k0 large enough. If
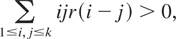
then nck,nα → 0 for any 0 ≤ α < 1/(H + 1). (We note that if (2.14) fails, then P(xk,n = 0) = 1, so T(xk,n) = T(0) has no effect on the limit.) So all the conditions of Theorem 2.2 are satisfied, and therefore
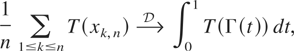
if |x|α−1T(x) is locally Lebesgue integrable with some 0 ≤ α < 1/(H + 1).
In all our applications so far, the random variables xk,n in (1.3) were normal. The following example, which extends Examples 2.4 and 2.5, shows that the long memory linear processes
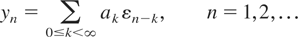
with weights ak ∼ ck−β, ½ < β < 1 satisfy the assumptions of Theorem 2.2 even if the generating random variables εj are not Gaussian. This extends the results of Pötscher (2004, Sec. 3) to long memory processes.
Let {εk,−∞ < k < ∞} be a sequence of independent, identically distributed random variables with Eε0 = 0, Eε02 = 1, Eε04 < ∞. Let {ak,k ≥ 0} be a positive sequence satisfying

Because [sum ]ak2 < ∞, the sum defining yj converges a.s. and Eyj = 0, Eyj2 < ∞. An easy calculation shows that
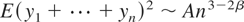
for some constant A > 0, and thus letting
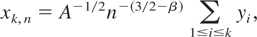
it follows from Davydov (1970, Thm. 2) that
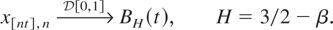
We now show that if the characteristic function φ of ε0 satisfies

for some γ > 0, then the random variables xn,n have uniformly bounded densities, and thus Theorem 2.2 applies with ck,n = (Exk,n2)1/2. Our argument follows Pötscher (2004). Let Ψn denote the characteristic function of xn,n. As is seen from the proof of Lemma 3.1 of Pötscher (2004) (cf. formulas (3.3) and (B.1) there), we have

where
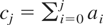
. By Eε0 = 0, Eε02 = 1 we have φ(t) = 1 − t2/2 + o(t2) as t → 0, and thus |φ(t)| ≤ (1 + t2/4)−1 in a neighborhood of 0. We now claim that

with some positive constant c. By the previous remark and the bound |φ(t)| = O(|t|−γ) (and assuming, without loss of generality, that γ ≤ 1) the claimed inequality holds with c = ¼ for |t| ≤ t0 and |t| ≥ t1, provided t0 is small enough and t1 is large enough. To prove it for t0 < |t| < t1 note that |φ(t)| < 1 for t ≠ 0 (otherwise |φ| would be periodic) and thus by the continuity of φ there exists a constant ϱamp; > 0 such that |φ(t)| ≤ 1 − ϱamp; for t0 ≤ |t| ≤ t1. Hence choosing c small enough, the claimed inequality holds also for t0 ≤ |t| ≤ t1. Because cj ∼ const·j1−β we get, using |φ(t)| ≤ 1,
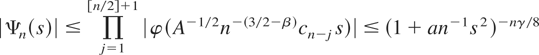
for some constant a > 0. Thus

Using 1/(1 + u2) ≤ exp(−c1u2) for |u| ≤ 1 and the substitution v = n1/2u we see that I1 ≤ C1 n−1/2 where C1 is a constant depending only on γ. On the other hand, for |u| > 1 we have

where C2 is a constant depending only on γ. Hence
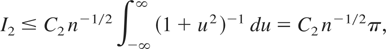
and thus we proved that
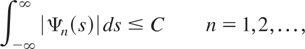
where C is a constant depending only on φ. By a well-known property of characteristic functions (see, e.g., Lukács, 1970, Thm. 3.2.2) it follows that the random variables xn,n have uniformly bounded densities, as claimed.
A minor variation of the preceding argument shows that the assumption |φ(t)| = O(|t|−γ), γ > 0 can be weakened to
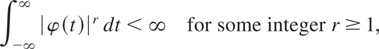
which is the condition assumed in Pötscher (2004). Indeed, using |φ(t)| ≤ 1 and cj ∼ const·j1−β we get, similarly as before,
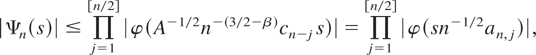
where the an,j are between positive bounds, independent of n,j. The last relation is very close to formula (B.1) in Pötscher (2004), and from there the proof can be completed by following his reasoning with minor changes.
So far we have replaced convergence to a Brownian motion in Pötscher's Theorem 1.2 with the convergence to a continuous Gaussian process. We showed that we still have the convergence in distribution of the integral functionals. Next we consider the case when (1.6) is not satisfied, i.e., if the distribution of xk,n is not necessarily smooth. The next example shows that (1.3) can fail if only (1.4) and (1.5) are assumed.
Let e1,e2,… be independent, identically distributed random variables with P(e1 = 1) = P(e1 = −1) = ½. Let T(x) = 1 if x is irrational and T(x) = 0 if x is rational. If n is a square number, then

However,

where W is a Brownian motion, so (1.3) cannot be true.
Our last result says that without assuming (1.6) or (2.7), the local Lebesgue integrability conditions in Theorems 1.2 and 2.2 should be replaced by the local Riemann integrability of T(x) to have (1.3).
THEOREM 2.3. If (1.1), (1.2), (1.4), (2.1), and (2.2) are satisfied and

then (1.3) holds.
Note that the integral in (2.15) is finite if and only if T is locally bounded, i.e., bounded on bounded intervals. The sufficiency of the last condition is obvious from 0 < α ≤ 1; to see the necessity note that if there exists a point x0 such that T is unbounded in any neighborhood of x0, then for any fixed h > 0 the integrand in (2.15) equals +∞ for |x − x0| < h, and thus the integral is infinite. The integrand is undefined for x = 0, but because we mean (2.15) as a Lebesgue integral, this does not cause any problem.
We would like to point out that (2.15) cannot be replaced by
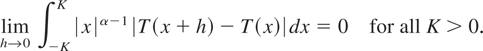
Indeed, the function T in Example 2.8 is bounded and Lebesgue measurable, and thus it satisfies

(see Hewitt and Stromberg, 1969, p. 199). From 0 < α < 1 and the Hölder inequality it follows that (2.16) is also valid, but according to Example 2.8, (1.3) cannot be true.
Remark 2.2. Condition (2.15) holds if and only if T is locally Riemann integrable, i.e., it is bounded and Riemann integrable on any bounded interval.
Proof of Theorem 1.1. By the Skorokhod–Dudley–Wichura representation theorem (cf. Shorack and Wellner, 1986, p. 47) there exist xk,n*, 1 ≤ k ≤ n, and Γn*(t), 0 ≤ t ≤ 1, such that
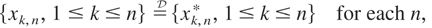
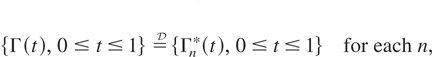
and
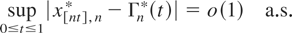
For any ε > 0 there is N such that
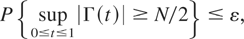
and therefore by (3.2) and (3.3) there is an integer n0 such that
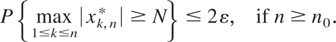
Let
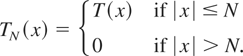
By (3.4) and (3.5) we have

Hence it is enough to prove that for any N ≥ 1
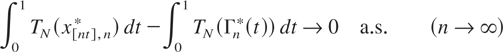
and
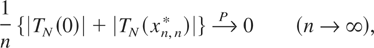
because
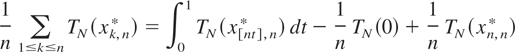
(x0,n* = 0 by definition). We note that TN is continuous on [−N,N], and therefore it is uniformly continuous on [−N,N]. Hence (3.6) follows from (3.3). Relation (3.7) is obvious, because by (3.1)–(3.5) and the continuity of TN on [−N,N] we have
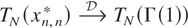
. █
Proof of Theorem 2.1. Clearly, it is enough to consider the case T ≥ 0. (Otherwise, write T as the difference between the positive and the negative parts and prove the existence for each part separately.) For any ε > 0 there is N ≥ 0 such that
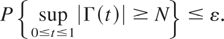
Also, there is a constant c such that
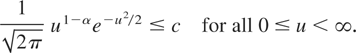
Because Γ(t) is normal with EΓ(t) = 0 and σ2(t) = EΓ2(t) we get, letting TN(x) denote the function defined in the previous proof,

The proof is complete. █
Proof of Theorem 2.2. For each ε > 0 there is N ≥ 0 such that (3.4) holds. So by (1.1) there is an integer n0 such that
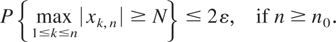
Thus

where TN(x) = T(x)I {|x| ≤ N}. Next we show that for any k0
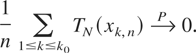
Indeed,

where K is defined in condition (2.7). Using (2.5) we get
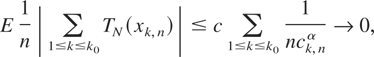
proving (3.11).
By Luzin's theorem (cf. Hewitt and Stromberg, 1969, Thm. 11.36) and (2.3) for any δ > 0 there is a continuous function T* on [−N,N] such that
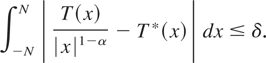
Let TN*(x) = T*(x) for |x| ≤ N and 0 otherwise. Using again (2.7) we get

where K is from condition (2.7). Also, (2.1) and (2.2) yield

where c = sup|u|1−αe−u2/2. Similarly to (3.11) one can easily show that
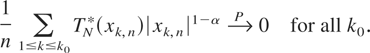
In view of (3.11)–(3.14), it is enough to show that
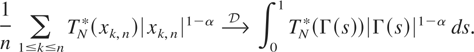
However, because of the continuity of TN*(x)|x|1−α on [−N,N], this is an immediate consequence of (3.1), (3.2), and (3.6). █
Proof of Theorem 2.3. We use again the Skorokhod–Dudley–Wichura representation theorem, so we assume that (3.1)–(3.3) hold. By (1.1) and (1.2) we also have (3.4) and (3.5). Hence, following the argument in the proof of Theorem 1.1, it is enough to prove
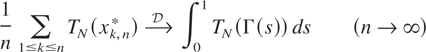
for all N, where TN(x) = T(x)I {|x| ≤ N}. As in the proof of Theorem 1.1 we have
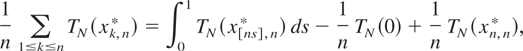
and thus

Hence

Because the distribution of Γn*(1) does not depend on n, we get
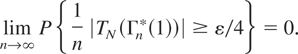
On the other hand,

if σ(1) > 0, where the last integral exists for all h by condition (2.15). If σ(1) = 0, then P{Γn*(1) = 0} = 1, and therefore
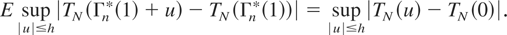
Thus by the Markov inequality we have in both cases
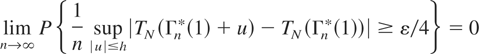
for all h. Similarly to (3.13) we have

Here the last integral tends to 0 as h → 0 by (2.15), and thus by (2.2) and the Markov inequality we have
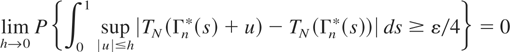
for all n. Now given δ > 0 we can choose h so small that I5 in (3.17) is at most δ for all n (note that the random variable in the probability I5 does not depend on n). Then choosing n sufficiently large, (3.3) and the preceding estimates show that I1,…,I4 will be less than δ. Thus (3.17) yields
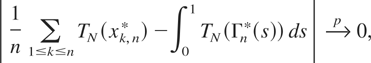
and the proof of (3.16) is complete. █
Proof of Remark 2.2. In view of the comments made after Theorem 2.3, we can assume that T is locally bounded. Let
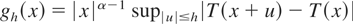
for x ≠ 0 and gh(0) = 0. The function gh(x) is Lebesgue integrable on [−K,K] if h is small. For any fixed x, the sequence gh(x) is nonincreasing as h ↓ 0, and thus it has a limit g(x) ≥ 0. Hence by the monotone convergence theorem the limit in (2.15) equals
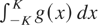
. So (2.15) holds if and only if
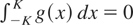
for all K. Because g(x) ≥ 0, this is true if and only if g(x) = 0 almost everywhere. Clearly, g(x0) = 0 for x0 ≠ 0 if and only if T is continuous at x0. So we proved that (2.15) is equivalent with the almost everywhere continuity of T. Recalling that a function is Riemann integrable on an interval if and only if it is bounded and almost everywhere continuous on the interval (cf. Riesz and Szőkefalvi-Nagy, 1990, p. 23), Remark 2.2 is proved. █