Nous construisons un espace adapté à l’étude de l’entropie des applications méromorphes en utilisant des limites projectives. Nous en déduisons un principe variationnel pour ces applications.

We develop a theory of $R$-module Thom spectra for a commutative symmetric ring spectrum $R$ and we analyze their multiplicative properties. As an interesting source of examples, we show that $R$-algebra Thom spectra associated to the special unitary groups can be described in terms of quotient constructions on $R$. We apply the general theory to obtain a description of the $R$-based topological Hochschild homology associated to an $R$-algebra Thom spectrum.

Let $\unicode[STIX]{x1D707}$ be the projection on 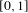$[0,1]$ of a Gibbs measure on 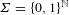$\unicode[STIX]{x1D6F4}=\{0,1\}^{\mathbb{N}}$ (or more generally a Gibbs capacity) associated with a Hölder potential. The thermodynamic and multifractal properties of $\unicode[STIX]{x1D707}$ are well known to be linked via the multifractal formalism. We study the impact of a random sampling procedure on this structure. More precisely, let 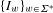$\{{I_{w}\}}_{w\in \unicode[STIX]{x1D6F4}^{\ast }}$ stand for the collection of dyadic subintervals of 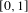$[0,1]$ naturally indexed by the finite dyadic words. Fix 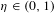$\unicode[STIX]{x1D702}\in (0,1)$, and a sequence 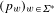$(p_{w})_{w\in \unicode[STIX]{x1D6F4}^{\ast }}$ of independent Bernoulli variables of parameters 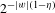$2^{-|w|(1-\unicode[STIX]{x1D702})}$. We consider the (very sparse) remaining values 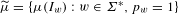$\widetilde{\unicode[STIX]{x1D707}}=\{\unicode[STIX]{x1D707}(I_{w}):w\in \unicode[STIX]{x1D6F4}^{\ast },p_{w}=1\}$. We study the geometric and statistical information associated with $\widetilde{\unicode[STIX]{x1D707}}$, and the relation between $\widetilde{\unicode[STIX]{x1D707}}$ and $\unicode[STIX]{x1D707}$. To do so, we construct a random capacity 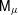$\mathsf{M}_{\unicode[STIX]{x1D707}}$ from 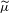$\widetilde{\unicode[STIX]{x1D707}}$. This new object fulfills the multifractal formalism, and its free energy is closely related to that of $\unicode[STIX]{x1D707}$. Moreover, the free energy of $\mathsf{M}_{\unicode[STIX]{x1D707}}$ generically exhibits one first order and one second order phase transition, while that of $\unicode[STIX]{x1D707}$ is analytic. The geometry of $\mathsf{M}_{\unicode[STIX]{x1D707}}$ is deeply related to the combination of approximation by dyadic numbers with geometric properties of Gibbs measures. The possibility to reconstruct $\unicode[STIX]{x1D707}$ from 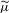$\widetilde{\unicode[STIX]{x1D707}}$ by using the almost multiplicativity of $\unicode[STIX]{x1D707}$ and concatenation of words is discussed as well.

Two measurable sets $S,\unicode[STIX]{x1D6EC}\subseteq \mathbb{R}^{d}$ form a Heisenberg uniqueness pair, if every bounded measure $\unicode[STIX]{x1D707}$ with support in $S$ whose Fourier transform vanishes on $\unicode[STIX]{x1D6EC}$ must be zero. We show that a quadratic hypersurface and the union of two hyperplanes in general position form a Heisenberg uniqueness pair in $\mathbb{R}^{d}$. As a corollary we obtain a new, surprising version of the classical Cramér–Wold theorem: a bounded measure supported on a quadratic hypersurface is uniquely determined by its projections onto two generic hyperplanes (whereas an arbitrary measure requires the knowledge of a dense set of projections). We also give an application to the unique continuation of eigenfunctions of second-order PDEs with constant coefficients.

Estimating averages of Dirichlet convolutions $1\ast \unicode[STIX]{x1D712}$, for some real Dirichlet character $\unicode[STIX]{x1D712}$ of fixed modulus, over the sparse set of values of binary forms defined over $\mathbb{Z}$ has been the focus of extensive investigations in recent years, with spectacular applications to Manin’s conjecture for Châtelet surfaces. We introduce a far-reaching generalisation of this problem, in particular replacing $\unicode[STIX]{x1D712}$ by Jacobi symbols with both arguments having varying size, possibly tending to infinity. The main results of this paper provide asymptotic estimates and lower bounds of the expected order of magnitude for the corresponding averages. All of this is performed over arbitrary number fields by adapting a technique of Daniel specific to $1\ast 1$. This is the first time that divisor sums over values of binary forms are asymptotically evaluated over any number field other than $\mathbb{Q}$. Our work is a key step in the proof, given in subsequent work, of the lower bound predicted by Manin’s conjecture for all del Pezzo surfaces over all number fields, under mild assumptions on the Picard number.

Colmez [Périodes des variétés abéliennes a multiplication complexe, Ann. of Math. (2)138(3) (1993), 625–683; available at http://www.math.jussieu.fr/∼colmez] conjectured a product formula for periods of abelian varieties over number fields with complex multiplication and proved it in some cases. His conjecture is equivalent to a formula for the Faltings height of CM abelian varieties in terms of the logarithmic derivatives at $s=0$ of certain Artin $L$-functions. In a series of articles we investigate the analog of Colmez’s theory in the arithmetic of function fields. There abelian varieties are replaced by Drinfeld modules and their higher-dimensional generalizations, so-called $A$-motives. In the present article we prove the product formula for the Carlitz module and we compute the valuations of the periods of a CM $A$-motive at all finite places in terms of Artin $L$-series. The latter is achieved by investigating the local shtukas associated with the $A$-motive.

In this paper, we construct the first examples of complex surfaces of general type with arbitrarily large geometric genus whose canonical maps induce non-hyperelliptic fibrations of genus $g=4$, and on the other hand, we prove that there is no complex surface of general type whose canonical map induces a hyperelliptic fibrations of genus $g\geqslant 4$ if the geometric genus is large.

In this paper, we consider the Stokes equations in a perforated domain. When the number of holes increases while their radius tends to 0, it is proven in Desvillettes et al. [J. Stat. Phys. 131 (2008) 941–967], under suitable dilution assumptions, that the solution is well approximated asymptotically by solving a Stokes–Brinkman equation. We provide here quantitative estimates in $L^{p}$-norms of this convergence.

We present a construction that enables one to find Banach spaces $X$ whose sets $\operatorname{NA}(X)$ of norm attaining functionals do not contain two-dimensional subspaces and such that, consequently, $X$ does not contain proximinal subspaces of finite codimension greater than one, extending the results recently provided by Read [Banach spaces with no proximinal subspaces of codimension 2, Israel J. Math. (to appear)] and Rmoutil [Norm-attaining functionals need not contain 2-dimensional subspaces, J. Funct. Anal. 272 (2017), 918–928]. Roughly speaking, we construct an equivalent renorming with the requested properties for every Banach space $X$ where the set $\operatorname{NA}(X)$ for the original norm is not “too large”. The construction can be applied to every Banach space containing $c_{0}$ and having a countable system of norming functionals, in particular, to separable Banach spaces containing $c_{0}$. We also provide some geometric properties of the norms we have constructed.