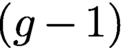1 Introduction
Let C be a complex smooth curve of genus
![]() $g \geq 3$
and
$g \geq 3$
and
 $\mathcal {SU}_C(r)$
the (coarse) moduli space of semistable vector bundles of rank r with trivial determinant on C. It is well known that this moduli space is a normal, projective, unirational variety of dimension
$\mathcal {SU}_C(r)$
the (coarse) moduli space of semistable vector bundles of rank r with trivial determinant on C. It is well known that this moduli space is a normal, projective, unirational variety of dimension
 $(r^2 - 1)(g - 1)$
. The study of the projective geometry of moduli spaces of vector bundles in low rank and genus has produced some beautiful descriptions, frequently mingling constructions issued in the context of classical algebraic geometry and the geometry of Jacobians and theta functions [Reference Desale and Ramanan11, Reference Ortega26, Reference Pauly28].
$(r^2 - 1)(g - 1)$
. The study of the projective geometry of moduli spaces of vector bundles in low rank and genus has produced some beautiful descriptions, frequently mingling constructions issued in the context of classical algebraic geometry and the geometry of Jacobians and theta functions [Reference Desale and Ramanan11, Reference Ortega26, Reference Pauly28].
Let
![]() $\mathcal {L}$
be the determinant line bundle on
$\mathcal {L}$
be the determinant line bundle on
 $\mathcal {SU}_C(r)$
and
$\mathcal {SU}_C(r)$
and

the map induced by global sections of
![]() $\mathcal {L}$
. The linear system
$\mathcal {L}$
. The linear system
 $|\mathcal {L}|^*$
is isomorphic to the
$|\mathcal {L}|^*$
is isomorphic to the
 $|r \Theta |$
linear series on the Jacobian variety
$|r \Theta |$
linear series on the Jacobian variety
 $\text {Jac}(C)$
, by the first declination of strange duality [Reference Beauville, Narasimhan and Ramanan3]. This way, we obtain a (in general) rational map
$\text {Jac}(C)$
, by the first declination of strange duality [Reference Beauville, Narasimhan and Ramanan3]. This way, we obtain a (in general) rational map
the celebrated theta map, which is canonically identified to
![]() $\varphi _{\mathcal {L}}$
[Reference Beauville, Narasimhan and Ramanan3] (see also [Reference Brivio and Verra10, Reference Hitching and Hoff16] for more details on the injectivity of
$\varphi _{\mathcal {L}}$
[Reference Beauville, Narasimhan and Ramanan3] (see also [Reference Brivio and Verra10, Reference Hitching and Hoff16] for more details on the injectivity of
![]() $\theta $
).
$\theta $
).
Let us now fix
![]() $r = 2$
. In this setting, the map
$r = 2$
. In this setting, the map
![]() $\theta $
is a finite morphism [Reference Raynaud29]. When
$\theta $
is a finite morphism [Reference Raynaud29]. When
![]() $g = 2$
, the map
$g = 2$
, the map
![]() $\theta $
is an isomorphism onto
$\theta $
is an isomorphism onto
![]() $\mathbb {P}^3$
[Reference Narasimhan and Ramanan25]. For
$\mathbb {P}^3$
[Reference Narasimhan and Ramanan25]. For
![]() $g \geq 3$
, the map
$g \geq 3$
, the map
![]() $\theta $
is an embedding if C is nonhyperelliptic, and it is a 2:1 map if C is hyperelliptic [Reference Brivio and Verra9, Reference Desale and Ramanan11, Reference van Geemen and Izadi30] (see Section 2.1 for more details).
$\theta $
is an embedding if C is nonhyperelliptic, and it is a 2:1 map if C is hyperelliptic [Reference Brivio and Verra9, Reference Desale and Ramanan11, Reference van Geemen and Izadi30] (see Section 2.1 for more details).
The goal of this paper is to describe the geometry associated to the map
![]() $\theta $
in the case
$\theta $
in the case
![]() $r = 2$
when C hyperelliptic. In the nonhyperelliptic case, the papers [Reference Bolognesi6] and [Reference Alzati and Bolognesi1] outline a connection between the moduli space
$r = 2$
when C hyperelliptic. In the nonhyperelliptic case, the papers [Reference Bolognesi6] and [Reference Alzati and Bolognesi1] outline a connection between the moduli space
 $\mathcal {SU}_C(2)$
and the moduli space
$\mathcal {SU}_C(2)$
and the moduli space
![]() $\mathcal {M}_{0,n}$
of rational curves with n ordered marked points. A generalization of [Reference Alzati and Bolognesi1] for higher rank vector bundles has been given in [Reference Bolognesi and Brivio8]. In the present work, we develop once again the interplay with the moduli space of pointed rational curves (more precisely with its GIT compactification
$\mathcal {M}_{0,n}$
of rational curves with n ordered marked points. A generalization of [Reference Alzati and Bolognesi1] for higher rank vector bundles has been given in [Reference Bolognesi and Brivio8]. In the present work, we develop once again the interplay with the moduli space of pointed rational curves (more precisely with its GIT compactification
 $\mathcal {M}_{0,n}^{GIT}$
). Thanks to some clever description of the GIT compactification in terms of linear systems on the projective space due to Kumar [Reference Kumar21], this also offers a new geometric description of the
$\mathcal {M}_{0,n}^{GIT}$
). Thanks to some clever description of the GIT compactification in terms of linear systems on the projective space due to Kumar [Reference Kumar21], this also offers a new geometric description of the
![]() $\theta $
-map if C is hyperelliptic.
$\theta $
-map if C is hyperelliptic.
Let C be a hyperelliptic curve of genus
![]() $g \geq 3$
and D an effective divisor of degree g on C.
$g \geq 3$
and D an effective divisor of degree g on C.
Let us set
 $\mathbb {P}_D^{3g-2} := \mathbb {P} \text {Ext}^1(\mathcal {O}(D), \mathcal {O}(-D)) = |K + 2D|^*,$
where K is the canonical divisor on C. The projective space
$\mathbb {P}_D^{3g-2} := \mathbb {P} \text {Ext}^1(\mathcal {O}(D), \mathcal {O}(-D)) = |K + 2D|^*,$
where K is the canonical divisor on C. The projective space
 $\mathbb {P}_D^{3g-2}$
parametrizes equivalence classes of extensions
$\mathbb {P}_D^{3g-2}$
parametrizes equivalence classes of extensions
and we denote by
 the natural tautological classifying map sending a semi-stable extension class onto its corresponding rank 2 vector bundle. Since the divisor
the natural tautological classifying map sending a semi-stable extension class onto its corresponding rank 2 vector bundle. Since the divisor
![]() $K + 2D$
is very ample, the linear system
$K + 2D$
is very ample, the linear system
 $|K + 2D|$
embeds the curve C in
$|K + 2D|$
embeds the curve C in
 $\mathbb {P}_D^{3g-2}$
. Let
$\mathbb {P}_D^{3g-2}$
. Let
![]() $N:=p_1+ \cdots + p_{2g}$
be a general reduced effective divisor in the linear system
$N:=p_1+ \cdots + p_{2g}$
be a general reduced effective divisor in the linear system
 $|2D|$
, and let
$|2D|$
, and let
 $\mathbb {P}_N^{2g-2}$
be the
$\mathbb {P}_N^{2g-2}$
be the
 $(2g-2)$
-dimensional linear span in
$(2g-2)$
-dimensional linear span in
 $\mathbb {P}_D^{3g-2}$
of the
$\mathbb {P}_D^{3g-2}$
of the
![]() $2g$
marked points
$2g$
marked points
![]() $p_1, \ldots , p_{2g}$
on C (
$p_1, \ldots , p_{2g}$
on C (
 $\mathbb {P}_N^{2g-2}$
has also a precise description in terms of extensions, see Section 3).
$\mathbb {P}_N^{2g-2}$
has also a precise description in terms of extensions, see Section 3).
Theorem A.
-
1. There exists a fibration
 whose general fiber is birational to
whose general fiber is birational to
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
.
$\mathcal {M}_{0,2g}^{\text {GIT}}$
. -
2. For every generic divisor
 $N \in |2D|$
, the restriction of
$N \in |2D|$
, the restriction of
 $f_D$
to the projective space
$f_D$
to the projective space
 $\mathbb {P}_N^{2g-2}\subset \mathbb {P}_D^{3g-2}$
dominates
$\mathbb {P}_N^{2g-2}\subset \mathbb {P}_D^{3g-2}$
dominates
 $p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
. The generic fiber of
$p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
. The generic fiber of
 $f_{D|\mathbb {P}_N^{2g-2}}$
is a rational normal curve passing through the
$f_{D|\mathbb {P}_N^{2g-2}}$
is a rational normal curve passing through the
 $2g$
marked points.
$2g$
marked points. -
3. The family of rational normal curves contracted by
 $f_{D|\mathbb {P}_N^{2g-2}}$
is the universal family of pointed rational curves over (an open subset of) the generic fiber
$f_{D|\mathbb {P}_N^{2g-2}}$
is the universal family of pointed rational curves over (an open subset of) the generic fiber
 $p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
.
$p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
.
In fact, the restriction of
![]() $f_D$
to
$f_D$
to
 $\mathbb {P}_N^{2g-2}$
coincides on an open subset with a dominant rational map
$\mathbb {P}_N^{2g-2}$
coincides on an open subset with a dominant rational map
 (see Section 4.3 for more details) that contracts all the rational normal curves passing through the
(see Section 4.3 for more details) that contracts all the rational normal curves passing through the
![]() $2g$
points of N. Via the Kapranov blow-up construction of
$2g$
points of N. Via the Kapranov blow-up construction of
 $\overline {\mathcal {M}}_{0,2g}$
(see Section 4.2.3) one sees that these rational normal curves, and the rational map
$\overline {\mathcal {M}}_{0,2g}$
(see Section 4.2.3) one sees that these rational normal curves, and the rational map
![]() $h_N$
, make up the universal family of pointed rational curves over an open subset of
$h_N$
, make up the universal family of pointed rational curves over an open subset of
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
.
$\mathcal {M}_{0,2g}^{\text {GIT}}$
.
Besides its independent interest, Thm. A is important since the map
![]() $\theta $
has a very explicit geometric description, once it is restricted to the generic fibers of the fibration
$\theta $
has a very explicit geometric description, once it is restricted to the generic fibers of the fibration
![]() $p_D$
. To this end, the following construction is crucial.
$p_D$
. To this end, the following construction is crucial.
Let
 $p, i(p)$
be two hyperelliptic involution-conjugate points in C; and consider the line
$p, i(p)$
be two hyperelliptic involution-conjugate points in C; and consider the line
 $l \subset \mathbb {P}_D^{3g-2}$
secant to C and passing through p and
$l \subset \mathbb {P}_D^{3g-2}$
secant to C and passing through p and
 $i(p)$
. We show that this line intersects the subspace
$i(p)$
. We show that this line intersects the subspace
 $\mathbb {P}_N^{2g-2}$
in a point. Moreover, the locus
$\mathbb {P}_N^{2g-2}$
in a point. Moreover, the locus
 $\Gamma \subset \mathbb {P}_N^{2g-2}$
of these intersections as we vary
$\Gamma \subset \mathbb {P}_N^{2g-2}$
of these intersections as we vary
![]() $p\in C$
is a rational normal curve passing by the points
$p\in C$
is a rational normal curve passing by the points
![]() $p_1, \ldots , p_{2g}$
. One of the consequences of Theorem A, is that the map
$p_1, \ldots , p_{2g}$
. One of the consequences of Theorem A, is that the map
![]() $f_D$
contracts the curve
$f_D$
contracts the curve
![]() $\Gamma $
onto a point
$\Gamma $
onto a point
 $w \in p_D^{-1}(N)$
(recall that
$w \in p_D^{-1}(N)$
(recall that
 $p_D^{-1}(N)$
is birational to
$p_D^{-1}(N)$
is birational to
![]() $\mathcal {M}_{0,2g}$
).
$\mathcal {M}_{0,2g}$
).
By using Kumar’s description [Reference Kumar21] of certain rational involutions on
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
, we can prove the following Theorem.
$\mathcal {M}_{0,2g}^{\text {GIT}}$
, we can prove the following Theorem.
Theorem B. The map
![]() $\theta $
restricted to the fibers
$\theta $
restricted to the fibers
 $p_D^{-1}(N)$
is a 2-to-1 osculating projection
$p_D^{-1}(N)$
is a 2-to-1 osculating projection
![]() $\pi _N$
of multiplicity
$\pi _N$
of multiplicity
![]() $g-2$
centered at the point
$g-2$
centered at the point
 $w = f_D(\Gamma )$
, up to composition with a birational map.
$w = f_D(\Gamma )$
, up to composition with a birational map.
In this theorem, and in the rest of the text, multiplicity one will mean the simple linear projection. Furthermore, the image of
![]() $\pi _N$
can be identified with a connected component of the moduli space
$\pi _N$
can be identified with a connected component of the moduli space
 $\mathcal {SU}_{C_w}(2)^{inv}$
of hyperelliptic invariant semistable vector bundles with trivial determinant on
$\mathcal {SU}_{C_w}(2)^{inv}$
of hyperelliptic invariant semistable vector bundles with trivial determinant on
![]() $C_w$
, where
$C_w$
, where
![]() $C_w$
is the hyperelliptic 2-to-1 cover of
$C_w$
is the hyperelliptic 2-to-1 cover of
![]() $\mathbb {P}^1$
ramifying over the
$\mathbb {P}^1$
ramifying over the
![]() $2g$
points defined by w. Thanks to [Reference Kumar21], we know that the ramification locus of the map
$2g$
points defined by w. Thanks to [Reference Kumar21], we know that the ramification locus of the map
![]() $\pi _N$
is the Kummer variety
$\pi _N$
is the Kummer variety
 $\text {Kum}(C_w) \subset \mathcal {SU}_{C_w}(2)^{inv}$
. These results, combined with Theorem B, allow us to give a quite accurate description of the ramification locus of the map
$\text {Kum}(C_w) \subset \mathcal {SU}_{C_w}(2)^{inv}$
. These results, combined with Theorem B, allow us to give a quite accurate description of the ramification locus of the map
![]() $\theta $
:
$\theta $
:
Theorem C. The ramification locus of the map
![]() $\theta $
has an irreducible component birational to a fibration in Kummer varieties of dimension
$\theta $
has an irreducible component birational to a fibration in Kummer varieties of dimension
![]() $g-1$
over
$g-1$
over
 $|2D| \cong \mathbb {P}^g$
.
$|2D| \cong \mathbb {P}^g$
.
In low genus, we are able to give a more precise description of the Theta map and its interplay with maps classifying extensions. Let us define
![]() $\varphi _D$
as
$\varphi _D$
as
![]() $\theta \circ f_D$
. The map
$\theta \circ f_D$
. The map
![]() $\varphi _D$
is defined by the linear system
$\varphi _D$
is defined by the linear system
 $|\mathcal {I}_{\text {Sec}^{g-2}(C)}(g)|$
(see Proposition 2.2).
$|\mathcal {I}_{\text {Sec}^{g-2}(C)}(g)|$
(see Proposition 2.2).
Theorem D. Let C be a hyperelliptic curve of genus 3. Then, for generic N, the restriction of
![]() $\varphi _D$
to the subspace
$\varphi _D$
to the subspace
 $\mathbb {P}_N^{2g-2}$
is exactly the composition
$\mathbb {P}_N^{2g-2}$
is exactly the composition
![]() $\pi _N \circ h_N$
. If
$\pi _N \circ h_N$
. If
![]() $g=4$
or
$g=4$
or
![]() $5$
, then
$5$
, then
 $\text {Sec}^{g-2}(C)\cap \mathbb {P}_N^{2g-2}$
is set-theoretically equal to the base locus of
$\text {Sec}^{g-2}(C)\cap \mathbb {P}_N^{2g-2}$
is set-theoretically equal to the base locus of
![]() $\pi _N \circ h_N$
.
$\pi _N \circ h_N$
.
Notation.
 $\mathbb {P}^n = \mathbb {P}(\mathbb {C}^{n+1})$
will denote the n-dimensional complex projective space of dim 1 subspaces. Throughout this paper, a form F of degree r on
$\mathbb {P}^n = \mathbb {P}(\mathbb {C}^{n+1})$
will denote the n-dimensional complex projective space of dim 1 subspaces. Throughout this paper, a form F of degree r on
![]() $\mathbb {P}^n$
will denote an element of the vector space
$\mathbb {P}^n$
will denote an element of the vector space
 $H^0(\mathbb {P}^n, \mathcal {O}_{\mathbb {P}^n}(r)) = \text {Sym}^r(\mathbb {C}^{n+1})^*$
. If we fix a basis
$H^0(\mathbb {P}^n, \mathcal {O}_{\mathbb {P}^n}(r)) = \text {Sym}^r(\mathbb {C}^{n+1})^*$
. If we fix a basis
![]() $x_0, \ldots , x_n$
of
$x_0, \ldots , x_n$
of
 $(\mathbb {C}^{n+1})^*$
, F is simply a homogeneous polynomial of degree r in
$(\mathbb {C}^{n+1})^*$
, F is simply a homogeneous polynomial of degree r in
![]() $x_0, \ldots , x_n$
. Most of the maps in this paper will be rational maps, hence we will often offend good taste by just dropping the adjective rational. We apologize for that.
$x_0, \ldots , x_n$
. Most of the maps in this paper will be rational maps, hence we will often offend good taste by just dropping the adjective rational. We apologize for that.
Plan of the paper: In Section 2, we introduce some general results about moduli of vector bundles and the maps classifying extension classes. Sections 3 and 4 are devoted to the study of the restriction of the classifying maps to
 $\mathbb {P}_N^{2g-2} \subset \mathbb {P}_D^{3g-2}$
(with N moving in
$\mathbb {P}_N^{2g-2} \subset \mathbb {P}_D^{3g-2}$
(with N moving in
 $|2D|$
) and to the relation of such maps with forgetful linear systems contracting rational normal curves. In Section 5, thanks to the projective geometry of the curve C embedded in
$|2D|$
) and to the relation of such maps with forgetful linear systems contracting rational normal curves. In Section 5, thanks to the projective geometry of the curve C embedded in
 $\mathbb {P}_D^{3g-2}$
the hyperelliptic involution comes into play and we show Theorems A, B, and C. Finally, Sections 6 and 7 are devoted to a more detailed study of the low genus cases, up to genus 6, which are resumed in Theorem D.
$\mathbb {P}_D^{3g-2}$
the hyperelliptic involution comes into play and we show Theorems A, B, and C. Finally, Sections 6 and 7 are devoted to a more detailed study of the low genus cases, up to genus 6, which are resumed in Theorem D.
2 Moduli of vector bundles
We briefly recall here some results about moduli of vector bundles.
2.1 Moduli of vector bundles and the map
 $\theta $
$\theta $
Let C be a smooth genus g algebraic curve with genus
![]() $g \geq 2$
. Let us denote by
$g \geq 2$
. Let us denote by
 $\text {Pic}^d(C)$
the Picard variety of degree d line bundles on C. The Jacobian of C is
$\text {Pic}^d(C)$
the Picard variety of degree d line bundles on C. The Jacobian of C is
 $\text {Jac}(C) = \text {Pic}^0(C)$
. As customary, we will denote by
$\text {Jac}(C) = \text {Pic}^0(C)$
. As customary, we will denote by
 $\Theta \subset \text {Pic}^{g-1}(C)$
the Riemann theta divisor.
$\Theta \subset \text {Pic}^{g-1}(C)$
the Riemann theta divisor.
The Picard group
![]() $\text {Pic}(\mathcal {SU}_C(2))$
is isomorphic to
$\text {Pic}(\mathcal {SU}_C(2))$
is isomorphic to
![]() $\mathbb {Z}$
, and it is generated by the determinant line bundle
$\mathbb {Z}$
, and it is generated by the determinant line bundle
![]() $\;\mathcal {L}$
[Reference Drezet and Narasimhan15]. For every
$\;\mathcal {L}$
[Reference Drezet and Narasimhan15]. For every
![]() $E \in \mathcal {SU}_C(2)$
, let us define the theta divisor
$E \in \mathcal {SU}_C(2)$
, let us define the theta divisor
 $$ \begin{align*}\theta(E) := \{ L \in \text{Pic}^{g-1}(C) \ | \ h^0(C, E \otimes L) \not = 0 \}.\end{align*} $$
$$ \begin{align*}\theta(E) := \{ L \in \text{Pic}^{g-1}(C) \ | \ h^0(C, E \otimes L) \not = 0 \}.\end{align*} $$
In the rank 2 case,
 $\theta (E)$
is a divisor in the linear system
$\theta (E)$
is a divisor in the linear system
 $|2 \Theta | \cong \mathbb {P}^{2^g - 1}$
and
$|2 \Theta | \cong \mathbb {P}^{2^g - 1}$
and
 $|2\Theta |$
is isomorphic to the linear system
$|2\Theta |$
is isomorphic to the linear system
 $|\mathcal {L}|^*$
[Reference Beauville, Narasimhan and Ramanan3]. It is well known that we can identify the map
$|\mathcal {L}|^*$
[Reference Beauville, Narasimhan and Ramanan3]. It is well known that we can identify the map
 $\mathcal {SU}_C(2) \to |\mathcal {L}|^*$
with the Theta map
$\mathcal {SU}_C(2) \to |\mathcal {L}|^*$
with the Theta map
 $$ \begin{align*} \theta : \mathcal{SU}_C(2) & \to |2 \Theta|;\\ E & \mapsto \theta(E). \end{align*} $$
$$ \begin{align*} \theta : \mathcal{SU}_C(2) & \to |2 \Theta|;\\ E & \mapsto \theta(E). \end{align*} $$
In rank 2, the map
![]() $\theta $
is a finite morphism. If C is not hyperelliptic,
$\theta $
is a finite morphism. If C is not hyperelliptic,
![]() $\theta $
is known to be an embedding [Reference Brivio and Verra9, Reference van Geemen and Izadi30]. This is also the case in genus 2, where
$\theta $
is known to be an embedding [Reference Brivio and Verra9, Reference van Geemen and Izadi30]. This is also the case in genus 2, where
![]() $\theta $
is an isomorphism onto
$\theta $
is an isomorphism onto
![]() $\mathbb {P}^3$
[Reference Narasimhan and Ramanan25]. If C is hyperelliptic of genus
$\mathbb {P}^3$
[Reference Narasimhan and Ramanan25]. If C is hyperelliptic of genus
![]() $g \geq 3$
, we have that
$g \geq 3$
, we have that
![]() $\theta $
factors through the involution
$\theta $
factors through the involution
induced by the hyperelliptic involution i, embedding the quotient
 $\mathcal {SU}_C(2)/i^*$
into
$\mathcal {SU}_C(2)/i^*$
into
 $|2 \Theta |$
[Reference Desale and Ramanan11]. An interesting explicit description of the image of the hyperelliptic theta map is given in [Reference Desale and Ramanan11].
$|2 \Theta |$
[Reference Desale and Ramanan11]. An interesting explicit description of the image of the hyperelliptic theta map is given in [Reference Desale and Ramanan11].
2.2 The classifying maps
Let D be a general degree g effective divisor on C. Let us consider isomorphism classes of extensions
These extensions are parametrized by the
 $(3g - 2)$
-dimensional projective space
$(3g - 2)$
-dimensional projective space
 $\mathbb {P}_D^{3g-2} := \mathbb {P} \text {Ext}^1(\mathcal {O}(D), \mathcal {O}(-D)) = |K + 2D|^*$
, where K is the canonical divisor of C. The divisor
$\mathbb {P}_D^{3g-2} := \mathbb {P} \text {Ext}^1(\mathcal {O}(D), \mathcal {O}(-D)) = |K + 2D|^*$
, where K is the canonical divisor of C. The divisor
![]() $K + 2D$
is very ample and embeds C as a degree
$K + 2D$
is very ample and embeds C as a degree
![]() $4g - 2$
curve in
$4g - 2$
curve in
 $\mathbb {P}_D^{3g-2}$
. Let us define the rational surjective classifying map
$\mathbb {P}_D^{3g-2}$
. Let us define the rational surjective classifying map
 which sends a semi-stable extension class
which sends a semi-stable extension class
 $(e)$
to the vector bundle
$(e)$
to the vector bundle
![]() $E_e$
. The composed map
$E_e$
. The composed map

can be described in terms of polynomial maps. From [Reference Bertram4, Theorem 2] we have an isomorphism
 $$ \begin{align} H^0(\mathcal{SU}_C(2), \mathcal{L}) \cong H^0(\mathbb{P}_D^{3g-2}, \mathcal{I}_C^{g-1}(g)), \end{align} $$
$$ \begin{align} H^0(\mathcal{SU}_C(2), \mathcal{L}) \cong H^0(\mathbb{P}_D^{3g-2}, \mathcal{I}_C^{g-1}(g)), \end{align} $$
where
![]() $\mathcal {I}_C$
is the ideal sheaf of C. In particular, we have
$\mathcal {I}_C$
is the ideal sheaf of C. In particular, we have
Theorem 2.1. The map
![]() $\varphi _D$
is given by the linear system
$\varphi _D$
is given by the linear system
 $|\mathcal {I}_C^{g-1}(g)|$
of forms of degree g vanishing with multiplicity at least
$|\mathcal {I}_C^{g-1}(g)|$
of forms of degree g vanishing with multiplicity at least
![]() $g - 1$
on C.
$g - 1$
on C.
Let us denote by
 $\text {Sec}^n(C)$
the variety of
$\text {Sec}^n(C)$
the variety of
![]() $(n + 1)$
-secant n-planes on C. We have that the singular locus of
$(n + 1)$
-secant n-planes on C. We have that the singular locus of
 $\text {Sec}^{n+1}(C)$
is the secant variety
$\text {Sec}^{n+1}(C)$
is the secant variety
![]() $\text {Sec}^{n}(C)$
for every n. The linear system
$\text {Sec}^{n}(C)$
for every n. The linear system
 $|\mathcal {I}_C^{g-1}(g)|$
can be alternatively characterized as follows (see e.g., [Reference Alzati and Bolognesi1, Lemma 2.5]):
$|\mathcal {I}_C^{g-1}(g)|$
can be alternatively characterized as follows (see e.g., [Reference Alzati and Bolognesi1, Lemma 2.5]):
Proposition 2.2. The linear system
 $|\mathcal {I}_C^{g-1}(g)|$
and
$|\mathcal {I}_C^{g-1}(g)|$
and
 $|\mathcal {I}_{\text {Sec}^{g-2} (C)}(g)|$
on
$|\mathcal {I}_{\text {Sec}^{g-2} (C)}(g)|$
on
 $\mathbb {P}_D^{3g-2}$
are the same.
$\mathbb {P}_D^{3g-2}$
are the same.
2.3 The exceptional fibers of the classifying map
 $f_D$
$f_D$
Since
 $\dim \mathcal {SU}_C(2) = 3g - 3$
, the generic fiber of
$\dim \mathcal {SU}_C(2) = 3g - 3$
, the generic fiber of
![]() $f_D$
has dimension one. The set of stable bundles for which
$f_D$
has dimension one. The set of stable bundles for which
 $\dim (f_D^{-1}(E))> 1$
is a proper subset of
$\dim (f_D^{-1}(E))> 1$
is a proper subset of
 $\mathcal {SU}_C(2)$
. For simplicity, let us define the “Serre dual” divisor
$\mathcal {SU}_C(2)$
. For simplicity, let us define the “Serre dual” divisor
![]() $B := K - D$
with
$B := K - D$
with
![]() $\deg (B) = g-2$
. As in the previous paragraphs, the isomorphism classes of extensions
$\deg (B) = g-2$
. As in the previous paragraphs, the isomorphism classes of extensions
are classified by the projective space
 $$ \begin{align*}\mathbb{P}_B^{3g-6} := \mathbb{P} \text{Ext}^1 (\mathcal{O}(B), \mathcal{O}(-B)) = |K + 2B|^*,\end{align*} $$
$$ \begin{align*}\mathbb{P}_B^{3g-6} := \mathbb{P} \text{Ext}^1 (\mathcal{O}(B), \mathcal{O}(-B)) = |K + 2B|^*,\end{align*} $$
which is endowed with the rational classifying map
 defined the same way as
defined the same way as
![]() $f_D$
.
$f_D$
.
Proposition 2.3. Let
 $E \in \mathcal {SU}_C(2)$
be a stable bundle. Then
$E \in \mathcal {SU}_C(2)$
be a stable bundle. Then
 $$ \begin{align*} \dim(f_D^{-1}(E)) \geq 2 \qquad \text{if and only if} \qquad E \in \overline{f_B(\mathbb{P}_B^{3g-6})}. \end{align*} $$
$$ \begin{align*} \dim(f_D^{-1}(E)) \geq 2 \qquad \text{if and only if} \qquad E \in \overline{f_B(\mathbb{P}_B^{3g-6})}. \end{align*} $$
Proof Let E be a stable bundle. Then, by Riemann-Roch and Serre duality theorems, the dimension of
 $f^{-1}_D(E)$
is given by
$f^{-1}_D(E)$
is given by
 $$ \begin{align*} h^0(C, E \otimes \mathcal{O}(D)) &= h^0(C, E \otimes \mathcal{O}(B)) + 2g - 2(g-1) \\ &= h^0(C, E \otimes \mathcal{O}(B)) + 1 \end{align*} $$
$$ \begin{align*} h^0(C, E \otimes \mathcal{O}(D)) &= h^0(C, E \otimes \mathcal{O}(B)) + 2g - 2(g-1) \\ &= h^0(C, E \otimes \mathcal{O}(B)) + 1 \end{align*} $$
Thus,
 $\dim (f_D^{-1}(E))> 2$
if and only if there exists a nonzero sheaf morphism
$\dim (f_D^{-1}(E))> 2$
if and only if there exists a nonzero sheaf morphism
![]() $\mathcal {O}(-B) \to E$
. This is equivalent to
$\mathcal {O}(-B) \to E$
. This is equivalent to
 $E \in \overline {f_B(\mathbb {P}_B^{3g-6})}$
.
$E \in \overline {f_B(\mathbb {P}_B^{3g-6})}$
.
If
![]() $g> 2$
, the divisor
$g> 2$
, the divisor
 $|K + 2B|$
embeds C as a degree
$|K + 2B|$
embeds C as a degree
![]() $4g - 6$
curve in
$4g - 6$
curve in
 $\mathbb {P}_B^{3g-6}$
(recall that
$\mathbb {P}_B^{3g-6}$
(recall that
 $\mathbb {P} \text {Ext}^1 (\mathcal {O}(B),\mathcal {O}(-B)) = |K + 2 B|^*$
). Again by Theorem 2.1, the map
$\mathbb {P} \text {Ext}^1 (\mathcal {O}(B),\mathcal {O}(-B)) = |K + 2 B|^*$
). Again by Theorem 2.1, the map
![]() $\varphi _B$
is given by the linear system
$\varphi _B$
is given by the linear system
 $|\mathcal {I}_C^{g-3}(g-2)|$
. Moreover, by [Reference Pareschi and Popa27, Theorem 4.1] this linear system has projective dimension
$|\mathcal {I}_C^{g-3}(g-2)|$
. Moreover, by [Reference Pareschi and Popa27, Theorem 4.1] this linear system has projective dimension
 $\left ( \sum _{i = 0}^{g-2} {\binom {g}{i}} \right ) - 1$
.
$\left ( \sum _{i = 0}^{g-2} {\binom {g}{i}} \right ) - 1$
.
Let us denote by
![]() $\mathbb {P}_c$
the linear span of
$\mathbb {P}_c$
the linear span of
 $\theta (\overline {f_B(\mathbb {P}_B^{3g-6})})$
in
$\theta (\overline {f_B(\mathbb {P}_B^{3g-6})})$
in
 $|2 \Theta |$
. Hence
$|2 \Theta |$
. Hence
![]() $\mathbb {P}_c$
has dimension
$\mathbb {P}_c$
has dimension
 $\left ( \sum _{i = 0}^{g-2} {\binom {g}{i}} \right ) - 1$
, and Proposition 2.3 also applies to
$\left ( \sum _{i = 0}^{g-2} {\binom {g}{i}} \right ) - 1$
, and Proposition 2.3 also applies to
![]() $\varphi _D$
: the fibers of
$\varphi _D$
: the fibers of
![]() $\varphi _D$
with dimension
$\varphi _D$
with dimension
![]() $\geq 2$
are those over
$\geq 2$
are those over
![]() $\mathbb {P}_c$
.
$\mathbb {P}_c$
.
3 A linear projection in
 $|2 \Theta |$
$|2 \Theta |$
The goal of this Section is to describe the map
 $\mathcal {SU}_C(2) \to \mathbb {P}^g$
whose fibers will be birational—and in some cases even biregular—to the GIT compactification of the moduli space of
$\mathcal {SU}_C(2) \to \mathbb {P}^g$
whose fibers will be birational—and in some cases even biregular—to the GIT compactification of the moduli space of
![]() $2g$
-pointed rational curves. In order to do this, we describe the projection with center
$2g$
-pointed rational curves. In order to do this, we describe the projection with center
![]() $\mathbb {P}_c$
, seen as a linear subspace of
$\mathbb {P}_c$
, seen as a linear subspace of
 $|2 \Theta |$
. So far we are not resricting to the case where C is hyperelliptic.
$|2 \Theta |$
. So far we are not resricting to the case where C is hyperelliptic.
Let
![]() $p_{\mathbb {P}_c}$
be the linear projection in
$p_{\mathbb {P}_c}$
be the linear projection in
 $|2 \Theta |$
with center
$|2 \Theta |$
with center
![]() $\mathbb {P}_c$
. Recall that
$\mathbb {P}_c$
. Recall that
 $\dim \mathbb {P}_c \,{=}\, \left [\! \sum _{i = 0}^{g-2} \binom {g}{i} \!\right ] \,{-}\, 1$
. A straightforward calculation shows that the supplementary linear subspaces of
$\dim \mathbb {P}_c \,{=}\, \left [\! \sum _{i = 0}^{g-2} \binom {g}{i} \!\right ] \,{-}\, 1$
. A straightforward calculation shows that the supplementary linear subspaces of
![]() $\mathbb {P}_c$
in
$\mathbb {P}_c$
in
 $|2 \Theta |$
are of projective dimension g. Thus, the image of
$|2 \Theta |$
are of projective dimension g. Thus, the image of
![]() $p_{\mathbb {P}_c}$
is a g-dimensional projective space. Let us set
$p_{\mathbb {P}_c}$
is a g-dimensional projective space. Let us set
 $$ \begin{align*}\widehat{\mathcal{SU}}_C(2) := \mathcal{SU}_C(2) \setminus (\text{Kum}(C) \cup \overline{\varphi_D(\mathbb{P}_B^{3g-6})}).\end{align*} $$
$$ \begin{align*}\widehat{\mathcal{SU}}_C(2) := \mathcal{SU}_C(2) \setminus (\text{Kum}(C) \cup \overline{\varphi_D(\mathbb{P}_B^{3g-6})}).\end{align*} $$
This is the open subset of
 $\mathcal {SU}_C(2)$
we will be mostly concerned by. Recall that the space
$\mathcal {SU}_C(2)$
we will be mostly concerned by. Recall that the space
 $H^0(C, E \otimes \mathcal {O}(D))$
has dimension 2 for
$H^0(C, E \otimes \mathcal {O}(D))$
has dimension 2 for
 $E \in \widehat {\mathcal {SU}}_C(2)$
. Consequently, we can pick two sections
$E \in \widehat {\mathcal {SU}}_C(2)$
. Consequently, we can pick two sections
![]() $s_1$
and
$s_1$
and
![]() $s_2$
that constitute a basis for this space.
$s_2$
that constitute a basis for this space.
Theorem 3.1. The image of the projection
![]() $p_{\mathbb {P}_c}$
can be identified with the linear system
$p_{\mathbb {P}_c}$
can be identified with the linear system
 $|2 D|$
on C, in a way such that the restriction of the projection
$|2 D|$
on C, in a way such that the restriction of the projection
![]() $p_{\mathbb {P}_c}$
to
$p_{\mathbb {P}_c}$
to
 $\theta (\widehat {\mathcal {SU}}_C(2))$
coincides with the map
$\theta (\widehat {\mathcal {SU}}_C(2))$
coincides with the map
 $$ \begin{align*} \theta(\widehat{\mathcal{SU}}_C(2)) \to |2D| \\ \theta(E) \mapsto \text{Zeroes}(s_1 \wedge s_2) \end{align*} $$
$$ \begin{align*} \theta(\widehat{\mathcal{SU}}_C(2)) \to |2D| \\ \theta(E) \mapsto \text{Zeroes}(s_1 \wedge s_2) \end{align*} $$
Proof A similar statement was proved in [Reference Alzati and Bolognesi1] for C non hyperelliptic, but the proof extends to the hyperelliptic case with no big problem. We recall briefly the lines of [Reference Alzati and Bolognesi1, Theorem 4.1] and will mention explicitly where the proof for C hyperelliptic differs. The Picard variety
 $\text {Pic}^{g-1}(C)$
contains a model
$\text {Pic}^{g-1}(C)$
contains a model
![]() $\widetilde {C}$
of C, made up by line bundles of type
$\widetilde {C}$
of C, made up by line bundles of type
 $\mathcal {O}(B + p)$
, with
$\mathcal {O}(B + p)$
, with
![]() $p \in C$
. The span of
$p \in C$
. The span of
![]() $\widetilde {C}$
inside
$\widetilde {C}$
inside
 $|2 \Theta |^*$
corresponds to the complete linear system
$|2 \Theta |^*$
corresponds to the complete linear system
 $|2 D|^*$
. Moreover, the linear span of
$|2 D|^*$
. Moreover, the linear span of
![]() $\widetilde {C}$
is the annihilator of
$\widetilde {C}$
is the annihilator of
![]() $\mathbb {P}_c$
. In particular, the projection
$\mathbb {P}_c$
. In particular, the projection
![]() $p_{\mathbb {P}_c|\theta (\widehat {\mathcal {SU}}_C(2))}$
determines a hyperplane in the annihilator of
$p_{\mathbb {P}_c|\theta (\widehat {\mathcal {SU}}_C(2))}$
determines a hyperplane in the annihilator of
![]() $\mathbb {P}_c$
, which is a point in
$\mathbb {P}_c$
, which is a point in
 $|2 D|$
. This projection can be identified with the map
$|2 D|$
. This projection can be identified with the map
 $$ \begin{align*} p_{\mathbb{P}_c\mid\theta(\widehat{\mathcal{SU}}_C(2))} : \theta(\widehat{\mathcal{SU}}_C(2)) & \to |2D|, \\ \theta(E) & \mapsto \Delta(E) , \end{align*} $$
$$ \begin{align*} p_{\mathbb{P}_c\mid\theta(\widehat{\mathcal{SU}}_C(2))} : \theta(\widehat{\mathcal{SU}}_C(2)) & \to |2D|, \\ \theta(E) & \mapsto \Delta(E) , \end{align*} $$
where
![]() $\Delta (E)$
is the divisor defined by
$\Delta (E)$
is the divisor defined by
 $$ \begin{align} \Delta (E):= \{p \in C \ | \ h^0(C,E \otimes \mathcal{O}(B + p)) \not = 0 \}. \end{align} $$
$$ \begin{align} \Delta (E):= \{p \in C \ | \ h^0(C,E \otimes \mathcal{O}(B + p)) \not = 0 \}. \end{align} $$
Equivalently, we have that
 $\Delta (E) = \theta (E) \cap \widetilde {C}$
. Now, in order to adapt to the hyperelliptic case, it is enough to observe that since
$\Delta (E) = \theta (E) \cap \widetilde {C}$
. Now, in order to adapt to the hyperelliptic case, it is enough to observe that since
 $\theta (E) = \theta (i^*E)$
, we directly obtain that
$\theta (E) = \theta (i^*E)$
, we directly obtain that
 $\Delta (E) = \Delta (i^* E)$
. Finally, an easy Riemann-Roch argument shows that that
$\Delta (E) = \Delta (i^* E)$
. Finally, an easy Riemann-Roch argument shows that that
 $\Delta (E)$
is the divisor of zeroes of
$\Delta (E)$
is the divisor of zeroes of
![]() $s_1 \wedge s_2$
.
$s_1 \wedge s_2$
.
Recall that the linear system
 $|K + 2D|$
embeds the curve C in the projective space
$|K + 2D|$
embeds the curve C in the projective space
 $\mathbb {P}_D^{3g-2}$
. Let
$\mathbb {P}_D^{3g-2}$
. Let
 $N \in |2D|$
be a generic effective reduced divisor and consider the linear span
$N \in |2D|$
be a generic effective reduced divisor and consider the linear span
 $\langle N \rangle \subset \mathbb {P}_D^{3g-2}$
. The annihilator of
$\langle N \rangle \subset \mathbb {P}_D^{3g-2}$
. The annihilator of
 $\langle N \rangle $
is the vector space
$\langle N \rangle $
is the vector space
 $H^0(C, 2D + K - N)$
, which has dimension g. In particular, the linear span
$H^0(C, 2D + K - N)$
, which has dimension g. In particular, the linear span
 $\langle N \rangle $
has dimension
$\langle N \rangle $
has dimension
 $(3g - 2) - g = 2g - 2$
. Let us write
$(3g - 2) - g = 2g - 2$
. Let us write
 $$ \begin{align*}\mathbb{P}_N^{2g-2} := \langle N \rangle \subset \mathbb{P}_D^{3g-2}.\end{align*} $$
$$ \begin{align*}\mathbb{P}_N^{2g-2} := \langle N \rangle \subset \mathbb{P}_D^{3g-2}.\end{align*} $$
We will study the classifying map
![]() $\varphi _D$
in relation with a fibration
$\varphi _D$
in relation with a fibration
 $\mathcal {SU}_C(2) \to \mathbb {P}^g$
by considering the restrictions of
$\mathcal {SU}_C(2) \to \mathbb {P}^g$
by considering the restrictions of
![]() $\varphi _D$
to
$\varphi _D$
to
 $\mathbb {P}_N^{2g-2}$
, as N varies in the linear system
$\mathbb {P}_N^{2g-2}$
, as N varies in the linear system
 $|2D|$
. The spaces
$|2D|$
. The spaces
 $\mathbb {P}_N^{2g-2}$
have a very explicit description in terms of extension classes (see [Reference Lange and Narasimhan23]).
$\mathbb {P}_N^{2g-2}$
have a very explicit description in terms of extension classes (see [Reference Lange and Narasimhan23]).
Notation. For simplicity, let us write
![]() $\varphi _{D,N}$
for the restricted map
$\varphi _{D,N}$
for the restricted map
![]() $\varphi _{D|\mathbb {P}_N^{2g-2}}$
.
$\varphi _{D|\mathbb {P}_N^{2g-2}}$
.
Before proceeding further, let us recall from [Reference Alzati and Bolognesi1], the following proposition, which is a consequence of [Reference Lange and Narasimhan23, Proposition 1.1].
Proposition 3.2. Let N in
 $|2D|$
be a general divisor on
$|2D|$
be a general divisor on
 $C \subset \mathbb {P}_D^{3g-2}$
. Then, the image of
$C \subset \mathbb {P}_D^{3g-2}$
. Then, the image of

is the closure in
 $\theta (\mathcal {SU}_C(2))$
of the fiber over
$\theta (\mathcal {SU}_C(2))$
of the fiber over
 $N \in |2D|$
of the projection
$N \in |2D|$
of the projection
![]() $p_{\mathbb {P}_c}$
.
$p_{\mathbb {P}_c}$
.
4 The modular fibration
 $\mathcal {SU}_C(2) \to \mathbb {P}^g$
$\mathcal {SU}_C(2) \to \mathbb {P}^g$
Let C be a smooth genus
![]() $g \geq 3$
curve (not necessarily hyperelliptic). Let D be a general degree g effective divisor on C. Let
$g \geq 3$
curve (not necessarily hyperelliptic). Let D be a general degree g effective divisor on C. Let
![]() $N = p_1 + \cdots + p_{2g}$
be a general divisor in the linear system
$N = p_1 + \cdots + p_{2g}$
be a general divisor in the linear system
 $|2D|$
. Consider the span
$|2D|$
. Consider the span
 $\mathbb {P}_N^{2g-2}$
in
$\mathbb {P}_N^{2g-2}$
in
 $\mathbb {P}_D^{3g-2}$
of the
$\mathbb {P}_D^{3g-2}$
of the
![]() $2g$
marked points
$2g$
marked points
![]() $p_1, \ldots , p_{2g}$
. In this section, building on [Reference Bolognesi7] and [Reference Alzati and Bolognesi1], we will give more information about the restricted map
$p_1, \ldots , p_{2g}$
. In this section, building on [Reference Bolognesi7] and [Reference Alzati and Bolognesi1], we will give more information about the restricted map
![]() $\varphi _{D,N}$
. In particular, we will explain the interplay between these maps, rational normal curves in
$\varphi _{D,N}$
. In particular, we will explain the interplay between these maps, rational normal curves in
 $\mathbb {P}_N^{2g-2}$
and moduli spaces of rational pointed curves.
$\mathbb {P}_N^{2g-2}$
and moduli spaces of rational pointed curves.
4.1 Linear systems in
 $\mathbb {P}_N^{2g-2}$
contracting rational normal curves
$\mathbb {P}_N^{2g-2}$
contracting rational normal curves
Recall that the secant variety
 $\text {Sec}^{g - 2}(C)$
is the base locus for
$\text {Sec}^{g - 2}(C)$
is the base locus for
![]() $\varphi _D$
(see Theorem 2.1 and Proposition 2.2). Hence we will distinguish the following two secant varieties in
$\varphi _D$
(see Theorem 2.1 and Proposition 2.2). Hence we will distinguish the following two secant varieties in
 $\mathbb {P}_N^{2g-2}$
:
$\mathbb {P}_N^{2g-2}$
:
 $$ \begin{align*} \text{Sec}^N &:= \text{Sec}^{g-2}(C) \cap \mathbb{P}_N^{2g-2} \ , \\ \text{Sec}^{g-2}(N) &:= \bigcup_{\substack{M \subset N \\ \#M = g - 1}} \text{span} \{M \} \ . \end{align*} $$
$$ \begin{align*} \text{Sec}^N &:= \text{Sec}^{g-2}(C) \cap \mathbb{P}_N^{2g-2} \ , \\ \text{Sec}^{g-2}(N) &:= \bigcup_{\substack{M \subset N \\ \#M = g - 1}} \text{span} \{M \} \ . \end{align*} $$
Note that, since the points of N are already in
 $\mathbb {P}_N^{2g-2}$
, we have the inclusion
$\mathbb {P}_N^{2g-2}$
, we have the inclusion
 $\text {Sec}^{g-2}(N) \subset \text {Sec}^N$
. We will also need to consider the linear systems on
$\text {Sec}^{g-2}(N) \subset \text {Sec}^N$
. We will also need to consider the linear systems on
 $\mathbb {P}_N^{2g-2}$
$\mathbb {P}_N^{2g-2}$
 $$ \begin{align*} \mathcal{I}_{\text{Sec}^N}(g), \quad \mathrm{and}\ \quad \mathcal{I}_{\text{Sec}^{g-2}(N)}(g) \end{align*} $$
$$ \begin{align*} \mathcal{I}_{\text{Sec}^N}(g), \quad \mathrm{and}\ \quad \mathcal{I}_{\text{Sec}^{g-2}(N)}(g) \end{align*} $$
of forms of degree g vanishing on the corresponding secant varieties. The previous inclusion of secant varieties implies that
 $\mathcal {I}_{\text {Sec}^N}(g)$
is in general a linear subsystem of
$\mathcal {I}_{\text {Sec}^N}(g)$
is in general a linear subsystem of
 $\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)$
.
$\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)$
.
Lemma 4.1. The restricted map
![]() $\varphi _{D,N}$
is given by a linear subsystem
$\varphi _{D,N}$
is given by a linear subsystem
![]() $\mathcal {R}$
of
$\mathcal {R}$
of
 $|\mathcal {I}_{\text {Sec}^N}(g)|$
.
$|\mathcal {I}_{\text {Sec}^N}(g)|$
.
4.2 Moduli spaces of pointed rational curves
In this section, we will outline the relation between the restricted map
![]() $\varphi _{D,N}$
and the moduli spaces of pointed rational curves.
$\varphi _{D,N}$
and the moduli spaces of pointed rational curves.
4.2.1 Two compactifications of
 $\mathcal {M}_{0,n}$
$\mathcal {M}_{0,n}$
The moduli space
![]() $\mathcal {M}_{0,n}$
of ordered configurations of n distinct points on the projective line is not compact. We will consider two compactifications of
$\mathcal {M}_{0,n}$
of ordered configurations of n distinct points on the projective line is not compact. We will consider two compactifications of
![]() $\mathcal {M}_{0,n}$
. The first one is the GIT quotient
$\mathcal {M}_{0,n}$
. The first one is the GIT quotient
 $$ \begin{align*}\mathcal{M}_{0,n}^{\text{GIT}} := (\mathbb{P}^1)^n // \text{PGL}(2, \mathbb{C})\end{align*} $$
$$ \begin{align*}\mathcal{M}_{0,n}^{\text{GIT}} := (\mathbb{P}^1)^n // \text{PGL}(2, \mathbb{C})\end{align*} $$
of
 $(\mathbb {P}^1)^n$
by the diagonal action of
$(\mathbb {P}^1)^n$
by the diagonal action of
 $G=\text {PGL}(2, \mathbb {C})$
for the natural G-linearization of the line bundle
$G=\text {PGL}(2, \mathbb {C})$
for the natural G-linearization of the line bundle
 (see [Reference Dolgachev and Ortland12, Reference Dolgachev13]). The quotient
(see [Reference Dolgachev and Ortland12, Reference Dolgachev13]). The quotient
 $\mathcal {M}_{0,n}^{\text {GIT}}$
is naturally embedded in the projective space
$\mathcal {M}_{0,n}^{\text {GIT}}$
is naturally embedded in the projective space
 $\mathbb {P} ( H^0 ((\mathbb {P}^1)^n, L )^{G} )$
of invariant sections.
$\mathbb {P} ( H^0 ((\mathbb {P}^1)^n, L )^{G} )$
of invariant sections.
The second one is the Mumford–Knudsen compactification
 $\overline {\mathcal {M}}_{0,n}$
[Reference Knudsen20]. The points of
$\overline {\mathcal {M}}_{0,n}$
[Reference Knudsen20]. The points of
 $\overline {\mathcal {M}}_{0,n}$
represent isomorphism classes of stable curves. More details on these constructions can be found in [Reference Kapranov18] and [Reference Knudsen20].
$\overline {\mathcal {M}}_{0,n}$
represent isomorphism classes of stable curves. More details on these constructions can be found in [Reference Kapranov18] and [Reference Knudsen20].
Both
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
and
$\mathcal {M}_{0,2g}^{\text {GIT}}$
and
 $\overline {\mathcal {M}}_{0,n}$
contain
$\overline {\mathcal {M}}_{0,n}$
contain
![]() $\mathcal {M}_{0,n}$
as an open set. However, the Mumford–Knudsen compactification is finer on the boundary: there exists a contraction dominant morphism
$\mathcal {M}_{0,n}$
as an open set. However, the Mumford–Knudsen compactification is finer on the boundary: there exists a contraction dominant morphism
 $$ \begin{align*}c_n: \overline{\mathcal{M}}_{0,n} \to \mathcal{M}_{0,n}^{\text{GIT}}\end{align*} $$
$$ \begin{align*}c_n: \overline{\mathcal{M}}_{0,n} \to \mathcal{M}_{0,n}^{\text{GIT}}\end{align*} $$
contracting some components of the boundary of
 $\overline {\mathcal {M}}_{0,n}$
, that restricts to the identity on
$\overline {\mathcal {M}}_{0,n}$
, that restricts to the identity on
![]() $\mathcal {M}_{0,n}$
[Reference Bolognesi7]. Moreover, we will denote by
$\mathcal {M}_{0,n}$
[Reference Bolognesi7]. Moreover, we will denote by
 $$ \begin{align*}\lambda_k: \overline{\mathcal{M}}_{0,n} \to \overline{\mathcal{M}}_{0,n-1},\end{align*} $$
$$ \begin{align*}\lambda_k: \overline{\mathcal{M}}_{0,n} \to \overline{\mathcal{M}}_{0,n-1},\end{align*} $$
for
![]() $k = 1,\ldots ,n$
, the forgetful morphism that forgets the labeling of the kth point.
$k = 1,\ldots ,n$
, the forgetful morphism that forgets the labeling of the kth point.
4.2.2 A variety of rational normal curves
Let
 $e_1, \ldots e_{n} \in \mathbb {P}^{n - 2}$
be n points in general position. Let
$e_1, \ldots e_{n} \in \mathbb {P}^{n - 2}$
be n points in general position. Let
![]() $\mathcal {H}$
be the Hilbert scheme of subschemes of
$\mathcal {H}$
be the Hilbert scheme of subschemes of
![]() $\mathbb {P}^{n-2}$
. Let
$\mathbb {P}^{n-2}$
. Let
 $V_0(e_1, \ldots , e_n) \subset \mathcal {H}$
be the subvariety of rational normal curves in
$V_0(e_1, \ldots , e_n) \subset \mathcal {H}$
be the subvariety of rational normal curves in
![]() $\mathbb {P}^{n - 2}$
passing through the points
$\mathbb {P}^{n - 2}$
passing through the points
![]() $e_1, \ldots , e_n$
, and let
$e_1, \ldots , e_n$
, and let
 $V(e_1, \ldots , e_n)$
be the closure of
$V(e_1, \ldots , e_n)$
be the closure of
 $V_0(e_1, \ldots , e_n)$
inside
$V_0(e_1, \ldots , e_n)$
inside
![]() $\mathcal {H}$
. The boundary
$\mathcal {H}$
. The boundary
 $V(e_1, \ldots , e_n) \setminus V_0(e_1, \ldots , e_n)$
consists on reducible rational normal curves, that is reducible nondegenerate curves of degree n such that each component is a rational normal curve in its projective span.
$V(e_1, \ldots , e_n) \setminus V_0(e_1, \ldots , e_n)$
consists on reducible rational normal curves, that is reducible nondegenerate curves of degree n such that each component is a rational normal curve in its projective span.
There exists an isomorphism
 $V_0(e_1, \ldots , e_{n}) \cong \mathcal {M}_{0,n}$
(see [Reference Dolgachev and Ortland12]) associating to a rational normal curve passing by
$V_0(e_1, \ldots , e_{n}) \cong \mathcal {M}_{0,n}$
(see [Reference Dolgachev and Ortland12]) associating to a rational normal curve passing by
![]() $e_1, \ldots , e_n$
the corresponding ordered configuration of n points in
$e_1, \ldots , e_n$
the corresponding ordered configuration of n points in
![]() $\mathbb {P}^1$
. This can be extended [Reference Kapranov18] to an isomorphism between
$\mathbb {P}^1$
. This can be extended [Reference Kapranov18] to an isomorphism between
 $V(e_1, \ldots , e_n)$
and
$V(e_1, \ldots , e_n)$
and
 $\overline {\mathcal {M}}_{0,n}$
.
$\overline {\mathcal {M}}_{0,n}$
.
4.2.3 The blow-up construction
The following construction is due to Kapranov [Reference Kapranov17]: let
 $e_1, \ldots , e_{n-1} \in \mathbb {P}^{n-3}$
be
$e_1, \ldots , e_{n-1} \in \mathbb {P}^{n-3}$
be
![]() $(n-1)$
points in general position. Consider the following sequence of blow-ups:
$(n-1)$
points in general position. Consider the following sequence of blow-ups:
-
1. Blow-up the points
 $e_1, \ldots , e_{n-1}$
.
$e_1, \ldots , e_{n-1}$
. -
2. Blow-up the proper transforms of lines spanned by pairs of points from
 $\{e_1, \ldots , e_{n-1} \}$
.
$\{e_1, \ldots , e_{n-1} \}$
. -
3. Blow-up the proper transforms of planes spanned by triples of points from
 $\{e_1, \ldots , e_{n-1} \}$
.
$\{e_1, \ldots , e_{n-1} \}$
. -
 $\vdots $
$\vdots $
-
(n-4). Blow-up the proper transforms of linear subspaces spanned by
 $(n-4)$
-ples of points from
$(n-4)$
-ples of points from
 $\{e_1, \ldots , e_{n-1} \}$
.
$\{e_1, \ldots , e_{n-1} \}$
.
Let
 $\text {Bl}(\mathbb {P}^{n-3})$
be the
$\text {Bl}(\mathbb {P}^{n-3})$
be the
![]() $(n - 3)$
-variety obtained in this way, and
$(n - 3)$
-variety obtained in this way, and
 $b : \text {Bl}(\mathbb {P}^{n-3}) \to \mathbb {P}^{n-3}$
the composition of this sequence of blow-ups. We will call this map the Kapranov blow-up map centered in the points
$b : \text {Bl}(\mathbb {P}^{n-3}) \to \mathbb {P}^{n-3}$
the composition of this sequence of blow-ups. We will call this map the Kapranov blow-up map centered in the points
![]() $e_1, \ldots , e_{n - 1}$
.
$e_1, \ldots , e_{n - 1}$
.
Theorem 4.2. (Kapranov [Reference Kapranov17])
Let
![]() $n \geq 4$
. Then, the moduli space
$n \geq 4$
. Then, the moduli space
 $\overline {\mathcal {M}}_{0,n}$
is isomorphic to
$\overline {\mathcal {M}}_{0,n}$
is isomorphic to
 $\text {Bl}(\mathbb {P}^{n-3})$
.
$\text {Bl}(\mathbb {P}^{n-3})$
.
Moreover, the images by b of the fibres of the map
![]() $\lambda _k$
over the points in the open set
$\lambda _k$
over the points in the open set
 $\mathcal {M}_{0,n-1} \subset \overline {\mathcal {M}}_{0,n-1}$
are the rational normal curves in
$\mathcal {M}_{0,n-1} \subset \overline {\mathcal {M}}_{0,n-1}$
are the rational normal curves in
![]() $\mathbb {P}^{n-3}$
passing through the
$\mathbb {P}^{n-3}$
passing through the
![]() $n - 1$
points
$n - 1$
points
![]() $e_1,\ldots , e_{n-1}$
(see [Reference Keel and McKernan19, Proposition 3.1]).
$e_1,\ldots , e_{n-1}$
(see [Reference Keel and McKernan19, Proposition 3.1]).
4.2.4 The Cremona inversion
Let
 $e_1, \ldots e_{n - 1} \in \mathbb {P}^{n - 3}$
in general position. Without loss of generality, we may assume
$e_1, \ldots e_{n - 1} \in \mathbb {P}^{n - 3}$
in general position. Without loss of generality, we may assume
![]() $e_k = [0: \cdots : 1 : \cdots : 0]$
for
$e_k = [0: \cdots : 1 : \cdots : 0]$
for
![]() $k = 1, \ldots , n - 2$
; and
$k = 1, \ldots , n - 2$
; and
 $e_{n - 1} = [1: \cdots : 1]$
. The Cremona inversion with respect to
$e_{n - 1} = [1: \cdots : 1]$
. The Cremona inversion with respect to
![]() $e_{n-1}$
is the birational map
$e_{n-1}$
is the birational map

On
![]() $\mathbb {P}^2$
the Cremona inversion is given by the linear system of quadrics passing through
$\mathbb {P}^2$
the Cremona inversion is given by the linear system of quadrics passing through
![]() $e_1,\ e_2$
, and
$e_1,\ e_2$
, and
![]() $e_3$
, on
$e_3$
, on
![]() $\mathbb {P}^3$
by the cubics that vanish on the six secant lines of
$\mathbb {P}^3$
by the cubics that vanish on the six secant lines of
![]() $e_1,\ e_2,\ e_3$
, and
$e_1,\ e_2,\ e_3$
, and
![]() $e_4$
, and so on. The Cremona inversion has the following property: any nondegenerate rational normal curve passing through the points
$e_4$
, and so on. The Cremona inversion has the following property: any nondegenerate rational normal curve passing through the points
![]() $e_1, \ldots , e_{n - 1}$
is transformed into a line passing by the point
$e_1, \ldots , e_{n - 1}$
is transformed into a line passing by the point
 $\text {Cr}_{n - 1}(e_{n - 1})$
. Let
$\text {Cr}_{n - 1}(e_{n - 1})$
. Let
![]() be the linear projection with center
be the linear projection with center
 $\text {Cr}_{n - 1}(e_{n - 1})$
. From the previous property, we obtain that the composition
$\text {Cr}_{n - 1}(e_{n - 1})$
. From the previous property, we obtain that the composition
![]() $\tau _{n - 1} \circ \text {Cr}_{n - 1}$
contracts nondegenerate rational normal curves passing through
$\tau _{n - 1} \circ \text {Cr}_{n - 1}$
contracts nondegenerate rational normal curves passing through
![]() $e_1, \ldots , e_{n - 1}$
.
$e_1, \ldots , e_{n - 1}$
.
Let
 $k \in \{1,\ldots ,n-1\}$
. It is straightforward to see that one can let
$k \in \{1,\ldots ,n-1\}$
. It is straightforward to see that one can let
![]() $e_k$
play the role of
$e_k$
play the role of
![]() $e_{n - 1}$
in the definition of
$e_{n - 1}$
in the definition of
![]() $\text {Cr}_{n - 1}$
, and define similarly the Cremona inversion
$\text {Cr}_{n - 1}$
, and define similarly the Cremona inversion
![]() $\text {Cr}_k$
. Let
$\text {Cr}_k$
. Let
![]() be the linear projection with center
be the linear projection with center
 $\text {Cr}_k(e_{k})$
.
$\text {Cr}_k(e_{k})$
.
Lemma 4.3. Let
 $e_1, \ldots e_{n - 1} \in \mathbb {P}^{n - 3}$
in general position. Then, the composition
$e_1, \ldots e_{n - 1} \in \mathbb {P}^{n - 3}$
in general position. Then, the composition
![]() $\tau _k \circ \text {Cr}_k$
contracts the nondegenerate rational normal curves passing through
$\tau _k \circ \text {Cr}_k$
contracts the nondegenerate rational normal curves passing through
![]() $e_1, \ldots , e_{n-1}$
.
$e_1, \ldots , e_{n-1}$
.
Let us denote
![]() $H_t$
, for
$H_t$
, for
![]() $t\neq k$
, the hyperplane in
$t\neq k$
, the hyperplane in
![]() $\mathbb {P}^{n-3}$
spanned the points
$\mathbb {P}^{n-3}$
spanned the points
![]() $e_i$
, with
$e_i$
, with
![]() $i\neq k,t.$
There are
$i\neq k,t.$
There are
![]() $n-2$
such hyperplanes and each one is contracted to a point by
$n-2$
such hyperplanes and each one is contracted to a point by
![]() $\text {Cr}_k$
.
$\text {Cr}_k$
.
Proposition 4.4. [Reference Kapranov18]
Let
 $e_1, \ldots e_{n - 1} \in \mathbb {P}^{n - 3}$
in general position. Let
$e_1, \ldots e_{n - 1} \in \mathbb {P}^{n - 3}$
in general position. Let
 $k \in \{1,\ldots ,n - 1\}$
. Then, the following diagram is commutative:
$k \in \{1,\ldots ,n - 1\}$
. Then, the following diagram is commutative:

Here, the map
![]() $b_k$
is the Kapranov blow-up map centered in the images of the hyperplanes
$b_k$
is the Kapranov blow-up map centered in the images of the hyperplanes
![]() $H_t$
, for
$H_t$
, for
![]() $1\leq t \leq n-1$
and
$1\leq t \leq n-1$
and
![]() $t \neq k$
, by
$t \neq k$
, by
![]() $\tau _k \circ \text {Cr}_k$
.
$\tau _k \circ \text {Cr}_k$
.
Remark. We observe here a little subtlety. We only get here
![]() $n-1$
forgetful maps through Cremona transformations, because we are tacitly assuming that Kapranov’s blow-up construction of
$n-1$
forgetful maps through Cremona transformations, because we are tacitly assuming that Kapranov’s blow-up construction of
 $\overline {\mathcal {M}}_{0,n}$
labels with integers from 1 to
$\overline {\mathcal {M}}_{0,n}$
labels with integers from 1 to
![]() $n-1$
the points
$n-1$
the points
![]() $e_1,\dots ,e_{n-1}$
of the projective base of
$e_1,\dots ,e_{n-1}$
of the projective base of
![]() $\mathbb {P}^{n-3}$
, and labels as n the last point (which is free to move inside the
$\mathbb {P}^{n-3}$
, and labels as n the last point (which is free to move inside the
![]() $\mathbb {P}^{n-3}$
, which is a birational model of
$\mathbb {P}^{n-3}$
, which is a birational model of
 $\overline {\mathcal {M}}_{0,n}$
). This is due to this small asymmetric aspect of Kapranov’s construction, but it is clear that one could assume that the last, freely moving point is labeled with any
$\overline {\mathcal {M}}_{0,n}$
). This is due to this small asymmetric aspect of Kapranov’s construction, but it is clear that one could assume that the last, freely moving point is labeled with any
 $k\in \{ 1, \dots , n-1\}$
, and obtain other forgetful maps.
$k\in \{ 1, \dots , n-1\}$
, and obtain other forgetful maps.
4.2.5 Rationalizations of
 $\mathcal {M}^{\text {GIT}}_{0,2g}$
$\mathcal {M}^{\text {GIT}}_{0,2g}$
Let
![]() $g \geq 3$
, and let
$g \geq 3$
, and let
 $e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
in general position. Let
$e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
in general position. Let
![]() $\Omega $
be the linear system of
$\Omega $
be the linear system of
 $(g-1)$
-forms in
$(g-1)$
-forms in
![]() $\mathbb {P}^{2g-3}$
vanishing with multiplicity
$\mathbb {P}^{2g-3}$
vanishing with multiplicity
![]() $g-2$
in
$g-2$
in
 $e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
.
$e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
.
Theorem 4.5. ([Reference Kumar21])
Let
![]() $g \geq 3$
, and let
$g \geq 3$
, and let
 $e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
be in general position. Then, the rational map
$e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
be in general position. Then, the rational map
induced by the linear system
![]() $\Omega $
maps
$\Omega $
maps
![]() $\mathbb {P}^{2g-3}$
birationally onto
$\mathbb {P}^{2g-3}$
birationally onto
 $\mathcal {M}^{\text {GIT}}_{0,2g}$
.
$\mathcal {M}^{\text {GIT}}_{0,2g}$
.
We also observe that the contraction map
![]() $c_{2n}$
can also be described in terms of Kumar’s linear system
$c_{2n}$
can also be described in terms of Kumar’s linear system
![]() $\Omega $
:
$\Omega $
:
Lemma 4.6. Let
![]() $g \geq 3$
, and let
$g \geq 3$
, and let
 $e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
in general position. Then, the following diagram is commutative:
$e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
in general position. Then, the following diagram is commutative:

Here, the map b is the Kapranov blow-up map centered in
![]() $p_1, \ldots , p_{2g - 1}$
.
$p_1, \ldots , p_{2g - 1}$
.
Let
![]() $e_0 \in \mathbb {P}^{2g - 3}$
such that
$e_0 \in \mathbb {P}^{2g - 3}$
such that
 $w = i_{\Omega }(e_0)$
lies in the open set
$w = i_{\Omega }(e_0)$
lies in the open set
 $\mathcal {M}_{0,2g} \subset \mathcal {M}^{\text {GIT}}_{0,2g}$
. The point w can represent a hyperelliptic genus
$\mathcal {M}_{0,2g} \subset \mathcal {M}^{\text {GIT}}_{0,2g}$
. The point w can represent a hyperelliptic genus
 $(g - 1)$
curve
$(g - 1)$
curve
![]() $C_w$
(namely the double cover of
$C_w$
(namely the double cover of
![]() $\mathbb {P}^1$
ramifying in the
$\mathbb {P}^1$
ramifying in the
![]() $2g$
marked points) together with an ordering of the Weierstrass points. Let
$2g$
marked points) together with an ordering of the Weierstrass points. Let
 $\mathcal {SU}_{C_w}(2)^{inv}$
be the moduli space of rank 2 semistable vector bundles with trivial determinant over the curve
$\mathcal {SU}_{C_w}(2)^{inv}$
be the moduli space of rank 2 semistable vector bundles with trivial determinant over the curve
![]() $C_w$
, that are invariant with respect to the hyperelliptic involution.
$C_w$
, that are invariant with respect to the hyperelliptic involution.
Consider the partial linear subsystem
![]() $\Lambda $
of
$\Lambda $
of
![]() $\Omega $
consisting of the
$\Omega $
consisting of the
 $(g - 1)$
-forms in
$(g - 1)$
-forms in
![]() $\mathbb {P}^{2g-3}$
vanishing with multiplicity
$\mathbb {P}^{2g-3}$
vanishing with multiplicity
![]() $g - 2$
in all the points
$g - 2$
in all the points
![]() $e_0, e_1, \ldots , e_{2g - 1}$
. Let
$e_0, e_1, \ldots , e_{2g - 1}$
. Let
 be the rational projection induced by the linear system
be the rational projection induced by the linear system
![]() $\Lambda $
.
$\Lambda $
.
Theorem 4.7. ([Reference Kumar21])
Let
![]() $g \geq 3$
, and let
$g \geq 3$
, and let
 $e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
be
$e_1, \ldots , e_{2g - 1} \in \mathbb {P}^{2g - 3}$
be
![]() $2g - 1$
points in general position. Let
$2g - 1$
points in general position. Let
![]() $e_0 \in \mathbb {P}^{2g - 3}$
such that
$e_0 \in \mathbb {P}^{2g - 3}$
such that
 $w = i_{\Omega }(e_0)$
lies in the open set
$w = i_{\Omega }(e_0)$
lies in the open set
 $\mathcal {M}_{0,2g} \subset \mathcal {M}^{\text {GIT}}_{0,2g}$
. Then, the map
$\mathcal {M}_{0,2g} \subset \mathcal {M}^{\text {GIT}}_{0,2g}$
. Then, the map
![]() $\kappa $
induced by the linear system
$\kappa $
induced by the linear system
![]() $\Lambda $
is a degree 2 osculating projection onto a connected component of the moduli space
$\Lambda $
is a degree 2 osculating projection onto a connected component of the moduli space
 $\mathcal {SU}_{C_w}(2)^{inv}$
. Furthermore, the map
$\mathcal {SU}_{C_w}(2)^{inv}$
. Furthermore, the map
![]() $\kappa $
ramifies along the Kummer variety
$\kappa $
ramifies along the Kummer variety
 $\text {Kum}(C_w) \subset \mathcal {SU}_{C_w}(2)^{inv}$
.
$\text {Kum}(C_w) \subset \mathcal {SU}_{C_w}(2)^{inv}$
.

In fact, one can talk of osculating projection (and this means
 $\mathcal {M}^{\text {GIT}}_{0,2g}$
is embedded in some known projective space) since
$\mathcal {M}^{\text {GIT}}_{0,2g}$
is embedded in some known projective space) since
![]() $i_\Omega $
embeds
$i_\Omega $
embeds
 $\mathcal {M}^{\text {GIT}}_{0,2g}$
in its natural projective space of invariants, defined by the democratic polarization with weights vector
$\mathcal {M}^{\text {GIT}}_{0,2g}$
in its natural projective space of invariants, defined by the democratic polarization with weights vector
 $(1,1,\dots ,1)$
(see also Section 5.2.3).
$(1,1,\dots ,1)$
(see also Section 5.2.3).
4.3 Forgetful linear systems and
 $\mathcal {M}^{\text {GIT}}_{0,2g}$
$\mathcal {M}^{\text {GIT}}_{0,2g}$
Let C be a smooth genus
![]() $g \geq 3$
curve (not necessarily hyperelliptic). Let D be a general degree g effective divisor on C. Let
$g \geq 3$
curve (not necessarily hyperelliptic). Let D be a general degree g effective divisor on C. Let
![]() $N = p_1 + \cdots + p_{2g}$
be a general reduced divisor in the linear system
$N = p_1 + \cdots + p_{2g}$
be a general reduced divisor in the linear system
 $|2D|$
. Consider the span
$|2D|$
. Consider the span
 $\mathbb {P}_N^{2g-2}$
in
$\mathbb {P}_N^{2g-2}$
in
 $\mathbb {P}_D^{3g-2}$
of the
$\mathbb {P}_D^{3g-2}$
of the
![]() $2g$
marked points
$2g$
marked points
![]() $p_1, \ldots , p_{2g}$
.
$p_1, \ldots , p_{2g}$
.
We will now apply the discussion of Section 4.2 to the general points
![]() $p_1, \ldots , p_{2g}$
in the projective space
$p_1, \ldots , p_{2g}$
in the projective space
 $\mathbb {P}_N^{2g-2}$
, taking
$\mathbb {P}_N^{2g-2}$
, taking
![]() $n = 2g + 1$
in the notation therein. For every
$n = 2g + 1$
in the notation therein. For every
![]() $k = 1, \ldots , 2g$
, we can compose Proposition 4.4 and Lemma 4.6 and get a commutative diagram
$k = 1, \ldots , 2g$
, we can compose Proposition 4.4 and Lemma 4.6 and get a commutative diagram

where
![]() $\Omega $
is the linear system of
$\Omega $
is the linear system of
 $(g-1)$
-forms in
$(g-1)$
-forms in
![]() $\mathbb {P}^{2g-3}$
vanishing with multiplicity
$\mathbb {P}^{2g-3}$
vanishing with multiplicity
![]() $g-2$
at the
$g-2$
at the
![]() $2g - 1$
points
$2g - 1$
points
![]() $\tau _{k} \circ \text {Cr}_{k}(H_i)$
, with
$\tau _{k} \circ \text {Cr}_{k}(H_i)$
, with
![]() $i\neq k$
and
$i\neq k$
and
![]() $1 \leq i \leq 2g$
. Let us define the rational map
$1 \leq i \leq 2g$
. Let us define the rational map

Proposition 4.8. ([Reference Bolognesi7])
Let
![]() $N = p_1 + \cdots + p_{2g}$
be a general reduced divisor in the linear system
$N = p_1 + \cdots + p_{2g}$
be a general reduced divisor in the linear system
 $|2D|$
. Then, the map
$|2D|$
. Then, the map
![]() $h_N$
coincides with the composition
$h_N$
coincides with the composition
![]() $i_{\Omega } \circ \tau _k \ \circ \ \text {Cr}_{k}$
for every
$i_{\Omega } \circ \tau _k \ \circ \ \text {Cr}_{k}$
for every
![]() $k = 1, \ldots , 2g$
. In particular, the composition
$k = 1, \ldots , 2g$
. In particular, the composition
![]() $i_{\Omega } \circ \tau _k \ \circ \ \text {Cr}_{k}$
does not depend on k.
$i_{\Omega } \circ \tau _k \ \circ \ \text {Cr}_{k}$
does not depend on k.
This is due to the fact that the linear system
 $|\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
is invariant with respect to the action of the symmetric group
$|\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
is invariant with respect to the action of the symmetric group
![]() $\Sigma _{2g}$
that operates on
$\Sigma _{2g}$
that operates on
 $\mathbb {P}_N^{2g-2}$
by linear automorphisms. Let us put together the results of Lemma 4.3, Theorem 4.5 and Proposition 4.8 in the following Proposition:
$\mathbb {P}_N^{2g-2}$
by linear automorphisms. Let us put together the results of Lemma 4.3, Theorem 4.5 and Proposition 4.8 in the following Proposition:
Proposition 4.9. The image of
![]() $h_N$
is isomorphic to the GIT moduli space
$h_N$
is isomorphic to the GIT moduli space
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
of ordered configurations of
$\mathcal {M}_{0,2g}^{\text {GIT}}$
of ordered configurations of
![]() $2g$
points in
$2g$
points in
![]() $\mathbb {P}^1$
. The map
$\mathbb {P}^1$
. The map
![]() $h_N$
is dominant and its general fiber is of dimension 1. More precisely,
$h_N$
is dominant and its general fiber is of dimension 1. More precisely,
![]() $h_N$
contracts every rational normal curve Z passing through the
$h_N$
contracts every rational normal curve Z passing through the
![]() $2g$
points N to a point z in
$2g$
points N to a point z in
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
. This point represents an ordered configuration of the
$\mathcal {M}_{0,2g}^{\text {GIT}}$
. This point represents an ordered configuration of the
![]() $2g$
points N on the rational curve Z.
$2g$
points N on the rational curve Z.
This is why these maps where dubbed “forgetful linear systems.” In fact the rational normal curves passing through the
![]() $2g$
points make up the universal curve over an open subset of
$2g$
points make up the universal curve over an open subset of
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
.
$\mathcal {M}_{0,2g}^{\text {GIT}}$
.
Remark. Since
![]() $\mathcal {R}$
is a linear subsystem of
$\mathcal {R}$
is a linear subsystem of
 $|\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
by Lemma 4.1, we have that
$|\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
by Lemma 4.1, we have that
![]() $\varphi _{D,N}$
factors through
$\varphi _{D,N}$
factors through
![]() $h_N$
:
$h_N$
:

4.3.1 A comparison of base loci
For future use, we need to compare the locus
 $\text {Sec}^{g-2}(N)$
and the more intricate locus
$\text {Sec}^{g-2}(N)$
and the more intricate locus
![]() $\text {Sec}^N$
obtained by intersecting the base locus of
$\text {Sec}^N$
obtained by intersecting the base locus of
![]() $\varphi _D$
with
$\varphi _D$
with
 $\mathbb {P}_N^{2g-2}$
. This section is devoted to this comparison.
$\mathbb {P}_N^{2g-2}$
. This section is devoted to this comparison.
By definition, the points in
![]() $\text {Sec}^N$
are given by the intersections
$\text {Sec}^N$
are given by the intersections
 $\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2} $
, where
$\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2} $
, where
![]() $L_{g-1}$
is an effective divisor of degree
$L_{g-1}$
is an effective divisor of degree
![]() $g-1$
and
$g-1$
and
 $\langle L_{g-1} \rangle $
is its linear span in
$\langle L_{g-1} \rangle $
is its linear span in
 $\mathbb {P}_D^{3g-2}$
. If
$\mathbb {P}_D^{3g-2}$
. If
![]() $L_{g-1}$
is contained in N, it is clear that
$L_{g-1}$
is contained in N, it is clear that
 $\langle L_{g-1} \rangle \subset \text {Sec}^{g-2}(N) \subset \mathbb {P}_N^{2g-2}$
.
$\langle L_{g-1} \rangle \subset \text {Sec}^{g-2}(N) \subset \mathbb {P}_N^{2g-2}$
.
Lemma 4.10. Let
![]() $L_{g-1}$
be an effective divisor on C of degree
$L_{g-1}$
be an effective divisor on C of degree
![]() $g - 1$
, not contained in N. Then,
$g - 1$
, not contained in N. Then,
 $$ \begin{align*} \langle L_{g-1} \rangle \cap \mathbb{P}_N^{2g-2} \not = \phi \quad \text{if and only if} \quad \dim|L_{g-1}| \geq 1. \end{align*} $$
$$ \begin{align*} \langle L_{g-1} \rangle \cap \mathbb{P}_N^{2g-2} \not = \phi \quad \text{if and only if} \quad \dim|L_{g-1}| \geq 1. \end{align*} $$
Moreover, if the intersection is nonempty, we have that
 $$ \begin{align*}\dim (\langle L_{g-1} \rangle \cap \mathbb{P}_N^{2g-2}) = \dim |L_{g-1}| - 1.\end{align*} $$
$$ \begin{align*}\dim (\langle L_{g-1} \rangle \cap \mathbb{P}_N^{2g-2}) = \dim |L_{g-1}| - 1.\end{align*} $$
Proof First, let us suppose that
![]() $L_{g-1}$
and N have no points in common. The vector space
$L_{g-1}$
and N have no points in common. The vector space
 $V := H^0(C, 2D + K - L_{g-1})$
is the annihilator of the span
$V := H^0(C, 2D + K - L_{g-1})$
is the annihilator of the span
 $\langle L_{g-1} \rangle $
in
$\langle L_{g-1} \rangle $
in
 $\mathbb {P}_D^{3g-2}$
. By the Riemann-Roch theorem, we see that V has dimension
$\mathbb {P}_D^{3g-2}$
. By the Riemann-Roch theorem, we see that V has dimension
![]() $2g$
, hence
$2g$
, hence
 $$ \begin{align*}\dim \langle L_{g-1} \rangle = (3g - 2) - 2g = g - 2.\end{align*} $$
$$ \begin{align*}\dim \langle L_{g-1} \rangle = (3g - 2) - 2g = g - 2.\end{align*} $$
Let d be the dimension of the span
 $\langle L_{g-1}, N \rangle $
of the points of
$\langle L_{g-1}, N \rangle $
of the points of
![]() $L_{g-1}$
and N. Since the dimension of
$L_{g-1}$
and N. Since the dimension of
 $\mathbb {P}_N^{2g-2} = \langle N \rangle $
is
$\mathbb {P}_N^{2g-2} = \langle N \rangle $
is
![]() $2g-2$
, we have that
$2g-2$
, we have that
 $d \leq (g-2) + (2g - 2) + 1 = 3g-3$
, where the equality holds iff
$d \leq (g-2) + (2g - 2) + 1 = 3g-3$
, where the equality holds iff
 $\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2}$
is empty.
$\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2}$
is empty.
In particular, this intersection is nonempty iff
![]() $d \leq 3g -4$
. Since
$d \leq 3g -4$
. Since
 $\dim |K + 2D|^* = \dim \mathbb {P}_D^{3g-2} = 3g - 2$
, this is equivalent to the annihilator space
$\dim |K + 2D|^* = \dim \mathbb {P}_D^{3g-2} = 3g - 2$
, this is equivalent to the annihilator space
 $$ \begin{align*}W := H^0(C, 2D + K - L_{g-1} - N) = H^0(C, K - L_{g-1})\end{align*} $$
$$ \begin{align*}W := H^0(C, 2D + K - L_{g-1} - N) = H^0(C, K - L_{g-1})\end{align*} $$
being of dimension
![]() $\geq 2$
. By Riemann-Roch and Serre duality, we obtain that this condition is equivalent to
$\geq 2$
. By Riemann-Roch and Serre duality, we obtain that this condition is equivalent to
 $\dim |L_{g-1}| \geq 1$
.
$\dim |L_{g-1}| \geq 1$
.
More precisely, let us suppose that
 $\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2}$
is nonempty and let
$\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2}$
is nonempty and let
 $e := \dim (\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2})$
. Then, we have that
$e := \dim (\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2})$
. Then, we have that
and the annihilator space W is of dimension
![]() $2 + e$
. Again by a Riemann-Roch computation, we conclude that
$2 + e$
. Again by a Riemann-Roch computation, we conclude that
 $e = \dim |L_{g-1}| - 1$
.
$e = \dim |L_{g-1}| - 1$
.
Finally, if
![]() $L_{g-1}$
and N have some points in common, we have to count them only once when defining the vector space W to avoid requiring higher vanishing multiplicity to the sections.
$L_{g-1}$
and N have some points in common, we have to count them only once when defining the vector space W to avoid requiring higher vanishing multiplicity to the sections.
From this Lemma, we conclude that
 $\text {Sec}^{g-2}(N)$
is a proper subset of
$\text {Sec}^{g-2}(N)$
is a proper subset of
![]() $\text {Sec}^N$
if and only if there exists a divisor
$\text {Sec}^N$
if and only if there exists a divisor
![]() $L_{g-1}$
not contained in N with
$L_{g-1}$
not contained in N with
 $\dim |L_{g-1}| \geq 1$
. By the Existence Theorem of Brill–Noether theory (see [Reference Arbarello, Cornalba, Griffiths and Harris2, Theorem 1.1, page 206]), this is possible only if
$\dim |L_{g-1}| \geq 1$
. By the Existence Theorem of Brill–Noether theory (see [Reference Arbarello, Cornalba, Griffiths and Harris2, Theorem 1.1, page 206]), this is possible only if
![]() $g \geq 4$
in the nonhyperelliptic case, whereas such a linear system may exist also when
$g \geq 4$
in the nonhyperelliptic case, whereas such a linear system may exist also when
![]() $g=3$
when C is hyperelliptic. We will discuss the first low genera cases in Section 7.
$g=3$
when C is hyperelliptic. We will discuss the first low genera cases in Section 7.
5 The hyperelliptic involution and rational normal curves
From now on, C will be a hyperelliptic curve of genus
![]() $g \geq 3$
.
$g \geq 3$
.
As we have seen in Lemma 4.1, the base locus of the map
![]() $\varphi _{D,N}$
contains
$\varphi _{D,N}$
contains
![]() $\text {Sec}^N$
. We have seen that the secant variety
$\text {Sec}^N$
. We have seen that the secant variety
 $\text {Sec}^{g-2}(N)$
is contained in
$\text {Sec}^{g-2}(N)$
is contained in
![]() $\text {Sec}^N$
and that this inclusion is strict for
$\text {Sec}^N$
and that this inclusion is strict for
![]() $g \geq 4$
in the nonhyperelliptic case.
$g \geq 4$
in the nonhyperelliptic case.
5.1 A rational normal curve coming from involution invariant secant lines
In the hyperelliptic case, we have an additional base locus for every
![]() $g \geq 3$
, which appears due to the hyperelliptic nature of the curve. This locus arises as follows. For each pair
$g \geq 3$
, which appears due to the hyperelliptic nature of the curve. This locus arises as follows. For each pair
 $\{ p, i(p) \}$
of involution-conjugate points in C, consider the secant line l in
$\{ p, i(p) \}$
of involution-conjugate points in C, consider the secant line l in
 $\mathbb {P}_D^{3g-2}$
passing through the points p and
$\mathbb {P}_D^{3g-2}$
passing through the points p and
 $i(p)$
. Let
$i(p)$
. Let
![]() $Q_p$
be the intersection of the line l with
$Q_p$
be the intersection of the line l with
 $\mathbb {P}_N^{2g-2}$
. Let us define
$\mathbb {P}_N^{2g-2}$
. Let us define
 $\Gamma \subset \mathbb {P}_N^{2g-2}$
as the locus of intersection points
$\Gamma \subset \mathbb {P}_N^{2g-2}$
as the locus of intersection points
![]() $Q_p$
when p moves inside C.
$Q_p$
when p moves inside C.

Figure 1 The situation in genus
![]() $3$
. The curves
$3$
. The curves
![]() $\Gamma $
and C intersect along the divisor D, of degree 6. The secant lines l cutting out the hyperelliptic pencil define the curve
$\Gamma $
and C intersect along the divisor D, of degree 6. The secant lines l cutting out the hyperelliptic pencil define the curve
![]() $\Gamma $
.
$\Gamma $
.
Lemma 5.1. The locus
 $\Gamma \subset \mathbb {P}_N^{2g-2}$
is a nondegenerate rational normal curve in
$\Gamma \subset \mathbb {P}_N^{2g-2}$
is a nondegenerate rational normal curve in
 $\mathbb {P}_N^{2g-2}$
. Moreover,
$\mathbb {P}_N^{2g-2}$
. Moreover,
![]() $\Gamma $
passes through the
$\Gamma $
passes through the
![]() $2g$
points of
$2g$
points of
![]() $N \subset C$
.
$N \subset C$
.
Proof Let us start by showing that the intersection
![]() $Q_p$
is nonempty for every line
$Q_p$
is nonempty for every line
 $l=\overline {p,i(p)}$
, with
$l=\overline {p,i(p)}$
, with
![]() $p\in C$
. Since
$p\in C$
. Since
 $\dim |p + i(p)| = \dim |h| = 1$
, the intersection
$\dim |p + i(p)| = \dim |h| = 1$
, the intersection
 $l \cap \mathbb {P}_N^{2g-2}$
is nonempty by Lemma 4.10.
$l \cap \mathbb {P}_N^{2g-2}$
is nonempty by Lemma 4.10.
Let us show that this intersection is a point, that is that the line l is not contained in
 $\mathbb {P}_N^{2g-2}$
. Recall that
$\mathbb {P}_N^{2g-2}$
. Recall that
 $\mathbb {P}_D^{3g-2} = |2D + K|^*$
; we will discuss three cases.
$\mathbb {P}_D^{3g-2} = |2D + K|^*$
; we will discuss three cases.
i) If the points p and
 $i(p)$
are both not contained in the divisor N, the vector space
$i(p)$
are both not contained in the divisor N, the vector space
 $$ \begin{align*}V := H^0(C,2D + K - N - (p + i(p))) = H^0(C,2D + K - N - h)\end{align*} $$
$$ \begin{align*}V := H^0(C,2D + K - N - (p + i(p))) = H^0(C,2D + K - N - h)\end{align*} $$
is exactly the annihilator of the span
 $\langle l, \mathbb {P}_N^{2g-2} \rangle $
in
$\langle l, \mathbb {P}_N^{2g-2} \rangle $
in
 $\mathbb {P}_D^{3g-2}$
. In particular, the codimension of
$\mathbb {P}_D^{3g-2}$
. In particular, the codimension of
 $\langle l, \mathbb {P}_N^{2g-2} \rangle $
in
$\langle l, \mathbb {P}_N^{2g-2} \rangle $
in
 $\mathbb {P}_D^{3g-2}$
is the dimension of V. By Riemann-Roch and Serre duality, we get that
$\mathbb {P}_D^{3g-2}$
is the dimension of V. By Riemann-Roch and Serre duality, we get that
![]() $\dim V = g - 2$
, thus
$\dim V = g - 2$
, thus
 $\dim \langle l, \mathbb {P}_N^{2g-2} \rangle = 3g - 2 - (g - 2) = 2g$
. This means that the intersection
$\dim \langle l, \mathbb {P}_N^{2g-2} \rangle = 3g - 2 - (g - 2) = 2g$
. This means that the intersection
 $l \cap \mathbb {P}_N^{2g-2}$
is a point.
$l \cap \mathbb {P}_N^{2g-2}$
is a point.
ii) For the case
![]() $p \in N$
and
$p \in N$
and
 $i(p) \not \in N$
, let us remark that the the annihilator of the span
$i(p) \not \in N$
, let us remark that the the annihilator of the span
 $\langle l, \mathbb {P}_N^{2g-2} \rangle $
is now the vector space
$\langle l, \mathbb {P}_N^{2g-2} \rangle $
is now the vector space
 $H^0(C,2D + K - N - i(p))$
. Since
$H^0(C,2D + K - N - i(p))$
. Since
 $$ \begin{align*}h^0(C,2D + K - N - i(p)) < h^0(C,2D + K - N),\end{align*} $$
$$ \begin{align*}h^0(C,2D + K - N - i(p)) < h^0(C,2D + K - N),\end{align*} $$
we conclude that the line l is not contained in
 $\mathbb {P}_N^{2g-2}$
.
$\mathbb {P}_N^{2g-2}$
.
iii) The case
 $\{p, i(p) \} \subset N$
is excluded by our genericity hypotheses on N. Hence we deduce that the locus
$\{p, i(p) \} \subset N$
is excluded by our genericity hypotheses on N. Hence we deduce that the locus
![]() $\Gamma $
is a curve in
$\Gamma $
is a curve in
 $\mathbb {P}_N^{2g-2}$
.
$\mathbb {P}_N^{2g-2}$
.
Let q be a point of
 $N \subset \mathbb {P}_N^{2g-2}$
. The line
$N \subset \mathbb {P}_N^{2g-2}$
. The line
 $\overline {q,i(q)}$
intersects the plane
$\overline {q,i(q)}$
intersects the plane
 $\mathbb {P}_N^{2g-2}$
at q. Thus
$\mathbb {P}_N^{2g-2}$
at q. Thus
![]() $\Gamma $
passes through all the points of N. Moreover, it is clear that N is the only intersection of
$\Gamma $
passes through all the points of N. Moreover, it is clear that N is the only intersection of
![]() $\Gamma $
and C, that is
$\Gamma $
and C, that is
![]() $\Gamma \cap C = N$
.
$\Gamma \cap C = N$
.
Let us prove now that
![]() $\Gamma $
is a rational normal curve. Since
$\Gamma $
is a rational normal curve. Since
![]() $\Gamma $
is defined by the hyperelliptic pencil, it is straightforward to see that
$\Gamma $
is defined by the hyperelliptic pencil, it is straightforward to see that
![]() $\Gamma $
is rational. Moreover, since the divisor D is general, the span of any subset of
$\Gamma $
is rational. Moreover, since the divisor D is general, the span of any subset of
![]() $2g - 1$
points of D is
$2g - 1$
points of D is
 $\mathbb {P}_N^{2g-2}$
. Thus, it suffices to show that the degree of
$\mathbb {P}_N^{2g-2}$
. Thus, it suffices to show that the degree of
 $\Gamma \subset \mathbb {P}_N^{2g-2}$
is precisely
$\Gamma \subset \mathbb {P}_N^{2g-2}$
is precisely
![]() $2g - 2$
.
$2g - 2$
.
Let us set
![]() $N = q_1 + \cdots + q_{2g}$
with
$N = q_1 + \cdots + q_{2g}$
with
![]() $q_1, \ldots , q_{2g} \in C$
. By the previous paragraph,
$q_1, \ldots , q_{2g} \in C$
. By the previous paragraph,
![]() $\Gamma $
passes through these
$\Gamma $
passes through these
![]() $2g$
points. Let us consider a hyperplane H of
$2g$
points. Let us consider a hyperplane H of
 $\mathbb {P}_N^{2g-2}$
spanned by
$\mathbb {P}_N^{2g-2}$
spanned by
![]() $2g - 2$
points of N. Without loss of generality, we can suppose that these points are the first
$2g - 2$
points of N. Without loss of generality, we can suppose that these points are the first
![]() $2g - 2$
points
$2g - 2$
points
![]() $q_1, \ldots , q_{2g - 2}$
. To show that the degree of
$q_1, \ldots , q_{2g - 2}$
. To show that the degree of
![]() $\Gamma $
is
$\Gamma $
is
![]() $2g - 2$
, we have to show that the intersection of
$2g - 2$
, we have to show that the intersection of
![]() $\Gamma $
with H consists exactly only of these points.
$\Gamma $
with H consists exactly only of these points.
Let l be the secant line
 $\overline {q,i(q)}$
,
$\overline {q,i(q)}$
,
![]() $q\in C$
. The intersection
$q\in C$
. The intersection
![]() $l \cap H$
is empty if and only if the linear span
$l \cap H$
is empty if and only if the linear span
 $\langle l, H \rangle $
of l and H in
$\langle l, H \rangle $
of l and H in
 $\mathbb {P}_D^{3g-2}$
is of maximal dimension
$\mathbb {P}_D^{3g-2}$
is of maximal dimension
![]() $2g - 1$
, that is of codimension
$2g - 1$
, that is of codimension
![]() $g - 1$
in
$g - 1$
in
 $\mathbb {P}_D^{3g-2}$
. Consider the divisors
$\mathbb {P}_D^{3g-2}$
. Consider the divisors
As before, if
 $\{q, i(q)\} \cap \{q_1, \ldots , q_{2g - 2} \}$
is empty, the vector space
$\{q, i(q)\} \cap \{q_1, \ldots , q_{2g - 2} \}$
is empty, the vector space
 $W = H^0(C,2D + K - D_H - D_l)$
is the annihilator of the span
$W = H^0(C,2D + K - D_H - D_l)$
is the annihilator of the span
 $\langle l, H \rangle $
in
$\langle l, H \rangle $
in
 $\mathbb {P}_D^{3g-2}$
. In particular, the codimension of
$\mathbb {P}_D^{3g-2}$
. In particular, the codimension of
 $\langle l, H \rangle $
in
$\langle l, H \rangle $
in
 $\mathbb {P}_D^{3g-2}$
is given by the dimension of W. Again by Riemann-Roch and Serre duality theorems, we can check that
$\mathbb {P}_D^{3g-2}$
is given by the dimension of W. Again by Riemann-Roch and Serre duality theorems, we can check that
 $$ \begin{align*}\dim W = h^0(C,-2D + D_H + D_l) + g - 1.\end{align*} $$
$$ \begin{align*}\dim W = h^0(C,-2D + D_H + D_l) + g - 1.\end{align*} $$
Thus, the codimension of
 $\langle l, H \rangle $
in
$\langle l, H \rangle $
in
 $\mathbb {P}_D^{3g-2}$
is greater than
$\mathbb {P}_D^{3g-2}$
is greater than
![]() $g - 1$
if and only if
$g - 1$
if and only if
 $h^0(C,-2D + D_H + D_l)> 0$
. Since
$h^0(C,-2D + D_H + D_l)> 0$
. Since
![]() $\deg (-2D + D_H + D_l) = 0$
, this is equivalent to
$\deg (-2D + D_H + D_l) = 0$
, this is equivalent to
![]() $-2D + D_H + D_l \sim 0$
. Since
$-2D + D_H + D_l \sim 0$
. Since
![]() $N = q_1 + \cdots + q_{2g} \sim 2D$
, we have that
$N = q_1 + \cdots + q_{2g} \sim 2D$
, we have that
 $$ \begin{align*} -2D + D_H + D_l \sim 0 &\iff q + i(q) \sim q_{2g - 1} + q_{2g} \\ &\iff h \sim q_{2g - 1} + q_{2g} \\ &\iff i(q_{2g - 1}) = q_{2g}. \end{align*} $$
$$ \begin{align*} -2D + D_H + D_l \sim 0 &\iff q + i(q) \sim q_{2g - 1} + q_{2g} \\ &\iff h \sim q_{2g - 1} + q_{2g} \\ &\iff i(q_{2g - 1}) = q_{2g}. \end{align*} $$
By our genericity hypothesis on N, the last condition is not satisfied. Consequently, we conclude that the line l intersects the hyperplane H iff
 $\{q, i(q)\} \cap \{q_1, \ldots , q_{2g - 2} \}$
is nonempty, that is iff q or
$\{q, i(q)\} \cap \{q_1, \ldots , q_{2g - 2} \}$
is nonempty, that is iff q or
![]() $i(q)$
is one of the
$i(q)$
is one of the
![]() $q_k$
for
$q_k$
for
![]() $k = 1, \ldots , 2g - 2$
. In particular,
$k = 1, \ldots , 2g - 2$
. In particular,
 $$ \begin{align*}\Gamma \cap H = \{q_1, \ldots, q_{2g - 2} \}\end{align*} $$
$$ \begin{align*}\Gamma \cap H = \{q_1, \ldots, q_{2g - 2} \}\end{align*} $$
as we wanted to show.
Hence, the curve
![]() $\Gamma $
is contracted by the map
$\Gamma $
is contracted by the map
![]() $h_N$
to a point
$h_N$
to a point
 $w \in \mathcal {M}_{0,2g}^{\text {GIT}}$
by Proposition 4.9. The point w represents a hyperelliptic curve
$w \in \mathcal {M}_{0,2g}^{\text {GIT}}$
by Proposition 4.9. The point w represents a hyperelliptic curve
![]() $C_{w}$
of genus
$C_{w}$
of genus
![]() $g-1$
together with an ordering of the Weierstrass points that correspond to the points of N on the rational curve
$g-1$
together with an ordering of the Weierstrass points that correspond to the points of N on the rational curve
![]() $\Gamma $
.
$\Gamma $
.
5.2 The restriction of the theta map to
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
$\mathcal {M}_{0,2g}^{\text {GIT}}$
Let us set once again
![]() $N = p_1 + \cdots + p_{2g}$
, a general divisor in the linear system
$N = p_1 + \cdots + p_{2g}$
, a general divisor in the linear system
 $|2D|$
, and consider the span
$|2D|$
, and consider the span
 $\mathbb {P}_N^{2g-2}$
in
$\mathbb {P}_N^{2g-2}$
in
 $\mathbb {P}_D^{3g-2}$
of the
$\mathbb {P}_D^{3g-2}$
of the
![]() $2g$
marked points
$2g$
marked points
![]() $p_1, \ldots , p_{2g}$
.
$p_1, \ldots , p_{2g}$
.
In this section, we describe the interplay between
![]() $\theta $
and the linear systems presented in Section 4.
$\theta $
and the linear systems presented in Section 4.
5.2.1 The factorization of the map
 $\varphi _D$
$\varphi _D$
Recall that the base locus of the map
![]() $\varphi _D$
is the secant variety
$\varphi _D$
is the secant variety
 $\text {Sec}^{g-2}(C)$
by Proposition 2.2. As in [Reference Bertram4], one can construct a resolution
$\text {Sec}^{g-2}(C)$
by Proposition 2.2. As in [Reference Bertram4], one can construct a resolution
![]() $\widetilde {\varphi _D}$
of the map
$\widetilde {\varphi _D}$
of the map
![]() $\varphi _D$
via a sequence of blow-ups
$\varphi _D$
via a sequence of blow-ups

along the secant varieties
 $$ \begin{align*}C = \text{Sec}^0(C) \subset \text{Sec}^1(C) \subset \cdots \subset \text{Sec}^{g-1}(C) \subset \mathbb{P}_D^{3g-2}.\end{align*} $$
$$ \begin{align*}C = \text{Sec}^0(C) \subset \text{Sec}^1(C) \subset \cdots \subset \text{Sec}^{g-1}(C) \subset \mathbb{P}_D^{3g-2}.\end{align*} $$
This chain of morphisms is defined inductively as follows: the center of the first blow-up
![]() $\text {Bl}_1$
is the curve
$\text {Bl}_1$
is the curve
 $C = \text {Sec}^0(C)$
. For
$C = \text {Sec}^0(C)$
. For
![]() $k = 2, \ldots , g-1$
, the center of the blow-up
$k = 2, \ldots , g-1$
, the center of the blow-up
![]() $\text {Bl}_k$
is the strict transform of the secant variety
$\text {Bl}_k$
is the strict transform of the secant variety
 $\text {Sec}^{k-1}(C)$
under the blow-up
$\text {Sec}^{k-1}(C)$
under the blow-up
![]() $\text {Bl}_{k-1}$
.
$\text {Bl}_{k-1}$
.
The map
![]() $\varphi _D$
is, by definition, the composition of the classifying map
$\varphi _D$
is, by definition, the composition of the classifying map
![]() $f_D$
and the degree 2 map
$f_D$
and the degree 2 map
![]() $\theta $
. Thus, the map
$\theta $
. Thus, the map
![]() $f_D$
lifts to a morphism
$f_D$
lifts to a morphism
 $\widetilde {f_D}$
which makes the following diagram commute:
$\widetilde {f_D}$
which makes the following diagram commute:

5.2.2 Osculating projections
We recall here a generalization of linear projections that will allow us to describe the map p in higher genus. For a more complete reference, see for example [Reference Massarenti and Rischter24]. Let
![]() $X \subset \mathbb {P}^N$
be an integral projective variety of dimension n, and
$X \subset \mathbb {P}^N$
be an integral projective variety of dimension n, and
![]() $p \in X$
a smooth point. Let
$p \in X$
a smooth point. Let
 $$ \begin{align*} \phi: \mathcal{U} \subset \mathbb{C}^n &\longrightarrow \mathbb{C}^N \\ (t_1, \ldots, t_n) &\longmapsto \phi(t_1, \ldots, t_n) \end{align*} $$
$$ \begin{align*} \phi: \mathcal{U} \subset \mathbb{C}^n &\longrightarrow \mathbb{C}^N \\ (t_1, \ldots, t_n) &\longmapsto \phi(t_1, \ldots, t_n) \end{align*} $$
be a local parametrization of X in a neighborhood of
 $p = \phi (0) \in X$
. For
$p = \phi (0) \in X$
. For
![]() $m \geq 0$
, let
$m \geq 0$
, let
 $O^m_p$
be the affine subspace of
$O^m_p$
be the affine subspace of
![]() $\mathbb {C}^N$
passing through
$\mathbb {C}^N$
passing through
![]() $p \in X$
and generated by the vectors
$p \in X$
and generated by the vectors
 $\phi _I(0)$
, where
$\phi _I(0)$
, where
![]() $\phi _I$
is a partial derivative of
$\phi _I$
is a partial derivative of
![]() $\phi $
of order
$\phi $
of order
![]() $\leq m$
.
$\leq m$
.
By definition, the m-osculating space
 $\;\,T_p^m X$
of X at p is the projective closure in
$\;\,T_p^m X$
of X at p is the projective closure in
![]() $\mathbb {P}^N$
of
$\mathbb {P}^N$
of
 $O^m_p$
. The m-osculating projection
$O^m_p$
. The m-osculating projection

is the corresponding linear projection with center
 $T_p^m$
.
$T_p^m$
.
5.2.3 Osculating projections of
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
$\mathcal {M}_{0,2g}^{\text {GIT}}$
In this section, we show how the map
![]() $\varphi _{D,N}$
induces an osculating projection on the copies of
$\varphi _{D,N}$
induces an osculating projection on the copies of
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
that appear as factors of the map in Diagram 4.
$\mathcal {M}_{0,2g}^{\text {GIT}}$
that appear as factors of the map in Diagram 4.
Lemma 5.2. Let Q be a r-form in
![]() $\mathbb {P}^n$
vanishing at the points
$\mathbb {P}^n$
vanishing at the points
![]() $P_1$
and
$P_1$
and
![]() $P_2$
with multiplicity
$P_2$
with multiplicity
![]() $l_1$
and
$l_1$
and
![]() $l_2$
respectively. Then, Q vanishes on the line passing through
$l_2$
respectively. Then, Q vanishes on the line passing through
![]() $P_1$
and
$P_1$
and
![]() $P_2$
with multiplicity at least
$P_2$
with multiplicity at least
![]() $l_1 + l_2 - r$
.
$l_1 + l_2 - r$
.
Proof See, for example, [Reference Kumar22, page 2].
Let us now consider the linear system
 $|\mathcal {I}_{\text {Sec}^N}(g)|$
on
$|\mathcal {I}_{\text {Sec}^N}(g)|$
on
 $\mathbb {P}_N^{2g-2}$
(see Section 4). The forms in
$\mathbb {P}_N^{2g-2}$
(see Section 4). The forms in
 $|\mathcal {I}_{\text {Sec}^N}(g)|$
vanish with multiplicity
$|\mathcal {I}_{\text {Sec}^N}(g)|$
vanish with multiplicity
![]() $g - 1$
along the points of C (see Lemma 2.2). By Lemma 5.2, these forms vanish then with multiplicity
$g - 1$
along the points of C (see Lemma 2.2). By Lemma 5.2, these forms vanish then with multiplicity
 $(g-1) + (g-1) - g = g-2$
along the secant lines l cutting out the hyperelliptic pencil. Thus, these forms vanish with multiplicity
$(g-1) + (g-1) - g = g-2$
along the secant lines l cutting out the hyperelliptic pencil. Thus, these forms vanish with multiplicity
![]() $g-2$
on the curve
$g-2$
on the curve
![]() $\Gamma $
.
$\Gamma $
.
Let us consider the linear system
 $|\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
. Let
$|\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
. Let
 $\mathcal {I}(\Gamma ) \subset |\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
be the partial linear system of forms vanishing (with multiplicity 1) along
$\mathcal {I}(\Gamma ) \subset |\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
be the partial linear system of forms vanishing (with multiplicity 1) along
 $\text {Sec}^{g-2}(N)$
, and with multiplicity
$\text {Sec}^{g-2}(N)$
, and with multiplicity
![]() $g - 2$
along
$g - 2$
along
![]() $\Gamma $
. By our previous observation and Lemma 4.1, we have the following inclusions of linear systems:
$\Gamma $
. By our previous observation and Lemma 4.1, we have the following inclusions of linear systems:
 $$ \begin{align*} \mathcal{R} \subset |\mathcal{I}_{\text{Sec}^N}(g)| \subset \mathcal{I}(\Gamma) \subset |\mathcal{I}_{\text{Sec}^{g-2}(N)}(g)|. \end{align*} $$
$$ \begin{align*} \mathcal{R} \subset |\mathcal{I}_{\text{Sec}^N}(g)| \subset \mathcal{I}(\Gamma) \subset |\mathcal{I}_{\text{Sec}^{g-2}(N)}(g)|. \end{align*} $$
Recall that the map
![]() $\varphi _{D,N}$
is induced by the linear system
$\varphi _{D,N}$
is induced by the linear system
![]() $\mathcal {R}$
. The above sequence of inclusions yields the following factorization of maps
$\mathcal {R}$
. The above sequence of inclusions yields the following factorization of maps

The first map
![]() $h_N$
is the one defined in Section 4.3, its image is the GIT quotient
$h_N$
is the one defined in Section 4.3, its image is the GIT quotient
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
. According to Proposition 4.9, this map contracts the curve
$\mathcal {M}_{0,2g}^{\text {GIT}}$
. According to Proposition 4.9, this map contracts the curve
![]() $\Gamma $
to a point
$\Gamma $
to a point
 $h_N(\Gamma )$
.
$h_N(\Gamma )$
.
Proposition 5.3. The map
![]() $\pi _N$
is the
$\pi _N$
is the
 $(g-3)$
-osculating projection
$(g-3)$
-osculating projection
 $\Pi ^{g-3}_{P}$
with center the point
$\Pi ^{g-3}_{P}$
with center the point
 $w = h_N(\Gamma )$
.
$w = h_N(\Gamma )$
.
Proof From the geometric description of the linear systems
 $\mathcal {I}(\Gamma )$
and
$\mathcal {I}(\Gamma )$
and
 $|\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
(Propositions 4.8 and 4.9), the base locus of the map
$|\mathcal {I}_{\text {Sec}^{g-2}(N)}(g)|$
(Propositions 4.8 and 4.9), the base locus of the map
![]() $\pi _N$
is the point
$\pi _N$
is the point
 $w = h_N(\Gamma )$
, with multiplicity
$w = h_N(\Gamma )$
, with multiplicity
![]() $g-2$
. In particular, since the forms in
$g-2$
. In particular, since the forms in
 $\mathcal {I}(\Gamma )$
vanish with multiplicity
$\mathcal {I}(\Gamma )$
vanish with multiplicity
![]() $g - 2$
along
$g - 2$
along
![]() $\Gamma $
, the order the projection
$\Gamma $
, the order the projection
![]() $\pi _N$
is
$\pi _N$
is
![]() $g-3$
.
$g-3$
.
According to Proposition 4.9, the map
![]() $h_N$
contracts the curve
$h_N$
contracts the curve
![]() $\Gamma $
to a point w in
$\Gamma $
to a point w in
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
representing an ordered configuration of the
$\mathcal {M}_{0,2g}^{\text {GIT}}$
representing an ordered configuration of the
![]() $2g$
marked points N. This point in turn corresponds to a hyperelliptic genus
$2g$
marked points N. This point in turn corresponds to a hyperelliptic genus
![]() $(g - 1)$
curve
$(g - 1)$
curve
![]() $C_w$
together with an ordering of the Weierstrass points. Now recall from Section 4.3 that the lower level composed map of Diagram 3 is the map
$C_w$
together with an ordering of the Weierstrass points. Now recall from Section 4.3 that the lower level composed map of Diagram 3 is the map
![]() $h_N$
. The rational normal curve
$h_N$
. The rational normal curve
 $\Gamma \subset \mathbb {P}_N^{2g-2}$
is contracted to a point
$\Gamma \subset \mathbb {P}_N^{2g-2}$
is contracted to a point
![]() $e_0\in \mathbb {P}^{2g-3}$
s.t.
$e_0\in \mathbb {P}^{2g-3}$
s.t.
 $w=i_\Omega (e_0)$
. Recall, once again from Section 4.3 that
$w=i_\Omega (e_0)$
. Recall, once again from Section 4.3 that
![]() $\mathbb {P}^{2g-3}$
also contains the
$\mathbb {P}^{2g-3}$
also contains the
![]() $2g-1$
points
$2g-1$
points
 $\tau _k\circ \text {Cr}_k(H_i)$
, images of the hyperplanes
$\tau _k\circ \text {Cr}_k(H_i)$
, images of the hyperplanes
 $H_i \subset \mathbb {P}_N^{2g-2}$
, with
$H_i \subset \mathbb {P}_N^{2g-2}$
, with
![]() $i\neq k$
and
$i\neq k$
and
![]() $1\leq i \leq 2g$
. Let us label them
$1\leq i \leq 2g$
. Let us label them
![]() $e_1, \dots , e_{2g-1}$
. Let now
$e_1, \dots , e_{2g-1}$
. Let now
![]() $\Lambda $
be the partial linear system of
$\Lambda $
be the partial linear system of
![]() $\Omega $
consisting of the
$\Omega $
consisting of the
 $(g - 1)$
-forms in
$(g - 1)$
-forms in
![]() $\mathbb {P}^{2g-3}$
vanishing with multiplicity
$\mathbb {P}^{2g-3}$
vanishing with multiplicity
![]() $g - 2$
in all the points
$g - 2$
in all the points
![]() $e_0, e_1, \ldots , e_{2g - 1}$
. As it is explained in Theorem 4.7, the rational map induced by the linear subsystem
$e_0, e_1, \ldots , e_{2g - 1}$
. As it is explained in Theorem 4.7, the rational map induced by the linear subsystem
![]() $\Lambda $
factors through
$\Lambda $
factors through
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
, and the second map
$\mathcal {M}_{0,2g}^{\text {GIT}}$
, and the second map
 is the osculating projection from the image of
is the osculating projection from the image of
![]() $e_0$
inside
$e_0$
inside
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
.
$\mathcal {M}_{0,2g}^{\text {GIT}}$
.
Theorem 5.4. The map
![]() $\pi _N$
coincides with the map
$\pi _N$
coincides with the map
![]() $\kappa $
. In particular, the map
$\kappa $
. In particular, the map
![]() $\pi _N$
is of degree 2.
$\pi _N$
is of degree 2.
Proof Consider the GIT quotient
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
embedded in
$\mathcal {M}_{0,2g}^{\text {GIT}}$
embedded in
 $|\Omega |^*$
as we have seen in Theorem 4.5. The osculating projection
$|\Omega |^*$
as we have seen in Theorem 4.5. The osculating projection
![]() $\pi _N$
is given by the linear system
$\pi _N$
is given by the linear system
 $|H - (g - 2) w|$
of hyperplanes vanishing in w with multiplicity
$|H - (g - 2) w|$
of hyperplanes vanishing in w with multiplicity
![]() $g-2$
. By definition of
$g-2$
. By definition of
![]() $\Omega $
, this linear system pulls back via
$\Omega $
, this linear system pulls back via
![]() $i_{\Omega }$
to the linear system of
$i_{\Omega }$
to the linear system of
![]() $(g - 1)$
-forms in
$(g - 1)$
-forms in
![]() $\mathbb {P}^{2g - 3}$
vanishing with multiplicity
$\mathbb {P}^{2g - 3}$
vanishing with multiplicity
![]() $g - 2$
in
$g - 2$
in
![]() $e_1, \ldots , e_{2g - 1}$
, and also with multiplicity
$e_1, \ldots , e_{2g - 1}$
, and also with multiplicity
![]() $g - 2$
in
$g - 2$
in
![]() $e_0$
, which is precisely
$e_0$
, which is precisely
![]() $\Lambda $
. Hence, the map
$\Lambda $
. Hence, the map
![]() $\pi _N$
is the map induced by the same linear system as
$\pi _N$
is the map induced by the same linear system as
![]() $\kappa $
(see Theorem 4.7).
$\kappa $
(see Theorem 4.7).
We will show in the next Section that the map
![]() $l_N$
from Diagram 6 is actually birational, and that the map
$l_N$
from Diagram 6 is actually birational, and that the map
![]() $\pi _N$
(birationally) coincides with the restriction of the map
$\pi _N$
(birationally) coincides with the restriction of the map
![]() $\theta $
.
$\theta $
.
5.3 The hyperelliptic theta map and rational involutions on
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
and
$\mathcal {M}_{0,2g}^{\text {GIT}}$
and
 $\mathcal {SU}_C(2)$
$\mathcal {SU}_C(2)$
The resolution
![]() $\widetilde {\varphi _D}$
of
$\widetilde {\varphi _D}$
of
![]() $\varphi _D$
factors through the degree 2 map
$\varphi _D$
factors through the degree 2 map
![]() $\theta $
as shown in Diagram 5. In the preceding section, we have shown that, when we restrict
$\theta $
as shown in Diagram 5. In the preceding section, we have shown that, when we restrict
![]() $\varphi _{D,N}$
to
$\varphi _{D,N}$
to
 $\mathbb {P}_N^{2g-2}$
, it factors through the degree 2 map
$\mathbb {P}_N^{2g-2}$
, it factors through the degree 2 map
![]() $\pi _N$
. Now, we link these two factorizations. The identification of maps in the following claim must be intended as rational maps, since for example
$\pi _N$
. Now, we link these two factorizations. The identification of maps in the following claim must be intended as rational maps, since for example
![]() $\pi _N$
is not everywhere defined.
$\pi _N$
is not everywhere defined.
Theorem 5.5. Let
 $N \in |2D|$
be a general effective divisor. Then, the restricted map
$N \in |2D|$
be a general effective divisor. Then, the restricted map
 $\theta |_{f_D\left (\mathbb {P}_N^{2g-2}\right )}$
is the map
$\theta |_{f_D\left (\mathbb {P}_N^{2g-2}\right )}$
is the map
![]() $\pi _N$
up to composition with a birational map.
$\pi _N$
up to composition with a birational map.
Proof Let us place ourselves on the open set
 $\widehat {\mathcal {SU}}_C(2) \subset \mathcal {SU}_C(2)$
of general stable bundles. First we remark that the factorization
$\widehat {\mathcal {SU}}_C(2) \subset \mathcal {SU}_C(2)$
of general stable bundles. First we remark that the factorization
 $\widetilde {\varphi _D} =\theta \circ \widetilde {f_D}$
of Diagram 5 is the Stein factorization of the map
$\widetilde {\varphi _D} =\theta \circ \widetilde {f_D}$
of Diagram 5 is the Stein factorization of the map
![]() $\widetilde {\varphi _D}$
along
$\widetilde {\varphi _D}$
along
 $\widetilde {\mathbb {P}_D^{3g-2}}$
. Indeed, the map
$\widetilde {\mathbb {P}_D^{3g-2}}$
. Indeed, the map
![]() $\theta $
is of degree 2 as explained in Section 1. Moreover, the preimage of a general stable bundle E by the map
$\theta $
is of degree 2 as explained in Section 1. Moreover, the preimage of a general stable bundle E by the map
![]() $f_D$
is the
$f_D$
is the
![]() $\mathbb {P}^1$
arising as the projectivization of the space of extensions of the form
$\mathbb {P}^1$
arising as the projectivization of the space of extensions of the form
In particular, the fibers of
 $\widetilde {f_D}$
over
$\widetilde {f_D}$
over
 $\widehat {\mathcal {SU}}_C(2)$
are connected.
$\widehat {\mathcal {SU}}_C(2)$
are connected.
The restriction of
![]() $\varphi _D$
to
$\varphi _D$
to
 $\mathbb {P}_N^{2g-2}$
factors through the maps
$\mathbb {P}_N^{2g-2}$
factors through the maps
![]() $h_N$
and
$h_N$
and
![]() $\pi _N$
(see Diagram 6), followed by the map
$\pi _N$
(see Diagram 6), followed by the map
![]() $l_N$
. According to Proposition 4.9, the fibers of
$l_N$
. According to Proposition 4.9, the fibers of
![]() $h_N$
are rational normal curves, thus connected. Moreover, the map
$h_N$
are rational normal curves, thus connected. Moreover, the map
![]() $\pi _N$
is degree 2 by Theorem 5.4. By unicity of the Stein factorization, we have our result.
$\pi _N$
is degree 2 by Theorem 5.4. By unicity of the Stein factorization, we have our result.
Comparing with the factorization
 $\widetilde {\varphi _D} =\theta \circ \widetilde {f_D}$
, we see that
$\widetilde {\varphi _D} =\theta \circ \widetilde {f_D}$
, we see that
![]() $l_N$
cannot have relative dimension
$l_N$
cannot have relative dimension
![]() $> 0$
. Hence,
$> 0$
. Hence,
![]() $l_N$
is a finite map. Since the degree of the map
$l_N$
is a finite map. Since the degree of the map
![]() $\theta $
in the Stein factorization is 2, which is equal to the degree of
$\theta $
in the Stein factorization is 2, which is equal to the degree of
![]() $\pi _N$
, we have that
$\pi _N$
, we have that
![]() $l_N$
cannot have degree
$l_N$
cannot have degree
![]() $> 1$
. In particular, we have that the map
$> 1$
. In particular, we have that the map
![]() $l_N$
is a birational map.
$l_N$
is a birational map.
We are now in the position to show the following.
Proposition 5.6.
-
1. There exists a fibration
 whose general fiber is birational to
whose general fiber is birational to
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
.
$\mathcal {M}_{0,2g}^{\text {GIT}}$
. -
2. For every generic divisor
 $N \in |2D|$
, the the restriction of
$N \in |2D|$
, the the restriction of
 $f_D$
to the
$f_D$
to the
 $2g$
-pointed projective space
$2g$
-pointed projective space
 $\mathbb {P}_N^{2g-2}\subset \mathbb {P}_D^{3g-2}$
dominates
$\mathbb {P}_N^{2g-2}\subset \mathbb {P}_D^{3g-2}$
dominates
 $p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
. The generic fiber of
$p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
. The generic fiber of
 $f_{D|\mathbb {P}_N^{2g-2}}$
is a rational normal curve passing through the
$f_{D|\mathbb {P}_N^{2g-2}}$
is a rational normal curve passing through the
 $2g$
marked points.
$2g$
marked points. -
3. The family of rational normal curves contracted by
 $f_{D|\mathbb {P}_N^{2g-2}}$
is the universal family of pointed rational curves over (an open subset of) the generic fiber
$f_{D|\mathbb {P}_N^{2g-2}}$
is the universal family of pointed rational curves over (an open subset of) the generic fiber
 $p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
.
$p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
.
Proof The fibration
![]() $p_D$
is defined by the composed map
$p_D$
is defined by the composed map
 . The birationality
. The birationality
 $p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
for a general
$p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
for a general
 $N\in |2D|$
is given by the classifying map
$N\in |2D|$
is given by the classifying map
![]() $f_D$
. In fact, if we fix
$f_D$
. In fact, if we fix
 $N\in |2D|$
, then by Proposition 3.2 we know that the (closure of the) image of the restricted map
$N\in |2D|$
, then by Proposition 3.2 we know that the (closure of the) image of the restricted map
![]() $\varphi _{D,N}$
is the fiber of
$\varphi _{D,N}$
is the fiber of
![]() $p_{\mathbb {P}_c}$
. Thanks to the discussion in Section 5.2.3 (see in particular Diagram 6 and Theorem 5.4) we know that birationally
$p_{\mathbb {P}_c}$
. Thanks to the discussion in Section 5.2.3 (see in particular Diagram 6 and Theorem 5.4) we know that birationally
![]() $\varphi _{D,N}$
factors via the map
$\varphi _{D,N}$
factors via the map
![]() $h_N$
that contracts rational normal curves through the
$h_N$
that contracts rational normal curves through the
![]() $2g$
points of N (see Proposition 4.9), and the degree 2 osculating projection
$2g$
points of N (see Proposition 4.9), and the degree 2 osculating projection
![]() $\pi _N$
. Finally, from Theorem 5.5 and its proof we see that birationally
$\pi _N$
. Finally, from Theorem 5.5 and its proof we see that birationally
![]() $h_N$
is equal to the restriction of
$h_N$
is equal to the restriction of
![]() $f_D$
to
$f_D$
to
 $\mathbb {P}_N^{2g-2}$
, the rational normal curves contracted by
$\mathbb {P}_N^{2g-2}$
, the rational normal curves contracted by
![]() $h_N$
are the fibers of the classifying map
$h_N$
are the fibers of the classifying map
![]() $f_D$
, and
$f_D$
, and
![]() $\pi _N$
is the restriction of
$\pi _N$
is the restriction of
![]() $\theta $
to
$\theta $
to
 $f_D(\mathbb {P}_N^{2g-2})$
. This implies claims
$f_D(\mathbb {P}_N^{2g-2})$
. This implies claims
 $(1)$
and
$(1)$
and
 $(2)$
. Claim
$(2)$
. Claim
 $(3)$
is a consequence of the properties of
$(3)$
is a consequence of the properties of
![]() $h_N$
described in Proposition 4.9 and the fact that over an open set
$h_N$
described in Proposition 4.9 and the fact that over an open set
 $f_{D|\mathbb {P}_N^{2g-2}}$
coincides with
$f_{D|\mathbb {P}_N^{2g-2}}$
coincides with
![]() $h_N$
. Remark that the existence of this universal family also induces, in a more intrinsic way, the birational map
$h_N$
. Remark that the existence of this universal family also induces, in a more intrinsic way, the birational map
 $p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
by means of the universal property of the categorical quotient
$p_D^{-1}(N)\stackrel {birat}{\cong } \mathcal {M}_{0,2g}^{\text {GIT}}$
by means of the universal property of the categorical quotient
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
.
$\mathcal {M}_{0,2g}^{\text {GIT}}$
.
Remark. With a little effort, it is also possible to reconstruct a semistable, rank 2 vector bundle on C with trivial determinant starting from a general configuration of points in
 $\mathcal {M}_{0,2g}^{\text {GIT}} \stackrel {birat}{\cong } p_D^{-1}(N)$
, thus producing an inverse to the birational map
$\mathcal {M}_{0,2g}^{\text {GIT}} \stackrel {birat}{\cong } p_D^{-1}(N)$
, thus producing an inverse to the birational map
 induced by
induced by
![]() $f_D$
, but we will refrain to develop the details.
$f_D$
, but we will refrain to develop the details.
The results proved and collected in the preceding sections put us now in the position to claim the following theorem.
Theorem 5.7. The restriction of
![]() $\theta $
to the general fiber of the fibration
$\theta $
to the general fiber of the fibration
 has a ramification locus birational to the Kummer variety of dimension
has a ramification locus birational to the Kummer variety of dimension
![]() $g - 1$
, obtained from the Jacobian of the hyperelliptic curve that is the double cover of
$g - 1$
, obtained from the Jacobian of the hyperelliptic curve that is the double cover of
![]() $\mathbb {P}^1$
ramified along the
$\mathbb {P}^1$
ramified along the
![]() $2g$
points represented by
$2g$
points represented by
 $w=h_N(\Gamma )$
.
$w=h_N(\Gamma )$
.
Proof The proof of this theorem is a collection of the results that we have developed so far. We will refer to Figure 2 as a guiding line. As we have observed (see Proposition 5.6 (2)—top right corner of Figure 2), the generic fiber of the projection
![]() $p_D$
is birational to
$p_D$
is birational to
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
, and on an open subset of the fiber the map
$\mathcal {M}_{0,2g}^{\text {GIT}}$
, and on an open subset of the fiber the map
![]() $\theta $
coincides with the degree 2 map
$\theta $
coincides with the degree 2 map
![]() $\pi _N$
(Theorem 5.5—vertical map on the RHS of the figure). In turn, the map
$\pi _N$
(Theorem 5.5—vertical map on the RHS of the figure). In turn, the map
![]() $\pi _N$
coincides with the osculating projection
$\pi _N$
coincides with the osculating projection
![]() $\kappa $
(Theorem 5.4) defined on
$\kappa $
(Theorem 5.4) defined on
 $\mathcal {M}_{0,2g}^{\text {GIT}}$
. Hence, by Kumar’s beautiful description (see [Reference Kumar21] and Theorem 4.7—bottom right corner of the figure) of the Kummer variety as the ramification locus of
$\mathcal {M}_{0,2g}^{\text {GIT}}$
. Hence, by Kumar’s beautiful description (see [Reference Kumar21] and Theorem 4.7—bottom right corner of the figure) of the Kummer variety as the ramification locus of
![]() $\kappa $
, we have the claim. Let us also underline that we are also tacitly showing that the map
$\kappa $
, we have the claim. Let us also underline that we are also tacitly showing that the map
![]() $p_D$
factors through the map
$p_D$
factors through the map
![]() $\theta $
(this is the full RHS of the diagram in Figure 2).
$\theta $
(this is the full RHS of the diagram in Figure 2).

Figure 2 An intuitive view of our construction.
Corollary 5.8. One of the irreducible components of the ramification locus of the theta map is birational to a fibration in Kummer
![]() $(g-1)$
-folds over
$(g-1)$
-folds over
![]() $\mathbb {P}^g$
.
$\mathbb {P}^g$
.
Results from [Reference Zelaci31, App. E] imply that the ramification locus is in fact nonirreducible.
6 The case
 $g = 3$
$g = 3$
Let us now illustrate the geometric situation by explaining in detail the first case in low genus. Let C be a hyperelliptic curve of genus 3. In this setting, we have that the map
![]() $\theta $
factors through the involution
$\theta $
factors through the involution
![]() $i^*$
, and embeds the quotient
$i^*$
, and embeds the quotient
 $\mathcal {SU}_C(2) / {\langle i^* \rangle }$
in
$\mathcal {SU}_C(2) / {\langle i^* \rangle }$
in
 $\mathbb {P}^7 = |2 \Theta |$
as a quadric hypersurface (see [Reference Desale and Ramanan11]). Let D be a general effective divisor of degree 3. The projective space
$\mathbb {P}^7 = |2 \Theta |$
as a quadric hypersurface (see [Reference Desale and Ramanan11]). Let D be a general effective divisor of degree 3. The projective space
 $\mathbb {P}^7_D$
, as defined in Section 1, parametrizes the extension classes in
$\mathbb {P}^7_D$
, as defined in Section 1, parametrizes the extension classes in
 $\text {Ext}^1(\mathcal {O}(D), \mathcal {O}(-D))$
. The classifying map
$\text {Ext}^1(\mathcal {O}(D), \mathcal {O}(-D))$
. The classifying map
![]() $\varphi _D$
is given in this case by the complete linear system
$\varphi _D$
is given in this case by the complete linear system
 $|\mathcal {I}_C^2(3)|$
of cubics vanishing on C with multiplicity 2. The forms from this linear system vanish along the secant lines of C, and in particular along the secant lines passing through involution-conjugate points. These form a pencil parametrized by the linear system
$|\mathcal {I}_C^2(3)|$
of cubics vanishing on C with multiplicity 2. The forms from this linear system vanish along the secant lines of C, and in particular along the secant lines passing through involution-conjugate points. These form a pencil parametrized by the linear system
![]() $|h|$
.
$|h|$
.
The image of the projection of
 $\theta (\mathcal {SU}_C(2))$
with center
$\theta (\mathcal {SU}_C(2))$
with center
 $\mathbb {P}_c = \mathbb {P}^3 \subset |2 \Theta |$
is also a
$\mathbb {P}_c = \mathbb {P}^3 \subset |2 \Theta |$
is also a
![]() $\mathbb {P}^3$
, that is identified with
$\mathbb {P}^3$
, that is identified with
 $|2 D|$
by Theorem 3.1. Let
$|2 D|$
by Theorem 3.1. Let
 $N \in |2D|$
be a general reduced divisor. By Proposition 3.2, the closure of the fiber
$N \in |2D|$
be a general reduced divisor. By Proposition 3.2, the closure of the fiber
 $p_{\mathbb {P}_c}^{-1}(N)$
is the image via
$p_{\mathbb {P}_c}^{-1}(N)$
is the image via
![]() $\varphi _D$
of the
$\varphi _D$
of the
 $\mathbb {P}_N^{4}$
spanned by the six points of N.
$\mathbb {P}_N^{4}$
spanned by the six points of N.
6.1 The restriction to
 $\mathbb {P}_N^4$
$\mathbb {P}_N^4$
The base locus of the restricted map
 $\varphi _{D,N} = \varphi _D|_{\mathbb {P}_N^{4}}$
contains
$\varphi _{D,N} = \varphi _D|_{\mathbb {P}_N^{4}}$
contains
 $\text {Sec}^N = \text {Sec}^1(C) \cap \mathbb {P}^4_N$
by Lemma 4.1. The secant variety
$\text {Sec}^N = \text {Sec}^1(C) \cap \mathbb {P}^4_N$
by Lemma 4.1. The secant variety
 $\text {Sec}^1(N) \subset \text {Sec}^N$
is the union of the 15 lines passing through pairs of the 6 points of N. According to Lemma 4.10, the further base locus
$\text {Sec}^1(N) \subset \text {Sec}^N$
is the union of the 15 lines passing through pairs of the 6 points of N. According to Lemma 4.10, the further base locus
 $\text {Sec}^N \setminus \text {Sec}^1(N)$
is given by the intersections of
$\text {Sec}^N \setminus \text {Sec}^1(N)$
is given by the intersections of
 $\mathbb {P}^4_N$
with the lines spanned by degree 2 divisors
$\mathbb {P}^4_N$
with the lines spanned by degree 2 divisors
![]() $L_2$
on C not contained in N satisfying
$L_2$
on C not contained in N satisfying
 $\dim |L_2| \geq 1$
. By Brill–Noether theory, there is only one linear system of such divisors on a genus 3 curve, namely the hyperelliptic linear system
$\dim |L_2| \geq 1$
. By Brill–Noether theory, there is only one linear system of such divisors on a genus 3 curve, namely the hyperelliptic linear system
![]() $|h|$
(see, e.g., [Reference Arbarello, Cornalba, Griffiths and Harris2], Chapter V). We will review these ideas in Section 7. This linear system traces the curve
$|h|$
(see, e.g., [Reference Arbarello, Cornalba, Griffiths and Harris2], Chapter V). We will review these ideas in Section 7. This linear system traces the curve
![]() $\Gamma $
that we introduced in Section 5 as the set of intersection points of
$\Gamma $
that we introduced in Section 5 as the set of intersection points of
 $\mathbb {P}_N^{2g-2}$
with the lines spanned by the divisors in the hyperelliptic pencil. Hence, we have that
$\mathbb {P}_N^{2g-2}$
with the lines spanned by the divisors in the hyperelliptic pencil. Hence, we have that
 $\text {Sec}^N = \{15 \text { lines} \} \cup \Gamma $
, and the restricted map
$\text {Sec}^N = \{15 \text { lines} \} \cup \Gamma $
, and the restricted map
![]() $\varphi _{D,N}$
factors as
$\varphi _{D,N}$
factors as

where
![]() $h_N$
is the map defined by the complete linear system
$h_N$
is the map defined by the complete linear system
 $|\mathcal {I}_{\text {Sec}^1(N)}(3)|$
of cubics vanishing along the 15 lines defined by the points of N, and
$|\mathcal {I}_{\text {Sec}^1(N)}(3)|$
of cubics vanishing along the 15 lines defined by the points of N, and
![]() $\pi _N$
is the projection with center the image via
$\pi _N$
is the projection with center the image via
![]() $h_N$
of the rational normal curve
$h_N$
of the rational normal curve
![]() $\Gamma $
.
$\Gamma $
.
The image of
![]() $\varphi _{D,N}$
is a
$\varphi _{D,N}$
is a
![]() $\mathbb {P}^3$
. Indeed, this image cannot have higher dimension, since the map factors through the projection from a point of
$\mathbb {P}^3$
. Indeed, this image cannot have higher dimension, since the map factors through the projection from a point of
 $\mathcal {M}_{0,6}^{\text {GIT}} \subset \mathbb {P}^4$
. Also, it cannot have dimension strictly smaller than 3 since otherwise the relative dimension of
$\mathcal {M}_{0,6}^{\text {GIT}} \subset \mathbb {P}^4$
. Also, it cannot have dimension strictly smaller than 3 since otherwise the relative dimension of
![]() $\varphi _{D,N}$
would be bigger than 1, or equivalently the global map
$\varphi _{D,N}$
would be bigger than 1, or equivalently the global map
![]() $\varphi _D$
would not surjet onto
$\varphi _D$
would not surjet onto
 $\mathcal {SU}_C(2)$
. Hence, in this case the map
$\mathcal {SU}_C(2)$
. Hence, in this case the map
![]() $\varphi _{D,N}$
is defined exactly by the system of cubics in
$\varphi _{D,N}$
is defined exactly by the system of cubics in
 $\mathbb {P}^4_N$
vanishing on
$\mathbb {P}^4_N$
vanishing on
![]() $\text {Sec}^N$
.
$\text {Sec}^N$
.
According to Proposition 4.9, the image of
![]() $h_N$
is the GIT moduli space
$h_N$
is the GIT moduli space
 $\mathcal {M}_{0,6}^{\text {GIT}}$
if N is general and reduced. It is a classical result that this GIT quotient is embedded in
$\mathcal {M}_{0,6}^{\text {GIT}}$
if N is general and reduced. It is a classical result that this GIT quotient is embedded in
![]() $\mathbb {P}^4$
as the Segre cubic
$\mathbb {P}^4$
as the Segre cubic
![]() $S_3$
(see for instance [Reference Dolgachev and Ortland12] or [Reference Dolgachev14]). This three-fold arises by considering the linear system of quadrics in
$S_3$
(see for instance [Reference Dolgachev and Ortland12] or [Reference Dolgachev14]). This three-fold arises by considering the linear system of quadrics in
![]() $\mathbb {P}^3$
that pass through five points in general position, thus it is isomorphic to the blow-up of
$\mathbb {P}^3$
that pass through five points in general position, thus it is isomorphic to the blow-up of
![]() $\mathbb {P}^3$
at these points, followed by the blow-down of all lines joining any two points. The composition of this map with the projection off a smooth point of
$\mathbb {P}^3$
at these points, followed by the blow-down of all lines joining any two points. The composition of this map with the projection off a smooth point of
![]() $S_3$
gives a
$S_3$
gives a
![]() $2:1$
rational map
$2:1$
rational map
![]() whose ramification locus is a Weddle surface [Reference Kumar21, Reference Bolognesi5]. The curve
whose ramification locus is a Weddle surface [Reference Kumar21, Reference Bolognesi5]. The curve
 $\Gamma \subset \mathbb {P}^4_N$
is a rational normal curve by Lemma 5.1, hence
$\Gamma \subset \mathbb {P}^4_N$
is a rational normal curve by Lemma 5.1, hence
![]() $\Gamma $
is contracted to a point w by
$\Gamma $
is contracted to a point w by
![]() $h_N$
again by Proposition 4.9.
$h_N$
again by Proposition 4.9.
By [Reference Bertram4] and Lemma 4.1, the linear system
 $|\mathcal {O}_{S_3}(1)|$
of hyperplanes in
$|\mathcal {O}_{S_3}(1)|$
of hyperplanes in
![]() $S_3$
is pulled back by
$S_3$
is pulled back by
![]() $h_N$
to
$h_N$
to
 $|\mathcal {I}_{\text {Sec}^1(N)}(3)|$
on
$|\mathcal {I}_{\text {Sec}^1(N)}(3)|$
on
 $\mathbb {P}_N^{4}$
. The linear system
$\mathbb {P}_N^{4}$
. The linear system
 $|\mathcal {O}_{S_3}(1) - w|$
of hyperplanes in
$|\mathcal {O}_{S_3}(1) - w|$
of hyperplanes in
![]() $S_3$
passing through w is pulled back to the complete linear system
$S_3$
passing through w is pulled back to the complete linear system
 $|\mathcal {I}_{\text {Sec}^N}(3)|$
defining
$|\mathcal {I}_{\text {Sec}^N}(3)|$
defining
![]() $\varphi _{D,N}$
. Hence, the map
$\varphi _{D,N}$
. Hence, the map
![]() $\pi _N$
is the linear projection with center w. Since
$\pi _N$
is the linear projection with center w. Since
![]() $S_3$
is a cubic, the projection
$S_3$
is a cubic, the projection
![]() $\pi _N$
is a degree 2 map. We will see in the next Section that this will be also the case for higher genus. The following proposition resumes what we have seen so far in this section.
$\pi _N$
is a degree 2 map. We will see in the next Section that this will be also the case for higher genus. The following proposition resumes what we have seen so far in this section.
Proposition 6.1. Let C be a hyperelliptic curve of genus 3. Then, for generic N, the restriction of
![]() $\varphi _D$
to the subspace
$\varphi _D$
to the subspace
 $\mathbb {P}_N^{2g-2}$
is exactly the composition
$\mathbb {P}_N^{2g-2}$
is exactly the composition
![]() $\pi _N \circ h_N$
.
$\pi _N \circ h_N$
.
The point w in
 $\mathcal {M}_{0,6}^{\text {GIT}}$
represents a rational curve with six marked points. Let
$\mathcal {M}_{0,6}^{\text {GIT}}$
represents a rational curve with six marked points. Let
![]() $C'$
be the hyperelliptic genus 2 curve constructed as the double cover of this rational curve ramified in these six points. According to Theorem 4.2 of [Reference Kumar21], the Kummer variety
$C'$
be the hyperelliptic genus 2 curve constructed as the double cover of this rational curve ramified in these six points. According to Theorem 4.2 of [Reference Kumar21], the Kummer variety
 $\text {Kum}(C')$
is contained in the image of
$\text {Kum}(C')$
is contained in the image of
![]() $\pi _N$
, and it is precisely its ramification locus. Recall that, when
$\pi _N$
, and it is precisely its ramification locus. Recall that, when
![]() $g=3$
, the linear system
$g=3$
, the linear system
 $|2D|$
is a
$|2D|$
is a
![]() $\mathbb {P}^3$
. By Proposition 3.2, the image of
$\mathbb {P}^3$
. By Proposition 3.2, the image of
 $\mathbb {P}_N^{4}$
by
$\mathbb {P}_N^{4}$
by
![]() $\varphi _D$
is the closure of the fiber
$\varphi _D$
is the closure of the fiber
 $p_{\mathbb {P}_c}^{-1}(N)$
. For each point N in
$p_{\mathbb {P}_c}^{-1}(N)$
. For each point N in
 $|2D|$
, this image is
$|2D|$
, this image is
 $\mathbb {P}^3 = |\mathcal {I}^2_{\text {Sec}^N}(3)|^*$
, which is the image of the Segre variety
$\mathbb {P}^3 = |\mathcal {I}^2_{\text {Sec}^N}(3)|^*$
, which is the image of the Segre variety
 $\mathcal {M}_{0,6}^{\text {GIT}}$
under the projection with center P. Thus, the image of the global map
$\mathcal {M}_{0,6}^{\text {GIT}}$
under the projection with center P. Thus, the image of the global map
![]() $\varphi _D$
is birational to a
$\varphi _D$
is birational to a
![]() $\mathbb {P}^3$
-bundle over
$\mathbb {P}^3$
-bundle over
 $|2D| = \mathbb {P}^3$
. Of course this is also the case since the image of the theta map is a quadric hypersurface in
$|2D| = \mathbb {P}^3$
. Of course this is also the case since the image of the theta map is a quadric hypersurface in
![]() $\mathbb {P}^7$
[Reference Desale and Ramanan11].
$\mathbb {P}^7$
[Reference Desale and Ramanan11].
7 Explicit descriptions in low genera
In this section, we will go through an explicit description of the classifying maps and how they factor through forgetful linear systems and osculating projections, for low values of the genus
![]() $g(C)$
of the hyperelliptic curve. In these cases the map remains fairly simple. These computations seem completely out of reach without the help of a computer for higher genus.
$g(C)$
of the hyperelliptic curve. In these cases the map remains fairly simple. These computations seem completely out of reach without the help of a computer for higher genus.
Recall from Section 4 that the intersection
 $ \text {Sec}^N = \text {Sec}^{g-2}(C) \cap \mathbb {P}_N^{2g-2}$
arises naturally as part of the base locus of the restricted map
$ \text {Sec}^N = \text {Sec}^{g-2}(C) \cap \mathbb {P}_N^{2g-2}$
arises naturally as part of the base locus of the restricted map
![]() $\varphi _{D,N}$
. The subvarieties
$\varphi _{D,N}$
. The subvarieties
 $\text {Sec}^{g-2}(N)$
and
$\text {Sec}^{g-2}(N)$
and
![]() $\Gamma $
of
$\Gamma $
of
![]() $\text {Sec}^N$
yield the factorization of
$\text {Sec}^N$
yield the factorization of
![]() $\varphi _{D,N}$
through the maps
$\varphi _{D,N}$
through the maps
![]() $h_N$
and
$h_N$
and
![]() $\pi _N$
of Proposition 5.3. Let us now describe the set
$\pi _N$
of Proposition 5.3. Let us now describe the set
 $$ \begin{align*} {\text{Sec}^N}' := \text{Sec}^N \setminus \{ \Gamma \cup \text{Sec}^{g-2}(N) \}. \end{align*} $$
$$ \begin{align*} {\text{Sec}^N}' := \text{Sec}^N \setminus \{ \Gamma \cup \text{Sec}^{g-2}(N) \}. \end{align*} $$
This set is empty for
![]() $g = 3$
, and the map
$g = 3$
, and the map
![]() $\varphi _{D,N}$
is exactly the composition of
$\varphi _{D,N}$
is exactly the composition of
![]() $h_N$
and
$h_N$
and
![]() $\pi _N$
, as described in Section 6. In higher genus, the existence of nonempty additional base locus
$\pi _N$
, as described in Section 6. In higher genus, the existence of nonempty additional base locus
![]() $\text {Sec}^N$
corresponds to the fact that the map
$\text {Sec}^N$
corresponds to the fact that the map
![]() $\varphi _{D,N}$
may not be exactly the composition of the maps
$\varphi _{D,N}$
may not be exactly the composition of the maps
![]() $h_N$
and
$h_N$
and
![]() $\pi _N$
. In other words, the map
$\pi _N$
. In other words, the map
![]() $l_N$
from Diagram 6 may not be nontrivial in higher genus.
$l_N$
from Diagram 6 may not be nontrivial in higher genus.
This supplementary base locus is given by the intersections of
 $\mathbb {P}_N^{2g-2}$
with
$\mathbb {P}_N^{2g-2}$
with
 $(g-2)$
-dimensional
$(g-2)$
-dimensional
![]() $(g-1)$
-secant planes of C in
$(g-1)$
-secant planes of C in
 $\mathbb {P}_D^{3g-2}$
, which are not already supported on
$\mathbb {P}_D^{3g-2}$
, which are not already supported on
 $\text {Sec}^{g-2}(N)$
and
$\text {Sec}^{g-2}(N)$
and
![]() $\Gamma $
. According to Lemma 4.10, these intersections are given by effective divisors
$\Gamma $
. According to Lemma 4.10, these intersections are given by effective divisors
![]() $L_{g-1}$
on C of degree
$L_{g-1}$
on C of degree
![]() $g-1$
, not contained in
$g-1$
, not contained in
 $\mathbb {P}_N^{2g-2}$
, and satisfying
$\mathbb {P}_N^{2g-2}$
, and satisfying
 $\dim |L_{g-1}| \geq 1$
. Again by Lemma 4.10, we obtain
$\dim |L_{g-1}| \geq 1$
. Again by Lemma 4.10, we obtain
 $\dim (\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2})=\dim |L_{g-1}| - 1$
.
$\dim (\langle L_{g-1} \rangle \cap \mathbb {P}_N^{2g-2})=\dim |L_{g-1}| - 1$
.
We will now give account of the situation in low genera.
Case
 $g = 4$
$g = 4$
In this case, the divisor N is of degree 8 and the map
 is given by the restriction of the linear system
is given by the restriction of the linear system
 $|\mathcal {I}_C^3(4)|$
to
$|\mathcal {I}_C^3(4)|$
to
 $\mathbb {P}_N^6$
. This map factors through the map
$\mathbb {P}_N^6$
. This map factors through the map
![]() $\pi _N$
which coincides with the one-osculating projection
$\pi _N$
which coincides with the one-osculating projection
 $\Pi ^1_w$
, where
$\Pi ^1_w$
, where
 $w = h_N(\Gamma )$
.
$w = h_N(\Gamma )$
.
We are looking for degree 3 divisors
![]() $L_3$
with
$L_3$
with
 $\dim |L_3| \geq 1$
. These satisfy all
$\dim |L_3| \geq 1$
. These satisfy all
 $\dim |L_3| = 1$
and are of the form
$\dim |L_3| = 1$
and are of the form
where h is the hyperelliptic divisor. Let p be a point of C. Then
 $L_3 = p + i(p) + q$
. Since
$L_3 = p + i(p) + q$
. Since
 $\dim |L_3| = 1$
, the secant plane
$\dim |L_3| = 1$
, the secant plane
 $\mathbb {P}^2_{L_3}$
in
$\mathbb {P}^2_{L_3}$
in
 $\mathbb {P}_D^{10}$
spanned by p,
$\mathbb {P}_D^{10}$
spanned by p,
![]() $i(p)$
and q intersects
$i(p)$
and q intersects
 $\mathbb {P}^6_N$
in a point. But this point necessarily lies on
$\mathbb {P}^6_N$
in a point. But this point necessarily lies on
![]() $\Gamma $
, since the line passing through p and
$\Gamma $
, since the line passing through p and
 $i(p)$
is already contained in this plane. Hence, we do not obtain any additional locus.
$i(p)$
is already contained in this plane. Hence, we do not obtain any additional locus.
Case
 $g = 5$
$g = 5$
In this case, the divisors
![]() $L_4$
of degree 4 are all of the form
$L_4$
of degree 4 are all of the form
and satisfy
 $\dim |L_4| = 1$
. Thus, the corresponding secant
$\dim |L_4| = 1$
. Thus, the corresponding secant
 $\mathbb {P}^3_{L_4}$
spanned by p,
$\mathbb {P}^3_{L_4}$
spanned by p,
 $i(p)$
, q and r intersects
$i(p)$
, q and r intersects
 $\mathbb {P}^{8}_N$
in a point. As before, this point lies on
$\mathbb {P}^{8}_N$
in a point. As before, this point lies on
![]() $\Gamma $
, thus we do not obtain any additional locus. The upshot is the following
$\Gamma $
, thus we do not obtain any additional locus. The upshot is the following
Proposition 7.1. Let C be a hyperelliptic curve of genus 4 or 5, then
![]() $\varphi _D$
is defined by a (possibly equal) linear subsystem of the linear system defining
$\varphi _D$
is defined by a (possibly equal) linear subsystem of the linear system defining
![]() $\pi _N \circ h_N$
, and set-theoretically the base locus of
$\pi _N \circ h_N$
, and set-theoretically the base locus of
![]() $\pi _N \circ h_N$
coincides with
$\pi _N \circ h_N$
coincides with
 $\text {Sec}^{g-2}(C)\cap \mathbb {P}_N^{2g-2}$
.
$\text {Sec}^{g-2}(C)\cap \mathbb {P}_N^{2g-2}$
.
Case
 $g = 6$
$g = 6$
Here we have, as in the genus 5 case, the divisors of the form
which do not give rise to any additional base locus. But there is a new family of divisors
These divisors satisfy
 $\dim |L_5| = 2$
. In particular, the intersection of the
$\dim |L_5| = 2$
. In particular, the intersection of the
 $\mathbb {P}^4_{L_5}$
spanned by p,
$\mathbb {P}^4_{L_5}$
spanned by p,
 $i(p)$
, q,
$i(p)$
, q,
![]() $i(q)$
, and r, for
$i(q)$
, and r, for
![]() $p, q \in C$
, with
$p, q \in C$
, with
 $\mathbb {P}^{10}_N$
is a line m in
$\mathbb {P}^{10}_N$
is a line m in
 $\mathbb {P}^{10}_N$
. The line
$\mathbb {P}^{10}_N$
. The line
![]() $l_1$
(resp.
$l_1$
(resp.
![]() $l_2$
) spanned by p and
$l_2$
) spanned by p and
![]() $i(p)$
(resp. q,
$i(p)$
(resp. q,
![]() $i(q)$
) intersects
$i(q)$
) intersects
![]() $\Gamma $
in a point
$\Gamma $
in a point
![]() $\widetilde {p}$
(resp.
$\widetilde {p}$
(resp.
![]() $\widetilde {q}$
). In particular, the line m is secant to
$\widetilde {q}$
). In particular, the line m is secant to
![]() $\Gamma $
and passes through
$\Gamma $
and passes through
![]() $\widetilde {p}$
and
$\widetilde {p}$
and
![]() $\widetilde {q}$
. Since every point of
$\widetilde {q}$
. Since every point of
![]() $\Gamma $
comes as an intersection of a secant line in C with
$\Gamma $
comes as an intersection of a secant line in C with
 $\mathbb {P}^{10}_N$
, we obtain the following description of the base locus of
$\mathbb {P}^{10}_N$
, we obtain the following description of the base locus of
![]() $\varphi _{D,N}$
:
$\varphi _{D,N}$
:
Proposition 7.2. Let C be a curve of genus
![]() $g = 6$
. Then, the base locus of the restricted map
$g = 6$
. Then, the base locus of the restricted map
![]() $\varphi _{D,N}$
contains the ruled three-fold
$\varphi _{D,N}$
contains the ruled three-fold
 $\text {Sec}^1(\Gamma )$
.
$\text {Sec}^1(\Gamma )$
.