2. EXPERIMENTAL SETUP

The experiment was performed at the Intense Laser Irradiation Laboratory of the CNR in Pisa. The laser system delivers pulses with an energy up to 100 mJ on target. In the described experiment, the energy on target was 80 mJ/pulse. The laser beam (800 nm, 40 fs) was focused by means of f/5 off-axis parabola into the gas-jet (See Fig. 1). The nominal peak laser intensity was 1.7 × 10¹⁸ W/cm² with a contrast of 5 × 10⁸ on a nanosecond time scale. The supersonic gas-jet nozzle exit was 4 mm long and 1.2 mm wide and the laser was propagating parallel to the shorter edge of the nozzle. The laser was focused close to the edge of the gas-jet closest to the focusing optics, at a vertical distance of 0.5 mm from the nozzle exit plane. As discussed below, the gas used in the experiment was Ar at a backing pressure between 45 and 50 bars, sufficient to produce clusterization of the gas. A Kodak Lanex Regular scintillating screen (marked as (1) in Fig. 1) is mounted at a distance of about 15 cm from the gas-jet nozzle for the characterization of the spatial profile of the electron beam. An imaging system is used to view the Lanex screen from outside the vacuum chamber. A magnetic spectrometer [marked as (2) in Fig. 1] with an entrance slit of 0.5 mm width is inserted between the nozzle and the Lanex screen at a distance of 8 mm from the Lanex screen for the characterization of the energy distribution of the accelerated electron beam. The charge of the electron beam is measured by means of a dosimetry film (Gafchromic MD-55) [marked as (3) in Figure 1]. A 15 μm thick Al filter is placed in front of the dosimetry film to avoid direct irradiation by the transmitted laser light and plasma self-emission.

Fig. 1. Experimental setup. (1) Lanex screen used for the electron spatial distribution measurements; (2) magnetic spectrometer used for the measurements of the electron energy distribution; (3) Gafchromic film used for the electron beam charge measurements; (4) a complex object was placed in contact with the radiochromic film detector for e-radiography.

3. EXPERIMENTAL RESULTS AND DISCUSSION

The spatial distribution of the electron beam detected by means of the scintillating screen as obtained from the interaction of a single laser pulse with an Ar-cluster target at a backing pressure of 46 bar is displayed in Figure 2 (top panel). The electron beam shows a very homogeneous spatial distribution over a wide region, well beyond the region imaged by the scintillating screen. In fact, in this case, the screen is set off-center, to image also the outer, lower intensity regions of the electron beam. Over the whole diameter of the scintillating screen of 5 cm the signal changes by less than a factor of two.

Fig. 2. Typical spatial distribution of the accelerated electron beam as detected by the scintillating screen at a distance of 15 cm from the gas-jet nozzle. The electron beam was obtained from the interaction of a 40 fs laser pulse at an intensity of 1.7 × 10¹⁸ W/cm² with an Ar-cluster target at a backing pressure of 46 bar (top) and an He gas target at a backing pressure of 40 bar (bottom).

For comparison, in Figure 2 (bottom panel) the typical spatial distribution of the electron beam accelerated in an He gas target in the case of using 40 bar backing pressure is shown. In this case, the electron beam is less divergent (note the different spatial scales of the two panels) and less homogeneous. From the comparison of the Lanex signals in the two cases, it is evident that the total charge of the electron beam accelerated in He gas is much lower than in the case of the Ar-cluster target, as will be shown in the following.

For a detailed characterization of the spatial distribution of the electron beam in the case of the Ar-cluster target, a lineout along the diameter of the graph in Figure 2 (top panel) is shown in Figure 3 together with a Gaussian fit f(x)=A exp[(x−x _c)²/(2σ²)]. The lineout of the data shows a smooth spatial profile and the width of the Gaussian fit results σ = 26.8 mm. Taking into account the distance from the nozzle to the scintillating screen the electron beam divergence is calculated to be 0.40 rad at full width at half maximum.

Fig. 3. Radial lineouts of the spatial distributions in Figure 2. The data obtained from the interaction with an Ar-cluster target was fitted with a Gaussian function (a) and the data obtained from the interaction with an He gas target with the sum of a Gaussian and a linear function (b).

The energy distribution of the electron beam above the lower spectral limit of our spectrometer (1.5 MeV) is shown in Figure 4 for the electron beam generated in the Ar-cluster target. In this case, the backing pressure was 46 bar. The spectrum shows a bright peak at about 1.9 MeV with a low-intensity tail at higher energies. As for the shot to shot variability at the laser intensity above, the electron energy was found to be always above the detection limit and below the 2 MeV, with the details of the spectrum changing moderately from shot to shot.

Fig. 4. Typical energy distribution of the electron beam obtained from the interaction of a 40 fs laser pulse at an intensity of 2 × 10¹⁸ W/cm² with an Ar-cluster target (backing pressure 46 bar). The sharp cut toward lower energies is due to the spectral limit of our spectrometer.

Information on the total charge of the electron beam accelerated in the Ar-cluster target was retrieved through the analysis of the signal detected on a dosimetry film for a series of 36 pulses of the driving laser. Taking into account the response curve of Gafchromic MD-55 film (Chair et al., Reference Chair, Blackwell, Coursey, Gall, Galvin, McLaughlin, Meigooni, Nath, Rodgers and Soares1998) and the measured optical density of the exposed film (OD = 0.77) we get a peak dose of about 25 Gy in the center of the spatial distribution of the electron beam. Considering the thickness (16 μm) of the two active layers and their density (1.08 g/cm³) we can obtain the surface mass density and finally the energy released by the energetic electrons on the dosimetry film which is found to be 8.64 × 10⁻⁵ J/cm². A Monte Carlo simulation on the energy released by energetic electrons on MD-55 dosimetry film is reported in Figure 5.

Fig. 5. Energy released in the active layers of a GAFCHROMIC MD-55 film as a function of incoming electron kinetic energy. The results are obtained from Monte Carlo simulations using Geant4 libraries for the experimental setup including an Al filter of 15 μm thickness.

As we can see, each 200 keV electron releases 22 keV, while an electron with energy of the order or greater than 1 MeV releases 6 keV. Thus the charge of the electron beam accelerated in the Ar-cluster target is in the range 5–18 nC, where the lower limit applies to a monoenergetic electron beam of 200 keV kinetic energy and the upper limit occurs for an electron beam with kinetic energy above 1 MeV. The electron energy distribution below 1 MeV was not measured during the experiment, as lower energy electrons are trapped inside the magnetic field of the spectrometer and thus are not detected on the Lanex screen. This generates a 50% uncertainty in the charge measurement of 12 ± 6 nC. From a comparison of the signal on the Lanex screen (Fig. 2) obtained in the case of the Ar-cluster target with the one obtained from He gas, the charge of the electron beam accelerated in He gas can be estimated. Both signals were integrated assuming circular symmetry. The charge of the electron beam obtained from the interaction of the laser pulse with the He target results to be of the order of 300 pC, more than one order of magnitude less than in the case of the Ar-cluster target. This value is consistent with values in literature, where the charge of the energetic electron beam, generated through laser-acceleration in gas targets, is typically of the order of tens to hundreds of pC (Mangles et al., Reference Mangles, Walton, And, Dangor, Krushelnick, Malka, Manclossi, Lopes, Carias, Mendes and Dorchies2006). Electron beams with such high charge of several nC in the case of the Ar-cluster target were generated with a high degree of reproducibility. In a sequence of 101 laser shots, only 23 shots with significantly weaker fluorescence signal from the Lanex screen were registered resulting in a reproducibility of 77%. The generated electron beam was then used to irradiate a sample of a few centimeters size at contact with the radiochromic film detector. A detailed description of the radiographic results can be found in Bussolino et al. (Reference Bussolino, Faenov, Giulietti, Giulietti, Koester, Labate, Levato, Pikuz and Gizzi2013). The spatial resolution was measured from the radiographic image of a sharp edge. Assuming a Gaussian point-spread-function, the RMS spot size was found to be 60 μm. It is necessary to stress the high sensitivity of the electron radiographic imaging in our case for low absorbing materials. As can be seen from Figure 6 (top left), Ni foils with a step thickness of only 10 μm could be clearly resolved despite of the fact that the total stopping range of 1 MeV electrons in Ni is about 680 μm. In Figure 6 (bottom right), a detail of the radiography showing a leaf is displayed. Internal structures of the leaf, which had thickness about 100–200 μm, are clearly visible. A very important property of our electron radiography scheme is the wide field of view. In fact, the whole sample (see the photograph in Fig. 6, top right) having a size of several centimeters could be irradiated without displacing the sample.

Fig. 6. Contact radiography performed with the electron beam obtained from the interaction of the laser pulse with the Ar-cluster target. Top left: Detail showing the radiography of two layers of a 10 μm thick Ni foil. The difference in absorption of 20 μm of Ni (light area), 10 μm of Ni (center diagonal), and no Ni (dark area) is visible. Bottom left: Lineout of the radiography in the top left panel along the black line. Top right: Photograph of one of the samples used for radiography. Bottom right: Detail (the leaf at the center) of the radiography of the sample in the top right panel. The internal structure of the leaf is visible.

These results on the characterization of the electron beam show that a high charge, homogeneous and divergent electron beam with moderate kinetic energy of 2 MeV can be generated through the interaction of the laser pulse with a clusterized Ar gas-jet target. It is therefore crucial to understand the role of clusters in this configuration.

In order to get information on the cluster parameters, simulations were performed for a conically shaped nozzle close to the one used in the experiments. The simulations show that Ar clusters with a radius between 40 nm (at 40 bar backing pressure) and 20 nm (at 60 bar) are generated. The concentration of clusters increases rapidly for backing pressures between 40 and 60 bar (see Fig. 7).

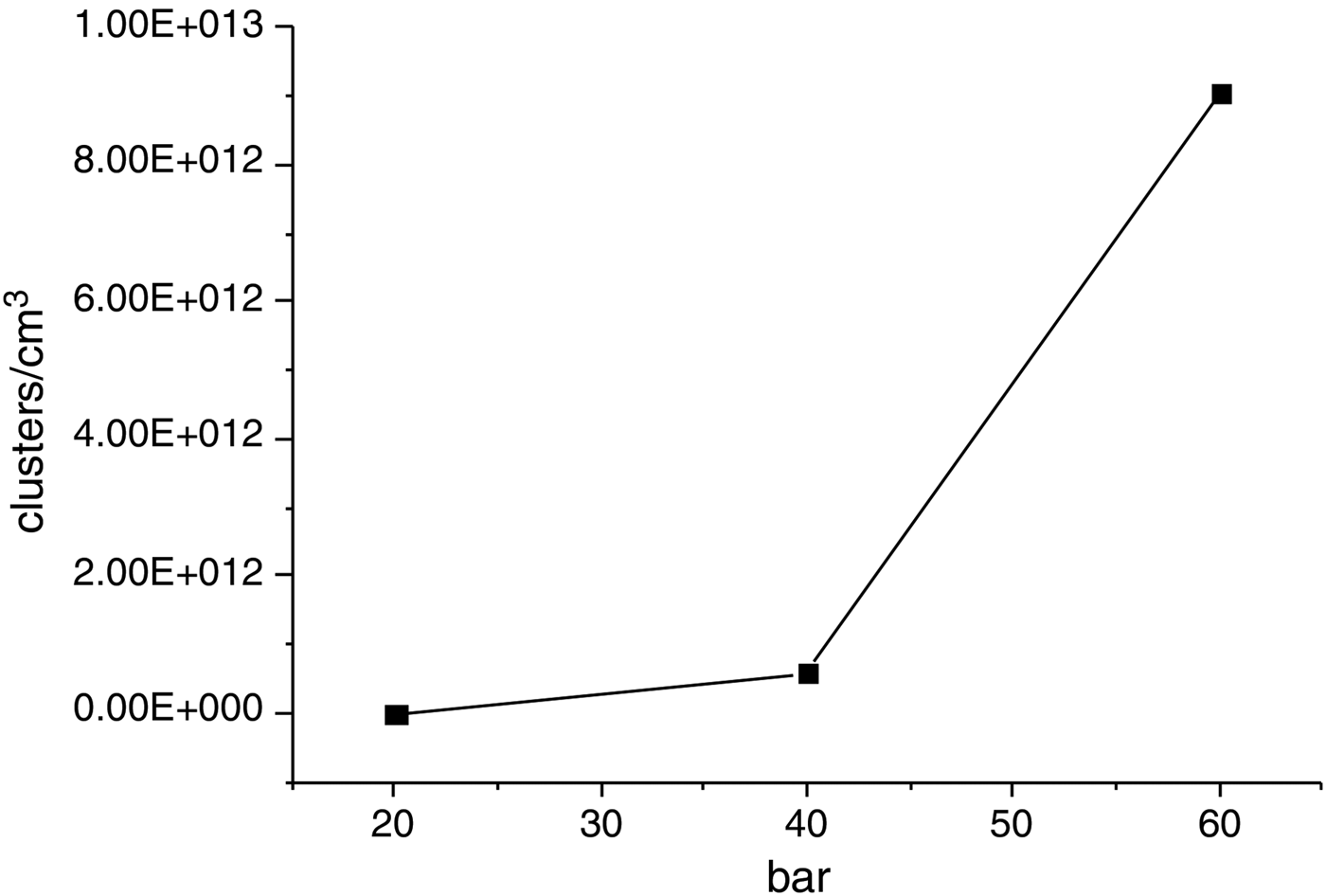
Fig. 7. Cluster density as a function of Ar gas backing pressure.

The efficient absorption of laser light in clusterized gases (Kishimoto & Tajima, Reference Kishimoto, Tajima, Tajima, Mima and Baldis2001) leads to high ionization stages of the Ar atoms and thus to a high electron density (Magunov et al., Reference Magunov, Pikuz, Skobelev, Faenov, Blasco, Dorchies, Caillaud, Bonte, Stenz, Salin, Loboda, Litvinenko, Popova, Baidin, Abdallah and Junkel-Vives2001; Sherrill et al., Reference Sherrill, Abdallah, Csanak, Dodd, Fukuda, Akahane, Aoyama, Inoue, Ueda, Yamakawa, Faenov, Magnov, Pikuz and Skobelev2006). Ionization stages up to 16 were reached in Ar-cluster targets for laser intensities similar to the ones used in the experiments (Abdallah et al., Reference Abdallah, Faenov, Skobelev, Magunov, Pikuz, Auguste, D'Oliveira, Hulin and Monot2001; Fukuda et al., Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Kishimoto, Yamakawa, Faenov, Magunov, Pikuz, Skobelev, Abdallah, Csanak, Boldarev and Gasilov2004; Faenov et al., Reference Faenov, Skobelev, Pikuz, Pikuz, Fortov, Fukuda, Hayashi, Pirozhkov, Kotaki, Shimomura, Kiriyama, Kanazawa, Kato, Colgan, Abdallah and Kando2012). Thus, for a neutral gas density of 4 × 10¹⁹ cm⁻³ as expected for the used backing pressure, plasma electron densities above 10²⁰ cm⁻³ are likely to be reached. This will contribute to increase the electron beam charge observed in the experiment. Given the very high electron density, strong self-focusing of the laser beam is expected to occur. In fact, the laser power of 2 TW largely exceeds the threshold power for self-focusing given by the relativistic critical power ${ P_c \! =\! \left({m_e c^5 \omega^2}/{e^2 \omega_p^2}\right)\!\approx\! 17 \left({\omega}/{\omega_p}\right)^2 }$ GW, where m _e is the electron mass, c the speed of light, ω is the laser radiation angular frequency, e the electron charge and ω_p is plasma frequency (P_c≈117 GW for a density of 10²⁰ cm⁻³). Also, in our experimental conditions the laser pulse duration of 40 fs is much longer than the inverse of the plasma frequency ω_p⁻¹~5 fs. In these circumstances, the accelerating wake field is expected to be driven through self-modulation of the laser pulse (Najmudin et al., Reference Najmudin, Krushelnick, Clark, Mangles, Walton, Dangor, Fritzler, Malka, Lefebvre, Gordon, Tsung and Joshi2003) in the case of a pure gas.

However, in the case of a cluster target, direct laser acceleration of the electrons contributes significantly to the overall energy gain as described in Chen et al. (Reference Chen, Yan, Li, Hu, Zhang, Wang, Hafz, Mao, Huang, Ma, Zhao, Ma, Li, Lu, Sheng, Wei, Gao and Zhang2013) and confirmed there by two-dimensional fully electromagnetic particle in cell simulations. Modeling clearly showed that in the case of the clustering gas target the electron density distribution has a large bow-like structure and the electron density exhibits a strong modulation in a broad region directly following the laser pulse. It was also demonstrated that a big size plasma cavity appears in the central area, which heats the most energetic electrons and accelerate them. It was also shown by modeling in Chen et al. (Reference Chen, Yan, Li, Hu, Zhang, Wang, Hafz, Mao, Huang, Ma, Zhao, Ma, Li, Lu, Sheng, Wei, Gao and Zhang2013) that in the case of a pure gas, the electron charge injected into wake fields and accelerated to the same energy is much lower. Simulations provided in Chen et al. (Reference Chen, Yan, Li, Hu, Zhang, Wang, Hafz, Mao, Huang, Ma, Zhao, Ma, Li, Lu, Sheng, Wei, Gao and Zhang2013) demonstrated that the direct laser acceleration (DLA) (Gahn et al., Reference Gahn, Tsakiris, Pukhov, Ter Vehn, Pretzler, Thirolf, Habs and Witte1999) constitutes a main contribution to drive electrons with large oscillation in the case of clusterized targets and could reach a value of about 80% of the total energy gain. At the same time modeling of electron acceleration for pure gas media shows that only about 1.5% of the energy gain originates from DLA, whereas the remaining gain was due to laser wake field acceleration.