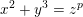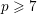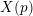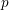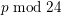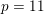1 Introduction
This paper considers the generalized Fermat equation
$$\begin{eqnarray}x^{2}+y^{3}=\pm z^{n}.\end{eqnarray}$$
Here
$n\geqslant 2$
is an integer and we are interested in non-trivial primitive integral solutions, where an integral solution is a triple
$(a,b,c)\in \mathbb{Z}^{3}$
such that
$a^{2}+b^{3}=\pm c^{n}$
; such a solution is trivial if
$abc=0$
and primitive if
$a$
,
$b$
and
$c$
are coprime. If
$n$
is odd, the sign can be absorbed into the
$n$
th power and there is only one equation to consider, whereas for even
$n$
the two sign choices lead to genuinely different equations.
It is known that for
$n\leqslant 5$
there are infinitely many primitive integral solutions, which come in finitely many families parameterized by binary forms evaluated at pairs of coprime integers satisfying some congruence conditions; see for example [Reference EdwardsEdw04] for details. It is also known that for (fixed)
$n\geqslant 6$
there are only finitely many coprime integral solutions; see [Reference Darmon and GranvilleDG95] for
$n\geqslant 7$
; the case
$n=6$
reduces to two elliptic curves of rank zero. Some non-trivial solutions are known for
$n\geqslant 7$
, namely (up to sign changes)
$$\begin{eqnarray}\displaystyle & 13^{2}+7^{3}=2^{9},\quad 71^{2}+(-17)^{3}=2^{7},\quad 21063928^{2}+(-76271)^{3}=17^{7}, & \displaystyle \nonumber\\ \displaystyle & 2213459^{2}+1414^{3}=65^{7},\quad 15312283^{2}+9262^{3}=113^{7}, & \displaystyle \nonumber\\ \displaystyle & 30042907^{2}+(-96222)^{3}=43^{8},\quad 1549034^{2}+(-15613)^{3}=-33^{8} & \displaystyle \nonumber\end{eqnarray}$$
and, for every
$n$
, there is the ‘Catalan solution’
$3^{2}+(-2)^{3}=1^{n}$
. It appears likely (and is in fact a special case of the ‘generalized Fermat conjecture’) that these are the only non-trivial primitive integral solutions for all
$n\geqslant 6$
. This has been verified for
$n=7$
[Reference Poonen, Schaefer and StollPSS07],
$n=8$
[Reference BruinBru99, Reference BruinBru03],
$n=9$
[Reference BruinBru05],
$n=10$
[Reference BrownBro12, Reference SiksekSik13] and
$n=15$
[Reference Siksek and StollSS14]. Since any integer
$n\geqslant 6$
is divisible by
$6$
,
$8$
,
$9$
,
$10$
,
$15$
,
$25$
or a prime
$p\geqslant 7$
, it suffices to deal with
$n=25$
and with
$n=p\geqslant 11$
a prime, given these results. The case
$n=25$
is considered in ongoing work by the authors of this paper; the results will be described elsewhere. So, we will from now on assume that
$n=p\geqslant 7$
(or
${\geqslant}11$
) is a prime number.
We note that an explicit version of the
$abc$
conjecture with a sufficiently good exponent would give an effective way of obtaining all solutions to (1.1). Namely, suppose that we know
$\unicode[STIX]{x1D6FE}>0$
and
$\unicode[STIX]{x1D700}<\frac{5}{61}$
such that for all coprime integers
$A,B,C$
with
$A+B=C$
, we have that
$$\begin{eqnarray}\displaystyle \max \{|A|,|B|,|C|\}\leqslant \unicode[STIX]{x1D6FE}\biggl(\mathop{\prod }_{p\mid ABC}p\biggr)^{1+\unicode[STIX]{x1D700}}, & & \displaystyle \nonumber\end{eqnarray}$$
where the product is over the prime divisors of
$ABC$
. Assume that
$a^{2}+b^{3}=\pm c^{n}$
with coprime
$a,b,c$
and set
$M=\max \{|a|^{2},|b|^{3},|c|^{n}\}$
. We then obtain that
$$\begin{eqnarray}\displaystyle M\leqslant \unicode[STIX]{x1D6FE}\biggl(\mathop{\prod }_{p\mid a^{2}b^{3}c^{n}}p\biggr)^{1+\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D6FE}\biggl(\mathop{\prod }_{p\mid abc}p\biggr)^{1+\unicode[STIX]{x1D700}}\leqslant \unicode[STIX]{x1D6FE}|abc|^{1+\unicode[STIX]{x1D700}}\leqslant \unicode[STIX]{x1D6FE}M^{(1/2+1/3+1/n)(1+\unicode[STIX]{x1D700})}, & & \displaystyle \nonumber\end{eqnarray}$$
so
$M^{1/6-1/n-(5/6+1/n)\unicode[STIX]{x1D700}}\leqslant \unicode[STIX]{x1D6FE}$
. Since
$\unicode[STIX]{x1D700}<\frac{5}{61}$
, the exponent on the left is positive as soon as
$n\geqslant 11$
and we get an effective bound on
$M$
in this case. Since (1.1) has been solved completely for
$n\leqslant 10$
, this then would give a complete solution. Whether this would result in a practical approach very much depends on the quality of the bound
$\unicode[STIX]{x1D6FE}$
in relation to
$\unicode[STIX]{x1D700}$
. (This is well known to experts; see for example [Reference CohenCoh07, Proposition 14.6.5 and Exercise 2 on p. 493].)
Our approach follows and refines the arguments of [Reference Poonen, Schaefer and StollPSS07] by combining new ideas around the modular method with recent approaches to the determination of the set of rational points on curves. We note that the existence of trivial solutions with
$c\neq 0$
and of the Catalan solutions prevents a successful application of the modular method alone; see the discussion below. Nevertheless, in the first part of this paper we will apply a refinement of it to obtain optimal
$2$
-adic and
$3$
-adic information, valid for an arbitrary prime exponent
$p$
. This information is then used as input for global methods in the second part when tackling concrete exponents. We now give a more detailed description of these two parts.
The modular method
The modular method for solving Diophantine equations typically proceeds in the following steps.
(1) To a putative solution associate a Frey elliptic curve
$E$
.(2) Use modularity and level-lowering results to show that (for a suitable prime
$p$
) the Galois representation on the
$p$
-torsion
$E[p]$
is isomorphic to the mod
$\mathfrak{p}$
representation associated to a newform
$f$
of weight
$2$
and small level
$N$
(for a suitable prime ideal
$\mathfrak{p}$
above
$p$
of the field of coefficients of
$f$
), (1.2)$$\begin{eqnarray}\overline{\unicode[STIX]{x1D70C}}_{E,p}\simeq \overline{\unicode[STIX]{x1D70C}}_{f,\mathfrak{p}}.\end{eqnarray}$$
(3) For each of the possible newforms, show that they cannot occur or find all possible associated solutions.
The most challenging step is often the very last, where we want to obtain a contradiction or list the corresponding solutions. In the proof of Fermat’s last theorem (where the modular method was born) we have
$N=2$
and there are no candidate newforms
$f$
, giving a simple contradiction. In essentially every other application of the method there are candidates for
$f$
; therefore, more work is needed to complete the argument. More precisely, we must show, for each newform
$f$
at the concrete small levels, that
$\overline{\unicode[STIX]{x1D70C}}_{E,p}\not \simeq \overline{\unicode[STIX]{x1D70C}}_{f,\mathfrak{p}}$
. This is for example the obstruction to proving Fermat’s last theorem over
$\mathbb{Q}(\sqrt{5})$
; see [Reference Freitas and SiksekFS15]. Thus, it is crucial to have methods for distinguishing Galois representations.
One such method is known as ‘the symplectic argument’; it originated in [Reference Halberstadt and KrausHK02] and it uses a ‘symplectic criterion’ (see Theorem 4.1) to decide if an isomorphism of the
$p$
-torsion of two elliptic curves having a common prime of (potentially) multiplicative reduction preserves the Weil pairing. In practice, it sometimes succeeds in distinguishing between the mod
$p$
Galois representations of elliptic curves having at least two primes of potentially multiplicative reduction. Extending the symplectic criteria to include elliptic curves with other types of reduction will clearly allow us to attack many more Diophantine equations. The main challenge in doing this comes from the fact that, in the presence of potentially good reduction, the inertia action either does not carry enough information or is hard to describe explicitly.
In the first part of this paper, we prove new symplectic criteria (Theorems 4.6 and 4.7) for certain cases of potentially good reduction at
$2$
and
$3$
and apply them to our concrete equation
$x^{2}+y^{3}=z^{p}$
. Previously the only such criterion available was [Reference Halberstadt and KrausHK02, Proposition A.2], which contains a large list of hypotheses making it hard to apply.
Remark 1.3. While completing this paper, the methods of this first part have been generalized in work of the first author [Reference FreitasFre16, Reference Freitas and KrausFK19]; furthermore, our symplectic results together with their more general variants have already allowed for applications to further Fermat-type equations, including the equation
$x^{3}+y^{3}=z^{p}$
; see [Reference FreitasFre16, Reference Bennett, Bruni and FreitasBBF18, Reference Freitas and KrausFK16].
Note that (1.1) admits, for all
$p$
, the Catalan solution mentioned above, but also the trivial solutions
$(\pm 1,1,0)$
,
$(\pm 1,0,1)$
,
$\pm (0,1,1)$
. We remark that the existence of these solutions is a powerful obstruction to the success of the modular method alone. Indeed, if by evaluating the Frey curve at these solutions we obtain a non-singular curve, then we will find the modular form corresponding to it via modularity among the forms with ‘small’ level. This means that we do obtain a ‘real’ isomorphism in (1.2), which for arbitrary
$p$
we cannot discard with current methods (except under highly favorable conditions). Nevertheless, we will apply our refinement of the symplectic argument together with a careful analysis of (1.2) restricted to certain decomposition groups to obtain finer local information, valid for an arbitrary exponent
$p$
. This information is then used as input for global methods in the second part when tackling concrete exponents.
More precisely, our goal is to reduce the study of (1.1) to the problem of determining the sets of rational points (satisfying some congruence conditions at
$2$
and
$3$
) on a small number of twists of the modular curve
$X(p)$
. For this, we apply our new symplectic criteria to reduce the list of twists that have to be considered (in the case of irreducible
$p$
-torsion on the Frey elliptic curve, which always holds for
$p\neq 7,13$
) that was obtained in [Reference Poonen, Schaefer and StollPSS07]. We also make use of fairly recent results regarding elliptic curves over
$\mathbb{Q}$
such that the image of the mod
$p$
Galois representation is contained in the normalizer of a split Cartan subgroup. Our results here are summarized in Table 5, which says that, depending on the residue class of
$p$
mod
$24$
, there are between four and 10 twists that have to be considered.
Rational points on curves
In the second part of the paper, our main goal is to give a proof of the following.
Theorem 1.4. Assume the generalized Riemann hypothesis (GRH). Then the only non-trivial primitive integral solutions of the equation
$$\begin{eqnarray}x^{2}+y^{3}=z^{11}\end{eqnarray}$$
are the Catalan solutions
$(a,b,c)=(\pm 3,-2,1)$
.
This appears to be only the second ‘hyperbolic’ instance (i.e. with
$1/p+1/q+1/r<1$
) of the generalized Fermat equation with pairwise distinct prime exponents
$p,q,r$
that could be solved completely. (The first instance was
$\{p,q,r\}=\{2,3,7\}$
, which was solved in [Reference Poonen, Schaefer and StollPSS07].)
We use several ingredients to obtain this result. One is the work of Fisher [Reference FisherFis14], who obtained an explicit description of the relevant twists of
$X(11)$
(which we determine in the first part). These curves have genus
$26$
and are therefore not amenable to any direct methods for determining their rational points. We can (and do) still use Fisher’s description to obtain local information, in particular on the location in
$\mathbb{Q}_{2}$
of the possible
$j$
-invariants of the Frey curves. The second ingredient is the observation that any rational point on one of the relevant twists of
$X(11)$
maps to a point on the elliptic curve
$X_{0}(11)$
that is defined over a certain number field
$K$
of degree (at most)
$12$
that only depends on
$E$
and such that the image of this point under the
$j$
-map is rational. This is the setting of ‘elliptic curve Chabauty’ [Reference BruinBru03]; this approach was already taken in an earlier unsuccessful attempt to solve (1.5) by David Zureick-Brown. To carry this out in the usual way, one needs to find generators of the group
$X_{0}(11)(K)$
(or at least of a subgroup of finite index), which proved to be infeasible in some of the cases. We get around this problem by invoking the third ingredient, which is ‘Selmer group Chabauty’ as described in [Reference StollSto17], applied in the elliptic curve Chabauty setting. We note that we need GRH to ensure the correctness of the class group computation for the number fields of degree
$36$
arising by adjoining to
$K$
the
$x$
-coordinate of a point of order
$2$
on
$X_{0}(11)$
. In principle, the class group can be verified unconditionally by a finite computation, which, however, would take too much time with the currently available implementations. We would like to stress that future improvements of the methods for computing class groups could result in removing the dependence of our result on GRH.
We also give some partial results for
$p=13$
, showing that the Frey curves cannot have reducible
$13$
-torsion and that the two CM curves in the list of Lemma 2.3 below can only give rise to trivial solutions.
Notation
Let
$K$
be a field of characteristic zero or a finite field. We write
$G_{K}$
for its absolute Galois group. If
$E/K$
is an elliptic curve, we denote by
$\overline{\unicode[STIX]{x1D70C}}_{E,p}$
the Galois representation of
$G_{K}$
arising from the
$p$
-torsion on
$E$
. We write
$N_{E}$
for the conductor of
$E$
when
$K$
is a
$p$
-adic field or a number field. For a modular form
$f$
and a prime
$\mathfrak{p}$
in its field of coefficients, we write
$\overline{\unicode[STIX]{x1D70C}}_{f,\mathfrak{p}}$
for its associated mod
$\mathfrak{p}$
Galois representation.
2 Irreducibility and level lowering
Suppose that
$(a,b,c)\in \mathbb{Z}^{3}$
is a solution to the equation
$$\begin{eqnarray}x^{2}+y^{3}=z^{p}\quad \text{with }p\geqslant 7\text{ prime.}\end{eqnarray}$$
Recall that
$(a,b,c)$
is trivial if
$abc=0$
and non-trivial otherwise. An integral solution is primitive if
$\gcd (a,b,c)=1$
and non-primitive otherwise. Note that (2.1) admits for all
$p$
the trivial primitive solutions
$(\pm 1,1,0)$
,
$(\pm 1,0,1)$
,
$\pm (0,1,1)$
and the pair of non-trivial primitive solutions
$(\pm 3,2,1)$
, which we refer to as the Catalan solution(s).
As in [Reference Poonen, Schaefer and StollPSS07], we can consider a putative solution
$(a,b,c)$
of (2.1) and the associated Frey elliptic curve
$$\begin{eqnarray}\displaystyle E_{(a,b,c)}:y^{2}=x^{3}+3bx-2a\quad \text{of discriminant }\unicode[STIX]{x1D6E5}=-12^{3}c^{p}. & & \displaystyle \nonumber\end{eqnarray}$$
This curve has invariants
$$\begin{eqnarray}c_{4}=-12^{2}b,\quad c_{6}=12^{3}a,\quad j=\frac{12^{3}b^{3}}{c^{p}}.\end{eqnarray}$$
We begin with a generalization and refinement of [Reference Poonen, Schaefer and StollPSS07, Lemma 6.1].
Lemma 2.3. Let
$p\geqslant 7$
and let
$(a,b,c)$
be coprime integers satisfying
$a^{2}+b^{3}=c^{p}$
and
$c\neq 0$
. Assume that the Galois representation on
$E_{(a,b,c)}[p]$
is irreducible. Then there is a quadratic twist
$E_{(a,b,c)}^{(d)}$
of
$E_{(a,b,c)}$
with
$d\in \{\pm 1,\pm 2,\pm 3,\pm 6\}$
such that
$E_{(a,b,c)}^{(d)}[p]$
is isomorphic to
$E[p]$
as a
$G_{\mathbb{Q}}$
-module, where
$E$
is one of the following seven elliptic curves (specified by their Cremona label):
$$\begin{eqnarray}\displaystyle 27a1,\quad 54a1,\quad 96a1,\quad 288a1,\quad 864a1,\quad 864b1,\quad 864c1. & & \displaystyle \nonumber\end{eqnarray}$$
For the convenience of the reader, we give equations of these elliptic curves.
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rlrl@{}}27a1 & :y^{2}+y=x^{3}-7,\qquad & 864a1 & :y^{2}=x^{3}-3x+6,\\ 54a1 & :y^{2}+xy=x^{3}-x^{2}+12x+8,\qquad & 864b1 & :y^{2}=x^{3}-24x+48,\\ 96a1, & :y^{2}=x^{3}+x^{2}-2x,\qquad & 864c1 & :y^{2}=x^{3}+24x-16,\\ 288a1 & :y^{2}=x^{3}+3x.\qquad \end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Proof. By the proof of [Reference Poonen, Schaefer and StollPSS07, Lemma 4.6], a twist
$E_{(a,b,c)}^{(d)}$
with
$d\in \{\pm 1,\pm 2,\pm 3,\pm 6\}$
of the Frey curve has conductor dividing
$12^{3}N^{\prime }$
, where
$N^{\prime }$
is the product of the primes
${\geqslant}5$
dividing
$c$
. In fact, carrying out Tate’s algorithm for
$E_{(a,b,c)}$
locally at
$2$
and
$3$
shows that the conductor can be taken to be
$2^{r}3^{s}N^{\prime }$
with
$r\in \{0,1,5\}$
and
$s\in \{1,2,3\}$
. (This uses the assumption that the solution is primitive.) Write
$E$
for this twist
$E_{(a,b,c)}^{(d)}$
.
Using level lowering as in the proof of [Reference Poonen, Schaefer and StollPSS07, Lemma 6.1], we find that
$\overline{\unicode[STIX]{x1D70C}}_{E,p}\simeq \overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}$
, where
$E^{\prime }$
is an elliptic curve of conductor
$27$
,
$54$
,
$96$
,
$288$
or
$864$
, or else
$\overline{\unicode[STIX]{x1D70C}}_{E,p}\simeq \overline{\unicode[STIX]{x1D70C}}_{f,\mathfrak{p}}$
, where
$f$
is a newform of level
$864$
with field of coefficients
$\mathbb{Q}(\sqrt{13})$
and
$\mathfrak{p}\mid p$
in this field. Let
$f$
be one of these newforms and write
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{f,\mathfrak{p}}|_{D_{3}}$
for the restriction of the Galois representation attached to
$f$
to a decomposition group at 3. We apply the Loeffler–Weinstein algorithmFootnote
1
[Reference Loeffler and WeinsteinLW12, Reference Loeffler and WeinsteinLW15] to determine
$\unicode[STIX]{x1D70C}$
and we obtain
$\unicode[STIX]{x1D70C}(I_{3})\simeq S_{3}$
, where
$I_{3}\subset D_{3}$
is the inertia group. Since
$p$
does not divide
$6=\#S_{3}$
, we also have that
$\overline{\unicode[STIX]{x1D70C}}(I_{3})\simeq S_{3}$
. On the other hand, it is well known that when
$\overline{\unicode[STIX]{x1D70C}}_{E,p}(I_{3})$
has order 6, it must be cyclic (see [Reference KrausKra90, p. 354]). Thus, we cannot have
$\overline{\unicode[STIX]{x1D70C}}_{E,p}\simeq \overline{\unicode[STIX]{x1D70C}}_{f,\mathfrak{p}}$
for any of these newforms
$f$
.
We then check that each elliptic curve with conductor
$27$
,
$54$
,
$96$
,
$288$
or
$864$
is isogenous (via an isogeny of degree prime to
$p$
) to a quadratic twist (with
$d$
in the specified set) of one of the seven curves mentioned in the statement of the lemma.◻
The following proposition shows that the irreducibility assumption in the previous lemma is automatically satisfied in most cases.
Proposition 2.4. Let
$(a,b,c)\in \mathbb{Z}^{3}$
be a non-trivial primitive solution of (2.1) for
$p\geqslant 11$
. Write
$E=E_{(a,b,c)}$
for the associated Frey curve. Then
$\overline{\unicode[STIX]{x1D70C}}_{E,p}$
is irreducible.
Proof. First assume that
$p\neq 13$
, so
$p=11$
or
$p\geqslant 17$
. Then, by Mazur’s results [Reference MazurMaz78], there is only a finite list of
$j$
-invariants of elliptic curves over
$\mathbb{Q}$
that have a reducible mod
$p$
Galois representation (see also [Reference DahmenDah08, Theorem 22]). More precisely, either we have that:
(i)
$p=11,19,43,67,163$
and the corresponding curves have integral
$j$
-invariant; or else(ii)
$p=17$
and the
$j$
-invariant is
$-17^{2}\cdot 101^{3}/2$
or
$-17\cdot 373^{3}/2^{17}$
.
Suppose that
$\overline{\unicode[STIX]{x1D70C}}_{E,p}$
is reducible; hence, the Frey curve
$E_{(a,b,c)}$
corresponds to one of the curves in (i) or (ii). Note that
$\gcd (a,b)=1$
. Suppose that we are in case (i). Since
$p\geqslant 11$
and the
$j$
-invariant is integral, it follows that
$c=\pm 1$
, which implies that we either have one of the trivial solutions
$(\pm 1,0,1)$
,
$\pm (0,1,1)$
or the ‘Catalan solution’
$(\pm 3,-2,1)$
, since the only integral points on the elliptic curves
$y^{2}=x^{3}\pm 1$
(which both have finite Mordell–Weil group) have
$x\in \{0,\pm 1,2\}$
. It remains to observe that the Frey curve associated to the Catalan solution (which is, up to quadratic twist,
$864b1$
) is the only curve in its isogeny class, so it has irreducible mod
$p$
Galois representations for all
$p$
(see [LMFDB17, Elliptic curves over
$\mathbb{Q}$
]). If we are in case (ii), then the
$17$
-adic valuation of the
$j$
-invariant contradicts (2.2).
For
$p=13$
, the claim is shown in Lemma 8.1.◻
We remark that the results of [Reference Poonen, Schaefer and StollPSS07] show that the statement of Proposition 2.4 is also true for
$p=7$
.
Note that some of the seven curves in Lemma 2.3 are realized by twists of the Frey curve evaluated at known solutions. Indeed,
$$\begin{eqnarray}\displaystyle E_{(1,0,1)}^{(6)}=27a1,\quad E_{(0,1,1)}=288a1,\quad E_{(0,-1,-1)}^{(2)}=288a2,\quad E_{(3,-2,1)}^{(-2)}=864b1 & & \displaystyle \nonumber\end{eqnarray}$$
and
$288a2$
and
$288a1$
are related by an isogeny of degree 2. The solutions
$(\pm 1,1,0)$
give rise to singular Frey curves. Note also that
$E_{(-a,b,c)}^{(-d)}=E_{(a,b,c)}^{(d)}$
, so that
$(-1,0,1)$
and
$(-3,-2,1)$
do not lead to new curves.
3 Local conditions and representations of inertia
Let
$\ell$
be a prime. We write
$\mathbb{Q}_{\ell }^{\operatorname{unr}}$
for the maximal unramified extension of
$\mathbb{Q}_{\ell }$
and
$I_{\ell }\subset G_{\mathbb{Q}_{\ell }}$
for the inertia subgroup.
Let
$E$
be an elliptic curve over
$\mathbb{Q}_{\ell }$
with potentially good reduction. Let
$p\geqslant 3$
,
$p\neq \ell$
and
$L=\mathbb{Q}_{\ell }^{\operatorname{unr}}(E[p])$
. The field
$L$
does not depend on
$p$
and is the smallest extension of
$\mathbb{Q}_{\ell }^{\operatorname{unr}}$
over which
$E$
acquires good reduction; see [Reference Serre and TateST68, § 2, Corollary 3]. We call
$L$
the inertial field of
$E/\mathbb{Q}_{\ell }$
or of
$E$
at
$\ell$
, when
$E$
is defined over
$\mathbb{Q}$
.
We write
$L_{2,96}$
and
$L_{2,288}$
for the inertial fields at
$2$
of the elliptic curves with Cremona labels
$96a1$
and
$288a1$
, respectively, and we write
$L_{3,27}$
and
$L_{3,54}$
for the inertial fields at
$3$
of the elliptic curves with Cremona labels
$27a1$
and
$54a1$
. The following theorem shows that these are all the inertial fields that can arise from certain types of elliptic curves.
Let
$H_{8}$
denote the quaternion group and
$\operatorname{Dic}_{12}\simeq C_{3}\rtimes C_{4}$
the dicyclic group of 12 elements. The properties of
$H_{8}$
and of
$\operatorname{Dic}_{12}$
that are used below can easily be verified using a suitable computer algebra system like for example Magma.
Theorem 3.1. Let
$E/\mathbb{Q}_{\ell }$
be an elliptic curve with potentially good reduction, conductor
$N_{E}$
and inertial field
$L$
. Assume further one of the following two sets of hypotheses:
(1)
$\ell =2$
,
$\operatorname{Gal}(L/\mathbb{Q}_{2}^{\operatorname{unr}})\simeq H_{8}$
and
$v_{2}(N_{E})=5$
;(2)
$\ell =3$
,
$\operatorname{Gal}(L/\mathbb{Q}_{3}^{\operatorname{unr}})\simeq \operatorname{Dic}_{12}$
and
$v_{3}(N_{E})=3$
.
Then
$L=L_{2,96}$
or
$L_{2,288}$
in case (1) and
$L=L_{3,27}$
or
$L_{3,54}$
in case (2).
Proof. For a finite extension
$K/\mathbb{Q}_{\ell }$
, we denote the Weil subgroup of the absolute Galois group
$G_{K}$
by
$W_{K}$
. We write
$W_{\ell }$
for
$W_{\mathbb{Q}_{\ell }}$
. We let
$r_{K}:K^{\times }\rightarrow W_{K}^{\operatorname{ab}}$
denote the reciprocity map from local class field theory. It allows us to identify a character
$\unicode[STIX]{x1D712}$
of
$W_{K}$
with the character
$\unicode[STIX]{x1D712}^{A}=\unicode[STIX]{x1D712}\circ r_{K}$
of
$K^{\times }$
.
There is a representation
$\unicode[STIX]{x1D70C}_{E}:W_{\ell }\rightarrow \operatorname{GL}_{2}(\mathbb{C})$
of conductor
$\ell ^{v_{\ell }(N_{E})}$
attached to
$E$
; see [Reference RohrlichRoh94, § 13] and [Reference Darmon, Diamond and TaylorDDT94, Remark 2.14]. This representation is either principal series or supercuspidal; see [Reference PacettiPac13, § 2], noting that the Steinberg representation corresponds to infinite inertia.
Hypotheses (1) and (2) both imply that
$E$
acquires good reduction over a non-abelian extension of
$\mathbb{Q}_{\ell }^{\operatorname{unr}}$
and hence
$\unicode[STIX]{x1D70C}_{E}$
is a supercuspidal representation. More precisely,
$\unicode[STIX]{x1D70C}_{E}=\operatorname{Ind}_{W_{M}}^{W_{\ell }}\unicode[STIX]{x1D712}$
, where
$M/\mathbb{Q}_{\ell }$
is a quadratic extension,
$W_{M}$
is the Weil group of
$M$
and
$\unicode[STIX]{x1D712}:W_{M}\rightarrow \mathbb{C}^{\times }$
is a character. If
$M/\mathbb{Q}_{\ell }$
is unramified, then
$\unicode[STIX]{x1D70C}_{E}|_{I_{\ell }}\simeq \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{s}$
, where
$\unicode[STIX]{x1D712}^{s}(g):=\unicode[STIX]{x1D712}(sgs^{-1})$
and
$s\in W_{\ell }$
lifts the non-trivial element of
$\operatorname{Gal}(M/\mathbb{Q}_{\ell })$
. Thus, inertia has abelian image, which is a contradiction. Therefore,
$M/\mathbb{Q}_{\ell }$
is ramified and we have that
$\unicode[STIX]{x1D70C}_{E}|_{I_{\ell }}=\operatorname{Ind}_{I_{M}}^{I_{\ell }}(\unicode[STIX]{x1D712}|_{I_{M}})$
, where
$I_{M}\subset W_{M}$
is the inertia subgroup.
Write
$\unicode[STIX]{x1D716}_{M}$
for the quadratic character of
$G_{\mathbb{Q}_{\ell }}$
fixing
$M$
. Then
$(\unicode[STIX]{x1D712}^{A}|_{\mathbb{Q}_{\ell }^{\times }})\,\cdot \,\unicode[STIX]{x1D716}_{M}^{A}=\Vert \cdot \Vert ^{-1}$
as characters of
$\mathbb{Q}_{\ell }^{\times }$
, where
$\Vert \cdot \Vert$
is the norm character. Furthermore, the conductor exponents of
$\unicode[STIX]{x1D70C}_{E}$
and
$\unicode[STIX]{x1D712}$
are related by
$\operatorname{cond}(\unicode[STIX]{x1D70C}_{E})=\operatorname{cond}(\unicode[STIX]{x1D712})+\operatorname{cond}(\unicode[STIX]{x1D716}_{M})$
; see [Reference GérardinGér78, 2.8].
We denote the maximal ideal of
$M$
by
$\mathfrak{p}$
.
Suppose hypothesis (1). From [Reference PacettiPac13, Corollary 4.1], it follows that
$M=\mathbb{Q}_{2}(d)$
with
$d=\sqrt{-1}$
or
$d=\sqrt{-5}$
; hence,
$\operatorname{cond}(\unicode[STIX]{x1D716}_{M})=2$
and
$\operatorname{cond}(\unicode[STIX]{x1D712})=5-2=3$
.
Since
$\operatorname{cond}(\unicode[STIX]{x1D712})=3$
, we have that
$\unicode[STIX]{x1D712}^{A}|_{{\mathcal{O}}_{M}^{\times }}$
factors via
$({\mathcal{O}}_{M}/\mathfrak{p}^{3})^{\times }$
, which has order
$4$
and is generated by
$2\,+\,d$
. The condition
$\unicode[STIX]{x1D712}^{A}|_{\mathbb{Z}_{2}^{\times }}=\unicode[STIX]{x1D716}_{M}^{A}$
implies that
$\unicode[STIX]{x1D712}^{A}(-1)=-1$
and thus
$\unicode[STIX]{x1D712}^{A}(2\,+\,d)=\pm i$
. We conclude that there are only two possibilities for
$\unicode[STIX]{x1D712}|_{I_{M}}$
, which are related by conjugation and hence giving the same induction
$\unicode[STIX]{x1D70C}_{E}|_{I_{2}}$
. Thus, for each possible extension
$M$
there is only one field
$L$
, so there are at most two possible fields
$L$
.
Finally, from [Reference KrausKra90, p. 357, Corollary], we see that the curves
$96a1$
and
$288a1$
satisfy hypothesis (1) and a direct computation in Magma using the
$3$
-torsion fields shows that
$L_{2,96}\neq L_{2,288}$
. This proves the theorem in case (1).
Now suppose hypothesis (2). We have
$M=\mathbb{Q}_{3}(d)$
, where
$d=\sqrt{\pm 3}$
, both fields satisfying
$v_{3}(\operatorname{disc}(M))=1$
. Thus,
$3=\operatorname{cond}(\unicode[STIX]{x1D712})+v_{3}(\operatorname{disc}(M))$
implies that
$\unicode[STIX]{x1D712}$
is of conductor
$\mathfrak{p}^{2}$
.
For both possible extensions
$M$
, the character
$\unicode[STIX]{x1D712}^{A}|_{{\mathcal{O}}_{M}^{\times }}$
factors through
$({\mathcal{O}}_{M}/\mathfrak{p}^{2})^{\times }$
, which is generated by
$-1$
and
$1+d$
of orders
$2$
and
$3$
, respectively. The condition
$\unicode[STIX]{x1D712}^{A}|_{\mathbb{Z}_{3}^{\times }}=\unicode[STIX]{x1D716}_{M}^{A}$
implies that
$\unicode[STIX]{x1D712}^{A}(-1)=-1$
and the conductor forces
$\unicode[STIX]{x1D712}^{A}(1+d)=\unicode[STIX]{x1D701}_{3}^{c}$
with
$c=1$
or
$2$
. Again, for each possible extension
$M$
there is only one field
$L$
, so there are at most two possible fields
$L$
.
Finally, from [Reference KrausKra90, p. 355, Corollary], we see that the curves
$27a1$
and
$54a1$
satisfy hypothesis (2) and again a direct computation with Magma (but now with
$5$
-torsion fields as we need
$\ell \neq p$
) shows that
$L_{3,27}\neq L_{3,54}$
. This concludes the proof.◻
In a similar way as in the preceding proof, using Magma to compute with the
$3$
-torsion fields over
$\mathbb{Q}_{2}$
, one checks that
$96a1$
and
$864c1$
have the same inertial field at
$2$
; the same is true for
$288a1$
,
$864a1$
and
$864b1$
. Similarly, working with the
$5$
-torsion fields over
$\mathbb{Q}_{3}$
, we also check that
$27a1$
,
$864b1$
and
$864c1$
have the same inertial field at
$3$
; the same is true for
$54a1$
and
$864a1$
.
Moreover, we reprove and refine Lemma 2.3 by determining the
$2$
-adic and
$3$
-adic conditions on
$a$
,
$b$
and the twists
$d\in \{\pm 1,\pm 2,\pm 3,\pm 6\}$
such that the inertial fields at
$2$
and
$3$
of
$E_{(a,b,c)}^{(d)}$
match those of the seven curves in Lemma 2.3. Indeed, the inertial field of
$E_{(a,b,c)}^{(d)}$
at
$2$
can be computed from the
$3$
-torsion field with only a finite amount of precision for the Weierstrass model of
$E_{(a,b,c)}^{(d)}/\mathbb{Q}_{2}$
. More precisely, there exists
$k$
such that if
$(x,y,z)\equiv (a,b,c)\hspace{0.2em}{\rm mod}\hspace{0.2em}2^{k}$
, then
$E_{(a,b,c)}^{(d)}$
and
$E_{(x,y,z)}^{(d)}$
have the same inertial field at
$2$
. We run over all congruence classes for
$x,y,z$
modulo
$2^{k}$
(with
$x,y$
not both even) and compute the inertial field in each case. We can use a version of Lemma 7.5 to show that
$k=3$
is sufficient. Analogously we compute the inertial fields at
$3$
using
$5$
-torsion (here
$k=2$
is sufficient).
The
$2$
-adic information can be found in Table 1. The last row is interesting: in this case the twists of the Frey curve that have good reduction at
$2$
have trace of Frobenius at
$2$
equal to
$\pm 2$
, so level lowering can never lead to a curve of conductor
$27$
(which is the only possible odd conductor dividing
$12^{3}$
), since these curves all have trace of Frobenius equal to
$0$
. The
$3$
-adic conditions can be found in Table 2. The first column in each table is just a line number; it will be useful as reference in a later section. The remaining columns contain the indicated data.
Table 1.
$2$
-adic conditions. Here
$E=E_{(a,b,c)}^{(d)}$
and
$j$
gives the possible values of the associated
$j$
-invariant, with
$t\in \mathbb{Z}_{2}$
.
Table 2.
$3$
-adic conditions;
$j$
is as in Table 1, with
$t\in \mathbb{Z}_{3}$
and
$E=E_{(a,b,c)}^{(d)}$
.
Table 3. Curves
$E$
determined by
$(a\hspace{0.2em}{\rm mod}\hspace{0.2em}36,b\hspace{0.2em}{\rm mod}\hspace{0.2em}24)$
.
Corollary 3.2. Let
$p\geqslant 11$
be a prime number. Let
$(a,b,c)\in \mathbb{Z}^{3}$
be coprime and satisfy
$a^{2}+b^{3}=c^{p}$
. Then
$b\not \equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
and, if
$c\neq 0$
, then
$c$
is not divisible by
$6$
.
Proof. Table 1 shows that
$b\equiv 4\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
is impossible. If
$c\neq 0$
, then we have a twisted Frey curve
$E_{(a,b,c)}^{(d)}$
, which if
$6\mid c$
would have to be
$p$
-congruent to
$54a1$
and to
$96a1$
at the same time; this is impossible.◻
We observe that the residue classes of
$a\hspace{0.2em}{\rm mod}\hspace{0.2em}36$
and
$b\hspace{0.2em}{\rm mod}\hspace{0.2em}24$
determine the corresponding curve in Lemma 2.3 uniquely, as given in Table 3. The line number
$i_{2}$
of Table 1 determines the row and the line number
$i_{3}$
of Table 2, the column.
A Magma script that performs the necessary computations for the results in this section is available as section3.magma at [Reference StollSto] and as supplementary material at https://doi.org/10.1112/S0010437X19007693.
4 Symplectic and anti-symplectic isomorphisms of
$p$
-torsion
Let
$p$
be a prime. Let
$K$
be a field of characteristic zero or a finite field of characteristic
$\neq p$
. Fix a primitive
$p$
th root of unity
$\unicode[STIX]{x1D701}_{p}\in \bar{K}$
. For
$E$
an elliptic curve defined over
$K$
, we write
$E[p]$
for its
$p$
-torsion
$G_{K}$
-module,
$\overline{\unicode[STIX]{x1D70C}}_{E,p}:G_{K}\rightarrow \operatorname{Aut}(E[p])$
for the corresponding Galois representation and
$e_{E,p}$
for the Weil pairing on
$E[p]$
. We say that an
$\mathbb{F}_{p}$
-basis
$(P,Q)$
of
$E[p]$
is symplectic if
$e_{E,p}(P,Q)=\unicode[STIX]{x1D701}_{p}$
.
Now let
$E/K$
and
$E^{\prime }/K$
be two elliptic curves over some field
$K$
and let
$\unicode[STIX]{x1D719}:E[p]\rightarrow E^{\prime }[p]$
be an isomorphism of
$G_{K}$
-modules. Then there is an element
$r(\unicode[STIX]{x1D719})\in \mathbb{F}_{p}^{\times }$
such that
$$\begin{eqnarray}\displaystyle e_{E^{\prime },p}(\unicode[STIX]{x1D719}(P),\unicode[STIX]{x1D719}(Q))=e_{E,p}(P,Q)^{r(\unicode[STIX]{x1D719})}\quad \text{for all }P,Q\in E[p]. & & \displaystyle \nonumber\end{eqnarray}$$
Note that for any
$a\in \mathbb{F}_{p}^{\times }$
, we have
$r(a\unicode[STIX]{x1D719})=a^{2}r(\unicode[STIX]{x1D719})$
. So, up to scaling
$\unicode[STIX]{x1D719}$
, only the class of
$r(\unicode[STIX]{x1D719})$
modulo squares matters. We say that
$\unicode[STIX]{x1D719}$
is a symplectic isomorphism if
$r(\unicode[STIX]{x1D719})$
is a square in
$\mathbb{F}_{p}^{\times }$
and an anti-symplectic isomorphism if
$r(\unicode[STIX]{x1D719})$
is a non-square. Fix a non-square
$r_{p}\in \mathbb{F}_{p}^{\times }$
. We say that
$\unicode[STIX]{x1D719}$
is strictly symplectic if
$r(\unicode[STIX]{x1D719})=1$
and strictly anti-symplectic if
$r(\unicode[STIX]{x1D719})=r_{p}$
. Finally, we say that
$E[p]$
and
$E^{\prime }[p]$
are symplectically (or anti-symplectically) isomorphic if there exists a symplectic (or anti-symplectic) isomorphism of
$G_{K}$
-modules between them. Note that it is possible that
$E[p]$
and
$E^{\prime }[p]$
are both symplectically and anti-symplectically isomorphic; this will be the case if and only if
$E[p]$
admits an anti-symplectic automorphism.
Note that an isogeny
$\unicode[STIX]{x1D719}:E\rightarrow E^{\prime }$
of degree
$n$
not divisible by
$p$
restricts to an isomorphism
$\unicode[STIX]{x1D719}:E[p]\rightarrow E^{\prime }[p]$
such that
$r(\unicode[STIX]{x1D719})=n$
. This can be seen from the following computation, where
$\hat{\unicode[STIX]{x1D719}}$
is the dual isogeny and where we use the fact that
$\unicode[STIX]{x1D719}$
and
$\hat{\unicode[STIX]{x1D719}}$
are adjoint with respect to the Weil pairing:
$$\begin{eqnarray}\displaystyle e_{E^{\prime },p}(\unicode[STIX]{x1D719}(P),\unicode[STIX]{x1D719}(Q))=e_{E,p}(P,\hat{\unicode[STIX]{x1D719}}\unicode[STIX]{x1D719}(Q))=e_{E,p}(P,nQ)=e_{E,p}(P,Q)^{n}. & & \displaystyle \nonumber\end{eqnarray}$$
In particular,
$\unicode[STIX]{x1D719}$
induces a symplectic isomorphism on
$p$
-torsion if
$(n/p)=1$
and an anti-symplectic isomorphism if
$(n/p)=-1$
.
For an elliptic curve
$E/\mathbb{Q}$
, there are two modular curves
$X_{E}^{+}(p)=X_{E}(p)$
and
$X_{E}^{-}(p)$
defined over
$\mathbb{Q}$
that parameterize pairs
$(E^{\prime },\unicode[STIX]{x1D719})$
consisting of an elliptic curve
$E^{\prime }$
and a strictly symplectic (respectively, strictly anti-symplectic) isomorphism
$\unicode[STIX]{x1D719}:E^{\prime }[p]\rightarrow E[p]$
. These two curves are twists of the standard modular curve
$X(p)$
that classifies pairs
$(E^{\prime },\unicode[STIX]{x1D719})$
such that
$\unicode[STIX]{x1D719}:E^{\prime }[p]\rightarrow M$
is a symplectic isomorphism, with
$M=\unicode[STIX]{x1D707}_{p}\times \mathbb{Z}/p\mathbb{Z}$
and a certain symplectic pairing on
$M$
; compare [Reference Poonen, Schaefer and StollPSS07, Definition 4.1]. As explained there, the existence of a non-trivial primitive solution
$(a,b,c)$
of (2.1) implies that some twisted Frey curve
$E_{(a,b,c)}^{(d)}$
gives rise to a rational point on one of the modular curves
$X_{E}(p)$
or
$X_{E}^{-}(p)$
, where
$E$
is one of the seven elliptic curves in Lemma 2.3. Thus, the resolution of (2.1) for any particular
$p\geqslant 11$
is reduced to the determination of the sets of rational points on 14 modular curves
$X_{E}(p)$
and
$X_{E}^{-}(p)$
.
We remark that taking quadratic twists by
$d$
of the pairs
$(E^{\prime },\unicode[STIX]{x1D719})$
induces canonical isomorphisms
$X_{E^{(d)}}(p)\simeq X_{E}(p)$
and
$X_{E^{(d)}}^{-}(p)\simeq X_{E}^{-}(p)$
. Also note that each twist
$X_{E}(p)$
has a ‘canonical rational point’ representing
$(E,\operatorname{id}_{E[p]})$
. On the other hand, it is possible that the twist
$X_{E}^{-}(p)$
does not have any rational point. If
$E^{\prime }$
is isogenous to
$E$
by an isogeny
$\unicode[STIX]{x1D719}$
of degree
$n$
prime to
$p$
, then
$(E^{\prime },\unicode[STIX]{x1D719}|_{E^{\prime }[p]})$
gives rise to a rational point on
$X_{E}(p)$
when
$(n/p)=+1$
and on
$X_{E}^{-}(p)$
when
$(n/p)=-1$
.
In this section we study carefully when isomorphisms of the torsion modules of elliptic curves preserve the Weil pairing. This will allow us to discard some of these 14 modular curves by local considerations. Of course, from the last paragraph of § 2, it follows that it is impossible to discard
$X_{27a1}(p)$
,
$X_{288a1}(p)$
or
$X_{864b1}(p)$
, since they have rational points arising from the known solutions. Moreover, if
$(2/p)=-1$
, we also have a rational point on
$X_{288a1}^{-}(p)\simeq X_{288a2}(p)$
.
We now recall a criterion from [Reference Kraus and OesterléKO92] to decide, under certain hypotheses, whether
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic, which will be useful later.
Theorem 4.1 [Reference Kraus and OesterléKO92, Proposition 2].
Let
$E$
,
$E^{\prime }$
be elliptic curves over
$\mathbb{Q}$
with minimal discriminants
$\unicode[STIX]{x1D6E5}$
,
$\unicode[STIX]{x1D6E5}^{\prime }$
. Let
$p$
be a prime such that
$\overline{\unicode[STIX]{x1D70C}}_{E,p}\simeq \overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}$
. Suppose that
$E$
and
$E^{\prime }$
have multiplicative reduction at a prime
$\ell \neq p$
and that
$p\nmid v_{\ell }(\unicode[STIX]{x1D6E5})$
. Then
$p\nmid v_{\ell }(\unicode[STIX]{x1D6E5}^{\prime })$
and the representations
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic if and only if
$v_{\ell }(\unicode[STIX]{x1D6E5})/v_{\ell }(\unicode[STIX]{x1D6E5}^{\prime })$
is a square mod
$p$
.
The objective of this section is to deduce similar results for certain types of additive reduction at
$\ell$
(see also [Reference FreitasFre16]), which we will then apply to our Diophantine problem in Theorem 5.1.
We will need the following auxiliary result.
Lemma 4.2. Let
$E$
and
$E^{\prime }$
be two elliptic curves defined over a field
$K$
and with isomorphic
$p$
-torsion. Fix symplectic bases for
$E[p]$
and
$E^{\prime }[p]$
. Let
$\unicode[STIX]{x1D719}:E[p]\rightarrow E^{\prime }[p]$
be an isomorphism of
$G_{K}$
-modules and write
$M_{\unicode[STIX]{x1D719}}$
for the matrix representing
$\unicode[STIX]{x1D719}$
with respect to these bases.
Then
$\unicode[STIX]{x1D719}$
is a symplectic isomorphism if and only if
$\det (M_{\unicode[STIX]{x1D719}})$
is a square mod
$p$
; otherwise
$\unicode[STIX]{x1D719}$
is anti-symplectic.
Moreover, if
$\overline{\unicode[STIX]{x1D70C}}_{E,p}(G_{K})$
is a non-abelian subgroup of
$\operatorname{GL}_{2}(\mathbb{F}_{p})$
, then
$E[p]$
and
$E^{\prime }[p]$
cannot be simultaneously symplectically and anti-symplectically isomorphic.
Proof. This is [Reference FreitasFre16, Lemma 1]. ◻
4.1 A little bit of group theory
Recall that
$H_{8}$
denotes the quaternion group and
$\operatorname{Dic}_{12}\simeq C_{3}\rtimes C_{4}$
is the dicyclic group of 12 elements; these are the two Galois groups occurring in Theorem 3.1. We now consider them as subgroups of
$\operatorname{GL}_{2}(\mathbb{F}_{p})$
.
Write
$D_{n}$
for the dihedral group with
$2n$
elements and
$S_{n}$
and
$A_{n}$
for the symmetric and alternating groups on
$n$
letters. We write
$C(G)$
for the center of a group
$G$
. If
$H$
is a subgroup of
$G$
, then we write
$N_{G}(H)$
for its normalizer and
$C_{G}(H)$
for its centralizer in
$G$
.
Lemma 4.3. Let
$p\geqslant 3$
and
$G=\operatorname{GL}_{2}(\mathbb{F}_{p})$
. Let
$H\subset G$
be a subgroup isomorphic to
$H_{8}$
. Then the group
$\operatorname{Aut}(H)$
of automorphisms of
$H$
satisfies
$$\begin{eqnarray}\displaystyle N_{G}(H)/C(G)\simeq \operatorname{Aut}(H)\simeq S_{4}. & & \displaystyle \nonumber\end{eqnarray}$$
Moreover:
(a) if
$(2/p)=1$
, then all the matrices in
$N_{G}(H)$
have square determinant;(b) if
$(2/p)=-1$
, then the matrices in
$N_{G}(H)$
with square determinant correspond to the subgroup of
$\operatorname{Aut}(H)$
isomorphic to
$A_{4}$
.
Proof. There is only one faithful two-dimensional representation of
$H_{8}$
over
$\mathbb{F}_{p}$
(
$H_{8}$
has exactly one irreducible two-dimensional representation and any direct sum of one-dimensional representations factors over the maximal abelian quotient), so all subgroups
$H$
as in the statement are conjugate. We can therefore assume that
$H$
is the subgroup generated by
$$\begin{eqnarray}\displaystyle g_{1}=\left(\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right)\quad \text{and}\quad g_{2}=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FD}\\ \unicode[STIX]{x1D6FD} & -\unicode[STIX]{x1D6FC}\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \mathbb{F}_{p}^{\times }$
satisfy
$\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2}=-1$
. It is easy to see that the elements of
$H$
span the
$\mathbb{F}_{p}$
-vector space of
$2\times 2$
matrices, which implies that
$C_{G}(H)=C(G)$
.
Now the action by conjugation induces a canonical group homomorphism
$N_{G}(H)\rightarrow \operatorname{Aut}(H)$
with kernel
$C_{G}(H)=C(G)$
, leading to an injection
$N_{G}(H)/C(G)\rightarrow \operatorname{Aut}(H)$
. To see that this map is also surjective (and hence an isomorphism), note that
$N_{G}(H)$
contains the matrices
$$\begin{eqnarray}\displaystyle n_{1}=\left(\begin{array}{@{}cc@{}}1 & -1\\ 1 & 1\end{array}\right)\quad \text{and}\quad n_{2}=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FD}-1\\ \unicode[STIX]{x1D6FD}+1 & -\unicode[STIX]{x1D6FC}\end{array}\right) & & \displaystyle \nonumber\end{eqnarray}$$
and that the subgroup of
$N_{G}(H)/C(G)$
generated by the images of
$H$
and of these matrices has order
$24$
. Since it can be easily checked that
$\operatorname{Aut}(H_{8})\simeq S_{4}$
, the first claim follows.
Note that
$A_{4}$
is the unique subgroup of
$S_{4}$
of index 2. The determinant induces a homomorphism
$S_{4}\simeq N_{G}(H)/C(G)\rightarrow \mathbb{F}_{p}^{\times }/\mathbb{F}_{p}^{\times 2}$
whose kernel is either
$S_{4}$
or
$A_{4}$
. Since
$H\subset \operatorname{SL}_{2}(\mathbb{F}_{p})$
and all matrices in
$C(G)$
have square determinant, it remains to compute
$\det (n_{1})$
and
$\det (n_{2})$
. But
$\det (n_{1})=2$
and
$$\begin{eqnarray}\displaystyle \det (n_{2})=-\unicode[STIX]{x1D6FC}^{2}-(\unicode[STIX]{x1D6FD}-1)(\unicode[STIX]{x1D6FD}+1)=-\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2}+1=2 & & \displaystyle \nonumber\end{eqnarray}$$
as well. The result is now clear. ◻
Lemma 4.4. Let
$p\geqslant 5$
and
$G=\operatorname{GL}_{2}(\mathbb{F}_{p})$
. Let
$H\subset G$
be a subgroup isomorphic to
$\operatorname{Dic}_{12}$
. Then the group of automorphisms of
$H$
satisfies
$$\begin{eqnarray}\displaystyle N_{G}(H)/C(G)\simeq \operatorname{Aut}(H)\simeq D_{6}. & & \displaystyle \nonumber\end{eqnarray}$$
Moreover:
(a) if
$(3/p)=1$
, then all the matrices in
$N_{G}(H)$
have square determinant;(b) if
$(3/p)=-1$
, then the matrices in
$N_{G}(H)$
with square determinant correspond to the subgroup of inner automorphisms in
$\operatorname{Aut}(H)$
.
Proof. The proof is similar to that of Lemma 4.3. Again, there is a unique conjugacy class of subgroups isomorphic to
$\operatorname{Dic}_{12}$
in
$G$
, so we can take
$H$
to be the subgroup generated by
$$\begin{eqnarray}\displaystyle g_{1}=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FD}\\ \unicode[STIX]{x1D6FD} & 1-\unicode[STIX]{x1D6FC}\end{array}\right)\quad \text{and}\quad g_{2}=\left(\begin{array}{@{}cc@{}}0 & -1\\ 1 & 0\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \mathbb{F}_{p}$
satisfy
$\unicode[STIX]{x1D6FD}^{2}=-\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}-1$
with
$\unicode[STIX]{x1D6FD}\neq 0$
. As before, one sees that
$C_{G}(H)=C(G)$
, so we again have an injective group homomorphism
$N_{G}(H)/C(G)\rightarrow \operatorname{Aut}(H)\simeq D_{6}$
.
The normalizer
$N_{G}(H)$
contains the matrix
$$\begin{eqnarray}\displaystyle M=\left(\begin{array}{@{}cc@{}}2\unicode[STIX]{x1D6FC}-1 & 2\unicode[STIX]{x1D6FD}\\ 2\unicode[STIX]{x1D6FD} & 1-2\unicode[STIX]{x1D6FC}\end{array}\right) & & \displaystyle \nonumber\end{eqnarray}$$
and the images of
$H$
and
$M$
generate a subgroup of order
$12$
of
$N_{G}(H)/C(G)$
, which shows that the homomorphism is also surjective.
Since
$H\subset \operatorname{SL}_{2}(\mathbb{F}_{p})$
, the determinant of any element of
$N_{G}(H)$
that induces an inner automorphism of
$H$
is a square. Also, the inner automorphism group of
$H$
has order
$6$
, so the homomorphism
$D_{6}\simeq N_{G}(H)/C(G)\rightarrow \mathbb{F}_{p}^{\times }/\mathbb{F}_{p}^{\times 2}$
induced by the determinant is either trivial or has kernel equal to the group of inner automorphisms. This depends on whether the determinant of
$M$
,
$$\begin{eqnarray}\displaystyle \det (M)=-4\unicode[STIX]{x1D6FC}^{2}+4\unicode[STIX]{x1D6FC}-1-4\unicode[STIX]{x1D6FD}^{2}=3, & & \displaystyle \nonumber\end{eqnarray}$$
is a square in
$\mathbb{F}_{p}$
or not.◻
4.2 The symplectic criteria
Let
$E$
,
$E^{\prime }$
be elliptic curves over
$\mathbb{Q}_{\ell }$
with potentially good reduction and respective inertial fields
$L=\mathbb{Q}_{\ell }^{\operatorname{unr}}(E[p])$
and
$L^{\prime }=\mathbb{Q}_{\ell }^{\operatorname{unr}}(E^{\prime }[p])$
. Suppose that
$E[p]$
and
$E^{\prime }[p]$
are isomorphic as
$G_{\mathbb{Q}_{\ell }}$
-modules; in particular,
$L=L^{\prime }$
. Write
$I=\operatorname{Gal}(L/\mathbb{Q}_{\ell }^{\operatorname{unr}})$
and recall that
$I_{\ell }$
denotes the inertia subgroup of
$G_{\mathbb{Q}_{\ell }}$
.
If
$I$
is not abelian, then Lemma 4.2 applied with
$K=\mathbb{Q}_{\ell }^{\operatorname{unr}}$
says that
$E[p]$
and
$E^{\prime }[p]$
cannot be both symplectically and anti-symplectically isomorphic
$I_{\ell }$
-modules. Since the symplectic type of an isomorphism
$\unicode[STIX]{x1D719}:E[p]\rightarrow E^{\prime }[p]$
does not depend on whether it is considered as an isomorphism of
$G_{\mathbb{Q}_{\ell }}$
-modules or of
$I_{\ell }$
-modules, we can conclude that
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic as
$G_{\mathbb{Q}_{\ell }}$
-modules if and only if they are symplectically isomorphic as
$I_{\ell }$
-modules. In Theorem 4.6, we provide a criterion to decide between the two possibilities when
$\ell =2$
and
$I\simeq H_{8}$
. In Theorem 4.7, we do the same for
$\ell =3$
and
$I\simeq \operatorname{Dic}_{12}$
.
We now introduce notation and recall facts from [Reference Serre and TateST68, § 2] and [Reference Freitas and KrausFK19]. We note that [Reference Freitas and KrausFK19], which originated as a continuation of the work done here, contains criteria similar to those stated below and also improvements of the second parts of Theorems 4.6 and 4.7.
Let
$p$
and
$\ell$
be primes such that
$p\geqslant 3$
and
$\ell \neq p$
. Let
$E/\mathbb{Q}_{\ell }$
,
$L$
and
$I$
be as above. Write
$\overline{E}$
for the elliptic curve over
$\overline{\mathbb{F}}_{\ell }$
obtained by reduction of a minimal model of
$E/L$
and
$\unicode[STIX]{x1D711}:E[p]\rightarrow \overline{E}[p]$
for the reduction morphism, which preserves the Weil pairing. Let
$\operatorname{Aut}(\overline{E})$
be the automorphism group of
$\overline{E}$
over
$\overline{\mathbb{F}}_{\ell }$
and write
$\unicode[STIX]{x1D713}:\operatorname{Aut}(\overline{E})\rightarrow \operatorname{GL}(\overline{E}[p])$
for the natural injective morphism. The action of
$I$
on
$L$
induces an injective morphism
$\unicode[STIX]{x1D6FE}_{E}:I\rightarrow \operatorname{Aut}(\overline{E})$
, so that
$\overline{E}[p]$
is an
$I$
-module via
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FE}_{E}$
in a natural way. Then
$\unicode[STIX]{x1D711}$
is actually an isomorphism of
$I$
-modules: for
$\unicode[STIX]{x1D70E}\in I$
, we have
$$\begin{eqnarray}\unicode[STIX]{x1D711}\circ \overline{\unicode[STIX]{x1D70C}}_{E,p}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE}_{E}(\unicode[STIX]{x1D70E}))\circ \unicode[STIX]{x1D711}.\end{eqnarray}$$
Theorem 4.6. Let
$p\geqslant 3$
be a prime. Let
$E$
and
$E^{\prime }$
be elliptic curves over
$\mathbb{Q}_{2}$
with potentially good reduction. Suppose that they have the same inertial field and that
$I\simeq H_{8}$
. Then
$E[p]$
and
$E^{\prime }[p]$
are isomorphic as
$I_{2}$
-modules. Moreover:
(1) if
$(2/p)=1$
, then
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic
$I_{2}$
-modules;(2) if
$(2/p)=-1$
, then
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic
$I_{2}$
-modules if and only if
$E[3]$
and
$E^{\prime }[3]$
are symplectically isomorphic
$I_{2}$
-modules.
Proof. Note that
$L=\mathbb{Q}_{2}^{\operatorname{unr}}(E[p])$
is the smallest extension of
$\mathbb{Q}_{2}^{\operatorname{unr}}$
over which
$E$
acquires good reduction and that the reduction map
$\unicode[STIX]{x1D711}$
is an isomorphism between the
$\mathbb{F}_{p}$
-vector spaces
$E[p](L)$
and
$\overline{E}[p](\overline{\mathbb{F}}_{2})$
. By hypothesis,
$E^{\prime }$
also has good reduction over
$L$
and
$\unicode[STIX]{x1D711}^{\prime }$
is an isomorphism. Applying (4.5) to both
$E$
and
$E^{\prime }$
, we see that
$E[p]$
and
$E^{\prime }[p]$
are isomorphic
$I_{2}$
-modules if we can show that
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FE}_{E}$
and
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FE}_{E^{\prime }}$
are isomorphic as representations into
$\operatorname{GL}(\overline{E}[p])$
and
$\operatorname{GL}(\overline{E}^{\prime }[p])$
, respectively.
Since the map
$\unicode[STIX]{x1D6FE}_{E}:I\rightarrow \operatorname{Aut}(\overline{E})$
is injective, we have
$H_{8}\subset \operatorname{Aut}(\overline{E})$
. From [Reference SilvermanSil09, Theorem III.10.1 and Example A.1 on p. 414], we see that
$\operatorname{Aut}(\overline{E})\simeq \operatorname{SL}_{2}(\mathbb{F}_{3})$
and
$j(\overline{E})=0$
. Similarly, we conclude that
$j(\overline{E}^{\prime })=0$
. Thus,
$\overline{E}$
and
$\overline{E}^{\prime }$
are isomorphic over
$\overline{\mathbb{F}}_{2}$
.
So, we can fix minimal models of
$E/L$
and
$E^{\prime }/L$
both reducing to the same
$\overline{E}$
.
There is only one (hence normal) subgroup
$H$
of
$\operatorname{SL}_{2}(\mathbb{F}_{3})$
isomorphic to
$H_{8}$
. Therefore, we have that
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE}_{E}(I))=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE}_{E^{\prime }}(I))=\unicode[STIX]{x1D713}(H)$
in
$\operatorname{GL}(\overline{E}[p])$
and there must be an automorphism
$\unicode[STIX]{x1D6FC}\in \operatorname{Aut}(\unicode[STIX]{x1D713}(H))$
such that
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FE}_{E}=\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FE}_{E^{\prime }}$
. The first statement of Lemma 4.3 shows that there is
$g\in \operatorname{GL}(\overline{E}[p])$
such that
$\unicode[STIX]{x1D6FC}(x)=gxg^{-1}$
for all
$x\in \unicode[STIX]{x1D713}(H)$
; thus,
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FE}_{E}$
and
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FE}_{E^{\prime }}$
are isomorphic representations.
Fix a symplectic basis of
$\overline{E}[p]$
, thus identifying
$\operatorname{GL}(\overline{E}[p])$
with
$\operatorname{GL}_{2}(\mathbb{F}_{p})$
. Let
$M_{g}$
denote the matrix representing
$g$
and observe that
$M_{g}\in N_{\operatorname{GL}_{2}(\mathbb{F}_{p})}(\unicode[STIX]{x1D713}(H))$
. Lift the fixed basis to bases of
$E[p]$
and
$E^{\prime }[p]$
via the corresponding reduction maps
$\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}^{\prime }$
. The lifted bases are symplectic. The matrices representing
$\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}^{\prime }$
with respect to these bases are the identity matrix in both cases. From (4.5), it follows that
$\overline{\unicode[STIX]{x1D70C}}_{E,p}(\unicode[STIX]{x1D70E})=M_{g}\overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}(\unicode[STIX]{x1D70E})M_{g}^{-1}$
for all
$\unicode[STIX]{x1D70E}\in I$
. Moreover,
$M_{g}$
represents some
$I_{2}$
-module isomorphism
$\unicode[STIX]{x1D719}:E[p]\rightarrow E^{\prime }[p]$
and, from Lemma 4.2, we have that
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic if and only if
$\det (M_{g})$
is a square mod
$p$
.
Part (1) then follows from Lemma 4.3(a).
We now prove (2). From Lemma 4.3(b), we see that
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic if and only if
$\unicode[STIX]{x1D6FC}$
is an automorphism in
$A_{4}\subset \operatorname{Aut}(\unicode[STIX]{x1D713}(H))\simeq S_{4}$
. Note that these are precisely the inner automorphisms or automorphisms of order 3. Note also that all the elements in
$S_{4}$
that are not in
$A_{4}$
are not inner and have order 2 or 4. For each
$p$
, the map
$\unicode[STIX]{x1D6FC}_{p}=\unicode[STIX]{x1D713}^{-1}\circ \unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D713}$
defines an automorphism of
$\unicode[STIX]{x1D6FE}_{E}(I)=H\subset \operatorname{Aut}(\overline{E})$
satisfying
$\unicode[STIX]{x1D6FC}_{p}\circ \unicode[STIX]{x1D6FE}_{E^{\prime }}=\unicode[STIX]{x1D6FE}_{E}$
.
We note that the unique automorphism of
$\operatorname{SL}_{2}(\mathbb{F}_{3})$
which fixes the order-8 subgroup pointwise is the identity. Since
$\unicode[STIX]{x1D6FE}_{E}$
,
$\unicode[STIX]{x1D6FE}_{E^{\prime }}$
are independent of
$p$
, it follows that
$\unicode[STIX]{x1D6FC}_{p}$
is the same for all
$p$
. Since
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}_{p}$
have the same order and are simultaneously inner or not, it follows that this property is independent of the prime
$p$
satisfying
$(2/p)=-1$
. This shows that
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic
$I_{2}$
-modules if and only if
$E[\ell ]$
and
$E^{\prime }[\ell ]$
are symplectically isomorphic
$I_{2}$
-modules for one (hence all)
$\ell$
satisfying
$(2/\ell )=-1$
. In particular, we can take
$\ell =3$
and the result follows.◻
Theorem 4.7. Let
$p\geqslant 5$
be a prime. Let
$E$
and
$E^{\prime }$
be elliptic curves over
$\mathbb{Q}_{3}$
with potentially good reduction. Suppose that they have the same inertial field and that
$I\simeq \operatorname{Dic}_{12}$
. Then
$E[p]$
and
$E^{\prime }[p]$
are isomorphic as
$I_{3}$
-modules. Moreover:
(1) if
$(3/p)=1$
, then
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic
$I_{3}$
-modules;(2) if
$(3/p)=-1$
, then
$E[p]$
and
$E^{\prime }[p]$
are symplectically isomorphic
$I_{3}$
-modules if and only if
$E[5]$
and
$E^{\prime }[5]$
are symplectically isomorphic
$I_{3}$
-modules.
Proof. This proof is analogous to the proof of Theorem 4.6, with 3 and 5 taking over the roles of 2 and 3, respectively.
In this case
$\operatorname{Aut}(\overline{E})\simeq \operatorname{Dic}_{12}$
[Reference SilvermanSil09, Theorem III.10.1], so
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE}_{E}(I))=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE}_{E^{\prime }}(I))=\unicode[STIX]{x1D713}(\operatorname{Aut}(\overline{E}))$
. We use Lemma 4.4 instead of Lemma 4.3 to conclude that
$\unicode[STIX]{x1D6FC}$
is given by a matrix
$M_{g}$
. Lemma 4.4(a) concludes the proof of (1) and Lemma 4.4(b) the proof of (2).◻
5 Reducing the number of relevant twists
Using the results of the previous section we will now show that one can discard some of the 14 twists of
$X(p)$
, depending on the residue class of
$p$
mod
$24$
.
Theorem 5.1. Let
$p\geqslant 11$
be prime and let
$(a,b,c)\in \mathbb{Z}^{3}$
be a non-trivial primitive solution of
$x^{2}+y^{3}=z^{p}$
. Then the associated Frey curve
$E_{(a,b,c)}^{(d)}$
gives rise to a rational point on one of the twists of
$X(p)$
listed in Table 4, depending on the residue class of
$p$
mod
$24$
.
Table 4. Relevant twists of
$X(p)$
.
Proof. Note that among the seven elliptic curves in Lemma 2.3,
$27a1$
and
$288a1$
have complex multiplication by
$\mathbb{Z}[\unicode[STIX]{x1D714}]$
and
$\mathbb{Z}[i]$
, respectively, where
$\unicode[STIX]{x1D714}$
is a primitive cube root of unity. The isogeny classes of the first four curves in the list of Lemma 2.3 have the following structure (the edges are labeled by the degree of the isogeny):
whereas the isogeny classes of the last three curves are trivial; see [Reference CremonaCre97, Table 1] or [LMFDB17]. Since
$27a3$
is the quadratic twist by
$-3$
of
$27a1$
, we have
$X_{27a1}(p)\simeq X_{27a3}(p)$
. If
$(3/p)=-1$
, then the
$3$
-isogeny between these curves induces an anti-symplectic isomorphism of the mod
$p$
Galois representations and we have that
$X_{27a1}(p)\simeq X_{27a3}(p)\simeq X_{27a1}^{-}(p)$
. So, when
$p\equiv 5,7,17,19\hspace{0.2em}{\rm mod}\hspace{0.2em}24$
, we only have one twist of
$X(p)$
coming from
$27a1$
. (For the other CM curve
$288a1$
, this argument does not apply, since it is its own
$-1$
-twist.)
For the twists associated to the curves
$54a1$
and
$96a1$
, we apply Theorem 4.1. From Table 1, we see that the Frey curve
$E_{(a,b,c)}^{(d)}$
has multiplicative reduction at
$\ell =2$
if and only if
$c$
is even and
$d=\pm 1,\pm 3$
, in which case its minimal discriminant is
$\unicode[STIX]{x1D6E5}=2^{-6}3^{3}d^{6}c^{p}$
(compare the proof of [Reference Poonen, Schaefer and StollPSS07, Lemma 4.6]); in particular,
$v_{2}(\unicode[STIX]{x1D6E5})\equiv -6\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
. Then the Frey curve must be
$p$
-congruent to
$E=54a1$
, which is the only curve in our list that has multiplicative reduction at
$2$
. On the other hand,
$\unicode[STIX]{x1D6E5}_{E}=-2^{3}3^{9}$
, so that the isomorphism between
$E_{(a,b,c)}^{(d)}[p]$
and
$E[p]$
is symplectic if and only if
$(-2/p)=1$
. So, for
$p\equiv 1,11,17,19\hspace{0.2em}{\rm mod}\hspace{0.2em}24$
, we get rational points at most on
$X_{54a1}(p)$
, whereas for
$p\equiv 5,7,13,23\hspace{0.2em}{\rm mod}\hspace{0.2em}24$
, we get rational points at most on
$X_{54a1}^{-}(p)$
(which is
$X_{54a2}(p)$
when
$(3/p)=-1$
). Similarly, Table 2 shows that the Frey curve has multiplicative reduction at
$\ell =3$
if and only if
$c$
is divisible by
$3$
. In this case
$d=\pm 3,\pm 6$
and the minimal discriminant is
$\unicode[STIX]{x1D6E5}=2^{6}3^{-3}c^{p}$
(see again the proof of [Reference Poonen, Schaefer and StollPSS07, Lemma 4.6]), so
$v_{3}(\unicode[STIX]{x1D6E5})\equiv -3\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
. Since
$E=96a1$
is the only curve in our list that has multiplicative reduction at
$3$
, the Frey curve must be
$p$
-congruent to it. Since
$\unicode[STIX]{x1D6E5}_{E}=2^{6}3^{2}$
, we find that the isomorphism between
$E_{(a,b,c)}^{(d)}[p]$
and
$E[p]$
is symplectic if and only if
$(-6/p)=1$
. So, for
$p\equiv 1,5,7,11\hspace{0.2em}{\rm mod}\hspace{0.2em}24$
, we get rational points at most on
$X_{96a1}(p)$
, whereas for
$p\equiv 13,17,19,23\hspace{0.2em}{\rm mod}\hspace{0.2em}24$
, we get rational points at most on
$X_{96a1}^{-}(p)$
(which is
$X_{96a2}$
when
$(2/p)=-1$
).
Now we consider the curves
$E$
with conductor at
$2$
equal to
$2^{5}$
; these are
$96a1$
,
$288a1$
,
$864a1$
,
$864b1$
and
$864c1$
. They all have potentially good reduction at
$2$
and
$I=\operatorname{Gal}(L/\mathbb{Q}_{2}^{\operatorname{unr}})\simeq H_{8}$
. As explained at the beginning of § 4.2, the fact that
$H_{8}$
is non-abelian implies that the isomorphism of mod
$p$
Galois representations is symplectic if and only if it is symplectic on the level of inertia groups. It follows from Theorem 4.6(1) that in the case that
$(2/p)=1$
, the isomorphism
$E_{(a,b,c)}^{(d)}[p]\simeq E[p]$
can only be symplectic. So, when
$p\equiv 1,7,17,23\hspace{0.2em}{\rm mod}\hspace{0.2em}24$
, we can exclude the ‘minus’ twists
$X_{E}^{-}(p)$
for
$E\in \{96a1,288a1,864a1,864b1,864c1\}$
.
We can use a similar argument over
$\mathbb{Q}_{3}$
for the curves
$E$
in our list whose conductor at
$3$
is
$3^{3}$
, namely
$E\in \{27a1,54a1,864a1,864b1,864c1\}$
. They all have potentially good reduction and
$I\simeq \operatorname{Dic}_{12}$
. By Theorem 4.7(1), we conclude that the isomorphism
$E_{(a,b,c)}^{(d)}[p]\simeq E[p]$
must be symplectic when
$(3/p)=1$
. Thus, we can exclude the twists
$X_{E}^{-}(p)$
for these curves when
$p\equiv 1,11,13,23\hspace{0.2em}{\rm mod}\hspace{0.2em}24$
.
Finally, from the isogeny diagrams we see that
$X_{96a2}(p)\simeq X_{96a1}^{-}(p)$
and
$X_{288a2}(p)\simeq X_{288a1}^{-}(p)$
when
$(2/p)=-1$
; and also
$X_{54a2}(p)\simeq X_{54a1}^{-}(p)$
when
$(3/p)=-1$
. This concludes the proof.◻
We have already observed that
$X_{E}(p)$
for
$E\in \{27a1,288a1,288a2,864b1\}$
always has a rational point coming from a primitive solution of (2.1), so these twists cannot be excluded. In a similar way, we see that we cannot exclude
$X_{E}(p)$
by local arguments over
$\mathbb{Q}_{\ell }$
with
$\ell =2$
or
$3$
if
$E/\mathbb{Q}_{\ell }$
can be obtained as the Frey curve evaluated at an
$\ell$
-adically primitive solution of (2.1). Note that, for
$\ell \in \{2,3\}$
and
$p\geqslant 5$
, any
$\ell$
-adic unit is a
$p$
th power in
$\mathbb{Q}_{\ell }$
. For
$\ell =2$
, we have the following triples
$(a,b,E)$
, where
$a,b\in \mathbb{Z}_{2}$
are coprime with
$a^{2}+b^{3}\in \mathbb{Z}_{2}^{\times }$
and
$E/\mathbb{Q}_{2}$
is the curve obtained as the associated (local) Frey curve:
$$\begin{eqnarray}\displaystyle (253,-40,27a2),\quad (10,-7,96a1),\quad (46,-13,96a2),\quad (1,2,864c1). & & \displaystyle \nonumber\end{eqnarray}$$
For
$\ell =3$
, we only obtain
$(13,7,54a1)$
and
$(3,-1,864a1)$
. The remaining combinations
$(E,\ell )$
, namely
$$\begin{eqnarray}\displaystyle & (27a2,3),(54a1,2),(54a2,2),(54a2,3),(54a3,2),(54a3,3),(96a1,3), & \displaystyle \nonumber\\ \displaystyle & (96a2,3),(96a3,2),(96a3,3),(96a4,2),(96a4,3),(864a1,2),(864c1,3), & \displaystyle \nonumber\end{eqnarray}$$
do not arise in this way. This can be verified by checking whether there is
$d\in \mathbb{Q}_{\ell }^{\times }$
such that
$a=c_{6}(E)d^{3}$
and
$b=-c_{4}(E)d^{2}$
are coprime
$\ell$
-adic integers such that
$a^{2}+b^{3}$
is an
$\ell$
-adic unit.
In the remainder of this section we will show that there are nevertheless always
$2$
-adic and
$3$
-adic points corresponding to primitive solutions on the twists
$X_{E}^{\pm }(p)$
listed in Theorem 5.1. This means that Theorem 5.1 is the optimal result obtainable from local information at
$2$
and
$3$
.
Lemma 5.2. Let
$p\geqslant 3$
be a prime such that
$(2/p)=-1$
. Then, up to unramified quadratic twist, the
$p$
-torsion
$G_{\mathbb{Q}_{2}}$
-modules of the following curves admit exclusively the following isomorphism types:
$$\begin{eqnarray}\displaystyle 96a1\stackrel{+}{\simeq }864c1,\quad 288a1\stackrel{-}{\simeq }864a1,\quad 288a1\stackrel{+}{\simeq }864b1,\quad 864a1\stackrel{-}{\simeq }864b1, & & \displaystyle \nonumber\end{eqnarray}$$
where
$+$
means symplectic and
$-$
anti-symplectic. Moreover, let
$a,b$
be coprime integers satisfying the congruences in line
$i_{2}$
of Table 1 and write
$E=E_{(a,b,c)}^{(d)}/\mathbb{Q}_{2}$
, where
$d$
is any of the possible values in the same line. Then, up to unramified quadratic twist, the
$p$
-torsion
$G_{\mathbb{Q}_{2}}$
-modules of the following curves admit exclusively the following isomorphism types:
$$\begin{eqnarray}\displaystyle \begin{array}{@{}llll@{}}i_{2}=2\text{ with }d=\pm 1,\pm 3\text{ or }i_{2}=6:\qquad & E\stackrel{+}{\simeq }288a1,\quad & E\stackrel{-}{\simeq }864a1,\quad & E\stackrel{+}{\simeq }864b1,\\ i_{2}=2\text{ with }d=\pm 2,\pm 6:\qquad & E\stackrel{-}{\simeq }288a1,\quad & E\stackrel{+}{\simeq }864a1,\quad & E\stackrel{-}{\simeq }864b1,\\ i_{2}=3\text{ with }d=\pm 1,\pm 3\text{ or }i_{2}=5:\qquad & E\stackrel{+}{\simeq }96a1,\quad & E\stackrel{+}{\simeq }864c1,\quad \\ i_{2}=3\text{ with }d=\pm 2,\pm 6:\qquad & E\stackrel{-}{\simeq }96a1,\quad & E\stackrel{-}{\simeq }864c1.\quad \end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Furthermore, if instead
$p\geqslant 3$
satisfies
$(2/p)=1$
, then all the previous isomorphisms are symplectic.
Proof. Let
$E$
and
$E^{\prime }$
be any choice of curves that are compared in the statement. We have seen in § 3 that
$E$
and
$E^{\prime }$
have the same inertial field at
$2$
. From Theorem 4.6, we know that there is an isomorphism of
$I_{2}$
-modules
$\unicode[STIX]{x1D719}:E[p]\rightarrow E^{\prime }[p]$
. We can then use [Reference Freitas and KrausFK19, Theorem 9] to decide whether this isomorphism is symplectic or anti-symplectic. We will now show that the
$I_{2}$
-module isomorphism between
$E[p]$
and
$E^{\prime }[p]$
extends to the whole of
$G_{\mathbb{Q}_{2}}$
up to unramified quadratic twist.
Write
$L_{p}=\mathbb{Q}_{2}(E[p])$
for the
$p$
-torsion field of
$E$
and let
$U_{p}$
be the maximal unramified extension of
$\mathbb{Q}_{2}$
contained in
$L_{p}$
. Note that all the curves in the statement acquire good reduction over
$L_{3}$
and have trace of Frobenius
$a_{L_{3}}=-4$
(this can be checked using Magma). Therefore, we know that
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D70C}}_{E,p}|_{I_{2}}\simeq \overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}|_{I_{2}}\quad \text{and}\quad \overline{\unicode[STIX]{x1D70C}}_{E,p}|_{G_{L_{3}}}\simeq \overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}|_{G_{L_{3}}}. & & \displaystyle \nonumber\end{eqnarray}$$
Note that
$G_{U_{3}}=G_{L_{3}}\cdot I_{2}$
. We now apply [Reference CentelegheCen16, Theorem 2] to find that there is a basis in which
$\overline{\unicode[STIX]{x1D70C}}_{E,p}(\operatorname{Frob}_{L_{3}})$
is the scalar matrix
$-2\cdot \text{Id}_{2}$
. Thus, the same is true in all bases; therefore,
$\overline{\unicode[STIX]{x1D70C}}_{E,p}(\operatorname{Frob}_{L_{3}})$
commutes with all matrices in
$\overline{\unicode[STIX]{x1D70C}}_{E,p}(I_{2})$
. Since the same is true for
$E^{\prime }$
, the isomorphism between
$\overline{\unicode[STIX]{x1D70C}}_{E,p}$
and
$\overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}$
on the subgroups
$I_{2}$
and
$G_{L_{3}}$
extends to
$G_{U_{3}}$
.
Since all the curves involved have conductor
$2^{5}$
, their discriminants are cubes in
$\mathbb{Q}_{2}$
. Thus, by [Reference Dokchitser and DokchitserDD08, Table 1], we conclude that
$\operatorname{Gal}(L_{3}/\mathbb{Q}_{2})$
is isomorphic to the semi-dihedral group with 16 elements and hence
$H_{8}\simeq I\subset G_{3}$
with index 2; thus,
$[U_{3}:\mathbb{Q}_{2}]=2$
. Therefore, because the representations
$\overline{\unicode[STIX]{x1D70C}}_{E,p}$
and
$\overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}$
are irreducible, they differ at most by the quadratic character
$\unicode[STIX]{x1D712}$
fixing
$U_{3}$
, that is, we have
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D70C}}_{E,p}\simeq \overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}\quad \text{or}\quad \overline{\unicode[STIX]{x1D70C}}_{E,p}\simeq \overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}\otimes \unicode[STIX]{x1D712}. & & \displaystyle \nonumber\end{eqnarray}$$
The last statement follows from Theorem 4.6(1). ◻
When
$(E,E^{\prime })$
is any of the pairs of curves in the first part of the statement of Lemma 5.2, the unramified quadratic twist is actually never necessary, whereas it is necessary for some of the Frey curves in the second part. This can be checked on the
$3$
-torsion by an explicit computation; the result for arbitrary
$p$
follows from this.
Since the isomorphism class of
$X_{E}(p)$
(or
$X_{E}^{-}(p)$
) depends only on the symplectic Galois module
$E[p]$
up to quadratic twist, Lemma 5.2 implies that over
$\mathbb{Q}_{2}$
,
$X_{96a1}^{\pm }(p)\simeq X_{864c1}^{\pm }(p)$
and
$X_{288a1}^{\pm }(p)\simeq X_{864b1}^{\pm }(p)$
(writing
$X_{E}^{+}(p)=X_{E}(p)$
) and also that
$X_{288a1}^{\pm }(p)\simeq X_{864a1}^{\pm }(p)$
when
$(2/p)=1$
, whereas
$X_{288a1}^{\pm }(p)\simeq X_{864a1}^{\mp }(p)$
when
$(2/p)=-1$
. In this latter case the Frey curve gives rise to ‘primitive’
$2$
-adic points on
$X_{E}^{-}(p)$
for
$E\in \{96a1,288a1,864a1,864b1,964c1\}$
.
Lemma 5.3. Let
$p\geqslant 5$
be a prime such that
$(3/p)=-1$
. Then, up to unramified quadratic twist, the
$p$
-torsion
$G_{\mathbb{Q}_{3}}$
-modules of the following curves admit exclusively the following isomorphism types:
$$\begin{eqnarray}\displaystyle 27a1\stackrel{+}{\simeq }864c1,\quad 27a1\stackrel{-}{\simeq }864b1,\quad 864b1\stackrel{-}{\simeq }864c1,\quad 54a1\stackrel{-}{\simeq }864a1, & & \displaystyle \nonumber\end{eqnarray}$$
where
$+$
means symplectic and
$-$
anti-symplectic. Moreover, let
$a,b$
be coprime integers satisfying the congruences in line
$i_{3}$
of Table 2 and write
$E=E_{(a,b,c)}^{(d)}/\mathbb{Q}_{3}$
, where
$d$
is any of the possible values in the same line. Then, up to unramified quadratic twist, the
$p$
-torsion
$G_{\mathbb{Q}_{3}}$
-modules of the following curves admit exclusively the following isomorphism types:
$$\begin{eqnarray}\displaystyle \begin{array}{@{}llll@{}}i_{3}=3\text{ or }5\text{ with }d=\pm 1,\pm 2:\qquad & E\stackrel{-}{\simeq }27a1,\quad & E\stackrel{+}{\simeq }864b1,\quad & E\stackrel{-}{\simeq }864c1,\\ i_{3}=3\text{ or }5\text{ with }d=\pm 3,\pm 6:\qquad & E\stackrel{+}{\simeq }27a1,\quad & E\stackrel{-}{\simeq }864b1,\quad & E\stackrel{+}{\simeq }864c1,\\ i_{3}=4\text{ or }7\text{ with }d=\pm 1,\pm 2:\qquad & E\stackrel{-}{\simeq }54a1,\quad & E\stackrel{+}{\simeq }864a1,\quad \\ i_{3}=4\text{ or }7\text{ with }d=\pm 3,\pm 6:\qquad & E\stackrel{+}{\simeq }54a1,\quad & E\stackrel{-}{\simeq }864a1.\quad \end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Furthermore, if instead
$p\geqslant 5$
satisfies
$(3/p)=1$
, then all the previous isomorphisms are symplectic.
Proof. The proof proceeds in the same way as for the previous lemma, replacing
$2$
and
$3$
by
$3$
and
$5$
, respectively. We now use [Reference Freitas and KrausFK19, Theorem 11] to obtain the result on the level of inertia. We then see that
$G_{U_{3}}=G_{L_{5}}\cdot I_{3}$
and that all the curves in the statement acquire good reduction over
$L_{5}$
and have trace of Frobenius
$a_{L_{5}}=-18$
. We conclude as before that
$\overline{\unicode[STIX]{x1D70C}}_{E,p}$
and
$\overline{\unicode[STIX]{x1D70C}}_{E^{\prime },p}$
are isomorphic when restricted to
$G_{U_{5}}$
. In the present case we have
$[U_{5}:\mathbb{Q}_{3}]=4$
, so it is a priori conceivable that the representations differ by an unramified quartic twist. However, this is not possible, because both representations have the same determinant. We conclude that they differ at most by an unramified quadratic twist.◻
The statements of this lemma can be translated in terms of isomorphisms over
$\mathbb{Q}_{3}$
and ‘primitive’
$\mathbb{Q}_{3}$
-points in the same way as for the previous lemma.
These results already show that all the curves
$X_{E}^{\pm }(p)$
listed in Theorem 5.1 have ‘primitive’
$2$
-adic and
$3$
-adic points (and therefore cannot be ruled out by local considerations at
$2$
and
$3$
), with the possible exception of
$2$
-adic points on
$X_{54a1}^{\pm }(p)$
and
$3$
-adic points on
$X_{96a1}^{\pm }(p)$
. The next proposition and corollary show that these curves also have these local ‘primitive’ points. This then implies that the information in Theorem 5.1 is optimal in the sense that we cannot exclude more of the twists using purely
$2$
-adic and
$3$
-adic arguments. Note that in some cases it is possible to use local arguments at other primes to rule out some further twists. For example, in [Reference Freitas and KrausFK19, § 32], it is shown that the twist
$X_{864a1}^{-}(p)$
can be excluded for
$p=19$
and
$43$
and that
$X_{864b1}^{-}(p)$
can be excluded for
$p=19$
,
$43$
and
$67$
, working at a suitable prime of good reduction.
Proposition 5.4. Let
$\ell \neq p$
be primes with
$p\geqslant 3$
and
$\ell \not \equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
. Let
$E_{1}$
and
$E_{2}$
be Tate curves over
$\mathbb{Q}_{\ell }$
with Tate parameters
$q_{1}$
and
$q_{2}$
. Write
$e_{1}=v_{\ell }(q_{1})$
and
$e_{2}=v_{\ell }(q_{2})$
and suppose that
$p\nmid e_{1}e_{2}$
. Then
$E_{1}[p]$
and
$E_{2}[p]$
are isomorphic
$G_{\mathbb{Q}_{\ell }}$
-modules.
Proof. Fix a primitive
$p$
th root of unity
$\unicode[STIX]{x1D701}\in \overline{\mathbb{Q}}_{\ell }$
. Since
$p\nmid e_{1}e_{2}$
, we can find integers
$n$
and
$m$
(with
$p\nmid n$
) satisfying
$e_{2}=ne_{1}+pm$
. Write
$a=q_{2}/q_{1}^{n}\ell ^{mp}$
; then
$a$
is a unit in
$\mathbb{Q}_{\ell }$
. Since by assumption
$p\neq \ell$
and
$\ell \not \equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
, every unit is a
$p$
th power and hence there is
$\unicode[STIX]{x1D6FC}\in \mathbb{Q}_{\ell }$
satisfying
$\unicode[STIX]{x1D6FC}^{p}=a$
. Thus,
$q_{2}=q_{1}^{n}(\ell ^{m}\unicode[STIX]{x1D6FC})^{p}$
with
$p\nmid n$
. Fix
$\unicode[STIX]{x1D6FE}_{1}\in \overline{\mathbb{Q}}_{\ell }$
with
$\unicode[STIX]{x1D6FE}_{1}^{p}=q_{1}$
. Setting
$\unicode[STIX]{x1D6FE}_{2}=\unicode[STIX]{x1D6FE}_{1}^{n}\ell ^{m}\unicode[STIX]{x1D6FC}$
, we have
$\unicode[STIX]{x1D6FE}_{2}^{p}=q_{2}$
. By the theory of the Tate curve, we can use
$(\unicode[STIX]{x1D701}q_{i}^{\mathbb{Z}},\unicode[STIX]{x1D6FE}_{i}q_{i}^{\mathbb{Z}})$
as an
$\mathbb{F}_{p}$
-basis for the
$p$
-torsion of
$E_{i}$
. We claim that the isomorphism
$\unicode[STIX]{x1D719}:E_{1}[p]\rightarrow E_{2}[p]$
of
$\mathbb{F}_{p}$
-vector spaces given by the matrix
$$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}cc@{}}n & 0\\ 0 & 1\end{array}\right)\in \operatorname{GL}_{2}(\mathbb{F}_{p}) & & \displaystyle \nonumber\end{eqnarray}$$
with respect to these bases is actually an isomorphism of
$G_{\mathbb{Q}_{\ell }}$
-modules. To see this, consider
$\unicode[STIX]{x1D70E}\in G_{\mathbb{Q}_{\ell }}$
. Then
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{r}$
for some
$r\in \mathbb{F}_{p}^{\times }$
and
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1})=\unicode[STIX]{x1D701}^{s}\unicode[STIX]{x1D6FE}_{1}$
for some
$s\in \mathbb{F}_{p}$
, which implies that
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2})=\unicode[STIX]{x1D701}^{ns}\unicode[STIX]{x1D6FE}_{2}$
. We then have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}q_{1}^{\mathbb{Z}}))=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D701}^{r}q_{1}^{\mathbb{Z}})=\unicode[STIX]{x1D701}^{nr}q_{2}^{\mathbb{Z}}=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{n}q_{2}^{\mathbb{Z}})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D701}q_{1}^{\mathbb{Z}})) & & \displaystyle \nonumber\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{1}q_{1}^{\mathbb{Z}}))=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D701}^{s}\unicode[STIX]{x1D6FE}_{1}q_{1}^{\mathbb{Z}})=\unicode[STIX]{x1D701}^{ns}\unicode[STIX]{x1D6FE}_{2}q_{2}^{\mathbb{Z}}=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE}_{2}q_{2}^{\mathbb{Z}})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE}_{1}q_{1}^{\mathbb{Z}})), & & \displaystyle \nonumber\end{eqnarray}$$
as desired. ◻
Corollary 5.5. For
$p\geqslant 5$
, there are primitive
$2$
-adic points on
$X_{54a1}^{\pm }(p)$
and primitive
$3$
-adic points on
$X_{96a1}^{\pm }(p)$
. The signs
$\pm$
here are as given by the entries in Table 5 (which for the curves considered here summarizes Theorem 5.1).
Proof. Note that
$2\not \equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
and
$3\not \equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
, so Proposition 5.4 applies for
$\ell =2$
and
$\ell =3$
.
Let
$W$
denote the curve
$54a1$
. From Table 1, we see that for the Frey curve
$E=E_{a,b,c}$
to be
$p$
-congruent to
$W$
we must have
$v_{2}(c)>0$
and
$v_{2}(a)=\unicode[STIX]{x1D710}_{2}(b)=0$
. Note that we can always find
$a,b,c\in \mathbb{Q}_{2}$
satisfying the previous conditions and
$a^{2}+b^{3}=c^{p}$
.
Up to unramified quadratic twist, the curves
$W/\mathbb{Q}_{2}$
and
$E/\mathbb{Q}_{2}$
are Tate curves with parameters
$q_{W}$
and
$q_{E}$
, respectively. We have
$v_{2}(q_{W})=v_{2}(\unicode[STIX]{x1D6E5}_{W})=3$
and
$v_{2}(q_{E})=-v_{2}(j_{E})=-6+pv_{2}(c)$
.
Since
$p\neq 3$
, from the previous proposition we conclude that (up to quadratic twist)
$E[p]$
and
$W[p]$
are isomorphic
$G_{\mathbb{Q}_{2}}$
-modules. Therefore, we get
$2$
-adic points on
$X_{54a1}^{+}(p)$
or
$X_{54a1}^{-}(p)$
according to the signs in Table 5.
For the curve
$96a1$
, we argue in the same way, but over
$\mathbb{Q}_{3}$
instead of
$\mathbb{Q}_{2}$
.◻
A Magma script that performs the necessary computations for the results in this section is available as section5.magma at [Reference StollSto] and as supplementary material.
6 Ruling out twists coming from CM curves
In [Reference Bilu, Parent and RebolledoBPR13, Corollary 1.2], it is shown that for
$p\geqslant 11$
,
$p\neq 13$
, the image of the mod
$p$
Galois representation of any elliptic curve
$E$
over
$\mathbb{Q}$
is never contained in the normalizer of a split Cartan subgroup unless
$E$
has complex multiplication. This allows us to deduce the following.
Lemma 6.1. Let
$p\geqslant 17$
be a prime number.
(1) If
$p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
, then the only primitive solutions of (2.1) coming from rational points on
$X_{27a1}^{\pm }(p)$
are the trivial solutions
$(\pm 1)^{2}+0^{3}=1^{p}$
.(2) If
$p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, then the only primitive solutions of (2.1) coming from rational points on
$X_{288a1}^{\pm }(p)$
are the trivial solutions
$0^{2}+(\pm 1)^{3}=(\pm 1)^{p}$
(with the same sign on both sides).
Proof. If a primitive solution
$(a,b,c)$
gives rise to a Frey curve
$E^{\prime }$
such that
$E^{\prime }[p]\cong E[p]$
for
$E=27a1$
, then the image of Galois in
$\operatorname{GL}(E^{\prime }[p])\cong \operatorname{GL}(E[p])$
is contained in the normalizer of a split Cartan subgroup, since
$E$
has complex multiplication by
$\mathbb{Z}[\unicode[STIX]{x1D714}]$
and
$p$
splits in this ring when
$p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. It follows that
$E^{\prime }$
also has complex multiplication, which implies that
$c=\pm 1$
. Since the Frey curve of the Catalan solution does not have CM, the solution must be trivial and then only the given solution corresponds to the right curve
$E$
. The other case is similar, using the fact that
$288a1$
has CM by
$\mathbb{Z}[i]$
.◻
A separate computation for the case
$p=13$
, see Lemma 8.2 below, shows that Lemma 6.1 remains valid in that case, even though the result of [Reference Bilu, Parent and RebolledoBPR13] does not apply.
We can therefore further reduce the list of twists of
$X(p)$
that have to be considered. This results in Table 5, where an entry ‘
$+$
’ (respectively, ‘
$-$
’) indicates that the twist
$X_{E}(p)$
(respectively,
$X_{E}^{-}(p)$
) cannot (so far) be ruled out to have rational points giving rise to a non-trivial primitive solution of (2.1).
Table 5. Twists of
$X(p)$
remaining after local considerations and using information on
$X_{\operatorname{sp}}^{+}(p)$
, according to
$p\hspace{0.2em}{\rm mod}\hspace{0.2em}24$
. This table is valid for
$p\geqslant 11$
.
Unfortunately, there is no similar result on mod
$p$
Galois representations whose image is contained in the normalizer of a non-split Cartan subgroup. Such a result would allow us to eliminate the curves
$27a1$
and
$288a1$
also in the remaining cases.
In § 7.1 below, we show how one can deal with the non-split case when
$p=11$
by considering the twists
$X_{\operatorname{ns}}^{(-1)}(p)$
and
$X_{\operatorname{ns}}^{(-3)}(p)$
of the double cover
$X_{\operatorname{ns}}(p)\rightarrow X_{\operatorname{ns}}^{+}(p)$
, where
$X_{\operatorname{ns}}(p)$
classifies elliptic curves such that the image of the mod
$p$
Galois representation is contained in a non-split Cartan subgroup and
$X_{\operatorname{ns}}^{+}(p)$
does the same for the normalizer of a non-split Cartan subgroup. It turns out that for
$p=11$
, the two curves
$X_{\operatorname{ns}}^{(-1)}(11)$
and
$X_{\operatorname{ns}}^{(-3)}(11)$
are not directly amenable to a Chabauty argument; instead one can use suitable coverings and elliptic curve Chabauty. The following argument shows that the failure of the Chabauty condition is a general phenomenon.
By a result of Chen [Reference ChenChe98] (see also [Reference de Smit and EdixhovendSE00]), the Jacobian variety
$J_{0}(p^{2})$
of
$X_{0}(p^{2})$
is isogenous to the product
$\operatorname{Jac}(X_{\operatorname{ns}}(p))\times \operatorname{Jac}(X_{0}(p))^{2}$
. On the other hand, a theorem of Shimura [Reference ShimuraShi94, Theorem 7.14] implies that
$J_{0}(p^{2})$
is isogenous to the product
$\prod _{f}A_{f}^{m_{f}}$
, where
$f$
runs over a system of representatives of the Galois orbits of newforms of weight
$2$
and level
$M_{f}$
dividing
$p^{2}$
,
$A_{f}$
is the abelian variety over
$\mathbb{Q}$
associated to
$f$
defined by Shimura and
$p^{3-m_{f}}=M_{f}$
. It follows that
$\operatorname{Jac}(X_{\operatorname{ns}}(p))$
is isogenous to the product of the
$A_{f}$
such that
$f$
is a newform in
$S_{2}(\unicode[STIX]{x1D6E4}_{0}(p^{2}))$
. Similarly, the Jacobian of
$X_{\operatorname{ns}}^{+}(p)$
corresponds to the product of the
$A_{f}$
for the subset of
$f$
invariant under the Atkin–Lehner involution
$W$
at level
$p^{2}$
.
If
$p\equiv -1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
, we need to exclude rational points on the twists
$X_{288a1}^{\pm }(p)$
; solutions associated to this curve will give rise to rational points on the
$(-1)$
-twist
$X_{\operatorname{ns}}^{(-1)}(p)$
of the double cover
$X_{\operatorname{ns}}(p)\rightarrow X_{\operatorname{ns}}^{+}(p)$
. Similarly, for
$p\equiv -1\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
, we need to exclude rational points on the twist
$X_{27a1}(p)$
and solutions associated to that curve will give rise to rational points on
$X_{\operatorname{ns}}^{(-3)}(p)$
. To be able to use Chabauty’s method, we would need to have a factor of the Jacobian
$J_{\operatorname{ns}}^{(d)}(p)$
(for
$d=-1$
and/or
$d=-3$
) of Mordell–Weil rank strictly less than its dimension. Since all these factors have real multiplication (defined over
$\mathbb{Q}$
), the Mordell–Weil rank is always a multiple of the dimension, so we actually need a factor of rank zero.
By the above, we know that
$J_{\operatorname{ns}}^{(d)}(p)$
splits up to isogeny as the product of the twists
$A_{f}^{(d)}$
for newforms
$f$
such that
$f|_{W}=-f$
and the untwisted
$A_{f}$
for
$f$
such that
$f|_{W}=f$
. The
$L$
-series of
$A_{f}^{(d)}$
is the product of
$L(\text{}^{\unicode[STIX]{x1D70E}}\!f_{\unicode[STIX]{x1D712}},s)$
, where
$\text{}^{\unicode[STIX]{x1D70E}}\!f$
runs through the newforms in the Galois orbit and
$\unicode[STIX]{x1D712}$
is the quadratic character associated to
$d$
; see [Reference ShimuraShi94, § 7.5]. By a theorem of Weil [Reference WeilWei67, Satz 1], all these
$L$
-series have root number
$-1$
when
$f|_{W}=-f$
and
$d<0$
is squarefree (note that
$C=1$
from
$f|_{W}=-f$
,
$\unicode[STIX]{x1D700}$
is trivial,
$\unicode[STIX]{x1D712}$
is real, so
$g(\unicode[STIX]{x1D712})=g(\bar{\unicode[STIX]{x1D712}})$
, and
$A=p^{2}$
, so that
$\unicode[STIX]{x1D712}(-A)=\unicode[STIX]{x1D712}(-1)=-1$
), so
$L(A_{f}^{(d)},s)$
vanishes at least to order
$\dim A_{f}^{(d)}$
at
$s=1$
. For the
$f$
that are invariant under
$W$
, we also have that the root number of
$L(\text{}^{\unicode[STIX]{x1D70E}}\!f,s)$
is
$-1$
, so
$L(A_{f},s)$
also vanishes to order at least
$\dim A_{f}$
. Assuming the Birch and Swinnerton-Dyer conjecture, it follows that all factors of
$J_{\operatorname{ns}}^{(d)}(p)$
have positive rank.
To conclude this section we mention that when
$p=13$
, we are in the split case for both CM curves. During the work on this paper, it was an open question whether the set of rational points on
$X_{\operatorname{sp}}^{+}(13)$
consists of cusps and CM points. (The curve is of genus
$3$
and its Jacobian has Mordell–Weil rank
$3$
; see [Reference BaranBar14] and [Reference Bruin, Poonen and StollBPS16].) We tried an approach similar to that used in § 7.1 below, but did not succeed. However, a different approach using twists of
$X_{1}(13)$
is successful; see Lemma 8.2.
After our work was finished, Steffen Müller announced at a workshop in Banff that in joint work with Balakrishnan, Dogra, Tuitman and Vonk the set
$X_{\operatorname{ns}}^{+}(13)(\mathbb{Q})$
could be determined using ‘quadratic Chabauty’ techniques. This work has now appeared as [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDMTV19]. Since there is an accidental isomorphism
$X_{\operatorname{ns}}^{+}(13)\simeq X_{\operatorname{sp}}^{+}(13)$
and there are no unexpected points, this gives another proof of Lemma 8.2.
7 The generalized Fermat equation with exponents 2, 3, 11
We now consider the case
$p=11$
. In this section we will prove the following theorem.
Theorem 7.1. Assume the generalized Riemann hypothesis. Then the only primitive integral solutions of the equation
$x^{2}+y^{3}=z^{11}$
are the trivial solutions
$(\pm 1,0,1)$
,
$\pm (0,1,1)$
,
$(\pm 1,-1,0)$
and the Catalan solutions
$(\pm 3,-2,1)$
.
We note at this point that GRH is only used to verify the correctness of the computation of the class groups of five specific number fields of degree
$36$
.
In the following we will say that
$j\in \mathbb{Q}$
is good if it is the
$j$
-invariant of a Frey curve associated to a primitive integral solution of
$x^{2}+y^{3}=z^{11}$
, which translates into
$j=(12b)^{3}/c^{11}$
and
$12^{3}-j=12^{3}a^{2}/c^{11}$
with coprime integers
$a$
,
$b$
,
$c$
. In a similar way, we say that
$j\in \mathbb{Q}_{2}$
is 2-adically good if it has this form for coprime
$2$
-adic integers
$a$
,
$b$
,
$c$
.
By Theorem 5.1, it suffices to find the rational points on the twisted modular curves
$X_{E}(11)$
for the elliptic curves
$E\in {\mathcal{E}}^{\prime }$
, where
$$\begin{eqnarray}\displaystyle {\mathcal{E}}^{\prime }=\{27a1,54a1,96a1,288a1,288a2,864a1,864b1,864c1\}, & & \displaystyle \nonumber\end{eqnarray}$$
such that their image on the
$j$
-line is good.
Some of the results in this section rely on computations that require a computer algebra system. We provide a script section7.magma at [Reference StollSto] and as supplementary material (which relies on localtest.magma, also provided there) that can be loaded into Magma and performs these computations.
7.1 The CM curves
In the case
$p=11$
, we can deal with the CM curves
$E\in \{27a1,288a1,288a2\}$
in the following way. Note that since
$(-1/11)=(-3/11)=-1$
, the images of both relevant Galois representations are contained in the normalizer of a non-split Cartan subgroup of
$\operatorname{GL}_{2}(\mathbb{F}_{11})$
. Elliptic curves with this property are parameterized by the modular curve
$X_{\operatorname{ns}}^{+}(11)$
, which is the elliptic curve
$121b1$
of rank
$1$
. It has as a double cover the curve
$X_{\operatorname{ns}}(11)$
parameterizing elliptic curves
$E$
such that the image of the mod
$11$
Galois representation is contained in a non-split Cartan subgroup. Elliptic curves whose mod
$11$
representation is isomorphic to that of
$288a1$
(or
$288a2$
) or
$27a1$
will give rise to rational points on the quadratic twists
$X_{\operatorname{ns}}^{(-1)}(11)$
and
$X_{\operatorname{ns}}^{(-3)}(11)$
of this double cover; see [Reference Dose, Fernández, González and SchoofDFGS14, Remark 1]. These curves are of genus
$4$
; the Jacobian of
$X_{\operatorname{ns}}(11)$
is isogenous to the product of the four elliptic curves
$121a1$
,
$121b1$
,
$121c1$
and
$121d1$
, so that the Jacobian of the twist
$X_{\operatorname{ns}}^{(d)}(11)$
splits into the four elliptic curves
$121b1$
,
$121a1^{(d)}$
,
$121c1^{(d)}$
and
$121d1^{(d)}$
. Unfortunately, for
$d=-1$
and
$d=-3$
, all of these curves have rank
$1$
, so the obvious approach does not work. However, we can use a covering collection combined with the elliptic curve Chabauty method [Reference BruinBru03], as follows. An equation for
$X_{\operatorname{ns}}^{+}(11)$
is (see [Reference LigozatLig77, Proposition II.4.3.8.1])
$$\begin{eqnarray}\displaystyle y^{2}=4x^{3}-4x^{2}-28x+41 & & \displaystyle \nonumber\end{eqnarray}$$
and the double cover
$X_{\operatorname{ns}}(11)\rightarrow X_{\operatorname{ns}}^{+}(11)$
is given by
$$\begin{eqnarray}\displaystyle t^{2}=-(4x^{3}+7x^{2}-6x+19) & & \displaystyle \nonumber\end{eqnarray}$$
(this is an equation for
$121c1$
); see [Reference Dose, Fernández, González and SchoofDFGS14, Proposition 1]. Therefore, our twists are given by
$$\begin{eqnarray}\displaystyle X_{\operatorname{ns}}^{(-1)}(11):\left\{\begin{array}{@{}rl@{}}y^{2}= & 4x^{3}-4x^{2}-28x+41,\\ t^{2}= & 4x^{3}+7x^{2}-6x+19,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle X_{\operatorname{ns}}^{(-3)}(11):\left\{\begin{array}{@{}rl@{}}y^{2}= & 4x^{3}-4x^{2}-28x+41,\\ t^{2}= & 3(4x^{3}+7x^{2}-6x+19).\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Let
$\unicode[STIX]{x1D6FC}$
be a root of
$f_{1}(x)=4x^{3}-4x^{2}-28x+41$
and set
$K=\mathbb{Q}(\unicode[STIX]{x1D6FC})$
. Write
$f_{1}(x)=(x-\unicode[STIX]{x1D6FC})g_{1}(x)$
in
$K[x]$
. Since
$E_{1}=121b1$
has Mordell–Weil group
$E_{1}(\mathbb{Q})$
isomorphic to
$\mathbb{Z}$
and
$P=(4,11)$
is a generator, it follows that each rational point on
$E_{1}$
gives rise to a
$K$
-rational point with rational
$x$
-coordinate on one of the two curves
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}rl@{}}y_{1}^{2}= & x-\unicode[STIX]{x1D6FC},\\ y_{2}^{2}= & g_{1}(x),\end{array}\right.\quad \text{and}\quad \left\{\begin{array}{@{}rl@{}}y_{1}^{2}= & (4-\unicode[STIX]{x1D6FC})(x-\unicode[STIX]{x1D6FC}),\\ y_{2}^{2}= & (4-\unicode[STIX]{x1D6FC})g_{1}(x).\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
(Here we use that the map
$E_{1}(\mathbb{Q})\rightarrow K^{\times }/K^{\times 2}$
that associates to a point
$P$
the square class of
$x(P)-\unicode[STIX]{x1D6FC}$
is a homomorphism.) So, a rational point on
$X_{\operatorname{ns}}^{(d)}(11)$
will give a
$K$
-rational point with rational
$x$
-coordinate on
$$\begin{eqnarray}\displaystyle u^{2}=-d(x-\unicode[STIX]{x1D6FC})(4x^{3}+7x^{2}-6x+19)\quad \text{or}\quad u^{2}=-d(4-\unicode[STIX]{x1D6FC})(x-\unicode[STIX]{x1D6FC})(4x^{3}+7x^{2}-6x+19). & & \displaystyle \nonumber\end{eqnarray}$$
These are elliptic curves over
$K$
, which turn out to both have Mordell–Weil rank
$1$
for
$d=-1$
and rank
$2$
for
$d=-3$
. Since the rank is strictly smaller than the degree of
$K$
in all cases, elliptic curve Chabauty applies and we find using Magma that the
$x$
-coordinates of the rational points on
$X_{\operatorname{ns}}^{(-1)}(11)$
and
$X_{\operatorname{ns}}^{(-3)}(11)$
are
$\infty ,5/4,4$
and
$-2$
, corresponding to
$O$
,
$\pm 3P$
,
$\pm P$
and
$\pm 4P$
on
$E_{1}$
. We compute the
$j$
-invariants of the elliptic curves represented by these points using the formula in [Reference Dose, Fernández, González and SchoofDFGS14] and find that only the curves corresponding to
$3P$
and to
$4P$
give rise to solutions of (2.1); they are the trivial solutions with
$a=0$
or
$b=0$
.
7.2 Dealing with the remaining curves
We now set
${\mathcal{E}}=\{54a1,96a1,864a1,864b1,864c1\}$
; this is the set of curves
$E$
such that we still have to consider
$X_{E}(11)$
.
We will denote any of the canonical morphisms
$$\begin{eqnarray}\displaystyle X(11)\rightarrow X(1)\simeq \mathbb{P}^{1},\quad X_{E}(11)\simeq _{\bar{\mathbb{Q}}}X(11)\rightarrow X(1)\simeq \mathbb{P}^{1}\quad \text{and}\quad X_{0}(11)\rightarrow X(1)\simeq \mathbb{P}^{1} & & \displaystyle \nonumber\end{eqnarray}$$
by
$j$
and we will also use
$j$
to denote the corresponding coordinate on
$\mathbb{P}^{1}$
.
Recall that
$X_{0}(11)$
is an elliptic curve. Let
$P\in X_{E}(11)(\mathbb{Q})$
be a rational point; then under the composition
$X_{E}(11)\simeq X(11)\rightarrow X_{0}(11)$
(where the isomorphism is defined over
$\bar{\mathbb{Q}}$
)
$P$
will be mapped to a point
$P^{\prime }$
on
$X_{0}(11)$
whose image
$j(P^{\prime })=j(P)$
on the
$j$
-line is rational. Since the
$j$
-map from
$X_{0}(11)$
has degree
$12$
, it follows that
$P^{\prime }$
is defined over a number field
$K$
of degree at most
$12$
. More precisely, the points in the fiber above
$j(P^{\prime })=j(P)$
in
$X_{0}(11)$
correspond to the 12 possible cyclic subgroups of order
$11$
in
$E[11]$
, so the Galois action on the fiber depends only on
$E$
and is the same as the Galois action on the fiber above the image
$j(E)$
on the
$j$
-line of the canonical point of
$X_{E}(11)$
. In particular, we can easily determine the isomorphism type of this fiber. It turns out that for our five curves
$E$
, the fiber is irreducible, with a (geometric) point defined over a field
$K=K_{E}$
of degree
$12$
. The problem can therefore be reduced to the determination of the set of
$K_{E}$
-points
$P^{\prime }$
on
$X_{0}(11)$
such that
$j(P^{\prime })\in \mathbb{Q}$
and is good. This kind of problem is the setting for the elliptic curve Chabauty method as introduced in [Reference BruinBru03] that we have already used in § 7.1 above. To apply the method, we need explicit generators of a finite-index subgroup of the group
$X_{0}(11)(K_{E})$
. This requires knowing the rank of this group, for which we can obtain an upper bound by computing a suitable Selmer group. We use the
$2$
-Selmer group, whose computation requires class and unit group information for the cubic extension
$L_{E}$
of
$K_{E}$
obtained by adjoining the
$x$
-coordinate of a point of order
$2$
on
$X_{0}(11)$
(no field
$K_{E}$
has a non-trivial subfield, so no point of order
$2$
on
$X_{0}(11)$
becomes rational over
$K_{E}$
). To make the relevant computation feasible, we assume GRH. With this assumption, the computation of the
$2$
-Selmer groups is done by Magma in reasonable time (up to a few hours). However, we now have the problem that we do not find sufficiently many independent points in
$X_{0}(11)(K_{E})$
to reach the upper bound. This is where an earlier attempt in 2006 along similar lines by David Zureick-Brown got stuck. We get around this stumbling block by making use of ‘Selmer group Chabauty’ as described in [Reference StollSto17]. This method allows us to work with the Selmer group information without having to find sufficiently many points in
$X_{0}(11)(K_{E})$
.
The idea of the Selmer group Chabauty method (when applied with the
$2$
-Selmer group) is to combine the global information from the Selmer group with local, here specifically
$2$
-adic, information. So, we first study our situation over
$\mathbb{Q}_{2}$
. Away from the branch points
$0$
,
$12^{3}$
and
$\infty$
of
$j:X_{0}(11)\rightarrow \mathbb{P}_{j}^{1}$
, the
$\mathbb{Q}_{2}$
-isomorphism type of the fiber is locally constant in the
$2$
-adic topology. In a suitable neighborhood of a branch point, the isomorphism type of the fiber will only depend on the class of the value of a suitable uniformizer on
$\mathbb{P}_{j}^{1}$
at the branch point modulo cubes (for
$0$
), squares (for
$12^{3}$
) or 11th powers (for
$\infty$
). We use the standard model given by
$$\begin{eqnarray}\displaystyle y^{2}+y=x^{3}-x^{2}-10x-20 & & \displaystyle \nonumber\end{eqnarray}$$
for the elliptic curve
$X_{0}(11)$
, with
$j$
-invariant map given by
$j=(a(x)+b(x)y)/(x-16)^{11}$
, where
$$\begin{eqnarray}\displaystyle a(x) & = & \displaystyle 743x^{11}+21559874x^{10}+19162005343x^{9}+2536749758583x^{8}\nonumber\\ \displaystyle & & \displaystyle +\,82165362766027x^{7}+576036867160006x^{6}-1895608370650736x^{5}\nonumber\\ \displaystyle & & \displaystyle -\,14545268641576841x^{4}+420015065507429x^{3}+74593328129816300x^{2}\nonumber\\ \displaystyle & & \displaystyle +\,108160113602504237x-39176677684144739\nonumber\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle b(x) & = & \displaystyle (x^{5}+4518x^{4}+1304157x^{3}+65058492x^{2}+271927184x-707351591)\nonumber\\ \displaystyle & & \displaystyle \cdot \,(x^{5}+192189x^{4}+3626752x^{3}-3406817x^{2}-37789861x-37315543).\nonumber\end{eqnarray}$$
We define the following set of subsets of
$\mathbb{P}^{1}(\mathbb{Q}_{2})$
:
$$\begin{eqnarray}\displaystyle {\mathcal{D}} & = & \displaystyle \{\!15\cdot 2^{6}+2^{11}\mathbb{Z}_{2},-2^{6}+2^{11}\mathbb{Z}_{2},2^{9}+2^{11}\mathbb{Z}_{2},-2^{9}+2^{11}\mathbb{Z}_{2},\{2^{-5}t^{-11}:t\in \mathbb{Z}_{2}\},\nonumber\\ \displaystyle & & \displaystyle \{12^{3}-3\cdot 2^{10}t^{2}:t\in \mathbb{Z}_{2}\},\{12^{3}-2^{10}t^{2}:t\in \mathbb{Z}_{2}\},\nonumber\\ \displaystyle & & \displaystyle \{12^{3}+2^{10}t^{2}:t\in \mathbb{Z}_{2}\},\{12^{3}+3\cdot 2^{10}t^{2}:t\in \mathbb{Z}_{2}\}\!\}\!.\end{eqnarray}$$
Note that according to Table 1, all elements in these sets are
$2$
-adically good
$j$
-invariants and, for each set, all fibers of the
$j$
-map
$X_{0}(11)\rightarrow \mathbb{P}^{1}$
over points in the set are isomorphic over
$\mathbb{Q}_{2}$
(excluding
$j=12^{3}$
and
$j=\infty$
).
Lemma 7.3. Let
$E\in {\mathcal{E}}$
and let
$P\in X_{E}(11)(\mathbb{Q}_{2})$
be such that
$j(P)$
is
$2$
-adically good. Then
$j(P)$
is in one of the following sets
$D\in {\mathcal{D}}$
, depending on
$E$
:
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rl@{}}54a1 & :\{2^{-5}t^{-11}:t\in \mathbb{Z}_{2}\},\\ 96a1 & :15\cdot 2^{6}+2^{11}\mathbb{Z}_{2},-2^{6}+2^{11}\mathbb{Z}_{2},-2^{9}+2^{11}\mathbb{Z}_{2},\\ 864a1 & :\{12^{3}-2^{10}t^{2}:t\in \mathbb{Z}_{2}\},\{12^{3}+3\cdot 2^{10}t^{2}:t\in \mathbb{Z}_{2}\},\\ 864b1 & :\{12^{3}-3\cdot 2^{10}t^{2}:t\in \mathbb{Z}_{2}\},\{12^{3}+2^{10}t^{2}:t\in \mathbb{Z}_{2}\},2^{9}+2^{11}\mathbb{Z}_{2},\\ 864c1 & :15\cdot 2^{6}+2^{11}\mathbb{Z}_{2},-2^{6}+2^{11}\mathbb{Z}_{2},-2^{9}+2^{11}\mathbb{Z}_{2}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Proof. This follows from the information in Table 1, together with Lemma 5.2, which allows us to distinguish between
$X_{E}(p)$
and
$X_{E}^{-}(p)$
(note that
$2$
is a non-square mod
$11$
).◻
Table 6. Fields
$K_{E}$
and dimensions of Selmer groups for
$E\in {\mathcal{E}}$
.
The next step is the computation of the
$2$
-Selmer groups of
$X_{0}(11)$
over the fields
$K_{E}$
, where
$E$
runs through the curves in
${\mathcal{E}}$
. This is where we assume GRH. Table 6 lists defining polynomials for the fields
$K_{E}$
and gives the
$\mathbb{F}_{2}$
-dimensions of the Selmer groups.
We eliminate
$y$
from the equation of
$X_{0}(11)$
and the relation between
$j$
and
$x,y$
. This results in
$$\begin{eqnarray}\displaystyle F(x,j) & = & \displaystyle (x^{4}-52820x^{3}+1333262x^{2}+4971236x+9789217)^{3}\nonumber\\ \displaystyle & & \displaystyle +(1486x^{11}+43119747x^{10}+38323813979x^{9}+5072626276355x^{8}\nonumber\\ \displaystyle & & \displaystyle +\,164063633585170x^{7}+1134855511654843x^{6}-4074814667347831x^{5}\nonumber\\ \displaystyle & & \displaystyle -\,29669709666741936x^{4}+6839041777752481x^{3}+159480622275659333x^{2}\nonumber\\ \displaystyle & & \displaystyle +\,199736619430410535x-104748564078368391)\!j\nonumber\\ \displaystyle & & \displaystyle -\,(x-16)^{11}j^{2}=0.\end{eqnarray}$$
We now state a technical lemma for later use.
Lemma 7.5. Let
$K$
be a field complete with respect to an absolute value
$|\cdot |$
. Consider a polynomial
$F=\sum _{i,j\geqslant 0}f_{ij}x^{i}y^{j}\in K[x,y]$
. Fix an integer
$e\geqslant 1$
such that the characteristic of
$K$
does not divide
$e$
. We assume that
$f_{0j}=0$
for
$0\leqslant j<e$
and that
$f_{0e}=1$
. Write
$F_{j}(t)=\sum _{i\geqslant 0}f_{ij}t^{i}\in K[t]$
for
$j\geqslant 0$
, so that
$F(x,y)=\sum _{j\geqslant 0}F_{j}(x)y^{j}$
. Assume that
$F_{0}(t)=-ct+\text{higher order terms}$
, with
$c\neq 0$
. For a real number
$r>0$
and a polynomial
$f(t)=a_{n}t^{n}+\cdots +a_{1}t+a_{0}\in K[t]$
, we set
$|f|_{r}=\max \{r^{i}|a_{i}|:0\leqslant i\leqslant n\}$
.
There are exactly
$e$
formal power series
$\unicode[STIX]{x1D719}_{0},\ldots ,\unicode[STIX]{x1D719}_{e-1}\in L[\![t]\!]$
, where
$L$
is the splitting field of
$X^{e}-c$
over
$K$
, such that
$\unicode[STIX]{x1D719}_{j}(0)=0$
and
$F(t^{e},\unicode[STIX]{x1D719}_{j}(t))=0$
. If
$\unicode[STIX]{x1D701}\in L$
is a primitive
$e$
th root of unity, then we can label the
$\unicode[STIX]{x1D719}_{j}$
in such a way that
$\unicode[STIX]{x1D719}_{j}(t)=\unicode[STIX]{x1D719}_{0}(\unicode[STIX]{x1D701}^{j}t)$
.
If
$r>0$
is such that
$|F_{m}(t^{e})|_{r}<|F_{0}(t^{e})|_{r}^{(e-m)/e}$
for
$0<m<e$
,
$|F_{e}(t^{e})-1|_{r}<1$
and
$|F_{0}(t^{e})|_{r}^{(m-e)/e}|F_{m}(t^{e})|_{r}<1$
for
$m>e$
, then the
$\unicode[STIX]{x1D719}_{j}$
converge on the closed disk of radius
$r$
in
$L$
and we have
$|\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x1D70F})|\leqslant |F_{0}(t^{e})|_{r}^{1/e}$
for all
$\unicode[STIX]{x1D70F}$
in this disk. If in addition
$|F_{0}(t^{e})+ct^{e}|_{r}<|F_{0}(t^{e})|_{r}$
, then
$|\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x1D70F})|=|c|^{1/e}|\unicode[STIX]{x1D70F}|$
for all these
$\unicode[STIX]{x1D70F}$
.
Proof. We consider the equation
$F(t^{e},y)=0$
over the field of Laurent series
$L(\!(t)\!)$
. The assumptions
$f_{0j}=0$
for
$0\leqslant j<e$
,
$f_{0e}=1$
and
$f_{10}=-c\neq 0$
imply that the Newton polygon of
$F(t^{e},y)$
has a segment of length
$e$
and slope
$-e$
and that all other slopes are
${\geqslant}0$
. This already shows that there are at most
$e$
power series with the required properties. Also, the reduction modulo
$t$
of
$t^{-e}F(t^{e},tz)$
is
$z^{e}-c$
, which is a separable polynomial splitting over
$L$
into linear factors. So, by Hensel’s lemma, there are exactly
$e$
solutions
$z\in L[\![t]\!]$
. Let
$\unicode[STIX]{x1D719}_{0}=tz_{0}$
for one such solution
$z_{0}$
. Clearly, each solution
$z$
gives rise to exactly one power series
$\unicode[STIX]{x1D719}_{j}$
. Since the original equation is invariant under the substitution
$t\mapsto \unicode[STIX]{x1D701}^{j}t$
,
$\unicode[STIX]{x1D719}_{j}(t):=\unicode[STIX]{x1D719}_{0}(\unicode[STIX]{x1D701}^{j}t)$
is a solution for each
$0\leqslant j<e$
. Since
$\unicode[STIX]{x1D6FE}=z_{0}(0)\neq 0$
(it is an
$e$
th root of
$c$
), we have
$\unicode[STIX]{x1D719}_{0}(t)=\unicode[STIX]{x1D6FE}t+\cdots \,$
and so all these
$\unicode[STIX]{x1D719}_{j}$
are pairwise distinct.
Now consider the completion of the polynomial ring
$L[t]$
with respect to
$|\cdot |_{r}$
. This is the Tate algebra
$T_{r}$
of power series converging on the closed disk of radius
$r$
(in the algebraic closure of
$L$
). The assumptions on
$r$
guarantee that the Newton polygon of
$F(t^{e},y)$
, considered over
$T_{r}$
, again has a unique segment of length
$e$
and slope corresponding to the absolute value
$|F_{0}(t^{e})|_{r}^{1/e}$
, whereas all other slopes correspond to larger absolute values. As can be seen by letting
$r$
tend to zero, the corresponding solutions must be given by the
$\unicode[STIX]{x1D719}_{j}$
. The claim that
$|\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x1D70F})|\leqslant |F_{0}(t^{e})|_{r}^{1/e}$
follows from
$|\unicode[STIX]{x1D719}_{j}|_{r}=|F_{0}(t^{e})|_{r}^{1/e}$
. For the last claim, note that
$|F_{0}(t^{e})|_{r}=|c|r^{e}$
and that if
$|\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x1D70F})|<|c|^{1/e}$
, then the term
$-c\unicode[STIX]{x1D70F}^{e}$
would be dominant in
$F(\unicode[STIX]{x1D70F}^{e},\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x1D70F}))$
, which gives a contradiction.◻
Recall that
$\unicode[STIX]{x1D703}$
denotes the
$x$
-coordinate of a point of order 2 on
$X_{0}(11)$
, so
$\unicode[STIX]{x1D703}$
is a root of the
$2$
-division polynomial
$$\begin{eqnarray}\displaystyle 4x^{3}-4x^{2}-40x-79 & & \displaystyle \nonumber\end{eqnarray}$$
of
$X_{0}(11)$
. We denote the
$2$
-adic valuation on
$\bar{\mathbb{Q}}_{2}$
by
$v_{2}$
, normalized so that
$v_{2}(2)=1$
. Then
$v_{2}(\unicode[STIX]{x1D703})=-2/3$
.
Lemma 7.6. Let
$K$
be a finite extension of
$\mathbb{Q}_{2}$
such that
$X_{0}(11)(K)[2]=0$
and set
$L=K(\unicode[STIX]{x1D703})$
. Let
$D\in {\mathcal{D}}$
, but different from
$\{2^{-5}t^{-11}:t\in \mathbb{Z}_{2}\}$
, and let
$\unicode[STIX]{x1D711}:\mathbb{Z}_{2}\rightarrow D$
be the parameterization in terms of
$t$
as given in (7.2). Let
$P\in X_{0}(11)(K)$
be such that
$j(P)\in D$
. Then
$P$
is in the image of an analytic map
$\unicode[STIX]{x1D719}:\mathbb{Z}_{2}\rightarrow X_{0}(11)(K)$
such that
$j\circ \unicode[STIX]{x1D719}=\unicode[STIX]{x1D711}$
and the square class of
$x(\unicode[STIX]{x1D719}(z))-\unicode[STIX]{x1D703}\in L^{\times }$
is constant for
$z\in \mathbb{Z}_{2}$
.
Proof. By the information in Table 1, the
$\mathbb{Q}_{2}$
-isomorphism type of the fiber of
$j$
above
$D$
is constant, say given by the disjoint union of
$\operatorname{Spec}K_{i}$
for certain
$2$
-adic fields
$K_{i}$
. We note that all
$K_{i}$
coming up in this way have the property that
$X_{0}(11)(K_{j})[2]=0$
, since the ramification indices are not divisible by
$3$
. We can then take
$K=K_{i}$
, since we will use a purely valuation-theoretic criterion for the second statement, so the choice of field will be largely irrelevant. In the following,
$F(x,j)=0$
is the relation between the
$x$
-coordinate on
$X_{0}(11)$
and the associated
$j$
-invariant given in (7.4).
If
$D$
is not one of the last four sets in (7.2), then we solve
$F(x_{0}+\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D711}(t))=0$
for a power series
$\unicode[STIX]{x1D719}_{0}$
with
$\unicode[STIX]{x1D719}_{0}(0)=0$
, where
$x_{0}\in K$
is any root of
$F(x,\unicode[STIX]{x1D711}(0))$
. For each possible
$D$
and
$x_{0}$
, Lemma 7.5 allows us to deduce that such a power series
$\unicode[STIX]{x1D719}_{0}$
exists, that it converges on an open disk containing
$\mathbb{Z}_{2}$
and that it satisfies
$v_{2}(\unicode[STIX]{x1D719}_{0}(\unicode[STIX]{x1D70F}))>4/3$
for all
$\unicode[STIX]{x1D70F}\in \mathbb{Z}_{2}$
. Since we obtain as many power series as there are roots of
$F(x,z)=0$
for any
$z\in D$
(this is because the fibers over
$D$
of the
$j$
-map are all isomorphic, so the number of roots in
$K$
is constant) and since the
$y$
-coordinate of a point on
$X_{0}(11)$
is uniquely determined by its
$x$
-coordinate and its image under the
$j$
-map (unless
$b(x)=0$
, but this never happens for the points we are considering), we obtain analytic maps
$\unicode[STIX]{x1D719}:\mathbb{Z}_{2}\rightarrow X_{0}(11)(K)$
whose images cover all points
$P$
as in the statement. Also,
$v_{2}(x(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F}))-x_{0})=v_{2}(\unicode[STIX]{x1D719}_{0}(\unicode[STIX]{x1D70F}))>4/3=2+v_{2}(x_{0}-\unicode[STIX]{x1D703})$
, which implies (compare [Reference StollSto01, Lemma 6.3]) that
$x(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F}))-\unicode[STIX]{x1D703}$
is in the same square class as
$x_{0}-\unicode[STIX]{x1D703}$
.
If
$D$
is one of the last four sets in (7.2), then we proceed in a similar way. Note that the four parameterizations
$\unicode[STIX]{x1D711}(t)=12^{3}+a2^{10}t^{2}$
all have
$2$
-adic units
$a$
and so can be converted one into another by scaling
$t$
by a
$2$
-adic unit (in some extension field of
$\mathbb{Q}_{2}$
). Since we only care about valuations in the argument, it is sufficient to just work with one of them. In the same way as before, we consider
$F(x_{0}+\unicode[STIX]{x1D719}_{0}(t),\unicode[STIX]{x1D711}(t))=0$
as an equation to be solved for a power series
$\unicode[STIX]{x1D719}_{0}$
with
$\unicode[STIX]{x1D719}_{0}(0)=0$
, where
$x_{0}\in K$
is such that
$F(x_{0},12^{3})=0$
. We apply Lemma 7.5 again, this time with
$e=2$
, and the remaining argument is similar to the previous case.◻
We now use the information coming from the Selmer group together with the preceding lemma to rule out most of the sets listed in Lemma 7.3.
Lemma 7.7. Let
$E\in {\mathcal{E}}$
and let
$P\in X_{E}(11)(\mathbb{Q})$
be such that
$j(P)$
is
$2$
-adically good. Then
$j(P)$
is in one of the following sets
$D\in {\mathcal{D}}$
, depending on
$E$
:
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rl@{}}54a1 & :\{2^{-5}t^{-11}:t\in \mathbb{Z}_{2}\},\\ 96a1 & :15\cdot 2^{6}+2^{11}\mathbb{Z}_{2},-2^{6}+2^{11}\mathbb{Z}_{2},\\ 864a1 & :\text{none},\\ 864b1 & :2^{9}+2^{11}\mathbb{Z}_{2},\\ 864c1 & :-2^{9}+2^{11}\mathbb{Z}_{2}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Note that the curve
$864a1$
can already be ruled out at this stage.
Proof. In view of Lemma 7.3, there is nothing to prove when
$E=54a1$
. So, we let
$E$
be one of the other four curves. Any rational point on
$X_{E}(11)$
whose image on the
$j$
-line is good will map to a point in
$X_{0}(11)(K_{E})$
with the same
$j$
-invariant and so will give rise to a
$K_{E}\otimes _{\mathbb{Q}}\mathbb{Q}_{2}$
-valued point on
$X_{0}(11)$
whose
$j$
-invariant is in one of the sets
$D$
listed in Lemma 7.3, depending on
$E$
. Recall that
$L_{E}=K_{E}(\unicode[STIX]{x1D703})$
. We write
$K_{E,2}=K_{E}\otimes _{\mathbb{Q}}\mathbb{Q}_{2}$
and
$L_{E,2}=L_{E}\otimes _{\mathbb{Q}}\mathbb{Q}_{2}$
;
$K_{E,2}$
and
$L_{E,2}$
are étale algebras over
$\mathbb{Q}_{2}$
. Then we have the following commutative diagram.
The composition of the two horizontal maps in the bottom row sends a point
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
to the square class of
$\unicode[STIX]{x1D709}-\unicode[STIX]{x1D703}$
in
$L_{E,2}^{\times }$
. By Lemma 7.6, the square class we obtain for a point in
$X_{0}(11)(K_{E,2})$
mapping into a fixed set
$D$
does not depend on the image point in
$D$
. It therefore suffices to compute the square class for the points above some representative point (for example, the ‘center’ if it is not a branch point) of
$D$
. Doing this, we find that the square classes we obtain are not in the image of the Selmer group except for the sets given in the statement. Since by the diagram above a point in
$X_{0}(11)(K_{E})$
has to map into the image of the Selmer group, this allows us to exclude these
$D$
.◻
It remains to deal with the remaining five sets
$D$
. All but one of them do actually contain the image of a point in
$X_{0}(11)(K_{E})$
, so we have to use a more sophisticated approach. The idea for the following statement comes from [Reference StollSto17].
Lemma 7.8. Let
$E\in {\mathcal{E}}$
and let
$D\in {\mathcal{D}}$
be one of the sets associated to
$E$
in Lemma 7.7. Assume that there is a point
$P\in X_{0}(11)(K_{E})$
with the following property.
(∗) For any point
$Q\in X_{0}(11)(K_{E,2})$
with
$Q\neq P$
and
$j(Q)\in D$
, there is
$n\geqslant 0$
such that
$Q=P+2^{n}Q^{\prime }$
with
$Q^{\prime }\in X_{0}(11)(K_{E,2})$
such that the image of
$Q^{\prime }$
in
$L_{E,2}^{\times }/L_{E,2}^{\times 2}$
is not in the image of the Selmer group.
Then, if
$j(P)\in D$
,
$P$
is the only point
$Q\in X_{0}(11)(K_{E})$
with
$j(Q)\in D$
and, if
$j(P)\notin D$
, then there is no such point.
Proof. For each
$E\in {\mathcal{E}}$
, we verify that the middle vertical map in the diagram in the proof of Lemma 7.7 is injective, by checking that the rightmost vertical map is injective on the image of the Selmer group. Note that the Selmer group is actually computed as a subgroup of the upper right group. Since
$X_{0}(11)(K_{E})/2X_{0}(11)(K_{E})$
maps injectively into the Selmer group, this means that a
$K_{E}$
-rational point that is divisible by
$2$
in
$X_{0}(11)(K_{E,2})$
is already divisible by
$2$
in
$X_{0}(11)(K_{E})$
. Since
$X_{0}(11)$
has no
$K_{E}$
-rational points of exact order
$2$
(none of the fields
$K_{E}$
have non-trivial subfields, so
$\unicode[STIX]{x1D703}\notin K_{E}$
, since
$[\mathbb{Q}(\unicode[STIX]{x1D703}):\mathbb{Q}]=3$
), there is a unique ‘half’ of a point, if there is any. So, if
$P\neq Q\in X_{0}(11)(K_{E})$
has
$j$
-invariant in
$D$
, then the point
$Q^{\prime }$
in the relation in property
$(\ast )$
is also
$K_{E}$
-rational. But then its image in
$L_{E,2}^{\times }/L_{E,2}^{\times 2}$
must be in the image of the Selmer group, which gives a contradiction to
$(\ast )$
. The only remaining possibility for a point
$Q\in X_{0}(11)(K_{E})$
with
$j(Q)\in D$
is then
$P$
and this possibility only exists when
$j(P)\in D$
.◻
It remains to exhibit a suitable point
$P$
for the remaining pairs
$(E,D)$
and to show that it has property
$(\ast )$
. We first have a look at the
$2$
-adic elliptic logarithm on
$X_{0}(11)$
. Let
${\mathcal{K}}\subset X_{0}(11)(\bar{\mathbb{Q}}_{2})$
denote the kernel of reduction. We take
$t=-x/y$
to be a uniformizer at the point at infinity on
$X_{0}(11)$
and write
${\mathcal{K}}_{\unicode[STIX]{x1D708}}=\{P\in {\mathcal{K}}:v_{2}(t(P))>\unicode[STIX]{x1D708}\}$
.
Lemma 7.9. The
$2$
-adic elliptic logarithm
$\log :{\mathcal{K}}\rightarrow \bar{\mathbb{Q}}_{2}$
induces a group isomorphism between
${\mathcal{K}}_{1/3}$
and the additive group
$D_{1/3}=\{\unicode[STIX]{x1D706}\in \bar{\mathbb{Q}}_{2}:v_{2}(\unicode[STIX]{x1D706})>1/3\}$
.
In particular, if
$K$
is a
$2$
-adic field and
$P\in {\mathcal{K}}_{4/3}\cap X_{0}(11)(K)$
, then
$P$
is divisible by
$2$
in
${\mathcal{K}}\cap X_{0}(11)(K)$
.
Proof. Note that the points
$T$
of order
$2$
on
$X_{0}(11)$
satisfy
$v_{2}(t(T))=1/3$
(the
$x$
-coordinate has valuation
$-2/3$
and the
$y$
-coordinate is
$-1/2$
). We also note that
$X_{0}(11)$
is supersingular at
$2$
, so
$X_{0}(11)(\bar{\mathbb{F}}_{2})$
consists of points of odd order. This implies that the kernel of
$\log$
on
${\mathcal{K}}$
consists exactly of the points of order a power of 2. There are no such points
$P$
with
$v_{2}(t(P))>1/3$
, so
$\log$
is injective on this set. Explicitly, we find that for
$P\in {\mathcal{K}}$
with
$t(P)=\unicode[STIX]{x1D70F}$
,
$$\begin{eqnarray}\displaystyle \log P=\unicode[STIX]{x1D70F}-{\textstyle \frac{1}{3}}\unicode[STIX]{x1D70F}^{3}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70F}^{4}-{\textstyle \frac{19}{5}}\unicode[STIX]{x1D70F}^{5}-\unicode[STIX]{x1D70F}^{6}+{\textstyle \frac{5}{7}}\unicode[STIX]{x1D70F}^{7}-{\textstyle \frac{27}{2}}\unicode[STIX]{x1D70F}^{8}+\cdots \,; & & \displaystyle \nonumber\end{eqnarray}$$
for
$v_{2}(\unicode[STIX]{x1D70F})>1/3$
, the first term is dominant, so the image is
$D_{1/3}$
, as claimed.
Now let
$P\in {\mathcal{K}}_{4/3}\cap X_{0}(11)(K)$
. Note that restricting
$\log$
gives us an isomorphism between
${\mathcal{K}}_{1/3}\cap X_{0}(11)(K)$
and
$D_{1/3}\cap K$
. Since
$v_{2}(\unicode[STIX]{x1D70F})>4/3$
, the image of
$P$
in
$D_{1/3}\cap K$
is divisible by
$2$
in
$D_{1/3}\cap K$
, so
$P$
must be divisible by
$2$
in
${\mathcal{K}}\cap X_{0}(11)(K)$
.◻
Lemma 7.10. Let
$K$
be some
$2$
-adic field such that
$X_{0}(11)(K)[2]=0$
and consider an analytic map
$\unicode[STIX]{x1D719}:\mathbb{Z}_{2}\rightarrow {\mathcal{K}}\cap X_{0}(11)(K)$
that converges on the open disk
$D_{-c}=\{\unicode[STIX]{x1D70F}\in \mathbb{C}_{2}:v_{2}(\unicode[STIX]{x1D70F})>-c\}$
for some
$c>0$
; we assume that there is some
$\unicode[STIX]{x1D708}\in \mathbb{Q}_{{>}1/3}$
such that
$|t(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F}))|=|2|^{\unicode[STIX]{x1D708}}\,|\unicode[STIX]{x1D70F}|$
for all
$\unicode[STIX]{x1D70F}\in D_{-c}$
. (This implies that
$\unicode[STIX]{x1D719}(0)$
is the point at infinity.) We set
$\unicode[STIX]{x1D707}=\lceil \unicode[STIX]{x1D708}-{\textstyle \frac{1}{3}}\rceil -1\in \mathbb{Z}_{{\geqslant}0}$
.
Then, for each
$\unicode[STIX]{x1D70F}\in \mathbb{Z}_{2}\setminus \{0\}$
, there is a unique
$Q_{\unicode[STIX]{x1D70F}}\in {\mathcal{K}}\cap X_{0}(11)(K)$
such that
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})=2^{\unicode[STIX]{x1D707}+v_{2}(\unicode[STIX]{x1D70F})}Q_{\unicode[STIX]{x1D70F}}$
. If
$\unicode[STIX]{x1D70F}\in \mathbb{Z}_{2}^{\times }$
, then
$Q_{\unicode[STIX]{x1D70F}}\equiv Q_{1}\hspace{0.2em}{\rm mod}\hspace{0.2em}2X_{0}(11)(K)$
. If
$\unicode[STIX]{x1D708}-\unicode[STIX]{x1D707}+\min \{1,c,\unicode[STIX]{x1D708}-{\textstyle \frac{1}{3}}\}>{\textstyle \frac{4}{3}}$
, then this remains true for arbitrary
$\unicode[STIX]{x1D70F}\in \mathbb{Z}_{2}\setminus \{0\}$
. Otherwise, we have that
$Q_{\unicode[STIX]{x1D70F}}\equiv Q_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}2X_{0}(11)(K)$
if
$\unicode[STIX]{x1D70F}\in 2\mathbb{Z}_{2}\setminus \{0\}$
.
Proof. Fix
$0\neq \unicode[STIX]{x1D70F}\in \mathbb{Z}_{2}$
and write
$n=v_{2}(\unicode[STIX]{x1D70F})$
. By assumption, we have that
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})\in {\mathcal{K}}_{\unicode[STIX]{x1D708}+n}$
. Since
$\unicode[STIX]{x1D708}>1/3+\unicode[STIX]{x1D707}$
, this implies that
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})$
is divisible by
$2^{\unicode[STIX]{x1D707}+n}$
in
${\mathcal{K}}\cap X_{0}(11)(K)$
by Lemma 7.9. Since
$X_{0}(11)(K)[2]=0$
, there is then a unique point
$Q_{\unicode[STIX]{x1D70F}}\in {\mathcal{K}}\cap X_{0}(11)(K)$
such that
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})=2^{\unicode[STIX]{x1D707}+n}Q_{\unicode[STIX]{x1D70F}}$
. We now consider
$$\begin{eqnarray}\displaystyle \log \unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70F}+a_{2}\unicode[STIX]{x1D70F}^{2}+a_{3}\unicode[STIX]{x1D70F}^{3}+\cdots \,). & & \displaystyle \nonumber\end{eqnarray}$$
We know by assumption and by Lemma 7.9 and its proof that
$|\text{log}\,\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})|=|t(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F}))|=|2|^{\unicode[STIX]{x1D708}}\,|\unicode[STIX]{x1D70F}|$
whenever
$v_{2}(\unicode[STIX]{x1D70F})>-\min \{c,\unicode[STIX]{x1D708}-{\textstyle \frac{1}{3}}\}$
(for
$\unicode[STIX]{x1D70F}\in \mathbb{C}_{2}$
). This implies that
$v_{2}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D708}$
and that
$$\begin{eqnarray}\displaystyle v_{2}(a_{k})\geqslant (k-1)\min \{c,\unicode[STIX]{x1D708}-{\textstyle \frac{1}{3}}\}\quad \text{for all }k\geqslant 2. & & \displaystyle \nonumber\end{eqnarray}$$
Writing
$\unicode[STIX]{x1D70F}=2^{n}u$
with
$u\in \mathbb{Z}_{2}^{\times }$
, we then have that
$$\begin{eqnarray}\displaystyle \log Q_{\unicode[STIX]{x1D70F}}=2^{-\unicode[STIX]{x1D707}-n}\log \unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6FE}2^{-\unicode[STIX]{x1D707}}(u+2^{n}a_{2}u^{2}+2^{2n}a_{3}u^{3}+\cdots \,) & & \displaystyle \nonumber\end{eqnarray}$$
and so
$$\begin{eqnarray}\displaystyle \log (Q_{\unicode[STIX]{x1D70F}}-Q_{1})=\log Q_{\unicode[STIX]{x1D70F}}-\log Q_{1}=\unicode[STIX]{x1D6FE}2^{-\unicode[STIX]{x1D707}}((u-1)+a_{2}(2^{n}u^{2}-1)+a_{3}(2^{2n}u^{3}-1)+\cdots \,). & & \displaystyle \nonumber\end{eqnarray}$$
If
$n=0$
, then
$v_{2}(\log (Q_{\unicode[STIX]{x1D70F}}-Q_{1}))\geqslant \unicode[STIX]{x1D708}-\unicode[STIX]{x1D707}+1>{\textstyle \frac{4}{3}}$
and, if
$\unicode[STIX]{x1D708}-\unicode[STIX]{x1D707}+\min \{1,c,\unicode[STIX]{x1D708}-{\textstyle \frac{1}{3}}\}>{\textstyle \frac{4}{3}}$
, then
$v_{2}(\log (Q_{\unicode[STIX]{x1D70F}}-Q_{1}))\geqslant \unicode[STIX]{x1D708}-\unicode[STIX]{x1D707}+\min \{1,v_{2}(a_{2}),v_{2}(a_{3}),\ldots \}>{\textstyle \frac{4}{3}}$
, so in both cases Lemma 7.9 shows that
$Q_{\unicode[STIX]{x1D70F}}-Q_{1}$
is divisible by
$2$
in
${\mathcal{K}}\cap X_{0}(11)(K)$
. If
$n\geqslant 1$
, then we find that
$$\begin{eqnarray}\displaystyle \log (Q_{\unicode[STIX]{x1D70F}}-Q_{2})=\unicode[STIX]{x1D6FE}2^{-\unicode[STIX]{x1D707}}((u-1)+2a_{2}(2^{n-1}u^{2}-1)+2^{2}a_{3}(2^{2n-2}u^{3}-1)+\cdots \,) & & \displaystyle \nonumber\end{eqnarray}$$
and we see that this has
$2$
-adic valuation
${>}{\textstyle \frac{4}{3}}$
, so
$Q_{\unicode[STIX]{x1D70F}}-Q_{2}$
is divisible by
$2$
.◻
Remark 7.11. We will apply this lemma in the following setting. We consider one of the remaining sets
$D\in {\mathcal{D}}$
and a point
$P\in X_{0}(11)(K_{E})$
such that
$j(P)\in D$
. Then there is an analytic map
$\unicode[STIX]{x1D713}:\mathbb{Z}_{2}\stackrel{\simeq }{\rightarrow }D\rightarrow X_{0}(11)(K_{E,2})$
such that
$\unicode[STIX]{x1D713}(0)=P$
and such that the second map in this composition inverts the
$j$
function. We set
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70F})-P$
; then
$\unicode[STIX]{x1D719}$
is an analytic map into
${\mathcal{K}}\cap X_{0}(11)(K_{E,2})$
which satisfies a polynomial relation
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70F},t(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})))=0$
, where
$\unicode[STIX]{x1D6F7}\in K_{E}[x,y]$
has degree 3 in
$x$
and degree
$12$
in
$y$
(this is because
$j:X_{0}(11)\rightarrow \mathbb{P}^{1}$
has degree
$12$
and
$t:X_{0}(11)\rightarrow \mathbb{P}^{1}$
has degree 3). We find
$\unicode[STIX]{x1D6F7}$
explicitly by interpolation: we compute the pairs
$(j(Q),t(Q))$
for all points
$Q=nP+T$
, where
$-5\leqslant n\leqslant 5$
and
$T\in X_{0}(11)(\mathbb{Q})_{\operatorname{tors}}\simeq \mathbb{Z}/5\mathbb{Z}$
. This gives us enough information to determine the
$52$
coefficients of
$\unicode[STIX]{x1D6F7}$
(up to scaling). We then use Lemma 7.5 to show that
$\unicode[STIX]{x1D719}$
actually converges for
$v_{2}(\unicode[STIX]{x1D70F})>-c$
for some
$c>1/3$
and that
$v_{2}(t(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F})))=\unicode[STIX]{x1D708}+v_{2}(\unicode[STIX]{x1D70F})$
for
$v_{2}(\unicode[STIX]{x1D70F})>-c$
(where
$\unicode[STIX]{x1D708}=2$
,
$3$
or
$5/11$
in the concrete cases considered). Finally, we check that
$Q_{1}$
does not map into the image of the Selmer group (and that
$Q_{2}$
does not, either, in the last case). This then verifies condition
$(\ast )$
for
$D$
,
$E$
and
$P$
.
Lemma 7.12. Let
$E\in {\mathcal{E}}$
and let
$D\in {\mathcal{D}}$
be one of the sets associated to
$E$
in Lemma 7.7. Then the point
$P$
given in the table below satisfies
$(\ast )$
for
$E$
and
$D$
. Here
$\operatorname{can}(E)$
stands for the image on
$X_{0}(11)$
of the canonical point on
$X_{E}(11)$
.
Proof. The points
$P$
given in the table have the property that their image in
$G=L_{E,2}^{\times }/L_{E,2}^{\times 2}$
agrees with the image of those points in
$j^{-1}(D)\cap X_{0}(11)(K_{E,2})$
whose image is in the image of the Selmer group. This means that for any point
$Q$
in one of the
$2$
-adic disks above
$D$
such that
$Q$
maps into the image of the Selmer group, we have that
$P-Q$
is divisible by 2 in
$X_{0}(11)(K_{E,2})$
.
We first consider the last three cases. In the last two cases only one (out of 16) of the disks above
$D$
maps into the image of the Selmer group; this must be the disk containing the image of the canonical point. For
$96a1$
, we use Fisher’s explicit description of
$X_{E}(11)$
and the
$j$
-map on it [Reference FisherFis14] to obtain a partition of
$X_{96a1}(11)(\mathbb{Q}_{2})$
into
$2$
-adic disks; we find that there is only one residue disk in
$X_{96a1}(11)(\mathbb{Q}_{2})$
that maps to
$D$
. Its image in
$X_{0}(11)(K_{96a1,2})$
must be one of the disks above
$D$
and this disk contains the image of the canonical point; the other disks above
$D$
can be excluded. So, in each of these three cases, the only disk in
$X_{0}(11)(K_{E,2})$
above
$D$
that we have to consider is the disk
$D^{\prime }$
containing the image of the canonical point. We then follow the approach outlined in Remark 7.11 above to verify
$(\ast )$
for each of the last three entries in the table.
Next we consider the other disk
$D$
for
$E=96a1$
; this is the second entry in the table. There are four disks
$D^{\prime }$
in
$X_{0}(11)(K_{E,2})$
above
$D$
such that the image of
$D^{\prime }$
in
$G$
is in the image of the Selmer group; this image is the same as that of
$P$
. Taking the difference with
$P$
and halving, we find that on three of these disks the image in
$G$
of the resulting points is not in the image of the Selmer group. On the fourth disk, the image is zero, so the points are again divisible by
$2$
. After halving again, we find that the resulting points have image in
$G$
not in the image of the Selmer group. This verifies
$(\ast )$
for this case (with
$n\leqslant 2$
).
Finally, we look at
$E=54a1$
. There is one unramified branch above
$j=\infty$
with the point at infinity of
$X_{0}(11)$
sitting in the center of the disk and there is one point (with coordinates
$(16,60)$
) with ramification index
$11$
. We can parameterize the disk relevant to us by setting
$j=2^{-5}\unicode[STIX]{x1D70F}^{-11}$
and solving for the
$x$
- and
$y$
-coordinates in
$\mathbb{Q}(\!\sqrt[11]{2})(\!(\unicode[STIX]{x1D70F})\!)$
. We use the alternative uniformizer
$t^{\prime }=-(x-5)/(y-5)$
at the origin (the standard uniformizer
$t$
does not work well in this case, because it is
$2$
-adically small on the other branch above
$j=\infty$
), which has the additional benefit that it is of degree
$2$
instead of
$3$
as a function on
$X_{0}(11)$
, leading to a smaller polynomial
$\unicode[STIX]{x1D6F7}$
. The statements of Lemmas 7.9 and 7.10 are unaffected by this change of uniformizer. Using the approach of Remark 7.11, we find that the series
$\unicode[STIX]{x1D719}$
of Lemma 7.10 converges for
$v_{2}(\unicode[STIX]{x1D70F})>-5/11$
and satisfies
$v_{2}(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70F}))=5/11+v_{2}(\unicode[STIX]{x1D70F})$
. We can also check that for
$\unicode[STIX]{x1D70F}=1$
and for
$\unicode[STIX]{x1D70F}=2$
, we obtain a point whose image in
$G$
is not in the image of the Selmer group, so
$(\ast )$
is verified in this case, too.◻
To conclude the proof of Theorem 7.1, it now only remains to observe that the
$j$
-invariants
$21952/9$
of
$96a1$
and
$1536$
of
$864c1$
are not good (the condition on the
$3$
-adic valuation is violated), so the only remaining point in
$X_{96a1}(11)(\mathbb{Q})$
and in
$X_{864c1}(11)(\mathbb{Q})$
does not lead to a primitive integral solution of our generalized Fermat equation. The only remaining point in
$X_{864b1}(11)(\mathbb{Q})$
is the canonical point; it corresponds to the Catalan solutions.
Remark 7.13. According to work by Ligozat [Reference LigozatLig77], the Jacobian
$J(11)$
of
$X(11)$
splits up to isogeny (and over
$\mathbb{Q}(\sqrt{-11})$
) into a product of 11 copies of
$X_{0}(11)$
, 10 copies of a second elliptic curve and five copies of a third elliptic curve (which is
$X_{\operatorname{ns}}^{+}(11)=121b1$
). The powers of these three elliptic curves correspond to isotypical components of the representation of the automorphism group of the
$j$
-map
$X(11)\rightarrow \mathbb{P}^{1}$
on the Lie algebra of
$J(11)$
; the splitting into these three powers therefore persists over
$\mathbb{Q}$
after twisting. Our approach uses the
$11$
-dimensional factor (it can be identified with the kernel of the trace map from
$R_{K_{E}/\mathbb{Q}}X_{0}(11)_{K_{E}}$
to
$X_{0}(11)$
, up to isogeny). It would be nice if one could use the five-dimensional factor instead in the hope of eliminating the dependence on GRH, but so far we have not found a description that would allow us to work over a smaller field.
8 The generalized Fermat equation with exponents 2, 3, 13
In this section we collect some partial results for the case
$p=13$
. More precisely, we show that the Frey curve associated to any putative solution must have an irreducible
$13$
-torsion Galois module and that only trivial solutions can be associated to the two CM curves in the list of Lemma 2.3.
8.1 Eliminating reducible 13-torsion
The case
$p=13$
is special in the sense that it is a priori possible to have Frey curves with reducible
$13$
-torsion Galois modules. In this respect, it is similar to
$p=7$
; compare [Reference Poonen, Schaefer and StollPSS07]. To deal with this possibility, we note that such a Frey curve
$E$
will have a Galois-stable subgroup
$C$
of order
$13$
and so gives rise to a rational point
$P_{E}$
on
$X_{0}(13)$
, which is a curve of genus
$0$
. The Galois action on
$C$
is via some character
$\unicode[STIX]{x1D712}:G_{\mathbb{Q}}\rightarrow \mathbb{F}_{13}^{\times }$
, which can be ramified at most at
$2$
,
$3$
and
$13$
. Associated to
$\unicode[STIX]{x1D712}$
is a twist
$X_{\unicode[STIX]{x1D712}}(13)$
of
$X_{1}(13)$
that classifies elliptic curves with a cyclic subgroup of order
$13$
on which the Galois group acts via
$\unicode[STIX]{x1D712}$
; the Frey curve
$E$
corresponds to a rational point on
$X_{\unicode[STIX]{x1D712}}(13)$
that maps to
$P_{E}$
under the canonical covering map
$X_{\unicode[STIX]{x1D712}}(13)\rightarrow X_{0}(13)$
. The covering
$X_{1}(13)\rightarrow X_{0}(13)$
is Galois of degree
$6$
with Galois group naturally isomorphic to
$\mathbb{F}_{13}^{\times }/\{\pm 1\}$
; the coverings
$X_{\unicode[STIX]{x1D712}}(13)\rightarrow X_{0}(13)$
are twisted forms of it, corresponding to the composition
$$\begin{eqnarray}\displaystyle G_{\mathbb{Q}}\stackrel{\unicode[STIX]{x1D712}}{\longrightarrow }\mathbb{F}_{13}^{\times }\longrightarrow \mathbb{F}_{13}^{\times }/\{\pm 1\}\simeq \mathbb{Z}/6\mathbb{Z}, & & \displaystyle \nonumber\end{eqnarray}$$
which is an element of
$H^{1}(\mathbb{Q},\mathbb{Z}/6\mathbb{Z};\{2,3,13\})$
(we write
$H^{1}(K,M;S)$
to denote the subgroup of
$H^{1}(K,M)$
of cocycle classes unramified outside
$S$
). We can describe this group in the form
where
$\unicode[STIX]{x1D714}$
is a primitive cube root of unity. One can check that a model of
$X_{1}(13)$
is given by
$$\begin{eqnarray}\displaystyle y^{2}=(v+2)^{2}+4,\quad z^{3}-vz^{2}-(v+3)z-1=0; & & \displaystyle \nonumber\end{eqnarray}$$
the map to
$X_{0}(13)\simeq \mathbb{P}^{1}$
is given by the
$v$
-coordinate. The second equation can be written in the form
$$\begin{eqnarray}\displaystyle \biggl(\frac{z-\unicode[STIX]{x1D714}}{z-\unicode[STIX]{x1D714}^{2}}\biggr)^{3}=\frac{v-3\unicode[STIX]{x1D714}}{v-3\unicode[STIX]{x1D714}^{2}}, & & \displaystyle \nonumber\end{eqnarray}$$
which shows that it indeed gives a cyclic covering of
$\mathbb{P}_{v}^{1}$
by
$\mathbb{P}_{z}^{1}$
. If
$d$
is a squarefree integer representing an element in
$\langle -1,2,3,13\rangle _{\mathbb{Q}^{\times }/\mathbb{Q}^{\times 2}}$
and
$\unicode[STIX]{x1D6FE}$
represents an element of
$\langle \unicode[STIX]{x1D714},(4+\unicode[STIX]{x1D714})/(3-\unicode[STIX]{x1D714})\rangle _{\mathbb{Q}(\unicode[STIX]{x1D714})^{\times }/\mathbb{Q}(\unicode[STIX]{x1D714})^{\times 3}}$
, then the corresponding twist is
$$\begin{eqnarray}\displaystyle X_{\unicode[STIX]{x1D712}}(13):dy^{2}=(v+2)^{2}+4,\quad \unicode[STIX]{x1D6FE}\biggl(\frac{z-\unicode[STIX]{x1D714}}{z-\unicode[STIX]{x1D714}^{2}}\biggr)^{3}=\frac{v-3\unicode[STIX]{x1D714}}{v-3\unicode[STIX]{x1D714}^{2}}. & & \displaystyle \nonumber\end{eqnarray}$$
We note that the first equation defines a conic that has no real points when
$d<0$
and has no
$3$
-adic points when
$3\mid d$
. This restricts us to
$d\in \{1,2,13,26\}$
. We find hyperelliptic equations for the
$36$
remaining curves (recall that
$X_{1}(13)$
has genus
$2$
). It turns out that only eight of them have
$\ell$
-adic points for
$\ell \in \{2,3,13\}$
. We list them in Table 7. In the table, we give
$d$
and
$\unicode[STIX]{x1D6FF}$
, where
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FF}/\bar{\unicode[STIX]{x1D6FF}}$
and the bar denotes the non-trivial automorphism of
$\mathbb{Q}(\unicode[STIX]{x1D714})$
. We denote the curve in row
$i$
of the table by
$C_{i}$
.
Table 7. Curves
$X_{\unicode[STIX]{x1D712}}(13)$
with local points, given as
$y^{2}=f(x)$
.
We see that the last four curves are isomorphic to the first four. This is because of the canonical isomorphism
$X_{1}(13)\simeq X_{\unicode[STIX]{x1D707}}(13)$
, where the latter classifies elliptic curves with a subgroup isomorphic to
$\unicode[STIX]{x1D707}_{13}$
. On the level of
$X_{0}(13)$
, this comes from the Atkin–Lehner involution, which in terms of our coordinate
$v$
is given by
$v\mapsto (v+12)/(v-1)$
.
The first curve
$C_{1}$
is
$X_{1}(13)$
; it is known that its Jacobian has Mordell–Weil rank zero and that the only rational points on
$X_{1}(13)$
are six cusps (there are no elliptic curves over
$\mathbb{Q}$
with a rational point of order
$13$
). For the curves
$C_{2}$
,
$C_{3}$
and
$C_{4}$
, a
$2$
-descent on the Jacobian as in [Reference StollSto01] gives an upper bound of 2 for the rank. The curves
$C_{2}$
and
$C_{4}$
each have six more or less obvious rational points; their differences generate a subgroup of rank
$2$
of the Mordell–Weil group, so their Jacobians indeed have rank
$2$
. On
$C_{3}$
, one does not find small rational points and indeed it turns out that its
$2$
-Selmer set is empty, which proves that it has no rational points. See [Reference Bruin and StollBS09] for how to compute the
$2$
-Selmer set. It remains to consider
$C_{2}$
and
$C_{4}$
.
We note that the
$j$
-invariant map on
$\mathbb{P}_{v}^{1}\simeq X_{0}(13)$
is given by
$$\begin{eqnarray}\displaystyle j=\frac{(v^{2}+3v+9)(v^{4}+3v^{3}+5v^{2}-4v-4)^{3}}{v-1}. & & \displaystyle \nonumber\end{eqnarray}$$
The obvious orbits of points on the six curves that do have rational points then give points on
$X_{0}(13)$
with
$v=\infty$
,
$0$
,
$-4$
,
$1$
,
$-12$
,
$-8/5$
and
$j$
-invariants
$$\begin{eqnarray}\displaystyle \infty ,\quad \frac{12^{3}}{3},\quad -\frac{12^{3}\cdot 13^{4}}{5},\quad \infty ,\quad -\frac{12^{3}\cdot 4079^{3}}{3},\quad -\frac{12^{3}\cdot (17\cdot 29)^{3}\cdot 13}{5^{13}}, & & \displaystyle \nonumber\end{eqnarray}$$
respectively. None of these correspond to primitive solutions of
$x^{2}+y^{3}=z^{13}$
, except
$j=\infty$
, which is related to the trivial solutions
$(\pm 1,-1,0)$
. So, to rule out solutions whose Frey curves have reducible
$13$
-torsion, it will suffice to show that there are no rational points on
$C_{2}$
and
$C_{4}$
other than the orbit of six points containing the points at infinity.
Computing the
$2$
-Selmer sets, we find in both cases that its elements are accounted for by the points in the known orbit. So, in each orbit of rational points under the action of the automorphism group, there is a point that lifts to the
$2$
-covering of the curve that lifts the two points at infinity. So, it is enough to look at rational points on this
$2$
-covering.
We first consider
$C_{2}$
. Its polynomial
$f$
splits off three linear factors over
$K$
, where
$K$
is the field obtained by adjoining one of the roots
$\unicode[STIX]{x1D6FC}$
of
$f$
to
$\mathbb{Q}$
. The relevant
$2$
-covering then maps over
$K$
to the curve
$y^{2}=(x-\unicode[STIX]{x1D6FC})g(x)$
, where
$g$
is the remaining cubic factor. This is an elliptic curve (with two
$K$
-points at infinity and one with
$x=\unicode[STIX]{x1D6FC}$
). Computing its
$2$
-Selmer group (this involves obtaining the class group of a number field of degree
$18$
, which we can do without assuming GRH; the computation took a few days), we find that it has rank
$1$
. We know three
$K$
-points on the elliptic curve; they map surjectively onto the Selmer group. So, we can do an elliptic curve Chabauty computation, which tells us that the only
$K$
-points whose
$x$
-coordinate is rational are the two points at infinity. This in turn implies that the known rational points on
$C_{2}$
are the six points in the orbit of the points at infinity.
Now we consider
$C_{4}$
. Here the field generated by a root of
$f$
is actually Galois (with group
$S_{3}$
). We work over its cubic subfield
$L$
. Over
$L$
,
$f$
splits as
$16$
times the product of three monic quadratic factors
$h_{1}$
,
$h_{2}$
,
$h_{3}$
and we consider the elliptic curve
$E$
given as
$y^{2}=h_{1}(x)h_{2}(x)$
, with one of the points at infinity as the origin. This curve has full
$2$
-torsion over
$L$
, so a
$2$
-descent is easily done unconditionally. We find that the
$2$
-Selmer group has rank
$3$
and that the difference of the two points at infinity has infinite order, so the Mordell–Weil rank of
$E$
over
$L$
is
$1$
. An elliptic curve Chabauty computation then shows that the only
$K$
-points on
$E$
with rational
$x$
-coordinate are those at infinity and those with
$x$
-coordinate
$-3$
. Since there are no rational points on
$C_{4}$
with
$x$
-coordinate
$-3$
, this shows as above for
$C_{2}$
that the only rational points are the six points in the orbit of the points at infinity.
This proves the following statement.
Lemma 8.1. Let
$(a,b,c)\in \mathbb{Z}^{3}$
be a non-trivial primitive solution of
$x^{2}+y^{3}=z^{13}$
. Then the
$13$
-torsion Galois module
$E_{(a,b,c)}[13]$
of the associated Frey curve is irreducible.
8.2 Dealing with the CM curves
The number
$13$
is congruent to
$1$
both mod
$3$
and mod
$4$
, so the
$13$
-torsion Galois representations on
$27a1$
and on
$288a1$
both have image contained in the normalizer of a split Cartan subgroup. But unfortunately the general result of [Reference Bilu, Parent and RebolledoBPR13] does not apply in this case. We can, however, use the approach taken in § 8.1 above. Since we are in the split case, the curves have cyclic subgroups of order
$13$
defined over a quadratic field
$K$
, which is
$\mathbb{Q}(\unicode[STIX]{x1D714})$
for
$27a1$
(with
$\unicode[STIX]{x1D714}$
a primitive cube root of unity) and
$\mathbb{Q}(i)$
for
$288a1$
. We find the twist of
$X_{1}(13)$
over
$K$
that corresponds to the Galois representation over
$K$
on this cyclic subgroup. Finding the twist is not entirely trivial, since the points on
$X_{0}(13)$
corresponding to
$27a1$
or to
$288a1$
are branch points for the covering
$X_{1}(13)\rightarrow X_{0}(13)$
(of ramification degree
$3$
, respectively
$2$
). In the case of
$27a1$
, we use a little trick: the isogenous curve
$27a2$
has isomorphic Galois representation, but
$j$
-invariant
$\neq 0$
, so the corresponding point in
$X_{0}(13)(K)$
lifts to a unique twist, which must be the correct one also for
$27a1$
. Since cube roots of unity are in
$K$
, we can make a coordinate change so that the automorphism of order 3 is given by multiplying the
$x$
-coordinate by
$\unicode[STIX]{x1D714}$
. We obtain the following simple model over
$K=\mathbb{Q}(\unicode[STIX]{x1D714})$
of the relevant twist of
$X_{1}(13)$
:
$$\begin{eqnarray}\displaystyle C_{27a1}:y^{2}=x^{6}+22x^{3}+13. & & \displaystyle \nonumber\end{eqnarray}$$
The points coming from
$27a1$
are the two points at infinity, and the points coming from
$27a2$
are the six points whose
$x$
-coordinate is a cube root of unity.
For
$288a1$
, we figure out the quadratic part of the sextic twist (the cubic part is unique in this case) by looking at the Galois action on the cyclic subgroup explicitly. We find that the correct twist of
$X_{1}(13)$
is
$$\begin{eqnarray}\displaystyle C_{288a1}:y^{2}=12ix^{5}+(30i+33)x^{4}+66x^{3}+(-30i+33)x^{2}-12ix. & & \displaystyle \nonumber\end{eqnarray}$$
Here the points coming from
$288a1$
are the ramification points
$(0,0)$
and
$(-1,0)$
and the (unique) point at infinity. There are (at least) six further points over
$\mathbb{Q}(i)$
on this curve, forming an orbit under the automorphism group, of which
$((4i-3)/6,35/36)$
is a representative.
As a first step, we compute the
$2$
-Selmer group of the Jacobian
$J$
of each of the two curves. In both cases, we find an upper bound of 2 for the rank of
$J(K)$
. The differences of the known points on the curve generate a group of rank 2, so we know a subgroup of finite index of
$J(K)$
. It is easy to determine the torsion subgroup, which is
$\mathbb{Z}/3\mathbb{Z}$
for
$C_{27a1}$
and
$\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
for
$C_{288a1}$
. Using the reduction modulo several good primes of
$K$
, we check that our subgroup is saturated at the primes dividing the group order of the reductions for the primes above
$7$
for
$C_{27a1}$
or the primes above
$5$
for
$C_{288a1}$
. We also use this reduction information for a bit of Mordell–Weil sieving (compare [Reference Bruin and StollBS10]) to show that any point in
$C_{27a1}(\mathbb{Q}(\unicode[STIX]{x1D714}))$
with rational
$j$
-invariant must reduce modulo both primes above
$7$
to the image of one of the known eight points (the same for both primes) and that any point in
$C_{288a1}(\mathbb{Q}(i))$
with rational
$j$
-invariant must reduce modulo both primes above
$5$
to the image of one of the three points coming from
$288a1$
(the other six points have
$j$
in
$\mathbb{Q}(i)\setminus \mathbb{Q}$
).
It remains to show that these points are the only points in their residue classes mod
$7$
(respectively, mod
$5$
). For this, we use the criterion in [Reference SiksekSik13, Theorem 2]. We compute the integrals to sufficient precision and then check that the pair of differentials killing
$J(K)$
is ‘transverse’ mod
$7$
(or mod
$5$
) at each of the relevant points, which comes down to verifying the assumption in Siksek’s criterion. Note that we apply Chabauty’s method for a genus
$2$
curve when the rank is 2; this is possible because we are working over a quadratic field. See the discussion in [Reference SiksekSik13, § 2].
We obtain the following result.
Lemma 8.2. Let
$(a,b,c)\in \mathbb{Z}^{3}$
be a non-trivial primitive solution of
$x^{2}+y^{3}=z^{13}$
. Then the
$13$
-torsion Galois module
$E_{(a,b,c)}[13]$
of the associated Frey curve is, up to quadratic twist, symplectically isomorphic to
$E[13]$
for some
$E\in \{96a2,864a1,864b1,864c1\}$
.
Proof. By Lemma 8.1,
$E_{(a,b,c)}[13]$
is irreducible, so, by Theorem 5.1, it is symplectically isomorphic to
$E[13]$
, where
$E$
is one of the given curves or one of the CM curves
$27a1$
,
$288a1$
or
$288a2$
. These latter three are excluded by the computations reported on above.◻
A Magma script that performs the necessary computations for the results in this section is available as section8.magma at [Reference StollSto] and as supplementary material. It relies on X1_13_opt.magma, which is available at the same locations.
9 Possible extensions
Since
$X_{0}(17)$
and
$X_{0}(19)$
are elliptic curves like
$X_{0}(11)$
, the approach taken in this paper to treat the case
$p=11$
has a chance to also work for
$p=17$
and/or
$p=19$
. Since
$X_{0}(17)$
has a rational point of order
$4$
and
$X_{0}(19)$
has a rational point of order
$3$
, suitable Selmer groups can be computed with roughly comparable effort (requiring arithmetic information of number fields of degree
$36$
or
$40$
). This is investigated in ongoing work by the authors. For
$p=13$
, results beyond those obtained in the preceding section are likely harder to obtain than for
$p=17$
or
$p=19$
, since
$X_{0}(13)$
is a curve of genus
$0$
. We can try to work with twists of
$X_{1}(13)$
, which is a curve of genus 2; our approach would require us to find the (relevant) points on such a twist over a field of degree
$14$
. The standard method of
$2$
-descent on the Jacobian of such a curve would require working with a number field of degree
$6\cdot 14=84$
, which is beyond the range of feasibility of current algorithms (even assuming GRH).
Source code
Magma scripts that perform the various computations are available at [Reference StollSto] and as supplementary material with the online version of this article available at https://doi.org/10.1112/S0010437X19007693.
Acknowledgements
We thank David Zureick-Brown for sharing his notes with us and Jean-Pierre Serre for pointing us to Ligozat’s work on the splitting of
$J(11)$
. We also thank an anonymous referee for some useful comments. We have used the Magma computer algebra system [Reference Bosma, Cannon and PlayoustBCP97] for the necessary computations.
