1. INTRODUCTION
In the last few years, significant progress in ultrashort pulse
generation (Batani & Wooton, 2004; Fuerbach et al., 2005) has obtained a pulse
duration τp compared to an oscillation period
corresponding to a fundamental frequency ω of laser radiation (Zavelani-Rossi et al., 2002; Schenkel et al., 2003). Such short pulses
react to a solid target by producing plasma at the target surface with a
solid-state density, n ≈ 1023–1024
cm−3, moreover, if the pulse power is relatively low, the
electron temperature is also low. If this is the case, a hydrodynamic
expansion of the plasma and the corresponding change of the density are
negligible at the time scale ∼τp, that is, one
can assume an abrupt plasma interface. Since the plasma density is high,
the frequency ν of electron collisions at an electron temperature of
tens of electron-volts significantly exceeds the fundamental frequency of
radiation ω and the mean free electron path l is much
smaller than the depth of the skin layer d that corresponds to
conditions of a normal skin effect. The electron heating is caused by
collisions with ions and their cooling is caused by heat removal deep into
the plasma, moreover, due to condition l << d, the
heat transport can be described within the Spitzer–Harm
approximation. Such representations of the ultrashort laser pulse
interaction with a dense plasma are on the basis of several theoretical
researches (Rozmus & Tikhonchuk, 1990; Rozmus et al., 1996; Honrubia & Tikhonchuk, 2004; Isakov et al., 2004), mainly devoted to the
studies of the influence of the electron temperature evolution in the skin
layer on the laser radiation absorption and reflection, as well as to
study the heat removal from the skin layer. In this connection, the
conditions where the electron temperature changes during the time above
the period of the light field oscillations ∼1/ω are under
consideration, and the pulse duration is so high that an influence of
effects arising due to its finiteness can be eliminated. At the same time,
an inverse situation is possible where the electron heating occurs during
the time shorter than ∼1/ω and the pulse duration is
commensurable to ∼1/ω. Under such conditions, first it is
necessary to take into account the change of the electron temperature in
the course of the field penetration into the plasma, and second the
moments of the laser pulse switching-on and switching-off must be taken
into account. An account for the influence of these effects on the
patterns of a high-power ultrashort laser pulse interaction with dense
plasma is the aim of this paper.
2. GENERAL RELATIONSHIPS
Let us consider the interaction of an electromagnetic pulse with
plasma occupying the space region z > 0. We assume that the
pulse normally incidences on the plasma surface and the distribution of
its electric and magnetic fields is described by relationships
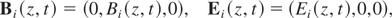
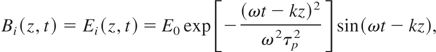
where E0 is the strength of the electric field,
k = (0,0,k) is the wave vector, ω = kc is
the fundamental radiation frequency, c is the speed of light, and
τp is the pulse duration. Fields of type (1) and
(2) satisfy the Maxwell equations in vacuum. The electromagnetic pulse is
partially reflected by the plasma. According to the Maxwell equations, the
reflected field is of the form
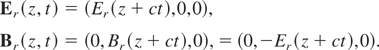
The incident and reflected fields are connected with the fields
E and B inside the plasma,
E(z,t) =
(E(z,t),0,0) and
B(z,t) =
(0,B(z,t),0). The electric field inside the
plasma significantly depends on the form of connection between the current
density j(z,t) and the field
E(z,t). Further we consider, sufficiently dense
hot plasmas where the electron plasma frequency
ωL =
(4πe2n/m)1/2
is much higher than the frequency of electron–ion collisions ν =
4πZe4nΛm−2vT−3,
where e and m are the electron charge and mass,
n and vT are the electron density
and thermal velocity, Λ is the Coulomb logarithm, and Z is
the ionization degree of ions. For a wide class of hot plasmas Z
>> 1 that is further assumed. We also assume that the collision
frequency ν is much higher than typical frequencies of changing the
electron temperature T and electric field E, and a mean
free path of thermal electrons [ell ] = vT
/ν are much less than typical scales of the field and temperature
inhomogeneities. Besides, let us assume that the electric field strength
is rather small, providing the following inequality:
.
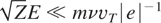
Within the framework of the assumptions made, a local in space and time
linear relation between the current density and the field takes place:
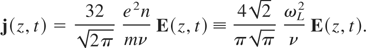
Using relation (4) for the field in the plasma, one has the following
approximate equation:
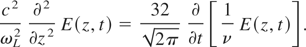
Eq. (5) should be supplemented by an initial and two boundary
conditions. The initial condition corresponds to the fact that for
t → −∞ there is no electromagnetic field in the
plasma,
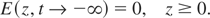
The tangential components of the electric and magnetic fields are
continuous at the plasma boundary. Taking this into account, one has with
the same accuracy as for Eq. (5)
The second boundary condition corresponds to the absence of the field
deep in the plasma,
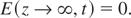
The frequency of electron–ion collisions, entering Eq. (5),
depends on the temperature. Since ∂ ln ν/∂t =
−(3/2)∂ ln T/∂t, the changing in
time of the collision frequency is determined by the corresponding
changing in time of the electron temperature. The evolution of the
electron temperature in the plasma is described by the following
equation
where kB is the Boltzmann constant,
Q(z,t) is the Joule heat released at point
z and at time t,
q(z,t) is the heat-flux density deep in the
plasma,
is the Spitzer–Harm factor of heat conductivity. Note that in
conditions under consideration an increase in temperature is
insignificant. That is why the ratio of the mean free electron path to the
typical scale of temperature inhomogeneity is relatively low during the
period of laser pulse action. Thus above-thermal electrons cannot
influence the energy removal from the skin layer to an extent providing
significant deviations from the Spitzer–Harm law and values of
temperature in the skin layer.
There is the following initial condition for Eq. (9):
where T0 is the electron temperature before the
laser pulse action, as well as two boundary conditions,
The boundary condition at z = 0 means the absence of the heat
flux at the plasma surface. Eqs. (5) and (9) allows one to study the
evolution of the field distribution and electron temperature in the dense
hot plasma under the action of an ultrashort laser pulse.
3. HEATING OF ELECTRONS AND NONLINEAR FIELD
PENETRATION INTO THE PLASMA
In the case of the action of laser pulses of high power inequality
I = cE02/8π >>
nkBTc/4 can be fulfilled. If
this inequality is satisfied and heat losses from the skin layer are low,
the time 1/ω is not short as compared to a typical time of the
electron temperature change. Under such conditions, it is necessary to
construct a solution for Eq. (5) taking into account a rather fast
evolution of the electron temperature described by Eq. (9). Obtaining a
numerical solution for Eqs. (5) and (9), let us introduce dimensionless
time- and space-variables τ = ωt, ξ =
z/d0, and dimensionless functions
y = T/T0 and u =
E/E(0) that describe the temperature and field
distribution inside the plasma. Here, the following notation is used:
where ν0 = ν(T0) is the
effective frequency of electron–ion collisions at temperature
T0. Using these variables, one obtains from (5) and
(9)
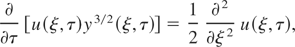
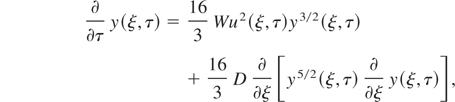
where the following notation is used:
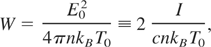
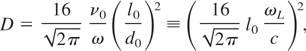
and
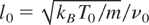
is the mean free path at temperature T0. In this
case, initial (6) and (13) and boundary (7), (8), and (14) conditions for
functions u(ξ,τ) and y(ξ,τ) are of the
form
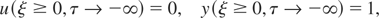
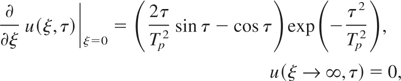
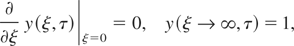
where Tp =
ωτp. Numerical solution for Eqs. (16) and
(17) for Tp = 2π, D =
10−3, and W = 0.1, 0.5, 2 are presented in
Figures 1 and 2. Figure 1 shows the space distribution of the squared
field in the plasma at the time moment τ = 0 for three values of
W = 0.1, 0.5, and 2. The electron temperature time-evolution at
the plasma surface (ξ = 0) for W = 0.1, 0.5, and 2 is shown
in Figure 2. As is seen from the dependences,
the electron temperature increases and the squared field at the plasma
surface decreases with an increase in the radiation flux density, that
is., with an increase in the parameter W. The space region of the
field concentration decreases with an increase in W. The
decreases in the effective depth of the skin layer and the modulus of the
field at the surface are due to fast electron heating.
Distribution of the squared field in the plasma at the time moment
τ = 0. The curves are obtained for D = 10−3
and Tp = 2π and correspond to three
values of the parameter W = 0.1 (solid curve), 0.5 (dashed
curve), and 2 (dotted curve).
Time dependence of the electron temperature at the plasma surface.
Calculations are carried out for Tp = 2π,
D = 10−3, and W = 0.1 (solid curve),
0.5 (dashed curve), and 2 (dotted curve).
Cooling of electrons due to the heat removal deep into the plasma is
characterized by the parameter D and can be seen in Figure 2. As a result of the electron heating, the
effective value of D increases providing the appearance of dips
of the curves in Figure 2 for time evolution of
the electron temperature at the plasma surface. The greater W,
the stronger the electron heating and the deeper the dips of the curves
y(ξ = 0,τ). In the course of time, at the laser pulse
shutdown, the electron heating becomes slower but the energy removal from
the skin layer is still high that results in a monotonic decrease in the
electron temperature at the surface (see Fig.
2).
4. ABSORPTION OF A HIGH-POWER PULSE AND
HARMONIC GENERATION
Changes in the features of the high-power laser pulse penetration into
the plasma caused by the fast heating of electrons result in changes in
the absorption coefficient and the spectrum of the reflected radiation.
Taking into account the explicit form of the incident pulse field (2), one
can obtain the following expression for the absorption coefficient:
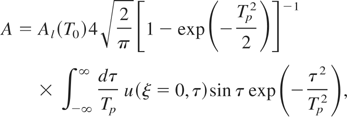
where
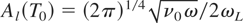
is the absorption coefficient for a long (Tp
>> 1) low-power pulse at temperature T0.
Calculation results for the absorption coefficient for a pulse with
Tp = 2π and D =
10−3 are presented in Figure 3.
According to the inset, in the case of a low radiation flux density where
the heating of electrons is low, the absorption coefficient A
(23) is close to Al(T0).
As the flux density increases the electron heating takes place during the
action of a pulse with Tp = 2π. The fast
heating is accompanied by the field reduction in the plasma and a decrease
in the effective depth of field penetration. This results in a decrease in
the dissipated fraction of the laser pulse energy, and therefore, in the
absorption coefficient. Figure 3 shows a
nonlinear reduction in the absorption coefficient caused by the increasing
parameter W. At large W the suppression of the
absorption coefficient becomes slower. The curve A(W) in
Figure 3 is of a variable bend. This is
connected with the fact that at large W, the electron temperature
significantly arises to the initial stage of the laser pulse action. Such
an increase in the temperature leads to a strong increase in the heat flux
deep into the plasma and to a slower growth of the temperature itself. The
major part of the laser pulse is absorbed under the conditions of slow
changing of the electron temperature that results in a relatively slower
decrease in A with the increasing W.
Absorption coefficient of a pulse with Tp
= 2π as a function of the radiation flux density W.
Calculation is carried out for D =
10−3.
A field of the reflected pulse is identically connected to the field
in the plasma. Taking into account notation (15), one obtains from the
continuity condition for the electric tangential component
where ur(ξ = 0,τ) =
Er(cτ/ω)/E(0).
The spectral composition of the reflected radiation is determined by the
Fourier component of the function ur(ξ =
0,τ),
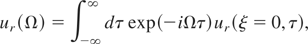
where Ω is dimensionless related to the frequency ω. Figure 4 shows plots of the function
|ur(Ω)| obtained for
Tp = 2π, D =
10−3,
Al(T0) = 0.1, and three
values of W = 0.01, 0.1, and 1. As the absorption coefficient
Al(T0) is small, the
reflected radiation is mainly concentrated near the frequency ω. The
width of the reflection band near the frequency ω is determined by
the reciprocal pulse duration. Broadening of the main band due to the
electron heating is relatively small, that is why the curves in Figure 4 corresponding to a different W
practically coincide each other in the vicinity of Ω ∼ 1. The
time change of the temperature causes a weak reflection at frequencies
above ω. According to Eq. (17), the energy absorbed by electrons is
proportional to the squared strength of the field that is concentrated
mainly near the frequency ω. As a result, the temperature is
modulated in time with a characteristic frequency 2ω. The electron
temperature modulation causes the generation of odd harmonics of the field
at frequencies (2n + 1)ω, n = 1,2… Amplitude
splashes of the Fourier component of the field near the frequencies
3ω and 5ω are seen in Figure 4.
Modulus of the Fourier component of the field of the reflected pulse
as a function of the dimensionless (related to ω) frequency Ω.
Calculations are carried out for Tp = 2π,
D = 10−3,
Al(T0) = 0.1, and three
values of W = 0.01 (solid curve), 0.1 (dashed curve), and 1
(dotted curve).
Generation of harmonics of a high-power high-frequency field due to
oscillations of the effective electron–ion collision frequency has
been known for a long time (Silin, 1965). In
Ferrante et al. (2003), the theory of
this phenomenon was developed as applied to conditions of the normal skin
effect, when ωL > ν > ω, the field
is low-power, and the electron heating occurs during the time much longer
than 1/ω. In Ferrante et al. (2003), the influence of electron-electron collisions
on the oscillating motion of electrons is assumed weak, that is, valid for
ω > νee = ν/Z, where
νee is the frequency of electron–electron
collisions. If νee > ω, the frequent
electron–electron collisions maintain the electron distribution
close to the Maxwellian one. Under such conditions, for description of
harmonic generation, one can not use a kinetic equation but a simpler
equation for the electron temperature. Within a such approach, as is shown
above, the odd harmonics arise due to the fact that the frequency of
electron–ion collisions is dependent on the thermal velocity
modulated at frequencies 2nω, n = 1,2,…
High-order harmonic generation by intense femtosecond laser pulses
irradiated at dense plasma surfaces is also discussed by Foldes et
al. (2003).
5. CONCLUSIONS
From the presentation above, it follows that there are specific
features in optical properties of dense plasma interacting with an
ultrashort laser pulse caused by fast heating of electrons. Let us
illustrate the conditions where the anomalies in optical properties
established above can manifest themselves. We assume as an estimate that
the plasma consists of fully ionized beryllium atoms with Z = 4
and electrons with a density n = 5·1023
cm−3 and temperature T0 = 60 eV and
the fundamental frequency in the pulse is ω =
2·1015 s−3. With such parameters of the
plasma and radiation one obtains Λ ∼ 1, ν0 ∼
ωL ≅ 4·1016
s−1 >> ω, l0 ≅
10−8 cm << d0 ≅
1.3·10−6 cm, and 2π/ω ≅ 3 fs.
The parameter W (18) determining a degree of the influence of
fast heating of electrons on optical properties of the plasma changes from
0.04 to 1 with an increase in the radiation flux density I from
2·1015 to 5·1016 W/cm2.
As is seen in Figure 3, an increase in
W from 0.04 to 1 result in a relative reduction in the absorption
coefficient from 0.8 to 0.3.
ACKNOWLEDGMENTS
This work was partially supported by the Program of Basic Research of
the Presidium of the Russian Academy of Sciences “Femtosecond Optics
and Physics of Super strong Laser Fields” and the Federal Research
Program on Priorities in Science and Technology, Subsection
“Femtosecond Laser Physics.”
