Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-06T07:39:43.895Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrated experiments for heavy ion fusion

Published online by Cambridge University Press:  25 March 2004

J.J. BARNARD ,
L.E. AHLE ,
F.M. BIENIOSEK ,
C.M. CELATA ,
R.C. DAVIDSON ,
E. HENESTROZA ,
A. FRIEDMAN ,
J.W. KWAN ,
B.G. LOGAN  and
E.P. LEE
...Show all authors
J.J. BARNARD
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
L.E. AHLE
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
F.M. BIENIOSEK
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
C.M. CELATA
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
R.C. DAVIDSON
Affiliation:
Princeton University, Princeton Plasma Physics Laboratory, Princeton, New Jersey
E. HENESTROZA
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
A. FRIEDMAN
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
J.W. KWAN
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
B.G. LOGAN
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
E.P. LEE
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
S.M. LUND
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
W.R. MEIER
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
G.-L. SABBI
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
P.A. SEIDL
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
W.M. SHARP
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
D.B. SHUMAN
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
W.L. WALDRON
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
H. QIN
Affiliation:
Princeton University, Princeton Plasma Physics Laboratory, Princeton, New Jersey
S.S. YU
Affiliation:
Lawrence Livermore National Laboratory, Livermore, California
Rights & Permissions [Opens in a new window]

Abstract

We describe the next set of experiments proposed in the U.S. Heavy Ion Fusion Virtual National Laboratory, the so-called Integrated Beam Experiment (IBX). The purpose of IBX is to investigate in an integrated manner the processes and manipulations necessary for a heavy ion fusion induction accelerator. The IBX experiment will demonstrate injection, acceleration, compression, bending, and final focus of a heavy ion beam at significant line charge density. Preliminary conceptual designs are presented and issues and trade-offs are discussed. Plans are also described for the step after IBX, the Integrated Research Experiment (IRE), which will carry out significant target experiments.

Keywords

AcceleratorDriverFusionHeavy ionInertial fusionSystems model
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 4 , October 2003 , pp. 553 - 560
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

The U.S. program in heavy ion fusion is currently embarking on an ambitious set of experiments (Logan et al., 2002) that focus on critical areas of a heavy ion fusion driver. Sources and injection (on the Source Test Stand, STS500; Ahle et al., 2002), transport at high line charge density (on the High Current Experiment, HCX; Seidl et al., 2002), and neutralized final focus (on the Neutralized Transport Experiment, NTX; Henestroza et al., 2003) will each be studied. This article focuses on the next set of proposed experiments, the so-called Integrated Beam Experiment (IBX). In Section 2, we will discuss the purpose of IBX, which, broadly speaking, is to investigate in an integrated manner the processes and manipulations necessary for a heavy ion fusion induction accelerator. These experiments will demonstrate injection, acceleration, compression, bending, and final focus of a heavy ion beam at significant line charge density. The scientific goals of IBX came about as a result of two workshops, whose conclusions are briefly discussed. In Section 3, two point designs from the second workshop are described and some design considerations are discussed that outline some of the constraints on the proposed accelerator. In Section 4, the design equations are presented. In Section 5, we discuss plans for the step after IBX, the Integrated Research Experiment (IRE), which will carry out significant target experiments, and which will provide the basis, along with results from the inertial confinement fusion program, to proceed to an engineering test facility for inertial fusion energy.

2. THE SCIENTIFIC GOALS OF THE IBX

Two workshops were held in 2001 that helped define the IBX scientific mission: The first was the Heavy Ion Fusion Science Workshop held May 30–31, 2001 at the Lawrence Berkeley National Laboratory that examined the critical issues facing heavy ion fusion generally. The workshop comprehensively identified and prioritized the scientific and engineering issues of the induction linac approach to heavy ion fusion In the second workshop (the so-called IBX workshop) held October 9–10 (cf. Celata, 2001), the discussion began regarding the IBX science mission and beam parameters. Prior to the IBX workshop, study groups were formed, focusing on specific physics and engineering areas and two illustrative designs were worked out (Barnard et al., 2001a; Lee, 2001).

Not all of the goals given high priority in the science workshop will be addressed on IBX, as many will be addressed in the near-term experiments, HCX, STS-500, and NTX, or later on the IRE. The main goals to be achieved on IBX can be divided into three broad areas: integrated physics, longitudinal physics, and transverse/longitudinal coupling physics. Integrated physics includes a demonstration of injection, acceleration, compression, bending, and focusing of a heavy ion beam at line charge density similar to the initial stages of a driver, so that physics involving interactions of beam ions with walls, residual gas, and stray electrons may be assessed. In parallel, simulations of a three-dimensional (3D) beam from source to target, predicting final spot radius, and current profile on target would demonstrate an integrated theoretical understanding. Longitudinal physics includes the physics of drift compression and stagnation. Stagnation here means the process whereby the longitudinal electric field of the beam's space charge is used to remove the velocity tilt at precisely the point where the beam passes through the final focus and hence minimizes chromatic aberrations of the spot. Measurement of the velocity tilt and velocity spread remaining after compression by a factor of ∼10, will be a key goal. The physics of longitudinal heating during acceleration and compression will be another focus. The third area to be explored is transverse/longitudinal coupling physics. The large velocity tilt required to compress the beam also manifests itself in the transverse dynamics, and so a number of topics related to coupling will be examined: matching and beam control with velocity tilt and acceleration, time dependent final-focus correction physics, bending physics, the transverse/longitudinal temperature anisotropy instability, and beam “end” physics.

3. TWO ILLUSTRATIVE CONCEPTUAL DESIGNS FOR IBX

In designing an accelerator with the physics goals described in Section 2, certain practical decisions need to be made. In carrying out the “straw man” or preconceptual designs in Barnard et al. (2001a) and Lee (2001) these decisions translate into certain design stategies. Among these are: maximize driver-relevant manipulations and beam physics to the extent possible; configure the machine to be able to carry out compression experiments in the drift section, but also to be flexible enough to carry out bunch compression and acceleration experiments in the accelerator itself; physics experiments are to be given higher priority than engineering demonstration (so technology limits are not pushed); and finally, simplicity should be stressed, maximizing modularity, so the project will fall within a cost envelope of approximately $50 million, the expected available project cost for a proof-of-principle experiment at this stage of fusion energy development. Using these considerations and the design equations in Section 4, the two teams independently obtained illustrative point designs. Figure 1 illustrates some of the more important parameters of the two point designs.

Layout and parameters of the two illustrative physics designs for the IBX. Parameters for the short pulse design in Lee et al. (2001) are above the sketch, and parameters for the longer pulse case in Barnard et al. (2001a) are below the sketch. Also note, that in Barnard et al., the bend extends for 180°, rather than 90° as indicated in the figure.

%3.1. Commonalities of the two designs

There are many commonalities to the accelerator point designs in Barnard et al. (2001a) and Lee (2001). The designs each consist of a number of sections where the beam undergoes a particular manipulation (such as the imposition of a velocity tilt or acceleration). Following the injector, there is a section that imposes an initial velocity tilt on the beam needed for bunch compression in the accelerator. This is followed by the main accelerator, followed by a shaping and velocity-tilt section where the current and velocity profiles are tailored to provide the correct initial conditions for the transfer of the beam into the drift-compression section. The beam is then bent and compressed in the drift-compression section, before it passes through the final focusing magnet section. Here the beam is expanded before its final convergence in the chamber section, where the beam space charge is neutralized before it arrives at the target with a spot size of a few millimeters. Both designs allow for testing of virtually all of the beam manipulations required in a driver, at line charge densities comparable to the initial line charge densities found in a driver. The discreteness of the sections in these point designs is largely due to conceptual simplicity. In more mature designs, the transitions would be more seamless, and, for example, the velocity tilt and shaping that follow acceleration would more likely occur in the accelerator itself.

Both preconceptual designs assume an ion species of singly charged potassium (atomic mass 39), an initial injection energy of 1.7 MeV, and an initial current of 0.69 A. This is based on extensive experience with potassium sources and the 2-MeV ESQ injector, together with the desire to create a single beam with the line charge density similar to what will be needed for a driver beam. Magnetic-quadrupole transport was chosen throughout both accelerators, as this choice has been made for the medium- to high-energy end of driver accelerators, and has largely been unexplored at these large line charge densities.

The principal differences in the two preconceptual designs are the initial pulse length and the consequences on the accelerator arising from this difference. Some induction linac heavy ion fusion power plant driver designs require initial pulse lengths as long as 20 μs. However, electron induction linacs have pulse lengths of the order of 10s of nanoseconds. In this article, “short” is relative to the pulse length of present experiments that have pulse durations of a few microseconds. The “longer” pulse design, although still shorter than a driver or many present experiments, has an initial flattop pulse duration of 1 μs, and a total pulse duration of 2 μs, whereas the “short” pulse design has an initial flattop pulse duration of 200 ns, and a total pulse duration of 300 ns.

3.2. Arguments in favor of short pulse

There are two principal arguments in favor of a short pulse. A short pulse allows a shorter drift compression section and short pulse requires fewer volt-seconds for a fixed final ion energy (and hence smaller induction cores). To understand the first argument, we may examine the scaling of a pulse with an initial parabolic distribution of current, and hence perveance Q: Q = Qmax(1 − 4Δz2/lbunch2), where Qmax is the perveance at the center of the bunch and hence is an evolving function of time, Δz is the longitudinal position relative to the bunch center, and lbunch is the full length of the bunch. The longitudinal electric field Ez is assumed to be approximately given by Ez ≅ −(g/[4πε0])∂λ/∂Δz where λ is the line charge density, ε0 is the free-space permeability, g = 2 ln rp /a, rp is the radius of the beam pipe, and a is the average beam radius. For these estimates, g is assumed to be constant, and it is also assumed that the space charge removes the velocity tilt at the end of the drift distance (to help mitigate the effects on the spot size of chromatic aberrations). A self-similar integration of the cold one-dimensional (1D) fluid equations yields a required velocity tilt Δv/v at the beginning of drift compression given by

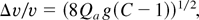
and a required drift distance d given by

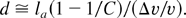
Here, Qa and la are the perveance and bunch length at the end of the accelerator, respectively, and C is the ratio of bunch length at the end of accelerator to the final bunch length. Although the actual pulse format used may not be parabolic, the scaling of velocity tilt and drift length are likely to be similar to a more exact calculation. Our science goals suggest that a final accelerator perveance Qa of 10−4, and a minimum compression ratio of 10 would be desired. With the variation of g limited, the initial velocity tilt will be of the order of 10% and will be insensitive to the pulse length, but the drift distance is directly proportional to the bunch length. Hence, cost savings can be accrued in the drift compression if the physics goals can be met with a shorter pulse.

The second advantage of short pulse is that fewer induction core volt-seconds are required for fixed final ion energy. From Faraday's law, the core cross-sectional area A times the material saturation magnetic field ΔB is proportional to the applied voltage times the pulse duration. The volume of the cores, and hence the mass of ferromagnetic material, is proportional to A for small outer radii and A2 if the outer radius becomes large compared to the inner radius. The engineering design is greatly simplified when the cores are smaller and more manageable, and the cost of the core material itself is greatly reduced. Although the loss rates per unit volume, Lloss, increase as Δt decreases (at worst being proportional to (dB/dt)2 Δt ∼ 1/Δt), the volume of magnetic material decreases as the pulse duration is decreased, thereby decreasing the total loss and reducing the total stored energy required for the pulsed power.

There are also some issues raised by going to very short pulse. The short-pulse option would reduce the ability to study potential electron/gas problems, because ions desorbed from the pipe walls require a large fraction of a microsecond to reach the beam. The long-pulse portion of the driver (the low energy end) would not be modeled well by this experiment, but it does model well the high-energy portion of the driver. (The issues for the low-energy end of a driver are well studied in HCX and STS500 so the need to study them again in IBX may be minimal.)

Some have argued that the diagnostics for a pulse length less than 100 ns may be expensive. Detailed cost estimates need to be made, but the time regime for the short pulse design is very similar to electron induction accelerators. There are differences between electron and ion diagnostics, but it does not appear to be a fundamental problem. The most serious concern for the short-pulse design is the simultaneous requirement of a 200-ns flattop pulse and the requirement of a current of 0.69 A of K+ at 1.7 MeV. For a simple planar diode, the Child–Langmuir law, yields a current of (1/9)(4πε0)(q/m)1/2(a/d)2V3/2, where q and m are the ion charge and mass, respectively, a is the radius of the source, d is the gap distance, and V is the voltage across the gap. Optics considerations generally require a/d < 0.5 (Kwan et al., 2001), so to obtain a current of 0.7 A of K+ requires a voltage of at least 280 kV. To avoid breakdown, an empirical expression (cf. Kwan et al., 2001) relating the maximum voltage Vmax allowed for a given gap separation d is commonly employed. This expression is

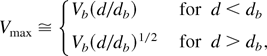
where Vb = 100 kV and db = 0.01 m. This relation suggests that for a 280-kV gap, the minimum distance d for this diode would be 0.078 m. Generally, to avoid transients in the current pulse, the flattop pulse duration must exceed the transit time of a particle through the gap (cf. Lampel & Tiefenback, 1983), given by ttrans = 3d(m/2qV)1/2. For d = 0.078 m, V = 280 kV, and singly charged K+, ttrans = 200 ns, so controlling transients and forming a flat usable current pulse needs to be carefully studied. One way to minimize transients would be to reduce the gap length (reducing the transit time), keeping the voltage constant. This would increase the voltage gradient beyond what is given in Eq. (3). But this has been successfully carried out on the injector for the RTA electron induction linac experiment at the Lawrence Berkeley National Laboratory (LBNL), possibly as a result of incorporating a solenoidal field to help prevent breakdown. This type of injector is slated to be investigated in more detail in fiscal year 2003, to see if a short pulse, single source injector would be feasible for IBX.

Another option, which would be manifestly compatible with short pulse, would be a multiple-beamlet injector, currently being investigated for use on an a heavy ion fusion driver or Integrated Research Experiment (Kwan et al., 2001). Each beamlet would be millimeter scale in radius, so transients would occur on a much shorter time scale. The development time for the multiple beamlet injector, however, will perhaps be longer than would be acceptable for inclusion in the IBX.

3.3. Additional differences between the two preconceptual designs

Besides pulse duration, the two reference designs differed in other ways.

3.3.1. Doublet versus singlet

In Lee (2002), the initial lattice period was based on the actual magnet design of the HCX (Sabbi et al., 2001; Seidel et al., 2002), so a syncopated lattice was introduced that allows for one longer drift space per lattice period for diagnostics, with minimal current reduction. This doublet configuration was maintained until 4.58 MeV, after which normal focus-drift-defocus-drift (FODO) focusing was used with equal drift spaces between quads. In Barnard et al. (2001a), a longer initial lattice period was chosen to accommodate separate cryostats for superconducting magnets, and a larger pipe radius was chosen to accommodate the reduced focusing.

3.3.2. 1 versus 4 beams

The Barnard et al. (2001a) design is a single-beam accelerator for simplicity and cost savings, whereas in the Lee (2001) design there are four beams to gain additional experience with multiple beams. The number of beams was not fundamental to either design and costing has been estimated in Meier et al. (2001) for versions with both one and four beams. The consensus of the IBX workshop was that the IBX should initially be a single-beam facility, but that the induction cores should have a large enough inner radius to accommodate four to nine beams, for a possible future upgrade.

3.3.3. Identical half-lattice period versus variable lattice

As the beam energy increases in a magnetic focusing system, the lattice period can be increased, as the focusing requirements are reduced. In Lee (2001), the lattice period increases as V1/2 until 4.58 MeV, and then increases as V1/4 to 18.34 MeV. In Barnard et al. (2001a), modularity was taken to a greater extreme, as the lattice half-period was held constant throughout the accelerator. This allowed identical magnets, as well as identical induction cells. This modularity advantage would be traded off against more half-lattice periods. More detailed estimates of engineering effort and fabrication costs required for different magnet and cell designs will be needed before choosing which of these strategies would be employed.

3.3.4. Compression schedules

In Lee (2001), a single compression schedule is suggested in which the line charge density was constant in the doublet section, and increased by a factor of two in the FODO section and by a factor of six in the drift section. In Barnard et al. (2001a), the strategy is to use different compression schemes when studying different aspects of accelerator physics. Each compression scheme can be characterized by the exponent α2, where the bunch length l ∼ Vα2 (see Tables 1 and 2). For example, to examine drift compression, the accelerator itself may operate with a simple “compression” scheme such as constant current (α2 = 0.5). Under that scenario, the current and pulse duration would remain constant, and so the bunch length would actually increase within the accelerator. But in the drift compression section, a factor of 10 bunch compression can take place, with a final perveance that would still be no higher than 10−3. On the other hand, to investigate acceleration and compression within the accelerator, bunch compression (with α2 = −0.25) by a factor of 0.64 would take place within the accelerator, but compression of a factor of only three in drift compression would be possible. The scenarios were constructed such that only the voltage waveforms needed to be modified for different compression schedules; the focusing would accommodate all four of the scenarios.

Summary of parameters for “short” and “longer” pulse conceptual design

Parameters for different compression schedules in the accelerator for the short pulse design (Lee et al., 2001)

3.3.5. Cost

In Meier et al. (2001), an approximate estimate of the costs of the short and longer pulse design was obtained. Estimates of the amount of ferromagnetic core material were made, and total cell costs were assumed proportional to weight, with the proportionality constant set by adopting the same coefficient as was found in the Dual Axis Hydrodynamic Radiography Test (DAHRT) accelerator now undergoing commissioning tests, and the Relativistic Two-Beam Accelerator experiments at LBNL, and detailed engineering costs of a previously proposed accelerator ILSE. Superconducting quadrupole and cryostat costs are based on work done by Sabbi et al. (2001). Pulsed magnet options were also costed. Pulsed power costs were based on the sum of stored energy and switching costs. Energy requirements were estimated from core losses, based on calculated core volumes and pulse durations. Spark gaps were chosen as the high power switch based on lower cost. The higher price of capacitors per joule in the short pulse case was included in the estimate. The cost estimates suggested that the one-beam short pulse design would have a total project cost (TPC) of ∼$38 million, whereas the four-beam longer pulse design would have a TPC of ∼$66 million, and the one-beam version of the longer pulse design would have a TPC of $57 million. Because pulse duration was not the only variable in the two designs, and the costs and designs are very rough, one should only infer that the cost and physics goals are not unrealistically out of line.

4. DESIGN EQUATIONS

In both Barnard et al. (2001a) and Lee (2001), algebraic relations were used to specify the lattice elements. We summarize below the major equations that specify the lattice (see, e.g., Lee, 1995).

The lattice parameters are related to the undepressed phase advance σ0 per lattice period approximately by the relation (Lee et al., 1985)

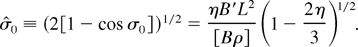
Here, B′ is the magnetic quadrupole gradient, η is the fraction of the half-lattice period occupied by the effective magnet length, L is the half-lattice period, and [Bρ] is the ion rigidity. Stability for space-charge-dominated beams requires σ0 to be less than ∼85°.

The equilibrium envelope equation relates the mean beam radius to σ0, L, the unnormalized beam emittance ε, and the generalized perveance Q. (In the nonrelativistic limit,

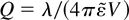
, where qV is the ion energy). This gives

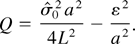
The velocity tilt Δv = vt − vh is defined as the difference between the velocity of the tail vt and the velocity of the head vh, at a fixed location, z, along the accelerator. If it is assumed that the bunch length varies continuously with the ion energy, and the energy varies continuously with z, then Δv is related to the voltage gradient dV/ds and pulse length l by

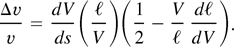
Here v is the velocity of the midpulse.

In the continuous half-lattice approximation, the number of half-lattice periods n increases as

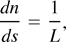
and the energy qV is related to the voltage gradient through the equation

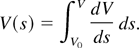
The total number of volt-seconds required to accelerate the flattop of the pulse per half-lattice period is

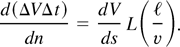
The additional voltage added to the beginning and end of the acceleration voltage required to keep the beam confined longitudinally against its own space charge is known as the “ear” voltage. Using the “g-factor model,” applied to a current pulse with quadratic current falloff, the required voltage increment per half-lattice period is given by

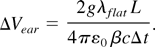
To maintain the velocity tilt implied by Eq. (6), a voltage increment of the tail relative to the head per half-lattice period must be applied, given by

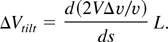
To obtain a specific physics design, additional assumptions are made. The voltage gradient, bunch length, and half-lattice period are all assumed to vary as a power of the voltage (defined as the beam energy/ion charge): dV/ds ∼ Vα1, lbunch ∼ Vα2, L ∼ Vα3. Using the equations above, constraints can then be placed on the exponents α1, α2, α3. Also, the pipe radius rp has been held constant (in both designs) for engineering simplicity, but this assumption has been relaxed in the drift compression section. The magnet length ηL has also been assumed (in both designs) to be constant to allow for more modularity and hence reduced engineering and fabrication costs. In the short pulse design, this modularity was extended to include a constant lattice period, and a constant cell design. Thus d(ΔVΔt)/dn is constant in the short-pulse design so the voltage increment per half-lattice period is held constant (single cell flavor). Table 1 summarizes major parameters of the linac portion of the illustrative designs based on these scaling laws, and Table 2 illustrates major beam parameters for the short-pulse design of Barnard et al. (2001a).

5. PARAMETER RANGES FOR THE IBX

The two point designs in Barnard et al. (2001a) and Lee (2001) give some confidence that a machine capable of carrying out the scientific goals of Section II can be manufactured within the expected cost envelope. At the IBX workshop a consensus based on scientific goals was obtained by three independent working groups on the energy (10–20 MeV), the ion species (K+), the final line charge density (1–2 μA/m), the minimum bunch compression needed ([gsim ]10), a final perveance of [lsim ]10−3, and initial pulse duration of between 0.2 and 2 μs. In some sense, the two point designs spanned the consensus parameter space.

6. LOOKING BEYOND THE IBX: THE IRE

With the insertion of an additional experiment (the IBX) into the experimental sequence leading to a heavy ion driver, the planned final pulse energy for the Integrated Research Experiment (IRE) has been increased to allow for more substantial target heating experiments. In Barnard et al. (2001b), a possible 200-MeV, 32-beam, K+ 30-kJ IRE is described. Recent considerations (Lee, 2002), have suggested that a considerable benefit to the target experiments could be achieved by going to a 800-MeV, Rb+, 250-kJ IRE. The total induction cell volt-seconds of such a machine might be ∼3 times that of the Barnard et al. (2001b) machine, even though the pulse energy was increased by nearly an order of magnitude. Detailed cost and physics designs of a more advanced IRE have not yet been carried out.

7. SUMMARY AND CONCLUSIONS

We have begun the process of defining the scientific goals and major accelerator parameters for the next heavy ion fusion induction accelerator, the IBX. The IBX will be an integrated test of most beam manipulations now being considered for an induction HIF driver. The energy will likely be between 10 and 20 MeV, with a final line charge density of ∼1–2 μC/m, and a bunch length compression of a factor of approximately 10. The beam will be focused to a spot, and the broadening of the beam spot from all of the processes that could potentially degrade the beam quality, including errors in acceleration, compression, focusing, and neutralization, will be assessed. It will be the first integrated experiment to carry out such a complete set of operations needed for HIF. The IBX will set the stage for the second integrated experiment on a larger scale, the IRE, where target heating experiments will be carried out. The IRE will lay the groundwork for the first engineering test facility on the pathway to a heavy ion driven inertial fusion energy power plant.

ACKNOWLEDGMENTS

Work was performed under the auspices of the U.S. Department of Energy under contract DE-AO33-76F0098 at the University of California LBNL, contract W-7405-ENG-48 at the University of California Lawrence Livermore National Laboratory, and contract DE-FG02-95ER40919 at the Princeton Plasma Physics Laboratory.

References

REFERENCES

Ahle, L., Grote, D. & Kwan, J. (2002). Developing high current and high brightness beams for HIF injectors. Laser Part. Beams 20, 603–608.Google Scholar
Barnard, J., Ahle, L., Friedman, A., Kwan, J., Logan, G., Lee, E., Lund, S., Meier, W., Sabbi, G., Sharp, W., Shuman, D., Waldron, W., Qin, H. & Yu, S. (2001a). IBX straw person design: Short pulse option. Proc. HIF-VNL Integrated Beam Experiment Workshop, p. 191–211.
Barnard, J.J., Ahle, L.E., Bangerter, R.O., Bieniosek, F.M., Celata, C.M., Faltens, A., Friedman, A., Grote, D.P., Haber, I., Henestroza, E., Kishek, R.A., de Hoon, M.J.L., Karpenko, V.P., Kwan, J.W., Lee, E.P., Logan, B.G., Lund, S.M., Meier, W.R., Molvik, A.W., Sangster, T.C., Seidl, P.A. & Sharp, W.M. (2001b). Planning for an integrated research experiment. Nucl. Instrum. Methods Phys. Res. A 464, 621.Google Scholar
Celata, C. (Ed.). (2001). Proc. HIF-VNL Integrated Beam Experiment Workshop.
Henestroza, E., Yu, S.S., Eylon, S., Anders, A., Sharp, W., Efthimion, P., Gilson, E., Welch, D. & Rose, D. (2003). Neutralized transport of high intensity beams. Particle Accelerator Confernece (APS, IEEE) WPPGO14.
Kwan, J.W., Ahle, L., Beck, D.N., Bieniosek, Faltens, A., Grote, D.P., Halaxa, E., Henestroza, E., Herrmannsfeldt, W.B., Karpenko, V., &Sangster, T.C. (2001). Ion sources and injectors for heavy ion fusion linacs. Nucl. Instrum. Methods Phys. Res. A 464, 379–387.Google Scholar
Lampel, M. & Tiefenback, M. (1983). An applied voltage to eliminate current transients in a one-dimensional diode. Appl. Phys. Lett. 43, 57–58.Google Scholar
Lee, E.P. (1995). Heavy ion driven LMF design concept UC-421. Report No. LBL-31248 revised, HIFAN721. Berkeley, CA: Lawrence Berkeley National Laboratory.
Lee, E.P. (2001). IBX rough design. Proc. HIF-VNL Integrated Beam Experiment Workshop, p. 166.
Lee, E.P. (2002). HIF IRE Driver Description. Snowmass 2002 Fusion Energy Sciences Summer Study, Presentations, July 10, 2002. Available at http://www.pppl.gove/snowmass_2002/presentations_july10.html.
Lee, E.P., Fessenden, T.J. & Laslett, L.J. (1985). Transportable charge in a periodic alternating gradient system. IEEE Trans. Nucl. Sci. NS-26, 2489–2492.Google Scholar
Logan, B.G., Celata, C.M., Kwan, J.W., Lee, E.P., Leitner, M., Seidl, P.A., Yu, S.S., Barnard, J.J., Friedman, A., Meier, W.R., Davidson, R.C. (2002). Overview of virtual national laboratory objectives, plans, and projects. Laser Part. Beams 20, 369–375.Google Scholar
Meier, W., Barnard, J., Sabbi, G., Shuman, D., Waldron, W. & Yu, S. (2001). Cost considerations for IBX. Proc. HIF-VNL Integrated Beam Experiment Workshop, p. 214.
Sabbi, J.L., Lietzke, A., Seidl, P.A., Shuman, D., Hinson, B., Meinke, R.B., Lund, S.M., Manahan, B., Martovetsky, N., Gung, C.-Y., Minervini, J., Myatt, L. & Schultz, J. (2001). Development of superconducting magnets for heavy ion fusion. Proc. 2001 Particle Accelerator Conference.
Seidl, P.A., Baca, D., Bieniosek, F.M., Faltens, A., Lund, S.M., Molvik, A.W., Prost, L.R. & Waldron, W.L. (2002). The high current experiment. Laser Part. Beams 21, 435–440.Google Scholar
Figure 0

Layout and parameters of the two illustrative physics designs for the IBX. Parameters for the short pulse design in Lee et al. (2001) are above the sketch, and parameters for the longer pulse case in Barnard et al. (2001a) are below the sketch. Also note, that in Barnard et al., the bend extends for 180°, rather than 90° as indicated in the figure.

Figure 1

Summary of parameters for “short” and “longer” pulse conceptual design

Figure 2

Parameters for different compression schedules in the accelerator for the short pulse design (Lee et al., 2001)