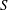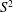1 Introduction
Deep-water breaking surface waves modulate the transfer of mass, momentum and energy between the atmosphere and ocean (Melville Reference Melville1996; Cavaleri, Fox-Kemper & Hemer Reference Cavaleri, Fox-Kemper and Hemer2012). Closing these integral budgets is of crucial importance in coupled ocean–atmosphere models describing both the weather and climate, and in particular they set the dynamics and statistics of air–sea interactions (Sullivan, McWilliams & Melville Reference Sullivan, McWilliams and Melville2007). Here we are interested in the wave-induced mass transport, which, besides having important implications for the momentum transfer between the atmosphere and ocean, has additional practical applications in better resolving the movement of jetsam and pollution at the ocean surface. To this end, this paper reports on laboratory experiments examining the mass transport induced by breaking and non-breaking focusing deep-water surface waves.
Recently, Deike, Pizzo & Melville (Reference Deike, Pizzo and Melville2017) used direct numerical simulations (DNS) to examine the mass transport induced by non-breaking and breaking deep-water focusing surface wave packets (Rapp & Melville Reference Rapp and Melville1990), finding that the transport induced by breaking can be significantly larger than the classical Stokes drift predictions for non-breaking waves. Pizzo, Melville & Deike (Reference Pizzo, Melville and Deike2019) then used the model of Deike et al. (Reference Deike, Pizzo and Melville2017) for the drift induced by one breaking wave, together with field observations of the statistics of wave breaking (Phillips Reference Phillips1985; Sutherland & Melville Reference Sutherland and Melville2013, Reference Sutherland and Melville2015), to estimate the total wave-breaking-induced transport at the ocean surface, and compared this with the predictions of Stokes drift (Kenyon Reference Kenyon1969). For the environmental conditions considered there, with wind speeds ranging from 1.6 to
![]() $16~\text{m}~\text{s}^{-1}$
, significant wave heights in the range 0.7–4.7 m and wave ages (defined here as
$16~\text{m}~\text{s}^{-1}$
, significant wave heights in the range 0.7–4.7 m and wave ages (defined here as
![]() $c_{m}/u_{\ast }$
, for
$c_{m}/u_{\ast }$
, for
![]() $c_{m}$
the spectrally weighted phase velocity (Sutherland & Melville Reference Sutherland and Melville2015) and
$c_{m}$
the spectrally weighted phase velocity (Sutherland & Melville Reference Sutherland and Melville2015) and
![]() $u_{\ast }$
the wind friction velocity) ranging from 16 to 150, it was found that the drift induced by breaking may be up to 30 % of the predicted Stokes drift, becoming increasingly important for younger seas. This estimate relied crucially on a scaling constant that was found by a best linear fit to the DNS data (the estimate of the drift induced by breaking is linearly proportional to the scaling constant). The uncertainty associated with the DNS estimate of the scaling constant partially motivated the present study.
$u_{\ast }$
the wind friction velocity) ranging from 16 to 150, it was found that the drift induced by breaking may be up to 30 % of the predicted Stokes drift, becoming increasingly important for younger seas. This estimate relied crucially on a scaling constant that was found by a best linear fit to the DNS data (the estimate of the drift induced by breaking is linearly proportional to the scaling constant). The uncertainty associated with the DNS estimate of the scaling constant partially motivated the present study.
Beginning with Rapp & Melville (Reference Rapp and Melville1990), dispersive focusing techniques (Longuet-Higgins Reference Longuet-Higgins1974) have been employed to conduct black box laboratory experiments, with measurements being conducted far upstream and downstream of the breaking region where the broadband wave packets are linear, yielding information about the turbulent two-phase unsteady breaking process without having to directly measure the process itself. This has included studies of the energy dissipated by breaking (Rapp & Melville Reference Rapp and Melville1990; Banner & Peirson Reference Banner and Peirson2007; Drazen, Melville & Lenain Reference Drazen, Melville and Lenain2008; Tian, Perlin & Choi Reference Tian, Perlin and Choi2010), the vorticity and circulation generated by breaking (Rapp & Melville Reference Rapp and Melville1990; Melville, Veron & White Reference Melville, Veron and White2002), and the turbulent flow generated by breaking (Melville et al. Reference Melville, Veron and White2002; Drazen & Melville Reference Drazen and Melville2009). In this paper, we study the mass transport induced by wave breaking by examining the particle positions before and after a breaking event.
Wave breaking introduces vorticity into the water column by topologically changing the free surface (Hornung, Willert & Turner Reference Hornung, Willert and Turner1995, see also Batchelor Reference Batchelor1967, Longuet-Higgins Reference Longuet-Higgins1998), creating gradients in the density of the two-phase fluid mixture, and by generating large surface curvatures. The vertical vorticity induced by breaking seeds the so-called CL2 mechanism, generating Langmuir circulation (Craik & Leibovich Reference Craik and Leibovich1976; Leibovich Reference Leibovich1983) by interacting with the mass transport induced by the waves, a consequence of Kelvin’s circulation theorem. The presence of vorticity in the water radically alters the dynamics and statistics of the resulting flow fields (Sullivan et al. Reference Sullivan, McWilliams and Melville2007) so that it is important to quantify the structure of the breaking-induced flow (Rapp & Melville Reference Rapp and Melville1990; Melville et al. Reference Melville, Veron and White2002; Pizzo & Melville Reference Pizzo and Melville2013), and its integral properties (Pizzo & Melville Reference Pizzo and Melville2016). By constraining the surface drift induced by breaking through laboratory experiments, this study provides an important step in closing the momentum budget between the atmosphere and ocean.
The outline of the paper is as follows. Section 2 discusses the experimental set-up and measurements. These measurements are analysed in § 3, and the results are discussed in § 4.
2 Experimental set-up
2.1 Hydraulics Laboratory facility
The laboratory experiments were conducted from November 2018 through January 2019 at the recently rebuilt (2017) Glass Channel Facility in the Hydraulics Laboratory at the Scripps Institution of Oceanography (SIO). The stainless steel and glass tank (see figure 1) is 32 m long, 0.5 m wide and 1 m deep. Waves are generated using a computer-controlled electromechanical wavemaker installed at one end, while a beach of
![]() $9^{\circ }$
slope covered with a thick fibrous mat is installed on the other end, to absorb and dissipate any waves that reach the end of the channel, minimizing wave reflections. The tank was filled with fresh water to a working depth of 0.5 m.
$9^{\circ }$
slope covered with a thick fibrous mat is installed on the other end, to absorb and dissipate any waves that reach the end of the channel, minimizing wave reflections. The tank was filled with fresh water to a working depth of 0.5 m.

Figure 1. Conceptual schematic of the experiment conducted at the Hydraulics Laboratory facility, SIO. The channel is 32 m long, 0.5 m wide and 1 m deep. Waves are generated using a computer-controlled electromechanical wave paddle installed at one end.
2.2 Wave packet generation
Breaking waves are generated using a dispersive focusing technique (Longuet-Higgins Reference Longuet-Higgins1974; Rapp & Melville Reference Rapp and Melville1990), in which the phase of a finite band of waves is tuned so that, according to linear theory, the amplitudes constructively add at a prescribed location
![]() $x_{b}^{\ell }$
and time
$x_{b}^{\ell }$
and time
![]() $t_{b}^{\ell }$
. That is, the linear free surface displacement takes the form
$t_{b}^{\ell }$
. That is, the linear free surface displacement takes the form
where
![]() $a_{n}$
is the amplitude of the
$a_{n}$
is the amplitude of the
![]() $n$
th component,
$n$
th component,
![]() $k_{n}$
is the wavenumber,
$k_{n}$
is the wavenumber,
![]() $\unicode[STIX]{x1D714}_{n}=2\unicode[STIX]{x03C0}f_{n}$
the angular frequency and
$\unicode[STIX]{x1D714}_{n}=2\unicode[STIX]{x03C0}f_{n}$
the angular frequency and
![]() $N$
the total number of frequency components. The wavenumber and frequency are connected by the linear dispersion relationship, namely
$N$
the total number of frequency components. The wavenumber and frequency are connected by the linear dispersion relationship, namely
![]() $\unicode[STIX]{x1D714}_{n}^{2}=gk_{n}\tanh (k_{n}H)$
, where
$\unicode[STIX]{x1D714}_{n}^{2}=gk_{n}\tanh (k_{n}H)$
, where
![]() $H$
is the water depth and
$H$
is the water depth and
![]() $g$
is the acceleration due to gravity. The amplitudes are chosen so that (Drazen et al.
Reference Drazen, Melville and Lenain2008)
$g$
is the acceleration due to gravity. The amplitudes are chosen so that (Drazen et al.
Reference Drazen, Melville and Lenain2008)
![]() $a_{n}=S/N$
, where
$a_{n}=S/N$
, where
![]() $S$
is the linear prediction of the maximum slope at focusing, and has the value
$S$
is the linear prediction of the maximum slope at focusing, and has the value
This parameter denotes the strength of focusing, and when it exceeds a critical value,
![]() $S_{\ast }$
, wave breaking is expected. For
$S_{\ast }$
, wave breaking is expected. For
![]() $S\geqslant S_{\ast }$
relatively small, spilling breaking waves are created, while for
$S\geqslant S_{\ast }$
relatively small, spilling breaking waves are created, while for
![]() $S\gg S_{\ast }$
relatively large, plunging breaking waves occur. The other relevant non-dimensional quantity characterizing the wave packet is the bandwidth
$S\gg S_{\ast }$
relatively large, plunging breaking waves occur. The other relevant non-dimensional quantity characterizing the wave packet is the bandwidth
![]() $\unicode[STIX]{x1D6FF}k/k_{c}$
, which sets the wavenumbers
$\unicode[STIX]{x1D6FF}k/k_{c}$
, which sets the wavenumbers
![]() $k_{n}=k_{c}(1+\unicode[STIX]{x1D6FF}k/k_{c}(n-N/2))$
, for
$k_{n}=k_{c}(1+\unicode[STIX]{x1D6FF}k/k_{c}(n-N/2))$
, for
![]() $k_{c}$
the central wavenumber (with corresponding central angular frequency
$k_{c}$
the central wavenumber (with corresponding central angular frequency
![]() $\unicode[STIX]{x1D714}_{c}^{2}=gk_{c}\tanh (k_{c}H)$
and frequency
$\unicode[STIX]{x1D714}_{c}^{2}=gk_{c}\tanh (k_{c}H)$
and frequency
![]() $f_{c}=\unicode[STIX]{x1D714}_{c}/2\unicode[STIX]{x03C0}$
).
$f_{c}=\unicode[STIX]{x1D714}_{c}/2\unicode[STIX]{x03C0}$
).
In the present study, the wave packet is composed of 32 frequency components (i.e.
![]() $N=32$
), with
$N=32$
), with
![]() $f_{c}=0.85$
Hz, bandwidth
$f_{c}=0.85$
Hz, bandwidth
![]() $\unicode[STIX]{x1D6FF}f/f=0.82$
, and the breaking location
$\unicode[STIX]{x1D6FF}f/f=0.82$
, and the breaking location
![]() $x_{b}$
set to 10.2 m. The input signal is windowed so that only one wave group is generated (Rapp & Melville Reference Rapp and Melville1990). The slope
$x_{b}$
set to 10.2 m. The input signal is windowed so that only one wave group is generated (Rapp & Melville Reference Rapp and Melville1990). The slope
![]() $S$
is varied from 0.172 to 0.334, which includes both non-breaking and breaking focusing wave packets.
$S$
is varied from 0.172 to 0.334, which includes both non-breaking and breaking focusing wave packets.
2.3 Measurements
A conceptual schematic of the experimental set-up is shown in figure 1. Surface wave heights in the channel were measured with an array of three resistance wire wave gauges using impedance-measuring electronics, from the Danish Hydraulics Institute (Model 80-74G), placed along the midline of the transverse direction of the tank, at along-channel distances
![]() $x=1.75$
, 4.75 and 19.75 m from the quiescent wave paddle location.
$x=1.75$
, 4.75 and 19.75 m from the quiescent wave paddle location.
The surface of the water was seeded with eight slightly buoyant coloured particles of
![]() $11.8~\text{mm}\pm 0.1~\text{mm}$
diameter. The material densities of the particles were calculated from their buoyant forces. Buoyancy was characterized by releasing the particles at depth and recording their rise velocity with a high-speed camera (Model Phantom M320s), giving a mean particle material density of
$11.8~\text{mm}\pm 0.1~\text{mm}$
diameter. The material densities of the particles were calculated from their buoyant forces. Buoyancy was characterized by releasing the particles at depth and recording their rise velocity with a high-speed camera (Model Phantom M320s), giving a mean particle material density of
![]() $0.996\pm 0.001~\text{g}~\text{cm}^{-3}$
. The particles were chosen based on the conditions that they scatter enough light to be detected over the duration of the breaking event and follow the flow streamlines without excessive slip (Melling Reference Melling1997; Prasad Reference Prasad2000). The former condition is met by painting the particles different colours (as is discussed in more detail below), while the latter condition is corroborated by noting that the particle rise velocities are found to be
$0.996\pm 0.001~\text{g}~\text{cm}^{-3}$
. The particles were chosen based on the conditions that they scatter enough light to be detected over the duration of the breaking event and follow the flow streamlines without excessive slip (Melling Reference Melling1997; Prasad Reference Prasad2000). The former condition is met by painting the particles different colours (as is discussed in more detail below), while the latter condition is corroborated by noting that the particle rise velocities are found to be
![]() $O(10^{-2})~\text{m}~\text{s}^{-1}$
(with corresponding Reynolds number
$O(10^{-2})~\text{m}~\text{s}^{-1}$
(with corresponding Reynolds number
![]() $O(10)$
) while typical speeds observed during breaking are
$O(10)$
) while typical speeds observed during breaking are
![]() $O(1)~\text{m}~\text{s}^{-1}$
(Rapp & Melville Reference Rapp and Melville1990; Melville et al.
Reference Melville, Veron and White2002; Drazen & Melville Reference Drazen and Melville2009), and therefore we expect the particles to faithfully follow the motion of the fluid during breaking (Melling Reference Melling1997).
$O(1)~\text{m}~\text{s}^{-1}$
(Rapp & Melville Reference Rapp and Melville1990; Melville et al.
Reference Melville, Veron and White2002; Drazen & Melville Reference Drazen and Melville2009), and therefore we expect the particles to faithfully follow the motion of the fluid during breaking (Melling Reference Melling1997).
The particles were placed approximately 10 cm apart along the midline, with an initial position shifted downstream for each repeated run to ensure that the desired spatial resolution was obtained along the channel. Each particle was painted with a distinct colour (cyan, blue, red, pink, purple, green, brown and silver) to obtain particle trajectories throughout the breaking process, with particles temporarily untrackable in regions of large bubble density due to breaking. Each repeated run was separated by a 12 min wait time to allow residual wave motion to attenuate in the channel. A total of 401 runs were conducted during the experiment – on average 25 and 50 runs were conducted per non-breaking and breaking case.
Video imagery of the free surface displacement in the region of focusing was recorded using a nadir-looking Nikon D810 SLR camera (
![]() $7360\times 4912~\text{px}$
,
$7360\times 4912~\text{px}$
,
![]() $35.9\times 24~\text{mm}$
full frame FX format CMOS sensor with
$35.9\times 24~\text{mm}$
full frame FX format CMOS sensor with
![]() $4.88~\unicode[STIX]{x03BC}\text{m}$
pixel size) that was mounted above the channel and equipped with a
$4.88~\unicode[STIX]{x03BC}\text{m}$
pixel size) that was mounted above the channel and equipped with a
![]() $14~\text{mm}~f/2.8D$
Nikon lens, and sampled at 5 Hz. In addition, a JaiPulnix AB800CL colour camera (
$14~\text{mm}~f/2.8D$
Nikon lens, and sampled at 5 Hz. In addition, a JaiPulnix AB800CL colour camera (
![]() $3296\times 2472~\text{px}$
,
$3296\times 2472~\text{px}$
,
![]() $18.13\times 13.6~\text{mm}~4/3$
inch format CCD with
$18.13\times 13.6~\text{mm}~4/3$
inch format CCD with
![]() $5.5~\unicode[STIX]{x03BC}\text{m}$
pixel size) with a 14 mm
$5.5~\unicode[STIX]{x03BC}\text{m}$
pixel size) with a 14 mm
![]() $f/2.8L$
Canon lens that was located adjacent to the channel and pointed to the side of the channel in the wave-breaking area where the coloured particles were located (see figure 1). This camera sampled images at 16 Hz. The two imaging devices were synchronized with the wavemaker and the resistance wave gauge data logger. All collected images were carefully corrected and calibrated to account for lens distortions.
$f/2.8L$
Canon lens that was located adjacent to the channel and pointed to the side of the channel in the wave-breaking area where the coloured particles were located (see figure 1). This camera sampled images at 16 Hz. The two imaging devices were synchronized with the wavemaker and the resistance wave gauge data logger. All collected images were carefully corrected and calibrated to account for lens distortions.

Figure 2. Sequence of images showing the trajectory of one particle (red dot) during wave propagation for a breaking focusing packet,
![]() $f_{c}=0.85~\text{Hz}$
,
$f_{c}=0.85~\text{Hz}$
,
![]() $\unicode[STIX]{x1D6FF}f/f=0.82$
and maximum linear slope
$\unicode[STIX]{x1D6FF}f/f=0.82$
and maximum linear slope
![]() $S=0.334$
. The particle trajectory is colour-coded by the non-dimensional time
$S=0.334$
. The particle trajectory is colour-coded by the non-dimensional time
![]() $t^{\ast }=(t-t_{b})\unicode[STIX]{x1D714}_{c}$
, relative to the focusing time
$t^{\ast }=(t-t_{b})\unicode[STIX]{x1D714}_{c}$
, relative to the focusing time
![]() $t_{b}$
. Snapshots before focusing,
$t_{b}$
. Snapshots before focusing,
![]() $t^{\ast }=-21.7$
, at the onset of breaking,
$t^{\ast }=-21.7$
, at the onset of breaking,
![]() $t^{\ast }=0$
, shortly after breaking,
$t^{\ast }=0$
, shortly after breaking,
![]() $t^{\ast }=3.3$
, and well after breaking,
$t^{\ast }=3.3$
, and well after breaking,
![]() $t^{\ast }=41.7$
, are shown in (a) through (d). The highlighted red dot represents the location of the particle at the time when the image was recorded. Note that the particle could not be tracked in the regions of large air entrainment, as shown in (c). The initial location of the particle is marked as a white asterisk in (b)–(d).
$t^{\ast }=41.7$
, are shown in (a) through (d). The highlighted red dot represents the location of the particle at the time when the image was recorded. Note that the particle could not be tracked in the regions of large air entrainment, as shown in (c). The initial location of the particle is marked as a white asterisk in (b)–(d).
Figure 2 shows a sequence of images of a plunging breaker collected from the side camera, along with a particle trajectory during the wave propagation for a breaking focusing packet of parameters
![]() $f_{c}=0.85$
Hz,
$f_{c}=0.85$
Hz,
![]() $\unicode[STIX]{x1D6FF}f/f=0.82$
and maximum linear slope
$\unicode[STIX]{x1D6FF}f/f=0.82$
and maximum linear slope
![]() $S=0.334$
. The onset of breaking occurs at
$S=0.334$
. The onset of breaking occurs at
![]() $t=t_{b}$
, which is determined by the imagery and is not the linear prediction discussed in the previous section (i.e.
$t=t_{b}$
, which is determined by the imagery and is not the linear prediction discussed in the previous section (i.e.
![]() $t_{b}\neq t_{b}^{\ell }$
). The selected particle, initially located close to the breaking point
$t_{b}\neq t_{b}^{\ell }$
). The selected particle, initially located close to the breaking point
![]() $x_{b}$
, experiences a large jump downstream during the breaking event, with a horizontal displacement
$x_{b}$
, experiences a large jump downstream during the breaking event, with a horizontal displacement
![]() $\unicode[STIX]{x0394}x$
on the order of
$\unicode[STIX]{x0394}x$
on the order of
![]() $\unicode[STIX]{x1D706}_{c}$
(consistent with the dye experiments of Rapp & Melville Reference Rapp and Melville1990), the characteristic wavelength of the packet. Note that the air entrainment in the area of active breaking (see figure 2
c) limits our ability to continuously track the particle location throughout the breaking process, but it does not limit our ability to measure the particle displacement for the whole breaking event.
$\unicode[STIX]{x1D706}_{c}$
(consistent with the dye experiments of Rapp & Melville Reference Rapp and Melville1990), the characteristic wavelength of the packet. Note that the air entrainment in the area of active breaking (see figure 2
c) limits our ability to continuously track the particle location throughout the breaking process, but it does not limit our ability to measure the particle displacement for the whole breaking event.
3 Measurements of the Lagrangian drift at the surface
In this study, the horizontal drift at the surface,
![]() $\unicode[STIX]{x0394}x$
, is computed using the position of particles that are initially at the surface before and after the breaking and non-breaking focusing events, at times
$\unicode[STIX]{x0394}x$
, is computed using the position of particles that are initially at the surface before and after the breaking and non-breaking focusing events, at times
![]() $t_{0}$
and
$t_{0}$
and
![]() $t_{f}$
, respectively, such that
$t_{f}$
, respectively, such that
![]() $\unicode[STIX]{x0394}x=x_{i}(t_{f})-x_{i}(t_{0})$
, where
$\unicode[STIX]{x0394}x=x_{i}(t_{f})-x_{i}(t_{0})$
, where
![]() $x_{i}$
represents the horizontal position of the
$x_{i}$
represents the horizontal position of the
![]() $i$
th particle. Using the nadir-looking imagery, the locations
$i$
th particle. Using the nadir-looking imagery, the locations
![]() $x_{i}(t_{0})$
, referred to as
$x_{i}(t_{0})$
, referred to as
![]() $x_{o}$
in the present work, and
$x_{o}$
in the present work, and
![]() $x_{i}(t_{f})$
were identified for all repeated runs using
$x_{i}(t_{f})$
were identified for all repeated runs using
![]() $t_{0}=4.5$
s and
$t_{0}=4.5$
s and
![]() $t_{f}=16.2$
s prior to and after the onset, respectively. These choices are based on allowing sufficient time for the breaking-induced turbulence to dissipate (Rapp & Melville Reference Rapp and Melville1990; Pizzo, Melville & Deike Reference Pizzo, Melville and Deike2016) so that the particles can be best observed. Note, the final time
$t_{f}=16.2$
s prior to and after the onset, respectively. These choices are based on allowing sufficient time for the breaking-induced turbulence to dissipate (Rapp & Melville Reference Rapp and Melville1990; Pizzo, Melville & Deike Reference Pizzo, Melville and Deike2016) so that the particles can be best observed. Note, the final time
![]() $t_{f}$
is constrained by the long waves possibly being reflected from the end of the channel back into the sampling area.
$t_{f}$
is constrained by the long waves possibly being reflected from the end of the channel back into the sampling area.
The duration of the breaking event, to lowest order in
![]() $S$
and
$S$
and
![]() $\unicode[STIX]{x1D6FF}f/f_{0}$
, scales with the central frequency of the wave packet (Rapp & Melville Reference Rapp and Melville1990; Drazen et al.
Reference Drazen, Melville and Lenain2008). The transport due to breaking then occurs largely over the time period defined above, with any additional transport between this time and
$\unicode[STIX]{x1D6FF}f/f_{0}$
, scales with the central frequency of the wave packet (Rapp & Melville Reference Rapp and Melville1990; Drazen et al.
Reference Drazen, Melville and Lenain2008). The transport due to breaking then occurs largely over the time period defined above, with any additional transport between this time and
![]() $t_{f}$
generated by residual wave motion or the mean flow induced by breaking (Melville et al.
Reference Melville, Veron and White2002; Pizzo & Melville Reference Pizzo and Melville2013), being assumed to be much weaker than the transport generated by breaking (Deike et al.
Reference Deike, Pizzo and Melville2017).
$t_{f}$
generated by residual wave motion or the mean flow induced by breaking (Melville et al.
Reference Melville, Veron and White2002; Pizzo & Melville Reference Pizzo and Melville2013), being assumed to be much weaker than the transport generated by breaking (Deike et al.
Reference Deike, Pizzo and Melville2017).

Figure 3. Measured horizontal drift
![]() $\unicode[STIX]{x0394}x$
for particles initially at the surface as a function of their initial horizontal position relative to the breaking location
$\unicode[STIX]{x0394}x$
for particles initially at the surface as a function of their initial horizontal position relative to the breaking location
![]() $(x_{0}-x_{b})$
, for all experimental runs. Data points are colour-coded for the linear prediction of the maximum slope at focusing,
$(x_{0}-x_{b})$
, for all experimental runs. Data points are colour-coded for the linear prediction of the maximum slope at focusing,
![]() $S$
.
$S$
.
Figure 3 shows the measured horizontal drift
![]() $\unicode[STIX]{x0394}x$
for all processed particles as a function of their initial horizontal position relative to the breaking location
$\unicode[STIX]{x0394}x$
for all processed particles as a function of their initial horizontal position relative to the breaking location
![]() $(x_{0}-x_{b})$
, for a range of slopes
$(x_{0}-x_{b})$
, for a range of slopes
![]() $S$
extending from non-breaking (
$S$
extending from non-breaking (
![]() $S=0.172$
) to energetic plunging breaking (
$S=0.172$
) to energetic plunging breaking (
![]() $S=0.334$
) cases. Note, multiple breakers were not observed for runs over this range of
$S=0.334$
) cases. Note, multiple breakers were not observed for runs over this range of
![]() $S$
. The initial position
$S$
. The initial position
![]() $x_{0}$
is defined as
$x_{0}$
is defined as
![]() $x_{0}=x_{i}(t_{0})$
, while the breaking location
$x_{0}=x_{i}(t_{0})$
, while the breaking location
![]() $x_{b}$
was carefully identified using the side camera imagery for each breaking packet slope, defined as the along-channel location at the onset of breaking. For the non-breaking packets,
$x_{b}$
was carefully identified using the side camera imagery for each breaking packet slope, defined as the along-channel location at the onset of breaking. For the non-breaking packets,
![]() $x_{b}$
was set to the location of breaking onset for the breaking packet of lowest slope
$x_{b}$
was set to the location of breaking onset for the breaking packet of lowest slope
![]() $S$
, equal to 0.282. Note,
$S$
, equal to 0.282. Note,
![]() $x_{b}$
varied by less than 5 % over the range of
$x_{b}$
varied by less than 5 % over the range of
![]() $S$
that we considered. For the larger slope cases, we find a sharp increase in surface drift, starting around the along-channel position of
$S$
that we considered. For the larger slope cases, we find a sharp increase in surface drift, starting around the along-channel position of
![]() $(x_{0}-x_{b})\approx -0.5$
m, ultimately reaching maximum surface drift values of up to approximately 2.5 m (exceeding
$(x_{0}-x_{b})\approx -0.5$
m, ultimately reaching maximum surface drift values of up to approximately 2.5 m (exceeding
![]() $\unicode[STIX]{x1D706}_{c}$
in that case), before a slow decay of surface drift with particles located further downstream of the focusing region.
$\unicode[STIX]{x1D706}_{c}$
in that case), before a slow decay of surface drift with particles located further downstream of the focusing region.
Figure 4(a) shows the corresponding running-average surface drift
![]() $\overline{\unicode[STIX]{x0394}x}$
normalized by the central wavenumber
$\overline{\unicode[STIX]{x0394}x}$
normalized by the central wavenumber
![]() $k_{c}$
as a function of the normalized along-channel initial position
$k_{c}$
as a function of the normalized along-channel initial position
![]() $\hat{x}=(x_{0}-x_{b})k_{c}$
. The quantity
$\hat{x}=(x_{0}-x_{b})k_{c}$
. The quantity
![]() $\overline{\unicode[STIX]{x0394}x}$
is computed using an averaging window of
$\overline{\unicode[STIX]{x0394}x}$
is computed using an averaging window of
![]() $\unicode[STIX]{x1D706}_{c}/4$
.
$\unicode[STIX]{x1D706}_{c}/4$
.
For
![]() $S$
larger than
$S$
larger than
![]() $S_{\ast }=0.28$
, the breaking threshold, we find that the normalized drift
$S_{\ast }=0.28$
, the breaking threshold, we find that the normalized drift
![]() $\overline{\unicode[STIX]{x0394}x}k_{c}$
rapidly increases, reaching a maximum value in the neighbourhood of
$\overline{\unicode[STIX]{x0394}x}k_{c}$
rapidly increases, reaching a maximum value in the neighbourhood of
![]() $x\approx x_{b}$
, then decaying down to levels similar to or lower than the drift measured upstream of the focusing region. Packets of slope
$x\approx x_{b}$
, then decaying down to levels similar to or lower than the drift measured upstream of the focusing region. Packets of slope
![]() $S<S_{\ast }$
do not show such a noticeable increase in surface drift (and asymmetry) around the focusing region, remaining approximately constant. Note, the breaking threshold
$S<S_{\ast }$
do not show such a noticeable increase in surface drift (and asymmetry) around the focusing region, remaining approximately constant. Note, the breaking threshold
![]() $S_{\ast }$
was characterized experimentally by slowly increasing
$S_{\ast }$
was characterized experimentally by slowly increasing
![]() $S$
until air entrainment was observed. We find both the maximum drift and the region of significant horizontal drift to be a function of
$S$
until air entrainment was observed. We find both the maximum drift and the region of significant horizontal drift to be a function of
![]() $S$
, with both quantities increasing monotonically with
$S$
, with both quantities increasing monotonically with
![]() $S$
.
$S$
.
Figure 4(b) shows the normalized total horizontal drift
![]() $\overline{\unicode[STIX]{x0394}x}k_{c}/\sqrt{S-S\ast }$
for the breaking cases only, as a function of the normalized initial horizontal position of the particles
$\overline{\unicode[STIX]{x0394}x}k_{c}/\sqrt{S-S\ast }$
for the breaking cases only, as a function of the normalized initial horizontal position of the particles
![]() $\hat{x}$
. The normalization, proportional to
$\hat{x}$
. The normalization, proportional to
![]() $h^{1/2}$
for
$h^{1/2}$
for
![]() $h$
, the height of the wave at breaking, and
$h$
, the height of the wave at breaking, and
![]() $S\sim (hk)$
(Drazen et al.
Reference Drazen, Melville and Lenain2008), implies that the magnitude of the drift scales with the ballistic velocity
$S\sim (hk)$
(Drazen et al.
Reference Drazen, Melville and Lenain2008), implies that the magnitude of the drift scales with the ballistic velocity
![]() $\sqrt{2gh}$
, which is consistent with the scaling arguments for the energy dissipation rate (Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero, Melville & Kleiss Reference Romero, Melville and Kleiss2012; Deike, Popinet & Melville Reference Deike, Popinet and Melville2015) and the circulation induced by breaking (Pizzo & Melville Reference Pizzo and Melville2013, Reference Pizzo and Melville2016).
$\sqrt{2gh}$
, which is consistent with the scaling arguments for the energy dissipation rate (Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero, Melville & Kleiss Reference Romero, Melville and Kleiss2012; Deike, Popinet & Melville Reference Deike, Popinet and Melville2015) and the circulation induced by breaking (Pizzo & Melville Reference Pizzo and Melville2013, Reference Pizzo and Melville2016).
Furthermore, we consider a best fit, taking the form of a gamma probability density function,
![]() ${\mathcal{F}}(\hat{x})$
, with
${\mathcal{F}}(\hat{x})$
, with
where
![]() $\unicode[STIX]{x1D6E4}$
is the gamma function, giving
$\unicode[STIX]{x1D6E4}$
is the gamma function, giving
![]() $\unicode[STIX]{x1D6FC}=5.04$
,
$\unicode[STIX]{x1D6FC}=5.04$
,
![]() $\unicode[STIX]{x1D6FD}=1.36$
,
$\unicode[STIX]{x1D6FD}=1.36$
,
![]() $a_{0}=5.12$
,
$a_{0}=5.12$
,
![]() $a_{1}=122.8$
and
$a_{1}=122.8$
and
![]() $a_{2}=-4.485$
. Here the choice of functional form for the fit is empirical; the development of a physical model that best describes the spatial evolution of the surface drift
$a_{2}=-4.485$
. Here the choice of functional form for the fit is empirical; the development of a physical model that best describes the spatial evolution of the surface drift
![]() $\overline{\unicode[STIX]{x0394}x}$
will be the primary focus of upcoming laboratory experiments, and is beyond the scope of the work presented here.
$\overline{\unicode[STIX]{x0394}x}$
will be the primary focus of upcoming laboratory experiments, and is beyond the scope of the work presented here.

Figure 4. (a) Total horizontal drift for particles initially at the surface, normalized by the wavenumber
![]() $k_{c}$
that is computed from the centre frequency
$k_{c}$
that is computed from the centre frequency
![]() $f_{c}$
, as a function of the normalized initial horizontal position of the particles
$f_{c}$
, as a function of the normalized initial horizontal position of the particles
![]() $\hat{x}=(x_{0}-x_{b})k_{c}$
. All data are colour-coded for the slope of the packet,
$\hat{x}=(x_{0}-x_{b})k_{c}$
. All data are colour-coded for the slope of the packet,
![]() $S$
. (b) Total horizontal drift for particles initially at the surface for the breaking cases only, normalized by the wavenumber
$S$
. (b) Total horizontal drift for particles initially at the surface for the breaking cases only, normalized by the wavenumber
![]() $k_{c}$
and
$k_{c}$
and
![]() $\sqrt{S-S_{\ast }}$
, as a function of the normalized initial horizontal position of the particles
$\sqrt{S-S_{\ast }}$
, as a function of the normalized initial horizontal position of the particles
![]() $(x_{0}-x_{b})k_{c}$
.
$(x_{0}-x_{b})k_{c}$
.
![]() $S_{\ast }$
is the measured breaking threshold slope. All data are colour-coded for the slope of the packet,
$S_{\ast }$
is the measured breaking threshold slope. All data are colour-coded for the slope of the packet,
![]() $S$
. The white circles represent the bin-averaged values, the grey dashed line a fit to a gamma distribution
$S$
. The white circles represent the bin-averaged values, the grey dashed line a fit to a gamma distribution
![]() ${\mathcal{F}}(\hat{x})$
, while the blue dashed line represents a fit to a Poisson functional form.
${\mathcal{F}}(\hat{x})$
, while the blue dashed line represents a fit to a Poisson functional form.

Figure 5. (a) Measured surface drift velocity
![]() $u_{L,s}/c$
, as a function of the wave slope
$u_{L,s}/c$
, as a function of the wave slope
![]() $S$
. Non-breaking cases are plotted in black, while the breaking cases are shown in red. The breaking threshold, identified experimentally, is represented by a black asterisk. We find two distinct regimes: for non-breaking waves we find
$S$
. Non-breaking cases are plotted in black, while the breaking cases are shown in red. The breaking threshold, identified experimentally, is represented by a black asterisk. We find two distinct regimes: for non-breaking waves we find
![]() $u_{L,s}/c\propto S^{2}$
and for the breaking cases we find
$u_{L,s}/c\propto S^{2}$
and for the breaking cases we find
![]() $u_{L,s}/c\propto S$
. (b) Same as in (a), with the results from the numerical studies of Deike et al. (Reference Deike, Pizzo and Melville2017) and an estimate from the experiments of Grue & Kolaas (Reference Grue and Kolaas2017) (yellow
$u_{L,s}/c\propto S$
. (b) Same as in (a), with the results from the numerical studies of Deike et al. (Reference Deike, Pizzo and Melville2017) and an estimate from the experiments of Grue & Kolaas (Reference Grue and Kolaas2017) (yellow
![]() $\ast$
) added. For the breaking case, we find that both the numerical simulations and laboratory results can be described as
$\ast$
) added. For the breaking case, we find that both the numerical simulations and laboratory results can be described as
![]() $u_{L,s}/c=\unicode[STIX]{x1D712}_{2}(S-S_{\ast })$
, with a fitted parameter
$u_{L,s}/c=\unicode[STIX]{x1D712}_{2}(S-S_{\ast })$
, with a fitted parameter
![]() $\unicode[STIX]{x1D712}_{2}$
of 8.2 and 9 for the laboratory and numerical experiments, respectively. In that case, the fit is forced to intersect the breaking threshold
$\unicode[STIX]{x1D712}_{2}$
of 8.2 and 9 for the laboratory and numerical experiments, respectively. In that case, the fit is forced to intersect the breaking threshold
![]() $S_{\ast }$
, measured at 0.28 in the present study, compared to 0.31 in the numerical simulations (Deike et al.
Reference Deike, Pizzo and Melville2017). Also shown is the unconstrained linear fit of the breaking cases, where
$S_{\ast }$
, measured at 0.28 in the present study, compared to 0.31 in the numerical simulations (Deike et al.
Reference Deike, Pizzo and Melville2017). Also shown is the unconstrained linear fit of the breaking cases, where
![]() $u_{L,s}/c=\unicode[STIX]{x1D712}_{3}(S-S_{o})$
. We find the fitting parameters
$u_{L,s}/c=\unicode[STIX]{x1D712}_{3}(S-S_{o})$
. We find the fitting parameters
![]() $\unicode[STIX]{x1D712}_{3}=6.1$
and
$\unicode[STIX]{x1D712}_{3}=6.1$
and
![]() $S_{o}=0.25$
.
$S_{o}=0.25$
.
Next, the drift velocity at the surface,
![]() $u_{L,s}$
, is defined as
$u_{L,s}$
, is defined as
where
![]() $T$
is the characteristic time scale of the packet, taken as
$T$
is the characteristic time scale of the packet, taken as
![]() $T=1/f_{c}$
(Rapp & Melville Reference Rapp and Melville1990). For the breaking cases, the surface drift
$T=1/f_{c}$
(Rapp & Melville Reference Rapp and Melville1990). For the breaking cases, the surface drift
![]() $\langle \overline{\unicode[STIX]{x0394}x}\rangle$
is computed by averaging
$\langle \overline{\unicode[STIX]{x0394}x}\rangle$
is computed by averaging
![]() $\overline{\unicode[STIX]{x0394}x}$
over a range of particle initial positions
$\overline{\unicode[STIX]{x0394}x}$
over a range of particle initial positions
![]() $x_{o}$
bounded by the locations where
$x_{o}$
bounded by the locations where
![]() $\overline{\unicode[STIX]{x0394}x}$
asymptotes upstream and downstream of the focusing region. For the non-breaking packets, the surface drift is averaged over all available measurements for a given
$\overline{\unicode[STIX]{x0394}x}$
asymptotes upstream and downstream of the focusing region. For the non-breaking packets, the surface drift is averaged over all available measurements for a given
![]() $S$
value.
$S$
value.
Figure 5(a) shows the normalized surface drift velocity
![]() $u_{L,s}/c$
as a function of slope
$u_{L,s}/c$
as a function of slope
![]() $S$
, where
$S$
, where
![]() $c$
is the characteristic phase velocity, corresponding to the phase velocity of the central frequency,
$c$
is the characteristic phase velocity, corresponding to the phase velocity of the central frequency,
![]() $f_{c}$
, of the wave packet. For non-breaking cases (black circles), we find the drift
$f_{c}$
, of the wave packet. For non-breaking cases (black circles), we find the drift
![]() $u_{L,s}/c\propto S^{2}$
, as expected for the Lagrangian drift of weakly nonlinear narrow-banded deep-water surface gravity waves; see the discussion in Deike et al. (Reference Deike, Pizzo and Melville2017) and van den Bremer & Taylor (Reference van den Bremer and Taylor2016). For larger slopes, above the breaking threshold, we find a distinct regime where the surface drift velocity is proportional to
$u_{L,s}/c\propto S^{2}$
, as expected for the Lagrangian drift of weakly nonlinear narrow-banded deep-water surface gravity waves; see the discussion in Deike et al. (Reference Deike, Pizzo and Melville2017) and van den Bremer & Taylor (Reference van den Bremer and Taylor2016). For larger slopes, above the breaking threshold, we find a distinct regime where the surface drift velocity is proportional to
![]() $S$
. This is in qualitative agreement with the scaling model of the Lagrangian transport due to wave breaking proposed by Deike et al. (Reference Deike, Pizzo and Melville2017), based on a theoretical argument due to Pizzo (Reference Pizzo2017) and numerical simulations over a much broader range of parameters.
$S$
. This is in qualitative agreement with the scaling model of the Lagrangian transport due to wave breaking proposed by Deike et al. (Reference Deike, Pizzo and Melville2017), based on a theoretical argument due to Pizzo (Reference Pizzo2017) and numerical simulations over a much broader range of parameters.
Figure 5(b) shows the same data that is already presented in figure 5(a), along with the results from Grue & Kolaas (Reference Grue and Kolaas2017) and Deike et al. (Reference Deike, Pizzo and Melville2017), labelled as DPM2017. For the latter, the colour-coding of the diamond symbols represents different packet configurations. Following their approach, the non-breaking cases, for
![]() $S<S_{\ast }$
, are described by
$S<S_{\ast }$
, are described by
with
![]() $\unicode[STIX]{x1D712}_{1}=1.28$
for the present study, as compared to
$\unicode[STIX]{x1D712}_{1}=1.28$
for the present study, as compared to
![]() $\unicode[STIX]{x1D712}_{1}=0.82$
for the numerical studies of Deike et al. (Reference Deike, Pizzo and Melville2017). This difference is likely due to the higher weighting of the largest
$\unicode[STIX]{x1D712}_{1}=0.82$
for the numerical studies of Deike et al. (Reference Deike, Pizzo and Melville2017). This difference is likely due to the higher weighting of the largest
![]() $S$
non-breaking cases. Above the breaking threshold
$S$
non-breaking cases. Above the breaking threshold
![]() $S_{\ast }$
, we find the drift to increase linearly with slope such that
$S_{\ast }$
, we find the drift to increase linearly with slope such that
with
![]() $\unicode[STIX]{x1D712}_{2}=8.2$
for the present study, close to the value found by Deike et al. (Reference Deike, Pizzo and Melville2017), namely
$\unicode[STIX]{x1D712}_{2}=8.2$
for the present study, close to the value found by Deike et al. (Reference Deike, Pizzo and Melville2017), namely
![]() $\unicode[STIX]{x1D712}_{2}=9$
; here the fit is forced to intersect the breaking threshold
$\unicode[STIX]{x1D712}_{2}=9$
; here the fit is forced to intersect the breaking threshold
![]() $S_{\ast }$
. Also shown is the unconstrained linear fit of the breaking cases, where
$S_{\ast }$
. Also shown is the unconstrained linear fit of the breaking cases, where
In that case, we find the fitting parameters
![]() $\unicode[STIX]{x1D712}_{3}=6.1$
and
$\unicode[STIX]{x1D712}_{3}=6.1$
and
![]() $S_{o}=0.25$
. These numbers are closer to the results of Grue & Jensen (Reference Grue and Jensen2012), where a linear relationship between Lagrangian drift velocity and a local wave slope,
$S_{o}=0.25$
. These numbers are closer to the results of Grue & Jensen (Reference Grue and Jensen2012), where a linear relationship between Lagrangian drift velocity and a local wave slope,
![]() $q$
, was found (see their figure 9 and related discussions).
$q$
, was found (see their figure 9 and related discussions).
Overall, we find good agreement between our laboratory measurements and the Deike et al. (Reference Deike, Pizzo and Melville2017) scaling model. The main difference being the value of the breaking threshold
![]() $S_{\ast }$
, which is found to be much larger in their numerical studies (
$S_{\ast }$
, which is found to be much larger in their numerical studies (
![]() $S_{\ast }=0.31$
). This is likely caused by the challenges of producing weakly breaking waves in a numerical tank, where the resolution required to properly resolve the fine-scale motion of incipient breaking waves was above the computational capabilities available at the time of their study. This numerical limitation is consistent with the DNS results of the energy dissipated by breaking (Deike et al.
Reference Deike, Popinet and Melville2015). Additionally, the fact that the particles considered in the laboratory experiments are slightly buoyant might contribute to this mismatch.
$S_{\ast }=0.31$
). This is likely caused by the challenges of producing weakly breaking waves in a numerical tank, where the resolution required to properly resolve the fine-scale motion of incipient breaking waves was above the computational capabilities available at the time of their study. This numerical limitation is consistent with the DNS results of the energy dissipated by breaking (Deike et al.
Reference Deike, Popinet and Melville2015). Additionally, the fact that the particles considered in the laboratory experiments are slightly buoyant might contribute to this mismatch.
4 Discussion and conclusion
In this paper we have observed the surface Lagrangian drift induced by a focusing deep-water surface wave packet. The averaged form of the drift, as a function of distance along the channel, was found, as was the total drift. For non-breaking waves, the drift measurements agree with the classical Stokes drift predictions (see § 2.2 of Deike et al. (Reference Deike, Pizzo and Melville2017), for details), while for breaking waves there is an agreement between the results found here and those presented in the numerical work of Deike et al. (Reference Deike, Pizzo and Melville2017), where the transport at the surface is found to scale with
![]() $S$
. In particular, the scaling constant
$S$
. In particular, the scaling constant
![]() $\unicode[STIX]{x1D712}_{2}$
was found to be in agreement with their DNS results.
$\unicode[STIX]{x1D712}_{2}$
was found to be in agreement with their DNS results.
This study only considered one packet bandwidth. The packet bandwidth is believed to modulate the duration of the breaking event, in both space and time. In particular, Drazen et al. (Reference Drazen, Melville and Lenain2008, see their figure 10) found that the duration of breaking has a weak dependence on
![]() $S$
, but depends more significantly (up to a factor of five for the packet parameters considered there) on the packet bandwidth. Therefore, a better understanding of this relationship would aid in improving the simple scaling arguments made by Deike et al. (Reference Deike, Pizzo and Melville2017) for the breaking cases, and will be the subject of future laboratory studies.
$S$
, but depends more significantly (up to a factor of five for the packet parameters considered there) on the packet bandwidth. Therefore, a better understanding of this relationship would aid in improving the simple scaling arguments made by Deike et al. (Reference Deike, Pizzo and Melville2017) for the breaking cases, and will be the subject of future laboratory studies.
Furthermore, the depth dependence of the breaking-induced drift is of significant interest, as it would allow us to estimate the total mass flux due to breaking. However, there is considerable difficulty in seeding and generating neutrally buoyant particles that are large enough to be observed over the duration of breaking, and small enough to faithfully follow the flow.
This paper serves to better constrain the Lagrangian drift induced by wave breaking. Together with the statistics describing wave breaking (Phillips Reference Phillips1985), following the framework of Pizzo et al. (Reference Pizzo, Melville and Deike2019), this paper will serve to better estimate and parameterize the surface drift induced by wave breaking in the ocean.
Acknowledgements
We thank R. Klidy and his staff at the Hydraulics Laboratory, Scripps Institution of Oceanography, for their assistance during the experiments. We thank J. Edara and J. Sinnis for their help processing and analysing the laboratory measurements, and L. Grare and N. Statom for reviewing earlier versions of the manuscript and support during the laboratory experiments. We are thankful to two anonymous reviewers for their suggestions, which improved the paper. This work was supported by NSF and ONR grants to W. K. Melville (OCE-1434694, OCE-1634289, N00014-14-1-0710 and N00014-17-1-3005).