I. INTRODUCTION
The miniature antennas have been and remain widely studied. Limits of the performances of these antennas in terms of quality factor, gain (efficiency) or bandwidth have been the subject of numerous studies and publications [Reference Wheeler1–Reference McLean5]. Properties of radiation of miniature antennas are less discussed and are mainly characterized via radiation efficiency. As a result, we are particularly interested in this work in limits of the maximum directivity (D max) with respect to the size of an antenna. The intrinsic gain G of an antenna is by definition bound to this parameter by means of the radiation efficiency η (G = ηD). From fundamental limits of electrically small antenna [Reference Harrington4], it is well known that the gain will be severely degraded due to the decreased efficiency when the antenna is miniaturized. The evolution of directivity versus antenna size is not widely reported. In consequence this document discusses the directivity properties of miniature antennas. It is based on a complete state of the art of directive compact antennas dealing with theoretical limits and identified the techniques to shape the radiation of compact antennas.
II. FUNDAMENTAL LIMITS OF ANTENNA DIRECTIVITY
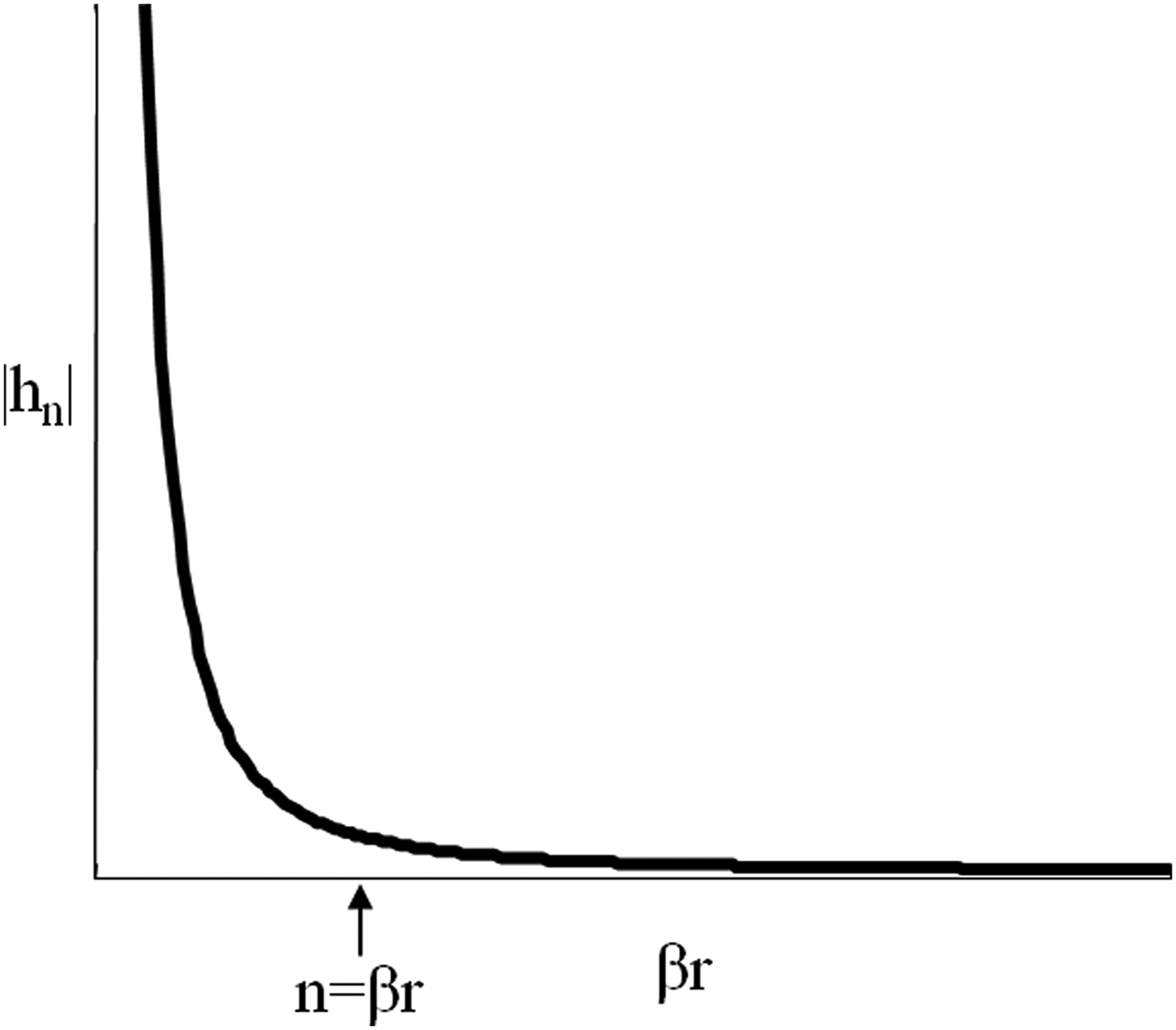
The term Superdirectivity was used for the first time by Taylor [Reference Taylor6] in his article of 1948 in response to the article by Riblet [Reference Riblet7] dealing with the maximum directivity of an antenna. While Riblet said that the gain of an antenna is only limited by the ohmic losses, latter Taylor sees limits related to areas of application of Hankel functions for spherical wave expansion radiation. Hansen [Reference Hansen8] in 1980 attributes the prior to a German book from 1922 written by Oseen [Reference Oseen9] which foresees the possibility of a superdirective antenna. As Riblet [Reference Riblet7], Hansen [Reference Hansen8], and Uzkov [Reference Uzkov10] state that any directivity can be reached for a given radiant aperture size. Therefore the limit in directivity does not exist. In 1958, Harrington [Reference Harrington3] establishes a limit on the maximum attainable directivity D in a given direction (θ 0, φ 0) depending on the order (N) of equivalent spherical modes in the radiation of an antenna as D max (θ 0, φ 0) = N 2 + 2N. In the same paper, Harrington pursues its analysis by providing, according to the Hankel functions, a relationship between the antenna size and N as N = βr, where β is the wave number and r is the radius of the sphere enclosing the entire antenna structure. With this relationship, Harrington proposes the first limit of the directivity as a function of the antenna size. He based this relationship on the inflection of Hankel function module (Fig. 1). He defines this as “the approximate transition point between the slow decay of the amplitude of the Hankel function of the second degree for βr high and rapid growth of the same magnitude for βr weak” [Reference Harrington3]. Although the relationship between the maximum directivity in one direction and the N order of spherical modes radiated seems absolute, the relationship linking the number of modes to the size of the antenna is questionable. In particular, if we trace the curve of the maximum directivity depending on 2r/λ (λ is the wavelength of the antenna), it is observed in Fig. 2 that for electrically small antenna sizes (βr < 1/(2π)) the maximum directivity becomes negative, which does not correspond to the theoretical definition of directivity. As Harrington himself says point N = βr is approximate and thus the relation linking D max(θ 0, φ 0) and r remains therefore to be determined for miniature antennas. Other articles [Reference Geyi11, Reference Pozar12] use the quality factor Q and its limit for miniaturized antennas in order to propose limits on the gain. Then, Geyi [Reference Geyi11] who says concerning Harrington's work that “the normal gain or supergain is kind of ambiguous since the cut-off point is an approximate transition point and in addition this is not clearly specified”, proposes a limit of gain compared with the limit of Harrington. For this new limit, infinite gain of miniaturized antennas is physically possible but implicitly assumes that the antennas remain efficient. Nevertheless even if for miniaturized antennas his limit appears physical, it does not represent a maximum outside this zone (lower than Harrington normal limit).
Fig. 1. Plot of the amplitude of a Hankel function of the second order as a function of βr
Fig. 2. Chart gathering the antenna examples.
Moreover, the directivity (equivalent to the gain if there are lossless antennas and no consideration on impedance mismatching) of an antenna will be stronger as the number of equivalent radiating spherical modes is high. Electrically small antennas are known to have a limited number of modes. Recent articles [Reference Belmkaddem, Rudant and Vuong13, Reference Belmkaddem, Rudant and Vuong14] analyzing electrically small antennas with the spherical wave expansion show that these antennas can be multi-modal. If these modes are well exploited, greater directivities than those currently produced could be achieved.
III. COMPACT DIRECTIVE ANTENNA: ANALYSE METHODOLOGY
In the following section, we will propose a classification of different kinds of compact directive antennas according to their size using a graph. Some clarifications are needed for a complete understanding of the approach. Firstly, in the graph used in Fig. 2, the antenna size is expressed as 2r/λ. Directivity D is expressed in dBi and corresponds to the maximum directivity achieved by the antenna to classify. This directivity is recorded directly in the articles, except for [Reference Grange15], where the directivity is recalculated from the gain and efficiency, and for the three patents [Reference Souny16–Reference Voronoff18], where the antennas have been simulated to get the directivity. In most cases, the positioning of the antennas on the graph is direct. Ambiguity appears, however, with antennas having a metallic plane. Except for patch antenna where this plane really grounds the antenna, in most cases thanks to the image theory this plane allows modifying the design of the antenna (by example monopole or Planar Inverted F Antenna (PIFA)). If in these cases, the metallic plane is of a finite size, smaller than one half-wavelength, it contributes to the directivity, by diffracting the field on the metallic plane edges for example [Reference Pfeiffer, Grbic, Xu and Forrest19]. Consequently, it must be taken into account in the effective size of the antenna. However, if this plane can be considered as infinite (large dimensions compared to the wavelength), we do not take it into account in the size of the antenna, but 3 dB (the radiation is considered in the half-space) are subtracted from the considered maximum directivity. For these cases the subtraction of 3 dB is mentioned in Table 1.
Table 1. Performances of miniature directive antennas in literature.
IV. (SUPER) DIRECTIVE AND MINIATURIZED ANTENNAS
Among the different compact and directive antenna topologies identified in the literature, we suggest to regroup them into four categories: antennas above reflector, Huygens source, loaded antenna, and compact antenna array. These four techniques to achieve high directivity antennas with compact size are detailed hereafter and the performances of all these antennas are gathered in Table 1.
A) Antennas above reflector
Two kinds of reflector exists for antenna, firstly the perfect electrical conductor (PEC) as metallic plane, which acts as mirror for electrical currents, and secondly the artificial (as perfect are purely theoretical) magnetic conductor (AMC) that acts as mirror for magnetic currents. These AMC are realized with high-impedance surface (HIS). The metallic ground plane can also be used for non-normal incident wave, as a mirror for normal electric currents as for monopole antennas [Reference Kim, Pivnenko and Breinbjerg20]. Thanks to the infinite metallic plane the size of the antenna is divided by two and the radiation pattern is focused on the half space where the antenna is set. Antennas over HIS as designed in [Reference Engheta and Ziolkowski31] are smaller in thickness than the antennas associated with classical metal reflectors. With a phase shift of the incident electric field of 0° against 180° for PEC, the antenna can be placed as close as possible from a HIS (λ/4 above PEC) and have stable behavior [Reference Engheta and Ziolkowski31]. First two examples [Reference Grange15, Reference Jin and Ziolkowski22] are presented for small antennas for which the HIS acts as an infinite reflector. As a limit case of the approach, one elementary cell of the HIS itself can also be used directly to resonate as shown by Luukkonen et al. [Reference Luukkonen, Karilainen, Vehmas, Simovski and Tretyakov21]. For this example, the whole size of the HIS has to be taken into account for antenna reference size and its directivity is not decreased of 3 dB. As shown on the graph in Fig. 2, where these antennas are represented by clear blue stars, their performances are slightly above the maximal normal limit of Harrington.
B) Huygens sources
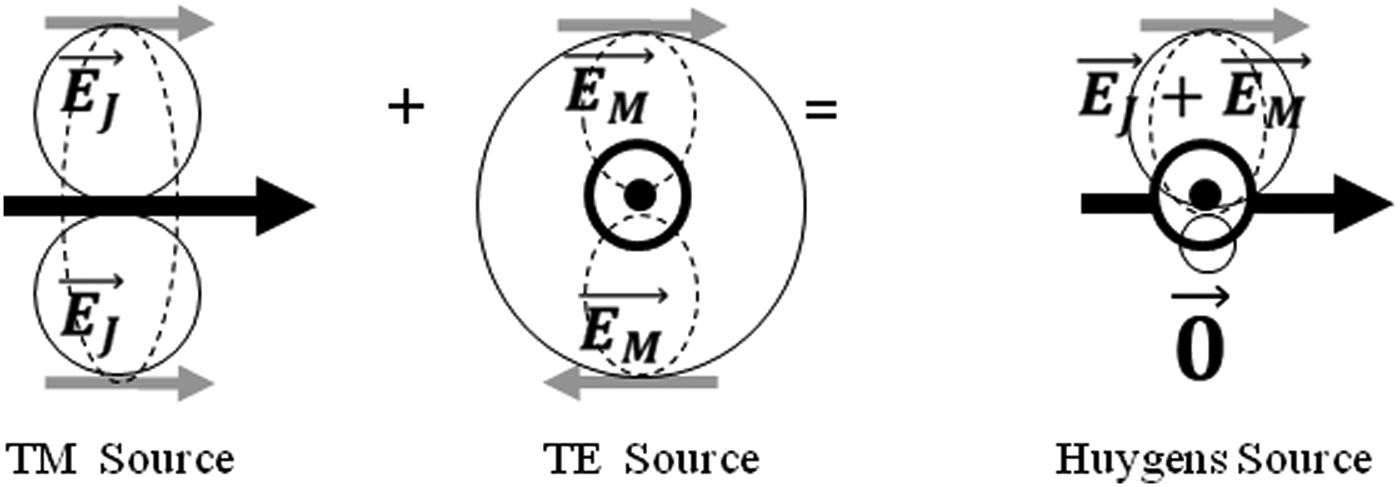
Secondly directivity can be created for compact antennas in using the natural radiation properties of the combination of a Transverse Electric (TE) mode in quadrature with a Transverse Magnetic (TM) mode of order N = 1 [Reference Yaghjian23], Fig. 3. This type of antenna is commonly called Huygens source or Poynting antenna or cross-field antenna (CFA). According to Yaghjian [Reference Yaghjian23] directivity of a Huygens source is up to 4.77 dBi (Harrington gives D = N 2 + 2N then for N = 1 we get D = 3 in linear so 4.77 dBi). Articles and patents [Reference Souny16, Reference Jin and Ziolkowski24–Reference Alitalo, Karilainen, Niemi, Simovski and Tretyakov26] use this technique to increase the directivity of miniaturized antennas (r between 0.1 and 0.2λ). Previous article as [Reference Clavin, Huebner and Kilburg32] have already detailed non-miniaturized Huygens sources (0.8 and 0.9λ). The structures of Huygens sources are very different, but in a general case the realization and feeding of the TE source (magnetic dipole) is quite complex and the association of both the sources is very tricky. These antennas are represented by red stars on the chart in Fig. 2. It is important to note that for [Reference Alitalo, Karilainen, Niemi, Simovski and Tretyakov26] the size of the antenna does not include the balun, which can be considered as part of the antenna is some cases. Moreover, the directivity announced by Jin and Ziolkowski [Reference Jin and Ziolkowski24] of 5.05 dBi is higher than the 4.77 dBi, which is the maximum for single Huygens sources. Some over phenomenon (possible array factor effect) due to the particular antenna configuration can explain this extra value of directivity. To conclude, the Huygens sources are quite complex antennas to realize and for single source the maximal directivity reachable is of 4.77 dBi.
Fig. 3. Principle of directivity by combining fields from TE and TM sources in phase quadrature.
C) Loaded antennas
The directivity of the antenna can also be increased by placing a resistor in a loop antenna [Reference Beverage33] to absorb unwanted currents and suppress a part of the reflected currents in each strand. Thus, this technique is used in [Reference Hadik-Barkoczy17, Reference Voronoff18, Reference Schantz27] to enhance the directivity of miniaturized antenna. The principle of these antennas has been exposed in 1920 by Beverage [Reference Beverage33] for non-miniaturized antenna and then realized long time after for miniaturized antenna and can be found in patents [Reference Hadik-Barkoczy17, Reference Voronoff18] or in very recent literature [Reference Schantz27]. These antennas are represented by green stars on the chart in Fig. 2. These antennas, incorporating a resistance, are proved low radiation efficiency due to the introduction of losses. Unfortunately, this information has not been verified because none of the concerned references provides efficiency data. However, these directive antennas are the smallest we have found in the literature. NB: Antennas can be loaded by inductance and capacitance as the microstrip antenna in [Reference Belmkaddem, Rudant and Vuong14]; nevertheless this kind of antennas shows worse directivity performances than the ones loaded by the resistance.
D) Compact antennas array
Finally, it is worth mentioning the compact antenna arrays. The combination of the radiation of multiple closely spaced compact sources increases the directivity of the whole system [Reference Kim, Pivnenko and Breinbjerg20]. Compact antennas arrays can be split in two different categories. The first one is an array composed of fed antennas; each antenna is fed individually, eventually by the use of a coupler to deal with the phase properties for the right combination. The second one is composed of one fed antenna and the others elements placed as parasitic (director or reflector) (Fig. 4). Gain (consequently directivity) of such compact antennas array, regardless of their topology, is theoretically infinite if no losses are taken into account (η = 1) and the distance d is null between an infinite number of elements [Reference Uzkov10]. For active arrays, the array factor and coupling phenomenon have to be optimized to increase the total radiating field. Thus, complex feeding circuits are developed to handle these specific problems [Reference Weber, Volmer, Blau, Stephan and Hein28]. For the parasitic array, the position of these elements and their loading play on the total radiated field and then can increase the directivity. Some examples of compact parasitic arrays can be found in the literature [Reference O'Donnell and Yaghjian29, Reference Yaghjian, O'Donnel, Altshuler and Best30]. By realizing an array of Huygens sources a directivity of 9 dBi (two sources) can be reached [Reference Yaghjian23]. The antenna arrays are represented by blue stars on the chart in Fig. 2. The compact antenna arrays are the most promising ones (infinite directivity, freedom degrees for optimization, miniaturization, and design).
Fig. 4. Antenna parasitic elements array, (a) dipole alone and (b) dipole with a directive parasitic element.
E) State-of-the-art chart
Antenna data are positioned in terms of size and directivity for the various items mentioned above on the chart in Fig. 2 for synthesis. The normal directivity limit of Harrington and miniature antennas limit defined by the radiansphere of Wheeler [Reference Wheeler1] are added to the chart as a guide. Geyi limit is also plotted for comparison in the area of miniature antennas. The pink star represents the half-wavelength dipole directivity.
V. CONCLUSIONS
Considering the position of the various referenced works on the chart, we can see that all the miniature directional antennas found in literature are above the maximal normal limit of Harrington. This justifies the term of super directivity due to antenna directivity higher than the normal directivity limit. Among these miniature and directional antennas, the smallest ones are loaded antennas or Huygens sources. It is important to notice that both of these antennas have significant drawbacks. Firstly, the loaded antennas have a very poor efficiency due to the introduction of losses inside the antenna. Secondly, for the Huygens sources their directivity is limited to 4.77 dBi and the magnetic source is really complex to realize. The most directive antennas are the Huygens multi-sources, the compact antenna arrays or the antenna above a reflector. Huygens multi-sources structure (which has never been realized experimentally) constitutes the research guidelines and can be classified as compact antenna arrays. Antennas on metamaterials (HIS) or on infinite ground planes are not promising because they are bulky and less directive. Eventually, the compact antenna arrays seem to be the most promising antennas by their manufacturing flexibility and optimization. This type of solution is to revisit with the contribution of new electronic and microelectronics technologies to design innovative miniature directive antennas.
ACKNOWLEDGEMENTS
This work is partially supported by ANR (ANR-11-INFR-014) through SOCRATE Project.
M. Pigeon received a degree in engineering from the National School of Civil Aviation (ENAC) in 2007 and received her Ph.D. degree in Microwave, Electromagnetism and Optoelectronics in 2011. She now holds a post-doctoral fellowship at the CEA-Leti. Her main research interests are design and optimization of small antennas as well as metamaterials and fundamental limitations.
C. Delaveaud completed a university curriculum resulting in a Ph.D. in Optical Communication and Microwave Techniques obtained in 1996 at the University of Limoges. After industrial experience in company Radiall (Voreppe, France), he joined in 2002 the Electronic and Information Technology Laboratory of the French Atomic Energy Commission (CEA-LETI) based in Grenoble (France). After his appointment as senior expert in 2003, he obtained his Accreditation to Direct Physics Research at the University of Grenoble (2010). His research areas range from electromagnetism applied to antennas (miniature antennas, multi-antenna systems, reconfigurable antennas), to propagation and microwave circuits for radio frequency transmitters. Since 2012, he heads the Antennas and Propagation Laboratory of CEA-LETI. To date, he has contributed to more than 150 papers and communications in major revues and conferences in the field of antennas and radio frequency circuits, and is the author or co-author of ten patents of invention.
L. Rudant was born in 1979. He prepared national selective exams in Saint-Denis, Reunion Island, France. He received the Electronic and Digital Technologies Engineering degree from Polytech'Nantes, the Graduate School of the University of Nantes, France, in 2003. In 2004, he received the Technology Research Engineering degree from Grenoble Institute of Technology, Grenoble, France. In 2004 and 2005, he was in charge of antenna projects for automotive in European research center of Radiall-Larsen Antenna Technology in Voiron, France. In 2006, he joined the Laboratory of Electronics and Information Technology (Leti), Grenoble, France. His main interests include small antenna design, MIMO antennas for terminals, Over-The-Air tests, reconfigurable antennas, superdirectivity. Since 2012, he is in charge with strategic programs and industrial partnerships for Leti activities in the field of wireless systems.
K. Belmkaddem received the M.Sc. degree in Electrical Engineering from Ecole Nationale Supérieure d'Electronique et de ses Applications (ENSEA) Cergy-Pontoise, France in 2009. From 2010 to 2012, she worked as a research engineer at CEA-LETI in Grenoble, France. Currently she is working toward the Ph.D. degree from University of Grenoble, France. Her current research interests include fundamental limitations and design of electrically small antennas.
