NOMENCLATURE
- AR
aspect ratio
- Deq
equivalent diameter of elliptic nozzle exit
- D
diameter of circular nozzle exit
- M
Mach number
- NPR
nozzle-pressure ratio, p 0s/pa
- pa
atmospheric pressure
- pb
backpressure
- pe
nozzle exit pressure
- p 0s
settling chamber pressure
- p 0t
pitot pressure
- x
coordinate along the jet axis
- y
coordinate along the minor axis
- z
coordinate along the major axis
1.0 INTRODUCTION
High-speed jet research is an active research field for a long time due to its wide-ranging application potential. Recent attention has been focused on the control of the jet to increase or decrease mixing of the jet fluid mass with the mass entrained by the jet from the environment to which it is discharged. To achieve the desired mixing, active and passive control techniques have been studied extensively. Compared to active control, passive control techniques have become more popular due to their simplicity. Passive controls, such as nozzle exit geometry modification and vortex generators in the form of tabs, notches and grooves, are popular because of their efficient mixing-promoting capability. Among the various passive control techniques, the use of non-circular geometries has gained importance due to their capability to generate mixing-promoting vortices right from the nozzle exit. It is well known that for mixing enhancement, the jet should have the mass entraining large-scale vortices and mass transporting small-scale vortices in proper proportion. Also, if the mass transporting or mixing-promoting small-scale vortices are of mixed size, it would result in immensely enhanced mixing. The non-circular nozzle exit geometries, such as rectangular and square shapes, were found to shed both small and large-scale vortices due to their azimuthal asymmetry. To exploit this inbuilt advantage, many researchers have carried out extensive studies on the use of rectangular geometry for effective jet control. But, even though the rectangular and square exits shed vortices of mixed size at their sharp corners, the vortices shed from the straight edges would be of uniform size and hence might not be efficient in promoting mixing right from the nozzle exit. Use of elliptic geometry as a passive jet control technique has also attracted many researchers because of their increased entrainment and enhanced mixing capabilities(Reference Ho and Gutmark1-Reference Gutmark, Schadow and Wilson6).
Some of the notable works pertinent to the present work are the following. Ho and Gutmark(Reference Ho and Gutmark1) studied the mass entrainment and its mechanism in an AR2 elliptic jet of exit velocity 21.9m/s. They noticed that the self-induction of the asymmetric coherent structure causing azimuthal distortions were responsible for engulfing large amount of surrounding fluid into the jet. Also, the growth rate of the jet in the minor axis plane is about 20% larger than that in the major axis plane, leading to three axis switches within the range of 40 equivalent diameters. As the mass entrainment ratio of an elliptic jet with a small aspect ratio (2:1) is several times higher than that of the equivalent circular jet, they argued that the small aspect ratio elliptic jet is a very effective passive control device for enhancing mass entrainment. Hussain and Husain(Reference Hussain and Husain2) performed detailed experimental studies on incompressible elliptic jets of different aspect ratios at an exit velocity of 29.26m/s, and inferred that the aspect ratio is one of the factors influencing the locations and frequency of axis-switching. They explained that the curvature-dependent self-advection of the vortical structures in an elliptic jet produces three-dimensional deformation leading to switching of axes and enhanced large-scale mixing. In addition, they(Reference Hussain and Husain3) also investigated the dynamics of coherent structures in the near-field of an AR2 elliptic jet. Quinn(Reference Quinn4) made an experimental study on a turbulent elliptic jet issuing from a sharp-edged AR5 elliptical slot at an exit velocity of 60m/s. He found that the elliptic slot jet entrains ambient fluid faster than an equivalent round-slot jet in both near and far fields of the jet. He observed reduction in potential core length and a higher far-field spreading rate of the elliptic jet. Schadow et al(Reference Schadow, Gutmark, Koshigoe and Wilson5) experimentally studied the mixing characteristics of cold and heated elliptic jets of AR3 and compared them to those of a circular jet. They found that, like subsonic jets, sonic and supersonic under-expanded elliptic jets from the sonic nozzle exhibit axis-switching and enjoy superior mixing characteristics than the circular jet. In the case of under-expanded elliptic jet, the major and minor axes switch at a distance of three diameters from the nozzle and the spreading rate is twice that of a subsonic jet. Gutmark et al(Reference Gutmark, Schadow and Wilson6) carried out experimental investigations on the circular, AR3 elliptic and AR3 rectangular jets issuing from sonic nozzles. The experiments carried out in both cold and hot flows showed that the mixing characteristics of an elliptic jet is are slightly better than those for the equivalent rectangular jet in the subsonic and under-expanded supersonic flows. Both elliptic and rectangular jets displayed higher spreading than the circular jet, particularly at the minor axis side. Verma and Rathakrishnan(Reference Verma and Rathakrishnan7) investigated the effect of aspect ratio on under-expanded elliptic-slot jets. They observed that at a moderately under-expanded condition (Mj = 1.5), a series of oblique shocks and expansion fans impinging on and reflecting from the jet shear layers resulted in a crossover point at the end of each cell giving the appearance of shock diamonds. At a highly under-expanded condition (Mj = 2), the crossover point was replaced by a normal shock known as Mach disk. Due to different growth rates along the two planes, a barrel shock was formed along the minor axis side while a bulb shock was formed along the major axis side for AR2 and AR3 jets. For an AR4 jet, a double bulb shock was formed due to stronger azimuthal deformations existing along the major axis side. Yoon and Lee(Reference Yoon and Lee8) investigated the flow characteristics and entrainment rate of a turbulent elliptic jet from an AR2 orifice at a Reynolds number of 104, using stereoscopic particle image velocimetry and found that the total entrainment rate of the elliptic jet is about 1.5% larger than that of the equivalent round jet. They reported axis-switching at about 2Deq and found that the entrainment of the surrounding fluid was more active on the minor axis as a result of the fast expansion of the jet along this axis due to the self-induction of the elliptic vortical structure in the near-field.
Baty et al(Reference Baty, Seiner and Ponton9) investigated the instability of a correctly expanded supersonic jet of Mach 1.5 from an AR2 convergent-divergent nozzle and revealed that the potential core extends to only about 5Deq. The Mach 1.5 convergent-divergent nozzle used by them had a convergence section of a circular to elliptic transition leading to an elliptic subsonic contraction of AR2, and the nozzle divergence section aspect ratio was held constant up to the exit. Menon and Skews(Reference Menon and Skews10) reported axis-switching and faster jet spread along the minor axis of the under-expanded elliptic nozzles and slots of AR2 and 4. Recently Mitchell et al(Reference Mitchell, Honnery and Soria11) made a quantitative measurement of velocity for an AR2 under-expanded elliptical jet issuing from a smoothly contoured elliptic sonic nozzle using high-resolution planar particle image velocimetry. As expected, the jet displayed axis-switching for all the pressure ratios studied, with the axis-switching gaining strength with increasing pressure ratio. They confirmed that some of the typical characteristics of under-expanded axisymmetric jets – namely, increase of shock spacing and strength with increasing pressure ratio – was also evident in the case of elliptic jet. Research on supersonic elliptic jets proved that the mixing characteristics of supersonic elliptic jets were similar to those of subsonic jets.
The increased entrainment and enhanced mixing capability of the elliptic jets (non-circular jets included) relative to the equivalent circular jet are due to the phenomenon of axis-switching which was unanimously supported by the literature. Axis-switching is a phenomenon in which the cross-section of an asymmetric jet evolves in such a manner that, after a certain distance from the nozzle, the major and the minor axes are interchanged(Reference Zaman12). As explained by Hussain and Husain(Reference Hussain and Husain2), “the curvature-dependent self-advection of the vortical structures in an elliptic jet produces three-dimensional deformation leading to switching of axes and enhanced large-scale mixing. Since the self-induced motion depends on the local curvature and on the core radius, the effect of initial boundary layer characteristics (which controls the core radius of rolled-up vortices) is more pronounced in elliptic jets than in circular jets”.
From the literature, it is clear that the most of the work done on elliptic jet is for subsonic incompressible elliptic jets from elliptic slots and nozzles. Also, the work done on sonic and under-expanded supersonic elliptic jets corresponds to jets issuing from elliptic slots and convergent nozzles with a smooth transition from circular inlet to elliptic exit. The supersonic Mach numbers reported in these cases are equivalent jet Mach numbers (Mj) corresponding to correctly expanded flow. Thus it can be stated that characterising supersonic elliptic jets from convergent-divergent nozzles with elliptic cross-sections from entry to exit at different levels of expansion of supersonic jets would be of great value to high-speed jet literature. With this in mind, in the present study, a Mach 2 jet issuing from a straight convergent-divergent elliptic nozzle of AR2, with elliptic cross-section right from the inlet to exit, was studied experimentally and the results were compared with the experimental results of equivalent Mach 2 circular jet carried out by Arun Kumar and RathakrishnanReference Arun Kumar and Rathakrishnan13.
2.0 EXPERIMENTAL DETAILS
2.1 Jet flow facility
The experiments were conducted in the open jet facility at the high-speed aerodynamics laboratory at the Indian Institute of Technology in Kanpur, India. Compressed air from storage tanks was ducted through a gate valve and a pressure-regulating valve to a settling chamber, where it was brought to an equilibrium stagnation condition (Fig. 1). To reduce the flow disturbance caused by the control valve, a mixing length of 2 m was placed between the pressure-regulating valve and the settling chamber. The flow was conditioned by two mesh screens placed within the settling chamber before entering into the nozzle. The desired nozzle pressure ratio (NPR) was achieved by controlling the settling chamber pressure (P 0s) since the backpressure (Pb) was the atmospheric pressure (Pa) into which the jet was discharging.

Figure 1. Schematic sketch of open jet facility.
2.2 Experimental model
The experimental model (Fig. 2) used in the present investigation is a Mach 2 convergent-divergent elliptic nozzle with a 2:1 aspect ratio, made of brass. The cross-section of the nozzle is elliptic right from the inlet to the exit, as shown in Fig. 2. The equivalent throat and exit diameters of the nozzle are 10mm and 13mm, respectively, which are the same as that of an equivalent circular nozzle(Reference Arun Kumar and Rathakrishnan13). The ratio of the exit area to the throat area is 1.69, which corresponds to the design Mach number of 2. The Reynolds numbers of the Mach 2 jet based on nozzle exit diameter are 7.12 × 105 and 16.6 × 105, respectively, for the minimum and maximum NPRs of 4 and 8 in the present investigation. The design Mach number of the elliptic nozzle is 2. After nozzle fabrication, it is essential to ensure whether the design Mach number is achieved. For this, the nozzle has to be calibrated over the range of nozzle pressure ratios. As the nozzle is elliptic in cross section, it has to be calibrated along the major and minor axes of the jet exit. The calibration results in the present case showed that the Mach number along the major and minor axes of the elliptic jet is uniform like that of axisymmetric nozzle. The flow Mach number at the exit of the nozzle was found to be 2 with an almost uniform distribution over the exit of the nozzle. Therefore, the quasi-one-dimensional isentropic approximation may be comfortably used for the supersonic elliptic nozzle as well, as in the case of a usual supersonic axisymmetric nozzle. Also, the jet is screech free since the jet Mach number 2 of the present study is beyond the screech-prone Mach number range of 1.5 to 1.8(Reference Rathakrishnan18).

Figure 2. Nozzle details: (a) CAD model of the nozzle, (b) fabricated nozzle model and (c) nozzle dimensions (in mm).
2.3 Instrumentation
Pressures were measured with a 16-channel Pressure Systems, Inc. 9010 transducer with a range of 0 to 2.1MPa. The software provided by the manufacturer was used to interface the transducer with a computer. The user-friendly menu-driven software acquires data and shows the pressure reading from all 16 channels simultaneously in a window-type display on the computer screen. The software can be used to choose the units of pressure from a list of available units, perform a re-zero/full calibration, etc. The transducer also has a facility to choose the number of samples to be averaged by means of dipswitch settings. The accuracy of the transducer (after the re-zero calibration) is specified to be ±0.15% full scale. The pressure measurement in the jet was done using a pitot tube with a 0.4mm inner diameter and 0.6mm outer diameter, mounted on a rigid three-dimensional traverse, with a resolution of 0.1mm in linear translation. Thus, the ratio of the nozzle exit to the probe area is (13/0.6)2 = 469.5, which is well above the limit of 64 for regarding the probe blockage negligible(Reference Rathakrishnan14). In all measurements, the sensing-probe stem was kept normal to the jet axis with its sensing hole facing the flow. Very low Reynolds numbers based on the probe diameter could significantly influence the pressures measured by the pitot probe. However, this effect is seldom a problem in supersonic streams because a probe of reasonable size will usually have a Reynolds number above 500, which is above the range of troublesome Reynolds numbers(Reference Phanindra and Rathakrishnan15). For the present probe of outer diameter 0.6mm, the Reynolds number at NPRs 4 and 8 are 4.4 × 104 and 5.8 × 104, respectively. Hence, the viscous effect will not cause any error in pitot-pressure measurements. However, it is important to note that the jet pressure field is essentially unsteady due to the vortices prevailing in the flow field. Therefore, what is measured is the mean value of the pitot pressure. To make this measurement with acceptable accuracy, the provision available in the transducer, namely, the average of 250 samples per second – has been exploited to record the pitot pressure. In the present study, the total number of samples taken was about 500, which corresponds to the time duration of two seconds. The measured values were found to be repeatable within ±3%. The waves prevailing in the supersonic jet core were visualised using a shadowgraph system with a helium spark arc light source in conjunction with a concave mirror. The shadowgraph images were recorded using a still camera.
2.4 Experimental procedure
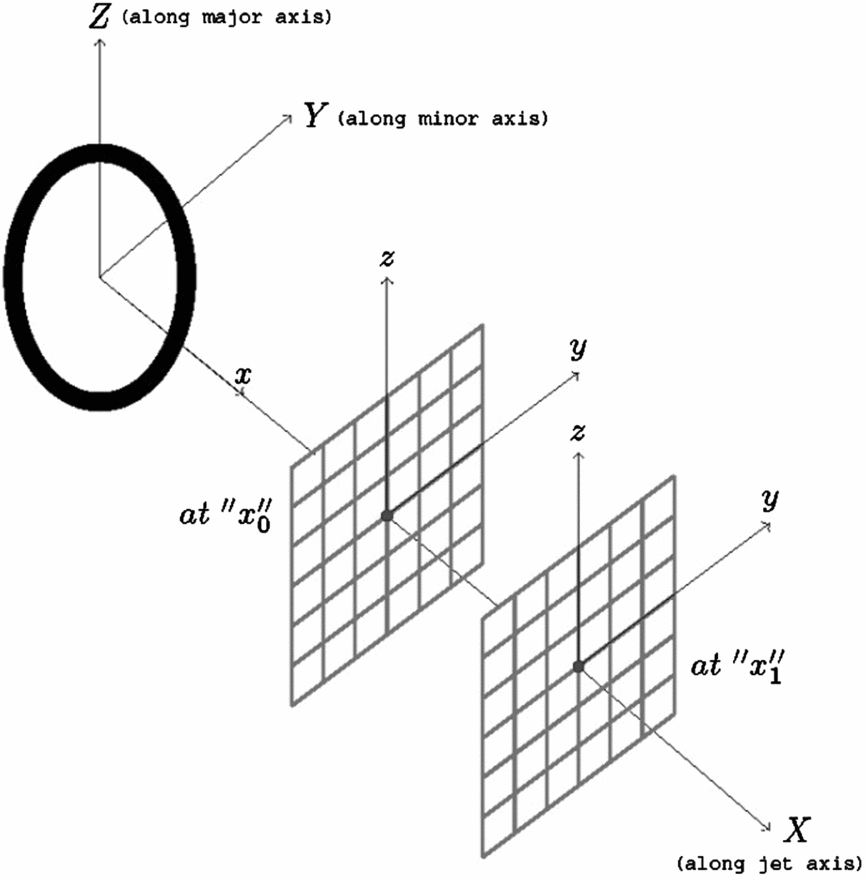
The stagnant air from the settling chamber was expanded through the convergent-divergent elliptic nozzle at five different settling chamber pressures. To study the mixing promoting capability of the elliptic jet, the pitot pressure along the jet centreline was measured at intervals of 1mm up to 260mm (20Deq), where Deq is the jet circular-equivalent diameter, defined as the diameter of the circular jet having the same exit cross-sectional area of the elliptic jet. The centreline pitot pressure was measured at NPRs 4-8 in increments of 1. To understand the evolution of elliptic jets, detailed pitot-pressure measurements were taken for the complete plane normal to the jet axis at different axial locations as shown in Fig. 3. The pressure distributions along the major (z-direction) and minor (y-direction) axis of the jet at different axial locations were also measured. The schematic diagram of the coordinates followed is shown in Fig. 3. The waves prevailing in the jet were visualised using shadowgraphs. The results obtained were compared with the Mach 2 equivalent circular jet(Reference Arun Kumar and Rathakrishnan13) under identical conditions.

Figure 3. Schematic diagram of the nozzle exit and the coordinates followed.
2.5 Data accuracy
The settling chamber pressure during the experiments of the present investigation was maintained within ±2% of the required NPR for all the NPRs studied. The repeatability of the pressure measurements was within ±3%. Since the traverse was manually operated, the linear movement of the pitot probe (mounted on the traverse) along the x, y and z directions had a resolution of ±0.1mm. The manual operation of pressure regulating valve introduced fluctuations in the measured values of stagnation pressure (P 0s). Therefore, the uncertainty in the measured pressure values (both pitot and stagnation) was about ±3%. The nozzle dimensions were accurate within ±0.8%. The uncertainty associated with the flow Mach number at the exit of the nozzle was estimated to be ±1.5%.
3.0 RESULTS AND DISCUSSION
3.1 Centreline pitot-pressure decay
The jet centreline pitot-pressure decay is a measure of jet mixing, indicating the mixing of the ambient fluid mass entrained at the jet boundary with the mass of the fluid inside the jet. Faster decay implies faster jet mixing. Therefore, to investigate the characteristics of a Mach 2 elliptic jet, the measured pitot pressure (P 0t) along the jet axis (X direction) up to 20Deq from the nozzle exit is non-dimensionalised with the settling chamber pressure (P 0s) and plotted as a function of non-dimensionalised axial distance, x/Deq. For all NPRs, the centreline pressure decay of the elliptic jet is compared to the equivalent Mach 2 circular jet available in open literature(Reference Arun Kumar and Rathakrishnan13). The equivalent diameter of elliptic jet (Deq) is the same as that of the circular jet diameter (D) in the present study.
In a supersonic flow, the measured pitot pressure, P 0t, is the total pressure behind the bow shock in front of the pitot probe. In a supersonic jet core, what the probe measures is the total pressure behind the bow shock that stands ahead of the probe nose. Thus it is not the actual total pressure. If the actual total pressure is required, one has to correct the measured pressure for the pressure loss across the shock. But the jet core is wave dominated and the Mach number in the core varies from point to point, and also the shocks in different shock cells are of different strengths. Therefore, it is difficult to correct the measured total pressure for shock loss. Furthermore, in supersonic regions, there is some measurement error due to probe interference with shock structure. Hence, the results in supersonic regions should be considered only as qualitative but are good enough for comparative purposes(Reference Rathakrishnan14). Nevertheless, the data are accurate enough to capture the overall features of the jet, such as the core length, characteristic decay, the decay in the fully developed zone, the number of shock-cells and the spacing between them. The pressure oscillations in the core region of the flow are due to the waves present in the jet. The core length of the supersonic jet may be defined as the axial distance from the nozzle exit, up to which supersonic flow prevails or the distance from the nozzle exit at which the characteristic decay begins(Reference Rathakrishnan14). The distance between two successive peaks of maximum or minimum pressures in the core region of the jet represents the shock-cell length.
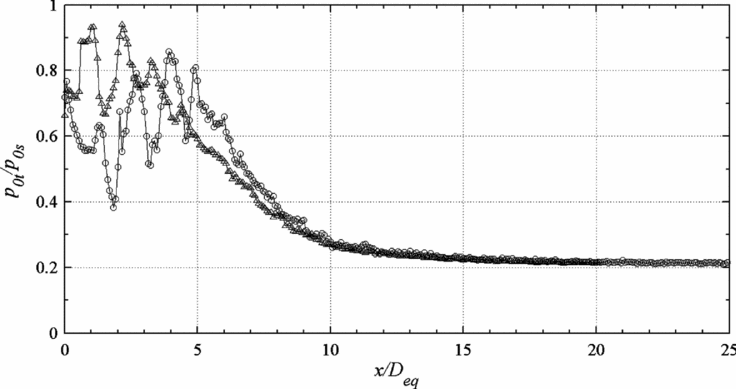
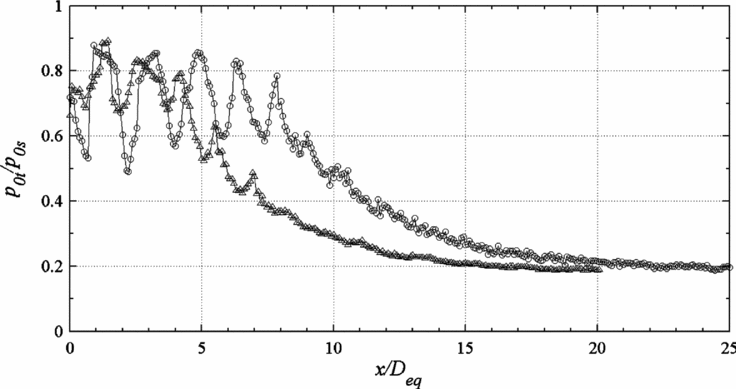
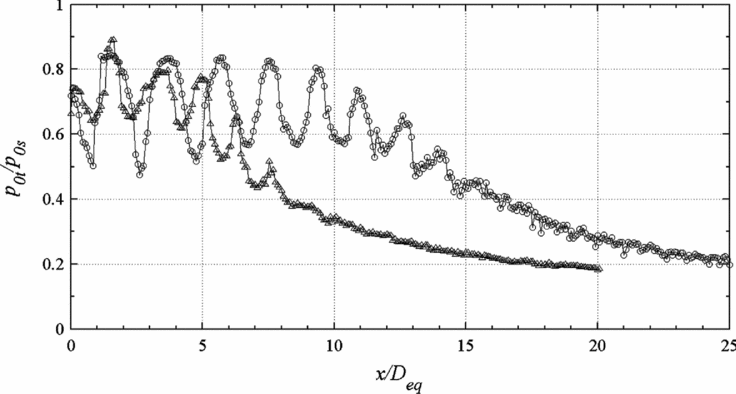
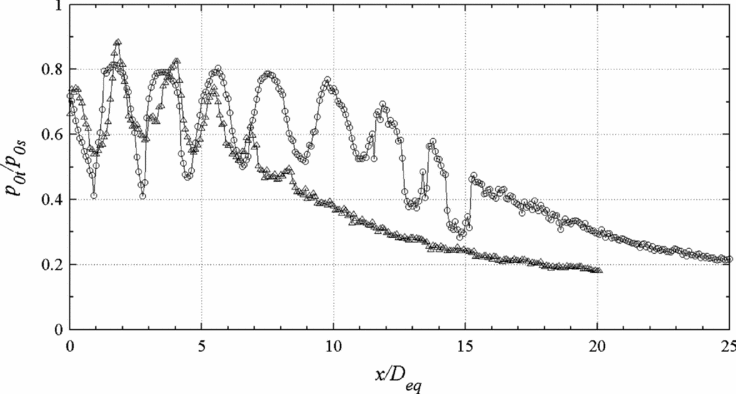
The centreline pitot-pressure decay of elliptic and the equivalent circular jets for NPRs 4-8, in increments of 1 are compared in Figs 4–8. The Mach 2 jet at NPRs 4, 5, 6 and 7 is over-expanded. At NPR 8, the jet is marginally under-expanded. At NPR 7.82, the jet is correctly expanded. From the results of centreline pressure decay (Figs 4–8), it is seen that the core length of the elliptic jet at NPRs 4, 5, 6, 7 and 8 are about 3.7Deq, 4.3Deq, 6.8Deq, 7.5Deq and 8.2Deq, respectively, which are significantly lower than the core of equivalent circular jet at all NPRs reported by Kumar and Rathakrishnan(Reference Arun Kumar and Rathakrishnan13). Also, at all the NPRs in the present study, the waves in the elliptic jet core are considerably weaker and the shock-cell length is smaller than in the circular jet core, as indicated by the amplitude of pitot pressure oscillations and the spacing between the two successive maximum or minimum pressure peaks in the core region.

Figure 4. (a): Centreline pressure decay of Mach 2 jet at NPR 4 (over-expanded). Circular jet (○)(Reference Arun Kumar and Rathakrishnan13), Elliptic jet (Δ). (b): Shadowgraph pictures of circular(Reference Arun Kumar and Rathakrishnan17) and elliptic jets at NPR 4 (over-expanded).

Figure 5. Centreline pressure decay of Mach 2 jet at NPR 5 (over-expanded). Circular jet (○)(Reference Arun Kumar and Rathakrishnan13), Elliptic jet (Δ).

Figure 6. Centreline pressure decay of Mach 2 jet at NPR 6 (over-expanded). Circular jet (○)(Reference Arun Kumar and Rathakrishnan13), Elliptic jet (Δ).

Figure 7. Centreline pressure decay of Mach 2 jet at NPR 7 (over-expanded). Circular jet (○)(Reference Arun Kumar and Rathakrishnan13), Elliptic jet (Δ).

Figure 8. Centreline pressure decay of Mach 2 jet at NPR 8 (marginally under-expanded). Circular jet (○)(Reference Arun Kumar and Rathakrishnan13), Elliptic jet (Δ).
At NPR 4 (Fig. 4(a)) with an over-expansion level of pe/pa = 0.511, the elliptic jet decays faster than the circular jet in the core region. The core for the elliptic jet is 3.7Deq, which is less than the core of the circular jet, as seen in Fig. 4(a). Another interesting effect of the faster mixing is that the waves (especially the compression waves) in the core of elliptic jet are considerably weaker than in the circular jet. Also, there is a Mach-disc formation at the end of the first shock cell for the circular jet(Reference Arun Kumar and Rathakrishnan17), whereas there is no Mach disc formation for the elliptic jet as seen in Fig. 4(b). The faster decay of the elliptic jet continues up to 6Deq and thereafter, the decay of circular jet is slightly faster than the elliptic jet and becomes fully developed at about 13Deq, whereas the elliptic becomes fully developed at about 16Deq. The faster decay of the circular jet beyond 6Deq may be because of the severe pressure loss encountered by the circular jet due to the stronger shocks in the near field. The number of shock-cells in the elliptic jet is three, whereas there are four shock-cells present in the circular jet. The moderate pitot pressure oscillations in the core region of the elliptic jet imply that the waves present in the elliptic jet field are weaker than the waves in the circular jet.
As the NPR increases from 4 to 5, the level of expansion changes from 0.511 to 0.639, indicating the decrease of adverse pressure gradient at the nozzle exit. At NPR 5 (Fig. 5), the elliptic jet when compared to the circular jet decays faster up to 8Deq. From 8Deq onwards, both the jets decay at the same rate and become fully developed at about 14Deq. Although the number of shock-cells in both the cases is four, the waves present in the core region of the circular jet are of considerably higher strength compared to the waves present in the core of the elliptic jet, as reflected by the pitot-pressure oscillations.
At NPRs 6, 7 and 8 (Figs. 6, 7 and 8), the elliptic jet shows superior mixing characteristic than the equivalent circular jet. This is evident from the significantly higher decay of elliptic jet at all the three zones of the jet field: the core, characteristic decay and fully developed regions. The number of shock-cells at NPRs 6, 7 and 8 for elliptic jet is five, which is significantly less than that of the circular jet at these NPRs. Also, the low amplitude of pitot-pressure oscillations in the elliptic jet core relative to the circular jet indicates that the waves in the elliptic jet core are weaker than the waves in the circular jet. At NPR 6, the elliptic jet becomes fully developed at about 15Deq, while the circular jet becomes fully developed at about 20Deq due to its slower rate of decay when compared to the elliptic jet. At NPRs 7 and 8, even at 20Deq, the elliptic and circular jets have yet to become fully developed, but the elliptic jet shows the tendency to become fully developed well before the circular jet.
In the case of the elliptic jet, the number of shock-cells increases from NPR 4 to 6 and thereafter remains the same. Also, the elliptic jet has a lower number of shock cells than the circular jet at all NPRs except NPR 5. As envisaged, for both elliptic and circular jets, the strength of the expansion waves, shock-cell length and core length increase with the increase in NPR. The point at which the jet becomes fully developed is also strongly influenced by the NPR. With increase in NPR, the location at which the fully developed flow begins progressively shifts downstream in case of the circular jet. But in the case of the elliptic jet, the location at which the jet becomes fully developed initially shifts upstream from NPR 4 to 5 and moves downstream from NPR 5 to 6.
From the centreline pressure decay plots, it is clearly seen that the elliptic jet decays faster than the circular jet and thus experiences higher mixing than the equivalent circular jet at all levels of expansion. At all NPRs, the core length of the elliptic jet is significantly less than the circular jet. Except at NPRs 4 and 5, the elliptic jet enjoys better mixing than the circular jet at all three zones of the jet, which is evident from the higher pitot-pressure decay of the elliptic jet. At NPR 4 (Fig. 4(a)), the circular jet decays slightly faster than the elliptic jet from about 6Deq onwards to become fully developed just before the elliptic jet. And at NPR 5 (Fig. 5), the elliptic jet decays faster than the circular jet up to 8Deq; from 8Deq onwards, both jets decay at the same rate and become fully developed at about 14Deq. However, the elliptic jet continues to enjoy better near-field mixing when compared to the circular jet at NPRs 4 and 5.
The reason for the faster decay of the elliptic jet is found to be the continuous variation in the size of the mixing-promoting vortices shed from the elliptic nozzle exit. This is because the elliptic jet has a built-in advantage of azimuthal asymmetry. The azimuthal asymmetry generates vortices of mixed sizes which themselves are asymmetric in nature. Therefore, the size of the vortices generated at the nozzle exit would vary continuously from the extremity of the minor axis to the extremity of the major axis in one quadrant, with the largest structure at the minor axis end and the smallest at the major axis end, in accordance with the vortex theory; the size of the vortex leaving a position at the nozzle exit edge is proportional to the radius of curvature of the edge at that point(Reference Rathakrishnan14). The asymmetric distribution of vorticity owing to azimuthal asymmetry leads to a higher mixing rate for the elliptic jet than for the equivalent circular jet.
3.2 Iso-pitot pressure contours
One of the unique and interesting features of the asymmetric jets is axis-switching. Axis-switching is a phenomenon in which the cross-section of an asymmetric jet evolves in such a manner that, after a certain distance from the nozzle exit, the major and the minor axes are interchangedReference Ho and Gutmark1. This is because of the faster jet spread along the minor axis owing to the azimuthal asymmetry of the elliptic nozzle exit. The vortices of continuously varying size that are shed at exit convect downstream at different rates due to their continuous varying radii of curvature. Therefore, the vortices at the major axis end, with smaller radii of curvature, move downstream faster than the vortices with larger radii of curvature at the minor axis end. This differential movement causes the jet to spread more along the minor axis side than on the major axis side. Also, it was found that the jet entrains more mass over the minor axis side than over the major axis side because the noncircular vortical structures do not remain in a plane and continuously deform when they move downstream, leading to self-induction. Thus, earlier axis-switching indicates faster jet spread and faster near-field mixing of the jet with the ambient fluid. To get an insight into the gross behaviour of jets and their axis-switching phenomena, detailed pitot-pressure measurements were taken at different planes normal to the jet axis and studied by constructing isobars. The pitot pressures were measured over the complete plane, without assuming any degree of jet symmetry.
From the contour plots of elliptic jet (Figs 9–13), it is seen that the jet cross-section initially takes the shape of ellipse after exiting the nozzle and further downstream it gradually changes to almost symmetric (i.e. circular) cross-section and thereafter switches its axes, at all the NPRs of the present study. In Figs 9–13, the pressure contour interval of 0.06 is kept same. The distance from the nozzle exit to the point where the minor and major axes of the jet become almost equal, causing the jet to become almost circular, can be taken as the axis-switching location, because after this location the jet begins to switch its axes completely, indicating that the minor axis of the jet ahead of this point has become the major axis.

Figure 9. Iso-pitot pressure contours of elliptic jet at NPR 4 (over-expanded).

Figure 10. Iso-pitot pressure contours of the elliptic jet at NPR 5 (over-expanded).

Figure 11. Iso-pitot pressure contours of elliptic jet at NPR 6 (over-expanded).

Figure 12. Iso-pitot pressure contours of elliptic jet at NPR 7 (over-expanded).

Figure 13. Iso-pitot pressure contours of elliptic jet at NPR 8 (marginally under-expanded).
At NPR 4 (Fig. 9), it is seen that the cross-section of the jet up to 2Deq is elliptic in nature and at about 4Deq, it develops nearly to rectangular cross-section. This is due to faster spreading of jet along the minor axis side than in the major axis side. Eventually, the jet switches its axes at about 7.5Deq, where it becomes almost axisymmetric, and thereafter at about 8De, it completely switches its axis in such a way that the minor axis becomes major and vice versa. The occurrence of axis-switching implies that the jet mixes faster in the upstream of the axis-switching location, which is clearly supported by the faster centreline pressure decay of the elliptic jet (Fig. 4(a)) up to 6Deq.
At NPR 5, with a decrease in over-expansion level, the jet becomes axisymmetric at about 5Deq as, seen in Fig. 10. At about 8Deq, the switched axes are explicitly seen. Compared to NPR 4, at NPR 5 (Fig. 5) elliptic jet decays faster to become fully developed at about 14Deq, which might be due to the earlier occurrence of axis-switching at NPR 5.
With further decrease in the over-expansion level at NPR 6 (Fig. 11), it is interesting to note that the axis-switching location, which initially shifted upstream from 7.5Deq to 5Deq from NPR 4 to 5, moves downstream to about 7Deq and also the location of the start of a fully developed flow shifts downstream to about 15Deq as shown by centreline pressure decay plot (Fig. 6).
As NPR increases from 6 to 7 (Fig. 12), the jet switches its axes at about 10Deq, whereas at a marginally under-expanded state of NPR 8 (Fig. 13), the axis-switching location of jet moves a little upstream and stays between 9Deq and 9.5Deq. For both NPR 7 and 8, even though the jet has not become fully developed even at about 20Deq (Figs 7 and 8), at NPR 8 it shows a tendency to become fully developed earlier than at NPR 7. This is due to slightly earlier occurrence of axis-switching at NPR 8 than NPR 7. From these results, it is evident that for all NPRs the axis-switching occurs at a location downstream of the supersonic core region, i.e. in the region of characteristic decay where the mixing action is predominant in the jet field.
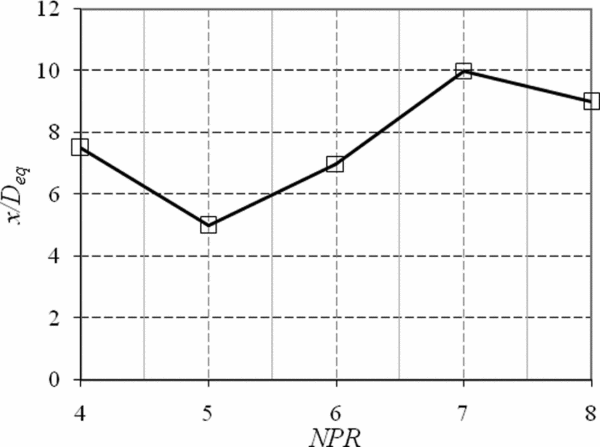
The variation of axis-switching location with increasing NPR is shown in Fig. 14. It is seen that as the NPR increases from 4 to 5, the location of axis-switching moves upstream from 7.5Deq to 5Deq. From NPR 5 onwards, the axis-switching location progressively moves downstream with increasing NPR up to NPR 7. The jet at NPR 6 and 7 switch their axes at around 7Deq and 10Deq. When NPR increases from 7 to 8, the state of the jet becomes marginally under-expanded and the axis-switching location shifts a little upstream to 9Deq.

Figure 14. Variation of axis-switching location with NPR.
From the above discussions, it may be inferred that the elliptic jet enjoys higher near-field mixing than the equivalent circular jet due to the phenomenon of axis-switching. The increased near-field mixing of the elliptic jet with the ambient fluid is evident from the faster decay of the elliptic jet displayed by the centreline pressure plots. The location of axis-switching might also influence the characteristic decay and fully developed zone of the jet. That is, the earlier occurrence of axis-switching, the faster the decay of the jet into the fully developed zone. Thus the elliptic jet, which enjoys the phenomenon of axis-switching associated with the self-induction of asymmetric vortices, clearly proves to be superior than an equivalent circular jet from mass entrainment and mixing points of view. This aspect of mixing superiority of elliptical jet is also reflected in the centreline pitot-pressure decay plots.
The selected iso-pitot contours at identical axial locations for elliptic and circular jets at NPRs 6 and 8 are compared in Figs 15 and 16. These results demonstrate that the elliptic jet spreads faster than the equivalent circular jet. At NPR 6, the over-expansion level of both the jets is 0.767. At this NPR, the iso-pitot pressure contours of elliptic jet show higher jet spread than the equivalent circular jet at all axial locations, as seen in Fig. 15. Along the major axis, the spread of the elliptic jet is faster than the circular jet up to 4Deq; beyond this location, the axis switching of the elliptic jet results in a higher spread along the minor axis, with jet spread along the major axis approximately same as for the circular jet as reflected by iso-pitot pressure contour at 8Deq. Similarly, at the marginally under-expanded condition corresponding to NPR 8, the elliptic jet shows higher spread than the circular jet at all axial locations, as seen in Fig. 16. At all these locations, the elliptic jet shows higher spread along the major axis than the minor axis up to 8Deq. At 8Deq, the jet minor axis shows higher spread than at 1Deq and 4Deq, indicating that the axis switching is likely to occur at downstream location. In general, the faster jet spread can be considered as a reasonable measure of jet mixing with the ambient fluid, which is indicated by the decay of jet centreline pressure(Reference Rathakrishnan14). Therefore, the elliptic jet enjoys higher mixing than the equivalent circular jet.

Figure 15. Iso-pitot pressure contours of elliptic and circular jets at NPR 6 (over-expanded). Elliptic jet: (a), (b) and (c). Circular jet: (d), (e) and (f)Reference Arun Kumar and Rathakrishnan13.

Figure 16. Iso-pitot pressure contours of elliptic and circular jets at NPR 8 (marginally under-expanded). Elliptic jet: (a), (b) and (c). Circular jet: (d), (e) and (f)(Reference Arun Kumar and Rathakrishnan13).
3.3 Pressure profiles
To authenticate the hypothesis that vortices of continuously varying size are shed from the end of the minor axis to the end of the major axis, the pressure distribution along the jet major and minor axis directions at NPR 4 to 8 in increments of one at different axial locations of x/Deq = 0.5, 1, 2, 3, 4, 5, 6, 8 and 10 were measured. As envisaged, for all NPRs, the pressure profile along the minor axis spreads faster than along the major axis, indicating faster jet spread along the minor axis plane than along the major one. Selective pressure profiles at x/Deq = 0.5, 4 and 10 that display these characteristics are shown in Fig. 17. At all NPRs, initially at 0.5Deq, the width of the jet along the minor axis is less than the jet width along the major axis. Thereafter, the jet spreads at a faster rate along the minor axis side than along the major axis side as reflected by pressure profiles at 4Deq. At about 10Deq, it is seen that the minor axis of the jet has become the major axis and vice versa at NPRs 4, 5, 6; at NPRs 7 and 8, the minor and major axes of the jet has just crossed over and the jet becomes almost axisymmetric. The reason for the faster jet spread along the minor axis than along the major axis side is because larger eddies around the minor axis extremities at the nozzle exit as well as other axial locations downstream would induce more mass from the surrounding into the jet, in accordance with the vortex theory that large eddies are very good suction creators(Reference Rathakrishnan14). This kind of differential jet spread along the major and minor axes leads to the phenomenon of axis-switching. This is attributed to the larger mixing enjoyed by the elliptic jet compared to the equivalent circular jet under identical conditions.

Figure 17. Elliptic Jet profiles; □ – major axis (z-direction), Δ – minor axis (y-direction).
3.4 Flow visualisation
The waves present in the jet core were visualised via shadowgraph. Views along the major and minor axes planes of the elliptic jet were recorded. The waves in the jet field at different NPRs are shown in Fig. 18. Due to azimuthal asymmetry of the elliptic shape, the compression/expansion waves in the core region of the elliptic jet are asymmetric in shape. Also, the intersections of the waves bouncing from the jet boundary are asymmetric and distorted as reported by Schadow et al for an under-expanded AR3 elliptic jet(Reference Schadow, Gutmark, Koshigoe and Wilson5). Therefore, the shock-cells of the elliptic jet are asymmetric in nature. The visualisation of the waves present in the major and minor axis planes clearly proves the asymmetry in the shock-cell structures. At NPRs 4 and 5, the first two shock-cells are more prominent than the rest, as seen in Figs. 18(a) and (b). Compared to NPR 4, the strength of the waves, core length and shock-cell spacing are higher at NPR 5. At NPRs 6, 7 and 8 (Figs. 18(c-e)), out of five shock-cells, only the first two are prominent in the core of the jet. The number of shock cells at these NPRs is the same, but the strength of the waves, core length and shock cell spacing increase with increasing NPR.

Figure 18. Shadowgraph pictures of elliptic jet.
At all NPRs, the waves present in the core region of the elliptic jet are considerably weaker than the waves present in the circular jet field reported by Arun and Rathakrishnan(Reference Arun Kumar and Rathakrishnan13). It is clearly seen in the shadowgraph pictures for circular and elliptic jets in Fig. 19, that the wave angle for the shocks at the nozzle exit for circular jet (Fig. 19(a)) are considerably higher than the shock angle at the exit of elliptic jet (Figs. 19(b) and (c)). The smaller angle of shock waves at the exit of elliptic jet clearly highlight that the waves present in the first cell of elliptic jet are weaker than the waves in the first cell of circular jet. Similar observation can be made at the highest NPR of 8 (Fig. 20). Also, the number of shock-cells, shock-cell spacing and the core length of the elliptic jet are significantly less than for the equivalent circular jet. Some selective shadowgraph images of the circular(Reference Arun Kumar and Rathakrishnan13) and elliptic jets at NPRs 6 and 8 showing these are compared in Figs 19 and 20.

Figure 19. Shadowgraph pictures of circular and elliptic jets at NPR 6 (over-expanded). (a) Circular jet(Reference Arun Kumar and Rathakrishnan13), (b) elliptic jet (major axis plane) and (c) elliptic jet (minor axis plane).

Figure 20. Shadowgraph pictures of circular and elliptic jets at NPR 8 (marginally under-expanded). (a) Circular jet(Reference Arun Kumar and Rathakrishnan13), (b) elliptic jet (major axis plane) and (c) elliptic jet (minor axis plane).
From the shadowgraph pictures of the elliptic jet, it is clearly seen that as the NPR increases, the strength of the expansion waves increases, but at the same time the strength of the compression waves in the first cell decreases and the length of the shock cell increases. It is also evident that the core length of the jet increases as NPR increases. This confirms the arguments based on centreline pressure decay. The waves in the core are made weaker and a substantial reduction in the core length is observed for the elliptic jet compared to the equivalent circular jet(Reference Arun Kumar and Rathakrishnan13) under identical conditions.
4.0 CONCLUSIONS
The results of the present study demonstrate that the continuously varying size of the mixing-promoting vortices shed by elliptic nozzle exit is an advantage from a mixing-enhancement point of view compared to results for the equivalent circular nozzle. Except at NPRs 4 and 5, the centreline pressure decay of elliptic jets at all the NPRs is faster than the equivalent circular jet in all the three zones of the jet field (the core, characteristic decay and fully developed regions). However, the elliptic jet also continues to enjoy better near-field mixing at NPRs 4 and 5. The elliptic jet spreads faster along the minor axis plane than the major axis plane and exhibits axis-switching at all levels of expansion, indicating enhanced near-field mixing of the elliptic jet. It is found that the axis-switching phenomenon is strongly influenced by the expansion level at the nozzle exit. The axis-switching location which initially shifted upstream with an increase in NPR from 4 to 5 later moved downstream from NPRs 5 to 7 at a faster rate. When the NPR is increased from 7 to 8, the jet level of expansion changed from over-expansion to a marginally under-expanded state, followed by a slight upstream movement of the axis-switching location. The shadowgraph visualisation of the elliptic jet showed that the waves (expansion/compression) present in the elliptic jet field are asymmetric due to the azimuthal asymmetry of the elliptic nozzle and are weaker than the waves present in the circular jet. Also, even though not measured, the weaker waves prevailing in the elliptical jet field can be seen as an advantage from an aero-acoustic point of view, since in accordance with Tam's theory(Reference Tam16), shorter shock-cells would result in lesser shock-associated noise than longer shock-cells.
ACKNOWLEDGEMENT
Authors would like to thank Arun Kumar, PhD scholar, High Speed Lab, Aerospace Engineering, IIT Kanpur, for giving the data for the Mach 2 circular jet used for comparison in this article.