1. INTRODUCTION
The rise of maritime trade in global commerce and the use of larger ships have led to increased maritime traffic density and associated accident risks, particularly during coastal navigation. Historical accident data shows that human error accounts for 80% of ship collisions (Tsou and Hsueh, Reference Tsou and Hsueh2010).
Technological advances and new maritime regulations demand that more novel marine instruments be installed on bridges to enhance the accuracy of navigational information, in turn complicating on-duty officers' decisions (Kwik, Reference Kwik1989). Collision-avoidance manoeuvring is a real-time decision-making process that contains five procedures (International Maritime Organization (IMO), 2007):
-
• When to act. This procedure calculates the timing of commencing action. In other words, decision makers must judge the relative bearing and distance at which they need to act.
-
• What actions to take. This step addresses the required rudder angles as effective collision-avoidance manoeuvres.
-
• Which new courses to adopt. The extent of the course change determines whether the target ship will leave the safety domain of the officer's own ship.
-
• When to return to the original route. This moment indicates the termination of collision avoidance.
-
• New course adopted for reorientation. The new course determines the reorientation trajectory, or the course to recover track.
Different decisions for the five procedures result in different collision-avoidance trajectories while also affecting bunker consumption during collision avoidance (Ronen, Reference Ronen1982). Therefore, making an optimal real-time decision for collision avoidance can achieve minimum energy use while also ensuring navigational safety.
The remainder of this paper is organised as follows. In Section 2 we review the relevant literature and identify knowledge gaps. In Section 3, we clarify the objective, scope, and intended contribution of this paper. Section 4 provides a brief introduction to ship collision avoidance. Section 5 depicts the parameter calculation and formulates the collision-avoidance manoeuvring process. Section 6 develops the mathematical model that optimises fuel use while ensuring navigational safety. Section 7 uses a numerical example to illustrate the model application. Section 8 summarises principal research findings and contributions. Section 9 suggests promising areas for future research.
2. LITERATURE REVIEW
There have been many studies on ship collision avoidance (Kwik, Reference Kwik1989; Sato and Ishii, Reference Sato and Ishii1998; Su et al., Reference Su, Chang and Cheng2012; Kao et al., Reference Kao, Cheng and Chang2007; Vincent et al., Reference Vincent, Cliff, Grantham and Peng1972; Merz, Reference Merz1973; Miloh and Sharma, Reference Miloh and Sharma1975; Wang et al., Reference Wang, Debnath and Chin2010; Van Amerongen and Van Nauta Lemke, Reference Van Amerongen and Van Nauta Lemke1978). Previous analytical methods can be classified into three items. The first study pertains to fuzzy neural networks, which use fuzzy rules to infer the static and dynamic degrees of danger (Hiraga et al., Reference Hiraga, Furuhashi, Uchikawa and Nakayama1995). The second analytical method uses fuzzy logic to describe an operator's recognition rules for collision avoidance (Hammer and Hara, Reference Hammer and Hara1990; Shimada et al., Reference Shimada, Mabuchi and Hara1991; Zhao et al., Reference Zhao, Tan, Price and Wilson1994). In addition to these methods, a probabilistic framework has been presented for designing and analysing existing Collision Avoidance (CA) algorithms, enabling on-line risk computation for faulty intervention and the consequences of different actions based on Monte Carlo techniques (Jansson and Gustafsson, Reference Jansson and Gustafsson2008). Smierzchalshi and Michalewica (Reference Smierzchalshi and Michalewica2000) used an evolutionary algorithm to model ship trajectories in the crossing situation. However, most previous studies either focused entirely on the shortest distance or did not explicitly account for fuel use. According to the speed-loss and the change in bunker consumption during ship turning, the shortest route may not represent the most energy-saving route. Table 1 summarises previous relevant studies and identified knowledge gaps.
Table 1. A review of previous navigation models
3. RESEARCH OBJECTIVE AND SCOPE
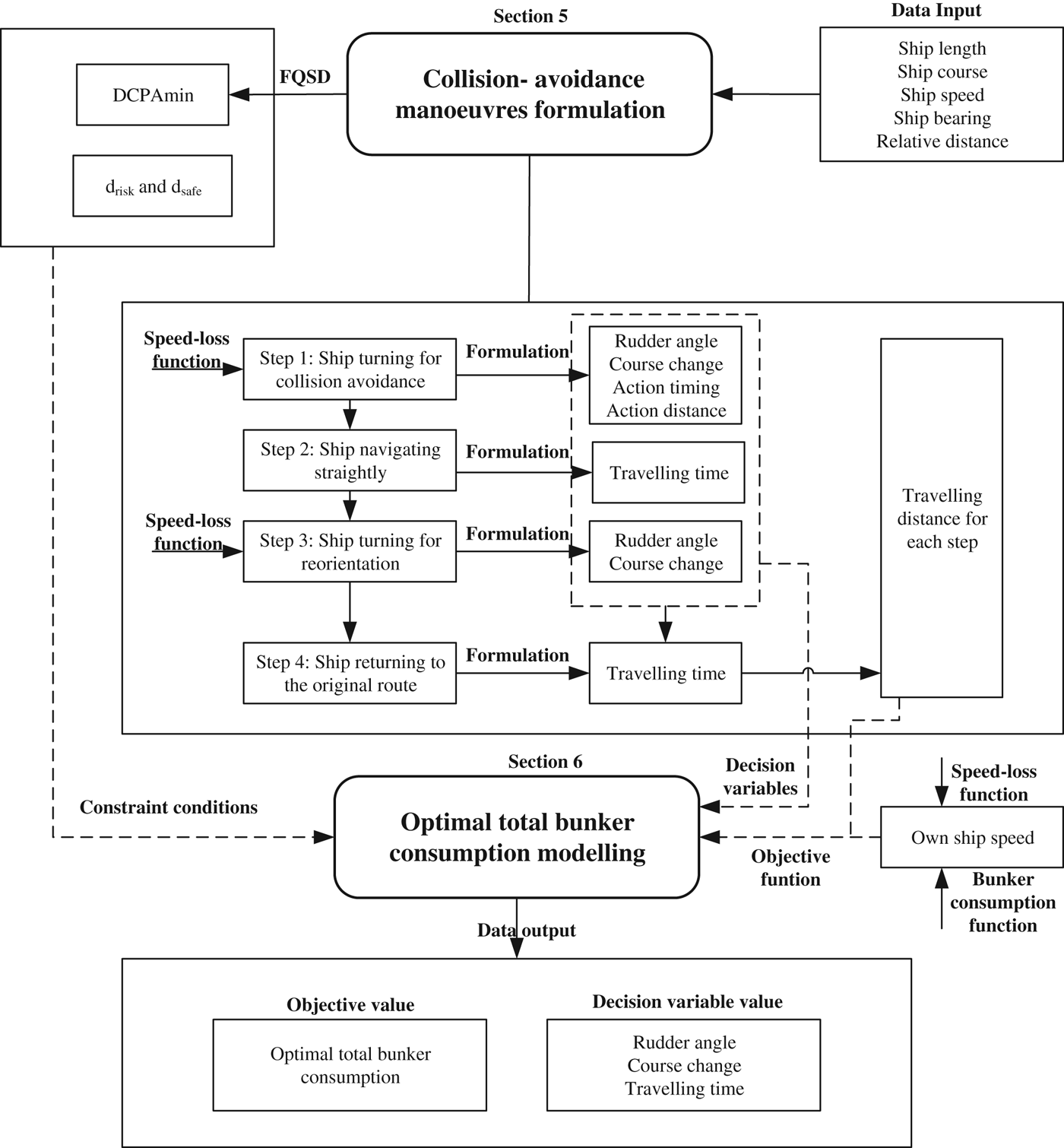
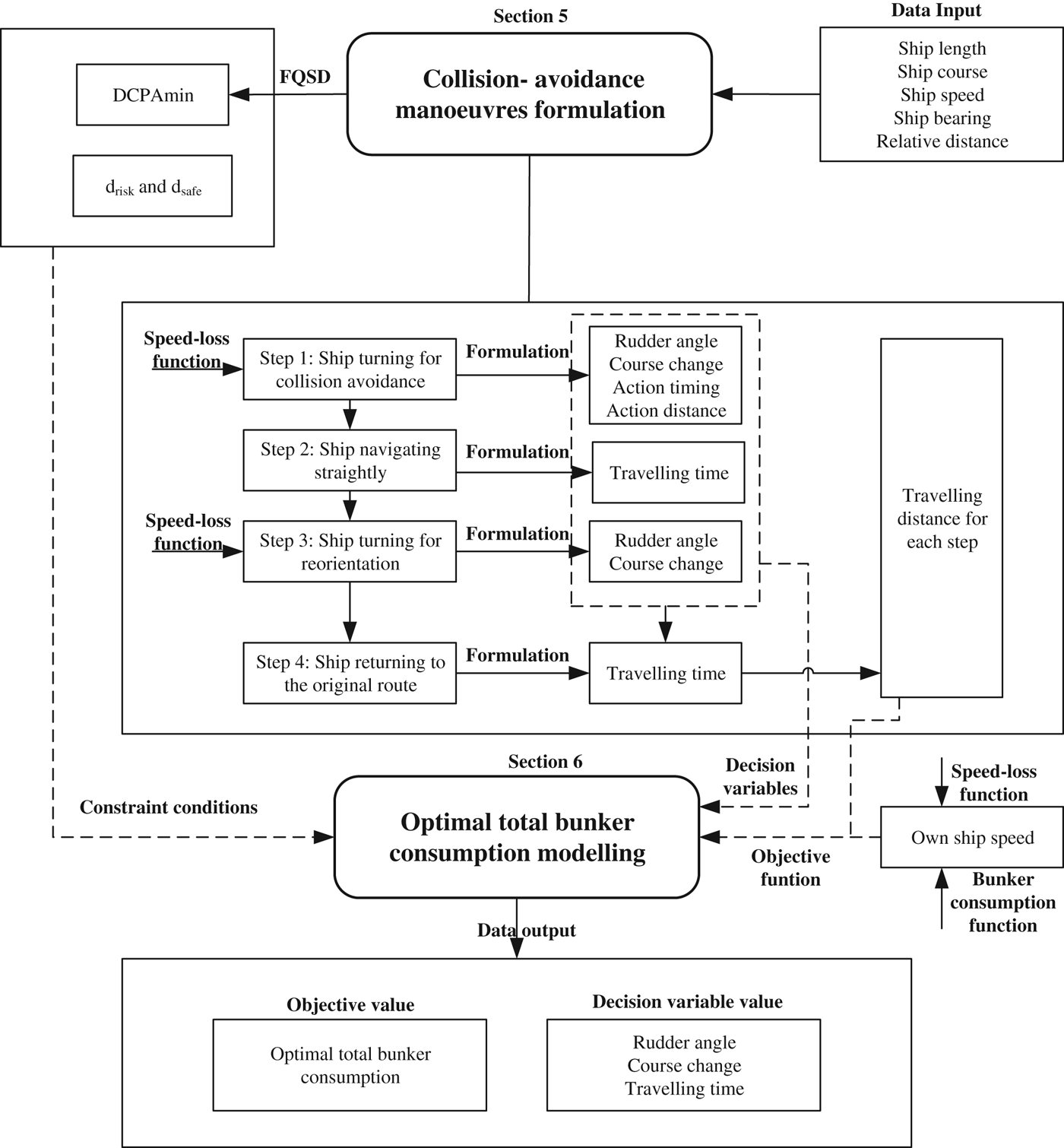
The International Regulations for Preventing Collisions at Sea 1972 (“COLREGS”) (IMO, 1972) proposed quantitative interpretations of widely adopted concepts such as “safety passing distance” and “early” action, etc. (Cockcroft and Lameijer, Reference Cockcroft and Lameijer2003). In addition, fuel use is a principal cost component of maritime transportation. The primary goal of this research is to develop an optimisation framework for collision-avoidance manoeuvres to minimise fuel use while maintaining a satisfactory safety level. The modelling framework will be developed as illustrated in Figure 1. Each section referred to in this framework will be explained explicitly in the corresponding parts.
4. BACKGROUND OF SHIP COLLISION AVOIDANCE
The vessel taking collision-avoidance manoeuvres is called “own ship,” and the ship that needs to be avoided is the “target ship” (Hong and Yang, Reference Hong and Yang2012). The COLREGS specify three encounter situations according to the point from which the target ship is approaching; these points are illustrated in Figure 2 (Tsou and Hsueh, Reference Tsou and Hsueh2010; Su et al., Reference Su, Chang and Cheng2012): head-on (region F); overtaking (region C, D) and crossing (region A, B, E). The definitions of these three encounter situations can be found in Hong and Yang (Reference Hong and Yang2012).
Figure 2. Encounter bearing distribution.
This paper focuses on the two-ship crossing situation in which only one ship is responsible for collision avoidance. Future research will account for other encounter situations. The ship taking collision-avoidance manoeuvres is called the “give-way” ship and the ship maintaining course and speed is called the “stand-on” ship.
As for collision avoidance, course change is the primary consideration for manoeuvres. Ship speed should change only when the environment does not allow a course change. Hence this paper focuses on course alteration as the crucial collision-avoidance manoeuvre.
5. COLLISION-AVOIDANCE MANOEUVRING FORMULATION
As the main preparation for mathematical modelling, this section contains three parts: parameter calculation, speed-loss effect and collision-avoidance process description.
5.1. Collision-Avoidance Parameter Calculation
Whether a ship should take collision-avoidance manoeuvres depends on the collision risk. We can also judge the manoeuvring efficiency through collision risk estimation.
Ship domain plays a very important role in collision risk evaluation. Many models in the literature use a binary criterion and define “safe” as “not located in the domain”, and “unsafe” as “located in the domain” (e.g. Davis et al., Reference Davis, Dove and Stockel1980; Fujii and Tanaka, Reference Fujii and Tanaka1971; Goodwin, Reference Goodwin1975; Wang et al., Reference Wang, Meng, Xu and Wang2009; Wang, Reference Wang2010). However, this paper uses fuzzy logic to describe the risk recognition for collision avoidance, and determines the collision risk value in the closed interval [0, 1] with respect to the relative distances. This so-called Fuzzy Quaternion Ship Domain (FQSD) methodology was originally proposed by Wang (Reference Wang2010), which has an advantage of merging risk uncertainty and fuzzy information into ship collision risk estimation. Compared to other approaches that define the risk as “0 or 1” binary variable, FQSD uses a continuous range “0 to 1” to measure the risk distribution, which is more generalised and accurate.
This paper will adopt the FQSD model to determine the minimum distance between the two ships at the closest point of approach (DCPA min) as the criterion of successful collision avoidance. Tables 2 and 3 present the parameter notations and decision variable notations used in the optimisation model.
Table 2. Associated parameter notations.
Table 3. Decision variables.
The FQSD model boundary can be formulated as follows:
$$\hbox{FQSD} \lpar \hbox{r} \rpar = \lcub \lpar \hbox{x}\comma \; \hbox{y} \rpar \vert \hbox{f} \lpar \hbox{x}\comma \; \hbox{y}\comma \; \hbox{Q} \lpar \hbox{r} \rpar \rpar \le 1 \rcub $$
Where
$$\eqalign{\hbox{f} \lpar \hbox{x}\comma \; \hbox{y}\comma \; \hbox{Q} \lpar \hbox{r} \rpar \rpar & = \left(\displaystyle{{2\hbox{x}}\over{\lpar 1 + \hbox{sgnx} \rpar \hbox{R}_{\rm starb} \lpar \hbox{r} \rpar - \lpar 1 - \hbox{sgnx} \rpar \hbox{R}_{\rm port} \lpar \hbox{r} \rpar }} \right)^{2} \cr & \quad + \left(\displaystyle{{2\hbox{y}} \over{\lpar 1 + \hbox{sgny} \rpar \hbox{R}_{\rm fore} \lpar \hbox{r} \rpar - \lpar 1 - \hbox{sgny} \rpar \hbox{R}_{\rm aft} \lpar \hbox{r} \rpar }}\right)^2} $$
$$\hbox{Q}\lpar \hbox{r}\rpar = \lcub \hbox{R}_{\rm fore} \lpar \hbox{r} \rpar \comma \; \hbox{R}_{\rm aft} \lpar \hbox{r} \rpar \comma \; \hbox{R}_{\rm starb} \lpar \hbox{r} \rpar \comma \; \hbox{R}_{\rm port} \lpar \hbox{r} \rpar \rcub $$
As for the manoeuvring timing, Zheng (Reference Zheng2002) proposed a collision risk membership function of objective distance based on fuzzy logic. drisk and dsafe denote the earliest and latest action points respectively. Thereafter we obtain a range (drisk, dsafe) in which the give-way ship should take action to avoid a potential collision. The manoeuvring distance range (drisk, dsafe) and DCPAmin obtained in this section will be the constraint conditions in the optimisation model.
5.2. Speed-Loss Effect
The ship may not keep a fixed speed during its turn. It will experience a speed-loss effect during a fixed throttle turn with no bunker consumption saving. Li (Reference Li2008) has proposed a mathematical model of the speed-loss effect. We introduce K and T as the ship manoeuvrability indices. K denotes the turning index, with a larger K denoting a better turning ability. T represents the adherence index. A smaller value indicates a better initial turning ability. K and T can be calculated as follows:
$$K^{\prime} = \displaystyle{{L}\over{V}}K $$
$$T^{\prime} = \displaystyle{{V}\over{L}}T $$
where L denotes the ship length and V denotes the ship speed.
With reference to Li (Reference Li2008), we can obtain
$$K^{\prime} = 1{\cdot}715 + 0{\cdot}964 \displaystyle{{L}\over{B}} - 0{\cdot}158 \displaystyle{{Ld}\over{A_{R}}}-1{\cdot}702C_{b}\displaystyle{{L}\over{B}}+0{\cdot}262C_{b}\displaystyle{{Ld}\over{A_{R}}} $$
$$T^{\, \prime} = 4{\cdot}664 + 0{\cdot}716 \displaystyle{{L}\over{B}} - 14{\cdot}491C_{b} - 0{\cdot}033\displaystyle{{L}\over{B}}\cdot \displaystyle{{Ld}\over{A_{R}}}+0{\cdot}396C_{b}\displaystyle{{Ld}\over{A_{R}}} $$
where B represents the ship's width, d represents the ship's draft and AR represents the area of the ship's rudder.
The ratio of the original speed V to the speed with loss which is denoted as Vloss is formulated as
$$\eqalign{\displaystyle{{V}\over{V_{loss}}} & = -8{\cdot}697+6{\cdot}361K^{\prime}+7{\cdot}960C_{N}-5{\cdot}295K^{\prime} \cdot C_{N}-0{\cdot}226C_{N}\cdot \displaystyle{{\varphi}\over{57{\cdot}3}} \cr & \quad +0{\cdot}067\lpar K^{\prime} \rpar ^{2}+0{\cdot}028\left(\displaystyle{{\varphi}\over{57{\cdot}3}}\right)^{2}} $$
Based on the Joessel Equation (Hong and Yang, Reference Hong and Yang2012), we obtain
$$C_{N} = \displaystyle{{0{\cdot}311 sin \delta}\over{0{\cdot}195 + 0{\cdot}305 sin \delta}} $$
Where δ is the rudder angle and φ denotes the course change.
5.3. Collision-Avoidance Process
The process can be formulated in four steps which are listed below (Figure 3). Meanwhile, the travelling distance for model parameters is expressed as a function of the decision variables.
-
• Step 1: ship turning for collision avoidance;
-
• Step 2: ship navigating straight on a new course;
-
• Step 3: ship turning for reorientation;
-
• Step 4: ship navigating directly to the original route.
Figure 3. Collision-avoidance trajectories of two encountering ships.
The research first establishes two x, y-coordinate systems: the Earth Reference Coordinate system (ERC) and the Own Ship Reference Coordinate system (ORC). The y-axis of the ERC indicates the direction of the initial speed v o and the x-axis is perpendicular to it and positive to starboard. The ORC system is relative to the Own Ship (OS) with the gravity of OS as the origin, the y-axis in the direction of v o , and the x-axis is perpendicular to it and positive to starboard. The initial coordinates of OS and the Target Ship (TS) in ERC are (x o , y o ) and (x t , y t ) respectively. The relative coordinates of TS are (x r , y r ). The following sub-sections model each of the above-mentioned steps.
5.3.1. Step 1: Ship turning for collision avoidance
After a period t
0, OS initiates the collision-avoidance manoeuvres. At this moment, the coordinates of OS and TS with respect to the ERC system are
$\lpar x_{o}^{0}\comma \; y_{o}^{0}\rpar $
and
$\lpar x_{t}^{0}\comma \; y_{t}^{0}\rpar $
. The relative distance between the two encountered ships reaches
$D_{r}^{0}$
when OS begins to take action to change the course with a rudder angle δ
t
∈ (10°, 30°) according to the COLREGS. We denote by
$C_{o}^{0}$
and
$C_{t}^{0}$
the present courses of OS and TS, respectively.
$$x_{o}^{0} = x_{0} $$
$$y_{o}^{0} = y_{o} + v_{o} t_{0} $$
$$x_{t}^{0} = x_{t} + v_{t} sin\lpar C_{t}^{0} - C_{o}^{0} \rpar t_{0} $$
$$y_{t}^{0} = y_{t} + v_{t} cos \lpar C_{t}^{0} - C_{o}^{0} \rpar t_{0} $$
$$D_{r}^{0} = \sqrt{\lpar x_{t}^{0}-x_{o}^{0} \rpar ^{2}+\lpar y_{t}^{0}-y_{o}^{0} \rpar ^{2}} $$
After time t
1, OS reaches the required turning angle φ
t
. The present coordinates of OS are
$\lpar x_{o}^{1}\comma \; y_{o}^{1}\rpar $
, and the present coordinates of TS are
$\lpar x_{t}^{1}\comma \; y_{t}^{1}\rpar $
. The relative distance between them is
$D_{r}^{1}$
. The new course of OS is denoted by
$C_{o}^{1}$
. The turning process is illustrated in Figure 4. Due to the speed-loss effect during the turn, the speed of OS decreases to the velocity
$v_{o}^{loss1}$
until the turn ends. To simplify the model, we assume that, during the turn, the own ship maintains constant speed
$v_{o}^{loss1}$
.
$$C_{o}^{1} = C_{o}^{0} + \varphi_{t} $$
Figure 4. Schematic figure for ship turning.
The ship will be navigating in compliance with a circle with a special diameter D t .
$$D_{t} = \displaystyle{{2v_{o}^{loss1}}\over{K\delta_{t}}} $$
OS travels l o1until reaching the required angle.
$$l_{o1} = v_{o}^{loss1} T + \displaystyle{{\varphi_{t}v_{o}^{loss1}} \over{K\delta_{t}}} $$
$$t_{1} = \displaystyle{{l_{o1}}\over{v_{o}^{loss1}}} = T+\displaystyle{{\varphi_{t}}\over{K\delta_{t}}} $$
$$x_{o}^{1} = x_{o}^{0}+\lpar R_{t}-R_{t}cos\varphi_{t} \rpar = x_{o}^{0}+\displaystyle{{v_{o}^{loss1}}\over{K\delta_{t}}}\lpar 1-cos\varphi_{t} \rpar $$
$$y_{o}^{1} = y_{o}^{0}+\lpar v_{o}^{loss1}T+R_{t}sin\varphi_{t} \rpar = y_{o}^{0}+v_{o}^{loss1}T+\displaystyle{{v_{o}^{loss1}sin\varphi_{t}}\over{K\delta_{t}}} $$
The turning angle φ t is constrained by the minimum safe passing distance DCPA min .
$$DCPA\ge {DCPA}_{min} $$
$$x_{t}^{1} = x_{t}^{0}+v_{t}t_{1}sin\lpar C_{t}-C_{o} \rpar $$
$$y_{t}^{1} = y_{t}^{0}+v_{t}t_{1}cos\lpar C_{t}-C_{o} \rpar $$
The relative coordinates of the TS position with respect to OS at the final situation are
$\lpar x_{r}^{1}y_{r}^{1}\rpar $
.
$$x_{r}^{1} = \lpar x_{t}^{1}-x_{o}^{1} \rpar cos\varphi_{t}-\lpar y_{t}^{1}-y_{o}^{1} \rpar sin\varphi_{t} $$
$$y_{r}^{1} = \lpar x_{t}^{1}-x_{o}^{1} \rpar sin\varphi_{t}+\lpar y_{t}^{1}-y_{o}^{1} \rpar cos\varphi_{t} $$
5.3.2. Step 2: Ship navigating straight on a new course
The speed-loss effect will cease once the turning terminates. Engine power will restore the original speed to v
o
in a very short time. To avoid collision, OS needs to navigate on the new course for a period of time to reach the closest point to TS. The time to approach the closest point to TS is denoted by TCPA. When OS reaches the closest point, the coordinates of OS are
$\lpar x_{o}^{\prime} y_{o}^{\prime}\rpar $
and the coordinates of TS are
$\lpar x_{t}^{\prime} y_{t}^{\prime}\rpar $
. The relative coordinates of TS with respect to the ORC system are
$\lpar x_{r}^{\prime} y_{r}^{\prime}\rpar $
. OS is navigating on a straight course for a period t
2. The navigating distance is denoted by l
o2. The coordinates of OS with respect to the ERC system are
$\lpar x_{o}^{2}y_{o}^{2}\rpar $
$$t_{2}\ge TCPA $$
$$l_{o2} = v_{o}t_{2} $$
$$x_{o}^{2} = x_{o}^{1}+v_{o}sin\varphi_{t}t_{2} $$
$$y_{o}^{2} = y_{o}^{1}+v_{o}cos\varphi_{t}t_{2} $$
The relative speed of TS and OS with respect to the ORC system is
$v_{r}^{2}$
. The relative heading of TS to the ORC system is
$\theta_{r\comma 2}^{h}$
.
$$\theta_{r\comma 2}^{h} = C_{t}-C_{o}-\varphi_{t} $$
$$v_{r\comma x}^{2} = v_{t}sin\lpar \theta_{r\comma 2}^{h} \rpar $$
$$v_{r\comma y}^{2} = v_{t}cos\lpar \theta_{r\comma 2}^{h} \rpar -v_{o} $$
$$TCPA = \displaystyle{{-\lpar x_{r}^{1}v_{r\comma x}^{2}+y_{r}^{1}v_{r\comma y}^{2} \rpar }\over{\lpar v_{r\comma x}^{2} \rpar ^{2}+\lpar v_{r\comma y}^{2} \rpar ^{2}}} $$
$$x_{r}^{\prime} = x_{r}^{1}+v_{r\comma x}^{2}TCPA $$
$$y_{r}^{\prime} = y_{r}^{1}+v_{r\comma y}^{2}TCPA $$
The required collision-avoidance manoeuvres should guarantee that the relative position of TS with respect to the ORC system should be outside the OS's domain, which can be formulated as
$$f\lpar x_{r}^{\prime}\comma \; y_{r}^{\prime}\comma \; Q\lpar r\rpar \rpar \ge 1 $$
5.3.3 Step 3: Ship turning for reorientation
The optimal reorientation timing with consideration of bunker consumption is the moment when the two encountered ships reach the closest point of approach (Hong and Yang, Reference Hong and Yang2012). We denote the reorientation rudder angle by δ
r
∈ (−30°, −10°). When the turning angle reaches φ
r
, the ship stops turning. OS also suffers from speed-loss effect and turns with speed
$v_{o}^{loss2}$
. The OS coordinates with respect to the ERC system are
$\lpar x_{o}^{3}\comma \; y_{o}^{3}\rpar $
.
$$t_{2} = TCPA $$
$$D_{r} = \displaystyle{{-2v_{o}^{loss2}}\over{K\delta_{r}}} $$
$$l_{o3} = v_{o}^{loss2}T+\displaystyle{{\varphi_{r}v_{o}^{loss2}}\over{K\delta_{r}}} $$
$$x_{o}^{3}\, { = }\, \left(\displaystyle{{v_{o}^{loss2}}\over{K\lpar -\delta_{r} \rpar }}\lpar cos\varphi_{r}\, {-}\, 1 \rpar \, {+}\, x_{o}^{2} \right)\!cos\lpar -\varphi_{t} \rpar {-}\left(\left(v_{o}^{loss2}T\, {+}\, \displaystyle{{v_{o}^{loss2}sin\lpar -\varphi_{r} \rpar }\over{K\lpar -\delta_{r} \rpar }}\right){+}\, y_{o}^{2} \right)\!sin\lpar -\varphi_{t} \rpar $$
$$y_{o}^{3}\, { = }\, \left(\left(v_{o}^{loss2}T\, {+}\, \displaystyle{{v_{o}^{loss2}\!\sin \lpar -{\varphi_{r}\rpar }}\over{K{\lpar -\delta }_{r}\rpar }} \right)\, {+}\, y_{o}^{2} \right)\!\cos {\lpar -\varphi_{t}\rpar }\, {+}\, \left(\displaystyle{{v_{o}^{loss2}}\over{K{\lpar -\delta }_{r}\rpar }}\lpar \cos \varphi_{r}-1 \rpar +x_{o}^{2} \right)\sin {\lpar -\varphi_{t}\rpar } $$
5.3.4 Step 4: Ship returning to the original route
OS navigates on the new course to the original route with a speed v
o
, and when the OS returns to the initial route, the OS coordinates with respect to the ERC system are
$\lpar x_{o}^{4}\comma \; y_{o}^{4}\rpar $
. The relative heading of OS with respect to the ERC system is
$C_{o}^{r}$
.
$$C_{o}^{r} = \varphi_{t}+\varphi_{r} $$
$$x_{o}^{4} = x_{o}^{0} $$
$$y_{o}^{4} = y_{o}^{3}+\lpar x_{o}^{0}-x_{o}^{3} \rpar cot $$
$$l_{o4} = \lpar x_{o}^{0}-x_{o}^{3} \rpar csc\lpar \varphi_{t}+\varphi_{r} \rpar $$
In conclusion, Section 5.3 presents the travelling distances for each step, which are the prerequisites for optimal bunker consumption modelling.
6. OPTIMAL BUNKER CONSUMPTION MODEL
6.1. Bunker Consumption Function
Bunker consumption has a complex relationship to environmental elements (e.g., water flow and wind) and other external navigation parameters (e.g., trim, draft, displacement). Wang and Meng (Reference Wang and Meng2012) and Wang et al. (Reference Wang, Meng and Liu2013) proposed that the daily bunker consumption Q (tons/day) and sailing average speed v (knot) during one day have the third power relationship below:
$$Q = a\times v^{3} $$
where a can be calibrated from real world data. The calibrated “a” will vary with the different ship types and sizes. However, ships' speed is routinely set to a fixed value when it navigates on the open sea (Zhang and Chen, Reference Zhang and Chen2013). So v in Equation (46) can be regarded as the constant speed at which the ship is navigating for one day.
Two-ship crossing is a dynamic encounter situation that lasts for a relatively short period. In this paper, we assume that there is no change in the environmental factors during collision-avoidance manoeuvres. We also use representative environmental conditions in our simulation-based quantitative study. The ship speed cannot remain unchanged during ship turning. We transform the bunker-speed relationship to the bunker-distance function. We denote by g i (v i ) the bunker consumption per nautical mile with speed v i . This transformation should be under the assumption that the ship keeps an almost constant speed over one day's navigation. Our future research will use real-time speed and fuel consumption information to calibrate a refined model to eliminate the possible limitations of this assumption.
$$g_{i}\lpar v_{i} \rpar = \displaystyle{{av_{i}^{3}}\over{24v_{i}}} = \displaystyle{{av_{i}^{2}}\over{24}} $$
Due to the speed-loss effect during ship turning with no bunker consumption change, the bunker consumption per nautical mile during ship turning can be formulated as follows:
$$g_{loss} \lpar v_{loss} \rpar = \displaystyle{{Q}\over{24\cdot v_{i}}}\times \displaystyle{{v_{i}}\over{v_{loss}}} = \displaystyle{{a\cdot v_{i}^{3}}\over{24\cdot v_{loss}}} $$
6.2. Mathematical Model
The ship collision-avoidance manoeuvring optimisation problem can determine optimal decision-making for each collision-avoidance process in order to fulfill the navigational safety demand while simultaneously minimising the bunker consumption.
The optimisation model will be established based on the following assumptions (Hong and Yang, Reference Hong and Yang2012):
-
• Rudders can turn to the required angle in a very short time.
-
• Tactical diameter equals the final diameter, which is the ship-steady turning diameter.
-
• OS returns to the original route after the collision-avoidance procedure.
-
• No collision-avoidance manoeuvres are made by other ships when OS takes collision-avoidance actions.
-
• No effect of Very High Frequency (VHF) collision-avoidance communication.
The collision-avoidance manoeuvring optimisation problem can be formulated as a mixed-integer nonlinear programming model:
$$\hbox{Minimise}\quad Q_{min} = \sum_{i\in I_{p}} {{l_{i}g}_{i}\lpar v_{i} \rpar -{\lpar y_{o}^{4}-y_{o}^{0} \rpar g}_{0}\lpar v_{0} \rpar }\ I_{p} = \lcub o1\comma \; o2\comma \; o3\comma \; o4 \rcub $$
$$\hbox{Subject to}\quad d_{risk}\le D_{r}^{0}\le d_{safe} $$
$$f\lpar x_{r}^{\prime}\comma \; y_{r}^{\prime}\comma \; Q\lpar r\rpar \rpar \ge 1 $$
$$t_{i}\ge 0i\in \lcub 0\comma \; 1\comma \; 2\comma \; 3\comma \; 4 \rcub $$
$$t_{2} = TCPA $$
$$0 \lt \varphi_{t}\le 90^{\circ} $$
$$-180^{\circ}\le \varphi_{r} \lt 0 $$
$$10^{\circ}\le \delta_{t}\le 30^{\circ} $$
$$-30^{\circ}\le \delta_{r}\le -10^{\circ} $$
$$t_{i}\comma \; \varphi_{t}\comma \; \varphi_{r}\comma \; \delta_{t}\comma \; \delta_{r}\in \hbox{Z} $$
The objective function Equation (49) minimises increased bunker consumption due to collision-avoidance manoeuvres. The first term represents bunker consumption during the collision-avoidance process. The second term represents bunker consumption without collision-avoidance manoeuvring. Constraint Equation (50) defines the relative distance range in which OS should take action. d risk and d safe are obtained in Section 5. Constraint Equation (51) ensures that TS is located outside the OS's domain. Constraint Equation (52) defines t i as a non-negative variable. Constraint Equation (53) enforces OS's reorientation timing. Constraint Equations (54) and (55) impose the course change ranges. We define a course change to starboard as positive and to port as negative. Constraint Equations (56) and (57) define that rudder angles for collision avoidance during manoeuvres should comply with the COLREGS requirement that collision-avoidance manoeuvres should be a ‘large action’ which requires a ‘large’ rudder angle. Constraint Equation (58) specifies the variable t i , φ t , φ r , δ t , δ r as integers. t i is measured in seconds.
Theoretically, these variables can be defined as continuous variables. However, according to navigational practice, the time period of collision-avoidance manoeuvring can only realistically be controlled in terms of seconds. Meanwhile, course changes and rudder angles usually vary from one integer to another. Taking these practical factors into account, we treat certain decision variables as integers.
7. NUMERICAL EXPERIMENT
Numerical examples are used to illustrate the model application. Owing to the complexity of navigational practice, we selected certain representative scenarios based on simulation data to draw managerial insights into the optimal ship collision-avoidance manoeuvres.
7.1. Input Data
This paper uses simulation data from maritime simulators at Dalian Maritime University, China. We fix the OS course at 000, and adjust the TS's course to obtain different scenarios. OS is a Very Large Crude Carrier (VLCC). OS's parameters are listed below:
-
• L(ship length) = 316·12 m
-
• B(ship width) = 60·0 m
-
• D (ship draft) = 21·8 m
-
• C b (cube coefficient) =0·8093
-
• A R (area of Rudder) = 150·22 m2
The manoeuvring characteristics are shown below:
-
• Main engine type: diesel
-
• Power output: 28,000 BHP (Brake Horsepower) × 68 RPM (Revolutions Per Minute)
-
• Propeller type: FPP (Fixed Pitch Propeller)
-
• Maximum rudder angle: 35°
In the numerical example, we consider a typical VLCC as TS. The TS's length is 220 m. This paper focuses on collision avoidance in open sea. The speed we apply in our scenarios varies in a reasonable domain from 15 knots to 20 knots. We choose the three special representative speeds as 15, 18, and 20 knots in our scenario simulations. According to the COLREGS, if the two encountered ships are in the crossing situation and OS is the responsible ship, TS should be in a bearing range from 5° to 112·5°. For generality, we choose three different relative bearings: “forward of the beam,” “abeam,” and “abaft the beam.” Correspondingly, we set 60°, 90°, and 110° as the three relative bearings of the TS. The ship speeds and bearings have been correlated with the TS's course. When the combination of ship speeds and bearing is determined, the TS course is correspondingly determined. We specify various scenarios with different combinations of OS speed, TS speed and relative distance under a special TS course.
7.2. Optimal Manoeuvring Strategies
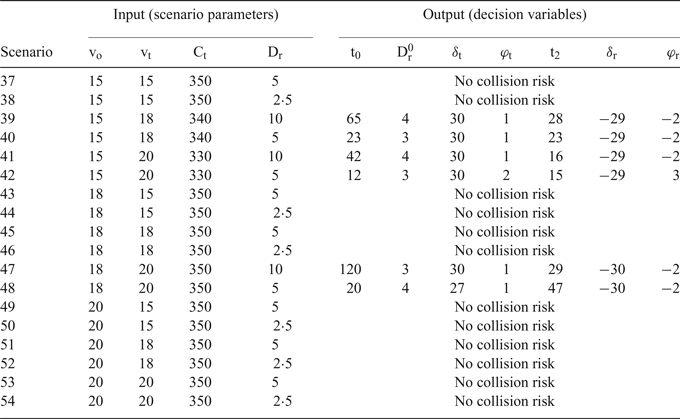
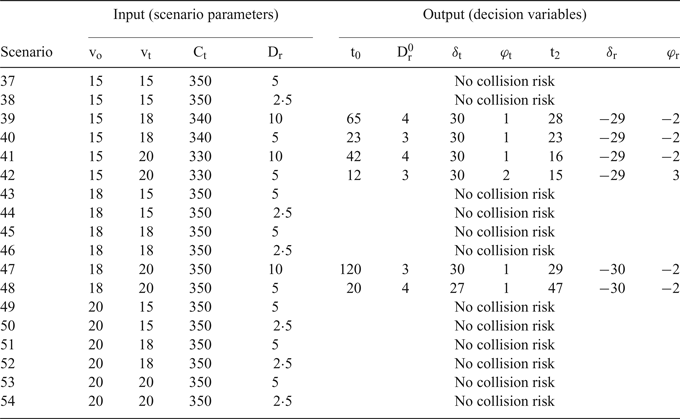
This mixed-integer nonlinear optimisation model contains trigonometric functions which increase the computational complexity. Commercial solvers may not obtain the global optimal solution. In this paper, we have simulated and optimised two-ship collision-avoidance manoeuvres in the Visual Basic Application (VBA) environment. We transformed the distance range to the time range when OS begins to act, measured in minutes. We analysed the optimal manoeuvring strategies under different scenarios with respect to the different ship speeds and relative positions (Table 4(a), Table 4(b) and Table 4(c)).
Table 4(a). Scenario simulation results with Br=60 (Target ship is forward the beam of own ship)
Table 4(b). Scenario simulation results with Br = 90 (Target ship is at the beam of own ship).
7.3. Scenario Simulation Result Analysis
Various scenarios in the crossing situation were simulated. Optimal manoeuvring strategies are determined in each scenario. Based on the simulation analysis, we draw the following observations from the viewpoints of relative ship motion and relative position, respectively.
7.3.1. Analysis with respect to the relative ship motion
The relative ship motion is illustrated mainly by the ratio of OS speed to TS speed. Different speed ratios will affect collision risk in the two-ship crossing situation. Figure 5 represents the number and percentage of collision risk scenarios at each speed ratio.
-
• In scenarios 20, 28 and 36, where v o = v t and TS is located at the beam of OS, the two encountered ships will approach each other very slowly. In these scenarios, OS does not need to take any manoeuvres until they are at a rather short relative distance. The output t 0 reflects the sufficient time period before the ship turning for collision-avoidance.
-
• As v o < v t and Br = 110, the optimum collision-avoidance manoeuvres for OS are to use a large rudder angle and a small course change for the purpose of bunker saving, i.e. scenarios 39 and 40, scenarios 41 and 42, and scenarios 47 and 48.
-
• For v o > v t , if TS is located at or abaft the beam of OS, then this crossing situation will not create a collision risk, i.e. scenarios 25 and 26, scenarios 31 through 34, scenarios 43 and 44, and scenarios 49 through 52.
-
• In scenarios 1, 9, and 17, the bearing, course, and initial relative distance are the same, but speed is different. This difference leads to different optimal solutions
$D_{r}^{{0}}$
(the relative distance during the action). The analysis indicates that ship speed affects the start timing of the collision-avoidance manoeuvres. A higher speed requires an earlier initiation of collision-avoidance manoeuvres. -
• In scenarios 4, 6, and 12, v o > v t . In scenario 4, OS might begin collision-avoidance actions when the relative distance falls to three nautical miles. In scenarios 6 and 12, OS needs to take the collision-avoidance manoeuvres immediately (i.e. t 0=0);. These results demonstrate that a larger speed difference requires an earlier collision-avoidance start time.
Figure 5. Collision risk distribution.
7.3.2. Analysis with respect to the relative ship position
The relative ship position is mainly determined by the bearing Br and relative distance (Dr). Different relative ship positions will impact the collision-avoidance timing and manoeuvres.
-
• If B r = 110, and v o = v t , no collision risk exists, even though D r is as small as 2.5 nautical miles, i.e. scenarios 37 and 38, scenarios 45 and 46, scenarios 53 and 54; if Br = 90 and v o = v t , whether the scenarios are involved in the collision risk depends on D r , i.e. scenarios 19 and 20, scenarios 27 and 28, and scenarios 35 and 36.
-
• For all scenarios, there will always be a relationship between φ t and φ r which is |φ r | = |φ t | + 1. OS (the give-way ship) should initiate the smallest possible course change to reorient to the designated route in order to minimise bunker consumption during collision avoidance.
-
• For all scenarios with a collision risk, the optimum manoeuvres recommend a maximal rudder angle if the action distance is the lower marginal safety collision-avoidance distance. This indicates that reaching the required course change as soon as possible can reduce bunker consumption when vessels implement larger rudder angles and travel only a short distance after the course change.
8. CONCLUSIONS
This paper develops an optimisation framework to determine optimal collision-avoidance manoeuvres while minimising fuel use. The research investigates the optimal manoeuvring strategies during each collision-avoidance phase. Numerical examples with representative scenarios are selected to illustrate the application of the optimisation model. The analysis of the results supports the effectiveness and reliability of the model. The analysis results provide four main indications. First, if the navigation environment allows, during the reorientation to the designed route, the ship should apply the smallest possible course change and shorten the course-changing period to minimise bunker consumption. This is consistent with a previous study by Hong and Yang (Reference Hong and Yang2012). Shortening the course-changing period could be realised through a relatively large applied rudder angle (i.e. 29° or 30°). Second, given enough manoeuvring space, during the turning process the ship should make a smaller course change when its speed is higher. This is probably due to the higher speed loss during ship turning with a higher speed. Third, regarding the collision-avoidance manoeuvres, the optimal manoeuvres for bunker saving depend on the relative distance and speed of the two encountered ships. The speed difference between the two ships could affect the optimal turning timing. A larger speed difference could result in an earlier turning. Finally, regarding the crossing situation, if the target ship is faster than the own ship, the crossing situation has a greater collision risk, especially when the target ship is located aft of the beam of the own ship.
The main contribution of this research can be considered in three aspects. First, the optimisation model in the framework takes into account the speed-loss effect during ship turning and the collision risk calculation based on the involved ships' parameters. Second, the optimisation model can obtain the specific magnitude of the operation (i.e. rudder angles, course changes) during each process. In the future, the model may ultimately be used to support the development of a computer-aided collision-avoidance system to further improve the safety and efficiency of maritime transportation.
9. SUGGESTED FUTURE RESEARCH
Because the current study focuses exclusively on the theoretical level with some assumptions, the following intensive future research might be conducted. When a rudder angle is required, it takes time for the rudder blades to reach the specified angle. A more accurate ship dynamic motion model with the consideration of the rudder response time may be needed in future research. The manoeuvres optimised by our current model may result in the own ship falling into a new crossing situation with another target ship. Our model did not consider that outcome. More future research can be developed in this direction. In navigation practice, multiple-ship crossing situations frequently exist, especially in busy waters. We suggest the future development of a more sophisticated model specific to multiple-ship crossing situations.
ACKNOWLEDGMENTS
The first author was funded by the Department of Civil and Environmental Engineering (CEE) through a research fellowship at Rutgers University. The second author was supported by the National Natural Science Foundation of China (Grant No. 51409157) and the Young Scholar Program of Humanities and Social Science of the Ministry of Education of China (14YJC630008). The third author was partially funded by the Department of Civil and Environmental Engineering and the School of Engineering, both at Rutgers University. However, the authors are solely responsible for all the views and analyses in this paper.
