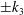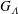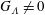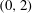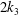1 Introduction
The presence of Görtler vortices in many flows of practical importance such as those occurring over turbine blades or aerofoils, has stimulated much research aimed at understanding their pre-transition phase as well as transition itself. Much progress has been made on receptivity, evolution and secondary instability of Görtler vortices. Reviews of the subject were given by Herbert (Reference Herbert1976), Hall (Reference Hall1990), Floryan (Reference Floryan1991) and Saric (Reference Saric1994). However, there has not yet been a complete theoretical framework, which treats these aspects in a unified manner. In this paper, we seek to take that step, and present a framework which will eventually allow us to predict the pre-transitional flow and the transition associated with Görtler vortices induced by free-stream turbulence (FST).
Görtler instability occurs in the boundary layer along a concave wall due to the imbalance between the centrifugal force and the wall-normal pressure gradient. It commonly results in generation of steady streamwise vortices, which develop into a mushroom-shaped structure in the cross-section. Görtler (Reference Görtler1941) made the first theoretical study of linear instability by normal-mode analysis, in which the instability modes were taken to be in the form of streamwise-oriented, counter-rotating vortices. The instability was shown to be controlled by the parameter
![]() $G_{\unicode[STIX]{x1D703}}=(U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D708})\sqrt{\unicode[STIX]{x1D703}/r_{0}^{\ast }}$
, where
$G_{\unicode[STIX]{x1D703}}=(U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D708})\sqrt{\unicode[STIX]{x1D703}/r_{0}^{\ast }}$
, where
![]() $U_{\infty }$
is the free-stream velocity,
$U_{\infty }$
is the free-stream velocity,
![]() $\unicode[STIX]{x1D703}$
is the boundary-layer (momentum) thickness,
$\unicode[STIX]{x1D703}$
is the boundary-layer (momentum) thickness,
![]() $r_{0}^{\ast }$
is the characteristic radius of curvature and
$r_{0}^{\ast }$
is the characteristic radius of curvature and
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity. The instability and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity. The instability and
![]() $G_{\unicode[STIX]{x1D703}}$
were therefore named after him. However, Görtler instability turned out to be far more complex than Görtler had envisaged. The spatial non-parallel effects and open-flow nature of the Görtler flow lead to difficulties in handling the instability.
$G_{\unicode[STIX]{x1D703}}$
were therefore named after him. However, Görtler instability turned out to be far more complex than Görtler had envisaged. The spatial non-parallel effects and open-flow nature of the Görtler flow lead to difficulties in handling the instability.
Normal-mode analysis and the marching method (or the method of parabolized stability equations) are the two main approaches for studying Görtler instability, both making the approximation that the radius of the wall curvature
![]() $r_{0}^{\ast }$
is much greater than the boundary-layer thickness
$r_{0}^{\ast }$
is much greater than the boundary-layer thickness
![]() $\unicode[STIX]{x1D703}$
so that the centrifugal force can be neglected in the description of the base flow. In the normal-mode approach, the base flow is assumed to be locally parallel, i.e. its dependence on the streamwise coordinate
$\unicode[STIX]{x1D703}$
so that the centrifugal force can be neglected in the description of the base flow. In the normal-mode approach, the base flow is assumed to be locally parallel, i.e. its dependence on the streamwise coordinate
![]() $x^{\ast }$
is treated as being parametric, so that the perturbation can be sought as an eigensolution. Although this approach has been successful for other types of instabilities such as inviscid or viscous shear instability, it led to unsatisfactory agreement of the predicted growth rate with experiments for Görtler instability. The reason of failure was explained by Hall (Reference Hall1983), who pointed out the instability should be formulated as an initial-value problem in the general case of
$x^{\ast }$
is treated as being parametric, so that the perturbation can be sought as an eigensolution. Although this approach has been successful for other types of instabilities such as inviscid or viscous shear instability, it led to unsatisfactory agreement of the predicted growth rate with experiments for Görtler instability. The reason of failure was explained by Hall (Reference Hall1983), who pointed out the instability should be formulated as an initial-value problem in the general case of
![]() $G_{\unicode[STIX]{x1D703}}=O(1)$
because Görtler vortices evolve on the same length scale as the background flow (Floryan & Saric Reference Floryan and Saric1982). Only when
$G_{\unicode[STIX]{x1D703}}=O(1)$
because Görtler vortices evolve on the same length scale as the background flow (Floryan & Saric Reference Floryan and Saric1982). Only when
![]() $G_{\unicode[STIX]{x1D703}}$
is asymptotically large, may the eigenvalue approach be justified. In the asymptotic limit
$G_{\unicode[STIX]{x1D703}}$
is asymptotically large, may the eigenvalue approach be justified. In the asymptotic limit
![]() $G_{\unicode[STIX]{x1D703}}\gg 1$
, Hall (Reference Hall1982) and Denier, Hall & Seddougui (Reference Denier, Hall and Seddougui1991) mapped out distinct regimes that operate at a fixed streamwise location for different spanwise wavelength
$G_{\unicode[STIX]{x1D703}}\gg 1$
, Hall (Reference Hall1982) and Denier, Hall & Seddougui (Reference Denier, Hall and Seddougui1991) mapped out distinct regimes that operate at a fixed streamwise location for different spanwise wavelength
![]() $\unicode[STIX]{x1D706}_{z}$
. These analyses and findings were recast for vortices with a fixed wavelength by Wu, Zhao & Luo (Reference Wu, Zhao and Luo2011) (referred to as WZL hereafter), who found that local eigenvalue formulations are mathematically justified from the position
$\unicode[STIX]{x1D706}_{z}$
. These analyses and findings were recast for vortices with a fixed wavelength by Wu, Zhao & Luo (Reference Wu, Zhao and Luo2011) (referred to as WZL hereafter), who found that local eigenvalue formulations are mathematically justified from the position
![]() $x^{\ast }\sim \unicode[STIX]{x1D6EC}R_{\unicode[STIX]{x1D6EC}}$
onwards for
$x^{\ast }\sim \unicode[STIX]{x1D6EC}R_{\unicode[STIX]{x1D6EC}}$
onwards for
![]() $G_{\unicode[STIX]{x1D6EC}}\equiv R_{\unicode[STIX]{x1D6EC}}^{2}\unicode[STIX]{x1D6EC}/r_{0}^{\ast }$
$G_{\unicode[STIX]{x1D6EC}}\equiv R_{\unicode[STIX]{x1D6EC}}^{2}\unicode[STIX]{x1D6EC}/r_{0}^{\ast }$
![]() $\gg 1$
, and showed how different regimes emerge in sequence when the vortices evolve downstream, where
$\gg 1$
, and showed how different regimes emerge in sequence when the vortices evolve downstream, where
![]() $R_{\unicode[STIX]{x1D6EC}}=U_{\infty }\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D708}$
is the Reynolds number based on the spanwise length scale
$R_{\unicode[STIX]{x1D6EC}}=U_{\infty }\unicode[STIX]{x1D6EC}/\unicode[STIX]{x1D708}$
is the Reynolds number based on the spanwise length scale
![]() $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D706}_{z}/(2\unicode[STIX]{x03C0})$
; however, the so-called inviscid–viscous interaction regime (which exists for the lowest-order normal mode) was unfortunately missed. Comparisons of eigenvalue (normal mode) and marching (initial value) solutions were made by Day, Herbert & Saric (Reference Day, Herbert and Saric1990) and Bottaro & Luchini (Reference Bottaro and Luchini1999). These studies confirmed that an initial-value problem needs to be considered, and the evolution of Görtler vortices depends on the initial conditions.
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D706}_{z}/(2\unicode[STIX]{x03C0})$
; however, the so-called inviscid–viscous interaction regime (which exists for the lowest-order normal mode) was unfortunately missed. Comparisons of eigenvalue (normal mode) and marching (initial value) solutions were made by Day, Herbert & Saric (Reference Day, Herbert and Saric1990) and Bottaro & Luchini (Reference Bottaro and Luchini1999). These studies confirmed that an initial-value problem needs to be considered, and the evolution of Görtler vortices depends on the initial conditions.
Many experiments have been conducted to investigate Görtler instability and resulting transition process, and the importance of initial conditions and external disturbances was noted. Bippes (Reference Bippes1972) was able to generate vortices of different wavelength by inserting a screen into the free stream, and measured the development of these vortices using hot wires. Initial/external conditions rather than intrinsic instability appeared to select the wavelength of the vortices that arose. Swearingen & Blackwelder (Reference Swearingen and Blackwelder1987) (referred to as SB hereafter) studied the detailed evolution and breakdown process of Görtler vortices, which arose without artificial triggering and were presumably generated by disturbances in the free stream. The deciding role of the latter in generating Görtler vortices was clearly demonstrated by the experiment of Kottke (Reference Kottke, Westfield and Brand1988), where a screen was placed upstream of the leading edge to manipulate free-stream disturbances. By varying the mesh size and the distance of the screen to the leading edge (thereby changing the free-stream disturbance intensity), Görtler vortices of different scale and strength appeared in the boundary layer. Similarly, by placing wire grids in the oncoming flow, Peerhossaini & Bahri (Reference Peerhossaini and Bahri1998) and the research group at the Singapore National University (Mitsudharmadi, Winoto & Shah Reference Mitsudharmadi, Winoto and Shah2004, Reference Mitsudharmadi, Winoto and Shah2005, Reference Mitsudharmadi, Winoto and Shah2006; Tandiono, Winoto & Shah Reference Tandiono, Winoto and Shah2008) succeed in triggering vortices with fixed wavelengths. Detailed measurements were then made to provide the information about the linear and nonlinear development, as well as breakdown, of these vortices. No attempt is made here to survey all the literature on Görtler vortex experiments. The reader is referred to Saric (Reference Saric1994) and Winoto, Shah & Mitsudharmadi (Reference Winoto, Shah and Mitsudharmadi2011) for reviews.
The theoretical analyses and experiments mentioned above both point to the crucial issue: the receptivity process, i.e. how external disturbances enter the boundary layer to trigger unstable modes, which are, in the case of the boundary layer over a concave wall, Görtler vortices. Relevant and realizable external disturbances include free-stream turbulence and surface roughness elements. A review of receptivity mechanisms for Görtler modes was presented by Bassom & Seddougui (Reference Bassom and Seddougui1995). Denier et al. (Reference Denier, Hall and Seddougui1991) considered the vortex motion induced by wall roughness, and reported that the most efficient excitation of instability is for wavelengths comparable with the boundary-layer thickness. Recently, Sescu & Thompson (Reference Sescu and Thompson2015) found that bell-shaped roughness elements excite Görtler vortices are more effective than sharp edged ones do.
Strong evidence exists that FST can excite Görtler vortices. Bippes & Görtler (Reference Bippes and Görtler1972), SB (1987), Kottke (Reference Kottke, Westfield and Brand1988) and Bippes & Deyhle (Reference Bippes and Deyhle1992) all found that the characteristics of FST influence the onset location and the amplitude of Görtler vortices. The recent direct numerical simulations of Schrader, Brandt & Zaki (Reference Schrader, Brandt and Zaki2011) suggest that Görtler boundary layers are highly receptive to free-stream vortical modes with zero or low frequencies, large spanwise wavelength and small wall-normal wavelength. However, the inlet disturbance is constructed by a superposition of continuous modes of the Orr–Sommerfeld and Squire operators. Such inlet disturbances were shown to be inappropriate by Dong & Wu (Reference Dong and Wu2013). A crucial issue for receptivity of Görtler vortices to FST is to account for properly the action of free-stream disturbances on the boundary layer.
Excitation of Görtler vortices by FST is very similar to generation of streaks (i.e. spanwise alternating low- and high-speed regions) in a flat-plate boundary layer, a problem related to bypass transition. FST consists of acoustic, vortical and entropy modes (Kovasznay Reference Kovasznay1953), of which free-stream vortical disturbances (FSVD) are considered to be the most significant. The parameters characterizing FSVD are the amplitude
![]() $\unicode[STIX]{x1D716}$
, the Reynolds number
$\unicode[STIX]{x1D716}$
, the Reynolds number
![]() $R_{\unicode[STIX]{x1D6EC}}$
and the typical frequency
$R_{\unicode[STIX]{x1D6EC}}$
and the typical frequency
![]() $k_{1}$
(normalized by
$k_{1}$
(normalized by
![]() $U_{\infty }/\unicode[STIX]{x1D6EC}$
). Goldstein, Leib & Cowley (Reference Goldstein, Leib and Cowley1992) studied the effect of steady vorticity normal to the wall on the boundary layer. The boundary layer responds to the vorticity by causing significant three-dimensional distortions, which were found to be governed by the nonlinear boundary-layer equations if
$U_{\infty }/\unicode[STIX]{x1D6EC}$
). Goldstein, Leib & Cowley (Reference Goldstein, Leib and Cowley1992) studied the effect of steady vorticity normal to the wall on the boundary layer. The boundary layer responds to the vorticity by causing significant three-dimensional distortions, which were found to be governed by the nonlinear boundary-layer equations if
![]() $\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}\gg 1$
, or the nonlinear boundary-region equations (NBRE) if
$\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}\gg 1$
, or the nonlinear boundary-region equations (NBRE) if
![]() $\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}=O(1)$
. The same methods were applied by Goldstein & Leib (Reference Goldstein and Leib1993) and Wundrow & Goldstein (Reference Wundrow and Goldstein2001) to steady streamwise vorticity. Leib, Wundrow & Goldstein (Reference Leib, Wundrow and Goldstein1999) (referred to as LWG hereafter) investigated the effect of long-wavelength, low-frequency FSVD on the pre-transitional flat-plate boundary layer. They showed that the induced perturbation is governed by the linearized unsteady boundary-region equations (LUBRE), and derived the appropriate initial and far-field boundary conditions that account for the action of FSVD on the boundary layer. The boundary layer was found to act like a filter, allowing only low-frequency components to penetrate into the layer while high-frequency ones are absorbed at the outer edge of the boundary layer (Dong & Wu Reference Dong and Wu2013). The LWG analysis was restricted to sufficiently weak FST, for which
$\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}=O(1)$
. The same methods were applied by Goldstein & Leib (Reference Goldstein and Leib1993) and Wundrow & Goldstein (Reference Wundrow and Goldstein2001) to steady streamwise vorticity. Leib, Wundrow & Goldstein (Reference Leib, Wundrow and Goldstein1999) (referred to as LWG hereafter) investigated the effect of long-wavelength, low-frequency FSVD on the pre-transitional flat-plate boundary layer. They showed that the induced perturbation is governed by the linearized unsteady boundary-region equations (LUBRE), and derived the appropriate initial and far-field boundary conditions that account for the action of FSVD on the boundary layer. The boundary layer was found to act like a filter, allowing only low-frequency components to penetrate into the layer while high-frequency ones are absorbed at the outer edge of the boundary layer (Dong & Wu Reference Dong and Wu2013). The LWG analysis was restricted to sufficiently weak FST, for which
![]() $\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}\ll 1$
. Ricco, Luo & Wu (Reference Ricco, Luo and Wu2011) studied the evolution and secondary instability of unsteady nonlinear streaks generated by FSVD with
$\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}\ll 1$
. Ricco, Luo & Wu (Reference Ricco, Luo and Wu2011) studied the evolution and secondary instability of unsteady nonlinear streaks generated by FSVD with
![]() $\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}=O(1)$
. Their work established in principle a quantitative relation between the characteristics of FST and secondary instability. Zhang et al. (Reference Zhang, Zaki, Sherwin and Wu2011) calculated the nonlinear response of a laminar boundary layer to FST with a broadband spectrum, and a fairly good quantitative agreement with experiments was obtained.
$\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}=O(1)$
. Their work established in principle a quantitative relation between the characteristics of FST and secondary instability. Zhang et al. (Reference Zhang, Zaki, Sherwin and Wu2011) calculated the nonlinear response of a laminar boundary layer to FST with a broadband spectrum, and a fairly good quantitative agreement with experiments was obtained.
WZL extended the formulation of LWG to a concave wall, and studied the excitation and linear evolution of Görtler vortices. Their work showed that Görtler vortices excited by FSVD are in agreement with experiments not only in their shape but also in their growth rate. Unlike streak formation in the flat-plate boundary layer, Görtler vortices amplify exponentially after their initial non-modal growth when
![]() $G_{\unicode[STIX]{x1D6EC}}$
exceeds a critical value. The analysis of WZL was restricted to sufficiently weak FSVD for which the induced Görtler vortices are governed by LUBRE. The analysis needs to be extended when FSVD is of sufficient strength that the boundary-layer response acquires an
$G_{\unicode[STIX]{x1D6EC}}$
exceeds a critical value. The analysis of WZL was restricted to sufficiently weak FSVD for which the induced Görtler vortices are governed by LUBRE. The analysis needs to be extended when FSVD is of sufficient strength that the boundary-layer response acquires an
![]() $O(1)$
amplitude either before or after evolving into Görtler vortices.
$O(1)$
amplitude either before or after evolving into Görtler vortices.
As was revealed by a series of experiments (SB, Peerhossaini & Bahri (Reference Peerhossaini and Bahri1998), Mitsudharmadi et al. (Reference Mitsudharmadi, Winoto and Shah2005) which will be referred to as MWS), Görtler vortices of
![]() $O(1)$
magnitude can significantly distort the velocity profile from that of the Blasius flow, and as vortices saturate, contours of the streamwise velocity feature a mushroom-shaped structure. Hall (Reference Hall1988) calculated the streamwise evolution of steady Görtler vortices that are governed by the NBRE. The initial (upstream) condition was however rather arbitrary. Sabry & Liu (Reference Sabry and Liu1991) tried to elucidate the nonlinear characteristics of Görtler vortices which were assumed to evolve in time (and thus were free from any effect of non-parallelism). Despite the artificial nature of the temporal formulation, the predicted distorted streamwise velocity profiles resembled those that were measured. Later, Lee & Liu (Reference Lee and Liu1992) solved the spatially evolving NBRE using a local eigensolution as the initial condition (cf. Hall Reference Hall1988). Their solution as well as that of Hall (Reference Hall1988) captured quite well the nonlinear features of the vortex flow, including saturation, mushroom-like structures and the skin friction. FSVD were not considered in either work, but need to be taken into account by a more complete formulation if their role in excitation and evolution of Görtler vortices is to be elucidated.
$O(1)$
magnitude can significantly distort the velocity profile from that of the Blasius flow, and as vortices saturate, contours of the streamwise velocity feature a mushroom-shaped structure. Hall (Reference Hall1988) calculated the streamwise evolution of steady Görtler vortices that are governed by the NBRE. The initial (upstream) condition was however rather arbitrary. Sabry & Liu (Reference Sabry and Liu1991) tried to elucidate the nonlinear characteristics of Görtler vortices which were assumed to evolve in time (and thus were free from any effect of non-parallelism). Despite the artificial nature of the temporal formulation, the predicted distorted streamwise velocity profiles resembled those that were measured. Later, Lee & Liu (Reference Lee and Liu1992) solved the spatially evolving NBRE using a local eigensolution as the initial condition (cf. Hall Reference Hall1988). Their solution as well as that of Hall (Reference Hall1988) captured quite well the nonlinear features of the vortex flow, including saturation, mushroom-like structures and the skin friction. FSVD were not considered in either work, but need to be taken into account by a more complete formulation if their role in excitation and evolution of Görtler vortices is to be elucidated.
Once Görtler vortices have acquired a significant amplitude and the mean flow is distorted into a three-dimensional pattern, the velocity profiles are highly unstable to high-frequency disturbances, which is referred to as secondary instability. It is SB who first provided the concrete evidence and the data base of secondary instability, although earlier experimental studies had been made by Aihara & Koyama (Reference Aihara and Koyama1981) among others. Inviscid secondary instability of Görtler vortices was first formulated by Hall & Horseman (Reference Hall and Horseman1991). Their analysis and calculations showed that odd and even (or sinuous and varicose) modes can exist. Li & Malik (Reference Li and Malik1995) performed extensive inviscid stability computations. Yu & Liu (Reference Yu and Liu1991, Reference Yu and Liu1994) analysed the stability of nonlinear vortices which evolved in time, and viscous effects were included. By examining the production terms in the kinetic energy equation, Yu & Liu (Reference Yu and Liu1994) demonstrated that sinuous and varicose modes are associated primarily with the spanwise and vertical gradients of the streamwise velocity of Görtler vortices, respectively. Recently, Ren & Fu (Reference Ren and Fu2015) found a new family of odd modes, which have relatively high frequencies and concentrate in the region nearer to the wall. Almost all previous studies of secondary instability focused on its linear characteristics. Very few researchers have considered nonlinear secondary instability. Li & Malik (Reference Li and Malik1995) investigated the nonlinear evolution of a single secondary (sinuous or varicose) mode using the approach of parabolized stability equations. Girgis & Liu (Reference Girgis and Liu2006) tackled the same problem for a sinuous mode by adopting a mean-field approximation, in which the self-interaction of the sinuous mode modifies the steady vortex flow through the time-averaged Reynolds stresses, whilst the modified vortex flow simultaneously affects the development of the sinuous mode. The latter was described by the parabolized stability equations. The effects of unsteady harmonics were neglected.
From the discussions above, one can conclude that the main characteristics of linear and nonlinear developments of steady Görtler vortices are fairly well understood, and relevant secondary instability modes have been identified. However, proper quantitative comparisons between theoretical predictions and experiments are still lacking. One of the reasons is that calculations for nonlinear evolutions were (with few exceptions) carried out for artificial upstream conditions. The predicted development and secondary instability results cannot readily be related to experiments where Görtler vortices were excited by external disturbances. For further progress, more effort needs to be devoted to generation of vortices by physically relevant external disturbances, which remains the least studied aspects of boundary-layer transition initiated by Görtler instability. FSVD are likely to generate unsteady Görtler vortices; nonlinear development and secondary instability of the latter have not been investigated. It is important to recognize that although the formation of Görtler vortices, their evolution and secondary instability are three distinct aspects of the entire transition, they are closely interlinked and are ultimately determined by external disturbances. The very purpose of studying transition is to predict transition events and location in terms of the characteristics of external disturbances. It is therefore crucial to develop an integrated framework, in which the action of the external disturbances are taken into account appropriately and quantitatively.
In the present paper, we will study the transition process in a concave wall boundary layer under the influence of FST. The intensity of FST is assumed to be strong enough to generate nonlinear Görtler vortices. We will treat the formation, evolution and secondary instability as interlinked stages, and describe them in an integrated framework. This is a necessary step towards predicting the pre-transitional flow and the transition location of the boundary layers over turbine blades. The present work is based upon the earlier investigations of Ricco et al. (Reference Ricco, Luo and Wu2011) and WZL, and indeed can be viewed as extending the former by including the centrifugal effects, while generalizing the latter to the nonlinear case. The rest of the paper will be organized as follows. In § 2, we describe FSVD and the relevant scalings, and formulate the initial-boundary-value problem, consisting of the nonlinear boundary-region equations as well as the upstream (initial) and far-field (boundary) conditions, which account for the impact of FSVD. The numerical procedure to solve the equations is explained in § 3. The results on steady and unsteady Görtler vortices excited are presented in § 4, and comprehensive comparisons with several experiments are made. Further secondary stability analyses of saturated steady and unsteady Görtler vortices are performed in § 5. A summary and concluding remarks are given in § 6.
2 Problem formulation
2.1 Scalings and governing equations
We consider the boundary-layer flow over a concave wall with a characteristic radius of curvature
![]() $r_{0}^{\ast }$
. The incompressible oncoming flow is assumed to be uniform with a speed
$r_{0}^{\ast }$
. The incompressible oncoming flow is assumed to be uniform with a speed
![]() $U_{\infty }$
, superimposed on which are small-amplitude vortical fluctuations. The FSVD has a characteristic spanwise length scale
$U_{\infty }$
, superimposed on which are small-amplitude vortical fluctuations. The FSVD has a characteristic spanwise length scale
![]() $\unicode[STIX]{x1D6EC}$
. The analysis is pertinent to low-frequency, including zero-frequency components, which can entrain into the boundary layer to excite Görtler vortices. For simplicity, we consider the case of a pair of free-stream vortical modes with opposite (dimensional) spanwise wavenumbers
$\unicode[STIX]{x1D6EC}$
. The analysis is pertinent to low-frequency, including zero-frequency components, which can entrain into the boundary layer to excite Görtler vortices. For simplicity, we consider the case of a pair of free-stream vortical modes with opposite (dimensional) spanwise wavenumbers
![]() $\pm k_{3}^{\ast }$
. Although this is a drastic idealization of physical reality, the assumed form of disturbances suffices for elucidating key physical mechanisms and transition process. The generalization of the formulation and calculation to realistic broadband FSVD is rather straightforward.
$\pm k_{3}^{\ast }$
. Although this is a drastic idealization of physical reality, the assumed form of disturbances suffices for elucidating key physical mechanisms and transition process. The generalization of the formulation and calculation to realistic broadband FSVD is rather straightforward.
We describe the flow in a curvilinear system
![]() $(x^{\ast },y^{\ast },z^{\ast })$
with its origin at the leading edge, where
$(x^{\ast },y^{\ast },z^{\ast })$
with its origin at the leading edge, where
![]() $x^{\ast }$
measures the distance to the leading edge along the wall,
$x^{\ast }$
measures the distance to the leading edge along the wall,
![]() $y^{\ast }$
is the distance to the wall and
$y^{\ast }$
is the distance to the wall and
![]() $z^{\ast }$
the spanwise coordinate normal to both
$z^{\ast }$
the spanwise coordinate normal to both
![]() $x^{\ast }$
and
$x^{\ast }$
and
![]() $y^{\ast }$
. Let
$y^{\ast }$
. Let
where
![]() $t^{\ast }$
is the dimensional time. The Reynolds number is defined as
$t^{\ast }$
is the dimensional time. The Reynolds number is defined as
and the global Görtler number as (WZL)
We assume that
![]() $R_{\unicode[STIX]{x1D6EC}}$
is asymptotically large, i.e.
$R_{\unicode[STIX]{x1D6EC}}$
is asymptotically large, i.e.
![]() $R_{\unicode[STIX]{x1D6EC}}\gg 1$
, but take
$R_{\unicode[STIX]{x1D6EC}}\gg 1$
, but take
![]() $G_{\unicode[STIX]{x1D6EC}}$
as being of
$G_{\unicode[STIX]{x1D6EC}}$
as being of
![]() $O(1)$
so that the resulting formulation accommodates all regimes of Görtler instability.
$O(1)$
so that the resulting formulation accommodates all regimes of Görtler instability.
Among the Fourier components of FSVD, of importance are those with low frequencies or equivalently long streamwise wavelengths
![]() $2\unicode[STIX]{x03C0}/k_{1}^{\ast }\gg \unicode[STIX]{x1D6EC}$
, where
$2\unicode[STIX]{x03C0}/k_{1}^{\ast }\gg \unicode[STIX]{x1D6EC}$
, where
![]() $k_{1}^{\ast }$
is the dimensional wavenumber. Specifically, when
$k_{1}^{\ast }$
is the dimensional wavenumber. Specifically, when
![]() $2\unicode[STIX]{x03C0}/k_{1}^{\ast }=O(\unicode[STIX]{x1D6EC}R_{\unicode[STIX]{x1D6EC}})$
, the induced response in the boundary layer takes on the character of Görtler vortices at distances
$2\unicode[STIX]{x03C0}/k_{1}^{\ast }=O(\unicode[STIX]{x1D6EC}R_{\unicode[STIX]{x1D6EC}})$
, the induced response in the boundary layer takes on the character of Görtler vortices at distances
![]() $x^{\ast }\sim \unicode[STIX]{x1D6EC}R_{\unicode[STIX]{x1D6EC}}$
, as was shown by WZL. We thus introduce the slow streamwise and time variables,
$x^{\ast }\sim \unicode[STIX]{x1D6EC}R_{\unicode[STIX]{x1D6EC}}$
, as was shown by WZL. We thus introduce the slow streamwise and time variables,
The disturbances in the upstream region are passively advected by the uniform background flow
![]() $U_{\infty }$
. It follows that the total velocity field can be written as
$U_{\infty }$
. It follows that the total velocity field can be written as
![]() $(u^{\ast },v^{\ast },w^{\ast })/U_{\infty }=(1,0,0)+\tilde{\boldsymbol{u}}_{\infty }$
, and the disturbance
$(u^{\ast },v^{\ast },w^{\ast })/U_{\infty }=(1,0,0)+\tilde{\boldsymbol{u}}_{\infty }$
, and the disturbance
![]() $\tilde{\boldsymbol{u}}_{\infty }$
takes the form
$\tilde{\boldsymbol{u}}_{\infty }$
takes the form
where
![]() $\unicode[STIX]{x1D716}$
is a measure of the disturbance intensity,
$\unicode[STIX]{x1D716}$
is a measure of the disturbance intensity,
![]() $\hat{\boldsymbol{u}}_{\pm }^{\infty }=\{\hat{u} _{1,\pm }^{\infty },\hat{u} _{2,\pm }^{\infty },\hat{u} _{3,\pm }^{\infty }\}=O(1)$
is the scaled velocity,
$\hat{\boldsymbol{u}}_{\pm }^{\infty }=\{\hat{u} _{1,\pm }^{\infty },\hat{u} _{2,\pm }^{\infty },\hat{u} _{3,\pm }^{\infty }\}=O(1)$
is the scaled velocity,
![]() $\boldsymbol{k}=\{k_{1},k_{2},k_{3}\}$
is the wavenumber vector and
$\boldsymbol{k}=\{k_{1},k_{2},k_{3}\}$
is the wavenumber vector and
![]() $\hat{k}_{1}=k_{1}R_{\unicode[STIX]{x1D6EC}}$
. The continuity condition implies that
$\hat{k}_{1}=k_{1}R_{\unicode[STIX]{x1D6EC}}$
. The continuity condition implies that
The turbulent Reynolds number is defined as (Goldstein et al. Reference Goldstein, Leib and Cowley1992, WZL)
It is necessary here to make a few remarks on FSVD and the so-called ‘free-stream coherent structures’, which have been described in recent studies; see for example Deguchi & Hall (Reference Deguchi and Hall2017) and references therein. The former are external disturbances characterizing the flow environment and present in the main inviscid part of the flow. In contrast, the latter are the nonlinearly self-sustained intrinsic disturbances, and decay to zero in the main inviscid region although they reside in the outer reach of the boundary layer, in the so-called ‘production layer’. FSVD and free-stream coherent structures are therefore different physical entities. Mathematically, there is a certain degree of similarity: both have a phase speed close to the free-stream velocity, and short-wavelength FSVD have an ‘edge layer’ (Dong & Wu Reference Dong and Wu2013; Wu & Dong Reference Wu and Dong2016), which is essentially the same as the ‘production layer’ of free-stream coherent structures. Recently, Deguchi & Hall (Reference Deguchi and Hall2017) showed that the nonlinear interactions of free-stream coherent structures in the production layer generate streaks, which can in turn excite Görtler vortices in the boundary layer if the wall is concave. We note that a similar excitation can take place for short-wavelength FSVD too. Presently, we consider long-wavelength FSVD, which are a more relevant and efficient agent for generating Görtler vortices.

Figure 1. Schematic illustration of the physical problem and the asymptotic structure.
Similar to the flat-plate case considered by LWG, the ensuing boundary layer over a concave wall evolves through four asymptotic regimes or regions (WZL), illustrated in figure 1. Near the leading edge is an inviscid region I, which is
![]() $O(\unicode[STIX]{x1D6EC})$
in all three directions, and the disturbance is governed by the linear rapid-distortion theory (LWG). Beneath region I is a viscous layer, region II, which has an
$O(\unicode[STIX]{x1D6EC})$
in all three directions, and the disturbance is governed by the linear rapid-distortion theory (LWG). Beneath region I is a viscous layer, region II, which has an
![]() $O(R_{\unicode[STIX]{x1D6EC}}^{-1/2}\unicode[STIX]{x1D6EC})$
thickness. In this region, the centrifugal force is negligible, and so as in the flat-plate case, the streamwise and spanwise components of FSVD induce a quasi two-dimensional disturbance and a three-dimensional disturbance respectively, both having an
$O(R_{\unicode[STIX]{x1D6EC}}^{-1/2}\unicode[STIX]{x1D6EC})$
thickness. In this region, the centrifugal force is negligible, and so as in the flat-plate case, the streamwise and spanwise components of FSVD induce a quasi two-dimensional disturbance and a three-dimensional disturbance respectively, both having an
![]() $O(\unicode[STIX]{x1D716})$
amplitude (LWG). Like WZL, we focus on the three-dimensional disturbance, which will develop into Görtler vortices further downstream. In region III, which has an
$O(\unicode[STIX]{x1D716})$
amplitude (LWG). Like WZL, we focus on the three-dimensional disturbance, which will develop into Görtler vortices further downstream. In region III, which has an
![]() $O(\unicode[STIX]{x1D6EC})$
thickness, the perturbations are governed by steady or unsteady nonlinear boundary-region equations, but with the centrifugal force appearing in the wall-normal momentum equation. An outer region IV above region III, where turbulence undergoes equilibrium decay, has a transversal scale of
$O(\unicode[STIX]{x1D6EC})$
thickness, the perturbations are governed by steady or unsteady nonlinear boundary-region equations, but with the centrifugal force appearing in the wall-normal momentum equation. An outer region IV above region III, where turbulence undergoes equilibrium decay, has a transversal scale of
![]() $O(\unicode[STIX]{x1D6EC}R_{\unicode[STIX]{x1D6EC}})$
. With the assumption
$O(\unicode[STIX]{x1D6EC}R_{\unicode[STIX]{x1D6EC}})$
. With the assumption
![]() $r_{t}\ll 1$
, the disturbance remains linear in all the regions. When
$r_{t}\ll 1$
, the disturbance remains linear in all the regions. When
![]() $r_{t}=O(1)$
, nonlinearity comes into play in regions III and IV (Wundrow & Goldstein Reference Wundrow and Goldstein2001). Görtler vortices then evolve nonlinearly, saturate and may undergo secondary instability.
$r_{t}=O(1)$
, nonlinearity comes into play in regions III and IV (Wundrow & Goldstein Reference Wundrow and Goldstein2001). Görtler vortices then evolve nonlinearly, saturate and may undergo secondary instability.
In the boundary region (region III), where
![]() $\hat{x}$
and
$\hat{x}$
and
![]() $y$
are both of
$y$
are both of
![]() $O(1)$
, the streamwise velocity has a magnitude greater than those of the normal and spanwise velocities by a factor of
$O(1)$
, the streamwise velocity has a magnitude greater than those of the normal and spanwise velocities by a factor of
![]() $O(R_{\unicode[STIX]{x1D6EC}})$
, while the pressure normalized by
$O(R_{\unicode[STIX]{x1D6EC}})$
, while the pressure normalized by
![]() $\unicode[STIX]{x1D70C}U_{\infty }^{2}$
is of
$\unicode[STIX]{x1D70C}U_{\infty }^{2}$
is of
![]() $O(R_{\unicode[STIX]{x1D6EC}}^{-2})$
. Therefore, we can write the velocity and pressure fields,
$O(R_{\unicode[STIX]{x1D6EC}}^{-2})$
. Therefore, we can write the velocity and pressure fields,
![]() $(u^{\ast },v^{\ast },w^{\ast })$
and
$(u^{\ast },v^{\ast },w^{\ast })$
and
![]() $p^{\ast }$
, as
$p^{\ast }$
, as
Substitution of (2.4) and (2.8) with the Lamè coefficients,
![]() $(h_{1},h_{2},h_{3})=((r_{0}^{\ast }-y^{\ast })/r_{0}^{\ast },1,1)$
, into the Navier–Stokes (N–S) equations gives at leading-order equations for rescaled velocity
$(h_{1},h_{2},h_{3})=((r_{0}^{\ast }-y^{\ast })/r_{0}^{\ast },1,1)$
, into the Navier–Stokes (N–S) equations gives at leading-order equations for rescaled velocity
![]() $\boldsymbol{u}\equiv (u,v,w)$
and pressure
$\boldsymbol{u}\equiv (u,v,w)$
and pressure
![]() $p$
(Hall Reference Hall1988),
$p$
(Hall Reference Hall1988),
where
![]() $\boldsymbol{j}$
is the unit vector in the wall-normal direction, the term containing
$\boldsymbol{j}$
is the unit vector in the wall-normal direction, the term containing
![]() $G_{\unicode[STIX]{x1D6EC}}$
reflects the essential influence of the wall curvature and
$G_{\unicode[STIX]{x1D6EC}}$
reflects the essential influence of the wall curvature and
![]() $\unicode[STIX]{x1D712}^{-1}(\hat{x})$
is the scaled local radius of wall curvature. The system (2.9), which holds under the assumption of large curvature radius, will be referred to as the nonlinear unsteady boundary-region equations (NUBRE). A noteworthy property of the system is that it is parabolic in the streamwise direction but retains ellipticity in the spanwise direction.
$\unicode[STIX]{x1D712}^{-1}(\hat{x})$
is the scaled local radius of wall curvature. The system (2.9), which holds under the assumption of large curvature radius, will be referred to as the nonlinear unsteady boundary-region equations (NUBRE). A noteworthy property of the system is that it is parabolic in the streamwise direction but retains ellipticity in the spanwise direction.
The flow can be decomposed as a sum of the Blasius flow and the perturbation which arises as the response to FSVD, namely
The Blasius boundary layer, taken as the unperturbed base flow, has the similarity solution,
where the prime denotes the differentiation with respect to
![]() $\unicode[STIX]{x1D702}$
, and the Blasius function
$\unicode[STIX]{x1D702}$
, and the Blasius function
![]() $F$
is determined by the boundary-value problem,
$F$
is determined by the boundary-value problem,
For
![]() $\unicode[STIX]{x1D702}\gg 1$
, the function
$\unicode[STIX]{x1D702}\gg 1$
, the function
![]() $F\rightarrow \unicode[STIX]{x1D702}-\unicode[STIX]{x1D6FD}$
with
$F\rightarrow \unicode[STIX]{x1D702}-\unicode[STIX]{x1D6FD}$
with
![]() $\unicode[STIX]{x1D6FD}\approx 1.217$
.
$\unicode[STIX]{x1D6FD}\approx 1.217$
.
Inserting (2.10) into (2.9), we obtain the governing equations for the perturbation,
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\hat{u} _{\hat{x}}+\hat{v}_{y}+{\hat{w}}_{z}=0,\\ \hat{u} _{\hat{\unicode[STIX]{x1D70F}}}+U\hat{u} _{\hat{x}}+\hat{u} U_{\hat{x}}+\hat{v}U_{y}+V\hat{u} _{y}=\hat{u} _{yy}+\hat{u} _{zz}+Q_{1},\\ \hat{v}_{\hat{\unicode[STIX]{x1D70F}}}+U\hat{v}_{\hat{x}}+\hat{u} V_{\hat{x}}+V\hat{v}_{y}+\hat{v}V_{y}+2G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}U\hat{u} =-\hat{p}_{y}+\hat{v}_{yy}+\hat{v}_{zz}+Q_{2},\\ {\hat{w}}_{\hat{\unicode[STIX]{x1D70F}}}+U{\hat{w}}_{\hat{x}}+V{\hat{w}}_{y}=-\hat{p}_{z}+{\hat{w}}_{yy}+{\hat{w}}_{zz}+Q_{3},\\ \end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\hat{u} _{\hat{x}}+\hat{v}_{y}+{\hat{w}}_{z}=0,\\ \hat{u} _{\hat{\unicode[STIX]{x1D70F}}}+U\hat{u} _{\hat{x}}+\hat{u} U_{\hat{x}}+\hat{v}U_{y}+V\hat{u} _{y}=\hat{u} _{yy}+\hat{u} _{zz}+Q_{1},\\ \hat{v}_{\hat{\unicode[STIX]{x1D70F}}}+U\hat{v}_{\hat{x}}+\hat{u} V_{\hat{x}}+V\hat{v}_{y}+\hat{v}V_{y}+2G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}U\hat{u} =-\hat{p}_{y}+\hat{v}_{yy}+\hat{v}_{zz}+Q_{2},\\ {\hat{w}}_{\hat{\unicode[STIX]{x1D70F}}}+U{\hat{w}}_{\hat{x}}+V{\hat{w}}_{y}=-\hat{p}_{z}+{\hat{w}}_{yy}+{\hat{w}}_{zz}+Q_{3},\\ \end{array}\right\}\end{eqnarray}$$
where
![]() $Q_{1}$
,
$Q_{1}$
,
![]() $Q_{2}$
and
$Q_{2}$
and
![]() $Q_{3}$
represent the components of the nonlinear term
$Q_{3}$
represent the components of the nonlinear term
![]() $-(\hat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\hat{\boldsymbol{u}}-G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}\hat{u} ^{2}\boldsymbol{j}$
.
$-(\hat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\hat{\boldsymbol{u}}-G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}\hat{u} ^{2}\boldsymbol{j}$
.
In the present nonlinear regime, the disturbance consists of all temporal and spanwise harmonics, and can be expressed as
 $$\begin{eqnarray}\displaystyle (\hat{u} ,\hat{v},{\hat{w}},\hat{p}) & = & \displaystyle r_{t}\mathop{\sum }_{m,n=-\infty }^{+\infty }((2\hat{x})\hat{u} _{m,n}(\hat{x},\unicode[STIX]{x1D702}),(2\hat{x})^{1/2}\hat{v}_{m,n}(\hat{x},\unicode[STIX]{x1D702}),{\hat{w}}_{m,n}(\hat{x},\unicode[STIX]{x1D702})/k_{3},\hat{p}_{m,n}(\hat{x},\unicode[STIX]{x1D702}))\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (-\text{i}m\hat{k}_{1}\hat{\unicode[STIX]{x1D70F}}+\text{i}nk_{3}z).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\hat{u} ,\hat{v},{\hat{w}},\hat{p}) & = & \displaystyle r_{t}\mathop{\sum }_{m,n=-\infty }^{+\infty }((2\hat{x})\hat{u} _{m,n}(\hat{x},\unicode[STIX]{x1D702}),(2\hat{x})^{1/2}\hat{v}_{m,n}(\hat{x},\unicode[STIX]{x1D702}),{\hat{w}}_{m,n}(\hat{x},\unicode[STIX]{x1D702})/k_{3},\hat{p}_{m,n}(\hat{x},\unicode[STIX]{x1D702}))\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (-\text{i}m\hat{k}_{1}\hat{\unicode[STIX]{x1D70F}}+\text{i}nk_{3}z).\end{eqnarray}$$
The factor
![]() $2\hat{x}$
in the streamwise velocity is introduced to offset the small divisor in numerical computations. The reality of the physical quality requires
$2\hat{x}$
in the streamwise velocity is introduced to offset the small divisor in numerical computations. The reality of the physical quality requires
where
![]() $\hat{q}_{m,n}$
stands for any of
$\hat{q}_{m,n}$
stands for any of
![]() $(\hat{u} _{m,n},\hat{v}_{m,n},{\hat{w}}_{m,n},\hat{p}_{m,n})$
and the subscript cc indicates the complex conjugate. Substitution of (2.14) into (2.13) yields the equations for the Fourier coefficients as follows.
$(\hat{u} _{m,n},\hat{v}_{m,n},{\hat{w}}_{m,n},\hat{p}_{m,n})$
and the subscript cc indicates the complex conjugate. Substitution of (2.14) into (2.13) yields the equations for the Fourier coefficients as follows.
The continuity equation:
The momentum equations:
 $$\begin{eqnarray}\displaystyle & & \displaystyle [2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})+2F^{\prime }-\unicode[STIX]{x1D702}F^{\prime \prime }]\hat{u} _{m,n}+2\hat{x}F^{\prime }{\displaystyle \frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\hat{x}}}-F{\displaystyle \frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}}+F^{\prime \prime }\hat{v}_{m,n}=-r_{t}(2\hat{x})\hat{l}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle [2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})+2F^{\prime }-\unicode[STIX]{x1D702}F^{\prime \prime }]\hat{u} _{m,n}+2\hat{x}F^{\prime }{\displaystyle \frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\hat{x}}}-F{\displaystyle \frac{\unicode[STIX]{x2202}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\hat{u} _{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}}+F^{\prime \prime }\hat{v}_{m,n}=-r_{t}(2\hat{x})\hat{l}_{m,n},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle [-\unicode[STIX]{x1D702}^{2}F^{\prime \prime }-\unicode[STIX]{x1D702}F^{\prime }+F+2(2\hat{x})^{3/2\;}G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}F^{\prime }]\hat{u} _{m,n}+[2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})+\!F^{\prime }+\unicode[STIX]{x1D702}F^{\prime \prime }]\hat{v}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,2\hat{x}F^{\prime }{\displaystyle \frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\hat{x}}}-F{\displaystyle \frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}-{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\hat{p}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}=-r_{t}(2\hat{x})\hat{e}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle [-\unicode[STIX]{x1D702}^{2}F^{\prime \prime }-\unicode[STIX]{x1D702}F^{\prime }+F+2(2\hat{x})^{3/2\;}G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}F^{\prime }]\hat{u} _{m,n}+[2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})+\!F^{\prime }+\unicode[STIX]{x1D702}F^{\prime \prime }]\hat{v}_{m,n}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,2\hat{x}F^{\prime }{\displaystyle \frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\hat{x}}}-F{\displaystyle \frac{\unicode[STIX]{x2202}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}-{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\hat{v}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\hat{p}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}=-r_{t}(2\hat{x})\hat{e}_{m,n},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle [2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2}){\hat{w}}_{m,n}]+2\hat{x}F^{\prime }{\displaystyle \frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\hat{x}}}-F^{\prime }{\displaystyle \frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,{\displaystyle \frac{\unicode[STIX]{x2202}^{2}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}}+2\hat{x}(\text{i}nk_{3}^{2})\hat{p}_{m,n}=-r_{t}(2\hat{x}){\hat{h}}_{m,n}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle [2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2}){\hat{w}}_{m,n}]+2\hat{x}F^{\prime }{\displaystyle \frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\hat{x}}}-F^{\prime }{\displaystyle \frac{\unicode[STIX]{x2202}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,{\displaystyle \frac{\unicode[STIX]{x2202}^{2}{\hat{w}}_{m,n}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}}+2\hat{x}(\text{i}nk_{3}^{2})\hat{p}_{m,n}=-r_{t}(2\hat{x}){\hat{h}}_{m,n}.\end{eqnarray}$$
In the above equations, we have put
 $$\begin{eqnarray}\displaystyle \hat{e}_{m,n} & = & \displaystyle \left\{\left(2\hat{x}\right)\frac{\unicode[STIX]{x2202}(\widehat{v_{a}u_{a}})}{\unicode[STIX]{x2202}\hat{x}}+3\widehat{v_{a}u_{a}}-\unicode[STIX]{x1D702}\frac{\unicode[STIX]{x2202}(\widehat{v_{a}u_{a}})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\unicode[STIX]{x2202}(\widehat{v_{a}v_{a}})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{1}{k_{3}}\frac{\unicode[STIX]{x2202}(\widehat{v_{a}w_{a}})}{\unicode[STIX]{x2202}z}+G_{\unicode[STIX]{x1D6EC}}\left(2\hat{x}\right)^{3/2}\unicode[STIX]{x1D712}\widehat{{u_{a}}^{2}}\right\}_{m,n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{e}_{m,n} & = & \displaystyle \left\{\left(2\hat{x}\right)\frac{\unicode[STIX]{x2202}(\widehat{v_{a}u_{a}})}{\unicode[STIX]{x2202}\hat{x}}+3\widehat{v_{a}u_{a}}-\unicode[STIX]{x1D702}\frac{\unicode[STIX]{x2202}(\widehat{v_{a}u_{a}})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\unicode[STIX]{x2202}(\widehat{v_{a}v_{a}})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}+\frac{1}{k_{3}}\frac{\unicode[STIX]{x2202}(\widehat{v_{a}w_{a}})}{\unicode[STIX]{x2202}z}+G_{\unicode[STIX]{x1D6EC}}\left(2\hat{x}\right)^{3/2}\unicode[STIX]{x1D712}\widehat{{u_{a}}^{2}}\right\}_{m,n},\end{eqnarray}$$
The new variables
![]() $(u_{a},v_{a},w_{a})$
are introduced for convenience of computation,
$(u_{a},v_{a},w_{a})$
are introduced for convenience of computation,
and the
![]() $\widehat{\qquad }$
symbol in the equations denotes Fourier transform. For
$\widehat{\qquad }$
symbol in the equations denotes Fourier transform. For
![]() $r_{t}\ll 1$
, the nonlinear terms in the NUBRE are of
$r_{t}\ll 1$
, the nonlinear terms in the NUBRE are of
![]() $O(r_{t}^{2})$
, and so the LUBRE are recovered by neglecting those terms (LWG, WZL). For
$O(r_{t}^{2})$
, and so the LUBRE are recovered by neglecting those terms (LWG, WZL). For
![]() $r_{t}=O(1)$
, the nonlinear terms in the streamwise and spanwise momentum equations are exactly the same as those in the flat-plate nonlinear problem (Ricco et al.
Reference Ricco, Luo and Wu2011), but the curved wall contributes an additional nonlinear terms
$r_{t}=O(1)$
, the nonlinear terms in the streamwise and spanwise momentum equations are exactly the same as those in the flat-plate nonlinear problem (Ricco et al.
Reference Ricco, Luo and Wu2011), but the curved wall contributes an additional nonlinear terms
![]() $G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}\widehat{u_{a}^{2}}$
(i.e.
$G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}\widehat{u_{a}^{2}}$
(i.e.
![]() $G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}\hat{u} ^{2}$
) in the normal-wall momentum equation.
$G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}\hat{u} ^{2}$
) in the normal-wall momentum equation.
2.2 Initial and outer boundary conditions
Since the velocity fluctuation induced in the boundary layer is of small amplitude near the leading edge, nonlinearity is weak in this region, and hence the initial condition remains the same as that in the linear case. For the special case, where the oncoming disturbance consists of a pair of oblique components, the upstream conditions can be expressed as (LWG, WZL)
 $$\begin{eqnarray}\displaystyle \hat{v}_{1,\pm 1} & \rightarrow & \displaystyle q_{\pm }\left\{V_{0}+(2\hat{x})^{1/2}V_{1}+\frac{\text{i}\text{e}^{\text{i}\hat{k}_{1}\hat{x}-\text{i}k_{2}(2\hat{x})^{1/2}\unicode[STIX]{x1D6FD}-(k_{3}^{2}+k_{2}^{2})\hat{x}}}{(k_{2}-\text{i}|k_{3}|)(2\hat{x})^{1/2}}[\text{e}^{\text{i}k_{2}(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}-\text{e}^{-|k_{3}|(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}]\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\text{e}^{-|k_{3}|(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}\left(\frac{\unicode[STIX]{x1D6FD}}{4}+\sqrt{2\hat{x}}c_{1}\right)-\bar{v}_{c}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{v}_{1,\pm 1} & \rightarrow & \displaystyle q_{\pm }\left\{V_{0}+(2\hat{x})^{1/2}V_{1}+\frac{\text{i}\text{e}^{\text{i}\hat{k}_{1}\hat{x}-\text{i}k_{2}(2\hat{x})^{1/2}\unicode[STIX]{x1D6FD}-(k_{3}^{2}+k_{2}^{2})\hat{x}}}{(k_{2}-\text{i}|k_{3}|)(2\hat{x})^{1/2}}[\text{e}^{\text{i}k_{2}(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}-\text{e}^{-|k_{3}|(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}]\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\text{e}^{-|k_{3}|(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}\left(\frac{\unicode[STIX]{x1D6FD}}{4}+\sqrt{2\hat{x}}c_{1}\right)-\bar{v}_{c}\right\},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\hat{w}}_{1,\pm 1} & \rightarrow & \displaystyle \mp \text{i}q_{\pm }\left\{W_{0}+(2\hat{x})^{1/2}W_{1}+{\displaystyle \frac{k_{2}\text{e}^{\text{i}\hat{k}_{1}\hat{x}-\text{i}k_{2}(2\hat{x})^{1/2}\unicode[STIX]{x1D6FD}-(k_{3}^{2}+k_{2}^{2})\hat{x}}}{(k_{2}-\text{i}|k_{3}|)}}[\text{e}^{\text{i}k_{2}(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}-\text{e}^{-|k_{3}|(2\hat{x})^{1/2\unicode[STIX]{x1D702}}}]\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\text{e}^{-|k_{3}|(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}\left[1-\unicode[STIX]{x1D6FD}\left(\text{i}(k_{2}+\text{i}|k_{3}|)+\frac{3}{4}|k_{3}|\right)\sqrt{2\hat{x}}\right]-\bar{w}_{c}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\hat{w}}_{1,\pm 1} & \rightarrow & \displaystyle \mp \text{i}q_{\pm }\left\{W_{0}+(2\hat{x})^{1/2}W_{1}+{\displaystyle \frac{k_{2}\text{e}^{\text{i}\hat{k}_{1}\hat{x}-\text{i}k_{2}(2\hat{x})^{1/2}\unicode[STIX]{x1D6FD}-(k_{3}^{2}+k_{2}^{2})\hat{x}}}{(k_{2}-\text{i}|k_{3}|)}}[\text{e}^{\text{i}k_{2}(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}-\text{e}^{-|k_{3}|(2\hat{x})^{1/2\unicode[STIX]{x1D702}}}]\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\text{e}^{-|k_{3}|(2\hat{x})^{1/2}\unicode[STIX]{x1D702}}\left[1-\unicode[STIX]{x1D6FD}\left(\text{i}(k_{2}+\text{i}|k_{3}|)+\frac{3}{4}|k_{3}|\right)\sqrt{2\hat{x}}\right]-\bar{w}_{c}\right\},\end{eqnarray}$$
as
![]() $\hat{x}\rightarrow 0$
, where
$\hat{x}\rightarrow 0$
, where
![]() $q_{\pm }=\pm \text{i}k_{3}(\hat{u} _{3,\pm }^{\infty }\pm \text{i}\hat{u} _{2,\pm }^{\infty })$
,
$q_{\pm }=\pm \text{i}k_{3}(\hat{u} _{3,\pm }^{\infty }\pm \text{i}\hat{u} _{2,\pm }^{\infty })$
,
The constant
![]() $c_{1}$
is obtained numerically along with
$c_{1}$
is obtained numerically along with
![]() $U_{k},V_{k}$
and
$U_{k},V_{k}$
and
![]() $W_{k}$
(
$W_{k}$
(
![]() $k=0,1$
) by solving the system (B 1)–(B 8) on page 200 in WZL. As in LWG and WZL, here we neglected the so-called ‘quasi two-dimensional’ particular solution as well as the homogeneous solution whose streamwise velocity behaves like
$k=0,1$
) by solving the system (B 1)–(B 8) on page 200 in WZL. As in LWG and WZL, here we neglected the so-called ‘quasi two-dimensional’ particular solution as well as the homogeneous solution whose streamwise velocity behaves like
![]() $x^{\unicode[STIX]{x1D70E}}$
(
$x^{\unicode[STIX]{x1D70E}}$
(
![]() $\unicode[STIX]{x1D70E}\approx 0.213$
). The latter is not excited by FSVD in the present context, but its nonlinear development (with an arbitrarily prescribed amplitude) and possible role in transition was studied by Martin et al. (Reference Martin, Martel, Paredes and Theofilis2015) and references therein.
$\unicode[STIX]{x1D70E}\approx 0.213$
). The latter is not excited by FSVD in the present context, but its nonlinear development (with an arbitrarily prescribed amplitude) and possible role in transition was studied by Martin et al. (Reference Martin, Martel, Paredes and Theofilis2015) and references therein.
The far-field condition is derived by considering the outer region IV. Similar to the flat-plate cases investigated by Wundrow & Goldstein (Reference Wundrow and Goldstein2001) and Ricco et al. (Reference Ricco, Luo and Wu2011), the perturbation in region IV is influenced by the viscous motion in region III through the displacement effect. It was shown there that the normal velocity has the asymptote
where
![]() $\bar{\unicode[STIX]{x1D6FF}}$
is the spanwise-averaged displacement thickness,
$\bar{\unicode[STIX]{x1D6FF}}$
is the spanwise-averaged displacement thickness,
The analysis of the outer region IV and its interaction with region III is presented in appendix A. Matching with the outer solution gives the far-field condition,
for
![]() $n\neq 0$
, where
$n\neq 0$
, where
![]() $v_{m,n}^{\dagger },w_{m,n}^{\dagger }$
and
$v_{m,n}^{\dagger },w_{m,n}^{\dagger }$
and
![]() $p_{m,n}^{\dagger }$
are given in appendix A.
$p_{m,n}^{\dagger }$
are given in appendix A.
For steady perturbations, the initial and far-field conditions can be further simplified. Since
![]() $\hat{k}_{1}$
is zero, only spanwise spectral components exist, and so
$\hat{k}_{1}$
is zero, only spanwise spectral components exist, and so
![]() $(\hat{u} _{-n},\hat{v}_{-n},{\hat{w}}_{-n},\hat{p}_{-n})=(\hat{u} _{n},\hat{u} _{n},{\hat{w}}_{n},\hat{p}_{n})_{cc}$
. The boundary conditions are matched with the outer solution in the same way as in the unsteady case.
$(\hat{u} _{-n},\hat{v}_{-n},{\hat{w}}_{-n},\hat{p}_{-n})=(\hat{u} _{n},\hat{u} _{n},{\hat{w}}_{n},\hat{p}_{n})_{cc}$
. The boundary conditions are matched with the outer solution in the same way as in the unsteady case.
The initial-boundary-value problem, consisting of (2.17)–(2.20), (2.25)–(2.27) and (2.31), governs the excitation, linear and nonlinear evolution of Görtler vortices in the presence of FSVD for the generic case of
![]() $G_{\unicode[STIX]{x1D6EC}}=O(1)$
. Several features of the formulation are worth emphasizing. First, the initial (upstream) and boundary conditions are interrelated, both being determined by FSVD. There is inherent consistency between them: the upstream limit (
$G_{\unicode[STIX]{x1D6EC}}=O(1)$
. Several features of the formulation are worth emphasizing. First, the initial (upstream) and boundary conditions are interrelated, both being determined by FSVD. There is inherent consistency between them: the upstream limit (
![]() $\hat{x}\rightarrow 0$
) of the latter matches the large-
$\hat{x}\rightarrow 0$
) of the latter matches the large-
![]() $y$
limit of the former. Second, throughout the entire course of development, including the fully developed phase when their streamwise velocity has acquired an
$y$
limit of the former. Second, throughout the entire course of development, including the fully developed phase when their streamwise velocity has acquired an
![]() $O(1)$
magnitude, Görtler vortices are continuingly influenced by FSVD via the forcing of the transverse velocities, that is, the boundary condition is as an inseparable part of the evolution just as the initial condition is. Finally, the viscous motion in the boundary layer is not a mere passive response to FSVD; it affects simultaneously the disturbances in the outer region as well.
$O(1)$
magnitude, Görtler vortices are continuingly influenced by FSVD via the forcing of the transverse velocities, that is, the boundary condition is as an inseparable part of the evolution just as the initial condition is. Finally, the viscous motion in the boundary layer is not a mere passive response to FSVD; it affects simultaneously the disturbances in the outer region as well.
3 Numerical method for NUBRE
3.1 Discretized equations
The initial-boundary-value problem, equations (2.17)–(2.20) supplemented by (2.25)–(2.27) and (2.31), is to be solved numerically by using appropriate finite-difference schemes.
For the purpose of computation, we define
![]() $\hat{f}=\hat{u} _{\unicode[STIX]{x1D702}}$
and
$\hat{f}=\hat{u} _{\unicode[STIX]{x1D702}}$
and
![]() ${\hat{g}}={\hat{w}}_{\unicode[STIX]{x1D702}}$
, and recast equations (2.17)–(2.20) into a system of first-order equations,
${\hat{g}}={\hat{w}}_{\unicode[STIX]{x1D702}}$
, and recast equations (2.17)–(2.20) into a system of first-order equations,
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\hat{u} _{\unicode[STIX]{x1D702}}=\hat{f},\quad \hat{v}_{\unicode[STIX]{x1D702}}=-2\hat{u} -\text{i}n{\hat{w}}+\unicode[STIX]{x1D702}\hat{f}-2\hat{x}\hat{u} _{\hat{x}},\quad {\hat{w}}_{\unicode[STIX]{x1D702}}={\hat{g}},\\ \hat{f}_{\unicode[STIX]{x1D702}}=[2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})+2F^{\prime }-\unicode[STIX]{x1D702}F^{\prime \prime }]\hat{u} +F^{\prime \prime }\hat{v}-F\hat{f}+2\hat{x}F^{\prime }\hat{u} _{\hat{x}}-\hat{l}_{m,n},\\ \hat{p}_{\unicode[STIX]{x1D702}}=[3\unicode[STIX]{x1D702}F^{\prime }-3F-2(2\hat{x})^{3/2}G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}F^{\prime }+\unicode[STIX]{x1D702}2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})]\hat{u} \\ +\,[-2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})-F^{\prime }]\hat{v}-\text{i}nF{\hat{w}}-\hat{f}-\text{i}n{\hat{g}}\\ +\,2\hat{x}(-F+\unicode[STIX]{x1D702}F^{\prime })\hat{u} _{\hat{x}}-2\hat{x}F^{\prime }\hat{v}_{\hat{x}}-2\hat{x}\hat{f}_{\hat{x}}-\unicode[STIX]{x1D702}\hat{l}_{m,n}+\hat{e}_{m,n},\\ {\hat{g}}_{\unicode[STIX]{x1D702}}=[2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})]{\hat{w}}+2\hat{x}(\text{i}nk_{3}^{2})\hat{p}-F^{\prime }{\hat{g}}+2\hat{x}F^{\prime }{\hat{w}}_{\hat{x}}-{\hat{h}}_{m,n},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\hat{u} _{\unicode[STIX]{x1D702}}=\hat{f},\quad \hat{v}_{\unicode[STIX]{x1D702}}=-2\hat{u} -\text{i}n{\hat{w}}+\unicode[STIX]{x1D702}\hat{f}-2\hat{x}\hat{u} _{\hat{x}},\quad {\hat{w}}_{\unicode[STIX]{x1D702}}={\hat{g}},\\ \hat{f}_{\unicode[STIX]{x1D702}}=[2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})+2F^{\prime }-\unicode[STIX]{x1D702}F^{\prime \prime }]\hat{u} +F^{\prime \prime }\hat{v}-F\hat{f}+2\hat{x}F^{\prime }\hat{u} _{\hat{x}}-\hat{l}_{m,n},\\ \hat{p}_{\unicode[STIX]{x1D702}}=[3\unicode[STIX]{x1D702}F^{\prime }-3F-2(2\hat{x})^{3/2}G_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D712}F^{\prime }+\unicode[STIX]{x1D702}2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})]\hat{u} \\ +\,[-2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})-F^{\prime }]\hat{v}-\text{i}nF{\hat{w}}-\hat{f}-\text{i}n{\hat{g}}\\ +\,2\hat{x}(-F+\unicode[STIX]{x1D702}F^{\prime })\hat{u} _{\hat{x}}-2\hat{x}F^{\prime }\hat{v}_{\hat{x}}-2\hat{x}\hat{f}_{\hat{x}}-\unicode[STIX]{x1D702}\hat{l}_{m,n}+\hat{e}_{m,n},\\ {\hat{g}}_{\unicode[STIX]{x1D702}}=[2\hat{x}(-\text{i}m\hat{k}_{1}+n^{2}k_{3}^{2})]{\hat{w}}+2\hat{x}(\text{i}nk_{3}^{2})\hat{p}-F^{\prime }{\hat{g}}+2\hat{x}F^{\prime }{\hat{w}}_{\hat{x}}-{\hat{h}}_{m,n},\end{array}\right\}\end{eqnarray}$$
which can be rewritten in a vector form,
where
![]() $\boldsymbol{U}=(\hat{u} ,\hat{v},{\hat{w}},\hat{f},\hat{p},{\hat{g}})$
is the solution vector,
$\boldsymbol{U}=(\hat{u} ,\hat{v},{\hat{w}},\hat{f},\hat{p},{\hat{g}})$
is the solution vector,
![]() $C_{0}$
and
$C_{0}$
and
![]() $C_{1}$
are the coefficient matrices and
$C_{1}$
are the coefficient matrices and
![]() $f(\boldsymbol{U})$
stands for nonlinear terms. For brevity, the subscripts ‘
$f(\boldsymbol{U})$
stands for nonlinear terms. For brevity, the subscripts ‘
![]() $m,n$
’ are omitted.
$m,n$
’ are omitted.
For components with
![]() $n=0$
,
$n=0$
,
![]() $\hat{u}$
and
$\hat{u}$
and
![]() $\hat{v}$
are decoupled from
$\hat{v}$
are decoupled from
![]() ${\hat{w}}$
, and the system (3.1) can be simplified to three equations for
${\hat{w}}$
, and the system (3.1) can be simplified to three equations for
![]() $\hat{u} ,\hat{v}$
and
$\hat{u} ,\hat{v}$
and
![]() $\hat{f}$
:
$\hat{f}$
:
and two equations for
![]() ${\hat{w}}$
and
${\hat{w}}$
and
![]() ${\hat{g}}$
,
${\hat{g}}$
,
The NUBRE are parabolic in the streamwise direction, and hence can be solved by a marching procedure in
![]() $\hat{x}$
-direction. The Malik scheme (Malik Reference Malik1990) is employed in
$\hat{x}$
-direction. The Malik scheme (Malik Reference Malik1990) is employed in
![]() $\unicode[STIX]{x1D702}$
-direction, and the second-order backward finite-difference scheme is applied in the streamwise direction, namely
$\unicode[STIX]{x1D702}$
-direction, and the second-order backward finite-difference scheme is applied in the streamwise direction, namely
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{U}_{j+1}-\boldsymbol{U}_{j}=\frac{h}{2}\left({\boldsymbol{U}^{\prime }}_{j+1}+{\boldsymbol{U}^{\prime }}_{j}\right),\\ \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{U}^{n+1}}{\unicode[STIX]{x2202}\hat{x}}=\left.\left[\frac{3}{2}\boldsymbol{U}^{n+1}-2\boldsymbol{U}^{n}+\frac{1}{2}\boldsymbol{U}^{n-1}\right]\right/\unicode[STIX]{x0394}\hat{x},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{U}_{j+1}-\boldsymbol{U}_{j}=\frac{h}{2}\left({\boldsymbol{U}^{\prime }}_{j+1}+{\boldsymbol{U}^{\prime }}_{j}\right),\\ \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{U}^{n+1}}{\unicode[STIX]{x2202}\hat{x}}=\left.\left[\frac{3}{2}\boldsymbol{U}^{n+1}-2\boldsymbol{U}^{n}+\frac{1}{2}\boldsymbol{U}^{n-1}\right]\right/\unicode[STIX]{x0394}\hat{x},\end{array}\right\}\end{eqnarray}$$
where
![]() $j$
and
$j$
and
![]() $n$
indicate the position of mesh points in the transverse and streamwise directions respectively. Grouping all terms at the streamwise location
$n$
indicate the position of mesh points in the transverse and streamwise directions respectively. Grouping all terms at the streamwise location
![]() $n+1$
on the left-hand side (except the nonlinear terms), we end up with the discrete equations,
$n+1$
on the left-hand side (except the nonlinear terms), we end up with the discrete equations,
where
![]() $\unicode[STIX]{x1D644}$
is the unit matrix, and we have put
$\unicode[STIX]{x1D644}$
is the unit matrix, and we have put
On introducing the discrete solution vector,
with
![]() $J$
being the number of mesh points in the wall-normal direction, the system of nonlinear algebraic equations, (3.6), is written in the matrix form,
$J$
being the number of mesh points in the wall-normal direction, the system of nonlinear algebraic equations, (3.6), is written in the matrix form,
where
![]() $\unicode[STIX]{x1D647}$
is the linear operator,
$\unicode[STIX]{x1D647}$
is the linear operator,
![]() $\boldsymbol{A}$
stands for the terms whose values are evaluated at upstream positions and
$\boldsymbol{A}$
stands for the terms whose values are evaluated at upstream positions and
![]() $\boldsymbol{N}_{n+1}$
denotes the nonlinear terms (see appendix B for their expressions). Only half of the Fourier modes needs to be computed since Fourier modes with negative indices
$\boldsymbol{N}_{n+1}$
denotes the nonlinear terms (see appendix B for their expressions). Only half of the Fourier modes needs to be computed since Fourier modes with negative indices
![]() $m$
can be evaluated by (2.15). The nonlinear terms are evaluated by applying the pseudo-spectral method, that is, the velocities in spectral space are transformed back to physical space, where multiplications are carried out, and then those products are Fourier transformed to obtain the nonlinear terms in spectral space. In order to prevent aliasing error, i.e. the spurious energy cascade from unresolved high-frequency modes into the resolved low-frequency ones, the 3/2-rule is applied (Kim, Moin & Moser Reference Kim, Moin and Moser1987). Seventeen Fourier modes are retained for capturing nonlinear effects. The domain size in the
$m$
can be evaluated by (2.15). The nonlinear terms are evaluated by applying the pseudo-spectral method, that is, the velocities in spectral space are transformed back to physical space, where multiplications are carried out, and then those products are Fourier transformed to obtain the nonlinear terms in spectral space. In order to prevent aliasing error, i.e. the spurious energy cascade from unresolved high-frequency modes into the resolved low-frequency ones, the 3/2-rule is applied (Kim, Moin & Moser Reference Kim, Moin and Moser1987). Seventeen Fourier modes are retained for capturing nonlinear effects. The domain size in the
![]() $\unicode[STIX]{x1D702}$
-direction is 30, within which 1000 grid points are deployed.
$\unicode[STIX]{x1D702}$
-direction is 30, within which 1000 grid points are deployed.
3.2 Solution procedure and validation of the algorithm
With the nonlinear terms being treated implicitly, the system (3.10) consists of nonlinear algebraic equations. It will be solved by using an iterative procedure involving a predictor–corrector and underrelaxation.
First, the nonlinear terms are evaluated by using the value at the previous streamwise point. This leads to a linear system of simultaneous equations,
in which the coefficient matrix
![]() $\unicode[STIX]{x1D647}$
is block tri-diagonal. This explicit method works when
$\unicode[STIX]{x1D647}$
is block tri-diagonal. This explicit method works when
![]() $G_{\unicode[STIX]{x1D6EC}}<20$
according to our computation, but fails to converge and a non-physical result appears when
$G_{\unicode[STIX]{x1D6EC}}<20$
according to our computation, but fails to converge and a non-physical result appears when
![]() $G_{\unicode[STIX]{x1D6EC}}>20$
.
$G_{\unicode[STIX]{x1D6EC}}>20$
.
An iteration method is thus applied in order to obtain the convergent solution. The
![]() $\unicode[STIX]{x1D6F7}_{n+1}^{\ast }$
predicted by the explicit scheme is used to re-evaluate the nonlinear terms. Then we solve the resulting equations to get a new value of
$\unicode[STIX]{x1D6F7}_{n+1}^{\ast }$
predicted by the explicit scheme is used to re-evaluate the nonlinear terms. Then we solve the resulting equations to get a new value of
![]() $\unicode[STIX]{x1D6F7}_{n+1}$
, which we use to compute
$\unicode[STIX]{x1D6F7}_{n+1}$
, which we use to compute
![]() $\boldsymbol{N}_{n+1}$
. This step is repeated, and the correct nonlinear terms and the solution are obtained when the difference between the two consecutive outcomes for
$\boldsymbol{N}_{n+1}$
. This step is repeated, and the correct nonlinear terms and the solution are obtained when the difference between the two consecutive outcomes for
![]() $\unicode[STIX]{x1D6F7}_{n+1}$
is less than a prescribed tolerance at all grid points. The non-physical result does not appear any more in the result, which is shown in symbols in figure 2(a). However, this iterative method is feasible only up to a certain streamwise position, beyond which it failed to converge, indicating that the predicted nonlinear terms are not suitable when the amplitude is sufficiently large and nonlinearity is strong.
$\unicode[STIX]{x1D6F7}_{n+1}$
is less than a prescribed tolerance at all grid points. The non-physical result does not appear any more in the result, which is shown in symbols in figure 2(a). However, this iterative method is feasible only up to a certain streamwise position, beyond which it failed to converge, indicating that the predicted nonlinear terms are not suitable when the amplitude is sufficiently large and nonlinearity is strong.

Figure 2. Comparison of the downstream development of the maximum streamwise velocity of different Fourier modes for
![]() $\unicode[STIX]{x1D716}=0.0001$
. (a) The results computed without the underrelaxation iteration (symbols) and with the underrelaxtion iteration (solid lines) for
$\unicode[STIX]{x1D716}=0.0001$
. (a) The results computed without the underrelaxation iteration (symbols) and with the underrelaxtion iteration (solid lines) for
![]() $G_{\unicode[STIX]{x1D6EC}}=1344$
and
$G_{\unicode[STIX]{x1D6EC}}=1344$
and
![]() $R_{\unicode[STIX]{x1D6EC}}=1222$
. (b) The results computed by using streamwise step
$R_{\unicode[STIX]{x1D6EC}}=1222$
. (b) The results computed by using streamwise step
![]() $\unicode[STIX]{x0394}\hat{x}=0.005$
(symbols) and
$\unicode[STIX]{x0394}\hat{x}=0.005$
(symbols) and
![]() $\unicode[STIX]{x0394}\hat{x}=0.001$
(solid lines) for
$\unicode[STIX]{x0394}\hat{x}=0.001$
(solid lines) for
![]() $G_{\unicode[STIX]{x1D6EC}}=1765$
and
$G_{\unicode[STIX]{x1D6EC}}=1765$
and
![]() $R_{\unicode[STIX]{x1D6EC}}=2298$
. The vertical dashed lines indicate the last streamwise position before the calculation without underrelaxation blows up.
$R_{\unicode[STIX]{x1D6EC}}=2298$
. The vertical dashed lines indicate the last streamwise position before the calculation without underrelaxation blows up.
Frequently, the convergence to a solution can be enhanced by a technique called underrelaxation, which was also used in solving the so-called parabolized stability equations (Zhao et al.
Reference Zhao, Zhang, Liu and Luo2016). We use the value of
![]() $\boldsymbol{N}_{n}$
obtained at the previous location, and
$\boldsymbol{N}_{n}$
obtained at the previous location, and
![]() $\boldsymbol{N}_{n+1}^{\ast }$
obtained by using
$\boldsymbol{N}_{n+1}^{\ast }$
obtained by using
![]() $\unicode[STIX]{x1D6F7}_{n+1}^{\ast }$
, to extrapolate a value for
$\unicode[STIX]{x1D6F7}_{n+1}^{\ast }$
, to extrapolate a value for
![]() $\hat{\boldsymbol{N}}_{n+1}$
as follows:
$\hat{\boldsymbol{N}}_{n+1}$
as follows:
where
![]() $0<\unicode[STIX]{x1D71B}<1$
is the parameter controlling underrelaxation, and
$0<\unicode[STIX]{x1D71B}<1$
is the parameter controlling underrelaxation, and
![]() $\hat{\boldsymbol{N}}_{n+1}$
is the new nonlinear terms for the next iterative step. Hence, our predictor–corrector procedure follows the steps below.
$\hat{\boldsymbol{N}}_{n+1}$
is the new nonlinear terms for the next iterative step. Hence, our predictor–corrector procedure follows the steps below.
Step 1: The nonlinear terms
![]() $\boldsymbol{N}_{n}$
is evaluated by using the value of
$\boldsymbol{N}_{n}$
is evaluated by using the value of
![]() $\unicode[STIX]{x1D731}_{n}$
at the last streamwise location.
$\unicode[STIX]{x1D731}_{n}$
at the last streamwise location.
Step 2: An estimated value of
![]() $\unicode[STIX]{x1D731}_{n+1}^{(i)}$
is obtained by solving the tri-diagonal form of the equations, and
$\unicode[STIX]{x1D731}_{n+1}^{(i)}$
is obtained by solving the tri-diagonal form of the equations, and
![]() $\unicode[STIX]{x1D731}_{n+1}^{(i)}$
is utilized to obtain upgraded nonlinear terms
$\unicode[STIX]{x1D731}_{n+1}^{(i)}$
is utilized to obtain upgraded nonlinear terms
![]() $\boldsymbol{N}_{n+1}^{(i)}$
, where
$\boldsymbol{N}_{n+1}^{(i)}$
, where
![]() $i$
refers to the number of iterations. Using
$i$
refers to the number of iterations. Using
![]() $\boldsymbol{N}_{(n+1)}^{(i+1)}=\boldsymbol{N}_{n}+\unicode[STIX]{x1D71B}(\boldsymbol{N}_{n+1}^{(i)}-\boldsymbol{N}_{n})$
, we can update the value of
$\boldsymbol{N}_{(n+1)}^{(i+1)}=\boldsymbol{N}_{n}+\unicode[STIX]{x1D71B}(\boldsymbol{N}_{n+1}^{(i)}-\boldsymbol{N}_{n})$
, we can update the value of
![]() $\unicode[STIX]{x1D731}_{n+1}$
, which is written as
$\unicode[STIX]{x1D731}_{n+1}$
, which is written as
![]() $\unicode[STIX]{x1D731}_{n+1}^{(i+1)}$
.
$\unicode[STIX]{x1D731}_{n+1}^{(i+1)}$
.
Step 3: Repeat step 2 until the amplitude of every Fourier mode converges. A satisfactory convergence is achieved rather rapidly by this method by choosing
![]() $\unicode[STIX]{x1D71B}=0.2$
.
$\unicode[STIX]{x1D71B}=0.2$
.
Different streamwise step lengths are also chosen to ensure convergence and accuracy of the solutions. Our numerical results indicate that the streamwise step needs to be reduced when the Görtler number is large. For instance, when
![]() $\unicode[STIX]{x0394}\hat{x}=0.005$
the computation converges for
$\unicode[STIX]{x0394}\hat{x}=0.005$
the computation converges for
![]() $G_{\unicode[STIX]{x1D6EC}}=1344$
as shown in figure 2(a), but diverges for
$G_{\unicode[STIX]{x1D6EC}}=1344$
as shown in figure 2(a), but diverges for
![]() $G_{\unicode[STIX]{x1D6EC}}=1765$
, which requires a smaller step size
$G_{\unicode[STIX]{x1D6EC}}=1765$
, which requires a smaller step size
![]() $\unicode[STIX]{x0394}\hat{x}=0.001$
. A comparison of the results using these two step sizes for
$\unicode[STIX]{x0394}\hat{x}=0.001$
. A comparison of the results using these two step sizes for
![]() $G_{\unicode[STIX]{x1D6EC}}=1765$
is displayed in figure 2(b). In all our calculations, we set
$G_{\unicode[STIX]{x1D6EC}}=1765$
is displayed in figure 2(b). In all our calculations, we set
![]() $\unicode[STIX]{x1D712}=1$
since the curved plates in experiments often have a constant curvature.
$\unicode[STIX]{x1D712}=1$
since the curved plates in experiments often have a constant curvature.

Figure 3. Validation of numerical algorithm and code. (a) Comparison of the downstream development of the maximum streamwise velocity of Görtler vortices with the linear results of WZL. The parameters are
![]() $G_{\unicode[STIX]{x1D6EC}}=1804$
,
$G_{\unicode[STIX]{x1D6EC}}=1804$
,
![]() $R_{\unicode[STIX]{x1D6EC}}=2192,\unicode[STIX]{x1D716}=7.0\times 10^{-7}$
and
$R_{\unicode[STIX]{x1D6EC}}=2192,\unicode[STIX]{x1D716}=7.0\times 10^{-7}$
and
![]() $G_{\unicode[STIX]{x1D6EC}}=1344,R_{\unicode[STIX]{x1D6EC}}=1222,\unicode[STIX]{x1D716}=7.0\times 10^{-6}$
. (b) Comparison of the nonlinear development of
$G_{\unicode[STIX]{x1D6EC}}=1344,R_{\unicode[STIX]{x1D6EC}}=1222,\unicode[STIX]{x1D716}=7.0\times 10^{-6}$
. (b) Comparison of the nonlinear development of
![]() $\max u_{rms}^{\prime }$
, the maximum root mean square of the time-dependent streamwise velocity of streaks (symbols), with the results of Ricco et al. (Reference Ricco, Luo and Wu2011) (lines) for fixed
$\max u_{rms}^{\prime }$
, the maximum root mean square of the time-dependent streamwise velocity of streaks (symbols), with the results of Ricco et al. (Reference Ricco, Luo and Wu2011) (lines) for fixed
![]() $\hat{k}_{1}=2$
, but different
$\hat{k}_{1}=2$
, but different
![]() $\unicode[STIX]{x1D716}=0.005$
(triangle and solid line), 0.01 (circle and dashed lines) and 0.015 (square and dash-dotted lines).
$\unicode[STIX]{x1D716}=0.005$
(triangle and solid line), 0.01 (circle and dashed lines) and 0.015 (square and dash-dotted lines).
In order to validate our code, two tests are carried out.
-
(i) Our code is designed primarily for nonlinear problems, but it must be able to reproduce the linear solution when
 $r_{t}\ll 1$
. The results obtained by the present method are compared in figure 3(a) with the linear results of WZL, shown in figure 11 of their paper. The parameters adopted are
$r_{t}\ll 1$
. The results obtained by the present method are compared in figure 3(a) with the linear results of WZL, shown in figure 11 of their paper. The parameters adopted are
 $R_{\unicode[STIX]{x1D6EC}}=1804,G_{\unicode[STIX]{x1D6EC}}=2192$
and
$R_{\unicode[STIX]{x1D6EC}}=1804,G_{\unicode[STIX]{x1D6EC}}=2192$
and
 $\unicode[STIX]{x1D716}=7.0\times 10^{-7}$
, and
$\unicode[STIX]{x1D716}=7.0\times 10^{-7}$
, and
 $R_{\unicode[STIX]{x1D6EC}}=1344$
,
$R_{\unicode[STIX]{x1D6EC}}=1344$
,
 $G_{\unicode[STIX]{x1D6EC}}=1222$
and
$G_{\unicode[STIX]{x1D6EC}}=1222$
and
 $\unicode[STIX]{x1D716}=7.0\times 10^{-6}$
. The linear result was rescaled to fit the nonlinear result at the first location. Excellent agreement is seen for the entire development of the maximum streamwise velocity as well as for the growth rate of steady vortices.
$\unicode[STIX]{x1D716}=7.0\times 10^{-6}$
. The linear result was rescaled to fit the nonlinear result at the first location. Excellent agreement is seen for the entire development of the maximum streamwise velocity as well as for the growth rate of steady vortices. -
(ii) Our code pertains to a boundary layer over a concave wall with
 $G_{\unicode[STIX]{x1D6EC}}>0$
. When
$G_{\unicode[STIX]{x1D6EC}}>0$
. When
 $G_{\unicode[STIX]{x1D6EC}}=0$
, it should be able to reproduce the results for the flat-plate case, which was computed by Ricco et al. (Reference Ricco, Luo and Wu2011) using a scheme entirely different from ours. The intensity of streaks or Görtler vortices is represented by the root mean square (r.m.s.) of the streamwise velocity, defined as (see Pope 2000, p. 687) (3.13)In order to measure time-dependent components, we also introduce
$G_{\unicode[STIX]{x1D6EC}}=0$
, it should be able to reproduce the results for the flat-plate case, which was computed by Ricco et al. (Reference Ricco, Luo and Wu2011) using a scheme entirely different from ours. The intensity of streaks or Görtler vortices is represented by the root mean square (r.m.s.) of the streamwise velocity, defined as (see Pope 2000, p. 687) (3.13)In order to measure time-dependent components, we also introduce $$\begin{eqnarray}u_{rms}\equiv r_{t}\left[\mathop{\sum }_{m,n}|2\hat{x}\hat{u} _{m,n}|^{2}\right]^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}u_{rms}\equiv r_{t}\left[\mathop{\sum }_{m,n}|2\hat{x}\hat{u} _{m,n}|^{2}\right]^{1/2}.\end{eqnarray}$$
 $u_{rms}^{\prime }$
, which has the same expression as
$u_{rms}^{\prime }$
, which has the same expression as
 $u_{rms}$
except that the zero-frequency components are excluded in the summation. The downstream development of
$u_{rms}$
except that the zero-frequency components are excluded in the summation. The downstream development of
 $\max u_{rms}^{\prime }$
for three different values of
$\max u_{rms}^{\prime }$
for three different values of
 $\unicode[STIX]{x1D716}$
is compared in figure 3(b), and an excellent agreement is seen for all three cases. This gives us the confidence that our code can correctly predict the nonlinear evolution of streaks or Görtler vortices.
$\unicode[STIX]{x1D716}$
is compared in figure 3(b), and an excellent agreement is seen for all three cases. This gives us the confidence that our code can correctly predict the nonlinear evolution of streaks or Görtler vortices.
4 Numerical results and quantitative comparisons with experiments
The initial-boundary-value problem is solved numerically using the method described in the previous section. Our theoretical predictions will be compared with the data from several experiments. The boundary layer is perturbed by a broad band of turbulent disturbances in experiments, while in our formulation free-stream disturbance is represented by a pair of convected gusts. Fortunately, vortices in the boundary layer typically exhibit a well-defined spanwise spacing
![]() $\unicode[STIX]{x1D6EC}$
. It is therefore reasonable to suggest that these vortices were excited by a pair of dominant oblique components in FST. In our asymptotic formulation, there are three parameters, the rescaled frequency
$\unicode[STIX]{x1D6EC}$
. It is therefore reasonable to suggest that these vortices were excited by a pair of dominant oblique components in FST. In our asymptotic formulation, there are three parameters, the rescaled frequency
![]() $\hat{k}_{1}$
, the wall-normal wavenumber
$\hat{k}_{1}$
, the wall-normal wavenumber
![]() $k_{2}$
and
$k_{2}$
and
![]() $r_{t}=\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}$
. The solutions for the vortices, obtained under the assumptions of
$r_{t}=\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}$
. The solutions for the vortices, obtained under the assumptions of
![]() $\unicode[STIX]{x1D716}\ll 1$
and
$\unicode[STIX]{x1D716}\ll 1$
and
![]() $R_{\unicode[STIX]{x1D6EC}}\gg 1$
with
$R_{\unicode[STIX]{x1D6EC}}\gg 1$
with
![]() $r_{t}=O(1)$
, will be applied to experiments, where
$r_{t}=O(1)$
, will be applied to experiments, where
![]() $R_{\unicode[STIX]{x1D6EC}}$
is finite and its values can be calculated using the observed value of
$R_{\unicode[STIX]{x1D6EC}}$
is finite and its values can be calculated using the observed value of
![]() $\unicode[STIX]{x1D6EC}$
. However, the FSVD amplitude
$\unicode[STIX]{x1D6EC}$
. However, the FSVD amplitude
![]() $\unicode[STIX]{x1D716}$
is not known, and so has to be determined by fitting the predicted amplitude at one streamwise location with the measured value.
$\unicode[STIX]{x1D716}$
is not known, and so has to be determined by fitting the predicted amplitude at one streamwise location with the measured value.
Table 1. The parameters and measurement locations in the experiments of Swearingen & Blackwelder (Reference Swearingen and Blackwelder1987), Ito (Reference Ito1985) and Mitsudharmadi et al. (Reference Mitsudharmadi, Winoto and Shah2005).

4.1 Comparison with Swearingen and Blackweld (1987)
SB studied the growth, breakdown and transition to turbulence of Görtler vortices by means of smoke-wire visualization and multiple-probe hot-wire measurements in a low-speed wind tunnel. The free-stream velocity
![]() $U_{\infty }=5~\text{ms}^{-1}$
and the boundary layer developed over a concave wall with a radius of curvature
$U_{\infty }=5~\text{ms}^{-1}$
and the boundary layer developed over a concave wall with a radius of curvature
![]() $r_{0}^{\ast }=3.20$
m. The spanwise wavelength of the Görtler vortices was
$r_{0}^{\ast }=3.20$
m. The spanwise wavelength of the Görtler vortices was
![]() $\unicode[STIX]{x1D706}_{z}\approx 2.3$
cm. These values are used to calculate the non-dimensional parameters,
$\unicode[STIX]{x1D706}_{z}\approx 2.3$
cm. These values are used to calculate the non-dimensional parameters,
![]() $R_{\unicode[STIX]{x1D6EC}}=U_{\infty }\unicode[STIX]{x1D706}_{z}/(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D708})=1145$
and
$R_{\unicode[STIX]{x1D6EC}}=U_{\infty }\unicode[STIX]{x1D706}_{z}/(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D708})=1145$
and
![]() $G_{\unicode[STIX]{x1D6EC}}=R_{\unicode[STIX]{x1D6EC}}^{2}\unicode[STIX]{x1D706}_{z}/(2\unicode[STIX]{x03C0}r_{0}^{\ast })=1501$
, where the kinematic viscosity coefficient of dry air
$G_{\unicode[STIX]{x1D6EC}}=R_{\unicode[STIX]{x1D6EC}}^{2}\unicode[STIX]{x1D706}_{z}/(2\unicode[STIX]{x03C0}r_{0}^{\ast })=1501$
, where the kinematic viscosity coefficient of dry air
![]() $\unicode[STIX]{x1D708}=1.6\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
is taken. The non-dimensional streamwise distance
$\unicode[STIX]{x1D708}=1.6\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
is taken. The non-dimensional streamwise distance
![]() $\hat{x}$
is calculated by the relation
$\hat{x}$
is calculated by the relation
The corresponding Reynolds and Görtler numbers as well as the non-dimensional streamwise locations of measurement are listed in table 1. We focus on the steady components
![]() $k_{1}=0$
, and take
$k_{1}=0$
, and take
![]() $\hat{u} _{3,\pm }^{\infty }=\pm 1$
and
$\hat{u} _{3,\pm }^{\infty }=\pm 1$
and
![]() $k_{2}=k_{3}=1$
, since the perturbation is likely to be isotropic. It follows that
$k_{2}=k_{3}=1$
, since the perturbation is likely to be isotropic. It follows that
![]() $\hat{u} _{2,\pm 1}^{\infty }=-1.0$
. The computation domain starts from
$\hat{u} _{2,\pm 1}^{\infty }=-1.0$
. The computation domain starts from
![]() $\hat{x}=0.001$
.
$\hat{x}=0.001$
.

Figure 4. Comparison of the downstream development of
![]() $\max u_{rms}$
for (a) fixed
$\max u_{rms}$
for (a) fixed
![]() $G_{\unicode[STIX]{x1D6EC}}$
but different values of
$G_{\unicode[STIX]{x1D6EC}}$
but different values of
![]() $\unicode[STIX]{x1D716}$
and (b) fixed
$\unicode[STIX]{x1D716}$
and (b) fixed
![]() $\unicode[STIX]{x1D716}$
but different values of
$\unicode[STIX]{x1D716}$
but different values of
![]() $G_{\unicode[STIX]{x1D6EC}}$
.
$G_{\unicode[STIX]{x1D6EC}}$
.
The two important parameters are
![]() $\unicode[STIX]{x1D716}$
and
$\unicode[STIX]{x1D716}$
and
![]() $G_{\unicode[STIX]{x1D6EC}}$
. In order to demonstrate their role, we solved the initial-boundary-value problems for several
$G_{\unicode[STIX]{x1D6EC}}$
. In order to demonstrate their role, we solved the initial-boundary-value problems for several
![]() $\unicode[STIX]{x1D716}$
and
$\unicode[STIX]{x1D716}$
and
![]() $G_{\unicode[STIX]{x1D6EC}}$
. We choose to measure the intensity of vortices by
$G_{\unicode[STIX]{x1D6EC}}$
. We choose to measure the intensity of vortices by
![]() $u_{rms}$
, the r.m.s of all harmonic components (as defined by (3.13) but with the double summation reducing to a single sum for the present steady limit). Figure 4(a) shows the downstream development of
$u_{rms}$
, the r.m.s of all harmonic components (as defined by (3.13) but with the double summation reducing to a single sum for the present steady limit). Figure 4(a) shows the downstream development of
![]() $\max u_{rms}$
for
$\max u_{rms}$
for
![]() $G_{\unicode[STIX]{x1D6EC}}=1501$
and four different values of
$G_{\unicode[STIX]{x1D6EC}}=1501$
and four different values of
![]() $\unicode[STIX]{x1D716}$
. The flat-plate case (
$\unicode[STIX]{x1D716}$
. The flat-plate case (
![]() $G_{\unicode[STIX]{x1D6EC}}=0$
) is also computed for comparison. When
$G_{\unicode[STIX]{x1D6EC}}=0$
) is also computed for comparison. When
![]() $\hat{x}\rightarrow 0$
, the centrifugal force vanishes, and so the solutions for
$\hat{x}\rightarrow 0$
, the centrifugal force vanishes, and so the solutions for
![]() $G_{\unicode[STIX]{x1D6EC}}=1501$
and
$G_{\unicode[STIX]{x1D6EC}}=1501$
and
![]() $G_{\unicode[STIX]{x1D6EC}}=0$
overlap for each value of
$G_{\unicode[STIX]{x1D6EC}}=0$
overlap for each value of
![]() $\unicode[STIX]{x1D716}$
. The centrifugal effect influences the evolution of the disturbance weakly in the range of
$\unicode[STIX]{x1D716}$
. The centrifugal effect influences the evolution of the disturbance weakly in the range of
![]() $\hat{x}=0.03-0.05$
. As
$\hat{x}=0.03-0.05$
. As
![]() $\unicode[STIX]{x1D716}$
increases, the response to the FSVD becomes stronger, and Görtler vortices and streaks saturate more quickly. For the case of strongest FSVD,
$\unicode[STIX]{x1D716}$
increases, the response to the FSVD becomes stronger, and Görtler vortices and streaks saturate more quickly. For the case of strongest FSVD,
![]() $\unicode[STIX]{x1D716}=0.035$
(which is characteristic of turbomachinery flow conditions), the linear amplification stage of Görtler vortices almost disappears, which means that it would be completely inappropriate to use local eigenmodes as initial conditions for integrating NUBRE. Interestingly, in the case of
$\unicode[STIX]{x1D716}=0.035$
(which is characteristic of turbomachinery flow conditions), the linear amplification stage of Görtler vortices almost disappears, which means that it would be completely inappropriate to use local eigenmodes as initial conditions for integrating NUBRE. Interestingly, in the case of
![]() $G_{\unicode[STIX]{x1D6EC}}\neq 0$
,
$G_{\unicode[STIX]{x1D6EC}}\neq 0$
,
![]() $u_{rms}$
eventually saturates at almost the same level for different values of
$u_{rms}$
eventually saturates at almost the same level for different values of
![]() $\unicode[STIX]{x1D716}$
, suggesting that the saturated state is an intrinsic property of the boundary-layer flow. This is however not the case for the flat-plate boundary layer. The responses of boundary layer to FSVD with
$\unicode[STIX]{x1D716}$
, suggesting that the saturated state is an intrinsic property of the boundary-layer flow. This is however not the case for the flat-plate boundary layer. The responses of boundary layer to FSVD with
![]() $\unicode[STIX]{x1D716}=0.0007$
are compared for different
$\unicode[STIX]{x1D716}=0.0007$
are compared for different
![]() $G_{\unicode[STIX]{x1D6EC}}$
in figure 4(b). It is found that
$G_{\unicode[STIX]{x1D6EC}}$
in figure 4(b). It is found that
![]() $u_{rms}$
with a larger
$u_{rms}$
with a larger
![]() $G_{\unicode[STIX]{x1D6EC}}$
has a greater linear growth rate as expected, and saturates at a higher level. In the limit of large Görtler number, an asymptotic theory for the fully nonlinear stage was proposed by Hall & Lakin (Reference Hall and Lakin1988), but a direct comparison is beyond the scope of the present study.
$G_{\unicode[STIX]{x1D6EC}}$
has a greater linear growth rate as expected, and saturates at a higher level. In the limit of large Görtler number, an asymptotic theory for the fully nonlinear stage was proposed by Hall & Lakin (Reference Hall and Lakin1988), but a direct comparison is beyond the scope of the present study.

Figure 5. The downstream development of
![]() $\max u_{1,rms}$
, the r.m.s. of the spanwise-dependent streamwise velocity: the solid line represents the theoretical prediction; the squares symbols indicate the experimental measurement of the steady components (SB), whereas the circle symbols indicate the unsteady contribution.
$\max u_{1,rms}$
, the r.m.s. of the spanwise-dependent streamwise velocity: the solid line represents the theoretical prediction; the squares symbols indicate the experimental measurement of the steady components (SB), whereas the circle symbols indicate the unsteady contribution.
The intensity of FSVD is controlled by
![]() $\unicode[STIX]{x1D716}$
, but an alternative and more common measure is turbulence level
$\unicode[STIX]{x1D716}$
, but an alternative and more common measure is turbulence level
![]() $Tu$
. For the assumed form of perturbations, equation (2.5), the two are related by the equation:
$Tu$
. For the assumed form of perturbations, equation (2.5), the two are related by the equation:
![]() $Tu=2\unicode[STIX]{x1D716}(\hat{u} _{1}^{\infty 2}+\hat{u} _{2}^{\infty 2}+\hat{u} _{3}^{\infty 2})^{1/2}/\sqrt{3}$
. Our theory shows that the streamwise velocity
$Tu=2\unicode[STIX]{x1D716}(\hat{u} _{1}^{\infty 2}+\hat{u} _{2}^{\infty 2}+\hat{u} _{3}^{\infty 2})^{1/2}/\sqrt{3}$
. Our theory shows that the streamwise velocity
![]() $\hat{u} _{1}^{\infty }$
does not play a leading-order role, suggesting that a modified form involving only the transverse velocities,
$\hat{u} _{1}^{\infty }$
does not play a leading-order role, suggesting that a modified form involving only the transverse velocities,
![]() $Tu^{\dagger }=2\unicode[STIX]{x1D716}(\hat{u} _{2}^{\infty 2}+\hat{u} _{3}^{\infty 2})^{1/2}/\sqrt{2}$
, is a more appropriate characterization. We choose
$Tu^{\dagger }=2\unicode[STIX]{x1D716}(\hat{u} _{2}^{\infty 2}+\hat{u} _{3}^{\infty 2})^{1/2}/\sqrt{2}$
, is a more appropriate characterization. We choose
![]() $\unicode[STIX]{x1D716}=0.0007$
in order to fit the measured streamwise velocity at the first location of measurement, and correspondingly
$\unicode[STIX]{x1D716}=0.0007$
in order to fit the measured streamwise velocity at the first location of measurement, and correspondingly
![]() $Tu^{\dagger }=0.14\,\%$
, and
$Tu^{\dagger }=0.14\,\%$
, and
![]() $Tu=0.14\,\%$
as well if one takes
$Tu=0.14\,\%$
as well if one takes
![]() $\hat{u} _{1}^{\infty }=1$
. In the experiment of SB, the FTS level was lower than
$\hat{u} _{1}^{\infty }=1$
. In the experiment of SB, the FTS level was lower than
![]() $0.07\,\%$
, but it most likely refers to unsteady fluctuations rather than steady components. Indeed SB stated that transverse variations of the steady flow were less than
$0.07\,\%$
, but it most likely refers to unsteady fluctuations rather than steady components. Indeed SB stated that transverse variations of the steady flow were less than
![]() $0.5\,\%$
. We believe that it is this part of the perturbation that excites Görtler vortices, but further detailed experiments are needed to characterize it.
$0.5\,\%$
. We believe that it is this part of the perturbation that excites Görtler vortices, but further detailed experiments are needed to characterize it.

Figure 6. Comparison of iso-
![]() $U$
contours at different streamwise locations: (a) theoretical prediction; (b) measurements of SB. The iso-
$U$
contours at different streamwise locations: (a) theoretical prediction; (b) measurements of SB. The iso-
![]() $U$
contours are plotted with an increment of 0.10
$U$
contours are plotted with an increment of 0.10
![]() $U_{\infty }$
as were the measurements of SB.
$U_{\infty }$
as were the measurements of SB.
As in the experiment of SB, we monitor the r.m.s. of the spanwise-dependent components in the streamwise velocity, defined as
 $$\begin{eqnarray}u_{1,rms}\equiv r_{t}\left[\mathop{\sum }_{n\neq 0}|2\hat{x}\hat{u} _{n}|^{2}\right]^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}u_{1,rms}\equiv r_{t}\left[\mathop{\sum }_{n\neq 0}|2\hat{x}\hat{u} _{n}|^{2}\right]^{1/2}.\end{eqnarray}$$
Note that the spanwise uniform mean-flow distortion is excluded. We compare the development of the computed
![]() $u_{1,rms}$
with the measurements of SB in figure 5. A perfect agreement is obtained up to
$u_{1,rms}$
with the measurements of SB in figure 5. A perfect agreement is obtained up to
![]() $\hat{x}=0.24$
. The r.m.s. of the fluctuations experiences an initial non-modal growth and then amplifies exponentially as indicated by the logarithmic scale of the figure. Nonlinear interactions take effect from approximately
$\hat{x}=0.24$
. The r.m.s. of the fluctuations experiences an initial non-modal growth and then amplifies exponentially as indicated by the logarithmic scale of the figure. Nonlinear interactions take effect from approximately
![]() $\hat{x}\approx 0.17$
. Disagreement is noted after
$\hat{x}\approx 0.17$
. Disagreement is noted after
![]() $\hat{x}=0.26$
, where secondary instability of Görtler vortices may have sufficiently developed, and high-frequency fluctuations become strong enough to interact nonlinearly to affect the evolution of the primary vortices (Girgis & Liu Reference Girgis and Liu2006). Disturbances in the experiments of SB contained time-dependent fluctuations. The unsteady contribution was obtained by subtracting the steady signals from the measured spanwise mean. The r.m.s. of unsteady fluctuations increases with
$\hat{x}=0.26$
, where secondary instability of Görtler vortices may have sufficiently developed, and high-frequency fluctuations become strong enough to interact nonlinearly to affect the evolution of the primary vortices (Girgis & Liu Reference Girgis and Liu2006). Disturbances in the experiments of SB contained time-dependent fluctuations. The unsteady contribution was obtained by subtracting the steady signals from the measured spanwise mean. The r.m.s. of unsteady fluctuations increases with
![]() $\hat{x}$
, but remains much smaller than that of steady vortices before
$\hat{x}$
, but remains much smaller than that of steady vortices before
![]() $\hat{x}=0.215$
(
$\hat{x}=0.215$
(
![]() $x^{\ast }=90$
cm). Unsteady perturbations apparently experienced fast exponential growth in the range of
$x^{\ast }=90$
cm). Unsteady perturbations apparently experienced fast exponential growth in the range of
![]() $\hat{x}=0.22$
–
$\hat{x}=0.22$
–
![]() $0.26$
, as indicated by the dashed line in figure 5. This issue will be discussed in connection with secondary instability of Görtler vortices.
$0.26$
, as indicated by the dashed line in figure 5. This issue will be discussed in connection with secondary instability of Görtler vortices.
Of particular interest is the streamwise velocity of the distorted boundary layer,
Contours of the predicted and measured
![]() $U$
in the cross-section (the
$U$
in the cross-section (the
![]() $y$
–
$y$
–
![]() $z$
plane) are displayed in figure 6 for comparison. The similarity variable
$z$
plane) are displayed in figure 6 for comparison. The similarity variable
![]() $\unicode[STIX]{x1D702}$
is related to the dimensional coordinate
$\unicode[STIX]{x1D702}$
is related to the dimensional coordinate
![]() $y^{\ast }$
via the relation
$y^{\ast }$
via the relation
The contours evolved into a mushroom-like structure, as was predicted by previous calculations (Hall Reference Hall1988; Lee & Liu Reference Lee and Liu1992; Li & Malik Reference Li and Malik1995). The present comparisons show that not only the intensity but also the shape of Görtler vortices are in good agreement up to
![]() $\hat{x}=0.238$
(
$\hat{x}=0.238$
(
![]() $x^{\ast }=100$
cm). The gross feature of vortices remains similar for
$x^{\ast }=100$
cm). The gross feature of vortices remains similar for
![]() $\hat{x}\geqslant 0.262$
(
$\hat{x}\geqslant 0.262$
(
![]() $x^{\ast }\geqslant 110$
cm), but the measured contours appear smoother. This is probably an indication that secondary instability has truly developed by
$x^{\ast }\geqslant 110$
cm), but the measured contours appear smoother. This is probably an indication that secondary instability has truly developed by
![]() $\hat{x}=0.262$
with the resulting high-frequency fluctuations affecting Görtler vortices through the Reynolds stresses (Girgis & Liu Reference Girgis and Liu2006).
$\hat{x}=0.262$
with the resulting high-frequency fluctuations affecting Görtler vortices through the Reynolds stresses (Girgis & Liu Reference Girgis and Liu2006).
Figure 7 displays the profiles of the streamwise velocity at different downstream locations and the two spanwise positions corresponding to a peak and a valley. A valley/peak refers to a low-/high-speed region, where the velocity exhibits a deficit/excess from the Blasius flow, respectively, We make comparison at these positions since only limited data were given by SB. There is a perfect agreement at every streamwise measurement location except at the valley of
![]() $\hat{x}=0.191$
(
$\hat{x}=0.191$
(
![]() $x^{\ast }=80$
cm). The reason for this discrepancy remains unclear.
$x^{\ast }=80$
cm). The reason for this discrepancy remains unclear.

Figure 7. Comparison of the predicted streamwise velocity profiles with the experimental measurements (SB 1987) at the spanwise positions corresponding to a valley (a) and a peak (b). Solid lines, theoretical predictions; symbols, experimental results. The parameters are
![]() $G_{\unicode[STIX]{x1D6EC}}=1501$
and
$G_{\unicode[STIX]{x1D6EC}}=1501$
and
![]() $R_{\unicode[STIX]{x1D6EC}}=1145$
.
$R_{\unicode[STIX]{x1D6EC}}=1145$
.

Figure 8. Comparisons of the predicted displacement thickness (a) and the skin friction (b) with the experimental measurements (SB 1987). Lines: theoretical results; circles: experimental measurement in the low-speed region; squares: experimental measurements in the high-speed region. The parameters are
![]() $G_{\unicode[STIX]{x1D6EC}}=1501$
and
$G_{\unicode[STIX]{x1D6EC}}=1501$
and
![]() $R_{\unicode[STIX]{x1D6EC}}=1145$
.
$R_{\unicode[STIX]{x1D6EC}}=1145$
.
Due to the presence of Görtler vortices, the local boundary-layer thickness differs from that of the Blasius flow and becomes spanwise dependent. The local displacement thickness is defined as
Figure 8(a) compares the predicted displacement thickness
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
with the experimental measurements of SB in the high-speed (peak) and low-speed (valley) regions. From
$\unicode[STIX]{x1D6FF}^{\ast }$
with the experimental measurements of SB in the high-speed (peak) and low-speed (valley) regions. From
![]() $x^{\ast }=20$
cm to 80 cm roughly, the displacement thickness in the low-speed region increases quickly while that in the high-speed region decreases, both because of exponential amplification of the vortices. The variations (increase and decrease) become moderate from
$x^{\ast }=20$
cm to 80 cm roughly, the displacement thickness in the low-speed region increases quickly while that in the high-speed region decreases, both because of exponential amplification of the vortices. The variations (increase and decrease) become moderate from
![]() $x^{\ast }=80$
cm to
$x^{\ast }=80$
cm to
![]() $90$
cm, due to saturation of Görtler vortices. The displacement thicknesses in the high- and low-speed regions are both in good agreement with the experimental data from
$90$
cm, due to saturation of Görtler vortices. The displacement thicknesses in the high- and low-speed regions are both in good agreement with the experimental data from
![]() $x^{\ast }=10$
cm to
$x^{\ast }=10$
cm to
![]() $90$
cm. The difference between the prediction and the measurement in the low-speed region near
$90$
cm. The difference between the prediction and the measurement in the low-speed region near
![]() $x^{\ast }=95$
cm may be attributed to inaccuracy of measurements since this difference almost disappears in the high-speed region. The displacement thickness in the low-speed region decreases slightly at
$x^{\ast }=95$
cm may be attributed to inaccuracy of measurements since this difference almost disappears in the high-speed region. The displacement thickness in the low-speed region decreases slightly at
![]() $x^{\ast }=100$
cm because of the over saturation of Görtler vortices, as indicated by figure 5. The comparison diverges downstream of
$x^{\ast }=100$
cm because of the over saturation of Görtler vortices, as indicated by figure 5. The comparison diverges downstream of
![]() $x^{\ast }=105$
cm, where secondary instability takes over and influences the displacement thickness substantially. Figure 8(b) displays the predicted skin friction values
$x^{\ast }=105$
cm, where secondary instability takes over and influences the displacement thickness substantially. Figure 8(b) displays the predicted skin friction values
![]() $\unicode[STIX]{x1D70F}^{\ast }=(\unicode[STIX]{x2202}u^{\ast }/\unicode[STIX]{x2202}y^{\ast })|_{y^{\ast }=0}$
. A good agreement with the experimental measurements is observed up to
$\unicode[STIX]{x1D70F}^{\ast }=(\unicode[STIX]{x2202}u^{\ast }/\unicode[STIX]{x2202}y^{\ast })|_{y^{\ast }=0}$
. A good agreement with the experimental measurements is observed up to
![]() $x^{\ast }=105$
cm. The predicted maximum of
$x^{\ast }=105$
cm. The predicted maximum of
![]() $\unicode[STIX]{x1D70F}^{\ast }$
in the high-speed region and the minimum for the low-speed region occur at almost the same streamwise positions as in the measurements. It is rather remarkable that the nonlinear development of a primary instability (i.e. steady Görtler vortices) causes a skin friction increase that is a hallmark of laminar–turbulent transition. Lee & Liu (Reference Lee and Liu1992) found that nonlinear amplitude development, structures of Görtler vortices and the skin friction were quite well predicted by the solutions to the NBRE with an eigensolution as the initial condition. The comparisons in the present paper are more comprehensive and arguably more satisfactory in terms of the required input and accuracy. In our complete initial-boundary-value formulation, the only input to the calculation is the amplitude of FSVD. Use of eigensolutions as initial conditions could only be justified if there exists a discernible linear modal growth stage. That in turn requires the Görtler numbers to be reasonably large and FSVD intensity to be fairly low because otherwise, the linear modal stage is unattainable or bypassed as figure 4(a) indicates. The somewhat better accuracy (e.g. our figure 5 versus figure 4 in Lee & Liu (Reference Lee and Liu1992)) probably resulted from taking into account the continuing action of FSVD on the vortices in the boundary layer.
$\unicode[STIX]{x1D70F}^{\ast }$
in the high-speed region and the minimum for the low-speed region occur at almost the same streamwise positions as in the measurements. It is rather remarkable that the nonlinear development of a primary instability (i.e. steady Görtler vortices) causes a skin friction increase that is a hallmark of laminar–turbulent transition. Lee & Liu (Reference Lee and Liu1992) found that nonlinear amplitude development, structures of Görtler vortices and the skin friction were quite well predicted by the solutions to the NBRE with an eigensolution as the initial condition. The comparisons in the present paper are more comprehensive and arguably more satisfactory in terms of the required input and accuracy. In our complete initial-boundary-value formulation, the only input to the calculation is the amplitude of FSVD. Use of eigensolutions as initial conditions could only be justified if there exists a discernible linear modal growth stage. That in turn requires the Görtler numbers to be reasonably large and FSVD intensity to be fairly low because otherwise, the linear modal stage is unattainable or bypassed as figure 4(a) indicates. The somewhat better accuracy (e.g. our figure 5 versus figure 4 in Lee & Liu (Reference Lee and Liu1992)) probably resulted from taking into account the continuing action of FSVD on the vortices in the boundary layer.

Figure 9. The nonlinear evolution of Görtler vortices as shown by contours of the streamwise velocity at different downstream locations for
![]() $G_{\unicode[STIX]{x1D6EC}}=1501$
and
$G_{\unicode[STIX]{x1D6EC}}=1501$
and
![]() $R_{\unicode[STIX]{x1D6EC}}=1145$
. The increment of the streamwise velocity in the contour values is 0.1
$R_{\unicode[STIX]{x1D6EC}}=1145$
. The increment of the streamwise velocity in the contour values is 0.1
![]() $U_{\infty }$
.
$U_{\infty }$
.
Figure 9 presents the predicted evolution and structure of Görtler vortices by our computation using the experimental parameters of SB. Contour plots of the streamwise velocity, (4.3), at several streamwise locations are assembled to create a perspective view of the vortical structure. The continued action of the upwelling and downwelling motions leads to formation of mushroom-shaped patterns, which have been observed by many researchers (Hall Reference Hall1988; Lee & Liu Reference Lee and Liu1992; Li & Malik Reference Li and Malik1995; Ren & Fu Reference Ren and Fu2015). It is worth noting that streaks in the corresponding flat-plate boundary layer do not develop into a mushroom-shaped structure (Ricco et al. Reference Ricco, Luo and Wu2011).
4.2 Comparison with Ito (Reference Ito1985)

Figure 10. Comparison of the predicted streamwise velocity profiles with the experimental measurements (Ito Reference Ito1985). Solid and dashed lines: theoretical results at the peak and valley, respectively; squares and circles: experimental results at the peak and valley, respectively. The parameters are
![]() $G_{\unicode[STIX]{x1D6EC}}=460$
and
$G_{\unicode[STIX]{x1D6EC}}=460$
and
![]() $R_{\unicode[STIX]{x1D6EC}}=425$
.
$R_{\unicode[STIX]{x1D6EC}}=425$
.

Figure 11. The nonlinear evolution of Görtler vortices as shown by contours of the streamwise velocity in the range of
![]() $0.05<\hat{x}<1.0$
for
$0.05<\hat{x}<1.0$
for
![]() $G_{\unicode[STIX]{x1D6EC}}=460$
and
$G_{\unicode[STIX]{x1D6EC}}=460$
and
![]() $R_{\unicode[STIX]{x1D6EC}}=425$
. The increment of the contour values is 0.1
$R_{\unicode[STIX]{x1D6EC}}=425$
. The increment of the contour values is 0.1
![]() $U_{\infty }$
.
$U_{\infty }$
.
The experiment of Ito (Reference Ito1985) was carried out for a boundary layer on a concave wall with a radius of curvature
![]() $r_{0}^{\ast }=1.0$
m, and the free-stream velocity
$r_{0}^{\ast }=1.0$
m, and the free-stream velocity
![]() $U_{\infty }=2.5~\text{ms}^{-1}$
. The spanwise wavelength of the Görtler vortices was
$U_{\infty }=2.5~\text{ms}^{-1}$
. The spanwise wavelength of the Görtler vortices was
![]() $\unicode[STIX]{x1D706}_{z}\approx 1.6$
cm. On using these parameters, the corresponding Reynolds number
$\unicode[STIX]{x1D706}_{z}\approx 1.6$
cm. On using these parameters, the corresponding Reynolds number
![]() $R_{\unicode[STIX]{x1D6EC}}=425$
and Görtler number
$R_{\unicode[STIX]{x1D6EC}}=425$
and Görtler number
![]() $G_{\unicode[STIX]{x1D6EC}}=460$
. The parameters and the non-dimensional streamwise locations are shown in table 1. We choose
$G_{\unicode[STIX]{x1D6EC}}=460$
. The parameters and the non-dimensional streamwise locations are shown in table 1. We choose
![]() $\unicode[STIX]{x1D716}=0.0022$
to fit the predicted amplitude with the experimental data at the first measurement position. The computational domain starts from
$\unicode[STIX]{x1D716}=0.0022$
to fit the predicted amplitude with the experimental data at the first measurement position. The computational domain starts from
![]() $\hat{x}=0.001$
.
$\hat{x}=0.001$
.
We calculated the streamwise velocity profiles at the peak and valley. The results are shown in figure 10, and compared with the experimental data of Ito (Reference Ito1985). The nonlinear effect is found to play a role from approximately
![]() $\hat{x}=0.35$
. A fairly good agreement is observed in both the linear and nonlinear development stages of the vortices. The predicted streamwise velocity profiles at the valley during nonlinear saturation at locations
$\hat{x}=0.35$
. A fairly good agreement is observed in both the linear and nonlinear development stages of the vortices. The predicted streamwise velocity profiles at the valley during nonlinear saturation at locations
![]() $\hat{x}=0.369$
,
$\hat{x}=0.369$
,
![]() $0.462$
,
$0.462$
,
![]() $0.554$
and
$0.554$
and
![]() $0.646$
agree quite well with the measurements over almost the entire boundary layer. The agreement starts to deteriorate downstream of
$0.646$
agree quite well with the measurements over almost the entire boundary layer. The agreement starts to deteriorate downstream of
![]() $\hat{x}=0.646$
, which suggests that secondary instability modes have become strong enough to influence the structure of saturated Görtler vortices.
$\hat{x}=0.646$
, which suggests that secondary instability modes have become strong enough to influence the structure of saturated Görtler vortices.
Figure 11 presents the predicted evolution of Görtler vortices using Ito’s experimental parameters. As the values of
![]() $R_{\unicode[STIX]{x1D6EC}}$
and
$R_{\unicode[STIX]{x1D6EC}}$
and
![]() $G_{\unicode[STIX]{x1D6EC}}$
are smaller than those in SB: see table 1, a longer distance is required for the vortices to develop into the mushroom-shaped structure, the head of which is farther away from the wall, and the stem of the mushroom is longer.
$G_{\unicode[STIX]{x1D6EC}}$
are smaller than those in SB: see table 1, a longer distance is required for the vortices to develop into the mushroom-shaped structure, the head of which is farther away from the wall, and the stem of the mushroom is longer.
4.3 Comparison with Mitsudharmadi et al. (Reference Mitsudharmadi, Winoto and Shah2004)
In the experiment of MWS, the surface has a radius of curvature
![]() $r_{0}^{\ast }=2$
m, and the free-stream velocity
$r_{0}^{\ast }=2$
m, and the free-stream velocity
![]() $U_{\infty }=3$
$U_{\infty }=3$
![]() $\text{ms}^{-1}$
. Thirteen vertical wires were placed upstream of the leading edge of the test plate to generate Görtler vortices with a fixed spanwise wavelength, as opposed to naturally occurring ones in SB and Ito (Reference Ito1985). The spanwise distance between the wires is 15 mm, which sets the wavelength of the vortices. The corresponding Reynolds number
$\text{ms}^{-1}$
. Thirteen vertical wires were placed upstream of the leading edge of the test plate to generate Görtler vortices with a fixed spanwise wavelength, as opposed to naturally occurring ones in SB and Ito (Reference Ito1985). The spanwise distance between the wires is 15 mm, which sets the wavelength of the vortices. The corresponding Reynolds number
![]() $R_{\unicode[STIX]{x1D6EC}}=478$
and Görtler number
$R_{\unicode[STIX]{x1D6EC}}=478$
and Görtler number
![]() $G_{\unicode[STIX]{x1D6EC}}=273$
. The presence of the vertical wires breaks isotropy, favouring components with longer length in the normal direction than that in the spanwise direction. For this reason,
$G_{\unicode[STIX]{x1D6EC}}=273$
. The presence of the vertical wires breaks isotropy, favouring components with longer length in the normal direction than that in the spanwise direction. For this reason,
![]() $k_{2}=0.6$
is adopted.
$k_{2}=0.6$
is adopted.
As a measure of the intensity of vortices, MWS defined the disturbance amplitude as
where
![]() $U_{D}$
and
$U_{D}$
and
![]() $U_{U}$
denote the velocities at the downwash (peak) and upwash (valley) positions. The predicted amplitude will fit with the measured value at the first location if we take
$U_{U}$
denote the velocities at the downwash (peak) and upwash (valley) positions. The predicted amplitude will fit with the measured value at the first location if we take
![]() $\unicode[STIX]{x1D716}=0.0007$
, which corresponds to
$\unicode[STIX]{x1D716}=0.0007$
, which corresponds to
![]() $Tu^{\dagger }=0.19\,\%$
, or
$Tu^{\dagger }=0.19\,\%$
, or
![]() $Tu=0.18\,\%$
if we take
$Tu=0.18\,\%$
if we take
![]() $\hat{u} _{1}^{\infty }=\hat{u} _{3}^{\infty }$
. The FST level in the test section is
$\hat{u} _{1}^{\infty }=\hat{u} _{3}^{\infty }$
. The FST level in the test section is
![]() $0.35\,\%$
, five times as high as that in SB experiment. Again, this turbulence level apparently refers to unsteady fluctuations. Figure 12 compares
$0.35\,\%$
, five times as high as that in SB experiment. Again, this turbulence level apparently refers to unsteady fluctuations. Figure 12 compares
![]() $\unicode[STIX]{x1D705}_{u}$
with the measurement, and a good agreement is observed. It is evident that Görtler vortices are linear, i.e. undergo exponential amplification, in the region from
$\unicode[STIX]{x1D705}_{u}$
with the measurement, and a good agreement is observed. It is evident that Görtler vortices are linear, i.e. undergo exponential amplification, in the region from
![]() $\hat{x}=0.1$
to 0.35, and then enter the nonlinear regime ranging from
$\hat{x}=0.1$
to 0.35, and then enter the nonlinear regime ranging from
![]() $\hat{x}=0.35$
to 0.75. Rapid growth of unsteady disturbances takes place from
$\hat{x}=0.35$
to 0.75. Rapid growth of unsteady disturbances takes place from
![]() $\hat{x}\approx 0.72$
(
$\hat{x}\approx 0.72$
(
![]() $x^{\ast }\approx 85$
cm), where Görtler vortices start meandering (MWS 2005). This is an indicator of secondary instability, which will be analysed in the next section.
$x^{\ast }\approx 85$
cm), where Görtler vortices start meandering (MWS 2005). This is an indicator of secondary instability, which will be analysed in the next section.
Figure 13 displays a comparison of the streamwise velocity profiles with the experimental measurements. There is a fair qualitative agreement from
![]() $x^{\ast }=31$
cm to
$x^{\ast }=31$
cm to
![]() $90.4$
cm (
$90.4$
cm (
![]() $\hat{x}=0.272$
to 0.792), but appreciable quantitative difference exists, even at the very first measurement point, where the vortices are weak and the base flow should be essentially Blasius. The difference suggests that a pressure gradient might be present. The discrepancy at
$\hat{x}=0.272$
to 0.792), but appreciable quantitative difference exists, even at the very first measurement point, where the vortices are weak and the base flow should be essentially Blasius. The difference suggests that a pressure gradient might be present. The discrepancy at
![]() $x^{\ast }=101.4$
cm (
$x^{\ast }=101.4$
cm (
![]() $\hat{x}=0.888$
) is most likely due to the onset and development of secondary instability.
$\hat{x}=0.888$
) is most likely due to the onset and development of secondary instability.
4.4 Unsteady Görtler vortices
The response of the boundary layer over a curved plate to unsteady FSVD is now presented. We focus on the nonlinear evolution of unsteady Görtler vortices, and choose parameters
![]() $G_{\unicode[STIX]{x1D6EC}}=1501$
and
$G_{\unicode[STIX]{x1D6EC}}=1501$
and
![]() $R_{\unicode[STIX]{x1D6EC}}=1145$
pertaining to the experiment of SB. The parameter
$R_{\unicode[STIX]{x1D6EC}}=1145$
pertaining to the experiment of SB. The parameter
![]() $\hat{k}_{1}$
is related to the dimensional frequency
$\hat{k}_{1}$
is related to the dimensional frequency
![]() $f^{\ast }$
via the relation
$f^{\ast }$
via the relation
Calculations were performed for three different frequencies
![]() $f^{\ast }=1$
Hz, 10 Hz and 20 Hz, corresponding to
$f^{\ast }=1$
Hz, 10 Hz and 20 Hz, corresponding to
![]() $\hat{k}_{1}=5.269$
, 52.691 and 104.382, respectively.
$\hat{k}_{1}=5.269$
, 52.691 and 104.382, respectively.

Figure 12. Comparison of the downstream development of the streamwise velocity fluctuation amplitude defined by (4.6): the line indicates the present computed results; the square symbols stand for the experimentally measured steady components (MWS 2005), whereas the circle symbols indicate the unsteady contributions.

Figure 13. Comparison of the streamwise velocity profiles with experimental measurements (Mitsudharmadi et al.
Reference Mitsudharmadi, Winoto and Shah2005). Solid and dashed lines represent the theoretical predictions at the peak and valley, respectively; delta and square symbols represent the experimental results at the peak and valley, respectively. The parameters are
![]() $G_{\unicode[STIX]{x1D6EC}}=273$
,
$G_{\unicode[STIX]{x1D6EC}}=273$
,
![]() $R_{\unicode[STIX]{x1D6EC}}=478$
and
$R_{\unicode[STIX]{x1D6EC}}=478$
and
![]() $k_{2}=0.6$
.
$k_{2}=0.6$
.

Figure 14. Comparison of the downstream development of
![]() $\max u_{rms}$
for different
$\max u_{rms}$
for different
![]() $\hat{k}_{1}$
. The parameters are
$\hat{k}_{1}$
. The parameters are
![]() $G_{\unicode[STIX]{x1D6EC}}=1501,R_{\unicode[STIX]{x1D6EC}}=1145$
and
$G_{\unicode[STIX]{x1D6EC}}=1501,R_{\unicode[STIX]{x1D6EC}}=1145$
and
![]() $\unicode[STIX]{x1D716}=0.0007$
.
$\unicode[STIX]{x1D716}=0.0007$
.

Figure 15. Development of the fundamental mode
![]() $\max |\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}2\hat{x}\hat{u} _{11}|$
and harmonic components
$\max |\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}2\hat{x}\hat{u} _{11}|$
and harmonic components
![]() $\max |\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}2\hat{x}\hat{u} _{m,n}|$
: (a)
$\max |\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}2\hat{x}\hat{u} _{m,n}|$
: (a)
![]() $\hat{k}_{1}=0$
; (b)
$\hat{k}_{1}=0$
; (b)
![]() $\hat{k}_{1}=5.269$
; (c)
$\hat{k}_{1}=5.269$
; (c)
![]() $\hat{k}_{1}=52.691$
; (d)
$\hat{k}_{1}=52.691$
; (d)
![]() $\hat{k}_{1}=104.382$
. The parameters are
$\hat{k}_{1}=104.382$
. The parameters are
![]() $G_{\unicode[STIX]{x1D6EC}}=1501$
,
$G_{\unicode[STIX]{x1D6EC}}=1501$
,
![]() $R_{\unicode[STIX]{x1D6EC}}=1145$
and
$R_{\unicode[STIX]{x1D6EC}}=1145$
and
![]() $\unicode[STIX]{x1D716}=0.0007$
.
$\unicode[STIX]{x1D716}=0.0007$
.
Figure 14 shows the development of
![]() $\max u_{rms}$
for these three frequencies with the steady case included for comparison. Vortices excited by lower-frequency disturbances acquire a larger amplitude prior to saturation. Interestingly,
$\max u_{rms}$
for these three frequencies with the steady case included for comparison. Vortices excited by lower-frequency disturbances acquire a larger amplitude prior to saturation. Interestingly,
![]() $\max u_{rms}$
saturates at almost the same level eventually. The saturation location shifts however downstream as the frequency increases. For the case of
$\max u_{rms}$
saturates at almost the same level eventually. The saturation location shifts however downstream as the frequency increases. For the case of
![]() $\hat{k}_{1}=52.691$
, there appears a rather sudden change of the slope at
$\hat{k}_{1}=52.691$
, there appears a rather sudden change of the slope at
![]() $\hat{x}\approx 0.22$
. For the case of
$\hat{x}\approx 0.22$
. For the case of
![]() $\hat{k}_{1}=104.382$
, the first linear growth stage disappears and instead
$\hat{k}_{1}=104.382$
, the first linear growth stage disappears and instead
![]() $\max u_{rms}$
decreases slightly after the transient growth. Starting from
$\max u_{rms}$
decreases slightly after the transient growth. Starting from
![]() $\hat{x}=0.18$
,
$\hat{x}=0.18$
,
![]() $\max u_{rms}$
grows exponentially at a fairly large rate until
$\max u_{rms}$
grows exponentially at a fairly large rate until
![]() $\hat{x}\approx 0.32$
, where saturation starts.
$\hat{x}\approx 0.32$
, where saturation starts.
In order to probe into the nature of nonlinear vortices, figure 15 shows the development of the maximum amplitudes of the fundamental and harmonic components for
![]() $\hat{k}_{1}=5.269,52.691$
and
$\hat{k}_{1}=5.269,52.691$
and
![]() $104.382$
. For the lower-frequency case (
$104.382$
. For the lower-frequency case (
![]() $\hat{k}_{1}=5.269$
), the mean-flow distortion acquires a magnitude appreciably greater than that of the seeded fundamental modes
$\hat{k}_{1}=5.269$
), the mean-flow distortion acquires a magnitude appreciably greater than that of the seeded fundamental modes
![]() $(1,\pm 1)$
; a similar feature was observed in the case of the flat-plate boundary layer (Ricco et al.
Reference Ricco, Luo and Wu2011). For the case of
$(1,\pm 1)$
; a similar feature was observed in the case of the flat-plate boundary layer (Ricco et al.
Reference Ricco, Luo and Wu2011). For the case of
![]() $\hat{k}_{1}=52.691$
, the amplitude of the mean-flow distortion
$\hat{k}_{1}=52.691$
, the amplitude of the mean-flow distortion
![]() $(0,0)$
is still larger than that of the fundamental modes, but the harmonic component (0,2) grows quickly from
$(0,0)$
is still larger than that of the fundamental modes, but the harmonic component (0,2) grows quickly from
![]() $\hat{x}\approx 0.23$
to overtake the fundamental modes
$\hat{x}\approx 0.23$
to overtake the fundamental modes
![]() $(1,\pm 1)$
. For the case
$(1,\pm 1)$
. For the case
![]() $\hat{k}_{1}=104.382$
, the fundamental modes
$\hat{k}_{1}=104.382$
, the fundamental modes
![]() $(1,\pm 1)$
do not grow any more after the transient growth, instead the (0,2) mode amplifies exponentially. The mean-flow distortion (0,0) undergoes rapid growth again from about
$(1,\pm 1)$
do not grow any more after the transient growth, instead the (0,2) mode amplifies exponentially. The mean-flow distortion (0,0) undergoes rapid growth again from about
![]() $\hat{x}=0.18$
to become the dominant component. It is worth noting that for both
$\hat{x}=0.18$
to become the dominant component. It is worth noting that for both
![]() $\hat{k}_{1}=52.691$
and
$\hat{k}_{1}=52.691$
and
![]() $104.382$
the rapid growth of the mean flow coincides with that of
$104.382$
the rapid growth of the mean flow coincides with that of
![]() $\max u_{rms}$
shown in figure 14. In all the four cases, the (0,0) mode saturates at the highest level, and in the steady case the dominance of this mode is in accordance with the nonlinear theory of Hall & Lakin (Reference Hall and Lakin1988). For the steady and low-frequency cases, the fundamental modes acquire the second largest saturation amplitude, but once the frequency exceeds a critical value, it is the nonlinearly generated (0,2) mode that takes the second place.
$\max u_{rms}$
shown in figure 14. In all the four cases, the (0,0) mode saturates at the highest level, and in the steady case the dominance of this mode is in accordance with the nonlinear theory of Hall & Lakin (Reference Hall and Lakin1988). For the steady and low-frequency cases, the fundamental modes acquire the second largest saturation amplitude, but once the frequency exceeds a critical value, it is the nonlinearly generated (0,2) mode that takes the second place.

Figure 16. Profiles of the instantaneous streamwise velocity
![]() $U$
at
$U$
at
![]() $z=0$
in different phases of time modulation: (a)
$z=0$
in different phases of time modulation: (a)
![]() $\hat{k}_{1}=5.269$
; (b)
$\hat{k}_{1}=5.269$
; (b)
![]() $\hat{k}_{1}=52.691$
; (c)
$\hat{k}_{1}=52.691$
; (c)
![]() $\hat{k}_{1}=104.382$
. The parameters are
$\hat{k}_{1}=104.382$
. The parameters are
![]() $G_{\unicode[STIX]{x1D6EC}}=1501,R_{\unicode[STIX]{x1D6EC}}=1145$
and
$G_{\unicode[STIX]{x1D6EC}}=1501,R_{\unicode[STIX]{x1D6EC}}=1145$
and
![]() $\unicode[STIX]{x1D716}=0.0007$
. The inserted window displays an enlarged view of the part in the dashed box.
$\unicode[STIX]{x1D716}=0.0007$
. The inserted window displays an enlarged view of the part in the dashed box.

Figure 17. Nonlinear evolution of Görtler vortices. (a,b)
![]() $\hat{k}_{1}=5.269,\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
(a) and
$\hat{k}_{1}=5.269,\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
(a) and
![]() $\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
(b); (c,d)
$\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
(b); (c,d)
![]() $\hat{k}_{1}=52.691$
,
$\hat{k}_{1}=52.691$
,
![]() $\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
(c) and
$\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
(c) and
![]() $\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
(d); (e,f)
$\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
(d); (e,f)
![]() $\hat{k}_{1}=104.382,\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
(e) and
$\hat{k}_{1}=104.382,\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
(e) and
![]() $\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
(f). The increments of the contour levels is 0.1
$\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
(f). The increments of the contour levels is 0.1
![]() $U_{0}$
. The parameters are
$U_{0}$
. The parameters are
![]() $G_{\unicode[STIX]{x1D6EC}}=1501,R_{\unicode[STIX]{x1D6EC}}=1145$
and
$G_{\unicode[STIX]{x1D6EC}}=1501,R_{\unicode[STIX]{x1D6EC}}=1145$
and
![]() $\unicode[STIX]{x1D716}=0.0007$
.
$\unicode[STIX]{x1D716}=0.0007$
.
Figure 16 shows the instantaneous streamwise velocity profiles at
![]() $z=0$
in different phases
$z=0$
in different phases
for three representative frequencies. For
![]() $\hat{k}_{1}=5.269$
, the velocity profile exhibits remarkable variation with the phase. The velocity may be larger or smaller than that of the Blasius flow. During certain time windows of the modulation, the instantaneous streamwise velocity profile becomes highly inflectional, suggesting that it may be inviscidly unstable. When
$\hat{k}_{1}=5.269$
, the velocity profile exhibits remarkable variation with the phase. The velocity may be larger or smaller than that of the Blasius flow. During certain time windows of the modulation, the instantaneous streamwise velocity profile becomes highly inflectional, suggesting that it may be inviscidly unstable. When
![]() $\hat{k}_{1}$
increases to
$\hat{k}_{1}$
increases to
![]() $52.691$
, the temporal variation of the streamwise velocity becomes less strong, and the profile maintains a similar shape. The velocity near the wall hardly changes, and is persistently faster than the Blasius flow. However, a persistent large velocity deficit occurs at the outer part of the boundary layer; a similar feature was observed in the flat-plate case (Ricco et al. (Reference Ricco, Luo and Wu2011) and references therein). For the case
$52.691$
, the temporal variation of the streamwise velocity becomes less strong, and the profile maintains a similar shape. The velocity near the wall hardly changes, and is persistently faster than the Blasius flow. However, a persistent large velocity deficit occurs at the outer part of the boundary layer; a similar feature was observed in the flat-plate case (Ricco et al. (Reference Ricco, Luo and Wu2011) and references therein). For the case
![]() $\hat{k}_{1}=104.382$
, the velocity profile changes moderately, i.e. Görtler vortices become almost stationary. This may be attributed to the dominance of the steady (0,0) and (0,2) modes. It is interesting to note that the profiles appear somewhat like the mean profile of fully developed turbulent boundary layer.
$\hat{k}_{1}=104.382$
, the velocity profile changes moderately, i.e. Görtler vortices become almost stationary. This may be attributed to the dominance of the steady (0,0) and (0,2) modes. It is interesting to note that the profiles appear somewhat like the mean profile of fully developed turbulent boundary layer.
Figure 17 displays perspective views of the contours of the streamwise velocity at different downstream locations for
![]() $\hat{k}_{1}=5.269,52.691$
and
$\hat{k}_{1}=5.269,52.691$
and
![]() $104.382$
. Two phases of time modulation
$104.382$
. Two phases of time modulation
![]() $\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
and
$\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
and
![]() $\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
, are chosen. The perturbation eventually develops into a mushroom structure as in the steady case. For
$\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
, are chosen. The perturbation eventually develops into a mushroom structure as in the steady case. For
![]() $\hat{k}_{1}=5.269$
, during a cycle of modulation, the mushrooms meander in the spanwise direction. For the case of
$\hat{k}_{1}=5.269$
, during a cycle of modulation, the mushrooms meander in the spanwise direction. For the case of
![]() $\hat{k}_{1}=52.691$
, the spanwise meandering is insignificant because the steady components, (0,0) and (0,2), dominate. Furthermore, since the (0,2) mode acquires a much larger amplitude than that of the fundamental, two mushrooms appear side by side within a fundamental spanwise wavelength. For the case of
$\hat{k}_{1}=52.691$
, the spanwise meandering is insignificant because the steady components, (0,0) and (0,2), dominate. Furthermore, since the (0,2) mode acquires a much larger amplitude than that of the fundamental, two mushrooms appear side by side within a fundamental spanwise wavelength. For the case of
![]() $\hat{k}_{1}=104.382$
, contour plots at the two phases are hardly distinguishable.
$\hat{k}_{1}=104.382$
, contour plots at the two phases are hardly distinguishable.
5 Secondary instability of Görtler vortices
5.1 Formulation and methodology
Once Görtler vortices have acquired a sufficiently large amplitude, the distorted velocity profile
![]() $U(y,z;x,t)$
usually becomes inflectional in the streamwise and spanwise directions, and therefore is a harbinger of secondary instability (Saric Reference Saric1994), which amplifies high-frequency fluctuations and ultimately causes transition to turbulence. As was mentioned earlier, linear secondary instability analyses have been performed by several investigators (Hall & Horseman Reference Hall and Horseman1991; Yu & Liu Reference Yu and Liu1991; Li & Malik Reference Li and Malik1995). Previous calculations were carried out for Görtler vortices that developed spatially (or temporally) from somewhat arbitrary upstream (or initial) conditions, which suffices for the aim of establishing salient characteristics of the instability. In the present paper, secondary instability analyses will be conducted as part of the integrated approach. Our purpose is to add more quantitative information on the one hand, and build up the capacity for predicting transition in terms of given FST on the other.
$U(y,z;x,t)$
usually becomes inflectional in the streamwise and spanwise directions, and therefore is a harbinger of secondary instability (Saric Reference Saric1994), which amplifies high-frequency fluctuations and ultimately causes transition to turbulence. As was mentioned earlier, linear secondary instability analyses have been performed by several investigators (Hall & Horseman Reference Hall and Horseman1991; Yu & Liu Reference Yu and Liu1991; Li & Malik Reference Li and Malik1995). Previous calculations were carried out for Görtler vortices that developed spatially (or temporally) from somewhat arbitrary upstream (or initial) conditions, which suffices for the aim of establishing salient characteristics of the instability. In the present paper, secondary instability analyses will be conducted as part of the integrated approach. Our purpose is to add more quantitative information on the one hand, and build up the capacity for predicting transition in terms of given FST on the other.
Since the flow field of Görtler vortices varies with
![]() $\hat{x}$
and
$\hat{x}$
and
![]() $\hat{\unicode[STIX]{x1D70F}}$
very slowly, the dependence on these two variables can be treated as being parametric when a short-wavelength (of order
$\hat{\unicode[STIX]{x1D70F}}$
very slowly, the dependence on these two variables can be treated as being parametric when a short-wavelength (of order
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
, with
$\unicode[STIX]{x1D6FF}^{\ast }$
, with
![]() $\unicode[STIX]{x1D6FF}^{\ast }$
being the dimensional boundary-larger thickness) and high-frequency (of order
$\unicode[STIX]{x1D6FF}^{\ast }$
being the dimensional boundary-larger thickness) and high-frequency (of order
![]() $U_{\infty }/\unicode[STIX]{x1D6FF}^{\ast }$
) instability is considered, just like the flat-plate case considered by Ricco et al. (Reference Ricco, Luo and Wu2011). With
$U_{\infty }/\unicode[STIX]{x1D6FF}^{\ast }$
) instability is considered, just like the flat-plate case considered by Ricco et al. (Reference Ricco, Luo and Wu2011). With
![]() $\hat{x}$
and
$\hat{x}$
and
![]() $\hat{\unicode[STIX]{x1D70F}}$
fixed, the base flow, comprising the Blasius flow and the Görtler vortices, depends only on
$\hat{\unicode[STIX]{x1D70F}}$
fixed, the base flow, comprising the Blasius flow and the Görtler vortices, depends only on
![]() $y$
and
$y$
and
![]() $z$
, and can be written as
$z$
, and can be written as
The transverse velocities of the vortex base flow,
![]() $V_{G}$
and
$V_{G}$
and
![]() $W_{G}$
, will be neglected since they are very small, of
$W_{G}$
, will be neglected since they are very small, of
![]() $O(R_{\unicode[STIX]{x1D6EC}}^{-1})$
, and so
$O(R_{\unicode[STIX]{x1D6EC}}^{-1})$
, and so
![]() $\boldsymbol{U}_{G}=(U,0,0)$
with
$\boldsymbol{U}_{G}=(U,0,0)$
with
![]() $U$
being given by (4.3). When the base flow is perturbed by a disturbance of
$U$
being given by (4.3). When the base flow is perturbed by a disturbance of
![]() $O(\unicode[STIX]{x1D716}_{s})$
, the instantaneous flow is
$O(\unicode[STIX]{x1D716}_{s})$
, the instantaneous flow is
where
![]() $\boldsymbol{u}_{s}^{\prime }=(u_{s}^{\prime },v_{s}^{\prime },w_{s}^{\prime })$
is the secondary perturbation velocity vector and
$\boldsymbol{u}_{s}^{\prime }=(u_{s}^{\prime },v_{s}^{\prime },w_{s}^{\prime })$
is the secondary perturbation velocity vector and
![]() $p_{s}^{\prime }$
the pressure. Substituting (5.2) into the N–S equations and neglecting the
$p_{s}^{\prime }$
the pressure. Substituting (5.2) into the N–S equations and neglecting the
![]() $O(\unicode[STIX]{x1D716}_{s}^{2})$
nonlinear terms, we obtain the linearized N–S equations,
$O(\unicode[STIX]{x1D716}_{s}^{2})$
nonlinear terms, we obtain the linearized N–S equations,
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x2202}_{t}\boldsymbol{u}_{s}^{\prime }=-(\boldsymbol{U}_{G}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}_{s}^{\prime }-(\boldsymbol{u}_{s}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{U}_{G}-\unicode[STIX]{x1D735}p_{s}^{\prime }+\frac{1}{R_{\unicode[STIX]{x1D6EC}}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}_{s}^{\prime },\\ \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{s}^{\prime }=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x2202}_{t}\boldsymbol{u}_{s}^{\prime }=-(\boldsymbol{U}_{G}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}_{s}^{\prime }-(\boldsymbol{u}_{s}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{U}_{G}-\unicode[STIX]{x1D735}p_{s}^{\prime }+\frac{1}{R_{\unicode[STIX]{x1D6EC}}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}_{s}^{\prime },\\ \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{s}^{\prime }=0.\end{array}\right\}\end{eqnarray}$$
These equations, together with the homogeneous boundary conditions,
define a linear evolution operator
![]() $\ell$
, which evolves perturbations forward in time.
$\ell$
, which evolves perturbations forward in time.
Given that the coefficients in (5.3) depend on
![]() $y$
and
$y$
and
![]() $z$
only, the solution for the secondary perturbation
$z$
only, the solution for the secondary perturbation
![]() $\unicode[STIX]{x1D753}_{s}^{\prime }(x,y,z,t)\equiv (\boldsymbol{u}_{s}^{\prime },\,p_{s}^{\prime })$
can be sought of the modal form,
$\unicode[STIX]{x1D753}_{s}^{\prime }(x,y,z,t)\equiv (\boldsymbol{u}_{s}^{\prime },\,p_{s}^{\prime })$
can be sought of the modal form,
where
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D714}$
are the non-dimensional streamwise wavenumber and frequency of the secondary disturbance respectively. The shape function
$\unicode[STIX]{x1D714}$
are the non-dimensional streamwise wavenumber and frequency of the secondary disturbance respectively. The shape function
![]() $\unicode[STIX]{x1D753}_{s}(y,z)$
is governed by a system of partial differential equations,
$\unicode[STIX]{x1D753}_{s}(y,z)$
is governed by a system of partial differential equations,
![]() ${\mathcal{L}}_{E}(\unicode[STIX]{x2202}_{y},\unicode[STIX]{x2202}_{z},U_{G};\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D714})\unicode[STIX]{x1D753}_{s}=0$
, which together with the homogeneous boundary conditions,
${\mathcal{L}}_{E}(\unicode[STIX]{x2202}_{y},\unicode[STIX]{x2202}_{z},U_{G};\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D714})\unicode[STIX]{x1D753}_{s}=0$
, which together with the homogeneous boundary conditions,
![]() $\boldsymbol{u}_{s}=0$
at
$\boldsymbol{u}_{s}=0$
at
![]() $y=0$
and
$y=0$
and
![]() $(\boldsymbol{u}_{s},\,p_{s})\rightarrow 0$
as
$(\boldsymbol{u}_{s},\,p_{s})\rightarrow 0$
as
![]() $y\rightarrow \infty$
, forms a so-called bi-global instability problem (Theofilis Reference Theofilis2011). In the temporal formulation,
$y\rightarrow \infty$
, forms a so-called bi-global instability problem (Theofilis Reference Theofilis2011). In the temporal formulation,
![]() $\unicode[STIX]{x1D6FC}$
is real, whereas
$\unicode[STIX]{x1D6FC}$
is real, whereas
![]() $\unicode[STIX]{x1D714}$
is complex valued and obtained as the eigenvalue. In the inviscid limit, the system for
$\unicode[STIX]{x1D714}$
is complex valued and obtained as the eigenvalue. In the inviscid limit, the system for
![]() $\unicode[STIX]{x1D753}_{s}(y,z)$
can be reduced to a single equation for the pressure
$\unicode[STIX]{x1D753}_{s}(y,z)$
can be reduced to a single equation for the pressure
![]() $p_{s}(y,z)$
(Hall & Horseman Reference Hall and Horseman1991),
$p_{s}(y,z)$
(Hall & Horseman Reference Hall and Horseman1991),
where
![]() $U$
stands for the streamwise velocity (4.3) of the vortex flow. Despite that the secondary instability is essentially inviscid and that we have taken
$U$
stands for the streamwise velocity (4.3) of the vortex flow. Despite that the secondary instability is essentially inviscid and that we have taken
![]() $R_{\unicode[STIX]{x1D6EC}}\gg 1$
in the analysis of the Görtler vortices, we will retain viscosity in the secondary instability calculations since this avoids the critical-layer singularity for neutral or nearly neutral modes, and furthermore may give more accurate results.
$R_{\unicode[STIX]{x1D6EC}}\gg 1$
in the analysis of the Görtler vortices, we will retain viscosity in the secondary instability calculations since this avoids the critical-layer singularity for neutral or nearly neutral modes, and furthermore may give more accurate results.
A discretization of the eigenvalue problem in two dimensions leads to a matrix, which is usually so large that it is difficult to compute its eigenvalues. To circumvent this obstacle, we use the Arnoldi method that makes use of time stepping. This method was developed by Barkley, Blackburn & Sherwin (Reference Barkley, Blackburn and Sherwin2008), and was recently adapted to finite-difference setting by one of the present authors (Zhang & Luo Reference Zhang and Luo2015). The method is based on integrating the evolution system (5.3)–(5.4a,b
) from
![]() $t=0$
to
$t=0$
to
![]() $t=T$
with
$t=T$
with
![]() $T$
being a preset time. In implementation, we write
$T$
being a preset time. In implementation, we write
![]() $\unicode[STIX]{x1D719}_{s}^{\prime }(x,y,z,t)=\bar{\unicode[STIX]{x1D719}}(y,z,t)\text{e}^{\text{i}\unicode[STIX]{x1D6FC}x}+\text{c.c}.$
, where
$\unicode[STIX]{x1D719}_{s}^{\prime }(x,y,z,t)=\bar{\unicode[STIX]{x1D719}}(y,z,t)\text{e}^{\text{i}\unicode[STIX]{x1D6FC}x}+\text{c.c}.$
, where
![]() $\unicode[STIX]{x1D719}_{s}^{\prime }$
stands for any of
$\unicode[STIX]{x1D719}_{s}^{\prime }$
stands for any of
![]() $u_{s}^{\prime }$
,
$u_{s}^{\prime }$
,
![]() $v_{s}^{\prime }$
,
$v_{s}^{\prime }$
,
![]() $w_{s}^{\prime }$
and
$w_{s}^{\prime }$
and
![]() $p_{s}^{\prime }$
. Since the coefficients of the governing equations are periodic functions of
$p_{s}^{\prime }$
. Since the coefficients of the governing equations are periodic functions of
![]() $z$
, according to Floquet theory the solution for
$z$
, according to Floquet theory the solution for
![]() $\bar{\unicode[STIX]{x1D719}}$
takes the form,
$\bar{\unicode[STIX]{x1D719}}$
takes the form,
where
![]() $\unicode[STIX]{x1D6FD}$
is the spanwise wavenumber and
$\unicode[STIX]{x1D6FD}$
is the spanwise wavenumber and
![]() $0\leqslant q\leqslant 1/2$
. Only fundamental modes (
$0\leqslant q\leqslant 1/2$
. Only fundamental modes (
![]() $q=0$
) will be presented because the differences between the growth rates of the fundamental and subharmonic (
$q=0$
) will be presented because the differences between the growth rates of the fundamental and subharmonic (
![]() $q=1/2$
) or detuned modes (
$q=1/2$
) or detuned modes (
![]() $0<q<1/2$
) are less than
$0<q<1/2$
) are less than
![]() $3.5\,\%$
(Ren & Fu Reference Ren and Fu2014). The discretization in the wall-normal direction is by a finite-difference scheme on variable grids, whose distribution is facilitated by a coordinate transformation from
$3.5\,\%$
(Ren & Fu Reference Ren and Fu2014). The discretization in the wall-normal direction is by a finite-difference scheme on variable grids, whose distribution is facilitated by a coordinate transformation from
![]() $y$
to
$y$
to
![]() $\tilde{\unicode[STIX]{x1D702}}$
(Zhang & Luo Reference Zhang and Luo2015),
$\tilde{\unicode[STIX]{x1D702}}$
(Zhang & Luo Reference Zhang and Luo2015),
![]() $y=y_{l}\tilde{\unicode[STIX]{x1D702}}/[1+b(1-\tilde{\unicode[STIX]{x1D702}}^{2})]$
with
$y=y_{l}\tilde{\unicode[STIX]{x1D702}}/[1+b(1-\tilde{\unicode[STIX]{x1D702}}^{2})]$
with
![]() $b=(\sqrt{1+8k}-3)/4$
; this maps the truncated physical domain
$b=(\sqrt{1+8k}-3)/4$
; this maps the truncated physical domain
![]() $0\leqslant y\leqslant y_{l}$
to
$0\leqslant y\leqslant y_{l}$
to
![]() $0\leqslant \widetilde{\unicode[STIX]{x1D702}}\leqslant 1$
, where
$0\leqslant \widetilde{\unicode[STIX]{x1D702}}\leqslant 1$
, where
![]() $k$
is the parameter controlling the mesh distribution. The interval (0,1) is divided into
$k$
is the parameter controlling the mesh distribution. The interval (0,1) is divided into
![]() $N_{y}$
equally spaced subintervals, and so
$N_{y}$
equally spaced subintervals, and so
![]() $\unicode[STIX]{x0394}\widetilde{\unicode[STIX]{x1D702}}=1/N_{y}$
. Typically, we use 300 points in the normal direction, and 64 terms in the Fourier series, but for modes concentrating in the wall region, refined grids are needed there in order to resolve the eigenfunctions.
$\unicode[STIX]{x0394}\widetilde{\unicode[STIX]{x1D702}}=1/N_{y}$
. Typically, we use 300 points in the normal direction, and 64 terms in the Fourier series, but for modes concentrating in the wall region, refined grids are needed there in order to resolve the eigenfunctions.
Let
![]() $\bar{\unicode[STIX]{x1D753}}$
denote the discretized solution vector. The integration from
$\bar{\unicode[STIX]{x1D753}}$
denote the discretized solution vector. The integration from
![]() $t=0$
to
$t=0$
to
![]() $t=T$
, starting with an initial perturbation
$t=T$
, starting with an initial perturbation
![]() $\bar{\unicode[STIX]{x1D753}}_{0}$
, may be viewed as a mapping,
$\bar{\unicode[STIX]{x1D753}}_{0}$
, may be viewed as a mapping,
by the evolution operator
![]() $\ell$
. Repeating this, one obtains
$\ell$
. Repeating this, one obtains
![]() $\ell ^{2}\bar{\unicode[STIX]{x1D753}}_{0},\ldots ,\ell ^{k}\bar{\unicode[STIX]{x1D753}}_{0}$
, which can be arranged to form the normalized Krylov sequence,
$\ell ^{2}\bar{\unicode[STIX]{x1D753}}_{0},\ldots ,\ell ^{k}\bar{\unicode[STIX]{x1D753}}_{0}$
, which can be arranged to form the normalized Krylov sequence,
where
![]() $a_{k}$
are the normalization factors to make each column a unit vector. A simple fundamental relation holds between
$a_{k}$
are the normalization factors to make each column a unit vector. A simple fundamental relation holds between
![]() ${\mathcal{T}}_{k+1}$
and
${\mathcal{T}}_{k+1}$
and
![]() $\ell (T){\mathcal{T}}_{k}$
. Using this relation and carrying out QR decompositions of
$\ell (T){\mathcal{T}}_{k}$
. Using this relation and carrying out QR decompositions of
![]() ${\mathcal{T}}_{k+1}$
and
${\mathcal{T}}_{k+1}$
and
![]() ${\mathcal{T}}_{k}$
, a
${\mathcal{T}}_{k}$
, a
![]() $k\times k$
Hessenberg matrix
$k\times k$
Hessenberg matrix
![]() $\unicode[STIX]{x1D643}_{k}$
can be constructed. Since
$\unicode[STIX]{x1D643}_{k}$
can be constructed. Since
![]() $k$
is rather small, eigenvalues of
$k$
is rather small, eigenvalues of
![]() $\unicode[STIX]{x1D643}_{k}$
,
$\unicode[STIX]{x1D643}_{k}$
,
![]() $\unicode[STIX]{x1D706}_{j}$
(
$\unicode[STIX]{x1D706}_{j}$
(
![]() $j=1,2,\ldots ,k$
), and the corresponding eigenvectors, can be computed at little cost. The eigenvalues for the original problem,
$j=1,2,\ldots ,k$
), and the corresponding eigenvectors, can be computed at little cost. The eigenvalues for the original problem,
![]() $\unicode[STIX]{x1D714}$
, are related to
$\unicode[STIX]{x1D714}$
, are related to
![]() $\unicode[STIX]{x1D706}_{j}$
by
$\unicode[STIX]{x1D706}_{j}$
by
![]() $\unicode[STIX]{x1D714}=(\text{i}/T)\ln \unicode[STIX]{x1D706}_{j}$
, and the eigenfunctions can be constructed by following the algorithm described in Barkley et al. (Reference Barkley, Blackburn and Sherwin2008).
$\unicode[STIX]{x1D714}=(\text{i}/T)\ln \unicode[STIX]{x1D706}_{j}$
, and the eigenfunctions can be constructed by following the algorithm described in Barkley et al. (Reference Barkley, Blackburn and Sherwin2008).
5.2 Secondary instability of steady Görtler vortices
5.2.1 Secondary instability calculations pertaining to the SB (1987) experiment
Although multiple unstable eigenmodes co-exist for each Görtler vortex flow profile, we focus on the most unstable ones. Both the computational results of the last section and the measurements of SB show that at
![]() $\hat{x}=0.227$
(
$\hat{x}=0.227$
(
![]() $x^{\ast }=95$
cm) Görtler vortices acquire their maximum amplitude. The experiment indicates that unsteady disturbances amplify abruptly from this position. The abrupt amplification is most likely due to the development of secondary instability modes, triggered by high-frequency components in FSVD, but the precise receptivity mechanism remains a complete mystery at the present. We select nine streamwise locations (listed in table 1), at which secondary stability analysis is to be performed.
$x^{\ast }=95$
cm) Görtler vortices acquire their maximum amplitude. The experiment indicates that unsteady disturbances amplify abruptly from this position. The abrupt amplification is most likely due to the development of secondary instability modes, triggered by high-frequency components in FSVD, but the precise receptivity mechanism remains a complete mystery at the present. We select nine streamwise locations (listed in table 1), at which secondary stability analysis is to be performed.

Figure 18. Characteristics of secondary instability of Görtler vortices in the experiment of SB: (a) the temporal growth rate and (b) the phase speed versus the streamwise wavenumber
![]() $\unicode[STIX]{x1D6FC}$
at
$\unicode[STIX]{x1D6FC}$
at
![]() $x^{\ast }=$
80, 85, 87 and 90 cm, corresponding to
$x^{\ast }=$
80, 85, 87 and 90 cm, corresponding to
![]() $\hat{x}=0.191,0.203$
,
$\hat{x}=0.191,0.203$
,
![]() $0.209$
and
$0.209$
and
![]() $0.215$
, respectively.
$0.215$
, respectively.

Figure 19. Eigenfunctions (absolute value, black line) of secondary unstable modes, shown by contours of the streamwise velocity at
![]() $\hat{x}=0.215$
. (a) The most unstable mode with
$\hat{x}=0.215$
. (a) The most unstable mode with
![]() $\unicode[STIX]{x1D6FC}=0.8$
(odd mode I); (b) the most unstable mode with
$\unicode[STIX]{x1D6FC}=0.8$
(odd mode I); (b) the most unstable mode with
![]() $\unicode[STIX]{x1D6FC}=1.5$
(even mode I). The grey contours represent the streamwise velocity of the vortex base flow. Nine levels are specified, ranging from 0.1 to 0.9.
$\unicode[STIX]{x1D6FC}=1.5$
(even mode I). The grey contours represent the streamwise velocity of the vortex base flow. Nine levels are specified, ranging from 0.1 to 0.9.
Figure 18 plots the growth rates and phase speeds at
![]() $\hat{x}=0.191,0.203,0.209$
and
$\hat{x}=0.191,0.203,0.209$
and
![]() $0.215$
. Figure 18(a) shows that at
$0.215$
. Figure 18(a) shows that at
![]() $\hat{x}=0.191$
, only unstable modes are found for
$\hat{x}=0.191$
, only unstable modes are found for
![]() $\unicode[STIX]{x1D6FC}<1$
, and these are sinuous modes, or odd modes I, as referred to by Li & Malik (Reference Li and Malik1995). Another family of modes with larger
$\unicode[STIX]{x1D6FC}<1$
, and these are sinuous modes, or odd modes I, as referred to by Li & Malik (Reference Li and Malik1995). Another family of modes with larger
![]() $\unicode[STIX]{x1D6FC}$
, referred to as even modes I by Li & Malik (Reference Li and Malik1995), start to emerge from
$\unicode[STIX]{x1D6FC}$
, referred to as even modes I by Li & Malik (Reference Li and Malik1995), start to emerge from
![]() $\hat{x}=0.203$
, and their growth rates increase. However, odd modes I remain dominant up to
$\hat{x}=0.203$
, and their growth rates increase. However, odd modes I remain dominant up to
![]() $\hat{x}=0.215$
. The maximum growth rates at the first three streamwise locations are attained for streamwise wavenumbers approximately between 0.6 and 0.8, corresponding to wavelengths between 3.8 and 2.9 cm. The growth rates of even modes I become almost equal to those of the odd modes I when
$\hat{x}=0.215$
. The maximum growth rates at the first three streamwise locations are attained for streamwise wavenumbers approximately between 0.6 and 0.8, corresponding to wavelengths between 3.8 and 2.9 cm. The growth rates of even modes I become almost equal to those of the odd modes I when
![]() $\hat{x}=0.215$
. The result in the figure also indicates that the band of unstable modes becomes broader at downstream positions. Figure 18(b) shows phase speeds of secondary instability modes. The phase speeds of sinuous modes decrease rather rapidly with
$\hat{x}=0.215$
. The result in the figure also indicates that the band of unstable modes becomes broader at downstream positions. Figure 18(b) shows phase speeds of secondary instability modes. The phase speeds of sinuous modes decrease rather rapidly with
![]() $\unicode[STIX]{x1D6FC}$
, whereas those of even modes I exhibit a weaker dependence on
$\unicode[STIX]{x1D6FC}$
, whereas those of even modes I exhibit a weaker dependence on
![]() $\unicode[STIX]{x1D6FC}$
. The variation of the growth rates with
$\unicode[STIX]{x1D6FC}$
. The variation of the growth rates with
![]() $\unicode[STIX]{x1D6FC}$
and streamwise location, is similar to the inviscid predictions of Li & Malik (Reference Li and Malik1995).
$\unicode[STIX]{x1D6FC}$
and streamwise location, is similar to the inviscid predictions of Li & Malik (Reference Li and Malik1995).
Figure 19 displays the eigenfunctions of typical sinuous and varicose modes in terms of their streamwise velocity. The eigenfunction is normalized such that its maximum value is unity. As figure 19(a) indicates, an odd mode I has two pairs of dominant peaks, one pair is located at the outer part of the boundary layer, while the other is well within the boundary layer. The modal shape is similar to the inviscid predictions of Hall & Horseman (Reference Hall and Horseman1991) and Li & Malik (Reference Li and Malik1995). A notable difference is that the inner peaks in Hall & Horseman (Reference Hall and Horseman1991) are farther out from the valley centre, whereas those in our calculation and in Li & Malik (Reference Li and Malik1995) are nearer to the valley centre, resembling more closely the measurement shown in figure 16 of SB. All these peaks appear to reside in the region where
![]() $U$
varies quickly with
$U$
varies quickly with
![]() $z$
. Figure 19(b) shows that an even mode I has three dominant peaks, which are in the region where
$z$
. Figure 19(b) shows that an even mode I has three dominant peaks, which are in the region where
![]() $U$
varies quickly with
$U$
varies quickly with
![]() $y$
.
$y$
.

Figure 20. Characteristics of secondary instability: (a) the temporal growth rate and (b) the phase speed versus the streamwise spanwise wavenumber
![]() $\unicode[STIX]{x1D6FC}$
at
$\unicode[STIX]{x1D6FC}$
at
![]() $x^{\ast }=90$
, 95, 100 and 105 cm corresponding to
$x^{\ast }=90$
, 95, 100 and 105 cm corresponding to
![]() $\hat{x}=0.215,0.227,0.238$
and
$\hat{x}=0.215,0.227,0.238$
and
![]() $0.250$
, respectively.
$0.250$
, respectively.

Figure 21. The characteristics of a sinuous mode II with a wavenumber
![]() $\unicode[STIX]{x1D6FC}=2.9$
at
$\unicode[STIX]{x1D6FC}=2.9$
at
![]() $\hat{x}=0.227$
(
$\hat{x}=0.227$
(
![]() $x^{\ast }=95$
cm). (a) Contours of the streamwise velocity eigenfunction (absolute value, solid line) and the base flow (dashed lines). Nine contour levels are specified ranging from 0.1 to 0.9. (b) The variation of growth rate (solid line) and frequency (dashed line) with
$x^{\ast }=95$
cm). (a) Contours of the streamwise velocity eigenfunction (absolute value, solid line) and the base flow (dashed lines). Nine contour levels are specified ranging from 0.1 to 0.9. (b) The variation of growth rate (solid line) and frequency (dashed line) with
![]() $R_{\unicode[STIX]{x1D6EC}}$
; the circle indicates the position
$R_{\unicode[STIX]{x1D6EC}}$
; the circle indicates the position
![]() $R_{\unicode[STIX]{x1D6EC}}=1145$
.
$R_{\unicode[STIX]{x1D6EC}}=1145$
.
Figure 20 shows the growth rates and phase speeds at
![]() $\hat{x}=0.215$
,
$\hat{x}=0.215$
,
![]() $0.227$
,
$0.227$
,
![]() $0.238$
and
$0.238$
and
![]() $0.250$
. Both even modes I and odd modes I are found at these four streamwise positions further downstream. The stability characteristics changes at
$0.250$
. Both even modes I and odd modes I are found at these four streamwise positions further downstream. The stability characteristics changes at
![]() $\hat{x}=0.215$
in that downstream of this position, there emerge odd modes II, which have larger wavenumbers. The existence of this family of modes was noted only recently by Ren & Fu (Reference Ren and Fu2015). From
$\hat{x}=0.215$
in that downstream of this position, there emerge odd modes II, which have larger wavenumbers. The existence of this family of modes was noted only recently by Ren & Fu (Reference Ren and Fu2015). From
![]() $\hat{x}=0.227$
, for
$\hat{x}=0.227$
, for
![]() $\unicode[STIX]{x1D6FC}$
less than approximately 1.0, odd modes I are dominant at all these streamwise positions, but for
$\unicode[STIX]{x1D6FC}$
less than approximately 1.0, odd modes I are dominant at all these streamwise positions, but for
![]() $\unicode[STIX]{x1D6FC}>1.0$
, even modes I dominate until
$\unicode[STIX]{x1D6FC}>1.0$
, even modes I dominate until
![]() $\unicode[STIX]{x1D6FC}$
reaches a certain value, where odd modes II take over. The growth rates of secondary instability modes increase until
$\unicode[STIX]{x1D6FC}$
reaches a certain value, where odd modes II take over. The growth rates of secondary instability modes increase until
![]() $\hat{x}=0.250$
, after which they drop as Görtler vortices attenuate, but interestingly the spectral range of unstable modes continues to expand. Figure 20(b) shows that the phase speeds of odd modes II are lower than those of other modes at every streamwise position. Hence odd modes II tend to concentrate in the wall region and may be difficult to detect, which might be the reason why they were not discovered by SB (1987).
$\hat{x}=0.250$
, after which they drop as Görtler vortices attenuate, but interestingly the spectral range of unstable modes continues to expand. Figure 20(b) shows that the phase speeds of odd modes II are lower than those of other modes at every streamwise position. Hence odd modes II tend to concentrate in the wall region and may be difficult to detect, which might be the reason why they were not discovered by SB (1987).
The eigenfunction of a typical odd mode II is shown in figure 21(a). The streamwise velocity
![]() $|u_{s}|$
of the odd mode II at
$|u_{s}|$
of the odd mode II at
![]() $x^{\ast }=95$
cm with a wavenumber
$x^{\ast }=95$
cm with a wavenumber
![]() $\unicode[STIX]{x1D6FC}=2.9$
is plotted. A question arises as to whether odd modes II are of viscous nature or essentially inviscid. In order to answer this question, we calculated the growth rates
$\unicode[STIX]{x1D6FC}=2.9$
is plotted. A question arises as to whether odd modes II are of viscous nature or essentially inviscid. In order to answer this question, we calculated the growth rates
![]() $\unicode[STIX]{x1D714}_{i}$
and frequencies
$\unicode[STIX]{x1D714}_{i}$
and frequencies
![]() $\unicode[STIX]{x1D714}_{r}$
of odd modes II for very high Reynolds numbers, which represent the inviscid asymptotic limit. As is shown in figure 21(b), the growth rate increases monotonically with
$\unicode[STIX]{x1D714}_{r}$
of odd modes II for very high Reynolds numbers, which represent the inviscid asymptotic limit. As is shown in figure 21(b), the growth rate increases monotonically with
![]() $R_{\unicode[STIX]{x1D6EC}}$
and finally approaches a constant, and the frequency
$R_{\unicode[STIX]{x1D6EC}}$
and finally approaches a constant, and the frequency
![]() $\unicode[STIX]{x1D714}_{r}$
becomes independent of
$\unicode[STIX]{x1D714}_{r}$
becomes independent of
![]() $R_{\unicode[STIX]{x1D6EC}}$
too, implying that odd modes II are inviscid in character.
$R_{\unicode[STIX]{x1D6EC}}$
too, implying that odd modes II are inviscid in character.

Figure 22. (a,b) The spatial growth rates of secondary instability versus the frequency at different streamwise locations.
When a temporal secondary mode (
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D714}$
) is found, the spatial growth rate can be obtained from the temporal rate by using Gaster transformation (Gaster 1962), according to which the complex wavenumber
$\unicode[STIX]{x1D714}$
) is found, the spatial growth rate can be obtained from the temporal rate by using Gaster transformation (Gaster 1962), according to which the complex wavenumber
![]() $\tilde{\unicode[STIX]{x1D6FC}}$
is related to
$\tilde{\unicode[STIX]{x1D6FC}}$
is related to
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D714}$
via
$\unicode[STIX]{x1D714}$
via
where
![]() $C_{g}=\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}\equiv |C_{g}|\text{e}^{\text{i}\unicode[STIX]{x1D712}}$
is the (complex-valued) group velocity with
$C_{g}=\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}\equiv |C_{g}|\text{e}^{\text{i}\unicode[STIX]{x1D712}}$
is the (complex-valued) group velocity with
![]() $\unicode[STIX]{x1D712}$
being the phase of
$\unicode[STIX]{x1D712}$
being the phase of
![]() $C_{g}$
. Figure 22 displays the spatial growth rates so obtained at several locations in the range of
$C_{g}$
. Figure 22 displays the spatial growth rates so obtained at several locations in the range of
![]() $x^{\ast }=80\sim 105$
cm. Lower frequency unstable waves (
$x^{\ast }=80\sim 105$
cm. Lower frequency unstable waves (
![]() $\unicode[STIX]{x1D714}_{r}<0.7$
) grow first but at smaller rates. The dimensional frequency
$\unicode[STIX]{x1D714}_{r}<0.7$
) grow first but at smaller rates. The dimensional frequency
![]() $f^{\ast }$
reported in experiments is related to
$f^{\ast }$
reported in experiments is related to
![]() $\unicode[STIX]{x1D714}_{r}$
by
$\unicode[STIX]{x1D714}_{r}$
by
Upstream of
![]() $\hat{x}=0.215$
, the most dangerous sinuous modes are centred at
$\hat{x}=0.215$
, the most dangerous sinuous modes are centred at
![]() $\unicode[STIX]{x1D714}_{r}=0.6$
, corresponding to
$\unicode[STIX]{x1D714}_{r}=0.6$
, corresponding to
![]() $f^{\ast }=128$
Hz. In the experiment of SB, the most dominant wave has a frequency of 130 Hz, which is very close to our theoretical prediction. In addition, the iso-contours of the streamwise velocity fluctuations at
$f^{\ast }=128$
Hz. In the experiment of SB, the most dominant wave has a frequency of 130 Hz, which is very close to our theoretical prediction. In addition, the iso-contours of the streamwise velocity fluctuations at
![]() $\hat{x}=0.191,0.215$
and
$\hat{x}=0.191,0.215$
and
![]() $0.238$
in figure 16 of SB, exhibit a structure very similar to that of odd modes I. Comparisons were made previously by Sabry & Liu (Reference Sabry and Liu1991) and Yu & Liu (Reference Yu and Liu1991), but their instability analysis was performed for temporally evolving vortices. For spatially evolving vortices, the inviscid calculations (Hall & Horseman Reference Hall and Horseman1991; Li & Malik Reference Li and Malik1995) gave the instability characteristics (including the range of frequency) broadly in agreement with experiments. The amplification of secondary instability modes may explain the abrupt change of the intensity of unsteady disturbances, shown in figure 6.
$0.238$
in figure 16 of SB, exhibit a structure very similar to that of odd modes I. Comparisons were made previously by Sabry & Liu (Reference Sabry and Liu1991) and Yu & Liu (Reference Yu and Liu1991), but their instability analysis was performed for temporally evolving vortices. For spatially evolving vortices, the inviscid calculations (Hall & Horseman Reference Hall and Horseman1991; Li & Malik Reference Li and Malik1995) gave the instability characteristics (including the range of frequency) broadly in agreement with experiments. The amplification of secondary instability modes may explain the abrupt change of the intensity of unsteady disturbances, shown in figure 6.
Figure 22 also shows that the growth rate of the most unstable higher-frequency even mode (
![]() $\unicode[STIX]{x1D714}=0.8$
) is comparable with that of the lower-frequency one (
$\unicode[STIX]{x1D714}=0.8$
) is comparable with that of the lower-frequency one (
![]() $\unicode[STIX]{x1D714}=0.4$
) at
$\unicode[STIX]{x1D714}=0.4$
) at
![]() $\hat{x}=0.215$
. The frequency of the former is about twice that of the latter, and will be even higher at locations farther downstream. The band of unstable modes becomes broader downstream despite the fact that the intensity of Görtler vortices decreases, implying that not only the amplitude but also the spatial structure of vortices is relevant to the instability characteristics.
$\hat{x}=0.215$
. The frequency of the former is about twice that of the latter, and will be even higher at locations farther downstream. The band of unstable modes becomes broader downstream despite the fact that the intensity of Görtler vortices decreases, implying that not only the amplitude but also the spatial structure of vortices is relevant to the instability characteristics.

Figure 23. The local spatial growth rates of modes each with a fixed frequency, and comparison with the experimental data of SB (1987). The results are shown for four different frequencies,
![]() $\unicode[STIX]{x1D714}=0.3$
(65 Hz),
$\unicode[STIX]{x1D714}=0.3$
(65 Hz),
![]() $0.5$
(107 Hz),
$0.5$
(107 Hz),
![]() $0.598$
(130 Hz) and
$0.598$
(130 Hz) and
![]() $0.8$
(174 Hz).
$0.8$
(174 Hz).
We also traced the downstream development of several modes, each with a fixed frequency. The variation of their growth rates with the streamwise distance is displayed in figure 23. Obviously, the mode with
![]() $\unicode[STIX]{x1D714}=0.598$
(
$\unicode[STIX]{x1D714}=0.598$
(
![]() $f^{\ast }=130$
Hz) starts to amplify from
$f^{\ast }=130$
Hz) starts to amplify from
![]() $\hat{x}=0.190$
(
$\hat{x}=0.190$
(
![]() $x^{\ast }=80$
cm). Its maximum growth occurs in the range of
$x^{\ast }=80$
cm). Its maximum growth occurs in the range of
![]() $\hat{x}=0.225\sim 0.250$
(
$\hat{x}=0.225\sim 0.250$
(
![]() $x^{\ast }=94\sim 105$
cm), which is same as the experimental observation. Also displayed in figure 23 is the growth rate of the r.m.s. of unsteady perturbations, calculated by
$x^{\ast }=94\sim 105$
cm), which is same as the experimental observation. Also displayed in figure 23 is the growth rate of the r.m.s. of unsteady perturbations, calculated by
where
![]() $u_{rms}^{\prime }$
denotes the experimentally measured r.m.s. of total unsteady perturbations. Since no experimental data on growth rates of secondary instability are available, we take
$u_{rms}^{\prime }$
denotes the experimentally measured r.m.s. of total unsteady perturbations. Since no experimental data on growth rates of secondary instability are available, we take
![]() $\unicode[STIX]{x1D70E}$
as their proxy. The predicted spatial growth rates
$\unicode[STIX]{x1D70E}$
as their proxy. The predicted spatial growth rates
![]() $-\unicode[STIX]{x1D6FC}_{i}$
are more or less of the same order of magnitude as the measured
$-\unicode[STIX]{x1D6FC}_{i}$
are more or less of the same order of magnitude as the measured
![]() $\unicode[STIX]{x1D70E}$
, but the former are several times larger than the latter. This quantitative discrepancy is not surprising because
$\unicode[STIX]{x1D70E}$
, but the former are several times larger than the latter. This quantitative discrepancy is not surprising because
![]() $-\unicode[STIX]{x1D6FC}_{i}$
and
$-\unicode[STIX]{x1D6FC}_{i}$
and
![]() $\unicode[STIX]{x1D70E}$
are, though related, not the same quantity. In experiment, rather than following the development of a well-defined mode, the growth rate
$\unicode[STIX]{x1D70E}$
are, though related, not the same quantity. In experiment, rather than following the development of a well-defined mode, the growth rate
![]() $\unicode[STIX]{x1D70E}$
of unsteady disturbances was computed from
$\unicode[STIX]{x1D70E}$
of unsteady disturbances was computed from
![]() $u_{rms}$
, which includes a broad band of components. The unstable mode is smeared, and thus
$u_{rms}$
, which includes a broad band of components. The unstable mode is smeared, and thus
![]() $\unicode[STIX]{x1D70E}$
, which measures the amplification rate of overall unsteady disturbances, is expected to be smaller than
$\unicode[STIX]{x1D70E}$
, which measures the amplification rate of overall unsteady disturbances, is expected to be smaller than
![]() $-\unicode[STIX]{x1D6FC}_{i}$
.
$-\unicode[STIX]{x1D6FC}_{i}$
.
The results in figures 22 and 23 indicate that higher-frequency even modes start to amplify later but at larger rates. Their presence and intensity in the boundary layer depend, like all modes, on the content of high-frequency FSVD and receptivity. If triggered, on the theoretical ground they are expected eventually to dominate farther downstream. We note that such even modes, which manifest themselves as horseshoe structures, were indeed observed by Aihara & Koyama (Reference Aihara and Koyama1981) and Ito (Reference Ito1985). However, in the experiment of SB even modes appeared rather infrequently, probably because they have not yet gained significant amplitudes in the region of measurement.
5.2.2 Secondary instability calculations pertaining to MWS (2005) experiment
MWS (2005) studied the onset of secondary instability of forced wavelength Görtler vortices by experiment. Through a spectral analysis of velocity fluctuations, they found that the peak frequency is approximately 150 Hz, and the spanwise wavelength is comparable with the spacing of the primary Görtler vortices, implying that the fundamental secondary instability is the dominant mode in their experiment. Secondary instability calculations are performed for Görtler vortices pertaining to this condition.

Figure 24. The characteristics of secondary instability of Görtler vortices in the experiment of MWS (2005): (a) the temporal growth rates, and (b) the phase speeds versus the streamwise wavenumber
![]() $\unicode[STIX]{x1D6FC}$
at different streamwise locations.
$\unicode[STIX]{x1D6FC}$
at different streamwise locations.

Figure 25. The spatial growth rate versus frequency at different streamwise locations.

Figure 26. The local spatial growth rates of modes each with a fixed frequency and comparison with the experimental data of MWS (2005). Results are shown for three unstable waves with
![]() $\unicode[STIX]{x1D714}=0.5$
(100 Hz),
$\unicode[STIX]{x1D714}=0.5$
(100 Hz),
![]() $0.75$
(150 Hz) and
$0.75$
(150 Hz) and
![]() $1.5$
(300 Hz).
$1.5$
(300 Hz).
Figure 24(a) displays the temporal growth rate for a range of the streamwise wavenumbers at different downstream locations. In the upstream region up to
![]() $x^{\ast }\approx 60$
cm, only odd modes I exist. Three families of modes, odd modes I, even modes I and odd modes II, are observed at
$x^{\ast }\approx 60$
cm, only odd modes I exist. Three families of modes, odd modes I, even modes I and odd modes II, are observed at
![]() $x^{\ast }=65$
cm. The growth rates of even modes increase until
$x^{\ast }=65$
cm. The growth rates of even modes increase until
![]() $x^{\ast }=70$
cm, after which they decrease. From
$x^{\ast }=70$
cm, after which they decrease. From
![]() $x^{\ast }=70$
cm, the growth rates of odd modes II increase to attain their respective maximum values, while those of odd modes I decrease slightly. The range of most unstable even modes I shrinks. At
$x^{\ast }=70$
cm, the growth rates of odd modes II increase to attain their respective maximum values, while those of odd modes I decrease slightly. The range of most unstable even modes I shrinks. At
![]() $x^{\ast }=95.2$
cm, odd modes II become most unstable. Figure 24(b) shows the phase speeds of the most unstable modes identified in different wavenumber ranges. The temporal growth rates are again converted into spatial ones using Gaster transformation. Figure 25 plots the spatial growth rates so obtained versus the frequency at different streamwise locations. The dominant frequencies of the odd mode I, even mode I and odd mode II are found to be 0.5 (100 Hz), 0.75 (150 Hz) and 1.5 (260 Hz), respectively. Obviously, large temporal growth rates translate broadly into large spatial amplification. Since strong spatial growth rates persisting over a streamwise region imply substantial accumulated amplification (see below), which determines which mode at a given location would dominate, it may be inferred that as vortices develop downstream the dominant disturbances are odd modes I first, then even modes follow, and odd modes II will dominate farther downstream. That odd modes I grow first is consistent with the experiment observation. MWS found that the fundamental frequency was in the range of 120–180 Hz, which is in reasonable agreement with our theoretical result. Given the eigenfunction of an odd mode II, fluctuations are expected to concentrate in the region near the ‘stem’ of the mushroom prior to turbulence. The turbulent intensity contours shown in figure 10 of Mitsudharmadi et al. (Reference Mitsudharmadi, Winoto and Shah2004) are consistent with this expectation, and may be taken as evidence for the existence of odd modes II.
$x^{\ast }=95.2$
cm, odd modes II become most unstable. Figure 24(b) shows the phase speeds of the most unstable modes identified in different wavenumber ranges. The temporal growth rates are again converted into spatial ones using Gaster transformation. Figure 25 plots the spatial growth rates so obtained versus the frequency at different streamwise locations. The dominant frequencies of the odd mode I, even mode I and odd mode II are found to be 0.5 (100 Hz), 0.75 (150 Hz) and 1.5 (260 Hz), respectively. Obviously, large temporal growth rates translate broadly into large spatial amplification. Since strong spatial growth rates persisting over a streamwise region imply substantial accumulated amplification (see below), which determines which mode at a given location would dominate, it may be inferred that as vortices develop downstream the dominant disturbances are odd modes I first, then even modes follow, and odd modes II will dominate farther downstream. That odd modes I grow first is consistent with the experiment observation. MWS found that the fundamental frequency was in the range of 120–180 Hz, which is in reasonable agreement with our theoretical result. Given the eigenfunction of an odd mode II, fluctuations are expected to concentrate in the region near the ‘stem’ of the mushroom prior to turbulence. The turbulent intensity contours shown in figure 10 of Mitsudharmadi et al. (Reference Mitsudharmadi, Winoto and Shah2004) are consistent with this expectation, and may be taken as evidence for the existence of odd modes II.
Figure 26 shows the variation with the streamwise distance of the spatial growth rates of secondary instability modes with fixed frequencies
![]() $\unicode[STIX]{x1D714}=0.5$
(100 Hz),
$\unicode[STIX]{x1D714}=0.5$
(100 Hz),
![]() $0.75$
(150 Hz) and
$0.75$
(150 Hz) and
![]() $1.5$
(300 Hz). As for the case of SB, lower-frequency waves grow first and expected to be observed upstream, but higher-frequency waves are likely to become significant too due to their accumulated amplification, over the regions
$1.5$
(300 Hz). As for the case of SB, lower-frequency waves grow first and expected to be observed upstream, but higher-frequency waves are likely to become significant too due to their accumulated amplification, over the regions
![]() $x^{\ast }>60$
and
$x^{\ast }>60$
and
![]() $x^{\ast }>65$
respectively for the two modes shown. Again, the predicted growth rates of secondary instability are compared with the measured
$x^{\ast }>65$
respectively for the two modes shown. Again, the predicted growth rates of secondary instability are compared with the measured
![]() $\unicode[STIX]{x1D70E}$
, and they are found to be of the same order of magnitude. However, significant difference exists, a possible reason for which was given earlier.
$\unicode[STIX]{x1D70E}$
, and they are found to be of the same order of magnitude. However, significant difference exists, a possible reason for which was given earlier.
5.3 Secondary instability of unsteady Görtler vortices
During the evolution of unsteady Görtler vortices, the distorted instantaneous velocity profiles appear, in certain phases, inflectional in the streamwise and spanwise directions, and thus may become inviscidly unstable. This expectation is confirmed by our secondary instability analysis.

Figure 27. Instability characteristics of unsteady Görtler vortices with
![]() $\hat{k}_{1}=5.291$
at
$\hat{k}_{1}=5.291$
at
![]() $\hat{x}=0.215$
(
$\hat{x}=0.215$
(
![]() $x^{\ast }=90$
cm) (a,b) and
$x^{\ast }=90$
cm) (a,b) and
![]() $\hat{x}=0.238$
(
$\hat{x}=0.238$
(
![]() $x^{\ast }=100$
cm) (c,d) the temporal growth rate
$x^{\ast }=100$
cm) (c,d) the temporal growth rate
![]() $\unicode[STIX]{x1D714}_{i}$
and the phase speed
$\unicode[STIX]{x1D714}_{i}$
and the phase speed
![]() $C_{r}$
versus the wavenumber
$C_{r}$
versus the wavenumber
![]() $\unicode[STIX]{x1D6FC}$
at seven instants.
$\unicode[STIX]{x1D6FC}$
at seven instants.
Figure 27(a,b) shows the instability characteristics at
![]() $\hat{x}=0.215$
(
$\hat{x}=0.215$
(
![]() $x^{\ast }=90$
cm), where unsteady Görtler vortices with frequency
$x^{\ast }=90$
cm), where unsteady Görtler vortices with frequency
![]() $\hat{k}_{1}=5.29$
(2 Hz) reach their maximum amplitude. Calculations were performed at seven instants corresponding to
$\hat{k}_{1}=5.29$
(2 Hz) reach their maximum amplitude. Calculations were performed at seven instants corresponding to
![]() $\unicode[STIX]{x1D719}=13\unicode[STIX]{x03C0}/16$
,
$\unicode[STIX]{x1D719}=13\unicode[STIX]{x03C0}/16$
,
![]() $\unicode[STIX]{x03C0},20\unicode[STIX]{x03C0}/16,22\unicode[STIX]{x03C0}/16$
,
$\unicode[STIX]{x03C0},20\unicode[STIX]{x03C0}/16,22\unicode[STIX]{x03C0}/16$
,
![]() $25\unicode[STIX]{x03C0}/16,30\unicode[STIX]{x03C0}/16$
and
$25\unicode[STIX]{x03C0}/16,30\unicode[STIX]{x03C0}/16$
and
![]() $31\unicode[STIX]{x03C0}/16$
, the streamwise velocity profiles at which are displayed in figure 16. Within a short time interval around
$31\unicode[STIX]{x03C0}/16$
, the streamwise velocity profiles at which are displayed in figure 16. Within a short time interval around
![]() $\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
, only a small band of weakly growing modes exists with
$\unicode[STIX]{x1D719}=25\unicode[STIX]{x03C0}/16$
, only a small band of weakly growing modes exists with
![]() $\unicode[STIX]{x1D6FC}$
near 0.9. Vigorous growth occurs around
$\unicode[STIX]{x1D6FC}$
near 0.9. Vigorous growth occurs around
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
and
$\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
and
![]() $31\unicode[STIX]{x03C0}/16$
. The secondary instability is thus intermittent in time, similar to the flat-plate case studied by Wu & Choudhari (Reference Wu and Choudhari2003) and Ricco et al. (Reference Ricco, Luo and Wu2011). The maximum growth rate is more than twice that of the steady case shown in figure 20 at the same streamwise location. Figure 27(b) plots the phase speeds, which fall in the range of
$31\unicode[STIX]{x03C0}/16$
. The secondary instability is thus intermittent in time, similar to the flat-plate case studied by Wu & Choudhari (Reference Wu and Choudhari2003) and Ricco et al. (Reference Ricco, Luo and Wu2011). The maximum growth rate is more than twice that of the steady case shown in figure 20 at the same streamwise location. Figure 27(b) plots the phase speeds, which fall in the range of
![]() $0.5{-}0.7U_{\infty }$
. Figure 27(c,d) presents the growth rates and phase speeds at
$0.5{-}0.7U_{\infty }$
. Figure 27(c,d) presents the growth rates and phase speeds at
![]() $\hat{x}=0.238$
(
$\hat{x}=0.238$
(
![]() $x^{\ast }=100$
cm). Both the growth rate and the phase speed are slightly larger in all phases than those at
$x^{\ast }=100$
cm). Both the growth rate and the phase speed are slightly larger in all phases than those at
![]() $\hat{x}=0.215$
. The temporal growth rates are merely suggestive of what kind of disturbances are likely to emerge. As in the steady case, the temporal growth rates can be converted to spatial ones, and the actual presence and intensity of the secondary disturbance depend on receptivity. However, for unsteady Görtler vortices the secondary disturbance is modulated both in time and space, tracing its development is more complicated than integrating the local spatial growth rate over the streamwise distance, and is not pursued in the present paper.
$\hat{x}=0.215$
. The temporal growth rates are merely suggestive of what kind of disturbances are likely to emerge. As in the steady case, the temporal growth rates can be converted to spatial ones, and the actual presence and intensity of the secondary disturbance depend on receptivity. However, for unsteady Görtler vortices the secondary disturbance is modulated both in time and space, tracing its development is more complicated than integrating the local spatial growth rate over the streamwise distance, and is not pursued in the present paper.

Figure 28. Contours of the eigenfunction (the streamwise velocity) at
![]() $\hat{x}=0.238$
(
$\hat{x}=0.238$
(
![]() $x^{\ast }=100$
cm) for
$x^{\ast }=100$
cm) for
![]() $\hat{k}_{1}=5.691$
: (a–c)
$\hat{k}_{1}=5.691$
: (a–c)
![]() $\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
; (a)
$\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
; (a)
![]() $\unicode[STIX]{x1D6FC}=1.2$
, (b)
$\unicode[STIX]{x1D6FC}=1.2$
, (b)
![]() $\unicode[STIX]{x1D6FC}=2.3$
, (c)
$\unicode[STIX]{x1D6FC}=2.3$
, (c)
![]() $\unicode[STIX]{x1D6FC}=3.7$
; (d–f)
$\unicode[STIX]{x1D6FC}=3.7$
; (d–f)
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
; (d)
$\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
; (d)
![]() $\unicode[STIX]{x1D6FC}=0.9$
, (e)
$\unicode[STIX]{x1D6FC}=0.9$
, (e)
![]() $\unicode[STIX]{x1D6FC}=2.1$
, (f)
$\unicode[STIX]{x1D6FC}=2.1$
, (f)
![]() $\unicode[STIX]{x1D6FC}=3.8$
.
$\unicode[STIX]{x1D6FC}=3.8$
.
Figure 28 plots the eigenfunctions of secondary instability at
![]() $\hat{x}=0.238$
, and contours of the instantaneous streamwise velocity of Görtler vortices are also included. Similar to the steady case, odd modes I, even modes I and odd modes II exist for small, intermediate and large
$\hat{x}=0.238$
, and contours of the instantaneous streamwise velocity of Görtler vortices are also included. Similar to the steady case, odd modes I, even modes I and odd modes II exist for small, intermediate and large
![]() $\unicode[STIX]{x1D6FC}$
. Note that for this frequency, unsteady Görtler vortices meander in the spanwise direction, and so do the eigenfunctions of secondary instability.
$\unicode[STIX]{x1D6FC}$
. Note that for this frequency, unsteady Görtler vortices meander in the spanwise direction, and so do the eigenfunctions of secondary instability.
Next we consider Görtler vortices with a moderate frequency
![]() $\hat{k}_{1}=52.916$
(
$\hat{k}_{1}=52.916$
(
![]() $f^{\ast }=10$
Hz). Since saturation occurs later than in the steady and lower-frequency cases, secondary instability calculations are carried at positions somewhat farther downstream, at
$f^{\ast }=10$
Hz). Since saturation occurs later than in the steady and lower-frequency cases, secondary instability calculations are carried at positions somewhat farther downstream, at
![]() $\hat{x}=0.288$
and
$\hat{x}=0.288$
and
![]() $0.336$
(
$0.336$
(
![]() $x^{\ast }=120$
cm and
$x^{\ast }=120$
cm and
![]() $140$
cm). The results are shown in figure 29. The variation of growth rates and phase speeds of dominant odd modes I becomes moderate, i.e. the intermittency of secondary instability weakens. The growth rates of odd modes II, centred at the second peak of these curves, still vary considerably with the phase at
$140$
cm). The results are shown in figure 29. The variation of growth rates and phase speeds of dominant odd modes I becomes moderate, i.e. the intermittency of secondary instability weakens. The growth rates of odd modes II, centred at the second peak of these curves, still vary considerably with the phase at
![]() $\hat{x}=0.288$
, but their variation becomes weaker too at
$\hat{x}=0.288$
, but their variation becomes weaker too at
![]() $\hat{x}=0.336$
even though their phase speeds exhibit strong dependence on the phase (figure 29
d).
$\hat{x}=0.336$
even though their phase speeds exhibit strong dependence on the phase (figure 29
d).

Figure 29. Instability characteristics of unsteady Görtler vortices with
![]() $\hat{k}_{1}=52.916$
at
$\hat{k}_{1}=52.916$
at
![]() $\hat{x}=0.288$
(
$\hat{x}=0.288$
(
![]() $x^{\ast }=120$
cm) (a,b) and
$x^{\ast }=120$
cm) (a,b) and
![]() $\hat{x}=0.336$
(
$\hat{x}=0.336$
(
![]() $x^{\ast }=140$
cm) (c,d) the temporal growth rate and the phase speed
$x^{\ast }=140$
cm) (c,d) the temporal growth rate and the phase speed
![]() $C_{r}$
versus
$C_{r}$
versus
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Figure 30 displays the eigenfunctions of secondary instability at
![]() $\hat{x}=0.336$
(
$\hat{x}=0.336$
(
![]() $x^{\ast }=140$
cm) for
$x^{\ast }=140$
cm) for
![]() $\hat{k}_{1}=52.691$
. At each of the two instants, eigenfunctions of an odd mode I, an even mode I and an odd mode II are shown. The spanwise wavelength of the odd mode I is half of the fundamental period of the vortices, indicating that odd modes are controlled primarily by the strong (0,2) component. They concentrate in the shoulder and stem regions of Görtler vortices. The even mode I and odd mode II have the same fundamental periodicity. They are intermittent, and reside on the top and in the stem region of the mushroom respectively.
$\hat{k}_{1}=52.691$
. At each of the two instants, eigenfunctions of an odd mode I, an even mode I and an odd mode II are shown. The spanwise wavelength of the odd mode I is half of the fundamental period of the vortices, indicating that odd modes are controlled primarily by the strong (0,2) component. They concentrate in the shoulder and stem regions of Görtler vortices. The even mode I and odd mode II have the same fundamental periodicity. They are intermittent, and reside on the top and in the stem region of the mushroom respectively.

Figure 30. Contours of the eigenfunctions (the streamwise velocity) at
![]() $\hat{x}=0.336$
(
$\hat{x}=0.336$
(
![]() $x^{\ast }=140$
cm) for
$x^{\ast }=140$
cm) for
![]() $\hat{k}_{1}=52.691$
: (a–c)
$\hat{k}_{1}=52.691$
: (a–c)
![]() $\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
; (a)
$\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
; (a)
![]() $\unicode[STIX]{x1D6FC}=1.3$
, (b)
$\unicode[STIX]{x1D6FC}=1.3$
, (b)
![]() $\unicode[STIX]{x1D6FC}=2.0$
, (c)
$\unicode[STIX]{x1D6FC}=2.0$
, (c)
![]() $\unicode[STIX]{x1D6FC}=3.1$
; (d–f)
$\unicode[STIX]{x1D6FC}=3.1$
; (d–f)
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
; (d)
$\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
; (d)
![]() $\unicode[STIX]{x1D6FC}=1.2$
, (e)
$\unicode[STIX]{x1D6FC}=1.2$
, (e)
![]() $\unicode[STIX]{x1D6FC}=2.1$
, (f)
$\unicode[STIX]{x1D6FC}=2.1$
, (f)
![]() $\unicode[STIX]{x1D6FC}=3.0$
.
$\unicode[STIX]{x1D6FC}=3.0$
.

Figure 31. Instability characteristics of unsteady Görtler vortices with
![]() $\hat{k}_{1}=104.382$
at
$\hat{k}_{1}=104.382$
at
![]() $\hat{x}=0.360$
(
$\hat{x}=0.360$
(
![]() $x^{\ast }=150$
cm) (a,b) and
$x^{\ast }=150$
cm) (a,b) and
![]() $\hat{x}=0.381$
(
$\hat{x}=0.381$
(
![]() $x^{\ast }=160$
cm) (c,d) the temporal growth rate and the phase speed
$x^{\ast }=160$
cm) (c,d) the temporal growth rate and the phase speed
![]() $C_{r}$
versus
$C_{r}$
versus
![]() $\unicode[STIX]{x1D6FC}$
at different phases.
$\unicode[STIX]{x1D6FC}$
at different phases.
Figure 31 shows the secondary instability characteristics of Görtler vortices with
![]() $\hat{k}_{1}=104.382$
(
$\hat{k}_{1}=104.382$
(
![]() $f^{\ast }=20$
Hz) at
$f^{\ast }=20$
Hz) at
![]() $\hat{x}=0.360$
and
$\hat{x}=0.360$
and
![]() $0.381$
(
$0.381$
(
![]() $x^{\ast }=150$
cm and
$x^{\ast }=150$
cm and
![]() $160$
cm). For such a high frequency, the intermittence of secondary instability almost disappears. Both the growth rates and phase speeds vary very little with the phase at each streamwise location. The maximum growth rates of odd and even modes I at
$160$
cm). For such a high frequency, the intermittence of secondary instability almost disappears. Both the growth rates and phase speeds vary very little with the phase at each streamwise location. The maximum growth rates of odd and even modes I at
![]() $\hat{x}=0.381$
become larger than those at
$\hat{x}=0.381$
become larger than those at
![]() $\hat{x}=0.360$
, but the growth rates of odd modes II decrease. Contours of the eigenfunction (the streamwise velocity) at
$\hat{x}=0.360$
, but the growth rates of odd modes II decrease. Contours of the eigenfunction (the streamwise velocity) at
![]() $\hat{x}=0.381$
(
$\hat{x}=0.381$
(
![]() $x^{\ast }=160$
cm) are shown in figure 32. For each of three types of modes, the eigenfunctions at the two phases appear almost identical (steady). Their spanwise wavelength is half of the fundamental period. We may conclude that the secondary instability is completely controlled by the (0,2) component.
$x^{\ast }=160$
cm) are shown in figure 32. For each of three types of modes, the eigenfunctions at the two phases appear almost identical (steady). Their spanwise wavelength is half of the fundamental period. We may conclude that the secondary instability is completely controlled by the (0,2) component.

Figure 32. Contours of the eigenfunction (the streamwise velocity) at
![]() $\hat{x}=0.381$
(
$\hat{x}=0.381$
(
![]() $x^{\ast }=160$
cm) for
$x^{\ast }=160$
cm) for
![]() $\hat{k}_{1}=104.382$
: (a–c)
$\hat{k}_{1}=104.382$
: (a–c)
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
; (a)
$\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
; (a)
![]() $\unicode[STIX]{x1D6FC}=1.3$
, (b)
$\unicode[STIX]{x1D6FC}=1.3$
, (b)
![]() $\unicode[STIX]{x1D6FC}=1.9$
, (c)
$\unicode[STIX]{x1D6FC}=1.9$
, (c)
![]() $\unicode[STIX]{x1D6FC}=3.0$
; (d–f)
$\unicode[STIX]{x1D6FC}=3.0$
; (d–f)
![]() $\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
; (d)
$\unicode[STIX]{x1D719}=31\unicode[STIX]{x03C0}/16$
; (d)
![]() $\unicode[STIX]{x1D6FC}=1.3$
, (e)
$\unicode[STIX]{x1D6FC}=1.3$
, (e)
![]() $\unicode[STIX]{x1D6FC}=2.0$
, (f)
$\unicode[STIX]{x1D6FC}=2.0$
, (f)
![]() $\unicode[STIX]{x1D6FC}=3.0$
.
$\unicode[STIX]{x1D6FC}=3.0$
.
6 Summary and conclusions
It is well known that free-stream disturbances can enter the boundary layer to excite instability modes, which are Görtler vortices for the boundary layer over a concave wall. Since Görtler instability must in general be treated as an initial-value problem (in space with the streamwise variable playing the role of time), it is of crucial importance to specify the appropriate initial (i.e. upstream) disturbance, and receptivity is thus an inseparable part of the instability. In this paper, we investigated the formation and nonlinear evolution of Görtler vortices which arise as response to FSVD of sufficiently long wavelength. Excitation of Görtler vortices by sufficiently weak disturbances of this kind has been studied by WZL, whose formulation relied on that of LWG. That formulation was in the present study extended to the nonlinear case, where FSVD are strong enough to generate Görtler vortices of
![]() $O(1)$
magnitude, altering completely the original Blasius flow in the generic region where the local boundary-layer thickness becomes comparable with the spanwise wavelength of vortices. The action of FSVD on the boundary layer is accounted for by specifying both appropriate initial (upstream) and boundary (far-field) conditions, and the ensuing response in the boundary layer, which affects simultaneously the outer disturbances, is governed by the NUBRE, leading to a nonlinear initial-boundary-value problem. It should be noted that the popular practice of using continuous spectra of the Orr-Sommerfeld/Squire equations to represent FSVD and inlet (initial) condition is inappropriate. The theoretical progress made in the present paper is significant because it enables us to implement properly the downstream marching approach (Hall Reference Hall1983, Reference Hall1988), the advantage of which was compromised in the past because without taking into account the initial and boundary conditions, arbitrary disturbances or local eigenmodes were used as an initial condition.
$O(1)$
magnitude, altering completely the original Blasius flow in the generic region where the local boundary-layer thickness becomes comparable with the spanwise wavelength of vortices. The action of FSVD on the boundary layer is accounted for by specifying both appropriate initial (upstream) and boundary (far-field) conditions, and the ensuing response in the boundary layer, which affects simultaneously the outer disturbances, is governed by the NUBRE, leading to a nonlinear initial-boundary-value problem. It should be noted that the popular practice of using continuous spectra of the Orr-Sommerfeld/Squire equations to represent FSVD and inlet (initial) condition is inappropriate. The theoretical progress made in the present paper is significant because it enables us to implement properly the downstream marching approach (Hall Reference Hall1983, Reference Hall1988), the advantage of which was compromised in the past because without taking into account the initial and boundary conditions, arbitrary disturbances or local eigenmodes were used as an initial condition.
The FSVD is represented by a simplified model, a pair of oblique waves with opposite spanwise wavenumbers. The nonlinear initial-boundary-value problem was solved numerically. A predictor–corrector procedure together with an underrelaxation technique was employed to handle the nonlinear terms in the equations. It was found that Görtler vortices are excited in a boundary layer over a concave wall. They undergo non-modal growth, quasi-exponential amplification and nonlinear saturation for moderate level of FSVD, but bypass the modal growth stage if FSVD is strong. The nonlinear interactions inhabit the response, causing saturation of Görtler vortices. The eventual saturated amplitude appears to be independent of the intensity of FSVD provided that the Görtler number is non-zero. We compared our theoretical predictions with three steady experimental measurements. The amplitude development and structure of the vortices, the boundary-layer thickness and wall shear stress were all in excellent quantitative agreement with the experimental data of SB. The predicted streamwise velocity profiles of the vortices were also found to agree very well with the measurement of Ito (Reference Ito1985). To the best of our knowledge, this is the first time that the nonlinear evolution of Görtler vortices induced by free-stream disturbances is found to be in quantitative agreement with experiments. The predicted profiles mimic closely those measured in the experiment of Mitsudharmadi et al. (Reference Mitsudharmadi, Winoto and Shah2005), but appreciable difference exists, which was most likely caused by the presence of a pressure gradient in the experimental set-up.
We also investigated, for the first time, nonlinear evolution of unsteady Görtler vortices excited by FSVD. For fairly low frequencies, the vortices exhibit time dependence. However, somewhat paradoxically as the frequency increases, the vortices appear increasingly steady. This is due to the fact that the nonlinearly generated harmonic component (0,2) attains a larger amplitude and eventually becomes dominant.
The streamwise velocity of the distorted base flow in the presence of Görtler vortices depends on both
![]() $y$
and
$y$
and
![]() $z$
, is inflectional in both directions, and thus may be inviscidly unstable. A secondary instability analysis with viscosity included was performed for nonlinear Görtler vortices induced by free-stream disturbances, specifically pertaining to the experiments of SB and MWS. Numerical results confirmed that steady Görtler vortices are susceptible to inviscid secondary instability. Three families of unstable modes, odd modes I, II and even modes I, were identified in our calculations. Each of them can be the most unstable for certain ranges of the streamwise wavenumber and distance. The results show that even modes I have larger growth rates, but they commence farther downstream than odd modes I do. The latter result in the so-called sinuous type of breakdown. Their eigenfunctions closely resemble the experimental measurements. The Gaster transformation was used to convert the temporal growth rates to spatial ones. The growth rates of unstable modes of different frequency were compared with experiments. For the SB experiment, the frequencies of the unstable modes were found to be centred at 130 Hz for
$z$
, is inflectional in both directions, and thus may be inviscidly unstable. A secondary instability analysis with viscosity included was performed for nonlinear Görtler vortices induced by free-stream disturbances, specifically pertaining to the experiments of SB and MWS. Numerical results confirmed that steady Görtler vortices are susceptible to inviscid secondary instability. Three families of unstable modes, odd modes I, II and even modes I, were identified in our calculations. Each of them can be the most unstable for certain ranges of the streamwise wavenumber and distance. The results show that even modes I have larger growth rates, but they commence farther downstream than odd modes I do. The latter result in the so-called sinuous type of breakdown. Their eigenfunctions closely resemble the experimental measurements. The Gaster transformation was used to convert the temporal growth rates to spatial ones. The growth rates of unstable modes of different frequency were compared with experiments. For the SB experiment, the frequencies of the unstable modes were found to be centred at 130 Hz for
![]() $x^{\ast }$
in the range of 95–105 cm, in agreement with the experimental observation. The dominant region of secondary instability was in agreement with the experiment of MWS as well. The predicted spatial growth rate
$x^{\ast }$
in the range of 95–105 cm, in agreement with the experimental observation. The dominant region of secondary instability was in agreement with the experiment of MWS as well. The predicted spatial growth rate
![]() $-\unicode[STIX]{x1D6FC}_{i}$
of secondary instability modes was compared with the measured growth rate of the r.m.s. of the total unsteady fluctuations,
$-\unicode[STIX]{x1D6FC}_{i}$
of secondary instability modes was compared with the measured growth rate of the r.m.s. of the total unsteady fluctuations,
![]() $\unicode[STIX]{x1D70E}$
, which is different from, but a proxy for, modal growth rates. The former is several times larger than the latter, nevertheless they are more or less of the same order of magnitude. The secondary instability of unsteady Görtler vortices was analysed for the first time. It was found that for low-frequency vortices, secondary instability is intermittent. However, the intermittence diminishes as the frequency increases.
$\unicode[STIX]{x1D70E}$
, which is different from, but a proxy for, modal growth rates. The former is several times larger than the latter, nevertheless they are more or less of the same order of magnitude. The secondary instability of unsteady Görtler vortices was analysed for the first time. It was found that for low-frequency vortices, secondary instability is intermittent. However, the intermittence diminishes as the frequency increases.
The present integrated theoretical framework allows a quantitative relation to be established between free-stream disturbances and the key transition processes: the formation, nonlinear evolution and secondary instability of Görtler vortices; high-frequency components of FSVD appear to trigger secondary instability modes but the receptivity to such disturbances is not considered. The formulation and calculation can readily be extended to the more general and realistic case of broadband free-stream turbulence. The resulting Görtler vortices and their secondary instability properties can be predicted and compared with experiment results. The present work considered only a zero-pressure-gradient boundary layer. However, a streamwise pressure gradient is usually present in many flows of practical interest, such as the boundary layers over turbomachinery blades (where a Coriolis force is also present due to the system rotation). Work is in progress to include the effects of the streamwise pressure gradient. By accounting for these factors and excitation of secondary instability modes by high-frequency components of FSVD, for which there was strong experimental evidence, it would be possible eventually to predict, on the first-principle basis, the characteristics and transition location of the boundary layers over blades in turbomachinery. Even before the receptivity of the secondary instability is resolved, an improved correlation of the transition location with free-stream turbulence may be attempted based on the onset and integrated amplification of the secondary instability.
Acknowledgement
The authors would like to thank Professor P. Hall as well as the referees for their helpful comments and suggestions. This research was supported by NSFC (grants 11172204, 11472190 and 11332007).
Appendix A. Disturbances in the outer region and the far-field condition
The outer region IV corresponds to
![]() $x,y=O(R_{\unicode[STIX]{x1D6EC}})$
, and thus we introduce the variable
$x,y=O(R_{\unicode[STIX]{x1D6EC}})$
, and thus we introduce the variable
in addition to
![]() $\hat{x}=x/R_{\unicode[STIX]{x1D6EC}}$
. As in the flat-plate case (Ricco et al.
Reference Ricco, Luo and Wu2011), the perturbation in this region consists of the three-dimensional vortical disturbances convected from upstream and a two-dimensional perturbation generated by the viscous motion within the boundary layer through the displacement effect. Similar to the steady perturbations considered by Wundrow & Goldstein (Reference Wundrow and Goldstein2001), the flow field can be decomposed as
$\hat{x}=x/R_{\unicode[STIX]{x1D6EC}}$
. As in the flat-plate case (Ricco et al.
Reference Ricco, Luo and Wu2011), the perturbation in this region consists of the three-dimensional vortical disturbances convected from upstream and a two-dimensional perturbation generated by the viscous motion within the boundary layer through the displacement effect. Similar to the steady perturbations considered by Wundrow & Goldstein (Reference Wundrow and Goldstein2001), the flow field can be decomposed as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u=1+\unicode[STIX]{x1D716}[\bar{u}_{0}(\hat{x},{\hat{y}},\hat{\unicode[STIX]{x1D70F}})+\hat{u} _{0}(\hat{x},y,z,\hat{\unicode[STIX]{x1D70F}})]+\cdots \,,\\ v=\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}[\bar{v}_{0}(\hat{x},{\hat{y}},\hat{\unicode[STIX]{x1D70F}})+\hat{v}_{0}(\hat{x},y,z,\hat{\unicode[STIX]{x1D70F}})]+\cdots \,,\\ w=\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}{\hat{w}}_{0}(\hat{x},y,z,\hat{\unicode[STIX]{x1D70F}})+\cdots \,,\\ p=-\frac{1}{2}+\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}^{2}[\bar{p}_{0}(\hat{x},y,\hat{\unicode[STIX]{x1D70F}})+\unicode[STIX]{x1D716}\hat{p}_{1}(\hat{x},y,z,\hat{\unicode[STIX]{x1D70F}})]+\cdots \,,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u=1+\unicode[STIX]{x1D716}[\bar{u}_{0}(\hat{x},{\hat{y}},\hat{\unicode[STIX]{x1D70F}})+\hat{u} _{0}(\hat{x},y,z,\hat{\unicode[STIX]{x1D70F}})]+\cdots \,,\\ v=\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}[\bar{v}_{0}(\hat{x},{\hat{y}},\hat{\unicode[STIX]{x1D70F}})+\hat{v}_{0}(\hat{x},y,z,\hat{\unicode[STIX]{x1D70F}})]+\cdots \,,\\ w=\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}{\hat{w}}_{0}(\hat{x},y,z,\hat{\unicode[STIX]{x1D70F}})+\cdots \,,\\ p=-\frac{1}{2}+\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}^{2}[\bar{p}_{0}(\hat{x},y,\hat{\unicode[STIX]{x1D70F}})+\unicode[STIX]{x1D716}\hat{p}_{1}(\hat{x},y,z,\hat{\unicode[STIX]{x1D70F}})]+\cdots \,,\end{array}\right\}\end{eqnarray}$$
where
![]() $\hat{\unicode[STIX]{x1D70F}}=t/R_{\unicode[STIX]{x1D6EC}}=O(1)$
. Here the factor
$\hat{\unicode[STIX]{x1D70F}}=t/R_{\unicode[STIX]{x1D6EC}}=O(1)$
. Here the factor
![]() $R_{\unicode[STIX]{x1D6EC}}$
in
$R_{\unicode[STIX]{x1D6EC}}$
in
![]() $v$
and
$v$
and
![]() $w$
, and
$w$
, and
![]() $R_{\unicode[STIX]{x1D6EC}}^{2}$
in
$R_{\unicode[STIX]{x1D6EC}}^{2}$
in
![]() $p$
, arise in order to undo the normalization introduced in (2.8) for the boundary-layer disturbance. The terms
$p$
, arise in order to undo the normalization introduced in (2.8) for the boundary-layer disturbance. The terms
![]() $\bar{u}_{0}$
,
$\bar{u}_{0}$
,
![]() $\bar{v}_{0}$
and
$\bar{v}_{0}$
and
![]() $\bar{p}_{0}$
represent the two-dimensional part and are governed by the linearized unsteady Euler equations,
$\bar{p}_{0}$
represent the two-dimensional part and are governed by the linearized unsteady Euler equations,
subject to the boundary condition,
The other boundary condition follows from matching
![]() $\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}\bar{v}_{0}$
with (2.29), the spanwise-averaged normal velocity at the outer edge of the boundary layer, and it reads
$\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}}\bar{v}_{0}$
with (2.29), the spanwise-averaged normal velocity at the outer edge of the boundary layer, and it reads
where
![]() $\bar{\unicode[STIX]{x1D6FF}}$
is the spanwise-averaged displacement thickness defined in (2.30).
$\bar{\unicode[STIX]{x1D6FF}}$
is the spanwise-averaged displacement thickness defined in (2.30).
The solution for
![]() $\bar{v}_{0}$
is found as
$\bar{v}_{0}$
is found as
![]() $\bar{v}_{0}=(1/\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}})\text{Re}(\bar{\unicode[STIX]{x1D6FF}}_{\hat{\unicode[STIX]{x1D709}}}(\hat{\unicode[STIX]{x1D709}},\hat{\unicode[STIX]{x1D70F}}))$
, where
$\bar{v}_{0}=(1/\unicode[STIX]{x1D716}R_{\unicode[STIX]{x1D6EC}})\text{Re}(\bar{\unicode[STIX]{x1D6FF}}_{\hat{\unicode[STIX]{x1D709}}}(\hat{\unicode[STIX]{x1D709}},\hat{\unicode[STIX]{x1D70F}}))$
, where
![]() $\bar{\unicode[STIX]{x1D6FF}}(\hat{\unicode[STIX]{x1D709}},\hat{\unicode[STIX]{x1D70F}})$
is the analytic continuation of
$\bar{\unicode[STIX]{x1D6FF}}(\hat{\unicode[STIX]{x1D709}},\hat{\unicode[STIX]{x1D70F}})$
is the analytic continuation of
![]() $\bar{\unicode[STIX]{x1D6FF}}(\hat{x},\hat{\unicode[STIX]{x1D70F}})$
to the complex plane
$\bar{\unicode[STIX]{x1D6FF}}(\hat{x},\hat{\unicode[STIX]{x1D70F}})$
to the complex plane
![]() $\hat{\unicode[STIX]{x1D709}}=\hat{x}+\text{i}{\hat{y}}$
, and
$\hat{\unicode[STIX]{x1D709}}=\hat{x}+\text{i}{\hat{y}}$
, and
![]() $\text{Re}$
stands for the real part. Substitution of (A 1) and (A 2) into the N–S equations shows that
$\text{Re}$
stands for the real part. Substitution of (A 1) and (A 2) into the N–S equations shows that
![]() $\bar{v}_{0}$
still appears in the governing equations of the three-dimensional component (
$\bar{v}_{0}$
still appears in the governing equations of the three-dimensional component (
![]() $\hat{u} _{0},\hat{v}_{0}$
,
$\hat{u} _{0},\hat{v}_{0}$
,
![]() ${\hat{w}}_{0}$
,
${\hat{w}}_{0}$
,
![]() $\hat{p}_{1}$
), indicating that the latter is also influenced by the viscous displacement effect. As was pointed out by Wundrow & Goldstein (Reference Wundrow and Goldstein2001) and Ricco et al. (Reference Ricco, Luo and Wu2011), the coupling with
$\hat{p}_{1}$
), indicating that the latter is also influenced by the viscous displacement effect. As was pointed out by Wundrow & Goldstein (Reference Wundrow and Goldstein2001) and Ricco et al. (Reference Ricco, Luo and Wu2011), the coupling with
![]() $\bar{v}_{0}$
can be removed by the Prandtl transformation,
$\bar{v}_{0}$
can be removed by the Prandtl transformation,
where
![]() $\hat{\unicode[STIX]{x1D6FF}}$
is to be chosen. By using the Prandtl transformation and the linearized Euler equations (A 3), the governing equations for (
$\hat{\unicode[STIX]{x1D6FF}}$
is to be chosen. By using the Prandtl transformation and the linearized Euler equations (A 3), the governing equations for (
![]() $\hat{u} _{0},\hat{v}_{0},{\hat{w}}_{0}$
) and
$\hat{u} _{0},\hat{v}_{0},{\hat{w}}_{0}$
) and
![]() $\hat{p}_{1}$
can be written as
$\hat{p}_{1}$
can be written as
 $$\begin{eqnarray}\displaystyle & \displaystyle \mathscr{L}\left(\begin{array}{@{}c@{}}\hat{u} _{0}\\ \hat{v}_{0}\\ {\hat{w}}_{0}\end{array}\right)=-r_{t}\left(\begin{array}{@{}c@{}}0\\ \hat{p}_{1\bar{y}}\\ \hat{p}_{1z}\end{array}\right)+\unicode[STIX]{x1D6FB}^{2}\left(\begin{array}{@{}c@{}}\hat{u} _{0}\\ \hat{v}_{0}\\ {\hat{w}}_{0}\end{array}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathscr{L}\left(\begin{array}{@{}c@{}}\hat{u} _{0}\\ \hat{v}_{0}\\ {\hat{w}}_{0}\end{array}\right)=-r_{t}\left(\begin{array}{@{}c@{}}0\\ \hat{p}_{1\bar{y}}\\ \hat{p}_{1z}\end{array}\right)+\unicode[STIX]{x1D6FB}^{2}\left(\begin{array}{@{}c@{}}\hat{u} _{0}\\ \hat{v}_{0}\\ {\hat{w}}_{0}\end{array}\right), & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FB}^{2}$
is the Laplacian operator in the
$\unicode[STIX]{x1D6FB}^{2}$
is the Laplacian operator in the
![]() $y$
–
$y$
–
![]() $z$
plane, and
$z$
plane, and
![]() $\mathscr{L}$
is the nonlinear differential operator,
$\mathscr{L}$
is the nonlinear differential operator,
Note that the fast variable
![]() $y$
or
$y$
or
![]() $\bar{y}$
defined in (A 6) describes the phase variation of FSVD, and so its presence should not obscure the fact that we are presently considering the far field, where the basic flow is uniform; see the expansion (A 2). As (A 9) indicates, the dependence on
$\bar{y}$
defined in (A 6) describes the phase variation of FSVD, and so its presence should not obscure the fact that we are presently considering the far field, where the basic flow is uniform; see the expansion (A 2). As (A 9) indicates, the dependence on
![]() $\bar{v}_{0}$
is removed if we choose
$\bar{v}_{0}$
is removed if we choose
![]() $\hat{\unicode[STIX]{x1D6FF}}$
to satisfy the equation and the ‘boundary condition’ (Ricco et al.
Reference Ricco, Luo and Wu2011),
$\hat{\unicode[STIX]{x1D6FF}}$
to satisfy the equation and the ‘boundary condition’ (Ricco et al.
Reference Ricco, Luo and Wu2011),
It suffices to obtain
![]() $\hat{\unicode[STIX]{x1D6FF}}$
for
$\hat{\unicode[STIX]{x1D6FF}}$
for
![]() ${\hat{y}}=0$
. Let
${\hat{y}}=0$
. Let
![]() $\displaystyle \bar{\unicode[STIX]{x1D6FF}}=\sum \bar{\unicode[STIX]{x1D6FF}}_{m}(\hat{x})\text{e}^{\text{i}m(\hat{x}-\hat{\unicode[STIX]{x1D70F}})}$
. Then the solution for
$\displaystyle \bar{\unicode[STIX]{x1D6FF}}=\sum \bar{\unicode[STIX]{x1D6FF}}_{m}(\hat{x})\text{e}^{\text{i}m(\hat{x}-\hat{\unicode[STIX]{x1D70F}})}$
. Then the solution for
![]() $\hat{\unicode[STIX]{x1D6FF}}$
can be written as
$\hat{\unicode[STIX]{x1D6FF}}$
can be written as
The transverse velocities
![]() $(\hat{v}_{0},{\hat{w}}_{0})$
are decoupled from the streamwise velocity
$(\hat{v}_{0},{\hat{w}}_{0})$
are decoupled from the streamwise velocity
![]() $\hat{u} _{0}$
. We are only concerned with the former as they act as the leading-order forcing of the free-stream disturbance on the boundary layer. We introduce the streamfunction
$\hat{u} _{0}$
. We are only concerned with the former as they act as the leading-order forcing of the free-stream disturbance on the boundary layer. We introduce the streamfunction
![]() $\hat{\unicode[STIX]{x1D713}}$
, such that
$\hat{\unicode[STIX]{x1D713}}$
, such that
![]() $\hat{v}_{0}=\hat{\unicode[STIX]{x1D713}}_{z}$
and
$\hat{v}_{0}=\hat{\unicode[STIX]{x1D713}}_{z}$
and
![]() ${\hat{w}}_{0}=-\hat{\unicode[STIX]{x1D713}}_{\bar{y}}$
, and then the wall-normal and spanwise momentum equations are simplified to a transport equation for the longitudinal vorticity
${\hat{w}}_{0}=-\hat{\unicode[STIX]{x1D713}}_{\bar{y}}$
, and then the wall-normal and spanwise momentum equations are simplified to a transport equation for the longitudinal vorticity
![]() $\unicode[STIX]{x1D6FB}^{2}\hat{\unicode[STIX]{x1D713}}$
,
$\unicode[STIX]{x1D6FB}^{2}\hat{\unicode[STIX]{x1D713}}$
,
and a Poisson equation for the pressure,
The equation can be solved using a spectral method, where the solution for
![]() $\hat{\unicode[STIX]{x1D713}}$
is sought in the form of Fourier series,
$\hat{\unicode[STIX]{x1D713}}$
is sought in the form of Fourier series,
Substitution of (A 14) into (A 12) leads to a system of coupled equations for
![]() $\hat{\unicode[STIX]{x1D713}}_{m,n}^{(j)}$
,
$\hat{\unicode[STIX]{x1D713}}_{m,n}^{(j)}$
,
where
![]() $\hat{N}_{m,n}^{(j)}$
denotes the Fourier transform of the nonlinear term
$\hat{N}_{m,n}^{(j)}$
denotes the Fourier transform of the nonlinear term
![]() $N(\hat{x},\bar{y},z,\hat{\unicode[STIX]{x1D70F}})$
. The solution for the pressure can be expressed as
$N(\hat{x},\bar{y},z,\hat{\unicode[STIX]{x1D70F}})$
. The solution for the pressure can be expressed as
where
![]() ${\hat{S}}_{m,n}^{(j)}$
denotes the Fourier transform of
${\hat{S}}_{m,n}^{(j)}$
denotes the Fourier transform of
![]() $S$
. To facilitate the matching with the solution in the boundary layer, the Prandtl transformation (A 6) is inserted into (A 14) and (A 16), and we rewrite
$S$
. To facilitate the matching with the solution in the boundary layer, the Prandtl transformation (A 6) is inserted into (A 14) and (A 16), and we rewrite
where the operations involved amount to Fourier transform, at each
![]() $\hat{x}$
, the left-hand side with respect to
$\hat{x}$
, the left-hand side with respect to
![]() $\hat{\unicode[STIX]{x1D70F}}$
for all
$\hat{\unicode[STIX]{x1D70F}}$
for all
![]() $n$
and
$n$
and
![]() $j$
. In terms of
$j$
. In terms of
![]() $(\unicode[STIX]{x1D719}_{m,n}^{(j)},\unicode[STIX]{x03C0}_{m,n}^{(j)})$
, the solution for
$(\unicode[STIX]{x1D719}_{m,n}^{(j)},\unicode[STIX]{x03C0}_{m,n}^{(j)})$
, the solution for
![]() $\hat{v}_{0}$
,
$\hat{v}_{0}$
,
![]() ${\hat{w}}_{0}$
and
${\hat{w}}_{0}$
and
![]() $\hat{p}_{1}$
can be written as
$\hat{p}_{1}$
can be written as
where
with
![]() $y$
being related to
$y$
being related to
![]() $\unicode[STIX]{x1D702}$
via
$\unicode[STIX]{x1D702}$
via
![]() $y=\sqrt{2\hat{x}}\unicode[STIX]{x1D702}$
. The flow field in region III is decomposed as (2.10), and so the matching condition becomes
$y=\sqrt{2\hat{x}}\unicode[STIX]{x1D702}$
. The flow field in region III is decomposed as (2.10), and so the matching condition becomes
It is worth pointing out that the effect of the interaction between the boundary-layer region III and the outer region IV through the displacement
![]() $\bar{\unicode[STIX]{x1D6FF}}$
is accounted for by the transformation
$\bar{\unicode[STIX]{x1D6FF}}$
is accounted for by the transformation
![]() $(\hat{\unicode[STIX]{x1D713}}_{m,n}^{(j)},\hat{p}_{m,n}^{(j)})\rightarrow (\unicode[STIX]{x1D719}_{m,n}^{(j)},\unicode[STIX]{x03C0}_{m,n}^{(j)})$
, defined in (A 17).
$(\hat{\unicode[STIX]{x1D713}}_{m,n}^{(j)},\hat{p}_{m,n}^{(j)})\rightarrow (\unicode[STIX]{x1D719}_{m,n}^{(j)},\unicode[STIX]{x03C0}_{m,n}^{(j)})$
, defined in (A 17).
Equation (A 15) has to be solved numerically in general. An exact solution can be obtained if the oncoming disturbance consists of a pair of oblique components with the same frequency and amplitude, but opposite spanwise wavenumbers. In this special case, the nonlinear terms in (A 15) vanish (Wundrow & Goldstein Reference Wundrow and Goldstein2001), and so
![]() $\hat{\unicode[STIX]{x1D713}}_{m,n}^{(j)}=0$
except that
$\hat{\unicode[STIX]{x1D713}}_{m,n}^{(j)}=0$
except that
where
![]() $c_{\infty }=-\hat{u} _{3}/k_{2}$
with
$c_{\infty }=-\hat{u} _{3}/k_{2}$
with
![]() $\hat{u} _{3}^{\infty }=\hat{u} _{3+}^{\infty }=\hat{u} _{3-}^{\infty }$
being the amplitude of the spanwise velocity of the FSVD. It follows that
$\hat{u} _{3}^{\infty }=\hat{u} _{3+}^{\infty }=\hat{u} _{3-}^{\infty }$
being the amplitude of the spanwise velocity of the FSVD. It follows that
![]() $\hat{\unicode[STIX]{x1D713}}=2c_{\infty }\sin (k_{3}z)\text{e}^{-(k_{2}^{2}+k_{3}^{2})\hat{x}+\text{i}\hat{k}_{1}(\hat{x}-\hat{\unicode[STIX]{x1D70F}})+\text{i}k_{2}\bar{y}}+\text{c.c}.$
, and
$\hat{\unicode[STIX]{x1D713}}=2c_{\infty }\sin (k_{3}z)\text{e}^{-(k_{2}^{2}+k_{3}^{2})\hat{x}+\text{i}\hat{k}_{1}(\hat{x}-\hat{\unicode[STIX]{x1D70F}})+\text{i}k_{2}\bar{y}}+\text{c.c}.$
, and
Then rewriting
![]() $\hat{v}_{0},{\hat{w}}_{0}$
, and
$\hat{v}_{0},{\hat{w}}_{0}$
, and
![]() $\hat{p}_{1}$
in terms of
$\hat{p}_{1}$
in terms of
![]() $y$
by using (A 6), we find that for
$y$
by using (A 6), we find that for
![]() $y=O(1)$
,
$y=O(1)$
,
where
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \hat{v}_{m,\pm 1}^{\dagger }=k_{3}c_{\infty }\text{e}^{-(k_{2}^{2}+k_{3}^{2})\hat{x}}[\text{e}^{\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x1D719}_{m}+\text{e}^{-\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x1D719}_{-m}^{\ast }],\\ \displaystyle {\hat{w}}_{m,\pm 1}^{\dagger }=\mp k_{2}c_{\infty }\text{e}^{-(k_{2}^{2}+k_{3}^{2})\hat{x}}[\text{e}^{\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x1D719}_{m}-\text{e}^{-\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x1D719}_{-m}^{\ast }],\\ \displaystyle \hat{p}_{m,0}^{\dagger }=-2k_{3}^{2}c_{\infty }^{2}\text{e}^{-2(k_{2}^{2}+k_{3}^{2})\hat{x}}[\text{e}^{2\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x03C0}_{m}+\text{e}^{-2\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x03C0}_{-m}^{\ast }],\\ \displaystyle \hat{p}_{\text{0},\pm 2}^{\dagger }=2k_{2}^{2}c_{\infty }^{2}\text{e}^{-2(k_{2}^{2}+k_{3}^{2})\hat{x}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \hat{v}_{m,\pm 1}^{\dagger }=k_{3}c_{\infty }\text{e}^{-(k_{2}^{2}+k_{3}^{2})\hat{x}}[\text{e}^{\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x1D719}_{m}+\text{e}^{-\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x1D719}_{-m}^{\ast }],\\ \displaystyle {\hat{w}}_{m,\pm 1}^{\dagger }=\mp k_{2}c_{\infty }\text{e}^{-(k_{2}^{2}+k_{3}^{2})\hat{x}}[\text{e}^{\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x1D719}_{m}-\text{e}^{-\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x1D719}_{-m}^{\ast }],\\ \displaystyle \hat{p}_{m,0}^{\dagger }=-2k_{3}^{2}c_{\infty }^{2}\text{e}^{-2(k_{2}^{2}+k_{3}^{2})\hat{x}}[\text{e}^{2\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x03C0}_{m}+\text{e}^{-2\text{i}(\hat{k}_{1}\hat{x}+k_{2}y)}\unicode[STIX]{x03C0}_{-m}^{\ast }],\\ \displaystyle \hat{p}_{\text{0},\pm 2}^{\dagger }=2k_{2}^{2}c_{\infty }^{2}\text{e}^{-2(k_{2}^{2}+k_{3}^{2})\hat{x}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D719}_{m}=\unicode[STIX]{x1D719}_{m,1}^{(1)}$
and
$\unicode[STIX]{x1D719}_{m}=\unicode[STIX]{x1D719}_{m,1}^{(1)}$
and
![]() $\unicode[STIX]{x03C0}_{m}=\unicode[STIX]{x03C0}_{m,1}^{(1)}$
. All other components
$\unicode[STIX]{x03C0}_{m}=\unicode[STIX]{x03C0}_{m,1}^{(1)}$
. All other components
![]() $\hat{v}_{m,n}^{\dagger }={\hat{w}}_{m,n}^{\dagger }=0$
$\hat{v}_{m,n}^{\dagger }={\hat{w}}_{m,n}^{\dagger }=0$
![]() $(n\neq \pm 1)$
and
$(n\neq \pm 1)$
and
![]() $\hat{p}_{m,n}^{\dagger }=0(n\neq 0,\pm 2)$
.
$\hat{p}_{m,n}^{\dagger }=0(n\neq 0,\pm 2)$
.
For the steady case, the disturbance frequency and streamwise wavenumber are zero, and so the disturbance in the outer region takes a simpler form,
Appendix B
The linear operator
![]() $\unicode[STIX]{x1D647}$
in (3.11) is defined as
$\unicode[STIX]{x1D647}$
in (3.11) is defined as
 $$\begin{eqnarray}\unicode[STIX]{x1D647}=\left[\begin{array}{@{}ccccccc@{}}I-\displaystyle \frac{h}{2}c_{J} & -I-\displaystyle \frac{h}{2}c_{J-1} & 0 & 0 & \cdots \, & 0 & 0\\ 0 & I-\displaystyle \frac{h}{2}c_{J-1} & -I-\displaystyle \frac{h}{2}c_{J-2} & 0 & \cdots \, & 0 & 0\\ \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \\ 0 & 0 & \cdots \, & 0 & I-\displaystyle \frac{h}{2}c_{2} & -I-\displaystyle \frac{h}{2}c_{1} & 0\\ 0 & 0 & \cdots \, & 0 & 0 & I-\displaystyle \frac{h}{2}c_{1} & -I-\displaystyle \frac{h}{2}c_{0}\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D647}=\left[\begin{array}{@{}ccccccc@{}}I-\displaystyle \frac{h}{2}c_{J} & -I-\displaystyle \frac{h}{2}c_{J-1} & 0 & 0 & \cdots \, & 0 & 0\\ 0 & I-\displaystyle \frac{h}{2}c_{J-1} & -I-\displaystyle \frac{h}{2}c_{J-2} & 0 & \cdots \, & 0 & 0\\ \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \, & \cdots \\ 0 & 0 & \cdots \, & 0 & I-\displaystyle \frac{h}{2}c_{2} & -I-\displaystyle \frac{h}{2}c_{1} & 0\\ 0 & 0 & \cdots \, & 0 & 0 & I-\displaystyle \frac{h}{2}c_{1} & -I-\displaystyle \frac{h}{2}c_{0}\end{array}\right].\end{eqnarray}$$
The vectors
![]() $\boldsymbol{A}$
and
$\boldsymbol{A}$
and
![]() $\boldsymbol{N}$
are expressed as
$\boldsymbol{N}$
are expressed as
 $$\begin{eqnarray}\boldsymbol{A}=\frac{h}{2}\left(\begin{array}{@{}c@{}}g_{J}+g_{J-1}\\ g_{J-1}+g_{J-2}\\ \cdots \\ g_{2}+g_{1}\\ g_{1}+g_{0}\end{array}\right),\quad \boldsymbol{N}_{n+1}=\frac{h}{2}\left(\begin{array}{@{}c@{}}f_{J}^{n+1}+f_{J-1}^{n+1}\\ f_{J-1}^{n+1}+f_{J-2}^{n+1}\\ \cdots \\ f_{2}^{n+1}+f_{1}^{n+1}\\ f_{1}^{n+1}+f_{0}^{n+1}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{A}=\frac{h}{2}\left(\begin{array}{@{}c@{}}g_{J}+g_{J-1}\\ g_{J-1}+g_{J-2}\\ \cdots \\ g_{2}+g_{1}\\ g_{1}+g_{0}\end{array}\right),\quad \boldsymbol{N}_{n+1}=\frac{h}{2}\left(\begin{array}{@{}c@{}}f_{J}^{n+1}+f_{J-1}^{n+1}\\ f_{J-1}^{n+1}+f_{J-2}^{n+1}\\ \cdots \\ f_{2}^{n+1}+f_{1}^{n+1}\\ f_{1}^{n+1}+f_{0}^{n+1}\end{array}\right),\end{eqnarray}$$
where
![]() $J$
denotes the number of mesh points in the wall-normal direction.
$J$
denotes the number of mesh points in the wall-normal direction.