1. INTRODUCTION
Recent developments in technology of high-intensity lasers have opened the way to accelerate the charged particles to high energies (Katsouleas et al., Reference Katsouleas and Bingham1996; Kar et al., Reference Kar, Markey, Simpson, Bellei, Green, Nagel, Kneip, Carroll, Dromey, Willingale, Clark, Mckenna, Najmudin, Krushelnick, Norreys, Clarke, Neely, Borghesi and Zepf2008; Gibbon, Reference Gibbon2005; Hoffmann et al., Reference Hoffmann, Blazevic, Rosmej, Spiller, Tahir, Weyrich, Dafni, Kuster, Ni, Roth, Udrea and Varentsov2007; Esirkepov et al., Reference Esirkepov, Bulanov, Yamagiwa and Tajima2006). Moreover, plasma has an important ability to generate energetic electrons from interaction with a high-intensity laser. Tajima et al. (Reference Tajima and Dawson1979) proposed that the ponderomotive force associated with the laser field (if the duration of the laser pulse is comparable or shorter to the plasma wave period) can excite a plasma wave (wakefield) that propagates with a velocity close to the speed of light. If electrons with sufficient energy matching the accelerating electric fields are injected into the wakefield, they can be trapped by the wakefield and accelerated to high energy. This scheme is known as the laser wakefield acceleration (LWFA), which may play a crucial role in developing future advanced accelerators. Recently, a major work has been carried out for achieving good quality and self-injected electron beam from the LWFA scheme. In the last 15 years, several major injection schemes have been proposed and performed by experiments successfully (Modena et al., Reference Modena, Dangor, Najmudin, Clayton, Marsh, Joshi, Malka, Darrow, Neely and Walsh1995; Faure et al., Reference Faure, Rechatin, Norlin, Lifschitz, Glinec and Malka2006; Sandhu et al., Reference Sandhu, Kumar, Sengupta, Das and Kaw2005). In 2004, few experiments on generation of monoenergetic electrons around 100 MeV were presented (Faure et al., Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004; Fritzler et al., Reference Fritzler, Lefebvre, Malka, Burgy, Dangor, Krushelnick, Mangles, Najmudin, Rousseau and Walton2004; Geddes et al., Reference Geddes, Toth, Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004). The possible mechanism accounting for the generation of monoenergetic electrons was the beam loading in the bubble region. The beam loading mechanism is a kind of self-injection of electrons into laser wakefield and depends strongly on the nonlinearity of pump laser propagation in plasmas.
Magnetic field is also very important in context of the plasma-based accelerators (Vieira et al., Reference Vieira, Martins, Pathak, Fonseca, Mori and Silva2011; Hur et al., Reference Hur, Gupta and Suk2008; Gupta et al., Reference Gupta and Suk2007). The application of magnetic field can modify the pre-pulse effect and can be a tool to control the electron self-injection. The number of particles in an electron beam from laser wakefield acceleration is determined at the moment of trapping of background electrons. A magnetic field applied in the longitudinal direction can suppress the transverse drift of the electrons and can turn them in the trapping region. The applied magnetic field can control the beam charge in laser-plasma accelerators, while keeping other parameters unmodified. Katsouleas et al. (Reference Katsouleas and Dawson1983) have proposed the surfatron concept in which a transverse magnetic field assists in electrons energy gain from the plasma wave by deflecting them across the wave front. Gahn et al. (Reference Gahn, Tsakiris, Pukhov, Mayer-Ter-Vehn, Pretzler, Thirolf, Habs and Wite1999) have reported simulation on the effect of azimuthal magnetic fields from the interactions of an intense short pulse laser with plasmas. They observed a strong magnetic field of the order of 100 MG in conjunction with strong flow of energetic electrons.
Wakefield wave is sensitive to the plasma density modulation (Suk et al., Reference Suk, Barov, Rosenzweig and Esarey2001) and leads to change in plasma frequency. The existence of a density ripple in the form of an ion wave excited by stimulated Brillouin scattering could greatly affect the coupling of plasma oscillations (Kaw et al., Reference Kaw, Lin and Dawson1973; Darrow et al., Reference Darrow, Umstadter, Katsouleas, Mori, Clayton and Joshi1986) and generate two sideband plasma waves. One sideband moves with lower phase velocity than the pump plasma wave and the other with higher phase velocity. The mode-coupling problem in this connection can be used to transfer energy to the main body of the electrons from plasma waves generated by density ripple. In this article, we propose to study the electron acceleration by the laser wakefield in the presence of plasma density ripple and the applied magnetic field in a limited width plasma channel. The fundamental wake wave decays in two harmonic waves while interacting with the periodic plasma density ripple, i.e., slow and fast waves. The slow wave assists in trapping the pre-accelerated background electrons in laser wakefield acceleration. The applied magnetic field helps in improving the self-injection of the electrons. The advantage of considering the limited width plasma channel is confined to the transverse electron in the interactions region. Therefore, overall, our study shows a significant improvement in electron energy gain in the LWFA scheme. Recently, we have studied the propagation of plasma beat-wave in density modulated plasma (Gupta et al., Reference Gupta, Nam and Suk2011). A plasma beat-wave interacting with periodic plasma-density-modulation generates two sideband plasma wave and the plasma electrons gains considerable energy in step by step accelerations.
The current work is related to laser wakefield acceleration, where the wakefield also generates two wake waves while interacting with the plasma density modulation. The slow can trap and inject the pre-accelerated electrons in the wakefield, hence, external injection is not required. We present two-dimensional (2D) particle-in-cell (PIC) simulations of the interaction of a laser pulse with density modulated plasma in order to study some of the features of electron acceleration in LWFA scheme in the presence of a magnetic field. The detailed study of this process is crucial in order to design a laser wakefield based accelerators in the presence of a magnetic field. In Section 2, we develop the theoretical framework for numerical/simulation estimation of the electron energy during acceleration by the LWFA in a density rippled plasma. In Section 3, we discuss the simulation results and the conclusions are summarized in the last section.
2. 1D-THEORETICAL MODEL
Consider a linearly polarized Gaussian laser pulse with the profile of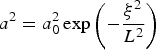 
$a^{2} = a_{0}^{2} \exp \left(-{{\rm \xi}^2 \over L^2} \right)$ for 0 < |ξ| < L, where 
$a= {eA_{\bot} \over mc^2}$, A ⊥ is the vector potential of the laser pulse, L = cτ0 is the laser pulse length, τ0 is the laser pulse duration, ξ = (z − v pt) is the moving coordinate normalized by the laser wavelength, v p is the phase velocity of the plasma wave, c is the speed of light in vacuum, and m and −e are the electron mass and charge, respectively. The plasma density is n 0 = 0.01n c, where 
$n_c = {m {\rm \omega}^2 \over 4{\rm \pi} e^2}$ is the critical density corresponding to the laser frequency ω. The motion of electrons in the laser field is described by the Hamiltonian (Esirkepov et al., 1996), 
$H = \left\{m^2 c^4 + c^2 p_{\parallel}^2 + \left(cp_{\bot} + eA_{\bot} \right)^2 \right\}^{1 \over 2} - e{\rm \phi}$, where ϕ is the electrostatic potential of the wakefield, 
$p_{\parallel}$ and p ⊥ are the longitudinal and transverse momentum of the electrons, respectively. Because of the large mass and the slow response of the ions, we consider them immobile. We consider the laser wakefield generation in the nonlinear regime for L ≃ λp0, where 
${\rm \lambda}_{\,p0} = {2{\rm \pi} v_p \over {\rm \omega}_{\,p0}}$ is the plasma wavelength and 
${\rm \omega}_{\,p0} = {4{\rm \pi} n_0 e^2 \over m}$ is the electron plasma frequency. We follow Esarey et al. (Reference Esarey, Sprangle, Krall and Ting1996) to write the density perturbation (δn/n) and electrostatic wakefield potential (φ = eϕ /mc 2) as
$$\displaystyle{{\rm \delta} n \over n} = - \displaystyle{{\rm \pi} \over 4} \displaystyle{a_0^2 \over 2} \left[1 + \displaystyle{8 \over k_p^2\, L^2} \left(1 - 2\displaystyle{{\rm \xi} ^2 \over L^2} \right)\right]\exp \left(- 2\displaystyle{{\rm \xi}^2 \over L^2} \right)$$and
$$\displaystyle{\partial ^2 {\rm \varphi} \over \partial {\rm \xi}^2} = k_p^2 {\rm \gamma}_p^2 \left[\displaystyle{{\rm \beta}_p {\rm \gamma}_p \left(1 + {\rm \varphi} \right)\over \left\{{\rm \gamma}_p^2 \left(1 + {\rm \varphi} \right)^2 - \left(1 + a^2 \right)\right\}^{1 \over 2}} - 1 \right]\comma \;$$
where 
${\rm \gamma}_p = {1 \over \left(1 - {\rm \beta}_p^2 \right)^{1 \over 2}}$ is the relativistic factor, 
${\rm \beta}_p = {v_p \over c}$, and 
$k_p = {2{\rm \pi} \over {\rm \lambda}_{\,p0}}$. The longitudinal electric field associated with the wake can be given by 
$\vec{E} = -\nabla {\rm \varphi}$. It is known that, in LWFA, the strength of accelerating and the de-phasing length are controlled by the plasma density. The increasing plasma density can increase the accelerating field strength and low plasma density can increases the acceleration length. Therefore, the plasma density variation is very important in determining the electron energy gain from LWFA mechanism.
In this work, the role of periodic plasma density variation on electron energy gain in LWFA was studied. We introduce a periodic density modulation in plasma in the form of n q = Re [n q0 exp (ik qz)] with the electron density of n 0, where 
$\vec{k}_q$ is the propagation vector of the modulation wave. Now, the resultant plasma density is n 0 + n q. Such kind of density modulation or ripple can be observed in tunnel ionized plasma through stimulated Brillouin scattering. Due to the density ripple (mildly varying over the plasma period), the wake wave is frequency modulated with amplitude modulation n q0 /2n 0 in the z-space. On the account of nonlinear interaction of an electrostatic wakefield with rippled plasma (if the amplitude of the modulation is small), the fundamental wake wave generates two significant sideband harmonics of the wave vectors of 
$\vec{k}_{\,p \pm} = \vec{k} \pm \vec{k}_q$, where ± sign is for slow and fast wave, respectively. The self-consistent fields of the sideband waves can be obtained by considering the amplitude of the modulation as a small parameter and expanding the electrostatic wakefield potential as
$$\displaystyle{\partial^2 {\rm \varphi}_{\pm} \over \partial {\rm \xi}^2} = k_{\,p \pm}^2 {\rm \gamma}_{\,p \pm}^2 \left[\displaystyle{{\rm \beta}_{\,p \pm} {\rm \gamma}_{\,p \pm} \left(1 + {\rm \varphi}_{\pm} \right)\over \left\{{\rm \gamma}_{\,p \pm}^2 \left(1 + {\rm \varphi}_{\pm} \right)^2 - \left(1 + a^2 \right)\right\}^{1 \over 2}} - 1 \right]\displaystyle{n_q^0 \over 2n_0}\comma \;$$On the account of nonlinear interaction of the wakefield with rippled plasma (if the amplitude of the modulation is small), the pump wave generates two significant sidebands during the interaction with a density ripple. We neglect the higher-order harmonics and keep only lower order sidebands because of the small modulation amplitude. If we consider the large density modulation then a large number of modes may be excited and the driver energy would be distributed among a large number of modes, hence, limiting the energy gain. Also, for nearly resonant excitation of wakefield, the pump wave is seen to grow linearly with space and time as in a parametric oscillator. Furthermore, the validity of linear wakefield equation can be verified by the numerical solution of the exact Lagrangian equations for the driven cold fluid oscillations (Darrow et al., Reference Darrow, Mori, Katsouleas, Joshi, Umstadter and Clayton1987).
The electrostatic wakefield of low-phase velocity injects the modest energy electrons to gain substantial energies. The electrons are accelerated to high energies by the main fundamental wakefield. They can be further accelerated to higher energies by the field of higher phase velocity. The wakefield also produce energetic electrons that carry an electric current and generate an azimuthal magnetic field, which is experienced by the electron that follow. Therefore, we also consider an azimuthal magnetic field in the wake of the laser field that can be expressed as (Gorbunov et al., Reference Gorbunov, Mora and Antonsen1996)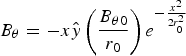 
$B_{{\rm \theta}} = - x \hat{y} \left({B_{{\rm \theta} 0} \over r_0} \right)e^{ - {x^2 \over 2r_0^2}}$, where r 0 is the radius of the wake.
3. SIMULATION RESULTS
In connection to our idea described by one-dimensional (1D) mathematical model in Section 2, we perform relativistic 2D simulations using a 2D PIC code for laser pulse propagation in density modulated plasma. We artificially introduce a fix width channel of width of 50 µm. We launch a laser pulse with a normalized intensity amplitude of a 0 = 2, 3, 5, central wavelength λ0 = 1 µm, focused to a spot size of r 0 = 10 µm. The pulse has a Gaussian transverse and temporal profile with 31.5 fs (1/e of field amplitude) pulse duration. The laser pulse propagate along the z-direction through a limited-width (of 50 µm) plasma slab with a background density of n 0 ≈ 1 × 1019 cm−3. The simulation box with dimensions of 50 × 50 µm2 moves at the speed of light, which is resolved with 1000 × 200 cells. Twenty particles per cell are used for simulations. The amplitude of periodic modulation is 10% (n q0 /n 0 = 0.1) of uniform plasma density. The ripple wave vector is chosen as k q = 0.2k p. The amplitude of the magnetic field is 100 Tesla. However, such a high magnetic field cannot be generated in the laboratory easily, but a quasi-static laser generated magnetic field of this magnitude or larger can in some cases is supported (Wilks et al., Reference Wilks, Kruer, Tabak and Langdon1992). For comparison, we simulate different cases with or without density modulation and with or without external magnetic field. The simulation results are presented as follow: Figure 1 shows the electron density distribution in LWFA for a 0 = 3 with a magnetic field of strength 100 Tesla and the plasma density ripple of 10% density modulation (n q0 = 0.1 n 00). Wakefield formation and consequently, electron beam generation can be seen from the results.
Figure 2 shows the energies of the macro-particles during LWFA in a density modulated plasma (where the density modulation is 10% of uniform plasma density) for different laser intensities. The strength of used magnetic field is about 100 Tesla. The main purpose of this simulation is to analyze the effects of laser intensity on the electron energy gain by the wakefield in the presence of a magnetic field. To observe this, we consider three cases of different intensity amplitudes of the laser pulses. The simulation results reveal that the higher laser intensity assists in increment of the electron energy gain during acceleration. Energy gained by the electron increases proportionally with increasing laser intensity parameter a 0. The key effect is to excite the strong fundamental wakefield by the laser so that large amplitude of the sideband can be excited. For higher laser intensity, the stronger sidebands can be excited. Strong self-injection of the pre-accelerated electrons in the coupling waves leads in electron energy enhancement.
Fig. 1. (Color online) Electron density distribution in LWFA for laser intensity amplitude parameters of a 0 = 3 with a magnetic field of strength 100 Tesla and the plasma density ripple of 10% density modulation (n q0 = 0.1n 00).
Fig. 2. (Color online) Electron energy (E, in MeV) as a function of the propagation time (1/ωp0) with plasma density ripple of 10% density modulation (n q0 = 0.1n 00) and with a magnetic field of strength 100 Tesla for different laser intensity amplitude parameters a 0 = 2 (red particles), a 0 = 3 (green particles), and a 0 = 5 (blue particles).
Figure 3 shows the effect of magnetic field on electron acceleration by the wakefield in a density modulated plasma. To understand the role of the magnetic field, we show the energies of the macro-particles during acceleration in simulations for the same parameter as those of in Figure 3 with magnetic field (red particles) and without applied magnetic field (black particles). The used laser intensity amplitude is a 0 = 2 and the magnetic field strength is about 100 Tesla. Magnetic field plays an important role in this mechanism. The magnetic field helps electrons gain much higher energy by trapping them around the wakefield potential trough. The electrons moving away from the propagation axis can be returned to the interaction region by the magnetic field. Hence, both the slow wakefield generated due to the plasma density modulation and the applied magnetic field assists together in self-injection and acceleration of the plasma electrons in LWFA.
Fig. 3. (Color online) Electron energy (E, in MeV) as a function of the propagation time (1/ωp0) with plasma density ripple of 10% density modulation (n q0 = 0.1n 00) for laser intensity amplitude parameters of a 0 = 2 with a magnetic field of strength 100 Tesla (red particles) and without a magnetic field (black particles).
In Figure 4, we explore more ranges of parameters in studying the electron energy gain during electron acceleration in this scheme, where the laser pulse propagates over the distance of about 250 µm (the laser pulse propagated the distance of 74c/ωp0). The variation of density modulation and strength of magnetic field for electron energy gains has been reported for this purpose. The role of density modulation and the magnetic field can be seen from these results. The amplitudes of the sidebands increase with the amplitude of density modulation. The stronger sideband can assist in electron energy gain in this scheme. Also, the stronger magnetic field also contributes significantly in electron energy gain by enhancement in electron trapping. Figure 5 shows the same for different acceleration length. Figure 5 is cut at the distance over which the laser pulse propagate about 500 µm (laser pulse propagated the distance of 297c/ωp0). The electrons in Figures 4 and 5 are in the acceleration phase and reach the deceleration phase, respectively, after the selected propagation distances.
Fig. 4. (Color online) Electron energy (E, in MeV) as a function of the propagation time [z(c/ωp0)] for B = 0T, n q0 = 0 (red particles); B = 0T, n q0 = 0.1n 00 (green particles); B = 100T, n q0 = 0.1n 00 (blue particles); and B = 0T, n q0 = 0.2n 00 (magenta particles).
Fig. 5. (Color online) Electron energy (E, in MeV)as a function of the propagation time (z(c/ωp0)) for B = 0T, n q0 = 0 (red particles); B = 0T, n q0 = 0.1n 00 (green particles); B = 100T, n q0 = 0.1n 00 (blue particles); and B = 0T, n q0 = 0.2n 00 (magenta particles).
Figure 6 shows the corresponding energy spectra of electrons at time of 15/ωp0. On the application of a magnetic field the electron can gain considerable energy. The magnetic field helps electrons to gain much higher energy by trapping them around the wakefield potential μ trough. In the presence of a magnetic field, however, the electrons will get enough energy due to the fundamental wakefield and the sidebands generated by the density modulation, but the particle will scatter from the interaction region due to the cyclotron frequency mismatch and, therefore, few of them will gain high energy in this scheme or the density of the accelerated electron will be reduced in comparison to the case of without magnetic field. The simulation results have demonstrated that the magnetic field is a very promising route to trap the plasma electrons in the interaction region for accelerations. Hence, particles will get more energy in LWFA. The accelerated electrons from density modulated plasma have an average energy of about 135 MeV (with magnetic field) and 100 MeV (without magnetic field). The plasma density modulation is reasonable for adequate number of accelerated particles and the applied magnetic field is desirable for energetic electron beam generation.
Fig. 6. (Color online) Electron energy spectra at the propagation time of 15/ωp0 with a magnetic field of strength 100 Tesla (red curve), without a magnetic field (black curve) and 10% density modulation.
Apart from the spectral information of the accelerated electron beam, we have also estimated other features of the accelerated electron beam from the simulation. For a 0 = 2, beam radius, beam length, emittance, and energy spread were estimated as 1.4 µm, 1 µm, 8.65 (pi mm mm rad), and 4.1%, respectively, in the absence of magnetic field for density rippled plasma. For a 0 = 2, beam radius, beam length, emittance, and energy spread were estimated as 1.4 µm, 1 µm, 16.5 (pi mm mm rad), 11%, respectively, in presence of magnetic field (100 Tesla) for density rippled plasma. From these calculations, it is obvious that the beam radius and the beam length are not affected by the magnetic field. But the emittance and the energy spread of the electron beam increases with the magnetic field. Because the electron beam interacts with the magnetic field in bubble regime and gets modulated. But in the absence of magnetic field electron beam affected along the propagation axis by the density modulation.
4. CONCLUSIONS
In conclusion, we study the laser wakefield acceleration of electrons in a density modulated plasma in the presence of a quasi-static magnetic field. Periodic plasma-density variation can be used to enhance the electron energy gain in LWFA. Periodic plasma density modulation can excite higher harmonics of different phase velocities of fundamental wakefield that can assist in improving the self-trapping of pre-accelerated electrons. Also, the magnetic field can assist in electrons energy gain by trapping them around the wakefield potential trough. Thus, both the slow wakefield generated due to the plasma density modulation and the applied magnetic field contributes together in self-injection and accelerations of the plasma electrons. In this way, most of the electrons can be in the acceleration phase of the wakefield, thus gaining more energy from the field. Emittance and energy spread of the accelerated beam can be improved by the application of a magnetic field while beam radius and beam length remains unchanged in this scheme.
ACKNOWLEDGMENTS
This work was financially supported by the Department of Science and Technology (DST), Govt. of India and Russian Foundation for Basic Research (RFBR), Russia (Grant number: 12-02-92702-IND_a and 13-02-01398_a). This research was also financially supported by the National Research Foundation of Korea (Grant number: 2012-0000165, R15-2008-006-01001-0). One of the authors (DNG) would like to thanks to University of Delhi for financial support under R&D program 2013–14. One of the authors (KG) would like to thanks to CSIR, Govt. of India for financial support during his Ph.D. thesis work.
