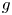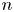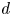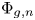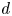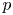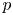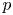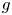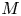1. Introduction
Let ![]() $K$ be an algebraically closed field of characteristic
$K$ be an algebraically closed field of characteristic ![]() $0$. Consider the (multi-valued) function
$0$. Consider the (multi-valued) function ![]() $\Phi _{g,n}$ that assigns to a general
$\Phi _{g,n}$ that assigns to a general ![]() $g$-dimensional principally polarized abelian
$g$-dimensional principally polarized abelian ![]() $K$-variety an
$K$-variety an ![]() $n$-torsion point. Thinking of
$n$-torsion point. Thinking of ![]() $\Phi _{g,n}$ as an algebraic function on the moduli space of principally polarized abelian varieties over
$\Phi _{g,n}$ as an algebraic function on the moduli space of principally polarized abelian varieties over ![]() $K,$ one can ask the following question.
$K,$ one can ask the following question.
Question 1 Let ![]() $g,n\geq 2$. What is the minimum
$g,n\geq 2$. What is the minimum ![]() $d$ such that, after a rational change of variables, the function
$d$ such that, after a rational change of variables, the function ![]() $\Phi _{g,n}$ can be written as an algebraic function of
$\Phi _{g,n}$ can be written as an algebraic function of ![]() $d$ variables?
$d$ variables?
Our interest in Question 1 was partly motivated by the work of Kronecker [Reference KroneckerKr1861, p. 309] and Klein (see [Reference KleinKl1888, p. 171] for the case ![]() $(g,n)=(2,3)$ and [Reference KleinKl1890, § II.16] for
$(g,n)=(2,3)$ and [Reference KleinKl1890, § II.16] for ![]() $(g,n)=(3,2)$) who asked about the analogous minimum integer
$(g,n)=(3,2)$) who asked about the analogous minimum integer ![]() $d$ for certain problems arising in classical algebraic geometry, and used ‘modular’ functions like
$d$ for certain problems arising in classical algebraic geometry, and used ‘modular’ functions like ![]() $\Phi _{g,n},$ to investigate these problems.
$\Phi _{g,n},$ to investigate these problems.
We can rephrase Question 1 in more modern language, using the moduli space of principally polarized abelian varieties and the notion of essential dimension introduced by Tschebotaröw [Reference TschebotaröwTsc34, § 4.8] (under the name ‘true transcendence degree’) and again by Buhler and Reichstein [Reference Buhler and ReichsteinBR97]. Let ![]() ${\mathcal {A}}_g$ denote the coarse moduli space of
${\mathcal {A}}_g$ denote the coarse moduli space of ![]() $g$-dimensional, principally polarized abelian varieties over
$g$-dimensional, principally polarized abelian varieties over ![]() $K$, and let
$K$, and let ![]() ${\mathcal {A}}_{g,n}^1$ be the coarse moduli space of pairs
${\mathcal {A}}_{g,n}^1$ be the coarse moduli space of pairs ![]() $(A,z)$ where
$(A,z)$ where ![]() $A$ is a principally polarized abelian variety of dimension
$A$ is a principally polarized abelian variety of dimension ![]() $g,$ and
$g,$ and ![]() $z$ is an
$z$ is an ![]() $n$-torsion point on
$n$-torsion point on ![]() $A$.
$A$.
For any finite, generically étale map of ![]() $K$-schemes,
$K$-schemes, ![]() $p:X'\to X$, define the essential dimension
$p:X'\to X$, define the essential dimension ![]() ${\rm ed}_K(X'\to X)$, or
${\rm ed}_K(X'\to X)$, or ![]() ${\rm ed}_K(X'/X)$ if the map is implicit, to be the minimal
${\rm ed}_K(X'/X)$ if the map is implicit, to be the minimal ![]() $d$ for which there is a dense Zariski open
$d$ for which there is a dense Zariski open ![]() $U\subset X,$ such that
$U\subset X,$ such that ![]() $X'|_U$ is the pullbackFootnote 1
$X'|_U$ is the pullbackFootnote 1

of a finite map ![]() $Y'\to Y$ of
$Y'\to Y$ of ![]() $d$-dimensional
$d$-dimensional ![]() $K$-varieties via a regular map
$K$-varieties via a regular map ![]() $f:U\to Y$. In this case we call
$f:U\to Y$. In this case we call ![]() $f$ a (rational) compression of
$f$ a (rational) compression of ![]() $p$. Question 1 can be rephrased as asking for the value of
$p$. Question 1 can be rephrased as asking for the value of ![]() ${\rm ed}_K({\mathcal {A}}_{g,n}^1\to {\mathcal {A}}_g)$.
${\rm ed}_K({\mathcal {A}}_{g,n}^1\to {\mathcal {A}}_g)$.
Following Klein [Reference KleinKl1884], we can ask a related question, where we allow certain accessory irrationalities; that is, we can ask for
for some class of finite, generically étale maps ![]() $E\to {\mathcal {A}}_g$. For example, Reichstein and Youssin [Reference Reichstein and YoussinRY00] define the essential
$E\to {\mathcal {A}}_g$. For example, Reichstein and Youssin [Reference Reichstein and YoussinRY00] define the essential ![]() $p$-dimension
$p$-dimension ![]() ${\rm ed}_K(X'/X; p)$ as the minimum of
${\rm ed}_K(X'/X; p)$ as the minimum of ![]() ${\rm ed}_K(X'\times _X E\to E)$ where
${\rm ed}_K(X'\times _X E\to E)$ where ![]() $E\to X$ runs over finite, generically étale maps of
$E\to X$ runs over finite, generically étale maps of ![]() $K$-varieties of degree prime to
$K$-varieties of degree prime to ![]() $p$. For any map
$p$. For any map ![]() $E \rightarrow X$ one always has
$E \rightarrow X$ one always has
where ![]() $\tilde X'$ denotes the composite of Galois closures of the connected components of
$\tilde X'$ denotes the composite of Galois closures of the connected components of ![]() $X'$ (see Lemmas 2.2.2, 2.2.3; cf. [Reference Buhler and ReichsteinBR97, Lemma 2.3]). In particular, for any class of maps
$X'$ (see Lemmas 2.2.2, 2.2.3; cf. [Reference Buhler and ReichsteinBR97, Lemma 2.3]). In particular, for any class of maps ![]() $E \to {\mathcal {A}}_g$, the answer to the question above does not change if we replace
$E \to {\mathcal {A}}_g$, the answer to the question above does not change if we replace ![]() ${\mathcal {A}}_{g,n}^1$ by
${\mathcal {A}}_{g,n}^1$ by ![]() ${\mathcal {A}}_{g,n},$ the coarse moduli space of pairs
${\mathcal {A}}_{g,n},$ the coarse moduli space of pairs ![]() $(A,\mathcal {B})$ where
$(A,\mathcal {B})$ where ![]() $A$ is a principally polarized abelian variety of dimension
$A$ is a principally polarized abelian variety of dimension ![]() $g,$ and
$g,$ and ![]() $\mathcal {B}$ is a symplectic basis for the
$\mathcal {B}$ is a symplectic basis for the ![]() $n$-torsion
$n$-torsion ![]() $A[n]$. (Here and below we fix once and for all an isomorphism
$A[n]$. (Here and below we fix once and for all an isomorphism ![]() $\mu _n(K) \overset \sim \longrightarrow {\mathbb {Z}}/n{\mathbb {Z}},$ so that we may speak of a symplectic basis for
$\mu _n(K) \overset \sim \longrightarrow {\mathbb {Z}}/n{\mathbb {Z}},$ so that we may speak of a symplectic basis for ![]() $A[n]$.)
$A[n]$.)
In this paper we apply techniques from the deformation theory of ![]() $p$-divisible groups and finite flat group schemes to compute the essential
$p$-divisible groups and finite flat group schemes to compute the essential ![]() $p$-dimension of congruence covers of certain locally symmetric varieties, such as
$p$-dimension of congruence covers of certain locally symmetric varieties, such as ![]() ${\mathcal {A}}_g$.
${\mathcal {A}}_g$.
Theorem 2 Let ![]() $g,n\geq 2$, and let
$g,n\geq 2$, and let ![]() $p$ be any prime with
$p$ be any prime with ![]() $p|n$. Then
$p|n$. Then
Theorem 2 thus answers Question 1: the minimal ![]() $d$ equals
$d$ equals ![]() $\binom {g+1}{2}$. We in fact prove a more general result, that for subvarieties of
$\binom {g+1}{2}$. We in fact prove a more general result, that for subvarieties of ![]() ${\mathcal {Z}} \subset {\mathcal {A}}_g$ satisfying some mild technical hypotheses,
${\mathcal {Z}} \subset {\mathcal {A}}_g$ satisfying some mild technical hypotheses, ![]() ${\rm ed}_K({\mathcal {A}}_{g,n}|_{{\mathcal {Z}}} / {\mathcal {Z}}) = {\rm dim}\,{\mathcal {Z}}$. More precisely, we prove the following theorem (see Theorem 3.2.6 below for a slightly more general formulation, which is important in some applications).
${\rm ed}_K({\mathcal {A}}_{g,n}|_{{\mathcal {Z}}} / {\mathcal {Z}}) = {\rm dim}\,{\mathcal {Z}}$. More precisely, we prove the following theorem (see Theorem 3.2.6 below for a slightly more general formulation, which is important in some applications).
Theorem 3 Let ![]() $p$ be prime and let
$p$ be prime and let ![]() $N\ge 3$ be an integer prime to
$N\ge 3$ be an integer prime to ![]() $p$. Suppose that
$p$. Suppose that ![]() $L = \bar {\mathbb {Q}}_p,$ an algebraic closure of
$L = \bar {\mathbb {Q}}_p,$ an algebraic closure of ![]() ${\mathbb {Q}}_p,$ let
${\mathbb {Q}}_p,$ let ![]() $\mathcal {O}_L$ be its ring of integers and let
$\mathcal {O}_L$ be its ring of integers and let ![]() $k$ be its residue field. Let
$k$ be its residue field. Let ![]() ${\mathcal {Z}} \subset {\mathcal {A}}_{g,N/\mathcal {O}_L}$ be a locally closed subscheme that is equidimensional and smooth over
${\mathcal {Z}} \subset {\mathcal {A}}_{g,N/\mathcal {O}_L}$ be a locally closed subscheme that is equidimensional and smooth over ![]() $\mathcal {O}_L$, and whose special fiber
$\mathcal {O}_L$, and whose special fiber ![]() ${\mathcal {Z}}_k$ meets the ordinary locus
${\mathcal {Z}}_k$ meets the ordinary locus ![]() ${\mathcal {A}}_{g,N}^{{\rm ord}} \subset {\mathcal {A}}_{g,N/k}$. Then
${\mathcal {A}}_{g,N}^{{\rm ord}} \subset {\mathcal {A}}_{g,N/k}$. Then
We give three applications of Theorem 3. The first is an analogue of Theorem 2 for ![]() ${\mathcal {M}}_g,$ the coarse moduli space of smooth, proper, genus
${\mathcal {M}}_g,$ the coarse moduli space of smooth, proper, genus ![]() $g\geq 2$ curves over
$g\geq 2$ curves over ![]() $K$. For any integer
$K$. For any integer ![]() $n,$ consider the level
$n,$ consider the level ![]() $n$ congruence cover
$n$ congruence cover ![]() ${\mathcal {M}}_g[n] \to {\mathcal {M}}_g$, where
${\mathcal {M}}_g[n] \to {\mathcal {M}}_g$, where ![]() ${\mathcal {M}}_g[n]$ denotes the moduli space of pairs
${\mathcal {M}}_g[n]$ denotes the moduli space of pairs ![]() $(C,{\mathcal {B}})$ consisting of a smooth, proper curve
$(C,{\mathcal {B}})$ consisting of a smooth, proper curve ![]() $C$ of genus
$C$ of genus ![]() $g,$ together with a symplectic basis
$g,$ together with a symplectic basis ![]() $\mathcal {B}$ for
$\mathcal {B}$ for ![]() $J(C)[n],$ where
$J(C)[n],$ where ![]() $J(C)$ is the Jacobian of
$J(C)$ is the Jacobian of ![]() $C$. Applying Theorem 3 and the Torelli theorem, we will deduce the following result.
$C$. Applying Theorem 3 and the Torelli theorem, we will deduce the following result.
Corollary 4 Let ![]() $g,n\geq 2$. Let
$g,n\geq 2$. Let ![]() $p$ be any prime with
$p$ be any prime with ![]() $p{{\mid}} n$. Then
$p{{\mid}} n$. Then
As a second application of Theorem 3, let ![]() $\mathcal {H}_g$ denote the coarse moduli of smooth, hyperelliptic curves of genus
$\mathcal {H}_g$ denote the coarse moduli of smooth, hyperelliptic curves of genus ![]() $g\geq 2$ over
$g\geq 2$ over ![]() $K$. For any integer
$K$. For any integer ![]() $n,$ consider the level
$n,$ consider the level ![]() $n$ congruence cover
$n$ congruence cover ![]() $\mathcal {H}_g[n] \to \mathcal {H}_g$, where
$\mathcal {H}_g[n] \to \mathcal {H}_g$, where ![]() $\mathcal {H}_g[n]$ denotes the moduli space of pairs
$\mathcal {H}_g[n]$ denotes the moduli space of pairs ![]() $(C,{\mathcal {B}})$ consisting of a hyperelliptic curve
$(C,{\mathcal {B}})$ consisting of a hyperelliptic curve ![]() $C$ together with a symplectic basis
$C$ together with a symplectic basis ![]() $\mathcal {B}$ for
$\mathcal {B}$ for ![]() $J(C)[n]$. Analogously to the case of
$J(C)[n]$. Analogously to the case of ![]() ${\mathcal {M}}_g$, we prove the following result.
${\mathcal {M}}_g$, we prove the following result.
Corollary 5 Let ![]() $g,n\geq 2$. Let
$g,n\geq 2$. Let ![]() $p {\mid} n$ be any odd prime. Then
$p {\mid} n$ be any odd prime. Then
For ![]() $g>2$, the hypothesis that
$g>2$, the hypothesis that ![]() $p$ is odd in Corollary 5 is necessary; see 3.3.5 below.
$p$ is odd in Corollary 5 is necessary; see 3.3.5 below.
Our third application of Theorem 3 generalizes Theorem 2 to many locally symmetric varieties. Recall that a locally symmetric variety is a variety whose complex points have the form ![]() $\Gamma \backslash X^+,$ where
$\Gamma \backslash X^+,$ where ![]() $X^+$ is a Hermitian symmetric domain and
$X^+$ is a Hermitian symmetric domain and ![]() $\Gamma$ is an arithmetic lattice in the corresponding real semisimple Lie group (see Lemma 4.2.3 below). Attached to
$\Gamma$ is an arithmetic lattice in the corresponding real semisimple Lie group (see Lemma 4.2.3 below). Attached to ![]() $\Gamma$ there is a semisimple algebraic group
$\Gamma$ there is a semisimple algebraic group ![]() $G$ over
$G$ over ![]() ${\mathbb {Q}},$ with
${\mathbb {Q}},$ with ![]() $X^+$ the connected component of the identity in
$X^+$ the connected component of the identity in ![]() $X = G({\mathbb {R}})/K_{\infty },$ for
$X = G({\mathbb {R}})/K_{\infty },$ for ![]() $K_{\infty } \subset G({\mathbb {R}})$ a maximal compact subgroup. By a principal
$K_{\infty } \subset G({\mathbb {R}})$ a maximal compact subgroup. By a principal ![]() $p$-level covering
$p$-level covering ![]() $\Gamma _1\backslash X^+ \to \Gamma \backslash X^+$ we mean that the definition of
$\Gamma _1\backslash X^+ \to \Gamma \backslash X^+$ we mean that the definition of ![]() $\Gamma$ does not involve any congruences at
$\Gamma$ does not involve any congruences at ![]() $p,$ and
$p,$ and ![]() $\Gamma _1 \subset \Gamma$ is the subgroup of elements that are trivial mod
$\Gamma _1 \subset \Gamma$ is the subgroup of elements that are trivial mod ![]() $p$. A sample of what we prove is the following theorem (see Theorem 4.3.6 below for the most general statement).
$p$. A sample of what we prove is the following theorem (see Theorem 4.3.6 below for the most general statement).
Theorem 6 Suppose that each irreducible factor of ![]() $G^{{\rm ad}}_{{\mathbb {R}}}$ is the adjoint group of one of
$G^{{\rm ad}}_{{\mathbb {R}}}$ is the adjoint group of one of ![]() $U(n,n),$
$U(n,n),$ ![]() ${\rm SO}(n,2)$ with
${\rm SO}(n,2)$ with ![]() $n+2 \neq 8,$ or
$n+2 \neq 8,$ or ![]() ${\rm Sp}(2n)$ for some positive integer
${\rm Sp}(2n)$ for some positive integer ![]() $n$. If
$n$. If ![]() $G$ is unramified at
$G$ is unramified at ![]() $p$ (a condition which holds for almost all
$p$ (a condition which holds for almost all ![]() $p$), then for any principal
$p$), then for any principal ![]() $p$-level covering
$p$-level covering ![]() $\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$, we have
$\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$, we have
In fact our results apply to any Hermitian symmetric domain of classical type, but in general they require a more involved condition on the ![]() ${\mathbb {Q}}$-group
${\mathbb {Q}}$-group ![]() $G$ giving rise to
$G$ giving rise to ![]() $\Gamma ;$ this condition always applies if
$\Gamma ;$ this condition always applies if ![]() $G$ splits over
$G$ splits over ![]() ${\mathbb {Q}}_p$. Note that these results include cases where the locally symmetric variety
${\mathbb {Q}}_p$. Note that these results include cases where the locally symmetric variety ![]() $\Gamma \backslash X^+$ is proper. As far as we know, these are the first examples of nontrivial lower bounds on the essential dimension of an unramified, nonabelian covering of a proper algebraic variety (although a certain abelian subgroup of the covering group plays an important role in the argument). The only prior result for unramified covers of proper varieties of which we are aware is due to Gabber [Reference Colliot-ThélèneCT02, Appendix], who proved that if
$\Gamma \backslash X^+$ is proper. As far as we know, these are the first examples of nontrivial lower bounds on the essential dimension of an unramified, nonabelian covering of a proper algebraic variety (although a certain abelian subgroup of the covering group plays an important role in the argument). The only prior result for unramified covers of proper varieties of which we are aware is due to Gabber [Reference Colliot-ThélèneCT02, Appendix], who proved that if ![]() $\{E'_i\to E_i\}$ is a collection of connected, unramified
$\{E'_i\to E_i\}$ is a collection of connected, unramified ![]() ${\mathbb {Z}}/p{\mathbb {Z}}$ covers of elliptic curves
${\mathbb {Z}}/p{\mathbb {Z}}$ covers of elliptic curves ![]() $E_i$, then under certain conditions, the cover
$E_i$, then under certain conditions, the cover ![]() $E_1'\times \cdots \times E_r'\to E_1\times \cdots \times E_r$ has essential dimension at
$E_1'\times \cdots \times E_r'\to E_1\times \cdots \times E_r$ has essential dimension at ![]() $p$ equal to
$p$ equal to ![]() $r$.
$r$.
When ![]() $\Gamma \backslash X$ is proper, the use of more standard techniques involving fixed points to bound
$\Gamma \backslash X$ is proper, the use of more standard techniques involving fixed points to bound ![]() ${\rm ed}$ from below (see, for example, [Reference ReichsteinRei11]) is precluded by the fact that one cannot use ‘ramification at infinity’. This is in analogy with Margulis superrigidity for irreducible lattices
${\rm ed}$ from below (see, for example, [Reference ReichsteinRei11]) is precluded by the fact that one cannot use ‘ramification at infinity’. This is in analogy with Margulis superrigidity for irreducible lattices ![]() $\Gamma$ in higher rank semisimple Lie groups where, for nonuniform
$\Gamma$ in higher rank semisimple Lie groups where, for nonuniform ![]() $\Gamma$ (equivalently, noncompact
$\Gamma$ (equivalently, noncompact ![]() $\Gamma \backslash X$), unipotents in
$\Gamma \backslash X$), unipotents in ![]() $\Gamma$ play a crucial role. When
$\Gamma$ play a crucial role. When ![]() $\Gamma$ is uniform it contains no unipotents, and new ideas were needed (and were provided only later, also by Margulis).
$\Gamma$ is uniform it contains no unipotents, and new ideas were needed (and were provided only later, also by Margulis).
There are many examples of finite simple groups of Lie type for which our methods give a lower bound on the essential ![]() $p$-dimension of a covering of locally symmetric varieties with that group. To state these, for
$p$-dimension of a covering of locally symmetric varieties with that group. To state these, for ![]() $H$ an absolutely simple (adjoint) algebraic group over
$H$ an absolutely simple (adjoint) algebraic group over ![]() ${\mathbb {F}}_q,$ denote by
${\mathbb {F}}_q,$ denote by ![]() $H(q)$ the image of
$H(q)$ the image of ![]() $H^{{\rm sc}}({\mathbb {F}}_q) \rightarrow H({\mathbb {F}}_q),$ where
$H^{{\rm sc}}({\mathbb {F}}_q) \rightarrow H({\mathbb {F}}_q),$ where ![]() $H^{{\rm sc}}$ denotes the simply connected cover of
$H^{{\rm sc}}$ denotes the simply connected cover of ![]() $H$.
$H$.
Corollary 7 Let ![]() $H$ be a classical, absolutely simple group over
$H$ be a classical, absolutely simple group over ![]() ${\mathbb {F}}_q,$ with
${\mathbb {F}}_q,$ with ![]() $q = p^r$. If
$q = p^r$. If ![]() $p=2$ we further assume that
$p=2$ we further assume that ![]() $8\nmid r,$ and
$8\nmid r,$ and ![]() $4\nmid r$ if
$4\nmid r$ if ![]() $H$ is not split over
$H$ is not split over ![]() ${\mathbb {F}}_q$.
${\mathbb {F}}_q$.
Then there is a congruence ![]() $H(q)$-cover of locally symmetric varieties
$H(q)$-cover of locally symmetric varieties ![]() $Y' \rightarrow Y,$ whose associated real Lie group is of the same type (
$Y' \rightarrow Y,$ whose associated real Lie group is of the same type (![]() $A,B,C$ or
$A,B,C$ or ![]() $D$) as
$D$) as ![]() $H,$ and such that
$H,$ and such that ![]() $e:= {\rm ed}_K(Y'/ Y; p)$ satisfies the following conditions.
$e:= {\rm ed}_K(Y'/ Y; p)$ satisfies the following conditions.
– If
 $H$ is a form of
$H$ is a form of  ${\rm PGL}_n$ which is split if
${\rm PGL}_n$ which is split if  $n$ is odd, then
$n$ is odd, then  $e = r\lfloor {n^2}/4 \rfloor$.
$e = r\lfloor {n^2}/4 \rfloor$.– If
 $H$ is
$H$ is  ${\rm PSp}_{2n}$ then
${\rm PSp}_{2n}$ then  $e = r({(n^2+n)}/2)$.
$e = r({(n^2+n)}/2)$.– If
 $H$ is a split form of
$H$ is a split form of  ${\rm PO}_{2n}$ then
${\rm PO}_{2n}$ then  $e = r({(n^2-n)}/2)$.
$e = r({(n^2-n)}/2)$.– If
 $H$ is a form of
$H$ is a form of  ${\rm PO}_n$ and
${\rm PO}_n$ and  $H$ is not of type
$H$ is not of type  $D_4,$ then
$D_4,$ then  $e = r(n-2)$.
$e = r(n-2)$.
Idea of the proof. To prove Theorem 2 and its generalization to subvarieties we use arithmetic techniques, specifically Serre–Tate theory, which describe the deformation theory of an ordinary abelian variety in characteristic ![]() $p$ in terms of its
$p$ in terms of its ![]() $p$-divisible group. Let
$p$-divisible group. Let ![]() $N \geq 3$ be an integer coprime to
$N \geq 3$ be an integer coprime to ![]() $p,$ and let
$p,$ and let ![]() ${\mathcal {A}}$ denote the universal abelian scheme over
${\mathcal {A}}$ denote the universal abelian scheme over ![]() ${\mathcal {A}}_{g,N}$ (now considered over
${\mathcal {A}}_{g,N}$ (now considered over ![]() $\mathbb {Z}[\zeta _N][1/N]$). Let
$\mathbb {Z}[\zeta _N][1/N]$). Let ![]() ${\mathcal {A}}[p]$ be its
${\mathcal {A}}[p]$ be its ![]() $p$-torsion group scheme, and let
$p$-torsion group scheme, and let ![]() ${\mathcal {A}}_x$ denote the fiber of
${\mathcal {A}}_x$ denote the fiber of ![]() ${\mathcal {A}}$ at
${\mathcal {A}}$ at ![]() $x$. Given a rational compression of
$x$. Given a rational compression of ![]() ${\mathcal {A}}_{g,pN}\to {\mathcal {A}}_{g,N}$ (in characteristic
${\mathcal {A}}_{g,pN}\to {\mathcal {A}}_{g,N}$ (in characteristic ![]() $0$) onto a smaller-dimensional variety, we show that there exists an ordinary mod
$0$) onto a smaller-dimensional variety, we show that there exists an ordinary mod ![]() $p$ point
$p$ point ![]() $x$ of
$x$ of ![]() ${\mathcal {A}}_{g,N}$, and a tangent direction
${\mathcal {A}}_{g,N}$, and a tangent direction ![]() $t_x$ at
$t_x$ at ![]() $x$ such that the deformation of
$x$ such that the deformation of ![]() ${\mathcal {A}}_x[p]$ corresponding to
${\mathcal {A}}_x[p]$ corresponding to ![]() $t_x$ is trivial. From this we deduce that the deformation of
$t_x$ is trivial. From this we deduce that the deformation of ![]() ${\mathcal {A}}_x$ corresponding to
${\mathcal {A}}_x$ corresponding to ![]() $t_x$ is trivial, a contradiction.
$t_x$ is trivial, a contradiction.
One might view our method as an arithmetic analogue of the ‘fixed point method’ in the theory of essential dimension (see [Reference ReichsteinRei11]), where the role of fixed points for a group action is now played by wild ramification at a prime. In the fixed point method one usually works over a field where the order of the group is invertible. In contrast, for us the presence of wild ramification plays an essential role.
Acknowledgements. We would like to thank Aaron Landesman and Zinovy Reichstein for detailed comments on an earlier version of this paper and for extensive helpful correspondence. We thank Frank Calegari for pointing out a mistake in an earlier version of this paper. We thank Yonathan Stone for help with the classical German literature. We also thank Maxime Bergeron, Mike Fried, Eric Rains, Alexander Polishchuk and Burt Totaro, for various helpful comments. Finally, we thank the referees for their incredibly thorough and thoughtful reports, and for many useful suggestions that helped to improve this paper.
2. Preliminary results
2.1 Finite étale maps
We begin with some general lemmas on finite étale maps.
2.1.1 Let ![]() $G \rightarrow G'$ be a homomorphism, and
$G \rightarrow G'$ be a homomorphism, and ![]() $S$ a finite set with an action of
$S$ a finite set with an action of ![]() $G$. We say that the action of
$G$. We say that the action of ![]() $G$ on
$G$ on ![]() $S$ lifts to
$S$ lifts to ![]() $G'$ if there is an action of
$G'$ if there is an action of ![]() $G'$ on
$G'$ on ![]() $S$, which induces the given action of
$S$, which induces the given action of ![]() $G$ on
$G$ on ![]() $S$. We call such a
$S$. We call such a ![]() $G'$-action a lifting of the
$G'$-action a lifting of the ![]() $G$-action on
$G$-action on ![]() $S$. We say that the action of
$S$. We say that the action of ![]() $G$ on
$G$ on ![]() $S$ virtually lifts to
$S$ virtually lifts to ![]() $G'$ if there is a finite index subgroup
$G'$ if there is a finite index subgroup ![]() $G'' \subset G',$ containing the image of
$G'' \subset G',$ containing the image of ![]() $G,$ such that the action of
$G,$ such that the action of ![]() $G$ on
$G$ on ![]() $S$ lifts to
$S$ lifts to ![]() $G''$.
$G''$.
For a positive integer ![]() $n$ we denote by
$n$ we denote by ![]() $S^n$ the
$S^n$ the ![]() $n$-fold product equipped with the diagonal action of
$n$-fold product equipped with the diagonal action of ![]() $G,$ and by
$G,$ and by ![]() $\pi _i: S^n \rightarrow S$,
$\pi _i: S^n \rightarrow S$, ![]() $i=1,\ldots , n$, the projections.
$i=1,\ldots , n$, the projections.
Lemma 2.1.2 Let ![]() $G \rightarrow G'$ be a map of groups, and
$G \rightarrow G'$ be a map of groups, and ![]() $S$ a finite set with an action of
$S$ a finite set with an action of ![]() $G$.
$G$.
(i) Suppose the action of
 $G$ on
$G$ on  $S$ admits a lifting to an action of
$S$ admits a lifting to an action of  $G'$ on
$G'$ on  $S,$ and fix such a lifting. Then there exists a finite index subgroup
$S,$ and fix such a lifting. Then there exists a finite index subgroup  $G'' \subset G'$ containing the image of
$G'' \subset G'$ containing the image of  $G,$ such that
$G,$ such that  $G$ and
$G$ and  $G''$ have the same image in
$G''$ have the same image in  ${\rm Aut}(S)$.
${\rm Aut}(S)$.(ii) Let
 $T \subset S^n$ be a
$T \subset S^n$ be a  $G$-stable subset such that
$G$-stable subset such that  $\bigcup _{i=1}^n \pi _i(T) = S$. Then the action of
$\bigcup _{i=1}^n \pi _i(T) = S$. Then the action of  $G$ on
$G$ on  $S$ virtually lifts to
$S$ virtually lifts to  $G'$ if and only if the action of
$G'$ if and only if the action of  $G$ on
$G$ on  $T$ virtually lifts to
$T$ virtually lifts to  $G'$.
$G'$.
Proof. Let ![]() $N \subset G'$ be the kernel of
$N \subset G'$ be the kernel of ![]() $G' \rightarrow {\rm Aut}(S),$ and
$G' \rightarrow {\rm Aut}(S),$ and ![]() $G'' \subset G'$ the subgroup generated by
$G'' \subset G'$ the subgroup generated by ![]() $N$ and the image of
$N$ and the image of ![]() $G$. Since
$G$. Since ![]() $S$ is finite,
$S$ is finite, ![]() $N$ and hence
$N$ and hence ![]() $G''$ has finite index in
$G''$ has finite index in ![]() $G^{\prime}$, and so
$G^{\prime}$, and so ![]() $G^{\prime\prime}$ satisfies the conditions in (i).
$G^{\prime\prime}$ satisfies the conditions in (i).
For (ii), suppose that the action of ![]() $G$ on
$G$ on ![]() $S$ virtually lifts to
$S$ virtually lifts to ![]() $G'$. By (i), after replacing
$G'$. By (i), after replacing ![]() $G'$ by a finite index subgroup containing the image of
$G'$ by a finite index subgroup containing the image of ![]() $G,$ we may assume that the action of
$G,$ we may assume that the action of ![]() $G$ on
$G$ on ![]() $S$ lifts to
$S$ lifts to ![]() $G',$ and that
$G',$ and that ![]() $G$ and
$G$ and ![]() $G'$ have the same image in
$G'$ have the same image in ![]() ${\rm Aut}(S)$. Then
${\rm Aut}(S)$. Then ![]() $T$ is
$T$ is ![]() $G'$-stable, so the action of
$G'$-stable, so the action of ![]() $G$ on
$G$ on ![]() $T$ lifts to
$T$ lifts to ![]() $G'$. Conversely, if the action of
$G'$. Conversely, if the action of ![]() $G$ on
$G$ on ![]() $T$ virtually lifts to
$T$ virtually lifts to ![]() $G',$ then, by (i), we may assume that the action of
$G',$ then, by (i), we may assume that the action of ![]() $G$ on
$G$ on ![]() $T$ lifts to
$T$ lifts to ![]() $G',$ and that
$G',$ and that ![]() $G$ and
$G$ and ![]() $G'$ have the same image in
$G'$ have the same image in ![]() ${\rm Aut}(T)$. In particular, any element of
${\rm Aut}(T)$. In particular, any element of ![]() $G'$ acts on
$G'$ acts on ![]() ${\rm Aut}(T)$ via an element of
${\rm Aut}(T)$ via an element of ![]() ${\rm Aut}(S)$. Since
${\rm Aut}(S)$. Since ![]() $\bigcup _{i=1}^n \pi _i(T) = S$ this element of
$\bigcup _{i=1}^n \pi _i(T) = S$ this element of ![]() ${\rm Aut}(S)$ is uniquely determined. The uniqueness implies that
${\rm Aut}(S)$ is uniquely determined. The uniqueness implies that ![]() $G' \rightarrow {\rm Aut}(T)$ factors through a homomorphism
$G' \rightarrow {\rm Aut}(T)$ factors through a homomorphism ![]() $G' \rightarrow {\rm Aut}(S),$ which lifts the action of
$G' \rightarrow {\rm Aut}(S),$ which lifts the action of ![]() $G$ on
$G$ on ![]() $S$.
$S$.
2.1.3 Let ![]() $X$ be a separated, locally Noetherian scheme and
$X$ be a separated, locally Noetherian scheme and ![]() $f:Y \rightarrow X$ a finite étale cover. We will say that
$f:Y \rightarrow X$ a finite étale cover. We will say that ![]() $f$ is Galois if any connected component of
$f$ is Galois if any connected component of ![]() $Y$ is Galois over its image.
$Y$ is Galois over its image.
Suppose that ![]() $X$ is connected, and let
$X$ is connected, and let ![]() $\bar x$ be a geometric point of
$\bar x$ be a geometric point of ![]() $X$. Let
$X$. Let ![]() $F_{\bar x}$ denote the functor which assigns to any finite étale cover
$F_{\bar x}$ denote the functor which assigns to any finite étale cover ![]() $Y \rightarrow X$ the underlying topological space
$Y \rightarrow X$ the underlying topological space ![]() $|Y_{\bar x}|$ of its fiber over
$|Y_{\bar x}|$ of its fiber over ![]() $\bar x$. Then
$\bar x$. Then ![]() ${\rm Aut}(F_{\bar x})$ is called the étale fundamental group and is denoted by
${\rm Aut}(F_{\bar x})$ is called the étale fundamental group and is denoted by ![]() $\pi _1(X,\bar x),$ [Reference GrothendieckSGA1, Exp. V, § 7]. It follows from [Reference GrothendieckSGA1, Exp. V, § 7] that the association
$\pi _1(X,\bar x),$ [Reference GrothendieckSGA1, Exp. V, § 7]. It follows from [Reference GrothendieckSGA1, Exp. V, § 7] that the association ![]() $Y \mapsto S(Y) : = |Y_{\bar x}|$ induces a bijection between isomorphism classes of finite étale covers, and of finite sets with
$Y \mapsto S(Y) : = |Y_{\bar x}|$ induces a bijection between isomorphism classes of finite étale covers, and of finite sets with ![]() $\pi _1(X,\bar x)$-action. If
$\pi _1(X,\bar x)$-action. If ![]() $X$ is connected and
$X$ is connected and ![]() $S$ is a finite set with an action of
$S$ is a finite set with an action of ![]() $\pi _1(X,\bar x),$ we denote by
$\pi _1(X,\bar x),$ we denote by ![]() $Y(S)$ the corresponding finite étale cover of
$Y(S)$ the corresponding finite étale cover of ![]() $X$.
$X$.
In the next three lemmas we consider a map of separated, locally Noetherian schemes ![]() $g: X \rightarrow X'$ and a finite étale cover
$g: X \rightarrow X'$ and a finite étale cover ![]() $f': Y' \rightarrow X'$ equipped with an isomorphism
$f': Y' \rightarrow X'$ equipped with an isomorphism ![]() $Y \overset \sim \longrightarrow Y'\times _{X'}X$. If
$Y \overset \sim \longrightarrow Y'\times _{X'}X$. If ![]() $X$ and
$X$ and ![]() $X'$ are connected, and
$X'$ are connected, and ![]() $\bar x$ again denotes the geometric point of
$\bar x$ again denotes the geometric point of ![]() $X'$ induced by
$X'$ induced by ![]() $\bar x,$ then such a
$\bar x,$ then such a ![]() $Y'$ exists if and only if the action of
$Y'$ exists if and only if the action of ![]() $\pi _1(X,\bar x)$ on
$\pi _1(X,\bar x)$ on ![]() $S(Y)$ lifts to
$S(Y)$ lifts to ![]() $\pi _1(X',\bar x)$.
$\pi _1(X',\bar x)$.
Lemma 2.1.4 If ![]() $f$ is Galois, then there is a finite étale
$f$ is Galois, then there is a finite étale ![]() $h: X'' \rightarrow X'$ such that
$h: X'' \rightarrow X'$ such that ![]() $g$ factors through
$g$ factors through ![]() $X''$ and
$X''$ and ![]() $Y'' = X''\times _{X'} Y' \rightarrow X''$ is Galois.
$Y'' = X''\times _{X'} Y' \rightarrow X''$ is Galois.
Proof. We may assume that ![]() $X$ and
$X$ and ![]() $X'$ are connected. We apply Lemma 2.1.2(i), to
$X'$ are connected. We apply Lemma 2.1.2(i), to ![]() $\pi _1(X,\bar x) \rightarrow \pi _1(X',\bar x)$ and
$\pi _1(X,\bar x) \rightarrow \pi _1(X',\bar x)$ and ![]() $S = S(Y) = S(Y')$. Let
$S = S(Y) = S(Y')$. Let ![]() $h: X'' \rightarrow X'$ be the finite étale map corresponding to the
$h: X'' \rightarrow X'$ be the finite étale map corresponding to the ![]() $\pi _1(X',\bar x)$-set
$\pi _1(X',\bar x)$-set ![]() $\pi _1(X',\bar x)/G''$. Since this set has a
$\pi _1(X',\bar x)/G''$. Since this set has a ![]() $\pi _1(X,\bar x)$ fixed point,
$\pi _1(X,\bar x)$ fixed point, ![]() $g$ factors through
$g$ factors through ![]() $X''$. By construction, the images of
$X''$. By construction, the images of ![]() $\pi _1(X'',\bar x)$ and
$\pi _1(X'',\bar x)$ and ![]() $\pi _1(X,\bar x)$ in
$\pi _1(X,\bar x)$ in ![]() ${\rm Aut}(S(Y')) = {\rm Aut}(S(Y))$ are equal. Denote this image by
${\rm Aut}(S(Y')) = {\rm Aut}(S(Y))$ are equal. Denote this image by ![]() $H,$ and for
$H,$ and for ![]() $s \in S(Y)$ denote the stabilizer by
$s \in S(Y)$ denote the stabilizer by ![]() $H_s$. Since
$H_s$. Since ![]() $Y\rightarrow X$ is Galois,
$Y\rightarrow X$ is Galois, ![]() $H_s$ is a normal subgroup which does not depend on
$H_s$ is a normal subgroup which does not depend on ![]() $s,$ which implies that
$s,$ which implies that ![]() $Y'' \rightarrow X''$ is Galois.
$Y'' \rightarrow X''$ is Galois.
2.1.5 Let ![]() $A$ be a finite ring. By an
$A$ be a finite ring. By an ![]() $A$-local system
$A$-local system ![]() ${\mathcal {F}}$ on
${\mathcal {F}}$ on ![]() $X$ we will mean an étale sheaf of
$X$ we will mean an étale sheaf of ![]() $A$-modules which is locally isomorphic to the constant
$A$-modules which is locally isomorphic to the constant ![]() $A$-module
$A$-module ![]() $A^n$ for some
$A^n$ for some ![]() $n$. Such an
$n$. Such an ![]() ${\mathcal {F}}$ is representable by a finite étale map
${\mathcal {F}}$ is representable by a finite étale map ![]() $Y({\mathcal {F}}) \rightarrow X$. This is clear étale locally on
$Y({\mathcal {F}}) \rightarrow X$. This is clear étale locally on ![]() $X,$ and follows from étale descent in general. If
$X,$ and follows from étale descent in general. If ![]() $X$ is connected, and equipped with a geometric point
$X$ is connected, and equipped with a geometric point ![]() $\bar x,$ then the association
$\bar x,$ then the association ![]() ${\mathcal {F}} \mapsto |Y({\mathcal {F}})|_{\bar x}$ induces a bijection between isomorphism classes of
${\mathcal {F}} \mapsto |Y({\mathcal {F}})|_{\bar x}$ induces a bijection between isomorphism classes of ![]() $A$-local systems and conjugacy classes of representations
$A$-local systems and conjugacy classes of representations ![]() $\pi _1(X,\bar x) \rightarrow {\rm GL}_n(A)$. Indeed, this follows easily from the bijection explained in 2.1.3.
$\pi _1(X,\bar x) \rightarrow {\rm GL}_n(A)$. Indeed, this follows easily from the bijection explained in 2.1.3.
For ![]() $X \rightarrow X_1$ a map of schemes, and
$X \rightarrow X_1$ a map of schemes, and ![]() $\mathcal {G}$ an
$\mathcal {G}$ an ![]() $A$-local system on
$A$-local system on ![]() $X_1,$ we will denote by
$X_1,$ we will denote by ![]() $\mathcal {G}|_X$ the pullback of
$\mathcal {G}|_X$ the pullback of ![]() $\mathcal {G}$ to
$\mathcal {G}$ to ![]() $X$.
$X$.
Lemma 2.1.6 Suppose that ![]() $f: Y = Y({\mathcal {F}}) \rightarrow X$ corresponds to an
$f: Y = Y({\mathcal {F}}) \rightarrow X$ corresponds to an ![]() $A$-local system
$A$-local system ![]() ${\mathcal {F}}$. Then there is a finite étale
${\mathcal {F}}$. Then there is a finite étale ![]() $h: X'' \rightarrow X'$ such that
$h: X'' \rightarrow X'$ such that ![]() $g$ factors through
$g$ factors through ![]() $X''$ and
$X''$ and ![]() $Y'' = X''\times _XY' \rightarrow X''$ represents an
$Y'' = X''\times _XY' \rightarrow X''$ represents an ![]() $A$-local system
$A$-local system ![]() ${\mathcal {F}}'',$ with
${\mathcal {F}}'',$ with ![]() ${\mathcal {F}}''|_X \overset \sim \longrightarrow {\mathcal {F}}$.
${\mathcal {F}}''|_X \overset \sim \longrightarrow {\mathcal {F}}$.
Proof. We may assume that ![]() $X$ and
$X$ and ![]() $X'$ are connected and choose
$X'$ are connected and choose ![]() $X''$ as in the proof of Lemma 2.1.4, using the construction in Lemma 2.1.2(i). Then the finite set
$X''$ as in the proof of Lemma 2.1.4, using the construction in Lemma 2.1.2(i). Then the finite set ![]() $S(Y) = S(Y')$ naturally has the structure of a finite free
$S(Y) = S(Y')$ naturally has the structure of a finite free ![]() $A$-module on which
$A$-module on which ![]() $\pi _1(X,\bar x)$ acts
$\pi _1(X,\bar x)$ acts ![]() $A$-linearly. Since the images of
$A$-linearly. Since the images of ![]() $\pi _1(X'',\bar x)$ and
$\pi _1(X'',\bar x)$ and ![]() $\pi _1(X,\bar x)$ in
$\pi _1(X,\bar x)$ in ![]() ${\rm Aut}(S(Y))$ are equal,
${\rm Aut}(S(Y))$ are equal, ![]() $\pi _1(X'',\bar x)$ acts on
$\pi _1(X'',\bar x)$ acts on ![]() $S(Y)$
$S(Y)$ ![]() $A$-linearly, which implies the statement of the lemma.
$A$-linearly, which implies the statement of the lemma.
2.1.7 We continue to assume that ![]() $X$ is separated and locally Noetherian.
$X$ is separated and locally Noetherian.
For any integer ![]() $N \geq 1$ we denote by
$N \geq 1$ we denote by ![]() $\mu _N$ the kernel of
$\mu _N$ the kernel of ![]() ${\mathbb {G}}_m \overset N \rightarrow {\mathbb {G}}_m$. This is a finite flat group scheme over
${\mathbb {G}}_m \overset N \rightarrow {\mathbb {G}}_m$. This is a finite flat group scheme over ![]() ${\mathbb {Z}},$ and we denote by the same symbol its pullback to any scheme
${\mathbb {Z}},$ and we denote by the same symbol its pullback to any scheme ![]() $X$. This pullback is étale if any only if
$X$. This pullback is étale if any only if ![]() $X$ is a
$X$ is a ![]() ${\mathbb {Z}}[1/N]$-scheme.
${\mathbb {Z}}[1/N]$-scheme.
Suppose ![]() $X$ is a
$X$ is a ![]() ${\mathbb {Z}}[1/N]$-scheme. For any
${\mathbb {Z}}[1/N]$-scheme. For any ![]() ${\mathbb {Z}}/N{\mathbb {Z}}$ algebra
${\mathbb {Z}}/N{\mathbb {Z}}$ algebra ![]() $A,$ we again denote by
$A,$ we again denote by ![]() $\mu _N$ or
$\mu _N$ or ![]() $A(1)$ the étale sheaf
$A(1)$ the étale sheaf ![]() $\mu _N\otimes _{{\mathbb {Z}}/N{\mathbb {Z}}}A$. For any nonnegative integer
$\mu _N\otimes _{{\mathbb {Z}}/N{\mathbb {Z}}}A$. For any nonnegative integer ![]() $i$ we write
$i$ we write ![]() $A(i) = A(1)^{\otimes i}$. For
$A(i) = A(1)^{\otimes i}$. For ![]() $i$ negative we set
$i$ negative we set ![]() $A(i)$ equal to the
$A(i)$ equal to the ![]() $A$-linear dual of
$A$-linear dual of ![]() $A(-i)$.
$A(-i)$.
Lemma 2.1.8 Let ![]() $N \geq 1$ be an integer,
$N \geq 1$ be an integer, ![]() $i,j$ integers, and
$i,j$ integers, and ![]() $A$ a finite
$A$ a finite ![]() ${\mathbb {Z}}/N{\mathbb {Z}}$-algebra. Suppose that
${\mathbb {Z}}/N{\mathbb {Z}}$-algebra. Suppose that ![]() $X$ is a
$X$ is a ![]() ${\mathbb {Z}}[1/N]$-scheme and that
${\mathbb {Z}}[1/N]$-scheme and that ![]() $f: Y = Y({\mathcal {F}}) \rightarrow X$ corresponds to an
$f: Y = Y({\mathcal {F}}) \rightarrow X$ corresponds to an ![]() $A$-local system
$A$-local system ![]() ${\mathcal {F}},$ which is an extension of
${\mathcal {F}},$ which is an extension of ![]() $A(i)^r$ by
$A(i)^r$ by ![]() $A(j)^s,$ for some positive integers
$A(j)^s,$ for some positive integers ![]() $r,s$.
$r,s$.
Then there is a finite étale map ![]() $X'' \rightarrow X'$ such that
$X'' \rightarrow X'$ such that ![]() $g$ factors through
$g$ factors through ![]() $X''$ and the cover
$X''$ and the cover ![]() $Y'' = X''\times _XY' \rightarrow X''$ represents an
$Y'' = X''\times _XY' \rightarrow X''$ represents an ![]() $A$-local system
$A$-local system ![]() ${\mathcal {F}}'',$ which is an extension of
${\mathcal {F}}'',$ which is an extension of ![]() $A(i)^r$ by
$A(i)^r$ by ![]() $A(j)^s,$ with
$A(j)^s,$ with ![]() ${\mathcal {F}}''|_X \overset \sim \longrightarrow {\mathcal {F}}$ as extensions.
${\mathcal {F}}''|_X \overset \sim \longrightarrow {\mathcal {F}}$ as extensions.
Proof. Replacing ![]() ${\mathcal {F}}$ by
${\mathcal {F}}$ by ![]() ${\mathcal {F}}(-j) : = {\mathcal {F}}\otimes _AA(-j)$, we may suppose that
${\mathcal {F}}(-j) : = {\mathcal {F}}\otimes _AA(-j)$, we may suppose that ![]() $j=0$. By Lemma 2.1.6, we may assume
$j=0$. By Lemma 2.1.6, we may assume ![]() $Y''$ represents an
$Y''$ represents an ![]() $A$-local system and
$A$-local system and ![]() $g^*({\mathcal {F}}') \overset \sim \longrightarrow {\mathcal {F}}$ as
$g^*({\mathcal {F}}') \overset \sim \longrightarrow {\mathcal {F}}$ as ![]() $A$-local systems. Let
$A$-local systems. Let ![]() ${\mathcal {F}}_1 \subset {\mathcal {F}}$ denote the sub
${\mathcal {F}}_1 \subset {\mathcal {F}}$ denote the sub ![]() $A$-local system corresponding to
$A$-local system corresponding to ![]() $A(j)^s,$ so that
$A(j)^s,$ so that ![]() ${\mathcal {F}}_1$ corresponds to an
${\mathcal {F}}_1$ corresponds to an ![]() $A$-submodule
$A$-submodule ![]() $S(Y')_1\subset S(Y')$.
$S(Y')_1\subset S(Y')$.
Let ![]() $X''$ and
$X''$ and ![]() $H$ be as in the proof of Lemma 2.1.4. Since the group
$H$ be as in the proof of Lemma 2.1.4. Since the group ![]() $H$ acts trivially on
$H$ acts trivially on ![]() $S(Y')_1,$ after replacing
$S(Y')_1,$ after replacing ![]() $X'$ by
$X'$ by ![]() $X'',$ we may assume that
$X'',$ we may assume that ![]() ${\mathcal {F}}'$ is an extension of
${\mathcal {F}}'$ is an extension of ![]() ${\mathcal {F}}'/A(i)^r$ by
${\mathcal {F}}'/A(i)^r$ by ![]() $A(j)^s,$ and
$A(j)^s,$ and ![]() $g^*({\mathcal {F}}') \overset \sim \longrightarrow {\mathcal {F}}$ is an isomorphism of extensions. A similar argument, applied to
$g^*({\mathcal {F}}') \overset \sim \longrightarrow {\mathcal {F}}$ is an isomorphism of extensions. A similar argument, applied to ![]() ${\mathcal {F}}/A(j)^s\otimes A(-i),$ shows that we may assume that
${\mathcal {F}}/A(j)^s\otimes A(-i),$ shows that we may assume that ![]() ${\mathcal {F}}'$ is an extension of
${\mathcal {F}}'$ is an extension of ![]() $A(i)^r$ by
$A(i)^r$ by ![]() $A(j)^s,$ with
$A(j)^s,$ with ![]() $g^*({\mathcal {F}}') \overset \sim \longrightarrow {\mathcal {F}}$ as extensions.
$g^*({\mathcal {F}}') \overset \sim \longrightarrow {\mathcal {F}}$ as extensions.
2.2 Essential dimension
2.2.1 Let ![]() $K$ be a field,
$K$ be a field, ![]() $X$ a
$X$ a ![]() $K$-scheme of finite type, and
$K$-scheme of finite type, and ![]() $f: Y \rightarrow X$ a finite étale cover. The essential dimension [Reference Buhler and ReichsteinBR97, § 2]
$f: Y \rightarrow X$ a finite étale cover. The essential dimension [Reference Buhler and ReichsteinBR97, § 2] ![]() ${\rm ed}_K(Y/X)$ of
${\rm ed}_K(Y/X)$ of ![]() $Y$ over
$Y$ over ![]() $X$ is the smallest integer
$X$ is the smallest integer ![]() $e$ such that there exists a finite type
$e$ such that there exists a finite type ![]() $K$-scheme
$K$-scheme ![]() $W$ of dimension
$W$ of dimension ![]() $e,$ a dense open subscheme
$e,$ a dense open subscheme ![]() $U \subset X,$ and a map
$U \subset X,$ and a map ![]() $U \rightarrow W,$ such that
$U \rightarrow W,$ such that ![]() $Y|_U$ is the pullback of a finite étale covering over
$Y|_U$ is the pullback of a finite étale covering over ![]() $W$. The essential
$W$. The essential ![]() $p$-dimension
$p$-dimension ![]() ${\rm ed}_K(Y/X;p)$ is defined as the minimum of
${\rm ed}_K(Y/X;p)$ is defined as the minimum of ![]() ${\rm ed}_K(Y\times _XE/E)$ where
${\rm ed}_K(Y\times _XE/E)$ where ![]() $E \rightarrow X$ runs over dominant, generically finite maps, which have degree prime to
$E \rightarrow X$ runs over dominant, generically finite maps, which have degree prime to ![]() $p$ at all generic points of
$p$ at all generic points of ![]() $X$.
$X$.
Note that when ![]() $X$ is irreducible, the definition does not change if we consider only coverings with
$X$ is irreducible, the definition does not change if we consider only coverings with ![]() $E$ irreducible. Indeed, for any
$E$ irreducible. Indeed, for any ![]() $E \rightarrow X,$ as above, one of the irreducible components of
$E \rightarrow X,$ as above, one of the irreducible components of ![]() $E$ will have degree prime to
$E$ will have degree prime to ![]() $p$ over the generic point of
$p$ over the generic point of ![]() $X$.
$X$.
Suppose ![]() $X$ is connected. A Galois closure of
$X$ is connected. A Galois closure of ![]() $Y \rightarrow X$ is a union of Galois closures of the connected components of
$Y \rightarrow X$ is a union of Galois closures of the connected components of ![]() $Y$. If
$Y$. If ![]() $Y_i \rightarrow X$,
$Y_i \rightarrow X$, ![]() $i=1, \ldots r$, are finite étale, Galois and connected, then a composite of the
$i=1, \ldots r$, are finite étale, Galois and connected, then a composite of the ![]() $Y_i$ is a connected component of
$Y_i$ is a connected component of ![]() $Y_1\times _X\cdots \times _X Y_r$. Up to isomorphism, this does not depend on the choice of connected component. If we drop the assumption that
$Y_1\times _X\cdots \times _X Y_r$. Up to isomorphism, this does not depend on the choice of connected component. If we drop the assumption that ![]() $X$ is connected, we define the Galois closure and composite by making these constructions over each connected component of
$X$ is connected, we define the Galois closure and composite by making these constructions over each connected component of ![]() $X$.
$X$.
Lemma 2.2.2 Let ![]() $f:Y\rightarrow X$ be a finite étale cover, and
$f:Y\rightarrow X$ be a finite étale cover, and ![]() $\tilde Y$ a Galois closure for
$\tilde Y$ a Galois closure for ![]() $Y$. For any map of
$Y$. For any map of ![]() $K$-schemes
$K$-schemes ![]() $E \rightarrow X,$ we have
$E \rightarrow X,$ we have
In particular, we have
Proof. We may assume that ![]() $X$ is connected. Let
$X$ is connected. Let ![]() $\bar x$ be a geometric point for
$\bar x$ be a geometric point for ![]() $X,$ and
$X,$ and ![]() $S$ a
$S$ a ![]() $\pi _1(X,\bar x)$-set with
$\pi _1(X,\bar x)$-set with ![]() $Y = Y(S)$. Suppose first that
$Y = Y(S)$. Suppose first that ![]() $Y$ is connected. Let
$Y$ is connected. Let ![]() $N \subset \pi _1(X,\bar x)$ be the (normal) subgroup which fixes
$N \subset \pi _1(X,\bar x)$ be the (normal) subgroup which fixes ![]() $S$ pointwise. If
$S$ pointwise. If ![]() $s \in S,$ and
$s \in S,$ and ![]() $\pi _1(X,\bar x)_s$ is the stabilizer of
$\pi _1(X,\bar x)_s$ is the stabilizer of ![]() $s,$ then
$s,$ then ![]() $N = \bigcap _{i=1}^n g_i\pi _1(X,\bar x)_sg_i^{-1}$ for a finite collection of elements
$N = \bigcap _{i=1}^n g_i\pi _1(X,\bar x)_sg_i^{-1}$ for a finite collection of elements ![]() $g_1,\ldots , g_n \in \pi _1(X,\bar x)$. Let
$g_1,\ldots , g_n \in \pi _1(X,\bar x)$. Let ![]() $\tilde S$ denote the
$\tilde S$ denote the ![]() $\pi _1(X,\bar x)$-orbit of
$\pi _1(X,\bar x)$-orbit of ![]() $(g_1\cdot s, \ldots , g_n\cdot s) \in S^n$. Then the stabilizer in
$(g_1\cdot s, \ldots , g_n\cdot s) \in S^n$. Then the stabilizer in ![]() $\pi _1(X,\bar x)$ of any point of
$\pi _1(X,\bar x)$ of any point of ![]() $\tilde S$ is
$\tilde S$ is ![]() $N,$ so
$N,$ so ![]() $\tilde Y = Y(\tilde S)$ is a Galois closure of
$\tilde Y = Y(\tilde S)$ is a Galois closure of ![]() $Y$.
$Y$.
Now we drop the assumption that ![]() $Y$ is connected, and let
$Y$ is connected, and let ![]() $Y_1, \ldots , Y_r$ denote the connected components of
$Y_1, \ldots , Y_r$ denote the connected components of ![]() $Y,$ with
$Y,$ with ![]() $Y_i$ corresponding to a subset
$Y_i$ corresponding to a subset ![]() $S_i \subset S$ on which
$S_i \subset S$ on which ![]() $\pi _1(X,\bar x)$ acts transitively. The above construction gives subsets
$\pi _1(X,\bar x)$ acts transitively. The above construction gives subsets ![]() $\tilde S_i \subset S_i^n,$ (we may assume without loss of generality that
$\tilde S_i \subset S_i^n,$ (we may assume without loss of generality that ![]() $n$ does not depend on
$n$ does not depend on ![]() $i$) with
$i$) with ![]() $\tilde Y_i = Y(\tilde S_i)$ a Galois closure of
$\tilde Y_i = Y(\tilde S_i)$ a Galois closure of ![]() $Y_i$. If
$Y_i$. If ![]() $\tilde S = \coprod _i \tilde S_i \subset S^n,$ then
$\tilde S = \coprod _i \tilde S_i \subset S^n,$ then ![]() $\tilde Y = Y(\tilde S) = \coprod _i \tilde Y_i$ is a Galois closure for
$\tilde Y = Y(\tilde S) = \coprod _i \tilde Y_i$ is a Galois closure for ![]() $Y$.
$Y$.
From the construction one sees that ![]() $S,$
$S,$ ![]() $T = \tilde S$ and
$T = \tilde S$ and ![]() $G = \pi _1(X,\bar x)$ satisfy the conditions in Lemma 2.1.2(ii) (note that these conditions do not depend on the choice of
$G = \pi _1(X,\bar x)$ satisfy the conditions in Lemma 2.1.2(ii) (note that these conditions do not depend on the choice of ![]() $G'$). For any homomorphism
$G'$). For any homomorphism ![]() $H \rightarrow G,$ these conditions continue to hold if we instead view
$H \rightarrow G,$ these conditions continue to hold if we instead view ![]() $S$ and
$S$ and ![]() $T$ as
$T$ as ![]() $H$-sets.
$H$-sets.
Now let ![]() $E \rightarrow X$ be a map of
$E \rightarrow X$ be a map of ![]() $K$-schemes,
$K$-schemes, ![]() $U \subset E$ a connected open subset, and
$U \subset E$ a connected open subset, and ![]() $U \rightarrow E'$ a map of
$U \rightarrow E'$ a map of ![]() $K$-schemes. Suppose
$K$-schemes. Suppose ![]() $U$ admits a geometric point
$U$ admits a geometric point ![]() $\bar y$ mapping to
$\bar y$ mapping to ![]() $\bar x$. Applying the above remark with
$\bar x$. Applying the above remark with ![]() $H = \pi _1(U,\bar y),$ Lemma 2.1.2(ii) implies that the action of
$H = \pi _1(U,\bar y),$ Lemma 2.1.2(ii) implies that the action of ![]() $H$ on
$H$ on ![]() $S$ virtually lifts to
$S$ virtually lifts to ![]() $\pi _1(E',\bar y)$ if and only the action of
$\pi _1(E',\bar y)$ if and only the action of ![]() $H$ on
$H$ on ![]() $T$ virtually lifts to
$T$ virtually lifts to ![]() $\pi _1(E',\bar y)$. As in the proof of Lemma 2.1.4, this implies that
$\pi _1(E',\bar y)$. As in the proof of Lemma 2.1.4, this implies that ![]() $Y|_U$ arises by pullback from a cover of
$Y|_U$ arises by pullback from a cover of ![]() $E''$ for some finite étale
$E''$ for some finite étale ![]() $E'' \rightarrow E',$ if and only if the same condition holds for
$E'' \rightarrow E',$ if and only if the same condition holds for ![]() $\tilde Y|_U$. Since
$\tilde Y|_U$. Since ![]() $\bar x$ was an arbitrary geometric point of
$\bar x$ was an arbitrary geometric point of ![]() $X,$ this implies
$X,$ this implies ![]() ${\rm ed}_K(Y|_E/E) = {\rm ed}_K(\tilde Y|_E/E)$.
${\rm ed}_K(Y|_E/E) = {\rm ed}_K(\tilde Y|_E/E)$.
Lemma 2.2.3 Let ![]() $Y_i \rightarrow X$,
$Y_i \rightarrow X$, ![]() $i=1,\ldots , r$, be connected Galois coverings of
$i=1,\ldots , r$, be connected Galois coverings of ![]() $K$-schemes, and
$K$-schemes, and ![]() $Y\rightarrow X$ a composite of the
$Y\rightarrow X$ a composite of the ![]() $Y_i$. Then for any map of
$Y_i$. Then for any map of ![]() $K$-schemes
$K$-schemes ![]() $E\rightarrow X,$ we have
$E\rightarrow X,$ we have
 \[ {\rm ed}_K(Y_E/E) = {\rm ed}_K\bigg(\bigg(\coprod_i Y_i\bigg)_E\bigg/E\bigg). \]
\[ {\rm ed}_K(Y_E/E) = {\rm ed}_K\bigg(\bigg(\coprod_i Y_i\bigg)_E\bigg/E\bigg). \]In particular, we have
 \[ {\rm ed}_K(Y/X;p) = {\rm ed}_K\bigg(\bigg(\coprod_i Y_i\bigg)\bigg/X; p\bigg). \]
\[ {\rm ed}_K(Y/X;p) = {\rm ed}_K\bigg(\bigg(\coprod_i Y_i\bigg)\bigg/X; p\bigg). \]Proof. Let ![]() $\bar x$ be a geometric point for
$\bar x$ be a geometric point for ![]() $X,$ and let
$X,$ and let ![]() $S_i$ be a
$S_i$ be a ![]() $\pi _1(X,\bar x)$-set with
$\pi _1(X,\bar x)$-set with ![]() $Y_i = Y(S_i)$. Let
$Y_i = Y(S_i)$. Let ![]() $S = \coprod _i S_i$. Then
$S = \coprod _i S_i$. Then ![]() $Y$ corresponds to a transitive
$Y$ corresponds to a transitive ![]() $\pi _1(X,\bar x)$ set
$\pi _1(X,\bar x)$ set ![]() $T \subset S_1\times \dots \times S_r$ which surjects onto each
$T \subset S_1\times \dots \times S_r$ which surjects onto each ![]() $S_i$. Viewing
$S_i$. Viewing ![]() $T \subset S^r,$ we see that
$T \subset S^r,$ we see that ![]() $T$ satisfies the conditions of Lemma 2.1.2. The lemma now follows as in the proof of Lemma 2.2.2.
$T$ satisfies the conditions of Lemma 2.1.2. The lemma now follows as in the proof of Lemma 2.2.2.
Lemma 2.2.4 Let ![]() $A$ be a finite ring,
$A$ be a finite ring, ![]() $K$ a field,
$K$ a field, ![]() ${\mathcal {F}}$ an
${\mathcal {F}}$ an ![]() $A$-local system on a connected
$A$-local system on a connected ![]() $K$-scheme
$K$-scheme ![]() $X$ equipped with a geometric point
$X$ equipped with a geometric point ![]() $\bar x,$ and
$\bar x,$ and ![]() $\rho _{{\mathcal {F}}}:\pi _1(X, \bar x) \rightarrow {\rm GL}_n(A)$ the representation corresponding to
$\rho _{{\mathcal {F}}}:\pi _1(X, \bar x) \rightarrow {\rm GL}_n(A)$ the representation corresponding to ![]() ${\mathcal {F}}$. Let
${\mathcal {F}}$. Let ![]() $Y$ be the covering of
$Y$ be the covering of ![]() $X$ corresponding to
$X$ corresponding to ![]() ${\rm ker}\, \rho _{{\mathcal {F}}}$.
${\rm ker}\, \rho _{{\mathcal {F}}}$.
Then ![]() $Y$ is the composite of Galois closures of the connected components of
$Y$ is the composite of Galois closures of the connected components of ![]() $Y({\mathcal {F}})$. In particular,
$Y({\mathcal {F}})$. In particular,
For any prime ![]() $p$ we also have
$p$ we also have
Proof. Consider the action of ![]() $\pi _1(X,\bar x)$ on
$\pi _1(X,\bar x)$ on ![]() $A^n$ corresponding to
$A^n$ corresponding to ![]() ${\mathcal {F}}$. The connected components of
${\mathcal {F}}$. The connected components of ![]() $Y({\mathcal {F}})$ correspond to the stabilizers
$Y({\mathcal {F}})$ correspond to the stabilizers ![]() $\pi _1(X)_s$ for
$\pi _1(X)_s$ for ![]() $s \in A^n$. A Galois closure of such a component corresponds to
$s \in A^n$. A Galois closure of such a component corresponds to
Thus the composite of such Galois closures corresponds to ![]() $\bigcap _s \pi _1(X)_s = {\rm ker}\, \rho _{{\mathcal {F}}}$.
$\bigcap _s \pi _1(X)_s = {\rm ker}\, \rho _{{\mathcal {F}}}$.
Lemma 2.2.5 Let ![]() $K' \subset K$ be algebraically closed fields. If
$K' \subset K$ be algebraically closed fields. If ![]() $Y \rightarrow X$ is a finite étale covering of finite type
$Y \rightarrow X$ is a finite étale covering of finite type ![]() $K'$-schemes then
$K'$-schemes then
Proof. Let ![]() $U_K \subset X_K$ be a dense open and
$U_K \subset X_K$ be a dense open and ![]() $U_K \rightarrow W_K$ a morphism with
$U_K \rightarrow W_K$ a morphism with ![]() ${\rm dim}\,W_K = {\rm ed}_K(Y_K/X_K)$ such that
${\rm dim}\,W_K = {\rm ed}_K(Y_K/X_K)$ such that ![]() $Y_K|_{U_K}$ arises from a finite cover
$Y_K|_{U_K}$ arises from a finite cover ![]() $f':Y'_K \rightarrow W_K$. Then
$f':Y'_K \rightarrow W_K$. Then ![]() $U_K,$ the finite cover
$U_K,$ the finite cover ![]() $f'$ and the isomorphism
$f'$ and the isomorphism ![]() $f^{\prime *} Y'_K \overset \sim \longrightarrow Y_K|_{U_K}$ are all defined over some finitely generated
$f^{\prime *} Y'_K \overset \sim \longrightarrow Y_K|_{U_K}$ are all defined over some finitely generated ![]() $K'$-algebra
$K'$-algebra ![]() $R \subset K$. Specializing by a map
$R \subset K$. Specializing by a map ![]() $R \rightarrow K'$ produces the required data for the covering
$R \rightarrow K'$ produces the required data for the covering ![]() $Y \rightarrow X$.
$Y \rightarrow X$.
2.2.6 It will be convenient to make the following definition. Suppose that ![]() $Y \rightarrow X$ is a finite étale covering of finite type
$Y \rightarrow X$ is a finite étale covering of finite type ![]() $R$-schemes, where
$R$-schemes, where ![]() $R$ is a domain of characteristic
$R$ is a domain of characteristic ![]() $0$. Set
$0$. Set ![]() $\overline {{\rm ed}}(Y/X) = {\rm ed}_{\bar K}(Y/X)$ where
$\overline {{\rm ed}}(Y/X) = {\rm ed}_{\bar K}(Y/X)$ where ![]() $\bar K$ is any algebraically closed field containing
$\bar K$ is any algebraically closed field containing ![]() $R,$ and similarly for
$R,$ and similarly for ![]() $\overline {{\rm ed}}(Y/X; p)$. By Lemma 2.2.5, this does not depend on the choice of
$\overline {{\rm ed}}(Y/X; p)$. By Lemma 2.2.5, this does not depend on the choice of ![]() $\bar K$.
$\bar K$.
Lemma 2.2.7 Let ![]() $K$ be an algebraically closed field, and
$K$ be an algebraically closed field, and ![]() $Y \rightarrow X$ a finite Galois covering of connected, finite type
$Y \rightarrow X$ a finite Galois covering of connected, finite type ![]() $K$-schemes with Galois group
$K$-schemes with Galois group ![]() $G$. Let
$G$. Let ![]() $H \subset G$ be a central, cyclic subgroup of order
$H \subset G$ be a central, cyclic subgroup of order ![]() $n$ with
$n$ with ![]() ${\rm char}(K)\nmid n$. Then for any prime
${\rm char}(K)\nmid n$. Then for any prime ![]() $p$ we have
$p$ we have
with equality if ![]() $p \nmid n$.
$p \nmid n$.
Proof. To show ![]() $\overline {{\rm ed}}(Y/X; p) \geq \overline {{\rm ed}}(Y/H\to X; p),$ after shrinking
$\overline {{\rm ed}}(Y/X; p) \geq \overline {{\rm ed}}(Y/H\to X; p),$ after shrinking ![]() $X,$ we may assume there is a map
$X,$ we may assume there is a map ![]() $f:X \rightarrow X'$ such that
$f:X \rightarrow X'$ such that ![]() $Y = f^*Y'$ for a finite étale covering
$Y = f^*Y'$ for a finite étale covering ![]() $Y' \rightarrow X',$ which may be assumed to be connected and Galois by Lemma 2.1.4. The Galois group of
$Y' \rightarrow X',$ which may be assumed to be connected and Galois by Lemma 2.1.4. The Galois group of ![]() $Y'/X'$ is necessarily equal to
$Y'/X'$ is necessarily equal to ![]() $G,$ and we have
$G,$ and we have ![]() $f^*(Y'/H) \overset \sim \longrightarrow Y/H$.
$f^*(Y'/H) \overset \sim \longrightarrow Y/H$.
For the converse inequality when ![]() $p \nmid n,$ we may assume there is a map
$p \nmid n,$ we may assume there is a map ![]() $f:X \rightarrow X'$ such that
$f:X \rightarrow X'$ such that ![]() $Y/H = f^*Y'$ for a finite étale covering
$Y/H = f^*Y'$ for a finite étale covering ![]() $Y' \rightarrow X',$ which we may again assume is connected and Galois with group
$Y' \rightarrow X',$ which we may again assume is connected and Galois with group ![]() $G/H$. The image,
$G/H$. The image, ![]() $c,$ of
$c,$ of ![]() $Y' \rightarrow X'$ under
$Y' \rightarrow X'$ under
is the obstruction to lifting ![]() $Y' \rightarrow X'$ to a
$Y' \rightarrow X'$ to a ![]() $G$-covering. Here, for the final isomorphism, we are using that
$G$-covering. Here, for the final isomorphism, we are using that ![]() $K$ is algebraically closed of characteristic prime to
$K$ is algebraically closed of characteristic prime to ![]() $n$. Viewing
$n$. Viewing ![]() $c$ as a Brauer class, we see that it has order dividing
$c$ as a Brauer class, we see that it has order dividing ![]() $n$. This implies that (after perhaps shrinking
$n$. This implies that (after perhaps shrinking ![]() $X$ further) there is an étale covering
$X$ further) there is an étale covering ![]() $X_1' \rightarrow X'$ of order dividing a power
$X_1' \rightarrow X'$ of order dividing a power ![]() $n$ such that
$n$ such that ![]() $c|_{X_1}$ is trivial [Reference Farb and DennisFD93, Lemma 4.17]. In particular,
$c|_{X_1}$ is trivial [Reference Farb and DennisFD93, Lemma 4.17]. In particular, ![]() $X_1' \rightarrow X'$ has order prime to
$X_1' \rightarrow X'$ has order prime to ![]() $p$. Replacing
$p$. Replacing ![]() $Y \rightarrow X \rightarrow X'$ by their pullbacks to
$Y \rightarrow X \rightarrow X'$ by their pullbacks to ![]() $X_1',$ we may assume that
$X_1',$ we may assume that ![]() $c = 0,$ and that
$c = 0,$ and that ![]() $Y' = Y''/H$ for some Galois covering
$Y' = Y''/H$ for some Galois covering ![]() $Y'' \rightarrow X'$ with group
$Y'' \rightarrow X'$ with group ![]() $G$.
$G$.
The difference between the ![]() $G$-coverings
$G$-coverings ![]() $Y \rightarrow X$ and
$Y \rightarrow X$ and ![]() $f^*Y'' \rightarrow X$ is measured by a class in
$f^*Y'' \rightarrow X$ is measured by a class in ![]() $H^1(X,H)$. After replacing
$H^1(X,H)$. After replacing ![]() $X$ by the
$X$ by the ![]() $H$-covering corresponding to this class, we may assume that this class is trivial, and so
$H$-covering corresponding to this class, we may assume that this class is trivial, and so ![]() $Y \overset \sim \longrightarrow f^*Y''$. This shows that
$Y \overset \sim \longrightarrow f^*Y''$. This shows that ![]() $\overline {{\rm ed}}(Y/X; p) \leq \overline {{\rm ed}}(Y/H\to X; p)$.
$\overline {{\rm ed}}(Y/X; p) \leq \overline {{\rm ed}}(Y/H\to X; p)$.
3. Essential dimension and moduli of abelian varieties
3.1 Ordinary finite flat group schemes
In this subsection we fix a prime ![]() $p,$ and we consider a complete discrete valuation ring
$p,$ and we consider a complete discrete valuation ring ![]() $V$ of characteristic
$V$ of characteristic ![]() $0,$ with perfect residue field
$0,$ with perfect residue field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p,$ and a uniformizer
$p,$ and a uniformizer ![]() $\pi \in V$.
$\pi \in V$.
By a finite flat group scheme on a ![]() ${\mathbb {Z}}_p$-scheme
${\mathbb {Z}}_p$-scheme ![]() $X$ we will always mean a finite flat, commutative, group scheme on
$X$ we will always mean a finite flat, commutative, group scheme on ![]() $X$ of
$X$ of ![]() $p$-power order. A finite flat group scheme on
$p$-power order. A finite flat group scheme on ![]() $X$ is called ordinary if étale locally on
$X$ is called ordinary if étale locally on ![]() $X,$ it is an extension of a constant group scheme
$X,$ it is an extension of a constant group scheme ![]() $\bigoplus _{i \in I} {\mathbb {Z}}/p^{n_i}{\mathbb {Z}}$ by a group scheme of the form
$\bigoplus _{i \in I} {\mathbb {Z}}/p^{n_i}{\mathbb {Z}}$ by a group scheme of the form ![]() $\bigoplus _{j \in J} \mu _{p^{m_j}}$ for integers
$\bigoplus _{j \in J} \mu _{p^{m_j}}$ for integers ![]() $n_i,m_j \geq 1$. In this subsection we study the classification of these extensions.
$n_i,m_j \geq 1$. In this subsection we study the classification of these extensions.
3.1.1 Now let ![]() $\tilde X = {\operatorname {Spec\,}} A$ be an affine
$\tilde X = {\operatorname {Spec\,}} A$ be an affine ![]() ${\mathbb {Z}}_p$-scheme, and set
${\mathbb {Z}}_p$-scheme, and set ![]() $X = \tilde X\otimes {\mathbb {Q}}$. Let
$X = \tilde X\otimes {\mathbb {Q}}$. Let ![]() $n \geq 1,$ and consider the exact sequence of sheaves
$n \geq 1,$ and consider the exact sequence of sheaves
in the flat topology of ![]() $\tilde X$. Taking flat cohomology of this sequence and its restriction to
$\tilde X$. Taking flat cohomology of this sequence and its restriction to ![]() $X$, we obtain the following commutative diagram with exact rows.
$X$, we obtain the following commutative diagram with exact rows.

The group ![]() $H^1(\tilde X, {\mathbb {G}}_m)$ classifies line bundles on
$H^1(\tilde X, {\mathbb {G}}_m)$ classifies line bundles on ![]() $\tilde X$. Hence, if
$\tilde X$. Hence, if ![]() $A$ is local it vanishes, and this can be used to classify extensions of
$A$ is local it vanishes, and this can be used to classify extensions of ![]() ${\mathbb {Z}}/p^n{\mathbb {Z}}$ by
${\mathbb {Z}}/p^n{\mathbb {Z}}$ by ![]() $\mu _{p^n}$ as finite flat group schemes. We have
$\mu _{p^n}$ as finite flat group schemes. We have
Here and below, the group on the left denotes extensions as sheaves of ![]() ${\mathbb {Z}}/p^n{\mathbb {Z}}$-modules.
${\mathbb {Z}}/p^n{\mathbb {Z}}$-modules.
Similarly, we can classify extensions of ![]() ${\mathbb {Q}}_p/{\mathbb {Z}}_p$ by
${\mathbb {Q}}_p/{\mathbb {Z}}_p$ by ![]() $\mu _{p^\infty } = \lim _n \mu _{p^n}$ as
$\mu _{p^\infty } = \lim _n \mu _{p^n}$ as ![]() $p$-divisible groups. If
$p$-divisible groups. If ![]() $\mathcal {E}$ is such an extension, then
$\mathcal {E}$ is such an extension, then ![]() $\mathcal {E}[p^n]$ is an extension of
$\mathcal {E}[p^n]$ is an extension of ![]() ${\mathbb {Z}}/p^n{\mathbb {Z}}$ by
${\mathbb {Z}}/p^n{\mathbb {Z}}$ by ![]() $\mu _{p^n}$ and we have
$\mu _{p^n}$ and we have
If ![]() $A$ is complete and local with residue field
$A$ is complete and local with residue field ![]() $k,$ then the right-hand side may be identified with
$k,$ then the right-hand side may be identified with ![]() $A^{\times ,1} \subset A^\times ,$ the subgroup of units which map to
$A^{\times ,1} \subset A^\times ,$ the subgroup of units which map to ![]() $1$ in
$1$ in ![]() $k^\times$. Thus we have
$k^\times$. Thus we have
3.1.2 For the rest of this subsection we assume that ![]() $A = V[\![ x_1, \ldots , x_n ]\!]$. Then
$A = V[\![ x_1, \ldots , x_n ]\!]$. Then ![]() $H^1(X, {\mathbb {G}}_m) = 0$ by [Reference GrothendieckSGA2, XI, Thm 3.13], and we have the following commutative diagram.
$H^1(X, {\mathbb {G}}_m) = 0$ by [Reference GrothendieckSGA2, XI, Thm 3.13], and we have the following commutative diagram.

3.1.3 We call an element of ![]() ${\rm Ext}^1_X({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n}) = H^1(X,\mu _{p^n})$ syntomic if it arises from an element of
${\rm Ext}^1_X({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n}) = H^1(X,\mu _{p^n})$ syntomic if it arises from an element of ![]() $A^\times ,$ or equivalently from a class in
$A^\times ,$ or equivalently from a class in ![]() ${\rm Ext}^1_{\tilde X}({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n}),$ and we denote the subgroup of syntomic elements by
${\rm Ext}^1_{\tilde X}({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n}),$ and we denote the subgroup of syntomic elements by ![]() ${\rm Ext}^{1,{\rm syn}}_X({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n}) \subset {\rm Ext}^1_X({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n})$
${\rm Ext}^{1,{\rm syn}}_X({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n}) \subset {\rm Ext}^1_X({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n})$
Lemma 3.1.4 The map ![]() ${\rm Ext}^1_{\tilde X}({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n}) \rightarrow {\rm Ext}^1_X({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n})$ is injective.
${\rm Ext}^1_{\tilde X}({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n}) \rightarrow {\rm Ext}^1_X({\mathbb {Z}}/p^n{\mathbb {Z}}, \mu _{p^n})$ is injective.
Proof. If ![]() $a \in A^\times$ is a
$a \in A^\times$ is a ![]() $p^{n}$th power in
$p^{n}$th power in ![]() $A[1/p]$ then it is a
$A[1/p]$ then it is a ![]() $p^{n}$th power in
$p^{n}$th power in ![]() $A,$ as
$A,$ as ![]() $A$ is normal. Hence the map
$A$ is normal. Hence the map ![]() $A^\times /(A^\times )^{p^n} \rightarrow A[1/p]^\times /(A[1/p]^\times )^{p^n}$ is injective, and the lemma follows from the description of
$A^\times /(A^\times )^{p^n} \rightarrow A[1/p]^\times /(A[1/p]^\times )^{p^n}$ is injective, and the lemma follows from the description of ![]() ${\rm Ext}^1$s above.
${\rm Ext}^1$s above.
Lemma 3.1.5 Let ![]() $B = V[\![ y_1, \ldots , y_s ]\!]$ for some integer
$B = V[\![ y_1, \ldots , y_s ]\!]$ for some integer ![]() $s \geq 0,$ and
$s \geq 0,$ and
a local flat map of complete local ![]() $V$-algebras. Let
$V$-algebras. Let ![]() $Y = {\operatorname {Spec\,}} B[1/p],$ and suppose that
$Y = {\operatorname {Spec\,}} B[1/p],$ and suppose that ![]() $c \in H^1(Y,\mu _{p^n}),$ and that
$c \in H^1(Y,\mu _{p^n}),$ and that ![]() $f^*(c) \in H^1(X,\mu _{p^n})$ is syntomic. Then
$f^*(c) \in H^1(X,\mu _{p^n})$ is syntomic. Then ![]() $c$ is syntomic.
$c$ is syntomic.
Proof. Let ![]() $b \in B[1/p]^\times$ be an element giving rise to
$b \in B[1/p]^\times$ be an element giving rise to ![]() $c$. Since
$c$. Since ![]() $B$ is a unique factorization domain we may write
$B$ is a unique factorization domain we may write ![]() $b = b_0\pi ^i$ with
$b = b_0\pi ^i$ with ![]() $b_0 \in B^\times$ and
$b_0 \in B^\times$ and ![]() $i \in {\mathbb {Z}}$. Since
$i \in {\mathbb {Z}}$. Since ![]() $f^*(c)$ is syntomic, we may write
$f^*(c)$ is syntomic, we may write ![]() $\pi ^i = a_0a^{p^n}$ with
$\pi ^i = a_0a^{p^n}$ with ![]() $a_0 \in A^\times$ and
$a_0 \in A^\times$ and ![]() $a \in A[1/p]^\times$. Comparing the images of both sides in the group of divisors on
$a \in A[1/p]^\times$. Comparing the images of both sides in the group of divisors on ![]() $A,$ one sees that
$A,$ one sees that ![]() $p^n|i$. So
$p^n|i$. So ![]() $c$ arises from
$c$ arises from ![]() $b_0$.
$b_0$.
3.1.6 Let ![]() ${\mathfrak m}_A$ be the maximal ideal of
${\mathfrak m}_A$ be the maximal ideal of ![]() $A,$ and
$A,$ and ![]() $\bar {\mathfrak m}_A$ its image in
$\bar {\mathfrak m}_A$ its image in ![]() $A/\pi A$. The natural map
$A/\pi A$. The natural map
is a bijection; both sides are ![]() $k$-vector spaces spanned by
$k$-vector spaces spanned by ![]() $x_1,\ldots , x_n$. We denote by
$x_1,\ldots , x_n$. We denote by ![]() $\theta _A$ the composite
$\theta _A$ the composite
Here we have used Lemma 3.1.4 to identify ![]() ${\rm Ext}_X^{1,{\rm syn}} ({\mathbb {Z}}/p{\mathbb {Z}}, \mu _p)$ and
${\rm Ext}_X^{1,{\rm syn}} ({\mathbb {Z}}/p{\mathbb {Z}}, \mu _p)$ and ![]() ${\rm Ext}_{\tilde X}^1 ({\mathbb {Z}}/p{\mathbb {Z}}, \mu _p)$.
${\rm Ext}_{\tilde X}^1 ({\mathbb {Z}}/p{\mathbb {Z}}, \mu _p)$.
Lemma 3.1.7 With the notation of Lemma 3.1.5, suppose that
is a subset such that the ![]() $k$-span of
$k$-span of ![]() $\theta _A(f^*(L))$ is
$\theta _A(f^*(L))$ is ![]() $\bar {\mathfrak m}_A/\bar {\mathfrak m}_A^2$. Then
$\bar {\mathfrak m}_A/\bar {\mathfrak m}_A^2$. Then ![]() $f$ is an isomorphism.
$f$ is an isomorphism.
Proof. By functoriality of the association ![]() $A \mapsto \theta _A,$ we have
$A \mapsto \theta _A,$ we have ![]() $\theta _A(f^*(L)) = f^*(\theta _B(L))$. Hence the
$\theta _A(f^*(L)) = f^*(\theta _B(L))$. Hence the ![]() $k$-span of
$k$-span of ![]() $\theta _A(f^*(L))$ is contained in image of
$\theta _A(f^*(L))$ is contained in image of ![]() $\bar {\mathfrak m}_B/\bar {\mathfrak m}_B^2$. It follows that
$\bar {\mathfrak m}_B/\bar {\mathfrak m}_B^2$. It follows that ![]() $\bar {\mathfrak m}_B/\bar {\mathfrak m}_B^2$ surjects onto
$\bar {\mathfrak m}_B/\bar {\mathfrak m}_B^2$ surjects onto ![]() $\bar {\mathfrak m}_A/\bar {\mathfrak m}_A^2$. Since
$\bar {\mathfrak m}_A/\bar {\mathfrak m}_A^2$. Since ![]() $A$ and
$A$ and ![]() $B$ are complete local
$B$ are complete local ![]() $V$-algebras, this implies that
$V$-algebras, this implies that ![]() $B,$ which is a subring of
$B,$ which is a subring of ![]() $A,$ surjects onto
$A,$ surjects onto ![]() $A$. Hence
$A$. Hence ![]() $f$ is an isomorphism.
$f$ is an isomorphism.
3.2 Monodromy of  $p$-torsion in an abelian scheme
$p$-torsion in an abelian scheme
We now use the results of the previous section to obtain results about the essential dimension of covers of the moduli space of abelian varieties.
3.2.1 Recall that an abelian scheme ![]() ${\mathcal {A}}$ over a
${\mathcal {A}}$ over a ![]() ${\mathbb {Z}}_p$-scheme is called ordinary if the group scheme
${\mathbb {Z}}_p$-scheme is called ordinary if the group scheme ![]() ${\mathcal {A}}[p^n]$ is ordinary for all
${\mathcal {A}}[p^n]$ is ordinary for all ![]() $n \geq 1$. This is equivalent to requiring the condition for
$n \geq 1$. This is equivalent to requiring the condition for ![]() $n=1$.
$n=1$.
Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p > 0,$ and let
$p > 0,$ and let ![]() $V$ be a complete discrete valuation ring with residue field
$V$ be a complete discrete valuation ring with residue field ![]() $k,$ so that
$k,$ so that ![]() $W(k) \subset V$. Let
$W(k) \subset V$. Let ![]() ${\mathcal {A}}_0$ be an abelian scheme over
${\mathcal {A}}_0$ be an abelian scheme over ![]() $k$ of dimension
$k$ of dimension ![]() $g$. We assume that
$g$. We assume that ![]() ${\mathcal {A}}_0$ is ordinary. Since
${\mathcal {A}}_0$ is ordinary. Since ![]() $k$ is algebraically closed, this implies that
$k$ is algebraically closed, this implies that ![]() ${\mathcal {A}}_0[p^\infty ]$ is isomorphic to
${\mathcal {A}}_0[p^\infty ]$ is isomorphic to ![]() $({\mathbb {Q}}_p/{\mathbb {Z}}_p)^g \oplus \mu _{p^\infty }^g$.
$({\mathbb {Q}}_p/{\mathbb {Z}}_p)^g \oplus \mu _{p^\infty }^g$.
Consider the functor ![]() $D_{{\mathcal {A}}_0}$ on the category of Artinian
$D_{{\mathcal {A}}_0}$ on the category of Artinian ![]() $V$-algebras
$V$-algebras ![]() $C$ with residue field
$C$ with residue field ![]() $k,$ which attaches to
$k,$ which attaches to ![]() $C$ the set of isomorphism classes of deformations of
$C$ the set of isomorphism classes of deformations of ![]() ${\mathcal {A}}_0$ to an abelian scheme over
${\mathcal {A}}_0$ to an abelian scheme over ![]() $C$. Recall [Reference KatzKat81, § 2] that
$C$. Recall [Reference KatzKat81, § 2] that ![]() $D_{{\mathcal {A}}_0}$ is equivalent to the functor which attaches to
$D_{{\mathcal {A}}_0}$ is equivalent to the functor which attaches to ![]() $C$ the set of isomorphism classes of deformations of
$C$ the set of isomorphism classes of deformations of ![]() ${\mathcal {A}}_0[p^\infty ],$ and that
${\mathcal {A}}_0[p^\infty ],$ and that ![]() $D_{{\mathcal {A}}_0}$ is pro-representable by a formally smooth
$D_{{\mathcal {A}}_0}$ is pro-representable by a formally smooth ![]() $V$-algebra
$V$-algebra ![]() $R$ of dimension
$R$ of dimension ![]() $g^2,$ called the universal deformation
$g^2,$ called the universal deformation ![]() $V$-algebra of
$V$-algebra of ![]() ${\mathcal {A}}_0$.
${\mathcal {A}}_0$.
Denote by ![]() ${\mathcal {A}}_R$ the universal (formal) abelian scheme over
${\mathcal {A}}_R$ the universal (formal) abelian scheme over ![]() $R$. Note that although
$R$. Note that although ![]() ${\mathcal {A}}_R$ is only a formal scheme over
${\mathcal {A}}_R$ is only a formal scheme over ![]() $R,$ the torsion group schemes
$R,$ the torsion group schemes ![]() ${\mathcal {A}}_R[p^n]$ are finite over
${\mathcal {A}}_R[p^n]$ are finite over ![]() $R,$ and so can be regarded as genuine
$R,$ and so can be regarded as genuine ![]() $R$-schemes. Since
$R$-schemes. Since ![]() ${\mathcal {A}}_0$ is ordinary the
${\mathcal {A}}_0$ is ordinary the ![]() $p$-divisible group,
$p$-divisible group, ![]() ${\mathcal {A}}_R[p^\infty ] = \lim _n {\mathcal {A}}_R[p^n]$ is an extension of
${\mathcal {A}}_R[p^\infty ] = \lim _n {\mathcal {A}}_R[p^n]$ is an extension of ![]() $({\mathbb {Q}}_p/{\mathbb {Z}}_p)^g$ by
$({\mathbb {Q}}_p/{\mathbb {Z}}_p)^g$ by ![]() $\mu _{p^\infty }^g$. Hence
$\mu _{p^\infty }^g$. Hence ![]() ${\mathcal {A}}_R[p]$ is an extension of
${\mathcal {A}}_R[p]$ is an extension of ![]() $({\mathbb {Z}}/p{\mathbb {Z}})^g$ by
$({\mathbb {Z}}/p{\mathbb {Z}})^g$ by ![]() $\mu _p^g$. This extension class is given by a
$\mu _p^g$. This extension class is given by a ![]() $g\times g$ matrix of classes
$g\times g$ matrix of classes ![]() $(c_{i,j})$ with
$(c_{i,j})$ with ![]() $c_{i,j} \in {\rm Ext}_R^1({\mathbb {Z}}/p{\mathbb {Z}}, \mu _p)$.
$c_{i,j} \in {\rm Ext}_R^1({\mathbb {Z}}/p{\mathbb {Z}}, \mu _p)$.
Lemma 3.2.2 With the notation of § 3.1, the elements ![]() $\theta _R(\{c_{i,j}\}_{i,j})$ span
$\theta _R(\{c_{i,j}\}_{i,j})$ span ![]() $\bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2$.
$\bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2$.
Proof. Consider the isomorphism
introduced in § 3.1. The universal extension of ![]() $p$-divisible groups over
$p$-divisible groups over ![]() $R$ gives rise to a
$R$ gives rise to a ![]() $g\times g$ matrix of elements
$g\times g$ matrix of elements ![]() $(\hat c_{i,j}) \in {\rm Ext}_R^1({\mathbb {Q}}_p/{\mathbb {Z}}_p, \mu _{p^\infty })$ which reduce to
$(\hat c_{i,j}) \in {\rm Ext}_R^1({\mathbb {Q}}_p/{\mathbb {Z}}_p, \mu _{p^\infty })$ which reduce to ![]() $(c_{i,j})$.
$(c_{i,j})$.
Let ![]() $L \subset \bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2$ be the
$L \subset \bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2$ be the ![]() $k$-span of the images of the elements
$k$-span of the images of the elements ![]() $\hat \theta _R(\hat c_{i,j})-1,$ or equivalently, the elements
$\hat \theta _R(\hat c_{i,j})-1,$ or equivalently, the elements ![]() $\theta _R(c_{i,j})-1,$ and set
$\theta _R(c_{i,j})-1,$ and set ![]() $R' = k \oplus L \subset R/(\pi ,{\mathfrak m}_R^2)$. Using the isomorphism
$R' = k \oplus L \subset R/(\pi ,{\mathfrak m}_R^2)$. Using the isomorphism ![]() $\hat \theta _{R'},$ one sees that
$\hat \theta _{R'},$ one sees that ![]() ${\mathcal {A}}_R[p^\infty ]|_{R/(\pi ,{\mathfrak m}_R^2)}$ is defined over
${\mathcal {A}}_R[p^\infty ]|_{R/(\pi ,{\mathfrak m}_R^2)}$ is defined over ![]() $R'$. If
$R'$. If ![]() $L \subsetneq \bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2,$ then there exists a surjective map
$L \subsetneq \bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2,$ then there exists a surjective map ![]() $R/(\pi ,{\mathfrak m}_R^2) \rightarrow k[x]/x^2$ which sends
$R/(\pi ,{\mathfrak m}_R^2) \rightarrow k[x]/x^2$ which sends ![]() $L$ to zero. Specializing
$L$ to zero. Specializing ![]() ${\mathcal {A}}_R[p^\infty ]|_{R/(\pi ,{\mathfrak m}_R^2)}$ by this map induces the trivial deformation of
${\mathcal {A}}_R[p^\infty ]|_{R/(\pi ,{\mathfrak m}_R^2)}$ by this map induces the trivial deformation of ![]() ${\mathcal {A}}_0[p^\infty ]$ (that is, the split extension of
${\mathcal {A}}_0[p^\infty ]$ (that is, the split extension of ![]() $({\mathbb {Q}}_p/{\mathbb {Z}}_p)^g$ by
$({\mathbb {Q}}_p/{\mathbb {Z}}_p)^g$ by ![]() $\mu _{p^\infty }$) over
$\mu _{p^\infty }$) over ![]() ${\operatorname {Spec\,}} k[x]/x^2$. This contradicts the fact that
${\operatorname {Spec\,}} k[x]/x^2$. This contradicts the fact that ![]() $R$ pro-represents
$R$ pro-represents ![]() $D_{{\mathcal {A}}_0}$. Hence
$D_{{\mathcal {A}}_0}$. Hence ![]() $L = \bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2,$ which proves the lemma.
$L = \bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2,$ which proves the lemma.
3.2.3 Let ![]() $A$ be a quotient of
$A$ be a quotient of ![]() $R$ which is formally smooth over
$R$ which is formally smooth over ![]() $V$. That is,
$V$. That is, ![]() $A$ is isomorphic as a complete
$A$ is isomorphic as a complete ![]() $V$-algebra to
$V$-algebra to ![]() $V[\![ x_1, \ldots x_n ]\!]$. As in § 3.1, we set
$V[\![ x_1, \ldots x_n ]\!]$. As in § 3.1, we set ![]() $X = {\operatorname {Spec\,}} A[1/p]$ and
$X = {\operatorname {Spec\,}} A[1/p]$ and ![]() $\tilde X = {\operatorname {Spec\,}} A$.
$\tilde X = {\operatorname {Spec\,}} A$.
Lemma 3.2.4 Let ![]() $B = V[\![ y_1, \ldots y_s ]\!]$ for some integer
$B = V[\![ y_1, \ldots y_s ]\!]$ for some integer ![]() $s \geq 0,$ and let
$s \geq 0,$ and let
be a local flat map of complete local ![]() $V$-algebras. Set
$V$-algebras. Set ![]() $Y = {\operatorname {Spec\,}} B[1/p]$. Suppose that
$Y = {\operatorname {Spec\,}} B[1/p]$. Suppose that ![]() $k$ is algebraically closed, and that there exists an
$k$ is algebraically closed, and that there exists an ![]() ${\mathbb {F}}_p$-local system
${\mathbb {F}}_p$-local system ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $Y$ which is an extension of
$Y$ which is an extension of ![]() $({\mathbb {Z}}/p{\mathbb {Z}})^g$ by
$({\mathbb {Z}}/p{\mathbb {Z}})^g$ by ![]() $\mu _p^g$ such that
$\mu _p^g$ such that ![]() $f^*\mathcal {L} \overset \sim \longrightarrow {\mathcal {A}}_R[p]|_X$ as extensions of
$f^*\mathcal {L} \overset \sim \longrightarrow {\mathcal {A}}_R[p]|_X$ as extensions of ![]() ${\mathbb {F}}_p$-local systems. Then
${\mathbb {F}}_p$-local systems. Then ![]() $f$ is an isomorphism.
$f$ is an isomorphism.
Proof. Using the notation of 3.2.1, we have that ![]() $\theta _R(\{c_{i,j}\}_{i,j})$ spans
$\theta _R(\{c_{i,j}\}_{i,j})$ spans ![]() $\bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2$ by Lemma 3.2.2. In particular, if we again denote by
$\bar {\mathfrak m}_R/\bar {\mathfrak m}_R^2$ by Lemma 3.2.2. In particular, if we again denote by ![]() $c_{i,j}$ the restrictions of these classes to
$c_{i,j}$ the restrictions of these classes to ![]() $A,$ then
$A,$ then ![]() $\theta _A(\{c_{i,j}\}_{i,j})$ spans
$\theta _A(\{c_{i,j}\}_{i,j})$ spans ![]() $\bar {\mathfrak m}_A/\bar {\mathfrak m}_A^2$.
$\bar {\mathfrak m}_A/\bar {\mathfrak m}_A^2$.
Now by Lemma 3.1.5 the ![]() $g^2$ extension classes defining
$g^2$ extension classes defining ![]() $\mathcal {L}$ are syntomic. So
$\mathcal {L}$ are syntomic. So ![]() $\mathcal {L}$ arises from an extension of
$\mathcal {L}$ arises from an extension of ![]() $({\mathbb {Z}}/p{\mathbb {Z}})^g$ by
$({\mathbb {Z}}/p{\mathbb {Z}})^g$ by ![]() $\mu _p^g$ as finite flat group schemes over
$\mu _p^g$ as finite flat group schemes over ![]() $\tilde Y$. If we denote by
$\tilde Y$. If we denote by ![]() $(d_{i,j})$ the corresponding
$(d_{i,j})$ the corresponding ![]() $g\times g$ matrix of elements of
$g\times g$ matrix of elements of ![]() ${\rm Ext}_{\tilde Y}^1({\mathbb {Z}}/p{\mathbb {Z}}, \mu _p),$ then Lemma 3.1.4, together with the fact that
${\rm Ext}_{\tilde Y}^1({\mathbb {Z}}/p{\mathbb {Z}}, \mu _p),$ then Lemma 3.1.4, together with the fact that ![]() $f^*\mathcal {L} \overset \sim \longrightarrow {\mathcal {A}}_R[p]|_X$, implies that
$f^*\mathcal {L} \overset \sim \longrightarrow {\mathcal {A}}_R[p]|_X$, implies that ![]() $f^*(d_{i,j}) = c_{i,j}$. It follows that the elements
$f^*(d_{i,j}) = c_{i,j}$. It follows that the elements ![]() $\theta _A(f^*(\{d_{i,j}\}))_{i,j}$ span
$\theta _A(f^*(\{d_{i,j}\}))_{i,j}$ span ![]() $\bar {\mathfrak m}_A/\bar {\mathfrak m}_A^2,$ which implies that
$\bar {\mathfrak m}_A/\bar {\mathfrak m}_A^2,$ which implies that ![]() $f$ is an isomorphism by Lemma 3.1.7.
$f$ is an isomorphism by Lemma 3.1.7.
3.2.5 Fix an integer ![]() $g \geq 1$, a prime
$g \geq 1$, a prime ![]() $p\geq 2$, and a positive integer
$p\geq 2$, and a positive integer ![]() $N \geq 2$ coprime to
$N \geq 2$ coprime to ![]() $p$. Consider the ring
$p$. Consider the ring ![]() ${\mathbb {Z}}[\zeta _N][1/N],$ where
${\mathbb {Z}}[\zeta _N][1/N],$ where ![]() $\zeta _N$ is a primitive
$\zeta _N$ is a primitive ![]() $N$th root of
$N$th root of ![]() $1$. Using the isomorphism
$1$. Using the isomorphism ![]() ${\mathbb {Z}}/N{\mathbb {Z}} \underset {1 \mapsto \zeta _N}{\overset \sim \longrightarrow }\mu _N,$ for any
${\mathbb {Z}}/N{\mathbb {Z}} \underset {1 \mapsto \zeta _N}{\overset \sim \longrightarrow }\mu _N,$ for any ![]() ${\mathbb {Z}}[\zeta _N][1/N]$-scheme
${\mathbb {Z}}[\zeta _N][1/N]$-scheme ![]() $T,$ and any principally polarized abelian scheme
$T,$ and any principally polarized abelian scheme ![]() $A$ over
$A$ over ![]() $T,$ the
$T,$ the ![]() $N$-torsion scheme
$N$-torsion scheme ![]() $A[N]$ is equipped with the (alternating) Weil pairing
$A[N]$ is equipped with the (alternating) Weil pairing
We denote by ![]() ${\mathcal {A}}_{g,N}$ the
${\mathcal {A}}_{g,N}$ the ![]() ${\mathbb {Z}}[\zeta _N][1/N]$-scheme which is the coarse moduli space of principally polarized abelian schemes
${\mathbb {Z}}[\zeta _N][1/N]$-scheme which is the coarse moduli space of principally polarized abelian schemes ![]() $A$ of dimension
$A$ of dimension ![]() $g$ equipped with a symplectic basis of
$g$ equipped with a symplectic basis of ![]() $A[N]$. When
$A[N]$. When ![]() $N \geq 3,$ this is a fine moduli space which is smooth over
$N \geq 3,$ this is a fine moduli space which is smooth over ![]() ${\mathbb {Z}}[\zeta _N][1/N]$. For a
${\mathbb {Z}}[\zeta _N][1/N]$. For a ![]() ${\mathbb {Z}}[\zeta _N][1/N]$-algebra
${\mathbb {Z}}[\zeta _N][1/N]$-algebra ![]() $B,$ we denote by
$B,$ we denote by ![]() ${\mathcal {A}}_{g,N/B}$ the base change of
${\mathcal {A}}_{g,N/B}$ the base change of ![]() ${\mathcal {A}}_{g,N}$ to
${\mathcal {A}}_{g,N}$ to ![]() $B$. If no confusion is likely to result we sometimes denote this base change simply by
$B$. If no confusion is likely to result we sometimes denote this base change simply by ![]() ${\mathcal {A}}_{g,N}$.
${\mathcal {A}}_{g,N}$.
Suppose that ![]() $N \geq 3,$ and let
$N \geq 3,$ and let ![]() ${\mathcal {A}} \rightarrow {\mathcal {A}}_{g,N}$ be the universal abelian scheme. The
${\mathcal {A}} \rightarrow {\mathcal {A}}_{g,N}$ be the universal abelian scheme. The ![]() $p$-torsion subgroup
$p$-torsion subgroup ![]() ${\mathcal {A}}[p] \subset {\mathcal {A}}$ is a finite flat group scheme over
${\mathcal {A}}[p] \subset {\mathcal {A}}$ is a finite flat group scheme over ![]() ${\mathcal {A}}_{g,N}$ which is étale over
${\mathcal {A}}_{g,N}$ which is étale over ![]() ${\mathbb {Z}}[\zeta _N][1/Np]$. Let
${\mathbb {Z}}[\zeta _N][1/Np]$. Let ![]() $x \in {\mathcal {A}}_{g,N}$ be a point with residue field
$x \in {\mathcal {A}}_{g,N}$ be a point with residue field ![]() $\kappa (x)$ of characteristic
$\kappa (x)$ of characteristic ![]() $p,$ and
$p,$ and ![]() ${\mathcal {A}}_x$ the corresponding abelian variety over
${\mathcal {A}}_x$ the corresponding abelian variety over ![]() $\kappa (x)$. The set of points
$\kappa (x)$. The set of points ![]() $x$ such that
$x$ such that ![]() ${\mathcal {A}}_x$ is ordinary is an open subscheme
${\mathcal {A}}_x$ is ordinary is an open subscheme ![]() ${\mathcal {A}}_{g,N}^{\rm ord} \subset {\mathcal {A}}_{g,N}\otimes {\mathbb {F}}_p$. For any
${\mathcal {A}}_{g,N}^{\rm ord} \subset {\mathcal {A}}_{g,N}\otimes {\mathbb {F}}_p$. For any ![]() $N,$ we denote by
$N,$ we denote by ![]() ${\mathcal {A}}_{g,N}^{\rm ord} \subset {\mathcal {A}}_{g,N}\otimes {\mathbb {F}}_p$ the image of
${\mathcal {A}}_{g,N}^{\rm ord} \subset {\mathcal {A}}_{g,N}\otimes {\mathbb {F}}_p$ the image of ![]() ${\mathcal {A}}_{g,NN'}$ for any
${\mathcal {A}}_{g,NN'}$ for any ![]() $N' \geq 3$ coprime to
$N' \geq 3$ coprime to ![]() $N$ and
$N$ and ![]() $p$.
$p$.
We now denote by ![]() $k$ a perfect field of characteristic
$k$ a perfect field of characteristic ![]() $p,$ and
$p,$ and ![]() $K/W[1/p]$ a finite extension with ring of integers
$K/W[1/p]$ a finite extension with ring of integers ![]() $\mathcal {O}_K$ and uniformizer
$\mathcal {O}_K$ and uniformizer ![]() $\pi$. We assume that
$\pi$. We assume that ![]() $K$ is equipped with a choice of primitive
$K$ is equipped with a choice of primitive ![]() $N$th root of
$N$th root of ![]() $1,$
$1,$ ![]() $\zeta _N \in K$. We remind the reader regarding the convention for the definition of
$\zeta _N \in K$. We remind the reader regarding the convention for the definition of ![]() $\overline {{\rm ed}}$ and
$\overline {{\rm ed}}$ and ![]() $\overline {{\rm ed}}(\,\cdot \, ; p)$ introduced in 2.2.6.
$\overline {{\rm ed}}(\,\cdot \, ; p)$ introduced in 2.2.6.
Theorem 3.2.6. Let ![]() $g\geq 1$ and let
$g\geq 1$ and let ![]() $p$ be any prime. Let
$p$ be any prime. Let ![]() $N \geq 3$ and coprime to
$N \geq 3$ and coprime to ![]() $p,$ and let
$p,$ and let
be a map of equidimensional, smooth ![]() $\mathcal {O}_K$-schemes, satisfying the following conditions.
$\mathcal {O}_K$-schemes, satisfying the following conditions.
(i) If
 $x \in {\mathcal {Z}}$ is a closed point with image
$x \in {\mathcal {Z}}$ is a closed point with image  $y \in {\mathcal {A}}_{g,N/\mathcal {O}_K},$ then
$y \in {\mathcal {A}}_{g,N/\mathcal {O}_K},$ then  $\iota$ induces a surjection of complete local rings
$\iota$ induces a surjection of complete local rings  $\widehat{\mathcal{O}}_{{\mathcal {A}}_{g,N/\mathcal {O}_K},y} \twoheadrightarrow \widehat{\mathcal{O}}_{{\mathcal {Z}},x}$.
$\widehat{\mathcal{O}}_{{\mathcal {A}}_{g,N/\mathcal {O}_K},y} \twoheadrightarrow \widehat{\mathcal{O}}_{{\mathcal {Z}},x}$.(ii) The image, under
 $\iota$, of the special fiber
$\iota$, of the special fiber  ${\mathcal {Z}}_k$ meets the ordinary locus
${\mathcal {Z}}_k$ meets the ordinary locus  ${\mathcal {A}}_{g,N}^{{\rm ord}} \subset {\mathcal {A}}_{g,N/k}$.
${\mathcal {A}}_{g,N}^{{\rm ord}} \subset {\mathcal {A}}_{g,N/k}$.
Then
Proof. It suffices to prove the theorem when ![]() $k$ is algebraically closed, which we assume from now on. Moreover, since
$k$ is algebraically closed, which we assume from now on. Moreover, since ![]() $K$ is an arbitrary finite extension of
$K$ is an arbitrary finite extension of ![]() $W[1/p],$ it is enough to show that
$W[1/p],$ it is enough to show that ![]() ${\rm ed}_K({\mathcal {A}}[p]|_{{\mathcal {Z}}_K}/{\mathcal {Z}}_K;p) = {\rm dim}\,{\mathcal {Z}}_K.$ We may replace
${\rm ed}_K({\mathcal {A}}[p]|_{{\mathcal {Z}}_K}/{\mathcal {Z}}_K;p) = {\rm dim}\,{\mathcal {Z}}_K.$ We may replace ![]() ${\mathcal {Z}}$ by a component whose special fiber meets the ordinary locus, and assume that
${\mathcal {Z}}$ by a component whose special fiber meets the ordinary locus, and assume that ![]() ${\mathcal {Z}}_K$ and
${\mathcal {Z}}_K$ and ![]() ${\mathcal {Z}}_k$ are geometrically connected.
${\mathcal {Z}}_k$ are geometrically connected.
Suppose that ![]() $\overline {{\rm ed}}({\mathcal {A}}[p]|_{{\mathcal {Z}}_K}/{\mathcal {Z}}_K; p) < {\rm dim}\,{\mathcal {Z}}_K$. Then there exists a dominant, generically finite map
$\overline {{\rm ed}}({\mathcal {A}}[p]|_{{\mathcal {Z}}_K}/{\mathcal {Z}}_K; p) < {\rm dim}\,{\mathcal {Z}}_K$. Then there exists a dominant, generically finite map ![]() $U_K \rightarrow {\mathcal {Z}}_K$ of degree prime to
$U_K \rightarrow {\mathcal {Z}}_K$ of degree prime to ![]() $p$ at the generic points of
$p$ at the generic points of ![]() $U_K,$ and a map
$U_K,$ and a map ![]() $h: U_K \rightarrow Y_K$ to a finite type
$h: U_K \rightarrow Y_K$ to a finite type ![]() $K$-scheme
$K$-scheme ![]() $Y_K$ with
$Y_K$ with ![]() ${\rm dim}\, Y_K < {\rm dim}\, {\mathcal {Z}}_K,$ such that
${\rm dim}\, Y_K < {\rm dim}\, {\mathcal {Z}}_K,$ such that ![]() ${\mathcal {A}}[p]|_{U_K}$ arises as the pullback of a finite étale covering of
${\mathcal {A}}[p]|_{U_K}$ arises as the pullback of a finite étale covering of ![]() $Y_K$. We may assume that
$Y_K$. We may assume that ![]() $Y_K$ is the scheme-theoretic image of
$Y_K$ is the scheme-theoretic image of ![]() $U_K$ under
$U_K$ under ![]() $h$. Next, after replacing both
$h$. Next, after replacing both ![]() $U_K$ and
$U_K$ and ![]() $Y_K$ by dense affine opens, we may assume that both these schemes are affine corresponding to
$Y_K$ by dense affine opens, we may assume that both these schemes are affine corresponding to ![]() $K$-algebras
$K$-algebras ![]() $B_K$ and
$B_K$ and ![]() $C_K$ respectively, and that
$C_K$ respectively, and that ![]() $U_K \rightarrow Y_K$ is flat.
$U_K \rightarrow Y_K$ is flat.
Let ![]() $\tilde {\mathcal {Z}}$ be the normalization of
$\tilde {\mathcal {Z}}$ be the normalization of ![]() ${\mathcal {Z}}$ in
${\mathcal {Z}}$ in ![]() $U_K$. Let
$U_K$. Let ![]() $\mathfrak p$ be the generic point of
$\mathfrak p$ be the generic point of ![]() ${\mathcal {Z}}_k,$ and
${\mathcal {Z}}_k,$ and ![]() $\mathfrak q_1, \ldots , \mathfrak q_m$ the primes of
$\mathfrak q_1, \ldots , \mathfrak q_m$ the primes of ![]() $\tilde {\mathcal {Z}}$ over
$\tilde {\mathcal {Z}}$ over ![]() $\mathfrak p$. Since the degree of
$\mathfrak p$. Since the degree of ![]() $\tilde {\mathcal {Z}} \rightarrow {\mathcal {Z}}$ over
$\tilde {\mathcal {Z}} \rightarrow {\mathcal {Z}}$ over ![]() $\mathfrak p$ is prime to
$\mathfrak p$ is prime to ![]() $p,$ for some
$p,$ for some ![]() $i$ the ramification degree
$i$ the ramification degree ![]() $e(\mathfrak q_i/\mathfrak p)$ and the degree of the residue field extension
$e(\mathfrak q_i/\mathfrak p)$ and the degree of the residue field extension ![]() $\kappa (\mathfrak q_i)/\kappa (\mathfrak p)$ are prime to
$\kappa (\mathfrak q_i)/\kappa (\mathfrak p)$ are prime to ![]() $p$. In particular, the residue field extension is separable. By Abhyankar's Lemma, it follows that, after replacing
$p$. In particular, the residue field extension is separable. By Abhyankar's Lemma, it follows that, after replacing ![]() $K$ by a finite extension, we may assume that
$K$ by a finite extension, we may assume that ![]() $e(\mathfrak q_i/\mathfrak p) = 1$ for some
$e(\mathfrak q_i/\mathfrak p) = 1$ for some ![]() $i,$ and that
$i,$ and that ![]() $\tilde {\mathcal {Z}} \rightarrow {\mathcal {Z}}$ is étale at
$\tilde {\mathcal {Z}} \rightarrow {\mathcal {Z}}$ is étale at ![]() $\mathfrak q_i$. Shrinking
$\mathfrak q_i$. Shrinking ![]() $U_K$ further if necessary, we may assume that there is an affine open
$U_K$ further if necessary, we may assume that there is an affine open ![]() ${\operatorname {Spec\,}} B = U \subset \tilde {\mathcal {Z}}$ such that
${\operatorname {Spec\,}} B = U \subset \tilde {\mathcal {Z}}$ such that ![]() $U_k \rightarrow {\mathcal {Z}}_k$ has dense image,
$U_k \rightarrow {\mathcal {Z}}_k$ has dense image, ![]() $U\otimes K = U_K,$ and
$U\otimes K = U_K,$ and ![]() $U \rightarrow {\mathcal {Z}}$ is étale. In particular,
$U \rightarrow {\mathcal {Z}}$ is étale. In particular, ![]() $U$ is smooth over
$U$ is smooth over ![]() $\mathcal {O}_K$.
$\mathcal {O}_K$.
Now choose a finitely generated ![]() $\mathcal {O}_K$-subalgebra
$\mathcal {O}_K$-subalgebra ![]() $C \subset C_K \cap B$ such that
$C \subset C_K \cap B$ such that ![]() $C\otimes K = C_K$. This is possible as
$C\otimes K = C_K$. This is possible as ![]() $C_K$ is finitely generated over
$C_K$ is finitely generated over ![]() $K$. Then
$K$. Then ![]() $h$ extends to a map
$h$ extends to a map ![]() $h: U \rightarrow Y = {\operatorname {Spec\,}} C$. Let
$h: U \rightarrow Y = {\operatorname {Spec\,}} C$. Let ![]() $J \supset (p)$ be an ideal of
$J \supset (p)$ be an ideal of ![]() $C,$ and
$C,$ and ![]() $Y_J \rightarrow Y$ the blow-up of
$Y_J \rightarrow Y$ the blow-up of ![]() $J$. Denote by
$J$. Denote by ![]() $U_J$ the proper transform of
$U_J$ the proper transform of ![]() $U$ by this blow-up. That is,
$U$ by this blow-up. That is, ![]() $U_J$ is the closure of
$U_J$ is the closure of ![]() $U_K$ in
$U_K$ in ![]() $U\times Y_J$. By the Raynaud–Gruson Flattening Theorem [Reference Raynaud and GrusonRG71, Theorem 5.2.2], we can choose
$U\times Y_J$. By the Raynaud–Gruson Flattening Theorem [Reference Raynaud and GrusonRG71, Theorem 5.2.2], we can choose ![]() $J$ so that
$J$ so that ![]() $U_J \rightarrow Y_J$ is flat. Since
$U_J \rightarrow Y_J$ is flat. Since ![]() $U$ is normal, the map
$U$ is normal, the map ![]() $U_J \rightarrow U$ is an isomorphism over the generic points of
$U_J \rightarrow U$ is an isomorphism over the generic points of ![]() $U\otimes k$. Hence, after replacing
$U\otimes k$. Hence, after replacing ![]() $Y$ by an affine open in
$Y$ by an affine open in ![]() $Y_J,$ and shrinking
$Y_J,$ and shrinking ![]() $U,$ we may assume that
$U,$ we may assume that ![]() $U \rightarrow Y$ is flat.
$U \rightarrow Y$ is flat.
Shrinking ![]() $U$ further, we may assume that the special fiber
$U$ further, we may assume that the special fiber ![]() $U_k$ maps to the ordinary locus of
$U_k$ maps to the ordinary locus of ![]() ${\mathcal {A}}_{g,N}$. Now let
${\mathcal {A}}_{g,N}$. Now let ![]() $\widehat B$ and
$\widehat B$ and ![]() $\widehat C$ denote the
$\widehat C$ denote the ![]() $p$-adic completions of
$p$-adic completions of ![]() $B$ and
$B$ and ![]() $C$ respectively, and set
$C$ respectively, and set ![]() $\widehat U = {\operatorname {Spec\,}} \widehat B$ and
$\widehat U = {\operatorname {Spec\,}} \widehat B$ and ![]() $\widehat Y = {\operatorname {Spec\,}} \widehat C$.Footnote 2 Since
$\widehat Y = {\operatorname {Spec\,}} \widehat C$.Footnote 2 Since ![]() ${\mathcal {A}}[p]|_{\widehat U}$ is ordinary, there is a finite étale covering
${\mathcal {A}}[p]|_{\widehat U}$ is ordinary, there is a finite étale covering ![]() $\widehat U' = {\operatorname {Spec\,}} \widehat B' \rightarrow \widehat U$ such that
$\widehat U' = {\operatorname {Spec\,}} \widehat B' \rightarrow \widehat U$ such that ![]() ${\mathcal {A}}[p]|_{\widehat U'}$ is an extension of
${\mathcal {A}}[p]|_{\widehat U'}$ is an extension of ![]() $({\mathbb {Z}}/p{\mathbb {Z}})^g$ by
$({\mathbb {Z}}/p{\mathbb {Z}})^g$ by ![]() $\mu _p^g$. Hence by Lemmas 2.1.6 and 2.1.8,
$\mu _p^g$. Hence by Lemmas 2.1.6 and 2.1.8, ![]() $\widehat U'_K \rightarrow \widehat Y_K$ factors through a finite étale map
$\widehat U'_K \rightarrow \widehat Y_K$ factors through a finite étale map ![]() $\widehat Y'_K \rightarrow \widehat Y_K$ such that
$\widehat Y'_K \rightarrow \widehat Y_K$ such that ![]() ${\mathcal {A}}[p]|_{\widehat U'_K}$ is the pullback of an extension
${\mathcal {A}}[p]|_{\widehat U'_K}$ is the pullback of an extension ![]() ${\mathcal {F}}'$ of
${\mathcal {F}}'$ of ![]() $({\mathbb {Z}}/p{\mathbb {Z}})^g$ by
$({\mathbb {Z}}/p{\mathbb {Z}})^g$ by ![]() $\mu _p^g$ on
$\mu _p^g$ on ![]() $\widehat Y'_K$. As
$\widehat Y'_K$. As ![]() $\widehat U'$ is normal, we may assume
$\widehat U'$ is normal, we may assume ![]() $\widehat Y'_K$ is normal.
$\widehat Y'_K$ is normal.
Let ![]() $\widehat Y' = {\operatorname {Spec\,}} \widehat C'$ be the normalization of
$\widehat Y' = {\operatorname {Spec\,}} \widehat C'$ be the normalization of ![]() $\widehat Y$ in
$\widehat Y$ in ![]() $\widehat Y'_K$. As
$\widehat Y'_K$. As ![]() $\widehat U'$ is normal, we have
$\widehat U'$ is normal, we have
As ![]() $\widehat Y'$ is normal,
$\widehat Y'$ is normal, ![]() $\widehat U' \rightarrow \widehat Y'$ is flat over the generic points of
$\widehat U' \rightarrow \widehat Y'$ is flat over the generic points of ![]() $\widehat Y'_k$. Hence, there exists
$\widehat Y'_k$. Hence, there exists ![]() $f_0 \in \widehat C'/\pi \widehat C'$ which is nowhere nilpotent on
$f_0 \in \widehat C'/\pi \widehat C'$ which is nowhere nilpotent on ![]() $\widehat Y'_k,$ and such that
$\widehat Y'_k,$ and such that ![]() $\widehat U'_k \rightarrow \widehat Y'_k$ is flat over the complement of the support of the ideal
$\widehat U'_k \rightarrow \widehat Y'_k$ is flat over the complement of the support of the ideal ![]() $(f_0)$. Now let
$(f_0)$. Now let ![]() $f \in \widehat C'$ be a lift of
$f \in \widehat C'$ be a lift of ![]() $f_0,$ and let
$f_0,$ and let ![]() $\widehat C'' = \widehat {C'[1/f]}$ and
$\widehat C'' = \widehat {C'[1/f]}$ and ![]() $\widehat B'' = \widehat {B'[1/f]},$ the
$\widehat B'' = \widehat {B'[1/f]},$ the ![]() $p$-adic completionsFootnote 3 of
$p$-adic completionsFootnote 3 of ![]() $C'[1/f]$ and
$C'[1/f]$ and ![]() $B'[1/f]$. Let
$B'[1/f]$. Let ![]() $\widehat U'' = {\operatorname {Spec\,}} B''$ and
$\widehat U'' = {\operatorname {Spec\,}} B''$ and ![]() $\widehat Y'' = {\operatorname {Spec\,}} \widehat C''$. Then
$\widehat Y'' = {\operatorname {Spec\,}} \widehat C''$. Then ![]() $\widehat U''$ is flat over
$\widehat U''$ is flat over ![]() $\widehat Y''$ by [Reference GrothendieckEGA, IV, 11.3.10.1]. Moreover, since
$\widehat Y''$ by [Reference GrothendieckEGA, IV, 11.3.10.1]. Moreover, since ![]() $\widehat U \rightarrow \widehat Y$ is flat, the generic points of
$\widehat U \rightarrow \widehat Y$ is flat, the generic points of ![]() $\widehat U'_k$ map to generic points of
$\widehat U'_k$ map to generic points of ![]() $\widehat Y'_k$. So the image of
$\widehat Y'_k$. So the image of ![]() $\widehat U''_k$ is dense in
$\widehat U''_k$ is dense in ![]() $\widehat U'_k,$ and in particular
$\widehat U'_k,$ and in particular ![]() $\widehat U''(k)$ is nonempty.
$\widehat U''(k)$ is nonempty.
Now choose a point ![]() $x \in \widehat U''(k),$ and denote by
$x \in \widehat U''(k),$ and denote by ![]() $y \in \widehat Y''(k)$ its image. We write
$y \in \widehat Y''(k)$ its image. We write ![]() $\mathcal {O}_{\widehat U'',x}$ and
$\mathcal {O}_{\widehat U'',x}$ and ![]() $\mathcal {O}_{\widehat Y'',y}$ for the complete local rings at
$\mathcal {O}_{\widehat Y'',y}$ for the complete local rings at ![]() $x$ and
$x$ and ![]() $y$. Since the maps
$y$. Since the maps
are formally étale, ![]() $\mathcal {O}_{\widehat U'',x}$ is naturally isomorphic to the complete local ring at the image of
$\mathcal {O}_{\widehat U'',x}$ is naturally isomorphic to the complete local ring at the image of ![]() $x$ in
$x$ in ![]() ${\mathcal {Z}}$. Let
${\mathcal {Z}}$. Let ![]() $R$ be the universal deformation
$R$ be the universal deformation ![]() $\mathcal {O}_K$-algebra of the abelian scheme
$\mathcal {O}_K$-algebra of the abelian scheme ![]() ${\mathcal {A}}_x$. By condition (i) of the theorem,
${\mathcal {A}}_x$. By condition (i) of the theorem, ![]() $\mathcal {O}_{\widehat U'',x}$ is naturally a quotient of
$\mathcal {O}_{\widehat U'',x}$ is naturally a quotient of ![]() $R$. The map
$R$. The map ![]() $\mathcal {O}_{\widehat Y'',y} \rightarrow \mathcal {O}_{\widehat U'',x}$ satisfies the conditions of Lemma 3.2.4 (cf. [Reference GrothendieckEGA, IV, 17.5.3]), and it follows that this map is an isomorphism. In particular, this implies that
$\mathcal {O}_{\widehat Y'',y} \rightarrow \mathcal {O}_{\widehat U'',x}$ satisfies the conditions of Lemma 3.2.4 (cf. [Reference GrothendieckEGA, IV, 17.5.3]), and it follows that this map is an isomorphism. In particular, this implies that
which contradicts our initial assumption.
Corollary 3.2.7. Let ![]() $g\geq 1,$ be an integer,
$g\geq 1,$ be an integer, ![]() $p$ any prime, and
$p$ any prime, and ![]() $N \geq 1$ an integer coprime to
$N \geq 1$ an integer coprime to ![]() $p$. Let
$p$. Let
be a map of equidimensional, smooth ![]() $\mathcal {O}_K$-schemes satisfying conditions (i) and (ii) of Theorem 3.2.6.
$\mathcal {O}_K$-schemes satisfying conditions (i) and (ii) of Theorem 3.2.6.
If ![]() $N=1,2$ we also assume the following condition: For any generic point
$N=1,2$ we also assume the following condition: For any generic point ![]() $\eta \in {\mathcal {Z}}_k,$ and
$\eta \in {\mathcal {Z}}_k,$ and ![]() $\bar \eta$ the spectrum of an algebraic closure of
$\bar \eta$ the spectrum of an algebraic closure of ![]() $\kappa (\eta ),$ the abelian variety
$\kappa (\eta ),$ the abelian variety ![]() ${\mathcal {A}}_{\bar \eta }$ over
${\mathcal {A}}_{\bar \eta }$ over ![]() $\bar \eta ,$ has automorphism group equal to
$\bar \eta ,$ has automorphism group equal to ![]() $\{\pm 1\}$. Then
$\{\pm 1\}$. Then
Proof. If ![]() $N \geq 3,$ the corollary follows from Theorem 3.2.6 and Lemma 2.2.4.
$N \geq 3,$ the corollary follows from Theorem 3.2.6 and Lemma 2.2.4.
Suppose ![]() $N=1$ or
$N=1$ or ![]() $2$. Let
$2$. Let ![]() $N' \geq 3$ be an integer coprime to
$N' \geq 3$ be an integer coprime to ![]() $pN$. We may assume that
$pN$. We may assume that ![]() $K$ is equipped with a primitive
$K$ is equipped with a primitive ![]() $pN^{\prime }$th root of
$pN^{\prime }$th root of ![]() $1,$
$1,$ ![]() $\zeta _{pN'}$. The map of
$\zeta _{pN'}$. The map of ![]() $K$-schemes
$K$-schemes ![]() ${\mathcal {A}}_{g,pN} \rightarrow {\mathcal {A}}_{g,N},$ is a covering with group
${\mathcal {A}}_{g,pN} \rightarrow {\mathcal {A}}_{g,N},$ is a covering with group ![]() ${\rm Sp}_{2g}(\mathbb {F}_p)/\{\pm 1\}$. Consider the maps
${\rm Sp}_{2g}(\mathbb {F}_p)/\{\pm 1\}$. Consider the maps
Then ![]() ${\mathcal {A}}'_{g,pNN'} \rightarrow {\mathcal {A}}_{g,NN'}$ again corresponds to a
${\mathcal {A}}'_{g,pNN'} \rightarrow {\mathcal {A}}_{g,NN'}$ again corresponds to a ![]() ${\rm Sp}_{2g}(\mathbb {F}_p)/\{\pm 1\}$ covering, and
${\rm Sp}_{2g}(\mathbb {F}_p)/\{\pm 1\}$ covering, and ![]() ${\mathcal {A}}_{g,pNN'} \rightarrow {\mathcal {A}}_{g,NN'}$ corresponds to a
${\mathcal {A}}_{g,pNN'} \rightarrow {\mathcal {A}}_{g,NN'}$ corresponds to a ![]() ${\rm Sp}_{2g}(\mathbb {F}_p)$ covering. When
${\rm Sp}_{2g}(\mathbb {F}_p)$ covering. When ![]() $p=2$ these two coverings coincide.
$p=2$ these two coverings coincide.
Let ![]() ${\mathcal {Z}}_{N'} = {\mathcal {Z}} \times _{{\mathcal {A}}_{g,N}}{\mathcal {A}}_{g,NN'}$. Our assumption on the automorphisms of
${\mathcal {Z}}_{N'} = {\mathcal {Z}} \times _{{\mathcal {A}}_{g,N}}{\mathcal {A}}_{g,NN'}$. Our assumption on the automorphisms of ![]() ${\mathcal {A}}_{\bar \eta }$ implies that at the generic points of
${\mathcal {A}}_{\bar \eta }$ implies that at the generic points of ![]() ${\mathcal {Z}}_k,$ the map
${\mathcal {Z}}_k,$ the map ![]() ${\mathcal {Z}}_{N'} \rightarrow {\mathcal {Z}}$ is étale. Thus, after replacing
${\mathcal {Z}}_{N'} \rightarrow {\mathcal {Z}}$ is étale. Thus, after replacing ![]() ${\mathcal {Z}}$ by a fiberwise dense open, we may assume that
${\mathcal {Z}}$ by a fiberwise dense open, we may assume that ![]() ${\mathcal {Z}}_{N'}$ is smooth over
${\mathcal {Z}}_{N'}$ is smooth over ![]() $\mathcal {O}_K$. The observations of the previous paragraph, Lemma 2.2.7 when
$\mathcal {O}_K$. The observations of the previous paragraph, Lemma 2.2.7 when ![]() $p >2,$ Lemma 2.2.4 and Theorem 3.2.6 imply that we have
$p >2,$ Lemma 2.2.4 and Theorem 3.2.6 imply that we have
 \begin{align} \overline{{\rm ed}}({\mathcal{A}}_{g,pN}|_{{\mathcal{Z}}_K}/{\mathcal{Z}}_K; p) &\geq \overline{{\rm ed}}({\mathcal{A}}'_{g,pNN'}|_{{\mathcal{Z}}_{N',K}}/{\mathcal{Z}}_{N',K}; p) \nonumber\\ &= \overline{{\rm ed}}({\mathcal{A}}_{g,pNN'}|_{{\mathcal{Z}}_{N',K}}/{\mathcal{Z}}_{N',K}; p)\nonumber\\ & = \overline{{\rm ed}}({\mathcal{A}}[p]|_{{\mathcal{Z}}_{N',K}}/{\mathcal{Z}}_{N',K}; p)\nonumber\\ & ={\rm dim}\, {\mathcal{Z}}_K.\end{align}
\begin{align} \overline{{\rm ed}}({\mathcal{A}}_{g,pN}|_{{\mathcal{Z}}_K}/{\mathcal{Z}}_K; p) &\geq \overline{{\rm ed}}({\mathcal{A}}'_{g,pNN'}|_{{\mathcal{Z}}_{N',K}}/{\mathcal{Z}}_{N',K}; p) \nonumber\\ &= \overline{{\rm ed}}({\mathcal{A}}_{g,pNN'}|_{{\mathcal{Z}}_{N',K}}/{\mathcal{Z}}_{N',K}; p)\nonumber\\ & = \overline{{\rm ed}}({\mathcal{A}}[p]|_{{\mathcal{Z}}_{N',K}}/{\mathcal{Z}}_{N',K}; p)\nonumber\\ & ={\rm dim}\, {\mathcal{Z}}_K.\end{align}Corollary 3.2.9. Let ![]() $g, n\geq 2$ and
$g, n\geq 2$ and ![]() $N$ a positive integer coprime to
$N$ a positive integer coprime to ![]() $n$. Consider the finite étale map of
$n$. Consider the finite étale map of ![]() ${\mathbb {Q}}(\zeta _{nN})$-schemes
${\mathbb {Q}}(\zeta _{nN})$-schemes ![]() ${\mathcal {A}}_{g,nN} \rightarrow {\mathcal {A}}_{g,N}$. Then for any
${\mathcal {A}}_{g,nN} \rightarrow {\mathcal {A}}_{g,N}$. Then for any ![]() $p{\mid} n$, we have
$p{\mid} n$, we have
Proof. A fortiori it suffices to consider the case when ![]() $n=p$ is prime, which is a special case of Corollary 3.2.7.
$n=p$ is prime, which is a special case of Corollary 3.2.7.
3.3 Moduli spaces of curves
Using the Torelli theorem one can use Theorem 3.2.6 to deduce the essential ![]() $p$-dimension of certain coverings of families of curves.
$p$-dimension of certain coverings of families of curves.
3.3.1 Let ![]() $g \geq 2,$ and let
$g \geq 2,$ and let ![]() ${\mathcal {M}}_g$ denote the coarse moduli space of smooth, proper, genus
${\mathcal {M}}_g$ denote the coarse moduli space of smooth, proper, genus ![]() $g$ curves. For any integer
$g$ curves. For any integer ![]() $n,$ let
$n,$ let ![]() ${\mathcal {M}}_g[n]$ denote the
${\mathcal {M}}_g[n]$ denote the ![]() ${\mathbb {Z}}[\zeta _n][1/n]$-scheme which is the coarse moduli space of pairs
${\mathbb {Z}}[\zeta _n][1/n]$-scheme which is the coarse moduli space of pairs ![]() $(C,{\mathcal {B}})$ consisting of a proper smooth curve
$(C,{\mathcal {B}})$ consisting of a proper smooth curve ![]() $C$ of genus
$C$ of genus ![]() $g$ together with a choice
$g$ together with a choice ![]() $\mathcal {B}$ of symplectic basis for
$\mathcal {B}$ of symplectic basis for ![]() $J(C)[n],$ where
$J(C)[n],$ where ![]() $J(C)$ denotes the Jacobian of
$J(C)$ denotes the Jacobian of ![]() $C$. For
$C$. For ![]() $n \geq 3$ this is a fine moduli space which is smooth over
$n \geq 3$ this is a fine moduli space which is smooth over ![]() ${\mathbb {Z}}[\zeta _n][1/n]$ [Reference Deligne and MumfordDM69].
${\mathbb {Z}}[\zeta _n][1/n]$ [Reference Deligne and MumfordDM69].
Theorem 3.3.2. Let ![]() $g,n \geq 2$, and let
$g,n \geq 2$, and let ![]() $p$ be any prime dividing
$p$ be any prime dividing ![]() $n$. Then
$n$. Then
Proof. Let ![]() $N \geq 3$ be an integer. There is a natural map of
$N \geq 3$ be an integer. There is a natural map of ![]() ${\mathbb {Z}}[\zeta _N][1/N]$-schemes
${\mathbb {Z}}[\zeta _N][1/N]$-schemes ![]() $\varpi : {\mathcal {M}}_g[N] \rightarrow A_{g,N}$ taking a curve to its Jacobian. For
$\varpi : {\mathcal {M}}_g[N] \rightarrow A_{g,N}$ taking a curve to its Jacobian. For ![]() $(C,\mathcal {B})$ in
$(C,\mathcal {B})$ in ![]() ${\mathcal {M}}_g[N]$ the pairs
${\mathcal {M}}_g[N]$ the pairs ![]() $(J(C), \mathcal {B})$ and
$(J(C), \mathcal {B})$ and ![]() $(J(C), -\mathcal {B})$ are isomorphic via
$(J(C), -\mathcal {B})$ are isomorphic via ![]() $-1$ on
$-1$ on ![]() $J(C)$. Thus
$J(C)$. Thus ![]() $(C,\mathcal {B}) \mapsto (C,-\mathcal {B})$ is an involution
$(C,\mathcal {B}) \mapsto (C,-\mathcal {B})$ is an involution ![]() $\Sigma$ of
$\Sigma$ of ![]() ${\mathcal {M}}_g[N],$ which is nontrivial, unless
${\mathcal {M}}_g[N],$ which is nontrivial, unless ![]() $g=2$. We denote by
$g=2$. We denote by ![]() ${\mathcal {M}}_g[N]'$ the quotient of
${\mathcal {M}}_g[N]'$ the quotient of ![]() ${\mathcal {M}}_g[N]$ by this involution. When
${\mathcal {M}}_g[N]$ by this involution. When ![]() $g \geq 3,$ the fixed points of
$g \geq 3,$ the fixed points of ![]() $\Sigma$ in any fiber of
$\Sigma$ in any fiber of ![]() ${\mathcal {M}}_g[N]$ over
${\mathcal {M}}_g[N]$ over ![]() ${\operatorname {Spec\,}} {\mathbb {Z}}[\zeta _N][1/N]$ are contained in a proper closed subset. Thus
${\operatorname {Spec\,}} {\mathbb {Z}}[\zeta _N][1/N]$ are contained in a proper closed subset. Thus ![]() ${\mathcal {M}}_g[N]'$ is generically smooth over every point of
${\mathcal {M}}_g[N]'$ is generically smooth over every point of ![]() ${\operatorname {Spec\,}} {\mathbb {Z}}[\zeta _N][1/N]$.
${\operatorname {Spec\,}} {\mathbb {Z}}[\zeta _N][1/N]$.
By [Reference Oort and SteenbrinkOS80, 1.11, 2.7, 2.8], the map of ![]() ${\mathbb {Z}}[\zeta _N][1/N]$-schemes
${\mathbb {Z}}[\zeta _N][1/N]$-schemes ![]() ${\mathcal {M}}_g[N] \rightarrow {\mathcal {A}}_{g,N}$ induces a map
${\mathcal {M}}_g[N] \rightarrow {\mathcal {A}}_{g,N}$ induces a map ![]() ${\mathcal {M}}_g[N]' \rightarrow {\mathcal {A}}_{g,N}$ which is injective, an immersion if
${\mathcal {M}}_g[N]' \rightarrow {\mathcal {A}}_{g,N}$ which is injective, an immersion if ![]() $g=2$ and an immersion outside the hyperelliptic locus if
$g=2$ and an immersion outside the hyperelliptic locus if ![]() $g \geq 3$.
$g \geq 3$.
It suffices to prove the theorem with ![]() $n$ replaced by the prime factor
$n$ replaced by the prime factor ![]() $p$. Let
$p$. Let ![]() $N \geq 3$ be coprime to
$N \geq 3$ be coprime to ![]() $p,$ and let
$p,$ and let ![]() ${\mathcal {M}}_g[pN]'' = {\mathcal {M}}_{g}[p]\times _{{\mathcal {M}}_g}{{\mathcal {M}}_g[N]}'$. It is enough to show that
${\mathcal {M}}_g[pN]'' = {\mathcal {M}}_{g}[p]\times _{{\mathcal {M}}_g}{{\mathcal {M}}_g[N]}'$. It is enough to show that ![]() $\overline {{\rm ed}}({\mathcal {M}}_g[pN]''/{\mathcal {M}}_g[N]'; p) = 3g-3$. If
$\overline {{\rm ed}}({\mathcal {M}}_g[pN]''/{\mathcal {M}}_g[N]'; p) = 3g-3$. If ![]() $p=2$ then
$p=2$ then ![]() ${\mathcal {M}}_g[pN]'' = {\mathcal {M}}_g[pN]'$ as coverings of
${\mathcal {M}}_g[pN]'' = {\mathcal {M}}_g[pN]'$ as coverings of ![]() ${\mathcal {M}}_g[N]',$ and if
${\mathcal {M}}_g[N]',$ and if ![]() $p \geq 3$ we have natural degree
$p \geq 3$ we have natural degree ![]() $2$ maps of coverings of
$2$ maps of coverings of ![]() ${\mathcal {M}}_g[N]'$,
${\mathcal {M}}_g[N]'$,
Thus, using Lemma 2.2.7 when ![]() $p \geq 3,$ it suffices to show that
$p \geq 3,$ it suffices to show that
Since ![]() ${\mathcal {M}}_g[pN]' = {\mathcal {A}}_{g,pN}|_{{\mathcal {M}}_g[N]'},$ for example by comparing the degrees of these coverings, and
${\mathcal {M}}_g[pN]' = {\mathcal {A}}_{g,pN}|_{{\mathcal {M}}_g[N]'},$ for example by comparing the degrees of these coverings, and ![]() ${\mathcal {M}}_g[N]'$ meets the ordinary locus in
${\mathcal {M}}_g[N]'$ meets the ordinary locus in ![]() ${\mathcal {A}}_{g,N}\otimes {\mathbb {F}}_p$ [Reference Faber and van der GeerFvdG04, 2.3], the theorem now follows from Theorem 3.2.6.
${\mathcal {A}}_{g,N}\otimes {\mathbb {F}}_p$ [Reference Faber and van der GeerFvdG04, 2.3], the theorem now follows from Theorem 3.2.6.
3.3.3 We now prove the analogue of Theorem 3.3.2 for the moduli space of hyperelliptic curves. Let ![]() $S$ be a
$S$ be a ![]() ${\mathbb {Z}}[1/2]$-scheme. Recall that a hyperelliptic curve over
${\mathbb {Z}}[1/2]$-scheme. Recall that a hyperelliptic curve over ![]() $S$ is a smooth proper curve
$S$ is a smooth proper curve ![]() $C/S$ of genus
$C/S$ of genus ![]() $g \geq 1,$ equipped with an involution
$g \geq 1,$ equipped with an involution ![]() $\sigma$ such that
$\sigma$ such that ![]() $P = C/\langle \sigma \rangle$ has genus
$P = C/\langle \sigma \rangle$ has genus ![]() $0$. Let
$0$. Let ![]() $\mathcal {H}_g$ denote the coarse moduli space of genus
$\mathcal {H}_g$ denote the coarse moduli space of genus ![]() $g$ hyperelliptic curves over
$g$ hyperelliptic curves over ![]() ${\mathbb {Z}}$. It is classical (and not hard to see) that over
${\mathbb {Z}}$. It is classical (and not hard to see) that over ![]() ${\mathbb {Z}}[1/2]$ one has
${\mathbb {Z}}[1/2]$ one has
where ![]() ${\mathcal {M}}_{0,2g+2}$ is the moduli space of genus
${\mathcal {M}}_{0,2g+2}$ is the moduli space of genus ![]() $0$ curves with
$0$ curves with ![]() $2g+2$ ordered marked points, and
$2g+2$ ordered marked points, and ![]() $S_{2g+2}$ is the symmetric group on
$S_{2g+2}$ is the symmetric group on ![]() $2g+2$ letters.
$2g+2$ letters.
For any integer ![]() $n,$ let
$n,$ let ![]() $\mathcal {H}_g[n]$ denote the
$\mathcal {H}_g[n]$ denote the ![]() ${\mathbb {Z}}[\zeta _n][1/n]$-scheme which is the coarse moduli space of pairs
${\mathbb {Z}}[\zeta _n][1/n]$-scheme which is the coarse moduli space of pairs ![]() $(C,{\mathcal {B}})$ consisting of a hyperelliptic curve
$(C,{\mathcal {B}})$ consisting of a hyperelliptic curve ![]() $C$ together with a symplectic basis
$C$ together with a symplectic basis ![]() $\mathcal {B}$ for
$\mathcal {B}$ for ![]() $J(C)[n]$. As above, for
$J(C)[n]$. As above, for ![]() $n \geq 3$ this is a fine moduli space which is smooth over
$n \geq 3$ this is a fine moduli space which is smooth over ![]() ${\mathbb {Z}}[\zeta _n][1/n]$.
${\mathbb {Z}}[\zeta _n][1/n]$.
Theorem 3.3.4. Let ![]() $g,n \geq 2$, and let
$g,n \geq 2$, and let ![]() $p$ be any odd prime dividing
$p$ be any odd prime dividing ![]() $n$. Then
$n$. Then
Proof. There is a natural map of ![]() ${\mathbb {Z}}[1/2]$-schemes
${\mathbb {Z}}[1/2]$-schemes ![]() $\mathcal {H}_g \rightarrow {\mathcal {M}}_g$ which is generically an injective immersion on every fiber over
$\mathcal {H}_g \rightarrow {\mathcal {M}}_g$ which is generically an injective immersion on every fiber over ![]() ${\mathbb {Z}}[1/2],$ as a general hyperelliptic curve has only one nontrivial automorphism [Reference PoonenPoo00, Theorem 1]. By the Torelli theorem and [Reference Oort and SteenbrinkOS80, Corollary 3.2], the map
${\mathbb {Z}}[1/2],$ as a general hyperelliptic curve has only one nontrivial automorphism [Reference PoonenPoo00, Theorem 1]. By the Torelli theorem and [Reference Oort and SteenbrinkOS80, Corollary 3.2], the map ![]() ${\mathcal {M}}_g \rightarrow {\mathcal {A}}_g$ is also generically an injective immersion on every fiber over
${\mathcal {M}}_g \rightarrow {\mathcal {A}}_g$ is also generically an injective immersion on every fiber over ![]() ${\mathbb {Z}}[1/2],$ and thus so is
${\mathbb {Z}}[1/2],$ and thus so is ![]() $\mathcal {H}_g \rightarrow {\mathcal {A}}_g$.
$\mathcal {H}_g \rightarrow {\mathcal {A}}_g$.
Now the Jacobian of a hyperelliptic curve over the generic point of ![]() $\mathcal {H}_g$ has automorphism group
$\mathcal {H}_g$ has automorphism group ![]() $\{\pm 1\}$ [Reference MatsusakaMat58, p. 790], and
$\{\pm 1\}$ [Reference MatsusakaMat58, p. 790], and ![]() $\mathcal {H}_g$ meets the ordinary locus of
$\mathcal {H}_g$ meets the ordinary locus of ![]() ${\mathcal {A}}_g\otimes {\mathbb {F}}_p$ by [Reference Glass and PriesGP05, Theorem 1]. Hence the theorem follows from Corollary 3.2.7.
${\mathcal {A}}_g\otimes {\mathbb {F}}_p$ by [Reference Glass and PriesGP05, Theorem 1]. Hence the theorem follows from Corollary 3.2.7.
3.3.5 We remark that when ![]() $g=2,$ Theorem 3.3.4 extends to
$g=2,$ Theorem 3.3.4 extends to ![]() $p=2,$ as this is a special case of Theorem 3.3.2. However, an extension to
$p=2,$ as this is a special case of Theorem 3.3.2. However, an extension to ![]() $p=2$ is not possible when
$p=2$ is not possible when ![]() $g> 2$. To explain this, recall that for a finite group
$g> 2$. To explain this, recall that for a finite group ![]() $G$ and a prime
$G$ and a prime ![]() $p$,
$p$, ![]() $\overline {{\rm ed}}(G;p)$ denotes the supremum of
$\overline {{\rm ed}}(G;p)$ denotes the supremum of ![]() ${\rm ed}_K(Y/X;p)$ taken over all
${\rm ed}_K(Y/X;p)$ taken over all ![]() $G$-covers
$G$-covers ![]() $Y/X$ of finite type
$Y/X$ of finite type ![]() $K$-schemes, for any algebraically closed field
$K$-schemes, for any algebraically closed field ![]() $K$ of characteristic
$K$ of characteristic ![]() $0$ (the definition being independent of
$0$ (the definition being independent of ![]() $K$). The covering
$K$). The covering
is a component of ![]() $\mathcal {H}_g[2];$ for
$\mathcal {H}_g[2];$ for ![]() $g>2$, the cover is disconnected, and all components are isomorphic.Footnote 4 We conclude that
$g>2$, the cover is disconnected, and all components are isomorphic.Footnote 4 We conclude that
 \begin{align*} \overline{{\rm ed}}(\mathcal{H}_g[2]/\mathcal{H}_g;2) &= \overline{{\rm ed}}({\mathcal{M}}_{0,2g+2}/\mathcal{H}_g;2) \\ & = \overline{{\rm ed}}(S_{2g+2};2)\\ & = g+1< 2g - 1 \end{align*}
\begin{align*} \overline{{\rm ed}}(\mathcal{H}_g[2]/\mathcal{H}_g;2) &= \overline{{\rm ed}}({\mathcal{M}}_{0,2g+2}/\mathcal{H}_g;2) \\ & = \overline{{\rm ed}}(S_{2g+2};2)\\ & = g+1< 2g - 1 \end{align*}
where the second equality follows from the versality of ![]() ${\mathcal {M}}_{0,2g+2}$ for
${\mathcal {M}}_{0,2g+2}$ for ![]() $S_{2g+2}$, and the third follows from [Reference Meyer and ReichsteinMR09, Cor. 4.2].
$S_{2g+2}$, and the third follows from [Reference Meyer and ReichsteinMR09, Cor. 4.2].
The lower bound ![]() $\overline {{\rm ed}}(\mathcal {H}_g[2]/\mathcal {H}_g;2) \geq g+1$ can actually be recovered using the techniques of this paper. The point is that although
$\overline {{\rm ed}}(\mathcal {H}_g[2]/\mathcal {H}_g;2) \geq g+1$ can actually be recovered using the techniques of this paper. The point is that although ![]() $\mathcal {H}_g \rightarrow {\mathcal {A}}_g$ is not generically an immersion in characteristic
$\mathcal {H}_g \rightarrow {\mathcal {A}}_g$ is not generically an immersion in characteristic ![]() $2,$ one can show that the image of the map on tangent spaces at a generic point has dimension
$2,$ one can show that the image of the map on tangent spaces at a generic point has dimension ![]() $g+1$. We are grateful to Aaron Landesman for showing us this calculation [Reference LandesmanLan19].
$g+1$. We are grateful to Aaron Landesman for showing us this calculation [Reference LandesmanLan19].
4. Essential dimension of congruence covers
4.1 Forms of reductive groups
In this subsection we prove a variant of a result of Harder and Borel showing that, under some mild conditions, for a reductive group over a number field one can always find a form with given specializations at finitely many places.
4.1.1 Let ![]() $F$ be a number field and
$F$ be a number field and ![]() $G = G^{{\rm ad}}$ an adjoint, connected reductive group over
$G = G^{{\rm ad}}$ an adjoint, connected reductive group over ![]() $F$. We fix algebraic closures
$F$. We fix algebraic closures ![]() $\bar F$ and
$\bar F$ and ![]() $\bar F_v$ of
$\bar F_v$ of ![]() $F$ and
$F$ and ![]() $F_v$ respectively, for every finite place
$F_v$ respectively, for every finite place ![]() $v$ of
$v$ of ![]() $F,$ as well as embeddings
$F,$ as well as embeddings ![]() $\bar F \hookrightarrow \bar F_v$.
$\bar F \hookrightarrow \bar F_v$.
Recall [Reference Demazure and GrothendieckSGA3, XXIV, Theorem 1.3] that the automorphism group scheme of ![]() $G$ is an extension
$G$ is an extension
where ![]() ${\rm Out}(G)$ is a finite group scheme. If
${\rm Out}(G)$ is a finite group scheme. If ![]() $G$ is split, then this extension is split and
$G$ is split, then this extension is split and ![]() ${\rm Out}(G)$ is a constant group scheme which can be identified with the group of automorphisms of the Dynkin diagram of
${\rm Out}(G)$ is a constant group scheme which can be identified with the group of automorphisms of the Dynkin diagram of ![]() $G$.
$G$.
We will also make use of the notion of the fundamental group ![]() $\pi _1(G)$ [Reference BorovoiBor96]. This is a finite abelian group equipped with a
$\pi _1(G)$ [Reference BorovoiBor96]. This is a finite abelian group equipped with a ![]() ${\rm Gal}(\bar F/F)$-action. As an étale sheaf on
${\rm Gal}(\bar F/F)$-action. As an étale sheaf on ![]() ${\operatorname {Spec\,}} F,$ one has
${\operatorname {Spec\,}} F,$ one has ![]() $\pi _1(G)\otimes \mu _n \overset \sim \longrightarrow {\rm ker}(G^{{\rm sc}}\rightarrow G)$ where
$\pi _1(G)\otimes \mu _n \overset \sim \longrightarrow {\rm ker}(G^{{\rm sc}}\rightarrow G)$ where ![]() $G^{{\rm sc}}$ is the simply connected cover of
$G^{{\rm sc}}$ is the simply connected cover of ![]() $G,$ and
$G,$ and ![]() $n$ is the order
$n$ is the order ![]() ${\rm ker}(G^{{\rm sc}} \rightarrow G)$. The following proposition is a variant of [Reference Harder and BorelHB78, Theorem B].
${\rm ker}(G^{{\rm sc}} \rightarrow G)$. The following proposition is a variant of [Reference Harder and BorelHB78, Theorem B].
Proposition 4.1.3 Let ![]() $G$ be a split, adjoint connected reductive group over
$G$ be a split, adjoint connected reductive group over ![]() $F,$ and
$F,$ and ![]() $S$ a finite set of places of
$S$ a finite set of places of ![]() $F$. Let
$F$. Let ![]() ${\rm Out}(G)' \subset {\rm Out}(G)$ be a subgroup and
${\rm Out}(G)' \subset {\rm Out}(G)$ be a subgroup and ![]() ${\rm Aut}'(G) \subset {\rm Aut}(G)$ the preimage of
${\rm Aut}'(G) \subset {\rm Aut}(G)$ the preimage of ![]() ${\rm Out}(G)'$. If the map of pointed sets
${\rm Out}(G)'$. If the map of pointed sets
is surjective, then the natural map of pointed sets
is surjective.
Proof. Recall the following facts about the cohomology of reductive groups over global and local fields [Reference KottwitzKot86]: Let ![]() $H$ be an adjoint connected reductive group over
$H$ be an adjoint connected reductive group over ![]() $F$. For any place
$F$. For any place ![]() $v$ of
$v$ of ![]() $F$, there is a map
$F$, there is a map
which is an isomorphism if ![]() $v$ is finite. For any finite set of places
$v$ is finite. For any finite set of places ![]() $T$ of
$T$ of ![]() $F,$ consider the composite map
$F,$ consider the composite map
Then by [Reference KottwitzKot86, § 2.2], ![]() $(x_v)_{v\in T} \in \prod _{v \in T} H^1(F_v, H)$ is in the image of
$(x_v)_{v\in T} \in \prod _{v \in T} H^1(F_v, H)$ is in the image of ![]() $H^1(F,H)$ if
$H^1(F,H)$ if ![]() $\xi ((x_v)) = 0$. Applying this to
$\xi ((x_v)) = 0$. Applying this to ![]() $T = S \cup \{v_0\}$ for some finite place
$T = S \cup \{v_0\}$ for some finite place ![]() $v_0 \notin S,$ we see that
$v_0 \notin S,$ we see that
is surjective.
Now let ![]() $(x_v) \in \prod _{v \in S} H^1(F_v, {\rm Aut}(G)')$ and let
$(x_v) \in \prod _{v \in S} H^1(F_v, {\rm Aut}(G)')$ and let ![]() $(\bar x_v) \in \prod _{v \in S} H^1(F_v, {\rm Out}(G)')$ be the image of
$(\bar x_v) \in \prod _{v \in S} H^1(F_v, {\rm Out}(G)')$ be the image of ![]() $(x_v)$. By our assumptions on
$(x_v)$. By our assumptions on ![]() ${\rm Out}(G)',$ there exists
${\rm Out}(G)',$ there exists ![]() $\bar x \in H^1(F, {\rm Out}(G)')$ mapping to
$\bar x \in H^1(F, {\rm Out}(G)')$ mapping to ![]() $(\bar x_v)$. Since we are assuming
$(\bar x_v)$. Since we are assuming ![]() $G$ is split, (4.1.2) is a split extension, so there is a
$G$ is split, (4.1.2) is a split extension, so there is a ![]() $x \in H^1(F,{\rm Aut}(G)')$ mapping to
$x \in H^1(F,{\rm Aut}(G)')$ mapping to ![]() $\bar x$. Let
$\bar x$. Let ![]() $H$ be the twist of
$H$ be the twist of ![]() $G$ by
$G$ by ![]() $x$. Recall that this means that if we choose a cocycle
$x$. Recall that this means that if we choose a cocycle ![]() $x = (x_\sigma )_{\sigma \in {\rm Gal}(\bar F/F)}$ representing
$x = (x_\sigma )_{\sigma \in {\rm Gal}(\bar F/F)}$ representing ![]() $x,$ then there is an isomorphism
$x,$ then there is an isomorphism ![]() $\tau : G \overset \sim \longrightarrow H$ over
$\tau : G \overset \sim \longrightarrow H$ over ![]() $\bar F,$ such that, for
$\bar F,$ such that, for ![]() $g \in G(\bar F)$ and
$g \in G(\bar F)$ and ![]() $\sigma \in {\rm Gal}(\bar F/F),$ we have
$\sigma \in {\rm Gal}(\bar F/F),$ we have ![]() $\tau (\sigma (g)) = (\sigma (\tau (g)))^{x_{\sigma }}$. We have a commutative diagram
$\tau (\sigma (g)) = (\sigma (\tau (g)))^{x_{\sigma }}$. We have a commutative diagram

such that the vertical maps send ![]() $x$ and
$x$ and ![]() $(x|_{F_v})_v$ to the trivial classes in the bottom line. Thus it suffices to show that
$(x|_{F_v})_v$ to the trivial classes in the bottom line. Thus it suffices to show that
is surjective, which we saw above.
Corollary 4.1.5. Let ![]() $G,$
$G,$ ![]() $S,$
$S,$ ![]() ${\rm Out}(G)'$ and
${\rm Out}(G)'$ and ![]() ${\rm Aut}(G)'$ be as in Proposition 4.1.3. Suppose that
${\rm Aut}(G)'$ be as in Proposition 4.1.3. Suppose that ![]() ${\rm Out}(G)'$ is an abelian group, and let
${\rm Out}(G)'$ is an abelian group, and let ![]() $2^s$ be the largest power of
$2^s$ be the largest power of ![]() $2$ such that
$2$ such that ![]() ${\rm Out}(G)'$ has an element of order
${\rm Out}(G)'$ has an element of order ![]() $2^s$. If
$2^s$. If ![]() $v \in S$ with
$v \in S$ with ![]() $v|2$ we assume that
$v|2$ we assume that ![]() $F_v(\zeta _{2^s})/F_v$ is cyclic, where
$F_v(\zeta _{2^s})/F_v$ is cyclic, where ![]() $\zeta _{2^s}$ is a primitive
$\zeta _{2^s}$ is a primitive ![]() $2^s$ root of
$2^s$ root of ![]() $1$.
$1$.
Then
is surjective.
Proof. By Proposition 4.1.3, it suffices to show that
is surjective. The elements of ![]() $H^1(F,{\rm Out}(G))$ are in bijection with conjugacy classes of maps
$H^1(F,{\rm Out}(G))$ are in bijection with conjugacy classes of maps ![]() ${\rm Gal}(\bar F/F) \rightarrow {\rm Out}(G),$ and similarly for the local classes, so this follows from [Reference SaltmanSal82, Theorem 5.10]. Note the condition there, that
${\rm Gal}(\bar F/F) \rightarrow {\rm Out}(G),$ and similarly for the local classes, so this follows from [Reference SaltmanSal82, Theorem 5.10]. Note the condition there, that ![]() $F_v(\zeta _{2^s})/F_v$ is cyclic is automatic unless
$F_v(\zeta _{2^s})/F_v$ is cyclic is automatic unless ![]() $v|2,$ as otherwise this is an unramified extension.
$v|2,$ as otherwise this is an unramified extension.
4.2 Shimura varieties
In this subsection we apply the results of § 3 to compute the essential dimension for congruence covers of Shimura varieties. This will be applied in the next subsection to give examples of congruence covers of locally symmetric varieties where our techniques give a lower bound on the essential dimension. Since our aim is to give lower bounds on essential dimension, it may seem odd that we work with the formalism of Shimura varieties rather than the locally symmetric varieties which are their geometrically connected components. However, many of the results we need are in the literature only in the former language, and it would take more effort to make the (routine) translation.
4.2.1 Recall [Reference DeligneDel79, § 1.2] that a Shimura datum is a pair ![]() $(G,X)$ consisting of a connected reductive group
$(G,X)$ consisting of a connected reductive group ![]() $G$ over
$G$ over ![]() ${\mathbb {Q}},$ and a
${\mathbb {Q}},$ and a ![]() $G({\mathbb {R}})$ conjugacy class of maps of algebraic groups over
$G({\mathbb {R}})$ conjugacy class of maps of algebraic groups over ![]() ${\mathbb {R}}$:
${\mathbb {R}}$:
This datum is required to satisfy certain properties which imply that the commutant of ![]() $h(\mathbb {S}({\mathbb {R}}))$ is a subgroup
$h(\mathbb {S}({\mathbb {R}}))$ is a subgroup ![]() $K_{\infty } \subset G({\mathbb {R}})$ whose image in
$K_{\infty } \subset G({\mathbb {R}})$ whose image in ![]() $G^{{\rm ad}}({\mathbb {R}})$ is maximal compact and
$G^{{\rm ad}}({\mathbb {R}})$ is maximal compact and ![]() $X = G({\mathbb {R}})/K_\infty$ is a union of finitely many Hermitian symmetric domains.
$X = G({\mathbb {R}})/K_\infty$ is a union of finitely many Hermitian symmetric domains.
Let ![]() $\mathbb {A}$ denote the adeles over
$\mathbb {A}$ denote the adeles over ![]() ${\mathbb {Q}}$ and
${\mathbb {Q}}$ and ![]() $\mathbb {A}_f$ the finite adeles. Let
$\mathbb {A}_f$ the finite adeles. Let ![]() $K \subset G(\mathbb {A}_f)$ be a compact open subgroup. Recall that
$K \subset G(\mathbb {A}_f)$ be a compact open subgroup. Recall that ![]() $K$ is called neat if
$K$ is called neat if ![]() $G({\mathbb {Q}}) \cap gKg^{-1}$ contains no torsion elements for all
$G({\mathbb {Q}}) \cap gKg^{-1}$ contains no torsion elements for all ![]() $g \in G(\mathbb {A}_f),$ and that sufficiently small compact open subgroups are neat. The conditions on
$g \in G(\mathbb {A}_f),$ and that sufficiently small compact open subgroups are neat. The conditions on ![]() $(G,X)$ imply that if
$(G,X)$ imply that if ![]() $K$ is neat, the quotient
$K$ is neat, the quotient
has a natural structure of (the complex points of) an algebraic variety over a number field ![]() $E = E(G,X) \subset {\mathbb {C}},$ called the reflex field of
$E = E(G,X) \subset {\mathbb {C}},$ called the reflex field of ![]() $(G,X),$ which does not depend on
$(G,X),$ which does not depend on ![]() $K$. We denote this algebraic variety by the same symbol,
$K$. We denote this algebraic variety by the same symbol, ![]() ${\rm Sh}_K(G,X),$ and we assume from now on that
${\rm Sh}_K(G,X),$ and we assume from now on that ![]() $K$ is neat.
$K$ is neat.
Now let ![]() $V_{{\mathbb {Z}}} = {\mathbb {Z}}^{2g}$ equipped with a perfect symplectic form
$V_{{\mathbb {Z}}} = {\mathbb {Z}}^{2g}$ equipped with a perfect symplectic form ![]() $\psi$. Set
$\psi$. Set ![]() $V = V_{{\mathbb {Z}}}\otimes _{{\mathbb {Z}}}{\mathbb {Q}}$ and
$V = V_{{\mathbb {Z}}}\otimes _{{\mathbb {Z}}}{\mathbb {Q}}$ and ![]() ${\rm GSp} = {\rm GSp}(V,\psi )$. As in [Reference DeligneDel79, 1.3.1], we denote by
${\rm GSp} = {\rm GSp}(V,\psi )$. As in [Reference DeligneDel79, 1.3.1], we denote by ![]() $S^{\pm }$ the conjugacy class of maps
$S^{\pm }$ the conjugacy class of maps ![]() $h: \mathbb {S} \rightarrow {\rm GSp}$ satisfying the following two properties
$h: \mathbb {S} \rightarrow {\rm GSp}$ satisfying the following two properties
(i) The action of the real Lie group
 $\mathbb {S}({\mathbb {R}}) = {\mathbb {C}}^\times$ on
$\mathbb {S}({\mathbb {R}}) = {\mathbb {C}}^\times$ on  $V_{{\mathbb {C}}}$ gives rise to a Hodge structure of type
$V_{{\mathbb {C}}}$ gives rise to a Hodge structure of type  $(-1,0)$
$(-1,0)$  $(0,-1):$
$(0,-1):$
 \[ V_{{\mathbb{C}}} \overset \sim \longrightarrow V^{{-}1,0} \oplus V^{0,-1}. \]
\[ V_{{\mathbb{C}}} \overset \sim \longrightarrow V^{{-}1,0} \oplus V^{0,-1}. \](ii) The pairing
 $(x,y) \mapsto \psi (x,h(i)y)$ on
$(x,y) \mapsto \psi (x,h(i)y)$ on  $V_{{\mathbb {R}}}$ is positive or negative definite.
$V_{{\mathbb {R}}}$ is positive or negative definite.
Then ![]() $({\rm GSp}, S^{\pm })$ is a Shimura datum called the Siegel datum, and
$({\rm GSp}, S^{\pm })$ is a Shimura datum called the Siegel datum, and ![]() ${\rm Sh}_K({\rm GSp}, S^{\pm })$ has an interpretation as the moduli space of principally polarized abelian varieties with suitable level structure.
${\rm Sh}_K({\rm GSp}, S^{\pm })$ has an interpretation as the moduli space of principally polarized abelian varieties with suitable level structure.
We say that ![]() $(G,X)$ is of Hodge type if there is a map of reductive groups over
$(G,X)$ is of Hodge type if there is a map of reductive groups over ![]() ${\mathbb {Q}},$
${\mathbb {Q}},$ ![]() $\iota : G \hookrightarrow {\rm GSp},$ which induces
$\iota : G \hookrightarrow {\rm GSp},$ which induces ![]() $X \rightarrow S^{\pm }$. By [Reference DeligneDel71, Prop. 1.15], there exists a neat compact open
$X \rightarrow S^{\pm }$. By [Reference DeligneDel71, Prop. 1.15], there exists a neat compact open ![]() $K' \subset {\rm GSp}(\mathbb {A}_f)$ such that
$K' \subset {\rm GSp}(\mathbb {A}_f)$ such that ![]() $K = K' \cap G(\mathbb {A}_f),$ and
$K = K' \cap G(\mathbb {A}_f),$ and ![]() $\iota$ induces a closed embedding of Shimura varieties
$\iota$ induces a closed embedding of Shimura varieties
Our conditions on ![]() $K$ and
$K$ and ![]() $K'$ imply that the right hand side carries a universal abelian scheme.
$K'$ imply that the right hand side carries a universal abelian scheme.
4.2.2 Now fix a prime ![]() $p,$ and suppose that
$p,$ and suppose that ![]() $G$ is the generic fiber of a reductive group
$G$ is the generic fiber of a reductive group ![]() $G_{{\mathbb {Z}}_{(p)}}$ over
$G_{{\mathbb {Z}}_{(p)}}$ over ![]() ${\mathbb {Z}}_{(p)}$. If no confusion is likely to result we will sometimes write simply
${\mathbb {Z}}_{(p)}$. If no confusion is likely to result we will sometimes write simply ![]() $G$ for
$G$ for ![]() $G_{{\mathbb {Z}}_{(p)}}$. We take
$G_{{\mathbb {Z}}_{(p)}}$. We take ![]() $K$ (still assumed neat) to be of the form
$K$ (still assumed neat) to be of the form ![]() $K_pK^p$ where
$K_pK^p$ where ![]() $K_p = G({\mathbb {Z}}_p)$ and
$K_p = G({\mathbb {Z}}_p)$ and ![]() $K^p \subset G(\mathbb {A}_f^p),$ where
$K^p \subset G(\mathbb {A}_f^p),$ where ![]() $\mathbb {A}_f^p$ denotes the finite adeles with trivial
$\mathbb {A}_f^p$ denotes the finite adeles with trivial ![]() $p$-component.
$p$-component.
Under these conditions, ![]() $p$ is unramified in
$p$ is unramified in ![]() $E,$ and for any prime
$E,$ and for any prime ![]() $\lambda |p$ of
$\lambda |p$ of ![]() $E,$
$E,$ ![]() ${\rm Sh}_K(G,X)$ has a canonical smooth model over
${\rm Sh}_K(G,X)$ has a canonical smooth model over ![]() $\mathcal {O}_{E_{\lambda }}$ [Reference KisinKis10, Theorem 2.3.8], [Reference Kim and PeraKMP16, Theorem 1], which we will denote by
$\mathcal {O}_{E_{\lambda }}$ [Reference KisinKis10, Theorem 2.3.8], [Reference Kim and PeraKMP16, Theorem 1], which we will denote by ![]() ${\mathscr S}_K(G,X)$. In particular, we may apply this to
${\mathscr S}_K(G,X)$. In particular, we may apply this to ![]() ${\rm Sh}_{K'}({\rm GSp}, S^{\pm })$ if we take
${\rm Sh}_{K'}({\rm GSp}, S^{\pm })$ if we take ![]() $K' = K'_pK^{\prime p}$ with
$K' = K'_pK^{\prime p}$ with ![]() $K'_p = {\rm GSp}(V_{{\mathbb {Z}}},\psi )({\mathbb {Z}}_p)$.
$K'_p = {\rm GSp}(V_{{\mathbb {Z}}},\psi )({\mathbb {Z}}_p)$.
Given ![]() $G_{{\mathbb {Z}}_{(p)}}$ and
$G_{{\mathbb {Z}}_{(p)}}$ and ![]() $(G,X)$ of Hodge type, we may always choose
$(G,X)$ of Hodge type, we may always choose ![]() $(V,\psi ),$
$(V,\psi ),$ ![]() $\iota$ and
$\iota$ and ![]() $K'$ with
$K'$ with ![]() $K'_p = {\rm GSp}(V_{{\mathbb {Z}}},\psi )({\mathbb {Z}}_p),$ such that
$K'_p = {\rm GSp}(V_{{\mathbb {Z}}},\psi )({\mathbb {Z}}_p),$ such that ![]() $K = K' \cap G(\mathbb {A}_f),$
$K = K' \cap G(\mathbb {A}_f),$ ![]() $\iota$ induces a map of smooth
$\iota$ induces a map of smooth ![]() $\mathcal {O}_{E_{\lambda }}$-schemes
$\mathcal {O}_{E_{\lambda }}$-schemes
and for any closed point ![]() $x \in {\mathscr S}_K(G,X)$, the complete local ring at
$x \in {\mathscr S}_K(G,X)$, the complete local ring at ![]() $x$ is a quotient of the complete local ring at
$x$ is a quotient of the complete local ring at ![]() $\iota (x)$ - see [Reference KisinKis10, Lem. 2.1.2, Prop. 2.3.5] when
$\iota (x)$ - see [Reference KisinKis10, Lem. 2.1.2, Prop. 2.3.5] when ![]() $p > 2,$ and [Reference Kim and PeraKMP16, Prop. 3.6] and its proof for the case
$p > 2,$ and [Reference Kim and PeraKMP16, Prop. 3.6] and its proof for the case ![]() $p=2$.
$p=2$.
As in § 3, we denote by ![]() ${\mathcal {A}}$ the universal abelian scheme over
${\mathcal {A}}$ the universal abelian scheme over ![]() ${\mathscr S}_{K'}({\rm GSp},S^{\pm })$. Then we have
${\mathscr S}_{K'}({\rm GSp},S^{\pm })$. Then we have
Lemma 4.2.3 Let ![]() $K_1 = K^pK_{1,p}$ where
$K_1 = K^pK_{1,p}$ where ![]() $K_{1,p} = {\rm ker}(G({\mathbb {Z}}_p) \rightarrow G({\mathbb {F}}_p)) \subset K_p$. Over any finite extension
$K_{1,p} = {\rm ker}(G({\mathbb {Z}}_p) \rightarrow G({\mathbb {F}}_p)) \subset K_p$. Over any finite extension ![]() $E'/E,$ the congruence cover
$E'/E,$ the congruence cover
is a union of copies of Galois closures of the étale local system ![]() ${\mathcal {A}}[p]|_{{\rm Sh}_K(G,X)}$ on
${\mathcal {A}}[p]|_{{\rm Sh}_K(G,X)}$ on ![]() ${\rm Sh}_K(G,X)$.
${\rm Sh}_K(G,X)$.
If ![]() $E,$ admits a prime
$E,$ admits a prime ![]() $\lambda |p$ with residue field
$\lambda |p$ with residue field ![]() ${\mathbb {F}}_p$ then
${\mathbb {F}}_p$ then
Proof. Write ![]() ${\rm Sh}_K = {\rm Sh}_K(G,X)$ and
${\rm Sh}_K = {\rm Sh}_K(G,X)$ and ![]() ${\rm Sh}_{K_1} = {\rm Sh}_{K_1}(G,X)$. Our assumptions imply that
${\rm Sh}_{K_1} = {\rm Sh}_{K_1}(G,X)$. Our assumptions imply that ![]() $K/K_1$ acts freely on
$K/K_1$ acts freely on ![]() ${\rm Sh}_{K_1},$ so that
${\rm Sh}_{K_1},$ so that ![]() ${\rm Sh}_{K_1} \rightarrow {\rm Sh}_K$ is a
${\rm Sh}_{K_1} \rightarrow {\rm Sh}_K$ is a ![]() $K/K_1 = G({\mathbb {F}}_p)$-torsor. As
$K/K_1 = G({\mathbb {F}}_p)$-torsor. As ![]() $G({\mathbb {F}}_p)$ acts faithfully on the fibers of
$G({\mathbb {F}}_p)$ acts faithfully on the fibers of ![]() ${\mathcal {A}}[p]|_{{\rm Sh}_K},$ this implies the first claim. By Lemma 2.2.4 applied to the geometrically connected components of
${\mathcal {A}}[p]|_{{\rm Sh}_K},$ this implies the first claim. By Lemma 2.2.4 applied to the geometrically connected components of ![]() ${\rm Sh}_K,$ we then have
${\rm Sh}_K,$ we then have
Now suppose that ![]() $E$ admits a prime
$E$ admits a prime ![]() $\lambda |p$ with residue field
$\lambda |p$ with residue field ![]() ${\mathbb {F}}_p,$ and consider the map of integral models
${\mathbb {F}}_p,$ and consider the map of integral models ![]() $\iota ,$ corresponding to
$\iota ,$ corresponding to ![]() $\lambda$. Since
$\lambda$. Since ![]() $\lambda$ has residue field
$\lambda$ has residue field ![]() $\mathbb {F}_p,$ every component of the image of
$\mathbb {F}_p,$ every component of the image of ![]() $\iota$ meets the ordinary locus of
$\iota$ meets the ordinary locus of ![]() ${\mathscr S}_{K'}({\rm GSp},S^{\pm })$ by [Reference WortmannWor, Theorem 1.1]. Now using that for some
${\mathscr S}_{K'}({\rm GSp},S^{\pm })$ by [Reference WortmannWor, Theorem 1.1]. Now using that for some ![]() $N$ with
$N$ with ![]() $(N,p) = 1,$ there is a surjective map
$(N,p) = 1,$ there is a surjective map ![]() ${\mathcal {A}}_{g,N} \rightarrow {\rm Sh}_{K'}({\rm GSp},S^{\pm }),$ and Theorem 3.2.6, we conclude
${\mathcal {A}}_{g,N} \rightarrow {\rm Sh}_{K'}({\rm GSp},S^{\pm }),$ and Theorem 3.2.6, we conclude
4.3 Congruence covers
It will be more convenient to state the results of this subsection in terms of locally symmetric varieties. These are geometrically connected components of the Shimura varieties discussed in the previous subsection.
4.3.1 For any reductive group ![]() $G$ over
$G$ over ![]() ${\mathbb {Q}}$, a congruence subgroup
${\mathbb {Q}}$, a congruence subgroup ![]() $\Gamma \subset G({\mathbb {Q}})$ is a group of the form
$\Gamma \subset G({\mathbb {Q}})$ is a group of the form ![]() $G({\mathbb {Q}}) \cap K$ for some compact open subgroup
$G({\mathbb {Q}}) \cap K$ for some compact open subgroup ![]() $K \subset G(\mathbb {A}_f)$. An arithmetic lattice
$K \subset G(\mathbb {A}_f)$. An arithmetic lattice ![]() $\Gamma \subset G({\mathbb {Q}})$ is a finite index subgroup of a congruence subgroup. If
$\Gamma \subset G({\mathbb {Q}})$ is a finite index subgroup of a congruence subgroup. If ![]() $i:G' \rightarrow G$ is a surjective map of reductive groups whose kernel is in the center of
$i:G' \rightarrow G$ is a surjective map of reductive groups whose kernel is in the center of ![]() $G',$ and
$G',$ and ![]() $\Gamma ' \subset G'({\mathbb {Q}})$ is an arithmetic lattice, then
$\Gamma ' \subset G'({\mathbb {Q}})$ is an arithmetic lattice, then ![]() $i(\Gamma ') \subset G({\mathbb {Q}})$ is an arithmetic lattice.
$i(\Gamma ') \subset G({\mathbb {Q}})$ is an arithmetic lattice.
Now suppose that ![]() $X = G({\mathbb {R}})/K_{\infty }$ is a union of Hermitian symmetric domains and let
$X = G({\mathbb {R}})/K_{\infty }$ is a union of Hermitian symmetric domains and let ![]() $X^+ \subset X$ be the connected component of the identity. If
$X^+ \subset X$ be the connected component of the identity. If ![]() $\Gamma \subset G^{{\rm ad}}({\mathbb {Q}})$ is an arithmetic lattice that acts freely on
$\Gamma \subset G^{{\rm ad}}({\mathbb {Q}})$ is an arithmetic lattice that acts freely on ![]() $X^+$ (so in particular leaves
$X^+$ (so in particular leaves ![]() $X^+$ stable), then
$X^+$ stable), then ![]() $\Gamma \backslash X^+$ has a natural structure of algebraic variety over
$\Gamma \backslash X^+$ has a natural structure of algebraic variety over ![]() $\bar {\mathbb {Q}}$ [Reference DeligneDel79, § 2]. For any arithmetic lattice
$\bar {\mathbb {Q}}$ [Reference DeligneDel79, § 2]. For any arithmetic lattice ![]() $\Gamma \subset G^{{\rm ad}}({\mathbb {Q}})$ there is a finite index subgroup which acts freely on
$\Gamma \subset G^{{\rm ad}}({\mathbb {Q}})$ there is a finite index subgroup which acts freely on ![]() $X^+$.
$X^+$.
If ![]() $(G,X)$ is a Shimura datum, then the geometrically connected components of
$(G,X)$ is a Shimura datum, then the geometrically connected components of ![]() ${\rm Sh}_K(G,X)$ have the form
${\rm Sh}_K(G,X)$ have the form ![]() $\Gamma \backslash X^+,$ where
$\Gamma \backslash X^+,$ where ![]() $X^+ \subset X$ is a connected component and
$X^+ \subset X$ is a connected component and ![]() $\Gamma \subset G^{{\rm ad}}({\mathbb {Q}})$ is the image of a congruence subgroup of
$\Gamma \subset G^{{\rm ad}}({\mathbb {Q}})$ is the image of a congruence subgroup of ![]() $G^{{\rm der}}({\mathbb {Q}})$ [Reference DeligneDel79, 2.1.2].
$G^{{\rm der}}({\mathbb {Q}})$ [Reference DeligneDel79, 2.1.2].
4.3.2 Now let ![]() $G$ be a semisimple, almost simple group over
$G$ be a semisimple, almost simple group over ![]() ${\mathbb {Q}}$. We will assume that
${\mathbb {Q}}$. We will assume that ![]() $G$ is of classical type, so that (the connected components of) its Dynkin diagram are of type
$G$ is of classical type, so that (the connected components of) its Dynkin diagram are of type ![]() $A,B,C$ or
$A,B,C$ or ![]() $D$.
$D$.
Let ![]() $K_\infty \subset G({\mathbb {R}})$ be a maximal compact subgroup, and denote by
$K_\infty \subset G({\mathbb {R}})$ be a maximal compact subgroup, and denote by ![]() $G({\mathbb {R}})^+ \subset G({\mathbb {R}})$ the connected component of the identity. We will assume that
$G({\mathbb {R}})^+ \subset G({\mathbb {R}})$ the connected component of the identity. We will assume that ![]() $X^+ = G({\mathbb {R}})^+/K_\infty$ is a Hermitian symmetric domain. The group
$X^+ = G({\mathbb {R}})^+/K_\infty$ is a Hermitian symmetric domain. The group ![]() $G^{{\rm ad}}({\mathbb {R}})$ is a product of simple groups
$G^{{\rm ad}}({\mathbb {R}})$ is a product of simple groups ![]() $G_i({\mathbb {R}}),$ for
$G_i({\mathbb {R}}),$ for ![]() $i$ in some index set
$i$ in some index set ![]() $I$. We denote by
$I$. We denote by ![]() $I_{{\rm nc}}$ (respectively,
$I_{{\rm nc}}$ (respectively, ![]() $I_{{\rm c}}$) the set of
$I_{{\rm c}}$) the set of ![]() $i$ with
$i$ with ![]() $G_i$ noncompact (respectively, compact). Then
$G_i$ noncompact (respectively, compact). Then ![]() $X^+$ is a product of the irreducible Hermitian symmetric domains
$X^+$ is a product of the irreducible Hermitian symmetric domains ![]() $X^+_i = G_i({\mathbb {R}})^+/K_i,$ for
$X^+_i = G_i({\mathbb {R}})^+/K_i,$ for ![]() $i \in I_{{\rm nc}},$ where
$i \in I_{{\rm nc}},$ where ![]() $K_i \subset G_i({\mathbb {R}})$ is maximal compact. We use Deligne's notation [Reference DeligneDel79] for the classification of these irreducible Hermitian symmetric domains. Since we are assuming
$K_i \subset G_i({\mathbb {R}})$ is maximal compact. We use Deligne's notation [Reference DeligneDel79] for the classification of these irreducible Hermitian symmetric domains. Since we are assuming ![]() $G$ is of classical type, for
$G$ is of classical type, for ![]() $i \in I_{{\rm nc}},$
$i \in I_{{\rm nc}},$ ![]() $X_i^+$ is of type
$X_i^+$ is of type ![]() $A, B, C$,
$A, B, C$, ![]() $D^{{\mathbb {R}}}$ or
$D^{{\mathbb {R}}}$ or ![]() $D^{\mathbb {H}}$. The group
$D^{\mathbb {H}}$. The group ![]() $G_i({\mathbb {R}})$ is either the adjoint group of
$G_i({\mathbb {R}})$ is either the adjoint group of ![]() $U(p,q)$ in the case of type
$U(p,q)$ in the case of type ![]() $A$, of
$A$, of ![]() ${\rm Sp}(2n)$ in the case of type
${\rm Sp}(2n)$ in the case of type ![]() $C$, of
$C$, of ![]() ${\rm SO}(n,2)$ in the case of type
${\rm SO}(n,2)$ in the case of type ![]() $B$ or
$B$ or ![]() $D^{{\mathbb {R}}},$ and of
$D^{{\mathbb {R}}},$ and of ![]() ${\rm SO}^*(2n),$ an inner form of
${\rm SO}^*(2n),$ an inner form of ![]() ${\rm SO}(2n)$, if
${\rm SO}(2n)$, if ![]() $G_i$ is of type
$G_i$ is of type ![]() $D^{\mathbb {H}}$.
$D^{\mathbb {H}}$.
Since ![]() $G$ is almost simple, for
$G$ is almost simple, for ![]() $i \in I_{{\rm nc}}$ the
$i \in I_{{\rm nc}}$ the ![]() $X^+_i$ are all of the same type, except possibly if
$X^+_i$ are all of the same type, except possibly if ![]() $G$ is of type
$G$ is of type ![]() $D,$ in which case it is possible that both factors of type
$D,$ in which case it is possible that both factors of type ![]() $D^{{\mathbb {R}}}$ and
$D^{{\mathbb {R}}}$ and ![]() $D^{\mathbb {H}}$ occur among the
$D^{\mathbb {H}}$ occur among the ![]() $X^+_i$. We will say that
$X^+_i$. We will say that ![]() $G$ is of Hodge type if all the factors
$G$ is of Hodge type if all the factors ![]() $X^+_i$ are of the same type
$X^+_i$ are of the same type ![]() $A,B,C,D^{{\mathbb {R}}}, D^{\mathbb {H}}$ and the following condition holds:
$A,B,C,D^{{\mathbb {R}}}, D^{\mathbb {H}}$ and the following condition holds: ![]() $G$ is simply connected unless the
$G$ is simply connected unless the ![]() $X^+_i$ are of type
$X^+_i$ are of type ![]() $D^{\mathbb {H}},$ in which case
$D^{\mathbb {H}},$ in which case ![]() $G({\mathbb {C}})$ is a product of special orthogonal groups.
$G({\mathbb {C}})$ is a product of special orthogonal groups.
4.3.3 The Dynkin diagram ![]() $\Delta (G)$ is equipped with a set of vertices
$\Delta (G)$ is equipped with a set of vertices ![]() $\Sigma (G)$ which is described as follows (cf. [Reference DeligneDel79], § 1.2, 1.3). For
$\Sigma (G)$ which is described as follows (cf. [Reference DeligneDel79], § 1.2, 1.3). For ![]() $i \in I_{{\rm nc}},$
$i \in I_{{\rm nc}},$ ![]() $K_i \subset G_i$ is the centralizer of a rank
$K_i \subset G_i$ is the centralizer of a rank ![]() $1$ compact torus
$1$ compact torus ![]() $U(1) \subset G_i,$ which is the center of
$U(1) \subset G_i,$ which is the center of ![]() $K_i$. Thus there are two cocharacters
$K_i$. Thus there are two cocharacters ![]() $h,h^{-1}: U(1) \rightarrow G_i$ which identify
$h,h^{-1}: U(1) \rightarrow G_i$ which identify ![]() $U(1)$ with this compact torus. These cocharacters are minuscule, and each corresponds to a vertex of
$U(1)$ with this compact torus. These cocharacters are minuscule, and each corresponds to a vertex of ![]() $\Delta (G_i)$. The two vertices are distinct exactly when
$\Delta (G_i)$. The two vertices are distinct exactly when ![]() $h,h^{-1}$ are not conjugate cocharacters. In this case, they are exchanged by the opposition involution of
$h,h^{-1}$ are not conjugate cocharacters. In this case, they are exchanged by the opposition involution of ![]() $\Delta (G_i),$ which also gives the action of complex conjugation on
$\Delta (G_i),$ which also gives the action of complex conjugation on ![]() $\Delta (G_i)$. We set
$\Delta (G_i)$. We set ![]() $\Sigma (G)$ to be the union of all the vertices above. Thus
$\Sigma (G)$ to be the union of all the vertices above. Thus ![]() $\Sigma (G) \cap \Delta (G_i)$ is empty if
$\Sigma (G) \cap \Delta (G_i)$ is empty if ![]() $i \in I_{{\rm c}}$, and consists of one or two vertices if
$i \in I_{{\rm c}}$, and consists of one or two vertices if ![]() $i \in I_{{\rm nc}}$. In the latter case it consists of two vertices if and only if
$i \in I_{{\rm nc}}$. In the latter case it consists of two vertices if and only if ![]() $G_i({\mathbb {R}})$ is either the adjoint group of
$G_i({\mathbb {R}})$ is either the adjoint group of ![]() $U(p,q)$ with
$U(p,q)$ with ![]() $p \neq q,$ or of
$p \neq q,$ or of ![]() ${\rm SO}^*(2n)$ with
${\rm SO}^*(2n)$ with ![]() $n$ odd.
$n$ odd.
4.3.4 Fix an embedding ![]() $\bar {\mathbb {Q}} \hookrightarrow \mathbb {C}$. The Galois group
$\bar {\mathbb {Q}} \hookrightarrow \mathbb {C}$. The Galois group ![]() ${\rm Gal}(\bar {\mathbb {Q}}/{\mathbb {Q}})$ acts on
${\rm Gal}(\bar {\mathbb {Q}}/{\mathbb {Q}})$ acts on ![]() $\Delta (G)$. We consider a subset
$\Delta (G)$. We consider a subset ![]() $\Sigma \subset \Sigma (G)$ such that
$\Sigma \subset \Sigma (G)$ such that ![]() $\Delta (G_i) \cap \Sigma$ consists of one element for
$\Delta (G_i) \cap \Sigma$ consists of one element for ![]() $i \in I_{{\rm nc}}$.
$i \in I_{{\rm nc}}$.
We say that ![]() $G$ is unramified at
$G$ is unramified at ![]() $p$ if
$p$ if ![]() $G$ is quasi-split over
$G$ is quasi-split over ![]() ${\mathbb {Q}}_p$ and splits over an unramified extension of
${\mathbb {Q}}_p$ and splits over an unramified extension of ![]() ${\mathbb {Q}}_p$. We call
${\mathbb {Q}}_p$. We call ![]() $G$
$G$ ![]() $p$-admissible if
$p$-admissible if ![]() $G$ is unramified, and for some embedding
$G$ is unramified, and for some embedding ![]() $\bar {\mathbb {Q}} \hookrightarrow \bar {\mathbb {Q}}_p,$ and some choice of
$\bar {\mathbb {Q}} \hookrightarrow \bar {\mathbb {Q}}_p,$ and some choice of ![]() $\Sigma ,$ the action of
$\Sigma ,$ the action of ![]() ${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$ leaves
${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$ leaves ![]() $\Sigma$ invariant. This definition may look slightly odd; it will be used to guarantee that the reflex field of a Shimura variety built out of
$\Sigma$ invariant. This definition may look slightly odd; it will be used to guarantee that the reflex field of a Shimura variety built out of ![]() $G$ has at least one prime where the Shimura variety has a nonempty ordinary locus.
$G$ has at least one prime where the Shimura variety has a nonempty ordinary locus.
4.3.5 Now suppose that ![]() $G$ is unramified at
$G$ is unramified at ![]() $p$. Then
$p$. Then ![]() $G$ extends to a reductive group
$G$ extends to a reductive group ![]() $G_{{\mathbb {Z}}_p}$ over
$G_{{\mathbb {Z}}_p}$ over ![]() ${\mathbb {Z}}_p$. The isomorphism class of the algebraic group
${\mathbb {Z}}_p$. The isomorphism class of the algebraic group ![]() $G_{{\mathbb {Z}}_p}\otimes _{{\mathbb {Z}}_p}{\mathbb {F}}_p$ over
$G_{{\mathbb {Z}}_p}\otimes _{{\mathbb {Z}}_p}{\mathbb {F}}_p$ over ![]() ${\mathbb {F}}_p$ depends only on
${\mathbb {F}}_p$ depends only on ![]() $G$ and not on
$G$ and not on ![]() $G_{{\mathbb {Z}}_p},$ and we call this group the reduction of
$G_{{\mathbb {Z}}_p},$ and we call this group the reduction of ![]() $G$.
$G$.
Let ![]() $K = K^pK_p \subset G(\mathbb {A}_f)$ and
$K = K^pK_p \subset G(\mathbb {A}_f)$ and ![]() $K_1 = K^pK_{1,p} \subset G(\mathbb {A}_f)$ be compact open, with
$K_1 = K^pK_{1,p} \subset G(\mathbb {A}_f)$ be compact open, with ![]() $K^p\subset G(\mathbb {A}_f^p),$
$K^p\subset G(\mathbb {A}_f^p),$ ![]() $K_p = G_{{\mathbb {Z}}_p}({\mathbb {Z}}_p)$ and
$K_p = G_{{\mathbb {Z}}_p}({\mathbb {Z}}_p)$ and ![]() $K_{1,p} = {\rm ker}(G_{{\mathbb {Z}}_p}({\mathbb {Z}}_p) \rightarrow G_{{\mathbb {Z}}_p}({\mathbb {F}}_p))$. Let
$K_{1,p} = {\rm ker}(G_{{\mathbb {Z}}_p}({\mathbb {Z}}_p) \rightarrow G_{{\mathbb {Z}}_p}({\mathbb {F}}_p))$. Let ![]() $\Gamma = G({\mathbb {Q}}) \cap K$ and
$\Gamma = G({\mathbb {Q}}) \cap K$ and ![]() $\Gamma _1 = G({\mathbb {Q}}) \cap K_1$. We will assume that
$\Gamma _1 = G({\mathbb {Q}}) \cap K_1$. We will assume that ![]() $\Gamma \subset G({\mathbb {R}})^+,$ and that
$\Gamma \subset G({\mathbb {R}})^+,$ and that ![]() $\Gamma$ acts freely on
$\Gamma$ acts freely on ![]() $X^+$. By [Reference DeligneDel79, 2.0.7], these conditions are satisfied if
$X^+$. By [Reference DeligneDel79, 2.0.7], these conditions are satisfied if ![]() $K^p$ is sufficiently small. In particular, this allows us to view
$K^p$ is sufficiently small. In particular, this allows us to view ![]() $\Gamma$ as an arithmetic subgroup of
$\Gamma$ as an arithmetic subgroup of ![]() $G^{{\rm ad}}({\mathbb {Q}})$. We call a covering of the form
$G^{{\rm ad}}({\mathbb {Q}})$. We call a covering of the form ![]() $\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+,$ with
$\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+,$ with ![]() $\Gamma$ satisfying the above conditions, a principal
$\Gamma$ satisfying the above conditions, a principal ![]() $p$-level covering.
$p$-level covering.
Theorem 4.3.6. Let ![]() $G$ be an almost simple,
$G$ be an almost simple, ![]() $p$-admissible group of Hodge type, and let
$p$-admissible group of Hodge type, and let ![]() $X^+ = G({\mathbb {R}})^+/K_{\infty }$. Then for any principal
$X^+ = G({\mathbb {R}})^+/K_{\infty }$. Then for any principal ![]() $p$-level covering
$p$-level covering ![]() $\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$, we have
$\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$, we have
Proof. Let ![]() $\Sigma \subset \Sigma (G)$ be a subset of the form described above. This corresponds to a
$\Sigma \subset \Sigma (G)$ be a subset of the form described above. This corresponds to a ![]() $G^{{\rm ad}}({\mathbb {R}})$-conjugacy class of cocharacters
$G^{{\rm ad}}({\mathbb {R}})$-conjugacy class of cocharacters ![]() $h: U(1) \rightarrow G^{{\rm ad}},$ which we denote by
$h: U(1) \rightarrow G^{{\rm ad}},$ which we denote by ![]() $X^{{\rm ad}}$. Then
$X^{{\rm ad}}$. Then ![]() $(G^{{\rm ad}}, X^{{\rm ad}})$ is a Shimura datum and its reflex field corresponds to the subgroup of
$(G^{{\rm ad}}, X^{{\rm ad}})$ is a Shimura datum and its reflex field corresponds to the subgroup of ![]() ${\rm Gal}(\bar {\mathbb {Q}}/{\mathbb {Q}})$ which takes
${\rm Gal}(\bar {\mathbb {Q}}/{\mathbb {Q}})$ which takes ![]() $\Sigma$ to itself [Reference DeligneDel79, Prop. 2.3.6]. Since
$\Sigma$ to itself [Reference DeligneDel79, Prop. 2.3.6]. Since ![]() $G$ is
$G$ is ![]() $p$-admissible, there is a choice of
$p$-admissible, there is a choice of ![]() $\Sigma ,$ and a prime
$\Sigma ,$ and a prime ![]() $\lambda '|p$ of
$\lambda '|p$ of ![]() $E(G^{{\rm ad}},X^{{\rm ad}})$ with
$E(G^{{\rm ad}},X^{{\rm ad}})$ with ![]() $\kappa (\lambda ') = {\mathbb {F}}_p$.
$\kappa (\lambda ') = {\mathbb {F}}_p$.
Then one sees using [Reference DeligneDel79, Prop. 2.3.10] that one can choose a Shimura datum of Hodge type ![]() $(G',X)$ with
$(G',X)$ with ![]() $G^{\prime {\rm der}} = G$ and adjoint Shimura datum
$G^{\prime {\rm der}} = G$ and adjoint Shimura datum ![]() $(G^{{\rm ad}}, X^{{\rm ad}}),$ and so that all primes of
$(G^{{\rm ad}}, X^{{\rm ad}}),$ and so that all primes of ![]() $E(G^{{\rm ad}},X^{{\rm ad}})$ above
$E(G^{{\rm ad}},X^{{\rm ad}})$ above ![]() $p$ split completely in
$p$ split completely in ![]() $E(G',X)$. In particular, any prime
$E(G',X)$. In particular, any prime ![]() $\lambda |\lambda '$ of
$\lambda |\lambda '$ of ![]() $E(G',X)$ has residue field
$E(G',X)$ has residue field ![]() ${\mathbb {F}}_p$. We have verified that
${\mathbb {F}}_p$. We have verified that ![]() $(G',X)$ satisfies the hypotheses of Lemma 4.2.3.
$(G',X)$ satisfies the hypotheses of Lemma 4.2.3.
Now let ![]() $G'_{{\mathbb {Z}}_p}$ be a reductive group over
$G'_{{\mathbb {Z}}_p}$ be a reductive group over ![]() ${\mathbb {Z}}_p,$ extending
${\mathbb {Z}}_p,$ extending ![]() $G',$ and containing
$G',$ and containing ![]() $G_{{\mathbb {Z}}_p}$. The existence of
$G_{{\mathbb {Z}}_p}$. The existence of ![]() $G'_{{\mathbb {Z}}_p}$ may be seen, for example, using the classification of split reductive groups in terms of root data [Reference Demazure and GrothendieckSGA3, Exp XXV, Theorem 1], and the fact that the inner forms of a reductive group and its derived group are in bijection. Set
$G'_{{\mathbb {Z}}_p}$ may be seen, for example, using the classification of split reductive groups in terms of root data [Reference Demazure and GrothendieckSGA3, Exp XXV, Theorem 1], and the fact that the inner forms of a reductive group and its derived group are in bijection. Set ![]() $K'_p = G'_{{\mathbb {Z}}_p}({\mathbb {Z}}_p)$ and
$K'_p = G'_{{\mathbb {Z}}_p}({\mathbb {Z}}_p)$ and ![]() $K'_{1,p} = {\rm ker}(G'_{{\mathbb {Z}}_p}({\mathbb {Z}}_p) \rightarrow G'_{{\mathbb {Z}}_p}({\mathbb {F}}_p))$. Choose
$K'_{1,p} = {\rm ker}(G'_{{\mathbb {Z}}_p}({\mathbb {Z}}_p) \rightarrow G'_{{\mathbb {Z}}_p}({\mathbb {F}}_p))$. Choose ![]() $K^{\prime p}\subset G'(\mathbb {A}^p_f)$ compact open such that
$K^{\prime p}\subset G'(\mathbb {A}^p_f)$ compact open such that ![]() $K' = K'_pK^{\prime p}$ is neat and
$K' = K'_pK^{\prime p}$ is neat and ![]() $K^{\prime p} \cap G(\mathbb {A}^p_f) \subset K^p,$ and set
$K^{\prime p} \cap G(\mathbb {A}^p_f) \subset K^p,$ and set ![]() $K'_1 = K'_{1,p}K^{\prime p}$.
$K'_1 = K'_{1,p}K^{\prime p}$.
Let ![]() $\Gamma ' = K' \cap G({\mathbb {Q}}) \subset \Gamma$ and
$\Gamma ' = K' \cap G({\mathbb {Q}}) \subset \Gamma$ and ![]() $\Gamma _1' = K'_1 \cap G({\mathbb {Q}})$. A fortiori, it suffices to prove that
$\Gamma _1' = K'_1 \cap G({\mathbb {Q}})$. A fortiori, it suffices to prove that
This follows from Lemma 4.2.3 applied to the groups ![]() $K'_1 \subset K',$ by restricting the map of that lemma to geometrically connected components, and using the description of these components in [Reference DeligneDel79, 2.1.2].
$K'_1 \subset K',$ by restricting the map of that lemma to geometrically connected components, and using the description of these components in [Reference DeligneDel79, 2.1.2].
4.3.7 We can make the condition of ![]() $p$-admissibility of
$p$-admissibility of ![]() $G$ in Theorem 4.3.6 somewhat more explicit if we assume that
$G$ in Theorem 4.3.6 somewhat more explicit if we assume that ![]() $G^{{\rm ad}}({\mathbb {R}})$ has no compact factors.
$G^{{\rm ad}}({\mathbb {R}})$ has no compact factors.
Corollary 4.3.8. Let ![]() $G$ be an almost simple group which is unramified at
$G$ be an almost simple group which is unramified at ![]() $p$. Suppose that either
$p$. Suppose that either
(i)
 $G$ splits over
$G$ splits over  ${\mathbb {Q}}_p$, or
${\mathbb {Q}}_p$, or(ii) the irreducible factors of
 $G^{{\rm ad}}({\mathbb {R}})$ are all isomorphic to the adjoint group of one of
$G^{{\rm ad}}({\mathbb {R}})$ are all isomorphic to the adjoint group of one of  $U(n,n),$
$U(n,n),$  ${\rm SO}(n,2)$ with
${\rm SO}(n,2)$ with  $n \neq 6,$ or
$n \neq 6,$ or  ${\rm Sp}(2n)$ for some positive integer
${\rm Sp}(2n)$ for some positive integer  $n$.
$n$.
Then ![]() $G$ is
$G$ is ![]() $p$-admissible, and for any principal
$p$-admissible, and for any principal ![]() $p$-level covering
$p$-level covering ![]() $\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$ we have
$\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$ we have
Proof. If ![]() $G$ splits over
$G$ splits over ![]() ${\mathbb {Q}}_p$ then
${\mathbb {Q}}_p$ then ![]() ${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$ acts trivially on
${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$ acts trivially on ![]() $\Delta (G),$ and so leaves any choice of
$\Delta (G),$ and so leaves any choice of ![]() $\Sigma$ stable. For (ii), one checks using the classification of [Reference DeligneDel79] that in each of these cases,
$\Sigma$ stable. For (ii), one checks using the classification of [Reference DeligneDel79] that in each of these cases, ![]() $\Sigma = \Sigma (G),$ and a vertex
$\Sigma = \Sigma (G),$ and a vertex ![]() $v \in \Sigma (G)$ is stable by any automorphism of the connected component of
$v \in \Sigma (G)$ is stable by any automorphism of the connected component of ![]() $\Delta (G)$ containing
$\Delta (G)$ containing ![]() $v$. It follows that
$v$. It follows that ![]() ${\rm Gal}(\bar {\mathbb {Q}}/{\mathbb {Q}})$ leaves
${\rm Gal}(\bar {\mathbb {Q}}/{\mathbb {Q}})$ leaves ![]() $\Sigma (G)$ stable.
$\Sigma (G)$ stable.
4.3.9 The above results give examples of coverings for which one can compute the essential ![]() $p$-dimension. These values are in general far from the essential
$p$-dimension. These values are in general far from the essential ![]() $p$-dimension of the corresponding group. For example, Hannah Knight [Reference KnightKni21] has shown that for
$p$-dimension of the corresponding group. For example, Hannah Knight [Reference KnightKni21] has shown that for ![]() $p\neq 2$,
$p\neq 2$,
The case ![]() $r=1$ was computed independently by D. Benson [Reference Brosnan and FakhruddinBF20, Appendix B].
$r=1$ was computed independently by D. Benson [Reference Brosnan and FakhruddinBF20, Appendix B].
We call a reductive group ![]() $H$ almost absolutely simple if
$H$ almost absolutely simple if ![]() $H$ is semisimple and
$H$ is semisimple and ![]() $H^{{\rm ad}}$ is absolutely simple. (That is, it remains simple over an algebraic closure). We have the following result.
$H^{{\rm ad}}$ is absolutely simple. (That is, it remains simple over an algebraic closure). We have the following result.
Proposition 4.3.10 Let ![]() $H$ be a classical, almost absolutely simple group over
$H$ be a classical, almost absolutely simple group over ![]() ${\mathbb {F}}_q,$ with
${\mathbb {F}}_q,$ with ![]() $q = p^r$. If
$q = p^r$. If ![]() $p=2$ we further assume that
$p=2$ we further assume that ![]() $8\nmid r,$ and
$8\nmid r,$ and ![]() $4\nmid r$ if
$4\nmid r$ if ![]() $H$ is not split over
$H$ is not split over ![]() ${\mathbb {F}}_q$.
${\mathbb {F}}_q$.
Then there exists a semisimple ![]() ${\mathbb {Q}}$-group
${\mathbb {Q}}$-group ![]() $G,$ such that
$G,$ such that ![]() $X^+ = G({\mathbb {R}})^+/K_{\infty }$ is a Hermitian symmetric domain, and
$X^+ = G({\mathbb {R}})^+/K_{\infty }$ is a Hermitian symmetric domain, and ![]() $G$ is unramified at
$G$ is unramified at ![]() $p$ with reduction isomorphic to
$p$ with reduction isomorphic to ![]() ${\rm Res}_{{\mathbb {F}}_q/{\mathbb {F}}_p} H,$ and a principal
${\rm Res}_{{\mathbb {F}}_q/{\mathbb {F}}_p} H,$ and a principal ![]() $p$-covering
$p$-covering ![]() $\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$ such that
$\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$ such that
satisfies the following properties.
– If
 $H$ is a form of
$H$ is a form of  ${\rm SL}_n$ which is split if
${\rm SL}_n$ which is split if  $n$ is odd, then
$n$ is odd, then  $e = r\lfloor {n^2}/4 \rfloor$.
$e = r\lfloor {n^2}/4 \rfloor$.– If
 $H$ is
$H$ is  ${\rm Sp}_{2n}$ then
${\rm Sp}_{2n}$ then  $e = r({(n^2+n)}/2)$.
$e = r({(n^2+n)}/2)$.– If
 $H$ is a split form of
$H$ is a split form of  ${\rm SO}_{2n}$ then
${\rm SO}_{2n}$ then  $e = r({(n^2-n)}/2)$.
$e = r({(n^2-n)}/2)$.– If
 $H$ is a form of
$H$ is a form of  ${\rm Spin}_n$ and
${\rm Spin}_n$ and  $H$ is not of type
$H$ is not of type  $D_4,$ then
$D_4,$ then  $e(H({\mathbb {F}}_q)) = r(n-2)$.
$e(H({\mathbb {F}}_q)) = r(n-2)$.
Proof. Let ![]() $\bar G = {\rm Res}_{{\mathbb {F}}_q/{\mathbb {F}}_p} H$. There is a unique (up to canonical isomorphism) connected reductive group
$\bar G = {\rm Res}_{{\mathbb {F}}_q/{\mathbb {F}}_p} H$. There is a unique (up to canonical isomorphism) connected reductive group ![]() $G_{{\mathbb {Z}}_p}$ over
$G_{{\mathbb {Z}}_p}$ over ![]() ${\mathbb {Z}}_p$ with
${\mathbb {Z}}_p$ with ![]() $G_{{\mathbb {Z}}_p}\otimes {\mathbb {F}}_p = \bar G$. If
$G_{{\mathbb {Z}}_p}\otimes {\mathbb {F}}_p = \bar G$. If ![]() $H$ is not one of the four types listed, then the condition on
$H$ is not one of the four types listed, then the condition on ![]() $e$ is vacuous, and the proposition follows easily from Corollary 4.1.5.
$e$ is vacuous, and the proposition follows easily from Corollary 4.1.5.
We may now assume that ![]() $H$ is one of the four types listed, and in each of these cases we define a semisimple Lie group
$H$ is one of the four types listed, and in each of these cases we define a semisimple Lie group ![]() $G_{{\mathbb {R}}}$ over
$G_{{\mathbb {R}}}$ over ![]() ${\mathbb {R}}$ as follows. If
${\mathbb {R}}$ as follows. If ![]() $H$ is a form of
$H$ is a form of ![]() ${\rm SL}_n,$ we take
${\rm SL}_n,$ we take ![]() $G_{{\mathbb {R}}}$ to be
$G_{{\mathbb {R}}}$ to be ![]() ${\rm SU}(n/2, n/2)^r$ if
${\rm SU}(n/2, n/2)^r$ if ![]() $n$ is even and
$n$ is even and ![]() ${\rm SU}({(n-1)}/2, {(n+1)}/2)^r$ if
${\rm SU}({(n-1)}/2, {(n+1)}/2)^r$ if ![]() $n$ is odd. If
$n$ is odd. If ![]() $H$ is
$H$ is ![]() ${\rm Sp}_{2n}$ we take
${\rm Sp}_{2n}$ we take ![]() $G_{{\mathbb {R}}} = {\rm Sp}_{2n}^r$. If
$G_{{\mathbb {R}}} = {\rm Sp}_{2n}^r$. If ![]() $H$ is a form of
$H$ is a form of ![]() ${\rm SO}_{2n}$ we take
${\rm SO}_{2n}$ we take ![]() $G_{{\mathbb {R}}}$ to be
$G_{{\mathbb {R}}}$ to be ![]() ${\rm SO}^*(2n)^r,$ the inner form of (the compact group)
${\rm SO}^*(2n)^r,$ the inner form of (the compact group) ![]() ${\rm SO}(2n)$ which gives rise to the Hermitian symmetric domain of type
${\rm SO}(2n)$ which gives rise to the Hermitian symmetric domain of type ![]() $D^{\mathbb {H}}_n$ (cf. [Reference DeligneDel79, 1.3.9, 1.3.10]). If
$D^{\mathbb {H}}_n$ (cf. [Reference DeligneDel79, 1.3.9, 1.3.10]). If ![]() $H$ is a form of
$H$ is a form of ![]() ${\rm Spin}_n$ we take
${\rm Spin}_n$ we take ![]() $G_{{\mathbb {R}}}$ to be
$G_{{\mathbb {R}}}$ to be ![]() ${\rm Spin}(n-2,2)^r$.
${\rm Spin}(n-2,2)^r$.
In all cases ![]() $G_{{\mathbb {R}}}$ and
$G_{{\mathbb {R}}}$ and ![]() $G_{{\mathbb {Z}}_p}$ are forms of the same split group
$G_{{\mathbb {Z}}_p}$ are forms of the same split group ![]() $G^{{\rm split}}$. The actions of
$G^{{\rm split}}$. The actions of ![]() ${\rm Gal}(\mathbb {C}/\mathbb {R})$ and
${\rm Gal}(\mathbb {C}/\mathbb {R})$ and ![]() ${\rm Gal}({\mathbb {Q}}_p^{{\rm ur}}/{\mathbb {Q}}_p)$ on
${\rm Gal}({\mathbb {Q}}_p^{{\rm ur}}/{\mathbb {Q}}_p)$ on ![]() $\Delta (G^{{\rm split}})$ generate a group which is isomorphic to either
$\Delta (G^{{\rm split}})$ generate a group which is isomorphic to either ![]() $C$ or
$C$ or ![]() $C \times \mathbb {Z}/2\mathbb {Z}$, with
$C \times \mathbb {Z}/2\mathbb {Z}$, with ![]() $C$ a cyclic group. Indeed, in each case
$C$ a cyclic group. Indeed, in each case ![]() ${\rm Gal}(\mathbb {C}/\mathbb {R})$ acts on
${\rm Gal}(\mathbb {C}/\mathbb {R})$ acts on ![]() $\Delta (G^{{\rm split}})$ by an automorphism of order
$\Delta (G^{{\rm split}})$ by an automorphism of order ![]() $1$ or
$1$ or ![]() $2$ which lies in the center of
$2$ which lies in the center of ![]() ${\rm Aut}(\Delta (G^{{\rm split}}))$. If
${\rm Aut}(\Delta (G^{{\rm split}}))$. If ![]() $p=2,$ our assumptions on
$p=2,$ our assumptions on ![]() $r$ imply that
$r$ imply that ![]() $8 \nmid |C|$. Thus by Corollary 4.1.5 there exists a semisimple reductive group
$8 \nmid |C|$. Thus by Corollary 4.1.5 there exists a semisimple reductive group ![]() $G$ over
$G$ over ![]() ${\mathbb {Q}},$ which gives rise to
${\mathbb {Q}},$ which gives rise to ![]() $G_{{\mathbb {R}}}$ and
$G_{{\mathbb {R}}}$ and ![]() $G_{{\mathbb {Z}}_p}$ over
$G_{{\mathbb {Z}}_p}$ over ![]() ${\mathbb {R}}$ and
${\mathbb {R}}$ and ![]() ${\mathbb {Z}}_p$ respectively.
${\mathbb {Z}}_p$ respectively.
By construction ![]() $G$ is of Hodge type, and we now check that it can be chosen to be
$G$ is of Hodge type, and we now check that it can be chosen to be ![]() $p$-admissible. This is necessarily the case by Corollary 4.3.8, except when
$p$-admissible. This is necessarily the case by Corollary 4.3.8, except when ![]() $n$ is odd and
$n$ is odd and ![]() $H$ is a form of
$H$ is a form of ![]() ${\rm SL}_n$ or
${\rm SL}_n$ or ![]() $H$ is a form of
$H$ is a form of ![]() ${\rm SO}(2n)$. In these cases, we are assuming that
${\rm SO}(2n)$. In these cases, we are assuming that ![]() $H$ is a split form, so
$H$ is a split form, so ![]() ${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$ permutes the components of
${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$ permutes the components of ![]() $\Delta (G)$ simply transitively. If
$\Delta (G)$ simply transitively. If ![]() $H$ is a form of
$H$ is a form of ![]() ${\rm SL}_n$ or
${\rm SL}_n$ or ![]() ${\rm SO}(2n)$ with
${\rm SO}(2n)$ with ![]() $n$ odd, then
$n$ odd, then ![]() $\Delta (G_i)$ contains two points in
$\Delta (G_i)$ contains two points in ![]() $\Sigma (G)$ (the opposition involution is nontrivial on
$\Sigma (G)$ (the opposition involution is nontrivial on ![]() $\Delta (G_i)$ in these cases), and we can take
$\Delta (G_i)$ in these cases), and we can take ![]() $\Sigma \subset \Sigma (G)$ to be a
$\Sigma \subset \Sigma (G)$ to be a ![]() ${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$-orbit of any point
${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$-orbit of any point ![]() $v \in \Sigma (G)$.
$v \in \Sigma (G)$.
When ![]() $H$ is a form of
$H$ is a form of ![]() ${\rm SO}(2n)$ with
${\rm SO}(2n)$ with ![]() $n$ even, then the opposition involution is trivial on
$n$ even, then the opposition involution is trivial on ![]() $\Delta (G_i),$ and hence so is the action of complex conjugation. The set
$\Delta (G_i),$ and hence so is the action of complex conjugation. The set ![]() $\Sigma (G)$ meets each component of
$\Sigma (G)$ meets each component of ![]() $\Delta (G)$ in one vertex. Let
$\Delta (G)$ in one vertex. Let ![]() $\Sigma _1$ be the
$\Sigma _1$ be the ![]() ${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$-orbit of any vertex in
${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p)$-orbit of any vertex in ![]() $\Sigma (G)$. There is an inner form
$\Sigma (G)$. There is an inner form ![]() $G_{1,{\mathbb {R}}}$ of
$G_{1,{\mathbb {R}}}$ of ![]() $G$ over
$G$ over ![]() ${\mathbb {R}}$ such that
${\mathbb {R}}$ such that ![]() $\Sigma (G_{1,{\mathbb {R}}}) = \Sigma _1$. (Note that the Dynkin diagrams of inner forms are identified, so this makes sense.) Explicitly, let
$\Sigma (G_{1,{\mathbb {R}}}) = \Sigma _1$. (Note that the Dynkin diagrams of inner forms are identified, so this makes sense.) Explicitly, let ![]() $a \in {\rm Out}(G)$ be an automorphism which preserves the connected components of
$a \in {\rm Out}(G)$ be an automorphism which preserves the connected components of ![]() $\Delta (G)$ and such that
$\Delta (G)$ and such that ![]() $a(\Sigma (G)) = \Sigma _1$. (Such an
$a(\Sigma (G)) = \Sigma _1$. (Such an ![]() $a$ is unique unless
$a$ is unique unless ![]() $H$ is of type
$H$ is of type ![]() $D_4$.) Then
$D_4$.) Then ![]() $G_{1,{\mathbb {R}}}$ is given by twisting
$G_{1,{\mathbb {R}}}$ is given by twisting ![]() $G$ by the cocycle
$G$ by the cocycle ![]() $\tilde a\sigma (\tilde a)^{-1}$ where
$\tilde a\sigma (\tilde a)^{-1}$ where ![]() $\tilde a \in {\rm Aut}(G)({\mathbb {C}})$ lifts
$\tilde a \in {\rm Aut}(G)({\mathbb {C}})$ lifts ![]() $a$. Using the surjection (4.1.4), we see that there is an inner twisting
$a$. Using the surjection (4.1.4), we see that there is an inner twisting ![]() $G_1$ of
$G_1$ of ![]() $G$ over
$G$ over ![]() ${\mathbb {Q}}$ which is isomorphic to
${\mathbb {Q}}$ which is isomorphic to ![]() $G_{1,{\mathbb {R}}}$ over
$G_{1,{\mathbb {R}}}$ over ![]() ${\mathbb {R}}$ and to
${\mathbb {R}}$ and to ![]() $G$ over
$G$ over ![]() ${\mathbb {Q}}_p,$ as an inner twist. As
${\mathbb {Q}}_p,$ as an inner twist. As ![]() $\Sigma (G_1) = \Sigma _1$ is stable by
$\Sigma (G_1) = \Sigma _1$ is stable by ![]() ${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p),$
${\rm Gal}(\bar {\mathbb {Q}}_p/{\mathbb {Q}}_p),$ ![]() $G_1$ is
$G_1$ is ![]() $p$-admissible.
$p$-admissible.
Thus, the proposition follows from Theorem 4.3.6 and the formulae for the dimensions of Hermitian symmetric domains.
4.3.11 As in the introduction, if ![]() $H$ is a simple reductive group over
$H$ is a simple reductive group over ![]() ${\mathbb {F}}_q,$ we denote by
${\mathbb {F}}_q,$ we denote by ![]() $H(q)$ the image of
$H(q)$ the image of ![]() $H^{{\rm sc}}({\mathbb {F}}_q)$ in
$H^{{\rm sc}}({\mathbb {F}}_q)$ in ![]() $H({\mathbb {F}}_q)$.
$H({\mathbb {F}}_q)$.
Corollary 4.3.12. Let ![]() $H$ be a classical, absolutely simple group over
$H$ be a classical, absolutely simple group over ![]() ${\mathbb {F}}_q,$ with
${\mathbb {F}}_q,$ with ![]() $q = p^r$. If
$q = p^r$. If ![]() $p=2$ we further assume that
$p=2$ we further assume that ![]() $8\nmid r,$ and
$8\nmid r,$ and ![]() $4\nmid r$ if
$4\nmid r$ if ![]() $H$ is not split over
$H$ is not split over ![]() ${\mathbb {F}}_q$.
${\mathbb {F}}_q$.
Then there is a congruence ![]() $H(q)$-cover of locally symmetric varieties
$H(q)$-cover of locally symmetric varieties ![]() $Y' \rightarrow Y$ whose associated real Lie group is of the same type (
$Y' \rightarrow Y$ whose associated real Lie group is of the same type (![]() $A,B,C$ or
$A,B,C$ or ![]() $D$) as
$D$) as ![]() $H,$ and such that
$H,$ and such that ![]() $e:= \overline {{\rm ed}}(Y'/ Y; p)$ satisfies the following properties.
$e:= \overline {{\rm ed}}(Y'/ Y; p)$ satisfies the following properties.
– If
 $H$ is a form of
$H$ is a form of  ${\rm PGL}_n$ which is split if
${\rm PGL}_n$ which is split if  $n$ is odd, then
$n$ is odd, then  $e = r\lfloor {n^2}/4 \rfloor$.
$e = r\lfloor {n^2}/4 \rfloor$.– If
 $H$ is
$H$ is  ${\rm PSp}_{2n}$ then
${\rm PSp}_{2n}$ then  $e = r({(n^2+n)}/2)$.
$e = r({(n^2+n)}/2)$.– If
 $H$ is a split form of
$H$ is a split form of  ${\rm PO}_{2n}$ then
${\rm PO}_{2n}$ then  $e = r({(n^2-n)}/2)$.
$e = r({(n^2-n)}/2)$.– If
 $H$ is a form of
$H$ is a form of  ${\rm PO}_n$ and
${\rm PO}_n$ and  $H$ is not of type
$H$ is not of type  $D_4,$ then
$D_4,$ then  $e = r(n-2)$.
$e = r(n-2)$.
Proof. The group ![]() $H$ has the form
$H$ has the form ![]() $\tilde H^{{\rm ad}},$ where
$\tilde H^{{\rm ad}},$ where ![]() $\tilde H$ is a group as in one of the four cases of Proposition 4.3.10. We apply Proposition 4.3.10 to
$\tilde H$ is a group as in one of the four cases of Proposition 4.3.10. We apply Proposition 4.3.10 to ![]() $\tilde H$ to obtain a semi-simple
$\tilde H$ to obtain a semi-simple ![]() ${\mathbb {Q}}$-group
${\mathbb {Q}}$-group ![]() $G$ and principal
$G$ and principal ![]() $p$-covering
$p$-covering ![]() $\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$. By assumption,
$\Gamma _1\backslash X^+ \rightarrow \Gamma \backslash X^+$. By assumption, ![]() $\Gamma$ acts freely on
$\Gamma$ acts freely on ![]() $X^+,$ so this covering has group
$X^+,$ so this covering has group ![]() $\Gamma /\Gamma _1$. We will show that
$\Gamma /\Gamma _1$. We will show that ![]() $H(q)$ is a subquotient of
$H(q)$ is a subquotient of ![]() $\Gamma /\Gamma _1,$ and take
$\Gamma /\Gamma _1,$ and take ![]() $Y' \rightarrow Y$ to be the corresponding
$Y' \rightarrow Y$ to be the corresponding ![]() $H(q)$ cover.
$H(q)$ cover.
Since ![]() $G$ has reduction isomorphic to
$G$ has reduction isomorphic to ![]() ${\rm Res}_{{\mathbb {F}}_q/{\mathbb {F}}_p} \tilde H,$ we have
${\rm Res}_{{\mathbb {F}}_q/{\mathbb {F}}_p} \tilde H,$ we have
Moreover, since ![]() $\tilde H$ is almost simple, and
$\tilde H$ is almost simple, and ![]() $G$ is associated to a Hermitian symmetric domain,
$G$ is associated to a Hermitian symmetric domain, ![]() $G$ does not have any compact factors over
$G$ does not have any compact factors over ![]() ${\mathbb {Q}}$. Thus, we may apply the strong approximation theorem to
${\mathbb {Q}}$. Thus, we may apply the strong approximation theorem to ![]() $G^{{\rm sc}}$ to conclude that
$G^{{\rm sc}}$ to conclude that ![]() $\Gamma /\Gamma _1$ contains
$\Gamma /\Gamma _1$ contains ![]() ${\rm Im}(H^{{\rm sc}}({\mathbb {F}}_q) \rightarrow \tilde H({\mathbb {F}}_q))$.
${\rm Im}(H^{{\rm sc}}({\mathbb {F}}_q) \rightarrow \tilde H({\mathbb {F}}_q))$.
If ![]() $Z_{H^{{\rm sc}}}$ denotes the center of
$Z_{H^{{\rm sc}}}$ denotes the center of ![]() $H^{{\rm sc}},$ then
$H^{{\rm sc}},$ then ![]() $H(q)$ is a normal subgroup of
$H(q)$ is a normal subgroup of ![]() $(\Gamma /\Gamma _1)/Z_{H^{{\rm sc}}}({\mathbb {F}}_q),$ and
$(\Gamma /\Gamma _1)/Z_{H^{{\rm sc}}}({\mathbb {F}}_q),$ and
Since ![]() $H$ is absolutely simple, there is a finite extension
$H$ is absolutely simple, there is a finite extension ![]() ${\mathbb {F}}_{q'}/{\mathbb {F}}_q,$ such that the group scheme
${\mathbb {F}}_{q'}/{\mathbb {F}}_q,$ such that the group scheme ![]() $Z_{H^{{\rm sc}}}$ is isomorphic to
$Z_{H^{{\rm sc}}}$ is isomorphic to ![]() $\mu _r$ over
$\mu _r$ over ![]() ${\mathbb {F}}_{q'},$ for some integer
${\mathbb {F}}_{q'},$ for some integer ![]() $r$. Thus
$r$. Thus ![]() $Z_{H^{{\rm sc}}}({\mathbb {F}}_q) \subset Z_{H^{{\rm sc}}}({\mathbb {F}}_{q'}) \subset {\mathbb {F}}_{q'}^\times ,$ and
$Z_{H^{{\rm sc}}}({\mathbb {F}}_q) \subset Z_{H^{{\rm sc}}}({\mathbb {F}}_{q'}) \subset {\mathbb {F}}_{q'}^\times ,$ and ![]() $H^1({\operatorname {Spec\,}} {\mathbb {F}}_q, Z_{H^{{\rm sc}}})$ is an extension of a subgroup of
$H^1({\operatorname {Spec\,}} {\mathbb {F}}_q, Z_{H^{{\rm sc}}})$ is an extension of a subgroup of ![]() ${\mathbb {F}}_{q'}^{\times }/({\mathbb {F}}_{q'}^{\times })^r$ by
${\mathbb {F}}_{q'}^{\times }/({\mathbb {F}}_{q'}^{\times })^r$ by ![]() $H^1({\rm Gal}({\mathbb {F}}_{q'}/{\mathbb {F}}_q), Z_{H^{{\rm sc}}}({\mathbb {F}}_{q'}))$. In particular,
$H^1({\rm Gal}({\mathbb {F}}_{q'}/{\mathbb {F}}_q), Z_{H^{{\rm sc}}}({\mathbb {F}}_{q'}))$. In particular, ![]() $Z_{H^{{\rm sc}}}({\mathbb {F}}_q)$ is cyclic of order prime to
$Z_{H^{{\rm sc}}}({\mathbb {F}}_q)$ is cyclic of order prime to ![]() $p,$ and
$p,$ and ![]() $H^1({\operatorname {Spec\,}} {\mathbb {F}}_q, Z_{H^{{\rm sc}}})$ has order prime to
$H^1({\operatorname {Spec\,}} {\mathbb {F}}_q, Z_{H^{{\rm sc}}})$ has order prime to ![]() $p$.
$p$.
That the cover corresponding to ![]() $H(q)$ satisfies the conclusion of the corollary now follows from Proposition 4.3.10 and Lemma 2.2.7.
$H(q)$ satisfies the conclusion of the corollary now follows from Proposition 4.3.10 and Lemma 2.2.7.
Remark 4.3.13 For ![]() $H={\rm PSL}_4$ and
$H={\rm PSL}_4$ and ![]() $q=2$ there is an exceptional isomorphism
$q=2$ there is an exceptional isomorphism ![]() $H(2)={\rm SL}_4({\mathbb {F}}_2)\cong A_8$. Corollary 4.3.12 thus gives examples of incompressible covers
$H(2)={\rm SL}_4({\mathbb {F}}_2)\cong A_8$. Corollary 4.3.12 thus gives examples of incompressible covers ![]() $\Gamma '\backslash X^+\to \Gamma \backslash X^+$ with Galois group
$\Gamma '\backslash X^+\to \Gamma \backslash X^+$ with Galois group ![]() $A_8$ where
$A_8$ where ![]() $\Gamma \backslash X^+$ is a 4-fold. It would be of interest to investigate these in connection with solutions of the general octic polynomial, for example as in Hilbert's Octic Conjecture [Reference HilbertHil27].
$\Gamma \backslash X^+$ is a 4-fold. It would be of interest to investigate these in connection with solutions of the general octic polynomial, for example as in Hilbert's Octic Conjecture [Reference HilbertHil27].