There have been many experiments in the past decade which have demonstrated that high-energy quasi-monoenergetic electron beams can be produced as a result of the interaction of intense laser pulses with underdense plasmas. Relativistic electron beams are generated via acceleration from large amplitude relativistic plasma waves (Faure et al., Reference Faure, Gilnec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004; Geddes et al., Reference Geddes, Toth, van Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004; Mangles et al., Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Foster, Divall, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick2004, Reference Mangles, Walton, Najmudin, Dangor, Krushelnick, Malka, Manclossi, Lopes, Carias, Mendes and Dorchies2006) which are created in the wake of the laser pulse as it propagates through the plasma. In the resonant regime at high power – where the laser pulse duration is less than the relativistic plasma wavelength, the plasma wave generated forms a “bubble”-shaped accelerating structure. Recently, electron beams with energies >1 GeV have been observed using short-pulse high repetition rate laser systems using plasma waveguides (Leemans et al., Reference Leemans, Nagler, Gonsalves, Toth, Nakamura, Geddes, Esarey, Schroeder and Hooker2006) or gases (Hafz et al., Reference Hafz, Jeong, Choi, Lee, Pae, Kulagin, Sung, Yu, Hong, Hosokai, Cary, Ko and Lee2008; Kneip et al., Reference Kneip, Nagel, Martins, Mangles, Bellei, Chekhlov, Clarke, Delerue, Divall, Doucas, Ertel, Fiuza, Fonseca, Foster, Hawkes, Hooker, Krushelnick, Mori, Palmer, Ta Phuoc, Rajeev, Schreiber, Streeter, Urner, Vieira, Silva and Najmudin2009) as the target.

One of the most important aspects of research in this field is to understand the injection of electrons into such wakefields. For best electron beam quality with regard to emittance, energy spread, reproducibility, and pulse duration, the injection of electrons into the “bubble” needs to be well controlled. There has been considerable research into the development of techniques to improve the beam quality in this way (Faure et al., Reference Faure, Rechatin, Norlin, Lifschitz, Glinec and Malka2006; Geddes et al., Reference Geddes, Nakamura, Plateau, Toth, Cormier-Michel, Esarey, Schroeder, Cary and Leemans2008; McGuffey et al., Reference McGuffey, Thomas, Schumaker, Matsuoka, Chvykov, Dollar, Kalintchenko, Yanovsky, Maksimchuk, Krushelnick, Bychenkov, Glazyrin and Karpeev2010).

In this paper, we discuss experimental measurements of scattered light from the interaction of an intense laser pulse with plasma as it accelerates mono-energetic electron beams from these interactions. These measurements suggest that prior to injection of the electrons into the wakefield, an instability occurs which drives non-linear short wavelength plasma oscillations in the bubble. The observed wavelength of the scattered emission agrees with the plasma frequency in the plasma “bubble” wall. Electron injection into the plasma wave occurs when the electric field in the plasma bubble reaches a “threshold” value which may also enable the generation of perturbations in the plasma wakefield structure and the production of plasma waves. Oscillations in the plasma bubble were previously observed in simulations to lead to injection and acceleration (Kalmykov et al., Reference Kalmykov, Yi, Khudik and Shvets2009). Our experimental observations are in general agreement with those results. The observed scattered light is most likely due to collective Thomson scattering from related oscillations in the plasma. Such measurements of scattered light with both high spectral and spatial resolution can provide detailed information about the dynamics of these accelerators as well as the injection mechanisms and also demonstrates the existence of this new “bubble instability” associated with laser wakefield self-injection.

The experiment used the Astra Titanium:Sapphire laser system at the Central Laser Facility of the Rutherford Appleton Laboratory in the UK. The laser pulses (λ = 800 nm, E = 350 mJ, τ = 40 fsec) were focused with an f/10 off-axis parabolic mirror onto the edge of a 2 mm-long supersonic jet of helium gas to produce intensities on the order of 1.3 × 10¹⁸ W/cm².

The plasma density was controlled by varying the backing pressure of the gas jet. The electron density as a function of backing pressure was determined by measuring the frequency shift (Δω = ω_pe where ω_pe is the electron plasma frequency) of satellite lines near the laser wavelength which result from forward Raman scattering. Direct interferometric measurements were also used. The plasma density was observed to vary linearly with backing pressure (agreeing with previous experiments using the same nozzle) and the electron density ranged from 3 × 10¹⁸ to 5 × 10¹⁹/cm³. In this density range, the wavelength of relativistic plasma waves produced (i.e., λ_p = 2πω_pe/c) is between one and ten times the laser pulse length (cτ, which is 12 µm here). For laser pulses which are less than the plasma wavelength, relativistic plasma waves can be generated “resonantly” in the wake of the pulse, while in the regime in which the laser pulse length is longer than the plasma wavelength, high-intensity interactions are required to drive an instability in which the plasma waves are produced via “self-modulation” of the laser pulse envelope at the plasma frequency or via the “forced” laser wakefield process.

In our experiments, the plasma waves are driven so that they generate a bubble-shaped wakefield which grows until “wave-breaking” or “self-injection” occurs. This is a phenomenon which takes place at very large amplitudes such that the non-linear wave energy is transferred directly into particle energy by the electric field in the “bubble-shaped” wave and plasma wave consequently can lose coherence. Electrons which reach relativistic energies from this process can become trapped (i.e., “injected” into the bubble) such that they can pick up even more energy. The cold wavebreaking electric-field amplitude for electron plasma waves is given by: E _p = mcω_p/e. The relativistic wave-breaking limit for high phase velocity waves is slightly modified and correspondingly given by: E _WB = [2(γ_p-1]^1/2mcω_p/e where γ_p is the Lorentz factor of the phase velocity of the plasma wave.

In our experiment, the electron energy spectrum was measured using an on-axis magnetic spectrometer. This consisted of an electromagnet that deflects electrons away from the axis of laser propagation. A high-resolution image plate detector (Fuji BAS1800II) was used to obtain the electron spectrum. The electrons were also simultaneously measured using a much lower resolution array of diodes which was situated behind the image plate and which could be used to calibrate the signal on the image plate. The spectrometer magnet, image plates, and diodes were set up to measure the spectrum over a wide energy range in a single shot. Other diagnostics used included the simultaneous measurement of the transmitted laser spectrum and a Rogowski coil to measure the total current in the electron beam.

An important tool in the study of such interactions are measurements of scattered radiation produced as a result of laser–plasma instabilities (Huntington et al., Reference Huntington, Thomas, McGuffey, Matsuoka, Chvykov, Kalintchenko, Kneip, Najmudin, Palmer, Yanovsky, Maksimchuk, Drake, Katsouleas and Krushelnick2011). Here we report a new observation of scattered radiation which is produced as a result of an interaction of the driving laser pulse with an oscillation of the thin walls of the plasma bubble, and which seems to be the “signature” of a bubble instability associated with self-injection.

As discussed previously, the onset of self-trapping of electrons from the background plasma in a laser wakefield accelerator is dependent on the peak vector potential a ₀ and the pulse shape for a given initial number density n _e. For pulses which are initially too long, wide, or too low in intensity, then self-focusing, pulse compression and photon deceleration result in a pulse closer to the “ideal” conditions for self-trapping to occur.

This is with the caveat that the pulse has a power greater than the critical power for self-focusing and a pulse length not much longer than a relativistic wavelength λ_p. Unless the pulse initially has well-matched conditions, electron injection will not take place until a certain time, after which self-focusing, compression, and photon deceleration have resulted in a matched pulse. The important thing to note is that, as the final energy of the accelerated electron bunch depends on the overall acceleration length, the time taken for the non-linear modification of the pulse to take place will be critical to the energy of the electron bunch produced in the interaction. Diagnosing this “evolution” time for the pulse would be highly useful in the development of the self-injecting LWFA, particularly for experiments with very high-power laser systems currently in development. There is experimental uncertainty in the acceleration length for the electron bunch due to the unknown time taken for the evolution of the laser pulse to electron trapping conditions. If this could be determined, then additional reference points could be obtained to confirm numerical modeling of these interactions. In addition, comparisons of this evolution time with three-dimensional particle-in-cell codes would prove a useful benchmark. The time for the pulse to evolve to trapping conditions is evidently bounded by the start of the plasma structure and the point at which electron trapping commences.

When trapping, or injection, occurs, a large bunch (~10⁸–10⁹) of electrons experience a violent change in velocity over a short period of time ω⁻¹_p from a small volume (λ³_p). This leads to a rapidly changing current density, and therefore radiation emission. The short timescale for the acceleration involved implies that the associated radiation spectrum is broadband. This radiation signature of injection [“wave-breaking” radiation (Thomas et al., Reference Thomas, Murphy, Mangles, Najmudin, Dangor, Kaluza and Krushelnick2007; Matsuoka et al., Reference Matsuoka, McGuffey, Horovitz, Dollar, Bulanov, Chvykov, Cummings, Kalintchenko, Rousseau, Yanovsky, Thomas, Maksimchuk and Krushelnick2010] is detectable in the direction transverse to the acceleration direction, and can be used to precisely measure where injection occurs in the interaction.

In the experiments, light scattered at 90° to the direction of propagation was re-imaged both perpendicular (top view) and parallel (side view) to the laser polarization plane. The principal diagnostic was an imaging spectrometer that gave both spectral and spatial information along the interaction length. The electron energies measured on the experiment in this density range typically consisted of peaked spectra (up to 60 MeV) but did not always have a single monoenergetic “spike”, although such spectra were often produced. In general, these energy spectra varied in charge and energy from shot-to-shot.

Electron beam profile measurements taken separately indicated that electron beams were consistently produced for n_e~1 × 10¹⁹/cm³. These took the form of one or more well-collimated beams, with the collimation increasing for decreasing density. However, a variation in pointing meant that often the electron beam was not collected within the relatively small solid angle (~10⁻⁵ steradian) of the spectrometer collimator (Thomas et al., Reference Thomas, Murphy, Mangles, Najmudin, Dangor, Kaluza and Krushelnick2007).

Figure 1 shows an example of simultaneous measurements of radiation emission in the optical wavelength range in the two orthogonal directions transverse to the laser propagation. In addition, the spatially resolved spectrum is also shown – Figure 1c shows the one-dimensional version of (a) but dispersed spectrally in the vertical direction.

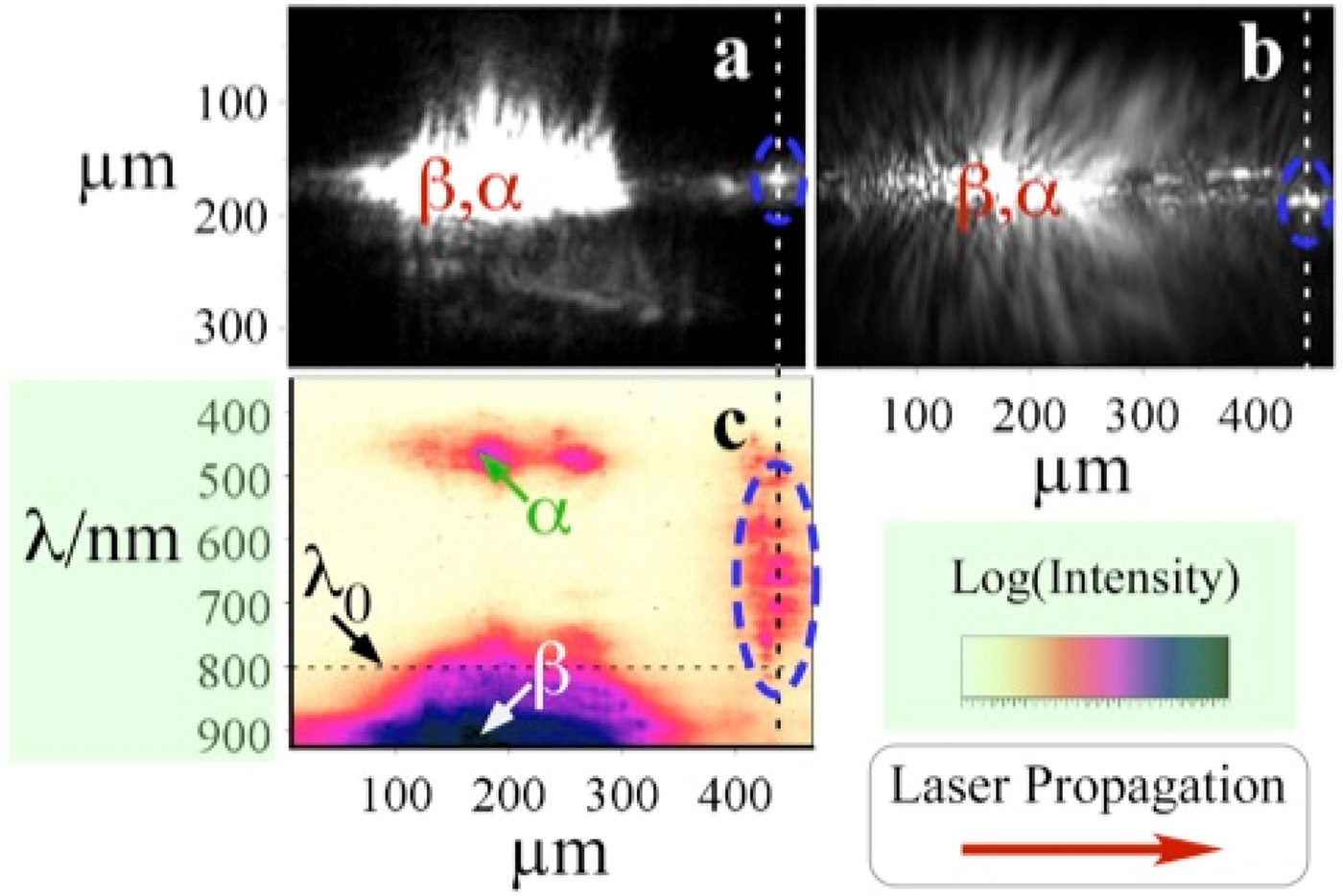
Fig. 1. Simultaneous measurement of (a) top view image, (b) side view image, and (c) imaging spectrometer for a shot at 3.2 × 10¹⁹/cm³. The laser propagates from left to right. α and β are the Stokes line of Raman side-scatter and its associated second harmonic. Circled is emission of broadband radiation occurring later in the interaction.

The imaging channels (a) and (b) were generally characterized by a short (~200–500 µm) bright burst of radiation (β). The imaging spectrometer reveals the brightest component of the light to be downshifted with respect to the laser fundamental wavelength. It is Raman side-scattering of the laser pulse (Matsuoka et al., Reference Matsuoka, McGuffey, Horovitz, Dollar, Bulanov, Chvykov, Cummings, Kalintchenko, Rousseau, Yanovsky, Thomas, Maksimchuk and Krushelnick2010), as it is shifted by –ω_p from the fundamental frequency. The corresponding up-shifted satellite ω_p + ω₀ is non-resonant for side-scatter. Although the pulse duration is extremely short for growth of side-scattered Raman instabilities, a real pulse is not Gaussian but is usually clipped by an aperture. This contributes to transverse k vectors in the pulse which increase amplification of side-scatter. The second harmonic of this scatter (α) is also evident (Krushelnick et al., Reference Krushelnick, Ting, Burris, Fisher, Manka and Esarey1995).

When the spectrometer filtering level is dramatically reduced, a cascade of up-shifted satellites are also evident. Figure 2 shows these imaged optical spectra over a variety of densities with this lower filtering level, and Figure 3 shows one of these spectra at n _e = 1.6 × 10¹⁹/cm³, with the different satellites annotated. These satellites are spaced by orders of frequency Δω = ω_pS from the laser fundamental frequency ω₀.

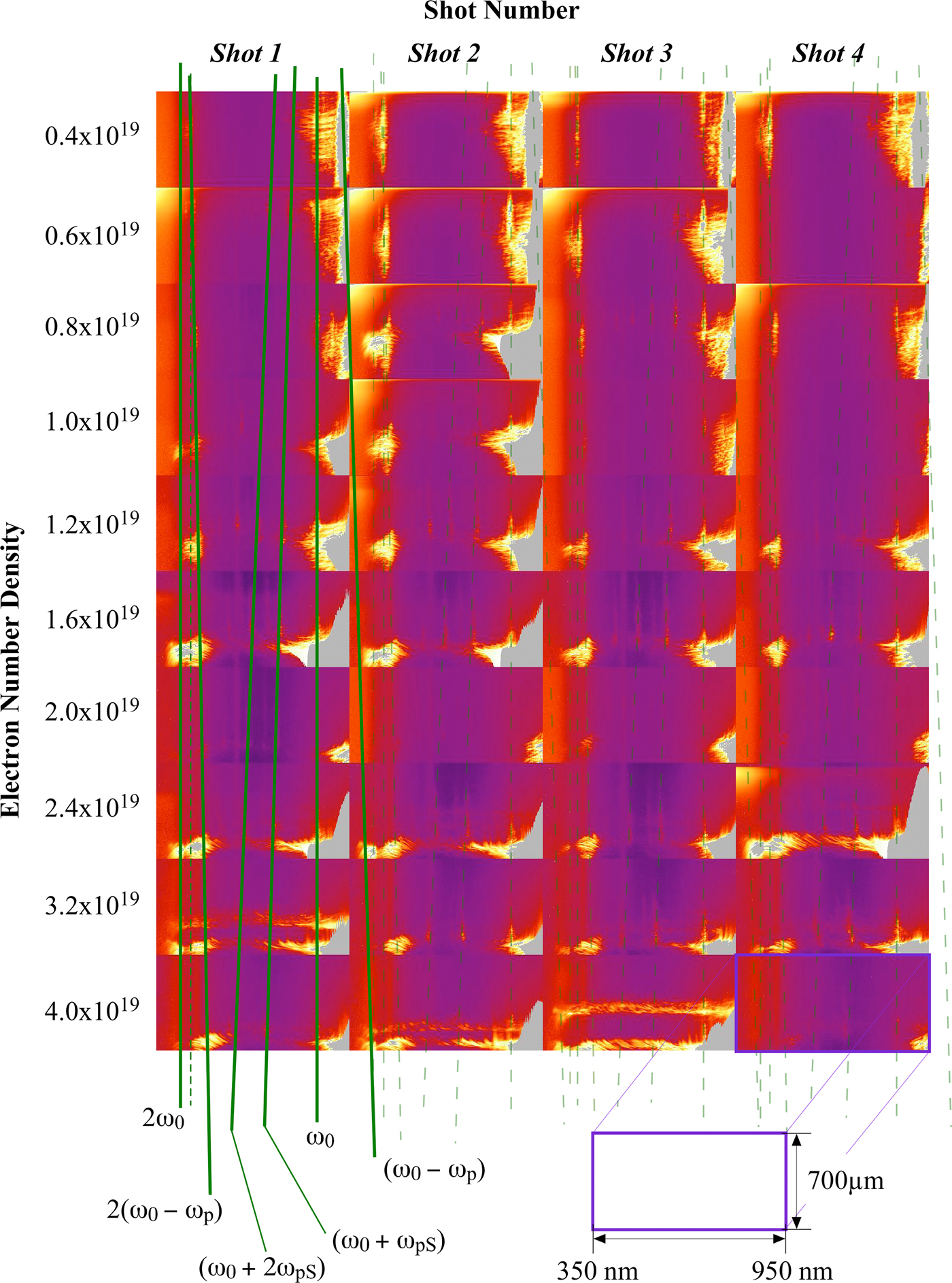
Fig. 2. The spectrum of light-emitted transverse to the laser direction as a function of distance of laser propagation for a range of densities. The vertical direction is length along the channel with the laser propagating from bottom to top. The horizontal direction is wavelength.

Fig. 3. The spectrum of light-emitted transverse to the laser direction as a function of distance of laser propagation for n _e = 3.2  × 10¹⁹/cm³. (a) Second harmonic of fundamental frequency ω₀. (b) Helium recombination emission line. (c) Second harmonic of Stokes line. (d–f) Cascade of satellites spaced at 1.7ω_p. (g) Laser pulse fundamental frequency ω₀. (h) Stokes line ω₀−ω_p.

However, the spacing ω_pS is not exactly ω_p, as would be expected from a linear Raman process, but closer to 1.7ω_p. This was an unexpected measurement but was confirmed when the different order satellites are plotted as a function of density as in Figure 4. The intercepts of the linear fits are at either ω = ω₀ or 2ω₀ as expected since ω_p → 0 as n _e → 0. The gradients are 1 for the second harmonic of the Stokes emission from SRS, also as expected, and 1.7 for the higher frequency satellites.

Fig. 4. The frequency of the satellites (ω₀ + mω_pS; a, b, c, m = 1, 2, 3, respectively), and (d) second harmonic of the Stokes line 2(ω₀−ω_p) as a function of plasma frequency ω_p. Also shown are linear fits to each data series with corresponding equations.

These observed anomalous satellites are at very low amplitude, implying that they result from a very non-resonant process. It is possible that this emission is from higher order wave-mixing processes, but this is quite unlikely since they are not spaced by the background plasma frequency. If such emission is due to non-linear plasma wave lengthening, this would need to act to decrease the local plasma frequency, and so there would have to be a four-wave-mixing process, or higher, to obtain satellites spaced at greater than the plasma frequency. This emission is also unusual in that it is observed in a specific spatial location in the laser–plasma interaction.

However, a simple calculation can show that the frequency 1.7ω_pe is approximately the plasma frequency in the shell of the non-linear plasma bubble – assuming only that the bubble has a radius of the relativistic plasma wavelength and a thickness which is just the plasma skin depth (implying that the laser pulse is mildly relativistic – as in our experiments) and that the laser intensity was about 10¹⁸ W/cm² so that a ₀ < 1.

The plasma density of the “shell” is thus given by:

$$\eqalign{n_{{\rm shell}}\,{\rm =}\, &n_{{\rm plasma}}\left( {\displaystyle{{V_{{\rm bubble}}} \over {V_{{\rm shell}}}}{\rm +} 1} \right) \cr {\rm \omega} _{{\rm shell}}^2 \,{\rm =}\, &{\rm \omega} _{{\rm plasma}}^2 \left( {\displaystyle{{V_{{\rm bubble}}} \over {V_{{\rm shell}}}}{\rm +} 1} \right) \cr V_{{\rm bubble}}\,{\rm =}\, &\displaystyle{{4{\rm \pi}} \over 3}\left( {\displaystyle{{{\rm \lambda}_{\rm p}} \over 2}} \right)^3{\rm =} \displaystyle{{\rm \pi} \over 6}{\rm \lambda} _{\rm p}^3 \cr V_{{\rm shell}}\,{\rm =}\, &4{\rm \pi} \left( {\displaystyle{{{\rm \lambda}_{\rm p}} \over 2}} \right)^2\Delta {\rm =} {\rm \pi \lambda} _{\rm p}^2 \Delta \cr \Delta \,{\rm =}\, &{\rm wall}\,{\rm thickness}\,{\rm =}\, \displaystyle{c \over {{\rm \omega} _{{\rm shell}}}}\,{\rm =}\, {\rm skin}\,{\rm depth}} $$

so

$$\displaystyle{{V_{{\rm bubble}}} \over {V_{{\rm shell}}}}\,{\rm =}\, \displaystyle{{{\rm \lambda} _{\rm p}} \over {6\Delta}}\,{\rm =}\,\displaystyle{{{\rm \omega} _{{\rm shell}}} \over {{\rm \omega} _{{\rm plasma}}}}\left( {\displaystyle{{\rm \pi} \over 3}} \right)$$

and

$$\left( {\displaystyle{{{\rm \omega}_{{\rm shell}}} \over {{\rm \omega}_{{\rm plasma}}}}} \right)^2{\rm -}\displaystyle{{\rm \pi} \over 3}\left( {\displaystyle{{{\rm \omega}_{{\rm shell}}} \over {{\rm \omega}_{{\rm plasma}}}}} \right){\rm -}1{\rm =} 0$$

so

$$\displaystyle{{{\rm \omega} _{{\rm shell}}} \over {{\rm \omega} _{{\rm plasma}}}}\approx 1.7$$

This shows that for a ₀ < 1, the frequency of plasma waves in the bubble shell should be about 1.7 times the background plasma frequency as measured in the experiment. Coherent Thomson scattering from such non-linear waves by the laser light will consequently produce an optical signature at multiples of the 1.7ω_pe shift.

The source of these large amplitude oscillations in the structure of the plasma bubble – just before the observation of wavebreaking – perhaps indicates that the bubble undergoes an instability which may be a prerequisite for self-injection. This is confirmed by recent numerical simulations of these interactions (Kalmykov et al., Reference Kalmykov, Yi, Khudik and Shvets2009).

In conclusion, we have made the first spatio-temporally resolved measurements of scattered emission from an instability in the structure of the bubble-shaped plasma wave produced during laser wakefield acceleration. This measurement was unexpected; however, it is likely that the scattering is caused by large amplitude perturbations in the bubble immediately prior to self-injection when the plasma bubble undergoes an instability which enhances the electric field in the bubble and induces electron injection. Further observations of this phenomenon may lead to improved understanding of the LWFA process and also enable improved control of the energetic electron beams produced in this way.