2.1 Governing equations

The two fluids are incompressible and fully miscible. The flow obeys Darcy’s law and the concentration of the injected fluid is described by an advection–diffusion equation,

(2.1) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}=-\frac{k}{\unicode[STIX]{x1D707}(c)}\unicode[STIX]{x1D735}p, & \displaystyle\end{eqnarray}$$

(2.3) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}c=\unicode[STIX]{x1D719}D\unicode[STIX]{x1D6FB}^{2}c. & \displaystyle\end{eqnarray}$$

Here $\boldsymbol{u}=(u,v)$ is the Darcy velocity or fluid flux, $p$ the pressure and $c$ the concentration, which varies between 0 (in the ambient fluid) and 1 (in the injected fluid). The viscosity $\unicode[STIX]{x1D707}(c)$ varies with the concentration, and we follow the convention of previous authors (e.g. Tan & Homsy Reference Tan and Homsy1986; Zimmerman & Homsy Reference Zimmerman and Homsy1991; Pramanik & Mishra Reference Pramanik and Mishra2015a ) by assuming an Arrhenius-like exponential dependence,

(2.4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(c)=\unicode[STIX]{x1D707}_{2}\text{e}^{-Rc}, & & \displaystyle\end{eqnarray}$$

where $R=-\text{ln}(\unicode[STIX]{x1D707}_{1}/\unicode[STIX]{x1D707}_{2})$ .

Figure 1. An illustration of the model set-up. The porous medium is taken to be an infinite strip of width $a$ initially filled with a fluid with viscosity $\unicode[STIX]{x1D707}_{2}$ . A fluid with viscosity $\unicode[STIX]{x1D707}_{1}$ is injected at a constant velocity $U\hat{\boldsymbol{x}}$ into the medium. We measure the concentration of the injected fluid, which is one upstream and zero downstream.

We non-dimensionalize the equations by the height of the domain $a$ , velocity $U$ , time $\unicode[STIX]{x1D719}a/U$ , permeability $k$ , viscosity of the ambient fluid $\unicode[STIX]{x1D707}_{2}$ and pressure $\unicode[STIX]{x1D707}_{2}Ua/k$ , leading to

(2.5) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}u^{\ast }}{\unicode[STIX]{x2202}x^{\ast }}+\frac{\unicode[STIX]{x2202}v^{\ast }}{\unicode[STIX]{x2202}y^{\ast }}=0, & & \displaystyle\end{eqnarray}$$

(2.6a,b ) $$\begin{eqnarray}\displaystyle -u^{\ast }\unicode[STIX]{x1D707}^{\ast }=\frac{\unicode[STIX]{x2202}p^{\ast }}{\unicode[STIX]{x2202}x^{\ast }},\quad -v^{\ast }\unicode[STIX]{x1D707}^{\ast }=\frac{\unicode[STIX]{x2202}p^{\ast }}{\unicode[STIX]{x2202}y^{\ast }}, & & \displaystyle\end{eqnarray}$$

(2.7) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}t^{\ast }}+u^{\ast }\frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}x^{\ast }}+v^{\ast }\frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}y^{\ast }}=\frac{1}{Pe}\left(\frac{\unicode[STIX]{x2202}^{2}c}{\unicode[STIX]{x2202}x^{\ast 2}}+\frac{\unicode[STIX]{x2202}^{2}c}{\unicode[STIX]{x2202}y^{\ast 2}}\right), & \displaystyle\end{eqnarray}$$

(2.8) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D707}^{\ast }(c)=\text{e}^{-Rc}, & \displaystyle\end{eqnarray}$$

where $(\cdot )^{\ast }$ denotes a dimensionless quantity. For notational simplicity, we drop the asterisks from all subsequent quantities. The key dimensionless parameters are the log-viscosity ratio and the Péclet number, defined as

(2.9a,b ) $$\begin{eqnarray}\displaystyle R=-\text{ln}\left(\frac{\unicode[STIX]{x1D707}_{1}}{\unicode[STIX]{x1D707}_{2}}\right),\quad Pe=\frac{Ua}{\unicode[STIX]{x1D719}D}. & & \displaystyle\end{eqnarray}$$

When the injected fluid is more viscous than the ambient ( $R<0$ ), the interface is stable and the concentration evolves by diffusion alone, with a classical error-function profile. However, when the injected fluid is less viscous than the ambient ( $R>0$ ), the interface can be unstable, leading to complex fingering patterns. We focus on the latter problem here. The Péclet number provides a ratio of the characteristic time scales for diffusion and advection: when $Pe\ll 1$ , diffusion dominates the dynamics, and when $Pe\gg 1$ , advection dominates. In the diffusive limit, as will be shown later, the instability can be suppressed so we will, therefore, focus predominantly on the limit $Pe\gg 1$ .

We note that the Péclet number here is a macroscopic quantity defined with respect to the width $a$ of the porous medium. It is distinct from the pore Péclet number, $Pe_{p}=Ub/D=(b/a)Pe$ , which is defined with respect to the intrinsic length scale $b$ of the medium, i.e. the pore size, or, in a Hele-Shaw cell, the gap width. The assumption of Darcy flow relies on the pore Péclet number being small, $Pe_{p}<O(1)$ (Yang & Yortsos Reference Yang and Yortsos1997), or, equivalently, $a/b>O(Pe)$ . In this limit, diffusion acts quickly to homogenize flow structures at the pore scale. This limit is assumed in all the work presented in this paper. If, instead, $Pe_{p}$ were not small, the flow structures across the pore or gap width would affect the global dynamics, leading to qualitatively different macroscopic behaviour (Paterson Reference Paterson1985; Lajeunesse et al. Reference Lajeunesse, Martin, Rakotomalala, Salin and Yortsos1999).

We work in a reference frame moving with the velocity of the injected fluid, and introduce transformed variables

(2.10a,b ) $$\begin{eqnarray}\displaystyle \tilde{u} =u-1,\quad \tilde{x}=x-t. & & \displaystyle\end{eqnarray}$$

In this frame, equations (2.5)–(2.7) become

(2.11) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\tilde{x}}+\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}=0, & & \displaystyle\end{eqnarray}$$

(2.12a,b ) $$\begin{eqnarray}\displaystyle -(\tilde{u} +1)\unicode[STIX]{x1D707}=\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}\tilde{x}},\quad -v\unicode[STIX]{x1D707}=\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}y}, & & \displaystyle\end{eqnarray}$$

(2.13) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}t}+\tilde{u} \frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}\tilde{x}}+v\frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}y}=\frac{1}{Pe}\left(\frac{\unicode[STIX]{x2202}^{2}c}{\unicode[STIX]{x2202}\tilde{x}^{2}}+\frac{\unicode[STIX]{x2202}^{2}c}{\unicode[STIX]{x2202}y^{2}}\right). & & \displaystyle\end{eqnarray}$$

Again, for notational convenience, we drop the tildes from all subsequent quantities.

2.2 Boundary conditions

Similar to previous work (Tan & Homsy Reference Tan and Homsy1988), we impose periodicity at the top and bottom boundaries. The upstream and downstream concentration are fixed at $c=1$ and $c=0$ respectively and the horizontal velocity is fixed at $u=0$ (in the moving frame). The boundary conditions are thus

(2.14a-c ) $$\begin{eqnarray}\displaystyle c(x,0,t)=c(x,1,t),\quad u(x,0,t)=u(x,1,t),\quad v(x,0,t)=v(x,1,t), & & \displaystyle\end{eqnarray}$$

(2.15a,b ) $$\begin{eqnarray}\displaystyle c(-\infty ,y,t)=1,\quad c(\infty ,y,t)=0, & & \displaystyle\end{eqnarray}$$

(2.16) $$\begin{eqnarray}\displaystyle u(-\infty ,y,t)=u(\infty ,y,t)=0. & & \displaystyle\end{eqnarray}$$

2.3 Diagnostic quantities

As the instability develops and an array of fine fingers form, the local fingering dynamics become chaotic and are controlled by nonlinear interactions between fingers. Instead of examining the behaviour of each individual finger, we aim to examine how the fingering dynamics evolve globally. To do so, we compute the average concentration over the transverse direction,

(2.17) $$\begin{eqnarray}\displaystyle \overline{c}(x,t)=\int _{0}^{1}c(x,y,t)\,\text{d}y. & & \displaystyle\end{eqnarray}$$

Using this definition, and defining the deviations $c^{\prime }(x,y)=c(x,y)-\overline{c}(x)$ , equation (2.13) can be written as two coupled equations for the mean and perturbed concentrations,

(2.18) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\overline{c}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\overline{uc^{\prime }}}{\unicode[STIX]{x2202}x}=\frac{1}{Pe}\frac{\unicode[STIX]{x2202}^{2}\overline{c}}{\unicode[STIX]{x2202}x^{2}}, & \displaystyle\end{eqnarray}$$

(2.19) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}c^{\prime }}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}uc^{\prime }}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}u\overline{c}}{\unicode[STIX]{x2202}x}-\frac{\unicode[STIX]{x2202}\overline{uc^{\prime }}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}vc^{\prime }}{\unicode[STIX]{x2202}y}=\frac{1}{Pe}\left(\frac{\unicode[STIX]{x2202}^{2}c^{\prime }}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}c^{\prime }}{\unicode[STIX]{x2202}y^{2}}\right). & \displaystyle\end{eqnarray}$$

We will use this decomposition in our derivation of the late-time solution in § 6.

We also examine three global quantities over time: the mixing length $h$ , which quantifies the width of the mixing zone; the average number of fingers $n$ , which gives an inverse measure of the transverse length scale; and the Nusselt number, $Nu$ , which quantifies the total convective mixing rate. These quantities are defined as

(2.20) $$\begin{eqnarray}\displaystyle & \displaystyle h=x|_{\overline{c}=0.01}-x|_{\overline{c}=0.99}, & \displaystyle\end{eqnarray}$$

(2.21) $$\begin{eqnarray}\displaystyle & \displaystyle n=\frac{1}{h}\int _{x|_{\overline{c}=0.99}}^{x|_{\overline{c}=0.01}}\unicode[STIX]{x1D702}(x)\,\text{d}x, & \displaystyle\end{eqnarray}$$

(2.22) $$\begin{eqnarray}\displaystyle & \displaystyle Nu=\int _{-\infty }^{\infty }\int _{0}^{1}u\left(c-\frac{1}{2}\right)\,\text{d}y\,\text{d}x, & \displaystyle\end{eqnarray}$$

where the number of fingers $\unicode[STIX]{x1D702}(x)$ is calculated by counting the number of local maxima in a vertical slice. Note that the Nusselt number is often defined as $Nu^{\ast }=1+Pe\,Nu$ , which is the ratio between total transport and diffusive transport (Zhou Reference Zhou2013). Here we instead use the Nusselt number simply to quantify the convective transport.

4.1 Scalings

At the start of all simulations, the interface is relatively sharp and the concentration and velocity perturbations are small. Diffusion across the interface dominates the growth of the mixing zone, and a diffusive balance $c/t\sim c/Peh^{2}$ gives the scaling for the mixing length $h\sim (t/Pe)^{1/2}$ , as can be seen in figure 4(a). In this linearly unstable regime, the aspect ratio of the fingers is $O(1)$ ; hence, from incompressibility, $u/x\sim v/y\Rightarrow u\sim v$ . The linearized elliptic equation (3.2) further suggests a balance $u/y\sim v/x\sim Rc/y$ , or $u\sim v\sim R$ . The linear scaling of the velocity with the log-viscosity ratio, together with an advection–diffusion balance in (2.13), indicates that $c/t\sim uc/x\sim c/Pex^{2}$ , or $t\sim 1/R^{2}Pe$ and $x\sim 1/RPe$ . That is, at early times, the number of fingers scales linearly with both $R$ and $Pe$ . Figure 4(c) shows a rescaled plot of the number of fingers which collapses well with this scaling. Finally, the Nusselt number is defined as the product of the exponentially growing velocity $u\sim R\text{e}^{\unicode[STIX]{x1D70E}t}$ and concentration perturbations $c^{\prime }\sim \text{e}^{\unicode[STIX]{x1D70E}t}$ integrated over the size of the perturbations $x\sim 1/RPe$ (where $\unicode[STIX]{x1D70E}$ is the growth rate of the instability). Given the time scale identified above, $t\sim 1/R^{2}Pe$ , we collapse the data for the Nusselt number with the scaling $Nu\sim \text{e}^{tR^{2}Pe}/Pe$ (figure 4 e).

At intermediate times the fingers interact nonlinearly causing them to elongate and coarsen. The horizontal velocity remains relatively constant and is solely a function of the log-viscosity ratio, $u=U(R)$ . An advective balance in (2.13) gives the scaling $Uc/h\sim c/t$ , or $h\sim U(R)t$ , and this linear growth of the mixing zone in time can be seen in figure 4(a,b). In fact, we return to the functional form of the velocity $U(R)$ in § 5.2, and find that it can be approximated by $U\sim R$ for small $R$ . The number of fingers, $n$ , in the intermediate regime, follows two distinct coalescence regimes. Initially the coalescence is advectively dominated, and in this limit (2.13) gives the scaling $vc/(1/n)\sim c/t$ . Assuming that the transverse velocity is $O(R)$ and constant, then $n\sim 1/Rt$ . Subsequently, the flow becomes diffusively dominated and (2.13) gives the scaling $c/t\sim c/(Pe/n^{2})\Rightarrow n\sim (t/Pe)^{-1/2}$ . These two scaling laws can be seen in figure 4(c,d). In the intermediate-time regime, the Nusselt number scales with the width of the mixing region ( $h\sim Rt$ ) and the average convective flux, which scales with the velocity $U\sim R$ . Together, this gives the scaling $Nu\sim R^{2}t$ (see figure 4 e,f). These observations suggest that the Nusselt number and growth of the mixing zone are independent of the Péclet number and, after a small amount of time spent advectively coalescing, the finger coalescence becomes independent of the viscosity ratio.

Finally, at late times, a single pair of long, thin fingers counter-propagate and decay through a background concentration gradient. As seen in figure 4(d), all simulations tend to this single-pair (single-maxima) state. Assuming that the concentration deviations from the background are small and applying a long, thin approximation to equation (3.2) results in the scaling $u\sim R$ (as discussed in more detail in § 6). Balancing longitudinal advection and transverse diffusion over a single finger yields the scaling $Rc/h\sim 1/Pe\Rightarrow h\sim RPe$ . This tendency towards a constant mixing length proportional to $RPe$ is shown in figure 4(b). A diffusive balance, $c/t\sim 1/Pe$ , suggests that the time should be scaled by the Péclet number in this late-time regime. Applying the same argument as before, the Nusselt number decays exponentially like $Nu\sim PeR^{2}\text{e}^{-t/Pe}$ .

The transitions between these different regimes are controlled by the relevant time scalings in each regime. The transition from the early-time to intermediate-time regime occurs once the concentration perturbations saturate and the flow becomes nonlinear. Since the perturbations grow exponentially, and the time scale of their growth is $t\sim 1/R^{2}Pe$ , the perturbations will reach a certain amplitude at a time, $t\sim O(1/R^{2}Pe)$ . The transition to the late-time regime occurs once the flow coarsens to a single finger. Since this coarsening process is diffusively dominated, the fingers will coarsen to one finger once the flow has diffused over the entire transverse length. This means the transition between the intermediate-time and late-time regime occurs at $t\sim O(Pe)$ .

The scalings are summarized in table 1. In the following sections, we discuss each of these regimes in more detail with an emphasis placed on understanding the evolution of the transversely averaged concentration.

5.1 Early times: linearly unstable regime

The concentration gradient between the two fluids, which are not moving relative to each other, is initially very high and spreads by diffusion. Neglecting the very small initial perturbations in (3.5), the resultant concentration profile is one-dimensional and given by

(5.1) $$\begin{eqnarray}\displaystyle c(x,t)=\frac{1}{2}+\frac{1}{2}\text{erf}\left(-\frac{x}{\sqrt{4t/Pe}}\right). & & \displaystyle\end{eqnarray}$$

Therefore, before the instability manifests itself, the concentration front widens like $(t/Pe)^{1/2}$ , which corresponds to the early-time scaling of $h$ (see figure 4 a).

Figure 5. (a) $Nu(t)$ , attained from direct numerical simulations, plotted on logarithmic axes for $R=2$ and different $Pe$ as marked. The Nusselt number is strictly decreasing for $Pe=20$ , but has a period of growth for $Pe=30$ , suggesting a point of marginal stability between $Pe=20$ and $30$ . (b,c) Marginal stability curves ( $\unicode[STIX]{x1D70E}=0$ , outlines) and regions of instability ( $\unicode[STIX]{x1D70E}>0$ , shaded areas), for $R=3$ and (b) $Pe=25,200,500$ and (c) $Pe=15,20,25$ . Wavenumbers less than $k=2\unicode[STIX]{x03C0}$ cannot be contained within the domain, and so the flow is stable for $k<2\unicode[STIX]{x03C0}$ , as indicated by the grey region in (c). (d) Plot of the critical Péclet number versus log-viscosity ratio based on the linear stability analysis (black line) and numerical simulations (blue ranges). The lower and upper estimated values of $Pe_{c}$ from our simulations in (d) are given, respectively, by the largest Pe for which $Nu(t)$ monotonically decreases, and by the smallest $Pe$ for which $Nu(t)$ increases at any time.

Table 1. Scalings for $h$ , $n$ and $Nu$ for early, intermediate and late times. The transition from the early-time to intermediate-time regime occurs at $t\sim O(1/R^{2}Pe)$ and the transition from the intermediate-time to late-time regime occurs at $t\sim O(Pe)$ .

When $R>0$ , the flow rapidly develops a viscous-fingering instability in which perturbations grow exponentially. Many authors have explored the onset of viscous fingering in a variety of contexts using linear stability theory. Tan & Homsy (Reference Tan and Homsy1987) found that the instability can be suppressed for all times, in a radial geometry, if the Péclet number is below some critical value. In a planar geometry, however, Pramanik & Mishra (Reference Pramanik and Mishra2015a ) found a time-dependent critical Péclet number which decreases in time, and suggested that there may be no Péclet number for which the flow is always stable.

In this section, we show that there is, in fact, a critical Péclet number below which the flow is always stable in a bounded planar geometry. To motivate the existence of this critical Péclet number, figure 5(a) shows $Nu(t)$ for $R=2$ and small Péclet numbers. For the range of Péclet numbers plotted, the Nusselt number never transitions to power-law growth, suggesting that there are choices of parameters where the flow never enters the nonlinear regime. In fact, we notice that for Péclet numbers less than or equal to 20, the Nusselt number is strictly decreasing, implying the configuration is stable for all times, while for Péclet numbers greater than or equal to 30, the Nusselt number goes through a period of growth. In this section, we perform a linear stability analysis to show the existence of a critical Péclet number for the instability.

We start with a diffusive base-state solution of the unperturbed system $c_{0}(x,t)$ given by (5.1). To accommodate the rapidly varying base state at early times we use a similarity transformation $\unicode[STIX]{x1D709}=x/\sqrt{t}$ , in terms of which (5.1) is steady,

(5.2) $$\begin{eqnarray}\displaystyle c_{0}(\unicode[STIX]{x1D709})=\frac{1}{2}\left[1+\text{erf}\left(\frac{-\unicode[STIX]{x1D709}\sqrt{Pe}}{2}\right)\right]. & & \displaystyle\end{eqnarray}$$

We then linearize equations (2.13), (3.1), and (3.2) about this base state and look for perturbations of the form $u^{\prime }(\unicode[STIX]{x1D709},y,t)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D709})\unicode[STIX]{x1D70F}(t)\text{e}^{\text{i}ky}$ and $c^{\prime }(\unicode[STIX]{x1D709},y,t)=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D709})\unicode[STIX]{x1D70F}(t)\text{e}^{\text{i}ky}$ , which satisfy

(5.3) $$\begin{eqnarray}\displaystyle & \displaystyle \left(\unicode[STIX]{x1D70E}(t_{0})-\frac{\unicode[STIX]{x1D709}}{2t_{0}}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}-\frac{1}{Pe\,t_{0}}\frac{\text{d}^{2}}{\text{d}\unicode[STIX]{x1D709}^{2}}+\frac{k^{2}}{Pe}\right)\unicode[STIX]{x1D6FD}=-\frac{1}{\sqrt{t_{0}}}\frac{\text{d}c_{0}}{\text{d}\unicode[STIX]{x1D709}}\unicode[STIX]{x1D719}, & \displaystyle\end{eqnarray}$$

(5.4) $$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{1}{t_{0}}\frac{\text{d}^{2}}{\text{d}\unicode[STIX]{x1D709}^{2}}-\frac{R}{t_{0}}\frac{\text{d}c_{0}}{\text{d}\unicode[STIX]{x1D709}}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}-k^{2}\right)\unicode[STIX]{x1D719}=-Rk^{2}\unicode[STIX]{x1D6FD}, & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D70E}(t_{0})\equiv (1/\unicode[STIX]{x1D70F})(\text{d}\unicode[STIX]{x1D70F}/\text{d}t)|_{t=t_{0}}$ is the instantaneous growth rate at $t=t_{0}$ , such that $\unicode[STIX]{x1D70F}=\text{e}^{\int _{0}^{t}\unicode[STIX]{x1D70E}\,\text{d}t_{0}}$ (see also Pramanik & Mishra Reference Pramanik and Mishra2015a ). We note that this formulation does not require any assumption of a slowly varying or quasi-steady background. We solve (5.3) and (5.4) by discretizing the domain using standard second-order finite-difference approximations for the differential operators, which yields the matrix eigenvalue problem

(5.5) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D648}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FD}. & & \displaystyle\end{eqnarray}$$

The growth rate of the most unstable mode is given by the maximum eigenvalue of the matrix $\unicode[STIX]{x1D648}$ . This growth rate depends on $Pe$ and $R$ , as well as, time $t_{0}$ and the wavenumber of the perturbation $k$ .

Figure 5(b) shows the marginal stability curve $\unicode[STIX]{x1D70E}(k,t_{0})=0$ , where $\unicode[STIX]{x1D70E}$ is the growth rate of the most unstable mode, for $R=3$ and a variety of Péclet numbers. The system is always initially stable and goes unstable at a critical time $t_{0}^{\ast }>0$ . Zooming into the region around wavenumber $k=2\unicode[STIX]{x03C0}$ (figure 5 c), which is the largest mode that is permissible inside the domain, we notice that for $Pe=20$ , the marginal stability curve lies above $k=2\unicode[STIX]{x03C0}$ for only a finite amount of time: once the marginal stability curve falls below this value, the flow is again stable. In fact, this transition back to stability at large $t_{0}$ is a general feature for all $R$ and $Pe$ and this intermittent stability suggests that if the interface is diffuse enough, the instability can be suppressed, in agreement with experimental evidence (Loggia et al. Reference Loggia, Rakotomalala, Salin and Yortsos1998). Finally, we notice that for Péclet numbers smaller than some critical value $Pe_{c}(R)$ , the growth rate is only positive for wavenumbers smaller than $2\unicode[STIX]{x03C0}$ . These modes do not fit in the domain and the interface is therefore always stable. For example, in figure 5(c) the critical Péclet number lies between 15 and 20.

The transitions out of, and back into, stability, occur as diffusion tends to arrest the instability. The system is initially stable because, for small $t$ , the growth of the interface ( $O(t^{-1/2})$ ) outpaces the exponential growth of the perturbations. Matching the diffusive length scale ( $t^{1/2}/Pe^{1/2}$ ) to the length scale of the most unstable perturbation ( $1/RPe$ ) gives a transition time $t\sim 1/R^{2}Pe$ . At sufficiently large times, the base flow is again stable, because the background concentration gradient has weakened to such an extent that transverse diffusion ( $1/Pey^{2}$ ) can smear out the advective growth of perturbations ( $u(\unicode[STIX]{x2202}\overline{c}/\unicode[STIX]{x2202}x)\sim R(Pe^{1/2}/t^{1/2})$ ). Balancing these two terms for $y\sim O(1)$ gives a transition time to return to stability, $t\sim R^{2}Pe^{3}$ . At some critical Péclet number, $Pe_{c}$ , the time scales of the initial instability and subsequent stabilization match, and the instability is completely suppressed. This balance gives $Pe_{c}\sim 1/R$ . The transition back to stability also indicates that fingering can be prevented by allowing the interface to diffuse before injection for a time $O(R^{2}Pe^{3})$ , or by initializing (for example by pre-mixing) a concentration gradient of width $O(RPe)$ .

Figure 5(d) shows $Pe_{c}(R)$ calculated from the linear stability analysis, which agrees with this predicted scaling. The figure also shows estimates of $Pe_{c}$ from direct numerical simulations, which give a reasonable agreement with the theory.

5.2 Intermediate times: nonlinear coalescence regime

The linear instability results in a number of fingers which grow exponentially and independently of their neighbours. After some time, the fingers begin to interact with each other. Although the nonlinear finger interactions exhibit complex and chaotic patterns and vary significantly over time and from simulation to simulation, the number of fingers, mixing length and Nusselt number are largely indifferent to the exact intermediary mechanisms (see rescaled data in figure 4). The transversely averaged concentration is asymmetric, nonlinear and evolves in a self-similar fashion (figure 6 a). There have been many attempts to model the behaviour of the transversely averaged concentration, with one of the simplest and most widely used models being the empirically derived formula of Koval (Reference Koval1963). While this model has been revisited by multiple authors (Yortsos & Salin Reference Yortsos and Salin2006; Booth Reference Booth2010), a fully closed model is yet to be derived. In this section we start by re-deriving the simple model that was first proposed by Koval (hereafter, the ‘simple Koval model’), and comment on its strengths and shortcomings. In order to address one of these shortcomings, we then propose a simple improvement to the model, which gives a qualitative improvement when compared with the numerical simulations.

Figure 6. (a) Plot of the transversely averaged concentration against the similarity variable $x/t$ . Here $R=2$ , $Pe=1000$ and the time, given by the colour, ranges from $10$ to $20$ . Each curve plotted represents the average of five different simulations. The dashed lines represent the three different model solutions: simple Koval (blue, dashed), fitted Koval (green, dotted) and parabolic Koval (black, dot-dashed). (b) Plot of the transverse variance in concentration for $Pe=2000$ , $4000$ , $8000$ and $16\,000$ at $t=8,4,2$ and $1$ . By sampling at these different times, we normalize for the effect of the onset of the instability. The variance calculated from the simple Koval model is given by the blue dashed line.

The simple Koval model can be derived in the limit where both the aspect ratio of the fingers and the Péclet number are large, ( $hn\gg 1$ and $Pe\gg 1$ respectively). Under these conditions the flow is predominantly horizontal and longitudinal diffusion is negligible. The velocity is calculated by taking the leading-order expansion in $hn$ in (3.2),

(5.6) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}-Ru\frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}y}=R\frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}y}, & & \displaystyle\end{eqnarray}$$

which has solution

(5.7) $$\begin{eqnarray}\displaystyle u=\frac{\text{e}^{Rc}}{\displaystyle \int _{0}^{1}\text{e}^{Rc}\,\text{d}y}-1. & & \displaystyle\end{eqnarray}$$

Substituting this form for the velocity into (2.18) and neglecting longitudinal diffusion gives

(5.8) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\overline{c}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{\displaystyle \int _{0}^{1}c\text{e}^{Rc}\,\text{d}y}{\displaystyle \int _{0}^{1}\text{e}^{Rc}\,\text{d}y}-\overline{c}\right)=0. & & \displaystyle\end{eqnarray}$$

The simple Koval model proceeds under the assumption that the fingered region consists of $\unicode[STIX]{x1D702}_{b}(x)$ leftward propagating fingers of width $w_{b}(x)$ with uniform concentration $c=0$ and $\unicode[STIX]{x1D702}_{f}(x)$ rightward propagating fingers of width $w_{f}(x)$ with uniform concentration $c=1$ . Under these assumptions, equation (5.8) becomes

(5.9) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\overline{c}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{\displaystyle \unicode[STIX]{x1D702}_{f}\int _{-w_{f}}^{w_{f}}\text{e}^{R}\,\text{d}y}{\displaystyle \unicode[STIX]{x1D702}_{f}\int _{-w_{f}}^{w_{f}}\text{e}^{R}\,\text{d}y+\unicode[STIX]{x1D702}_{b}\int _{-w_{b}}^{w_{b}}1\,\text{d}y}-\overline{c}\right)=0. & & \displaystyle\end{eqnarray}$$

In addition, the total area of the fingers has to add up to one, $\unicode[STIX]{x1D702}_{f}w_{f}+\unicode[STIX]{x1D702}_{b}w_{b}=1$ and the total concentration in the forward propagating fingers has to equal the transverse average, $\unicode[STIX]{x1D702}_{f}w_{f}=\overline{c}$ . Combining these constraints and simplifying (5.9) results in a hyperbolic equation for $\overline{c}$ ,

(5.10) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\overline{c}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{M\overline{c}}{M\overline{c}+1-\overline{c}}-\overline{c}\right)=0, & & \displaystyle\end{eqnarray}$$

where $M\equiv \text{e}^{R}=\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{1}$ is the viscosity ratio between the two unmixed fluids. The solution to (5.10) is

(5.11) $$\begin{eqnarray}\displaystyle \overline{c}(x,t)=\left\{\begin{array}{@{}ll@{}}1 & x/t<\displaystyle \frac{1}{M}-1,\\ \displaystyle \frac{1}{M-1}\left(\sqrt{\frac{M}{x/t+1}}-1\right) & \displaystyle \frac{1}{M}-1\leqslant x/t\leqslant M-1,\\ 0 & x/t>M-1.\end{array}\right. & & \displaystyle\end{eqnarray}$$

Although coalescence occurs through a nonlinear diffusive process, the longitudinal spreading of the interface is advectively dominated. As a result, the flow is self-similar in the variable $x/t$ and has finite forward velocity $M-1$ and finite backward velocity $1/M-1$ . This asymmetry comes from the fact that in order to maintain a transversely uniform pressure, the leading, less viscous fingers must travel $M$ times faster than the more viscous surrounding fluid downstream, and the trailing more viscous fingers must travel $1/M$ times as fast as the less viscous surrounding fluid upstream, in the non-travelling frame. Figure 6(a) compares (5.11) to the numerical simulations. The simple Koval model accurately predicts two qualitative features of the nonlinear spreading process: an asymmetric concentration profile, and self-similarity in the variable $x/t$ . However, this model greatly overpredicts the spreading of the mixing zone (figure 6 a). To account for the difference between the model and experiments, Koval, in his original work, empirically fit an effective viscosity $M_{e}$ to the experiments of Blackwell, Rayne & Terry (Reference Blackwell, Rayne and Terry1959), yielding

(5.12) $$\begin{eqnarray}\displaystyle M_{e}=[0.22\text{e}^{R/4}+(1-0.22)]^{4}. & & \displaystyle\end{eqnarray}$$

The prediction of (5.11) with $M$ replaced by $M_{e}$ in (5.12), which we denote the ‘fitted Koval’ model, gives a remarkably good fit with our numerical results (figure 6 a). Indeed, the agreement in figure 6(a) is all the more surprising given that (5.12) was fitted for fluids with a different relationship between viscosity and concentration than we are using here. Nonetheless, in spite of recent attempts, there is no rigorous derivation of this form of effective viscosity ratio. Furthermore, this fitted model tends to break down for large $M$ (Malhotra, Sharma & Lehman Reference Malhotra, Sharma and Lehman2015).

Figure 7. (a) Snapshot of the concentration profile at $t=1$ for a simulation with $Pe=16\,000$ and $R=2$ . Superimposed are lines which follow the peaks (orange) and troughs (blue) in concentration. (b) Concentration profile along peaks (orange) and troughs (blue). (c) Concentration profile in the transverse direction at $x=0$ centred around the peaks (orange) and troughs (blue).

One of the critical assumptions of the Koval model is that the concentration is either exactly one or exactly zero. We interrogate this assumption by plotting the concentration field from a simulation with a large Péclet number ( $Pe=16\,000$ ) in figure 7(a). We find that even at very large $Pe$ , the concentration is not just one or zero but varies in both the horizontal and vertical direction. The concentration along the local maxima and minima of the fingers (figure 7 b) decreases and increases towards the tips, respectively. In the transverse direction, the concentration takes on a single maximum or minimum in each finger, which, in its simplest form, can be approximated by a parabola (figure 7 c). These two factors together result in a much smaller prediction for the transverse variance in concentration than the simple Koval model predicts (figure 6 b). Interestingly, in this limit of large $Pe$ , the variance is independent of the Péclet number, which suggests that the Péclet number has no effect on the effective viscosity in this regime in agreement with the fact that (5.11) and (5.12) have no dependence on $Pe$ .

Motivated by these observations, we suggest a very simple improvement to the simple Koval model, which addresses one of its main assumptions. In the simple Koval model, the viscosity is uniformly given by $e^{R}$ or $1$ in each finger, which follows from the assumption of uniform concentration in each finger. However, we observe that the concentration actually varies across the fingers, and we can approximate this variation as being parabolic. In fact, the significant improvement to the simple model by the empirical fit (5.12) suggests that the main consequence of ignoring this variation is an inaccurate calculation of the effective viscosity. We therefore propose a simple modification of the Koval model in which the viscosity varies with a quadratic concentration profile across each finger; that is, $\unicode[STIX]{x1D707}(y)=\text{e}^{R(1-y^{2}/w_{f}^{2})}$ and $\unicode[STIX]{x1D707}(y)=\text{e}^{R(y^{2}/w_{b}^{2})}$ in the forward and backward propagating fingers, respectively. In all other respects, we retain the same assumptions as in the simple Koval model: the fingers are still assumed to be horizontally uniform, and to obtain a simple analytical solution with the same functional form as the simple Koval model, the mean concentration in each finger is still assumed to be either zero or one.

Under these assumptions, equation (5.9) instead becomes

(5.13) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\overline{c}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{\unicode[STIX]{x1D702}_{f}\displaystyle \int _{-w_{f}}^{w_{f}}\text{e}^{R(1-y^{2}/w_{f}^{2})}\,\text{d}y}{\unicode[STIX]{x1D702}_{f}\displaystyle \int _{-w_{f}}^{w_{f}}\text{e}^{R(1-y^{2}/w_{f}^{2})}\,\text{d}y+\unicode[STIX]{x1D702}_{b}\int _{-w_{b}}^{w_{b}}\text{e}^{R(y^{2}/w_{b}^{2})}\,\text{d}y}-\overline{c}\right)=0. & & \displaystyle\end{eqnarray}$$

Combining (5.13) with the same constraints as before, and solving, results in the same expression for $\overline{c}$ as (5.11) but with an effective viscosity ratio

(5.14) $$\begin{eqnarray}\displaystyle M_{e}=\frac{e^{R}\text{erf}(\sqrt{R})}{\text{erfi}(\sqrt{R})}, & & \displaystyle\end{eqnarray}$$

where $\text{erfi}(x)$ is the imaginary error function. We denote this model as the ‘parabolic Koval’ model. As with the original Koval model, the effective viscosity does not depend on the width or the number of fingers.

Figure 8. Plot of the effective viscosity ratio measured for different values of $R$ and $Pe$ . Each point plotted is calculated by extracting the value of $M$ from a least-squares fit of (5.11) to the transversely averaged concentration profiles $\overline{c}(x,t)$ , at five different times $t=10,11,12,13,14$ and five different simulations. These measurements are then averaged and the error bars represent one standard deviation in these measurements. The three different model predictions are: simple Koval (blue, dashed), fitted Koval (green, dotted) and parabolic Koval (black, dot-dashed).

Figure 8 plots the effective viscosity ratio extracted from the numerical simulations (dots), together with the predictions of the simple Koval model (S-K), the empirically fit effective viscosity (F-K) (5.12) and the analytically derived model with parabolic transverse profiles (P-K) (5.14). The simple Koval model overpredicts the effective viscosity of the fingered region, whereas the parabolic model agrees well with both the empirical fit and numerical experiments. In fact, the parabolic model predicts smaller effective viscosities than the empirical fit for $R>3$ in qualitative agreement with experiments by Malhotra et al. (Reference Malhotra, Sharma and Lehman2015). Although the model agrees well with the data, it remains, of course, an approximation: it does not take into account the along-flow variations in concentration, and it still assumes the concentration (but not the viscosity) is either one or zero in each finger. Nevertheless, we have shown that an accurate effective viscosity in the Koval model can be derived simply by assuming the viscosity varies smoothly in the transverse direction. Accounting for the other approximations in the model is the subject of future work.

Figure 9. Snapshots at $t=500$ for $R=2$ , $Pe=2000$ . (a) Colour map of the concentration with overlaid contours of the raw (solid) and transversely averaged (dashed) concentration. (b) Colour map of $c^{\prime }(x,y)=c(x,y)-\overline{c}(x)$ . (c) Colour map of the horizontal velocity $u$ . (d) Colour map of the vertical velocity $v$ . Note that the $x$ -axis has been compressed by a factor of 10 in these plots.

6.1 Numerical observations

At late times, we find a new flow regime which, to leading order, involves a single pair of fingers counter-propagating through a linear background concentration gradient as shown by the snapshots in figure 9. The concentration field is dominated by a nearly uniform background gradient in the horizontal direction with some small transverse deviations superimposed (figure 9 a). The concentration deviations (figure 9 b) are horizontally uniform and have a single maximum (i.e. they form a single finger). The horizontal velocity $u$ (figure 9 c) tracks closely the concentration deviations while the vertical velocity $v$ (figure 9 d) is only appreciable at the tips.

Figure 10. (a) Plot of the transversely averaged concentration. (b) Plot of the longitudinally averaged concentration $\overline{c}_{L}(y)=\int _{-\unicode[STIX]{x1D6E4}/2}^{\unicode[STIX]{x1D6E4}/2}c(x,y)\,\text{d}x=1/2+\int _{-\unicode[STIX]{x1D6E4}/2}^{\unicode[STIX]{x1D6E4}/2}c^{\prime }(x,y)\,\text{d}x$ . A sinusoidal fit for $t=150$ is given by the dashed black line. In both plots $R=2$ , $Pe=2000$ and the time, given by the colour, ranges from $150$ to $550$ .

Figure 10 shows how the concentration field evolves over time. We find that the transversely averaged concentration, $\overline{c}(x)$ , is linear and steady in the interior. The fluid flow only widens the mixing region by filling in the linear profile (inset to figure 10 a). In addition, we find that $\overline{c}$ is no longer skewed and $\overline{c}=1/2$ is in the middle of the domain. These features are in stark contrast to the previous regime in which $\overline{c}(x)$ was asymmetric and nonlinear. Superimposed on this background concentration field are horizontally uniform deviations which are sinusoidal in the transverse direction (figure 10 b). These deviations decay in time, which ultimately results in a one-dimensional linear concentration field that evolves purely by diffusion in the $x$ direction.

We find that the single-finger state is stable, that is, no tip splitting occurs. The manner by which these fingers are stabilized is distinct from the classical Saffman–Taylor finger where surface tension acts as the stabilizing force. In this case, weak longitudinal concentration gradients and transverse diffusion not only stabilize the fingers but also cause them to decay.

6.2 Asymptotic model

The late-time regime is characterized by a linear background gradient with a single pair of counter-propagating fingers superimposed. The fingers have a very large aspect ratio, and so the velocity is given by (5.7), which for small deviations $c^{\prime }$ reduces to

(6.1) $$\begin{eqnarray}\displaystyle u=Rc^{\prime }+O(c^{\prime 2}). & & \displaystyle\end{eqnarray}$$

We look for a steady interior solution for $\overline{c}$ , for which (2.18) becomes

(6.2) $$\begin{eqnarray}\displaystyle \frac{1}{Pe}\frac{\unicode[STIX]{x2202}^{2}\overline{c}}{\unicode[STIX]{x2202}x^{2}}=O(c^{\prime 2}), & & \displaystyle\end{eqnarray}$$

or

(6.3) $$\begin{eqnarray}\displaystyle \overline{c}=-\unicode[STIX]{x1D6FC}x+{\textstyle \frac{1}{2}}+O(c^{\prime 2}). & & \displaystyle\end{eqnarray}$$

Given that the net change in concentration of the two fluids must be equal and opposite, the concentration at the mid-plane must be $1/2$ , which determines the constant of integration in (6.3).

Substituting the steady transversely averaged concentration (6.3) and velocity (6.1) into equation (2.19) results in a partial differential equation for the evolution of the deviations,

(6.4) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}c^{\prime }}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FC}Rc^{\prime }=\frac{1}{Pe}\frac{\unicode[STIX]{x2202}^{2}c^{\prime }}{\unicode[STIX]{x2202}y^{2}}+O\left(\frac{c^{\prime }}{Peh^{2}}\right)+O(c^{\prime 2}). & & \displaystyle\end{eqnarray}$$

The leading-order behaviour of (6.4) is a balance between the growth/decay of the concentration deviations, advection of the background concentration gradient and transverse diffusion. Advection of the background tends to cause the deviations to grow since positive deviations tend to move high concentrations downstream (and negative deviations move low concentrations upstream), while diffusion causes them to attenuate. This competition results in the exponential decay of the fingers and eventual shutdown of the instability. Furthermore, this equation is independent of $x$ ; therefore, the deviations must be horizontally uniform, as observed. The single-finger solution to the leading-order truncation of (6.4) is

(6.5) $$\begin{eqnarray}\displaystyle c^{\prime }(y,t)=\text{sin}(2\unicode[STIX]{x03C0}y)\text{e}^{-\unicode[STIX]{x1D6FE}(t-t^{\ast })}, & & \displaystyle\end{eqnarray}$$

where $t^{\ast }$ is a virtual origin relating to the transition between regimes and

(6.6) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}=\frac{4\unicode[STIX]{x03C0}^{2}}{Pe}-\unicode[STIX]{x1D6FC}R. & & \displaystyle\end{eqnarray}$$

Note that, while a solution of (6.4) with any integer number of fingers is permissible, solutions with more fingers decay more rapidly over time, and the solution with $k=2\unicode[STIX]{x03C0}$ (6.5) is the slowest decaying mode.

The slope $\unicode[STIX]{x1D6FC}$ of the interior profile in (6.3) is set by the amount of mixing that occurs during the intermediate, nonlinear regime. That regime lasts for a time $t\sim O(Pe)$ during which the mixing zone grows linearly in time, $h\sim Rt$ . Therefore, once the system has reached the single-finger regime, the width of the mixing zone will have become $h\approx 1/\unicode[STIX]{x1D6FC}\sim RPe$ , such that $\unicode[STIX]{x1D6FC}R=\hat{A}/Pe$ , for some constant $\hat{A}$ . We fit $\hat{A}=24.9$ to the collapsed transversely averaged concentration profiles (figure 11 b).

We verify this model by measuring $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D6FE}$ from the numerical simulations. We calculate $\unicode[STIX]{x1D6FC}$ by measuring the slope of $\overline{c}$ at $x=0$ at some late time, and $\unicode[STIX]{x1D6FE}$ by measuring the decay rate of the maximum of $c^{\prime }$ at the mid-plane. Plots of the numerically measured $\unicode[STIX]{x1D6FE}$ and $\unicode[STIX]{x1D6FC}R$ are given in figure 12(a) and both quantities exhibit the predicted $1/Pe$ scaling. Finally, the validity of (6.6) is tested by plotting the ratio of $\unicode[STIX]{x1D6FE}$ measured from the simulations and $\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC})$ calculated using (6.6). This quantity is plotted in figure 12(b) and deviates by a maximum of 4 % over a range of Péclet numbers and log-viscosity ratios.

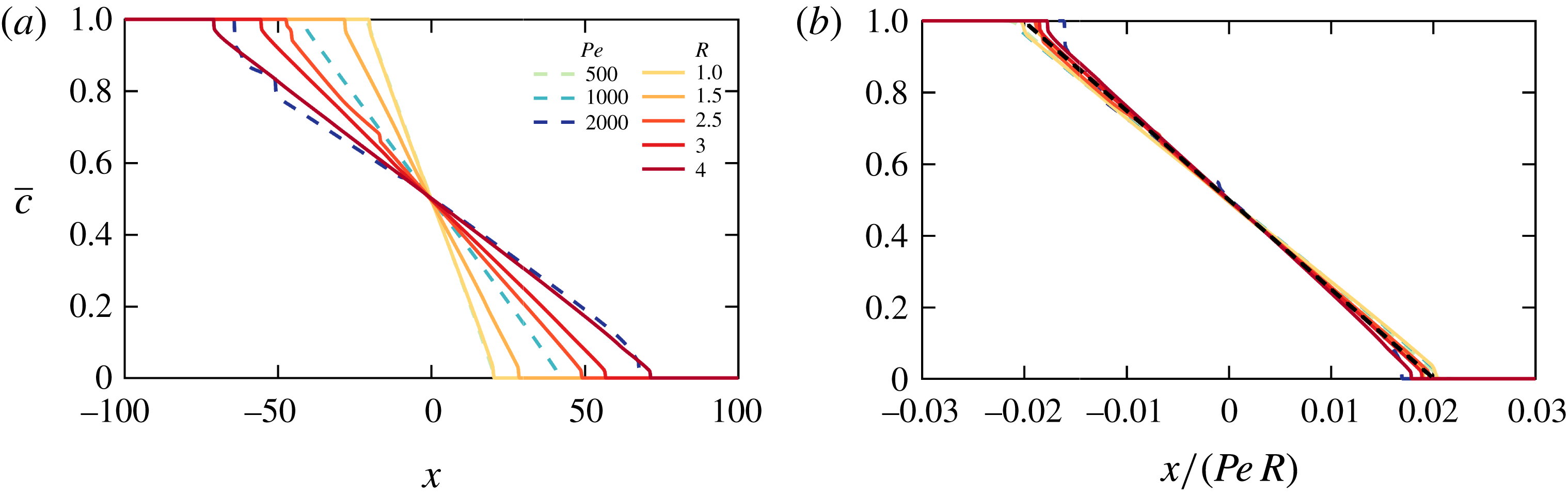
Figure 11. (a) Plots of $\overline{c}(x)$ for $R=2$ , $Pe=500,1000,2000$ (dashed) and $Pe=1000$ and $R=1,1.5,2.5,3,4$ (solid) at $t=200$ . (b) $\overline{c}$ as a function of $x/(RPe)$ , with the fitted line $\overline{c}=1/2-24.9x/RPe$ (black, dashed).

Figure 12. (a) Plot of $\unicode[STIX]{x1D6FE}$ (circles) and $\unicode[STIX]{x1D6FC}R$ (diamonds) as functions of $Pe$ and $R$ (colours). (b) Ratio of $\unicode[STIX]{x1D6FE}$ , measured from the simulations as the decay rate of the maximum of $c^{\prime }$ at $x=0$ , to $\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D6FC}R)$ , calculated using (6.6) where $\unicode[STIX]{x1D6FC}$ is the slope of $\overline{c}$ measured at $t>200$ .

6.3 Total convective mixing

One of the major implications of this final single-finger exchange-flow regime is that the viscous-fingering instability can only generate a finite amount of convective mixing. In figure 13(a) we plot the time integral of the convective flux through the mid-plane,

(6.7) $$\begin{eqnarray}\displaystyle F=\int _{0}^{\infty }\int _{0}^{1}uc^{\prime }|_{x=0}\,\text{d}y\,\text{d}t, & & \displaystyle\end{eqnarray}$$

as a function of the Péclet number and log-viscosity ratio. We find that the flux increases linearly with both $Pe$ and $R$ for $Pe\gg 1$ , and can be fit by the functional form $F=\hat{a}R(Pe-\hat{b}/R)$ , where the shift in the Péclet number, $\hat{b}/R$ , corresponds to the onset of the instability as described in § 5.1. We find that the numerical data are best fit with $\hat{a}=5.3\times 10^{-3}$ and $\hat{b}=45$ (solid lines in figure 13 a).

Of course, provided advection dominates the horizontal transport, the quantity $F$ can also be directly related to the slope $\unicode[STIX]{x1D6FC}$ of the late-time profiles, by mass conservation. Such a balance gives

(6.8) $$\begin{eqnarray}\displaystyle F\approx \int _{0}^{\infty }\bar{c}\,\text{d}x\approx \frac{1}{8\unicode[STIX]{x1D6FC}}. & & \displaystyle\end{eqnarray}$$

For the three values of $R$ plotted, we find that this prediction gives good agreement for $Pe>O(100)$ (figure 13 b), which suggests that for the range of $R$ plotted, horizontal diffusion plays a negligible role in mixing for $Pe>O(100)$ .

Figure 13. (a) Time-integrated convective exchange flux $F$ (6.7) between the two fluids as a function of $Pe$ and $R$ (colours), as calculated from the numerical simulations. In order to calculate the infinite time integral in (6.7), we integrate the numerical data out to $t=200$ , which is well into the late-time regime in all simulations, and fit a decaying exponential function $E(t)$ to the flux $\int _{0}^{1}uc^{\prime }|_{x=0}\,\text{d}y$ for subsequent times such that $F=\int _{0}^{200}\int _{0}^{1}uc^{\prime }|_{x=0}\,\text{d}y\,\text{d}t+\int _{200}^{\infty }E(t)\,\text{d}t$ . The lines of best fit (black) correspond to the fit $F=5.3\times 10^{-3}R(Pe-45/R)$ . (b) Ratio of the time-integrated convective exchange flux and the final slope of the transversely averaged concentration.