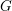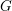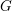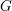1 Introduction
Let
![]() ${\mathcal{C}}$
be a triangulated category equipped with a compatible symmetric monoidal structure. A central problem in studying
${\mathcal{C}}$
be a triangulated category equipped with a compatible symmetric monoidal structure. A central problem in studying
![]() ${\mathcal{C}}$
is the classification of its thick tensor ideals. This problem can be reformulated [Reference BalmerBal05] as determining the Balmer spectrum
${\mathcal{C}}$
is the classification of its thick tensor ideals. This problem can be reformulated [Reference BalmerBal05] as determining the Balmer spectrum
![]() $\operatorname{Spc}({\mathcal{C}})$
, a topological space associated to
$\operatorname{Spc}({\mathcal{C}})$
, a topological space associated to
![]() ${\mathcal{C}}$
whose points are the prime ideals of
${\mathcal{C}}$
whose points are the prime ideals of
![]() ${\mathcal{C}}$
. One of the first examples where a complete description of
${\mathcal{C}}$
. One of the first examples where a complete description of
![]() $\operatorname{Spc}({\mathcal{C}})$
was obtained is the thick subcategory theorem of Hopkins–Smith [Reference Hopkins and SmithHS98] for the category of finite spectra, which is fundamental to our understanding of the stable homotopy category. In recent years there has been significant progress towards obtaining such a description also for the category of finite genuine
$\operatorname{Spc}({\mathcal{C}})$
was obtained is the thick subcategory theorem of Hopkins–Smith [Reference Hopkins and SmithHS98] for the category of finite spectra, which is fundamental to our understanding of the stable homotopy category. In recent years there has been significant progress towards obtaining such a description also for the category of finite genuine
![]() $G$
-spectra
$G$
-spectra
![]() ${\mathcal{S}}{\mathcal{H}}_{G}^{c}$
for a finite group
${\mathcal{S}}{\mathcal{H}}_{G}^{c}$
for a finite group
![]() $G$
. Balmer–Sanders [Reference Balmer and SandersBS17], building on unpublished work of Strickland, gave a description of the underlying set of
$G$
. Balmer–Sanders [Reference Balmer and SandersBS17], building on unpublished work of Strickland, gave a description of the underlying set of
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G}^{c})$
and showed that the topology and hence the classification of thick tensor ideals is determined by the inclusions between the prime ideals. They further determined which inclusions occur for
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G}^{c})$
and showed that the topology and hence the classification of thick tensor ideals is determined by the inclusions between the prime ideals. They further determined which inclusions occur for
![]() $G=\mathbb{Z}/p$
and deduced a complete description of the Balmer spectrum for all finite groups
$G=\mathbb{Z}/p$
and deduced a complete description of the Balmer spectrum for all finite groups
![]() $G$
of square-free order. This classification was extended to all finite abelian groups in [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19], by computing the height shift of the generalized Tate construction for Lubin–Tate theory as well as making use of fixed-point properties of explicit finite equivariant complexes previously considered by Arone [Reference AroneAro98] and Arone–Lesh [Reference Arone and LeshAL17].
$G$
of square-free order. This classification was extended to all finite abelian groups in [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19], by computing the height shift of the generalized Tate construction for Lubin–Tate theory as well as making use of fixed-point properties of explicit finite equivariant complexes previously considered by Arone [Reference AroneAro98] and Arone–Lesh [Reference Arone and LeshAL17].
The goal of the present paper is to generalize these results to the category
![]() ${\mathcal{S}}{\mathcal{H}}_{G}^{c}$
of finite genuine
${\mathcal{S}}{\mathcal{H}}_{G}^{c}$
of finite genuine
![]() $G$
-spectra for a compact Lie group
$G$
-spectra for a compact Lie group
![]() $G$
. Similarly to the finite group case, we obtain a complete description of
$G$
. Similarly to the finite group case, we obtain a complete description of
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G}^{c})$
as a set for all compact Lie groups, and a classification of the Balmer topology and the tt-ideals for all abelian compact Lie groups, in particular tori. While some of the structural properties are similar to the finite group case, there are also new phenomena, the most notable being the interplay of the Hausdorff topology on the space of closed subgroups of
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G}^{c})$
as a set for all compact Lie groups, and a classification of the Balmer topology and the tt-ideals for all abelian compact Lie groups, in particular tori. While some of the structural properties are similar to the finite group case, there are also new phenomena, the most notable being the interplay of the Hausdorff topology on the space of closed subgroups of
![]() $G$
(which is discrete for finite groups) and the Balmer topology on
$G$
(which is discrete for finite groups) and the Balmer topology on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G}^{c})$
. In particular, it is no longer true that the Balmer topology is determined by the inclusions among prime ideals alone. Another difference to the finite group case is that even in the
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G}^{c})$
. In particular, it is no longer true that the Balmer topology is determined by the inclusions among prime ideals alone. Another difference to the finite group case is that even in the
![]() $p$
-local category
$p$
-local category
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, not every thick tensor ideal is finitely generated.
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, not every thick tensor ideal is finitely generated.
Statement of the results
We now describe the results of this paper in more detail. Recall that a thick tensor ideal (
![]() $=$
tt-ideal) in a tensor triangulated category
$=$
tt-ideal) in a tensor triangulated category
![]() $({\mathcal{C}},\otimes ,\unicode[STIX]{x1D7D9})$
is a triangulated subcategory that is closed under retracts and tensor product with an arbitrary object of
$({\mathcal{C}},\otimes ,\unicode[STIX]{x1D7D9})$
is a triangulated subcategory that is closed under retracts and tensor product with an arbitrary object of
![]() ${\mathcal{C}}$
. A proper tt-ideal
${\mathcal{C}}$
. A proper tt-ideal
![]() $I$
is said to be prime if
$I$
is said to be prime if
![]() $X\otimes Y\in I$
implies that
$X\otimes Y\in I$
implies that
![]() $X\in I$
or
$X\in I$
or
![]() $Y\in I$
. The Balmer spectrum is the set of all prime tt-ideals, with Balmer topology generated by the closed sets
$Y\in I$
. The Balmer spectrum is the set of all prime tt-ideals, with Balmer topology generated by the closed sets
![]() $\operatorname{supp}(X)=\{{\wp}\mid X\notin {\wp}\}$
for all
$\operatorname{supp}(X)=\{{\wp}\mid X\notin {\wp}\}$
for all
![]() $X\in {\mathcal{C}}$
. We are interested in determining this spectrum
$X\in {\mathcal{C}}$
. We are interested in determining this spectrum
![]() $\operatorname{Spc}({\mathcal{C}})$
in the case where
$\operatorname{Spc}({\mathcal{C}})$
in the case where
![]() ${\mathcal{C}}$
is the homotopy category
${\mathcal{C}}$
is the homotopy category
![]() ${\mathcal{S}}{\mathcal{H}}_{G}^{c}$
of finite
${\mathcal{S}}{\mathcal{H}}_{G}^{c}$
of finite
![]() $G$
-spectra for a compact Lie group
$G$
-spectra for a compact Lie group
![]() $G$
with the smash product
$G$
with the smash product
![]() $\wedge$
as the monoidal product. For simplicity, we work in the
$\wedge$
as the monoidal product. For simplicity, we work in the
![]() $p$
-local homotopy category
$p$
-local homotopy category
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, from which the global result can be reconstructed as explained in [Reference Balmer and SandersBS17, § 6]. We rely on the computation of the spectrum of the homotopy category of non-equivariant finite
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, from which the global result can be reconstructed as explained in [Reference Balmer and SandersBS17, § 6]. We rely on the computation of the spectrum of the homotopy category of non-equivariant finite
![]() $p$
-local spectra, due to Hopkins and Smith [Reference Hopkins and SmithHS98], which we briefly recall. Let
$p$
-local spectra, due to Hopkins and Smith [Reference Hopkins and SmithHS98], which we briefly recall. Let
![]() $\overline{\mathbb{N}}=\mathbb{Z}_{{\geqslant}0}\cup \{\infty \}$
. Then every prime ideal is of the form
$\overline{\mathbb{N}}=\mathbb{Z}_{{\geqslant}0}\cup \{\infty \}$
. Then every prime ideal is of the form
![]() $P(n)=\{X\mid K(n-1)_{\ast }(X)=0\}$
for some
$P(n)=\{X\mid K(n-1)_{\ast }(X)=0\}$
for some
![]() $n\in \overline{\mathbb{N}}_{{>}0}$
, where
$n\in \overline{\mathbb{N}}_{{>}0}$
, where
![]() $K(n)$
denotes the
$K(n)$
denotes the
![]() $n$
th Morava
$n$
th Morava
![]() $K$
-theory. These primes
$K$
-theory. These primes
![]() $P(n)$
are pairwise distinct and form a descending chain
$P(n)$
are pairwise distinct and form a descending chain
In order to construct prime ideals for finite
![]() $G$
-spectra, one makes use of the geometric fixed point functors
$G$
-spectra, one makes use of the geometric fixed point functors
for all closed subgroups
![]() $H$
of
$H$
of
![]() $G$
. Since these functors are symmetric monoidal, the subcategories
$G$
. Since these functors are symmetric monoidal, the subcategories
are again prime ideals. Our first result (Theorem 3.14) then says the following.
Theorem 1.1 (The underlying set of
 $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
).
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
).
Let
![]() $G$
be a compact Lie group. Then every prime ideal of the homotopy category of finite
$G$
be a compact Lie group. Then every prime ideal of the homotopy category of finite
![]() $p$
-local
$p$
-local
![]() $G$
-spectra
$G$
-spectra
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
is of the form
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
is of the form
![]() $P_{G}(H,n)$
for some closed subgroup
$P_{G}(H,n)$
for some closed subgroup
![]() $H$
of
$H$
of
![]() $G$
and
$G$
and
![]() $n\in \overline{\mathbb{N}}_{{>}0}$
. Moreover,
$n\in \overline{\mathbb{N}}_{{>}0}$
. Moreover,
![]() $P_{G}(H,m)=P_{G}(K,n)$
if and only if
$P_{G}(H,m)=P_{G}(K,n)$
if and only if
![]() $H$
is
$H$
is
![]() $G$
-conjugate to
$G$
-conjugate to
![]() $K$
and
$K$
and
![]() $m=n$
.
$m=n$
.
The case of finite groups is due to Balmer–Sanders [Reference Balmer and SandersBS17]. Our proof is a bit different and builds on a general method introduced by Hovey–Palmieri–Strickland in [Reference Hovey, Palmieri and StricklandHPS97].
We then study the Balmer topology on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
. For general
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
. For general
![]() $G$
, our main result says that it can be expressed in terms of the inclusions between prime ideals and the Hausdorff topology on the set
$G$
, our main result says that it can be expressed in terms of the inclusions between prime ideals and the Hausdorff topology on the set
![]() $\operatorname{Sub}(G)$
of closed subgroups of
$\operatorname{Sub}(G)$
of closed subgroups of
![]() $G$
. Let
$G$
. Let
![]() $\operatorname{Sub}(G)/G$
denote the orbit space by the conjugation
$\operatorname{Sub}(G)/G$
denote the orbit space by the conjugation
![]() $G$
-action, equipped with the quotient topology making it a compact and totally disconnected Hausdorff space [Reference tom DiecktD79, Theorem 5.6.1]. Using the poset structure on the set of prime ideals, we define a function
$G$
-action, equipped with the quotient topology making it a compact and totally disconnected Hausdorff space [Reference tom DiecktD79, Theorem 5.6.1]. Using the poset structure on the set of prime ideals, we define a function
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
to be admissible if
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
to be admissible if
![]() $P_{G}(K,f(K))$
is not contained in
$P_{G}(K,f(K))$
is not contained in
![]() $P_{G}(H,f(H)+1)$
for all subgroups
$P_{G}(H,f(H)+1)$
for all subgroups
![]() $K,H$
with
$K,H$
with
![]() $f(H)<\infty$
. The Balmer topology can then be described in the following way (Corollary 5.8).
$f(H)<\infty$
. The Balmer topology can then be described in the following way (Corollary 5.8).
Theorem 1.2 (The topology on
 $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
).
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
).
For every compact Lie group
![]() $G$
, the open sets
$G$
, the open sets
are a basis for the Balmer topology on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
, where
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
, where
![]() $f$
ranges through all locally constant admissible functions
$f$
ranges through all locally constant admissible functions
![]() $\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
.
$\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
.
Since admissibility depends only on the poset structure on the set of prime ideals, the Balmer topology depends only on this poset structure and the Hausdorff topology on
![]() $\operatorname{Sub}(G)/G$
. Consequently, the classification of tt-ideals can also be described in terms of admissible functions. Given a finite
$\operatorname{Sub}(G)/G$
. Consequently, the classification of tt-ideals can also be described in terms of admissible functions. Given a finite
![]() $p$
-local
$p$
-local
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
, let
$X$
, let
![]() $\text{type}_{X}:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
be the type function of
$\text{type}_{X}:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
be the type function of
![]() $X$
, which assigns to a conjugacy class
$X$
, which assigns to a conjugacy class
![]() $[H]$
the chromatic type of the geometric fixed points
$[H]$
the chromatic type of the geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{H}(X)$
, i.e., the minimal
$\unicode[STIX]{x1D6F7}^{H}(X)$
, i.e., the minimal
![]() $n$
such that
$n$
such that
![]() $\unicode[STIX]{x1D6F7}^{H}(X)\notin P(n+1)$
. This definition extends to tt-ideals
$\unicode[STIX]{x1D6F7}^{H}(X)\notin P(n+1)$
. This definition extends to tt-ideals
![]() $I$
, via
$I$
, via
![]() $\text{type}_{I}(H)=\min (\text{type}_{X}(H)\mid X\in I)$
. Then we have the following (Theorem 5.3).
$\text{type}_{I}(H)=\min (\text{type}_{X}(H)\mid X\in I)$
. Then we have the following (Theorem 5.3).
Theorem 1.3 (Classification of tt-ideals in
 ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
).
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
).
Let
![]() $G$
be a compact Lie group.
$G$
be a compact Lie group.
(i) The assignment
 $I\mapsto \text{type}_{I}$
defines a bijection from the set of tt-ideals in the homotopy category of finite
$I\mapsto \text{type}_{I}$
defines a bijection from the set of tt-ideals in the homotopy category of finite
 $p$
-local
$p$
-local
 $G$
-spectra
$G$
-spectra
 ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
to the set of upper semi-continuous admissible functions, i.e., those admissible functions
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
to the set of upper semi-continuous admissible functions, i.e., those admissible functions
 $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
for which the preimage
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
for which the preimage
 $f^{-1}([0,n))$
is open for all
$f^{-1}([0,n))$
is open for all
 $n\in \overline{\mathbb{N}}$
.
$n\in \overline{\mathbb{N}}$
.(ii) Such a tt-ideal
 $I$
is finitely generated if and only if its type function
$I$
is finitely generated if and only if its type function
 $\text{type}_{I}$
is locally constant.
$\text{type}_{I}$
is locally constant.
The last item can be reformulated as saying that given a function
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
, there exists a finite
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
, there exists a finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
with
$X$
with
![]() $\text{type}_{X}=f$
if and only if
$\text{type}_{X}=f$
if and only if
![]() $f$
is admissible and locally constant.
$f$
is admissible and locally constant.
In order to obtain an explicit description of the Balmer topology and the classification of tt-ideals, it is hence necessary to understand the poset structure on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
and the topology on
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
and the topology on
![]() $\operatorname{Sub}(G)/G$
. The latter topology is fairly well understood thanks to work of Montgomery–Zippin [Reference Montgomery and ZippinMZ42] and tom Dieck [Reference tom DiecktD79, § 5.6]. Unravelling the definitions, determining the poset structure boils down to the following basic geometric question: Given two closed subgroups
$\operatorname{Sub}(G)/G$
. The latter topology is fairly well understood thanks to work of Montgomery–Zippin [Reference Montgomery and ZippinMZ42] and tom Dieck [Reference tom DiecktD79, § 5.6]. Unravelling the definitions, determining the poset structure boils down to the following basic geometric question: Given two closed subgroups
![]() $K$
and
$K$
and
![]() $H$
of
$H$
of
![]() $G$
and numbers
$G$
and numbers
![]() $n,m\in \overline{\mathbb{N}}_{{>}0}$
, does there exist a finite
$n,m\in \overline{\mathbb{N}}_{{>}0}$
, does there exist a finite
![]() $G$
-CW complex
$G$
-CW complex
![]() $X$
such that the
$X$
such that the
![]() $K$
-fixed points
$K$
-fixed points
![]() $X^{K}$
have type
$X^{K}$
have type
![]() ${\geqslant}n$
and the
${\geqslant}n$
and the
![]() $H$
-fixed points
$H$
-fixed points
![]() $X^{H}$
have type
$X^{H}$
have type
![]() ${<}m$
? The answer to this question is ‘yes’ if and only if
${<}m$
? The answer to this question is ‘yes’ if and only if
![]() $P_{G}(K,n)\not \subseteq P_{G}(H,m)$
.
$P_{G}(K,n)\not \subseteq P_{G}(H,m)$
.
This problem appears to be difficult in general and is already wide open for general finite groups
![]() $G$
. For abelian compact Lie groups
$G$
. For abelian compact Lie groups
![]() $A$
, however, the answer is as follows (Theorem 7.1). Here, we write
$A$
, however, the answer is as follows (Theorem 7.1). Here, we write
![]() $rk_{p}(A^{\prime })$
for the
$rk_{p}(A^{\prime })$
for the
![]() $p$
-rank of a finite abelian group
$p$
-rank of a finite abelian group
![]() $A^{\prime }$
, i.e., the dimension of
$A^{\prime }$
, i.e., the dimension of
![]() $A^{\prime }\otimes \mathbb{Z}/p$
over
$A^{\prime }\otimes \mathbb{Z}/p$
over
![]() $\mathbb{Z}/p$
.
$\mathbb{Z}/p$
.
Theorem 1.4 (Abelian groups).
Let
![]() $A$
be an abelian compact Lie group. Then we have an inclusion
$A$
be an abelian compact Lie group. Then we have an inclusion
![]() $P_{A}(K,n)\subseteq P_{A}(H,m)$
if and only if
$P_{A}(K,n)\subseteq P_{A}(H,m)$
if and only if
![]() $K$
is a subgroup of
$K$
is a subgroup of
![]() $H$
,
$H$
,
![]() $\unicode[STIX]{x1D70B}_{0}(H/K)$
is a
$\unicode[STIX]{x1D70B}_{0}(H/K)$
is a
![]() $p$
-group and
$p$
-group and
Hence, a function
![]() $f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
is admissible if and only if
$f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
is admissible if and only if
for all
![]() $K\subseteq H$
with
$K\subseteq H$
with
![]() $\unicode[STIX]{x1D70B}_{0}(H/K)$
a
$\unicode[STIX]{x1D70B}_{0}(H/K)$
a
![]() $p$
-group.
$p$
-group.
Figure 1 is a depiction of the Balmer spectrum for the circle group. Note in particular that if
![]() $K\subseteq H$
is a subgroup with quotient
$K\subseteq H$
is a subgroup with quotient
![]() $H/K$
a torus, then there is an inclusion
$H/K$
a torus, then there is an inclusion
![]() $P_{A}(K,n)\subseteq P_{A}(H,n)$
for every
$P_{A}(K,n)\subseteq P_{A}(H,n)$
for every
![]() $n$
, as follows from a Morava
$n$
, as follows from a Morava
![]() $K$
-theory version of the classical Borel Localization Theorem. This is the main new ingredient in addition to the finite abelian case of [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19].
$K$
-theory version of the classical Borel Localization Theorem. This is the main new ingredient in addition to the finite abelian case of [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19].

Figure 1. An illustration of the
![]() $p$
-local Balmer spectrum for the circle group
$p$
-local Balmer spectrum for the circle group
![]() $\mathbb{T}$
. We refer to Figure 3 for an interpretation of this picture.
$\mathbb{T}$
. We refer to Figure 3 for an interpretation of this picture.
For general compact Lie groups
![]() $G$
, we get a complete answer for all but finitely many
$G$
, we get a complete answer for all but finitely many
![]() $p$
, namely those
$p$
, namely those
![]() $p$
appearing as divisors of the order of Weyl groups
$p$
appearing as divisors of the order of Weyl groups
![]() $|W_{G}H|$
, where
$|W_{G}H|$
, where
![]() $H$
ranges through all closed subgroups with finite Weyl group in
$H$
ranges through all closed subgroups with finite Weyl group in
![]() $G$
(that this number is indeed finite is a theorem of tom Dieck [Reference tom DiecktD77, Theorem 1]). This is described in Theorem 8.1. Finally, if one is willing to study the question simultaneously for all compact Lie groups, it is possible to reduce it to the case where
$G$
(that this number is indeed finite is a theorem of tom Dieck [Reference tom DiecktD77, Theorem 1]). This is described in Theorem 8.1. Finally, if one is willing to study the question simultaneously for all compact Lie groups, it is possible to reduce it to the case where
![]() $G$
is an extension of a finite
$G$
is an extension of a finite
![]() $p$
-group by an abelian compact Lie group, see § 6.5.
$p$
-group by an abelian compact Lie group, see § 6.5.
Remark 1.5. The Balmer spectrum
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,\mathbb{Q}}^{c})$
of the homotopy category of finite rational
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,\mathbb{Q}}^{c})$
of the homotopy category of finite rational
![]() $G$
-spectra was determined for all compact Lie groups
$G$
-spectra was determined for all compact Lie groups
![]() $G$
in [Reference GreenleesGre19], but this also follows from Theorem 6.2 (poset structure) and Corollary 5.8 (topology).
$G$
in [Reference GreenleesGre19], but this also follows from Theorem 6.2 (poset structure) and Corollary 5.8 (topology).
2 Recollections
Let us begin by quickly recalling the proof of the classical thick subcategory theorem as well as collecting some basic notions from stable equivariant homotopy theory that will be used throughout the paper.
As explained in [Reference Balmer and SandersBS17, § 6] for finite groups, the computation of
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G}^{c})$
for a compact Lie group
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G}^{c})$
for a compact Lie group
![]() $G$
may be separated into that of
$G$
may be separated into that of
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
for all primes
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
for all primes
![]() $p$
. Throughout the paper, we will therefore work in the
$p$
. Throughout the paper, we will therefore work in the
![]() $p$
-local homotopy category for a fixed prime
$p$
-local homotopy category for a fixed prime
![]() $p$
, and all our constructions are implicitly
$p$
, and all our constructions are implicitly
![]() $p$
-local.
$p$
-local.
2.1 The classical thick subcategory theorem
As the prototypical example, we quickly recall the key steps in the computation of the Balmer spectrum of the homotopy category of finite non-equivariant
![]() $p$
-local spectra
$p$
-local spectra
![]() ${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
, following Hopkins and Smith [Reference Hopkins and SmithHS98].
${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
, following Hopkins and Smith [Reference Hopkins and SmithHS98].
For
![]() $n\in \mathbb{N}_{{>}0}$
, let
$n\in \mathbb{N}_{{>}0}$
, let
![]() $K(n)$
denote the
$K(n)$
denote the
![]() $n$
th Morava
$n$
th Morava
![]() $K$
-theory spectrum at
$K$
-theory spectrum at
![]() $p$
, with coefficients
$p$
, with coefficients
![]() $K(n)_{\ast }=\mathbb{F}_{p}[v_{n}^{\pm 1}]$
and
$K(n)_{\ast }=\mathbb{F}_{p}[v_{n}^{\pm 1}]$
and
![]() $|v_{n}|=2(p^{n}-1)$
. Furthermore,
$|v_{n}|=2(p^{n}-1)$
. Furthermore,
![]() $K(0)$
is defined to be the rational Eilenberg–MacLane spectrum
$K(0)$
is defined to be the rational Eilenberg–MacLane spectrum
![]() $H\mathbb{Q}$
. For
$H\mathbb{Q}$
. For
![]() $n>0$
we write
$n>0$
we write
and
![]() $P(\infty )=\bigcap _{n\in \mathbb{N}}P(n)$
for the set of all contractible finite
$P(\infty )=\bigcap _{n\in \mathbb{N}}P(n)$
for the set of all contractible finite
![]() $p$
-local spectra. Every
$p$
-local spectra. Every
![]() $P(n)$
is a prime ideal, since the
$P(n)$
is a prime ideal, since the
![]() $K(n)$
satisfy a Künneth formula. Moreover, note that
$K(n)$
satisfy a Künneth formula. Moreover, note that
![]() ${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
is generated by the unit of the smash product, the
${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
is generated by the unit of the smash product, the
![]() $p$
-local sphere spectrum, so any thick subcategory is automatically a tensor ideal. The thick subcategory theorem [Reference Hopkins and SmithHS98, Theorem 7] for
$p$
-local sphere spectrum, so any thick subcategory is automatically a tensor ideal. The thick subcategory theorem [Reference Hopkins and SmithHS98, Theorem 7] for
![]() ${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
provides a complete computation of the Balmer spectrum
${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
provides a complete computation of the Balmer spectrum
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{(p)}^{c})$
.
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{(p)}^{c})$
.
Theorem 2.1 (Hopkins–Smith).
If
![]() ${\mathcal{C}}\subseteq {\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
is a proper thick subcategory, then there exists a unique
${\mathcal{C}}\subseteq {\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
is a proper thick subcategory, then there exists a unique
![]() $n\in \overline{\mathbb{N}}_{{>}0}$
such that
$n\in \overline{\mathbb{N}}_{{>}0}$
such that
![]() ${\mathcal{C}}=P(n)$
. Moreover, there are proper inclusions
${\mathcal{C}}=P(n)$
. Moreover, there are proper inclusions
The proof can be divided into three steps.
(i) Firstly, Ravenel [Reference RavenelRav84, Theorem 2.11] showed that if
 $n>0$
and
$n>0$
and
 $X$
is a finite spectrum for which
$X$
is a finite spectrum for which
 $K(n)_{\ast }(X)=0$
, then also
$K(n)_{\ast }(X)=0$
, then also
 $K(n-1)_{\ast }(X)=0$
. This translates into the inclusion
$K(n-1)_{\ast }(X)=0$
. This translates into the inclusion
 $P(n+1)\subseteq P(n)$
. Given a finite spectrum
$P(n+1)\subseteq P(n)$
. Given a finite spectrum
 $X$
, there hence exists a maximal
$X$
, there hence exists a maximal
 $n$
such that
$n$
such that
 $X\in P(n)$
. This
$X\in P(n)$
. This
 $n$
is called the type of
$n$
is called the type of
 $X$
. If
$X$
. If
 $X\notin P(1)$
, or in other words, if the rational homology of
$X\notin P(1)$
, or in other words, if the rational homology of
 $X$
is non-trivial,
$X$
is non-trivial,
 $X$
is said to be of type
$X$
is said to be of type
 $0$
.
$0$
.(ii) Secondly, these inclusions are all proper, as was first shown by Mitchell [Reference MitchellMit85], by constructing a finite spectrum
 $F(n)$
with
$F(n)$
with
 $K(n)_{\ast }(F(n))\neq 0$
and
$K(n)_{\ast }(F(n))\neq 0$
and
 $K(n-1)_{\ast }(F(n))=0$
.
$K(n-1)_{\ast }(F(n))=0$
.(iii) Thirdly, as an application of the nilpotence theorem, Hopkins and Smith showed that if another finite spectrum
 $Y$
has type larger than or equal to the type of
$Y$
has type larger than or equal to the type of
 $X$
, then
$X$
, then
 $Y$
already lies in the tt-ideal
$Y$
already lies in the tt-ideal
 $\text{thick}^{\otimes }(X)$
generated by
$\text{thick}^{\otimes }(X)$
generated by
 $X$
. As a consequence, any finite spectrum of type
$X$
. As a consequence, any finite spectrum of type
 $n$
generates
$n$
generates
 $P(n)$
. It follows that the
$P(n)$
. It follows that the
 $P(n)$
make up all the proper thick tensor ideals and in particular all the prime ideals in
$P(n)$
make up all the proper thick tensor ideals and in particular all the prime ideals in
 ${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
. Moreover, the topology on
${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
. Moreover, the topology on
 $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{(p)}^{c})$
is determined by the closure of points, which is given by
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{(p)}^{c})$
is determined by the closure of points, which is given by
 $\overline{\{P(n)\}}=\{P(n),P(n+1),\ldots ,P(\infty )\}$
.
$\overline{\{P(n)\}}=\{P(n),P(n+1),\ldots ,P(\infty )\}$
.
These steps are also manifest in the computation of the Balmer spectrum of the stable equivariant homotopy category. The goal of the next section is to establish an analogue of (3) for all compact Lie groups
![]() $G$
as well as an equivariant generalization of the nilpotence theorem. In contrast, Steps (1) and (2) turn out to be more subtle in the equivariant context, and so far only partial generalizations are known; this will be the subject of the remainder of the paper.
$G$
as well as an equivariant generalization of the nilpotence theorem. In contrast, Steps (1) and (2) turn out to be more subtle in the equivariant context, and so far only partial generalizations are known; this will be the subject of the remainder of the paper.
2.2 Stable equivariant homotopy theory
We recall some notions and results from equivariant stable homotopy theory for a compact Lie group
![]() $G$
that we will need throughout the paper. Classical references in the Lewis–May approach are [Reference Lewis, May, Steinberger and McClureLMSM86, Reference Greenlees and MayGM95a, Reference MayMay96], a treatment of
$G$
that we will need throughout the paper. Classical references in the Lewis–May approach are [Reference Lewis, May, Steinberger and McClureLMSM86, Reference Greenlees and MayGM95a, Reference MayMay96], a treatment of
![]() $G$
-orthogonal spectra is given in [Reference Mandell and MayMM02], and [Reference Mathew, Naumann and NoelMNN17, §§ 5 and 6] contains a discussion of some of the constructions in an
$G$
-orthogonal spectra is given in [Reference Mandell and MayMM02], and [Reference Mathew, Naumann and NoelMNN17, §§ 5 and 6] contains a discussion of some of the constructions in an
![]() $\infty$
-categorical setting.
$\infty$
-categorical setting.
We denote by
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
the homotopy category of
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
the homotopy category of
![]() $p$
-local
$p$
-local
![]() $G$
-spectra for a compact Lie group
$G$
-spectra for a compact Lie group
![]() $G$
indexed on a complete universe and write
$G$
indexed on a complete universe and write
![]() $\operatorname{Sub}(G)$
for the set of closed subgroups of
$\operatorname{Sub}(G)$
for the set of closed subgroups of
![]() $G$
. For
$G$
. For
![]() $H\in \operatorname{Sub}(G)$
, the suspension spectrum
$H\in \operatorname{Sub}(G)$
, the suspension spectrum
![]() $G/H_{+}=\unicode[STIX]{x1D6F4}^{\infty }G/H_{+}$
is a
$G/H_{+}=\unicode[STIX]{x1D6F4}^{\infty }G/H_{+}$
is a
![]() $G$
-spectrum, and the
$G$
-spectrum, and the
![]() $H$
-homotopy groups of
$H$
-homotopy groups of
![]() $X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
are defined as
$X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
are defined as
i.e., the graded maps in
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
from the suspension spectrum of
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
from the suspension spectrum of
![]() $G/H_{+}$
into
$G/H_{+}$
into
![]() $X$
. A map of
$X$
. A map of
![]() $G$
-spectra is an equivalence if and only if it induces an isomorphism on
$G$
-spectra is an equivalence if and only if it induces an isomorphism on
![]() $\unicode[STIX]{x1D70B}_{\ast }^{H}$
for all closed subgroups
$\unicode[STIX]{x1D70B}_{\ast }^{H}$
for all closed subgroups
![]() $H$
of
$H$
of
![]() $G$
.
$G$
.
The category
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}=({\mathcal{S}}{\mathcal{H}}_{G,(p)},\wedge ,\mathbb{S}_{G})$
is a tensor triangulated category which is compactly generated by the set of dualizable objects
${\mathcal{S}}{\mathcal{H}}_{G,(p)}=({\mathcal{S}}{\mathcal{H}}_{G,(p)},\wedge ,\mathbb{S}_{G})$
is a tensor triangulated category which is compactly generated by the set of dualizable objects
![]() $\{G/{H_{+}\}}_{H\in \operatorname{Sub}(G)}$
and with compact unit given by the
$\{G/{H_{+}\}}_{H\in \operatorname{Sub}(G)}$
and with compact unit given by the
![]() $G$
-equivariant sphere spectrum
$G$
-equivariant sphere spectrum
![]() $\mathbb{S}_{G}=G/G_{+}$
. For every real
$\mathbb{S}_{G}=G/G_{+}$
. For every real
![]() $G$
-representation
$G$
-representation
![]() $V$
, the suspension spectrum of the one-point compactification
$V$
, the suspension spectrum of the one-point compactification
![]() $S^{V}$
is an invertible object in
$S^{V}$
is an invertible object in
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
. As usual, the full subcategory of
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
. As usual, the full subcategory of
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
spanned by the compact objects is denoted by
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
spanned by the compact objects is denoted by
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
. The objects of
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
. The objects of
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, which we call the finite
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, which we call the finite
![]() $G$
-spectra, can be described in the following way.
$G$
-spectra, can be described in the following way.
Lemma 2.2. Every finite
![]() $p$
-local
$p$
-local
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
is of the form
$X$
is of the form
![]() $S^{-V}\wedge \unicode[STIX]{x1D6F4}^{\infty }A$
, where
$S^{-V}\wedge \unicode[STIX]{x1D6F4}^{\infty }A$
, where
![]() $V$
is a
$V$
is a
![]() $G$
-representation and
$G$
-representation and
![]() $A$
is a homotopy retract of the
$A$
is a homotopy retract of the
![]() $p$
-localization of a based finite
$p$
-localization of a based finite
![]() $G$
-CW complex.
$G$
-CW complex.
Here, to avoid subtleties with
![]() $p$
-localization of
$p$
-localization of
![]() $G$
-spaces, the finite
$G$
-spaces, the finite
![]() $G$
-CW complex can always be chosen to be a double suspension, so all fixed points are simply connected and the
$G$
-CW complex can always be chosen to be a double suspension, so all fixed points are simply connected and the
![]() $p$
-localization is given by the mapping telescope over repeated multiplication by
$p$
-localization is given by the mapping telescope over repeated multiplication by
![]() $q$
for all primes
$q$
for all primes
![]() $q\neq p$
, using the comultiplication from the suspension coordinates. The lemma is (a
$q\neq p$
, using the comultiplication from the suspension coordinates. The lemma is (a
![]() $p$
-local variation of) a classical fact about
$p$
-local variation of) a classical fact about
![]() $G$
-spectra and follows from every
$G$
-spectra and follows from every
![]() $G$
-spectrum being a filtered homotopy colimit over
$G$
-spectrum being a filtered homotopy colimit over
![]() $G$
-spectra of the form
$G$
-spectra of the form
![]() $S^{-V}\wedge \unicode[STIX]{x1D6F4}^{\infty }(-)$
, see [Reference Lewis, May, Steinberger and McClureLMSM86, Proposition I.4.7].
$S^{-V}\wedge \unicode[STIX]{x1D6F4}^{\infty }(-)$
, see [Reference Lewis, May, Steinberger and McClureLMSM86, Proposition I.4.7].
2.2.1 Pullback along a group homomorphism
Let
![]() $\unicode[STIX]{x1D711}:G\rightarrow K$
be a continuous group homomorphism. Then every
$\unicode[STIX]{x1D711}:G\rightarrow K$
be a continuous group homomorphism. Then every
![]() $K$
-space
$K$
-space
![]() $A$
gives rise to a
$A$
gives rise to a
![]() $G$
-space
$G$
-space
![]() $\unicode[STIX]{x1D711}^{\ast }(A)$
by taking the same underlying space and pulling back the
$\unicode[STIX]{x1D711}^{\ast }(A)$
by taking the same underlying space and pulling back the
![]() $K$
-action to a
$K$
-action to a
![]() $G$
-action along
$G$
-action along
![]() $\unicode[STIX]{x1D711}$
. There is a spectrum analogue
$\unicode[STIX]{x1D711}$
. There is a spectrum analogue
![]() $\unicode[STIX]{x1D711}^{\ast }:{\mathcal{S}}{\mathcal{H}}_{K,(p)}\rightarrow {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
, technically obtained as a composite of a space-level pullback functor and a change of universe functor, see [Reference Lewis, May, Steinberger and McClureLMSM86, §§ II.1–4] or [Reference Mandell and MayMM02, §§ V.1–3]. It is uniquely determined by the fact that it is exact, symmetric monoidal, preserves all coproducts and sends a suspension spectrum
$\unicode[STIX]{x1D711}^{\ast }:{\mathcal{S}}{\mathcal{H}}_{K,(p)}\rightarrow {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
, technically obtained as a composite of a space-level pullback functor and a change of universe functor, see [Reference Lewis, May, Steinberger and McClureLMSM86, §§ II.1–4] or [Reference Mandell and MayMM02, §§ V.1–3]. It is uniquely determined by the fact that it is exact, symmetric monoidal, preserves all coproducts and sends a suspension spectrum
![]() $\unicode[STIX]{x1D6F4}^{\infty }A$
to the suspension spectrum
$\unicode[STIX]{x1D6F4}^{\infty }A$
to the suspension spectrum
![]() $\unicode[STIX]{x1D6F4}^{\infty }\unicode[STIX]{x1D711}^{\ast }(A)$
. In particular,
$\unicode[STIX]{x1D6F4}^{\infty }\unicode[STIX]{x1D711}^{\ast }(A)$
. In particular,
![]() $\unicode[STIX]{x1D711}^{\ast }$
preserves dualizable objects and hence restricts to a functor
$\unicode[STIX]{x1D711}^{\ast }$
preserves dualizable objects and hence restricts to a functor
![]() $\unicode[STIX]{x1D711}^{\ast }:{\mathcal{S}}{\mathcal{H}}_{K,(p)}^{c}\rightarrow {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
.
$\unicode[STIX]{x1D711}^{\ast }:{\mathcal{S}}{\mathcal{H}}_{K,(p)}^{c}\rightarrow {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
.
We need two special cases of this construction, called restriction and inflation.
2.2.2 Restriction and induction
In the case where
![]() $\unicode[STIX]{x1D711}$
is the inclusion of a closed subgroup
$\unicode[STIX]{x1D711}$
is the inclusion of a closed subgroup
![]() $H$
into
$H$
into
![]() $G$
, the pullback functor is called restriction and denoted
$G$
, the pullback functor is called restriction and denoted
![]() $\operatorname{Res}_{H}^{G}$
. In that case it has a left adjoint called induction that is denoted
$\operatorname{Res}_{H}^{G}$
. In that case it has a left adjoint called induction that is denoted
![]() $\operatorname{Ind}_{H}^{G}$
. When
$\operatorname{Ind}_{H}^{G}$
. When
![]() $A$
is a based
$A$
is a based
![]() $H$
-space, there is a natural equivalence
$H$
-space, there is a natural equivalence
![]() $\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A)\simeq \unicode[STIX]{x1D6F4}^{\infty }(G_{+}\wedge _{H}A)$
, which follows from the analogous property of
$\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A)\simeq \unicode[STIX]{x1D6F4}^{\infty }(G_{+}\wedge _{H}A)$
, which follows from the analogous property of
![]() $\operatorname{Res}_{H}^{G}$
. Furthermore, for a pair of an
$\operatorname{Res}_{H}^{G}$
. Furthermore, for a pair of an
![]() $H$
-spectrum
$H$
-spectrum
![]() $X$
and a
$X$
and a
![]() $G$
-spectrum
$G$
-spectrum
![]() $Y$
, Frobenius reciprocity provides an equivalence
$Y$
, Frobenius reciprocity provides an equivalence
One way to see this is to note that adjunction gives a natural map from the left to the right, and it is enough to check that this map is an equivalence in the case where
![]() $X$
and
$X$
and
![]() $Y$
vary through the compact generators. Since these are suspension spectra and
$Y$
vary through the compact generators. Since these are suspension spectra and
![]() $\operatorname{Ind}_{H}^{G},\operatorname{Res}_{H}^{G}$
, and
$\operatorname{Ind}_{H}^{G},\operatorname{Res}_{H}^{G}$
, and
![]() $\wedge$
commute with
$\wedge$
commute with
![]() $\unicode[STIX]{x1D6F4}^{\infty }$
, this reduces to the space-level analogue, which is easily checked.
$\unicode[STIX]{x1D6F4}^{\infty }$
, this reduces to the space-level analogue, which is easily checked.
2.2.3 Inflation
When
![]() $\unicode[STIX]{x1D711}$
is the projection
$\unicode[STIX]{x1D711}$
is the projection
![]() $p:G\rightarrow G/N$
for a closed normal subgroup of
$p:G\rightarrow G/N$
for a closed normal subgroup of
![]() $G$
, the pullback functor is called inflation and denoted by
$G$
, the pullback functor is called inflation and denoted by
![]() $i_{N}^{\ast }$
. Most important for us is the case
$i_{N}^{\ast }$
. Most important for us is the case
![]() $N=G$
, in which case the inflation functor turns an ordinary spectrum into a
$N=G$
, in which case the inflation functor turns an ordinary spectrum into a
![]() $G$
-spectrum with ‘trivial action’.
$G$
-spectrum with ‘trivial action’.
2.2.4 Geometric fixed points
For every closed subgroup
![]() $H$
of
$H$
of
![]() $G$
, there is a geometric fixed point functor
$G$
, there is a geometric fixed point functor
obtained by composing the restriction
![]() $\operatorname{Res}_{H}^{G}:{\mathcal{S}}{\mathcal{H}}_{G,(p)}\rightarrow {\mathcal{S}}{\mathcal{H}}_{H,(p)}$
with the (absolute) geometric fixed point functor for
$\operatorname{Res}_{H}^{G}:{\mathcal{S}}{\mathcal{H}}_{G,(p)}\rightarrow {\mathcal{S}}{\mathcal{H}}_{H,(p)}$
with the (absolute) geometric fixed point functor for
![]() $H$
, see [Reference Lewis, May, Steinberger and McClureLMSM86, § II.9], [Reference Mandell and MayMM02, § V.4] or [Reference Mathew, Naumann and NoelMNN17, § 6.2]. This functor is exact, symmetric monoidal, preserves all coproducts, and satisfies
$H$
, see [Reference Lewis, May, Steinberger and McClureLMSM86, § II.9], [Reference Mandell and MayMM02, § V.4] or [Reference Mathew, Naumann and NoelMNN17, § 6.2]. This functor is exact, symmetric monoidal, preserves all coproducts, and satisfies
![]() $\unicode[STIX]{x1D6F7}^{H}(\unicode[STIX]{x1D6F4}^{\infty }A)\simeq \unicode[STIX]{x1D6F4}^{\infty }(A^{H})$
for all based
$\unicode[STIX]{x1D6F7}^{H}(\unicode[STIX]{x1D6F4}^{\infty }A)\simeq \unicode[STIX]{x1D6F4}^{\infty }(A^{H})$
for all based
![]() $G$
-CW complexes
$G$
-CW complexes
![]() $A$
. Since the dualizable objects and the compact objects coincide in
$A$
. Since the dualizable objects and the compact objects coincide in
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
, the geometric fixed point functor
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
, the geometric fixed point functor
![]() $\unicode[STIX]{x1D6F7}^{H}$
preserves compact objects and hence restricts to a functor
$\unicode[STIX]{x1D6F7}^{H}$
preserves compact objects and hence restricts to a functor
![]() $\unicode[STIX]{x1D6F7}^{H}:{\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}\rightarrow {\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
. Every element
$\unicode[STIX]{x1D6F7}^{H}:{\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}\rightarrow {\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
. Every element
![]() $g\in G$
induces conjugation equivalences
$g\in G$
induces conjugation equivalences
![]() $\unicode[STIX]{x1D6F7}^{H}\simeq \unicode[STIX]{x1D6F7}^{H^{g}}$
, where
$\unicode[STIX]{x1D6F7}^{H}\simeq \unicode[STIX]{x1D6F7}^{H^{g}}$
, where
![]() $H^{g}=g^{-1}Hg$
. Hence, up to equivalence, the geometric fixed point functors depend only on the conjugacy class of
$H^{g}=g^{-1}Hg$
. Hence, up to equivalence, the geometric fixed point functors depend only on the conjugacy class of
![]() $H$
. Moreover, the collection
$H$
. Moreover, the collection
![]() ${\{\unicode[STIX]{x1D6F7}^{H}\}}_{H\in \operatorname{Sub}(G)}$
is jointly conservative, i.e., a map
${\{\unicode[STIX]{x1D6F7}^{H}\}}_{H\in \operatorname{Sub}(G)}$
is jointly conservative, i.e., a map
![]() $f$
in
$f$
in
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
is an equivalence if and only if
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
is an equivalence if and only if
![]() $\unicode[STIX]{x1D6F7}^{H}(f)$
is an equivalence in
$\unicode[STIX]{x1D6F7}^{H}(f)$
is an equivalence in
![]() ${\mathcal{S}}{\mathcal{H}}_{(p)}$
for all
${\mathcal{S}}{\mathcal{H}}_{(p)}$
for all
![]() $H\in \operatorname{Sub}(G)$
(see [Reference SchwedeSch18, Proposition 3.3.10] for a proof).
$H\in \operatorname{Sub}(G)$
(see [Reference SchwedeSch18, Proposition 3.3.10] for a proof).
Finally, geometric fixed points have the following behaviour with respect to pullback along a continuous group homomorphism
![]() $\unicode[STIX]{x1D711}:G\rightarrow K$
. For a closed subgroup
$\unicode[STIX]{x1D711}:G\rightarrow K$
. For a closed subgroup
![]() $H$
of
$H$
of
![]() $G$
there are natural equivalences
$G$
there are natural equivalences
These can be derived from their space-level analogues using that both sides are exact, symmetric monoidal, coproduct-preserving functors in
![]() $X$
.
$X$
.
2.2.5 Borel completion
A
![]() $G$
-spectrum
$G$
-spectrum
![]() $Y$
is called Borel-complete if the map
$Y$
is called Borel-complete if the map
![]() $Y\rightarrow F(EG_{+},Y)$
is an equivalence, see [Reference Mathew, Naumann and NoelMNN17, § 6.3] for a recent reference. Here,
$Y\rightarrow F(EG_{+},Y)$
is an equivalence, see [Reference Mathew, Naumann and NoelMNN17, § 6.3] for a recent reference. Here,
![]() $F(-,-)$
denotes the function
$F(-,-)$
denotes the function
![]() $G$
-spectrum between two
$G$
-spectrum between two
![]() $G$
-spectra. If the underlying non-equivariant spectrum of a Borel-complete
$G$
-spectra. If the underlying non-equivariant spectrum of a Borel-complete
![]() $G$
-spectrum
$G$
-spectrum
![]() $Y$
is contractible, then
$Y$
is contractible, then
![]() $Y$
is already contractible as a
$Y$
is already contractible as a
![]() $G$
-spectrum, which follows from an induction over the cells of
$G$
-spectrum, which follows from an induction over the cells of
![]() $EG_{+}$
. For every spectrum
$EG_{+}$
. For every spectrum
![]() $Z$
equipped with a
$Z$
equipped with a
![]() $G$
-action in the naive sense (i.e., a module over the spherical group ring
$G$
-action in the naive sense (i.e., a module over the spherical group ring
![]() $\unicode[STIX]{x1D6F4}^{\infty }G_{+}$
, or in
$\unicode[STIX]{x1D6F4}^{\infty }G_{+}$
, or in
![]() $\infty$
-categorical language, a functor from
$\infty$
-categorical language, a functor from
![]() $BG$
to the
$BG$
to the
![]() $\infty$
-category of spectra) there exists a Borel spectrum
$\infty$
-category of spectra) there exists a Borel spectrum
![]() $\text{}\underline{Z}\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
uniquely determined by the property that it is Borel complete and that its underlying spectrum with naive
$\text{}\underline{Z}\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
uniquely determined by the property that it is Borel complete and that its underlying spectrum with naive
![]() $G$
-action is equivalent to
$G$
-action is equivalent to
![]() $Z$
.
$Z$
.
3 Equivariant support, equivariant prime ideals and the equivariant nilpotence theorem
In this section, we use the geometric fixed point functors and the non-equivariant nilpotence theorem to construct a support theory that allows us to detect inclusions between equivariant tt-ideals, thereby providing an equivariant generalization of Step (3) in the proof of Theorem 2.1. We then use these results to determine the underlying set of the Balmer spectrum of the category of finite
![]() $p$
-local
$p$
-local
![]() $G$
-spectra. Although not needed in the remainder of the paper, we also prove an equivariant version of the nilpotence theorem for all compact Lie groups.
$G$
-spectra. Although not needed in the remainder of the paper, we also prove an equivariant version of the nilpotence theorem for all compact Lie groups.
3.1 An abstract thick tensor ideal theorem
Let
![]() ${\mathcal{C}}=({\mathcal{C}},\otimes ,1)$
be a closed symmetric monoidal triangulated category with arbitrary coproducts and compact unit
${\mathcal{C}}=({\mathcal{C}},\otimes ,1)$
be a closed symmetric monoidal triangulated category with arbitrary coproducts and compact unit
![]() $1$
, which implies that every dualizable object in
$1$
, which implies that every dualizable object in
![]() ${\mathcal{C}}$
is compact. Following Hovey, Palmieri, and Strickland [Reference Hovey, Palmieri and StricklandHPS97], we say that
${\mathcal{C}}$
is compact. Following Hovey, Palmieri, and Strickland [Reference Hovey, Palmieri and StricklandHPS97], we say that
![]() ${\mathcal{C}}$
is a unital algebraic stable homotopy category if it is compactly generated by a set of dualizable objects.
${\mathcal{C}}$
is a unital algebraic stable homotopy category if it is compactly generated by a set of dualizable objects.
Given an indexing set
![]() $I$
, consider a collection of graded abelian categories
$I$
, consider a collection of graded abelian categories
![]() $({\mathcal{D}}_{i})_{i\in I}$
with zero objects
$({\mathcal{D}}_{i})_{i\in I}$
with zero objects
![]() $0\in {\mathcal{D}}_{i}$
and a collection of stable homological functors
$0\in {\mathcal{D}}_{i}$
and a collection of stable homological functors
![]() $(\unicode[STIX]{x1D705}_{i}:{\mathcal{C}}\rightarrow {\mathcal{D}}_{i})_{i\in I}$
satisfying the following two conditions.
$(\unicode[STIX]{x1D705}_{i}:{\mathcal{C}}\rightarrow {\mathcal{D}}_{i})_{i\in I}$
satisfying the following two conditions.
(i) Let
 $i\in I$
and
$i\in I$
and
 $X,Y\in {\mathcal{C}}$
. Then
$X,Y\in {\mathcal{C}}$
. Then
 $\unicode[STIX]{x1D705}_{i}(X\otimes Y)=0$
if and only if
$\unicode[STIX]{x1D705}_{i}(X\otimes Y)=0$
if and only if
 $\unicode[STIX]{x1D705}_{i}(X)=0$
or
$\unicode[STIX]{x1D705}_{i}(X)=0$
or
 $\unicode[STIX]{x1D705}_{i}(Y)=0$
.
$\unicode[STIX]{x1D705}_{i}(Y)=0$
.(ii) If
 $R\in \operatorname{Alg}({\mathcal{C}})$
is a monoid in
$R\in \operatorname{Alg}({\mathcal{C}})$
is a monoid in
 ${\mathcal{C}}$
with
${\mathcal{C}}$
with
 $\unicode[STIX]{x1D705}_{i}(R)=0$
for all
$\unicode[STIX]{x1D705}_{i}(R)=0$
for all
 $i\in I$
, then
$i\in I$
, then
 $R=0$
.
$R=0$
.
We will refer to such a collection of functors as a coarse support theory for
![]() ${\mathcal{C}}$
. The corresponding notion of support is then defined for any
${\mathcal{C}}$
. The corresponding notion of support is then defined for any
![]() $X\in {\mathcal{C}}$
as
$X\in {\mathcal{C}}$
as
This extends to any collection
![]() ${\mathcal{X}}\subseteq {\mathcal{C}}$
of objects in
${\mathcal{X}}\subseteq {\mathcal{C}}$
of objects in
![]() ${\mathcal{C}}$
by setting
${\mathcal{C}}$
by setting
![]() $\operatorname{supp}({\mathcal{X}})=\bigcup _{X\in {\mathcal{X}}}\operatorname{supp}(X)$
. Since the functors
$\operatorname{supp}({\mathcal{X}})=\bigcup _{X\in {\mathcal{X}}}\operatorname{supp}(X)$
. Since the functors
![]() $\unicode[STIX]{x1D705}_{i}$
are stable homological to graded abelian categories
$\unicode[STIX]{x1D705}_{i}$
are stable homological to graded abelian categories
![]() ${\mathcal{D}}_{i}$
, then
${\mathcal{D}}_{i}$
, then
![]() $\operatorname{supp}(X)=\operatorname{supp}(\text{thick}^{\otimes }(X))$
.
$\operatorname{supp}(X)=\operatorname{supp}(\text{thick}^{\otimes }(X))$
.
Remark 3.1. Conditions (1) and (2) translate to the following two properties of the corresponding notion of support.
- (
 $1^{\prime }$
)
$1^{\prime }$
) For any two objects
 $X,Y\in {\mathcal{C}}$
, we have
$X,Y\in {\mathcal{C}}$
, we have
 $\operatorname{supp}(X\otimes Y)=\operatorname{supp}(X)\cap \operatorname{supp}(Y)$
.
$\operatorname{supp}(X\otimes Y)=\operatorname{supp}(X)\cap \operatorname{supp}(Y)$
.- (
 $2^{\prime }$
)
$2^{\prime }$
) A monoid
 $R\in {\mathcal{C}}$
is trivial if and only if
$R\in {\mathcal{C}}$
is trivial if and only if
 $\operatorname{supp}(R)=\varnothing$
.
$\operatorname{supp}(R)=\varnothing$
.
A coarse support theory thus satisfies part of the defining conditions of a support datum as axiomatized by Balmer in [Reference BalmerBal05, Definition 3.1], thereby justifying our choice of terminology.
The next result is an abstract version of the support-theoretic part of the thick subcategory theorem; the proof is a modification of the argument in [Reference Hovey, Palmieri and StricklandHPS97, Proof of Theorem 5.2.2] and thus essentially due to Hovey, Palmieri, and Strickland.
Proposition 3.2. Suppose
![]() $(\unicode[STIX]{x1D705}_{i}:{\mathcal{C}}\rightarrow {\mathcal{D}}_{i})_{i\in I}$
is a coarse support theory on a unital algebraic stable homotopy category
$(\unicode[STIX]{x1D705}_{i}:{\mathcal{C}}\rightarrow {\mathcal{D}}_{i})_{i\in I}$
is a coarse support theory on a unital algebraic stable homotopy category
![]() ${\mathcal{C}}$
, and let
${\mathcal{C}}$
, and let
![]() $X\in {\mathcal{C}}^{c}$
be a compact object and
$X\in {\mathcal{C}}^{c}$
be a compact object and
![]() ${\mathcal{D}}\subseteq {\mathcal{C}}^{c}$
a thick tensor ideal. If
${\mathcal{D}}\subseteq {\mathcal{C}}^{c}$
a thick tensor ideal. If
![]() $\operatorname{supp}(X)\subseteq \operatorname{supp}({\mathcal{D}})$
, then
$\operatorname{supp}(X)\subseteq \operatorname{supp}({\mathcal{D}})$
, then
![]() $X\in {\mathcal{D}}$
.
$X\in {\mathcal{D}}$
.
Proof. For a full subcategory
![]() ${\mathcal{S}}\subseteq {\mathcal{C}}$
, let
${\mathcal{S}}\subseteq {\mathcal{C}}$
, let
![]() $\operatorname{Loc}^{\otimes }({\mathcal{S}})$
be the smallest localizing ideal of
$\operatorname{Loc}^{\otimes }({\mathcal{S}})$
be the smallest localizing ideal of
![]() ${\mathcal{C}}$
containing
${\mathcal{C}}$
containing
![]() ${\mathcal{S}}$
, i.e., the smallest triangulated subcategory of
${\mathcal{S}}$
, i.e., the smallest triangulated subcategory of
![]() ${\mathcal{C}}$
containing
${\mathcal{C}}$
containing
![]() ${\mathcal{S}}$
which is closed under tensor products with objects of
${\mathcal{S}}$
which is closed under tensor products with objects of
![]() ${\mathcal{C}}$
. The natural inclusion
${\mathcal{C}}$
. The natural inclusion
![]() ${\mathcal{D}}\rightarrow {\mathcal{C}}$
then gives rise to a (Verdier) localization sequence
${\mathcal{D}}\rightarrow {\mathcal{C}}$
then gives rise to a (Verdier) localization sequence
By [Reference Hovey, Palmieri and StricklandHPS97, Lemma 3.1.6(e) and Theorem 3.3.3], the functor
![]() ${\mathcal{C}}\rightarrow {\mathcal{C}}/\operatorname{Loc}^{\otimes }({\mathcal{D}})$
admits a right adjoint. The corresponding composite
${\mathcal{C}}\rightarrow {\mathcal{C}}/\operatorname{Loc}^{\otimes }({\mathcal{D}})$
admits a right adjoint. The corresponding composite
![]() $L_{{\mathcal{D}}}^{f}:{\mathcal{C}}\rightarrow {\mathcal{C}}/\operatorname{Loc}^{\otimes }({\mathcal{D}})\rightarrow {\mathcal{C}}$
is then a smashing localization functor on
$L_{{\mathcal{D}}}^{f}:{\mathcal{C}}\rightarrow {\mathcal{C}}/\operatorname{Loc}^{\otimes }({\mathcal{D}})\rightarrow {\mathcal{C}}$
is then a smashing localization functor on
![]() ${\mathcal{C}}$
, so there is a canonical isomorphism
${\mathcal{C}}$
, so there is a canonical isomorphism
![]() $L_{{\mathcal{D}}}^{f}Y=Y\otimes L_{{\mathcal{D}}}^{f}1$
for all
$L_{{\mathcal{D}}}^{f}Y=Y\otimes L_{{\mathcal{D}}}^{f}1$
for all
![]() $Y\in {\mathcal{C}}$
. Suppose
$Y\in {\mathcal{C}}$
. Suppose
![]() $X$
satisfies the assumptions of the proposition, then the conclusion is equivalent to
$X$
satisfies the assumptions of the proposition, then the conclusion is equivalent to
![]() $L_{{\mathcal{D}}}^{f}X=0$
, since
$L_{{\mathcal{D}}}^{f}X=0$
, since
![]() $\operatorname{Loc}^{\otimes }({\mathcal{D}})\cap {\mathcal{C}}^{c}={\mathcal{D}}$
by Thomason’s Theorem in the form of [Reference GreenleesGre19, Theorem 7.1(ii)].
$\operatorname{Loc}^{\otimes }({\mathcal{D}})\cap {\mathcal{C}}^{c}={\mathcal{D}}$
by Thomason’s Theorem in the form of [Reference GreenleesGre19, Theorem 7.1(ii)].
Note that we may assume without loss of generality that
![]() $X\in \operatorname{Alg}({\mathcal{C}})$
: indeed, since
$X\in \operatorname{Alg}({\mathcal{C}})$
: indeed, since
![]() $X$
is a retract of
$X$
is a retract of
![]() $X\otimes DX\otimes X$
by dualizability,
$X\otimes DX\otimes X$
by dualizability,
![]() $X$
and the monoid
$X$
and the monoid
![]() $X\otimes DX$
have the same support. Moreover, the same observation shows that
$X\otimes DX$
have the same support. Moreover, the same observation shows that
![]() $X\in {\mathcal{D}}$
if and only if
$X\in {\mathcal{D}}$
if and only if
![]() $X\otimes DX\in {\mathcal{D}}$
.
$X\otimes DX\in {\mathcal{D}}$
.
We now claim that
![]() $\unicode[STIX]{x1D705}_{i}(L_{{\mathcal{D}}}^{f}X)=0$
for all
$\unicode[STIX]{x1D705}_{i}(L_{{\mathcal{D}}}^{f}X)=0$
for all
![]() $i\in I$
. To this end, let
$i\in I$
. To this end, let
![]() $i\in I$
and assume that
$i\in I$
and assume that
![]() $\unicode[STIX]{x1D705}_{i}(X)=0$
. It follows that
$\unicode[STIX]{x1D705}_{i}(X)=0$
. It follows that
![]() $\unicode[STIX]{x1D705}_{i}(L_{{\mathcal{D}}}^{f}(X))=\unicode[STIX]{x1D705}_{i}(X\otimes L_{{\mathcal{D}}}^{f}1)=0$
. If
$\unicode[STIX]{x1D705}_{i}(L_{{\mathcal{D}}}^{f}(X))=\unicode[STIX]{x1D705}_{i}(X\otimes L_{{\mathcal{D}}}^{f}1)=0$
. If
![]() $i\in I$
is instead such that
$i\in I$
is instead such that
![]() $\unicode[STIX]{x1D705}_{i}(X)\neq 0$
, then
$\unicode[STIX]{x1D705}_{i}(X)\neq 0$
, then
![]() $i\in \operatorname{supp}(X)\subseteq \operatorname{supp}({\mathcal{D}})$
, so there exists
$i\in \operatorname{supp}(X)\subseteq \operatorname{supp}({\mathcal{D}})$
, so there exists
![]() $Y\in {\mathcal{D}}$
with
$Y\in {\mathcal{D}}$
with
![]() $\unicode[STIX]{x1D705}_{i}(Y)\neq 0$
. But
$\unicode[STIX]{x1D705}_{i}(Y)\neq 0$
. But
![]() $L_{{\mathcal{D}}}^{f}Y=0$
, and hence
$L_{{\mathcal{D}}}^{f}Y=0$
, and hence
![]() $\unicode[STIX]{x1D705}_{i}((X\otimes L_{{\mathcal{D}}}^{f}1)\otimes Y)=0$
. Therefore
$\unicode[STIX]{x1D705}_{i}((X\otimes L_{{\mathcal{D}}}^{f}1)\otimes Y)=0$
. Therefore
![]() $\unicode[STIX]{x1D705}_{i}(X\otimes L_{{\mathcal{D}}}^{f}1)=0$
in this case as well. Consequently,
$\unicode[STIX]{x1D705}_{i}(X\otimes L_{{\mathcal{D}}}^{f}1)=0$
in this case as well. Consequently,
![]() $L_{{\mathcal{D}}}^{f}X$
is a monoid in
$L_{{\mathcal{D}}}^{f}X$
is a monoid in
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $\unicode[STIX]{x1D705}_{i}(L_{{\mathcal{D}}}^{f}X)=0$
for all
$\unicode[STIX]{x1D705}_{i}(L_{{\mathcal{D}}}^{f}X)=0$
for all
![]() $i\in I$
, and thus
$i\in I$
, and thus
![]() $L_{{\mathcal{D}}}^{f}X=0$
.◻
$L_{{\mathcal{D}}}^{f}X=0$
.◻
We note that the proposition in particular implies that every thick tensor ideal
![]() ${\mathcal{D}}$
in
${\mathcal{D}}$
in
![]() ${\mathcal{C}}^{c}$
is determined by its support: it consists of all
${\mathcal{C}}^{c}$
is determined by its support: it consists of all
![]() $X\in {\mathcal{C}}^{c}$
such that
$X\in {\mathcal{C}}^{c}$
such that
![]() $\operatorname{supp}(X)\subseteq \operatorname{supp}({\mathcal{D}})$
.
$\operatorname{supp}(X)\subseteq \operatorname{supp}({\mathcal{D}})$
.
Example 3.3. Let
![]() ${\mathcal{S}}{\mathcal{H}}_{(p)}$
be the
${\mathcal{S}}{\mathcal{H}}_{(p)}$
be the
![]() $p$
-local stable homotopy category at a prime
$p$
-local stable homotopy category at a prime
![]() $p$
. For any
$p$
. For any
![]() $n\in \overline{\mathbb{N}}=\{0,1,\ldots \}\cup \{\infty \}$
, write
$n\in \overline{\mathbb{N}}=\{0,1,\ldots \}\cup \{\infty \}$
, write
![]() $K(n)$
for the
$K(n)$
for the
![]() $p$
-local height
$p$
-local height
![]() $n$
Morava
$n$
Morava
![]() $K$
-theory spectrum, where we set
$K$
-theory spectrum, where we set
![]() $K(\infty )=H\mathbb{F}_{p}$
. The nilpotence theorem of Devinatz, Hopkins, and Smith [Reference Devinatz, Hopkins and SmithDHS88, Reference Hopkins and SmithHS98] implies that the collection of homological and symmetric monoidal functors
$K(\infty )=H\mathbb{F}_{p}$
. The nilpotence theorem of Devinatz, Hopkins, and Smith [Reference Devinatz, Hopkins and SmithDHS88, Reference Hopkins and SmithHS98] implies that the collection of homological and symmetric monoidal functors
forms a coarse support theory for
![]() ${\mathcal{S}}{\mathcal{H}}_{(p)}$
. In this case, Proposition 3.2 recovers the thick subcategory theorem [Reference Hopkins and SmithHS98, Theorem 7] of Hopkins and Smith, as explained in § 2.1.
${\mathcal{S}}{\mathcal{H}}_{(p)}$
. In this case, Proposition 3.2 recovers the thick subcategory theorem [Reference Hopkins and SmithHS98, Theorem 7] of Hopkins and Smith, as explained in § 2.1.
3.2 Equivariant support and type functions of finite
 $G$
-spectra
$G$
-spectra
In order to apply the abstract result of the previous subsection to equivariant stable homotopy theory for a compact Lie group
![]() $G$
, we need to construct an appropriate coarse support theory. Fix a prime
$G$
, we need to construct an appropriate coarse support theory. Fix a prime
![]() $p$
and write
$p$
and write
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
for the category of
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
for the category of
![]() $p$
-local
$p$
-local
![]() $G$
-spectra. Recall from Example 3.3 that for each
$G$
-spectra. Recall from Example 3.3 that for each
![]() $n\in \overline{\mathbb{N}}$
there is a Morava
$n\in \overline{\mathbb{N}}$
there is a Morava
![]() $K$
-theory spectrum
$K$
-theory spectrum
![]() $K(n)\in {\mathcal{S}}{\mathcal{H}}_{(p)}$
of height
$K(n)\in {\mathcal{S}}{\mathcal{H}}_{(p)}$
of height
![]() $n$
.
$n$
.
Definition 3.4. Let
![]() $I=\operatorname{Sub}(G)\times \overline{\mathbb{N}}$
and define for each
$I=\operatorname{Sub}(G)\times \overline{\mathbb{N}}$
and define for each
![]() $(H,n)\in I$
functors
$(H,n)\in I$
functors
As in the previous subsection, we shall write
![]() $\operatorname{supp}(X)$
for the support of
$\operatorname{supp}(X)$
for the support of
![]() $X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
corresponding to the collection of functors
$X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
corresponding to the collection of functors
![]() $\{{\unicode[STIX]{x1D705}_{(H,n)}\}}_{(H,n)\in I}$
.
$\{{\unicode[STIX]{x1D705}_{(H,n)}\}}_{(H,n)\in I}$
.
As before, this notion of support extends to any collection
![]() ${\mathcal{X}}\subseteq {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
. Since each
${\mathcal{X}}\subseteq {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
. Since each
![]() $\unicode[STIX]{x1D6F7}^{H}$
is exact as well as symmetric monoidal and
$\unicode[STIX]{x1D6F7}^{H}$
is exact as well as symmetric monoidal and
![]() $K(n)$
has a Künneth isomorphism, we have
$K(n)$
has a Künneth isomorphism, we have
![]() $\operatorname{supp}(X)=\operatorname{supp}(\text{thick}^{\otimes }(X))$
for all
$\operatorname{supp}(X)=\operatorname{supp}(\text{thick}^{\otimes }(X))$
for all
![]() $X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
. Then we have the following result, which was also obtained in unpublished work of Strickland.
$X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
. Then we have the following result, which was also obtained in unpublished work of Strickland.
Proposition 3.5. The collection
![]() $\{{\unicode[STIX]{x1D705}_{(H,n)}\}}_{(H,n)\in \operatorname{Sub}(G)\times \overline{\mathbb{N}}}$
is a coarse support theory for
$\{{\unicode[STIX]{x1D705}_{(H,n)}\}}_{(H,n)\in \operatorname{Sub}(G)\times \overline{\mathbb{N}}}$
is a coarse support theory for
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
.
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
.
Proof. We have to verify conditions (1) and (2) above. For any
![]() $(H,n)\in \operatorname{Sub}(G)\times \overline{\mathbb{N}}$
and all
$(H,n)\in \operatorname{Sub}(G)\times \overline{\mathbb{N}}$
and all
![]() $X,Y\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
, there is a canonical isomorphism
$X,Y\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}$
, there is a canonical isomorphism
Since
![]() $K(n)_{\ast }$
is a graded field, this implies that the first condition is satisfied. To see that
$K(n)_{\ast }$
is a graded field, this implies that the first condition is satisfied. To see that
![]() $\operatorname{supp}$
detects ring objects, suppose that
$\operatorname{supp}$
detects ring objects, suppose that
![]() $R\in \operatorname{Alg}({\mathcal{S}}{\mathcal{H}}_{G,(p)})$
with
$R\in \operatorname{Alg}({\mathcal{S}}{\mathcal{H}}_{G,(p)})$
with
![]() $\operatorname{supp}(R)=\varnothing$
. By the nilpotence theorem in the form of [Reference Hopkins and SmithHS98, Theorem 3 i)], this implies that
$\operatorname{supp}(R)=\varnothing$
. By the nilpotence theorem in the form of [Reference Hopkins and SmithHS98, Theorem 3 i)], this implies that
![]() $\unicode[STIX]{x1D6F7}^{H}(R)=0$
for all
$\unicode[STIX]{x1D6F7}^{H}(R)=0$
for all
![]() $H\in \operatorname{Sub}(G)$
, and hence
$H\in \operatorname{Sub}(G)$
, and hence
![]() $R=0$
because
$R=0$
because
![]() ${\{\unicode[STIX]{x1D6F7}^{H}\}}_{H\in \operatorname{Sub}(G)}$
is jointly conservative.◻
${\{\unicode[STIX]{x1D6F7}^{H}\}}_{H\in \operatorname{Sub}(G)}$
is jointly conservative.◻
For any non-zero finite (
![]() $p$
-local) spectrum
$p$
-local) spectrum
![]() $F$
there exists an
$F$
there exists an
![]() $n\in \mathbb{N}$
such that
$n\in \mathbb{N}$
such that
![]() $K(n)_{\ast }(F)\neq 0$
, which can be seen using the Atiyah–Hirzebruch spectral sequence.
$K(n)_{\ast }(F)\neq 0$
, which can be seen using the Atiyah–Hirzebruch spectral sequence.
Definition 3.6. If
![]() $X$
is a finite
$X$
is a finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
, we define its type function as the function
$X$
, we define its type function as the function
![]() $\text{type}_{X}:\operatorname{Sub}(G)\rightarrow \overline{\mathbb{N}}$
defined by
$\text{type}_{X}:\operatorname{Sub}(G)\rightarrow \overline{\mathbb{N}}$
defined by
It turns out that the central problem for determining the topology on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
and classifying the tt-ideals is the question of which functions can occur as
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
and classifying the tt-ideals is the question of which functions can occur as
![]() $\text{type}_{X}$
for some
$\text{type}_{X}$
for some
![]() $X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
.
$X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
.
By a theorem due to Ravenel [Reference RavenelRav84, Theorem 2.11], if
![]() $F\in {\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
has
$F\in {\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
has
![]() $K(n)_{\ast }(F)=0$
, then
$K(n)_{\ast }(F)=0$
, then
![]() $K(n-1)_{\ast }(F)$
as well; so for finite
$K(n-1)_{\ast }(F)$
as well; so for finite
![]() $G$
-spectra
$G$
-spectra
![]() $X$
, the function
$X$
, the function
![]() $\text{type}_{X}$
contains the same information as
$\text{type}_{X}$
contains the same information as
![]() $\operatorname{supp}(X)$
. As before, we may extend
$\operatorname{supp}(X)$
. As before, we may extend
![]() $\text{type}_{}$
to subcategories
$\text{type}_{}$
to subcategories
![]() ${\mathcal{X}}\subseteq {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
by defining
${\mathcal{X}}\subseteq {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
by defining
We write
![]() $f\geqslant g$
for two functions
$f\geqslant g$
for two functions
![]() $f,g:\operatorname{Sub}(G)\rightarrow \overline{\mathbb{N}}$
if
$f,g:\operatorname{Sub}(G)\rightarrow \overline{\mathbb{N}}$
if
![]() $f(H)\geqslant g(H)$
for all
$f(H)\geqslant g(H)$
for all
![]() $H\in \operatorname{Sub}(G)$
. The next corollary is now an immediate consequence of Propositions 3.2 and 3.5.
$H\in \operatorname{Sub}(G)$
. The next corollary is now an immediate consequence of Propositions 3.2 and 3.5.
Corollary 3.7. Let
![]() $X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
be a finite
$X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
be a finite
![]() $G$
-spectrum and
$G$
-spectrum and
![]() $I\subseteq {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
a tt-ideal such that
$I\subseteq {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
a tt-ideal such that
![]() $\text{type}_{X}\geqslant \text{type}_{I}$
. Then
$\text{type}_{X}\geqslant \text{type}_{I}$
. Then
![]() $X\in I$
.
$X\in I$
.
In particular, the type function
![]() $\text{type}_{I}$
determines the tt-ideal
$\text{type}_{I}$
determines the tt-ideal
![]() $I$
: it is given by all
$I$
: it is given by all
![]() $X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
such that
$X\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
such that
![]() $\text{type}_{X}\geqslant \text{type}_{I}$
.
$\text{type}_{X}\geqslant \text{type}_{I}$
.
When
![]() $I$
is given by
$I$
is given by
![]() $\text{thick}^{\otimes }(Y)$
for another finite
$\text{thick}^{\otimes }(Y)$
for another finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $Y$
, the corollary implies that
$Y$
, the corollary implies that
![]() $X\in \text{thick}^{\otimes }(Y)$
if and only if
$X\in \text{thick}^{\otimes }(Y)$
if and only if
![]() $\text{type}_{X}\geqslant \text{type}_{Y}$
. This statement is perhaps slightly surprising, because it means that
$\text{type}_{X}\geqslant \text{type}_{Y}$
. This statement is perhaps slightly surprising, because it means that
![]() $X$
lies in
$X$
lies in
![]() $\text{thick}^{\otimes }(Y)$
if and only if
$\text{thick}^{\otimes }(Y)$
if and only if
![]() $\unicode[STIX]{x1D6F7}^{H}(X)$
lies in
$\unicode[STIX]{x1D6F7}^{H}(X)$
lies in
![]() $\text{thick}^{\otimes }(\unicode[STIX]{x1D6F7}^{H}(Y))$
for all closed subgroups
$\text{thick}^{\otimes }(\unicode[STIX]{x1D6F7}^{H}(Y))$
for all closed subgroups
![]() $H$
, with no condition on how the various geometric fixed points are glued together.
$H$
, with no condition on how the various geometric fixed points are glued together.
Remark 3.8. Bousfield has extended Ravenel’s theorem to all
![]() $p$
-torsion suspension spectra, see [Reference BousfieldBou99]; hence, the notion of type is well-defined for this larger class of spectra. We are not aware of an analogue of the classification of thick subcategories in this setting.
$p$
-torsion suspension spectra, see [Reference BousfieldBou99]; hence, the notion of type is well-defined for this larger class of spectra. We are not aware of an analogue of the classification of thick subcategories in this setting.
We end this subsection with a result concerning the type function of induced
![]() $G$
-spectra, which we shall make repeated use of. Recall from § 2.2.2 that for a closed subgroup
$G$
-spectra, which we shall make repeated use of. Recall from § 2.2.2 that for a closed subgroup
![]() $H$
of a compact Lie group
$H$
of a compact Lie group
![]() $G$
, the restriction functor
$G$
, the restriction functor
has a left adjoint denoted
![]() $\operatorname{Ind}_{H}^{G}$
.
$\operatorname{Ind}_{H}^{G}$
.
Lemma 3.9. Let
![]() $H$
be a closed subgroup of a compact Lie group
$H$
be a closed subgroup of a compact Lie group
![]() $G$
, and
$G$
, and
![]() $X$
a finite
$X$
a finite
![]() $H$
-spectrum. Then the following hold.
$H$
-spectrum. Then the following hold.
(i) The type of
 $\unicode[STIX]{x1D6F7}^{H}(\operatorname{Ind}_{H}^{G}(X))$
is equal to the type of
$\unicode[STIX]{x1D6F7}^{H}(\operatorname{Ind}_{H}^{G}(X))$
is equal to the type of
 $\unicode[STIX]{x1D6F7}^{H}(X)$
.
$\unicode[STIX]{x1D6F7}^{H}(X)$
.(ii) If
 $K$
is another closed subgroup of
$K$
is another closed subgroup of
 $G$
, then the type of
$G$
, then the type of
 $\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
is at least the minimum of the types of
$\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
is at least the minimum of the types of
 $\unicode[STIX]{x1D6F7}^{K^{\prime }}(X)$
for all subgroups
$\unicode[STIX]{x1D6F7}^{K^{\prime }}(X)$
for all subgroups
 $K^{\prime }$
of
$K^{\prime }$
of
 $H$
that are conjugate to
$H$
that are conjugate to
 $K$
in
$K$
in
 $G$
.
$G$
.(iii) If
 $K$
is not subconjugate to
$K$
is not subconjugate to
 $H$
, then the geometric fixed points
$H$
, then the geometric fixed points
 $\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
are trivial.
$\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
are trivial.
A proof of this result is given in Appendix A.
Remark 3.10. When
![]() $G$
is a finite group, there is in fact an equality in part (ii) above, i.e., in that case the type of
$G$
is a finite group, there is in fact an equality in part (ii) above, i.e., in that case the type of
![]() $\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
equals the minimum of the types of
$\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
equals the minimum of the types of
![]() $\unicode[STIX]{x1D6F7}^{K^{\prime }}(\operatorname{Ind}_{H}^{G}(X))$
for all subgroups
$\unicode[STIX]{x1D6F7}^{K^{\prime }}(\operatorname{Ind}_{H}^{G}(X))$
for all subgroups
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $H$
that are conjugate to
$H$
that are conjugate to
![]() $K$
in
$K$
in
![]() $G$
, see Remark A.3 in Appendix A.
$G$
, see Remark A.3 in Appendix A.
This is not generally true for compact Lie groups. Note that when
![]() $K$
is the trivial group, an equality in part (ii) would mean that the type of
$K$
is the trivial group, an equality in part (ii) would mean that the type of
![]() $\unicode[STIX]{x1D6F7}^{e}\operatorname{Ind}_{H}^{G}(X)$
is always the same as the type of
$\unicode[STIX]{x1D6F7}^{e}\operatorname{Ind}_{H}^{G}(X)$
is always the same as the type of
![]() $\unicode[STIX]{x1D6F7}^{e}(X)$
. Counterexamples to such an equality are given by the following complexes, which play a central role in [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19] and were studied extensively by Arone, Lesh, and Mahowald [Reference AroneAro98, Reference Arone and MahowaldAM99, Reference Arone and LeshAL17]. We refer to [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19, § 4] for more details. Let
$\unicode[STIX]{x1D6F7}^{e}(X)$
. Counterexamples to such an equality are given by the following complexes, which play a central role in [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19] and were studied extensively by Arone, Lesh, and Mahowald [Reference AroneAro98, Reference Arone and MahowaldAM99, Reference Arone and LeshAL17]. We refer to [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19, § 4] for more details. Let
![]() $n>0$
and let
$n>0$
and let
![]() ${\mathcal{P}}_{p^{n}}^{\diamond }$
denote the unreduced suspension of the complex of proper non-trivial partitions of the set
${\mathcal{P}}_{p^{n}}^{\diamond }$
denote the unreduced suspension of the complex of proper non-trivial partitions of the set
![]() $\{1,\ldots ,p^{n}\}$
, equipped with the action of
$\{1,\ldots ,p^{n}\}$
, equipped with the action of
![]() $\unicode[STIX]{x1D6F4}_{p^{n}}$
by permuting the partitions. Further, let
$\unicode[STIX]{x1D6F4}_{p^{n}}$
by permuting the partitions. Further, let
![]() $\overline{\unicode[STIX]{x1D70C}}$
denote the reduced standard representation of
$\overline{\unicode[STIX]{x1D70C}}$
denote the reduced standard representation of
![]() $\unicode[STIX]{x1D6F4}_{p^{n}}$
, and define
$\unicode[STIX]{x1D6F4}_{p^{n}}$
, and define
![]() $X\in {\mathcal{S}}{\mathcal{H}}_{\unicode[STIX]{x1D6F4}_{p^{n}},(p)}^{c}$
by
$X\in {\mathcal{S}}{\mathcal{H}}_{\unicode[STIX]{x1D6F4}_{p^{n}},(p)}^{c}$
by
The reduced standard representation (this time over
![]() $\mathbb{C}$
) defines an embedding
$\mathbb{C}$
) defines an embedding
![]() $\unicode[STIX]{x1D6F4}_{p^{n}}{\hookrightarrow}U(p^{n}-1)$
, so we can consider
$\unicode[STIX]{x1D6F4}_{p^{n}}{\hookrightarrow}U(p^{n}-1)$
, so we can consider
![]() $\operatorname{Ind}_{\unicode[STIX]{x1D6F4}_{p^{n}}}^{U(p^{n}-1)}X$
. Since
$\operatorname{Ind}_{\unicode[STIX]{x1D6F4}_{p^{n}}}^{U(p^{n}-1)}X$
. Since
![]() ${\mathcal{P}}_{p^{n}}$
is a non-trivial wedge of spheres (see [Reference Orlik and TeraoOT92, 4.109]), the underlying non-equivariant spectrum of
${\mathcal{P}}_{p^{n}}$
is a non-trivial wedge of spheres (see [Reference Orlik and TeraoOT92, 4.109]), the underlying non-equivariant spectrum of
![]() $X$
, i.e.,
$X$
, i.e.,
![]() $\unicode[STIX]{x1D6F7}^{e}(X)$
, has type
$\unicode[STIX]{x1D6F7}^{e}(X)$
, has type
![]() $0$
. On the other hand, by work of Arone–Mahowald [Reference Arone and MahowaldAM99] and Arone [Reference AroneAro98], the underlying non-equivariant spectrum of
$0$
. On the other hand, by work of Arone–Mahowald [Reference Arone and MahowaldAM99] and Arone [Reference AroneAro98], the underlying non-equivariant spectrum of
![]() $\operatorname{Ind}_{\unicode[STIX]{x1D6F4}_{p^{n}}}^{U(p^{n}-1)}X$
has type
$\operatorname{Ind}_{\unicode[STIX]{x1D6F4}_{p^{n}}}^{U(p^{n}-1)}X$
has type
![]() $n$
, see also the proof of [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19, Theorem 2.2].
$n$
, see also the proof of [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19, Theorem 2.2].
3.3 The underlying set of
 $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
In this subsection we describe the set of prime ideals in
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, using the geometric fixed point functors to pull back prime ideals from
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, using the geometric fixed point functors to pull back prime ideals from
![]() ${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
and applying results of the previous subsections to deduce that every prime ideal is obtained in this way. For any
${\mathcal{S}}{\mathcal{H}}_{(p)}^{c}$
and applying results of the previous subsections to deduce that every prime ideal is obtained in this way. For any
![]() $(H,n)\in \operatorname{Sub}(G)\times \overline{\mathbb{N}}_{{>}0}$
, we write
$(H,n)\in \operatorname{Sub}(G)\times \overline{\mathbb{N}}_{{>}0}$
, we write
Since
![]() $\unicode[STIX]{x1D6F7}^{H}$
is symmetric monoidal, it follows that each
$\unicode[STIX]{x1D6F7}^{H}$
is symmetric monoidal, it follows that each
![]() $P_{G}(H,n)$
is again a prime.
$P_{G}(H,n)$
is again a prime.
We now show that every prime ideal in
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
is of the form
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
is of the form
![]() $P_{G}(H,n)$
for some closed subgroup
$P_{G}(H,n)$
for some closed subgroup
![]() $H$
and
$H$
and
![]() $n\in \overline{\mathbb{N}}_{{>}0}$
, where
$n\in \overline{\mathbb{N}}_{{>}0}$
, where
![]() $n$
is unique and
$n$
is unique and
![]() $H$
is unique up to conjugacy. We first prove uniqueness, for which we make use of finite
$H$
is unique up to conjugacy. We first prove uniqueness, for which we make use of finite
![]() $G$
-spectra of the following form.
$G$
-spectra of the following form.
Definition 3.11. Let
![]() $H\in \operatorname{Sub}(G)$
and
$H\in \operatorname{Sub}(G)$
and
![]() $n\in \overline{\mathbb{N}}$
. A finite
$n\in \overline{\mathbb{N}}$
. A finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
is said to be of type
$X$
is said to be of type
![]() $({\leqslant}^{G}\!H,n)$
if
$({\leqslant}^{G}\!H,n)$
if
![]() $\text{type}_{X}(K)=n$
for all subgroups
$\text{type}_{X}(K)=n$
for all subgroups
![]() $K$
which are conjugate in
$K$
which are conjugate in
![]() $G$
to a subgroup of
$G$
to a subgroup of
![]() $H$
and
$H$
and
![]() $\text{type}_{X}(K)=\infty$
for all other
$\text{type}_{X}(K)=\infty$
for all other
![]() $K$
.
$K$
.
Such finite
![]() $G$
-spectra always exist, by the following simple construction. Let
$G$
-spectra always exist, by the following simple construction. Let
![]() $Y$
be a non-equivariant finite type
$Y$
be a non-equivariant finite type
![]() $n$
spectrum. We consider the finite
$n$
spectrum. We consider the finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X=G/H_{+}\wedge i_{G}^{\ast }(Y)$
, i.e., the smash product of the based
$X=G/H_{+}\wedge i_{G}^{\ast }(Y)$
, i.e., the smash product of the based
![]() $G$
-space
$G$
-space
![]() $G/H_{+}$
with the inflation of
$G/H_{+}$
with the inflation of
![]() $Y$
to a
$Y$
to a
![]() $G$
-spectrum.
$G$
-spectrum.
Lemma 3.12. For every non-equivariant finite type
![]() $n$
spectrum
$n$
spectrum
![]() $Y$
the finite
$Y$
the finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X=G/H_{+}\wedge i_{G}^{\ast }(Y)$
is of type
$X=G/H_{+}\wedge i_{G}^{\ast }(Y)$
is of type
![]() $({\leqslant}^{G}\!H,n)$
.
$({\leqslant}^{G}\!H,n)$
.
Proof. For a subgroup
![]() $K$
of
$K$
of
![]() $G$
we have an equivalence
$G$
we have an equivalence
which follows from the behaviour of geometric fixed points with respect to smash product, suspension spectra, and inflation, as recalled in § 2.2. Now, if
![]() $K$
is conjugate to a subgroup
$K$
is conjugate to a subgroup
![]() $K^{g}$
of
$K^{g}$
of
![]() $H$
, then
$H$
, then
![]() $(G/H)^{K}$
is non-empty, since it contains the coset
$(G/H)^{K}$
is non-empty, since it contains the coset
![]() $g^{-1}H$
. Hence
$g^{-1}H$
. Hence
![]() $(G/H)_{+}^{K}$
contains
$(G/H)_{+}^{K}$
contains
![]() $S^{0}$
as a retract, and it follows that the type of
$S^{0}$
as a retract, and it follows that the type of
![]() $(G/H)_{+}^{K}\wedge Y$
is equal to the type of
$(G/H)_{+}^{K}\wedge Y$
is equal to the type of
![]() $Y$
, namely
$Y$
, namely
![]() $n$
. If, on the other hand,
$n$
. If, on the other hand,
![]() $K$
is not conjugate to a subgroup of
$K$
is not conjugate to a subgroup of
![]() $H$
, then the fixed points
$H$
, then the fixed points
![]() $(G/H)^{K}$
are empty, and hence
$(G/H)^{K}$
are empty, and hence
![]() $\unicode[STIX]{x1D6F7}^{K}(X)$
is trivial.◻
$\unicode[STIX]{x1D6F7}^{K}(X)$
is trivial.◻
The existence of such finite
![]() $G$
-spectra directly implies the following.
$G$
-spectra directly implies the following.
Lemma 3.13. Let
![]() $H$
and
$H$
and
![]() $K$
be closed subgroups of
$K$
be closed subgroups of
![]() $G$
, and
$G$
, and
![]() $n,m\in \overline{\mathbb{N}}_{{>}0}$
. We have:
$n,m\in \overline{\mathbb{N}}_{{>}0}$
. We have:
(i) if there is an inclusion
 $P_{G}(K,n)\subseteq P_{G}(H,m)$
, then
$P_{G}(K,n)\subseteq P_{G}(H,m)$
, then
 $n\geqslant m$
and
$n\geqslant m$
and
 $K$
is conjugate to a subgroup of
$K$
is conjugate to a subgroup of
 $H$
;
$H$
;(ii) if
 $P_{G}(K,n)=P_{G}(H,m)$
, then
$P_{G}(K,n)=P_{G}(H,m)$
, then
 $n=m$
and
$n=m$
and
 $K$
is conjugate to
$K$
is conjugate to
 $H$
.
$H$
.
Proof. Part (1): If
![]() $n<m$
, then any finite
$n<m$
, then any finite
![]() $G$
-spectrum of type
$G$
-spectrum of type
![]() $({\leqslant}^{G}\!G,n)$
lies in
$({\leqslant}^{G}\!G,n)$
lies in
![]() $P_{G}(K,n)$
but not in
$P_{G}(K,n)$
but not in
![]() $P_{G}(H,m)$
. If
$P_{G}(H,m)$
. If
![]() $K$
is not conjugate to a subgroup of
$K$
is not conjugate to a subgroup of
![]() $H$
, then any finite
$H$
, then any finite
![]() $G$
-spectrum of type
$G$
-spectrum of type
![]() $({\leqslant}^{G}\!H,m-1)$
lies in
$({\leqslant}^{G}\!H,m-1)$
lies in
![]() $P_{G}(K,n)$
but not in
$P_{G}(K,n)$
but not in
![]() $P_{G}(H,m)$
.
$P_{G}(H,m)$
.
Part (2) is a direct consequence of Part (1), since a closed subgroup of a compact Lie group cannot be conjugate to a proper subgroup of itself. Indeed, suppose
![]() $H$
is conjugate to
$H$
is conjugate to
![]() $H^{\prime }\subseteq H$
. Then by compactness,
$H^{\prime }\subseteq H$
. Then by compactness,
![]() $H^{\prime }$
has to be both closed and open in
$H^{\prime }$
has to be both closed and open in
![]() $H$
and hence a union of finitely many components of
$H$
and hence a union of finitely many components of
![]() $H$
. But we also have a bijection
$H$
. But we also have a bijection
![]() $\unicode[STIX]{x1D70B}_{0}(H)\cong \unicode[STIX]{x1D70B}_{0}(H^{\prime })$
, and hence
$\unicode[STIX]{x1D70B}_{0}(H)\cong \unicode[STIX]{x1D70B}_{0}(H^{\prime })$
, and hence
![]() $H^{\prime }=H$
as desired.◻
$H^{\prime }=H$
as desired.◻
Theorem 3.14. Let
![]() $G$
be a compact Lie group. Then the assignment
$G$
be a compact Lie group. Then the assignment
![]() $(H,n)\mapsto P_{G}(H,n)$
defines a bijection
$(H,n)\mapsto P_{G}(H,n)$
defines a bijection
Proof. Lemma 3.13 shows that the map is injective; hence it suffices to see that every prime ideal
![]() ${\wp}$
is of the form
${\wp}$
is of the form
![]() $P_{G}(H,n)$
for some subgroup
$P_{G}(H,n)$
for some subgroup
![]() $H$
and
$H$
and
![]() $n\in \mathbb{N}$
. By Corollary 3.7, we have
$n\in \mathbb{N}$
. By Corollary 3.7, we have
where we take
![]() $P_{G}(H,\text{type}_{{\wp}}(H))$
to mean the full category
$P_{G}(H,\text{type}_{{\wp}}(H))$
to mean the full category
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
if
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
if
![]() $\text{type}_{{\wp}}(H)=0$
. Since
$\text{type}_{{\wp}}(H)=0$
. Since
![]() ${\wp}$
is prime, it is in particular not the full tt-ideal of all finite
${\wp}$
is prime, it is in particular not the full tt-ideal of all finite
![]() $G$
-spectra, so there exists a subgroup
$G$
-spectra, so there exists a subgroup
![]() $H$
such that
$H$
such that
![]() $\text{type}_{{\wp}}(H)>0$
. Without loss of generality, we can assume that
$\text{type}_{{\wp}}(H)>0$
. Without loss of generality, we can assume that
![]() $H$
is minimal with this property, since every descending chain of compact Lie groups stabilizes after finitely many steps. We claim that
$H$
is minimal with this property, since every descending chain of compact Lie groups stabilizes after finitely many steps. We claim that
![]() ${\wp}$
is equal to
${\wp}$
is equal to
![]() $P_{G}(H,\text{type}_{{\wp}}(H))$
. If not, there would exist an element
$P_{G}(H,\text{type}_{{\wp}}(H))$
. If not, there would exist an element
![]() $X\in P_{G}(H,\text{type}_{{\wp}}(H))\setminus {\wp}$
. Furthermore, any finite
$X\in P_{G}(H,\text{type}_{{\wp}}(H))\setminus {\wp}$
. Furthermore, any finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $Y$
of type
$Y$
of type
![]() $({\leqslant}^{G}\!H,0)$
does not lie in
$({\leqslant}^{G}\!H,0)$
does not lie in
![]() ${\wp}$
, but we claim it is contained in
${\wp}$
, but we claim it is contained in
![]() $\bigcap _{H^{\prime }\not \sim H}P_{G}(H^{\prime },\text{type}_{{\wp}}(H^{\prime }))$
. Indeed, if
$\bigcap _{H^{\prime }\not \sim H}P_{G}(H^{\prime },\text{type}_{{\wp}}(H^{\prime }))$
. Indeed, if
![]() $H^{\prime }$
is conjugate to a proper subgroup of
$H^{\prime }$
is conjugate to a proper subgroup of
![]() $H$
, then
$H$
, then
![]() $\text{type}_{{\wp}}(H^{\prime })=0$
by the minimality of
$\text{type}_{{\wp}}(H^{\prime })=0$
by the minimality of
![]() $H$
, and hence
$H$
, and hence
![]() $P_{G}(H^{\prime },\text{type}_{{\wp}}(H^{\prime }))$
is the ideal of all finite
$P_{G}(H^{\prime },\text{type}_{{\wp}}(H^{\prime }))$
is the ideal of all finite
![]() $G$
-spectra. If
$G$
-spectra. If
![]() $H^{\prime }$
is not conjugate to a subgroup of
$H^{\prime }$
is not conjugate to a subgroup of
![]() $H$
, then
$H$
, then
![]() $\text{type}_{Y}(H^{\prime })=\infty$
and hence
$\text{type}_{Y}(H^{\prime })=\infty$
and hence
![]() $Y$
is contained in
$Y$
is contained in
![]() $P_{G}(H^{\prime },n)$
for all
$P_{G}(H^{\prime },n)$
for all
![]() $n$
. However, the smash product
$n$
. However, the smash product
![]() $X\wedge Y$
lies in the intersection
$X\wedge Y$
lies in the intersection
contradicting the fact that
![]() ${\wp}$
is prime. Hence, such an
${\wp}$
is prime. Hence, such an
![]() $X$
cannot exist, which implies that
$X$
cannot exist, which implies that
![]() ${\wp}=P_{G}(H,\text{type}_{{\wp}}(H))$
as desired.◻
${\wp}=P_{G}(H,\text{type}_{{\wp}}(H))$
as desired.◻
3.4 The equivariant nilpotence theorem
The goal of this subsection is to strengthen the observation made in the proof of Proposition 3.5 that
![]() $\{{\unicode[STIX]{x1D705}_{(H,n)}\}}_{(H,n)\in \operatorname{Sub}(G)\times \overline{\mathbb{N}}}$
detects ring objects to an equivariant version of the nilpotence theorem. This generalizes [Reference Balmer and SandersBS17, Theorem 4.15] from finite groups to arbitrary compact Lie groups; however, unlike their proof, our argument does not rely on the classification of prime ideals in
$\{{\unicode[STIX]{x1D705}_{(H,n)}\}}_{(H,n)\in \operatorname{Sub}(G)\times \overline{\mathbb{N}}}$
detects ring objects to an equivariant version of the nilpotence theorem. This generalizes [Reference Balmer and SandersBS17, Theorem 4.15] from finite groups to arbitrary compact Lie groups; however, unlike their proof, our argument does not rely on the classification of prime ideals in
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
, but rather exploits properties of the geometric fixed point functors to reduce to the non-equivariant nilpotence theorem by Devinatz, Hopkins, and Smith.
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
, but rather exploits properties of the geometric fixed point functors to reduce to the non-equivariant nilpotence theorem by Devinatz, Hopkins, and Smith.
Lemma 3.15. Let
![]() $R$
be a homotopy
$R$
be a homotopy
![]() $G$
-ring spectrum (i.e., an object of
$G$
-ring spectrum (i.e., an object of
![]() $\operatorname{Alg}({\mathcal{S}}{\mathcal{H}}_{G})$
) and
$\operatorname{Alg}({\mathcal{S}}{\mathcal{H}}_{G})$
) and
![]() $x\in \unicode[STIX]{x1D70B}_{n}^{G}(R)$
an element. Then
$x\in \unicode[STIX]{x1D70B}_{n}^{G}(R)$
an element. Then
![]() $x$
is nilpotent if and only if the mapping telescope
$x$
is nilpotent if and only if the mapping telescope
is contractible.
Proof. First we note that the homotopy ring
![]() $\unicode[STIX]{x1D70B}_{\ast }^{G}(\operatorname{tel}(x))$
is isomorphic to the colimit
$\unicode[STIX]{x1D70B}_{\ast }^{G}(\operatorname{tel}(x))$
is isomorphic to the colimit
Now, if
![]() $\operatorname{tel}(x)$
is contractible, then this colimit must be trivial. In particular, the element represented by the class of the element
$\operatorname{tel}(x)$
is contractible, then this colimit must be trivial. In particular, the element represented by the class of the element
![]() $1\in \unicode[STIX]{x1D70B}_{0}^{G}(R)$
under the inclusion of the first term in the colimit system must be trivial. By standard facts about sequential colimits, this means that
$1\in \unicode[STIX]{x1D70B}_{0}^{G}(R)$
under the inclusion of the first term in the colimit system must be trivial. By standard facts about sequential colimits, this means that
![]() $x^{n}\cdot 1=x^{n}$
must be trivial for some
$x^{n}\cdot 1=x^{n}$
must be trivial for some
![]() $n\in \mathbb{N}$
, and hence
$n\in \mathbb{N}$
, and hence
![]() $x$
is nilpotent.
$x$
is nilpotent.
If
![]() $x$
is nilpotent, say
$x$
is nilpotent, say
![]() $x^{n}=0$
, then clearly the colimit above is trivial, since any composition of
$x^{n}=0$
, then clearly the colimit above is trivial, since any composition of
![]() $n$
maps in the colimit system is trivial. So we find that
$n$
maps in the colimit system is trivial. So we find that
![]() $\unicode[STIX]{x1D70B}_{\ast }^{G}(\operatorname{tel}(x))=0$
. Furthermore, all restrictions
$\unicode[STIX]{x1D70B}_{\ast }^{G}(\operatorname{tel}(x))=0$
. Furthermore, all restrictions
![]() $\operatorname{Res}_{H}^{G}(x)$
to closed subgroups
$\operatorname{Res}_{H}^{G}(x)$
to closed subgroups
![]() $H$
are also nilpotent, since restriction maps are ring homomorphisms. So we conclude that
$H$
are also nilpotent, since restriction maps are ring homomorphisms. So we conclude that
![]() $\unicode[STIX]{x1D70B}_{\ast }^{H}(\operatorname{tel}(\operatorname{Res}_{H}^{G}(x)))$
is trivial for all closed subgroups
$\unicode[STIX]{x1D70B}_{\ast }^{H}(\operatorname{tel}(\operatorname{Res}_{H}^{G}(x)))$
is trivial for all closed subgroups
![]() $H$
. Since we have an equivalence
$H$
. Since we have an equivalence
this shows that all the equivariant homotopy groups of
![]() $\operatorname{tel}(x)$
vanish, and hence
$\operatorname{tel}(x)$
vanish, and hence
![]() $\operatorname{tel}(x)$
is contractible.◻
$\operatorname{tel}(x)$
is contractible.◻
Remark 3.16. In fact, the statement holds more generally for
![]() $x\in \unicode[STIX]{x1D70B}_{V}^{G}(R)$
an element in the
$x\in \unicode[STIX]{x1D70B}_{V}^{G}(R)$
an element in the
![]() $RO(G)$
-graded homotopy ring of
$RO(G)$
-graded homotopy ring of
![]() $R$
, with the same proof.
$R$
, with the same proof.
Recall that there is a comparison map
which is a ring map if
![]() $X$
is a homotopy
$X$
is a homotopy
![]() $G$
-ring spectrum. Given an element
$G$
-ring spectrum. Given an element
![]() $x\in \unicode[STIX]{x1D70B}_{\ast }^{G}(X)$
, we also use the notation
$x\in \unicode[STIX]{x1D70B}_{\ast }^{G}(X)$
, we also use the notation
![]() $\unicode[STIX]{x1D6F7}^{H}(x)$
for the element
$\unicode[STIX]{x1D6F7}^{H}(x)$
for the element
![]() $\unicode[STIX]{x1D6F7}^{H}(\operatorname{Res}_{H}^{G}(x))\in \unicode[STIX]{x1D6F7}_{\ast }^{H}(X)$
.
$\unicode[STIX]{x1D6F7}^{H}(\operatorname{Res}_{H}^{G}(x))\in \unicode[STIX]{x1D6F7}_{\ast }^{H}(X)$
.
Proposition 3.17. Let
![]() $R$
be a homotopy
$R$
be a homotopy
![]() $G$
-ring spectrum and
$G$
-ring spectrum and
![]() $x\in \unicode[STIX]{x1D70B}_{\ast }^{G}(X)$
. Then
$x\in \unicode[STIX]{x1D70B}_{\ast }^{G}(X)$
. Then
![]() $x$
is nilpotent if and only if all its geometric fixed points
$x$
is nilpotent if and only if all its geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{H}(x)$
are nilpotent in
$\unicode[STIX]{x1D6F7}^{H}(x)$
are nilpotent in
![]() $\unicode[STIX]{x1D6F7}_{\ast }^{H}(R)$
.
$\unicode[STIX]{x1D6F7}_{\ast }^{H}(R)$
.
Proof. By the previous lemma we know that
![]() $x$
is nilpotent if and only if its mapping telescope
$x$
is nilpotent if and only if its mapping telescope
![]() $\operatorname{tel}(x)$
is contractible. But this is the case if and only if all the geometric fixed points
$\operatorname{tel}(x)$
is contractible. But this is the case if and only if all the geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{H}(\operatorname{tel}(x))$
are contractible. Since we have an equivalence
$\unicode[STIX]{x1D6F7}^{H}(\operatorname{tel}(x))$
are contractible. Since we have an equivalence
![]() $\unicode[STIX]{x1D6F7}^{H}(\operatorname{tel}(x))\simeq \operatorname{tel}(\unicode[STIX]{x1D6F7}^{H}(x))$
, this in turn is equivalent to all the geometric fixed points
$\unicode[STIX]{x1D6F7}^{H}(\operatorname{tel}(x))\simeq \operatorname{tel}(\unicode[STIX]{x1D6F7}^{H}(x))$
, this in turn is equivalent to all the geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{H}(x)$
being nilpotent, again by the previous lemma. This finishes the proof.◻
$\unicode[STIX]{x1D6F7}^{H}(x)$
being nilpotent, again by the previous lemma. This finishes the proof.◻
Recall that
![]() $F(-,-)$
denotes the function
$F(-,-)$
denotes the function
![]() $G$
-spectrum between two
$G$
-spectrum between two
![]() $G$
-spectra, see [Reference Lewis, May, Steinberger and McClureLMSM86, § II.3] or [Reference Mandell and MayMM02, § II.3]. The function
$G$
-spectra, see [Reference Lewis, May, Steinberger and McClureLMSM86, § II.3] or [Reference Mandell and MayMM02, § II.3]. The function
![]() $G$
-spectra are uniquely determined by being right adjoint to the smash product and make
$G$
-spectra are uniquely determined by being right adjoint to the smash product and make
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
a closed symmetric monoidal category. In particular, as is generally the case for closed symmetric monoidal categories (see, for example, [Reference KellyKel82, §§ 1.5–1.8]), the function
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
a closed symmetric monoidal category. In particular, as is generally the case for closed symmetric monoidal categories (see, for example, [Reference KellyKel82, §§ 1.5–1.8]), the function
![]() $G$
-spectra
$G$
-spectra
![]() $F(-,-)$
define a canonical enrichment of
$F(-,-)$
define a canonical enrichment of
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
over itself, and the smash product canonically extends to an enriched bi-functor. As a formal consequence, for any pair of
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
over itself, and the smash product canonically extends to an enriched bi-functor. As a formal consequence, for any pair of
![]() $G$
-spectra
$G$
-spectra
![]() $X$
and
$X$
and
![]() $Y$
, one can form a homotopy
$Y$
, one can form a homotopy
![]() $G$
-ring spectrum
$G$
-ring spectrum
![]() $R_{X,Y}=\vee _{n}F(X^{\wedge n},Y^{\wedge n})$
with multiplication given by the enriched smash product
$R_{X,Y}=\vee _{n}F(X^{\wedge n},Y^{\wedge n})$
with multiplication given by the enriched smash product
Its homotopy ring is given by
Now, if
![]() $X$
is a finite
$X$
is a finite
![]() $G$
-spectrum, the geometric fixed points
$G$
-spectrum, the geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{H}(F(X^{\wedge n},Y^{\wedge n}))$
are naturally equivalent to the non-equivariant function spectrum
$\unicode[STIX]{x1D6F7}^{H}(F(X^{\wedge n},Y^{\wedge n}))$
are naturally equivalent to the non-equivariant function spectrum
![]() $F(\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n},\unicode[STIX]{x1D6F7}^{H}(Y)^{\wedge n})$
. One way to see this is the following. Since
$F(\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n},\unicode[STIX]{x1D6F7}^{H}(Y)^{\wedge n})$
. One way to see this is the following. Since
![]() $X$
is dualizable,
$X$
is dualizable,
![]() $F(X^{\wedge n},Y^{\wedge n})$
is canonically equivalent to
$F(X^{\wedge n},Y^{\wedge n})$
is canonically equivalent to
![]() $F(X^{\wedge n},\mathbb{S}_{G})\,\wedge \,Y^{\wedge n}$
(see [Reference Greenlees and MayGM95a, Theorem 4.17]). Now
$F(X^{\wedge n},\mathbb{S}_{G})\,\wedge \,Y^{\wedge n}$
(see [Reference Greenlees and MayGM95a, Theorem 4.17]). Now
![]() $F(X^{\wedge n},\mathbb{S}_{G})$
is the dual of
$F(X^{\wedge n},\mathbb{S}_{G})$
is the dual of
![]() $X^{\wedge n}$
, whose
$X^{\wedge n}$
, whose
![]() $H$
-geometric fixed points are equivalent to the dual of
$H$
-geometric fixed points are equivalent to the dual of
![]() $\unicode[STIX]{x1D6F7}^{H}(X^{\wedge n})\simeq \unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n}$
, since
$\unicode[STIX]{x1D6F7}^{H}(X^{\wedge n})\simeq \unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n}$
, since
![]() $\unicode[STIX]{x1D6F7}^{H}$
is symmetric monoidal. Hence we obtain the above equivalence via
$\unicode[STIX]{x1D6F7}^{H}$
is symmetric monoidal. Hence we obtain the above equivalence via
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{H}(F(X^{\wedge n},Y^{\wedge n})) & \simeq & \displaystyle \unicode[STIX]{x1D6F7}^{H}(F(X^{\wedge n},\mathbb{S}_{G}))\wedge \unicode[STIX]{x1D6F7}^{H}(Y^{\wedge n})\nonumber\\ \displaystyle & \simeq & \displaystyle F(\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n},\mathbb{S})\wedge \unicode[STIX]{x1D6F7}^{H}(Y)^{\wedge n}\nonumber\\ \displaystyle & \simeq & \displaystyle F(\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n},\unicode[STIX]{x1D6F7}^{H}(Y)^{\wedge n}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{H}(F(X^{\wedge n},Y^{\wedge n})) & \simeq & \displaystyle \unicode[STIX]{x1D6F7}^{H}(F(X^{\wedge n},\mathbb{S}_{G}))\wedge \unicode[STIX]{x1D6F7}^{H}(Y^{\wedge n})\nonumber\\ \displaystyle & \simeq & \displaystyle F(\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n},\mathbb{S})\wedge \unicode[STIX]{x1D6F7}^{H}(Y)^{\wedge n}\nonumber\\ \displaystyle & \simeq & \displaystyle F(\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n},\unicode[STIX]{x1D6F7}^{H}(Y)^{\wedge n}),\nonumber\end{eqnarray}$$
where the last step uses dualizability of
![]() $\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n}$
.
$\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n}$
.
The above equivalences are compatible with taking smash products, so it follows that, for finite
![]() $X$
,
$X$
,
![]() $\unicode[STIX]{x1D6F7}^{H}(R_{X,Y})$
is equivalent as a homotopy ring spectrum to
$\unicode[STIX]{x1D6F7}^{H}(R_{X,Y})$
is equivalent as a homotopy ring spectrum to
![]() $R_{\unicode[STIX]{x1D6F7}^{H}(X),\unicode[STIX]{x1D6F7}^{H}(Y)}$
. Furthermore, the geometric fixed point map takes a map
$R_{\unicode[STIX]{x1D6F7}^{H}(X),\unicode[STIX]{x1D6F7}^{H}(Y)}$
. Furthermore, the geometric fixed point map takes a map
![]() $g:X^{\wedge n}\rightarrow Y^{\wedge n}$
to
$g:X^{\wedge n}\rightarrow Y^{\wedge n}$
to
![]() $\unicode[STIX]{x1D6F7}^{H}(g):\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n}\rightarrow \unicode[STIX]{x1D6F7}^{H}(Y)^{\wedge n}$
. Applying Proposition 3.17 to
$\unicode[STIX]{x1D6F7}^{H}(g):\unicode[STIX]{x1D6F7}^{H}(X)^{\wedge n}\rightarrow \unicode[STIX]{x1D6F7}^{H}(Y)^{\wedge n}$
. Applying Proposition 3.17 to
![]() $R_{X,Y}$
hence implies the following.
$R_{X,Y}$
hence implies the following.
Corollary 3.18. A map
![]() $f:X\rightarrow Y$
of
$f:X\rightarrow Y$
of
![]() $G$
-spectra, with
$G$
-spectra, with
![]() $X$
finite, is smash-nilpotent if and only if
$X$
finite, is smash-nilpotent if and only if
![]() $\unicode[STIX]{x1D6F7}^{H}(f):\unicode[STIX]{x1D6F7}^{H}(X)\rightarrow \unicode[STIX]{x1D6F7}^{H}(Y)$
is smash-nilpotent for all closed subgroups
$\unicode[STIX]{x1D6F7}^{H}(f):\unicode[STIX]{x1D6F7}^{H}(X)\rightarrow \unicode[STIX]{x1D6F7}^{H}(Y)$
is smash-nilpotent for all closed subgroups
![]() $H$
.
$H$
.
These results allow us to transport non-equivariant nilpotence theorems to the equivariant world, by testing on all geometric fixed points. In particular, we obtain the following equivariant version of the nilpotence theorem as a consequence of the non-equivariant nilpotence theorem.
Theorem 3.19. A map
![]() $f:X\rightarrow Y$
of
$f:X\rightarrow Y$
of
![]() $p$
-local
$p$
-local
![]() $G$
-spectra, with
$G$
-spectra, with
![]() $X$
finite, is smash-nilpotent if and only if
$X$
finite, is smash-nilpotent if and only if
![]() $K(n)_{\ast }\unicode[STIX]{x1D6F7}^{H}(f):K(n)_{\ast }\unicode[STIX]{x1D6F7}^{H}(X)\rightarrow K(n)_{\ast }\unicode[STIX]{x1D6F7}^{H}(Y)$
is smash-nilpotent in the category of graded
$K(n)_{\ast }\unicode[STIX]{x1D6F7}^{H}(f):K(n)_{\ast }\unicode[STIX]{x1D6F7}^{H}(X)\rightarrow K(n)_{\ast }\unicode[STIX]{x1D6F7}^{H}(Y)$
is smash-nilpotent in the category of graded
![]() $K(n)_{\ast }$
-modules for all closed subgroups
$K(n)_{\ast }$
-modules for all closed subgroups
![]() $H$
of
$H$
of
![]() $G$
and all
$G$
and all
![]() $n\in \overline{\mathbb{N}}$
.
$n\in \overline{\mathbb{N}}$
.
As mentioned previously, for finite groups
![]() $G$
this theorem was proven using tt-geometric techniques and induction on the order of
$G$
this theorem was proven using tt-geometric techniques and induction on the order of
![]() $G$
by Balmer and Sanders. We close this section with a remark about alternative versions of the equivariant nilpotence theorem.
$G$
by Balmer and Sanders. We close this section with a remark about alternative versions of the equivariant nilpotence theorem.
Remark 3.20. Let
![]() $MU_{G}$
be the homotopical
$MU_{G}$
be the homotopical
![]() $G$
-equivariant complex cobordism spectrum in the sense of tom Dieck [Reference tom DiecktD70]. For any closed subgroup
$G$
-equivariant complex cobordism spectrum in the sense of tom Dieck [Reference tom DiecktD70]. For any closed subgroup
![]() $H\subseteq G$
, the geometric fixed points
$H\subseteq G$
, the geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{H}MU_{G}$
split into a non-trivial wedge of shifted copies of non-equivariant
$\unicode[STIX]{x1D6F7}^{H}MU_{G}$
split into a non-trivial wedge of shifted copies of non-equivariant
![]() $MU$
, see [Reference SinhaSin01, Theorem 4.10], so it follows from Corollary 3.18 and the classical nilpotence theorem [Reference Devinatz, Hopkins and SmithDHS88] for
$MU$
, see [Reference SinhaSin01, Theorem 4.10], so it follows from Corollary 3.18 and the classical nilpotence theorem [Reference Devinatz, Hopkins and SmithDHS88] for
![]() $MU$
that
$MU$
that
![]() $MU_{G}$
detects smash-nilpotence of maps between finite
$MU_{G}$
detects smash-nilpotence of maps between finite
![]() $G$
-spectra.
$G$
-spectra.
When
![]() $G=C_{2}$
one can also consider the real cobordism spectrum
$G=C_{2}$
one can also consider the real cobordism spectrum
![]() $MU_{\mathbb{R}}$
, where
$MU_{\mathbb{R}}$
, where
![]() $C_{2}$
acts on the underlying spectrum
$C_{2}$
acts on the underlying spectrum
![]() $MU$
via complex conjugation [Reference LandweberLan68]. This one does not detect smash-nilpotence since its geometric fixed points
$MU$
via complex conjugation [Reference LandweberLan68]. This one does not detect smash-nilpotence since its geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{C_{2}}MU_{\mathbb{R}}\simeq MO$
see only
$\unicode[STIX]{x1D6F7}^{C_{2}}MU_{\mathbb{R}}\simeq MO$
see only
![]() $2$
-primary information. For a concrete example of a non smash-nilpotent map between finite
$2$
-primary information. For a concrete example of a non smash-nilpotent map between finite
![]() $C_{2}$
-spectra which is nilpotent in
$C_{2}$
-spectra which is nilpotent in
![]() $MU_{\mathbb{R}}$
, let
$MU_{\mathbb{R}}$
, let
![]() $C$
be the cofibre of the transfer map
$C$
be the cofibre of the transfer map
![]() $S^{0}\rightarrow (C_{2})_{+}\rightarrow S^{0}$
and consider the multiplication by
$S^{0}\rightarrow (C_{2})_{+}\rightarrow S^{0}$
and consider the multiplication by
![]() $2$
map
$2$
map
We claim that
![]() $(MU_{\mathbb{R}})_{\ast }(v)$
is nilpotent, while
$(MU_{\mathbb{R}})_{\ast }(v)$
is nilpotent, while
![]() $v$
is not. To this end, first observe that
$v$
is not. To this end, first observe that
![]() $\unicode[STIX]{x1D6F7}^{e}(v)$
induces multiplication by
$\unicode[STIX]{x1D6F7}^{e}(v)$
induces multiplication by
![]() $2$
on the mod-
$2$
on the mod-
![]() $2$
Moore spectrum
$2$
Moore spectrum
![]() $\unicode[STIX]{x1D6F7}^{e}C\simeq S^{0}/2$
and hence is smash-nilpotent. Secondly, applying
$\unicode[STIX]{x1D6F7}^{e}C\simeq S^{0}/2$
and hence is smash-nilpotent. Secondly, applying
![]() $C_{2}$
-geometric fixed points yields the map
$C_{2}$
-geometric fixed points yields the map
which induces the null map after smashing with
![]() $H\mathbb{Z}/2$
and hence also
$H\mathbb{Z}/2$
and hence also
![]() $MO$
. Therefore, the map
$MO$
. Therefore, the map
![]() $MO_{\ast }(\unicode[STIX]{x1D6F7}^{C^{2}}(v))$
is nilpotent. However, multiplication by
$MO_{\ast }(\unicode[STIX]{x1D6F7}^{C^{2}}(v))$
is nilpotent. However, multiplication by
![]() $2$
is not nilpotent on
$2$
is not nilpotent on
![]() $\unicode[STIX]{x1D6F7}^{C_{2}}C\simeq S^{0}\vee S^{1}$
and consequently
$\unicode[STIX]{x1D6F7}^{C_{2}}C\simeq S^{0}\vee S^{1}$
and consequently
![]() $v$
cannot be smash-nilpotent.
$v$
cannot be smash-nilpotent.
4 Type functions of finite
 $G$
-spectra are locally constant
$G$
-spectra are locally constant
In this section we discuss an essential property of the type functions
![]() $\text{type}_{X}$
for finite
$\text{type}_{X}$
for finite
![]() $G$
-spectra
$G$
-spectra
![]() $X$
: they are locally constant with respect to the Hausdorff topology on the space of conjugacy classes of closed subgroups
$X$
: they are locally constant with respect to the Hausdorff topology on the space of conjugacy classes of closed subgroups
![]() $\operatorname{Sub}(G)/G$
. This property plays a central role in the description of the Balmer topology, as we explain in § 5.
$\operatorname{Sub}(G)/G$
. This property plays a central role in the description of the Balmer topology, as we explain in § 5.
We now recall the topology on the set
![]() $\operatorname{Sub}(G)/G$
. First we choose a bi-invariant metric
$\operatorname{Sub}(G)/G$
. First we choose a bi-invariant metric
![]() $d$
on the Lie group
$d$
on the Lie group
![]() $G$
, and also write
$G$
, and also write
![]() $d$
for the induced Hausdorff metric on
$d$
for the induced Hausdorff metric on
![]() $\operatorname{Sub}(G)$
, defined via
$\operatorname{Sub}(G)$
, defined via
where
![]() $d(h,K)$
denotes the distance from the point
$d(h,K)$
denotes the distance from the point
![]() $h$
to the compact subset
$h$
to the compact subset
![]() $K$
, and likewise for
$K$
, and likewise for
![]() $d(H,k)$
. One can show that the resulting topology on
$d(H,k)$
. One can show that the resulting topology on
![]() $\operatorname{Sub}(G)$
is independent of the chosen metric on
$\operatorname{Sub}(G)$
is independent of the chosen metric on
![]() $G$
. See Figure 2 for an illustration of
$G$
. See Figure 2 for an illustration of
![]() $\operatorname{Sub}(\mathbb{T})$
. The topology on
$\operatorname{Sub}(\mathbb{T})$
. The topology on
![]() $\operatorname{Sub}(G)/G$
is then defined as the quotient topology from the projection
$\operatorname{Sub}(G)/G$
is then defined as the quotient topology from the projection
![]() $\operatorname{Sub}(G)\rightarrow \operatorname{Sub}(G)/G$
. We collect the following properties of the spaces
$\operatorname{Sub}(G)\rightarrow \operatorname{Sub}(G)/G$
. We collect the following properties of the spaces
![]() $\operatorname{Sub}(G)$
and
$\operatorname{Sub}(G)$
and
![]() $\operatorname{Sub}(G)/G$
.
$\operatorname{Sub}(G)/G$
.
Proposition 4.1. For any compact Lie group
![]() $G$
, the space of subgroups
$G$
, the space of subgroups
![]() $\operatorname{Sub}(G)$
is compact. If a sequence of subgroups
$\operatorname{Sub}(G)$
is compact. If a sequence of subgroups
![]() $(H_{i})_{i\in \mathbb{N}}$
converges to a subgroup
$(H_{i})_{i\in \mathbb{N}}$
converges to a subgroup
![]() $H$
of
$H$
of
![]() $G$
in
$G$
in
![]() $\operatorname{Sub}(G)$
, then
$\operatorname{Sub}(G)$
, then
![]() $H_{i}$
is conjugate to a subgroup of
$H_{i}$
is conjugate to a subgroup of
![]() $H$
for almost all
$H$
for almost all
![]() $i\in \mathbb{N}$
. Moreover, the conjugation action of
$i\in \mathbb{N}$
. Moreover, the conjugation action of
![]() $G$
on
$G$
on
![]() $\operatorname{Sub}(G)$
is continuous, and the quotient
$\operatorname{Sub}(G)$
is continuous, and the quotient
![]() $\operatorname{Sub}(G)/G$
is a compact, totally disconnected Hausdorff space.
$\operatorname{Sub}(G)/G$
is a compact, totally disconnected Hausdorff space.
A proof is given in [Reference tom DiecktD79, Propositions 5.6.1 and 5.6.2]. The part about convergent sequences of subgroups is a consequence of the Montgomery–Zippin theorem [Reference Montgomery and ZippinMZ42].
Example 4.2. The subgroups of the circle group
![]() $\mathbb{T}$
are given by the cyclic subgroups
$\mathbb{T}$
are given by the cyclic subgroups
![]() $C_{n}$
for
$C_{n}$
for
![]() $n\in \mathbb{N}$
and the full group
$n\in \mathbb{N}$
and the full group
![]() $\mathbb{T}$
. The Hausdorff topology on
$\mathbb{T}$
. The Hausdorff topology on
![]() $\operatorname{Sub}(\mathbb{T})$
is that of a converging sequence, i.e., the subspace
$\operatorname{Sub}(\mathbb{T})$
is that of a converging sequence, i.e., the subspace
![]() $\{{C_{n}\}}_{n\in \mathbb{N}}$
is discrete and the sets
$\{{C_{n}\}}_{n\in \mathbb{N}}$
is discrete and the sets
![]() $\{{C_{n}\}}_{n\geqslant m}\cup \{\mathbb{T}\}$
for
$\{{C_{n}\}}_{n\geqslant m}\cup \{\mathbb{T}\}$
for
![]() $m\in \mathbb{N}$
form a neighbourhood basis for the point
$m\in \mathbb{N}$
form a neighbourhood basis for the point
![]() $\mathbb{T}$
.
$\mathbb{T}$
.

Figure 2. A schematic illustration of
![]() $\operatorname{Sub}(\mathbb{T})$
.
$\operatorname{Sub}(\mathbb{T})$
.
As claimed above, we have the following proposition.
Proposition 4.3. For every finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
, the type function
$X$
, the type function
is locally constant.
Proof. Let
![]() $X$
be a finite
$X$
be a finite
![]() $G$
-spectrum. By Lemma 2.2,
$G$
-spectrum. By Lemma 2.2,
![]() $X$
is of the form
$X$
is of the form
![]() $S^{-V}\wedge \unicode[STIX]{x1D6F4}^{\infty }A$
, where
$S^{-V}\wedge \unicode[STIX]{x1D6F4}^{\infty }A$
, where
![]() $A$
is a homotopy retract of the
$A$
is a homotopy retract of the
![]() $p$
-localization of a finite based
$p$
-localization of a finite based
![]() $G$
-CW complex
$G$
-CW complex
![]() $B$
. Since smashing with a representation sphere does not change the type function, we can reduce to showing the proposition in the case where
$B$
. Since smashing with a representation sphere does not change the type function, we can reduce to showing the proposition in the case where
![]() $V=0$
and hence
$V=0$
and hence
![]() $X\simeq \unicode[STIX]{x1D6F4}^{\infty }A$
. We have to show that each
$X\simeq \unicode[STIX]{x1D6F4}^{\infty }A$
. We have to show that each
![]() $\text{type}_{X}^{-1}(n)$
is open. Let
$\text{type}_{X}^{-1}(n)$
is open. Let
![]() $H\in \operatorname{Sub}(G)$
such that
$H\in \operatorname{Sub}(G)$
such that
![]() $\text{type}_{X}(H)=n$
. If the class of
$\text{type}_{X}(H)=n$
. If the class of
![]() $H$
did not lie in the interior of
$H$
did not lie in the interior of
![]() $\text{type}_{X}^{-1}(n)$
, there would be a sequence
$\text{type}_{X}^{-1}(n)$
, there would be a sequence
![]() $H_{i}$
converging to
$H_{i}$
converging to
![]() $H$
with each
$H$
with each
![]() $H_{i}\notin \text{type}_{X}^{-1}(n)$
. By the Montgomery–Zippin theorem, we can assume that the
$H_{i}\notin \text{type}_{X}^{-1}(n)$
. By the Montgomery–Zippin theorem, we can assume that the
![]() $H_{i}$
are subgroups of
$H_{i}$
are subgroups of
![]() $H$
. Now the restriction
$H$
. Now the restriction
![]() $\operatorname{Res}_{H}^{G}B$
to an
$\operatorname{Res}_{H}^{G}B$
to an
![]() $H$
-space admits the structure of a finite
$H$
-space admits the structure of a finite
![]() $H$
-cell complex, and thus the isotropy of its points consist of only finitely many conjugacy classes of subgroups of
$H$
-cell complex, and thus the isotropy of its points consist of only finitely many conjugacy classes of subgroups of
![]() $H$
. Let
$H$
. Let
![]() $K_{1},\ldots ,K_{m},H$
be a choice of representatives for these conjugacy classes, where the full group
$K_{1},\ldots ,K_{m},H$
be a choice of representatives for these conjugacy classes, where the full group
![]() $H$
is among the isotropy groups since
$H$
is among the isotropy groups since
![]() $\operatorname{Res}_{H}^{G}B$
has a fixed basepoint. It follows that if
$\operatorname{Res}_{H}^{G}B$
has a fixed basepoint. It follows that if
![]() $K\subseteq H$
is not
$K\subseteq H$
is not
![]() $H$
-subconjugate to one of the
$H$
-subconjugate to one of the
![]() $K_{j}$
, then the restriction map
$K_{j}$
, then the restriction map
![]() $B^{H}\rightarrow B^{K}$
is a homeomorphism. Since
$B^{H}\rightarrow B^{K}$
is a homeomorphism. Since
![]() $A$
is a homotopy retract of the
$A$
is a homotopy retract of the
![]() $p$
-localization of
$p$
-localization of
![]() $B$
, this means that for these
$B$
, this means that for these
![]() $K$
the restriction map
$K$
the restriction map
![]() $A^{H}\rightarrow A^{K}$
is a homotopy equivalence. In particular,
$A^{H}\rightarrow A^{K}$
is a homotopy equivalence. In particular,
![]() $\text{type}_{X}(K)=\text{type}_{X}(H)$
for all such
$\text{type}_{X}(K)=\text{type}_{X}(H)$
for all such
![]() $K$
, since
$K$
, since
Thus, each
![]() $H_{i}$
above must be subconjugate to one of the
$H_{i}$
above must be subconjugate to one of the
![]() $K_{j}$
, and consequently, some
$K_{j}$
, and consequently, some
![]() $K_{j}$
, say
$K_{j}$
, say
![]() $K_{1}$
, is superconjugate to infinitely many of the
$K_{1}$
, is superconjugate to infinitely many of the
![]() $H_{i}$
. But this implies that
$H_{i}$
. But this implies that
![]() $d(H,H_{i})\geqslant d(H,K_{1})$
for all these
$d(H,H_{i})\geqslant d(H,K_{1})$
for all these
![]() $i$
, contradicting the facts that (1)
$i$
, contradicting the facts that (1)
![]() $K_{1}$
is a proper subgroup of
$K_{1}$
is a proper subgroup of
![]() $H$
and (2) the
$H$
and (2) the
![]() $H_{i}$
converge to
$H_{i}$
converge to
![]() $H$
.◻
$H$
.◻
Remark 4.4. When
![]() $G$
is finite, the Hausdorff topology on
$G$
is finite, the Hausdorff topology on
![]() $\operatorname{Sub}(G)$
is discrete and thus every function on it is automatically locally constant. In contrast to this, it will turn out in Theorem 5.3 below that the topology on
$\operatorname{Sub}(G)$
is discrete and thus every function on it is automatically locally constant. In contrast to this, it will turn out in Theorem 5.3 below that the topology on
![]() $\operatorname{Sub}(G)$
is one of the novel ingredients in the study of the Balmer spectrum for general compact Lie groups.
$\operatorname{Sub}(G)$
is one of the novel ingredients in the study of the Balmer spectrum for general compact Lie groups.
It is not generally true that the type functions of arbitrary tt-ideals
![]() $I$
are locally constant, as we will see in Theorem 5.3 and Example 5.5. However, we will need that they can be approximated by type functions
$I$
are locally constant, as we will see in Theorem 5.3 and Example 5.5. However, we will need that they can be approximated by type functions
![]() $\text{type}_{X}$
for
$\text{type}_{X}$
for
![]() $X\in I$
, in the following sense.
$X\in I$
, in the following sense.
Proposition 4.5. Let
![]() $G$
be a compact Lie group,
$G$
be a compact Lie group,
![]() $I$
a tt-ideal of
$I$
a tt-ideal of
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, and
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, and
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
a locally constant function such that
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
a locally constant function such that
![]() $f\geqslant \text{type}_{I}$
. Then there exists an
$f\geqslant \text{type}_{I}$
. Then there exists an
![]() $X\in I$
such that
$X\in I$
such that
![]() $f\geqslant \text{type}_{X}$
.
$f\geqslant \text{type}_{X}$
.
Proof. For every
![]() $H\in \operatorname{Sub}(G)/G$
we choose an object
$H\in \operatorname{Sub}(G)/G$
we choose an object
![]() $Y_{H}\in I$
such that
$Y_{H}\in I$
such that
![]() $\text{type}_{Y_{H}}(H)\leqslant f(H)$
, which exists by assumption. We note that since both
$\text{type}_{Y_{H}}(H)\leqslant f(H)$
, which exists by assumption. We note that since both
![]() $f$
and
$f$
and
![]() $\text{type}_{Y_{H}}$
are locally constant, there exists an open neighbourhood
$\text{type}_{Y_{H}}$
are locally constant, there exists an open neighbourhood
![]() $U_{H}$
of
$U_{H}$
of
![]() $H$
on which both
$H$
on which both
![]() $f$
and
$f$
and
![]() $\text{type}_{Y_{H}}$
are constant, and hence
$\text{type}_{Y_{H}}$
are constant, and hence
![]() $\text{type}_{Y_{H}}\leqslant f$
on that neighbourhood. The open sets
$\text{type}_{Y_{H}}\leqslant f$
on that neighbourhood. The open sets
![]() $U_{H}$
cover
$U_{H}$
cover
![]() $\operatorname{Sub}(G)/G$
, which is compact. Hence there exists a finite subcover
$\operatorname{Sub}(G)/G$
, which is compact. Hence there exists a finite subcover
![]() $U_{H_{1}},\ldots ,U_{H_{n}}$
. We now define
$U_{H_{1}},\ldots ,U_{H_{n}}$
. We now define
![]() $X$
via
$X$
via
Then on each
![]() $U_{H_{i}}$
we have
$U_{H_{i}}$
we have
![]() $\text{type}_{X}\leqslant \text{type}_{Y_{H_{i}}}\leqslant f$
. Since the
$\text{type}_{X}\leqslant \text{type}_{Y_{H_{i}}}\leqslant f$
. Since the
![]() $U_{H_{i}}$
cover
$U_{H_{i}}$
cover
![]() $\operatorname{Sub}(G)/G$
, it follows that
$\operatorname{Sub}(G)/G$
, it follows that
![]() $\text{type}_{X}\leqslant f$
on all of
$\text{type}_{X}\leqslant f$
on all of
![]() $\operatorname{Sub}(G)/G$
, which shows that
$\operatorname{Sub}(G)/G$
, which shows that
![]() $X$
has the desired property.◻
$X$
has the desired property.◻
5 The Balmer topology and classification of tt-ideals
For finite groups
![]() $G$
, it is shown in [Reference Balmer and SandersBS17] that the Balmer topology on
$G$
, it is shown in [Reference Balmer and SandersBS17] that the Balmer topology on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
and the classification of tt-ideals can be expressed in terms of the poset structure on the Balmer spectrum. In this section we show that in the case of compact Lie groups, the Balmer topology and the classification of tt-ideals are again determined by the poset structure on the set of prime ideals, provided one also remembers the Hausdorff topology on
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
and the classification of tt-ideals can be expressed in terms of the poset structure on the Balmer spectrum. In this section we show that in the case of compact Lie groups, the Balmer topology and the classification of tt-ideals are again determined by the poset structure on the set of prime ideals, provided one also remembers the Hausdorff topology on
![]() $\operatorname{Sub}(G)/G$
. We will return to the study of the poset structure in § 6.
$\operatorname{Sub}(G)/G$
. We will return to the study of the poset structure in § 6.
We first recall from Corollary 3.7 that every tt-ideal
![]() $I$
is determined by its type function
$I$
is determined by its type function
![]() $\text{type}_{I}$
. Hence, we obtain a classification of tt-ideals if we can describe which functions
$\text{type}_{I}$
. Hence, we obtain a classification of tt-ideals if we can describe which functions
![]() $\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
occur as the type function of a tt-ideal. It turns out that the type functions are detected by the following two properties, the first relying on the poset structure on the Balmer spectrum and the second on the topology on
$\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
occur as the type function of a tt-ideal. It turns out that the type functions are detected by the following two properties, the first relying on the poset structure on the Balmer spectrum and the second on the topology on
![]() $\operatorname{Sub}(G)/G$
.
$\operatorname{Sub}(G)/G$
.
Definition 5.1. We say a function
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
is admissible if
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
is admissible if
![]() $P_{G}(K,f(K))$
is not contained in
$P_{G}(K,f(K))$
is not contained in
![]() $P_{G}(H,f(H)+1)$
for all subgroups
$P_{G}(H,f(H)+1)$
for all subgroups
![]() $K,H$
with
$K,H$
with
![]() $f(H)<\infty$
.
$f(H)<\infty$
.
Definition 5.2. A function
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
is upper semi-continuous if
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
is upper semi-continuous if
![]() $f^{-1}([0,n))$
is open for all
$f^{-1}([0,n))$
is open for all
![]() $n\in \overline{\mathbb{N}}$
.
$n\in \overline{\mathbb{N}}$
.
Theorem 5.3. Let
![]() $G$
be a compact Lie group and
$G$
be a compact Lie group and
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
be a function. Then the following hold.
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
be a function. Then the following hold.
(i) The function
 $f$
is of the form
$f$
is of the form
 $\text{type}_{I}$
for some tt-ideal
$\text{type}_{I}$
for some tt-ideal
 $I$
if and only if it is admissible and upper semi-continuous.
$I$
if and only if it is admissible and upper semi-continuous.(ii) The function
 $f$
is of the form
$f$
is of the form
 $\text{type}_{X}$
for some finite
$\text{type}_{X}$
for some finite
 $G$
-spectrum
$G$
-spectrum
 $X$
if and only if it is admissible and locally constant.
$X$
if and only if it is admissible and locally constant.
Remark 5.4. We will see later in Lemma 7.2 that when
![]() $G$
is abelian, every admissible function is automatically upper semi-continuous, but this is not the case in general, for example for
$G$
is abelian, every admissible function is automatically upper semi-continuous, but this is not the case in general, for example for
![]() $G=O(2)$
, see Remark 7.5.
$G=O(2)$
, see Remark 7.5.
Example 5.5. An example of a tt-ideal
![]() $I$
that is not finitely generated is the prime ideal
$I$
that is not finitely generated is the prime ideal
![]() ${\wp}=P_{\mathbb{T}}(\mathbb{T},1)$
for the circle group
${\wp}=P_{\mathbb{T}}(\mathbb{T},1)$
for the circle group
![]() $\mathbb{T}$
. For any finite subgroup
$\mathbb{T}$
. For any finite subgroup
![]() $C_{n}$
of
$C_{n}$
of
![]() $\mathbb{T}$
, the finite
$\mathbb{T}$
, the finite
![]() $\mathbb{T}$
-spectrum
$\mathbb{T}$
-spectrum
![]() $\unicode[STIX]{x1D6F4}^{\infty }(\mathbb{T}/C_{n})_{+}$
has trivial
$\unicode[STIX]{x1D6F4}^{\infty }(\mathbb{T}/C_{n})_{+}$
has trivial
![]() $\mathbb{T}$
-geometric fixed points; hence it is contained in
$\mathbb{T}$
-geometric fixed points; hence it is contained in
![]() ${\wp}$
, but its
${\wp}$
, but its
![]() $C_{n}$
-geometric fixed points have type
$C_{n}$
-geometric fixed points have type
![]() $0$
. It follows that the type function
$0$
. It follows that the type function
![]() $\text{type}_{{\wp}}$
sends all finite subgroups
$\text{type}_{{\wp}}$
sends all finite subgroups
![]() $C_{n}$
to
$C_{n}$
to
![]() $0$
and the full group
$0$
and the full group
![]() $\mathbb{T}$
to
$\mathbb{T}$
to
![]() $1$
; hence it is not locally constant.
$1$
; hence it is not locally constant.
Before we prove the theorem, we need two preparatory lemmas.
Lemma 5.6. Let
![]() $X$
and
$X$
and
![]() $Y$
be finite
$Y$
be finite
![]() $G$
-spectra and
$G$
-spectra and
![]() $f:\unicode[STIX]{x1D6F7}^{G}(X)\rightarrow \unicode[STIX]{x1D6F7}^{G}(Y)$
a map between their geometric fixed points. Then there exists a
$f:\unicode[STIX]{x1D6F7}^{G}(X)\rightarrow \unicode[STIX]{x1D6F7}^{G}(Y)$
a map between their geometric fixed points. Then there exists a
![]() $G$
-representation
$G$
-representation
![]() $V$
satisfying
$V$
satisfying
![]() $V^{G}=0$
and a
$V^{G}=0$
and a
![]() $G$
-map
$G$
-map
![]() $\widetilde{f}:X\rightarrow Y\wedge S^{V}$
such that
$\widetilde{f}:X\rightarrow Y\wedge S^{V}$
such that
equals
![]() $f$
.
$f$
.
Proof. There is a natural isomorphism (for which finiteness of
![]() $X$
is not required)
$X$
is not required)
where
![]() $\widetilde{E}P$
is the cofibre of the map
$\widetilde{E}P$
is the cofibre of the map
![]() $EP_{+}\rightarrow S^{0}$
and
$EP_{+}\rightarrow S^{0}$
and
![]() $EP$
is a universal space for the family of proper subgroups of
$EP$
is a universal space for the family of proper subgroups of
![]() $G$
. This isomorphism is a consequence of the fact that
$G$
. This isomorphism is a consequence of the fact that
![]() $\widetilde{E}P\wedge -$
is a smashing localization on the homotopy category of
$\widetilde{E}P\wedge -$
is a smashing localization on the homotopy category of
![]() $G$
-spectra, whose category of local objects is equivalent to the homotopy category of non-equivariant spectra via taking geometric fixed points, see [Reference Lewis, May, Steinberger and McClureLMSM86, Corollary II.9.6], [Reference MayMay96, Theorem XVI.6.6] or [Reference Mathew, Naumann and NoelMNN17, Theorem 6.11]. The isomorphism assigns to a
$G$
-spectra, whose category of local objects is equivalent to the homotopy category of non-equivariant spectra via taking geometric fixed points, see [Reference Lewis, May, Steinberger and McClureLMSM86, Corollary II.9.6], [Reference MayMay96, Theorem XVI.6.6] or [Reference Mathew, Naumann and NoelMNN17, Theorem 6.11]. The isomorphism assigns to a
![]() $G$
-map
$G$
-map
![]() $X\rightarrow \widetilde{E}P\wedge Y$
its induced map on geometric fixed points, using that
$X\rightarrow \widetilde{E}P\wedge Y$
its induced map on geometric fixed points, using that
![]() $\unicode[STIX]{x1D6F7}^{G}(\widetilde{E}P)\simeq S^{0}$
. A model for
$\unicode[STIX]{x1D6F7}^{G}(\widetilde{E}P)\simeq S^{0}$
. A model for
![]() $\widetilde{E}P$
is given by the homotopy colimit over
$\widetilde{E}P$
is given by the homotopy colimit over
![]() $S^{V}$
, where
$S^{V}$
, where
![]() $V$
runs through the poset of all finite-dimensional subrepresentations of a complete
$V$
runs through the poset of all finite-dimensional subrepresentations of a complete
![]() $G$
-universe
$G$
-universe
![]() ${\mathcal{U}}_{G}$
which have trivial
${\mathcal{U}}_{G}$
which have trivial
![]() $G$
-fixed points; this is a consequence of the fact that for every proper closed subgroup
$G$
-fixed points; this is a consequence of the fact that for every proper closed subgroup
![]() $H$
of
$H$
of
![]() $G$
there exists a
$G$
there exists a
![]() $G$
-representation
$G$
-representation
![]() $V$
such that
$V$
such that
![]() $V^{G}=0$
but
$V^{G}=0$
but
![]() $V^{H}\neq 0$
, see [Reference Bröcker and tom DieckBtD85, Proposition III.4.2]. Hence,
$V^{H}\neq 0$
, see [Reference Bröcker and tom DieckBtD85, Proposition III.4.2]. Hence,
Now if
![]() $f:\unicode[STIX]{x1D6F7}^{G}(X)\rightarrow \unicode[STIX]{x1D6F7}^{G}(Y)$
is given as above, it corresponds to a
$f:\unicode[STIX]{x1D6F7}^{G}(X)\rightarrow \unicode[STIX]{x1D6F7}^{G}(Y)$
is given as above, it corresponds to a
![]() $G$
-map
$G$
-map
Since
![]() $X$
is finite, the map
$X$
is finite, the map
![]() $F$
factors through a finite stage
$F$
factors through a finite stage
![]() $S^{V}\wedge Y$
, yielding the desired
$S^{V}\wedge Y$
, yielding the desired
![]() $\widetilde{f}$
.◻
$\widetilde{f}$
.◻
Lemma 5.7. Let
![]() $K$
and
$K$
and
![]() $H$
be subgroups of
$H$
be subgroups of
![]() $G$
, and
$G$
, and
![]() $n\in \overline{\mathbb{N}}$
and
$n\in \overline{\mathbb{N}}$
and
![]() $m\in \mathbb{N}$
. If
$m\in \mathbb{N}$
. If
![]() $P_{G}(K,n)$
is not contained in
$P_{G}(K,n)$
is not contained in
![]() $P_{G}(H,m+1)$
, then there exists a finite
$P_{G}(H,m+1)$
, then there exists a finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
such that
$X$
such that
![]() $\text{type}_{X}(K)\geqslant n$
and
$\text{type}_{X}(K)\geqslant n$
and
![]() $\text{type}_{X}(H)=m$
.
$\text{type}_{X}(H)=m$
.
Proof. Since
![]() $P_{G}(K,n)$
is not contained in
$P_{G}(K,n)$
is not contained in
![]() $P_{G}(H,m+1)$
, there exists a finite
$P_{G}(H,m+1)$
, there exists a finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $Y$
such that
$Y$
such that
![]() $\text{type}_{Y}(K)\geqslant n$
and
$\text{type}_{Y}(K)\geqslant n$
and
![]() $\text{type}_{Y}(H)\leqslant m$
. If
$\text{type}_{Y}(H)\leqslant m$
. If
![]() $\text{type}_{Y}(H)=m$
, we are done. If not, we will explain how to use
$\text{type}_{Y}(H)=m$
, we are done. If not, we will explain how to use
![]() $Y$
to construct another finite
$Y$
to construct another finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $Y^{\prime }$
such that
$Y^{\prime }$
such that
![]() $\text{type}_{Y^{\prime }}(K)\geqslant n$
and
$\text{type}_{Y^{\prime }}(K)\geqslant n$
and
![]() $\text{type}_{Y^{\prime }}(H)=\text{type}_{Y}(H)+1$
. Iterating this process leads to the desired finite
$\text{type}_{Y^{\prime }}(H)=\text{type}_{Y}(H)+1$
. Iterating this process leads to the desired finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
.
$X$
.
The construction of
![]() $Y^{\prime }$
goes as follows. We first consider the case where
$Y^{\prime }$
goes as follows. We first consider the case where
![]() $H$
equals the ambient group
$H$
equals the ambient group
![]() $G$
. By the periodicity theorem of Hopkins and Smith [Reference Hopkins and SmithHS98, Theorem 9], there exists a
$G$
. By the periodicity theorem of Hopkins and Smith [Reference Hopkins and SmithHS98, Theorem 9], there exists a
![]() $v_{\text{type}_{Y}(G)}$
-self map
$v_{\text{type}_{Y}(G)}$
-self map
![]() $f:\unicode[STIX]{x1D6F4}^{k}\unicode[STIX]{x1D6F7}^{G}(Y)\rightarrow \unicode[STIX]{x1D6F7}^{G}(Y)$
, i.e., a self-map which induces an isomorphism on
$f:\unicode[STIX]{x1D6F4}^{k}\unicode[STIX]{x1D6F7}^{G}(Y)\rightarrow \unicode[STIX]{x1D6F7}^{G}(Y)$
, i.e., a self-map which induces an isomorphism on
![]() $K(\text{type}_{Y}(G))_{\ast }$
and is trivial on all other Morava
$K(\text{type}_{Y}(G))_{\ast }$
and is trivial on all other Morava
![]() $K$
-theories. Applying Lemma 5.6 to this
$K$
-theories. Applying Lemma 5.6 to this
![]() $f$
, we obtain a
$f$
, we obtain a
![]() $G$
-map
$G$
-map
![]() $\widetilde{f}:\unicode[STIX]{x1D6F4}^{k}Y\rightarrow Y\wedge S^{V}$
for some
$\widetilde{f}:\unicode[STIX]{x1D6F4}^{k}Y\rightarrow Y\wedge S^{V}$
for some
![]() $G$
-representation
$G$
-representation
![]() $V$
with trivial fixed points, such that the geometric fixed points
$V$
with trivial fixed points, such that the geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{H}(\widetilde{f})$
give back
$\unicode[STIX]{x1D6F7}^{H}(\widetilde{f})$
give back
![]() $f$
. Then the cofibre
$f$
. Then the cofibre
![]() $Y^{\prime }=\operatorname{cone}(\widetilde{f})$
has the desired properties: the geometric fixed points
$Y^{\prime }=\operatorname{cone}(\widetilde{f})$
has the desired properties: the geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{G}(Y^{\prime })$
are given by the cofibre of
$\unicode[STIX]{x1D6F7}^{G}(Y^{\prime })$
are given by the cofibre of
![]() $f$
, whose type equals
$f$
, whose type equals
![]() $\text{type}_{Y}(G)+1$
, since
$\text{type}_{Y}(G)+1$
, since
![]() $f$
is a
$f$
is a
![]() $v_{\text{type}_{Y}(G)}$
-self map. Furthermore, since
$v_{\text{type}_{Y}(G)}$
-self map. Furthermore, since
![]() $Y^{\prime }$
lies in the tt-ideal generated by
$Y^{\prime }$
lies in the tt-ideal generated by
![]() $Y$
, the type of
$Y$
, the type of
![]() $\unicode[STIX]{x1D6F7}^{K}(Y^{\prime })$
cannot be smaller than that of
$\unicode[STIX]{x1D6F7}^{K}(Y^{\prime })$
cannot be smaller than that of
![]() $\unicode[STIX]{x1D6F7}^{K}(Y)$
.
$\unicode[STIX]{x1D6F7}^{K}(Y)$
.
If
![]() $H$
is a proper subgroup of
$H$
is a proper subgroup of
![]() $G$
, one repeats the same argument for
$G$
, one repeats the same argument for
![]() $G=H$
applied to the restriction
$G=H$
applied to the restriction
![]() $\operatorname{Res}_{H}^{G}(Y)$
. This leads to a finite
$\operatorname{Res}_{H}^{G}(Y)$
. This leads to a finite
![]() $H$
-spectrum
$H$
-spectrum
![]() $\widetilde{Y}$
, defined as the cofibre of an
$\widetilde{Y}$
, defined as the cofibre of an
![]() $H$
-map
$H$
-map
![]() $\widetilde{f}:\operatorname{Res}_{H}^{G}(Y)\rightarrow \operatorname{Res}_{H}^{G}(Y)\wedge S^{V}$
, where
$\widetilde{f}:\operatorname{Res}_{H}^{G}(Y)\rightarrow \operatorname{Res}_{H}^{G}(Y)\wedge S^{V}$
, where
![]() $V$
is an
$V$
is an
![]() $H$
-representation with trivial fixed points. By the same argument as in the absolute case, the type of its
$H$
-representation with trivial fixed points. By the same argument as in the absolute case, the type of its
![]() $H$
-geometric fixed points is given by
$H$
-geometric fixed points is given by
![]() $\text{type}_{Y}(H)+1$
, and the type of
$\text{type}_{Y}(H)+1$
, and the type of
![]() $\unicode[STIX]{x1D6F7}^{J}(\widetilde{Y})$
is at least that of
$\unicode[STIX]{x1D6F7}^{J}(\widetilde{Y})$
is at least that of
![]() $\unicode[STIX]{x1D6F7}^{J}(Y)$
for all other subgroups
$\unicode[STIX]{x1D6F7}^{J}(Y)$
for all other subgroups
![]() $J$
of
$J$
of
![]() $H$
. Let
$H$
. Let
![]() $Y^{\prime }=\operatorname{Ind}_{H}^{G}(\widetilde{Y})$
. Then Lemma 3.9 shows that
$Y^{\prime }=\operatorname{Ind}_{H}^{G}(\widetilde{Y})$
. Then Lemma 3.9 shows that
![]() $\text{type}_{Y^{\prime }}(H)=\text{type}_{Y}(H)+1$
, and that
$\text{type}_{Y^{\prime }}(H)=\text{type}_{Y}(H)+1$
, and that
 $$\begin{eqnarray}\displaystyle \text{type}_{Y^{\prime }}(K) & {\geqslant} & \displaystyle \min (\text{type}_{\widetilde{Y}}(K^{\prime })~|~K^{\prime }\subseteq H,K^{\prime }\sim K)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \min (\text{type}_{Y}(K^{\prime })|~K^{\prime }\subseteq H,K^{\prime }\sim K)\nonumber\\ \displaystyle & = & \displaystyle \text{type}_{Y}(K),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{type}_{Y^{\prime }}(K) & {\geqslant} & \displaystyle \min (\text{type}_{\widetilde{Y}}(K^{\prime })~|~K^{\prime }\subseteq H,K^{\prime }\sim K)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \min (\text{type}_{Y}(K^{\prime })|~K^{\prime }\subseteq H,K^{\prime }\sim K)\nonumber\\ \displaystyle & = & \displaystyle \text{type}_{Y}(K),\nonumber\end{eqnarray}$$
where the last equality follows from the fact that
![]() $\text{type}_{Y}$
takes the same value on all
$\text{type}_{Y}$
takes the same value on all
![]() $K^{\prime }$
that are conjugate to
$K^{\prime }$
that are conjugate to
![]() $K$
, because
$K$
, because
![]() $Y$
is a
$Y$
is a
![]() $G$
-spectrum. Hence
$G$
-spectrum. Hence
![]() $Y^{\prime }$
has the desired property, which finishes the proof.◻
$Y^{\prime }$
has the desired property, which finishes the proof.◻
Proof of Theorem 5.3.
We start by showing that if
![]() $I$
is a tt-ideal in
$I$
is a tt-ideal in
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, then the type function
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
, then the type function
![]() $\text{type}_{I}$
is admissible and upper semi-continuous. Let
$\text{type}_{I}$
is admissible and upper semi-continuous. Let
![]() $H$
and
$H$
and
![]() $K$
be two closed subgroups of
$K$
be two closed subgroups of
![]() $G$
such that
$G$
such that
![]() $\text{type}_{I}(H)<\infty$
. Further, let
$\text{type}_{I}(H)<\infty$
. Further, let
![]() $X\in I$
be a finite
$X\in I$
be a finite
![]() $G$
-spectrum with
$G$
-spectrum with
![]() $\text{type}_{X}(H)=\text{type}_{I}(H)$
. Then
$\text{type}_{X}(H)=\text{type}_{I}(H)$
. Then
![]() $X\notin P_{G}(H,\text{type}_{I}(H)\,+\,1)$
, but
$X\notin P_{G}(H,\text{type}_{I}(H)\,+\,1)$
, but
![]() $X\in I\subseteq P_{G}(K,\text{type}_{I}(K))$
. Thus,
$X\in I\subseteq P_{G}(K,\text{type}_{I}(K))$
. Thus,
![]() $P_{G}(K,\text{type}_{I}(K))$
cannot be contained in
$P_{G}(K,\text{type}_{I}(K))$
cannot be contained in
![]() $P_{G}(H,\text{type}_{I}(H)+1)$
and hence
$P_{G}(H,\text{type}_{I}(H)+1)$
and hence
![]() $\text{type}_{I}$
is admissible. Furthermore, by Proposition 4.3 we know that
$\text{type}_{I}$
is admissible. Furthermore, by Proposition 4.3 we know that
![]() $\text{type}_{X}$
is locally constant for every finite
$\text{type}_{X}$
is locally constant for every finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
, and thus
$X$
, and thus
![]() $\text{type}_{X}^{-1}([0,n))$
is in particular open, for all
$\text{type}_{X}^{-1}([0,n))$
is in particular open, for all
![]() $n\in \overline{\mathbb{N}}$
. Hence,
$n\in \overline{\mathbb{N}}$
. Hence,
is also open, and thus
![]() $\text{type}_{I}$
is upper semi-continuous.
$\text{type}_{I}$
is upper semi-continuous.
Now let
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
be an admissible and upper semi-continuous function. We wish to construct a tt-ideal
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
be an admissible and upper semi-continuous function. We wish to construct a tt-ideal
![]() $I$
such that
$I$
such that
![]() $\text{type}_{I}=f$
. For this we let
$\text{type}_{I}=f$
. For this we let
![]() $H$
be a closed subgroup of
$H$
be a closed subgroup of
![]() $G$
. Our first aim is to construct an
$G$
. Our first aim is to construct an
![]() $X_{H}\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
such that
$X_{H}\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
such that
![]() $\text{type}_{X_{H}}(H)=f(H)$
and
$\text{type}_{X_{H}}(H)=f(H)$
and
![]() $\text{type}_{X_{H}}(K)\geqslant f(K)$
for all other subgroups
$\text{type}_{X_{H}}(K)\geqslant f(K)$
for all other subgroups
![]() $K$
of
$K$
of
![]() $G$
. We first fix such a
$G$
. We first fix such a
![]() $K$
in addition to
$K$
in addition to
![]() $H$
. Since
$H$
. Since
![]() $P_{G}(K,f(K))$
is not contained in
$P_{G}(K,f(K))$
is not contained in
![]() $P_{G}(H,f(H)+1)$
, Lemma 5.7 shows that there exists an
$P_{G}(H,f(H)+1)$
, Lemma 5.7 shows that there exists an
![]() $X_{H,K}\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
such that
$X_{H,K}\in {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
such that
![]() $\text{type}_{X_{H,K}}(H)=f(H)$
and
$\text{type}_{X_{H,K}}(H)=f(H)$
and
![]() $\text{type}_{X_{H,K}}(K)\geqslant f(K)$
. Since
$\text{type}_{X_{H,K}}(K)\geqslant f(K)$
. Since
![]() $f$
is upper semi-continuous and
$f$
is upper semi-continuous and
![]() $\text{type}_{X_{H,K}}$
is locally constant (Proposition 4.3), there is an open neighbourhood
$\text{type}_{X_{H,K}}$
is locally constant (Proposition 4.3), there is an open neighbourhood
![]() $U_{H,K}$
of
$U_{H,K}$
of
![]() $K$
on which
$K$
on which
![]() $\text{type}_{X_{H,K}}$
is constant with value
$\text{type}_{X_{H,K}}$
is constant with value
![]() $\text{type}_{X_{H,K}}(K)=f(K)$
and
$\text{type}_{X_{H,K}}(K)=f(K)$
and
![]() $f$
is bounded above by
$f$
is bounded above by
![]() $f(K)$
. The space
$f(K)$
. The space
![]() $\operatorname{Sub}(G)/G$
is compact, and thus it is covered by finitely many
$\operatorname{Sub}(G)/G$
is compact, and thus it is covered by finitely many
![]() $U_{H,K_{1}},\ldots ,U_{H,K_{n}}$
. We then define
$U_{H,K_{1}},\ldots ,U_{H,K_{n}}$
. We then define
![]() $X_{H}$
as the smash product
$X_{H}$
as the smash product
Then,
![]() $\text{type}_{X_{H}}(K)=\max \{\text{type}_{X_{H,K_{i}}}(K)\mid i=1,\ldots ,n\}$
. Since
$\text{type}_{X_{H}}(K)=\max \{\text{type}_{X_{H,K_{i}}}(K)\mid i=1,\ldots ,n\}$
. Since
![]() $\text{type}_{X_{H,K_{i}}}(H)=f(H)$
for all
$\text{type}_{X_{H,K_{i}}}(H)=f(H)$
for all
![]() $i$
, it follows that also
$i$
, it follows that also
![]() $\text{type}_{X_{H}}(H)=f(H)$
. Moreover, for
$\text{type}_{X_{H}}(H)=f(H)$
. Moreover, for
![]() $K\in U_{H,K_{i}}$
, we have
$K\in U_{H,K_{i}}$
, we have
![]() $\text{type}_{X_{H,K_{i}}}(K)=f(K_{i})\geqslant f(K)$
. Thus,
$\text{type}_{X_{H,K_{i}}}(K)=f(K_{i})\geqslant f(K)$
. Thus,
![]() $\text{type}_{X_{H}}(K)\geqslant f(K)$
. The
$\text{type}_{X_{H}}(K)\geqslant f(K)$
. The
![]() $U_{H,K_{i}}$
cover
$U_{H,K_{i}}$
cover
![]() $\operatorname{Sub}(G)/G$
, so it follows that
$\operatorname{Sub}(G)/G$
, so it follows that
![]() $\text{type}_{X_{H}}\geqslant f$
, as desired. Now we set
$\text{type}_{X_{H}}\geqslant f$
, as desired. Now we set
Then
![]() $\text{type}_{I}\geqslant f$
, since
$\text{type}_{I}\geqslant f$
, since
![]() $\text{type}_{X_{H}}\geqslant f$
for all
$\text{type}_{X_{H}}\geqslant f$
for all
![]() $H$
. On the other hand we have
$H$
. On the other hand we have
![]() $\text{type}_{X_{H}}=f(H)$
, and hence
$\text{type}_{X_{H}}=f(H)$
, and hence
![]() $\text{type}_{I}\leqslant f$
. Therefore,
$\text{type}_{I}\leqslant f$
. Therefore,
![]() $\text{type}_{I}$
is equal to
$\text{type}_{I}$
is equal to
![]() $f$
, which concludes the proof of the first part of the theorem.
$f$
, which concludes the proof of the first part of the theorem.
For the second part of the theorem we need to show that a function
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
is equal to
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
is equal to
![]() $\text{type}_{X}$
for some finite
$\text{type}_{X}$
for some finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
if and only if it is admissible and locally constant. We first show the ‘only if’ direction. We know that
$X$
if and only if it is admissible and locally constant. We first show the ‘only if’ direction. We know that
![]() $\text{type}_{X}$
is locally constant for every finite
$\text{type}_{X}$
is locally constant for every finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
, again by Proposition 4.3. From the first part of the theorem it follows that
$X$
, again by Proposition 4.3. From the first part of the theorem it follows that
![]() $\text{type}_{X}$
is also admissible, since
$\text{type}_{X}$
is also admissible, since
![]() $\text{type}_{X}=\text{type}_{\text{thick}^{\otimes }(X)}$
. For the other direction let
$\text{type}_{X}=\text{type}_{\text{thick}^{\otimes }(X)}$
. For the other direction let
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
be an admissible and locally constant function. Again using the first part, it follows that there exists a tt-ideal
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
be an admissible and locally constant function. Again using the first part, it follows that there exists a tt-ideal
![]() $I$
such that
$I$
such that
![]() $f=\text{type}_{I}$
, since locally constant in particular implies upper semi-continuous. We can now apply Proposition 4.5 to
$f=\text{type}_{I}$
, since locally constant in particular implies upper semi-continuous. We can now apply Proposition 4.5 to
![]() $I$
and the locally constant function
$I$
and the locally constant function
![]() $\text{type}_{I}$
, and see that there is an
$\text{type}_{I}$
, and see that there is an
![]() $X\in I$
such that
$X\in I$
such that
![]() $\text{type}_{X}\leqslant \text{type}_{I}$
. But
$\text{type}_{X}\leqslant \text{type}_{I}$
. But
![]() $X\in I$
also implies
$X\in I$
also implies
![]() $\text{type}_{X}\geqslant \text{type}_{I}$
. Hence,
$\text{type}_{X}\geqslant \text{type}_{I}$
. Hence,
![]() $\text{type}_{X}=\text{type}_{I}=f$
, which concludes the proof.◻
$\text{type}_{X}=\text{type}_{I}=f$
, which concludes the proof.◻
We obtain the following characterization of the Balmer topology on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
.
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
.
Corollary 5.8. For
![]() $G$
a compact Lie group, the Balmer topology on
$G$
a compact Lie group, the Balmer topology on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
has as a basis the open sets
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
has as a basis the open sets
where
![]() $f$
ranges through all locally constant admissible functions
$f$
ranges through all locally constant admissible functions
![]() $\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
.
$\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
.
Proof. By definition, the Balmer topology has as basis the open sets
where
![]() $X$
ranges through all finite
$X$
ranges through all finite
![]() $G$
-spectra. By Theorem 3.14, all prime ideals are of the form
$G$
-spectra. By Theorem 3.14, all prime ideals are of the form
![]() $P_{G}(H,n)$
. Moreover, by definition,
$P_{G}(H,n)$
. Moreover, by definition,
![]() $X$
lies in
$X$
lies in
![]() $P_{G}(H,n)$
if and only if
$P_{G}(H,n)$
if and only if
![]() $n\leqslant \text{type}_{X}(H)$
. Thus we have
$n\leqslant \text{type}_{X}(H)$
. Thus we have
Hence,
![]() $U_{X}$
depends only on the function
$U_{X}$
depends only on the function
![]() $\text{type}_{X}$
. By the previous theorem, we know that
$\text{type}_{X}$
. By the previous theorem, we know that
![]() $\text{type}_{X}$
ranges through all admissible locally constant functions. This finishes the proof.◻
$\text{type}_{X}$
ranges through all admissible locally constant functions. This finishes the proof.◻
Since admissibility depends only on the poset structure of
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
, this shows that the Balmer topology is indeed determined by the inclusions among prime ideals together with the topology on
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
, this shows that the Balmer topology is indeed determined by the inclusions among prime ideals together with the topology on
![]() $\operatorname{Sub}(G)/G$
, as claimed.
$\operatorname{Sub}(G)/G$
, as claimed.
6 Inclusions of prime ideals
We continue to let
![]() $G$
be a compact Lie group and work
$G$
be a compact Lie group and work
![]() $p$
-locally. In order to obtain a complete description of the topology on the Balmer spectrum
$p$
-locally. In order to obtain a complete description of the topology on the Balmer spectrum
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
and a classification of the tt-ideals, we are hence left to determine the poset structure on
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
and a classification of the tt-ideals, we are hence left to determine the poset structure on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
. By Lemma 3.13, we know that a prime
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
. By Lemma 3.13, we know that a prime
![]() $P_{G}(K,m)$
can only be contained in
$P_{G}(K,m)$
can only be contained in
![]() $P_{G}(H,n)$
if
$P_{G}(H,n)$
if
![]() $K$
is conjugate to a subgroup of
$K$
is conjugate to a subgroup of
![]() $H$
and
$H$
and
![]() $m\geqslant n$
. Moreover, if
$m\geqslant n$
. Moreover, if
![]() $P_{G}(K,m)\subseteq P_{G}(H,n)$
, then also
$P_{G}(K,m)\subseteq P_{G}(H,n)$
, then also
![]() $P_{G}(K,m+1)\subseteq P_{G}(H,n)$
, since
$P_{G}(K,m+1)\subseteq P_{G}(H,n)$
, since
![]() $P_{G}(K,m+1)\subseteq P_{G}(K,m)$
. The remaining problem can thus be phrased as the following question.
$P_{G}(K,m+1)\subseteq P_{G}(K,m)$
. The remaining problem can thus be phrased as the following question.
Question 6.1. Given an inclusion of subgroups
![]() $K\subseteq H$
and
$K\subseteq H$
and
![]() $n\in \overline{\mathbb{N}}_{{>}0}$
, what is the minimal
$n\in \overline{\mathbb{N}}_{{>}0}$
, what is the minimal
![]() $i\in \overline{\mathbb{N}}$
, if any, for which there is an inclusion
$i\in \overline{\mathbb{N}}$
, if any, for which there is an inclusion
Phrased more concretely, given a finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
such that
$X$
such that
![]() $\unicode[STIX]{x1D6F7}^{K}(X)$
is of type
$\unicode[STIX]{x1D6F7}^{K}(X)$
is of type
![]() ${\geqslant}n+i$
, is
${\geqslant}n+i$
, is
![]() $\unicode[STIX]{x1D6F7}^{H}(X)$
necessarily of type
$\unicode[STIX]{x1D6F7}^{H}(X)$
necessarily of type
![]() ${\geqslant}n$
?
${\geqslant}n$
?
This problem appears to be difficult and is open in general, already for finite groups
![]() $G$
where it is linked to the blue-shift phenomenon for generalized Tate constructions [Reference Balmer and SandersBS17, § 9]. In this section we show that the question can be reduced to the case where
$G$
where it is linked to the blue-shift phenomenon for generalized Tate constructions [Reference Balmer and SandersBS17, § 9]. In this section we show that the question can be reduced to the case where
![]() $K\subseteq H$
is a ‘
$K\subseteq H$
is a ‘
![]() $p$
-subcotoral’ inclusion. We also give lower and upper bounds for the minimal
$p$
-subcotoral’ inclusion. We also give lower and upper bounds for the minimal
![]() $i$
in Question 6.1, building on the previously obtained bounds for finite groups from [Reference Balmer and SandersBS17] and [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19]. In § 7 we then use these bounds to derive a complete classification for abelian compact Lie groups. For a general compact Lie group
$i$
in Question 6.1, building on the previously obtained bounds for finite groups from [Reference Balmer and SandersBS17] and [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19]. In § 7 we then use these bounds to derive a complete classification for abelian compact Lie groups. For a general compact Lie group
![]() $G$
, we obtain an answer away from finitely many critical primes
$G$
, we obtain an answer away from finitely many critical primes
![]() $p$
, those that divide the ‘order’
$p$
, those that divide the ‘order’
![]() $|G|$
of
$|G|$
of
![]() $G$
, as we explain in § 8.
$G$
, as we explain in § 8.
We first need to introduce some terminology. An inclusion
![]() $K\subseteq H$
of subgroups of
$K\subseteq H$
of subgroups of
![]() $G$
is said to be cotoral if it is normal and the quotient is a torus. For every subgroup
$G$
is said to be cotoral if it is normal and the quotient is a torus. For every subgroup
![]() $K$
there exists a maximal cotoral inclusion
$K$
there exists a maximal cotoral inclusion
![]() $K\subseteq \unicode[STIX]{x1D714}_{G}(K)$
in
$K\subseteq \unicode[STIX]{x1D714}_{G}(K)$
in
![]() $G$
, unique up to conjugacy. Moreover, the group
$G$
, unique up to conjugacy. Moreover, the group
![]() $\unicode[STIX]{x1D714}_{G}(K)$
has finite Weyl group and is hence cotorally maximal, i.e., there exists no proper cotoral inclusion of the form
$\unicode[STIX]{x1D714}_{G}(K)$
has finite Weyl group and is hence cotorally maximal, i.e., there exists no proper cotoral inclusion of the form
![]() $\unicode[STIX]{x1D714}_{G}(K)\subset H$
. In fact, the function
$\unicode[STIX]{x1D714}_{G}(K)\subset H$
. In fact, the function
![]() $K\mapsto \unicode[STIX]{x1D714}_{G}(K)$
defines a continuous retraction of
$K\mapsto \unicode[STIX]{x1D714}_{G}(K)$
defines a continuous retraction of
![]() $\operatorname{Sub}(G)/G$
onto the closed subspace of conjugacy classes of subgroups with finite Weyl group (see [Reference Fausk and OliverFO05, Definition 1.2f.] for a discussion of all these properties). Given a subgroup
$\operatorname{Sub}(G)/G$
onto the closed subspace of conjugacy classes of subgroups with finite Weyl group (see [Reference Fausk and OliverFO05, Definition 1.2f.] for a discussion of all these properties). Given a subgroup
![]() $H$
of
$H$
of
![]() $G$
, we further write
$G$
, we further write
![]() ${\mathcal{O}}(H)$
for the minimal normal subgroup of
${\mathcal{O}}(H)$
for the minimal normal subgroup of
![]() $H$
with quotient a finite
$H$
with quotient a finite
![]() $p$
-group. We say that a subgroup
$p$
-group. We say that a subgroup
![]() $K\subseteq H$
is
$K\subseteq H$
is
![]() $p$
-subcotoral if
$p$
-subcotoral if
![]() ${\mathcal{O}}(K)$
sits inside
${\mathcal{O}}(K)$
sits inside
![]() ${\mathcal{O}}(H)$
and the inclusion
${\mathcal{O}}(H)$
and the inclusion
![]() ${\mathcal{O}}(K)\subseteq {\mathcal{O}}(H)$
is cotoral. When
${\mathcal{O}}(K)\subseteq {\mathcal{O}}(H)$
is cotoral. When
![]() $G$
is finite, this notion reduces to the notion of
$G$
is finite, this notion reduces to the notion of
![]() $p$
-subnormal subgroup studied by Balmer and Sanders, see [Reference Balmer and SandersBS17, Lemma 3.3].
$p$
-subnormal subgroup studied by Balmer and Sanders, see [Reference Balmer and SandersBS17, Lemma 3.3].
Then the following theorem summarizes what we know about inclusions of primes.
Theorem 6.2. The following hold for subgroups
![]() $K$
and
$K$
and
![]() $H$
of
$H$
of
![]() $G$
and
$G$
and
![]() $n,m\in \overline{\mathbb{N}}_{{>}0}$
.
$n,m\in \overline{\mathbb{N}}_{{>}0}$
.
(i) If there is an inclusion
 $P_{G}(K,m)\subseteq P_{G}(H,n)$
, then
$P_{G}(K,m)\subseteq P_{G}(H,n)$
, then
 $K$
is
$K$
is
 $G$
-conjugate to a
$G$
-conjugate to a
 $p$
-subcotoral subgroup of
$p$
-subcotoral subgroup of
 $H$
and
$H$
and
 $m\geqslant n$
.
$m\geqslant n$
.(ii) If there is an inclusion
 $P_{G}(K,1)\subseteq P_{G}(H,1)$
, then
$P_{G}(K,1)\subseteq P_{G}(H,1)$
, then
 $K$
is
$K$
is
 $G$
-conjugate to a cotoral subgroup of
$G$
-conjugate to a cotoral subgroup of
 $H$
.
$H$
.(iii) If
 $K$
is
$K$
is
 $G$
-conjugate to a cotoral subgroup of
$G$
-conjugate to a cotoral subgroup of
 $H$
, then
$H$
, then
 $P_{G}(K,n)\subseteq P_{G}(H,n)$
for all
$P_{G}(K,n)\subseteq P_{G}(H,n)$
for all
 $n$
.
$n$
.(iv) If
 $K$
is
$K$
is
 $G$
-conjugate to a normal subgroup of
$G$
-conjugate to a normal subgroup of
 $H$
with quotient a cyclic
$H$
with quotient a cyclic
 $p$
-group, then
$p$
-group, then
 $P_{G}(K,n+1)\subseteq P_{G}(H,n)$
for all
$P_{G}(K,n+1)\subseteq P_{G}(H,n)$
for all
 $n$
.
$n$
.(v) If
 $K$
is
$K$
is
 $G$
-conjugate to a
$G$
-conjugate to a
 $p$
-subcotoral subgroup of
$p$
-subcotoral subgroup of
 $H$
, then
$H$
, then
 $P_{G}(K,\infty )\subseteq P_{G}(H,\infty )$
.
$P_{G}(K,\infty )\subseteq P_{G}(H,\infty )$
.(vi) If
 $K\subseteq H$
is normal in
$K\subseteq H$
is normal in
 $G$
and
$G$
and
 $H/K$
is an elementary abelian
$H/K$
is an elementary abelian
 $p$
-group of rank
$p$
-group of rank
 $k$
, then for all
$k$
, then for all $$\begin{eqnarray}P_{G}(K,n+k-1)\not \subseteq P_{G}(H,n)\end{eqnarray}$$
$$\begin{eqnarray}P_{G}(K,n+k-1)\not \subseteq P_{G}(H,n)\end{eqnarray}$$
 $k,n\in \mathbb{N}$
.
$k,n\in \mathbb{N}$
.
The proof is given in §§ 6.2 and 6.3. Using the change of groups properties of Proposition 6.4 below, items (iv) and (vi) are immediate consequences of the main result of [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19], with the case
![]() $H/K\cong \mathbb{Z}/p$
previously shown in [Reference Balmer and SandersBS17].
$H/K\cong \mathbb{Z}/p$
previously shown in [Reference Balmer and SandersBS17].
Remark 6.3. Note that the conclusion of (vi) translates into the existence of a finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
with the property that
$X$
with the property that
![]() $\text{type}_{X}(K)\geqslant n+k-1$
and
$\text{type}_{X}(K)\geqslant n+k-1$
and
![]() $\text{type}_{X}(H)<n$
. Under the condition that
$\text{type}_{X}(H)<n$
. Under the condition that
![]() $H/K$
is elementary abelian, suitable complexes can be formally constructed from the Arone–Lesh complexes [Reference Arone and LeshAL17], which thus form the crucial ingredient in our proof of (vi). We currently do not know how to extend this result beyond the case of abelian groups.
$H/K$
is elementary abelian, suitable complexes can be formally constructed from the Arone–Lesh complexes [Reference Arone and LeshAL17], which thus form the crucial ingredient in our proof of (vi). We currently do not know how to extend this result beyond the case of abelian groups.
We note that (ii) and (iii) imply that
![]() $P_{G}(K,1)\subseteq P_{G}(H,1)$
if and only if
$P_{G}(K,1)\subseteq P_{G}(H,1)$
if and only if
![]() $K$
is
$K$
is
![]() $G$
-conjugate to a cotoral subgroup of
$G$
-conjugate to a cotoral subgroup of
![]() $H$
. This gives back the computation of the Balmer spectrum of the homotopy category of finite rational
$H$
. This gives back the computation of the Balmer spectrum of the homotopy category of finite rational
![]() $G$
-spectra of [Reference GreenleesGre19]. Parts (iii) and (iv) can be used to obtain many more inclusions of primes by inducting on subnormal chains
$G$
-spectra of [Reference GreenleesGre19]. Parts (iii) and (iv) can be used to obtain many more inclusions of primes by inducting on subnormal chains
![]() $K=H_{1}\subseteq H_{2}\subseteq \cdots \subseteq H_{n}=H$
with each quotient
$K=H_{1}\subseteq H_{2}\subseteq \cdots \subseteq H_{n}=H$
with each quotient
![]() $H_{i+1}/H_{i}$
a torus or a cyclic
$H_{i+1}/H_{i}$
a torus or a cyclic
![]() $p$
-group.
$p$
-group.
6.1 Change of groups
We begin by proving the following change of groups properties regarding Question 6.1.
Proposition 6.4. Let
![]() $G$
be a compact Lie group and consider
$G$
be a compact Lie group and consider
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
.
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
.
(i) There is an inclusion
 $P_{G}(K,n)\subseteq P_{G}(H,m)$
if and only if there exists an element
$P_{G}(K,n)\subseteq P_{G}(H,m)$
if and only if there exists an element
 $g\in G$
such that the conjugate
$g\in G$
such that the conjugate
 $K^{g}$
is a subgroup of
$K^{g}$
is a subgroup of
 $H$
and
$H$
and
 $P_{H}(K^{g},n)\subseteq P_{H}(H,m)$
.
$P_{H}(K^{g},n)\subseteq P_{H}(H,m)$
.(ii) If
 $K^{\prime }$
is a normal subgroup of
$K^{\prime }$
is a normal subgroup of
 $G$
contained in
$G$
contained in
 $K$
and
$K$
and
 $H$
, then there is an inclusion
$H$
, then there is an inclusion
 $P_{G}(K,n)\subseteq P_{G}(H,m)$
if and only if there is an inclusion
$P_{G}(K,n)\subseteq P_{G}(H,m)$
if and only if there is an inclusion
 $P_{G/K^{\prime }}(K/K^{\prime },n)\subseteq P_{G/K^{\prime }}(H/K^{\prime },m)$
.
$P_{G/K^{\prime }}(K/K^{\prime },n)\subseteq P_{G/K^{\prime }}(H/K^{\prime },m)$
.(iii) Let
 $K^{\prime }\subseteq K\subseteq H$
be subgroups of
$K^{\prime }\subseteq K\subseteq H$
be subgroups of
 $G$
such that
$G$
such that
 $K$
is normal in
$K$
is normal in
 $G$
. If
$G$
. If
 $P_{G}(K^{\prime },n)\subseteq P_{G}(H,m)$
, then also
$P_{G}(K^{\prime },n)\subseteq P_{G}(H,m)$
, then also
 $P_{G}(K,n)\subseteq P_{G}(H,m)$
.
$P_{G}(K,n)\subseteq P_{G}(H,m)$
.
The first part can be interpreted as a ‘Going-Up’ theorem for restriction to subgroup functors, see [Reference Balmer and SandersBS17, Proposition 6.9] in the finite group case.
Proof. (i) If
![]() $P_{H}(K^{g},n)\subseteq P_{H}(H,m)$
, then also
$P_{H}(K^{g},n)\subseteq P_{H}(H,m)$
, then also
![]() $P_{G}(K^{g},n)\subseteq P_{G}(H,m)$
, since the question of whether a finite
$P_{G}(K^{g},n)\subseteq P_{G}(H,m)$
, since the question of whether a finite
![]() $G$
-spectrum
$G$
-spectrum
![]() $X$
lies in
$X$
lies in
![]() $P_{G}(H,m)$
depends only on the restriction
$P_{G}(H,m)$
depends only on the restriction
![]() $\operatorname{Res}_{H}^{G}(X)$
to an
$\operatorname{Res}_{H}^{G}(X)$
to an
![]() $H$
-spectrum. Since
$H$
-spectrum. Since
![]() $K^{g}$
is conjugate to
$K^{g}$
is conjugate to
![]() $K$
, it follows that also
$K$
, it follows that also
![]() $P_{G}(K,n)\subseteq P_{G}(H,m)$
. We now show that if
$P_{G}(K,n)\subseteq P_{G}(H,m)$
. We now show that if
![]() $P_{H}(K^{g},n)\not \subseteq P_{H}(H,m)$
for all conjugates
$P_{H}(K^{g},n)\not \subseteq P_{H}(H,m)$
for all conjugates
![]() $K^{g}$
of
$K^{g}$
of
![]() $K$
which are subgroups of
$K$
which are subgroups of
![]() $H$
, then also
$H$
, then also
![]() $P_{G}(K,n)\not \subseteq P_{G}(H,m)$
. We want to apply induction
$P_{G}(K,n)\not \subseteq P_{G}(H,m)$
. We want to apply induction
![]() $\operatorname{Ind}_{H}^{G}(-)$
to a suitable
$\operatorname{Ind}_{H}^{G}(-)$
to a suitable
![]() $H$
-spectrum
$H$
-spectrum
![]() $X$
. Recall from Lemma 3.9 that the type of
$X$
. Recall from Lemma 3.9 that the type of
![]() $\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}X)$
is at least as large as the minimum of the types of all
$\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}X)$
is at least as large as the minimum of the types of all
![]() $\unicode[STIX]{x1D6F7}^{K^{g}}(X)$
for
$\unicode[STIX]{x1D6F7}^{K^{g}}(X)$
for
![]() $G$
-conjugates
$G$
-conjugates
![]() $K^{g}$
contained in
$K^{g}$
contained in
![]() $H$
, and that the type of
$H$
, and that the type of
![]() $\unicode[STIX]{x1D6F7}^{H}(\operatorname{Ind}_{H}^{G}X)$
is the same as that of
$\unicode[STIX]{x1D6F7}^{H}(\operatorname{Ind}_{H}^{G}X)$
is the same as that of
![]() $\unicode[STIX]{x1D6F7}^{H}(X)$
. It is hence sufficient to construct a finite
$\unicode[STIX]{x1D6F7}^{H}(X)$
. It is hence sufficient to construct a finite
![]() $H$
-spectrum
$H$
-spectrum
![]() $X$
such that
$X$
such that
![]() $\unicode[STIX]{x1D6F7}^{H}(X)$
has type
$\unicode[STIX]{x1D6F7}^{H}(X)$
has type
![]() ${<}m$
and
${<}m$
and
![]() $\unicode[STIX]{x1D6F7}^{K^{g}}(X)$
has type
$\unicode[STIX]{x1D6F7}^{K^{g}}(X)$
has type
![]() ${\geqslant}n$
for all conjugates
${\geqslant}n$
for all conjugates
![]() $K^{g}$
. For every conjugate
$K^{g}$
. For every conjugate
![]() $K^{g}$
, we choose a finite
$K^{g}$
, we choose a finite
![]() $H$
-spectrum
$H$
-spectrum
![]() $X_{K^{g}}$
with the property that
$X_{K^{g}}$
with the property that
![]() $\unicode[STIX]{x1D6F7}^{K^{g}}(X_{K^{g}})$
has type
$\unicode[STIX]{x1D6F7}^{K^{g}}(X_{K^{g}})$
has type
![]() ${\geqslant}n$
and
${\geqslant}n$
and
![]() $\unicode[STIX]{x1D6F7}^{H}(X_{K^{g}})$
has type
$\unicode[STIX]{x1D6F7}^{H}(X_{K^{g}})$
has type
![]() ${<}m$
, which exists by assumption. Note that, up to
${<}m$
, which exists by assumption. Note that, up to
![]() $H$
-conjugacy, there are only finitely many
$H$
-conjugacy, there are only finitely many
![]() $K^{g}\subseteq H$
(see Remark A.2). Hence, we can consider the smash product
$K^{g}\subseteq H$
(see Remark A.2). Hence, we can consider the smash product
This has the desired property, since the type of a smash product is the maximum of the types of the smash factors.
(ii) This follows from the fact that
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G/K^{\prime },(p)}^{c})$
sits inside
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G/K^{\prime },(p)}^{c})$
sits inside
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
as a retract, as the subspace of all
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
as a retract, as the subspace of all
![]() $P_{G}(H,-)$
with
$P_{G}(H,-)$
with
![]() $H$
containing
$H$
containing
![]() $K^{\prime }$
. The inclusion
$K^{\prime }$
. The inclusion
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G/K^{\prime },(p)}^{c})\rightarrow \operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
is induced by the refined version of the geometric fixed point functor
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G/K^{\prime },(p)}^{c})\rightarrow \operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
is induced by the refined version of the geometric fixed point functor
![]() $\unicode[STIX]{x1D6F7}^{K^{\prime }}$
which remembers the
$\unicode[STIX]{x1D6F7}^{K^{\prime }}$
which remembers the
![]() $G/K^{\prime }$
-action. The projection
$G/K^{\prime }$
-action. The projection
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})\rightarrow \operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G/K^{\prime }}^{c})$
is induced by the inflation functor
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})\rightarrow \operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G/K^{\prime }}^{c})$
is induced by the inflation functor
![]() $i_{K^{\prime }}:{\mathcal{S}}{\mathcal{H}}_{G/K^{\prime }}^{c}\rightarrow {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
(§ 2.2.3).
$i_{K^{\prime }}:{\mathcal{S}}{\mathcal{H}}_{G/K^{\prime }}^{c}\rightarrow {\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
(§ 2.2.3).
(iii) The third statement also follows from the previous argument, this time applied to the projection
![]() $p:G\rightarrow G/K$
. The self-map
$p:G\rightarrow G/K$
. The self-map
![]() $(\unicode[STIX]{x1D6F7}^{K})^{\ast }\circ (i_{K})^{\ast }$
of
$(\unicode[STIX]{x1D6F7}^{K})^{\ast }\circ (i_{K})^{\ast }$
of
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
sends the ideal
${\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c}$
sends the ideal
![]() $P_{G}(H,m)$
to itself, since
$P_{G}(H,m)$
to itself, since
![]() $H$
contains the normal subgroup
$H$
contains the normal subgroup
![]() $K$
. On the other hand,
$K$
. On the other hand,
![]() $(i_{K})^{\ast }$
sends
$(i_{K})^{\ast }$
sends
![]() $P_{G}(K^{\prime },n)$
to
$P_{G}(K^{\prime },n)$
to
![]() $P_{G/K}(p(K^{\prime }),n)$
, as a consequence of the equivalence (1) of § 2.2.3. Since
$P_{G/K}(p(K^{\prime }),n)$
, as a consequence of the equivalence (1) of § 2.2.3. Since
![]() $K^{\prime }$
is contained in
$K^{\prime }$
is contained in
![]() $K$
, the image
$K$
, the image
![]() $p(K^{\prime })$
is the trivial subgroup
$p(K^{\prime })$
is the trivial subgroup
![]() $K/K$
. Thus
$K/K$
. Thus
As the composite
![]() $(\unicode[STIX]{x1D6F7}^{K})^{\ast }\circ (i_{K})^{\ast }$
preserves inclusions, this shows the claim.◻
$(\unicode[STIX]{x1D6F7}^{K})^{\ast }\circ (i_{K})^{\ast }$
preserves inclusions, this shows the claim.◻
If one is willing to study Question 6.1 simultaneously for all compact Lie groups, Proposition 6.4 allows us to reduce to the case where
![]() $H$
equals the ambient group
$H$
equals the ambient group
![]() $G$
and
$G$
and
![]() $K$
contains no non-trivial subgroup normal in
$K$
contains no non-trivial subgroup normal in
![]() $H$
. In § 6.5 we explain how this can be used to reduce to the case where
$H$
. In § 6.5 we explain how this can be used to reduce to the case where
![]() $H$
is an extension
$H$
is an extension
of a finite
![]() $p$
-group
$p$
-group
![]() $P$
by an abelian compact Lie group
$P$
by an abelian compact Lie group
![]() $A$
with
$A$
with
![]() $|\unicode[STIX]{x1D70B}_{0}(A)|$
coprime to
$|\unicode[STIX]{x1D70B}_{0}(A)|$
coprime to
![]() $p$
. In the case where
$p$
. In the case where
![]() $K$
is a normal subgroup of
$K$
is a normal subgroup of
![]() $H$
, it can be further reduced to
$H$
, it can be further reduced to
![]() $H$
a finite
$H$
a finite
![]() $p$
-group.
$p$
-group.
6.2 The spectrum of the Burnside ring
We now start with the proof of Theorem 6.2. Inspired by [Reference Balmer and SandersBS17], we use the comparison map to the spectrum of the Burnside ring
![]() $A(G)=\unicode[STIX]{x1D70B}_{0}^{G}(\mathbb{S}_{G})$
to rule out certain inclusions between the primes. The spectrum of the Burnside ring was computed by Dress in the case of finite groups [Reference DressDre69] and by tom Dieck [Reference tom DiecktD75b] for compact Lie groups. We now recall this computation, or more precisely its
$A(G)=\unicode[STIX]{x1D70B}_{0}^{G}(\mathbb{S}_{G})$
to rule out certain inclusions between the primes. The spectrum of the Burnside ring was computed by Dress in the case of finite groups [Reference DressDre69] and by tom Dieck [Reference tom DiecktD75b] for compact Lie groups. We now recall this computation, or more precisely its
![]() $p$
-local version. For every closed subgroup
$p$
-local version. For every closed subgroup
![]() $H$
, the geometric fixed point map induces a ring homomorphism on endomorphism rings
$H$
, the geometric fixed point map induces a ring homomorphism on endomorphism rings
These homomorphisms are called the marks of
![]() $A(G)_{(p)}$
.
$A(G)_{(p)}$
.
Remark 6.5. The marks were originally studied by tom Dieck in [Reference tom DiecktD75b]. There he defined the Burnside ring of a compact Lie group as the ring of certain equivalence classes of closed differentiable
![]() $G$
-manifolds. The mark homomorphism
$G$
-manifolds. The mark homomorphism
![]() $\unicode[STIX]{x1D711}^{H}$
assigns to such a
$\unicode[STIX]{x1D711}^{H}$
assigns to such a
![]() $G$
-manifold
$G$
-manifold
![]() $X$
the Euler characteristic of its fixed space
$X$
the Euler characteristic of its fixed space
![]() $X^{H}$
(in fact the equivalence relation is exactly defined as considering two
$X^{H}$
(in fact the equivalence relation is exactly defined as considering two
![]() $G$
-manifolds to be equivalent if these Euler characteristics are the same for all closed subgroups
$G$
-manifolds to be equivalent if these Euler characteristics are the same for all closed subgroups
![]() $H$
of
$H$
of
![]() $G$
). In [Reference tom DiecktD75a] tom Dieck proved that his version of the Burnside ring agrees with
$G$
). In [Reference tom DiecktD75a] tom Dieck proved that his version of the Burnside ring agrees with
![]() $\unicode[STIX]{x1D70B}_{0}^{G}\mathbb{S}_{G}$
. The isomorphism sends a closed
$\unicode[STIX]{x1D70B}_{0}^{G}\mathbb{S}_{G}$
. The isomorphism sends a closed
![]() $G$
-manifold
$G$
-manifold
![]() $X$
to the composite
$X$
to the composite
using that
![]() $\unicode[STIX]{x1D6F4}^{\infty }X_{+}$
is dualizable in
$\unicode[STIX]{x1D6F4}^{\infty }X_{+}$
is dualizable in
![]() ${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
. This construction is called the categorical Euler characteristic or trace, see [Reference Lewis, May, Steinberger and McClureLMSM86, §§ III.7 and V.1]. Since geometric fixed points
${\mathcal{S}}{\mathcal{H}}_{G,(p)}$
. This construction is called the categorical Euler characteristic or trace, see [Reference Lewis, May, Steinberger and McClureLMSM86, §§ III.7 and V.1]. Since geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{H}$
are symmetric monoidal, it follows that they send the categorical Euler characteristic of
$\unicode[STIX]{x1D6F7}^{H}$
are symmetric monoidal, it follows that they send the categorical Euler characteristic of
![]() $\unicode[STIX]{x1D6F4}^{\infty }X_{+}$
to the categorical Euler characteristic of
$\unicode[STIX]{x1D6F4}^{\infty }X_{+}$
to the categorical Euler characteristic of
![]() $\unicode[STIX]{x1D6F7}^{H}(\unicode[STIX]{x1D6F4}^{\infty }X_{+})\simeq \unicode[STIX]{x1D6F4}^{\infty }X_{+}^{H}$
in the non-equivariant stable homotopy category. It is a classical fact that this categorical Euler characteristic equals the usual Euler characteristic for any finite CW-complex. Hence tom Dieck’s definition of the mark homomorphisms agrees with the one given above (see also [Reference Lewis, May, Steinberger and McClureLMSM86, § V.2] for more details on this discussion).
$\unicode[STIX]{x1D6F7}^{H}(\unicode[STIX]{x1D6F4}^{\infty }X_{+})\simeq \unicode[STIX]{x1D6F4}^{\infty }X_{+}^{H}$
in the non-equivariant stable homotopy category. It is a classical fact that this categorical Euler characteristic equals the usual Euler characteristic for any finite CW-complex. Hence tom Dieck’s definition of the mark homomorphisms agrees with the one given above (see also [Reference Lewis, May, Steinberger and McClureLMSM86, § V.2] for more details on this discussion).
It turns out that the marks determine the spectrum of
![]() $A(G)_{(p)}$
. For the two primes
$A(G)_{(p)}$
. For the two primes
![]() $(0)$
and
$(0)$
and
![]() $(p)$
of
$(p)$
of
![]() $\mathbb{Z}_{(p)}$
, we denote by
$\mathbb{Z}_{(p)}$
, we denote by
![]() $q(H,1)$
and
$q(H,1)$
and
![]() $q(H,\infty )$
the respective pullbacks along
$q(H,\infty )$
the respective pullbacks along
![]() $\unicode[STIX]{x1D711}^{H}$
. Recall that, given a subgroup
$\unicode[STIX]{x1D711}^{H}$
. Recall that, given a subgroup
![]() $H$
of
$H$
of
![]() $G$
, we write
$G$
, we write
![]() $\unicode[STIX]{x1D714}_{G}(H)$
for a maximal cotoral extension of
$\unicode[STIX]{x1D714}_{G}(H)$
for a maximal cotoral extension of
![]() $H$
in
$H$
in
![]() $G$
and
$G$
and
![]() ${\mathcal{O}}(H)$
for the minimal normal subgroup of
${\mathcal{O}}(H)$
for the minimal normal subgroup of
![]() $H$
whose quotient is a finite
$H$
whose quotient is a finite
![]() $p$
-group. Finally we call
$p$
-group. Finally we call
![]() $\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
the
$\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
the
![]() $p$
-perfection of
$p$
-perfection of
![]() $H$
in
$H$
in
![]() $G$
(see [Reference Fausk and OliverFO05]). Note that, unlike
$G$
(see [Reference Fausk and OliverFO05]). Note that, unlike
![]() ${\mathcal{O}}(H)$
, the
${\mathcal{O}}(H)$
, the
![]() $p$
-perfection depends on the ambient group
$p$
-perfection depends on the ambient group
![]() $G$
.
$G$
.
Theorem 6.6 [Reference tom DiecktD75b, § 4], [Reference FauskFau08, § 12].
Let
![]() $G$
be a compact Lie group. All prime ideals of
$G$
be a compact Lie group. All prime ideals of
![]() $A(G)_{(p)}$
are of the form
$A(G)_{(p)}$
are of the form
![]() $q(H,1)$
or
$q(H,1)$
or
![]() $q(H,\infty )$
. They are related as follows:
$q(H,\infty )$
. They are related as follows:
(i)
 $q(H,1)=q(H^{\prime },1)$
if and only if
$q(H,1)=q(H^{\prime },1)$
if and only if
 $\unicode[STIX]{x1D714}_{G}(H)$
is conjugate to
$\unicode[STIX]{x1D714}_{G}(H)$
is conjugate to
 $\unicode[STIX]{x1D714}_{G}(H^{\prime })$
, and there are no proper inclusions of the form
$\unicode[STIX]{x1D714}_{G}(H^{\prime })$
, and there are no proper inclusions of the form
 $q(H,1)\subset q(H^{\prime },1)$
;
$q(H,1)\subset q(H^{\prime },1)$
;(ii)
 $q(H,\infty )=q(H^{\prime },\infty )$
if and only if
$q(H,\infty )=q(H^{\prime },\infty )$
if and only if
 $\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
is conjugate to
$\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
is conjugate to
 $\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H^{\prime }))$
, and there are no proper inclusions of the form
$\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H^{\prime }))$
, and there are no proper inclusions of the form
 $q(H,\infty )\subset q(H^{\prime },\infty )$
;
$q(H,\infty )\subset q(H^{\prime },\infty )$
;(iii)
 $q(H,1)\subseteq q(H^{\prime },\infty )$
if and only if
$q(H,1)\subseteq q(H^{\prime },\infty )$
if and only if
 $q(H,\infty )=q(H^{\prime },\infty )$
;
$q(H,\infty )=q(H^{\prime },\infty )$
;(iv) there are no inclusions of the form
 $q(H,\infty )\subseteq q(H^{\prime },1)$
.
$q(H,\infty )\subseteq q(H^{\prime },1)$
.
Proof. The fact that all prime ideals are of this form is given by [Reference tom DiecktD75b, Theorem 4]. By [Reference tom DiecktD75b, Proposition 8], the primes of the form
![]() $q(H,1)$
depend only on the conjugacy class of
$q(H,1)$
depend only on the conjugacy class of
![]() $\unicode[STIX]{x1D714}_{G}(H)$
and the primes of the form
$\unicode[STIX]{x1D714}_{G}(H)$
and the primes of the form
![]() $q(H,\infty )$
depend only on the conjugacy class of
$q(H,\infty )$
depend only on the conjugacy class of
![]() $\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
. Combining this with [Reference tom DiecktD75b, Propositions 9 and 12] gives part (i). Part (ii) can be derived from [Reference tom DiecktD75b, Proposition 16], but is stated more explicitly in this form in [Reference FauskFau08, Lemma 12.5]. Part (iii) is given by [Reference tom DiecktD75b, Proposition 9], while part (iv) follows from the fact that the element
$\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
. Combining this with [Reference tom DiecktD75b, Propositions 9 and 12] gives part (i). Part (ii) can be derived from [Reference tom DiecktD75b, Proposition 16], but is stated more explicitly in this form in [Reference FauskFau08, Lemma 12.5]. Part (iii) is given by [Reference tom DiecktD75b, Proposition 9], while part (iv) follows from the fact that the element
![]() $p\in A(G)_{(p)}$
lies in
$p\in A(G)_{(p)}$
lies in
![]() $q(H^{\prime },1)$
but not in
$q(H^{\prime },1)$
but not in
![]() $q(H,\infty )$
for any pair of closed subgroups
$q(H,\infty )$
for any pair of closed subgroups
![]() $H,H^{\prime }$
of
$H,H^{\prime }$
of
![]() $G$
.◻
$G$
.◻
The comparison map
![]() $\unicode[STIX]{x1D713}:\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})\rightarrow \operatorname{Spec}(A(G)_{(p)})$
is defined to send
$\unicode[STIX]{x1D713}:\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})\rightarrow \operatorname{Spec}(A(G)_{(p)})$
is defined to send
![]() ${\wp}\in \operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
to the prime ideal of all
${\wp}\in \operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
to the prime ideal of all
![]() $\unicode[STIX]{x1D6FC}\in A(G)_{(p)}$
such that the cofibre
$\unicode[STIX]{x1D6FC}\in A(G)_{(p)}$
such that the cofibre
![]() $C(\unicode[STIX]{x1D6FC})$
is not contained in
$C(\unicode[STIX]{x1D6FC})$
is not contained in
![]() ${\wp}$
, see [Reference BalmerBal10]. This computes as follows.
${\wp}$
, see [Reference BalmerBal10]. This computes as follows.
Proposition 6.7. Given
![]() $P_{G}(H,n)\in \operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
, we have
$P_{G}(H,n)\in \operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
, we have
Proof. The proof builds on the following commutative comparison diagram.

Since
![]() $P_{G}(H,n)$
is by definition equal to
$P_{G}(H,n)$
is by definition equal to
![]() $(\unicode[STIX]{x1D6F7}^{H})^{\ast }(P(n))$
, it is enough to compute
$(\unicode[STIX]{x1D6F7}^{H})^{\ast }(P(n))$
, it is enough to compute
![]() $\unicode[STIX]{x1D713}(P(n))$
. First note that if
$\unicode[STIX]{x1D713}(P(n))$
. First note that if
![]() $x\in \mathbb{Z}_{(p)}$
is non-trivial, then it becomes a unit in
$x\in \mathbb{Z}_{(p)}$
is non-trivial, then it becomes a unit in
![]() $\mathbb{Q}$
, and hence
$\mathbb{Q}$
, and hence
![]() $K(0)_{\ast }(C(x))=H\mathbb{Q}_{\ast }(C(x))=0$
, and thus
$K(0)_{\ast }(C(x))=H\mathbb{Q}_{\ast }(C(x))=0$
, and thus
![]() $x\notin \unicode[STIX]{x1D713}(P(1))$
. It follows that
$x\notin \unicode[STIX]{x1D713}(P(1))$
. It follows that
![]() $\unicode[STIX]{x1D713}(P(1))$
is the
$\unicode[STIX]{x1D713}(P(1))$
is the
![]() $0$
-ideal, as claimed. Now, if
$0$
-ideal, as claimed. Now, if
![]() $x\in \mathbb{Z}_{(p)}$
is divisible by
$x\in \mathbb{Z}_{(p)}$
is divisible by
![]() $p$
, then its image in
$p$
, then its image in
![]() $K(n-1)_{\ast }$
for
$K(n-1)_{\ast }$
for
![]() $n>1$
is zero, and hence
$n>1$
is zero, and hence
![]() $C(x)\notin P(n)$
, and thus
$C(x)\notin P(n)$
, and thus
![]() $x\in \unicode[STIX]{x1D713}(P(n))$
. This shows that for all
$x\in \unicode[STIX]{x1D713}(P(n))$
. This shows that for all
![]() $n>1$
we have
$n>1$
we have
![]() $(p)\subseteq \unicode[STIX]{x1D713}(P(n))$
, and hence
$(p)\subseteq \unicode[STIX]{x1D713}(P(n))$
, and hence
![]() $(p)=\unicode[STIX]{x1D713}(P(n))$
, since
$(p)=\unicode[STIX]{x1D713}(P(n))$
, since
![]() $(p)$
is maximal. The statement now follows from the commutativity of the above diagram and the facts that
$(p)$
is maximal. The statement now follows from the commutativity of the above diagram and the facts that
![]() $q(H,1)=(\unicode[STIX]{x1D711}^{H})^{\ast }((0))$
and
$q(H,1)=(\unicode[STIX]{x1D711}^{H})^{\ast }((0))$
and
![]() $q(H,\infty )=(\unicode[STIX]{x1D711}^{H})^{\ast }((p))$
.◻
$q(H,\infty )=(\unicode[STIX]{x1D711}^{H})^{\ast }((p))$
.◻
Since the comparison map is inclusion reversing, we see the following.
Corollary 6.8. If
![]() $P_{G}(K,n)\subseteq P_{G}(H,m)$
is an inclusion in
$P_{G}(K,n)\subseteq P_{G}(H,m)$
is an inclusion in
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
, then
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
, then
![]() $\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(K))$
is conjugate to
$\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(K))$
is conjugate to
![]() $\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
. If
$\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
. If
![]() $n=1$
, then
$n=1$
, then
![]() $\unicode[STIX]{x1D714}_{G}(K)$
is conjugate to
$\unicode[STIX]{x1D714}_{G}(K)$
is conjugate to
![]() $\unicode[STIX]{x1D714}_{G}(H)$
.
$\unicode[STIX]{x1D714}_{G}(H)$
.
In order to prove parts (i) and (ii) of Theorem 6.2, one combines this corollary with the first part of Proposition 6.4 on change of groups: if
![]() $P_{G}(K,n)\subseteq P_{G}(H,m)$
, then there exists a
$P_{G}(K,n)\subseteq P_{G}(H,m)$
, then there exists a
![]() $G$
-conjugate
$G$
-conjugate
![]() $K^{g}\subseteq H$
such that
$K^{g}\subseteq H$
such that
![]() $P_{H}(K^{g},n)\subseteq P_{H}(H,m)$
. Hence, by the corollary,
$P_{H}(K^{g},n)\subseteq P_{H}(H,m)$
. Hence, by the corollary,
![]() $\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K^{g}))\sim \unicode[STIX]{x1D714}_{H}({\mathcal{O}}(H))={\mathcal{O}}(H)$
and it follows that
$\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K^{g}))\sim \unicode[STIX]{x1D714}_{H}({\mathcal{O}}(H))={\mathcal{O}}(H)$
and it follows that
![]() $K^{g}$
is
$K^{g}$
is
![]() $p$
-subcotoral in
$p$
-subcotoral in
![]() $H$
, as desired. If
$H$
, as desired. If
![]() $n=1$
, then even
$n=1$
, then even
![]() $\unicode[STIX]{x1D714}_{H}(K^{g})\sim \unicode[STIX]{x1D714}_{H}(H)=H$
and
$\unicode[STIX]{x1D714}_{H}(K^{g})\sim \unicode[STIX]{x1D714}_{H}(H)=H$
and
![]() $K^{g}$
is cotoral in
$K^{g}$
is cotoral in
![]() $H$
. In summary, this proves parts (i) and (ii) of Theorem 6.2.
$H$
. In summary, this proves parts (i) and (ii) of Theorem 6.2.
Corollary 6.9. If
![]() $P_{G}(K,n)\subseteq P_{G}(H,m)$
, then
$P_{G}(K,n)\subseteq P_{G}(H,m)$
, then
![]() $K$
is
$K$
is
![]() $G$
-conjugate to a
$G$
-conjugate to a
![]() $p$
-subcotoral subgroup of
$p$
-subcotoral subgroup of
![]() $H$
and
$H$
and
![]() $n\geqslant m$
. If
$n\geqslant m$
. If
![]() $n=1$
, then
$n=1$
, then
![]() $K$
is even
$K$
is even
![]() $G$
-conjugate to a cotoral subgroup of
$G$
-conjugate to a cotoral subgroup of
![]() $H$
.
$H$
.
6.3 Inclusions for
 $p$
-cotoral and
$p$
-cotoral and
 $p$
-subcotoral subgroups
$p$
-subcotoral subgroups
While the previous subsection was about establishing necessary conditions for the inclusion of prime ideals, we now turn to sufficient ones. We begin with parts (iii) and (iv) of Theorem 6.2, which via Proposition 6.4 reduce to the following.
Proposition 6.10. Let
![]() $K\subseteq H$
be a normal inclusion of closed subgroups in
$K\subseteq H$
be a normal inclusion of closed subgroups in
![]() $G$
.
$G$
.
(i) If
 $H/K$
is a torus, then
$H/K$
is a torus, then
 $P_{G}(K,n)\subseteq P_{G}(H,n)$
for all
$P_{G}(K,n)\subseteq P_{G}(H,n)$
for all
 $n\in \overline{\mathbb{N}}$
.
$n\in \overline{\mathbb{N}}$
.(ii) If
 $H/K$
is a cyclic
$H/K$
is a cyclic
 $p$
-group, then
$p$
-group, then
 $P_{G}(K,n+1)\subseteq P_{G}(H,n)$
for all
$P_{G}(K,n+1)\subseteq P_{G}(H,n)$
for all
 $n\in \overline{\mathbb{N}}$
.
$n\in \overline{\mathbb{N}}$
.
As mentioned above, the second item is [Reference Barthel, Hausmann, Naumann, Nikolaus, Noel and StapletonBHN+19, Theorem 2.6]. In order to prove the first, we will use a small computation of the geometric
![]() $\mathbb{T}$
-fixed points of Morava
$\mathbb{T}$
-fixed points of Morava
![]() $K$
-theories proved in § 6.4 below.
$K$
-theories proved in § 6.4 below.
Proof of Proposition 6.10.
It only remains to prove the first item. Since the enhanced version of the geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{K}(X)$
is a finite
$\unicode[STIX]{x1D6F7}^{K}(X)$
is a finite
![]() $H/K$
-spectrum satisfying
$H/K$
-spectrum satisfying
![]() $\unicode[STIX]{x1D6F7}^{H/K}(\unicode[STIX]{x1D6F7}^{K}(X))\simeq \unicode[STIX]{x1D6F7}^{H}(X)$
, it suffices to consider the case where
$\unicode[STIX]{x1D6F7}^{H/K}(\unicode[STIX]{x1D6F7}^{K}(X))\simeq \unicode[STIX]{x1D6F7}^{H}(X)$
, it suffices to consider the case where
![]() $K$
is the trivial group and
$K$
is the trivial group and
![]() $H=G=\mathbb{T}^{k}$
is a torus. By induction on
$H=G=\mathbb{T}^{k}$
is a torus. By induction on
![]() $k$
we can further reduce to
$k$
we can further reduce to
![]() $k=1$
.
$k=1$
.
Hence we are given a finite
![]() $\mathbb{T}$
-spectrum
$\mathbb{T}$
-spectrum
![]() $X$
such that
$X$
such that
![]() $K(n)_{\ast }(\unicode[STIX]{x1D6F7}^{\{e\}}(X))=0$
, and we want to show that
$K(n)_{\ast }(\unicode[STIX]{x1D6F7}^{\{e\}}(X))=0$
, and we want to show that
![]() $K(n)_{\ast }(\unicode[STIX]{x1D6F7}^{\mathbb{T}}(X))$
is also trivial. We consider the function spectrum
$K(n)_{\ast }(\unicode[STIX]{x1D6F7}^{\mathbb{T}}(X))$
is also trivial. We consider the function spectrum
![]() $F_{\mathbb{T}}(X,\text{}\underline{K(n)})$
from
$F_{\mathbb{T}}(X,\text{}\underline{K(n)})$
from
![]() $X$
into the
$X$
into the
![]() $\mathbb{T}$
-Borel spectrum for
$\mathbb{T}$
-Borel spectrum for
![]() $K(n)$
(with trivial naive
$K(n)$
(with trivial naive
![]() $\mathbb{T}$
-action), see § 2.2.5. Then
$\mathbb{T}$
-action), see § 2.2.5. Then
![]() $F_{\mathbb{T}}(X,\text{}\underline{K(n)})$
is itself Borel complete, since there is an equivalence
$F_{\mathbb{T}}(X,\text{}\underline{K(n)})$
is itself Borel complete, since there is an equivalence
Moreover, the underlying non-equivariant spectrum of
![]() $F_{\mathbb{T}}(X,\text{}\underline{K(n)})$
is
$F_{\mathbb{T}}(X,\text{}\underline{K(n)})$
is
![]() $F(\unicode[STIX]{x1D6F7}^{\{e\}}(X),K(n))$
(since
$F(\unicode[STIX]{x1D6F7}^{\{e\}}(X),K(n))$
(since
![]() $\unicode[STIX]{x1D6F7}^{\{e\}}(X)\simeq \operatorname{Res}_{e}^{\mathbb{T}}(X)$
), which is contractible by assumption. Hence
$\unicode[STIX]{x1D6F7}^{\{e\}}(X)\simeq \operatorname{Res}_{e}^{\mathbb{T}}(X)$
), which is contractible by assumption. Hence
![]() $F_{\mathbb{T}}(X,\text{}\underline{K(n)})$
is equivariantly contractible and therefore its geometric fixed points
$F_{\mathbb{T}}(X,\text{}\underline{K(n)})$
is equivariantly contractible and therefore its geometric fixed points
![]() $\unicode[STIX]{x1D6F7}^{\mathbb{T}}(F_{\mathbb{T}}(X,\text{}\underline{K(n)}))$
are also contractible. Since
$\unicode[STIX]{x1D6F7}^{\mathbb{T}}(F_{\mathbb{T}}(X,\text{}\underline{K(n)}))$
are also contractible. Since
![]() $X$
is finite, we can compute these geometric fixed points as
$X$
is finite, we can compute these geometric fixed points as
see the discussion preceding Corollary 3.18. By Theorem 6.12,
![]() $\unicode[STIX]{x1D6F7}^{\mathbb{T}}(\text{}\underline{K(n)})$
is a non-trivial
$\unicode[STIX]{x1D6F7}^{\mathbb{T}}(\text{}\underline{K(n)})$
is a non-trivial
![]() $K(n)$
-module and hence contains
$K(n)$
-module and hence contains
![]() $K(n)$
as a retract. So we conclude that
$K(n)$
as a retract. So we conclude that
![]() $F_{\mathbb{T}}(\unicode[STIX]{x1D6F7}^{\mathbb{T}}(X),\mathbb{S})\wedge K(n)$
is trivial and hence so is
$F_{\mathbb{T}}(\unicode[STIX]{x1D6F7}^{\mathbb{T}}(X),\mathbb{S})\wedge K(n)$
is trivial and hence so is
![]() $\unicode[STIX]{x1D6F7}^{\mathbb{T}}(X)\wedge K(n)$
, using the Künneth formula for Morava
$\unicode[STIX]{x1D6F7}^{\mathbb{T}}(X)\wedge K(n)$
, using the Künneth formula for Morava
![]() $K$
-theory.
$K$
-theory.
To obtain the statement also for
![]() $n=\infty$
, one uses that
$n=\infty$
, one uses that
![]() $P_{G}(H,\infty )$
is the intersection of all
$P_{G}(H,\infty )$
is the intersection of all
![]() $P_{G}(H,n)$
with
$P_{G}(H,n)$
with
![]() $n<\infty$
.◻
$n<\infty$
.◻
We are left with showing part (v) of Theorem 6.2.
Proposition 6.11. Let
![]() $K$
and
$K$
and
![]() $H$
be two closed subgroups of
$H$
be two closed subgroups of
![]() $G$
. If
$G$
. If
![]() $K$
is
$K$
is
![]() $p$
-subcotoral in
$p$
-subcotoral in
![]() $H$
, then there is an inclusion
$H$
, then there is an inclusion
![]() $P_{G}(K,\infty )\subseteq P_{G}(H,\infty )$
.
$P_{G}(K,\infty )\subseteq P_{G}(H,\infty )$
.
Proof. The key to the proof is the following statement, due to tom Dieck [Reference tom DiecktD75b, Theorem 4]: if
![]() $K\subseteq H$
is
$K\subseteq H$
is
![]() $p$
-subcotoral and
$p$
-subcotoral and
![]() $K\neq H$
, then either
$K\neq H$
, then either
![]() $K$
has infinite Weyl group
$K$
has infinite Weyl group
![]() $W_{H}K$
or the order of
$W_{H}K$
or the order of
![]() $W_{H}K$
is divisible by
$W_{H}K$
is divisible by
![]() $p$
. This leads to the following algorithm to construct
$p$
. This leads to the following algorithm to construct
![]() $H$
out of
$H$
out of
![]() $K$
. First replace
$K$
. First replace
![]() $K$
by
$K$
by
![]() $\unicode[STIX]{x1D714}_{H}(K)$
, which we can do since we know that
$\unicode[STIX]{x1D714}_{H}(K)$
, which we can do since we know that
![]() $P_{G}(K,\infty )\subseteq P_{G}(\unicode[STIX]{x1D714}_{H}(K),\infty )$
and
$P_{G}(K,\infty )\subseteq P_{G}(\unicode[STIX]{x1D714}_{H}(K),\infty )$
and
![]() $\unicode[STIX]{x1D714}_{H}(K)$
is again
$\unicode[STIX]{x1D714}_{H}(K)$
is again
![]() $p$
-subcotoral in
$p$
-subcotoral in
![]() $H$
. Hence, it is enough to consider the case where
$H$
. Hence, it is enough to consider the case where
![]() $K$
has finite Weyl group. If
$K$
has finite Weyl group. If
![]() $K=H$
, we are done. If not, we can find a normal extension
$K=H$
, we are done. If not, we can find a normal extension
![]() $K\subseteq K_{1}$
(inside
$K\subseteq K_{1}$
(inside
![]() $H$
) of index
$H$
) of index
![]() $p^{k}$
with
$p^{k}$
with
![]() $k\geqslant 1$
. Then
$k\geqslant 1$
. Then
![]() $P_{G}(K,\infty )\subseteq P_{G}(K_{1},\infty )$
and
$P_{G}(K,\infty )\subseteq P_{G}(K_{1},\infty )$
and
![]() ${\mathcal{O}}(K_{1})={\mathcal{O}}(K)$
. Hence,
${\mathcal{O}}(K_{1})={\mathcal{O}}(K)$
. Hence,
![]() $K_{1}$
is also
$K_{1}$
is also
![]() $p$
-subcotoral in
$p$
-subcotoral in
![]() $H$
and we can replace
$H$
and we can replace
![]() $K$
by
$K$
by
![]() $K_{1}$
. This way we obtain a subnormal chain
$K_{1}$
. This way we obtain a subnormal chain
![]() $K\subseteq K_{1}\subseteq K_{2}\subseteq \cdots \,$
. If at some point we have
$K\subseteq K_{1}\subseteq K_{2}\subseteq \cdots \,$
. If at some point we have
![]() $K_{i}=H$
, we are done. If not, we consider the closure
$K_{i}=H$
, we are done. If not, we consider the closure
![]() $L$
of the union of the
$L$
of the union of the
![]() $K_{i}$
. Since we have
$K_{i}$
. Since we have
![]() $P_{G}(K,\infty )\subseteq P_{G}(K_{i},\infty )$
for all
$P_{G}(K,\infty )\subseteq P_{G}(K_{i},\infty )$
for all
![]() $i$
, it follows that we also have
$i$
, it follows that we also have
![]() $P_{G}(K,\infty )\subseteq P_{G}(L,\infty )$
, since the type function
$P_{G}(K,\infty )\subseteq P_{G}(L,\infty )$
, since the type function
![]() $\text{type}_{X}$
of every finite
$\text{type}_{X}$
of every finite
![]() $G$
-spectrum is locally constant and the
$G$
-spectrum is locally constant and the
![]() $K_{i}$
converge to
$K_{i}$
converge to
![]() $L$
in
$L$
in
![]() $\operatorname{Sub}(G)$
.
$\operatorname{Sub}(G)$
.
Further, we claim that
![]() $L$
is also
$L$
is also
![]() $p$
-subcotoral in
$p$
-subcotoral in
![]() $H$
. There are different ways to see this. One is to use tom Dieck’s theorem (Theorem 6.6, Part (ii)) that
$H$
. There are different ways to see this. One is to use tom Dieck’s theorem (Theorem 6.6, Part (ii)) that
![]() $L\subseteq H$
is
$L\subseteq H$
is
![]() $p$
-subcotoral if and only if the primes
$p$
-subcotoral if and only if the primes
![]() $q(L,\infty )$
and
$q(L,\infty )$
and
![]() $q(H,\infty )$
are the same in the Burnside ring of
$q(H,\infty )$
are the same in the Burnside ring of
![]() $H$
. We know that
$H$
. We know that
![]() $q(H,\infty )$
is equal to
$q(H,\infty )$
is equal to
![]() $q(K_{i},\infty )$
for all
$q(K_{i},\infty )$
for all
![]() $i$
, and a similar argument as in the proof of Proposition 4.3 shows that then also
$i$
, and a similar argument as in the proof of Proposition 4.3 shows that then also
![]() $q(H,\infty )$
is equal to
$q(H,\infty )$
is equal to
![]() $q(L,\infty )$
, using that for every
$q(L,\infty )$
, using that for every
![]() $H$
-representation
$H$
-representation
![]() $V$
we have
$V$
we have
![]() $V^{L}=V^{K_{i}}$
for almost all
$V^{L}=V^{K_{i}}$
for almost all
![]() $i$
. Hence, we can replace
$i$
. Hence, we can replace
![]() $K$
by
$K$
by
![]() $L$
and proceed. Since the dimension of
$L$
and proceed. Since the dimension of
![]() $L$
is larger than that of
$L$
is larger than that of
![]() $K$
, this process must eventually terminate at the full group
$K$
, this process must eventually terminate at the full group
![]() $H$
. This finishes the proof.◻
$H$
. This finishes the proof.◻
6.4 Geometric fixed points of Borel-equivariant Morava
 $K$
-theories
$K$
-theories
We now give the computation needed for the proof of the first part of Proposition 6.10, and also explain that this argument is special for tori. Let
![]() $\text{}\underline{K(n)}$
denote the
$\text{}\underline{K(n)}$
denote the
![]() $G$
-equivariant Borel spectrum for the
$G$
-equivariant Borel spectrum for the
![]() $n$
th Morava
$n$
th Morava
![]() $K$
-theory
$K$
-theory
![]() $K(n)$
, see § 2.2.5. Then we have the following theorem.
$K(n)$
, see § 2.2.5. Then we have the following theorem.
Theorem 6.12. Suppose
![]() $G$
is a compact Lie group,
$G$
is a compact Lie group,
![]() $n\geqslant 0$
, and
$n\geqslant 0$
, and
![]() $r\geqslant 0$
. Then
$r\geqslant 0$
. Then
Proof. We start with the case where
![]() $G=\mathbb{T}$
is the circle group. Since
$G=\mathbb{T}$
is the circle group. Since
![]() $K(n)$
is a complex oriented cohomology theory, and using [Reference Greenlees and MayGM95a, Proposition 3.20], we can compute
$K(n)$
is a complex oriented cohomology theory, and using [Reference Greenlees and MayGM95a, Proposition 3.20], we can compute
![]() $\unicode[STIX]{x1D6F7}_{\ast }^{\mathbb{T}}(\text{}\underline{K(n)})$
as the localization of
$\unicode[STIX]{x1D6F7}_{\ast }^{\mathbb{T}}(\text{}\underline{K(n)})$
as the localization of
at Euler classes
![]() $e_{V}$
, where
$e_{V}$
, where
![]() $V$
ranges through a countable collection
$V$
ranges through a countable collection
![]() ${\mathcal{C}}$
of complex
${\mathcal{C}}$
of complex
![]() $\mathbb{T}$
-representations satisfying two properties.
$\mathbb{T}$
-representations satisfying two properties.
(i) The fixed points
 $V^{\mathbb{T}}$
are trivial for all
$V^{\mathbb{T}}$
are trivial for all
 $V\in {\mathcal{C}}$
.
$V\in {\mathcal{C}}$
.(ii) For every proper closed subgroup
 $H$
of
$H$
of
 $\mathbb{T}$
there exists a representation
$\mathbb{T}$
there exists a representation
 $V\in {\mathcal{C}}$
such that
$V\in {\mathcal{C}}$
such that
 $V^{H}\neq 0$
.
$V^{H}\neq 0$
.
This fact uses that under these assumptions the unit sphere in the representation
![]() $\sum _{\mathbb{N}}\sum _{V\in {\mathcal{C}}}V$
is a model for the universal space for the family of proper subgroups. For
$\sum _{\mathbb{N}}\sum _{V\in {\mathcal{C}}}V$
is a model for the universal space for the family of proper subgroups. For
![]() $n>0$
, let
$n>0$
, let
![]() $\unicode[STIX]{x1D70C}_{n}$
be the one-dimensional complex representation given by the
$\unicode[STIX]{x1D70C}_{n}$
be the one-dimensional complex representation given by the
![]() $n$
-fold tensor power of the tautological representation
$n$
-fold tensor power of the tautological representation
![]() $\unicode[STIX]{x1D70C}_{1}$
. Then the collection
$\unicode[STIX]{x1D70C}_{1}$
. Then the collection
![]() $\{{\unicode[STIX]{x1D70C}_{n}\}}_{n>0}$
satisfies the two properties above. The Euler class of
$\{{\unicode[STIX]{x1D70C}_{n}\}}_{n>0}$
satisfies the two properties above. The Euler class of
![]() $\unicode[STIX]{x1D70C}_{n}$
is given by the
$\unicode[STIX]{x1D70C}_{n}$
is given by the
![]() $n$
-series
$n$
-series
![]() $[n]_{F}(x)$
, where
$[n]_{F}(x)$
, where
![]() $F$
is the formal group law associated to the complex orientation of
$F$
is the formal group law associated to the complex orientation of
![]() $K(n)$
. We claim that it is in fact enough to invert the single element
$K(n)$
. We claim that it is in fact enough to invert the single element
![]() $x$
, i.e., the
$x$
, i.e., the
![]() $1$
-series
$1$
-series
![]() $[1]_{F}(x)$
, and hence that we have an isomorphism
$[1]_{F}(x)$
, and hence that we have an isomorphism
as claimed. To show that, it is enough to see that the leading term of
![]() $[n]_{F}(x)$
is a unit for all
$[n]_{F}(x)$
is a unit for all
![]() $n>1$
. We first consider the case where
$n>1$
. We first consider the case where
![]() $n=p^{k}$
is a power of
$n=p^{k}$
is a power of
![]() $p$
. If
$p$
. If
![]() $k=1$
, then
$k=1$
, then
![]() $[p]_{F}(x)$
has leading term
$[p]_{F}(x)$
has leading term
![]() $v_{n}\cdot x^{p^{n}}$
, and
$v_{n}\cdot x^{p^{n}}$
, and
![]() $v_{n}$
is a unit in
$v_{n}$
is a unit in
![]() $K(n)_{\ast }$
. For larger
$K(n)_{\ast }$
. For larger
![]() $k$
, we can use the formula
$k$
, we can use the formula
![]() $[p^{k}]_{F}(x)=[p]_{F}([p^{k-1}]_{F}(x))$
to see that the leading coefficient of
$[p^{k}]_{F}(x)=[p]_{F}([p^{k-1}]_{F}(x))$
to see that the leading coefficient of
![]() $[p^{k}]_{F}(x)$
is given by
$[p^{k}]_{F}(x)$
is given by
![]() $v_{n}$
multiplied with the
$v_{n}$
multiplied with the
![]() $p^{n}$
-fold power of the leading coefficient of the
$p^{n}$
-fold power of the leading coefficient of the
![]() $p^{k-1}$
-series, which is a unit by induction. Finally we can write a general
$p^{k-1}$
-series, which is a unit by induction. Finally we can write a general
![]() $n$
as
$n$
as
![]() $p^{k}\cdot q$
with
$p^{k}\cdot q$
with
![]() $q$
not divisible by
$q$
not divisible by
![]() $p$
. Then
$p$
. Then
![]() $[n]_{F}(x)=[q]_{F}([p^{k}]_{F}(x))$
. Since
$[n]_{F}(x)=[q]_{F}([p^{k}]_{F}(x))$
. Since
![]() $[q]_{F}(x)$
has leading term
$[q]_{F}(x)$
has leading term
![]() $q\cdot x$
, we see that the leading coefficient of
$q\cdot x$
, we see that the leading coefficient of
![]() $[n]_{F}(x)$
is given by
$[n]_{F}(x)$
is given by
![]() $q$
times the leading coefficient of
$q$
times the leading coefficient of
![]() $[p^{k}]_{F}(x)$
and is hence a unit.
$[p^{k}]_{F}(x)$
and is hence a unit.
Next we deal with the case
![]() $G=\mathbb{T}^{\times r}$
of a higher rank torus. There is an isomorphism
$G=\mathbb{T}^{\times r}$
of a higher rank torus. There is an isomorphism
and the ring
![]() $\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F7}^{\mathbb{T}^{\times r}}(\text{}\underline{K(n)})$
is obtained from this by inverting all Euler classes of non-trivial irreducible complex representations of
$\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F7}^{\mathbb{T}^{\times r}}(\text{}\underline{K(n)})$
is obtained from this by inverting all Euler classes of non-trivial irreducible complex representations of
![]() $\mathbb{T}^{\times r}$
. The
$\mathbb{T}^{\times r}$
. The
![]() $x_{i}$
are the Euler classes associated to the projections
$x_{i}$
are the Euler classes associated to the projections
![]() $\mathbb{T}^{\times r}\rightarrow \mathbb{T}$
, and hence we need to see that after inverting all
$\mathbb{T}^{\times r}\rightarrow \mathbb{T}$
, and hence we need to see that after inverting all
![]() $x_{i}$
the Euler class of any non-trivial irreducible complex representation becomes invertible. Every such irreducible representation
$x_{i}$
the Euler class of any non-trivial irreducible complex representation becomes invertible. Every such irreducible representation
![]() $V$
is of the form
$V$
is of the form
![]() $V_{1}\otimes _{\mathbb{C}}\cdots \otimes _{\mathbb{C}}V_{r}$
, where
$V_{1}\otimes _{\mathbb{C}}\cdots \otimes _{\mathbb{C}}V_{r}$
, where
![]() $V_{i}$
is the pullback of an irreducible representation of
$V_{i}$
is the pullback of an irreducible representation of
![]() $\mathbb{T}$
along the
$\mathbb{T}$
along the
![]() $i$
th projection. Since
$i$
th projection. Since
![]() $V$
is non-trivial, one of the
$V$
is non-trivial, one of the
![]() $V_{i}$
needs to be non-trivial, which by symmetry we can assume to be
$V_{i}$
needs to be non-trivial, which by symmetry we can assume to be
![]() $V_{1}$
. Since the Euler class of a tensor product of one-dimensional representations is given by the formal sum of the Euler classes of the factors, we see that
$V_{1}$
. Since the Euler class of a tensor product of one-dimensional representations is given by the formal sum of the Euler classes of the factors, we see that
Now, each
![]() $e_{V_{i}}$
is a power series in the variable
$e_{V_{i}}$
is a power series in the variable
![]() $x_{i}$
. Furthermore, since
$x_{i}$
. Furthermore, since
![]() $V_{1}$
is non-trivial, we have seen in the rank
$V_{1}$
is non-trivial, we have seen in the rank
![]() $1$
case above that
$1$
case above that
![]() $e_{V_{1}}$
becomes invertible after adjoining
$e_{V_{1}}$
becomes invertible after adjoining
![]() $x_{1}^{-1}$
. But this implies that
$x_{1}^{-1}$
. But this implies that
![]() $e_{V}$
also becomes invertible in
$e_{V}$
also becomes invertible in
![]() $K(n)_{\ast }\unicode[STIX]{x27E6}x_{1},\ldots ,x_{r}\unicode[STIX]{x27E7}(x_{1}^{-1})$
, and therefore in particular in
$K(n)_{\ast }\unicode[STIX]{x27E6}x_{1},\ldots ,x_{r}\unicode[STIX]{x27E7}(x_{1}^{-1})$
, and therefore in particular in
![]() $K(n)_{\ast }\unicode[STIX]{x27E6}x_{1},\ldots ,x_{r}\unicode[STIX]{x27E7}(x_{1}^{-1},\ldots ,x_{r}^{-1})$
, since when viewed as a power series over
$K(n)_{\ast }\unicode[STIX]{x27E6}x_{1},\ldots ,x_{r}\unicode[STIX]{x27E7}(x_{1}^{-1},\ldots ,x_{r}^{-1})$
, since when viewed as a power series over
![]() $K(n)_{\ast }\unicode[STIX]{x27E6}x_{1}\unicode[STIX]{x27E7}$
it is given by
$K(n)_{\ast }\unicode[STIX]{x27E6}x_{1}\unicode[STIX]{x27E7}$
it is given by
![]() $e_{V_{1}}$
plus higher order terms. This finishes the proof of the torus case.
$e_{V_{1}}$
plus higher order terms. This finishes the proof of the torus case.
We now turn to the second part and show that if
![]() $G$
is not a torus, the
$G$
is not a torus, the
![]() $G$
-geometric fixed points of
$G$
-geometric fixed points of
![]() $\text{}\underline{K(n)}$
are trivial. We begin with the case where
$\text{}\underline{K(n)}$
are trivial. We begin with the case where
![]() $G$
is a non-trivial finite group, which follows directly from the Tate vanishing of
$G$
is a non-trivial finite group, which follows directly from the Tate vanishing of
![]() $K(n)$
. By [Reference Greenlees and SadofskyGS96, Theorem 1.1], the
$K(n)$
. By [Reference Greenlees and SadofskyGS96, Theorem 1.1], the
![]() $G$
-spectrum
$G$
-spectrum
![]() $\text{}\underline{K(n)}\wedge \tilde{E}G$
is trivial, where
$\text{}\underline{K(n)}\wedge \tilde{E}G$
is trivial, where
![]() $\tilde{E}G$
is the cofibre of
$\tilde{E}G$
is the cofibre of
![]() $EG_{+}\rightarrow S^{0}$
. But
$EG_{+}\rightarrow S^{0}$
. But
![]() $\unicode[STIX]{x1D6F7}^{G}(\tilde{E}G)$
is equivalent to the sphere
$\unicode[STIX]{x1D6F7}^{G}(\tilde{E}G)$
is equivalent to the sphere
![]() $S^{0}$
, so
$S^{0}$
, so
Next we consider the case where
![]() $G$
is disconnected but not necessarily discrete. The quotient map
$G$
is disconnected but not necessarily discrete. The quotient map
![]() $p:G\rightarrow \unicode[STIX]{x1D70B}_{0}(G)$
induces a ring map
$p:G\rightarrow \unicode[STIX]{x1D70B}_{0}(G)$
induces a ring map
sending an Euler class
![]() $e_{V}$
to the pulled-back Euler class
$e_{V}$
to the pulled-back Euler class
![]() $e_{p^{\ast }(V)}$
. As
$e_{p^{\ast }(V)}$
. As
![]() $p$
is surjective, the
$p$
is surjective, the
![]() $G$
-fixed points of
$G$
-fixed points of
![]() $p^{\ast }(V)$
are trivial if the
$p^{\ast }(V)$
are trivial if the
![]() $\unicode[STIX]{x1D70B}_{0}(G)$
-fixed points of
$\unicode[STIX]{x1D70B}_{0}(G)$
-fixed points of
![]() $V$
are trivial. It follows that the geometric fixed point map
$V$
are trivial. It follows that the geometric fixed point map
![]() $K(n)^{\ast }(BG)\rightarrow \unicode[STIX]{x1D6F7}_{\ast }^{G}(\text{}\underline{K(n)})$
factors through the localization of
$K(n)^{\ast }(BG)\rightarrow \unicode[STIX]{x1D6F7}_{\ast }^{G}(\text{}\underline{K(n)})$
factors through the localization of
![]() $K(n)^{\ast }(BG)$
at the Euler classes of the form
$K(n)^{\ast }(BG)$
at the Euler classes of the form
![]() $e_{p^{\ast }(V)}$
with
$e_{p^{\ast }(V)}$
with
![]() $V^{\unicode[STIX]{x1D70B}_{0}(G)}=0$
. But this localization is trivial, since it is an algebra over
$V^{\unicode[STIX]{x1D70B}_{0}(G)}=0$
. But this localization is trivial, since it is an algebra over
which we have just seen to be trivial.
The remaining case of
![]() $G$
connected holds in fact more generally than for Morava
$G$
connected holds in fact more generally than for Morava
![]() $K$
-theory.
$K$
-theory.
Lemma 6.13. Let
![]() $E$
be any Borel-complete
$E$
be any Borel-complete
![]() $G$
-spectrum for
$G$
-spectrum for
![]() $G$
a connected compact Lie group which is not a torus. Then
$G$
a connected compact Lie group which is not a torus. Then
![]() $\unicode[STIX]{x1D6F7}^{G}(E)$
is contractible.
$\unicode[STIX]{x1D6F7}^{G}(E)$
is contractible.
Proof. Write
![]() $T$
for a maximal torus in
$T$
for a maximal torus in
![]() $G$
and
$G$
and
![]() $N=N_{G}(T)$
for the normalizer of
$N=N_{G}(T)$
for the normalizer of
![]() $T$
in
$T$
in
![]() $G$
. Since
$G$
. Since
![]() $N$
is a proper subgroup of
$N$
is a proper subgroup of
![]() $G$
, the Peter–Weyl theorem implies that there exists an orthogonal representation
$G$
, the Peter–Weyl theorem implies that there exists an orthogonal representation
![]() $V$
of
$V$
of
![]() $G$
with the property that
$G$
with the property that
![]() $V^{G}=0$
but
$V^{G}=0$
but
![]() $V^{N}\neq 0$
. We claim that the map
$V^{N}\neq 0$
. We claim that the map
is trivial. Since
![]() $e_{V}$
induces the identity on geometric fixed points and consequently so does
$e_{V}$
induces the identity on geometric fixed points and consequently so does
![]() $E\,\wedge \,e_{V}$
, this implies that
$E\,\wedge \,e_{V}$
, this implies that
![]() $\unicode[STIX]{x1D6F7}^{G}(E)$
is contractible.
$\unicode[STIX]{x1D6F7}^{G}(E)$
is contractible.
The proof of the claim is a standard transfer argument, using that the Euler characteristic of the quotient
![]() $G/N$
is
$G/N$
is
![]() $1$
. We consider the composition
$1$
. We consider the composition
obtained by smashing the transfer map
![]() $G/G_{+}\rightarrow G/N_{+}$
and the restriction map
$G/G_{+}\rightarrow G/N_{+}$
and the restriction map
![]() $G/N_{+}\rightarrow G/G_{+}$
with
$G/N_{+}\rightarrow G/G_{+}$
with
![]() $G_{+}$
. This composition is given by multiplication with the Euler characteristic of
$G_{+}$
. This composition is given by multiplication with the Euler characteristic of
![]() $G/N$
and hence an equivalence. It follows that
$G/N$
and hence an equivalence. It follows that
![]() $X\rightarrow X\wedge G/N_{+}\rightarrow X$
is an equivalence for any spectrum
$X\rightarrow X\wedge G/N_{+}\rightarrow X$
is an equivalence for any spectrum
![]() $X$
built out of free cells, and in particular for
$X$
built out of free cells, and in particular for
![]() $X$
the suspension spectrum of
$X$
the suspension spectrum of
![]() $EG_{+}$
. Using that
$EG_{+}$
. Using that
![]() $E\simeq F(EG_{+},E)$
by assumption, it follows that
$E\simeq F(EG_{+},E)$
by assumption, it follows that
![]() $E$
is naturally a retract of the function spectrum
$E$
is naturally a retract of the function spectrum
![]() $F(G/N_{+},E)$
. Hence it suffices to show that
$F(G/N_{+},E)$
. Hence it suffices to show that
![]() $F(G/N_{+},E)\wedge e_{V}\simeq F(G/N_{+},E\wedge e_{V})$
is trivial. But this follows from the fact that
$F(G/N_{+},E)\wedge e_{V}\simeq F(G/N_{+},E\wedge e_{V})$
is trivial. But this follows from the fact that
![]() $e_{V}$
is trivial when restricted to
$e_{V}$
is trivial when restricted to
![]() $N$
-spectra (as
$N$
-spectra (as
![]() $V^{N}\neq 0$
), since the functor
$V^{N}\neq 0$
), since the functor
![]() $F(G/N_{+},-)$
is equivalent to the composition of the restriction to
$F(G/N_{+},-)$
is equivalent to the composition of the restriction to
![]() $N$
-spectra followed by coinduction back up to
$N$
-spectra followed by coinduction back up to
![]() $G$
-spectra.◻
$G$
-spectra.◻
This finishes the proof of Theorem 6.12.◻
Example 6.14. We note that the corresponding vanishing statement for the Tate construction does not hold. Indeed, if
![]() $G$
is a compact Lie group which is not finite, then
$G$
is a compact Lie group which is not finite, then
![]() $\unicode[STIX]{x1D70B}_{\ast }(H\mathbb{Q}^{hG})=H^{-\ast }(BG;\mathbb{Q})$
is non-zero in arbitrarily large negative degrees. The norm sequence [Reference Greenlees and MayGM95b, p. 5] shows that
$\unicode[STIX]{x1D70B}_{\ast }(H\mathbb{Q}^{hG})=H^{-\ast }(BG;\mathbb{Q})$
is non-zero in arbitrarily large negative degrees. The norm sequence [Reference Greenlees and MayGM95b, p. 5] shows that
![]() $H^{-\ast }(BG)=H\mathbb{Q}_{\ast }^{hG}\rightarrow H\mathbb{Q}_{\ast }^{tG}$
is an isomorphism in negative degrees, so in particular
$H^{-\ast }(BG)=H\mathbb{Q}_{\ast }^{hG}\rightarrow H\mathbb{Q}_{\ast }^{tG}$
is an isomorphism in negative degrees, so in particular
![]() $H\mathbb{Q}_{\ast }^{tG}\neq 0$
.
$H\mathbb{Q}_{\ast }^{tG}\neq 0$
.
6.5 Reduction to extensions of
 $p$
-groups by abelian groups
$p$
-groups by abelian groups
In the final part of this section we show that the change of group results of Proposition 6.4 can be used to reduce Question 6.1 to extensions of finite
![]() $p$
-groups
$p$
-groups
![]() $P$
by abelian compact Lie groups
$P$
by abelian compact Lie groups
![]() $A$
with
$A$
with
![]() $|\unicode[STIX]{x1D70B}_{0}(A)|$
coprime to
$|\unicode[STIX]{x1D70B}_{0}(A)|$
coprime to
![]() $p$
.
$p$
.
Proposition 6.15. Let
![]() $G$
be a compact Lie group. The poset structure on
$G$
be a compact Lie group. The poset structure on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
is determined by the poset structure on
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
is determined by the poset structure on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{Q,(p)}^{c})$
for all subquotients
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{Q,(p)}^{c})$
for all subquotients
![]() $Q$
of
$Q$
of
![]() $G$
which are extensions of a finite
$G$
which are extensions of a finite
![]() $p$
-group by an abelian compact Lie group
$p$
-group by an abelian compact Lie group
![]() $A$
with
$A$
with
![]() $|\unicode[STIX]{x1D70B}_{0}(A)|$
coprime to
$|\unicode[STIX]{x1D70B}_{0}(A)|$
coprime to
![]() $p$
.
$p$
.
Proof. Recall that by Proposition 6.4(i) and Corollary 6.9, a complete understanding of the poset structure on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
will follow from understanding inclusions
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
will follow from understanding inclusions
![]() $P_{H}(K,n+i)\subseteq P_{H}(H,n)$
, where
$P_{H}(K,n+i)\subseteq P_{H}(H,n)$
, where
![]() $K$
is a
$K$
is a
![]() $p$
-subcotoral subgroup of
$p$
-subcotoral subgroup of
![]() $H$
. We now fix such a
$H$
. We now fix such a
![]() $p$
-subcotoral extension
$p$
-subcotoral extension
![]() $K\subseteq H$
and consider the commutator subgroup
$K\subseteq H$
and consider the commutator subgroup
![]() $C=[{\mathcal{O}}(H),{\mathcal{O}}(H)]$
of the minimal normal subgroup
$C=[{\mathcal{O}}(H),{\mathcal{O}}(H)]$
of the minimal normal subgroup
![]() ${\mathcal{O}}(H)$
of
${\mathcal{O}}(H)$
of
![]() $H$
of
$H$
of
![]() $p$
-power index. Since
$p$
-power index. Since
![]() $K$
is
$K$
is
![]() $p$
-subcotoral, the group
$p$
-subcotoral, the group
![]() ${\mathcal{O}}(K)$
sits cotorally inside
${\mathcal{O}}(K)$
sits cotorally inside
![]() ${\mathcal{O}}(H)$
. Hence, it must contain the commutator subgroup
${\mathcal{O}}(H)$
. Hence, it must contain the commutator subgroup
![]() $C$
. It follows that so does
$C$
. It follows that so does
![]() $K$
. Moreover, since
$K$
. Moreover, since
![]() ${\mathcal{O}}(H)$
is normal in
${\mathcal{O}}(H)$
is normal in
![]() $H$
and
$H$
and
![]() $C$
is preserved by any automorphism of
$C$
is preserved by any automorphism of
![]() ${\mathcal{O}}(H)$
, it follows that
${\mathcal{O}}(H)$
, it follows that
![]() $C$
is also normal in
$C$
is also normal in
![]() $H$
. Thus we can apply part (ii) of Proposition 6.4 to find that there is an inclusion
$H$
. Thus we can apply part (ii) of Proposition 6.4 to find that there is an inclusion
![]() $P_{H}(K,n+i)\subseteq P_{H}(H,n)$
if and only if there is an inclusion
$P_{H}(K,n+i)\subseteq P_{H}(H,n)$
if and only if there is an inclusion
![]() $P_{H/C}(K/C,n+i)\subseteq P_{H/C}(H/C,n)$
.
$P_{H/C}(K/C,n+i)\subseteq P_{H/C}(H/C,n)$
.
Now the group
![]() $H/C$
sits in the short exact sequence
$H/C$
sits in the short exact sequence
The group
![]() $P=H/{\mathcal{O}}(H)$
is a finite
$P=H/{\mathcal{O}}(H)$
is a finite
![]() $p$
-group. Moreover,
$p$
-group. Moreover,
![]() $A={\mathcal{O}}(H)/C$
is an abelian compact Lie group whose group of components
$A={\mathcal{O}}(H)/C$
is an abelian compact Lie group whose group of components
![]() $\unicode[STIX]{x1D70B}_{0}(A)$
is
$\unicode[STIX]{x1D70B}_{0}(A)$
is
![]() $p$
-perfect since it is a quotient of the
$p$
-perfect since it is a quotient of the
![]() $p$
-perfect group
$p$
-perfect group
![]() $\unicode[STIX]{x1D70B}_{0}({\mathcal{O}}(H))$
. Thus, the order of
$\unicode[STIX]{x1D70B}_{0}({\mathcal{O}}(H))$
. Thus, the order of
![]() $\unicode[STIX]{x1D70B}_{0}(A)$
is coprime to
$\unicode[STIX]{x1D70B}_{0}(A)$
is coprime to
![]() $p$
. This yields the desired reduction.◻
$p$
. This yields the desired reduction.◻
Remark 6.16. If
![]() $G$
is finite, the poset structure on
$G$
is finite, the poset structure on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
is in fact determined by the poset structure on
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
is in fact determined by the poset structure on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{Q,(p)}^{c})$
for all subquotients
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{Q,(p)}^{c})$
for all subquotients
![]() $Q$
that are
$Q$
that are
![]() $p$
-groups, see [Reference Balmer and SandersBS17, Proposition 6.11]. This is because for every
$p$
-groups, see [Reference Balmer and SandersBS17, Proposition 6.11]. This is because for every
![]() $p$
-subnormal inclusion
$p$
-subnormal inclusion
![]() $K\subseteq H$
, the
$K\subseteq H$
, the
![]() $p$
-perfection
$p$
-perfection
![]() ${\mathcal{O}}(H)$
is a normal subgroup of
${\mathcal{O}}(H)$
is a normal subgroup of
![]() $H$
that is contained in
$H$
that is contained in
![]() $K$
and such that
$K$
and such that
![]() $H/{\mathcal{O}}(H)$
is a
$H/{\mathcal{O}}(H)$
is a
![]() $p$
-group. By Proposition 6.4, there is an inclusion
$p$
-group. By Proposition 6.4, there is an inclusion
![]() $P_{H}(K,n+i)\subseteq P_{H}(H,n)$
if and only if there is an inclusion
$P_{H}(K,n+i)\subseteq P_{H}(H,n)$
if and only if there is an inclusion
![]() $P_{H/{\mathcal{O}}(H)}(K/{\mathcal{O}}(H),n+i)\subseteq P_{H/{\mathcal{O}}(H)}(H/{\mathcal{O}}(H),n)$
, reducing the problem to the poset structure on
$P_{H/{\mathcal{O}}(H)}(K/{\mathcal{O}}(H),n+i)\subseteq P_{H/{\mathcal{O}}(H)}(H/{\mathcal{O}}(H),n)$
, reducing the problem to the poset structure on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{H/{\mathcal{O}}(H),(p)}^{c})$
.
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{H/{\mathcal{O}}(H),(p)}^{c})$
.
One could hope that for compact Lie groups, the poset structure can be reduced to the poset structure for those subquotients which are extensions of finite
![]() $p$
-groups by tori (i.e.,
$p$
-groups by tori (i.e.,
![]() $p$
-toral groups), but we have been unable to see this. The problem is that given a
$p$
-toral groups), but we have been unable to see this. The problem is that given a
![]() $p$
-subcotoral inclusion
$p$
-subcotoral inclusion
![]() $K\subseteq H$
, in general there exists no subgroup
$K\subseteq H$
, in general there exists no subgroup
![]() $K^{\prime }\subseteq K$
that is normal in
$K^{\prime }\subseteq K$
that is normal in
![]() $H$
and for which
$H$
and for which
![]() $H/K^{\prime }$
is a
$H/K^{\prime }$
is a
![]() $p$
-toral group.
$p$
-toral group.
7 Abelian compact Lie groups
The results of the previous section allow us to give a complete description of the Balmer spectrum for abelian compact Lie groups
![]() $A$
. Recall from § 5 that the topology on
$A$
. Recall from § 5 that the topology on
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{A,(p)}^{c})$
and the classification of its tt-ideals are determined by the set of admissible functions
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{A,(p)}^{c})$
and the classification of its tt-ideals are determined by the set of admissible functions
![]() $f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
and the Hausdorff topology on
$f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
and the Hausdorff topology on
![]() $\operatorname{Sub}(A)$
. We say that a compact Lie group is p-toral if it is an extension of a finite
$\operatorname{Sub}(A)$
. We say that a compact Lie group is p-toral if it is an extension of a finite
![]() $p$
-group by a torus, and that an inclusion
$p$
-group by a torus, and that an inclusion
![]() $K\subseteq H$
is
$K\subseteq H$
is
![]() $p$
-cotoral if it is normal with
$p$
-cotoral if it is normal with
![]() $p$
-toral quotient
$p$
-toral quotient
![]() $H/K$
. Furthermore, given a finite abelian
$H/K$
. Furthermore, given a finite abelian
![]() $p$
-group
$p$
-group
![]() $A^{\prime }$
, we write
$A^{\prime }$
, we write
![]() $rk_{p}(A^{\prime })$
for the rank of
$rk_{p}(A^{\prime })$
for the rank of
![]() $A^{\prime }$
, i.e., the dimension of
$A^{\prime }$
, i.e., the dimension of
![]() $A^{\prime }\otimes \mathbb{Z}/p$
over
$A^{\prime }\otimes \mathbb{Z}/p$
over
![]() $\mathbb{Z}/p$
.
$\mathbb{Z}/p$
.
Theorem 7.1. Let
![]() $A$
be an abelian compact Lie group. A function
$A$
be an abelian compact Lie group. A function
![]() $f:\operatorname{Sub}(A)/A\rightarrow \overline{\mathbb{N}}$
is admissible if and only if for all
$f:\operatorname{Sub}(A)/A\rightarrow \overline{\mathbb{N}}$
is admissible if and only if for all
![]() $p$
-cotoral inclusions
$p$
-cotoral inclusions
![]() $K\subseteq H$
of closed subgroups of
$K\subseteq H$
of closed subgroups of
![]() $A$
, the inequality
$A$
, the inequality
holds.
For later reference, we call (⋆) the
![]() $p$
-cotoral rank property.
$p$
-cotoral rank property.
Proof. Recall that
![]() $f$
was defined to be admissible if for all subgroups
$f$
was defined to be admissible if for all subgroups
![]() $K$
and
$K$
and
![]() $H$
there is no inclusion
$H$
there is no inclusion
![]() $P_{A}(K,f(K))\subseteq P_{A}(H,f(H)+1)$
if
$P_{A}(K,f(K))\subseteq P_{A}(H,f(H)+1)$
if
![]() $f(H)<\infty$
. By part (i) of Theorem 6.2, we know that such an inclusion can only happen if
$f(H)<\infty$
. By part (i) of Theorem 6.2, we know that such an inclusion can only happen if
![]() $K$
is a
$K$
is a
![]() $p$
-subcotoral subgroup of
$p$
-subcotoral subgroup of
![]() $H$
. We claim that for abelian groups,
$H$
. We claim that for abelian groups,
![]() $K$
being
$K$
being
![]() $p$
-subcotoral in
$p$
-subcotoral in
![]() $H$
is equivalent to the quotient
$H$
is equivalent to the quotient
![]() $H/K$
being
$H/K$
being
![]() $p$
-toral: if there is a cotoral inclusion
$p$
-toral: if there is a cotoral inclusion
![]() ${\mathcal{O}}(K)\subseteq {\mathcal{O}}(H)$
, then
${\mathcal{O}}(K)\subseteq {\mathcal{O}}(H)$
, then
![]() ${\mathcal{O}}(K)\subseteq H$
is a
${\mathcal{O}}(K)\subseteq H$
is a
![]() $p$
-toral extension, and hence so is
$p$
-toral extension, and hence so is
![]() $K\subseteq H$
since the quotient of a
$K\subseteq H$
since the quotient of a
![]() $p$
-toral group is again
$p$
-toral group is again
![]() $p$
-toral. Conversely, if
$p$
-toral. Conversely, if
![]() $H/K$
is
$H/K$
is
![]() $p$
-toral, then so is
$p$
-toral, then so is
![]() $H/{\mathcal{O}}(K)$
as an extension of a
$H/{\mathcal{O}}(K)$
as an extension of a
![]() $p$
-toral group by a finite
$p$
-toral group by a finite
![]() $p$
-group. Thus,
$p$
-group. Thus,
![]() $H/\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K))$
is a finite
$H/\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K))$
is a finite
![]() $p$
-group and
$p$
-group and
![]() $\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K))$
contains
$\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K))$
contains
![]() ${\mathcal{O}}(H)$
as a finite index subgroup. Furthermore,
${\mathcal{O}}(H)$
as a finite index subgroup. Furthermore,
![]() $K/(K\cap {\mathcal{O}}(H))$
is a finite
$K/(K\cap {\mathcal{O}}(H))$
is a finite
![]() $p$
-group, since it is isomorphic to a subgroup of
$p$
-group, since it is isomorphic to a subgroup of
![]() $H/{\mathcal{O}}(H)$
. Thus,
$H/{\mathcal{O}}(H)$
. Thus,
![]() $K\cap {\mathcal{O}}(H)$
contains
$K\cap {\mathcal{O}}(H)$
contains
![]() ${\mathcal{O}}(K)$
. It follows that
${\mathcal{O}}(K)$
. It follows that
![]() ${\mathcal{O}}(H)/{\mathcal{O}}(K)$
is a finite index subgroup of the torus
${\mathcal{O}}(H)/{\mathcal{O}}(K)$
is a finite index subgroup of the torus
![]() $\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K))/K$
, and hence
$\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K))/K$
, and hence
![]() ${\mathcal{O}}(H)=\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K))$
. This proves the claim.
${\mathcal{O}}(H)=\unicode[STIX]{x1D714}_{H}({\mathcal{O}}(K))$
. This proves the claim.
Hence, it remains to show that for a
![]() $p$
-cotoral inclusion
$p$
-cotoral inclusion
![]() $K\subseteq H$
, we have
$K\subseteq H$
, we have
and
The first statement follows from the fact that there is a chain of inclusions
where each
![]() $H_{i}/H_{i-1}$
is
$H_{i}/H_{i-1}$
is
![]() $p$
-power cyclic. Hence, by parts (iii) and (iv) of Theorem 6.2, we find that
$p$
-power cyclic. Hence, by parts (iii) and (iv) of Theorem 6.2, we find that
 $$\begin{eqnarray}\displaystyle P_{A}(K,n+rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K))) & \subseteq & \displaystyle P_{A}(\unicode[STIX]{x1D714}_{H}(K),n+rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K)))\nonumber\\ \displaystyle & \subseteq & \displaystyle P_{A}(H_{1},n+rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K))-1)\nonumber\\ \displaystyle & \subseteq & \displaystyle \cdots \subseteq P_{A}(H,n),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{A}(K,n+rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K))) & \subseteq & \displaystyle P_{A}(\unicode[STIX]{x1D714}_{H}(K),n+rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K)))\nonumber\\ \displaystyle & \subseteq & \displaystyle P_{A}(H_{1},n+rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K))-1)\nonumber\\ \displaystyle & \subseteq & \displaystyle \cdots \subseteq P_{A}(H,n),\nonumber\end{eqnarray}$$
as desired. Finally, that
![]() $P_{A}(K,n+rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K))-1)\not \subseteq P_{A}(H,n)$
follows from part (vi) of Theorem 6.2 and part (iii) of Proposition 6.4 applied to the subgroup chain
$P_{A}(K,n+rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K))-1)\not \subseteq P_{A}(H,n)$
follows from part (vi) of Theorem 6.2 and part (iii) of Proposition 6.4 applied to the subgroup chain
![]() $K\subseteq \unicode[STIX]{x1D714}_{H}(K)\subseteq H$
.◻
$K\subseteq \unicode[STIX]{x1D714}_{H}(K)\subseteq H$
.◻
Hence, by Theorem 5.3, the tt-ideals of
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{A,(p)}^{c})$
correspond bijectively to upper semi-continuous functions
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{A,(p)}^{c})$
correspond bijectively to upper semi-continuous functions
![]() $\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
satisfying property (⋆) above. In fact, it turns out that property
$\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
satisfying property (⋆) above. In fact, it turns out that property
![]() $(\star )$
implies upper semi-continuity.
$(\star )$
implies upper semi-continuity.
Lemma 7.2. Let
![]() $A$
be an abelian compact Lie group and
$A$
be an abelian compact Lie group and
![]() $f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
a function such that
$f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
a function such that
![]() $f(K)\leqslant f(H)$
for every cotoral inclusion
$f(K)\leqslant f(H)$
for every cotoral inclusion
![]() $K\subseteq H$
. Then
$K\subseteq H$
. Then
![]() $f$
is upper semi-continuous.
$f$
is upper semi-continuous.
Proof. Let
![]() $n\in \overline{\mathbb{N}}$
and
$n\in \overline{\mathbb{N}}$
and
![]() $H$
be a closed subgroup of
$H$
be a closed subgroup of
![]() $A$
such that
$A$
such that
![]() $f(H)<n$
. We have to show that some open neighbourhood of
$f(H)<n$
. We have to show that some open neighbourhood of
![]() $H$
is also contained in
$H$
is also contained in
![]() $f^{-1}([0,n))$
. We claim that the set of subgroups
$f^{-1}([0,n))$
. We claim that the set of subgroups
![]() $K$
of
$K$
of
![]() $H$
for which
$H$
for which
![]() $K\subseteq H$
is a cotoral inclusion forms an open neighbourhood of
$K\subseteq H$
is a cotoral inclusion forms an open neighbourhood of
![]() $H$
in
$H$
in
![]() $\operatorname{Sub}(A)$
. Note that for any such
$\operatorname{Sub}(A)$
. Note that for any such
![]() $K$
we have
$K$
we have
![]() $f(K)\leqslant f(H)<n$
by assumption, and hence
$f(K)\leqslant f(H)<n$
by assumption, and hence
![]() $K\in f^{-1}([0,n))$
. Thus, we are done once we have shown the claim. Now, by the Montgomery–Zippin theorem (see Proposition 4.1), the set of all subgroups of
$K\in f^{-1}([0,n))$
. Thus, we are done once we have shown the claim. Now, by the Montgomery–Zippin theorem (see Proposition 4.1), the set of all subgroups of
![]() $H$
is open in
$H$
is open in
![]() $\operatorname{Sub}(A)$
; hence it suffices to show that the set of cotoral subgroups
$\operatorname{Sub}(A)$
; hence it suffices to show that the set of cotoral subgroups
![]() $K\subseteq H$
is open in
$K\subseteq H$
is open in
![]() $\operatorname{Sub}(H)$
. But this follows from the fact that the projection
$\operatorname{Sub}(H)$
. But this follows from the fact that the projection
![]() $H\rightarrow \unicode[STIX]{x1D70B}_{0}(H)$
induces a continuous map
$H\rightarrow \unicode[STIX]{x1D70B}_{0}(H)$
induces a continuous map
![]() $\operatorname{Sub}(H)\rightarrow \operatorname{Sub}(\unicode[STIX]{x1D70B}_{0}(H))$
and the cotoral subgroups are exactly the ones that surject onto
$\operatorname{Sub}(H)\rightarrow \operatorname{Sub}(\unicode[STIX]{x1D70B}_{0}(H))$
and the cotoral subgroups are exactly the ones that surject onto
![]() $\unicode[STIX]{x1D70B}_{0}(H)$
.◻
$\unicode[STIX]{x1D70B}_{0}(H)$
.◻
Corollary 7.3. Let
![]() $A$
be an abelian compact Lie group. Then we have:
$A$
be an abelian compact Lie group. Then we have:
(i) the tt-ideals of
 $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{A,(p)}^{c})$
correspond bijectively to functions
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{A,(p)}^{c})$
correspond bijectively to functions
 $f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
satisfying the
$f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
satisfying the
 $p$
-cotoral rank property (⋆) above;
$p$
-cotoral rank property (⋆) above;(ii) given a function
 $f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
, there exists a finite
$f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
, there exists a finite
 $G$
-spectrum
$G$
-spectrum
 $X$
with
$X$
with
 $\text{type}_{X}=f$
if and only if
$\text{type}_{X}=f$
if and only if
 $f$
satisfies the
$f$
satisfies the
 $p$
-cotoral rank property (⋆) above and is locally constant.
$p$
-cotoral rank property (⋆) above and is locally constant.
Proof. Every function
![]() $f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
satisfying the
$f:\operatorname{Sub}(A)\rightarrow \overline{\mathbb{N}}$
satisfying the
![]() $p$
-cotoral rank property in particular satisfies the conditions for Lemma 7.2. Hence, the corollary is a direct consequence of Theorems 5.3 and 7.1 and this lemma.◻
$p$
-cotoral rank property in particular satisfies the conditions for Lemma 7.2. Hence, the corollary is a direct consequence of Theorems 5.3 and 7.1 and this lemma.◻
Example 7.4 (
 $A=\mathbb{T}$
).
$A=\mathbb{T}$
).
The subgroups of
![]() $\mathbb{T}$
are given by the finite cyclic subgroups
$\mathbb{T}$
are given by the finite cyclic subgroups
![]() $C_{n}$
for
$C_{n}$
for
![]() $n\geqslant 1$
, and the full group
$n\geqslant 1$
, and the full group
![]() $\mathbb{T}$
. Therefore, we can identify
$\mathbb{T}$
. Therefore, we can identify
![]() $\operatorname{Sub}(\mathbb{T})$
with
$\operatorname{Sub}(\mathbb{T})$
with
![]() $\{1,2,\ldots \}\cup \{\infty \}$
. The tt-ideals of
$\{1,2,\ldots \}\cup \{\infty \}$
. The tt-ideals of
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{\mathbb{T},(p)}^{c})$
hence correspond to functions
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{\mathbb{T},(p)}^{c})$
hence correspond to functions
such that
![]() $f(\infty )\geqslant f(n)$
for all
$f(\infty )\geqslant f(n)$
for all
![]() $n$
, and
$n$
, and
![]() $f(p^{k}\cdot n)\,+\,1\geqslant f(n)$
for all
$f(p^{k}\cdot n)\,+\,1\geqslant f(n)$
for all
![]() $n$
and
$n$
and
![]() $k$
. The tt-ideal corresponding to such a function is finitely generated if and only if
$k$
. The tt-ideal corresponding to such a function is finitely generated if and only if
![]() $f(n)=f(\infty )$
for almost all
$f(n)=f(\infty )$
for almost all
![]() $n$
. See Figure 3 for an illustration.
$n$
. See Figure 3 for an illustration.

Figure 3.
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{\mathbb{T},(p)}^{c})$
: This figure depicts the poset structure of
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{\mathbb{T},(p)}^{c})$
: This figure depicts the poset structure of
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{\mathbb{T},(p)}^{c})$
, inclusions going from left to right and top to bottom. Each natural number
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{\mathbb{T},(p)}^{c})$
, inclusions going from left to right and top to bottom. Each natural number
![]() $m$
that is not divisible by
$m$
that is not divisible by
![]() $p$
gives rise to a page as above, the different pages overlapping in the primes
$p$
gives rise to a page as above, the different pages overlapping in the primes
![]() $P_{\mathbb{T}}(\mathbb{T},n)$
of the full group
$P_{\mathbb{T}}(\mathbb{T},n)$
of the full group
![]() $\mathbb{T}$
. The inclusions
$\mathbb{T}$
. The inclusions
![]() $P_{\mathbb{T}}(C_{p^{k}m},n+1)\subseteq P_{\mathbb{T}}(C_{p^{k+l}m},n)$
with
$P_{\mathbb{T}}(C_{p^{k}m},n+1)\subseteq P_{\mathbb{T}}(C_{p^{k+l}m},n)$
with
![]() $l>3$
are omitted in the picture, while the dashed lines indicate the inclusions
$l>3$
are omitted in the picture, while the dashed lines indicate the inclusions
![]() $P_{\mathbb{T}}(C_{p^{k}m},n)\subseteq P_{\mathbb{T}}(\mathbb{T},n)$
for all
$P_{\mathbb{T}}(C_{p^{k}m},n)\subseteq P_{\mathbb{T}}(\mathbb{T},n)$
for all
![]() $k\in \mathbb{N}$
.
$k\in \mathbb{N}$
.
Remark 7.5. One might wonder whether upper semi-continuity is always implied by admissibility, but this is not the case in general. We consider the orthogonal group
![]() $O(2)$
for any prime
$O(2)$
for any prime
![]() $p$
and the function
$p$
and the function
defined by
Then
![]() $f$
is admissible, since no subgroup
$f$
is admissible, since no subgroup
![]() $K$
of
$K$
of
![]() $O(2)$
sits cotorally inside
$O(2)$
sits cotorally inside
![]() $O(2)$
, and therefore
$O(2)$
, and therefore
![]() $P_{O(2)}(K,1)\not \subseteq P_{O(2)}(O(2),1)$
by part (ii) of Theorem 6.2. But
$P_{O(2)}(K,1)\not \subseteq P_{O(2)}(O(2),1)$
by part (ii) of Theorem 6.2. But
![]() $f$
is not upper semi-continuous as the preimage of
$f$
is not upper semi-continuous as the preimage of
![]() $[0,1)$
is not open.
$[0,1)$
is not open.
8 Away from
 $|G|$
$|G|$
Finally, we explain that for a fixed compact Lie group
![]() $G$
, the results in this paper determine the Balmer spectrum of
$G$
, the results in this paper determine the Balmer spectrum of
![]() $\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
for all but finitely many
$\operatorname{Spc}({\mathcal{S}}{\mathcal{H}}_{G,(p)}^{c})$
for all but finitely many
![]() $p$
.
$p$
.
It is a result of tom Dieck [Reference tom DiecktD77, Theorem 1] that the set of orders of finite Weyl groups
is bounded. We denote the least common multiple of this set by
![]() $|G|$
and call it the order of
$|G|$
and call it the order of
![]() $G$
. Note that for finite
$G$
. Note that for finite
![]() $G$
this coincides with the usual definition of
$G$
this coincides with the usual definition of
![]() $|G|$
. Then we have the following theorem.
$|G|$
. Then we have the following theorem.
Theorem 8.1. Let
![]() $G$
be a compact Lie group and
$G$
be a compact Lie group and
![]() $p$
be a prime not dividing the order
$p$
be a prime not dividing the order
![]() $|G|$
. Then a function
$|G|$
. Then a function
![]() $f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
is admissible if and only if for all normal inclusions
$f:\operatorname{Sub}(G)/G\rightarrow \overline{\mathbb{N}}$
is admissible if and only if for all normal inclusions
![]() $K\subseteq H$
with
$K\subseteq H$
with
![]() $H/K$
an abelian
$H/K$
an abelian
![]() $p$
-toral group, the inequality
$p$
-toral group, the inequality
holds.
In other words, if
![]() $p$
does not divide
$p$
does not divide
![]() $|G|$
, there is an inclusion
$|G|$
, there is an inclusion
if and only if
![]() $K$
is
$K$
is
![]() $G$
-conjugate to a normal subgroup
$G$
-conjugate to a normal subgroup
![]() $K^{g}$
of
$K^{g}$
of
![]() $H$
with
$H$
with
![]() $H/K^{g}$
an abelian
$H/K^{g}$
an abelian
![]() $p$
-toral group such that
$p$
-toral group such that
![]() $i\geqslant rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K^{g}))$
. In particular, this determines the Balmer spectrum of finite
$i\geqslant rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K^{g}))$
. In particular, this determines the Balmer spectrum of finite
![]() $G$
-spectra away from the order
$G$
-spectra away from the order
![]() $|G|$
. Note that for finite groups
$|G|$
. Note that for finite groups
![]() $G$
the statement of Theorem 8.1 follows directly from Theorem 6.2, since for
$G$
the statement of Theorem 8.1 follows directly from Theorem 6.2, since for
![]() $p$
not dividing
$p$
not dividing
![]() $|G|$
there exist no proper
$|G|$
there exist no proper
![]() $p$
-subcotoral inclusions
$p$
-subcotoral inclusions
![]() $K\subseteq H$
. For general compact Lie groups we still need to take care of the maximal torus and its
$K\subseteq H$
. For general compact Lie groups we still need to take care of the maximal torus and its
![]() $p$
-toral subgroups and hence rely on understanding the inclusions for abelian groups as worked out in the previous section.
$p$
-toral subgroups and hence rely on understanding the inclusions for abelian groups as worked out in the previous section.
Proof of Theorem 8.1.
We first show that when
![]() $p$
does not divide the order
$p$
does not divide the order
![]() $|G|$
and
$|G|$
and
![]() $K\subseteq H$
is a
$K\subseteq H$
is a
![]() $p$
-subcotoral inclusion of closed subgroups of
$p$
-subcotoral inclusion of closed subgroups of
![]() $G$
, then
$G$
, then
![]() $K$
is normal in
$K$
is normal in
![]() $H$
and the quotient
$H$
and the quotient
![]() $H/K$
is an abelian
$H/K$
is an abelian
![]() $p$
-toral group. To see this, we first note that when
$p$
-toral group. To see this, we first note that when
![]() $K\subseteq H$
is
$K\subseteq H$
is
![]() $p$
-subcotoral,
$p$
-subcotoral,
![]() $K$
and
$K$
and
![]() $H$
in particular have the same
$H$
in particular have the same
![]() $p$
-perfection inside
$p$
-perfection inside
![]() $G$
, i.e.,
$G$
, i.e.,
![]() $\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(K))=\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
. We recall from [Reference tom DiecktD75b, Theorem 4] that the set of conjugacy classes of subgroups of
$\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(K))=\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(H))$
. We recall from [Reference tom DiecktD75b, Theorem 4] that the set of conjugacy classes of subgroups of
![]() $G$
sharing this
$G$
sharing this
![]() $p$
-perfection with
$p$
-perfection with
![]() $H$
and
$H$
and
![]() $K$
has a unique maximal element
$K$
has a unique maximal element
![]() $M$
, which is characterized by the property that its Weyl group is finite and of order coprime to
$M$
, which is characterized by the property that its Weyl group is finite and of order coprime to
![]() $p$
. Without loss of generality, we can choose an
$p$
. Without loss of generality, we can choose an
![]() $M$
which contains
$M$
which contains
![]() $H$
. Since
$H$
. Since
![]() ${\mathcal{O}}(M)$
has the same
${\mathcal{O}}(M)$
has the same
![]() $p$
-perfection as
$p$
-perfection as
![]() $M$
and is contained inside
$M$
and is contained inside
![]() $M$
with finite
$M$
with finite
![]() $p$
-power index, it follows that
$p$
-power index, it follows that
![]() ${\mathcal{O}}(M)$
must have finite Weyl group (since otherwise
${\mathcal{O}}(M)$
must have finite Weyl group (since otherwise
![]() $\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(M))$
could not be contained in a subgroup conjugate to
$\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(M))$
could not be contained in a subgroup conjugate to
![]() $M$
). Now, by assumption,
$M$
). Now, by assumption,
![]() $|W_{G}{\mathcal{O}}(M)|$
is coprime to
$|W_{G}{\mathcal{O}}(M)|$
is coprime to
![]() $p$
, and thus
$p$
, and thus
![]() $M$
must equal
$M$
must equal
![]() ${\mathcal{O}}(M)$
. But this implies that
${\mathcal{O}}(M)$
. But this implies that
![]() $H$
is contained in
$H$
is contained in
![]() ${\mathcal{O}}(M)=\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(K))$
. Thus, there is a chain of inclusions
${\mathcal{O}}(M)=\unicode[STIX]{x1D714}_{G}({\mathcal{O}}(K))$
. Thus, there is a chain of inclusions
Since
![]() ${\mathcal{O}}(K)\subseteq \unicode[STIX]{x1D714}_{G}({\mathcal{O}}(K))$
is a cotoral inclusion, we find that
${\mathcal{O}}(K)\subseteq \unicode[STIX]{x1D714}_{G}({\mathcal{O}}(K))$
is a cotoral inclusion, we find that
![]() $K$
must be normal in
$K$
must be normal in
![]() $H$
with abelian quotient. Since
$H$
with abelian quotient. Since
![]() $K$
is further
$K$
is further
![]() $p$
-subcotoral in
$p$
-subcotoral in
![]() $H$
, the quotient must be a
$H$
, the quotient must be a
![]() $p$
-toral compact Lie group as desired.
$p$
-toral compact Lie group as desired.
Now we let
![]() $K$
and
$K$
and
![]() $H$
be arbitrary closed subgroups of
$H$
be arbitrary closed subgroups of
![]() $G$
and show the statement of the theorem, i.e., that there is an inclusion
$G$
and show the statement of the theorem, i.e., that there is an inclusion
![]() $P_{G}(K,n\,+\,i)\subseteq P_{G}(H,n)$
if and only if
$P_{G}(K,n\,+\,i)\subseteq P_{G}(H,n)$
if and only if
![]() $K$
is
$K$
is
![]() $G$
-conjugate to a normal subgroup
$G$
-conjugate to a normal subgroup
![]() $K^{g}$
of
$K^{g}$
of
![]() $H$
with
$H$
with
![]() $H/K^{g}$
an abelian
$H/K^{g}$
an abelian
![]() $p$
-toral group such that
$p$
-toral group such that
![]() $i\geqslant rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K^{g}))$
. By Proposition 6.4 we know that there is an inclusion
$i\geqslant rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K^{g}))$
. By Proposition 6.4 we know that there is an inclusion
![]() $P_{G}(K,n\,+\,i)\subseteq P_{G}(H,n)$
if and only if there is an inclusion
$P_{G}(K,n\,+\,i)\subseteq P_{G}(H,n)$
if and only if there is an inclusion
![]() $P_{H}(K^{g},n+i)\subseteq P_{H}(H,n)$
for some conjugate
$P_{H}(K^{g},n+i)\subseteq P_{H}(H,n)$
for some conjugate
![]() $K^{g}$
contained in
$K^{g}$
contained in
![]() $H$
. Theorem 6.2 shows that the latter inclusion can only happen when
$H$
. Theorem 6.2 shows that the latter inclusion can only happen when
![]() $K^{g}\subseteq H$
is
$K^{g}\subseteq H$
is
![]() $p$
-subcotoral, which, as we just saw, implies that
$p$
-subcotoral, which, as we just saw, implies that
![]() $K^{g}\subseteq H$
is normal with abelian
$K^{g}\subseteq H$
is normal with abelian
![]() $p$
-toral quotient. Applying Proposition 6.4 once more gives that in this case there is an inclusion
$p$
-toral quotient. Applying Proposition 6.4 once more gives that in this case there is an inclusion
![]() $P_{H}(K^{g},n+i)\subseteq P_{H}(H,n)$
if and only if there is an inclusion
$P_{H}(K^{g},n+i)\subseteq P_{H}(H,n)$
if and only if there is an inclusion
![]() $P_{H/K^{g}}(K^{g}/K^{g},n+i)\subseteq P_{H/K^{g}}(H/K^{g},n)$
. Since the group
$P_{H/K^{g}}(K^{g}/K^{g},n+i)\subseteq P_{H/K^{g}}(H/K^{g},n)$
. Since the group
![]() $H/K^{g}$
is abelian
$H/K^{g}$
is abelian
![]() $p$
-toral, Theorem 7.1 implies that the latter inclusion happens if and only if
$p$
-toral, Theorem 7.1 implies that the latter inclusion happens if and only if
![]() $i\geqslant rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K^{g}))$
, which finishes the proof.◻
$i\geqslant rk_{p}(\unicode[STIX]{x1D70B}_{0}(H/K^{g}))$
, which finishes the proof.◻
Acknowledgements
We would like to thank the two anonymous referees for helpful comments on an earlier version of this paper. All three authors are grateful to the Isaac Newton Institute (funded by EPSRC Grant number EP/R014604/1) for the opportunity to talk during the Homotopy Harnessing Higher Structures Programme.
Appendix A
In this appendix we give the proof of Lemma 3.9, the statement of which we recall for convenience.
Lemma A.1. Let
![]() $H$
be a closed subgroup of a compact Lie group
$H$
be a closed subgroup of a compact Lie group
![]() $G$
, and let
$G$
, and let
![]() $X$
be a finite
$X$
be a finite
![]() $H$
-spectrum. Then the following hold.
$H$
-spectrum. Then the following hold.
(i) The type of
 $\unicode[STIX]{x1D6F7}^{H}(\operatorname{Ind}_{H}^{G}(X))$
is equal to the type of
$\unicode[STIX]{x1D6F7}^{H}(\operatorname{Ind}_{H}^{G}(X))$
is equal to the type of
 $\unicode[STIX]{x1D6F7}^{H}(X)$
.
$\unicode[STIX]{x1D6F7}^{H}(X)$
.(ii) If
 $K$
is another closed subgroup of
$K$
is another closed subgroup of
 $G$
, then the type of
$G$
, then the type of
 $\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
is at least the minimum of the types of
$\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
is at least the minimum of the types of
 $\unicode[STIX]{x1D6F7}^{K^{\prime }}(X)$
for all subgroups
$\unicode[STIX]{x1D6F7}^{K^{\prime }}(X)$
for all subgroups
 $K^{\prime }$
of
$K^{\prime }$
of
 $H$
that are conjugate to
$H$
that are conjugate to
 $K$
in
$K$
in
 $G$
.
$G$
.(iii) If
 $K$
is not subconjugate to
$K$
is not subconjugate to
 $H$
, then the geometric fixed points
$H$
, then the geometric fixed points
 $\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
are trivial.
$\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(X))$
are trivial.
Remark A.2. Before we prove the lemma, we note that the set of
![]() $H$
-conjugacy classes of such subgroups
$H$
-conjugacy classes of such subgroups
![]() $K^{\prime }$
is always finite, by the following argument. For an element
$K^{\prime }$
is always finite, by the following argument. For an element
![]() $g\in G$
, the conjugate
$g\in G$
, the conjugate
![]() $K^{g}=g^{-1}Kg$
is a subgroup of
$K^{g}=g^{-1}Kg$
is a subgroup of
![]() $H$
if and only if
$H$
if and only if
![]() $gH$
is a
$gH$
is a
![]() $K$
-fixed point in
$K$
-fixed point in
![]() $G/H$
. Moreover, if two elements
$G/H$
. Moreover, if two elements
![]() $g$
and
$g$
and
![]() $\widetilde{g}$
represent the same coset in this
$\widetilde{g}$
represent the same coset in this
![]() $K$
-fixed space, then the conjugates
$K$
-fixed space, then the conjugates
![]() $K^{g}$
and
$K^{g}$
and
![]() $K^{\widetilde{g}}$
are
$K^{\widetilde{g}}$
are
![]() $H$
-conjugate. Hence, one obtains a well-defined surjective map
$H$
-conjugate. Hence, one obtains a well-defined surjective map
This map is not injective, but it becomes so after quotienting out by the residual action of the normalizer
![]() $N_{G}(K)$
on
$N_{G}(K)$
on
![]() $(G/H)^{K}$
. Indeed, if
$(G/H)^{K}$
. Indeed, if
![]() $n\in N_{G}(K)$
, then
$n\in N_{G}(K)$
, then
![]() $K^{ng}=(K^{n})^{g}=K^{g}$
; hence the map factors through the quotient, and if
$K^{ng}=(K^{n})^{g}=K^{g}$
; hence the map factors through the quotient, and if
![]() $K^{g}=(K^{\widetilde{g}})^{h}$
for some
$K^{g}=(K^{\widetilde{g}})^{h}$
for some
![]() $h\in H$
, then
$h\in H$
, then
![]() $\widetilde{g}hg^{-1}\in N_{G}(K)$
and
$\widetilde{g}hg^{-1}\in N_{G}(K)$
and
![]() $(\widetilde{g}hg^{-1})gH=\widetilde{g}H$
. Now, the set
$(\widetilde{g}hg^{-1})gH=\widetilde{g}H$
. Now, the set
![]() $(G/H)^{K}/N_{G}(K)$
is finite as a consequence of the Montgomery–Zippin theorem, see [Reference BredonBre72, Corollary II.5.7]. We note also that this implies that the
$(G/H)^{K}/N_{G}(K)$
is finite as a consequence of the Montgomery–Zippin theorem, see [Reference BredonBre72, Corollary II.5.7]. We note also that this implies that the
![]() $N_{G}(K)$
-orbits of
$N_{G}(K)$
-orbits of
![]() $(G/H)^{K}$
are open, and hence
$(G/H)^{K}$
are open, and hence
![]() $(G/H)^{K}$
decomposes as the topological disjoint union over these.
$(G/H)^{K}$
decomposes as the topological disjoint union over these.
Proof of Lemma 3.9.
Let
![]() $K$
be a closed subgroup of
$K$
be a closed subgroup of
![]() $G$
; later in the proof we check what happens in the special case where
$G$
; later in the proof we check what happens in the special case where
![]() $K=H$
. We start by showing the claims for suspension spectra. Let
$K=H$
. We start by showing the claims for suspension spectra. Let
![]() $A$
be a (not necessarily finite) based
$A$
be a (not necessarily finite) based
![]() $H$
-CW complex and consider the based
$H$
-CW complex and consider the based
![]() $G$
-space
$G$
-space
![]() $G_{+}\wedge _{H}A$
, i.e., the space-level induction of
$G_{+}\wedge _{H}A$
, i.e., the space-level induction of
![]() $A$
to a
$A$
to a
![]() $G$
-space. We want to understand the
$G$
-space. We want to understand the
![]() $K$
-fixed points
$K$
-fixed points
![]() $(G_{+}\wedge _{H}A)^{K}$
. Let
$(G_{+}\wedge _{H}A)^{K}$
. Let
![]() $g_{1},\ldots ,g_{s}\in G$
be a set of representatives of the
$g_{1},\ldots ,g_{s}\in G$
be a set of representatives of the
![]() $N_{G}(K)$
-orbits of
$N_{G}(K)$
-orbits of
![]() $(G/H)^{K}$
, as in the above remark. Note that if
$(G/H)^{K}$
, as in the above remark. Note that if
![]() $n\in N_{G}(K)$
and
$n\in N_{G}(K)$
and
![]() $a\in A^{K^{g_{i}}}$
, then the class
$a\in A^{K^{g_{i}}}$
, then the class
![]() $[(ng_{i},a)]\in G_{+}\wedge _{H}A$
is
$[(ng_{i},a)]\in G_{+}\wedge _{H}A$
is
![]() $K$
-fixed, since
$K$
-fixed, since
The last step uses that
![]() $g_{i}^{-1}n^{-1}kng_{i}\in K^{g_{i}}$
, because
$g_{i}^{-1}n^{-1}kng_{i}\in K^{g_{i}}$
, because
![]() $n$
normalizes
$n$
normalizes
![]() $K$
. Moreover, if
$K$
. Moreover, if
![]() $\widetilde{n}\in N_{H}(K^{g_{i}})$
, then
$\widetilde{n}\in N_{H}(K^{g_{i}})$
, then
![]() $g_{i}\widetilde{n}g_{i}^{-1}\in N_{G}(K)$
and
$g_{i}\widetilde{n}g_{i}^{-1}\in N_{G}(K)$
and
Thus we obtain a continuous map
 $$\begin{eqnarray}\displaystyle \mathop{\vee }_{g_{1},\ldots ,g_{s}}(N_{G}(K)\cdot g_{i})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}} & \rightarrow & \displaystyle (G_{+}\wedge _{H}A)^{K}\nonumber\\ \displaystyle [(ng_{i},a)] & \mapsto & \displaystyle [(ng_{i},a)]\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\vee }_{g_{1},\ldots ,g_{s}}(N_{G}(K)\cdot g_{i})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}} & \rightarrow & \displaystyle (G_{+}\wedge _{H}A)^{K}\nonumber\\ \displaystyle [(ng_{i},a)] & \mapsto & \displaystyle [(ng_{i},a)]\nonumber\end{eqnarray}$$
with
![]() $N_{H}(K^{g_{i}})$
acting on
$N_{H}(K^{g_{i}})$
acting on
![]() $N_{G}(K)\cdot g_{i}$
by right multiplication. We leave it to the reader to check that this map is bijective. It is then not hard to show that it is a homeomorphism, using that
$N_{G}(K)\cdot g_{i}$
by right multiplication. We leave it to the reader to check that this map is bijective. It is then not hard to show that it is a homeomorphism, using that
![]() $(G/H)^{K}$
decomposes as a topological disjoint union of its
$(G/H)^{K}$
decomposes as a topological disjoint union of its
![]() $N_{G}(K)$
-orbits, as explained in Remark A.2 (see also the proof of [Reference SchwedeSch18, Proposition B.17]). Thus, in summary, for based
$N_{G}(K)$
-orbits, as explained in Remark A.2 (see also the proof of [Reference SchwedeSch18, Proposition B.17]). Thus, in summary, for based
![]() $H$
-spaces
$H$
-spaces
![]() $A$
there is a natural homeomorphism
$A$
there is a natural homeomorphism
where the
![]() $g_{i}$
are elements of
$g_{i}$
are elements of
![]() $G$
such that
$G$
such that
![]() $K^{g_{1}},\ldots ,K^{g_{s}}$
are representatives of
$K^{g_{1}},\ldots ,K^{g_{s}}$
are representatives of
![]() $H$
-conjugacy classes of subgroups of
$H$
-conjugacy classes of subgroups of
![]() $H$
that are conjugate to
$H$
that are conjugate to
![]() $K$
in
$K$
in
![]() $G$
. Hence, using that geometric fixed points and induction commute with suspension spectra (§§ 2.2.4 and 2.2.2), we obtain an equivalence
$G$
. Hence, using that geometric fixed points and induction commute with suspension spectra (§§ 2.2.4 and 2.2.2), we obtain an equivalence
Now we assume that (the
![]() $p$
-localization of)
$p$
-localization of)
![]() $\unicode[STIX]{x1D6F4}^{\infty }A$
is a finite
$\unicode[STIX]{x1D6F4}^{\infty }A$
is a finite
![]() $p$
-local
$p$
-local
![]() $H$
-spectrum. Then, in order to prove part (ii) we need to show that the type of
$H$
-spectrum. Then, in order to prove part (ii) we need to show that the type of
![]() $(N_{G}(K)\cdot g_{i})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}}$
is at least the type of
$(N_{G}(K)\cdot g_{i})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}}$
is at least the type of
![]() $A^{K^{g_{i}}}$
. This follows from the fact that the
$A^{K^{g_{i}}}$
. This follows from the fact that the
![]() $N_{H}(K^{g_{i}})$
-action on
$N_{H}(K^{g_{i}})$
-action on
![]() $N_{G}(K)$
is free; hence
$N_{G}(K)$
is free; hence
![]() $N_{G}(K)$
is
$N_{G}(K)$
is
![]() $N_{H}(K^{g_{i}})$
-equivariantly built out of cells of the form
$N_{H}(K^{g_{i}})$
-equivariantly built out of cells of the form
![]() $N_{H}(K^{g_{i}})_{+}\wedge D^{n}$
. Therefore,
$N_{H}(K^{g_{i}})_{+}\wedge D^{n}$
. Therefore,
![]() $\unicode[STIX]{x1D6F4}^{\infty }(N_{G}(K)\cdot g_{i})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}}$
lies in the thick subcategory generated by
$\unicode[STIX]{x1D6F4}^{\infty }(N_{G}(K)\cdot g_{i})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}}$
lies in the thick subcategory generated by
![]() $\unicode[STIX]{x1D6F4}^{\infty }(N_{H}(K^{g_{i}})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}})\simeq \unicode[STIX]{x1D6F4}^{\infty }A^{K^{g_{i}}}$
, and hence its type is at least as large. Furthermore, if no conjugate of
$\unicode[STIX]{x1D6F4}^{\infty }(N_{H}(K^{g_{i}})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}})\simeq \unicode[STIX]{x1D6F4}^{\infty }A^{K^{g_{i}}}$
, and hence its type is at least as large. Furthermore, if no conjugate of
![]() $K$
is a subgroup of
$K$
is a subgroup of
![]() $H$
, then
$H$
, then
![]() $(G_{+}\wedge _{H}A)^{K}$
consists of a point, and hence
$(G_{+}\wedge _{H}A)^{K}$
consists of a point, and hence
![]() $\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A))$
is trivial, proving part (iii) for suspension spectra.
$\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A))$
is trivial, proving part (iii) for suspension spectra.
Remark A.3. If
![]() $G$
is finite, then
$G$
is finite, then
![]() $N_{G}(K)\cdot g_{i}$
is discrete, so picking a set of representatives of
$N_{G}(K)\cdot g_{i}$
is discrete, so picking a set of representatives of
![]() $N_{H}(K^{g_{i}})$
-orbits gives rise to a homeomorphism
$N_{H}(K^{g_{i}})$
-orbits gives rise to a homeomorphism
and hence the type of
![]() $(N_{G}(K)\cdot g_{i})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}}$
is in fact equal to that of
$(N_{G}(K)\cdot g_{i})_{+}\wedge _{N_{H}(K^{g_{i}})}A^{K^{g_{i}}}$
is in fact equal to that of
![]() $A^{K^{g_{i}}}$
. Such an argument does not work for general compact Lie groups, because the projection
$A^{K^{g_{i}}}$
. Such an argument does not work for general compact Lie groups, because the projection
![]() $N_{G}(K)\cdot g_{i}\rightarrow (N_{G}(K)\cdot g_{i})/N_{H}(K^{g_{i}})$
need not split. See Remark 3.10 for a counterexample.
$N_{G}(K)\cdot g_{i}\rightarrow (N_{G}(K)\cdot g_{i})/N_{H}(K^{g_{i}})$
need not split. See Remark 3.10 for a counterexample.
When
![]() $K$
is equal to
$K$
is equal to
![]() $H$
, the formula above consists of only one summand corresponding to
$H$
, the formula above consists of only one summand corresponding to
![]() $H$
itself, since
$H$
itself, since
![]() $H$
is not conjugate to a proper subgroup of itself (see the proof of Lemma 3.13). As
$H$
is not conjugate to a proper subgroup of itself (see the proof of Lemma 3.13). As
![]() $N_{H}(H)=H$
, this summand is given by
$N_{H}(H)=H$
, this summand is given by
![]() $\unicode[STIX]{x1D6F4}^{\infty }N_{G}(H)_{+}\wedge _{H}A^{H}$
. The
$\unicode[STIX]{x1D6F4}^{\infty }N_{G}(H)_{+}\wedge _{H}A^{H}$
. The
![]() $H$
-action on
$H$
-action on
![]() $A^{H}$
is trivial, and hence
$A^{H}$
is trivial, and hence
![]() $N_{G}(H)_{+}\wedge _{H}A^{H}$
is homeomorphic to
$N_{G}(H)_{+}\wedge _{H}A^{H}$
is homeomorphic to
![]() $(N_{G}(H)/H)_{+}\wedge A^{H}$
, whose type equals that of
$(N_{G}(H)/H)_{+}\wedge A^{H}$
, whose type equals that of
![]() $A^{H}$
since it contains
$A^{H}$
since it contains
![]() $A^{H}$
as a retract (and on the other hand lies in the thick subcategory generated by
$A^{H}$
as a retract (and on the other hand lies in the thick subcategory generated by
![]() $A^{H}$
). Therefore, the type of
$A^{H}$
). Therefore, the type of
![]() $\unicode[STIX]{x1D6F7}^{H}(\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A))$
equals the type of
$\unicode[STIX]{x1D6F7}^{H}(\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A))$
equals the type of
![]() $\unicode[STIX]{x1D6F7}^{H}(\unicode[STIX]{x1D6F4}^{\infty }A)$
, as desired. This finishes the proof of the lemma for finite
$\unicode[STIX]{x1D6F7}^{H}(\unicode[STIX]{x1D6F4}^{\infty }A)$
, as desired. This finishes the proof of the lemma for finite
![]() $G$
-spectra of the form
$G$
-spectra of the form
![]() $\unicode[STIX]{x1D6F4}^{\infty }A$
.
$\unicode[STIX]{x1D6F4}^{\infty }A$
.
Now, by Lemma 2.2, a general finite
![]() $H$
-spectrum
$H$
-spectrum
![]() $X$
is of the form
$X$
is of the form
![]() $S^{-V}\wedge \unicode[STIX]{x1D6F4}^{\infty }A$
for
$S^{-V}\wedge \unicode[STIX]{x1D6F4}^{\infty }A$
for
![]() $A$
a homotopy retract of the
$A$
a homotopy retract of the
![]() $p$
-localization of a finite
$p$
-localization of a finite
![]() $H$
-CW complex and an
$H$
-CW complex and an
![]() $H$
-representation
$H$
-representation
![]() $V$
. By a standard fact in representation theory of compact Lie groups (see for example [Reference Bröcker and tom DieckBtD85, Theorem III.4.5]), there exists a
$V$
. By a standard fact in representation theory of compact Lie groups (see for example [Reference Bröcker and tom DieckBtD85, Theorem III.4.5]), there exists a
![]() $G$
-representation
$G$
-representation
![]() $W$
such that
$W$
such that
![]() $V$
sits inside the restriction
$V$
sits inside the restriction
![]() $\operatorname{Res}_{H}^{G}W$
of
$\operatorname{Res}_{H}^{G}W$
of
![]() $W$
to an
$W$
to an
![]() $H$
-representation. Then
$H$
-representation. Then
Let
![]() $A^{\prime }=S^{(\operatorname{Res}_{H}^{G}W)-V}\wedge A$
, which is again a homotopy retract of the
$A^{\prime }=S^{(\operatorname{Res}_{H}^{G}W)-V}\wedge A$
, which is again a homotopy retract of the
![]() $p$
-localization of a finite
$p$
-localization of a finite
![]() $H$
-CW complex, and hence
$H$
-CW complex, and hence
![]() $\unicode[STIX]{x1D6F4}^{\infty }A^{\prime }$
is a finite
$\unicode[STIX]{x1D6F4}^{\infty }A^{\prime }$
is a finite
![]() $p$
-local
$p$
-local
![]() $H$
-spectrum. Then
$H$
-spectrum. Then
![]() $X\simeq \operatorname{Res}_{H}^{G}S^{-W}\wedge \unicode[STIX]{x1D6F4}^{\infty }A^{\prime }$
, and by Frobenius reciprocity (see § 2.2.2) there is an equivalence
$X\simeq \operatorname{Res}_{H}^{G}S^{-W}\wedge \unicode[STIX]{x1D6F4}^{\infty }A^{\prime }$
, and by Frobenius reciprocity (see § 2.2.2) there is an equivalence
Note that smashing with a representation sphere has no effect on the type of the geometric fixed points for any subgroup. Hence, for a closed subgroup
![]() $K$
of
$K$
of
![]() $G$
we obtain
$G$
we obtain
 $$\begin{eqnarray}\displaystyle \text{type}_{K}(\operatorname{Ind}_{H}^{G}(X)) & = & \displaystyle \text{type}_{K}(\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A^{\prime }))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \min (\text{type}_{K^{\prime }}(\unicode[STIX]{x1D6F4}^{\infty }A^{\prime })~|~K^{\prime }\subseteq H,K^{\prime }\sim K)\nonumber\\ \displaystyle & = & \displaystyle \min (\text{type}_{K^{\prime }}(X)~|~K^{\prime }\subseteq H,K^{\prime }\sim K)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{type}_{K}(\operatorname{Ind}_{H}^{G}(X)) & = & \displaystyle \text{type}_{K}(\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A^{\prime }))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \min (\text{type}_{K^{\prime }}(\unicode[STIX]{x1D6F4}^{\infty }A^{\prime })~|~K^{\prime }\subseteq H,K^{\prime }\sim K)\nonumber\\ \displaystyle & = & \displaystyle \min (\text{type}_{K^{\prime }}(X)~|~K^{\prime }\subseteq H,K^{\prime }\sim K)\nonumber\end{eqnarray}$$
as desired, with equality in the case
![]() $K=H$
. Finally, if
$K=H$
. Finally, if
![]() $K$
is not conjugate to a subgroup of
$K$
is not conjugate to a subgroup of
![]() $H$
, then
$H$
, then
since
![]() $\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A^{\prime }))\simeq \ast$
.◻
$\unicode[STIX]{x1D6F7}^{K}(\operatorname{Ind}_{H}^{G}(\unicode[STIX]{x1D6F4}^{\infty }A^{\prime }))\simeq \ast$
.◻