Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-06T15:52:30.385Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of microstructure on shock propagation in foams

Published online by Cambridge University Press:  01 June 2004

F. PHILIPPE ,
B. CANAUD ,
X. FORTIN ,
F. GARAUDE  and
H. JOURDREN
F. PHILIPPE
Affiliation:
Département de Physique Théorique et Appliquée, Commissariat à l'Energie Atomique/DAM Ile-de-France, Bruyères-le-Châtel, France
B. CANAUD
Affiliation:
Département de Physique Théorique et Appliquée, Commissariat à l'Energie Atomique/DAM Ile-de-France, Bruyères-le-Châtel, France
X. FORTIN
Affiliation:
Département de Physique Théorique et Appliquée, Commissariat à l'Energie Atomique/DAM Ile-de-France, Bruyères-le-Châtel, France
F. GARAUDE
Affiliation:
Département de Physique Théorique et Appliquée, Commissariat à l'Energie Atomique/DAM Ile-de-France, Bruyères-le-Châtel, France
H. JOURDREN
Affiliation:
Département Sciences de la Simulation et de l'Information, Commissariat à l'Energie Atomique/DAM Ile-de-France, Bruyères-le-Châtel, France
Rights & Permissions [Opens in a new window]

Abstract

Foams are an important component of various inertial confinement fusion target schemes. The propagation of shock waves in foams is also an important issue for many other laser experiments (e.g., laboratory astrophysics experiments). The usual approach is to assume that the foam can be considered as a homogeneous mixture. Taking into account the effects of foam heterogeneity leads to increased shock velocity and reduced compressibility. Evidence of this effect is obtained using two-dimensional adaptive mesh refinement Eulerian numerical simulations. Nonetheless, for the very low density foams filled with DT ice used in recent direct drive target designs, the homogeneous mixture model provides adequate shock timing, density, and pressure profiles.

Keywords

FoamHeterogeneous mediaShock
Type
Research Article
Information
Laser and Particle Beams , Volume 22 , Issue 2 , June 2004 , pp. 171 - 174
Copyright
© 2004 Cambridge University Press

1. INTRODUCTION

Foams are an important component of various inertial confinement fusion (ICF) target schemes. Recent target designs for direct-drive ICF use either a wetted foam ablator to provide both high ablation velocity and efficient laser absorption (following the earlier proposal of Sacks and Darling, 1987) or a very low density foam buffer for density profile tailoring and imprint reduction (Metzler et al., 2002). The double shell targets designed for indirect drive ICF (Amendt et al., 2002) also include a foam layer. Finally, the propagation of shocks in foam is an important issue in laboratory astrophysics experiments (Remington et al., 2000), where their use is very widespread.

In this context, foams are usually modeled as homogeneous mixtures. Although this may seem a reasonable approximation on intuitive grounds when pore size is small, to assess the reliability and accuracy of the results obtained with this simple model, a detailed understanding of the effect of foam microstructure is needed. From a microscopic point of view, the foam structure appears like a solid fiber tangle with open cells, either empty or filled by another fluid (“wetted foams”). The first computational study of shock propagation in a foam with this more realistic model was done by Kotelnikov and Montgomery (1998) with a two-dimensional (2D) Eulerian code. But these calculations were made with a regular, periodic cylinder array model without dealing with the random aspect of foam structure. Moreover, uniform mesh resolution lead to a prohibitive computational cost for large-scale calculations. In this article, we present the first description of that kind of foam with a 2D Eulerian code with adaptive mesh refinement (AMR) and interface tracking, which makes it possible to tackle large-scale simulations. In addition, a random distribution of fiber positions has been considered.

Section 2 is devoted to the mathematical formalism describing shock propagation in a heterogeneous medium. Simulations and their results are detailed in Section 3.

2. GENERALIZED RANKINE-HUGONIOT EQUATIONS

If the size of the foam structure is small compared to the resolution of experimental measurements or numerical simulation, it is interesting to consider all physical quantities A(x,y) averaged over the direction transverse to the shock front and in the direction of propagation over the characteristic scale length L of heterogeneities. This double averaging process is hereafter denoted by double angle brackets:

where x is the direction of shock propagation, y the transverse direction, and V the averaging volume.

It was shown by Hazak et al. (1998) that the double averaged values on each side of a shock front are related by equations analogous to the well-known Rankine–Hugoniot set:

where P is the pressure, ρ the density, ε the internal energy, and u the fluid velocity. The subscripts 0 and 1 denote, respectively, the preshock and postshock values.

These generalized Rankine–Hugoniot equations differ from the classical ones due to the existence of nonvanishing correlation terms defined by the following generic expression:

Therefore, the averaged quantities behind the shock are different from the values that would be predicted for an homogeneous medium with the same averaged density. If Ah is the value predicted for the quantity A in the homogeneous case, we define the deviation ΔA by

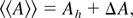
and the shock speed deviation ΔD by

For a given piston velocity, and assuming the preshock medium is at rest, taking the difference of the generalized and classical Rankine–Hugoniot relations leads to

An additional relation is given by the equation of state of the fiber/background mixture, which links the internal energy deviation to pressure and density. In the following simulations, we will consider a perfect gas equation of state:

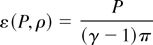
The deviations Δρ, ΔD, ΔP, Δε are thus implicitly given as functions of the homogeneous values and correlation terms.

According to Hazak et al. (1998), the effect of correlations is to increase shock velocity and reduce pressure and density behind the shock front. A physical interpretation of this effect is that part of the energy is stored in the transverse fluid motions associated with the vortices generated when the shock crosses a fiber, rather than used for compression.

Unfortunately, there is no simple analytical expression for the needed correlation terms, and numerical simulation is needed to evaluate them.

3. NUMERICAL SIMULATIONS RESULTS

Numerical simulations were performed with the HERA 2D hydrocode, developed at the Commissariat à l'Energie Atomique (CEA). HERA 2D is a multifluid two-dimensional Eulerian hydrodynamic code with tree-based AMR capability. Its hydrodynamic solver uses a time-explicit Godounov-type scheme with interface reconstruction. The code supports various parallel modes, from full MPI to full multithread or hybrid multithread/MPI with dynamic load balancing via subdomain migrations. The code is available on various computer architectures (HP-Compaq Tru64, Sun Solaris, PC Linux). Implicit thermal conduction and paraxial laser propagation solvers are also available in HERA 2D, but were not used in this study.

We focused our study on shock propagation in two samples of foam relevant for direct drive target designs, with a CH fibers network embedded in DT ice. Simulations were conducted for a low density (20 mg/cc before DT filling) foam, and for a higher density one (100 mg/cc before DT filling). In each case, simulations of the structured foam were compared to simulations of a homogeneous one with the same average density. The fibrous foam structure was modeled as a random distribution of transverse, infinite CH cylinders on a DT ice background (cf. Fig. 1). The initial sample size was 2 μm across and 8 μm along the shock propagation axis.

Initial random distribution of CH cylinders on a DT ice background.

A simple perfect gas equation of state was used in the simulation, with γ = 5/3. The initial fluid velocity of the sample is 40 km/s toward the left, with inflow boundary conditions on the right side and wall boundaries everywhere else. This generates a shock propagating from left to right in the foam, with velocities and pressure typical of the first shock in direct-drive targets. These initial and boundary conditions place the simulation in the piston rest frame. From a numerical point of view, it ensures a more accurate description of the vortices and mixing behind the shock front, as the medium is at rest on average after shock passage.

Figure 2 is a snapshot of the foam density 144 ps after the beginning of shock propagation. As seen in Figure 2, when the shock crosses a fiber, baroclinic instability leads to vorticity deposition at the interface between fiber and ice. The fiber is then quickly destroyed and mixed with the surrounding background.

Density map at t = 144 ps in a 20-mg/cc foam filled with DT ice (upper part) and in a homogeneous mixture of the same average density (lower part). The vertical dashed line represents the shock front.

The evolution of a single cylinder subject to a shock wave was experimentally studied by Jacobs (1993), and is accurately reproduced in our simulation, thanks to the high resolution permitted by AMR and interface reconstruction. In a random foam structure, interactions between neighboring cylinders can occur, which has been shown experimentally to affect the first stages of evolution of the instability (Tomkins et al., 2003).

The comparison of the shock average position between the heterogeneous and homogeneous cases shows no noticeable difference in shock velocity. This can be confirmed using previous formulae. We find ΔD/Dh < 0.3% in this case. Moreover, pressure and density profiles with and without foam structure are in good agreement (cf. Fig. 3) even if heterogeneous structure introduces random fluctuations behind the shock. Therefore, the homogeneous mixture model is found to be adequate in this particular case.

Pressure (right, bars) and density (left, g/cc) profiles along the shock propagation axis at t = 144 ps for the heterogeneous (full line) and homogeneous (dashed line) cases.

Concerning the denser foam, the results are quite different. As seen in Figure 4, interactions between fibers are greater. In this case, the difference in shock velocity with respect to the homogeneous case is more significant. In addition, pressure and density profiles with and without foam structure are very different, the heterogeneous case exhibiting strong undercompression (cf. Fig. 5). The shock velocity deviation deduced from generalized Rankine–Hugoniot equations and correlation terms extracted from the simulation is found to be in good agreement with the numerical value ΔD/Dh = 1% ± 0.3%.

Density map at t = 60 ps in a 100-mg/cc foam filled with DT ice (upper part) and in a homogeneous mixture of the same average density (lower part). The vertical dashed line represents the shock front.

Pressure (right, bars) and density (left, g/cc) profiles along the shock propagation axis at t = 60 ps for the heterogeneous (full line) and homogeneous (dashed line) cases.

Finally, perturbations of the shock front start to appear in the denser case, and could seed Richtmyer–Meshkov instability at the interface of the foam with another medium.

4. CONCLUSION

AMR simulations of shock propagation in wetted foams have been performed, including a random initial distribution of fibers. The study of shock propagation in low density foams (20 mg/cc) shows no discrepancy with the homogeneous mixture model. Designs involving higher density foams (100 mg/cc) should take into account the effect of foam structure, because changes in shock timing will have consequences on the choice of laser pulse shape for optimal gain. It can be expected that besides modifying shock propagation, the foam structure can have effects on foam ablation physics and instabilities at foam interfaces. These latter topics are the subject of further investigations.

References

REFERENCES

Amendt, P., Colvin, J.D., Tipton, R.E., Hinkel, D.E., Edwards, M.J., Landen, O.L., Ramshaw, J.D., Suter, L.J., Varnum, W.S. & Watt, R.G. (2002). Phys. Plasmas 9, 2221.
Hazak, G., Velikovich, A.L., Gardner, J.H. & Dahlburg, J.P. (1998). Phys. Plasmas 5, 4357.
Jacobs, J.W. (1993). Phys. Fluids A 5, 2239.
Kotelnikov, A.D. & Montgomery, D.C. (1998). Phys. Fluids 10, 2037.
Metzler, N., Velikovich, A.L. & Gardner, J.H. (2002). Phys. Plasmas 9, 5050.
Remington, B.A., Drake, R.P., Takabe, H. & Arnett, D. (2000). Phys. Plasmas 7, 1641.
Sacks, R.A. & Darling, D.H. (1987). Nucl. Fusion 27, 447.
Tomkins, C., Prestridge, K., Rightley, P., Marr-Lyon, M., Vorobieff, P. & Benjamin (2003). Phys. Fluids 15, 986.
Figure 0

Initial random distribution of CH cylinders on a DT ice background.

Figure 1

Density map at t = 144 ps in a 20-mg/cc foam filled with DT ice (upper part) and in a homogeneous mixture of the same average density (lower part). The vertical dashed line represents the shock front.

Figure 2

Pressure (right, bars) and density (left, g/cc) profiles along the shock propagation axis at t = 144 ps for the heterogeneous (full line) and homogeneous (dashed line) cases.

Figure 3

Density map at t = 60 ps in a 100-mg/cc foam filled with DT ice (upper part) and in a homogeneous mixture of the same average density (lower part). The vertical dashed line represents the shock front.

Figure 4

Pressure (right, bars) and density (left, g/cc) profiles along the shock propagation axis at t = 60 ps for the heterogeneous (full line) and homogeneous (dashed line) cases.