Introduction
Studies with hair sheep have generated a considerable amount of data, contributing to our understanding of nutritional patterns (Mendes et al., Reference Mendes, Souza, Herbster, Brito Neto, Silva, Rodrigues, Marcondes, Oliveira, Bezerra and Pereira2021). The hair lambs' body weight (BW) may vary throughout the year according to various factors such as feed quality and availability, mainly in grazing systems and warm areas. Thus, estimates of growth rates, adult weight (Lôbo et al., Reference Lôbo, Villela, Lobo, Passos and Oliveira2006) and weight at maturity (NRC, 1996) are economically important variables to be determined, both for selection programs with multiple characteristics (MacNeil and Newman, Reference MacNeil and Newman1994) and for fitting nutritional requirement equations.
Knowledge of weight at maturity is an essential step in balancing diets (Almeida et al., Reference Almeida, Resende, Tedeschi, Fernandes, Regadas Filho and Teixeira2016; Marcondes et al., Reference Marcondes, Tedeschi, Valadares Filho, Silva and Silva2016), and most committees take into account maturity to adjust nutrient requirements for the animals (NRC, 2000; CSIRO, 2007). However, the definition of mature weight is not standardized, even among simulation models (Arnold and Bennett, Reference Arnold and Bennett1991). The CSIRO (2007) considers that weight at maturity is characterized by the BW reached when the animal completes skeletal development. However, the NRC (2000) considers the point when the protein and ash deposition rates are similar to the empty body weight (EBW). The fixed value of 25 g of fat content/100 g of EBW is referred to by the NRC (2007). In these systems, sheep reach maturity with an average BW of 60 kg. However, hair sheep have a relatively small body frame and slow growth rates (López-Carlos et al., Reference López-Carlos, Ramírez, Aguilera-Soto, Aréchiga and Rodríguez2010) and there is a lack in mature weight information. The use of adjusted equations by committees could result in estimation errors when used in hair sheep feeding systems.
Therefore, the hypothesis investigated in this paper is that the chemical constituents, ash, protein and/or fat, can be used to predict the mature weight of intact male sheep. The objective of this study was to provide an approach to estimate mature weight for hair sheep male.
Materials and methods
Inclusion criteria for the studies
The database used to estimate the maturity weight consisted of eight experimental studies based on a comparative slaughter methodology, comprising a total of 250 animals (Table 1). The feedlot feeding system was used. Only studies containing information on individual animals, fed at maintenance levels, and animals fed at least two levels above maintenance were included. Furthermore, only experiments conducted with hair sheep or crosses raised in the tropical region of Brazil that contained the following quantitative data on each animal were included: BW, EBW; information about chemical composition: water-free EBW protein content (EBP), water-free EBW fat content (EBF), water-free EBW ash content (EBA) and EBW water content (EBWt). The descriptive statistics of the variables used to fit the models are shown in Table 2.
Table 1. Descriptive table of the studies that make up the database used to estimate the weight at maturity

a Range of adult body weight according to Sousa et al. (Reference Sousa, Lôbo and Morais2003).
b ME diet, metabolizable energy of diet.
c CP diet, crude protein of diet.
d Experimental diets composed of Elephant grass hay (Pennisetum purpureum Shum.), ground maize, soybean meal and mineral premix.
e Experimental diets composed of Tifton 85 grass hay (Cynodon spp.), ground maize, soybean meal and mineral premix.
Table 2. Descriptive statistics of the variables used to fit the equations
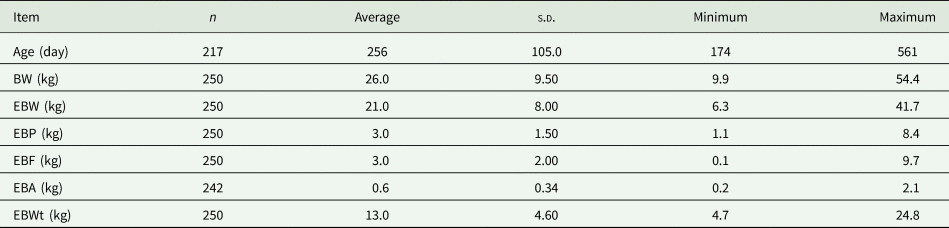
s.d., standard deviation; EBW, empty BW; EBP, water-free EBW protein content; EBF, water-free EBW fat content; EBA, water-free EBW ash content; EBWt, EBW water content.
Slaughtering
Similar slaughter procedures were adopted by all experimental studies. Before slaughter, fasting body weight (FBW) was obtained as the animals' BW after 18 h without feed and water. Slaughtering was carried out by stunning using a captive bolt pistol (EFA Cash Special 22), causing brain concussion and subsequently sectioning the jugular vein until the animals bled out completely, followed by skinning and evisceration. The blood was weighed and sampled. The gastrointestinal tract was washed, and after draining, it was weighed with other organs (liver, heart, trachea + lungs + tongue + oesophagus, bladder, kidneys, reproductive tract, spleen), body parts (carcass, head, blood and hooves) and visceral fat (omental, mesenteric, heart and perirenal). The EBW was calculated by subtracting the weight of gastrointestinal and bladder contents from FBW. The hides were weighed, sampled in bands and frozen.
The carcasses were refrigerated at 4°C for 24 h and then were divided into right and left half-carcasses. Subsequently, the right half-carcasses, non-carcass components (blood, head, hooves, internal organs and the cleaned gastrointestinal tract) and hides were frozen and then cut with a band saw and ground in an industrial cutter.
Chemical analysis
After grinding and homogenization, samples of 500 g of the combined mass of the non-carcass components, right half-carcass and hides were taken and then frozen at −20°C. All samples were stored frozen until laboratory chemical analyses were performed. Posteriorly, they were placed in a forced ventilation oven at 55°C for 72 h. Subsequently, the triplicate samples were defatted by extraction with ether in a Soxhlet apparatus (AOAC, 1990; method number 920.39) for 12 h, followed by grinding in a ball mill and storing in closed containers. The dry matter (DM) contents were determined by AOAC (1990) (method 967.03). The ash (AOAC, 1990; method 942.05) and crude protein (CP) (AOAC, 1990; method 981.10) levels were determined in fat-free samples, and the EBWt was determined as 100−DM (g/kg EBW).
Statistical analysis
The non-linear regressions were fitted to predict EBP, EBF, EBA and EBWt, expressed as amounts of the EBW and water-free EBW (i.e. EBW−EBWt). Initially, candidate equations were evaluated on the basis of preliminary graphical examination of the observed body composition of the database according to Almeida et al. (Reference Almeida, Resende, Tedeschi, Fernandes, Regadas Filho and Teixeira2016). The variables were tested on different bases of water-free EBW and fat-free EBW and as ratios between nutrients (protein:fat and ash:fat). Models of the Richards family (Richards, Reference Richards1959), an allometric model and an exponential model, were tested (Eqns (1) and (2), respectively).
In these equations, y is the dependent variable, which may be fat as a proportion of the EBW or protein or ash as a proportion of the water-free EBW; exp is the base of natural numbers; β 0 and β 1 are parameters to be estimated in the model; ɛ is the residual term. Previously, for the estimates of these models, the data were adjusted by the MIXED procedure of the SAS software (SAS Inst. Inc., Cary, NC, USA) to remove the effects of the differences among the studies. Based on the predicted values, the linear models described above were estimated by the NLIN procedure in SAS. The best model was chosen considering the achievement of convergence and the capacity for biological explanation. The allometric model was adopted, and the analyses were performed using the NLMIXED procedure of the SAS program, applying the Newton-Raphson algorithm for the maximum likelihood solution.
To estimate the mature EBW, asymptotic values were used, algebraically solving the first derivative of the selected model (Eqn (1)):
where EBW is the asymptotic EBW and β 0 and β 1 are the parameter estimates of Eqn (1). The standard deviation of the asymptotic EBW was computed using a simulation method based on a Monte Carlo approach.
Results
The relationships among the proportions of water, fat, protein and ash in hair sheep are shown in Fig. 1.

Fig. 1. Relationships among the proportions (g/kg EBW) of water, fat, ash and protein from 6.3 to 41.7 kg of EBW in hair sheep.
The amounts (g) of protein, and ash on the water-free EBW and fat on EBW are shown in Fig. 2. By plotting the amount of EBP (g) against water-free EBW (Fig. 2(a)), using an allometric function (Eqn (1)), we obtained an estimate mature weight of 47.3 kg EBW at 54.0 kg BW. Plotting the amount of EBF (g) against EBW (kg) (Fig. 2(b)), using an allometric function (Eqn (1)), we obtained an estimate mature weight of 57.5 kg of EBW at 64.0 kg of BW (Table 3).

Fig. 2. Protein and ash contents in water-free EBW (g/kg) and fat content in EBW (g/kg) of hair sheep.
Table 3. Estimated EBW and BW at maturity of intact male hair sheep using fat in the EBW (EBF g/kg EBW) and the amount (g) of protein in the water-free EBW

s.e., standard error; s.d., standard deviation.
a Empty body weight at maturity.
b Referent body weight at maturity.
c Estimated solving the allometric equation for EBW at 294 g fat/EBW using a Monte Carlo simulation; EBF = β 0 × ${\rm EB}{\rm W}^{\beta _1}$![]() (P < 0.001, σ e2 = 2756.63, σ s2 = 172.31).
(P < 0.001, σ e2 = 2756.63, σ s2 = 172.31).
d s.d. for mature weight estimations were computed applying a Monte Carlo-based method.
e Estimated solving the allometric equation for EBW at 7280 g protein/water-free EBW using a Monte Carlo simulation; EBP = β 0 × ${\rm EB}{\rm W}^{\beta _1}$![]() (P < 0.001, σ e2 = 170 207.93, σ s2 = 53.66).
(P < 0.001, σ e2 = 170 207.93, σ s2 = 53.66).
Protein and fat were able to predict estimates within the capacity to biological explanation. However, protein presents lower data dispersion when compared to fat in the animal's body. The ash content (Fig. 2(c)) was not a reliable predictor to describe weight at maturity (i.e. the analyses did not meet the convergence criteria).
Discussion
Body composition affects nutritional requirements, mainly due to the differences among the metabolic activities of tissues that make up the animals' body. Furthermore, when the chemical constituents of the animals' body (water, protein, fat and minerals) reach a plateau, the weight at maturity is defined. In hair sheep, the lack in the knowledge of mature weight can lead to a major restriction in the interpretation of body composition and consequently of the growth.
In the present study, the water and protein contents in the EBW were closely associated. The fat contents increased from 16.8 to 181.6 g/kg EBW as the EBW increased from 6.3 to 41.7 kg.
On the other hand, the protein and water levels decreased from 701.7 to 450.5 g/kg water-free EBW and 741.2 to 595.4 g/kg EBW for intact males, respectively. For each 1 kg of CP deposited in the body, 4–5 kg of water is deposited as well, whereas in the case of fat, each 1 kg deposited is associated with the deposition of <1 kg of water (Marcondes et al., Reference Marcondes, Tedeschi, Valadares Filho and Gionbelli2013). The reduction in protein deposition is related to a concomitant reduction in the amount of water in the empty body (Morand-Fehr, Reference Morand-Fehr and Gall1981) due to the reduction in muscle growth. The opposite occurs for fat, whose deposition increases as the animal grows; after maturity, the deposition is exponential (NRC, 2007). Compared to temperate genotypes, tropical genotypes are generally not selected for muscle deposition (Salah et al., Reference Salah, Sauvant and Archimède2014), thus depositing more fat in the gain. In our studies on nutritional requirements, we observed that hair sheep exhibit higher amounts of visceral, abdominal and pelvic fat at high weights.
In our study, regarding the ash, it did not show asymptotic stability, as observed in goats (Almeida et al., Reference Almeida, Resende, Tedeschi, Fernandes, Regadas Filho and Teixeira2016) and Nellore cattle (Marcondes et al., Reference Marcondes, Tedeschi, Valadares Filho, Silva and Silva2016). The ash contains the sum of all inorganic elements such as Ca, P and Mg, which are mainly present in bones, in addition to other macro- and microelements, such as oxides, carbonates, sulphates, metal-organic molecules and ions in bones, teeth, cartilage and soft tissues (Underwood and Suttle, Reference Underwood and Suttle1999). Unlike the other components, the ash content was unstable in the empty body of sheep.
Mature body size or mature weight can be defined in various ways. The definition of mature BW proposed by Taylor and Young (Reference Taylor and Young1967) was discussed by Keele et al. (Reference Keele, Williams and Bennett1992). By that definition, mature weight is the point of BW equilibrium for cattle fed forage diets. At this point, the chemical fat content of the empty body is approximately 25 g/100 g of EBW. The point at which protein accretion ceases as an estimate of mature BW was used by Brody and Lardy (Reference Brody and Lardy1946) and Fox and Black (Reference Fox and Black1984). We were able to identify the point when the CP became constant. The stabilization of the protein content occurred when the animal reached 47.3 kg of EBW, which corresponds to 54.0 kg of BW.
Thus, mature weight is defined as the point at which the protein mass reaches a plateau. Beyond this point, the animals may have a continued fat deposition and weight gain, but protein accretion presumably would be null. According to the NRC (2000), chemical maturity may be achieved through the stabilization of protein accretion in the EBW.
The NRC (2007) considers that maturity occurs when the skeleton is complete and exhibits a fixed fat content. In our study, the value of 57.5 kg of EBW was found when using fat as a predictor, corresponding to 294 g fat/kg EBW. A value of 340 g/kg was employed previously by Wang and Dickerson (Reference Wang and Dickerson1991) in modelling lamb growth, whereas 368 g/kg as used by Almeida et al. (Reference Almeida, Resende, Tedeschi, Fernandes, Regadas Filho and Teixeira2016) for goats. Therefore, as the animal grows, a change in priority of addition to the tissue occurs. Our analysis suggests that, irrespective of the chemical constituents used to estimate maturity, the weight at maturity would remain between 47.3 and 57.5 kg of EBW (corresponding to an average EBW of 52.4 kg). The fat content of the animals' body may vary depending on the metabolizable energy of the diet (Coleman et al., Reference Coleman, Evans and Guenther1993; Marcondes et al., Reference Marcondes, Tedeschi, Valadares Filho, Silva and Silva2016) and could compromise the understanding of the body composition (Almeida et al., Reference Almeida, Resende, Tedeschi, Fernandes, Regadas Filho and Teixeira2016). Thus, it could not indicate maturity since it would be highly variable (Marcondes et al., Reference Marcondes, Tedeschi, Valadares Filho, Silva and Silva2016), this was observed in our study, which implies the choice of protein as the best predictor. Therefore, we understand that protein in water-free EBW is a good predictor of the maturity for intact male hair sheep. The BR-CORTE (2016) and NRC (2000) consider the idea that maturity may be achieved through the stabilization of protein accretion in the empty body. Protein rate accretion declines markedly as animals reach maturity, reaching zero at mature size.
Our study has provided a greater understanding of the possibility of using chemical constituents in predicting mature weight. It is an important step to understand the nutritional requirements, especially for growing sheep. However, more information of studies with weighing more than 40 kg of EBW would provide more robust estimates. Extrapolation of values presented out of the x-space (6.3–41.7 kg) must be used with great care, because while we can mathematically obtain a predicted value for the response at point x, we should have some additional knowledge that the equation in it validates over a wider region of x-space.
Conclusion
Animal maturity can be estimated mathematically using body composition. The allometric model suggests that hair sheep reach maturity at EBW of 47.3 and 57.5 kg when using protein and fat as a predictor, respectively. We conclude that protein is a best predictor of maturity for intact male hair sheep.
Acknowledgements
The authors thank the grants provided by Conselho Nacional de Desenvolvimento Científico e Tecnológico – CNPq and Coordenação de Aperfeiçoamento de Pessoal de Nível superior – CAPES.
Financial support
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Conflict of interest
None.
Ethical standards
The approval of the ethics committee regarding the use of animals was not necessary in this study. The data were collected from previously published sources.








