1. Introduction
Electro-vortex flows (EVF) develop in conductive liquids due to an electric current which interacts with its own magnetic field (Bojarevich et al. Reference Bojarevich, Freibergs, Shilova and Shcherbinin1989). The EVF essentially affect many engineering devices such as electric arc furnaces (Kazak & Semko Reference Kazak and Semko2011; Kazak Reference Kazak2013), liquid metal pumps (Khripchenko, Kolesnichenko & Dolgikh Reference Khripchenko, Kolesnichenko and Dolgikh2008; Denisov et al. Reference Denisov, Dolgikh, Khripchenko and Kolesnichenko2016) and liquid metal batteries (LMB), (Kelley & Weier Reference Kelley and Weier2018; Herreman et al. Reference Herreman, Nore, Cappanera and Guermond2021). The canonical problem in EVF studies concerns the liquid metal flows in axisymmetric cells with an electrode localized on its axis (at the solid end or on a free surface). The cylindrical geometry has been widely used starting from early experiments (Millere, Sharamkin & Shcherbinin Reference Millere, Sharamkin and Shcherbinin1980; Zhilin et al. Reference Zhilin, Ivochkin, Oksman, Lurinsh, Chaikovskii, Chudnovskii and Shcherbinin1986), and becomes quite popular in the context of LMB (Herreman et al. Reference Herreman, Nore, Ziebell Ramos, Cappanera, Guermond and Weber2019; Kolesnichenko et al. Reference Kolesnichenko, Frick, Eltishchev, Mandrykin and Stefani2020; Liu et al. Reference Liu, Stefani, Weber, Weier and Li2020; Herreman et al. Reference Herreman, Nore, Cappanera and Guermond2021).
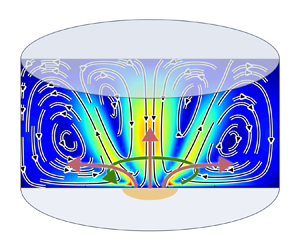
A scheme of the considered cylindrical EVF cell is given in figure 1. A strong electric current (![]() $\boldsymbol {j}$ is its density) diverges from the axial electrode located at the cell bottom and produces the magnetic field
$\boldsymbol {j}$ is its density) diverges from the axial electrode located at the cell bottom and produces the magnetic field ![]() $\boldsymbol {B}_j$. The interaction of this field with the current gives rise to the poloidal volumetric Lorentz force
$\boldsymbol {B}_j$. The interaction of this field with the current gives rise to the poloidal volumetric Lorentz force ![]() $\boldsymbol {f}_L$ responsible for the EVF generation. The role of a second electrode is played in our case by the sidewall. Conventionally, a solid upper end face serves as a second electrode, but we prefer the side electrode because it makes it possible to consider both the solid and free upper boundaries by applying electrodes of the same geometry.
$\boldsymbol {f}_L$ responsible for the EVF generation. The role of a second electrode is played in our case by the sidewall. Conventionally, a solid upper end face serves as a second electrode, but we prefer the side electrode because it makes it possible to consider both the solid and free upper boundaries by applying electrodes of the same geometry.

Figure 1. Current, magnetic field and forces in the EVF cell with a central electrode.
The EVF in this configuration has a purely poloidal structure, comprising only a radial and a vertical velocity. However, any external vertical magnetic field ![]() $\boldsymbol {B}_{ext}$ produces the azimuthal Lorentz force
$\boldsymbol {B}_{ext}$ produces the azimuthal Lorentz force ![]() $\boldsymbol {f}_{az}$, spinning the flow and making the EVF sensitive to external magnetic fields. For example, EVF experiments in a semispherical cell showed that the Earth's magnetic field causes an intense azimuthal flow under any conditions (Vinogradov, Ivochkin & Teplyakov Reference Vinogradov, Ivochkin and Teplyakov2018). Moreover, the weak azimuthal volumetric force (
$\boldsymbol {f}_{az}$, spinning the flow and making the EVF sensitive to external magnetic fields. For example, EVF experiments in a semispherical cell showed that the Earth's magnetic field causes an intense azimuthal flow under any conditions (Vinogradov, Ivochkin & Teplyakov Reference Vinogradov, Ivochkin and Teplyakov2018). Moreover, the weak azimuthal volumetric force (![]() $|\boldsymbol {f}_{az}| \ll |\boldsymbol {f}_L|$) can effectively suppress the EVF by a kind of Ekman pumping (Davidson et al. Reference Davidson, Kinner, Lingwood, Short and He1999). The experimental and numerical study of the EVF in a cylindrical cell showed that the Earth's magnetic field is strong enough to reduce the EVF (in a saturated state) several times (Liu et al. Reference Liu, Stefani, Weber, Weier and Li2020).
$|\boldsymbol {f}_{az}| \ll |\boldsymbol {f}_L|$) can effectively suppress the EVF by a kind of Ekman pumping (Davidson et al. Reference Davidson, Kinner, Lingwood, Short and He1999). The experimental and numerical study of the EVF in a cylindrical cell showed that the Earth's magnetic field is strong enough to reduce the EVF (in a saturated state) several times (Liu et al. Reference Liu, Stefani, Weber, Weier and Li2020).
It is worth noting here that the characteristic time needed to generate the EVF is usually much shorter than the evolution time of the rotating flow. That is the reason why strong transient states appear when the electric current is switched on. These states were recently studied in detail by Kolesnichenko et al. (Reference Kolesnichenko, Frick, Eltishchev, Mandrykin and Stefani2020) and the mechanism of poloidal flow suppression, as proposed by Davidson et al. (Reference Davidson, Kinner, Lingwood, Short and He1999), was confirmed experimentally and numerically. It was shown that EVF in large-scale LMB, especially during the switch-on process when the transient poloidal flows are up to two orders of magnitude stronger than those existing in the saturated state, require a great deal of care. Note that Kolesnichenko et al. (Reference Kolesnichenko, Frick, Eltishchev, Mandrykin and Stefani2020) performed the experiment in a cell where the liquid metal surface was free, while the simulations were done for a solid upper boundary. Nevertheless, the results obtained were very similar. This fact deserves attention because the conventional Ekman pumping is sensitive to viscous boundary layers. Moreover, the Ekman pumping produced by the bottom boundary layer acts not against the EVF (as in the case of the electrode located on the upper free surface, which was considered by Davidson et al. (Reference Davidson, Kinner, Lingwood, Short and He1999)), but is codirected with the EVF. So, the mechanism of poloidal flow suppression is not fully understood.
In this paper, we revisit the EVF in cylindrical cells with the intent to analyse in detail the mechanism of poloidal flow suppression by a weak axial magnetic field and to clarify the influence of boundary conditions and governing parameters on the saturated flow. For this purpose, we performed a series of laboratory experiments and numerical simulations of the EVF in a cylindrical cell placed in an external magnetic field. The cell was filled with a gallium alloy. The electric current was supplied to the centre of the cell bottom and collected on the entire sidewall of the cylinder. The external magnetic field was directed vertically, so that it coincides with the cell axis. In both numerical and experimental studies, the electric current and the external magnetic field were varied. The experiments were performed in a liquid gallium alloy with a free surface and a solid cover, while the simulations were done for a solid boundary only.
2. Experimental set-up and methods
A schematic of the experimental set-up is shown in figure 2. The sidewall (labelled 1) of the cylindrical cell of inner diameter ![]() $D=201.4$ mm is made of stainless steel and it is tinned on the inside. The bottom end of the cell (labelled 2) is made of Plexiglas. It has eight slots for the ultrasonic Doppler velocimeter (UDV) probes (labelled 7) located at radius
$D=201.4$ mm is made of stainless steel and it is tinned on the inside. The bottom end of the cell (labelled 2) is made of Plexiglas. It has eight slots for the ultrasonic Doppler velocimeter (UDV) probes (labelled 7) located at radius ![]() $r=90$ mm. A Plexiglas lid can be placed on the liquid metal surface. The cylindrical copper cathode (labelled 4) of diameter
$r=90$ mm. A Plexiglas lid can be placed on the liquid metal surface. The cylindrical copper cathode (labelled 4) of diameter ![]() $d=30$ mm is located on the cell axis. The end face of the cathode is tinned and aligned with the bottom. The sidewall serves as an anode which is connected to the power supply by the copper tube (labelled 5) coaxially mounted from the outside of the cathode. This compensates the magnetic field of the supply cables to a large extent. The power supply provides a direct current up to 1200 A.
$d=30$ mm is located on the cell axis. The end face of the cathode is tinned and aligned with the bottom. The sidewall serves as an anode which is connected to the power supply by the copper tube (labelled 5) coaxially mounted from the outside of the cathode. This compensates the magnetic field of the supply cables to a large extent. The power supply provides a direct current up to 1200 A.

Figure 2. Photograph and scheme of the experimental set-up (cut view): 1, sidewall; 2, Plexiglas bottom end face; 3, gallium alloy; 4, cathode; 5, anode; 6, Helmholtz coils; 7, UDV transducers. The beam direction of the UDV probe is indicated with a dashed magenta line.
The cell was filled with a ![]() $\mathrm {Ga}_{86.3} \mathrm {Zn}_{10.8} \mathrm {Sn}_{2.9}$ (wt.%) liquid alloy (labelled 3). The melting temperature of this alloy is 17
$\mathrm {Ga}_{86.3} \mathrm {Zn}_{10.8} \mathrm {Sn}_{2.9}$ (wt.%) liquid alloy (labelled 3). The melting temperature of this alloy is 17![]() $^{\circ }$C. Its main physical properties at room temperature are as follows: density
$^{\circ }$C. Its main physical properties at room temperature are as follows: density ![]() $\rho = 6256$ kg m
$\rho = 6256$ kg m![]() $^{-3}$; kinematic viscosity
$^{-3}$; kinematic viscosity ![]() $\nu = 3\times 10^{-7}$ m
$\nu = 3\times 10^{-7}$ m![]() $^{2}$ s
$^{2}$ s![]() $^{-1}$; electric conductivity
$^{-1}$; electric conductivity ![]() $\sigma = 3.56 \times 10^{6}$ S m
$\sigma = 3.56 \times 10^{6}$ S m![]() $^{-1}$; and sound velocity
$^{-1}$; and sound velocity ![]() $V_{s}=2740$ m s
$V_{s}=2740$ m s![]() $^{-1}$. The distance between the vessel bottom and the free surface of the liquid metal was
$^{-1}$. The distance between the vessel bottom and the free surface of the liquid metal was ![]() $H=100$ mm. Two flow configurations were considered in the experiments, with a solid cover and with a free surface.
$H=100$ mm. Two flow configurations were considered in the experiments, with a solid cover and with a free surface.
The cell was placed in an external vertical magnetic field, which was created by the Helmholtz coils (labelled 6). The average radius of the coils was ![]() $240$ mm, which made it possible to get a sufficiently uniform magnetic field inside the cell (its inhomogeneity was less than 1 %).
$240$ mm, which made it possible to get a sufficiently uniform magnetic field inside the cell (its inhomogeneity was less than 1 %).
The main governing parameter of the EVF, which characterizes the ratio between the Lorentz and viscous forces, is the so-called EVF parameter (Bojarevich et al. Reference Bojarevich, Freibergs, Shilova and Shcherbinin1989):
In our experiments, we applied a direct electric current ![]() $400\leq I\leq 1200$ A, which corresponds to
$400\leq I\leq 1200$ A, which corresponds to ![]() $8.5 \times 10^{6}\leq S\leq 7.6 \times 10^{7}$.
$8.5 \times 10^{6}\leq S\leq 7.6 \times 10^{7}$.
The study of the structure of the EVF was carried out using a UDV. Eight UDV transducers were located at the bottom of the cell. The positions of the UDV probes are shown in figure 3(b). Each probe allowed us to record the vertical component of the flow velocity of the liquid metal along the vertical beam.

Figure 3. Computational domain (a) and UDV probe positioning (b).
The experimental work included two parts: a study of the EVF in the Earth's magnetic field at different values of electric current in a range from 400 to 1200 A; a study of the influence of an external vertical magnetic field on the flow at a constant electric current of 1000 A. The magnetic field ![]() $B_{ext}$ varied from 0.02 to 5 mT.
$B_{ext}$ varied from 0.02 to 5 mT.
3. Mathematical model and numerical simulations
The computational domain is a cylinder with a height ![]() $H = 100$ mm and a diameter
$H = 100$ mm and a diameter ![]() $D = 200$ mm (see figure 3a). The electric current flows through the electrode (labelled 1),
$D = 200$ mm (see figure 3a). The electric current flows through the electrode (labelled 1), ![]() $30$ mm in diameter located in the centre of the bottom end face of the cylinder. The circuit is completed at the entire sidewall (labelled 2). The external magnetic field is considered homogeneous and its direction coincides with the cylinder axis. In the computations and graphical representation of the results, we use a right-handed Cartesian coordinate system, the origin of which is located at the centre of the cell bottom. The
$30$ mm in diameter located in the centre of the bottom end face of the cylinder. The circuit is completed at the entire sidewall (labelled 2). The external magnetic field is considered homogeneous and its direction coincides with the cylinder axis. In the computations and graphical representation of the results, we use a right-handed Cartesian coordinate system, the origin of which is located at the centre of the cell bottom. The ![]() $z$-axis of this system coinciding with the symmetry axis of the cell is directed upwards from the centre of the bottom end face.
$z$-axis of this system coinciding with the symmetry axis of the cell is directed upwards from the centre of the bottom end face.
The cylindrical cell is filled with a gallium alloy, the material properties of which are the same as in the experimental study.
We consider the flow of an incompressible fluid described by the Navier–Stokes and continuity equations
where ![]() $\boldsymbol {v}$ is the velocity vector,
$\boldsymbol {v}$ is the velocity vector, ![]() $p$ is the pressure and
$p$ is the pressure and ![]() $\nu$ is the kinematic viscosity. Here,
$\nu$ is the kinematic viscosity. Here, ![]() $\boldsymbol {f}_L$ is the volumetric Lorentz force responsible for the EVF generation, and it is determined as
$\boldsymbol {f}_L$ is the volumetric Lorentz force responsible for the EVF generation, and it is determined as
where ![]() $\boldsymbol {j}$ is the electric current density,
$\boldsymbol {j}$ is the electric current density, ![]() $\boldsymbol {B}_j$ is the own magnetic field of the electric current, and
$\boldsymbol {B}_j$ is the own magnetic field of the electric current, and ![]() $\boldsymbol {B}_{ext}$ is the external magnetic field.
$\boldsymbol {B}_{ext}$ is the external magnetic field.
Since the magnetic Reynolds number of the flow is much smaller than 1, we employ the inductionless approximation. This means that the Lorentz force field is only computed once at the beginning of the simulations, while the induction effects of the arising velocity are neglected The current density is found by solving the equations for electric potential:
Then, the magnetic field is determined by using the Biot–Savart law, and the Lorentz force distribution is calculated following (3.3).
The scheme of the EVF generation is presented in figure 1.
The boundary conditions for the electric potential on the anode (labelled 1) (see figure 3a) and cathode (labelled 2) are set with fixed electric potentials, whereas at the insulating parts ![]() $\partial \varphi / \partial \boldsymbol {n} = 0$ is applied. The no-slip conditions for the velocity are employed on all boundaries.
$\partial \varphi / \partial \boldsymbol {n} = 0$ is applied. The no-slip conditions for the velocity are employed on all boundaries.
The numerical simulations were performed using the ANSYS software. The problem was solved in two steps. First, the electromagnetic force field was computed in ANSYS Emag and then it was transferred into ANSYS Fluent and involved in the simulations of the hydrodynamics. The block-structured mesh, consisting of ![]() $268\,800$ hexahedrons, was used in computations, and the fixed time step was
$268\,800$ hexahedrons, was used in computations, and the fixed time step was ![]() $0.1$ s. The standard
$0.1$ s. The standard ![]() $k$-
$k$-![]() $\omega$ turbulence model was used. All computations started from the zero-velocity state of the system.
$\omega$ turbulence model was used. All computations started from the zero-velocity state of the system.
4. The EVF in the absence of an external magnetic field
In the laboratory, the experimental set-up is always exposed to a weak magnetic field, at least the Earth's field. For this reason, the evolution of a pure EVF with increasing current was examined in numerical simulations, which were performed for the cell with a solid upper boundary. The structure of the poloidal velocity field for different current values is shown in figure 4. Figure 4(a–c) corresponds to the instant velocity fields in the ![]() $zOx$ plane at
$zOx$ plane at ![]() $t = 350$ s. The colour represents the poloidal velocity magnitude, and the lines with arrows visualize the vector velocity field (trajectories of Lagrangian particles). At weak electric current
$t = 350$ s. The colour represents the poloidal velocity magnitude, and the lines with arrows visualize the vector velocity field (trajectories of Lagrangian particles). At weak electric current ![]() $I=50$ A, a stable upward jet is formed at the cell axis, and one stable axisymmetric vortex occupies the whole cell. This large-scale vortex of toroidal shape dominates at any current, but with increasing current
$I=50$ A, a stable upward jet is formed at the cell axis, and one stable axisymmetric vortex occupies the whole cell. This large-scale vortex of toroidal shape dominates at any current, but with increasing current ![]() $I$ the stability is lost and the flow starts oscillating (the fields for
$I$ the stability is lost and the flow starts oscillating (the fields for ![]() $I=250$ A and
$I=250$ A and ![]() $I=750$ A). At high current, the axial upward jet becomes more divergent and the vortex central line moves down. This tendency can be observed in the time-averaged velocity fields (averaged over 1000 s), shown in figure 4(d–f).
$I=750$ A). At high current, the axial upward jet becomes more divergent and the vortex central line moves down. This tendency can be observed in the time-averaged velocity fields (averaged over 1000 s), shown in figure 4(d–f).

Figure 4. Instant (a–c) and time-averaged over 1000 s (d,e) and 500 s ( f) fields of poloidal velocity in the ![]() $xOz$ plane in a pure EVF flow (no external magnetic field) at the electric current
$xOz$ plane in a pure EVF flow (no external magnetic field) at the electric current ![]() $I=50$ A (a,d),
$I=50$ A (a,d), ![]() $I=250$ A (b,e) and
$I=250$ A (b,e) and ![]() $I=750$ A (c, f), which correspond to the values of EVF parameter
$I=750$ A (c, f), which correspond to the values of EVF parameter ![]() $S=4 \times 10^{5}$,
$S=4 \times 10^{5}$, ![]() $S= 10^{7}$ and
$S= 10^{7}$ and ![]() $S=10^{8}$, respectively. The magenta line indicates the direction of the UDV beams.
$S=10^{8}$, respectively. The magenta line indicates the direction of the UDV beams.
For the EVF at strong currents, a linear dependence of the flow velocity on the current is expected (Bojarevich et al. Reference Bojarevich, Freibergs, Shilova and Shcherbinin1989). This linear dependence was first confirmed in the experimental study of EVF performed by Zhilin et al. (Reference Zhilin, Ivochkin, Oksman, Lurinsh, Chaikovskii, Chudnovskii and Shcherbinin1986) for the electric current in the range ![]() $0 < I < 1500$ A (
$0 < I < 1500$ A (![]() $10^{3} < S < 10^{6}$) passing through the cylindrical cell of a diameter
$10^{3} < S < 10^{6}$) passing through the cylindrical cell of a diameter ![]() $60$ mm, which was filled with mercury.
$60$ mm, which was filled with mercury.
In figure 5, we present our numerical results (together with the experimental data) for the dependence of the Reynolds numbers on the EVF parameter ![]() $S$. Because the experimental results concern the vertical velocity along the UDV beam only (shown in figure 4 by dashed red lines), we used for numerical data the same information. Two Reynolds numbers are shown:
$S$. Because the experimental results concern the vertical velocity along the UDV beam only (shown in figure 4 by dashed red lines), we used for numerical data the same information. Two Reynolds numbers are shown:
The first, ![]() $Re$, is defined through the maximal mean velocity along the UDV beam,
$Re$, is defined through the maximal mean velocity along the UDV beam, ![]() $U_{max}$ (
$U_{max}$ (![]() $R$ is the cell radius), and it characterizes the large-scale flow in the cell. The second,
$R$ is the cell radius), and it characterizes the large-scale flow in the cell. The second, ![]() $Re_t$, is defined through the root mean square (r.m.s.) fluctuations of the vertical velocity, and it characterizes the intensity of fluctuations. Note that
$Re_t$, is defined through the root mean square (r.m.s.) fluctuations of the vertical velocity, and it characterizes the intensity of fluctuations. Note that ![]() $Re$ was calculated in a similar way in the experiments and in the numerical simulations, while
$Re$ was calculated in a similar way in the experiments and in the numerical simulations, while ![]() $Re_t$ was calculated in the numerical experiments only. The plot includes three sets of points, which correspond to two experimental series with the free and solid upper boundaries, and to numerical simulations. All the points follow the dependence
$Re_t$ was calculated in the numerical experiments only. The plot includes three sets of points, which correspond to two experimental series with the free and solid upper boundaries, and to numerical simulations. All the points follow the dependence ![]() $Re \sim \sqrt {S}$, demonstrating some small but systematic excess of the experimental points of the first group (solid boundary) over the second one (free boundary). Again, there is a good agreement between the experiment and simulation results. The second Reynolds number,
$Re \sim \sqrt {S}$, demonstrating some small but systematic excess of the experimental points of the first group (solid boundary) over the second one (free boundary). Again, there is a good agreement between the experiment and simulation results. The second Reynolds number, ![]() $Re_t$, shows that strong fluctuations occur at
$Re_t$, shows that strong fluctuations occur at ![]() $S\approx 3 \times 10^{6}$ (
$S\approx 3 \times 10^{6}$ (![]() $I = 250$ A). Then
$I = 250$ A). Then ![]() $Re_t\approx 0.2 Re$, and it grows like
$Re_t\approx 0.2 Re$, and it grows like ![]() $Re_t \sim \sqrt {S}$ at higher
$Re_t \sim \sqrt {S}$ at higher ![]() $S$.
$S$.

Figure 5. Reynolds numbers ![]() $Re$ (points) and
$Re$ (points) and ![]() $Re_t$ (black crosses) versus the EVF parameter
$Re_t$ (black crosses) versus the EVF parameter ![]() $S$. The experimental data for
$S$. The experimental data for ![]() $Re$ are shown by green points for the solid upper boundary and by blue points for the free surface. Numerical data are indicated by red points (
$Re$ are shown by green points for the solid upper boundary and by blue points for the free surface. Numerical data are indicated by red points (![]() $Re$) and black crosses (
$Re$) and black crosses (![]() $Re_t$).
$Re_t$).
Two series of experiments were performed under different upper boundary conditions: for free surface and for solid cover. The electric current varies in both series from ![]() $I=400$ A to
$I=400$ A to ![]() $I=1200$ A with a step
$I=1200$ A with a step ![]() $100$ A. No external magnetic field was applied. The magnetic field measured in the cell in the absence of the electric current and the applied magnetic field was
$100$ A. No external magnetic field was applied. The magnetic field measured in the cell in the absence of the electric current and the applied magnetic field was ![]() $B_y=0.01$ mT,
$B_y=0.01$ mT, ![]() $B_z=0.02$ mT. In each experiment, the vertical velocity was measured by the UDV along eight vertical beams. The sensor locations are shown in figures 3(b) and 4. The velocity was recorded during
$B_z=0.02$ mT. In each experiment, the vertical velocity was measured by the UDV along eight vertical beams. The sensor locations are shown in figures 3(b) and 4. The velocity was recorded during ![]() $500$ s at saturated state (at
$500$ s at saturated state (at ![]() $t>100$ s). The mean velocity profiles, averaged over all eight beams, are shown in figure 6. The increasing current provides a monotonic increasing velocity – the typical EVF velocity is expected to grow linearly with
$t>100$ s). The mean velocity profiles, averaged over all eight beams, are shown in figure 6. The increasing current provides a monotonic increasing velocity – the typical EVF velocity is expected to grow linearly with ![]() $I$ (Zhilin et al. Reference Zhilin, Ivochkin, Oksman, Lurinsh, Chaikovskii, Chudnovskii and Shcherbinin1986), see figure 5. At any state in the considered range of current
$I$ (Zhilin et al. Reference Zhilin, Ivochkin, Oksman, Lurinsh, Chaikovskii, Chudnovskii and Shcherbinin1986), see figure 5. At any state in the considered range of current ![]() $I$, the velocity profiles demonstrate a general downward flow at the cell periphery, which corresponds to the expected EVF in the form of a large-scale toroidal vortex. The only difference is that, with increasing current, the velocity extremum shifts to the upper boundary if this boundary is free and shifts to the bottom if it is solid.
$I$, the velocity profiles demonstrate a general downward flow at the cell periphery, which corresponds to the expected EVF in the form of a large-scale toroidal vortex. The only difference is that, with increasing current, the velocity extremum shifts to the upper boundary if this boundary is free and shifts to the bottom if it is solid.

Figure 6. Experimental profiles of the mean vertical velocity ![]() $v_z$ averaged over the UDV probes 1–8 for different values of the electric current
$v_z$ averaged over the UDV probes 1–8 for different values of the electric current ![]() $I$ for the EVF in the cell with a free surface (a) and a solid upper boundary (b). Here
$I$ for the EVF in the cell with a free surface (a) and a solid upper boundary (b). Here ![]() ${B_{ext}}=0$.
${B_{ext}}=0$.
5. The EVF under the influence of an external magnetic field
For the fixed electric current ![]() $I=1000$ A, two series of experiments (for free surface and for solid cover) were performed for different external magnetic fields
$I=1000$ A, two series of experiments (for free surface and for solid cover) were performed for different external magnetic fields ![]() $0 < {B_{ext}} \leq 5$ mT. The measurements were done at a saturated state. The corresponding mean velocity profiles are shown in figure 7. Two sets of the profiles are qualitatively similar, demonstrating a weak dependence on the boundary condition at the upper boundary. In the presence of a weak magnetic field (
$0 < {B_{ext}} \leq 5$ mT. The measurements were done at a saturated state. The corresponding mean velocity profiles are shown in figure 7. Two sets of the profiles are qualitatively similar, demonstrating a weak dependence on the boundary condition at the upper boundary. In the presence of a weak magnetic field (![]() ${B_{ext}} \leq 0.1$ mT), the EVF is poorly affected by the field, and the velocity profile keeps the structure of the pure EVF. At a larger magnetic field, the velocity decreases and at
${B_{ext}} \leq 0.1$ mT), the EVF is poorly affected by the field, and the velocity profile keeps the structure of the pure EVF. At a larger magnetic field, the velocity decreases and at ![]() ${B_{ext}} \approx 0.5$ mT an upward flow occurs at the cell periphery. Again, the velocity maximum observed in the case of a free surface shifts upward as compared with that of a solid boundary.
${B_{ext}} \approx 0.5$ mT an upward flow occurs at the cell periphery. Again, the velocity maximum observed in the case of a free surface shifts upward as compared with that of a solid boundary.

Figure 7. Experimental profiles of the mean vertical velocity ![]() $v_z$ averaged over UDV probes 1–8 for fixed electric current
$v_z$ averaged over UDV probes 1–8 for fixed electric current ![]() $I=1000$ A and different magnetic fields
$I=1000$ A and different magnetic fields ![]() ${B_{ext}}$: free surface (a); solid upper boundary (b).
${B_{ext}}$: free surface (a); solid upper boundary (b).
Numerical simulations allow us to study the entire three-dimensional velocity field. However, we are first interested in a comparison with experimental data. In this connection, we calculated in the numerical simulations the same velocity profiles which were recorded in experiments. Figure 8 presents the numerical and experimental velocity profiles determined in the presence of a weak external magnetic field, i.e. the experimental results obtained without the applied magnetic field (the Earth's magnetic field remains, of course) are compared with the results of simulations made for the applied magnetic field: ![]() ${B_{ext}} = 0.01$ mT;
${B_{ext}} = 0.01$ mT; ![]() ${B_{ext}} = B_{Earth}$;
${B_{ext}} = B_{Earth}$; ![]() ${B_{ext}} = 0.03$ mT. This set of the applied magnetic field values was chosen because EVF are very sensitive to the vertical external field. Figure 8 shows that the experimental profile is similar to the profile calculated for
${B_{ext}} = 0.03$ mT. This set of the applied magnetic field values was chosen because EVF are very sensitive to the vertical external field. Figure 8 shows that the experimental profile is similar to the profile calculated for ![]() ${B_{ext}} = 0.01$ mT, i.e. for the field weaker than the Earth's field. In the simulations, the critical magnetic field of the poloidal suppression is lower than the one in the experiments, which is to be shown in detail below.
${B_{ext}} = 0.01$ mT, i.e. for the field weaker than the Earth's field. In the simulations, the critical magnetic field of the poloidal suppression is lower than the one in the experiments, which is to be shown in detail below.

Figure 8. Experimental and numerical profiles (NS) of the mean vertical velocity ![]() $v_z$ under weak external magnetic field. Solid upper boundary.
$v_z$ under weak external magnetic field. Solid upper boundary.
Now, we fix the electric current at ![]() $I=1000$ A (
$I=1000$ A (![]() $S = 5.3 \times 10^{7}$) and investigate in numerical simulations the EVF under various external magnetic fields. As a reference case, we simulate the EVF without the external magnetic field. The corresponding poloidal and azimuthal velocity fields are presented in figure 9(a,d). The poloidal flow exhibits one fluctuating vortex; similar vortex was shown above for the low electric current. No stable mean azimuthal flow exists in the absence of a vertical magnetic field. The instant distribution of
$S = 5.3 \times 10^{7}$) and investigate in numerical simulations the EVF under various external magnetic fields. As a reference case, we simulate the EVF without the external magnetic field. The corresponding poloidal and azimuthal velocity fields are presented in figure 9(a,d). The poloidal flow exhibits one fluctuating vortex; similar vortex was shown above for the low electric current. No stable mean azimuthal flow exists in the absence of a vertical magnetic field. The instant distribution of ![]() $v_y$ indicates some azimuthal fluctuations.
$v_y$ indicates some azimuthal fluctuations.

Figure 9. Instant fields of the poloidal (a–c) and azimuthal (d–f) velocities in the ![]() $xOz$ plane in the absence of an external magnetic field (a,d), in the magnetic field
$xOz$ plane in the absence of an external magnetic field (a,d), in the magnetic field ![]() ${B_{ext}} = 0.05$ mT (b,e) and in a strong vertical magnetic field
${B_{ext}} = 0.05$ mT (b,e) and in a strong vertical magnetic field ![]() ${B_{ext}} = 1$ mT (c, f).
${B_{ext}} = 1$ mT (c, f).
Next, we simulate the flow in the Earth's magnetic field, namely, in the field measured near the laboratory experimental set-up, ![]() $B_z=0.05$ mT,
$B_z=0.05$ mT, ![]() $B_x=0.015$ mT. Note that these values differ from those previously described in § 2. This is due to the fact that the magnetic field value used in numerical simulations was measured in the absence of the laboratory set-up. For the experiments, the magnetic field was measured in the same spot, but inside the cell filled with liquid gallium alloy (in the switched-off set-up). The simulations showed that this weak magnetic field is sufficient to essentially suppress the poloidal motion (see figure 9b,e). The remains of the poloidal motion are concentrated in the vicinity of the electrode edges. The azimuthal velocity field shows a developed swirl. Note that the rotation is highly inhomogeneous – the strongest rotation is located in a narrow ring domain, which coincides with the domain of a more intense poloidal flow.
$B_x=0.015$ mT. Note that these values differ from those previously described in § 2. This is due to the fact that the magnetic field value used in numerical simulations was measured in the absence of the laboratory set-up. For the experiments, the magnetic field was measured in the same spot, but inside the cell filled with liquid gallium alloy (in the switched-off set-up). The simulations showed that this weak magnetic field is sufficient to essentially suppress the poloidal motion (see figure 9b,e). The remains of the poloidal motion are concentrated in the vicinity of the electrode edges. The azimuthal velocity field shows a developed swirl. Note that the rotation is highly inhomogeneous – the strongest rotation is located in a narrow ring domain, which coincides with the domain of a more intense poloidal flow.
In the strong vertical magnetic field ![]() ${B_{ext}} = 1$ mT, the rotational flow penetrates the entire height of the cell, and the azimuthal velocity becomes practically uniform along the height, with the exception of a thin boundary layer near the solid walls (see figure 9a,d). The poloidal flow is manifested by only two pairs of small-scale vortices observed near the upper and lower ends of the cylinder and occurred due to Ekman pumping in viscous layers. Note that the velocity field is symmetric with respect to the vertical field (transferring the electrode to the upper surface will not change the picture).
${B_{ext}} = 1$ mT, the rotational flow penetrates the entire height of the cell, and the azimuthal velocity becomes practically uniform along the height, with the exception of a thin boundary layer near the solid walls (see figure 9a,d). The poloidal flow is manifested by only two pairs of small-scale vortices observed near the upper and lower ends of the cylinder and occurred due to Ekman pumping in viscous layers. Note that the velocity field is symmetric with respect to the vertical field (transferring the electrode to the upper surface will not change the picture).
For a quantitative comparison of the intensities of the poloidal and rotational motions of the metal, we calculate the energy of each flow
where ![]() $v_r$ and
$v_r$ and ![]() $v_\varphi$ are the radial and azimuthal velocity components. Then, the total energy is
$v_\varphi$ are the radial and azimuthal velocity components. Then, the total energy is ![]() ${E_{tot}} = {E_{pol}} + {E_{az}}$. The dependence of these energies on the external magnetic field (see figure 10) shows that the critical value of the field is a value that is sufficient to swirl the metal in such a way that the rotational motion energy becomes comparable to the poloidal EVF energy. This fact was first established by Davidson et al. (Reference Davidson, Kinner, Lingwood, Short and He1999) and illustrated with an EVF in a hemispherical cell with an electrode on the upper free surface. For a cylindrical cell with a bottom electrode, this result has been recently confirmed by Kolesnichenko et al. (Reference Kolesnichenko, Frick, Eltishchev, Mandrykin and Stefani2020). Figure 10 shows that the weak magnetic field (
${E_{tot}} = {E_{pol}} + {E_{az}}$. The dependence of these energies on the external magnetic field (see figure 10) shows that the critical value of the field is a value that is sufficient to swirl the metal in such a way that the rotational motion energy becomes comparable to the poloidal EVF energy. This fact was first established by Davidson et al. (Reference Davidson, Kinner, Lingwood, Short and He1999) and illustrated with an EVF in a hemispherical cell with an electrode on the upper free surface. For a cylindrical cell with a bottom electrode, this result has been recently confirmed by Kolesnichenko et al. (Reference Kolesnichenko, Frick, Eltishchev, Mandrykin and Stefani2020). Figure 10 shows that the weak magnetic field (![]() ${B_{ext}} \leq 0.01$ mT) does not affect the poloidal motion. At this
${B_{ext}} \leq 0.01$ mT) does not affect the poloidal motion. At this ![]() ${B_{ext}}$, the finite azimuthal energy
${B_{ext}}$, the finite azimuthal energy ![]() ${E_{az}}$ is provided by small-scale velocity fluctuations. The global rotational flow develops monotonically with increasing
${E_{az}}$ is provided by small-scale velocity fluctuations. The global rotational flow develops monotonically with increasing ![]() ${B_{ext}}$ as demonstrated in figure 11, where the mean azimuthal velocity at the cell periphery (namely, at
${B_{ext}}$ as demonstrated in figure 11, where the mean azimuthal velocity at the cell periphery (namely, at ![]() $r=0.9R$) is plotted against the applied magnetic field.
$r=0.9R$) is plotted against the applied magnetic field.

Figure 10. Poloidal and azimuthal energies as a function of the external vertical magnetic field. ![]() $I=1000$ A. Numerical simulations. An extended version of figure 9 from Kolesnichenko et al. (Reference Kolesnichenko, Frick, Eltishchev, Mandrykin and Stefani2020).
$I=1000$ A. Numerical simulations. An extended version of figure 9 from Kolesnichenko et al. (Reference Kolesnichenko, Frick, Eltishchev, Mandrykin and Stefani2020).

Figure 11. Mean azimuthal velocity at ![]() $r=0.9R$ versus the external magnetic field. Here
$r=0.9R$ versus the external magnetic field. Here ![]() $I=1000$ A.
$I=1000$ A.
At ![]() ${B_{ext}} \approx 0.01$ mT, the poloidal energy
${B_{ext}} \approx 0.01$ mT, the poloidal energy ![]() ${E_{pol}}$ starts to decrease and, after the point at which
${E_{pol}}$ starts to decrease and, after the point at which ![]() ${E_{pol}} \approx {E_{az}}$, it falls down by two orders of magnitude. Upon reaching the magnetic field
${E_{pol}} \approx {E_{az}}$, it falls down by two orders of magnitude. Upon reaching the magnetic field ![]() ${B_{ext}} \approx 0.04$ mT, both energies
${B_{ext}} \approx 0.04$ mT, both energies ![]() ${E_{pol}}$ and
${E_{pol}}$ and ![]() ${E_{az}}$ increase, which causes an increase in the magnetic field, and follow a similar power law dependence (close to the linear one), and the poloidal flow energy remains approximately two orders of magnitude less than the azimuthal flow energy. Note that this sharp decrease in the flow energy is accompanied by an equally strong decrease in the level of fluctuations of the flow energy (see figure 12).
${E_{az}}$ increase, which causes an increase in the magnetic field, and follow a similar power law dependence (close to the linear one), and the poloidal flow energy remains approximately two orders of magnitude less than the azimuthal flow energy. Note that this sharp decrease in the flow energy is accompanied by an equally strong decrease in the level of fluctuations of the flow energy (see figure 12).

Figure 12. Standard deviation (SD) of the poloidal and azimuthal energies versus the external vertical magnetic field. Here ![]() $I=1000$ A.
$I=1000$ A.
The ![]() $E(B)$ dependencies shown in figure 10 cannot be verified experimentally because only the vertical velocity
$E(B)$ dependencies shown in figure 10 cannot be verified experimentally because only the vertical velocity ![]() $v_z$ is available for measurement along a few fixed lines (UDV beams). Therefore, we plot the dependence of the Reynolds number
$v_z$ is available for measurement along a few fixed lines (UDV beams). Therefore, we plot the dependence of the Reynolds number ![]() $Re$, which characterizes the poloidal motion defined as above through the maximal mean vertical velocity averaged over eight beams, on the external vertical magnetic field. Figure 13 presents the experimental points for the free and solid upper boundary, as well as the results of simulations performed in the same way. The latter (red points in figure 13) confirm that the Reynolds number defined in a localized periphery domain correctly reproduces the dependence
$Re$, which characterizes the poloidal motion defined as above through the maximal mean vertical velocity averaged over eight beams, on the external vertical magnetic field. Figure 13 presents the experimental points for the free and solid upper boundary, as well as the results of simulations performed in the same way. The latter (red points in figure 13) confirm that the Reynolds number defined in a localized periphery domain correctly reproduces the dependence ![]() ${E_{pol}}({B_{ext}})$ presented in figure 10. The experimental points follow a similar behaviour, but the strong poloidal motion suppression occurs at a stronger external magnetic field, namely, the decrease starts at
${E_{pol}}({B_{ext}})$ presented in figure 10. The experimental points follow a similar behaviour, but the strong poloidal motion suppression occurs at a stronger external magnetic field, namely, the decrease starts at ![]() ${B_{ext}} \approx 0.1$ mT versus
${B_{ext}} \approx 0.1$ mT versus ![]() ${B_{ext}} \approx 0.02$ mT observed in the numerical simulations. This shift cannot be explained by the presence of the Earth's magnetic field in experiments, because it should provide a shift of the experimental points in the opposite direction. However, the set-up is powered by strong currents and the magnetic fields of the power supply cables can induce fields that are substantially larger than the Earth's field. The current is distributed to the model through a few coaxial cables (see figure 2), but at a distance of approximately
${B_{ext}} \approx 0.02$ mT observed in the numerical simulations. This shift cannot be explained by the presence of the Earth's magnetic field in experiments, because it should provide a shift of the experimental points in the opposite direction. However, the set-up is powered by strong currents and the magnetic fields of the power supply cables can induce fields that are substantially larger than the Earth's field. The current is distributed to the model through a few coaxial cables (see figure 2), but at a distance of approximately ![]() $0.7$ m below the cell bottom the cables diverge in opposite directions. Additional numerical studies have shown that the EVF is sensitive to the magnetic field distortion, which can be induced, say, by the power supply cables. Note that the Reynolds numbers calculated in the experiments and simulations are close at a pure EVF (weak magnetic field) and similar at a suppressed state (minimal
$0.7$ m below the cell bottom the cables diverge in opposite directions. Additional numerical studies have shown that the EVF is sensitive to the magnetic field distortion, which can be induced, say, by the power supply cables. Note that the Reynolds numbers calculated in the experiments and simulations are close at a pure EVF (weak magnetic field) and similar at a suppressed state (minimal ![]() $Re$), while at a strong field (
$Re$), while at a strong field (![]() $1$ mT and more) the experiments demonstrate a stronger intensity of the poloidal motion. The influence of the horizontal component of the magnetic field was studied as well (see the Appendix).
$1$ mT and more) the experiments demonstrate a stronger intensity of the poloidal motion. The influence of the horizontal component of the magnetic field was studied as well (see the Appendix).

Figure 13. Reynolds number defined through the maximal vertical velocity along the UDV beam vs the applied vertical magnetic field. Results of numerical simulations (red) and experiments with solid (green) and free (blue) upper boundary. Here ![]() $I=1000$ A.
$I=1000$ A.
6. Dynamics and mechanism of EVF suppression under a vertical magnetic field
We have seen above that the EVF is strongly affected by the magnetic field and demonstrates dramatic changes in the flow pattern even under a weak vertical magnetic field. This flow reorganization is provided by the general metal rotation driven by the Lorentz force produced by the radial component of electric current and applied vertical magnetic field. The general suppression of poloidal motion, as shown by Davidson et al. (Reference Davidson, Kinner, Lingwood, Short and He1999), is due to the typical rotating flows redistribution of the pressure field (Ekman pumping). However, linear combinations of the original EVF and Ekman flows do not yield the structures observed in laboratory and numerical experiments.
For illustration, we show in figure 14 a simple scheme of the vertical velocity profiles along the UDV beam for the pure EVF (curve a) and for the EVF in a vertical magnetic field (curve d). This plot also presents two profiles expected for the flow induced in the cell by a homogeneous radial current in a vertical magnetic field if the surface is free (curve b) or solid (curve c). In both later cases, the poloidal flow is produced by Ekman pumping – note that in the cell with a free surface the flow pattern should be similar to the EVF pattern, and the solid cover causes a two-vortex flow structure to occur. To explain the origin of these profiles, we provide in the same figure schematics of corresponding poloidal flows in the cylindrical cell. It is also worth noting that the EVF under the applied magnetic field (curve d) practically does not depend on the upper boundary, and no direct combination of the EVF and Ekman flows can yield such curves (see figure 7).

Figure 14. Schematic of four kinds of poloidal flow in the cylindrical cell: a pure EVF (a); flows induced by the homogeneous radial current in a vertical magnetic field in the cell with a free surface (b) and with a solid cover (c); a flow associated with the velocity profile, observed in the EVF under a moderate vertical magnetic field (d). Corresponding sketches of vertical velocity profiles along the UDV beam (which is indicated by dashed magenta lines) are shown in the left-hand subpanel.
To understand the flow formation mechanism under the combined action of the poloidal and azimuthal forces, it is essential to analyse the time evolution of the flow pattern after the electric current is turned on. The point is that the evolution of the metal rotation in a relatively weak external magnetic field is a slow process in comparison with the evolution of the EVF itself. Therefore, if the current is switched on at ![]() $t=0$, the poloidal flow develops first and dominates until the azimuthal rotation becomes strong enough. Figure 15 illustrates the evolution of the energy of both poloidal and azimuthal flows for approximately 1000 s after the electric current
$t=0$, the poloidal flow develops first and dominates until the azimuthal rotation becomes strong enough. Figure 15 illustrates the evolution of the energy of both poloidal and azimuthal flows for approximately 1000 s after the electric current ![]() $I=1000$ A was switched on. Two cases are considered: the weak vertical magnetic field (
$I=1000$ A was switched on. Two cases are considered: the weak vertical magnetic field (![]() ${B_{ext}} = 0.01$ mT), which decreases the poloidal EVF, but is not sufficient to suppress it; and the moderate field (
${B_{ext}} = 0.01$ mT), which decreases the poloidal EVF, but is not sufficient to suppress it; and the moderate field (![]() ${B_{ext}} = 0.1$ mT), at which the poloidal flow reaches the minimal level of energy at saturated state.
${B_{ext}} = 0.1$ mT), at which the poloidal flow reaches the minimal level of energy at saturated state.

Figure 15. Evolution of the energy of poloidal and azimuthal flows under weak (![]() ${B_{ext}} = 0.01$ mT, panel a) and moderate (
${B_{ext}} = 0.01$ mT, panel a) and moderate (![]() ${B_{ext}} = 0.1$ mT, panel b) magnetic fields after the electric current
${B_{ext}} = 0.1$ mT, panel b) magnetic fields after the electric current ![]() $I=1000$ A is switched on.
$I=1000$ A is switched on.
At the very beginning of the process (the graphs start at time ![]() $t=0.1$ s), the poloidal energy is two to three orders of magnitude greater than the azimuthal energy and grows like
$t=0.1$ s), the poloidal energy is two to three orders of magnitude greater than the azimuthal energy and grows like ![]() ${\sim } t^{3/2}$ during the first second. Later the poloidal energy growth slows down and the azimuthal energy gradually increases, slower in a weak field, faster and more steadily in a moderate field, but interestingly, in both cases it approaches the poloidal flow energy (approximately
${\sim } t^{3/2}$ during the first second. Later the poloidal energy growth slows down and the azimuthal energy gradually increases, slower in a weak field, faster and more steadily in a moderate field, but interestingly, in both cases it approaches the poloidal flow energy (approximately ![]() $10^{-3}$ (m s
$10^{-3}$ (m s![]() $^{-1}$)
$^{-1}$)![]() $^{-2}$) in roughly the same time,
$^{-2}$) in roughly the same time, ![]() $t \sim 40$–
$t \sim 40$–![]() $50$ s. After this point, the flows evolve according to very different scenarios. The field
$50$ s. After this point, the flows evolve according to very different scenarios. The field ![]() ${B_{ext}} = 0.01$ mT is not sufficient to suppress the EVF and an oscillatory mode occurs – both energies oscillate remaining in relation
${B_{ext}} = 0.01$ mT is not sufficient to suppress the EVF and an oscillatory mode occurs – both energies oscillate remaining in relation ![]() ${E_{pol}}/{E_{az}} \sim 10$. The field
${E_{pol}}/{E_{az}} \sim 10$. The field ![]() ${B_{ext}} = 0.1$ mT completely suppresses the initial EVF, whose energy drops by almost three orders of magnitude. The azimuthal energy continues to rise and the system reaches a state in which
${B_{ext}} = 0.1$ mT completely suppresses the initial EVF, whose energy drops by almost three orders of magnitude. The azimuthal energy continues to rise and the system reaches a state in which ![]() ${E_{az}} \sim 500{E_{pol}}$.
${E_{az}} \sim 500{E_{pol}}$.
We note that if the flow evolves in a spin-up mode, i.e. spinning the metal under a moderate magnetic field after the fast formation of the EVF, the system qualitatively passes through all modes arising for the given current at varying external field. Therefore, we will reproduce step by step such a spin-up mode; but we do this for a lower current, namely ![]() $I=100$ A, because it provides more monotonic flow evolution and more stable flow structure.
$I=100$ A, because it provides more monotonic flow evolution and more stable flow structure.
The poloidal and azimuthal energy at a saturated state versus the external magnetic field for ![]() $I=100$ A is shown in figure 16. This figure should be compared with figure 10, in which same graphs are drawn for
$I=100$ A is shown in figure 16. This figure should be compared with figure 10, in which same graphs are drawn for ![]() $I=1000$ A. Both figures are similar. They show that the weaker EVF is suppressed by the lower external field (
$I=1000$ A. Both figures are similar. They show that the weaker EVF is suppressed by the lower external field (![]() $5\times 10^{-6}$ T at
$5\times 10^{-6}$ T at ![]() $I=100$ A versus
$I=100$ A versus ![]() $4 \times 10^{-5}$ T at
$4 \times 10^{-5}$ T at ![]() $I=1000$ A). The only significant difference concerns the behaviour of azimuthal energy at
$I=1000$ A). The only significant difference concerns the behaviour of azimuthal energy at ![]() ${B_{ext}} \to 0$. At
${B_{ext}} \to 0$. At ![]() $I=100$ A, the azimuthal flow monotonically decreases as the field decreases, while at
$I=100$ A, the azimuthal flow monotonically decreases as the field decreases, while at ![]() $I=1000$ A the azimuthal energy does not decrease further at
$I=1000$ A the azimuthal energy does not decrease further at ![]() ${B_{ext}} < 2 \times 10^{-5}$ T. As mentioned above, this is due to the fact that at strong currents the EVF flow is unstable and the final level of azimuthal energy in the absence of swirl is due to velocity fluctuations.
${B_{ext}} < 2 \times 10^{-5}$ T. As mentioned above, this is due to the fact that at strong currents the EVF flow is unstable and the final level of azimuthal energy in the absence of swirl is due to velocity fluctuations.

Figure 16. Flow energy as a function of the external magnetic field, ![]() $I = 100$ A.
$I = 100$ A.
Figure 17 illustrates the time evolution of the flow energy at ![]() $I=100$A for four different external magnetic fields:
$I=100$A for four different external magnetic fields: ![]() ${B_{ext}}=0$ mT (pure EVF);
${B_{ext}}=0$ mT (pure EVF); ![]() ${B_{ext}}=0.003$ mT (corresponding to the saturated state with
${B_{ext}}=0.003$ mT (corresponding to the saturated state with ![]() ${E_{pol}} \approx {E_{az}}$);
${E_{pol}} \approx {E_{az}}$); ![]() ${B_{ext}} = 0.1$ mT; and
${B_{ext}} = 0.1$ mT; and ![]() ${B_{ext}} = 1$ mT. Figure 17(a) shows that without magnetic field the EVF energy starts to increase as
${B_{ext}} = 1$ mT. Figure 17(a) shows that without magnetic field the EVF energy starts to increase as ![]() $E(t)\sim t^{3/2}$ and follows this law for approximately
$E(t)\sim t^{3/2}$ and follows this law for approximately ![]() $10$ s. The growth slows down thereafter, reaching the saturation at
$10$ s. The growth slows down thereafter, reaching the saturation at ![]() $t\approx 300$ s. Note, that there is no regular rotation in a pure EVF and the energy of azimuthal flow in figure 17(a) is due to small-scale fluctuations. During the first second
$t\approx 300$ s. Note, that there is no regular rotation in a pure EVF and the energy of azimuthal flow in figure 17(a) is due to small-scale fluctuations. During the first second ![]() ${E_{az}}\sim t^{3/2}$ following the growth of the poloidal energy, but then lags behind remaining at a very weak level.
${E_{az}}\sim t^{3/2}$ following the growth of the poloidal energy, but then lags behind remaining at a very weak level.

Figure 17. Evolution of the energy of poloidal and azimuthal flows without an external magnetic field (pure EVF, panel a), ![]() ${B_{ext}} = 0.003$ mT (b),
${B_{ext}} = 0.003$ mT (b), ![]() ${B_{ext}} = 0.1$ mT (c) and
${B_{ext}} = 0.1$ mT (c) and ![]() ${B_{ext}} = 1$ mT (d) after the electric current
${B_{ext}} = 1$ mT (d) after the electric current ![]() $I=100$ A is switched on.
$I=100$ A is switched on.
At ![]() ${B_{ext}} = 0.003$ mT (figure 17b), after a long slow acceleration (approximately 3000 s), the azimuthal flow accumulates the energy comparable with the poloidal flow energy, and this quasi-equilibrium keeps at a saturated state.
${B_{ext}} = 0.003$ mT (figure 17b), after a long slow acceleration (approximately 3000 s), the azimuthal flow accumulates the energy comparable with the poloidal flow energy, and this quasi-equilibrium keeps at a saturated state.
Under the external vertical magnetic field ![]() ${B_{ext}} = 0.1$ mT (figure 17c), the EVF develops during the first few seconds in the same way as without the field (although its energy is approximately half as weak), but the global rotation grows much faster. Here
${B_{ext}} = 0.1$ mT (figure 17c), the EVF develops during the first few seconds in the same way as without the field (although its energy is approximately half as weak), but the global rotation grows much faster. Here ![]() ${E_{az}}\sim t^{2}$ (the angular velocity grows linearly with time) and
${E_{az}}\sim t^{2}$ (the angular velocity grows linearly with time) and ![]() ${E_{az}}$ catches up
${E_{az}}$ catches up ![]() ${E_{pol}}$ at
${E_{pol}}$ at ![]() $t\approx 10$ s. After that, the poloidal flow energy decreases, and then the transient process is saturated at
$t\approx 10$ s. After that, the poloidal flow energy decreases, and then the transient process is saturated at ![]() ${E_{pol}}\sim 0.003 {E_{az}}$.
${E_{pol}}\sim 0.003 {E_{az}}$.
Figure 17(d) depicts the evolution of energy under the influence of the strong magnetic field in which the azimuthal flow develops faster than the poloidal one. The poloidal energy increases following the azimuthal energy, but it does not reach it and drops after approximately 30 s, approaching approximately the same level ![]() ${E_{pol}}\sim 0.003 {E_{az}}$.
${E_{pol}}\sim 0.003 {E_{az}}$.
Note that, at saturated states, the flow energy can be stable or can exhibit periodic or chaotic fluctuations. To illustrate this statement, the wavelet spectrograms of normalized poloidal energy fluctuations in a saturated state are shown in figure 18 for three cases. The first corresponds to the mode from figure 15(a), in which the poloidal motion dominates. The second concerns the opposite case (a strong swirl and a very weak poloidal flow), shown in figure 15(b). Both spectrograms demonstrate stochastic fluctuations in the range of characteristic frequencies. The third spectrogram shows very strong regular fluctuations that occur at a lower current and a stronger magnetic field (![]() $I=100$ A,
$I=100$ A, ![]() ${B_{ext}} = 1$ mT); the energy evolution is shown in figure 17(d).
${B_{ext}} = 1$ mT); the energy evolution is shown in figure 17(d).

Figure 18. Wavelet spectrograms of the poloidal energy fluctuations at saturated state. Here (a) ![]() $I = 1000$ A,
$I = 1000$ A, ![]() ${B_{ext}} = 0.01$ mT, (b)
${B_{ext}} = 0.01$ mT, (b) ![]() $I = 1000$ A,
$I = 1000$ A, ![]() ${B_{ext}} = 0.1$ mT, (c)
${B_{ext}} = 0.1$ mT, (c) ![]() $I = 100$ A,
$I = 100$ A, ![]() ${B_{ext}} = 1$ mT.
${B_{ext}} = 1$ mT.
Figure 19 shows how the flow pattern changes during this evolution for the case ![]() ${B_{ext}}=0.1$ mT,
${B_{ext}}=0.1$ mT, ![]() $I=100$ A considered in figure 17(c). At the beginning of the evolution (figure 19a–c) the poloidal EVF is similar to a pure EVF, and the rotating flow is concentrated near the electrode. The maximal angular velocity is quite high (figure 19c, f,i,l,o,r), but the total angular momentum is weak. Thus, the inhomogeneous current distribution provides strong axial and radial differential rotations.
$I=100$ A considered in figure 17(c). At the beginning of the evolution (figure 19a–c) the poloidal EVF is similar to a pure EVF, and the rotating flow is concentrated near the electrode. The maximal angular velocity is quite high (figure 19c, f,i,l,o,r), but the total angular momentum is weak. Thus, the inhomogeneous current distribution provides strong axial and radial differential rotations.

Figure 19. Evolution of the EVF flow at ![]() $I=100$ A and
$I=100$ A and ![]() ${B_{ext}} = 0.1$ mT. The poloidal (a,d,g,j,m,p) and azimuthal (b,e,h,k,n,q) velocity fields in the
${B_{ext}} = 0.1$ mT. The poloidal (a,d,g,j,m,p) and azimuthal (b,e,h,k,n,q) velocity fields in the ![]() $x0z$ plane, and the angular velocity along the cell axis (c, f,i,l,o,r) for six time moments,
$x0z$ plane, and the angular velocity along the cell axis (c, f,i,l,o,r) for six time moments, ![]() $t=6.2$,
$t=6.2$, ![]() $60$,
$60$, ![]() $92$,
$92$, ![]() $122.1$,
$122.1$, ![]() $160.6$ and
$160.6$ and ![]() $478.6$ s.
$478.6$ s.
Figure 19(c, f,i,l,o,r) shows the distribution of the flow angular velocity ![]() $\omega$ along the cell axis. The developing azimuthal flow with a strong decrease of the angular velocity with height leads to the formation of a domain with reduced pressure above the electrode. The vertical pressure drop causes a downward flow to occur along the cell axis. This downward flow results in a second large-scale poloidal cone-shaped vortex in the upper central part of the cell (figure 19d–f). The azimuthal flow is still concentrated close to the electrode, but it is stretched along the cone.
$\omega$ along the cell axis. The developing azimuthal flow with a strong decrease of the angular velocity with height leads to the formation of a domain with reduced pressure above the electrode. The vertical pressure drop causes a downward flow to occur along the cell axis. This downward flow results in a second large-scale poloidal cone-shaped vortex in the upper central part of the cell (figure 19d–f). The azimuthal flow is still concentrated close to the electrode, but it is stretched along the cone.
The downward poloidal vortex is formed at ![]() $t \approx 100$ s, being accompanied by a sharp decrease in the poloidal flow energy. The increase of the swirl leads to further suppression of the poloidal flow (figure 19g–i). The upper toroidal vortex begins to dominate in the cell, and the azimuthal flow spreads up to the upper boundary.
$t \approx 100$ s, being accompanied by a sharp decrease in the poloidal flow energy. The increase of the swirl leads to further suppression of the poloidal flow (figure 19g–i). The upper toroidal vortex begins to dominate in the cell, and the azimuthal flow spreads up to the upper boundary.
Figure 19(j–l) corresponds to the minimal energy of the poloidal flow (the strongest suppression). The upper vortex continues to grow and the azimuthal flow occupies practically the whole cell. As the swirl is increased further, the one-vortex flow develops. Only a weak residual toroidal vortex survives at the periphery of the bottom, which is the result of Ekman pumping (figure 19m–o). At fast rotation, this poloidal flow becomes unstable (figure 19p–r) , while the azimuthal flow demonstrates a solid-like rotation. The angular velocity is constant along the most part of the cell axis, keeping a maximum near the electrode. This domain of the highest swirl provides the stable axial downward flow.
Figure 20 illustrates the flow pattern evolution in the presence of a strong magnetic field (![]() ${B_{ext}} = 1$ mT), in which the azimuthal flow develops first (the case shown in figure 17d). Then the intense azimuthal swirl appears as a localized vortex in the vicinity of the electrode, providing a downward axial flow (figure 20a–c). The swirl spreads rapidly through the cell and at
${B_{ext}} = 1$ mT), in which the azimuthal flow develops first (the case shown in figure 17d). Then the intense azimuthal swirl appears as a localized vortex in the vicinity of the electrode, providing a downward axial flow (figure 20a–c). The swirl spreads rapidly through the cell and at ![]() $t\approx 25$ s it occupies the entire domain. It is at this moment that the poloidal motion begins to decrease and saturate. The final state is similar to that observed in the previous case (compare figures 19p–r and 20g–i).
$t\approx 25$ s it occupies the entire domain. It is at this moment that the poloidal motion begins to decrease and saturate. The final state is similar to that observed in the previous case (compare figures 19p–r and 20g–i).

Figure 20. Evolution of the EVF flow at ![]() $I=100$ A and
$I=100$ A and ![]() ${B_{ext}} = 1$ mT. The poloidal (a,d,g) and azimuthal (b,e,h) velocity fields in the
${B_{ext}} = 1$ mT. The poloidal (a,d,g) and azimuthal (b,e,h) velocity fields in the ![]() $x0z$ plane, and the angular velocity along the cell axis (c, f,i) for three time moments
$x0z$ plane, and the angular velocity along the cell axis (c, f,i) for three time moments ![]() $t = 5$,
$t = 5$, ![]() $25$ and
$25$ and ![]() $300$ s.
$300$ s.
7. Discussion and conclusions
We start our discussion by highlighting the most important conclusions of the work by Davidson et al. (Reference Davidson, Kinner, Lingwood, Short and He1999), which explains the key points of the suppression of poloidal flow by swirl under the joint action of poloidal and azimuthal forces in a confined domain. First, they showed that the dominant swirl is not the result of any instability. In fact, the swirl develops until the balance of dissipative forces with the acting azimuthal forces occurs and the main dissipation in the cavity is then localized in the Ekman layers. Second, the magnitude of the azimuthal velocity is simply governed by the prescribed magnitude of the azimuthal force, but the poloidal flow, being compensated by the centrifugal forces, becomes unexpectedly weak. Third, the effect of poloidal flow suppression is quite general for confined flows under the joint action of poloidal and azimuthal mass forces, and it weakly depends on the specific structure of the force field, e.g. in the case of EVF, on the structure of the electric current field. The dominance of the swirl occurs in turbulent flows if the ratio ![]() ${F_{az}}/{F_{pol}} \gtrsim 0.01$, where
${F_{az}}/{F_{pol}} \gtrsim 0.01$, where ![]() ${F_{az}}$ and
${F_{az}}$ and ![]() ${F_{pol}}$ are the typical azimuthal and poloidal forces. These conclusions were illustrated by Davidson et al. (Reference Davidson, Kinner, Lingwood, Short and He1999) via numerical simulations of the liquid metal flows induced in a hemisphere by the electric current of different configurations in the presence of a vertical magnetic field. In the context of our study it is important to note that all considered current distributions were smooth, and no localized electrodes were considered.
${F_{pol}}$ are the typical azimuthal and poloidal forces. These conclusions were illustrated by Davidson et al. (Reference Davidson, Kinner, Lingwood, Short and He1999) via numerical simulations of the liquid metal flows induced in a hemisphere by the electric current of different configurations in the presence of a vertical magnetic field. In the context of our study it is important to note that all considered current distributions were smooth, and no localized electrodes were considered.
It is worth mentioning that Davidson et al. (Reference Davidson, Kinner, Lingwood, Short and He1999) investigated the steady-state flows, i.e. saturated states. Analysis of the results of the EVF experiment performed recently by Kolesnichenko et al. (Reference Kolesnichenko, Frick, Eltishchev, Mandrykin and Stefani2020) has revealed that, during the switch-on regime, the transient poloidal flows can be up to two orders of magnitude stronger than those observed in the saturated state. This finding motivated us to revisit the problem in order to study in detail the dynamics of transient modes following the evolution of the flow structure at different ratios of azimuthal and poloidal Lorentz forces, governed by the current and vertical magnetic field. An important difference in our formulation of the problem is that the Lorentz forces are concentrated near the central electrode at the bottom of the cell and the evolution of the vortex (including the suppression of the poloidal component) can take place before the swirl involves the whole cell. The considered problem is also interesting because the bottom Ekman pumping is directed in the same way as the original poloidal EVF flow. We have also investigated the effect of the upper boundary (solid or free).
First, we made sure that a pure poloidal EVF mode occurs in numerical simulations and experiments despite the fact that the weak magnetic fields cannot be eliminated in the laboratory set-up. The dependence of the observed Reynolds number on the EVF parameter is consistent with the available data. In the absence of the external magnetic field, the EVF follows the ![]() $Re\sim S^{1/2}$ law.
$Re\sim S^{1/2}$ law.
The azimuthal force occurs in the liquid metal due to the vertical component of the magnetic field interacting with the radial component of the electric current flowing away from the central electrode. The vertical magnetic field leads to the EVF suppression as soon as the azimuthal Lorentz force becomes sufficient to provide the swirl energy comparable with the EVF energy. The above-mentioned criterion ![]() ${F_{az}}/{F_{pol}} \gtrsim 0.01$ (Davidson et al. Reference Davidson, Kinner, Lingwood, Short and He1999) is approximately valid, but it cannot be verified precisely because the Lorentz forces are distributed highly heterogeneously, and the choice of typical values
${F_{az}}/{F_{pol}} \gtrsim 0.01$ (Davidson et al. Reference Davidson, Kinner, Lingwood, Short and He1999) is approximately valid, but it cannot be verified precisely because the Lorentz forces are distributed highly heterogeneously, and the choice of typical values ![]() ${F_{az}}$ and
${F_{az}}$ and ![]() ${F_{pol}}$ is not unambiguous. A rough estimate gives
${F_{pol}}$ is not unambiguous. A rough estimate gives ![]() ${F_{az}}/{F_{pol}} \sim {B_{ext}}R/\mu _0 I$, from which it follows that the critical field is proportional to the applied current, which has been qualitatively confirmed by the experiments described above.
${F_{az}}/{F_{pol}} \sim {B_{ext}}R/\mu _0 I$, from which it follows that the critical field is proportional to the applied current, which has been qualitatively confirmed by the experiments described above.
In our experiments, the suppression of the poloidal motion was observed at stronger external magnetic field (as compared with the numerical simulations). This shift may be caused by the presence of the magnetic field induced by the power supply cables. Our numerical simulations have shown that the effect of horizontal magnetic field on the flow structure is negligible.
The structure of the saturated flow strongly depends on the ratio of forces. In the suppressed state (corresponding to the minimum in the curve ![]() ${E_{pol}}({B_{ext}})$), the vortex is strongly localized near the electrode edge (see figure 9b for
${E_{pol}}({B_{ext}})$), the vortex is strongly localized near the electrode edge (see figure 9b for ![]() $I=1000$ A and
$I=1000$ A and ![]() ${B_{ext}}=5 \times 10^{-5}$ T). The increased azimuthal forcing leads to the formation of a Proudman column (see figure 9c for
${B_{ext}}=5 \times 10^{-5}$ T). The increased azimuthal forcing leads to the formation of a Proudman column (see figure 9c for ![]() $I=1000$ A and
$I=1000$ A and ![]() ${B_{ext}} = 10^{-3}$ T) – the swirl becomes vertically homogeneous, but only the weak swirl reaches the sidewall. On the contrary, almost uniform rotation with thin boundary layers is observed at low current (see figure 17c,d for
${B_{ext}} = 10^{-3}$ T) – the swirl becomes vertically homogeneous, but only the weak swirl reaches the sidewall. On the contrary, almost uniform rotation with thin boundary layers is observed at low current (see figure 17c,d for ![]() $I=100$ A and
$I=100$ A and ![]() ${B_{ext}} = 10^{-4}$ T).
${B_{ext}} = 10^{-4}$ T).
The classification of flow modes on the control parameter plane (![]() $S$,
$S$, ![]() $Ha$),
$Ha$), ![]() $Ha$ is the Hartmann number, has been recently performed based on computations for a cylindrical magnetohydrodynamic cell with a bottom localized electrode (the second electrode is the upper solid cap) and applied vertical magnetic field (Kharicha et al. Reference Kharicha, Al-Nasser, Barati, Karimi-Sibaki, Vakhrushev, Abdi, Ludwig and Wu2022). In the comparable range of parameters, the structure of the resulting flows is qualitatively the same as that obtained in our simulations.
$Ha$ is the Hartmann number, has been recently performed based on computations for a cylindrical magnetohydrodynamic cell with a bottom localized electrode (the second electrode is the upper solid cap) and applied vertical magnetic field (Kharicha et al. Reference Kharicha, Al-Nasser, Barati, Karimi-Sibaki, Vakhrushev, Abdi, Ludwig and Wu2022). In the comparable range of parameters, the structure of the resulting flows is qualitatively the same as that obtained in our simulations.
The azimuthal velocity field induces a pressure field, which gives rise not only to the Ekman pumping associated with the fall in centripetal acceleration in viscous (horizontal) boundary layers, but also to an axial downward stream occurring due to the pressure gradient associated with the dependence of rotational velocity on vertical coordinate.
Because of the near-bottom localization of the Lorentz force domain, the impact of the upper boundary on the flow dynamics and its final state is rather weak. The experiments with free surface and solid upper boundary have shown that a solid surface slightly changes the flow pattern. Furthermore, by no means does it not contribute to the reduction in the intensity of the resulting flow (more viscous layers – more dissipation), but, on the contrary, slightly increases its energy (Reynolds number).
In the problem under study, the peculiarities of transient modes responsible for the poloidal flow suppression are associated with the fact that the domain of acting forces is localized in the vicinity of the bottom electrode – the vortex forces (causing EVF) are concentrated near the electrode and the forces (creating the swirl of the whole mass of liquid metal) are localized therein as well. The scenario of the flow evolution depends again on the ratio of the electro-vortex and rotational forces, i.e. on whether the EVF has time to form before a noticeable swirl of the metal or the swirl dominates from the beginning of the flow evolution.
These two scenarios of the flow evolution have been studied by numerical simulations of the whole process of flow evolution after the current ![]() $I=100$ A was switched on. The computations were performed for a moderate
$I=100$ A was switched on. The computations were performed for a moderate ![]() ${B_{ext}} = 10^{-4}$ T and strong
${B_{ext}} = 10^{-4}$ T and strong ![]() ${B_{ext}} = 10^{-3}$ T external magnetic field.
${B_{ext}} = 10^{-3}$ T external magnetic field.
It is important to emphasize that in the presence of a moderate or strong external field the poloidal vortex suppression starts when the vortex is still localized near the electrode. There is no Ekman pumping in the literal sense yet. Then, the vortex is destroyed due to the vertical pressure gradient caused by the change of angular velocity along the cell axis (see figures 19c, f,i,l,o,r and 20c, f,i). At moderate fields, this gradient provides a downward flow, which results in a second large-scale poloidal cone-shaped vortex in the upper central part of the cell. This vortex expands, pushing the original counter-rotating EVF vortex towards the periphery of the bottom. Note that the vertical angular velocity gradient persists then even at a saturated state (figure 19r), supporting a weak but stable axial downward flow. In the case of a strong magnetic field, the original EVF failed to evolve at all. A strong swirl occurred immediately after the current was switched on providing an axial downward flow (figure 20).
Finally, we would like to note that the transient states associated with the development of poloidal EVF and their suppression by the rotational motion developing in the liquid metal are of no less importance in technological magnetohydrodynamic systems than the steady-state flows. Therefore, proper understanding of the features of transient modes and possible scenarios of their development may be the key to control the processes occurring at the electrodes of LMB or the melt bath in an arc furnace.
Declaration of interests
The authors report no conflict of interest.
Appendix
This paragraph concerns how the external magnetic fields with different ratios of the horizontal to vertical components affect the EVF. To do this, we perform simulations for the magnetic fields of different magnitudes and different tilt angles ![]() $\alpha$ between the field direction and the
$\alpha$ between the field direction and the ![]() $Oz$ axis. The obtained dependencies of the Reynolds number on the magnitude of the magnetic field and its tilt angle
$Oz$ axis. The obtained dependencies of the Reynolds number on the magnitude of the magnetic field and its tilt angle ![]() $\alpha$ (figure 21), as well as the instant and time-averaged poloidal velocity fields (see figure 22), showed the absence of a pronounced effect of the horizontal component of the external magnetic field on the flow. Namely, the dependence
$\alpha$ (figure 21), as well as the instant and time-averaged poloidal velocity fields (see figure 22), showed the absence of a pronounced effect of the horizontal component of the external magnetic field on the flow. Namely, the dependence ![]() $Re({B_{ext}})$ becomes weaker with increasing angle
$Re({B_{ext}})$ becomes weaker with increasing angle ![]() $\alpha$.
$\alpha$.

Figure 21. Reynolds number ![]() $Re$ versus the external magnetic field for different inclination angles (
$Re$ versus the external magnetic field for different inclination angles (![]() $\alpha =0$ corresponds to the vertical magnetic field,
$\alpha =0$ corresponds to the vertical magnetic field, ![]() $\alpha =90^{\circ }$ corresponds to the horizontal magnetic field).
$\alpha =90^{\circ }$ corresponds to the horizontal magnetic field).

Figure 22. Instant (a) and time-averaged (b) fields of poloidal velocity in the ![]() $xOz$ plane in a horizontal magnetic field
$xOz$ plane in a horizontal magnetic field ![]() ${B_{ext}} = 0.1$ mT. The averaging time interval is 200 s.
${B_{ext}} = 0.1$ mT. The averaging time interval is 200 s.