Introduction
Permafrost is the layer of soil that remains frozen throughout the year and is found in the polar regions or at high elevations. Typically, cold regions are wet because of low evaporation rates and thus permafrost is usually cemented by ice. The McMurdo Dry Valleys are an Antarctic desert with moisture levels so low that permafrost that is not ice-cemented is observed, particularly at elevations above ~1000 m (Campbell & Claridge Reference Campbell and Claridge2006, Bockheim et al. Reference Bockheim, Campbell and McLeod2007). In these high elevation Antarctic soils, the thermal and moisture content define three key zones in the shallow subsurface (e.g. Marchant & Head Reference Marchant and Head2007). The active layer is the uppermost soil layer in which summer temperatures rise above freezing. Below this there may be a layer in which temperatures never rise above freezing but contain no ice - dry permafrost. Further down there may be a layer of ice-cemented ground or, in some cases, massive ice. For example, at Linnaeus Terrace in Upper Wright Valley at an elevation of 1600–1650 m the thickness of the active layer is 12.5 cm, the dry permafrost extends to a depth of 25 cm, and ice-cemented soil is below that level (McKay et al. Reference McKay, Mellon and Friedmann1998).
Campbell & Claridge (Reference Campbell and Claridge1987, 2006) pointed out that for older surfaces the incidence of ice-cemented ground decreases and dry permafrost becomes more extensive. They suggested that the depth to ice-cemented ground reflected the age of the soil surface due to the gradual evaporation of the ground ice. However, the age of the surface may be up to several million years and recent estimates of the rate of ice evaporation from deep ice-cemented ground suggest rates of 0.5 mm yr -1, or 500 m in a Myr (Hindmarsh et al. Reference Hindmarsh, Van der Wateren and Verbers1998, McKay et al. Reference McKay, Mellon and Friedmann1998). This would suggest that the equilibrium time for the ground ice is short compared to the age of the surface and that age is not the determining factor. Campbell & Claridge (2007) point out that older land surfaces are most commonly found at higher elevation, inland areas where the climate is colder and drier, thus local climate conditions rather than age may determine the presence of ice-cemented ground.
Hagedorn et al. (Reference Hagedorn, Sletten and Hallet2007) studied ice-cemented ground in Victoria Valley at an elevation of 450 m on 10 000 yr old surfaces. The depth to ground ice was from 20–40 cm and average ground temperatures were -23.1°C. They found that the ice at this location was evaporating over the period from 2002–2005 at a typical rate of 0.2 mm yr -1 but that summer snow cover affected the rate of evaporation and even reversed it.
Most datasets used for the analysis of permafrost in Antarctica have been based on measurements over a year or at most a few years (McKay et al. Reference McKay, Mellon and Friedmann1998, Schorghofer Reference Schorghofer2005, Kowalewski et al. Reference Kowalewski, Marchant, Levy and Head2006, Hagedorn et al. Reference Hagedorn, Sletten and Hallet2007). However, Doran et al. (Reference Doran, McKay, Fountain, Nylen, McKnight, Jaros and Barrett2008) have presented a study of the 40 year record of meltwater flow into the lakes that are found at the bottom of the Dry Valleys. They show that there is considerable variation from year to year over decadal timescales.
The work of Doran et al. (Reference Doran, McKay, Fountain, Nylen, McKnight, Jaros and Barrett2008) highlights the variability of the polar desert environment of the McMurdo Dry Valleys and suggests that climatic events on decadal timescales may be key to understanding the distribution of ice-cemented ground. The most likely factor that varies between years is the occurrence of snow.
Ground ice stability
In this section I consider the role of surface snow in setting the depth to ground ice using a mathematical description of the movement of water vapour through the soil for a typical soil temperature profile. Water vapour in the soil moves in response to gradients in the water vapour density. The water vapour density over ice or snow depends only on the temperature. The water vapour density in the atmosphere can be expressed as the product of the atmospheric relative humidity with respect to ice and the vapour density of ice at the temperature of the atmosphere. If the atmospheric water vapour density is lower than the water vapour density at the subsurface ice interface, then water vapour will move away from the ground ice and toward the atmosphere. If the gradient is reversed the flux will reverse. Typically throughout the year there will be times when the water vapour flux is into the ground and times when the flux is out of the ground ice (e.g. McKay et al. 1988). For this reason it is convenient to consider the average value of the water vapour density. Ground ice will be stable when its water vapour density averaged over the entire year is equal to the atmospheric water vapour density averaged over the year.
A convenient way to express the annual average water vapour density is with the concept of frost point temperature. The frost point temperature, T f, for a location is the temperature at which ice will have the same vapour density as the vapour density at that location averaged over the year. The yearly average density of water vapour, <[H2O]>, in the atmosphere or at any depth is then given by
where RH is the relative humidity and [H2O](T) is the instantaneous water vapour density which is a function of temperature, T. The integral in Eq. (1) is over the year. Note that the RH is unity for ice-cemented ground and for snow and is less than unity in the atmosphere. [H2O](T) is the water vapour density of ice as a function of temperature and can be expressed as Ae -b/T/RT, using a standard expression for the vapour pressure of water, Ae -b/T, and the ideal gas law. The coefficients A and b are 3.459 × 1012 Pa and 6137.2 K, respectively, R is the gas constant, 8.316 J mol-1 K-1. The frost point temperature, T f, is the temperature for which [H2O](T f) = <[H2O]> . In general, the frost point is not equal to the average temperature because of the non-linear dependence of water vapour pressure on temperature. The frost point temperature is warmer than, or equal to, the average temperature, and is equal only when seasonal temperature variation is negligibly small.
Given values for temperature throughout the year, Eq. (1) can be evaluated. As an example we use an analytic solution for the ground temperature (Campbell Reference Campbell1977) that corresponds to the solution of the thermal diffussion equation in a semi-infinite plane parallel homogeneous soil with a sinusoidal surface temperature boundary conditions.
where T 0 is the mean annual temperature at the surface, z is the depth measured positive downward, t is time, ω is the frequency of the annual wave (ω = 2π/yr), ΔT is the half amplitude of the seasonal temperature variation and δ is the depth of penetration (damping depth) of the annual thermal wave equal to (2k/ωρc)1/2 where, ρ is the bulk density of the ground, k is the thermal conductivity, and c is the heat capacity. For dry ground, where k = 0.6 W m-1 K-1, the annual thermal skin depth (δ) is 1.4 m. For ice-cemented ground, k = 2.5 W m-1 K-1 and δ = 2.8 m based on values in McKay et al. (Reference McKay, Mellon and Friedmann1998).
Substituting Eq. (2) for T in Eq. (1) gives an analytical solution for the mean water vapour density in the subsurface and provides a direct expression for the frost point temperature.
Figure 1 shows the frost point temperature as a function of depth computed using Eqs (1) & (2). The air temperature has a mean, T 0, of -25°C, a value of ΔT = 25°C, and constant atmospheric relative humidity of 35%. These values are illustrative of conditions in the high elevations of the Dry Valleys (McKay et al. Reference McKay, Mellon and Friedmann1998). The solid line in Fig. 1 shows the ground frost point temperature for ice-cemented conditions at all depths (RH = 1). The frost point temperature for ice-cemented ground at the surface is -15°C and decreases with depth until it becomes equal to the mean annual temperature, -25°C, at depths below about 2–3 damping depths. At three damping depths the seasonal temperature variation is reduced to 5% of its surface value.
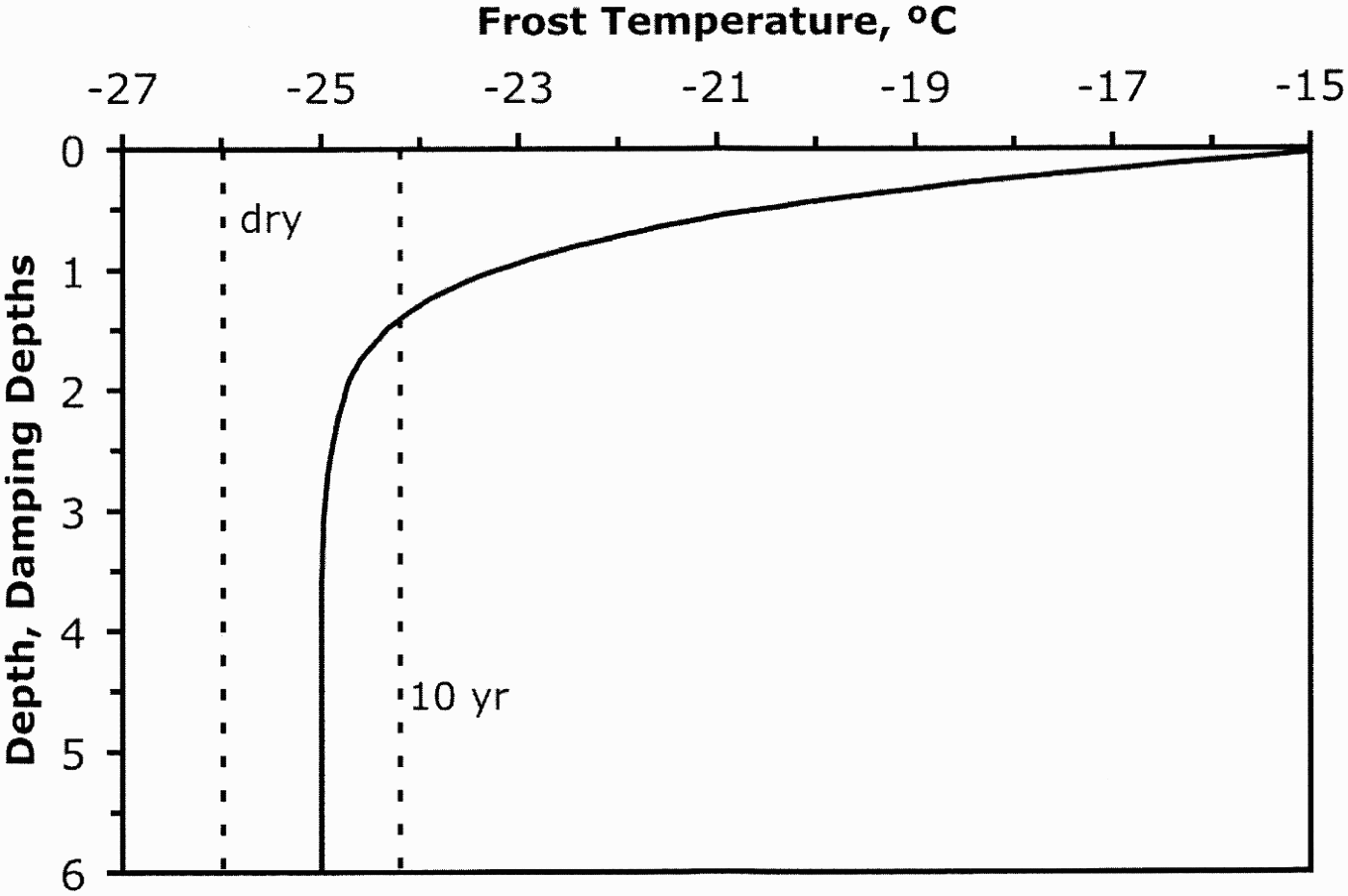
Fig. 1. Frost point temperature as a function of depth for ice-cemented ground for an idealized case with sinusoidal temperature variation at the surface. The depth is expressed in units of the damping depth, δ = (2k/ωρc)1/2. For ice-cemented ground δ = 2.8 m, while for dry ground δ = 1.4 m. Dotted lines show the frost point temperature for an atmospheric humidity of 35% and no snow recurrence, and for a snow recurrence of 10 years. For no snow recurrence there is only dry permafrost. For a 10 year recurrence the depth to ground ice is 1.5 damping depths.
Because of the low air humidity, the atmospheric frost point temperature is -26°C (dotted line labelled “dry”), which is colder than the frost point temperature for ice-cemented ground at all depths. If the atmospheric frost point temperature is colder than the minimum frost point temperature for ice-cemented ground in the subsurface, then completely dry permafrost would be expected. This is the case in Fig. 1, as the frost point temperatures for ice-cemented ground at all depths (solid line) exceeds the atmospheric frost point temperature. Any initial ground ice would evaporate over time.
However, if the surface is occasionally snow covered, the stability changes. The “10 yr” snow recurrence dotted line in Fig. 1 shows the frost point temperature at the surface averaged between nine years of atmospheric humidity and one year of snow cover (RH = 1) at the surface. In this case the frost point temperature is -24.2°C and ice is stable at a depth of ~1.5 damping depths. For snow recurrence more frequent than once in 10 years, the depth of the ice stability would move upward. For longer intervals between snow recurrence the depth to the ice-cemented ground moves downward but if the recurrence interval exceeds 19 years in this example, subsurface ice is unstable. The shape of the curve in Fig. 1 shows that if a stable ice-table is present at all, it will be present in the top ~2 damping depths.
I have approximated snow either entirely present or entirely absent for a given year, and without altering the temperature profile. While the real distribution of snow is certainly more complex and snow will alter the temperature profile by changing the albedo and the thermal conductivity of the surface, the effect of snow is demonstrated by this approximation. The essential features of snow recurrence controlling the depth to the ice-table are illustrated in Fig. 1. However, it is useful to consider a real example using measured ground temperatures and ice-table depths.
McMurdo Dry Valley sites
There are several observations of ground ice and datasets of ground temperature from the upper elevations of the Dry Valleys that can be reviewed for consistency with the concept developed above of snow recurrence controlling depth to ground ice. A detailed year-round ground temperature record exists for Linnaeus Terrace at 77.6°S, 161.1°E, elevation 1600 m (McKay et al. 1988) and the depth to ground ice has been measured. In Beacon Valley (77.85°S, 163.6°E, elevation 1351 m) there are many locations where there is no ground ice down to several metres below the surface. Also in Beacon Valley there are locations with massive ground ice less than 50 cm below the surface. This massive ground ice is overlain by fine dust, presumably an ablation till left behind from the evaporation of the massive ice. University Valley (77.86°S, 163.75°E, elevation 1700 m), a hanging valley above Beacon Valley has a permanent snowfield at one end and shallow ice-cemented ground on the valley floor, in contrast to Beacon Valley. These three sites are mostly free of snow but over the past decades, snow covers of a few centimetres have been observed in the summer months. Unfortunately, there is no systematic dataset for snow recurrence in this area. Nevertheless, I review the temperature data and ground ice observations that exist from these sites to show that they are consistent with the depth to ice-cemented ground set by snow recurrence.
A detailed record of temperature over a complete year at several depths has been published for Linnaeus Terrace (McKay et al. Reference McKay, Mellon and Friedmann1998). Below the annual damping depth they found average ground temperature of -24.9°C, an average air temperature of -23.3°C, and an atmospheric frost point temperature of -25.7°C. The frost point temperature stated here is different from the value reported in McKay et al. (Reference McKay, Mellon and Friedmann1998). It has been corrected, because the value is computed with respect to the relative humidity of ice instead of water as used by McKay et al. (Reference McKay, Mellon and Friedmann1998). The observed depth of the ice table at Linnaeus Terrace is 25 cm, 12.5 cm below the depth at which temperatures never exceed freezing. Thus, there are 12.5 cm of dry permafrost at this site. The ice loss rate is 0.4 to 0.6 mm yr-1 (McKay et al. Reference McKay, Mellon and Friedmann1998), thus requiring less than 500 years for the ice table to reach its current depth.
Figure 2 shows a plot of the average surface frost point temperature computed using the data of McKay et al. (Reference McKay, Mellon and Friedmann1998) for a range of snow recurrence intervals from 1 to 100 years. A snow recurrence of one year implies constant snow conditions. The average surface frost point temperature is calculated from the vapour density (Eq. 1), which was computed from temperature measurements taken every 10 min at a series of depths. To determine the average frost point temperature at the surface of the soil, the water vapour for a snow-free year was averaged with the water vapour for a snow-covered year as weighted by the recurrence interval. When computing the average water vapour density for a snow covered year, any measured surface temperatures that were above 0°C were set equal to 0°. As seen in Fig. 2 of McKay et al. (Reference McKay, Mellon and Friedmann1998) surface temperatures were rarely above 0°C so this correction is a minor (< 0.01°C) change in the frost point temperature. A more important consideration may be the effect that a layer of snow will have in reducing the sunlight absorbed by the soil and insulating the soil. These effects probably reduce the soil surface temperatures implying that the recurrence intervals reported here may be lower limits.
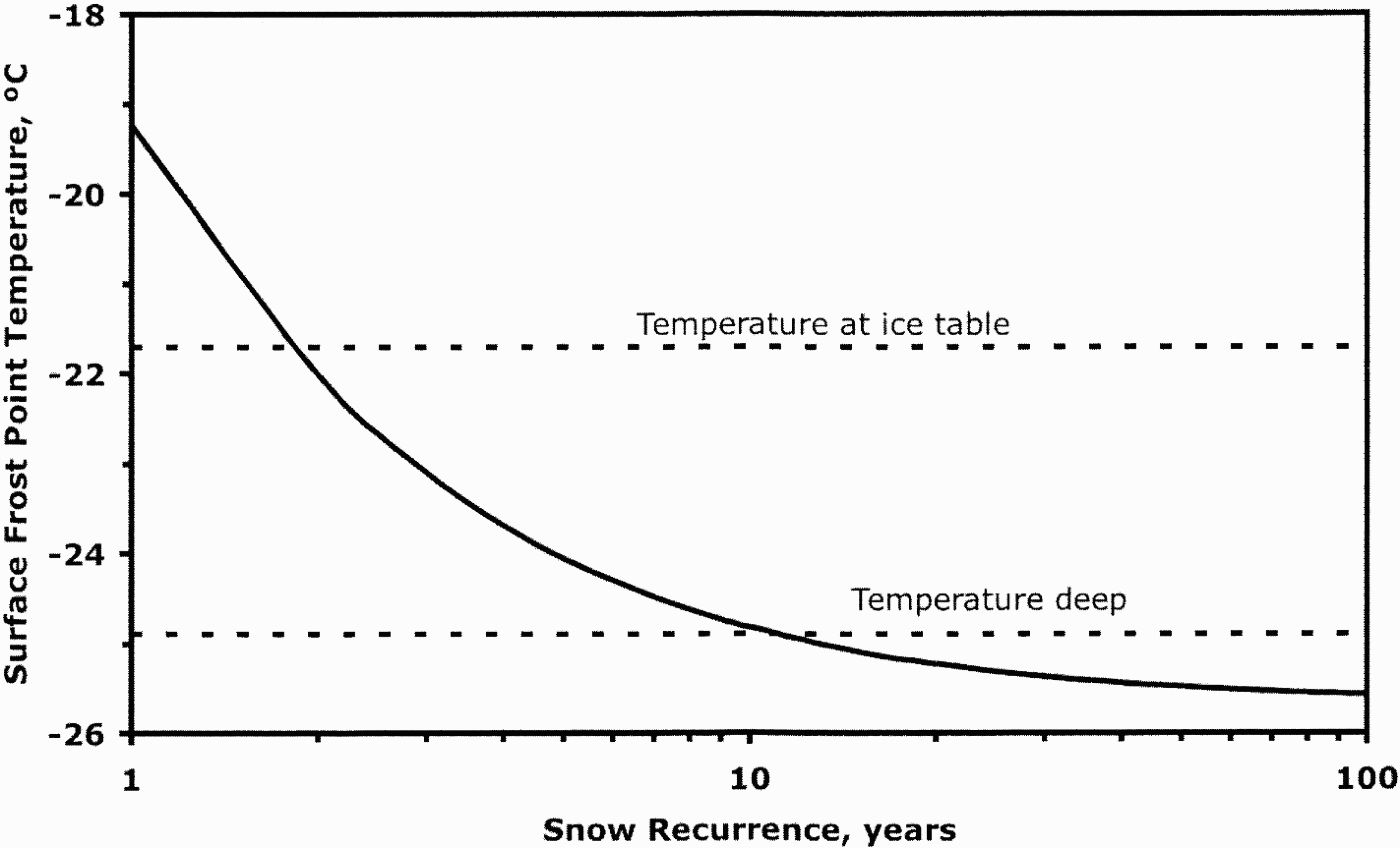
Fig. 2. Average Linnaeus Terrace surface frost point temperature as a function of snow recurrence based on detailed temperature data (McKay et al. Reference McKay, Mellon and Friedmann1998). The frost point temperature is computed by averaging the vapour density of snow-free years with the vapour density of snow-covered years recurring once in the specified interval. The equilibrium frost point temperature for the observed ice table at 25 cm is shown as the dotted line labelled ice. The minimum equilibrium frost point temperature at depths below many (> 5) damping depths is shown as the dotted line labelled deep. A snow recurrence of ~2 yr would explain the observed ice table and a snow recurrence of more than 10 yr would result in only dry permafrost.
The data from Linnaeus Terrace show that the depth to ice-cemented ground can be explained by snow cover with a two to ten year recurrence interval. Snow recurrence periods longer than 10 years would create only dry permafrost at this site. The use of average boundary conditions to calculate the surface frost point temperature can be justified by noting that at the computed loss rate, ~0.5 mm yr-1, the ice table at Linnaeus Terrace would move only 0.5 cm over a decade; much less than the depth of the ice, 25 cm.
Another example of the control of snow cover in determining the depth of dry permafrost comes from University Valley. This valley floor is at an elevation of ~1650 m and ground and air temperatures should be close to those measured at Linnaeus Terrace which is at a similar elevation. However, unlike Linnaeus Terrace, University Valley has a small glacier at one end (Fig. 3). This glacier is sustained by snow blown into the valley from the Polar Plateau.

Fig. 3. View of University Valley, January 2008, showing the glacier at the end of the valley. Length across the glacier is ~1 km.
The glacier has been present in the valley for at least the past 27 years based on personal observation. Personal observation also indicates that there is often snow, a few centimetres thick, on the floor of the valley away from the glacier, with the persistence and thickness of the snow diminishing away from the glacier.
The depth to the ice table in University Valley increases with distance away from the glacier as shown in Fig. 4. Distance from the glacier was determined using global positioning readings with an error of 6 m for each reading. Depth to ground ice was determined by digging a pit and measuring the depth with an error of about 1 cm. The solid line shows a least squares fit to the data giving a slope of 0.068 cm m-1 and a correlation coefficient of 0.98. The floor of University Valley is relatively flat (Fig. 3). The soil texture and particle size was uniform at all sites and dominated by sand derived from the sandstone cliffs that ring the valley. Given the uniform surface and soil properties and the small spatial scale it is plausible that snow recurrence and not soil or climate variation is determining the trend seen in Fig. 4. The distances involved are too small for any significant change in climate and there is no systematic change in surface albedo, aspect, or rock abundance. The only variation that can explain the large increase in depth to ground ice is the presence of snow. However, the data shown in Fig. 4 represent a preliminary assessment of the distribution of ground ice in University Valley and a more detailed mapping is required to substantiate this initial result. It is also important to note that snow recurrence is assumed to increase with distance from the glacier but this has not yet been demonstrated. Observations over many years would be required to established this.

Fig. 4. University Valley depth to ground ice as a function of distance from the small glacier at the end of the valley during January 2008.
By comparison to the analysis of the Linnaeus Terrace data presented in Fig. 2, we can estimate the snow recurrence interval 500 m away from the glacier in University Valley. The ice-cemented ground measured at this distance is at 35 cm depth, which corresponds to a frost point temperature of between -22°C and -23°C based on the data from Linnaeus Terrance (McKay et al. Reference McKay, Mellon and Friedmann1998). From Fig. 2 this implies a snow recurrence interval of between two and three years.
Beacon Valley, located ~300 m below University Valley, is another interesting site with respect to ground ice and dry permafrost. On the floor of Beacon Valley there is massive glacial ice buried under 20–50 cm of fine grain material (Sugden et al. Reference Sugden, Marchant, Potter, Souchez, Denton, Swisher and Tison1995). This material appears to be glacial till left behind from the evaporation of the ice. There is some uncertainty about the age of the ice but estimates range from 2–8 Myr (Sudgen et al. 1995, Gilichinsky et al. Reference Gilichinsky, Wilson, Friedmann, McKay, Sletten, Rivkina, Vishnivetskaya, Erokhina, Ivanushkina, Kochkina, Shcherbakova, Soina, Spirina, Vorobyova, Fyodorov-Davydov, Hallet, Ozerskaya, Sorokovikov, Laurinavichyus, Shatilovich, Chanton, Ostroumov and Tiedje2007). The presence of recoverable bacteria in the ice is, therefore, of great interest (Gilichinsky et al. Reference Gilichinsky, Wilson, Friedmann, McKay, Sletten, Rivkina, Vishnivetskaya, Erokhina, Ivanushkina, Kochkina, Shcherbakova, Soina, Spirina, Vorobyova, Fyodorov-Davydov, Hallet, Ozerskaya, Sorokovikov, Laurinavichyus, Shatilovich, Chanton, Ostroumov and Tiedje2007). Recent models have speculated that the ice may be maintained by variations in climate from present conditions (Schorghofer 2005, Kowalewski et al. Reference Kowalewski, Marchant, Levy and Head2006). Snow recurrence is one such mechanism. In this case the effect of snow would not be to create ice-cemented layers but to preserve the massive subsurface ice. However, in other locations on the floor of Beacon Valley there is no ancient glacier ice and in these locations there is no ice-cemented ground either. The presence of dry permafrost to depths greater than ~2 damping depths indicates conditions unsuitable for creation of ice-cemented ground. I suggest that this is due to a snow recurrence of more than 10–20 years. Observations during many field seasons also suggest that extensive snow on the floor of Beacon Valley has a recurrence of more than two decades. From this I conclude that ground ice is not stable on the floor of Beacon Valley and the ancient Beacon Valley ice is systematically evaporating under present and recent climatic conditions in contrast to the suggestions of Schorghofer (2005) and Kowalewski et al. (Reference Kowalewski, Marchant, Levy and Head2006).
Conclusions
Based on theoretical consideration of the effect of snow on subsurface water vapour transport and comparisons to field observations, I conclude that snow recurrence controls the depth to ice-cemented ground in the high elevations of the Dry Valleys.
The presence of ice-cemented ground, or its complete absence, reflects variations in current climatic conditions that determine snow recurrence, and not ancient formational events.
The calculations presented here assume that water is transported by vapour diffusion through the active layer and the dry permafrost. This may be a reasonable assumption given the low temperatures and dry conditions at the upper elevations in the Dry Valleys. However, it is possible that thin films of liquid water could play an important role in transporting water through the active zone and possibly even in the dry permafrost due to the presence of salt. These effects would alter the details of the calculations presented here but not the main conclusions. Long term observations comparable to the network of stations at lower elevation established by Clow et al. (Reference Clow, McKay, Simmons and Wharton1988) and reported on 17 years later by Doran et al. (Reference Doran, McKay, Clow, Dana, Fountain, Nylen and Lyons2002) are required to quantitatively test the role of snow recurrence in ground ice stability.
On Earth, dry permafrost is only found in the arid upland regions of Antarctica (Bockheim et al. Reference Bockheim, Campbell and McLeod2007) but it has also been shown to be present on Mars (Mellon & Jakosky Reference Mellon and Jakosky1993, Mellon et al. Reference Mellon, Feldman and Prettyman2004). Ice-cemented ground in the polar regions of Mars may hold clues to the biological history of that planet (Smith & McKay Reference Smith and McKay2005) and are therefore a target for current (Smith et al. Reference Smith, Tampari, Arvidson, Bass, Blaney, Boynton, Carswell, Catling, Clark, Duck, DeJong, Fisher, Goetz, Gunnlaugsson, Hecht, Hipkin, Hoffman, Hviid, Keller, Kounaves, Lange, Lemmon, Madsen, Malin, Markiewicz, Marshall, McKay, Mellon, Michelangeli, Ming, Morris, Renno, Pike, Staufer, Stoker, Taylor, Whiteway, Young and Zent2008) and future missions. On Mars, snow recurrence may occur on timescales set by annual cycles near the polar caps, but in the mid-latitudes it may be on timescales set by obliquity cycles of many thousands of years. In the polar regions obliquity cycles may result in a persistent snow cover for extended periods of time. Unlike the Dry Valleys, Mars has two condensable species, CO2 as well as H2O, and trapping of H2O in CO2 ice may alter the boundary condition associated with “snow” in significant ways.
The upper elevations of the Antarctic Dry Valleys are the best terrestrial analogue to conditions of ground ice on Mars. Thus, studies of the factors that control the distribution of dry permafrost in Antarctica may provide a basis for understanding its distribution on Mars - another arid polar environment.
Acknowledgements
This work was supported by the NASA IPY program. The able assistance of the other members of the field team and the excellent logistics support from the NSF Office of Polar Programs allowed the field work to be completed. I thank the editor and two reviewers for comments that greatly improved the paper.






