Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-14T15:25:38.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Transport equation for the mean turbulent energy dissipation rate on the centreline of a fully developed channel flow

Published online by Cambridge University Press:  15 July 2015

S. L. Tang ,
R. A. Antonia ,
L. Djenidi ,
H. Abe ,
T. Zhou ,
L. Danaila  and
Y. Zhou
S. L. Tang
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, PR China School of Engineering, University of Newcastle, NSW 2308, Australia
R. A. Antonia*
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
L. Djenidi
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
H. Abe
Affiliation:
Japan Aerospace Exploration Agency, Jindaiji-higashi, Chofu, Tokyo 182-8522, Japan
T. Zhou
Affiliation:
School of Civil and Resource Engineering, University of Western Australia, WA 6009, Australia
L. Danaila
Affiliation:
CORIA CNRS UMR 6614, Université de Rouen, 77801 Saint Etienne du Rouvray, France
Y. Zhou
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, PR China
*
†Email address for correspondence: robert.antonia@newcastle.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

The transport equation for the mean turbulent energy dissipation rate $\overline{{\it\epsilon}}$ along the centreline of a fully developed channel flow is derived by applying the limit at small separations to the two-point budget equation. Since the ratio of the isotropic energy dissipation rate to the mean turbulent energy dissipation rate 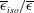$\overline{{\it\epsilon}}_{iso}/\overline{{\it\epsilon}}$ is sufficiently close to 1 on the centreline, our main focus is on the isotropic form of the transport equation. It is found that the imbalance between the production of $\overline{{\it\epsilon}}$ due to vortex stretching and the destruction of $\overline{{\it\epsilon}}$ caused by the action of viscosity is governed by the diffusion of $\overline{{\it\epsilon}}$ by the wall-normal velocity fluctuation. This imbalance is intrinsically different from the advection-driven imbalance in decaying-type flows, such as grid turbulence, jets and wakes. In effect, the different types of imbalance represent different constraints on the relation between the skewness of the longitudinal velocity derivative 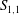$S_{1,1}$ and the destruction coefficient $G$ of enstrophy in different flows, thus resulting in non-universal approaches of 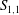$S_{1,1}$ towards a constant value as the Taylor microscale Reynolds number, $R_{{\it\lambda}}$, increases. For example, the approach is slower for the measured values of 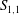$S_{1,1}$ along either the channel or pipe centreline than along the axis in the self-preserving region of a round jet. The data for 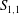$S_{1,1}$ collected in different flows strongly suggest that, in each flow, the magnitude of 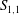$S_{1,1}$ is bounded, the value being slightly larger than 0.5.

JFM classification

Waves/Free-surface Flows: Channel flow Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 777 , 25 August 2015 , pp. 151 - 177
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H. & Antonia, R. A. 2011 Scaling of normalized mean energy and scalar dissipation rates in a turbulent channel flow. Phys. Fluids 23, 055104.Google Scholar
Abe, H., Antonia, R. A. & Kawamura, H. 2009 Correlation between small-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.Google Scholar
Anselmet, F., Gagne, Y., Hopfinger, E. J. & Antonia, R. A. 1984 Higher-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 140, 63–89.Google Scholar
Antonia, R. A., Abe, H. & Kawamura, H. 2009 Analogy between velocity and scalar fields in a turbulent channel flow. J. Fluid Mech. 628, 241–268.CrossRefGoogle Scholar
Antonia, R. A., Anselmet, F. & Chambers, A. J. 1986 Assessment of local isotropy using measurements in a turbulent plane jet. J. Fluid Mech. 163, 365–391.Google Scholar
Antonia, R. A., Djenidi, L. & Danaila, L. 2014 Collapse of the turbulent dissipation range on Kolmogorov scales. Phys. Fluids 26, 045105.CrossRefGoogle Scholar
Antonia, R. A. & Kim, J. 1994 Low-Reynolds-number effects on near-wall turbulence. J. Fluid Mech. 276, 61–80.CrossRefGoogle Scholar
Antonia, R. A., Kim, J. & Browne, L. W. B. 1991 Some characteristics of small-scale turbulence in a turbulent duct flow. J. Fluid Mech. 233, 369–388.CrossRefGoogle Scholar
Antonia, R. A. & Pearson, B. R. 2000a Reynolds number dependence of velocity structure functions in a turbulent pipe flow. Flow Turbul. Combust. 64, 95–117.CrossRefGoogle Scholar
Antonia, R. A., Satyaprakash, B. R. & Hussain, A. K. M. F. 1982 Statistics of fine-scale velocity in turbulent plane and circular jets. J. Fluid Mech. 119, 55–89.CrossRefGoogle Scholar
Antonia, R. A., Zhou, T., Danaila, L. & Anselmet, F. 2000b Streamwise inhomogeneity of decaying grid turbulence. Phys. Fluids 12, 3086.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1947 Decay of vorticity in isotropic turbulence. Proc. R. Soc. Lond. A 190, 534–550.Google Scholar
Bernardini, M., Pirozolli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to $Re_{{\it\tau}}=4000$ . J. Fluid Mech. 742, 171–191.CrossRefGoogle Scholar
Bos, W. J. T., Chevillard, L., Scott, J. F. & Rubinstein, R. 2012 Reynolds number effect on the velocity increment skewness in isotropic turbulence. Phys. Fluids 24, 015108.CrossRefGoogle Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2005 On the normalised turbulent energy dissipation rate. Phys. Fluids 17, 098103.Google Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2008 Velocity derivative skewness in isotropic turbulence and its measurement with hot wires. Exp. Fluids 45, 523–535.Google Scholar
Camussi, R. & Guj, G. 1995 Experimental analysis of scaling laws in low and moderate $Re$ grid generated turbulence. Exp. Fluids 24, 63–67.Google Scholar
Champagne, F. H. 1978 The fine-scale structure of the turbulent velocity field. J. Fluid Mech. 86, 67–108.Google Scholar
Comte-Bellot, G.1963 Contribution à l’étude de la turbulence de conduite. PhD thesis, University of Grenoble.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 2001 Turbulent energy scale-budget equations in a fully developed channel flow. J. Fluid Mech. 430, 87–109.Google Scholar
Djenidi, L., Tardu, S. F., Antonia, R. A. & Danaila, L. 2014 Breakdown of Kolmogorov’s first similarity hypothesis in grid turbulence. J. Turbul. 15, 596–610.Google Scholar
Friehe, C. A., Van Atta, C. W. & Gibson, C. H. 1971 Jet turbulence: dissipation rate measurements and correlations. AGARD Turbul. Shear Flows 18, 1–7.Google Scholar
Frisch, U., Sulem, P. L. & Nelkin, M. 1978 A simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 87, 719–736.Google Scholar
Hearst, R. J. & Lavoie, P. 2014 Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 741, 567–584.Google Scholar
Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.Google Scholar
Jimenez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.Google Scholar
Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Kahalerras, H., Malecot, Y. & Gagne, Y. 1998 Intermittency and Reynolds number. Phys. Fluids 10, 910–921.Google Scholar
von Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164, 192–215.Google Scholar
von Kármán, T. 1937 The fundamentals of statistical theory of turbulence. J. Aero. Sci. 4, 131–138.Google Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.Google Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.Google Scholar
Kim, J. & Antonia, R. A. 1993 Isotropy of the small-scales of turbulence at small Reynolds numbers. J. Fluid Mech. 251, 219–238.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kolmogorov, A. 1941 Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 125, 15–17.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Larssen, J. V. & Devenport, W. J. 2011 On the generation of large-scale homogeneous turbulence. Exp. Fluids 50, 1207–1223.CrossRefGoogle Scholar
Laufer, J. 1954 The structure of turbulence in fully developed pipe flow. NACA Rep. 1174, 417–434.Google Scholar
Lee, S. K., Djenidi, L., Antonia, R. A. & Danaila, L. 2013 On the destruction coefficients for slightly heated decaying grid turbulence. Intl J. Heat Fluid Flow 43, 129–136.Google Scholar
Lefeuvre, N., Djenidi, L. & Antonia, R. A.2015 Decay of mean energy dissipation rate on the axis of a turbulent round jet. The 9th Symposium on Turbulence and Shear Flow Phenomena (TSFP-9) (June 30th–July 3rd, Melbourne, Austalia).Google Scholar
Meldi, M. & Sagaut, P. 2013 Further insights into self-similarity and self-preservation in freely decaying isotropic turbulence. J. Turbul. 14, 24–53.Google Scholar
Mi, J., Xu, M. & Zhou, T. 2013 Reynolds number influence on statistical behaviors of turbulence in a circular free jet. Phys. Fluids 25, 075101.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulations of turbulent channel flow up to $Re_{{\it\tau}}=590$ . Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Qian, J. 1994 Skewness factor of turbulent velocity derivative. Acta Mechanica Sin. 10, 12–15.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.Google Scholar
Saffman, P. G. 1970 Dependence on Reynolds number of high-order moments of velocity derivatives in isotropic turbulence. Phys. Fluids 13, 2193–2194.Google Scholar
Shah, D. A.1988 Scaling of the ‘bursting’ and ‘pulse’ periods in wall bounded turbulent flows. PhD thesis, The University of Newcastle.Google Scholar
Shah, D. A. & Antonia, R. A. 1986 Isotropic forms of vorticity and velocity structure function equations in several turbulent shear flows. Phys. Fluids 29 (12), 4016–4024.Google Scholar
Sreenivasan, K. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10, 528–529.Google Scholar
Sreenivasan, K. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Tennekes, H. 1968 Simple model for the small-scale structure of turbulence. Phys. Fluids 11, 669–671.Google Scholar
Tennekes, H. & Wyngaard, J. C. 1972 The intermittent small-scale structure of turbulence: data-processing hazards. J. Fluid Mech. 55, 93–103.Google Scholar
Thiesset, F., Antonia, R. A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, (R2).Google Scholar
Townsend, A. A. 1951 On the fine-scale structure of turbulence. Proc. R. Soc. Lond. A 208, 534–542.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Universal dissipation scaling for non-equilibrium turbulence. Phys. Rev. Lett. 108, 214503.Google Scholar
Van Atta, C. W. & Antonia, R. A. 1980 Reynolds number dependence of skewness and flatness factors of turbulent velocity derivatives. Phys. Fluids 23, 252–257.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.Google Scholar
Vreman, A. W. & Kuerten, J. G. M. 2014 a Comparison of direct numerical simulation databases of turbulent channel flow at $Re_{{\it\tau}}=180$ . Phys. Fluids 26, 015102.CrossRefGoogle Scholar
Vreman, A. W. & Kuerten, J. G. M. 2014b Statistics of spatial derivatives of velocity and pressure in turbulent channel flow. Phys. Fluids 26, 085103.Google Scholar
Wallace, J. M., Brodkey, R. S. & Eckelmann, H. 1977 Pattern-recognized structures in bounded turbulent shear flows. J. Fluid Mech. 83, 673–693.CrossRefGoogle Scholar
Wang, L.-P., Chen, S., Brasseur, J. G. & Wyngaard, J. C. 1996 Examination of hypotheses in Kolmogorov refined turbulence theory through high-resolution simulations. Part 1. Velocity field. J. Fluid Mech. 309, 113–156.CrossRefGoogle Scholar
Wyngaard, J. C. 2010 Turbulence in the Atmosphere. Cambridge University Press.Google Scholar
Zhou, T. & Antonia, R. A. 2000 Reynolds number dependence of the small-scale structure of grid turbulence. J. Fluid Mech. 406, 81–107.Google Scholar
Zhou, T., Antonia, R. A., Zhu, Y., Orlandi, P. & Esposito, P. 1998 Performance of a transverse vorticity probe in a turbulent channel flow. Exp. Fluids 24, 510–517.Google Scholar