2.1. Relationship between the number of satellites and GDOP

The DOP is an important index used to measure the performance of positioning, and a good satellite sky distribution structure is the premise of high position precision. The index indirectly reflects the spatial distribution structure of the satellites, and GDOP can reflect the magnification factor of positioning and clock precision directly because of the satellite spatial distribution structure and is calculated as Equation (1):

(1)$$GDOP=\sqrt{\lpar Q_{11}+Q_{22}+Q_{33}+Q_{44}\rpar } $$

where Q _jj (j = 1, 2, 3, 4) denotes an element of Q = (H ^TH)⁻¹ and H denotes the coefficient matrix, which is calculated by the satellite azimuth α _i and elevation angle β _i $\lpar i=1\cdots n\rpar $ as Equation (2):

(2)$$H = \left[{\matrix{ {\sin \alpha_1} & {\cos \alpha_1\sin \beta_1} & {\cos \alpha_1\cos \beta_1} & 1 & 0 & 0 \cr \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \cr {\sin \alpha_{i-1}} & {\cos \alpha_{i-1}\cos \beta_{i-1}} & {\cos \alpha_{i-1}\cos \beta_{i-1}} & 1 & 0 & 0 \cr {\sin \alpha_i} & {\cos \alpha_i\cos \beta_i} & {\cos \alpha_i\cos \beta_i} & 0 & 1 & 0 \cr \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \cr {\sin \alpha_{j-1}} & {\cos \alpha_{j-1}\cos \beta_{j-1}} & {\cos \alpha_{j-1}\cos \beta_{j-1}} & 0 & 1 & 0 \cr {\sin \alpha_j} & {\cos \alpha_j\cos \beta_j} & {\cos \alpha_j\cos \beta_j} & 0 & 0 & 1 \cr \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \cr {\sin \alpha_n} & {\cos \alpha_n\cos \beta_n} & {\cos \alpha_n\cos \beta_n} & 0 & 0 & 1 \cr } } \right]\matrix{ {\left. {\matrix{ {} \hfill \cr {} \hfill \cr {} \hfill \cr } } \right\}{\rm nsys}1} \cr {\left. {\matrix{ {} \hfill \cr {} \hfill \cr {} \hfill \cr } } \right\}{\rm nsys2}} \cr {\left. {\matrix{ {} \hfill \cr {} \hfill \cr {} \hfill \cr } } \right\}{\rm nsys3}} \cr } $$

where nsys1, nsys2, and nsys3 represent different GNSS systems. If there are any other systems, then H can be expanded as required.

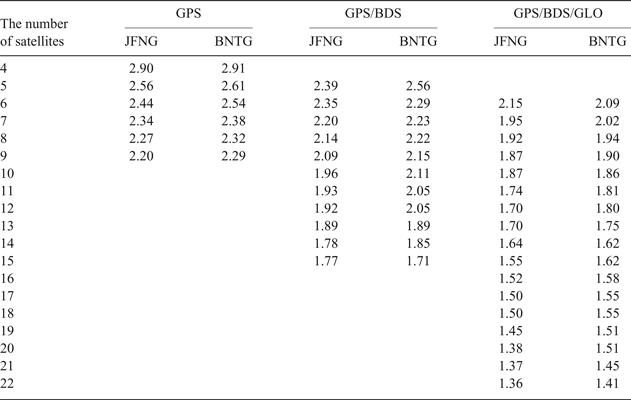
To verify the effects of system combination and the number of satellites on GDOP, data from International GNSS Service (IGS) stations were collected on 1 October 2016 and are used to calculate the minimum DOP of GPS, GPS/BDS, and GPS/BDS/GLO for a changing number of satellites. The results are shown in Table 1.

Table 1. Minimum GDOP change with the change of satellites number

2.2. Effect of one satellite on GDOP

Many factors affect GDOP, and the most important are the satellite constellation configuration parameters and spatial distribution of satellites. The satellite constellation configuration parameters are not discussed in this paper because they are determined when designing the system; hence, we only discuss the effect of a single satellite on GDOP.

M satellites in the field of view are selected for positioning, and the GDOP of m satellites is GDOP _m and the GDOP of $m-1$ satellites is $GDOP_{m-1}^{i}$ after removing the i-th satellite, whose coefficient matrix h _i is [e _i1 e _i2 e _i3 1]. The relationship between GDOP _m and $GDOP_{m-1}^{i} $ can be deduced as Equation (3) (Cong et al., Reference Cong, Abidat and Tan2006; Teng and Wang, Reference Teng and Wang2016):

(3)$$\eqalign{GDOP_{m-1}^{i2} & =traceQ_{m-1}^{i} \cr & =traceQ_{m} +trace \displaystyle{{Q_{m}^{T} h_{i}^{T} h_{i} Q_{m}}\over{1-h_{i} Q_{m} h_{i}^{T}}} \cr & =GDOP_{m}^{2}+trace \displaystyle{{Q_{m}^{T} h_{i}^{T} h_{i} Q_{m}}\over{1-h_{i} Q_{m} h_{i}^{T}}}} $$

From the above reasoning, the i-th satellite GDOP contribution $\Delta GDOP_{m}^{i} $ is described as Equation (4):

(4)$$\lpar \Delta GDOP_{m}^{i}\rpar ^{2}=trace \displaystyle{{Q_{m}^{T} h_{i}^{T} h_{i} Q_{m}}\over{1-h_{i} Q_{m} h_{i}^{T}}} $$

From Equation (4), we can see that the larger $\Delta GDOP_{m}^{i}$, the greater the satellite's contribution, and we could indirectly infer that GDOP decreases as the number of satellites increases in the calculation.

3.1. Satellite selection step of rotating partition algorithm

The fundamental aspect of GNSS satellite selection is to select a few satellites in the field of view that satisfy the positioning requirements. There are $\hbox{C}_{{\rm n}}^{{\rm m}}$ types of combinations if m satellites are used for positioning among n satellites in the field. The optimal DOP satellite selection algorithm often uses the minimum DOP to select satellites in traditional algorithms; however, the optimal DOP satellite selection algorithm cannot meet the requirements of real-time multi-GNSS because the computation time would increase several times as the number of satellites increases. To reduce the computational complexity without affecting positioning accuracy, we propose a fast satellite selection algorithm based on equal distribution of sky. The schematic diagram is shown in Figure 1.

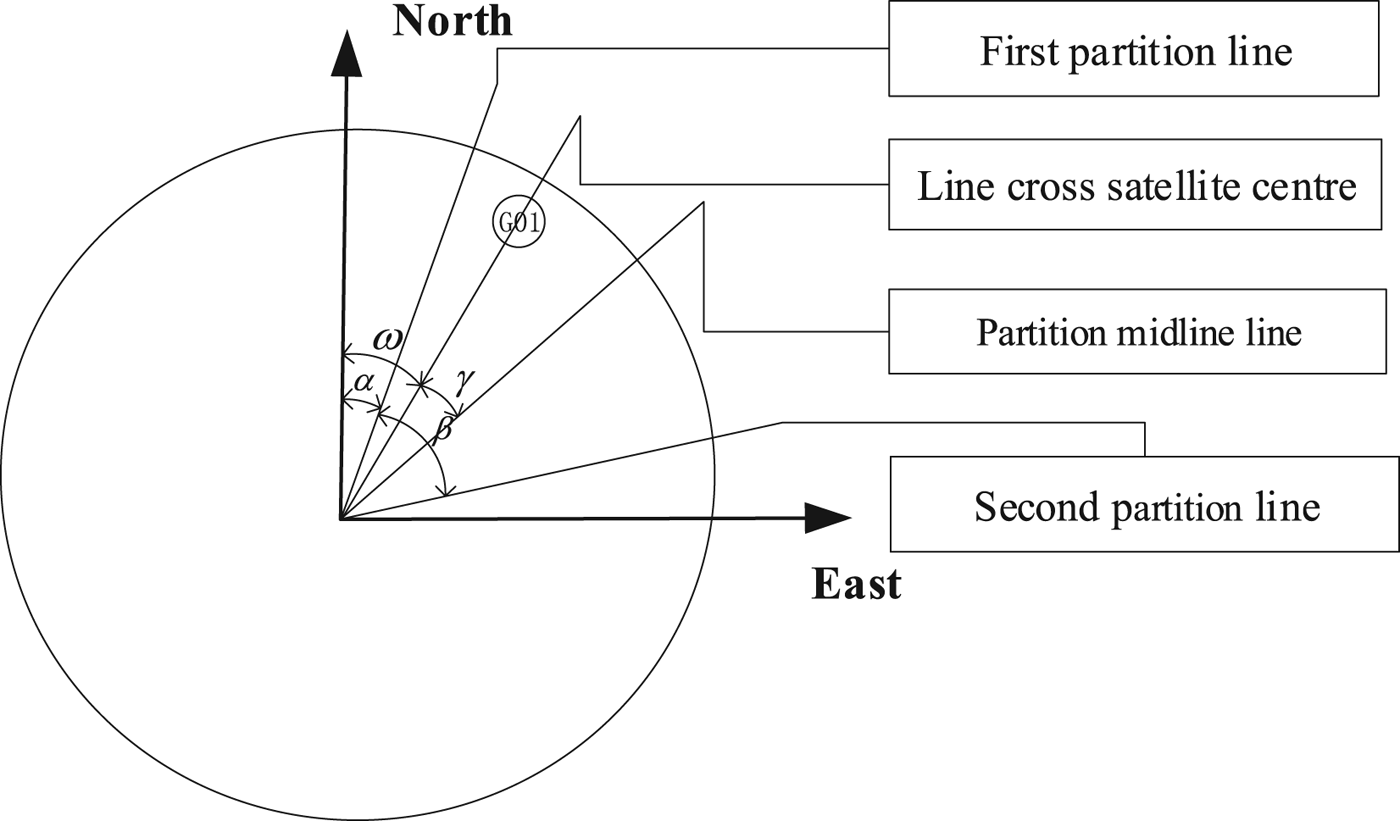
Figure 1. Sketch map of the rotating partition satellite selection algorithm.

In Figure 1, ω denotes the satellite azimuth, α denotes the rotation angle, β denotes the partition angle and γ denotes the angle distance. The steps of the rotating partition satellite selection algorithm are as follows:

• Step 1: Remove satellites whose elevation angle θ is less than cut-off elevation angle θ ₀ and which are unhealthy according to Space Vehicle (SV) Health.

• Step 2: Execute step 3 if visible satellites number is more than selecting satellites number. Conversely, remove the system with the fewest satellites and continue to assess whether the number of satellites meets the condition for selecting satellites circularly.

• Step 3: Traverse all satellites to select the satellite with maximum elevation angle θ _max as the first satellite to select.

• Step 4: Divide the satellites' sky equally based on the number of satellites selected ($\beta =360/nsat$). Match the satellite to the middle line of each partition using the minimum angle distance $\lpar \gamma=\alpha+\beta/2-\omega\rpar _{\min}$. Temporarily skip the partition and match for the other partitions preferentially if the minimum angle is greater than half the portion angle ($\gamma \gt \beta/2\rpar $.

• Step 5: Average the minimum angle distances of all partitions, and the scheme is one of optional schemes.

• Step 6: Increase the rotation angle for the re-partition (enlarge α) and repeat the above process to calculate the average minimum distance of the corresponding partition. The final satellite selection scheme is the minimum value of the average minimum distance partition $\lpar \lpar \hbox{sum}\lpar \gamma_{i\min}\rpar /nsat\rpar _{\min}\rpar $.

• Step 7: Test the DOP of the satellite selection result. If the satellite selection result can pass the test, the selected satellites will be used for positioning. Conversely, if the satellite selection result cannot pass the test, all of the healthy satellites will be used for positioning.

The scheme to select satellites is based on the elevation angle and spatial distribution of the satellite. The algorithm is fast and simple because it does not calculate a complex inverse matrix. The number of satellites to be selected is determined arbitrarily according to positioning systems. However, the GDOP of the rotating partition algorithm is not the minimum GDOP, so the rotating partition algorithm can be considered a suboptimal algorithm. The flowchart for satellite selection is shown in Figure 2.

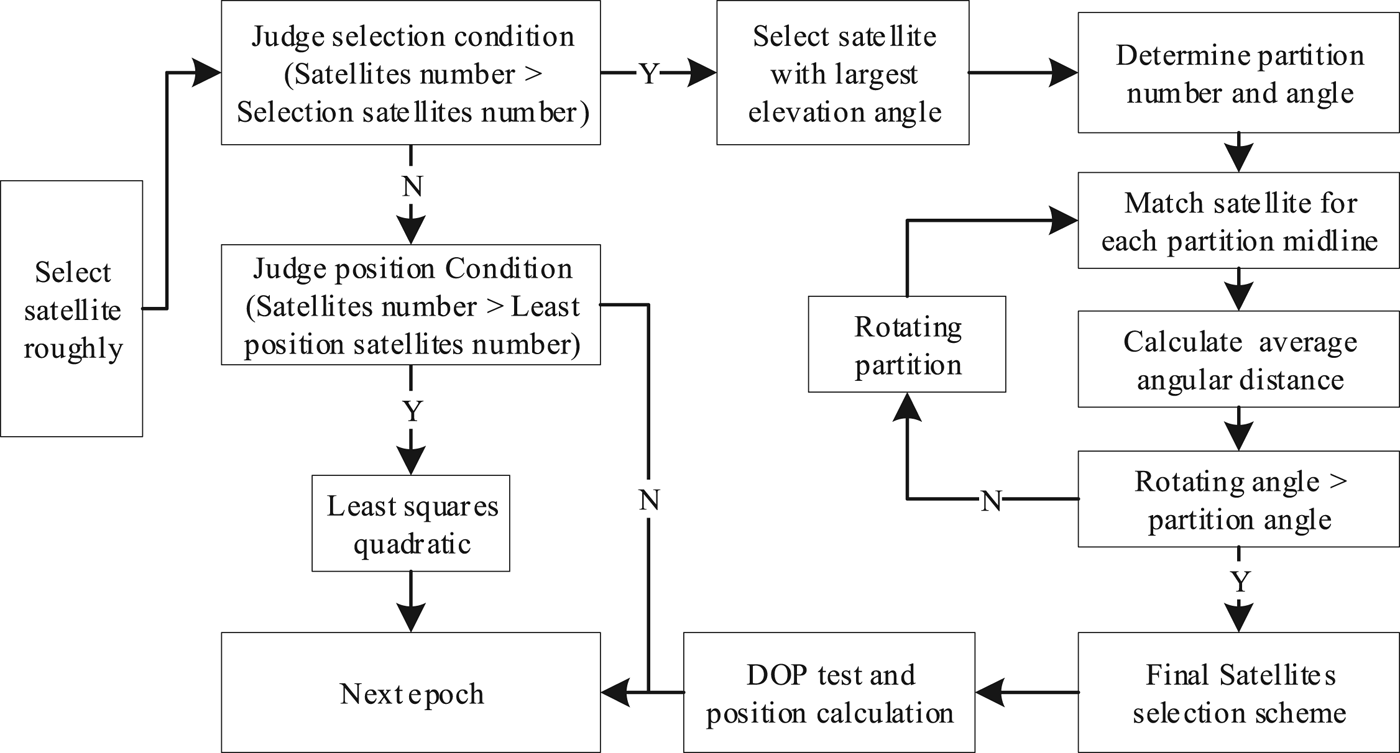
Figure 2. Flowchart for rotating partition satellite selection algorithm.

3.2. An example of a rotating partition satellite selection

Data measured on 1 October 2016 from IGS Multi-GNSS Experiment (MGEX) station JFNG is used as an example. 24 satellites could be observed in the sky for a GPS/GLO/BDS triple system at the first epoch including nine GPS satellites, six GLONASS satellites and nine BDS satellites. The satellite health identifiers were extracted from broadcast ephemeris and altitude and azimuth angle of the visible satellites for the station were calculated. The results are shown in Table 2.

Table 2. The SV Health, Azimuth and elevation angle of satellites in the field of view

The G represents GPS satellite, the R represents GLONASS satellite and the C represents BDS satellite.

3.2.1. Rough satellite selection

• Step 1: The unhealthy satellites BDS C04 and BDS C05 are eliminated based on the SV Health from broadcast ephemeris, and GLO R06 based on masking angle (cut-off elevation angle = 10^°). The sky plot after rough satellite selection is shown as Figure 3.

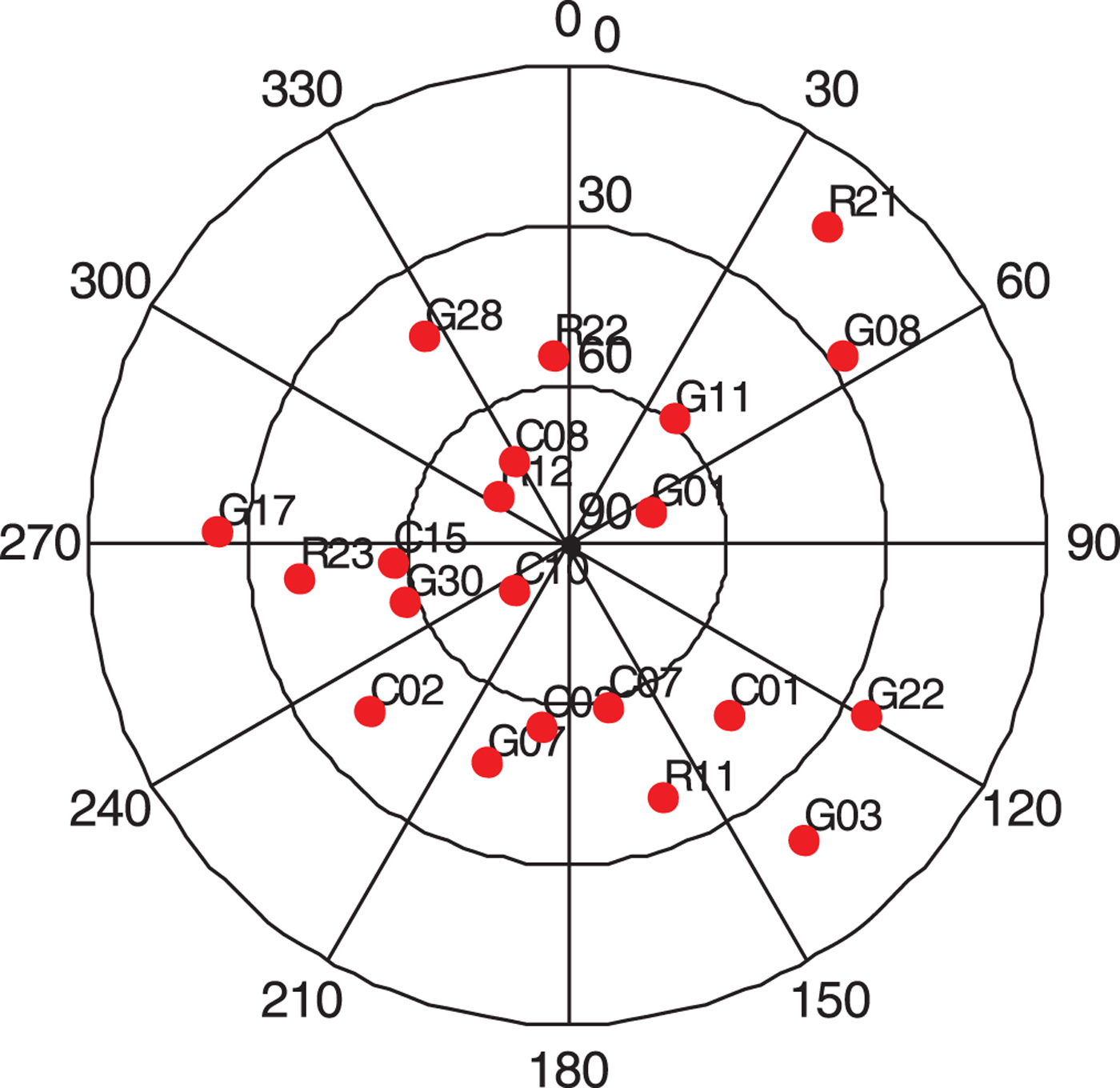
Figure 3. The sky plot of all satellites in the field of view.

3.2.2. Detailed satellite selection

• Step 2: There are 22 healthy satellites in the field, which is more than the number of satellites to be selected, so Step 3 is executed next.

• Step 3: All satellites are traversed to select the satellite with maximum elevation angle as the first satellite to select. BDS C10 is taken as the first satellite whose elevation angle is 77.01^°.

• Step 4: To detect and process the gross error, six satellites are used for a single system, eight satellites for a double system and ten satellites for a triple system. As the satellite with the largest elevation angle has been chosen, the sky is divided into nine regions for satellite selection and the partition angle is 40^°. The first partition midline is 0^°, the second is 40^°, and the n-th is $\lpar n-1\rpar \times 40^{\circ}$.

• Step 5: The satellites for each partition midline whose angle distance is minimum are then chosen. The sky plot is shown as Figure 4 when the rotation angle is 0^° and the average minimum angle distance is 4.56^°.

• Step 6: The partition line is then rotated, increasing 1^° each time. 40 rotations are made to search the minimum average minimum angle distance whose value is 4.41^° by increasing the rotation angle from 0^° to 40^°. The final satellite selection scheme is shown in Figure 5.

• Step 7: The satellite selection result can pass the DOP test, so we use the satellites selected and shown in Figure 5 for positioning.

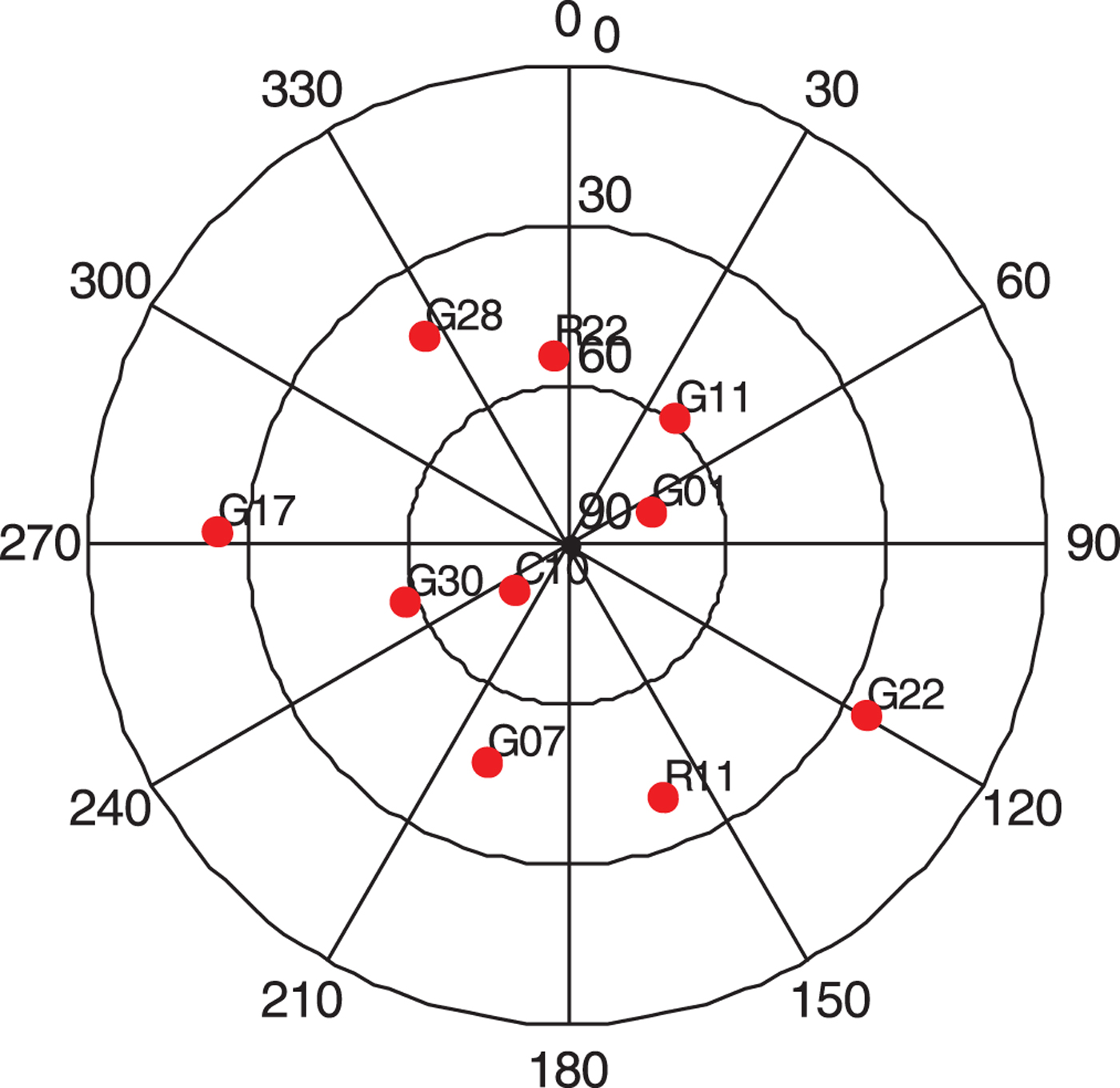
Figure 4. The sky plot of the partition satellite selection algorithm when the rotation angle is 0^°.

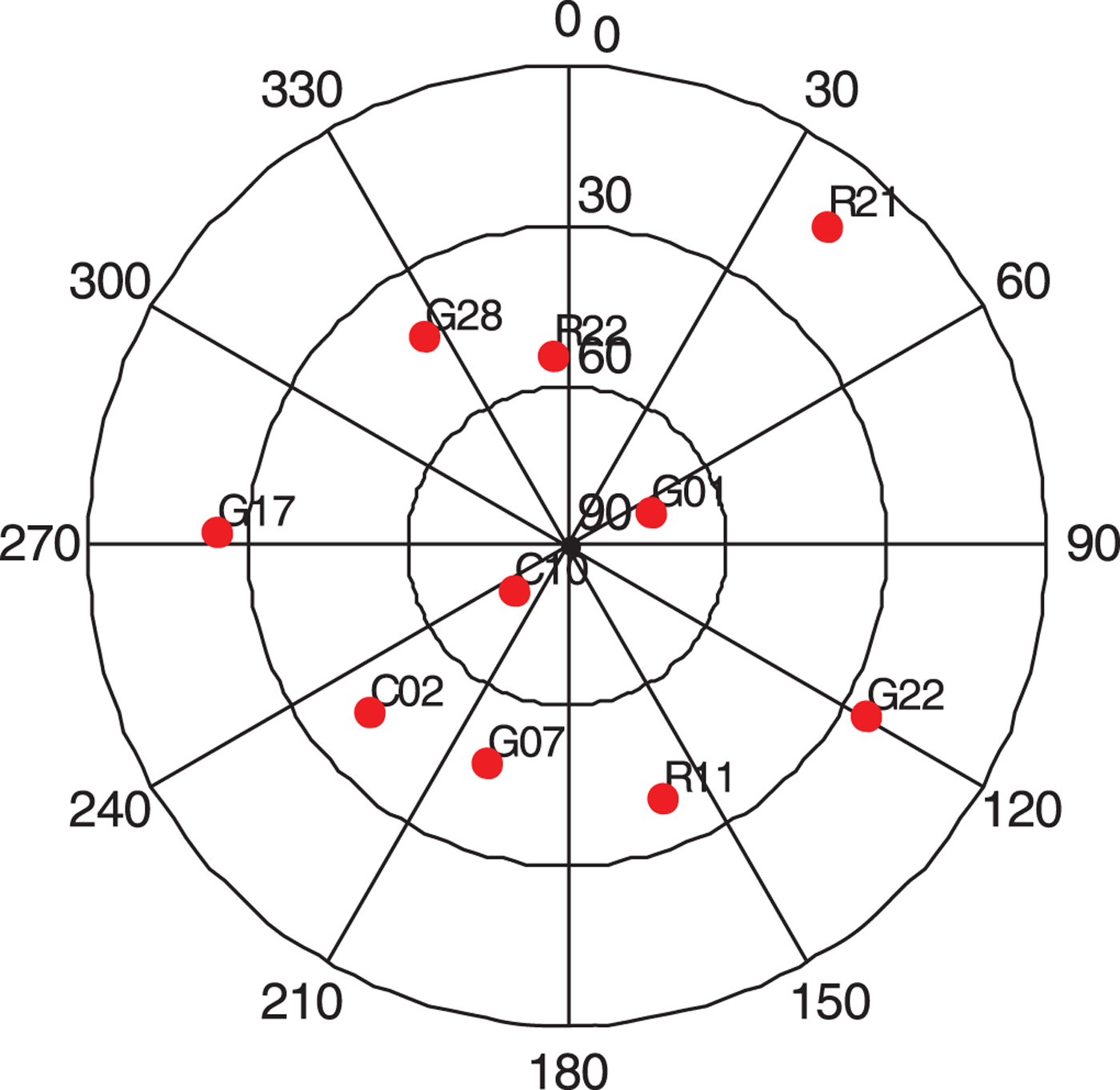
Figure 5. The sky plot of final satellite selection result by the rotating partition algorithm.

4.1. Comparative efficiency analysis

First, the computation time was compared as this is one of main indicators of satellite selection, and one of the main reasons that the application scope of the optimal DOP algorithm is limited. There are $\hbox{C}_{{\rm n}}^{{\rm m}}$ types of combination if m satellites are used for positioning among n satellites in the field of view. However, there are often more than 25 satellites in the field of view for multi-GNSS. If we choose seven satellites, then there are more than 480 possible combinations and if we choose ten satellites, then there are more than three million possible combinations, and an inverse matrix is calculated for each combination; thus, the burden on an ordinary receiver's processing element is unbearable. The new algorithm proposed in this paper only requires addition, subtraction, multiplication and division operations, no inversion; hence, computation time is greatly reduced and the calculation speed is greatly accelerated. To describe the computation time of two algorithms, the GNSS data of the IGS MGEX JNFG station collected on 1 October 2016 was used to measure the computation time in this paper, and the results are shown in Table 3.

Table 3. Average computation time of the rotating partition and optimal DOP algorithm (ms)

The G represents GPS satellite, the R represents GLONASS satellite and the C represents BDS satellite in Table 2.

The results demonstrate that the computation time of the rotating partition algorithm is essentially unaffected as the positioning satellite number increases. This is because the wasting time equals the saving time, and the two offset each other and achieve balance. Respectively, the rotation angle reduced as the positioning satellite number increased if the partition number increased. The angle of each rotation of the selected satellite was set to 1^° degree in this study. The computation time of the rotating partition algorithm was affected by only dozens of milliseconds as the number of positioning satellites increased. This demonstrates that the speed of the rotating partition algorithm outclassed the optimal DOP algorithm. If we use the optimal DOP algorithm to select satellites, the computation time will increase several times with increasing satellites number in the field. If we use the rotating partition algorithm, the time delay is, at the shortest, 21 ms and, at the longest, 73 ms to obtain a result if three or more systems are used for positioning, and such efficiency can easily satisfy the real-time positioning requirement.

4.2. GDOP comparative analysis of the algorithm

GDOP is the main measure for evaluating the accuracy of positioning to evaluate the results of the rotating partition algorithm objectively. The GNSS data of the IGS MGEX JNFG station collected on 1 October 2016 was used to compare the GDOP of the two algorithms in a single system including six satellites, a double system including eight satellites, and a triple system including ten satellites in different circumstances. The GDOP of the rotating partition and optimal DOP algorithm are shown in Figures 6–8.

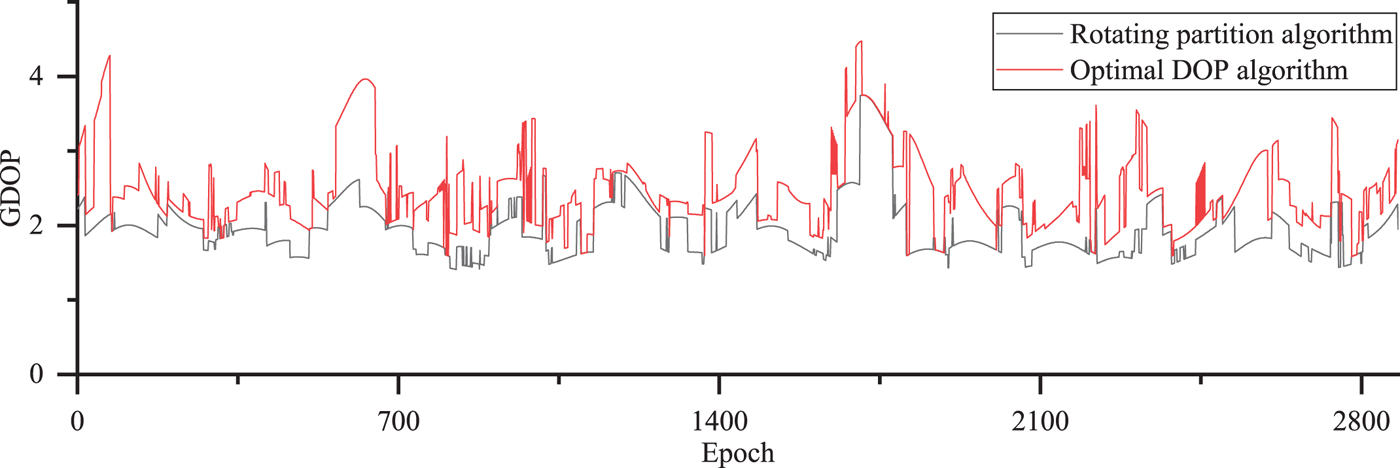
Figure 6. The GDOP of single system for GPS selecting six satellites by rotating partition and optimal DOP algorithm.

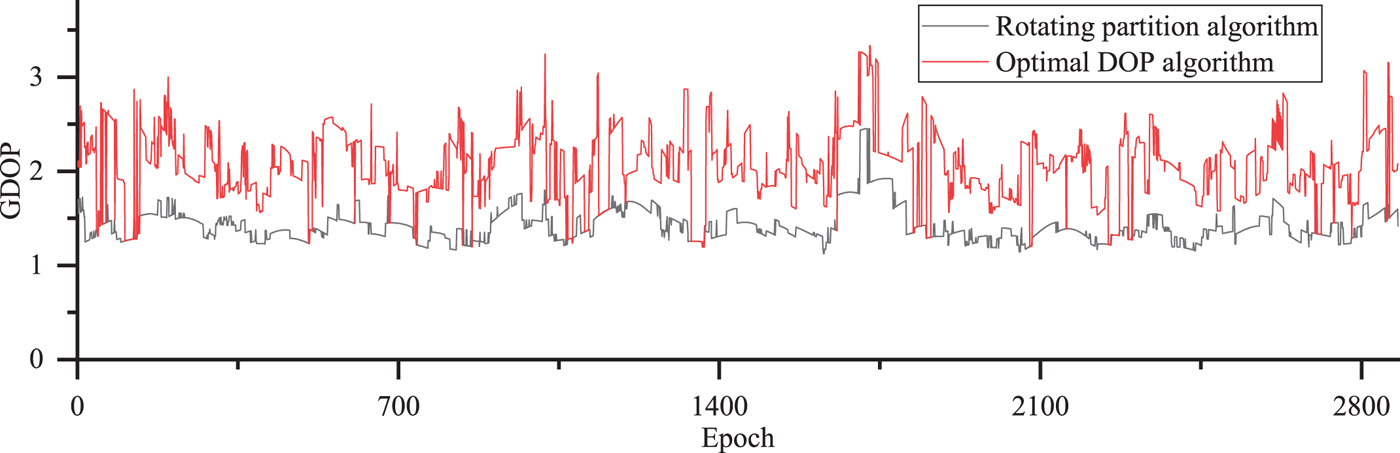
Figure 7. The GDOP of double system for GPS/GLO selecting eight satellites by rotating partition and optimal DOP algorithm.

Figure 8. The GDOP of triple system for GPS/GLO/BDS selecting ten satellites by rotating partition and optimal DOP algorithm.

The results illustrated in Figure 6 demonstrate where a system using just GPS that selected six satellites is used for positioning. If the rotating partition algorithm is used to select satellites, the GDOP less than 4.0 accounts for 98.9%, and the GDOP less than 3.0 accounts for 86.1%. Moreover, The GDOP ratio of the rotating partition algorithm to the optimal DOP algorithm is also statistically analysed. The GDOP ratio less than 2.0 accounts for 99.9%, the GDOP ratio less than 1.8 accounts for 96.8% and the GDOP ratio less than 1.5 accounts for 56.9%.

The results illustrated in Figure 7 demonstrate where a double system of GPS and GLONASS that selected eight satellites was used for positioning. If the rotating partition algorithm is used to select satellites, the GDOP less than 3.0 accounts for 98.3%, the GDOP less than 2.5 accounts for 90.0%, and the GDOP less than 2.0 accounts for 43.5%. Moreover, the GDOP ratio of the rotating partition algorithm to the optimal DOP algorithm is statistically analysed. The GDOP ratio less than 2.0 accounts for 96.6%, the GDOP ratio less than 1.8 accounts for 88.3% and the GDOP ratio less than 1.5 accounts for 85.0%.

The results illustrated in Figure 8 demonstrate where a triple system of GPS, GLONASS and BDS that selected ten satellites was used for positioning If the rotating partition algorithm is used to select satellites, the GDOP less than 3.0 accounts for 100%, the GDOP less than 2.5 accounts for 99.7%, and the GDOP less than 2.0 accounts for 97.8%. Moreover, the GDOP ratio of the rotating partition algorithm to the optimal DOP algorithm is also statistically analysed. The GDOP ratio less than 2.0 accounts for 74.7% and the GDOP ratio less than 1.8 accounts for 56.7%.

From the above results, we deduce that the number of satellites for a position were reduced greatly, particularly in the triple system, which led to an increase of GDOP; however, GDOP remained in a normal range with the rotating partition algorithm. It could be ensured that the GDOP ratio of the rotating partition to optimal DOP algorithm was less than 1.8 for single-system GPS, less than 1.5 for double system GPS/GLO, and only 2.2% GDOP for triple system GPS/GLO/BDS, where the epoch is greater than three. The satellite spatial distribution fully meets the requirements for general navigation and positioning such that the satellite GDOP of the position should be less than five.

4.3. Performance analysis of static data for SPP

Data utilisation and accuracy are the main indices used to evaluate the GNSS algorithm. Generally speaking, the data rejection rate should be less than 10% in the same period in engineering, and the availability and point positioning accuracy of GNSS is evaluated on a global scale by Li et al. (Reference Li, Gao, Wang and Yao2017). To evaluate the rotating partition algorithm, data utilisation and position residuals of the rotating partition algorithm and a traditional optimal DOP algorithm were comparatively analysed in different surroundings, such as a single system that selected six satellites, a double system that selected eight satellites, and a triple system that selected ten satellites. IGS MGEX JNFG station data collected by a Trimble R9 receiver on 1 October 2016, located in Wuhan, Hubei Province was used for the study. The sampling interval was 30 s and continued for 86,400 s (including 2,880 epochs). The GNSS data was processed using the Standard Point Positioning (SPP) strategy according to a single system for GPS, a dual system for combination GPS/GLO, and a three-system combination for GPS/GLO/BDS. The residuals of the rotating partition and optimal DOP algorithm are shown in Figures 9–11.

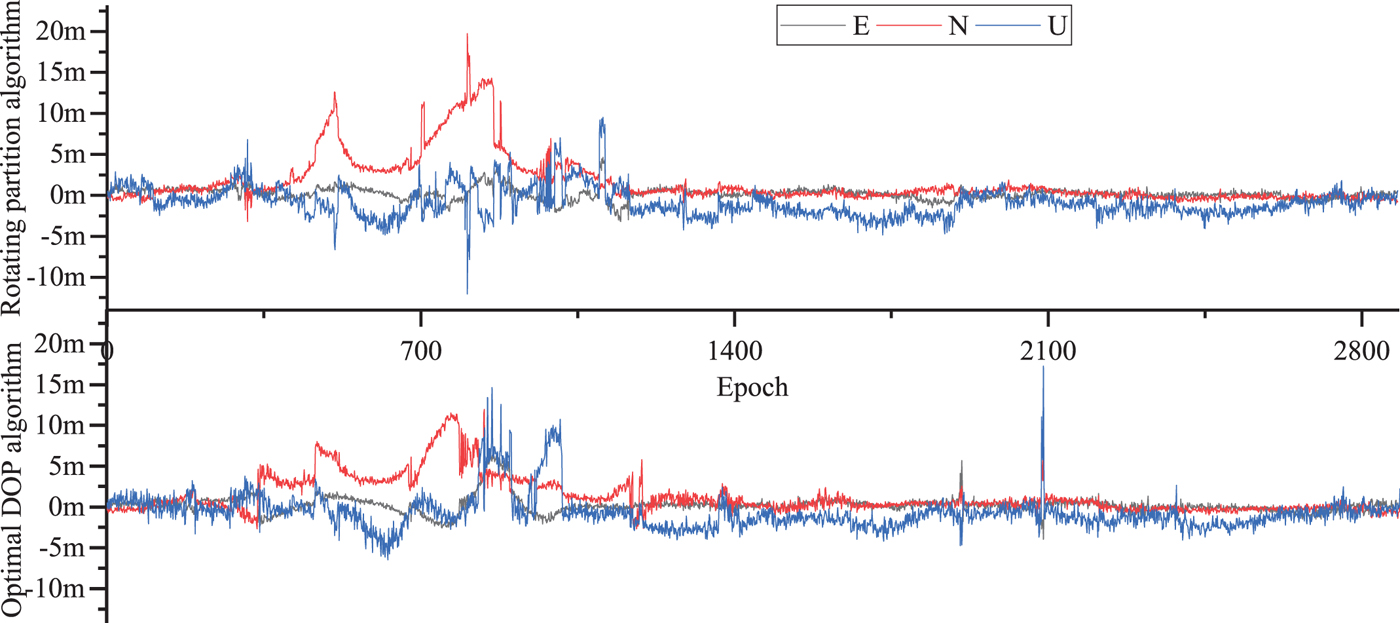
Figure 9. The static position residuals of single system for GPS with six selected satellites.

Figure 10. The static position residuals of double system for GPS/GLO with eight selected satellites.

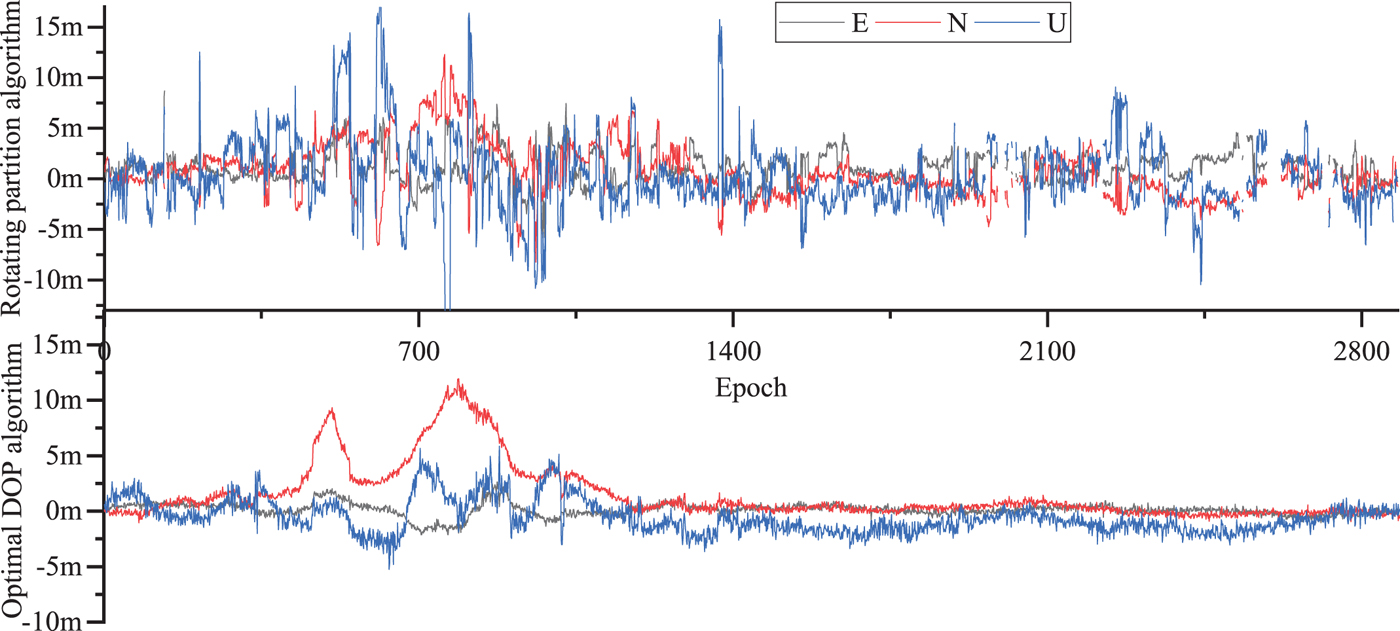
Figure 11. The static position residuals of triple system for GPS/GLO/BDS with ten selected satellites.

The results shows that there are partial epochs that cannot output positioning results because the parameter estimation result fails to pass the Chi-square hypothesis test. For the single system GPS test, the result is 0.2%, for a double GPS/GLO system, it is 0.4% and for a triple GPS/GLO/BDS system, the result is 23.4% if we do not select satellites before parameter estimation. The single, double and triple systems all passed the hypothesis test for the optimal DOP algorithm. All the epochs of the single and double system could pass the hypothesis test, and the pass rate for the triple system increased from 76.4% to 95.8% with the rotating partition algorithm.

The residual error of the two algorithms was compared: the accuracy of a single system for GPS was 0.730 m in the East (E) direction, 3.310 m in the North (N) direction, and 1.999 m in the Up (U) direction with the rotating partition algorithm. The accuracy of the single GPS system was 1.083 m in the E direction, 2.578 m in the N direction and 2.309 m in the U direction with the optimal DOP algorithm. The accuracy of the double GPS/GLO system was 0.664 m in the E direction, 2.715 m in the N direction and 2.208 m in the U direction with the rotating partition algorithm. The accuracy of the double GPS/GLO system was 0.889 m in the E direction, 2.774 m in the N direction, and 2.280 m in the U direction with the optimal DOP algorithm. The accuracy of the triple GPS/GLO/BDS system was 1.833 m in the E direction, 2.615 m in the N direction, and 3.626 m in the U direction with the rotating partition algorithm. The accuracy of the triple GPS/GLO/BDS system was 0.603 m in the E direction, 2.945 m in the N direction, and 1.598 m in the U direction with optimal DOP algorithm. Statistical results are shown in Table 4.

Table 4. Static data accuracy comparison for JFNG station

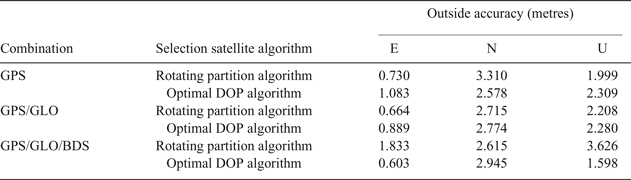
Statistical information from the two types of algorithm shows that the precision was better than 5 m in three directions, which meets the requirement of navigation. Thus, we could consider that there is small difference between the two algorithms, but the speed of the rotating partition algorithm satellite selection algorithm was far higher than the traditional optimal DOP satellite selection algorithm.

4.4. Performance analysis of dynamic data for SPP

To analyse the performance of the rotating partition algorithm more objectively, dynamic GNSS data collected on 17 June 2017 using a Trimble R10 receiver was used to verify the new satellite selection algorithm. The collection area was at CUMT in Xuzhou, Jiangsu province the sampling frequency was 1 Hz and continued for approximately 400 s.

The base station was the CUMT Continuously Operating Reference Stations (CORS) whose coordinates are known accurately, and the result of the dynamic baseline solution was a reference true value for the SPP result; the residual in three directions of the data is shown in Figures 12–14.

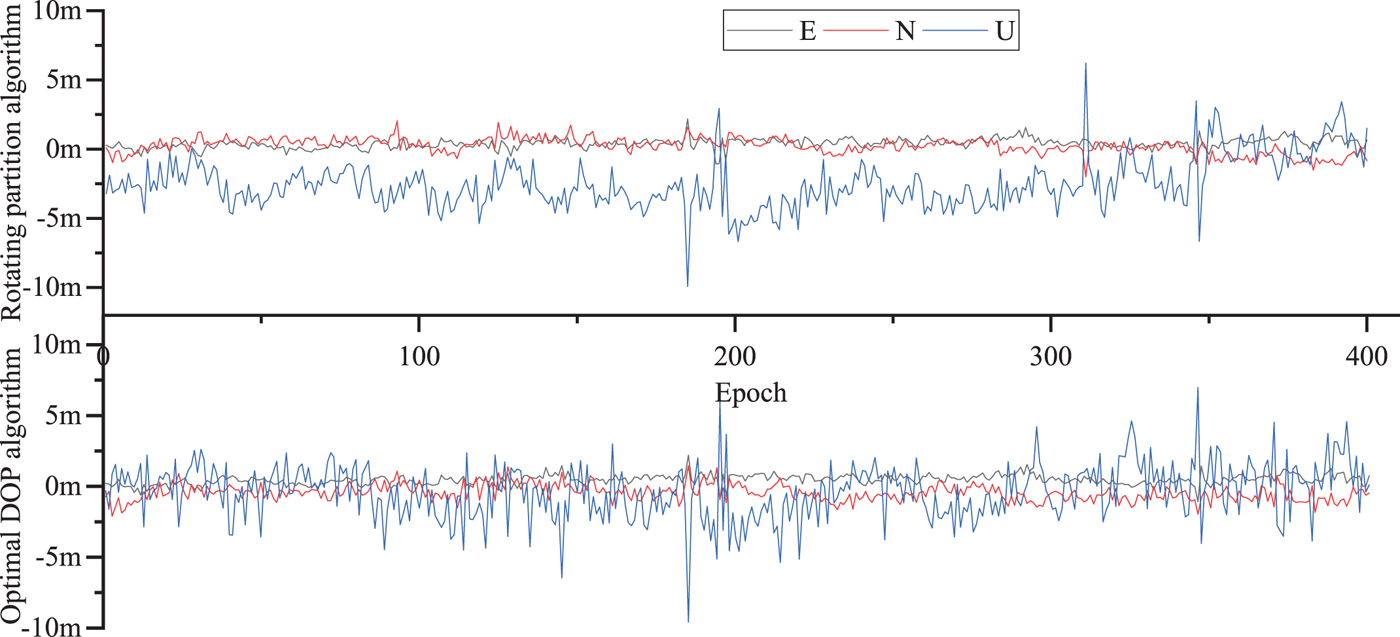
Figure 12. The dynamic position residuals of single system for GPS with six selected satellites.

Figure 13. The dynamic position residuals of double system for GPS/GLO with eight selected satellites.

Figure 14. The dynamic position residuals of triple system for GPS/GLO/BDS with ten selected satellites.

The results show that the single, double and triple systems all passed the hypothesis test using the optimal DOP algorithm. The single and double systems passed the hypothesis test, and the pass rate of the triple system increased to 98.6% with the rotating partition algorithm.

We compared the residual error of the two algorithms: the accuracy of the single system for GPS was 1.719 m in the E direction, 1.914 m in the N direction, and 9.743 m in the U direction with the rotating partition algorithm. The accuracy of the single GPS system was 1.845 m in the E direction, 2.302 m in the N direction, and 6.366 m in the U direction with the optimal DOP. The accuracy of the double GPS/GLO system was 1.984 m in the E direction, 1.633 m in the N direction, and 9.820 m in the U direction with the rotating partition algorithm. The accuracy of the double GPS/GLO system was 1.470 m in the E direction, 1.343 m in the N direction, and 6.763 m in the U direction with optimal DOP. The accuracy of the triple GPS/GLO/BDS system was 2.906 m in the E direction, 3.418 m in the N direction and 6.065 m in the U direction with the rotating partition algorithm. The accuracy of the triple GPS/GLO/BDS system was 1.567 m in the E direction, 1.477 m in the N direction, 7.362 m in the U direction with the optimal DOP algorithm. Statistical results are shown in Table 5.

Table 5. Dynamic data accuracy comparison

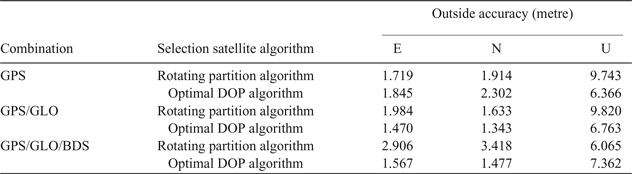
The statistical information for the two types of algorithm demonstrates that the precision was better than 5 m in three directions, which meets the requirement of positioning and navigation. Thus, we could consider that there was small difference between the two algorithms, but the speed of the rotating partition satellite selection algorithm was far higher than the traditional optimal DOP satellite selection algorithm.