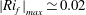1 Introduction
1.1 Reasons for the study
This study was prompted by questions of effectiveness arising from industrial studies on air handling devices for separating climatic environments by means of dynamic air barriers. In many factories, especially in the food and pharmaceutical industries, a zonal approach tends to be needed, even inside cleanrooms, to maintain different levels of temperature and air cleanliness between non-separate adjacent spaces. The first example is the separation of an open volume containing products susceptible to biological contamination from the atmosphere surrounding the workers. In such a case, techniques have been proposed consisting of flowing horizontal or inclined clean cold air flows. In other situations, zonal separation is achieved with vertical air curtains. Generally, each dynamic separation between two atmospheres is analogous to a plane turbulent mixing layer developing between two streams of different velocities and temperatures.
As long as a temperature gradient is maintained across that shear layer, buoyancy has to be taken into account as a force acting on the different dynamic mechanisms involved in entrainment and turbulent mixing and leading to the continuous spread of the mixing layer. Locally, the relative weight of the buoyancy force can be estimated by the flux Richardson number (ratio of buoyancy and turbulent productions, see Tennekes & Lumley Reference Tennekes and Lumley1972; Townsend Reference Townsend1976), while both locally and overall the orientation of the mixing layer plane modifies the way the vertical buoyancy acts on the longitudinal and transverse dynamic mechanisms.
We focused in this study on the case of a horizontal plane shear layer corresponding to devices designed for the food industry. In such a case, cold air is blown on the high-velocity side of the mixing layer, hot air is blown on the low-velocity side of the mixing layer and cold air can be either above or below the hot air. Figure 1 illustrates the two possible configurations encountered in which the mean vertical velocity and temperature gradients are of opposite sign (and then mean vertical velocity and density gradients are of the same sign). The overall temperature gradient between the two streams gives an overall buoyancy level that can be weighed against the dynamic forces through a bulk Richardson number
![]() $Ri_{b}=-(g_{y}\unicode[STIX]{x1D6FF})/(\unicode[STIX]{x0394}U^{2})\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
(see figure 1 for the definitions of the variables). Inside the mixing layer, local gradients have to be considered to investigate the action of buoyancy on the dynamics through a gradient Richardson number
$Ri_{b}=-(g_{y}\unicode[STIX]{x1D6FF})/(\unicode[STIX]{x0394}U^{2})\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
(see figure 1 for the definitions of the variables). Inside the mixing layer, local gradients have to be considered to investigate the action of buoyancy on the dynamics through a gradient Richardson number
![]() $Ri_{g}=-g_{y}\unicode[STIX]{x1D6FD}\unicode[STIX]{x2202}\unicode[STIX]{x1D703}/\unicode[STIX]{x2202}y(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-2}$
. Both overall and locally, a near zero Richardson number corresponds to a very weak action of buoyancy on the flow. Temperature can then be considered as a passive scalar. With a positive Richardson number (high temperature above, see figure 1
a), buoyancy tends to prevent the movement of fluid parcels towards the central plane of the mixing layer, which is believed to produce a stabilizing effect on the thermal stratification (note however that this behaviour can produce oscillations called Brunt-Väisälä oscillations within a stable geophysical environment). With a negative Richardson number (high temperature below, see figure 1
b), some kind of amplification of the mixing of the two layers is expected. We call these two opposite configurations stably stratified and unstably stratified, respectively.
$Ri_{g}=-g_{y}\unicode[STIX]{x1D6FD}\unicode[STIX]{x2202}\unicode[STIX]{x1D703}/\unicode[STIX]{x2202}y(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-2}$
. Both overall and locally, a near zero Richardson number corresponds to a very weak action of buoyancy on the flow. Temperature can then be considered as a passive scalar. With a positive Richardson number (high temperature above, see figure 1
a), buoyancy tends to prevent the movement of fluid parcels towards the central plane of the mixing layer, which is believed to produce a stabilizing effect on the thermal stratification (note however that this behaviour can produce oscillations called Brunt-Väisälä oscillations within a stable geophysical environment). With a negative Richardson number (high temperature below, see figure 1
b), some kind of amplification of the mixing of the two layers is expected. We call these two opposite configurations stably stratified and unstably stratified, respectively.

Figure 1. Illustration of horizontal plane mixing layer with mean shear and stratification. The mean vertical velocity and temperature gradients are of opposite sign.
![]() $\boldsymbol{U}$
,
$\boldsymbol{U}$
,
![]() $\unicode[STIX]{x1D6E9}$
and
$\unicode[STIX]{x1D6E9}$
and
![]() $\unicode[STIX]{x1D70C}$
are the velocity vector, temperature and density of the flow, respectively.
$\unicode[STIX]{x1D70C}$
are the velocity vector, temperature and density of the flow, respectively.
![]() $\unicode[STIX]{x0394}U$
,
$\unicode[STIX]{x0394}U$
,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
are velocity, temperature and density differences between the two streams, respectively.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
are velocity, temperature and density differences between the two streams, respectively.
![]() $\boldsymbol{g}$
is the gravity vector.
$\boldsymbol{g}$
is the gravity vector.
![]() $\unicode[STIX]{x1D6FF}$
is the thickness of the mixing layer. The Richardson number can be defined using gradients and is then written
$\unicode[STIX]{x1D6FF}$
is the thickness of the mixing layer. The Richardson number can be defined using gradients and is then written
![]() $Ri_{g}=+g_{y}1/\unicode[STIX]{x1D70C}(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}y)(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-2}$
or
$Ri_{g}=+g_{y}1/\unicode[STIX]{x1D70C}(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}y)(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-2}$
or
![]() $-g_{y}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x2202}\unicode[STIX]{x1D703}/\unicode[STIX]{x2202}y)(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-2}$
where
$-g_{y}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x2202}\unicode[STIX]{x1D703}/\unicode[STIX]{x2202}y)(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-2}$
where
![]() $g_{y}$
is the
$g_{y}$
is the
![]() $y$
-component of the gravity vector (usually
$y$
-component of the gravity vector (usually
![]() $g_{y}=-g$
with
$g_{y}=-g$
with
![]() $g$
the standard acceleration due to gravity equal to
$g$
the standard acceleration due to gravity equal to
![]() $9.81~\text{m}^{2}~\text{s}^{-1}$
) and
$9.81~\text{m}^{2}~\text{s}^{-1}$
) and
![]() $\unicode[STIX]{x1D6FD}$
is the thermal expansion coefficient. (a) With a positive Richardson number, the heavy fluid is below the lighter fluid and the buoyancy-weight resulting force acting on a parcel of fluid
$\unicode[STIX]{x1D6FD}$
is the thermal expansion coefficient. (a) With a positive Richardson number, the heavy fluid is below the lighter fluid and the buoyancy-weight resulting force acting on a parcel of fluid
![]() $p$
tends to oppose vertical displacement, giving a stably stratified configuration. (b) With a negative Richardson number, the heavy fluid is above the lighter fluid and the buoyancy-weight resulting force acting on a parcel of fluid
$p$
tends to oppose vertical displacement, giving a stably stratified configuration. (b) With a negative Richardson number, the heavy fluid is above the lighter fluid and the buoyancy-weight resulting force acting on a parcel of fluid
![]() $p$
tends to amplify vertical displacement, giving an unstably stratified configuration.
$p$
tends to amplify vertical displacement, giving an unstably stratified configuration.
The overall temperature and velocity gradients at stake in the industrial situations considered (roughly
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=20~\text{K}$
and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=20~\text{K}$
and
![]() $\unicode[STIX]{x0394}U=2~\text{m}~\text{s}^{-1}$
for a layer thickness
$\unicode[STIX]{x0394}U=2~\text{m}~\text{s}^{-1}$
for a layer thickness
![]() $\unicode[STIX]{x1D6FF}$
of approximately 10 cm) mean that Boussinesq approximation can be used for the equations of motion, and the Richardson number value has a moderate negative or positive value. Our aim was therefore to evaluate the action of such relatively moderate buoyancy forces, in stably and unstably stratified conditions, on the behaviour of the mixing layer and, more precisely, on the entrainment and turbulent mixing mechanisms.
$\unicode[STIX]{x1D6FF}$
of approximately 10 cm) mean that Boussinesq approximation can be used for the equations of motion, and the Richardson number value has a moderate negative or positive value. Our aim was therefore to evaluate the action of such relatively moderate buoyancy forces, in stably and unstably stratified conditions, on the behaviour of the mixing layer and, more precisely, on the entrainment and turbulent mixing mechanisms.
1.2 Entrainment and mixing in shear layers
Many visualization experiments have shown the presence of large-scale coherent structures in shear flows. For a plane mixing layer, visualizations by Brown & Roshko (Reference Brown and Roshko1974) and Bernal & Roshko (Reference Bernal and Roshko1986) revealed large spanwise roller vortices surrounded by smaller quasi-streamwise rib vortices. Roller vortices originate from the development of Kelvin–Helmholtz instabilities at the Strouhal frequency and at the inflection point of the velocity profile (Michalke Reference Michalke1965). The evolution of the roller vortices follows the downstream expansion rate of the mixing layer through the pairing process (Winant & Browand Reference Winant and Browand1974) and/or individual growth (Hernan & Jimenez Reference Hernan and Jimenez1982; D’Ovidio & Coats Reference D’Ovidio and Coats2013). The pairing process results from subharmonic excitations and consists of the merging of two neighbouring roller vortices rolling around each other giving rise to a single structure of larger size (Ho & Huang Reference Ho and Huang1982). Rib vortices come from three-dimensional shear instabilities in the thin vortical braid region between the rollers (Corcos & Lin Reference Corcos and Lin1984). Together with the spanwise oscillations of rollers reported by Pierrehumbert & Widnall (Reference Pierrehumbert and Widnall1982), they speed up the transition to three-dimensional turbulence.
The entrainment process results from the introduction of the surrounding fluid into the mixing layer by eddies of turbulence. Corrsin & Kistler (Reference Corrsin and Kistler1954) emphasized the importance of the interface between non-turbulent and turbulent flows for the entrainment of irrotational flow into the rotational region. Identification and characterization of this interface has been the subject of intensive research (see review by da Silva et al. Reference da Silva, Hunt, Eames and Westerweel2014). Engulfing and nibbling are regarded as the two main contributing mechanisms in the entrainment process. Engulfing corresponds to an inviscid mechanism in which large packets of surrounding irrotational flow are drawn into the turbulent region and nibbling corresponds to a small-scale viscous mechanism occurring at the interface. Although engulfing has been considered to be predominant in entrainment since the work of Townsend (Reference Townsend1966), recent investigations of jet flows suggest that entrainment can mainly be caused by nibbling (Mathew & Basu Reference Mathew and Basu2002; Westerweel et al. Reference Westerweel, Fukushima, Pedersen and Hunt2005), as originally assumed by Corrsin & Kistler (Reference Corrsin and Kistler1954). However, Philip et al. (Reference Philip, Meneveau, de Silva and Marusic2014) considered that the two mechanisms can be viewed as describing the same entrainment process but on different scales that are necessarily linked since engulfing increases the size of the interface where nibbling occurs. In a plane mixing layer, the velocity difference between the two streams is sustained and thus roller vortices persist far downstream. Lasheras, Cho & Maxworthy (Reference Lasheras, Cho and Maxworthy1986) and Bell & Mehta (Reference Bell and Mehta1990) showed that the entrainment process results from both the action of rib vortices at the interface (nibbling) and from that of the roller vortices (engulfing), but to our knowledge there has been no recent investigation of the mixing layer interface going into more detail about this combined mechanism, except for the work by Gampert et al. (Reference Gampert, Boschung, Hennig, Gauding and Peters2014) who focused their study only on detection of the interface.
The mixing process leading to the homogenization of two fluids can be broken down into three stages (Eckart Reference Eckart1948): entrainment, dispersion (or stirring) and molecular diffusion. Following Broadwell & Breidenthal (Reference Broadwell and Breidenthal1982), Masutani & Bowman (Reference Masutani and Bowman1986) summarized the mixing process in a plane mixing layer as a combination of tongues of unmixed fluid transported across the layer by large-scale movements (engulfing), interfacial diffusion zones of finite thickness separating the zones of unmixed fluid (nibbling) and cores of mixed fluid with a nearly homogeneous composition. Meyer, Dutton & Lucht (Reference Meyer, Dutton and Lucht2006) showed however that the interfacial diffusion layers may be dominated by intermediate scales leading to regions of inhomogeneously mixed fluid. The mixing process spans the full spectrum of space–time scales of the flow and depends on the Reynolds number
![]() $Re$
and the Prandtl–Schmidt number
$Re$
and the Prandtl–Schmidt number
![]() $Sc=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
, i.e. the ratio between the kinematic viscosity
$Sc=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
, i.e. the ratio between the kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
and the molecular or thermal diffusivity
$\unicode[STIX]{x1D708}$
and the molecular or thermal diffusivity
![]() $\unicode[STIX]{x1D705}$
. Turbulent kinetic energy in three-dimensional turbulence flow cascades down from large velocity length scales
$\unicode[STIX]{x1D705}$
. Turbulent kinetic energy in three-dimensional turbulence flow cascades down from large velocity length scales
![]() $\unicode[STIX]{x1D6EC}_{u}$
, where turbulent kinetic energy is injected, to the smallest velocity length scale of the flow, where turbulent kinetic energy is dissipated into heat by the viscosity of the fluid. The turbulent kinetic energy cascade is characterized by an inertial subrange described by the
$\unicode[STIX]{x1D6EC}_{u}$
, where turbulent kinetic energy is injected, to the smallest velocity length scale of the flow, where turbulent kinetic energy is dissipated into heat by the viscosity of the fluid. The turbulent kinetic energy cascade is characterized by an inertial subrange described by the
![]() $k^{-5/3}$
law (
$k^{-5/3}$
law (
![]() $k$
is a wavenumber) established by Kolmogorov, and by a viscous subrange. The smallest velocity length scale is known as the Kolmogorov length scale
$k$
is a wavenumber) established by Kolmogorov, and by a viscous subrange. The smallest velocity length scale is known as the Kolmogorov length scale
![]() $\unicode[STIX]{x1D702}_{K}=(\unicode[STIX]{x1D708}^{3}/\langle \unicode[STIX]{x1D716}_{u}\rangle )^{1/4}$
(where
$\unicode[STIX]{x1D702}_{K}=(\unicode[STIX]{x1D708}^{3}/\langle \unicode[STIX]{x1D716}_{u}\rangle )^{1/4}$
(where
![]() $\langle \unicode[STIX]{x1D716}_{u}\rangle$
is the mean dissipation rate) and its value depends on the Reynolds number (
$\langle \unicode[STIX]{x1D716}_{u}\rangle$
is the mean dissipation rate) and its value depends on the Reynolds number (
![]() $\unicode[STIX]{x1D702}_{K}/\unicode[STIX]{x1D6EC}_{u}\sim Re^{-3/4}$
). Similarly, scalar variance cascades down to the smallest scalar length scales of the flow, where the scalar fluctuations are damped by the molecular diffusion. In the inertial subrange of the velocity, the scalar variance cascade is characterized by an inertial–convective subrange described by the
$\unicode[STIX]{x1D702}_{K}/\unicode[STIX]{x1D6EC}_{u}\sim Re^{-3/4}$
). Similarly, scalar variance cascades down to the smallest scalar length scales of the flow, where the scalar fluctuations are damped by the molecular diffusion. In the inertial subrange of the velocity, the scalar variance cascade is characterized by an inertial–convective subrange described by the
![]() $k^{-5/3}$
law established by Corrsin and Obukhov. At a higher wavenumber, it is characterized by a viscous–convective subrange described by the
$k^{-5/3}$
law established by Corrsin and Obukhov. At a higher wavenumber, it is characterized by a viscous–convective subrange described by the
![]() $k^{-1}$
law established by Batchelor, and by a viscous–diffusive subrange. If
$k^{-1}$
law established by Batchelor, and by a viscous–diffusive subrange. If
![]() $Sc\leqslant 1$
(i.e.
$Sc\leqslant 1$
(i.e.
![]() $\unicode[STIX]{x1D708}\leqslant \unicode[STIX]{x1D705}$
), molecular diffusion appears in the inertial subrange of the velocity, at a scale larger than the Kolmogorov scale. In this case, the molecular diffusive scale is known as the Corrsin–Obukhov scale
$\unicode[STIX]{x1D708}\leqslant \unicode[STIX]{x1D705}$
), molecular diffusion appears in the inertial subrange of the velocity, at a scale larger than the Kolmogorov scale. In this case, the molecular diffusive scale is known as the Corrsin–Obukhov scale
![]() $\unicode[STIX]{x1D702}_{CO}$
with
$\unicode[STIX]{x1D702}_{CO}$
with
![]() $\unicode[STIX]{x1D702}_{CO}/\unicode[STIX]{x1D702}_{K}\sim \text{Sc}^{-3/4}$
. If
$\unicode[STIX]{x1D702}_{CO}/\unicode[STIX]{x1D702}_{K}\sim \text{Sc}^{-3/4}$
. If
![]() $Sc\gg 1$
(i.e.
$Sc\gg 1$
(i.e.
![]() $\unicode[STIX]{x1D708}\gg \unicode[STIX]{x1D705}$
), molecular diffusion appears at a scale smaller than the Kolmogorov scale. In this case, the molecular diffusive scale is known as the Batchelor scale
$\unicode[STIX]{x1D708}\gg \unicode[STIX]{x1D705}$
), molecular diffusion appears at a scale smaller than the Kolmogorov scale. In this case, the molecular diffusive scale is known as the Batchelor scale
![]() $\unicode[STIX]{x1D702}_{B}$
with
$\unicode[STIX]{x1D702}_{B}$
with
![]() $\unicode[STIX]{x1D702}_{B}/\unicode[STIX]{x1D702}_{K}\sim \text{Sc}^{-1/2}$
. When carrying out an analysis of turbulent mixing from experimental data, it is then of importance to evaluate the resolution of the measuring technique and see whether it measures fluctuations coming from the different mechanisms taking place above and under these scales.
$\unicode[STIX]{x1D702}_{B}/\unicode[STIX]{x1D702}_{K}\sim \text{Sc}^{-1/2}$
. When carrying out an analysis of turbulent mixing from experimental data, it is then of importance to evaluate the resolution of the measuring technique and see whether it measures fluctuations coming from the different mechanisms taking place above and under these scales.
1.3 Effects of stratification
Stratified shear flows have been the subject of numerous studies mainly motivated by geophysical and engineering situations that are generally modelled by two types of flow configurations. The first is a flow with uniform shear and stratification behind a grid-generated turbulence (see for example Lienhard & Van Atta Reference Lienhard and Van Atta1990; Yoon & Warhaft Reference Yoon and Warhaft1990; Piccirillo & Van Atta Reference Piccirillo and Van Atta1997; Jacobitz, Sarkar & Van Atta Reference Jacobitz, Sarkar and Van Atta1997). The second is a flow with shear and stratification localized in a layer. The thermally stratified mixing layers studied in the present paper belong to the second type.
When stratification is present, the vorticity transport equation of the flow is supplemented by a baroclinic torque resulting from the misalignment between the pressure and density gradients. At the inviscid limit, this baroclinic torque can be rewritten as the vector product between the acceleration and density gradient fields. This baroclinic torque is a source or sink of vorticity in the roller vortices and in the braid region. Illustrations of the effects of baroclinic vorticity generation can be seen in Schowalter, Van Atta & Lasheras (Reference Schowalter, Van Atta and Lasheras1994) and Soteriou & Ghoniem (Reference Soteriou and Ghoniem1995). This baroclinic torque influences the roller and rib vortices and leads to so-called baroclinic instabilities evolving into additional vortices. Density gradient effects on the structure of the mixing layer can be seen in Soteriou & Ghoniem (Reference Soteriou and Ghoniem1995), Reinaud, Joly & Chassaing (Reference Reinaud, Joly and Chassaing2000) and Fontane & Joly (Reference Fontane and Joly2008) for an acceleration field resulting from unsteadiness and in Klaassen & Peltier (Reference Klaassen and Peltier1991), Schowalter et al. (Reference Schowalter, Van Atta and Lasheras1994), Staquet (Reference Staquet1995) and Smyth (Reference Smyth2003) for an acceleration field primarily due to gravity.
It has been shown in both numerical simulations and experiments that the measured development of a mixing layer is influenced by differences in the inflow conditions such as turbulence intensity in the free streams or the state of the boundary layer on the upstream separating plate. However, the spreading rate is mainly governed by the velocity and the density ratios between the two streams. Experimental evidence of the influence of the density ratio can be seen in the reports of Brown & Roshko (Reference Brown and Roshko1974), Fiedler (Reference Fiedler1974) and Konrad (Reference Konrad1977). In the case of an inertia-dominated variable-density mixing layer (Brown & Roshko Reference Brown and Roshko1974; Konrad Reference Konrad1977; Soteriou & Ghoniem Reference Soteriou and Ghoniem1995; Reinaud et al.
Reference Reinaud, Joly and Chassaing2000), models proposed by Brown & Roshko (Reference Brown and Roshko1974) and Dimotakis (Reference Dimotakis1986) can predict the spreading rate of the mixing layer, the entrainment ratio of the two streams and the convection velocity of the roller vortices in relation to the velocity and density ratios. In the case of horizontal gravity-dominated variable-density mixing layers, the flow can be stably or unstably stratified depending on whether the vertical density gradient is positive or negative and furthermore its downstream evolution can be influenced by the increase in the bulk Richardson number in relation to the growth of the mixing layer thickness
![]() $\unicode[STIX]{x1D6FF}$
.
$\unicode[STIX]{x1D6FF}$
.
Unstably stratified mixing layers have been investigated in a few studies. Nagata & Komori (Reference Nagata and Komori2000) investigated the separate effects of shear and stratification on the development of a mixing layer downstream a turbulence-generating grid (the case of sheared and stratified flow was not considered in their study). In particular, they showed that turbulent mixing increases significantly either at large scale, by shear, in the case of sheared and neutrally stratified flow or at both large and small scales, by buoyancy, in the case of unsheared and unstably stratified flow. Akula, Andrews & Ranjan (Reference Akula, Andrews and Ranjan2013) reported that the mixing layer is initially dominated by shear associated with roller vortices originating from Kelvin–Helmholtz instability and further downstream the mixing layer is governed by buoyancy with vertical plume structures originating from Rayleigh–Taylor instability. Transition occurs within a wide critical bulk Richardson number range (
![]() $Ri_{b}$
from
$Ri_{b}$
from
![]() $-1.5$
to
$-1.5$
to
![]() $-2.5$
) for an Atwood number
$-2.5$
) for an Atwood number
![]() $A=0.035$
(
$A=0.035$
(
![]() $A=(\unicode[STIX]{x1D70C}_{1}-\unicode[STIX]{x1D70C}_{2})/(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})$
where
$A=(\unicode[STIX]{x1D70C}_{1}-\unicode[STIX]{x1D70C}_{2})/(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})$
where
![]() $\unicode[STIX]{x1D70C}_{1}$
is the density of the heavier fluid and
$\unicode[STIX]{x1D70C}_{1}$
is the density of the heavier fluid and
![]() $\unicode[STIX]{x1D70C}_{2}$
the density of the lighter fluid).
$\unicode[STIX]{x1D70C}_{2}$
the density of the lighter fluid).
Stably stratified mixing layers with a Richardson number above a quarter everywhere in the flow are stable against small perturbations (Howard Reference Howard1961; Miles Reference Miles1961). As long as the critical Richardson number is not reached, turbulence can develop in the flow, and the stably stratified configuration has been used to study Reynolds, Schmidt and Richardson number effects on the vortex dynamics (Staquet Reference Staquet1995; Smyth Reference Smyth2003).
1.4 Main focus of the study
We began from the starting point that, although the mixing layer is an academically relatively well documented flow, there is still a lack of differentiation and quantification of the contributions of dynamic and buoyancy forces in the entrainment and mixing processes taking place in the case of mixing layers with velocity and temperature differences. Further investigations should lead to more complete models for Reynolds, Schmidt and Richardson number dependence.
One prerequisite for such studies appears to be the operability of measurement techniques able simultaneously to extract instantaneous velocity and temperature at a high frequency and on a space scale consistent with the mixing scale. The difficulty of velocity–temperature correlation measurements lies in the instantaneous measuring of velocity and temperature both with a fine spatial resolution and a short integration time in relation to the turbulence scales. Our work follows on the studies by Ndoye et al. (Reference Ndoye, Delville, Heitz and Arroyo2010) and Sodjavi & Carlier (Reference Sodjavi and Carlier2013) who used the variable temperature hot-wire thermo-anemometry initially proposed by Corrsin (Reference Corrsin1947) to meet these requirements. In Sodjavi & Carlier (Reference Sodjavi and Carlier2013), measurements were carried out in two stratified configurations denominated stably and unstably stratified mixing layers in relation to the sign of the vertical temperature gradient applied (note again that, in the present study, the mean vertical velocity and temperature gradients remain of opposite sign, the velocity gradient being reversed in opposition to the temperature gradient by always associating high velocity with low temperature, see figure 1), and in an isothermal configuration denominated neutrally stratified mixing layer. The influence of buoyancy on the flow was evaluated and analysed by comparison of the evolution of the different terms of the transport equations for turbulent kinetic energy and temperature variance.
Here, we recommenced from the point at which the velocity vector (
![]() $\boldsymbol{u}$
) and temperature (
$\boldsymbol{u}$
) and temperature (
![]() $\unicode[STIX]{x1D703}$
) coupling appear in the buoyancy term
$\unicode[STIX]{x1D703}$
) coupling appear in the buoyancy term
![]() $-\unicode[STIX]{x1D6FD}g_{j}\langle \unicode[STIX]{x1D703}^{\prime }{u_{j}}^{\prime }\rangle$
of the transport equations for turbulent kinetic energy
$-\unicode[STIX]{x1D6FD}g_{j}\langle \unicode[STIX]{x1D703}^{\prime }{u_{j}}^{\prime }\rangle$
of the transport equations for turbulent kinetic energy
![]() $\langle k^{\prime }\rangle$
(
$\langle k^{\prime }\rangle$
(
![]() $\unicode[STIX]{x1D6FD}$
is the thermal expansion coefficient and
$\unicode[STIX]{x1D6FD}$
is the thermal expansion coefficient and
![]() $g_{j}$
is the
$g_{j}$
is the
![]() $j$
th component of the gravity vector) and in the production term
$j$
th component of the gravity vector) and in the production term
![]() $-\langle \unicode[STIX]{x1D703}^{\prime }{u_{j}}^{\prime }\rangle (\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D703}\rangle /\unicode[STIX]{x2202}x_{j})$
of the transport equations for temperature variance
$-\langle \unicode[STIX]{x1D703}^{\prime }{u_{j}}^{\prime }\rangle (\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D703}\rangle /\unicode[STIX]{x2202}x_{j})$
of the transport equations for temperature variance
![]() $\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
, both buoyancy and production terms being written using Einstein’s summation convention. These buoyancy and production terms are often evaluated against the production term
$\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
, both buoyancy and production terms being written using Einstein’s summation convention. These buoyancy and production terms are often evaluated against the production term
![]() $-\langle {u_{i}}^{\prime }{u_{j}}^{\prime }\rangle (\unicode[STIX]{x2202}\langle u_{i}\rangle /\unicode[STIX]{x2202}x_{j})$
in the transport equations of turbulent kinetic energy. In our flow configuration, with gravity aligned with the transverse axis of the mixing layer, the active cross-correlations were the heat flux
$-\langle {u_{i}}^{\prime }{u_{j}}^{\prime }\rangle (\unicode[STIX]{x2202}\langle u_{i}\rangle /\unicode[STIX]{x2202}x_{j})$
in the transport equations of turbulent kinetic energy. In our flow configuration, with gravity aligned with the transverse axis of the mixing layer, the active cross-correlations were the heat flux
![]() $\langle \unicode[STIX]{x1D703}^{\prime }v^{\prime }\rangle$
for both the buoyancy and the production terms and the momentum flux (or shear stress)
$\langle \unicode[STIX]{x1D703}^{\prime }v^{\prime }\rangle$
for both the buoyancy and the production terms and the momentum flux (or shear stress)
![]() $\langle u^{\prime }v^{\prime }\rangle$
for the production term. The ratios between these quantities can be found in the flux Richardson number
$\langle u^{\prime }v^{\prime }\rangle$
for the production term. The ratios between these quantities can be found in the flux Richardson number
 $$\begin{eqnarray}Ri_{f}=-\frac{\displaystyle \unicode[STIX]{x1D6FD}g_{y}\langle \unicode[STIX]{x1D703}^{\prime }v^{\prime }\rangle }{\displaystyle \frac{\unicode[STIX]{x2202}\langle u\rangle }{\unicode[STIX]{x2202}y}\langle u^{\prime }v^{\prime }\rangle },\end{eqnarray}$$
$$\begin{eqnarray}Ri_{f}=-\frac{\displaystyle \unicode[STIX]{x1D6FD}g_{y}\langle \unicode[STIX]{x1D703}^{\prime }v^{\prime }\rangle }{\displaystyle \frac{\unicode[STIX]{x2202}\langle u\rangle }{\unicode[STIX]{x2202}y}\langle u^{\prime }v^{\prime }\rangle },\end{eqnarray}$$
and the turbulent Prandtl number
 $$\begin{eqnarray}Pr_{t}=\frac{\displaystyle \langle u^{\prime }v^{\prime }\rangle \frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D703}\rangle }{\unicode[STIX]{x2202}y}}{\displaystyle \langle \unicode[STIX]{x1D703}^{\prime }v^{\prime }\rangle \frac{\unicode[STIX]{x2202}\langle u\rangle }{\unicode[STIX]{x2202}y}},\end{eqnarray}$$
$$\begin{eqnarray}Pr_{t}=\frac{\displaystyle \langle u^{\prime }v^{\prime }\rangle \frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D703}\rangle }{\unicode[STIX]{x2202}y}}{\displaystyle \langle \unicode[STIX]{x1D703}^{\prime }v^{\prime }\rangle \frac{\unicode[STIX]{x2202}\langle u\rangle }{\unicode[STIX]{x2202}y}},\end{eqnarray}$$
where
![]() $g_{y}$
is the
$g_{y}$
is the
![]() $y$
-component of the gravity vector with
$y$
-component of the gravity vector with
![]() $g_{y}=-9.81~\text{m}^{2}~\text{s}^{-1}$
. In the face of difficulties in velocity–temperature correlation measurements, the values of these ratios have often been deduced from bulk scales or by recourse to a Boussinesq gradient diffusion hypothesis.
$g_{y}=-9.81~\text{m}^{2}~\text{s}^{-1}$
. In the face of difficulties in velocity–temperature correlation measurements, the values of these ratios have often been deduced from bulk scales or by recourse to a Boussinesq gradient diffusion hypothesis.
With direct access to the cross-correlation quantities, hot-wire thermo-anemometry gave us the opportunity to use joint measurements to highlight mechanisms and events that significantly contribute to the transverse momentum and heat fluxes, and to obtain information on the buoyancy effects. In view of the bulk Richardson number values at stake in our experiments (
![]() $|Ri_{b}|\simeq 0.03$
), it was expected that the stratified mixing layer would be dominated by shears associated with roller vortices from the Kelvin–Helmholtz instability, and the buoyancy force would be very small compared to the main driving forces. In Sodjavi & Carlier (Reference Sodjavi and Carlier2013), we showed it was the case but surprisingly, in the unstably stratified configuration, such a small buoyancy force involved significant changes, as for example in the equilibrium between the different terms of the transport equation for turbulent kinetic energy. It seemed that the baroclinic torque associated with the acceleration field due to gravity changed significantly the entrainment and mixing processes in the unstably stratified configurations. In the present paper, the experimental data already exploited in Sodjavi & Carlier (Reference Sodjavi and Carlier2013) were reworked to further investigate measurable effects of stratification in the self-similar region of the mixing layer. Section 2 describes the experimental configuration and the measurement method, with a focus on the assessment of measurement resolution. The results are then analysed in § 3. The characteristics of the mixing layer are summarized in § 3.1, with a focus on the a priori noticeable effects of stratification. The probability density functions (PDFs) of velocity and temperature and the joint PDFs (JPDFs) of velocity and temperature are analysed in §§ 3.2–3.5 to point out in an original way some physical mechanisms (entrained and mixed fluid events) and clarify their contributions through quantification from the statistical quantity profiles. A conditional analysis is performed in § 3.6, which consists in splitting the flow into several categories of fluid particles in order to separately analyse the behaviours of entrained and mixed fluids. The analysis is associated with a separate movement quantification that enables, in § 3.7, an evaluation of the effect of stratification on entrainment velocities on the two sides of the thermally stratified mixing layer. Finally some hypothesis are proposed on the effect of buoyancy on the mechanisms involved in the entrainment and mixing processes.
$|Ri_{b}|\simeq 0.03$
), it was expected that the stratified mixing layer would be dominated by shears associated with roller vortices from the Kelvin–Helmholtz instability, and the buoyancy force would be very small compared to the main driving forces. In Sodjavi & Carlier (Reference Sodjavi and Carlier2013), we showed it was the case but surprisingly, in the unstably stratified configuration, such a small buoyancy force involved significant changes, as for example in the equilibrium between the different terms of the transport equation for turbulent kinetic energy. It seemed that the baroclinic torque associated with the acceleration field due to gravity changed significantly the entrainment and mixing processes in the unstably stratified configurations. In the present paper, the experimental data already exploited in Sodjavi & Carlier (Reference Sodjavi and Carlier2013) were reworked to further investigate measurable effects of stratification in the self-similar region of the mixing layer. Section 2 describes the experimental configuration and the measurement method, with a focus on the assessment of measurement resolution. The results are then analysed in § 3. The characteristics of the mixing layer are summarized in § 3.1, with a focus on the a priori noticeable effects of stratification. The probability density functions (PDFs) of velocity and temperature and the joint PDFs (JPDFs) of velocity and temperature are analysed in §§ 3.2–3.5 to point out in an original way some physical mechanisms (entrained and mixed fluid events) and clarify their contributions through quantification from the statistical quantity profiles. A conditional analysis is performed in § 3.6, which consists in splitting the flow into several categories of fluid particles in order to separately analyse the behaviours of entrained and mixed fluids. The analysis is associated with a separate movement quantification that enables, in § 3.7, an evaluation of the effect of stratification on entrainment velocities on the two sides of the thermally stratified mixing layer. Finally some hypothesis are proposed on the effect of buoyancy on the mechanisms involved in the entrainment and mixing processes.
2 Experimental configuration and measurement method
The data used in the present study originate from experiments fully described in Sodjavi & Carlier (Reference Sodjavi and Carlier2013). This section first presents the wind tunnel and the generating conditions for the thermally stratified mixing layer. The variable-temperature hot-wire thermo-anemometry method is then described in its enhanced variant specially designed for the simultaneous measurement of temperature and two components of velocity. Finally, the flow configurations explored are detailed and the measurement resolution is discussed.

Figure 2. Side view schematic representation and two pictures of the wind tunnel specifically designed for the study of thermally stratified shear layers. Image (a) is a wind tunnel overview, while (b) focuses on the test section with the splitter plate and a laser-sheet flow visualization of the mixing layer.
2.1 Presentation of the wind tunnel
The wind tunnel used has been specifically designed for the study of thermally stratified mixing layers. A detailed sketch and two images of this wind tunnel are given in figure 2. The wind tunnel is equipped with two juxtaposed open circuits. Two parallel air streams are blown separately through two independent halves of a conditioning chamber comprising several screens and a convergent entrance cone with a contraction coefficient of 2.5. The two streams are separated by a thick horizontal thermal insulating plate with a tapering angle of approximately
![]() $3^{\circ }$
at the trailing edge. These two streams merge and initiate the mixing process downstream from the trailing edge of the splitter plate. The test section of the tunnel is
$3^{\circ }$
at the trailing edge. These two streams merge and initiate the mixing process downstream from the trailing edge of the splitter plate. The test section of the tunnel is
![]() $1\times 1~\text{m}^{2}$
and its length is 3 m. Downstream from the test section, the mixed flow is evacuated through a divergent exit cone. The origin of the coordinate system
$1\times 1~\text{m}^{2}$
and its length is 3 m. Downstream from the test section, the mixed flow is evacuated through a divergent exit cone. The origin of the coordinate system
![]() $(x,y,z)$
is located at the centre of the trailing edge of the separating plate. The
$(x,y,z)$
is located at the centre of the trailing edge of the separating plate. The
![]() $x$
axis coincides with the longitudinal streamwise direction, the
$x$
axis coincides with the longitudinal streamwise direction, the
![]() $y$
axis with the upward transverse direction (parallel to the gravity or buoyancy force direction) and the
$y$
axis with the upward transverse direction (parallel to the gravity or buoyancy force direction) and the
![]() $z$
axis with the spanwise direction of the mixing layer (see figures 1 and 2). Classically,
$z$
axis with the spanwise direction of the mixing layer (see figures 1 and 2). Classically,
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
are the velocity components associated with
$w$
are the velocity components associated with
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
. The velocity and temperature profiles are uniform at the entrance of the test section (maintained very close to pure uniformity outside the boundary layers). The velocity and temperature can be chosen continuously and independently, from 0.5 to
$z$
. The velocity and temperature profiles are uniform at the entrance of the test section (maintained very close to pure uniformity outside the boundary layers). The velocity and temperature can be chosen continuously and independently, from 0.5 to
![]() $5~\text{m}~\text{s}^{-1}$
and from 5 to
$5~\text{m}~\text{s}^{-1}$
and from 5 to
![]() $35\,^{\circ }\text{C}$
. The turbulence levels are lower than 1 % for velocity and
$35\,^{\circ }\text{C}$
. The turbulence levels are lower than 1 % for velocity and
![]() $0.2\,^{\circ }\text{C}$
for temperature in the free stream outside the boundary and mixing layers. The boundary layers over the separating plate faces are tripped downstream to establish the turbulence state and the onset of the transition. The displacement thickness
$0.2\,^{\circ }\text{C}$
for temperature in the free stream outside the boundary and mixing layers. The boundary layers over the separating plate faces are tripped downstream to establish the turbulence state and the onset of the transition. The displacement thickness
![]() $\unicode[STIX]{x1D6FF}_{h}^{\ast }=\int _{0}^{\infty }(1-U(y)/U_{h})\,\text{d}y$
and the momentum thickness
$\unicode[STIX]{x1D6FF}_{h}^{\ast }=\int _{0}^{\infty }(1-U(y)/U_{h})\,\text{d}y$
and the momentum thickness
![]() $\unicode[STIX]{x1D703}_{h}=\int _{0}^{\infty }U(y)/U_{h}(1-U(y)/U_{h})\,\text{d}y$
of the boundary layer on the high-speed side are approximately 2.8 mm and 2 mm, respectively, (
$\unicode[STIX]{x1D703}_{h}=\int _{0}^{\infty }U(y)/U_{h}(1-U(y)/U_{h})\,\text{d}y$
of the boundary layer on the high-speed side are approximately 2.8 mm and 2 mm, respectively, (
![]() $U(y)$
is the mean transverse profile of the longitudinal velocity for an
$U(y)$
is the mean transverse profile of the longitudinal velocity for an
![]() $x$
location on the plate and
$x$
location on the plate and
![]() $U_{h}$
is the velocity in the free stream). This results in a shape factor
$U_{h}$
is the velocity in the free stream). This results in a shape factor
![]() $H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D703}_{h}$
of around 1.4, as expected for the turbulence state (
$H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D703}_{h}$
of around 1.4, as expected for the turbulence state (
![]() $H\simeq 2.6$
for laminar boundary layers and
$H\simeq 2.6$
for laminar boundary layers and
![]() $H\simeq 1.4$
for turbulent boundary layers).
$H\simeq 1.4$
for turbulent boundary layers).
2.2 Description of the variable-temperature hot-wire thermo-anemometry method
The multiple overheat thermo-anemometry was initially proposed by Corrsin (Reference Corrsin1947). Assuming that hot-wire is sensitive to velocity for a high overheat and to temperature for a low overheat, information can be obtained simultaneously on velocity and temperature by submitting hot-wire(s) to different overheats. The overheats may be applied either simultaneously to different wires or sequentially to a single wire or several wires of a single probe. The second method has the advantage of minimizing the number of wires, and therefore both reducing the measurement volume and avoiding interference problems, the drawback being that sequential measurements are not strictly instantaneous.
This second method was implemented by Ndoye et al. (Reference Ndoye, Delville, Heitz and Arroyo2010) and Sodjavi & Carlier (Reference Sodjavi and Carlier2013) in a variable-temperature hot-wire thermo-anemometer invented by Joël Delville (from Pprime Institute, Poitiers, France). In Ndoye et al. (Reference Ndoye, Delville, Heitz and Arroyo2010), the method was designed to use a single hot-wire probe to measure the temperature and the longitudinal velocity component simultaneously. In Sodjavi & Carlier (Reference Sodjavi and Carlier2013), the method was extended to use a
![]() $\times$
-wire probe, thus allowing in addition the measurement of the transverse velocity component.
$\times$
-wire probe, thus allowing in addition the measurement of the transverse velocity component.
In practice, several overheat steps are applied cyclically so that the wire changes suddenly from one constant-temperature step to another, which provides an output voltage response featuring sequences in which well-marked voltage levels correspond to the different overheats applied. Figure 3 shows a typical output voltage response of the anemometer during three cycles, each cycle having two overheat steps. The instantaneous velocity and temperature of the flow, assumed to be constant throughout each short cycle, are deduced from the resolution of a previously calibrated system linking the velocity and the temperature to the voltages of the different overheat steps.

Figure 3. Typical output voltage response of the anemometer during three cycles, each cycle having two overheat steps (
![]() $O_{l}$
and
$O_{l}$
and
![]() $O_{h}$
are the low and the high overheat ratios, respectively). For each cycle, the combination of the two voltage levels extracted from the two plateaus directly gives an estimate of the instantaneous velocity and temperature measured during this cycle.
$O_{h}$
are the low and the high overheat ratios, respectively). For each cycle, the combination of the two voltage levels extracted from the two plateaus directly gives an estimate of the instantaneous velocity and temperature measured during this cycle.
2.3 Flow configurations and measurements
A flow configuration is defined by the convection velocity
![]() $U_{c}=(U_{h}+U_{l})/2$
, the velocity difference between the two parallel flows
$U_{c}=(U_{h}+U_{l})/2$
, the velocity difference between the two parallel flows
![]() $\unicode[STIX]{x0394}U=U_{h}-U_{l}$
(or the modified velocity ratio
$\unicode[STIX]{x0394}U=U_{h}-U_{l}$
(or the modified velocity ratio
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x0394}U/2U_{c}$
) and the temperature difference
$\unicode[STIX]{x1D706}=\unicode[STIX]{x0394}U/2U_{c}$
) and the temperature difference
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D6E9}_{h}-\unicode[STIX]{x1D6E9}_{l}$
. The subscripts
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D6E9}_{h}-\unicode[STIX]{x1D6E9}_{l}$
. The subscripts
![]() $h$
and
$h$
and
![]() $l$
correspond to the high and low free-stream velocity and temperature, respectively. In addition to these parameters, it is necessary to specify whether the mean vertical velocity and temperature gradients are of the same or opposite sign and whether the temperature stratification (the mixing layer is horizontal) is stably stratified (
$l$
correspond to the high and low free-stream velocity and temperature, respectively. In addition to these parameters, it is necessary to specify whether the mean vertical velocity and temperature gradients are of the same or opposite sign and whether the temperature stratification (the mixing layer is horizontal) is stably stratified (
![]() $\unicode[STIX]{x1D6E9}_{h}$
above) or unstably stratified (
$\unicode[STIX]{x1D6E9}_{h}$
above) or unstably stratified (
![]() $\unicode[STIX]{x1D6E9}_{h}$
below). In this study, the analysis of the results was based on three mixing layer configurations with
$\unicode[STIX]{x1D6E9}_{h}$
below). In this study, the analysis of the results was based on three mixing layer configurations with
![]() $U_{h}\simeq 4~\text{m}~\text{s}^{-1}$
and
$U_{h}\simeq 4~\text{m}~\text{s}^{-1}$
and
![]() $U_{l}\simeq 2~\text{m}~\text{s}^{-1}$
corresponding to
$U_{l}\simeq 2~\text{m}~\text{s}^{-1}$
corresponding to
![]() $U_{c}\simeq 3~\text{m}~\text{s}^{-1}$
and
$U_{c}\simeq 3~\text{m}~\text{s}^{-1}$
and
![]() $\unicode[STIX]{x1D706}\simeq 0.33$
:
$\unicode[STIX]{x1D706}\simeq 0.33$
:
-
(i) one stably stratified mixing layer configuration with
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=21.2~\text{K}$
and mean vertical velocity and temperature gradients of opposite sign;
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=21.2~\text{K}$
and mean vertical velocity and temperature gradients of opposite sign; -
(ii) one unstably stratified mixing layer configuration with
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=21~\text{K}$
and mean vertical velocity and temperature gradients of opposite sign; and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=21~\text{K}$
and mean vertical velocity and temperature gradients of opposite sign; and -
(iii) one neutrally stratified mixing layer configuration with
 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=0~\text{K}$
.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=0~\text{K}$
.

Figure 4. Flow visualizations of the mixing layer in stably and unstably stratified configurations. Images come from laser tomography experiments. The cold high-velocity stream was seeded with particles while the hot low-velocity stream was clean. Colour palette from blue to red was used to give an image of the temperature distribution induced by the turbulence stirring process, with a slight error due to the absence of molecular diffusion with particles. Mirroring is applied to the unstably stratified condition, with the gravity vector turned upwards. Dots distributed along 11 transverse profiles correspond to the hot-wire measurement locations.
Two flow visualizations of the mixing layer are presented in figure 4 for the stably and unstably stratified configurations. With this figure, we present the stratified mixing layer configurations investigated in this study and give an illustration of the enhancement of the downstream spreading of the mixing layer in both stably and unstably stratified configurations. For the unstably stratified configuration, the
![]() $y$
axis was turned upside down, thus placing the high-velocity stream on the negative side of the
$y$
axis was turned upside down, thus placing the high-velocity stream on the negative side of the
![]() $y$
axis and the low-velocity stream on the positive side, as for the neutrally and the stably stratified configurations. This mirroring was systematically applied throughout the study to make it easier to describe the comparison between the three configurations (the only difference between the three configurations now being the
$y$
axis and the low-velocity stream on the positive side, as for the neutrally and the stably stratified configurations. This mirroring was systematically applied throughout the study to make it easier to describe the comparison between the three configurations (the only difference between the three configurations now being the
![]() $y$
-component of gravity vector:
$y$
-component of gravity vector:
![]() $g_{y}=-9.81~\text{m}^{2}~\text{s}^{-1}$
for the stably and neutrally stratified configurations and
$g_{y}=-9.81~\text{m}^{2}~\text{s}^{-1}$
for the stably and neutrally stratified configurations and
![]() $g_{y}=+9.81~\text{m}^{2}~\text{s}^{-1}$
for the unstably stratified configuration). This figure thus provides a concrete depiction to facilitate the introduction to the changes induced by buoyancy in the following section (§ 3, Results).
$g_{y}=+9.81~\text{m}^{2}~\text{s}^{-1}$
for the unstably stratified configuration). This figure thus provides a concrete depiction to facilitate the introduction to the changes induced by buoyancy in the following section (§ 3, Results).
The measurement grid (overlain on the visualizations) comprised 911 points distributed along 11 transverse profiles downstream from the trailing edge of the splitter plate. This paper mainly focuses on the eleventh and last profile located in the self-similar region of the mixing layer. Table 1 summarizes the characteristics of the mixing layer at
![]() $x=2400~\text{mm}$
, the furthest downstream measurement location from the trailing edge. These characteristics provide information on the state, the length scales and the intensity of the turbulent mixing layer at this location and on the effects of stable and unstable stratifications.
$x=2400~\text{mm}$
, the furthest downstream measurement location from the trailing edge. These characteristics provide information on the state, the length scales and the intensity of the turbulent mixing layer at this location and on the effects of stable and unstable stratifications.
Table 1. Characteristics of the mixing layer at the
![]() $x$
position considered. The wavelength of the initial structure
$x$
position considered. The wavelength of the initial structure
![]() $L_{0}$
is approximated by
$L_{0}$
is approximated by
![]() $30\,\unicode[STIX]{x1D703}_{h}$
(Monkewitz & Huerre Reference Monkewitz and Huerre1982). The velocity-based shear layer thickness
$30\,\unicode[STIX]{x1D703}_{h}$
(Monkewitz & Huerre Reference Monkewitz and Huerre1982). The velocity-based shear layer thickness
![]() $\unicode[STIX]{x1D6FF}_{u}$
is defined as the distance between transverse locations where
$\unicode[STIX]{x1D6FF}_{u}$
is defined as the distance between transverse locations where
![]() $(\langle u\rangle -U_{l})/\unicode[STIX]{x0394}U=0.1$
and 0.9. The velocity-based deflection angle
$(\langle u\rangle -U_{l})/\unicode[STIX]{x0394}U=0.1$
and 0.9. The velocity-based deflection angle
![]() $\unicode[STIX]{x1D6FC}_{u}$
of the axis of the mixing layer is deduced from the transverse location where
$\unicode[STIX]{x1D6FC}_{u}$
of the axis of the mixing layer is deduced from the transverse location where
![]() $(\langle u\rangle -U_{l})/\unicode[STIX]{x0394}U=0.5$
. The same definitions are used for temperature-based characteristics. The subscript
$(\langle u\rangle -U_{l})/\unicode[STIX]{x0394}U=0.5$
. The same definitions are used for temperature-based characteristics. The subscript
![]() $u$
indicates that the quantities
$u$
indicates that the quantities
![]() $\unicode[STIX]{x1D702}_{u}$
and
$\unicode[STIX]{x1D702}_{u}$
and
![]() $\unicode[STIX]{x1D6FF}_{u}$
are extracted from the velocity profiles, otherwise from the temperature profiles the subscript would be
$\unicode[STIX]{x1D6FF}_{u}$
are extracted from the velocity profiles, otherwise from the temperature profiles the subscript would be
![]() $\unicode[STIX]{x1D703}$
. As with covariances, flux Richardson number, gradient Richardson number and turbulent Prandtl number values are the ones obtained on the axis of the mixing layer, knowing that these values correspond to extremum values for the flux Richardson number profiles and minimum values for the turbulent Prandtl number profiles.
$\unicode[STIX]{x1D703}$
. As with covariances, flux Richardson number, gradient Richardson number and turbulent Prandtl number values are the ones obtained on the axis of the mixing layer, knowing that these values correspond to extremum values for the flux Richardson number profiles and minimum values for the turbulent Prandtl number profiles.

2.4 Assessment of measurement resolution
In Ndoye et al. (Reference Ndoye, Delville, Heitz and Arroyo2010), a new variable-temperature hot-wire thermo-anemometry method was developed for simultaneous measurement of temperature
![]() $\unicode[STIX]{x1D703}$
and the longitudinal component of the velocity
$\unicode[STIX]{x1D703}$
and the longitudinal component of the velocity
![]() $u$
by using a single wire probe. The accuracy of this method with a single wire probe was evaluated by successively estimating the uncertainties associated with the dynamic calibration, the measurement procedure and the post-processing technique using a Monte Carlo simulation method.
$u$
by using a single wire probe. The accuracy of this method with a single wire probe was evaluated by successively estimating the uncertainties associated with the dynamic calibration, the measurement procedure and the post-processing technique using a Monte Carlo simulation method.
In Sodjavi & Carlier (Reference Sodjavi and Carlier2013), we extended this method to the use of a
![]() $\times$
-wire probe to measure, in addition, the transverse component of the velocity
$\times$
-wire probe to measure, in addition, the transverse component of the velocity
![]() $v$
, the fluctuations of which are involved in the transverse heat flux
$v$
, the fluctuations of which are involved in the transverse heat flux
![]() $\langle \unicode[STIX]{x1D703}^{\prime }v^{\prime }\rangle$
and momentum flux
$\langle \unicode[STIX]{x1D703}^{\prime }v^{\prime }\rangle$
and momentum flux
![]() $\langle u^{\prime }v^{\prime }\rangle$
across the mixing layer. The accuracy of the hot-wire thermo-anemometry method with a
$\langle u^{\prime }v^{\prime }\rangle$
across the mixing layer. The accuracy of the hot-wire thermo-anemometry method with a
![]() $\times$
-wire probe was evaluated by comparing its measurements with parallel measurements obtained from proven methods (constant-current anemometry for temperature and constant-temperature anemometry and particle image velocimetry for velocity) for the mean and fluctuating flow.
$\times$
-wire probe was evaluated by comparing its measurements with parallel measurements obtained from proven methods (constant-current anemometry for temperature and constant-temperature anemometry and particle image velocimetry for velocity) for the mean and fluctuating flow.
Variable-temperature hot-wire thermo-anemometry is a scalar measuring technique, as opposed to the chemical reaction measuring techniques generally used to study entrainment and mixing processes. The former type overestimates the amount of mixing if the sampling volume is greater than the molecular or thermal diffusion scale. It is therefore generally restricted to low Schmidt numbers (
![]() $Sc\leqslant 1$
). In contrast, the latter is inherently far less sensitive to sampling volume inadequacy and its use is more suitable at high Schmidt numbers (
$Sc\leqslant 1$
). In contrast, the latter is inherently far less sensitive to sampling volume inadequacy and its use is more suitable at high Schmidt numbers (
![]() $Sc\gg 1$
).
$Sc\gg 1$
).
To evaluate whether the measurement resolution is fine enough, the relevant quantities are first the ratio between the measurement scale and the dissipative scale and second the ratio between the measurement scale and the molecular diffusive scale. For
![]() $Sc\leqslant 1$
, the thermal diffusive scale is known as the Corrsin–Obukhov scale (
$Sc\leqslant 1$
, the thermal diffusive scale is known as the Corrsin–Obukhov scale (
![]() $\unicode[STIX]{x1D702}_{CO}$
) and is calculated in the same way as the Kolmogorov scale (
$\unicode[STIX]{x1D702}_{CO}$
) and is calculated in the same way as the Kolmogorov scale (
![]() $\unicode[STIX]{x1D702}_{K}$
):
$\unicode[STIX]{x1D702}_{K}$
):
where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity,
![]() $\unicode[STIX]{x1D705}$
the thermal diffusivity and
$\unicode[STIX]{x1D705}$
the thermal diffusivity and
![]() $\langle \unicode[STIX]{x1D716}_{u}\rangle$
the mean dissipation rate for velocity fluctuations. In the present study, estimation of the mean dissipation rate from hot-wire anemometry measurements required a frozen and locally isotropic turbulence hypothesis. In such a flow configuration, expression of the mean dissipation rate is reduced to:
$\langle \unicode[STIX]{x1D716}_{u}\rangle$
the mean dissipation rate for velocity fluctuations. In the present study, estimation of the mean dissipation rate from hot-wire anemometry measurements required a frozen and locally isotropic turbulence hypothesis. In such a flow configuration, expression of the mean dissipation rate is reduced to:
where
![]() $\langle {u^{\prime }}^{2}\rangle$
is the variance of the longitudinal velocity fluctuations and
$\langle {u^{\prime }}^{2}\rangle$
is the variance of the longitudinal velocity fluctuations and
![]() $\unicode[STIX]{x1D706}_{u}$
the Taylor microscale defined as the intercept of the osculating parabola to the autocorrelation coefficient
$\unicode[STIX]{x1D706}_{u}$
the Taylor microscale defined as the intercept of the osculating parabola to the autocorrelation coefficient
![]() $\unicode[STIX]{x1D70C}_{uu}(\text{d}x)$
at
$\unicode[STIX]{x1D70C}_{uu}(\text{d}x)$
at
![]() $\text{d}x=0$
with the
$\text{d}x=0$
with the
![]() $\text{d}x$
-axis,
$\text{d}x$
-axis,
![]() $\langle {u^{\prime }}^{2}\rangle$
and
$\langle {u^{\prime }}^{2}\rangle$
and
![]() $\unicode[STIX]{x1D706}_{u}$
, two quantities that are easy to evaluate from hot-wire anemometry. We showed in Sodjavi & Carlier (Reference Sodjavi and Carlier2013) that application of (2.3) to our results of hot-wire anemometry provided a good estimate of the mean dissipation rate as this estimation led to a compliant balance between the different terms involved in the transport equation of the turbulent kinetic energy (convection, production, turbulent diffusion, buoyancy and dissipation were all computed from hot-wire anemometry measurements), although the hot-wire probe used was not specifically designed for accurate estimation of dissipation and despite the fact that the validity of the local isotropy hypothesis (tested with different methods) has been called into question in a significant body of academic literature, especially for shear and stratified turbulent flows at a ‘moderate’ Reynolds number (see for example Piccirillo & Van Atta Reference Piccirillo and Van Atta1997).
$\unicode[STIX]{x1D706}_{u}$
, two quantities that are easy to evaluate from hot-wire anemometry. We showed in Sodjavi & Carlier (Reference Sodjavi and Carlier2013) that application of (2.3) to our results of hot-wire anemometry provided a good estimate of the mean dissipation rate as this estimation led to a compliant balance between the different terms involved in the transport equation of the turbulent kinetic energy (convection, production, turbulent diffusion, buoyancy and dissipation were all computed from hot-wire anemometry measurements), although the hot-wire probe used was not specifically designed for accurate estimation of dissipation and despite the fact that the validity of the local isotropy hypothesis (tested with different methods) has been called into question in a significant body of academic literature, especially for shear and stratified turbulent flows at a ‘moderate’ Reynolds number (see for example Piccirillo & Van Atta Reference Piccirillo and Van Atta1997).
In our study, laboratory-made miniature
![]() $\times$
-wire probes had
$\times$
-wire probes had
![]() $2.5~\unicode[STIX]{x03BC}\text{m}$
diameter and 0.8 mm long plated tungsten wire sensors. These probes connected to multiple overheat thermo-anemometers were operated with two overheat steps and a 1 ms cycle, enabling an acquisition frequency of 1 kHz . The hot-wire length was twofold greater than the thermal diffusion scale (
$2.5~\unicode[STIX]{x03BC}\text{m}$
diameter and 0.8 mm long plated tungsten wire sensors. These probes connected to multiple overheat thermo-anemometers were operated with two overheat steps and a 1 ms cycle, enabling an acquisition frequency of 1 kHz . The hot-wire length was twofold greater than the thermal diffusion scale (
![]() $l/\unicode[STIX]{x1D702}_{CO}=2$
, for
$l/\unicode[STIX]{x1D702}_{CO}=2$
, for
![]() $Re\sim 20\,000$
and
$Re\sim 20\,000$
and
![]() $Sc=0.7$
). No sub-resolution stirring was expected since Buch & Dahm (Reference Buch and Dahm1998) have reported that the mean dissipation layer thickness in flows is approximately 11.2 times greater than the usual estimation using Schmidt and Reynolds numbers. Moreover, the 1 kHz acquisition frequency and the 60 s acquisition time were sufficient to resolve the turbulent flow scales and to ensure the convergence of second- and third-order moments at each point of the grid.
$Sc=0.7$
). No sub-resolution stirring was expected since Buch & Dahm (Reference Buch and Dahm1998) have reported that the mean dissipation layer thickness in flows is approximately 11.2 times greater than the usual estimation using Schmidt and Reynolds numbers. Moreover, the 1 kHz acquisition frequency and the 60 s acquisition time were sufficient to resolve the turbulent flow scales and to ensure the convergence of second- and third-order moments at each point of the grid.
This multiple overheat thermo-anemometry method can be considered an alternative to the measurement method used by Lienhard & Van Atta (Reference Lienhard and Van Atta1990) and Piccirillo & Van Atta (Reference Piccirillo and Van Atta1997) who obtained a comparable resolution for a linearly stratified shear flow with large Kolmogorov and Corrsin–Obukhov scales. Their experiments were carried out with the thermo-anemometry method developed by Lienhard (Reference Lienhard1988) which combined hot-wire probes operating in constant-temperature anemometry mode with a cold-wire probe operating in constant-current anemometry mode. The present multiple overheat thermo-anemometry method is only based on hot-wire probes operating in constant-temperature anemometry mode with different overheats applied sequentially, the probe dimensions being comparable to the ones used by Lienhard & Van Atta (Reference Lienhard and Van Atta1990) and Piccirillo & Van Atta (Reference Piccirillo and Van Atta1997) who worked with a
![]() $\times$
-wire probe of similar size, with a sensor diameter of
$\times$
-wire probe of similar size, with a sensor diameter of
![]() $5~\unicode[STIX]{x03BC}\text{m}$
, a sensor length of 1.25 mm and an additional thermometer probe having a sensor diameter of
$5~\unicode[STIX]{x03BC}\text{m}$
, a sensor length of 1.25 mm and an additional thermometer probe having a sensor diameter of
![]() $1~\unicode[STIX]{x03BC}\text{m}$
and a sensor length of 0.4 mm.
$1~\unicode[STIX]{x03BC}\text{m}$
and a sensor length of 0.4 mm.
Table 2. Ratio between the measurement scale
![]() $l$
and the Corrsin–Obukhov scale
$l$
and the Corrsin–Obukhov scale
![]() $\unicode[STIX]{x1D702}_{CO}$
from different papers with Schmidt number close to unity.
$\unicode[STIX]{x1D702}_{CO}$
from different papers with Schmidt number close to unity.

Table 2 gives the ratios between the measurement scale
![]() $l$
and the Corrsin–Obukhov scale
$l$
and the Corrsin–Obukhov scale
![]() $\unicode[STIX]{x1D702}_{CO}$
collected in different publications on stratified and sheared mixing layers. Looking at scalar measuring techniques in flows with
$\unicode[STIX]{x1D702}_{CO}$
collected in different publications on stratified and sheared mixing layers. Looking at scalar measuring techniques in flows with
![]() $Sc\sim 1$
, the low resolutions (high length ratios) used by Konrad (Reference Konrad1977), Pickett & Ghandhi (Reference Pickett and Ghandhi2001) and Meyer et al. (Reference Meyer, Dutton and Lucht2006) were found to be without any strong effect on the PDFs of the scalar, which was not the case with the even lower resolution ratio used by Batt (Reference Batt1977) (as suggested in Mungal & Dimotakis Reference Mungal and Dimotakis1984; Karasso & Mungal Reference Karasso and Mungal1996) and by Masutani & Bowman (Reference Masutani and Bowman1986). Our conclusion is that the measurement resolution reached in our experiment was sufficient to avoid false mixing enhancement by sub-resolution stirring and then to measure the velocity and temperature fluctuations and to extract the turbulent quantities across the mixing layer.
$Sc\sim 1$
, the low resolutions (high length ratios) used by Konrad (Reference Konrad1977), Pickett & Ghandhi (Reference Pickett and Ghandhi2001) and Meyer et al. (Reference Meyer, Dutton and Lucht2006) were found to be without any strong effect on the PDFs of the scalar, which was not the case with the even lower resolution ratio used by Batt (Reference Batt1977) (as suggested in Mungal & Dimotakis Reference Mungal and Dimotakis1984; Karasso & Mungal Reference Karasso and Mungal1996) and by Masutani & Bowman (Reference Masutani and Bowman1986). Our conclusion is that the measurement resolution reached in our experiment was sufficient to avoid false mixing enhancement by sub-resolution stirring and then to measure the velocity and temperature fluctuations and to extract the turbulent quantities across the mixing layer.
3 Results
3.1 Characteristics of the mixing layer
Table 1 confirms that requirements were met at this location to obtain self-similar behaviour, i.e. geometric affinity of the statistical quantity profiles and linear growth of the mixing layer thickness. Indeed, Bradshaw (Reference Bradshaw1966) showed that transition typically comes to an end at around
![]() $x/\unicode[STIX]{x1D703}_{h}\sim 1000$
, where
$x/\unicode[STIX]{x1D703}_{h}\sim 1000$
, where
![]() $\unicode[STIX]{x1D703}_{h}$
is the momentum thickness of the boundary layer on the high-speed side. Moreover, Huang & Ho (Reference Huang and Ho1990) showed that a high Reynolds number (
$\unicode[STIX]{x1D703}_{h}$
is the momentum thickness of the boundary layer on the high-speed side. Moreover, Huang & Ho (Reference Huang and Ho1990) showed that a high Reynolds number (
![]() $Re>10\,000{-}20\,000$
) and a high pairing parameter (
$Re>10\,000{-}20\,000$
) and a high pairing parameter (
![]() $\unicode[STIX]{x1D706}(x/L_{0})>8$
, where
$\unicode[STIX]{x1D706}(x/L_{0})>8$
, where
![]() $\unicode[STIX]{x1D706}$
is the modified velocity ratio and
$\unicode[STIX]{x1D706}$
is the modified velocity ratio and
![]() $L_{0}$
the wavelength of the initial structure) are also required to support small-scale turbulence. Figure 5 shows the downstream evolution of the mixing layer thicknesses
$L_{0}$
the wavelength of the initial structure) are also required to support small-scale turbulence. Figure 5 shows the downstream evolution of the mixing layer thicknesses
![]() $\unicode[STIX]{x1D6FF}_{u}$
and
$\unicode[STIX]{x1D6FF}_{u}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. The self-similar state was also confirmed by the linear growth of the mixing layer thicknesses shown in this figure and the geometric affinity of the turbulence profiles with an asymptotic behaviour achieved by turbulence intensities (see Ndoye et al.
Reference Ndoye, Delville, Heitz and Arroyo2010; Sodjavi & Carlier Reference Sodjavi and Carlier2013). Note again that, in the presence of thermal stratification, that self-similar state would not be valid further downstream because of the growing influence of buoyancy (see § 1.3, Effects of stratification). The spreading rates were higher for the unstably stratified configuration than for the neutrally and stably stratified configurations. In parallel, comparing figure 5(a,b), a classical result can be seen for the ratios between the velocity and temperature spreading rates (0.82 and 0.74 for the stably and unstably stratified configurations, respectively), corresponding to faster spread values for temperature than for velocity.
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. The self-similar state was also confirmed by the linear growth of the mixing layer thicknesses shown in this figure and the geometric affinity of the turbulence profiles with an asymptotic behaviour achieved by turbulence intensities (see Ndoye et al.
Reference Ndoye, Delville, Heitz and Arroyo2010; Sodjavi & Carlier Reference Sodjavi and Carlier2013). Note again that, in the presence of thermal stratification, that self-similar state would not be valid further downstream because of the growing influence of buoyancy (see § 1.3, Effects of stratification). The spreading rates were higher for the unstably stratified configuration than for the neutrally and stably stratified configurations. In parallel, comparing figure 5(a,b), a classical result can be seen for the ratios between the velocity and temperature spreading rates (0.82 and 0.74 for the stably and unstably stratified configurations, respectively), corresponding to faster spread values for temperature than for velocity.

Figure 5. Linear velocity and temperature spreads of the mixing layer for neutrally, stably and unstably stratified configurations (figure reproduced from Sodjavi & Carlier (Reference Sodjavi and Carlier2013) with permission of Springer). Mixing layer thicknesses
![]() $\unicode[STIX]{x1D6FF}_{u}$
and
$\unicode[STIX]{x1D6FF}_{u}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
and downstream location
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
and downstream location
![]() $x$
relatively to the virtual origin
$x$
relatively to the virtual origin
![]() $x_{o}$
of the mixing layer are made dimensionless using the boundary layer momentum thickness on the high-speed side
$x_{o}$
of the mixing layer are made dimensionless using the boundary layer momentum thickness on the high-speed side
![]() $\unicode[STIX]{x1D703}_{h}$
.
$\unicode[STIX]{x1D703}_{h}$
.
The mixing layer in this type of configuration is not a symmetrical flow. Symmetry with respect to the
![]() $y=0$
plane can be obtained for a temporally developing mixing layer, but not for a spatially developing mixing layer, for which there is a slight deviation of the central plane of the mixing layer (or the axis in two dimensional analysis) towards the low-velocity side (see Pope Reference Pope2000, for example). This deflection stems from the greater volumetric flux coming from the high-speed stream (asymmetric entrainment of fluid into the mixing layer) as shown by Dimotakis (Reference Dimotakis1986) and D’Ovidio & Coats (Reference D’Ovidio and Coats2013). Statistical quantities based only on velocity are symmetric if this deflection is taken into account using the similarity variable
$y=0$
plane can be obtained for a temporally developing mixing layer, but not for a spatially developing mixing layer, for which there is a slight deviation of the central plane of the mixing layer (or the axis in two dimensional analysis) towards the low-velocity side (see Pope Reference Pope2000, for example). This deflection stems from the greater volumetric flux coming from the high-speed stream (asymmetric entrainment of fluid into the mixing layer) as shown by Dimotakis (Reference Dimotakis1986) and D’Ovidio & Coats (Reference D’Ovidio and Coats2013). Statistical quantities based only on velocity are symmetric if this deflection is taken into account using the similarity variable
![]() $\unicode[STIX]{x1D702}_{u}=(y-y_{o})/\unicode[STIX]{x1D6FF}_{u}$
for the ordinate axis, where
$\unicode[STIX]{x1D702}_{u}=(y-y_{o})/\unicode[STIX]{x1D6FF}_{u}$
for the ordinate axis, where
![]() $y_{o}$
is the half-profile location used to compute the deflection angle (see caption of table 1 for definitions). Even so, dissymmetry remains noticeable as soon as temperature is involved (see figure 6). For instance, the mean longitudinal velocity profile was symmetric with one single inflection point located on the axis of the mixing layer. In contrast, the mean temperature profile had three inflection points (see also Ndoye et al.
Reference Ndoye, Delville, Heitz and Arroyo2010). The
$y_{o}$
is the half-profile location used to compute the deflection angle (see caption of table 1 for definitions). Even so, dissymmetry remains noticeable as soon as temperature is involved (see figure 6). For instance, the mean longitudinal velocity profile was symmetric with one single inflection point located on the axis of the mixing layer. In contrast, the mean temperature profile had three inflection points (see also Ndoye et al.
Reference Ndoye, Delville, Heitz and Arroyo2010). The
![]() $\langle u^{\prime }u^{\prime }\rangle$
and
$\langle u^{\prime }u^{\prime }\rangle$
and
![]() $\langle v^{\prime }v^{\prime }\rangle$
were symmetric. However, the peak of
$\langle v^{\prime }v^{\prime }\rangle$
were symmetric. However, the peak of
![]() $\langle v^{\prime }v^{\prime }\rangle$
often appeared slightly shifted toward the low-velocity side, as reported by Wygnanski & Fiedler (Reference Wygnanski and Fiedler1970). The two peaks of
$\langle v^{\prime }v^{\prime }\rangle$
often appeared slightly shifted toward the low-velocity side, as reported by Wygnanski & Fiedler (Reference Wygnanski and Fiedler1970). The two peaks of
![]() $\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
were not symmetric, the largest peak being on the low-velocity side. Heat fluxes
$\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
were not symmetric, the largest peak being on the low-velocity side. Heat fluxes
![]() $\langle u^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
and
$\langle u^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
and
![]() $\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
, rarely measured and often inferred, are discussed in relation to JPDFs and conditional analysis in the dedicated sections below.
$\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
, rarely measured and often inferred, are discussed in relation to JPDFs and conditional analysis in the dedicated sections below.

Figure 6. Evolution of turbulence statistics through the mixing layer in the self-similar region for neutrally, stably and unstably stratified configurations. Note: for the unstably stratified configuration, the
![]() $y$
axis was turned upside down to make the comparison easier; dimensionless vertical position
$y$
axis was turned upside down to make the comparison easier; dimensionless vertical position
![]() $\unicode[STIX]{x1D702}_{u}$
then stands for
$\unicode[STIX]{x1D702}_{u}$
then stands for
![]() $-\unicode[STIX]{x1D702}_{u}$
in this figure and figures thereafter.
$-\unicode[STIX]{x1D702}_{u}$
in this figure and figures thereafter.
The effects of buoyancy on the mixing layer can be seen through the spreading rates (figure 5) and turbulence quantities (figure 6). In view of the Richardson numbers involved in this study (
![]() $|Ri_{f}|_{max}\simeq 0.02$
), the mixing layer can be considered to be dominated by shears associated with roller vortices from the Kelvin–Helmholtz instability, and the buoyancy force was very small compared to the main driving forces. In the stably stratified configuration, the curves were close to those of the neutrally stratified configuration and therefore temperature seemed to behave as a passive scalar. In the unstably stratified configuration, such a small buoyancy force appeared to be sufficient to significantly increase turbulence quantities (up to 60 % for the shear stress), spreading rates being affected to a lesser extent (10 % and 20 % for the velocity and temperature spreading rates, respectively, see figure 5). We pointed out in Sodjavi & Carlier (Reference Sodjavi and Carlier2013) that the buoyancy-driven increase in turbulence production involved changes in the equilibrium between the different terms of the transport equation for turbulent kinetic energy, whereas it seemed not to modify the balance in the temperature variance budget, thus leading to a greater direct effect on the temperature spreading rate than on the velocity spreading rate.
$|Ri_{f}|_{max}\simeq 0.02$
), the mixing layer can be considered to be dominated by shears associated with roller vortices from the Kelvin–Helmholtz instability, and the buoyancy force was very small compared to the main driving forces. In the stably stratified configuration, the curves were close to those of the neutrally stratified configuration and therefore temperature seemed to behave as a passive scalar. In the unstably stratified configuration, such a small buoyancy force appeared to be sufficient to significantly increase turbulence quantities (up to 60 % for the shear stress), spreading rates being affected to a lesser extent (10 % and 20 % for the velocity and temperature spreading rates, respectively, see figure 5). We pointed out in Sodjavi & Carlier (Reference Sodjavi and Carlier2013) that the buoyancy-driven increase in turbulence production involved changes in the equilibrium between the different terms of the transport equation for turbulent kinetic energy, whereas it seemed not to modify the balance in the temperature variance budget, thus leading to a greater direct effect on the temperature spreading rate than on the velocity spreading rate.
3.2 A priori illustration of the topology of mixing
With a view to analysing mixing and entrainment through PDF analysis, an illustration of the organization of the turbulent mixing layer in the self-similar region is proposed as an a priori in figure 7. This illustration is based on previous studies found in the literature representing streamlines of the flow in a moving or fixed reference frame (Coles Reference Coles1981; Broadwell & Breidenthal Reference Broadwell and Breidenthal1982; Lasheras & Choi Reference Lasheras and Choi1988). The spatio-temporal organization of the flow is described as a succession of well-identified events:
-
(i) Entrained fluid from free streams (potential flow with
 $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
and
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
and
 $\unicode[STIX]{x1D735}\times \boldsymbol{u}=0$
) into the turbulence region bounded by the turbulent/non-turbulent interfaces. Entrained fluid by the entrainment process can be either nibbled at these boundaries or engulfed into the outermost boundaries of the mixing layer under the effect of individual growth or pairing of roller vortices.
$\unicode[STIX]{x1D735}\times \boldsymbol{u}=0$
) into the turbulence region bounded by the turbulent/non-turbulent interfaces. Entrained fluid by the entrainment process can be either nibbled at these boundaries or engulfed into the outermost boundaries of the mixing layer under the effect of individual growth or pairing of roller vortices. -
(ii) Mixed fluid due to the mixing process. Mixed fluid and entrained fluid are mainly located in large roller vortices. In the context of mixing by turbulence, the region of mixed fluid can be seen as a turbulence region, but bearing in mind that heterogeneities exist between ‘mixed fluid’ and ‘unmixed fluid’ associated with entrainment and engulfment.
-
(iii) Fronts of high shear in the braid region, the shear being located between two roller vortices and aligned with the divergent axis of the saddle point (or stagnation point).
Mixed, entrained and engulfed fluids are entities described by Sandham et al. (Reference Sandham, Mungal, Broadwell and Reynolds1988). A measurement probe immersed in the mixing layer is likely to be submitted to a complex time sequence of events corresponding to entrained fluid from the slower stream, the front, entrained fluid from the faster stream and mixed fluid movement. The front is then seen as a temperature jump corresponding to the border crossing between entrained fluid from the slower and faster streams.

Figure 7. Illustration of the organization of the turbulent mixing layer in the self-similar region and in fixed reference frame. The underlying image came from flow visualization by laser tomography (Sobel operator was applied on the image to emphasize turbulence regions and turbulent/non-turbulent interfaces). The solid lines
![]() $-\unicode[STIX]{x1D6FF}/2$
and
$-\unicode[STIX]{x1D6FF}/2$
and
![]() $+\unicode[STIX]{x1D6FF}/2$
correspond to the velocity-based expansion of the mixing layer and the dash-dotted line corresponds to the axis of the mixing layer, with a slight deflection angle toward the low-velocity free stream.
$+\unicode[STIX]{x1D6FF}/2$
correspond to the velocity-based expansion of the mixing layer and the dash-dotted line corresponds to the axis of the mixing layer, with a slight deflection angle toward the low-velocity free stream.
3.3 Skewness and kurtosis
Overall information on PDF shapes can be deduced from the skewness factor
![]() $S=\unicode[STIX]{x1D707}_{3}/\unicode[STIX]{x1D70E}^{3}$
and the kurtosis factor
$S=\unicode[STIX]{x1D707}_{3}/\unicode[STIX]{x1D70E}^{3}$
and the kurtosis factor
![]() $K=\unicode[STIX]{x1D707}_{4}/\unicode[STIX]{x1D70E}^{4}$
where
$K=\unicode[STIX]{x1D707}_{4}/\unicode[STIX]{x1D70E}^{4}$
where
![]() $\unicode[STIX]{x1D70E}$
is the standard deviation and
$\unicode[STIX]{x1D70E}$
is the standard deviation and
![]() $\unicode[STIX]{x1D707}_{3}$
and
$\unicode[STIX]{x1D707}_{3}$
and
![]() $\unicode[STIX]{x1D707}_{4}$
are the third and fourth moments around the mean, respectively. The skewness factor measures the symmetry of the fluctuations around the mean and the kurtosis factor measures the peaked or flat shape characterizing a deviation from a Gaussian distribution (
$\unicode[STIX]{x1D707}_{4}$
are the third and fourth moments around the mean, respectively. The skewness factor measures the symmetry of the fluctuations around the mean and the kurtosis factor measures the peaked or flat shape characterizing a deviation from a Gaussian distribution (
![]() $S=0$
and
$S=0$
and
![]() $K=3$
for a Gaussian distribution). Figure 8 gives distributions of these factors computed from
$K=3$
for a Gaussian distribution). Figure 8 gives distributions of these factors computed from
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $\unicode[STIX]{x1D703}$
signals across the mixing layer for neutrally, stably and unstably stratified configurations. In the free streams (
$\unicode[STIX]{x1D703}$
signals across the mixing layer for neutrally, stably and unstably stratified configurations. In the free streams (
![]() $|\unicode[STIX]{x1D702}_{u}|>1$
), skewness and kurtosis factors were equal to
$|\unicode[STIX]{x1D702}_{u}|>1$
), skewness and kurtosis factors were equal to
![]() $0$
and
$0$
and
![]() $3$
, respectively, suggesting a Gaussian distribution of the residual turbulence. The skewness and kurtosis factors values changed suddenly near the border of the mixing layer (
$3$
, respectively, suggesting a Gaussian distribution of the residual turbulence. The skewness and kurtosis factors values changed suddenly near the border of the mixing layer (
![]() $|\unicode[STIX]{x1D702}_{u}|\simeq 1$
), more significantly for
$|\unicode[STIX]{x1D702}_{u}|\simeq 1$
), more significantly for
![]() $S_{\unicode[STIX]{x1D703}}$
and
$S_{\unicode[STIX]{x1D703}}$
and
![]() $K_{\unicode[STIX]{x1D703}}$
. These changes resulted from intermittencies between turbulent puffs (mixed fluid) into the free stream and fluid incursions into the mixing layer (entrained fluid). From the free stream, this can be roughly seen as follows:
$K_{\unicode[STIX]{x1D703}}$
. These changes resulted from intermittencies between turbulent puffs (mixed fluid) into the free stream and fluid incursions into the mixing layer (entrained fluid). From the free stream, this can be roughly seen as follows:

Figure 8. Skewness and kurtosis for
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $\unicode[STIX]{x1D703}$
through the mixing layer in the self-similar region for neutrally, stably and unstably stratified configurations.
$\unicode[STIX]{x1D703}$
through the mixing layer in the self-similar region for neutrally, stably and unstably stratified configurations.
-
(i) On the high-velocity side (
 $\unicode[STIX]{x1D702}_{u}<0$
), events that disturbed the flow were fluid particles coming from the ‘turbulence region’. These fluid particles were then hotter (
$\unicode[STIX]{x1D702}_{u}<0$
), events that disturbed the flow were fluid particles coming from the ‘turbulence region’. These fluid particles were then hotter (
 $\unicode[STIX]{x1D703}^{\prime }>0$
), slower (
$\unicode[STIX]{x1D703}^{\prime }>0$
), slower (
 $u^{\prime }<0$
) and pointing downwards (
$u^{\prime }<0$
) and pointing downwards (
 $v^{\prime }<0$
) so that
$v^{\prime }<0$
) so that
 $S_{\unicode[STIX]{x1D703}}>0$
,
$S_{\unicode[STIX]{x1D703}}>0$
,
 $S_{u}<0$
and
$S_{u}<0$
and
 $S_{v}<0$
.
$S_{v}<0$
. -
(ii) On the low-velocity side (
 $\unicode[STIX]{x1D702}_{u}>0$
), the corresponding fluid particles were colder (
$\unicode[STIX]{x1D702}_{u}>0$
), the corresponding fluid particles were colder (
 $\unicode[STIX]{x1D703}^{\prime }<0$
), faster (
$\unicode[STIX]{x1D703}^{\prime }<0$
), faster (
 $u^{\prime }>0$
) and pointing upwards (
$u^{\prime }>0$
) and pointing upwards (
 $v^{\prime }>0$
) so that
$v^{\prime }>0$
) so that
 $S_{\unicode[STIX]{x1D703}}<0$
,
$S_{\unicode[STIX]{x1D703}}<0$
,
 $S_{u}>0$
and
$S_{u}>0$
and
 $S_{v}>0$
.
$S_{v}>0$
.
The particularly high extreme values of
![]() $S_{\unicode[STIX]{x1D703}}$
and
$S_{\unicode[STIX]{x1D703}}$
and
![]() $K_{\unicode[STIX]{x1D703}}$
expressed stronger intermittency for temperature than for velocity. Deeper inside the mixing layer (
$K_{\unicode[STIX]{x1D703}}$
expressed stronger intermittency for temperature than for velocity. Deeper inside the mixing layer (
![]() $|\unicode[STIX]{x1D702}_{u}|<1$
), progressive deviations from Gaussian distribution reflected the extension of this phenomenon from the corresponding boundaries into the mixing layer. Skewness distributions were not exactly antisymmetric, nor were kurtosis distributions, defined in terms of even power, strictly symmetric. This was particularly noticeable for temperatures near the centre of the mixing layer where the
$|\unicode[STIX]{x1D702}_{u}|<1$
), progressive deviations from Gaussian distribution reflected the extension of this phenomenon from the corresponding boundaries into the mixing layer. Skewness distributions were not exactly antisymmetric, nor were kurtosis distributions, defined in terms of even power, strictly symmetric. This was particularly noticeable for temperatures near the centre of the mixing layer where the
![]() $S_{\unicode[STIX]{x1D703}}$
value was slightly positive, while the
$S_{\unicode[STIX]{x1D703}}$
value was slightly positive, while the
![]() $K_{\unicode[STIX]{x1D703}}$
value was
$K_{\unicode[STIX]{x1D703}}$
value was
![]() $3$
on the high-velocity side but below
$3$
on the high-velocity side but below
![]() $3$
on the low-velocity side. All of this is in line with the hypothesis of asymmetry between entrainment of fluid from the high- and low-speed streams into the mixing layer.
$3$
on the low-velocity side. All of this is in line with the hypothesis of asymmetry between entrainment of fluid from the high- and low-speed streams into the mixing layer.

Figure 9. Evolution through the mixing layer of the probability density function of temperature
![]() $P_{\unicode[STIX]{x1D703}}$
in the self-similar region: left panels (a) and (c) for the stably stratified configuration and right panels (b) and (d) for the unstably stratified configuration. Three-dimensional graphs
$P_{\unicode[STIX]{x1D703}}$
in the self-similar region: left panels (a) and (c) for the stably stratified configuration and right panels (b) and (d) for the unstably stratified configuration. Three-dimensional graphs
![]() $P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D702}_{u})$
are shown in top panels (a) and (b) as colour map views and two-dimensional graphs
$P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D702}_{u})$
are shown in top panels (a) and (b) as colour map views and two-dimensional graphs
![]() $P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D703})$
are shown in bottom panels (c) and (d) for various
$P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D703})$
are shown in bottom panels (c) and (d) for various
![]() $\unicode[STIX]{x1D702}_{u}$
coordinates (red–blue colour palette). The mean temperature profiles are superimposed on the top views.
$\unicode[STIX]{x1D702}_{u}$
coordinates (red–blue colour palette). The mean temperature profiles are superimposed on the top views.
3.4 Probability density function of temperature
Figure 9 shows the evolution through the mixing layer of the PDF of temperature
![]() $P_{\unicode[STIX]{x1D703}}$
in the self-similar region for stably and unstably stratified configurations. For all the views,
$P_{\unicode[STIX]{x1D703}}$
in the self-similar region for stably and unstably stratified configurations. For all the views,
![]() $(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
was chosen as abscissa variable and
$(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
was chosen as abscissa variable and
![]() $P_{\unicode[STIX]{x1D703}}$
has been normalized to integrate to one. The multimodal shape of
$P_{\unicode[STIX]{x1D703}}$
has been normalized to integrate to one. The multimodal shape of
![]() $P_{\unicode[STIX]{x1D703}}$
is striking, with one large ellipsoidal central mode and two pointed lateral modes. The large ellipsoidal central mode corresponds to the temperature distribution in the mixed fluid region where the mixing takes place inside the roller vortices, and in the braid region between these vortices. The pointed lateral modes correspond to surrounding fluid (free stream) entrained into the mixing layer.
$P_{\unicode[STIX]{x1D703}}$
is striking, with one large ellipsoidal central mode and two pointed lateral modes. The large ellipsoidal central mode corresponds to the temperature distribution in the mixed fluid region where the mixing takes place inside the roller vortices, and in the braid region between these vortices. The pointed lateral modes correspond to surrounding fluid (free stream) entrained into the mixing layer.
Typical PDF shapes involving one central mode and two lateral modes have been described, for different flow conditions, in several published results and a distinction has been made between ‘marching’ and ‘non-marching’ types. If the most probable value of the scalar in the mixed fluid core is independent of the transverse position, the PDF is called non-marching, otherwise the PDF is called marching (or tilted or hybrid, depending on how this value varies across the layer). A non-marching PDF has been attributed to homogeneous mixing by turbulence transport in the roller vortices. The stirring process leads to molecular diffusion at the Kolmogorov scale and produces a uniform scalar distribution across the layer. A marching PDF is due to molecular diffusion taking place directly in the high shear of the braid region, allowing lateral variation in PDF. These two processes are the foundation of the PDF-based mixing models proposed by Broadwell & Breidenthal (Reference Broadwell and Breidenthal1982), Dimotakis (Reference Dimotakis1989) and Broadwell & Mungal (Reference Broadwell and Mungal1991). Although in most studies a high Péclet number (
![]() $Pe=Re\times Sc$
) suggests that turbulent transport diffusion dominates over molecular diffusion, experimental and numerical results (see compilation in Cortesi et al.
Reference Cortesi, Smith, Sigg and Banerjee2001) have shown the PDF shape to be dependent on the Reynolds and Schmidt numbers, and also on the initial conditions the effects of which on the structure of the flow persist far downstream. Non-marching PDFs (Konrad Reference Konrad1977; Mungal & Dimotakis Reference Mungal and Dimotakis1984; Koochesfahani & Dimotakis Reference Koochesfahani and Dimotakis1986; Masutani & Bowman Reference Masutani and Bowman1986; Pickett & Ghandhi Reference Pickett and Ghandhi2001; Wiltse & Glezer Reference Wiltse and Glezer2004) and marching PDFs (Batt Reference Batt1977; Karasso & Mungal Reference Karasso and Mungal1996; Pickett & Ghandhi Reference Pickett and Ghandhi2002; Meyer et al.
Reference Meyer, Dutton and Lucht2006) have often been described in the literature, but a clear distinction between the shapes has still to be established. In figure 9, the most probable value did not follow the mean temperature profile and scrolled very slightly from the high-velocity side to the low-velocity side, giving a non-marching PDF for this experiment conducted at a high Reynolds number, low Schmidt number and beyond the mixing transition. This non-marching PDF suggests that, in this experiment, roller vortices were coherent and turbulent enough to promote the stirring process while preventing non-mixed fluid penetrating into the core of the mixing layer, at least from a statistical point of view.
$Pe=Re\times Sc$
) suggests that turbulent transport diffusion dominates over molecular diffusion, experimental and numerical results (see compilation in Cortesi et al.
Reference Cortesi, Smith, Sigg and Banerjee2001) have shown the PDF shape to be dependent on the Reynolds and Schmidt numbers, and also on the initial conditions the effects of which on the structure of the flow persist far downstream. Non-marching PDFs (Konrad Reference Konrad1977; Mungal & Dimotakis Reference Mungal and Dimotakis1984; Koochesfahani & Dimotakis Reference Koochesfahani and Dimotakis1986; Masutani & Bowman Reference Masutani and Bowman1986; Pickett & Ghandhi Reference Pickett and Ghandhi2001; Wiltse & Glezer Reference Wiltse and Glezer2004) and marching PDFs (Batt Reference Batt1977; Karasso & Mungal Reference Karasso and Mungal1996; Pickett & Ghandhi Reference Pickett and Ghandhi2002; Meyer et al.
Reference Meyer, Dutton and Lucht2006) have often been described in the literature, but a clear distinction between the shapes has still to be established. In figure 9, the most probable value did not follow the mean temperature profile and scrolled very slightly from the high-velocity side to the low-velocity side, giving a non-marching PDF for this experiment conducted at a high Reynolds number, low Schmidt number and beyond the mixing transition. This non-marching PDF suggests that, in this experiment, roller vortices were coherent and turbulent enough to promote the stirring process while preventing non-mixed fluid penetrating into the core of the mixing layer, at least from a statistical point of view.
There was no visible difference between the PDF distributions of the stably and unstably stratified configurations. The most probable value of the mixed fluid was approximately
![]() $(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}\simeq 0.4$
. The temperature in the roller vortices was therefore colder than the average of the two free-stream temperatures. According to Koochesfahani & Dimotakis (Reference Koochesfahani and Dimotakis1986) and Pickett & Ghandhi (Reference Pickett and Ghandhi2002), asymmetry of the mixed fluid composition is not only due to preferential entrainment from the faster stream but also to the initial composition of the first rolling, with excess from the faster stream (as we chose mean vertical velocity and temperature gradients of opposite sign for both the stably and unstably stratified configurations, high speed was always associated with low temperature). However, we can assume that this initial contribution so far away from the trailing edge of the splitter plate would be small compared to the continuous entrainment process in the self-similar region, this process then being clearly asymmetric.
$(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}\simeq 0.4$
. The temperature in the roller vortices was therefore colder than the average of the two free-stream temperatures. According to Koochesfahani & Dimotakis (Reference Koochesfahani and Dimotakis1986) and Pickett & Ghandhi (Reference Pickett and Ghandhi2002), asymmetry of the mixed fluid composition is not only due to preferential entrainment from the faster stream but also to the initial composition of the first rolling, with excess from the faster stream (as we chose mean vertical velocity and temperature gradients of opposite sign for both the stably and unstably stratified configurations, high speed was always associated with low temperature). However, we can assume that this initial contribution so far away from the trailing edge of the splitter plate would be small compared to the continuous entrainment process in the self-similar region, this process then being clearly asymmetric.
The asymmetry and the bimodal shape on both sides of the axis of the mixing layer were consistent with the previously shown turbulence statistics. First, the temperature difference between entrained and mixed fluids was higher on the low-speed side than on the high-speed side, and moreover temperature variations were preferentially a consequence of this temperature jump between entrained and mixed fluids, rather than of the temperature fluctuations in the roller vortices. This explains, in particular, the large peak on the low-velocity side of the temperature variance curve in figure 6(g).
3.5 Joint probability density functions
Variable-temperature hot-wire thermo-anemometry was developed to measure both velocity and temperature of the flow instantaneously. The joint nature of the measurement was used in a previous study (Sodjavi & Carlier Reference Sodjavi and Carlier2013) to evaluate the heat fluxes involved in the production of temperature fluctuation and buoyancy, and then to calculate and compare the profiles of the separate terms of the transport equations for turbulent kinetic energy and temperature variance. In the present study, we benefited from the joint measurements to obtain JPDFs of velocity and temperature, with a view to obtaining information on the respective influences of the movements in the mixing process corresponding to entrained and mixed fluids. It is of note that quantitative measurements of heat or scalar fluxes in turbulent mixing layers are very rare. We only found them in Koochesfahani, Cohn & MacKinnon (Reference Koochesfahani, Cohn and MacKinnon2000), Li, Balaras & Wallace (Reference Li, Balaras and Wallace2010b ), Ndoye et al. (Reference Ndoye, Delville, Heitz and Arroyo2010) and Sodjavi & Carlier (Reference Sodjavi and Carlier2013), and only Li et al. (Reference Li, Balaras and Wallace2010b ) focused their study on JPDFs.

Figure 10. Normally distributed JPDFs associated with the distributions of
![]() $(u^{\prime },v^{\prime })$
through the mixing layer in the self-similar region for stably and unstably stratified configurations.
$(u^{\prime },v^{\prime })$
through the mixing layer in the self-similar region for stably and unstably stratified configurations.

Figure 11. Normally distributed JPDFs associated with the distributions of
![]() $(u^{\prime },\unicode[STIX]{x1D703}^{\prime })$
through the mixing layer in the self-similar region for stably and unstably stratified configurations.
$(u^{\prime },\unicode[STIX]{x1D703}^{\prime })$
through the mixing layer in the self-similar region for stably and unstably stratified configurations.

Figure 12. Normally distributed JPDFs associated with the distributions of
![]() $(v^{\prime },\unicode[STIX]{x1D703}^{\prime })$
through the mixing layer in the self-similar region for stably and unstably stratified configurations.
$(v^{\prime },\unicode[STIX]{x1D703}^{\prime })$
through the mixing layer in the self-similar region for stably and unstably stratified configurations.
Figures 10, 11 and 12 present the JPDFs
![]() $P_{u^{\prime },v^{\prime }}$
,
$P_{u^{\prime },v^{\prime }}$
,
![]() $P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
$P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
![]() $P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
at five locations across the mixing layer in the self-similar region for stably and unstably stratified configurations. Each small illustration gives a two-dimensional view of the different JPDFs for a given transverse
$P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
at five locations across the mixing layer in the self-similar region for stably and unstably stratified configurations. Each small illustration gives a two-dimensional view of the different JPDFs for a given transverse
![]() $y$
location measured in proportion to the velocity-based thickness of the mixing layer
$y$
location measured in proportion to the velocity-based thickness of the mixing layer
![]() $\unicode[STIX]{x1D6FF}_{u}$
. The JPDFs are normally distributed with mean values
$\unicode[STIX]{x1D6FF}_{u}$
. The JPDFs are normally distributed with mean values
![]() $\langle u\rangle$
,
$\langle u\rangle$
,
![]() $\langle v\rangle$
or
$\langle v\rangle$
or
![]() $\langle \unicode[STIX]{x1D703}\rangle$
and standard deviations
$\langle \unicode[STIX]{x1D703}\rangle$
and standard deviations
![]() $\unicode[STIX]{x1D70E}_{u}$
,
$\unicode[STIX]{x1D70E}_{u}$
,
![]() $\unicode[STIX]{x1D70E}_{v}$
or
$\unicode[STIX]{x1D70E}_{v}$
or
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}$
. To facilitate a step by step analysis, we chose to divide each of them into only quadrants identified by numbers (i for northeast, ii for northwest, iii for southwest and iv for southeast) as proposed by Wallace, Eckelmann & Brodkey (Reference Wallace, Eckelmann and Brodkey1972) and Willmarth & Lu (Reference Willmarth and Lu1972), while aware that the octant decomposition proposed by Vinçont et al. (Reference Vinçont, Simoëns, Ayrault and Wallace2000) could have been used to consider the three-dimensional JPDFs
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}$
. To facilitate a step by step analysis, we chose to divide each of them into only quadrants identified by numbers (i for northeast, ii for northwest, iii for southwest and iv for southeast) as proposed by Wallace, Eckelmann & Brodkey (Reference Wallace, Eckelmann and Brodkey1972) and Willmarth & Lu (Reference Willmarth and Lu1972), while aware that the octant decomposition proposed by Vinçont et al. (Reference Vinçont, Simoëns, Ayrault and Wallace2000) could have been used to consider the three-dimensional JPDFs
![]() $P_{u^{\prime },v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
.
$P_{u^{\prime },v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
.
It can be seen that near the velocity-based border of the mixing layer (
![]() $|\unicode[STIX]{x1D702}_{u}|\simeq 1$
),
$|\unicode[STIX]{x1D702}_{u}|\simeq 1$
),
![]() $P_{u^{\prime },v^{\prime }}$
had a circular shape centred on the origin, while
$P_{u^{\prime },v^{\prime }}$
had a circular shape centred on the origin, while
![]() $P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
$P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
![]() $P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
had an elliptical shape with the minor axis aligned with the
$P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
had an elliptical shape with the minor axis aligned with the
![]() $\unicode[STIX]{x1D703}^{\prime }$
axis and the major axis aligned with the
$\unicode[STIX]{x1D703}^{\prime }$
axis and the major axis aligned with the
![]() $u^{\prime }$
or
$u^{\prime }$
or
![]() $v^{\prime }$
axis. Note that, as these JPDFs were normally distributed, their shapes only translated the correlations and distributions of
$v^{\prime }$
axis. Note that, as these JPDFs were normally distributed, their shapes only translated the correlations and distributions of
![]() $u^{\prime }$
,
$u^{\prime }$
,
![]() $v^{\prime }$
and
$v^{\prime }$
and
![]() $\unicode[STIX]{x1D703}^{\prime }$
and not the intensity of their fluctuations. The symmetry of these JPDFs about the
$\unicode[STIX]{x1D703}^{\prime }$
and not the intensity of their fluctuations. The symmetry of these JPDFs about the
![]() $\unicode[STIX]{x1D703}^{\prime }$
axis and the
$\unicode[STIX]{x1D703}^{\prime }$
axis and the
![]() $u^{\prime }$
or
$u^{\prime }$
or
![]() $v^{\prime }$
axis corresponds to patterns associated with low correlation levels at this location (see figure 6). The circular shape of
$v^{\prime }$
axis corresponds to patterns associated with low correlation levels at this location (see figure 6). The circular shape of
![]() $P_{u^{\prime },v^{\prime }}$
corresponds with residual turbulence in the free stream where PDFs of
$P_{u^{\prime },v^{\prime }}$
corresponds with residual turbulence in the free stream where PDFs of
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
were Gaussian without significant Reynolds stress. The elliptical shape of
$v^{\prime }$
were Gaussian without significant Reynolds stress. The elliptical shape of
![]() $P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
$P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
![]() $P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
was derived from the temperature distribution at this location situated within the temperature-based border of the mixing layer (the expansion rate was greater for the temperature than for velocity). At this location, the PDFs of
$P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
was derived from the temperature distribution at this location situated within the temperature-based border of the mixing layer (the expansion rate was greater for the temperature than for velocity). At this location, the PDFs of
![]() $\unicode[STIX]{x1D703}^{\prime }$
were non-Gaussian with a flatness factor for temperature much higher than the flatness factor for velocity (see figure 8).
$\unicode[STIX]{x1D703}^{\prime }$
were non-Gaussian with a flatness factor for temperature much higher than the flatness factor for velocity (see figure 8).
Near the axis of the mixing layer (
![]() $|\unicode[STIX]{x1D702}_{u}|\leqslant 0.2$
),
$|\unicode[STIX]{x1D702}_{u}|\leqslant 0.2$
),
![]() $P_{u^{\prime },v^{\prime }}$
had an elliptical shape with a major axis oriented toward quadrants i and iii. This result agrees very well with
$P_{u^{\prime },v^{\prime }}$
had an elliptical shape with a major axis oriented toward quadrants i and iii. This result agrees very well with
![]() $P_{u^{\prime },v^{\prime }}$
patterns presented in Li, Chang & Wang (Reference Li, Chang and Wang2010a
).
$P_{u^{\prime },v^{\prime }}$
patterns presented in Li, Chang & Wang (Reference Li, Chang and Wang2010a
).
![]() $P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
$P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
![]() $P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
had a completely different shape, with a centred mode corresponding to the velocity–temperature distribution in the mixed fluid and two lateral modes, located in quadrants ii and iv, corresponding to entrained fluid from the low- and high-speed streams.
$P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
had a completely different shape, with a centred mode corresponding to the velocity–temperature distribution in the mixed fluid and two lateral modes, located in quadrants ii and iv, corresponding to entrained fluid from the low- and high-speed streams.
A break-down analysis can be proposed as follows:
-
(i) Fluid entrained from the low-speed stream was hotter (
 $\unicode[STIX]{x1D703}^{\prime }>0$
), slower (
$\unicode[STIX]{x1D703}^{\prime }>0$
), slower (
 $u^{\prime }<0$
) and pointing downward (
$u^{\prime }<0$
) and pointing downward (
 $v^{\prime }<0$
), corresponding to the lateral mode in quadrant ii for
$v^{\prime }<0$
), corresponding to the lateral mode in quadrant ii for
 $P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
$P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
 $P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
.
$P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
. -
(ii) Fluid entrained from the high-speed stream was colder (
 $\unicode[STIX]{x1D703}^{\prime }<0$
), faster (
$\unicode[STIX]{x1D703}^{\prime }<0$
), faster (
 $u^{\prime }>0$
) and pointing upward (
$u^{\prime }>0$
) and pointing upward (
 $v^{\prime }>0$
), corresponding to the lateral mode in quadrant iv for
$v^{\prime }>0$
), corresponding to the lateral mode in quadrant iv for
 $P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
$P_{u^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
and
 $P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
.
$P_{v^{\prime },\unicode[STIX]{x1D703}^{\prime }}$
.
The privileged orientations of
![]() $P_{u^{\prime },v^{\prime }}$
,
$P_{u^{\prime },v^{\prime }}$
,
![]() $P_{u^{\prime }\unicode[STIX]{x1D703}^{\prime }}$
and
$P_{u^{\prime }\unicode[STIX]{x1D703}^{\prime }}$
and
![]() $P_{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}$
were consistent with positive production terms in transport equations for turbulent kinetic energy and temperature variance:
$P_{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}$
were consistent with positive production terms in transport equations for turbulent kinetic energy and temperature variance:
-
(i) Production of turbulence (
 $-\langle u^{\prime }v^{\prime }\rangle (\unicode[STIX]{x2202}\langle u\rangle /\unicode[STIX]{x2202}y)>0$
) with a negative velocity gradient (
$-\langle u^{\prime }v^{\prime }\rangle (\unicode[STIX]{x2202}\langle u\rangle /\unicode[STIX]{x2202}y)>0$
) with a negative velocity gradient (
 $(\unicode[STIX]{x2202}\langle u\rangle /\unicode[STIX]{x2202}y)<0$
) gave a positive transverse mass flux (
$(\unicode[STIX]{x2202}\langle u\rangle /\unicode[STIX]{x2202}y)<0$
) gave a positive transverse mass flux (
 $\langle u^{\prime }v^{\prime }\rangle >0$
).
$\langle u^{\prime }v^{\prime }\rangle >0$
). -
(ii) Production of temperature variance (
 $-\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle (\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D703}\rangle /\unicode[STIX]{x2202}y)>0$
) with a positive temperature gradient (
$-\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle (\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D703}\rangle /\unicode[STIX]{x2202}y)>0$
) with a positive temperature gradient (
 $(\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D703}\rangle /\unicode[STIX]{x2202}y)>0$
) gave a negative transverse heat flux (
$(\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D703}\rangle /\unicode[STIX]{x2202}y)>0$
) gave a negative transverse heat flux (
 $\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle <0$
).
$\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle <0$
). -
(iii) Positive mass flux and negative heat flux (
 $\langle u^{\prime }v^{\prime }\rangle >0$
and
$\langle u^{\prime }v^{\prime }\rangle >0$
and
 $\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle <0$
) gave a negative longitudinal heat flux (
$\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle <0$
) gave a negative longitudinal heat flux (
 $\langle u^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle <0$
).
$\langle u^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle <0$
).
JPDF analysis based on quadrant decomposition thus indicated that movements of entrainment into the mixing layer contributed significantly to heat and mass fluxes. In the following section, we propose to go further in discriminating between entrained and mixed fluid within these fluxes by using a conditional analysis.
3.6 Conditional analysis
One way to separate the contributions of mixing and entrainment in the heat and mass fluxes is to perform conditional analysis. The approach we chose was to use the instantaneous value of temperature as a tag value to differentiate particles according to their origin (hot, cold or mixed region) and to apply a conditional analysis to the measurements affected by such a tag, or indicator function. The multimodal shape of the PDFs of temperature (see figure 9), with clear valleys and peaks, allowed simple thresholding to construct an indicator function (Antonia Reference Antonia1981; Prasad & Sreenivasan Reference Prasad and Sreenivasan1989), where two thresholds could be set to distinguish between mixed fluid, entrained fluid from the high-velocity side and entrained fluid from the low-velocity side:
-
(i) The first threshold
 $(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=0.1$
selected was the valley point between the centred mode (high probability of mixed fluid) and the left lateral mode (high probability of entrained fluid from the high-velocity side).
$(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=0.1$
selected was the valley point between the centred mode (high probability of mixed fluid) and the left lateral mode (high probability of entrained fluid from the high-velocity side). -
(ii) The second threshold
 $(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=0.9$
selected was the valley point between the centred mode (high probability of mixed fluid) and the right lateral mode (high probability of entrained fluid from the low-velocity side).
$(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}=0.9$
selected was the valley point between the centred mode (high probability of mixed fluid) and the right lateral mode (high probability of entrained fluid from the low-velocity side).
The indicator functions were then:
 $$\begin{eqnarray}\left.\begin{array}{@{}lll@{}}I_{h}(t)=1, & \text{if}~{\displaystyle \frac{\unicode[STIX]{x1D703}(t)-\unicode[STIX]{x1D6E9}_{l}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}}}<0.1 & \text{and 0 otherwise,}\\ I_{m}(t)=1, & \text{if}~0.1<{\displaystyle \frac{\unicode[STIX]{x1D703}(t)-\unicode[STIX]{x1D6E9}_{l}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}}}<0.9 & \text{and 0 otherwise,}\\ I_{l}(t)=1, & \text{if}~0.9<{\displaystyle \frac{\unicode[STIX]{x1D703}(t)-\unicode[STIX]{x1D6E9}_{l}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}}} & \text{and 0 otherwise,}\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}lll@{}}I_{h}(t)=1, & \text{if}~{\displaystyle \frac{\unicode[STIX]{x1D703}(t)-\unicode[STIX]{x1D6E9}_{l}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}}}<0.1 & \text{and 0 otherwise,}\\ I_{m}(t)=1, & \text{if}~0.1<{\displaystyle \frac{\unicode[STIX]{x1D703}(t)-\unicode[STIX]{x1D6E9}_{l}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}}}<0.9 & \text{and 0 otherwise,}\\ I_{l}(t)=1, & \text{if}~0.9<{\displaystyle \frac{\unicode[STIX]{x1D703}(t)-\unicode[STIX]{x1D6E9}_{l}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}}} & \text{and 0 otherwise,}\end{array}\right\}\end{eqnarray}$$
with
![]() $I_{m}$
for fluid parcels tagged as mixed fluid,
$I_{m}$
for fluid parcels tagged as mixed fluid,
![]() $I_{h}$
for fluid parcels tagged as entrained fluid from the high-velocity side and
$I_{h}$
for fluid parcels tagged as entrained fluid from the high-velocity side and
![]() $I_{l}$
for fluid parcels tagged as entrained fluid from the low-velocity side. Morphological filtering (opening and closing) was applied on the indicator functions to remove single detections due to the overlap of the modes while preserving
$I_{l}$
for fluid parcels tagged as entrained fluid from the low-velocity side. Morphological filtering (opening and closing) was applied on the indicator functions to remove single detections due to the overlap of the modes while preserving
![]() $I_{h}+I_{m}+I_{l}=1$
. Due to the selection of temperature for the indication function, no differentiation was made between entrained fluid and engulfed fluid (engulfed fluid is the fluid entrained intermittently into the two outermost turbulent/non-turbulent boundaries of the mixing layer). The region of fluid mixed by turbulence can be considered or not as a turbulence region, depending on whether or not engulfed fluid is considered as turbulent. Such an indicator function can therefore be an alternative to a velocity-based indicator for marking the position of the turbulent/non-turbulent interfaces, giving a slightly different light on the separation.
$I_{h}+I_{m}+I_{l}=1$
. Due to the selection of temperature for the indication function, no differentiation was made between entrained fluid and engulfed fluid (engulfed fluid is the fluid entrained intermittently into the two outermost turbulent/non-turbulent boundaries of the mixing layer). The region of fluid mixed by turbulence can be considered or not as a turbulence region, depending on whether or not engulfed fluid is considered as turbulent. Such an indicator function can therefore be an alternative to a velocity-based indicator for marking the position of the turbulent/non-turbulent interfaces, giving a slightly different light on the separation.
The conditional expectation of
![]() $X$
given the event
$X$
given the event
![]() $I$
is defined by:
$I$
is defined by:
and in this paper is simply noted
![]() $\langle X\rangle _{\mid I}$
. The conditional covariance of
$\langle X\rangle _{\mid I}$
. The conditional covariance of
![]() $X$
and
$X$
and
![]() $Y$
, given
$Y$
, given
![]() $I$
, is defined by:
$I$
, is defined by:
and simply noted
![]() $\langle X^{\prime }Y^{\prime }\rangle _{\mid I}$
.
$\langle X^{\prime }Y^{\prime }\rangle _{\mid I}$
.
As the indicator functions
![]() $I$
are binary, the conditional expectation and covariance of
$I$
are binary, the conditional expectation and covariance of
![]() $X$
and
$X$
and
![]() $Y$
to
$Y$
to
![]() $I$
defined by (3.2) and (3.3) can be regarded as expectation and covariance of
$I$
defined by (3.2) and (3.3) can be regarded as expectation and covariance of
![]() $X$
and
$X$
and
![]() $Y$
in fluid parcels tagged by
$Y$
in fluid parcels tagged by
![]() $I$
. The expectation of
$I$
. The expectation of
![]() $X$
can be broken down into three terms:
$X$
can be broken down into three terms:
and can be considered as the weighted sum of the conditional expectations using their respective contributions. Similarly the covariance of
![]() $X$
and
$X$
and
![]() $Y$
is given by:
$Y$
is given by:
where the weighted sum of the conditional covariances is supplemented by cross-products between conditional expectations.
Figures 13 and 14 present the conditional expectations and covariances of velocity and temperature across the mixing layer, given the indicator functions for the mixed fluid
![]() $I_{m}$
and for the entrained fluid from both sides
$I_{m}$
and for the entrained fluid from both sides
![]() $I_{h}$
and
$I_{h}$
and
![]() $I_{l}$
. Expectations of these indicator functions can be viewed as probabilities of presence of these events and are also given in figure 13(a).
$I_{l}$
. Expectations of these indicator functions can be viewed as probabilities of presence of these events and are also given in figure 13(a).
The profiles of these probabilities of presence (
![]() $\langle I_{m}\rangle$
,
$\langle I_{m}\rangle$
,
![]() $\langle I_{h}\rangle$
and
$\langle I_{h}\rangle$
and
![]() $\langle I_{l}\rangle$
in figure 13
a) behaved similarly to those computed from concentration data in Konrad (Reference Konrad1977) and Koochesfahani & Dimotakis (Reference Koochesfahani and Dimotakis1986). The mixed fluid probability
$\langle I_{l}\rangle$
in figure 13
a) behaved similarly to those computed from concentration data in Konrad (Reference Konrad1977) and Koochesfahani & Dimotakis (Reference Koochesfahani and Dimotakis1986). The mixed fluid probability
![]() $\langle I_{m}\rangle$
was bell shaped and symmetrical with regard to the mixing layer axis. It is equivalent to the intermittency factor (flatness factor of the velocity time derivative) computed by Wygnanski & Fiedler (Reference Wygnanski and Fiedler1970) and Spencer & Jones (Reference Spencer and Jones1971), i.e. the ratio between the observed turbulence time and the total observation time. The entrained fluid probabilities
$\langle I_{m}\rangle$
was bell shaped and symmetrical with regard to the mixing layer axis. It is equivalent to the intermittency factor (flatness factor of the velocity time derivative) computed by Wygnanski & Fiedler (Reference Wygnanski and Fiedler1970) and Spencer & Jones (Reference Spencer and Jones1971), i.e. the ratio between the observed turbulence time and the total observation time. The entrained fluid probabilities
![]() $\langle I_{h}\rangle$
and
$\langle I_{h}\rangle$
and
![]() $\langle I_{l}\rangle$
decreased inside the mixing layer so that there was low probability of finding unmixed fluid at the centre of the mixing layer (approximately 8 %). This suggests very active nibbling at the border of the entrained region which allowed only a small proportion of entrained fluid to reach the centre of the mixing layer. Neither imbalance between the entrained fluid from the high- and low-velocity sides nor differences between the stably and unstably stratified configurations could be observed from these curves of probability of presence.
$\langle I_{l}\rangle$
decreased inside the mixing layer so that there was low probability of finding unmixed fluid at the centre of the mixing layer (approximately 8 %). This suggests very active nibbling at the border of the entrained region which allowed only a small proportion of entrained fluid to reach the centre of the mixing layer. Neither imbalance between the entrained fluid from the high- and low-velocity sides nor differences between the stably and unstably stratified configurations could be observed from these curves of probability of presence.

Figure 13. Expectation of the indicator functions for the mixed fluid
![]() $I_{m}$
and for the entrained fluid from both sides
$I_{m}$
and for the entrained fluid from both sides
![]() $I_{h}$
and
$I_{h}$
and
![]() $I_{l}$
and conditional expectations for the velocity and temperature (profiles across the mixing layer in the self-similar region for stably and unstably stratified configurations).
$I_{l}$
and conditional expectations for the velocity and temperature (profiles across the mixing layer in the self-similar region for stably and unstably stratified configurations).

Figure 14. Conditional covariances for the velocity and temperature (profiles across the mixing layer in the self-similar region for stably and unstably stratified configurations).
The conditional expectations of temperature
![]() $\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{h}}$
and
$\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{h}}$
and
![]() $\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{l}}$
shown in figure 13(b) represent the expectations of temperature in the entrained fluid. As expected, the normalized values were constant across the layer,
$\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{l}}$
shown in figure 13(b) represent the expectations of temperature in the entrained fluid. As expected, the normalized values were constant across the layer,
![]() $0$
for the entrained cold fluid from the high-speed stream and
$0$
for the entrained cold fluid from the high-speed stream and
![]() $1$
for the entrained hot fluid from the low-speed stream. The conditional expectation of temperature
$1$
for the entrained hot fluid from the low-speed stream. The conditional expectation of temperature
![]() $\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
represents the expectation of temperature in the mixed fluid. The profiles across the layer were fairly flat and homogeneous, as was the conditional variance of temperature
$\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
represents the expectation of temperature in the mixed fluid. The profiles across the layer were fairly flat and homogeneous, as was the conditional variance of temperature
![]() $\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle _{\mid I_{m}}$
in figure 14(e). These behaviours have already been described by Fiedler (Reference Fiedler1974), Koochesfahani & Dimotakis (Reference Koochesfahani and Dimotakis1986) and Karasso & Mungal (Reference Karasso and Mungal1996), indicating an active stirring process in the turbulent roller vortices before molecular diffusion, as expected with a high Péclet number. As observed in figure 9, these results were consistent with non-marching PDFs.
$\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle _{\mid I_{m}}$
in figure 14(e). These behaviours have already been described by Fiedler (Reference Fiedler1974), Koochesfahani & Dimotakis (Reference Koochesfahani and Dimotakis1986) and Karasso & Mungal (Reference Karasso and Mungal1996), indicating an active stirring process in the turbulent roller vortices before molecular diffusion, as expected with a high Péclet number. As observed in figure 9, these results were consistent with non-marching PDFs.
The conditional expectation of temperature
![]() $\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
averaged over the layer can provide an estimate of the entrainment ratio
$\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
averaged over the layer can provide an estimate of the entrainment ratio
![]() $E=Q_{h}/Q_{l}$
, which is the ratio between the fractional flow rates
$E=Q_{h}/Q_{l}$
, which is the ratio between the fractional flow rates
![]() $Q_{h}$
and
$Q_{h}$
and
![]() $Q_{l}$
originating from the high- and low-velocity streams, respectively, and entrained into the mixing layer. Indeed, the entrainment balance equation yields:
$Q_{l}$
originating from the high- and low-velocity streams, respectively, and entrained into the mixing layer. Indeed, the entrainment balance equation yields:
(n.b. cold air
![]() $\unicode[STIX]{x1D6E9}_{l}$
blown on the high-velocity side
$\unicode[STIX]{x1D6E9}_{l}$
blown on the high-velocity side
![]() $U_{h}$
and hot air
$U_{h}$
and hot air
![]() $\unicode[STIX]{x1D6E9}_{h}$
blown on the low-velocity side
$\unicode[STIX]{x1D6E9}_{h}$
blown on the low-velocity side
![]() $U_{l}$
), leading to:
$U_{l}$
), leading to:
The entrainment balance is simply depicted in Dimotakis (Reference Dimotakis1991) as a bucket filled by hot and cold water faucets running with unequal flow rates, the average temperature in the bucket being only a function of the ratio of the two flow rates. The average value of
![]() $\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
integrated across the layer was approximately
$\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
integrated across the layer was approximately
![]() $0.43$
in the stably stratified configuration and 0.47 in the unstably stratified configuration, giving entrainment ratios of approximately 1.38 and 1.17, respectively. This greater entrainment from the high-speed stream was also found in the literature, namely 1.58 by Fiedler (Reference Fiedler1974),
$0.43$
in the stably stratified configuration and 0.47 in the unstably stratified configuration, giving entrainment ratios of approximately 1.38 and 1.17, respectively. This greater entrainment from the high-speed stream was also found in the literature, namely 1.58 by Fiedler (Reference Fiedler1974),
![]() $1.32$
by Koochesfahani & Dimotakis (Reference Koochesfahani and Dimotakis1986) and 1.37 by Karasso & Mungal (Reference Karasso and Mungal1996).
$1.32$
by Koochesfahani & Dimotakis (Reference Koochesfahani and Dimotakis1986) and 1.37 by Karasso & Mungal (Reference Karasso and Mungal1996).
The conditional expectations of the streamwise velocity are shown in figure 13(c). The expectations of the streamwise velocity in the entrained fluid
![]() $\langle u\rangle _{\mid I_{h}}$
and
$\langle u\rangle _{\mid I_{h}}$
and
![]() $\langle u\rangle _{\mid I_{l}}$
tended to retain the free-stream velocity value, as in Spencer & Jones (Reference Spencer and Jones1971). In contrast to the conditional expectation of the temperature
$\langle u\rangle _{\mid I_{l}}$
tended to retain the free-stream velocity value, as in Spencer & Jones (Reference Spencer and Jones1971). In contrast to the conditional expectation of the temperature
![]() $\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
, the conditional expectation of the streamwise velocity
$\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
, the conditional expectation of the streamwise velocity
![]() $\langle u\rangle _{\mid I_{m}}$
followed the mean streamwise velocity in the mixing layer. Indeed, the turbulent roller vortices trap the engulfed fluid and a significant part of the mixed fluid. The thresholding we made isolates the mixed fluid and associates it with
$\langle u\rangle _{\mid I_{m}}$
followed the mean streamwise velocity in the mixing layer. Indeed, the turbulent roller vortices trap the engulfed fluid and a significant part of the mixed fluid. The thresholding we made isolates the mixed fluid and associates it with
![]() $I_{m}$
while engulfed fluid remains with particles contributing to
$I_{m}$
while engulfed fluid remains with particles contributing to
![]() $I_{l}$
and
$I_{l}$
and
![]() $I_{h}$
. The conditional expectations in the mixed fluid account for the active stirring process in the turbulent roller vortices, leading to homogeneous distribution of the conditional expectation of the temperature in the mixed fluid
$I_{h}$
. The conditional expectations in the mixed fluid account for the active stirring process in the turbulent roller vortices, leading to homogeneous distribution of the conditional expectation of the temperature in the mixed fluid
![]() $\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
and, with the rotation of the roller vortices, leading to the evolution of the conditional expectation of the streamwise velocity in the mixed fluid
$\langle \unicode[STIX]{x1D703}\rangle _{\mid I_{m}}$
and, with the rotation of the roller vortices, leading to the evolution of the conditional expectation of the streamwise velocity in the mixed fluid
![]() $\langle u\rangle _{\mid I_{m}}$
from
$\langle u\rangle _{\mid I_{m}}$
from
![]() $U_{l}$
at the low-speed side to
$U_{l}$
at the low-speed side to
![]() $U_{h}$
at the high-speed side. Let us note that this describes only the mixing and movement of mixed fluid but engulfed fluid may also be present in the turbulent roller vortices, adding some heterogeneity or intermittency in the covered region.
$U_{h}$
at the high-speed side. Let us note that this describes only the mixing and movement of mixed fluid but engulfed fluid may also be present in the turbulent roller vortices, adding some heterogeneity or intermittency in the covered region.
The conditional expectations of transverse velocity are shown in figure 13(d). Entrained fluid dived into the mixing layer faster and faster because of entrainment by roller vortices and the values were higher for entrained fluid from the high-speed stream due to greater momentum. The expectation of the transverse velocity in the mixed fluid was negative for
![]() $\unicode[STIX]{x1D702}_{u}<0$
and positive for
$\unicode[STIX]{x1D702}_{u}<0$
and positive for
![]() $\unicode[STIX]{x1D702}_{u}>0$
, in line with the expansion of the mixing layer.
$\unicode[STIX]{x1D702}_{u}>0$
, in line with the expansion of the mixing layer.
Moving on to the conditional variance profiles in figure 14, for
![]() $\langle u^{\prime }u^{\prime }\rangle$
,
$\langle u^{\prime }u^{\prime }\rangle$
,
![]() $\langle u^{\prime }v^{\prime }\rangle$
and
$\langle u^{\prime }v^{\prime }\rangle$
and
![]() $\langle v^{\prime }v^{\prime }\rangle$
in figure 14(a–c), the values of the conditional variances to
$\langle v^{\prime }v^{\prime }\rangle$
in figure 14(a–c), the values of the conditional variances to
![]() $I_{h}$
and
$I_{h}$
and
![]() $I_{l}$
(i.e. relating to the entrained fluid) were much lower than the respective total variances (in black) and values decreased from the mixing layer axis to the borders. Indeed, the velocity variances in the entrained fluid were both produced by velocity fluctuations inside these regions and by variability of the velocity of successive entrainment events from one event to another. In the same figure, the values of the conditional variances to
$I_{l}$
(i.e. relating to the entrained fluid) were much lower than the respective total variances (in black) and values decreased from the mixing layer axis to the borders. Indeed, the velocity variances in the entrained fluid were both produced by velocity fluctuations inside these regions and by variability of the velocity of successive entrainment events from one event to another. In the same figure, the values of the conditional variances to
![]() $I_{m}$
(i.e. related to the mixed fluid) and the total variances were similar near the mixing layer axis, suggesting negligible effects of intermittency between entrained and mixed fluids on the fully velocity-based variances. These results can be clarified by applying (3.5) near the mixing layer axis in which the first term was governed by the conditional variances to
$I_{m}$
(i.e. related to the mixed fluid) and the total variances were similar near the mixing layer axis, suggesting negligible effects of intermittency between entrained and mixed fluids on the fully velocity-based variances. These results can be clarified by applying (3.5) near the mixing layer axis in which the first term was governed by the conditional variances to
![]() $I_{m}$
(
$I_{m}$
(
![]() $\langle I_{m}\rangle =0.92$
and
$\langle I_{m}\rangle =0.92$
and
![]() $\langle I_{h}\rangle +\langle I_{l}\rangle =0.08$
) and the second term was negligible due to the small difference between the expected velocities in the central regions (see figure 13
c).
$\langle I_{h}\rangle +\langle I_{l}\rangle =0.08$
) and the second term was negligible due to the small difference between the expected velocities in the central regions (see figure 13
c).
For
![]() $\langle u^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
,
$\langle u^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
,
![]() $\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
and
$\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
and
![]() $\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
in figure 14(d–f), the conditional variances to
$\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
in figure 14(d–f), the conditional variances to
![]() $I_{h}$
and
$I_{h}$
and
![]() $I_{l}$
were very low. This result was consistent as it was related to entrained fluid which carried unmixed fluid with a temperature remaining near that of the free stream from which it came. In the same figure, the profiles of the conditional variances to
$I_{l}$
were very low. This result was consistent as it was related to entrained fluid which carried unmixed fluid with a temperature remaining near that of the free stream from which it came. In the same figure, the profiles of the conditional variances to
![]() $I_{m}$
were more homogeneous than for the total variances. In contrast to the fully velocity-based variances, there was a small gap between the conditional variances to
$I_{m}$
were more homogeneous than for the total variances. In contrast to the fully velocity-based variances, there was a small gap between the conditional variances to
![]() $I_{m}$
for
$I_{m}$
for
![]() $\langle u^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
,
$\langle u^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
,
![]() $\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
and
$\langle v^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
and
![]() $\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
and the total variances near the mixing layer axis. The second term in (3.5) contributed significantly to the total variances here due to the high levels of difference between the expected temperatures in the entrained fluids (see figure 13
b). As there was very little temperature fluctuation in the entrained fluid, the temperature variance resulted mainly from the homogeneous turbulence in the mixed fluid and the level of temperature difference between mixed and entrained fluids. As already described in § 3.4, the double peak of
$\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
and the total variances near the mixing layer axis. The second term in (3.5) contributed significantly to the total variances here due to the high levels of difference between the expected temperatures in the entrained fluids (see figure 13
b). As there was very little temperature fluctuation in the entrained fluid, the temperature variance resulted mainly from the homogeneous turbulence in the mixed fluid and the level of temperature difference between mixed and entrained fluids. As already described in § 3.4, the double peak of
![]() $\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
in figure 14(e) (also displayed on figure 6
g) was due to the temperature jumps that occurred at the fronts, and thus the larger peak on the low-velocity side can be explained by the greater temperature difference between entrained and mixed fluids on the low-speed side (around
$\langle \unicode[STIX]{x1D703}^{\prime }\unicode[STIX]{x1D703}^{\prime }\rangle$
in figure 14(e) (also displayed on figure 6
g) was due to the temperature jumps that occurred at the fronts, and thus the larger peak on the low-velocity side can be explained by the greater temperature difference between entrained and mixed fluids on the low-speed side (around
![]() $0.45\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
) than on the high-speed (low-temperature) side (around
$0.45\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
) than on the high-speed (low-temperature) side (around
![]() $0.35\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
).
$0.35\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
).
In conclusion, this kind of conditional analysis gives a more complete view of the separate contributions of the entrainment and mixing to the velocity and temperature fluctuations and their expectations and covariances.
3.7 Effects of buoyancy on entrainment velocity
Entrainment velocity was defined by Townsend (Reference Townsend1976, p. 231) as the mean rate of formation of turbulent fluid in a mixing layer:
By using the Leibniz integral rule and the similarity variable
![]() $\unicode[STIX]{x1D702}_{u}$
, this definition becomes:
$\unicode[STIX]{x1D702}_{u}$
, this definition becomes:
It should be noted that the velocity-based spreading rate
![]() ${\unicode[STIX]{x1D6FF}^{\prime }}_{u}=(\text{d}\unicode[STIX]{x1D6FF}_{u}/\text{d}x)$
is then proportional to the entrainment velocity. According to Brown (Reference Brown1974) and Konrad (Reference Konrad1977), entrainment velocity can also be broken down into the sum of the entrainment velocities across the two boundaries between non-turbulent and turbulent regions:
${\unicode[STIX]{x1D6FF}^{\prime }}_{u}=(\text{d}\unicode[STIX]{x1D6FF}_{u}/\text{d}x)$
is then proportional to the entrainment velocity. According to Brown (Reference Brown1974) and Konrad (Reference Konrad1977), entrainment velocity can also be broken down into the sum of the entrainment velocities across the two boundaries between non-turbulent and turbulent regions:
with
where
![]() $Ve_{l}$
is the entrainment velocity from the low-velocity side and
$Ve_{l}$
is the entrainment velocity from the low-velocity side and
![]() $Ve_{h}$
the entrainment velocity from the high-velocity side. The scalar quantity
$Ve_{h}$
the entrainment velocity from the high-velocity side. The scalar quantity
![]() $\unicode[STIX]{x1D709}$
transported by the flow makes it possible to discriminate between entrainments from the low- and high-velocity sides. It can be
$\unicode[STIX]{x1D709}$
transported by the flow makes it possible to discriminate between entrainments from the low- and high-velocity sides. It can be
![]() $(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
for heat flux or
$(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6E9}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}$
for heat flux or
![]() $(\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
for mass flux.
$(\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}_{l})/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
for mass flux.
In many studies (e.g. Brown Reference Brown1974; Masutani & Bowman Reference Masutani and Bowman1986; Zhou & Pereira Reference Zhou and Pereira2000; D’Ovidio & Coats Reference D’Ovidio and Coats2013), simplifications were used to cope with the lack of turbulence detection and joint measurements
![]() $\unicode[STIX]{x1D709}\cdot u$
. Integrations were limited to the boundaries (based on mean quantities) and the mean of the product was estimated by the product of the means. In the present study, no simplification was necessary but entrainment velocity was related to the mean rate of formation of mixed fluid rather than turbulent fluid, and hence
$\unicode[STIX]{x1D709}\cdot u$
. Integrations were limited to the boundaries (based on mean quantities) and the mean of the product was estimated by the product of the means. In the present study, no simplification was necessary but entrainment velocity was related to the mean rate of formation of mixed fluid rather than turbulent fluid, and hence
![]() $I_{t}$
was replaced by
$I_{t}$
was replaced by
![]() $I_{m}$
in (3.11) and (3.12).
$I_{m}$
in (3.11) and (3.12).
Table 3 gives entrainment velocities and their sums and ratios in the self-similar region for stably and unstably stratified configurations. Buoyancy amplified entrainment from both sides in the unstably stratified configuration, the increase being higher on the low-velocity side, while the total entrainment velocity
![]() $Ve$
was increased in the same proportion as the velocity-based spreading rate
$Ve$
was increased in the same proportion as the velocity-based spreading rate
![]() ${\unicode[STIX]{x1D6FF}^{\prime }}_{u}$
was (see table 1). The entrainment ratios (1.4 and 1.2) appeared to confirm the estimate obtained by (3.7) (1.38 and 1.17, respectively) and its dependence on buoyancy. The lower asymmetry for the unstably stratified configuration is consistent with the lower deflection angle (see table 1).
${\unicode[STIX]{x1D6FF}^{\prime }}_{u}$
was (see table 1). The entrainment ratios (1.4 and 1.2) appeared to confirm the estimate obtained by (3.7) (1.38 and 1.17, respectively) and its dependence on buoyancy. The lower asymmetry for the unstably stratified configuration is consistent with the lower deflection angle (see table 1).
Table 3. Entrainment velocities and their sum and ratio in the self-similar region for stably and unstably stratified configurations.

Dimotakis (Reference Dimotakis1986) proposed a model based on the work of Brown (Reference Brown1974) to predict the volumetric flux entrainment ratio
![]() $E_{Ve}$
, in addition to the vortex convection velocity
$E_{Ve}$
, in addition to the vortex convection velocity
![]() $U_{v}$
and the velocity-based spreading rate
$U_{v}$
and the velocity-based spreading rate
![]() ${\unicode[STIX]{x1D6FF}^{\prime }}_{u}$
:
${\unicode[STIX]{x1D6FF}^{\prime }}_{u}$
:
 $$\begin{eqnarray}\displaystyle & \displaystyle {\unicode[STIX]{x1D6FF}^{\prime }}_{\unicode[STIX]{x1D714}}=0.085\frac{1-r}{1+r\sqrt{s}}\left(1+\sqrt{s}-\frac{1-\sqrt{s}}{\displaystyle 1+2.9\frac{1+r}{1-r}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\unicode[STIX]{x1D6FF}^{\prime }}_{\unicode[STIX]{x1D714}}=0.085\frac{1-r}{1+r\sqrt{s}}\left(1+\sqrt{s}-\frac{1-\sqrt{s}}{\displaystyle 1+2.9\frac{1+r}{1-r}}\right), & \displaystyle\end{eqnarray}$$
where
![]() $r=(U_{l}/U_{h})$
is the velocity ratio,
$r=(U_{l}/U_{h})$
is the velocity ratio,
![]() ${\unicode[STIX]{x1D6FF}^{\prime }}_{\unicode[STIX]{x1D714}}$
the vorticity-based spreading rate (with
${\unicode[STIX]{x1D6FF}^{\prime }}_{\unicode[STIX]{x1D714}}$
the vorticity-based spreading rate (with
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=0.91\unicode[STIX]{x1D6FF}_{u}$
) and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=0.91\unicode[STIX]{x1D6FF}_{u}$
) and
![]() $s=(\unicode[STIX]{x1D70C}_{h}/\unicode[STIX]{x1D70C}_{l})$
the density ratio.
$s=(\unicode[STIX]{x1D70C}_{h}/\unicode[STIX]{x1D70C}_{l})$
the density ratio.
Through this model, Dimotakis found a way to introduce the asymmetry between the entrainments in the case of a spatially developing mixing layer, by considering a differential in fluid entrainment between the upstream and downstream sides of a roller vortex, the differential being related to the expansion of the mixing layer. The Dimotakis models also introduced density gradient effects through dependence on mean roller vortex spacing to position ratio
![]() $l/x$
and the density ratio function
$l/x$
and the density ratio function
![]() $\sqrt{s}$
. In case of density gradient effects due to unsteadiness-induced acceleration, he assumed the ratio between the mean roller vortex spacing and the position to be
$\sqrt{s}$
. In case of density gradient effects due to unsteadiness-induced acceleration, he assumed the ratio between the mean roller vortex spacing and the position to be
![]() $l/x=3.9{\unicode[STIX]{x1D6FF}^{\prime }}_{\unicode[STIX]{x1D714}}$
(Koochesfahani et al.
Reference Koochesfahani, Dimotakis, Catherasoo, Gharib and Lang1979) with
$l/x=3.9{\unicode[STIX]{x1D6FF}^{\prime }}_{\unicode[STIX]{x1D714}}$
(Koochesfahani et al.
Reference Koochesfahani, Dimotakis, Catherasoo, Gharib and Lang1979) with
![]() ${\unicode[STIX]{x1D6FF}^{\prime }}_{\unicode[STIX]{x1D714}}=0.17(1-r)/(1+r)$
or
${\unicode[STIX]{x1D6FF}^{\prime }}_{\unicode[STIX]{x1D714}}=0.17(1-r)/(1+r)$
or
![]() $0.17\unicode[STIX]{x1D706}$
(Brown & Roshko Reference Brown and Roshko1974), providing the
$0.17\unicode[STIX]{x1D706}$
(Brown & Roshko Reference Brown and Roshko1974), providing the
![]() $0.68$
coefficient in the expression of
$0.68$
coefficient in the expression of
![]() $E_{Ve}$
(3.13). Soteriou & Ghoniem (Reference Soteriou and Ghoniem1995) stated that the dependence on
$E_{Ve}$
(3.13). Soteriou & Ghoniem (Reference Soteriou and Ghoniem1995) stated that the dependence on
![]() $\sqrt{s}$
, initially quasi-empirically assumed by Brown (Reference Brown1974) and later based on Bernoulli’s equation applied along a line through the saddle point by Dimotakis (Reference Dimotakis1986), provides coarse modelling of the effects of the baroclinic torque on entrainment (see § 1.3, Effects of stratification). These effects mainly take place through the generation, amplification and damping of eddy structures, on intermediate scales, similar to those of rib vortices. Together with gravity-induced acceleration, by its construction (3.13) the model integrates buoyancy effects, but only through the large-scale topological length values (spacing and expansion of roller vortices).
$\sqrt{s}$
, initially quasi-empirically assumed by Brown (Reference Brown1974) and later based on Bernoulli’s equation applied along a line through the saddle point by Dimotakis (Reference Dimotakis1986), provides coarse modelling of the effects of the baroclinic torque on entrainment (see § 1.3, Effects of stratification). These effects mainly take place through the generation, amplification and damping of eddy structures, on intermediate scales, similar to those of rib vortices. Together with gravity-induced acceleration, by its construction (3.13) the model integrates buoyancy effects, but only through the large-scale topological length values (spacing and expansion of roller vortices).

Figure 15. Volumetric flux entrainment ratio
![]() $E_{Ve}$
against density ratio
$E_{Ve}$
against density ratio
![]() $s$
for three velocity ratios
$s$
for three velocity ratios
![]() $r$
. The solid lines are the predictions of the Dimotakis model, while the symbols are results from numerical simulations or experiments.
$r$
. The solid lines are the predictions of the Dimotakis model, while the symbols are results from numerical simulations or experiments.
Figure 15 shows that the volumetric flux entrainment ratio for a mixing layer with or without an unsteadiness-induced acceleration was fairly well predicted by the Dimotakis model for a wide range of density ratios, including experimental results from Brown (Reference Brown1974) and Konrad (Reference Konrad1977) and numerical results from Soteriou & Ghoniem (Reference Soteriou and Ghoniem1995). It should be noted however that the excellent agreement between the Dimotakis model and the results of Konrad (Reference Konrad1977) and Soteriou & Ghoniem (Reference Soteriou and Ghoniem1995) was probably biased by adjustment artefacts, bearing in mind that Dimotakis constructed his model using results from Konrad (Reference Konrad1977), and that Soteriou & Ghoniem (Reference Soteriou and Ghoniem1995) corrected their results to take into account confinement in their numerical simulations. In the study presented here, the mixing layer configurations were all characterized by
![]() $r=0.5$
and
$r=0.5$
and
![]() $s=0.93$
but led to different values for the mean roller vortex spacing and spreading rate, due to differences in buoyancy magnitude. For the neutrally stratified configuration, the Dimotakis model provided
$s=0.93$
but led to different values for the mean roller vortex spacing and spreading rate, due to differences in buoyancy magnitude. For the neutrally stratified configuration, the Dimotakis model provided
![]() $E_{Ve}=1.21$
. For the stably and unstably stratified configurations with both unsteadiness- and gravity-induced acceleration, the Dimotakis model provided
$E_{Ve}=1.21$
. For the stably and unstably stratified configurations with both unsteadiness- and gravity-induced acceleration, the Dimotakis model provided
![]() $E_{Ve}=1.19$
and 1.23, respectively, which were still different from the measured values 1.4 and 1.2 (see table 3).
$E_{Ve}=1.19$
and 1.23, respectively, which were still different from the measured values 1.4 and 1.2 (see table 3).
As the neutrally and stably stratified configurations of the mixing layer in this study provided similar characteristics (see table 1) and turbulence profiles (see figures 5, 6 and 8), we conclude that the density gradient effects were too weak to be observed in that particular case of weak stably stratified condition. We do not consider that the gap between our measured values and the Dimotakis model prediction for the neutrally and stably stratified configurations invalidates the model per se, bearing in mind that the gap may have been at least partially due to differences in the initial conditions and in the development length of the mixing layer (Dimotakis himself suggested such dependence), but an inadequacy of the model emerges in that it could not predict the buoyancy effect on the unstably stratified configuration. The inability to predict the buoyancy effect mainly shows that the modifications in the large-scale topological lengths (spacing and expansion of roller vortices) are not sufficient to capture and model the difference in asymmetry that buoyancy induces. The modifications in smaller-scale eddy structures are relatively significant, as shown by Piccirillo & Van Atta (Reference Piccirillo and Van Atta1997) in the case of uniform shear and stratification and Nagata & Komori (Reference Nagata and Komori2000) in the case of localized shear and stratification. To improve the model prediction, the modifications in the smaller-scale eddy structures should be better taken into account, in addition to the unsteadiness- and gravity-induced effects on roller vortices.
In the present configuration of a stratified mixing layer dominated by shear, the entrainment process results from both engulfing by large roller vortices (individual growth and pairing process) and nibbling by intermediate-scale eddy structures. In unstably stratified conditions with
![]() ${Ri_{f}}_{min}\simeq -0.02$
, we can assume that the lower entrainment ratio measured can be attributed to enhanced nibbling as compared with engulfing. In stably stratified conditions with
${Ri_{f}}_{min}\simeq -0.02$
, we can assume that the lower entrainment ratio measured can be attributed to enhanced nibbling as compared with engulfing. In stably stratified conditions with
![]() ${Ri_{f}}_{max}\simeq 0.02$
, it is of note that, in our experiment, almost no difference appeared between the neutrally and stably stratified configurations, but higher Richardson numbers would probably provide measurable effects of buoyancy on the entrainment process. This could then be observed further downstream, as the Richardson number grows with
${Ri_{f}}_{max}\simeq 0.02$
, it is of note that, in our experiment, almost no difference appeared between the neutrally and stably stratified configurations, but higher Richardson numbers would probably provide measurable effects of buoyancy on the entrainment process. This could then be observed further downstream, as the Richardson number grows with
![]() $x$
, in a longer wind tunnel. We therefore conclude that, for flow configurations where buoyancy significantly acts on the entrainment and turbulent mixing processes, at least some complement to the Dimotakis model (or even a new model) should be devised from more complete experiments, to account for the separate effects of buoyancy on engulfing and nibbling.
$x$
, in a longer wind tunnel. We therefore conclude that, for flow configurations where buoyancy significantly acts on the entrainment and turbulent mixing processes, at least some complement to the Dimotakis model (or even a new model) should be devised from more complete experiments, to account for the separate effects of buoyancy on engulfing and nibbling.
4 Conclusion
Hot-wire thermo-anemometry adapted to the use of
![]() $\times$
-wire probes proved to be an effective method to deliver clear information on the turbulence structure of the flow and on the separate contributions of entrainments and core mixing to the development of the mixing layer.
$\times$
-wire probes proved to be an effective method to deliver clear information on the turbulence structure of the flow and on the separate contributions of entrainments and core mixing to the development of the mixing layer.
It should be noted that this was made possible by the combination of a small probe, relatively low velocities and large set-up dimensions, leading to a correct ratio between the spatial and temporal measurement scales and the flow turbulence and dissipative scales. Together with the use of temperature as the scalar creating the density gradients, this produced an experimental situation where a scalar method could provide precise results which are generally only provided by chemical reaction measuring methods.
Derived from industrial situations, the experimental conditions led to the study of a mixing layer where buoyancy was quantitatively weak compared to turbulence production but where it appeared to have marked effects on the turbulence mechanisms involved in transverse heat and mass fluxes. In the ‘stably’ stratified condition, almost no difference was found from the neutral non-buoyant condition. In the ‘unstably’ stratified condition, clear differences appeared in turbulence quantities involving temperature and transverse velocity. The PDFs and JPDFs did not show any clear differentiation between the stably and unstably stratified conditions, but the PDF and JPDF maps showed the coexistence of separately discernible movements through multimodal shapes, corresponding to strong turbulent mixing in the roller vortices on the one hand and entrainment from the free streams on both sides of the mixing layer on the other.
Taking advantage of the simultaneity of the temperature and velocity measurements at the same point and at high frequency, it was then possible to perform conditional analysis of the measurements using instantaneous temperature thresholds to separate events and tag them as related to mixed fluid or entrained fluid from the low-velocity side or entrained fluid from the high-velocity side. This made possible separate study of movements according to their origin and finally allowed evaluation of the entrainment velocities on both sides of the mixing layer. The entrainment ratios calculated between these two velocities were different for the stably and unstably stratified conditions, and it was hypothesised that this arose from a difference in the effects of gravity on the different mechanisms involved in entrainment, namely nibbling and engulfing. These new results suggest the need for further experiments to pursue the physically consistent approach proposed by Dimotakis and to design a more complete model for the prediction of the entrainment ratio, in particular for situations where buoyancy acts significantly on a spatially developing free shear layer.
Acknowledgements
We are grateful to the Region Bretagne of France for their financial support. We thank G. Arroyo for his constant support and valuable advice throughout all these years. This paper is dedicated to the memory of J. Delville and C. Fourment, two colleagues who passed away prematurely.