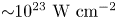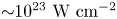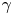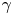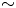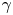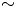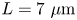Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-06T19:20:43.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Plasma scale length and quantum electrodynamics effects on particle acceleration at extreme laser plasmas

Published online by Cambridge University Press:  15 November 2021

Ozgur Culfa Open the ORCID record for Ozgur Culfa [Opens in a new window]  and
Sinan Sagir Open the ORCID record for Sinan Sagir [Opens in a new window]
Ozgur Culfa*
Affiliation:
Department of Physics, Karamanoglu Mehmetbey University, Karaman 70200, Turkey
Sinan Sagir
Affiliation:
Vocational School of Health Services, Karamanoglu Mehmetbey University, Karaman, 70200, Turkey
*
†Email address for correspondence: ozgurculfa@kmu.edu.tr
Rights & Permissions [Opens in a new window]

Abstract

In this work, simulations of multipetawatt lasers at irradiances ${\sim }10^{23} \ \mathrm {W}\ \mathrm {cm}^{-2}$, striking solid targets and implementing two-dimensional particle-in-cell code was used to study particle acceleration. Preformed plasma at the front surface of a solid target increases both the efficiency of particle acceleration and the reached maximum energy by the accelerated charged particles via nonlinear plasma processes. Here, we have investigated the preformed plasma scale length effects on particle acceleration in the presence and absence of nonlinear quantum electrodynamic (QED) effects, including quantum radiation reaction and multiphoton Breit–Wheeler pair production, which become important at irradiances ${\sim } 10^{23}\ \mathrm {W}\ \mathrm {cm}^{-2}$. Our results show that QED effects help particles gain higher energies with the presence of preformed plasma. In the results for all cases, preplasma leads to more efficient laser absorption and produces more energetic charged particles, as expected. In the case where QED is included, however, physical mechanisms changed and generated secondary particles ($\gamma$-rays and positrons) reversing this trend. That is, the hot electrons cool down due to QED effects, while ions gain more energy due to different acceleration methods. It is found that more energetic $\gamma$-rays and positrons are created with increasing scale length due to high laser conversion efficiency (${\sim }$24 % for $\gamma$-rays and $\sim$4 % for positrons at $L = 7\ \mathrm {\mu }\textrm {m}$ scale length), which affects the ion and electron acceleration mechanisms. It is also observed that the QED effect reduces the collimation of angular distribution of accelerated ions because the dominant ion acceleration mechanism is changing when QED is involved in the process.

Keywords

PIC simulationsparticle accelerationlaser-plasma interactions
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 6 , December 2021 , 905870602
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

1. Introduction

The strong electromagnetic fields in the focus of high-intensity laser pulses ionize matter to produce a plasma in a very short time. Charged particles can be accelerated to very high energies in short distances by the electromagnetic fields generated in this plasma (Daido, Nishiuchi & Pirozhkov Reference Daido, Nishiuchi and Pirozhkov2012; Macchi, Borghesi & Passoni Reference Macchi, Borghesi and Passoni2013). Therefore, laser–plasma interactions have many potential applications varying from hadron therapy (Bulanov et al. Reference Bulanov, Wilkens, Esirkepov, Korn, Kraft, Kraft, Molls and Khoroshkov2014) and radiation generation for femtosecond time scale imaging (Blaga et al. Reference Blaga, Xu, DiChiara, Sistrunk, Zhang, Agostini, Miller, DiMauro and Lin2011), to next-generation particle accelerators (if they can be staged) (Tajima & Dawson Reference Tajima and Dawson1979; Esarey, Schroeder & Leemans Reference Esarey, Schroeder and Leemans2009; Steinke et al. Reference Steinke, van Tilborg, Benedetti, Geddes, Schroeder, Daniels, Swanson, Gonsalves, Nakamura and Matlis2016). Recent theoretical studies with high intensity laser–solid interactions (${>}10^{20} \ \mathrm {W}\ \mathrm {cm}^{-2}$) show that monoenergetic ions can be accelerated to GeV energy levels (Xu et al. Reference Xu, Wang, Hora, Qi, Xing, Yang and Zhu2018), and by altering the target, maximum ion energies can be increased (Sadighi-Bonabi et al. Reference Sadighi-Bonabi, Yazdani, Cang and Hora2010; Yazdani et al. Reference Yazdani, Sadighi-Bonabi, Afarideh, Yazdanpanah and Hora2014). At the extreme intensities reaching laser irradiances ${>}10^{22}\ \mathrm {W}\ \mathrm {cm}^{-2}$, the solid target is ionized rapidly and the electrons in the generated plasma are accelerated to such ultrarelativistic energies that the electric field they experience in their rest frame may reach the critical or Schwinger field of quantum electrodynamics (QED), $E_s = 1.3\times 10^{18}\ \mathrm {V}\ \mathrm {m}^{-1}$ (Schwinger Reference Schwinger1951). This field is the threshold where QED effects start to become important (Bell & Kirk Reference Bell and Kirk2008; Kirk, Bell & Arka Reference Kirk, Bell and Arka2009). The radiation-dominant regime starts at $a_0 \simeq 400$ where $a_0$ is the dimensionless laser amplitude given by

(1.1)\begin{equation} a_0 = \sqrt{\frac{I_{\mathrm{W}\ \mathrm{cm}^{{-}2}}\lambda^2_{\mathrm{\mu} \mathrm{m}}}{1.37\times 10^{18}}} , \end{equation}

where $I$ is the intensity (in $\mathrm {W}\ \mathrm {cm}^{-2}$) and $\lambda$ (in microns) is the wavelength of the incident laser. Furthermore, quantum physics effects begin to present at $a_0 \simeq 2500$ ($I\simeq 1.38\times 10^{26}\ \mathrm {W}\ \mathrm {cm}^{-2}$). When $a_0= 5\times 10^5$ and $I \simeq 3\times 10^{29}\ \mathrm {W}\ \mathrm {cm}^{-2}$, the laser pulse electric field becomes equal to the Schwinger electric field $E_s=m_e^2c^3/e\hbar$ and nonlinear QED effects are present, creating electron–positron pairs in the vacuum (Mourou, Tajima & Bulanov Reference Mourou, Tajima and Bulanov2006).

The development of multipetawatt class lasers (up to 100 PW) mean that intensities of ${\sim }10^{23}\ \mathrm {W}\ \mathrm {cm}^{-2}$ will be achievable (Piazza, Muller & Hatsagortsyan Reference Piazza, Muller, Hatsagortsyan and Keitel2012; Danson et al. Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein and Hillier2019), raising a new regime in physics which includes the ion acceleration to GeV energies by the radiation pressure of the laser (Shen et al. Reference Shen, Li, Yu and Cary2007; Zhang et al. Reference Zhang, Shen, Ji, Wang, Wen, Wang, Xu and Yu2010; Qiao et al. Reference Qiao, Kar, Geissler, Gibbon, Zeph and Borghesi2012) and the onset of nonlinear QED effects. In this paper, the acceleration of protons, fast electrons, positrons and photons in extreme laser irradiances (${>}10^{23}\ \mathrm {W}\ \mathrm {cm}^{-2}$) have been studied in the presence of QED effects and defined preformed plasma scale lengths.

Particle acceleration with high irradiance laser plasma interactions has been extensively investigated with current PW-class lasers (up to ${\sim }10^{21}\ \mathrm {W}\ \mathrm {cm}^{-2}$) (Wilks et al. Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001; McKenna et al. Reference McKenna, Carroll, Lundh, Nürnberg, Markey, Bandyopadhyay, Batani, Evans, Jafer and Kar2008; Culfa et al. Reference Culfa, Tallents, Rossall, Wagenaars, Ridgers, Murphy, Dance, Gray, McKenna and Brown2016, Reference Culfa, Tallents, Korkmaz, Rossall, Wagenaars, Ridgers, Murphy, Booth, Carroll and Wilson2017). Hot electrons can reach GeV energies when interacting with gas targets (Leemans et al. Reference Leemans, Nagler, Gonsalves, Tóth, Nakamura, Geddes, Esarey, Schroeder and Hooker2006; Kneip et al. Reference Kneip, Nagel, Martins, Mangles, Bellei, Chekhlov, Clarke, Delerue, Divall and Doucas2009) and 150 MeV with solid targets (Culfa et al. Reference Culfa, Tallents, Wagenaars, Ridgers, Dance, Rossall, Gray, McKenna, Brown and James2014, Reference Culfa, Tallents, Rossall, Wagenaars, Ridgers, Murphy, Dance, Gray, McKenna and Brown2016, Reference Culfa, Tallents, Korkmaz, Rossall, Wagenaars, Ridgers, Murphy, Booth, Carroll and Wilson2017). Moreover, these generated electrons also lead to the acceleration of protons inside the plasma via several mechanisms (Wilks et al. Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001; Albright et al. Reference Albright, Yin, Bowers, Hegelich, Flippo, Kwan and Fernández2007; Yin et al. Reference Yin, Albright, Hegelich, Bowers, Flippo, Kwan and Fernández2007; Jung et al. Reference Jung, Yin, Gautier, Wu, Letzring, Dromey, Shah, Palaniyappan, Shimada and Johnson2013). It is well known that laser absorption and electron acceleration mechanisms have a strong dependence on preformed plasma scale length $L$ and electron number density $n_e$ given by

(1.2)\begin{equation} n_e = \frac{\omega_p^2 m_e \epsilon_0}{e^2} \end{equation}

where $\omega _p$ is the plasma frequency, $m_e$ and $e$ is the electron mass and charge, respectively.

Recent simulations with different foil thicknesses between 0.1 and $0.9\ \mathrm {\mu }\mathrm {m}$ showed that a 110 nm preformed plasma scale length is optimum for proton acceleration at the relatively lower intensities (${\sim }10^{22}\ \mathrm {W}\ \mathrm {cm}^{-2}$) possible with 10 PW laser systems (Hadjisolomou et al. Reference Hadjisolomou, Tsygvintsev, Sasorov, Gasilov, Korn and Bulanov2020). For thicker targets with foil thicknesses of a few $\mathrm {\mu }\textrm {m}$, it is seen that the optimum preformed plasma scale length is around $8\ \mathrm {\mu }\mathrm {m}$ for proton acceleration with similar laser intensities (${\sim }10^{21}\text {--}10^{22}\ \mathrm {W}\ \mathrm {cm}^{{-2}}$) (Esirkepov et al. Reference Esirkepov, Koga, Sunahara, Morita, Nishikino, Kageyama, Nagatomo, Nishihara, Sagisaka and Kotaki2014). The interaction of a laser pulse with an overdense plasma ($n_e > n_{c}$), depends on the plasma scale length $L$. When the scale length is much larger than the electron quiver radius, $r = eE/m\omega ^2 \ll L$, the main laser absorption mechanism is due to nonlinear processes in the plasma resonance region where $n_e \simeq n_c$. Varying density scale length enables an optimum absorption by the resonance absorption mechanism (Kruer Reference Kruer1988). For the case of $L\gg r$, the mechanism of electron vacuum heating (Brunel Reference Brunel1987) is the process. The vacuum heating mechanism vanishes when the plasma scale length surpasses the electromagnetic field skin depth. The $\boldsymbol {J} \times \boldsymbol {B}$ (Wilks et al. Reference Wilks, Kruer, Tabak and Langdon1992) electron acceleration mechanism dominates with longer underdense pulse propagation. Self-focusing (Max, Arons & Langdon Reference Max, Arons and Langdon1974) and other factors, including channel formation (Najmudin et al. Reference Najmudin, Krushelnick, Tatarakis, Clark, Danson, Malka, Neely, Santala and Dangor2003) which affects the energy coupling to electrons, modifies the laser pulse propagation in longer scale lengths. Recent simulations with $a_0\gg 1$ and $n_e \gg n_c$ showed that ultraintense (${>}10^{23}\ \mathrm {W}\ \mathrm {cm}^{{-2}}$) laser–solid interactions generate a new electron acceleration mechanism called the zero-vector-potential (ZVP) absorption mechanism, which produces electrons with higher temperatures (Savin et al. Reference Savin, Ross, Aboushelbaya, Mayr, Spiers, Wang and Norreys2019). The qualitative evidence of the ZVP mechanism can be seen graphically through high momentum spikes on the laser propagation axis. These spikes can verify that the high momentum of the electrons only occur for pulses where the vector potential passes through zero (Savin et al. Reference Savin, Ross, Serzans, Trines, Ceurvorst, Ratan, Spiers, Bingham, Robinson and Norreys2017).

Such high laser irradiances of $I > 10^{23}\ \mathrm {W}\ \mathrm {cm}^{{-2}}$ generate extremely strong electromagnetic fields ($E_L \gtrsim 10^{15}\ \mathrm {V}\ \mathrm {m}^{-1}$). These electromagnetic fields can accelerate electrons significantly, such that a large fraction of their energy is radiated as $\gamma$-rays, by nonlinear Compton scattering, within a single laser cycle, resulting in the radiation reaction (RR) force becoming vital in determining the electron trajectories (Dirac Reference Dirac1938). Thus, quantum aspects of the radiation emission are important (Kirk et al. Reference Kirk, Bell and Arka2009; Sokolov et al. Reference Sokolov, Nees, Yanovsky, Naumova and Mourou2010; Duclous, Kirk & Bell Reference Duclous, Kirk and Bell2011) and electron–positron pairs can be generated by the emitted photons on interaction with the laser fields via multiphoton Breit–Wheeler pair production (Breit & Wheeler Reference Breit and Wheeler1934; Bell & Kirk Reference Bell and Kirk2008; Fedotov et al. Reference Fedotov, Narozhny, Mourou and Korn2010). The plasma dynamics created by next generation 10 and 100 PW lasers will be dominated by these emission processes (Nerush et al. Reference Nerush, Kostyukov, Fedotov, Narozhny, Elkina and Ruhl2011; Sokolov, Naumova & Nees Reference Sokolov, Naumova and Nees2011; Ridgers et al. Reference Ridgers, Brady, Duclous, Kirk, Bennett, Arber, Robinson and Bell2012). Quantum RR and multiphoton Breit–Wheeler pair production have a strong effect on particle acceleration in multipetawatt laser–solid interactions as shown in recent studies (Tamburini et al. Reference Tamburini, Pegoraro, Piazza, Keitel and Macchi2010; Zhang, Ridgers & Thomas Reference Zhang, Ridgers and Thomas2015). Current theoretical studies show that $\gamma$-ray and pair production can be done experimentally by using the flying mirror technique, which increases the laser pulse power up to the level where the laser electric field reaches the Schwinger limit at which electron positron pairs are produced (Bulanov et al. Reference Bulanov, Esirkepov, Hayashi, Kando, Kiriyama, Koga, Kondo, Kotaki, Pirozhkov and Bulanov2011).

Another important process in the interaction of lasers having $a_0 \gg 1$ with plasmas is relativistically induced transparency (RIT). In the ultrarelativistic regime, the effective mass of electrons in the plasma with high energies is much greater than the their rest mass. Therefore, the plasma frequency is reduced by a factor of $1/\sqrt {\langle \gamma \rangle }$, where $\langle \gamma \rangle$ is the average Lorentz factor of the electrons and the electron number density $n_e$ is reduced by $1/\langle \gamma \rangle$. Consequently, an opaque plasma can be expected to become transparent if the $\langle \gamma \rangle$ is sufficiently high. This RIT (Palaniyappan et al. Reference Palaniyappan, Hegelich, Wu, Jung, Gautier, Yin, Albright, Johnson, Shimada and Letzring2012) optically switches the plasma from opaque to transparent and enables light propagation. Thus, when the plasma frequency drops lower than the laser frequency, the laser propagates far behind the target because the light is no longer reflected at the critical surface (Lefebvre & Bonnaud Reference Lefebvre and Bonnaud1995). Reaching this state with currently developed lasers requires foils thinner than a micron. These extreme laser intensities (${>}10^{21}\ \mathrm {W}\ \mathrm {cm}^{{-2}}$) turn the initially defined plasma into relativistically defined plasma and increases the mass of the electrons by the Lorentz factor $\langle \gamma \rangle = \sqrt {(1+a_0^2/2)}$; subsequently, the critical plasma density turns to relativistic critical density ($n_{rc}= \gamma n_{c}$) which is far greater than our initially defined plasma density. Critical plasma density $n_{c}$ can be defined as

(1.3a,b)\begin{equation} n_{rc}= \gamma n_{c},\quad n_c = \frac{4{\rm \pi}^2m_e \epsilon_0c^2}{e^2} \frac{1}{\lambda^2} \simeq \frac{1.11\times 10^{21}}{\lambda^2_{\mathrm{\mu} \textrm{m}}}\mathrm{cm}^{{-3}}, \end{equation}

where $e$ and $m_e$ are the electrical charge and rest mass of the electron, $\epsilon _0$ is the free space permittivity and $c$ is the speed of light. The measure of transparency or opaqueness of the plasma can be given with the equation (Vshivkov et al. Reference Vshivkov, Naumova, Pegoraro and Bulanov1998)

(1.4)\begin{equation} \zeta = \frac{\omega_p^2l}{2\omega_Lc} = \frac{\lambda l }{4{\rm \pi} \delta^2 }, \end{equation}

where $l$ is the plasma thickness, $\omega _p$ and $\omega _L$ are the plasma and laser frequency, respectively, and $\delta$ is the plasma skin depth ($\delta = c/\omega _p$). The plasma is transparent when the dimensionless parameter $\zeta \ll 1$, but when $\zeta \gg 1$, the plasma is opaque. When the laser intensities $a_0\gg 1$, a foil with $\zeta \gg$1 is transparent as long as $a_0\gg \zeta$. Our initial case before the interaction, $a_0 \simeq 483$, $\zeta \simeq 112$, shows that our plasma is transparent for the relativistic case which can be expressed as $\omega _L \gg {\omega _p^2l}/{2a_0c}$.

However, if we enter the QED-plasma regime as the electromagnetic fields increase, RR becomes important, the electron motion is damped and thus $\langle \gamma \rangle$ is expected to be reduced. Furthermore, RR leads to absorption of the electromagnetic wave (Mourou et al. Reference Mourou, Tajima and Bulanov2006; Bashinov & Kim Reference Bashinov and Kim2013).

Such high intensity lasers can accelerate ions with light pressure, known as radiation pressure acceleration (RPA) (Esirkepov et al. Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Robinson et al. Reference Robinson, Zepf, Kar, Evans and Bellei2008; Sorbo et al. Reference Sorbo, Blackman, Capdessus, Small, Slade-Lowther, Luo, Duff, Robinson, McKenna and Sheng2018). The related radiation pressure can go up to $2I/c$, where $I$ is the laser intensity and $c$ is the speed of light. In this mechanism, the charge separation field leads the transfer of the radiation momentum to the accelerated ions. The electrons are pushed forward into the target (via radiation pressure) which causes a charge separation behind and generates an electrostatic field which accelerates background ions. In our simulations, we find that the laser bores a hole in the plasma due to the ponderomotive force as the laser pushes away electrons from the underdense region. This helps to create a dense local build-up of the electrons just beyond the critical layer, referred to as a snowplough (Sahai et al. Reference Sahai, Tsung, Tableman, Mori and Katsouleas2013) as seen in figure 1. The electron snowplough forms only when the transparency conditions are valid and its speed is less than the laser group velocity $v_g/c = \sqrt {1-n_e/ n_c \gamma }$. For short laser pulses, ions stay undisturbed and effectively stationary by the ponderomotive force. In long scale length plasmas, this leads to a new ion acceleration mechanism, called relativistically induced transparency acceleration (RITA) (Sahai et al. Reference Sahai, Tsung, Tableman, Mori and Katsouleas2013; Powell et al. Reference Powell, King, Gray, MacLellan, Gonzalez-Izquierdo, Stockhausen, Hicks, Dover, Rusby and Carroll2015). The RITA mechanism is different than previously described laser–plasma ion acceleration mechanisms in several aspects. The background ions are mainly stable over the RITA time scales, whereas the ion motion is critical in other schemes (Gibbon Reference Gibbon2000; Silva et al. Reference Silva, Marti, Davies, Fonseca, Ren, Tsung and Mori2004). In this mechanism, femtosecond relativistic laser pulses accelerate protons to produce quasimonoenergetic clusters with peak energies.

Figure 1. (a) Electron and (b) proton number densities for $5\ \mathrm {\mu }\textrm {m}$ scale length at several time steps, including QED effects.

Recent studies have shown that QED effects reduce the energy of laser pulses in relativistically underdense plasmas with short-scale preplasma ($1\ \mathrm {\mu }\textrm {m}$), which is in disagreement with previous studies (plasmas without QED effects) where the preplasma actually becomes more transparent with increasing laser intensity (Wang et al. Reference Wang, Gibbon, Sheng, Li and Zhang2017).

To the best of our knowledge, in previous studies with QED particle-in-cell (PIC) simulations investigating the laser–plasma interactions at the multipetawatt level, a significant preplasma (up to $7\ \mathrm {\mu }\textrm {m}$) has not been included and laser absorption mechanisms for protons and electrons with and without QED effects have not been compared at different scale lengths (Brady, Ridgers & Arber Reference Brady, Ridgers, Arber, Bell and Kirk2012; Ridgers et al. Reference Ridgers, Brady, Duclous, Kirk, Bennett, Arber, Robinson and Bell2012; Zhang et al. Reference Zhang, Ridgers and Thomas2015; Kostyukov & Nerush Reference Kostyukov and Nerush2016; Wang et al. Reference Wang, Gibbon, Sheng, Li and Zhang2017; Levy et al. Reference Levy, Blackburn, Ratan, Sadler, Ridgers, Kasim, Ceurvorst, Holloway, Baring and Bell2019). We have employed the two-dimensional (2-D) EPOCH PIC code with the aforementioned QED effects (Ridgers et al. Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Blackburn, Arber and Bell2014; Arber et al. Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers2015). In reality, the laser prepulse will create a preplasma at the front surface of the target which dramatically increases electron acceleration efficiency (Culfa et al. Reference Culfa, Tallents, Wagenaars, Ridgers, Dance, Rossall, Gray, McKenna, Brown and James2014, Reference Culfa, Tallents, Rossall, Wagenaars, Ridgers, Murphy, Dance, Gray, McKenna and Brown2016, Reference Culfa, Tallents, Korkmaz, Rossall, Wagenaars, Ridgers, Murphy, Booth, Carroll and Wilson2017). Here, we investigate the effects of preformed plasma and nonlinear QED processes on particle acceleration in extreme laser plasma interactions ($I \sim 10^{23}\ \mbox {W}\ \mbox {cm}^{-2}$).

2. EPOCH 2-D PIC code simulations

We used a 2-D EPOCH PIC code to simulate the laser–solid interactions with preformed plasma and QED effects on particle acceleration. The system size was $220\ \mathrm {\mu }\textrm {m} \times 30 \ \mathrm {\mu }\textrm {m}$ with a mesh resolution of $6875 \times 1000$ cells with each cell containing 100 electrons and 25 protons. The simulated laser irradiance was $5\times 10^{23}\ \mathrm {W}\ \mathrm {cm}^{{-2}}$ in a p-polarized beam with a $5\ \mathrm {\mu }\textrm {m}$ full width at half maximum (FWHM) focal spot and a laser incident angle of $0^{\circ }$. The laser wavelength and pulse duration were $0.8\ \mathrm {\mu }\textrm {m}$ and 30 fs, respectively. The solid hydrogen foil was chosen as a target and peak electron density was limited to $29n_c$ initially (Polz et al. Reference Polz, Robinson, Kalinin, Becker, Costa Fraga, Hellwing, Hornung, Keppler, Kessler and Klöpfel2019), where $n_c$ is the critical density. In the case of preplasma, an exponential density profile was assumed with a maximum scale length of $L=7\ \mathrm {\mu }\textrm {m}$ and a cutoff to zero density at 0.001 $n_c$ in front of a $1\ \mathrm {\mu }\textrm {m}$ foil. Plasma scale length $L$ can be defined as $[ -(\partial n_e/\partial x)/n_e]^{-1}$ where $n_e$ is the electron number density.

We have performed simulations with QED, without QED and only with RR (where positron generation is artificially turned off) for several scale lengths ranging between 0 and $7 \ \mathrm {\mu }\textrm {m}$. Our simulations suggest particle acceleration mechanisms change when QED or RR is implemented. For irradiances greater than $10^{22}\ \mathrm {W}\ \mathrm {cm}^{{-2}}$, we expect radiation pressure ion acceleration (RPA) (Esirkepov et al. Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Robinson et al. Reference Robinson, Zepf, Kar, Evans and Bellei2008; Tamburini et al. Reference Tamburini, Pegoraro, Piazza, Keitel and Macchi2010) to be the dominating acceleration type mechanism of protons. However, in our simulations, we observed two different acceleration mechanisms – with and without QED – which impacted the plasma transparency.

Figure 2 shows the electron and ion average kinetic energy for $L = 5\ \mathrm {\mu }\textrm {m}$ without QED effects. It can be seen that the ponderomotive force first pushes the electrons away and then the ions start gaining energy by light pressure (RPA mechanism). Figure 3 shows the electron, ion, photon and positron average kinetic energy for $L = 5\ \mathrm {\mu }\textrm {m}$ with QED effects. It can be seen that, similar to figure 2, the initial acceleration mechanism and ion behaviour is similar to cases without QED effects. The accelerated electrons cause the acceleration of ions because of a moving electrostatic potential formed by an increase in the local electron density (RITA mechanism) at the later stage of the simulations. It can be seen that, especially for the RR case, there are monoenergetic ion beams produced for longer scale length cases ($L > 3\ \mathrm {\mu }\textrm {m}$). Figure 3 shows that initially ions and electrons accelerate and behave similarly to non-QED cases; however, with increasing time, their behaviours are changing due to the RITA mechanism, and monoenergetic ions are created. In the electron-depleted region before the snowplough, a propagating electrostatic potential $\varPhi _{sp}$ that follows the snowplough is set up due to the spatial charge separation between protons and electrons. If the potential difference is large enough, then protons can be picked up and accelerated to speeds twice that of the snowplough. Figure 4 shows the $E_x$ longitudinal electric field due to charge separation which results in RITA acceleration when QED and RR is the process and the ions are moving with the longitudinal electric field. Figure 5 shows the proton longitudinal phase space on the $x$-axis for all three cases and all scale lengths at 400 fs time, where reflected RITA accelerated protons can be seen for the QED and RR-only cases. Similar to ions, we observed that electron acceleration mechanisms also have dependence on QED (or RR) effects. Figure 6 shows the longitudinal electron momentum on the $x$-axis ($P_x - x$) for all three cases and all plasma scale lengths at 400 fs time. One of the well known and proposed acceleration mechanisms when QED is implemented is $\boldsymbol {J} \times \boldsymbol {B}$ where electron oscillation frequency by the ponderomotive force is $2\omega _L$, where $\omega _L$ is the laser frequency (Wilks et al. Reference Wilks, Kruer, Tabak and Langdon1992; Jiao et al. Reference Jiao, Zhang, Yu, Zhang, Yan, He, Deng, Teng, Hong and Gu2017). It is seen in figure 6 that the electron oscillation frequency is 2$\omega _L$ ($d = \lambda /2$) which suggests that $\boldsymbol {J} \times \boldsymbol {B}$ is the main mechanism accelerating the electrons (see figure 6). However, we also noticed that without QED, there is another electron acceleration method involved in addition to the $\boldsymbol {J} \times \boldsymbol {B}$ electron acceleration mechanism. The observed momentum spikes of the electrons on the $x$-axis suggest that the ZVP acceleration mechanism is involved (see figure 6) (Savin et al. Reference Savin, Ross, Serzans, Trines, Ceurvorst, Ratan, Spiers, Bingham, Robinson and Norreys2017). In the ZVP mechanism case, electrons are not directly accelerated by the $\boldsymbol {J} \times \boldsymbol {B}$ force, instead they are confined in a ‘plasma capacitor’ and perform finite oscillations which are much higher than the frequency of the relativistic electron oscillations caused by the ponderomotive force. The spatial duration of the electron cluster is given as $\varDelta _{eb} \propto \lambda S/a_0^2$, where $S = n_e/n_ca_0$ which indicates that the fast electron clusters’ spatial duration is much shorter than the period of the laser pulse (Baeva et al. Reference Baeva, Gordienko, Robinson and Norreys2011).

Figure 2. (a) Electron and (b) proton average kinetic energies for $5\ \mathrm {\mu }\textrm {m}$ scale length at several time steps, without QED effects.

Figure 3. (a) Electron and (b) proton average kinetic energies for $5 \ \mathrm {\mu }\textrm {m}$ scale length at several time steps, including QED effects.

Figure 4. Longitudinal laser electric field ($E_x$) and proton number density for no QED, QED and only RR cases at different simulation time steps for $L = 5\ \mathrm {\mu }\textrm {m}$ scale length.

Figure 5. Proton phase space ($P_x-x$) distributions at different scale lengths for the cases of without (a) and with (b) the effects of QED and RR-only (c). Colourbar shows the weight of protons in arbitrary units.

Figure 6. Electron phase space ($P_x-x$) distributions at different scale lengths for the cases of without (a) and with (b) the effects of QED and RR-only (c). Colourbar shows the weight of electrons in arbitrary units.

3. Energy spectra of accelerated particles

Electron, proton, $\gamma$-ray and positron energy spectra were examined in order to study the effects of both QED and plasma density scale length on particle acceleration. The energy spectra of electrons and protons at different time steps with a preformed plasma scale length $L$ of $5\ \mathrm {\mu }\textrm {m}$ at the front surface are shown in figure 7 when QED effects are artificially switched off, switched on and when only RR effects are included (the laser is focused on 29$n_{c}$ plasma slab at $t=240\ \textrm {fs}$ for $L = 5\ \mathrm {\mu }\textrm {m}$ case). It is seen that the accelerated particles’ energy increased with time. Proton energy spectra shows that protons have a monoenergetic beam with increasing time and indicates that, the laser absorption mechanism changed during the simulation for the QED and RR cases. Figure 8 shows the energy spectra of electrons and protons with varied preformed plasma – extracted at the end of the simulation time ($t = 500\ \textrm {fs}$) – for when QED effects are artificially switched off, switched on and when only the RR effect is included. When there is no preplasma ($L=0\ \mathrm {\mu }\textrm {m}$), electron and ion energies reach a similar maximum energy for all cases. While electrons have continuous energy spectra in the cases of QED and RR-only, a peak is observed in the electron energy spectrum at around 2 GeV when QED is not included. However, increasing scale length ($L > 0\ \mathrm {\mu }\textrm {m}$) accelerates more energetic electrons for the non-QED case, and higher energetic electrons (${>}4\ \textrm {GeV}$) are cooled down when the QED effect is more dominant. For the ions, it is clear that the QED and RR have a positive effect on ion acceleration which might be because of the increase in absorbed laser energy by ions (increase $\sim$2 % when QED and RR is on) or the change in the dominant ion acceleration mechanism from RPA to RITA.

Figure 7. Electron (a–c) and proton (d–f) energy spectra for the cases of without (a,d) and with (b,e) the effects of QED and RR-only (c,f) for the $L = 5\ \mathrm {\mu }\textrm {m}$ scale length case at different time steps.

Figure 8. Electron (a–c) and proton (d–f) energy spectra for the cases of without (a,d) and with (b,e) the effects of QED and RR-only (c,f) for different scale lengths varying from 0 to $7\ \mathrm {\mu }\textrm {m}$ at the end of the simulation time.

For cases without QED effects, the electron energies are higher, while ion energies are lower when compared with RR and QED effect cases. However, QED effects cause significant cooling of very hot electrons while accelerating protons, as seen in figure 8. Results without QED effects show that increasing preplasma scale lengths ($L > 0\ \mathrm {\mu }\textrm {m}$) leads to more efficient laser absorption and, therefore, generates more energetic electrons and ions, as expected (Santala et al. Reference Santala, Zeph, Watts, Beg, Clark, Tatarakis, Krushelnick, Dangor, McCanny and Spencer2000; Peebles et al. Reference Peebles, Wei, Arefiev, McGuffey, Stephens, Theobald, Haberberger, Jarrott, Link and Chen2017). In the QED case, we see even stronger laser absorption as the preplasma scale length increases when compared with cases without QED effects, due to pair productions.

We have also performed simulations excluding pair production to determine whether RR or pair production has the stronger effect on particle acceleration. As shown in figure 8, QED and RR have a negligible effect on particle acceleration without preplasma, while RR is the key effect with preplasma. Pair production reduces the energy of accelerated ions as scale length increases. In the QED and RR cases, the energy of the accelerated electrons is reduced, while ions are accelerated to higher energies due to different dominant acceleration mechanisms caused by increased plasma opaqueness.

Comparing figures 8(b) and 8(c), one can see that hot electrons are cooled down by RR, which leads to significant absorption of the laser pulse and, therefore, a drop in the radiation pressure available to accelerate the protons by RPA (Sorbo et al. Reference Sorbo, Blackman, Capdessus, Small, Slade-Lowther, Luo, Duff, Robinson, McKenna and Sheng2018) (see figures 8d–f and 9). This is due to extremely dense (${\approx }10^{23}\ \mathrm {cm}^{{-3}}$) pair-plasma when pair production is present.

Figure 9. Radiation reaction effects on single electron dynamics are shown for classical plasma without RR effect (red line), for classical RR (blue line) and QED and for quantum corrected RR effect (black line).

In the QED-plasma regime, since the electromagnetic fields increase and RR becomes important, $\langle \gamma \rangle$ is expected to be reduced and RR helps to absorb more of the electromagnetic waves. Calculations for classical, semiclassical and QED plasmas show that $\gamma$ is reduced when QED effects are included (Zhang et al. Reference Zhang, Ridgers and Thomas2015). For the classical plasma (QED-off), $\gamma = \sqrt {1+a_0^2}$. For the classical RR, dimensionless laser amplitude is given as:

(3.1)\begin{equation} a_0^2=\tau_R^2\omega_L^2\gamma^8 + \gamma^2, \end{equation}

where $\tau _R$ is a production rate per electron per laser period and defined as $\tau _R = 0.06(I_{24}\lambda ^2_{\mathrm {\mu } \textrm {m}})^{1/2} \eta ^{1/4} \exp (-8/\sqrt {3\eta })$ and $\eta = {\gamma E \sin \theta }/{E_s}$ (Bell & Kirk Reference Bell and Kirk2008). For the relativistic plasma with QED effects, $\gamma$ for the quantum corrected RR effects can be calculated from

(3.2)\begin{equation} \frac{\varGamma\gamma^2}{a_0^2 }= \sqrt{1-\frac{\gamma^2}{a_0^2}} \end{equation}

by using the definitions $\gamma = a_0 \sin \theta$ and $\varGamma \sin ^2\theta - \cos \theta = 0$, where $\varGamma = \tau _R\omega _La_0\gamma ^2$. By using (3.1) for classical RR, (3.2) for QED plasma and $\gamma = \sqrt {1+a_0^2}$ for classical plasma, we can obtain the plot given in figure 9  and can show the reduction in $\gamma$ values for QED plasmas which affects the plasma opaqueness.

Figure 10 shows the total laser energy ($E_L$) – propagated in the $x$ direction – and plasma electron number density when QED is off, on and RR-only cases at different simulation times for $L = 5\ \mathrm {\mu }\textrm {m}$ scale length. It is seen that without QED, the ponderomotive force pushes the particles away but the laser absorption is lower when compared with QED and RR cases due to RIT. In our simulations, the plasma becomes totally transparent and there is very little laser reflection ($n_{rc} = 5.86\times 10^{23} \ \mathrm {cm}^{{-3}}$). Laser absorption is around 8 % without QED and 30 % with QED. In particular, for the cases without QED, at the maximum plasma scale length of $L = 7 \ \mathrm {\mu }\textrm {m}$, the laser absorption is only ${\sim }10\,\%$ and the rest of the laser passes through the target. When QED is turned on, laser absorption increases dramatically, mainly due to RR caused by $\gamma$-ray radiation (which is around 24 % conversion efficiency for the $L = 7\ \mathrm {\mu }\textrm {m}$ case).

Figure 10. Laser energy $E_L$ and plasma number density without QED, with QED and only RR cases at different simulation time steps for $L = 5\ \mathrm {\mu }\textrm {m}$ scale length.

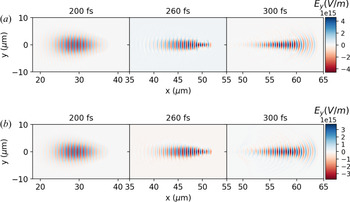
Figure 11 shows the laser $E_y$ electric field before and after laser focusing for cases without and with QED effects. It is seen that the laser is self-focused in both cases due to long plasma scale lengths of up to a few $\mathrm {\mu }\textrm {m}$ FWHM, which increases the initially defined laser intensity up to ${\sim }10^{24} \ \mathrm {W}\ \mathrm {cm}^{{-2}}$ for all cases. While laser self-focusing does have an effect on accelerating particles, because of its very similar character in all cases, we can neglect this effect in our comparisons.

Figure 11. The $E_y$ laser electric field for $5\ \mathrm {\mu }\textrm {m}$ scale length at several time steps (a) without QED and (b) with QED cases.

Figure 12 shows the energy spectra of generated photons for different preformed plasma scale lengths with QED and RR. Preformed plasma increases the energy of generated photons. Previous studies showed that there is a threshold limit for the photon energy with increasing scale length and that for 30 fs, ${\sim }10$ PW laser systems, the gamma conversion rate is at a maximum when the scale length is around $L \simeq 20\ \mathrm {\mu }\textrm {m}$ but if the laser pulse duration is longer (150 fs), optimum plasma scale length is reduced to $L \simeq 10\ \mathrm {\mu }\textrm {m}$ (Lezhnin et al. Reference Lezhnin, Sasorov, Korn and Bulanov2018). The generated photon energies are slightly higher in the QED cases due to the density of relativistic plasma and laser conversion efficiency, which is 24 % in the QED case (21 % for RR cases) when $L = 7\ \mathrm {\mu }\textrm {m}$.

Figure 12. Photon energy spectra with QED (a) and RR (b) effects for several plasma scale lengths.

The generated positron energy spectra for different plasma scale lengths are shown in figure 13. Adding a preformed plasma in next generation laser–solid interactions leads to the generation of higher energy photons and positrons (Nakamura et al. Reference Nakamura, Koga, Esirkepov, Kando, Korn and Bulanov2012). Initially, for all cases, the results are not surprising with preformed plasma, since the accelerated electrons are more energetic. In the QED cases the positrons can, just as the electrons, be accelerated in the preformed plasma to higher energies, as seen in figure 13. Laser–positron conversion efficiency increases with increasing plasma scale length up to $\sim$4 %.

Figure 13. Positron energy spectra for (a) several different time steps when $L = 3\ \mathrm {\mu }\textrm {m}$ and (b) for several plasma scale lengths at the end of the simulation ($t = 500\ \textrm {fs}$).

Figure 14 shows the conversion efficiency of intense laser pulses into energetic particles – via absorption – for no QED, QED and RR cases at different scale lengths. It is seen that QED and RR-only effects increase the plasma opacity and cause higher laser absorption (up to 40 % when $L = 7\ \mathrm {\mu }\textrm {m}$ mainly by $\gamma$-rays). We also show the laser absorption by each particle species and the total conversion efficiency as a function of plasma scale length in figure 15.

Figure 14. The conversion efficiency of intense laser pulse into energetic particles via absorption for no QED (a), QED (b) and RR (c) cases at different scale lengths.

Figure 15. Total laser absorption by the plasma and by the particles inside the plasma as a function of plasma scale length for the cases with no QED (a), QED (b) and RR (c) at different scale lengths.

Figure 15 shows the total laser absorption as a function of plasma scale length for the cases with QED, without QED and RR-only. The results in this work are consistent with those quoted in Levy et al. (Reference Levy, Blackburn, Ratan, Sadler, Ridgers, Kasim, Ceurvorst, Holloway, Baring and Bell2019), where total laser absorption efficiency is around 40 % with the laser intensities $10^{23}\ \mathrm {W}\ \mathrm {cm}^{{-2}}$. Our studies show the importance of target design, i.e. adding preformed plasma to increase the efficiency of $\gamma$-ray generation for the future laser plasma experiments.

Figure 16 shows the extracted electron temperature with and without QED effects as a function of plasma scale length. We determined the electron temperature ($kT_e$) by fitting the hot tail of electron spectra with an exponential function of the form $\exp (-E/kT_e)$. For such intensities, if the QED effect is not taken into account, the calculated temperature has a similar trend in terms of having an optimum temperature, which is at $L = 3\ \mathrm {\mu }\textrm {m}$ in this study, whereas it was measured $L \simeq 8\ \mathrm {\mu }\textrm {m}$ experimentally with lower laser irradiances (${\sim }10^{20} \ \mathrm {W}\ \mathrm {cm}^{{-2}}$) due to laser filamentation and absorption in longer preformed plasmas (Culfa et al. Reference Culfa, Tallents, Wagenaars, Ridgers, Dance, Rossall, Gray, McKenna, Brown and James2014, Reference Culfa, Tallents, Rossall, Wagenaars, Ridgers, Murphy, Dance, Gray, McKenna and Brown2016). However, the hot electron temperature $T_e$ follows a different trend when QED effects are present. Our results show that if there is no scale length, the number of generated hot electrons is lower when compared with $L > 0 \ \mathrm {\mu }\textrm {m}$ scale length cases. When there is a preformed plasma with a scale length of $L = 1\ \mathrm {\mu }\textrm {m}$, more electrons are generated but their temperatures are decreased. However, increasing scale length helps generate more electrons with higher temperatures due to increased plasma opacity (caused by QED effects). Recent studies show that if the QED effect is in the process, electron temperature ($T_e$) is proportional to normalized laser amplitude ($a_o$). Savin et al. (Reference Savin, Ross, Aboushelbaya, Mayr, Spiers, Wang and Norreys2019) claims that $T_e \propto a_o^2$ without QED and $T_e \propto a_o^5$ with QED effects. Since a small fixed amount of scale length ($L = 0.2\ \mathrm {\mu }\textrm {m}$) was used in their simulations, Savin et al. did not take into account the effect of varied preformed plasma scale length, which has a high impact on electron acceleration calculations. Our studies are in agreement with the Savin et al. (Reference Savin, Ross, Aboushelbaya, Mayr, Spiers, Wang and Norreys2019) calculated results for corresponding $a_o \sim 483$ and $L$ scale length between 0 and $1\ \mathrm {\mu }\textrm {m}$ with and without QED cases.

Figure 16. Calculated electron temperature $T_e$ as a function of plasma scale length with ($\square$, blue) and without ($\circ$, red) QED cases.

Figure 17 shows average electron and proton energies as a function of time for non-QED, QED and RR-only cases. Optimum scale length is found to be around $3\ \mathrm {\mu }\textrm {m}$ for electron and proton acceleration. Since the average photon energy is nearly the same for QED and RR cases, as seen in figure 18, it is understood that RR is the effect which accelerates charged particles to higher energies for extreme laser intensities. When there is an absence of preplasma ($L = 0\ \mathrm {\mu }\textrm {m}$), no QED, QED and RR have similar trends for ion acceleration due to the lack of photon and positron generation. Accelerated protons reach their maximum average energy at $\sim$150 fs and remain almost constant until the end of the simulation, indicating that QED and RR effects are very small.

Figure 17. Electron (a–c) and proton (d–f) average energy for the cases without (a–d) and with (b–e) the effects of QED and RR-only (c–f) as a function of time for several scale lengths.

Figure 18. Average photon energy as a function of time with QED (a) and RR-only(b) effects for several plasma scale lengths.

With increasing scale length, QED and RR effects help to accelerate more electrons with moderate energies (1–4 GeV), while in No-QED cases only a small fraction of electrons are accelerated to very high energies (>4 GeV). Although very hot electrons are cooled down with QED effects, the average energy increases due to a larger fraction of electrons being at moderate energies.

When preplasma is present, QED and RR cases show that ions are accelerated dramatically up to some point (depending on scale length) then continue to accelerate with a smaller growth until the end of the simulation due to effects of plasma opacity. Figure 18 shows that photons gain energy, then start losing their energy before a point at which the ions have a second acceleration increase which emphasizes that RR has an effect on ion heating by increasing plasma opacity. The drop in the average energy of photons indicates that the number of generated $\gamma$-rays are increasing with energies below 1 GeV.

Figure 19 shows the average positron energy generated through nonlinear QED effects during the laser plasma interactions with different preformed plasma scale lengths. When the number of positrons is increased with increasing scale length, QED effects become important and the amount of laser absorption inside the plasma starts increasing, while the energy of accelerated protons decreases (when compared with the RR-only case), as shown in figures 8, 13 and 19.

Figure 19. Average positron energy as a function of time for several scale lengths.

4. Angular distribution of ions

The angular distribution of charged particles has significant importance for future applications. Figure 20 shows the angular distribution of the accelerated ions behind the target with kinetic energies greater than 0.5 MeV for different plasma scale lengths with and without QED and RR effects. We see that increasing plasma scale length helps to accelerate more collimated ion beams with higher energies when there is no QED effect. It shows that RPA is in the process and accelerates more focused, higher energy ions without QED effects. However, once the QED (or RR) is introduced to our simulations, RPA is changing to RITA acceleration which spreads out the collimated ion beam (proton reflection). Increasing plasma scale length still helps generate more energetic ions with QED and RR cases. However, for scale lengths greater than $3\ \mathrm {\mu }\textrm {m}$, higher laser absorption is observed due to high photon and positron generation. Ions are heated by the RITA acceleration mechanism and, therefore, accelerated ions scatter around so their angular distribution is increased and they are no longer collimated. It is clear that QED or RR-only will be the more effective case for future laser–plasma experiments with higher laser intensities in next generation laser facilities. Generating a high energy focused proton beam is essential for accelerated ion applications. Our study shows that if QED or RR is in the process for future experimental studies, the optimum plasma scale length $L$ should be around $3\ \mathrm {\mu }\textrm {m}$ in order to be used in different applications.

Figure 20. Proton angular distributions at different scale lengths for the cases of without (a) and with (b) the effects of QED and RR-only (c). Colourbar shows the weight of protons in arbitrary units.

5. Conclusion

In conclusion, we investigated the effect of plasma scale length and QED processes on particle acceleration and the angular distribution of protons in laser–matter interactions for laser intensities of $5\times 10^{23}\ \textrm {W}\ \textrm {cm}^{-2}$. On simulating the case with varied preformed plasma scale length, we have found that in the case without QED, more efficient laser absorption occurs due to the preformed plasma and generated electrons and ions having more energy compared with cases without preplasma. However, in the case where QED is included, physical mechanisms change and strong laser absorption in the preplasma reverses this trend. That is, the hot electrons are cooled down due to QED effects, whereas ions have more energy due to the new dominant laser absorption mechanism (RITA) and the increase in laser energy conversion efficiency.

We have also found that the electron energy is reduced due to RR, but in the case of no scale length, QED processes (RR and pair production from the emitted photons) have no effect since the generated number of photons and positrons is minimal. For QED processes with scale lengths, pair production significantly affected the particles’ energy; the increase in the particles’ energy is mainly because of RR effects which increase plasma opacity. We have shown that more energetic $\gamma$-rays and positrons are created with increasing scale length due to high laser conversion efficiency (24 % for photons and 4 % for positrons for $L = 7\ \mathrm {\mu }\textrm {m}$) which affected our ion and electron acceleration mechanisms. The QED effect also has an important impact on ion angular distribution. We showed that if there is no QED effect, ions are collimated more, but the QED effect scatters ions due to the different laser absorption mechanism (RITA) and less collimated angular distribution is obtained. For the best collimated ion beam, $L \leqslant 3\mathrm {\mu }\ \textrm {m}$ scale length should be achieved.

Acknowledgements

We would like to thank Dr C. Ridgers for his useful comments and feedback. We also would like to thank S. North for proofreading.

Editor Victor Malka thanks the referees for their advice in evaluating this article.

Funding

The research was supported by TUBITAK (grant number 118F077). This work was in part funded by the UK EPSRC (grant numbers EP/G054950/1, EP/G056803/1, EP/G055165/1, EP/M018156/1, EP/ M022463/1).

Declaration of interests

The authors report no conflict of interest.

References

REFERENCES

Albright, B., Yin, L., Bowers, K.J., Hegelich, B.M., Flippo, K.A., Kwan, T.J.T. & Fernández, J.C. 2007 Relativistic buneman instability in the laser breakout afterburner. Phys. Plasmas 14, 094502.10.1063/1.2768933CrossRefGoogle Scholar
Arber, T., Bennett, K., Brady, C., Lawrence-Douglas, A., Ramsay, M.G., Sircombe, N.J., Gillies, P., Evans, R.G., Schmitz, H., Bell, A.R. & Ridgers, C.P. 2015 Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys. Control. Fusion 57, 113001.10.1088/0741-3335/57/11/113001CrossRefGoogle Scholar
Baeva, T., Gordienko, S., Robinson, A. & Norreys, P. 2011 Efficient laser-driven proton acceleration from a cryogenic solid hydrogen target. Phys. Plasmas 18, 056702.10.1063/1.3566068CrossRefGoogle Scholar
Bashinov, A. & Kim, A. 2013 On the electrodynamic model of ultra-relativistic laser-plasma interactions caused by radiation reaction effects. Phys. Plasmas 20, 113111.10.1063/1.4835215CrossRefGoogle Scholar
Bell, A. & Kirk, J. 2008 Possibility of prolific pair production with high-power lasers. Phys. Rev. Lett. 101, 200403.10.1103/PhysRevLett.101.200403CrossRefGoogle ScholarPubMed
Blaga, C., Xu, J., DiChiara, A., Sistrunk, E., Zhang, K., Agostini, P., Miller, T.A., DiMauro, L.F. & Lin, C.D. 2011 Imaging ultrafast molecular dynamics with laser-induced electron diffraction. Nature 483, 194–197.10.1038/nature10820CrossRefGoogle Scholar
Brady, C., Ridgers, C., Arber, T., Bell, A.R. & Kirk, J.G. 2012 Laser absorption in relativistically underdense plasmas by synchrotron radiation. Phys. Rev. Lett. 109, 245006.10.1103/PhysRevLett.109.245006CrossRefGoogle ScholarPubMed
Breit, G. & Wheeler, J.A. 1934 Collision of two light quanta. Phys. Rev. 46, 1087.10.1103/PhysRev.46.1087CrossRefGoogle Scholar
Brunel, F. 1987 Not-so-resonant, resonant absorption. Phys. Rev. Lett. 59, 52–55.10.1103/PhysRevLett.59.52CrossRefGoogle ScholarPubMed
Bulanov, S., Esirkepov, T., Hayashi, Y., Kando, M., Kiriyama, H., Koga, J.K., Kondo, K., Kotaki, H., Pirozhkov, A.S., Bulanov, S.S., et al. 2011 On the design of experiments for the study of extreme field limits in the interaction of laser with ultrarelativistic electron beam. Nucl. Instrum. Meth. Phys. Res. 660, 31–42.10.1016/j.nima.2011.09.029CrossRefGoogle Scholar
Bulanov, S.V., Wilkens, J.J., Esirkepov, T., Korn, G., Kraft, G., Kraft, S.D., Molls, M. & Khoroshkov, V.S. 2014 Laser ion acceleration for hadron therapy. Phys. Uspekhi 57, 1149–1179.10.3367/UFNe.0184.201412a.1265CrossRefGoogle Scholar
Culfa, O., Tallents, G.J., Korkmaz, M., Rossall, A.K., Wagenaars, E., Ridgers, C.P., Murphy, C.D., Booth, N., Carroll, D.C., Wilson, L.A., et al. 2017 Plasma scale length effects on protons generated in ultra intense laser plasmas. Laser Particle Beams 35, 58–63.10.1017/S0263034616000811CrossRefGoogle Scholar
Culfa, O., Tallents, G.J., Rossall, A.K., Wagenaars, E., Ridgers, C.P., Murphy, C.D., Dance, R.J., Gray, R.J., McKenna, P., Brown, C.D.R., et al. 2016 Plasma scale-length effects on electron energy spectra in high-irradiance laser plasmas. Phys. Rev. E 93, 043201.10.1103/PhysRevE.93.043201CrossRefGoogle ScholarPubMed
Culfa, O., Tallents, G.J., Wagenaars, E., Ridgers, C.P., Dance, R.J., Rossall, A.K., Gray, R.J., McKenna, P., Brown, C.D.R., James, S.F., et al. 2014 Hot electron production in laser solid interactions with a controlled pre-pulse. Phys. Plasmas 21, 043106.10.1063/1.4870633CrossRefGoogle Scholar
Daido, H., Nishiuchi, M. & Pirozhkov, A. 2012 Review of laser-driven ion sources and their applications. Rep. Prog. Phys. 75, 056401.10.1088/0034-4885/75/5/056401CrossRefGoogle ScholarPubMed
Danson, C.N., Haefner, C., Bromage, J., Butcher, T., Chanteloup, J-C. F., Chowdhury, E.A., Galvanauskas, A., Gizzi, L.A., Hein, J., Hillier, D.I., et al. 2019 Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Engng 7, e54.10.1017/hpl.2019.36CrossRefGoogle Scholar
Dirac, P. 1938 Classical theory of radiating electrons. Proc. R. Soc. Lond. A 167, 148.Google Scholar
Duclous, R., Kirk, J. & Bell, A. 2011 Monte Carlo calculations of pair production in high-intensity laser–plasma interactions. Plasma. Phys. Control. Fusion 53, 015009.10.1088/0741-3335/53/1/015009CrossRefGoogle Scholar
Esarey, E., Schroeder, C. & Leemans, W. 2009 Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 81, 1229–1285.10.1103/RevModPhys.81.1229CrossRefGoogle Scholar
Esirkepov, T., Borghesi, M., Bulanov, S., Mourou, G. & Tajima, T. 2004 Highly efficient relativistic-ion generation in the laser-piston regime. Phys. Rev. Lett. 92, 175003.10.1103/PhysRevLett.92.175003CrossRefGoogle ScholarPubMed
Esirkepov, T., Koga, J., Sunahara, A., Morita, T., Nishikino, M., Kageyama, K., Nagatomo, H., Nishihara, K., Sagisaka, A., Kotaki, H., et al. 2014 Prepulse and amplified spontaneous emission effects on theinteraction of a petawatt class laser with thin solid targets. Nucl. Instrum. Meth. Phys. Res. 745, 150–163.10.1016/j.nima.2014.01.056CrossRefGoogle Scholar
Fedotov, A., Narozhny, N.B., Mourou, G. & Korn, G. 2010 Limitations on the attainable intensity of high power lasers. Phys. Rev. Lett. 105, 080402.10.1103/PhysRevLett.105.080402CrossRefGoogle ScholarPubMed
Gibbon, P. 2000 Short Pulse Laser Interactions with Matter. Imperial College Press.Google Scholar
Hadjisolomou, P., Tsygvintsev, I., Sasorov, P., Gasilov, V., Korn, G. & Bulanov, S. 2020 Preplasma effects on laser ion generation from thin foil targets. Phys. Plasmas 27, 013107.10.1063/1.5124457CrossRefGoogle Scholar
Jiao, J., Zhang, B., Yu, J. , Zhang, Z., Yan, Y., He, S., Deng, Z., Teng, J., Hong, W. & Gu, Y. 2017 Generating high-yield positrons and relativistic collisionless shocks by 10 PW laser. Laser Particle Beams 35, 234–240.10.1017/S0263034617000106CrossRefGoogle Scholar
Jung, D., Yin, L., Gautier, D., Wu, H.-C., Letzring, S., Dromey, B., Shah, R., Palaniyappan, S., Shimada, T., Johnson, R.P., et al. 2013 Laser-driven 1 GeV carbon ions from preheated diamond targets in the break-out afterburner regime. Phys. Plasmas 20, 083103.10.1063/1.4817287CrossRefGoogle Scholar
Kirk, J., Bell, A. & Arka, I. 2009 Pair production in counter-propagating laser beams. Plasma Phys. Control. Fusion 51, 085008.10.1088/0741-3335/51/8/085008CrossRefGoogle Scholar
Kneip, S., Nagel, S., Martins, S., Mangles, S.P.D., Bellei, C., Chekhlov, O., Clarke, R.J., Delerue, N., Divall, E.J., Doucas, G., et al. 2009 Near-GeV acceleration of electrons by a nonlinear plasma wave driven by a self-guided laser pulse. Phys. Rev. Lett. 103 (3), 035002.10.1103/PhysRevLett.103.035002CrossRefGoogle ScholarPubMed
Kostyukov, I. & Nerush, E. 2016 Production and dynamics of positrons in ultrahigh intensity laser-foil interactions. Phys. Plasmas 23, 093119.10.1063/1.4962567CrossRefGoogle Scholar
Kruer, W. 1988 The Physics of Laser Plasma Interactions. Addison-Wesley.Google Scholar
Leemans, W., Nagler, B., Gonsalves, A., Tóth, Cs., Nakamura, K., Geddes, C.G.R., Esarey, E., Schroeder, C.B. & Hooker, S.M. 2006 GeV electron beams from a centimetre-scale accelerator. Nat. Phys. 2, 696–699.10.1038/nphys418CrossRefGoogle Scholar
Lefebvre, E. & Bonnaud, G. 1995 Transparency/opacity of a solid target illuminated by an ultrahigh-intensity laser pulse. Phys. Rev. Lett. 74, 2002.10.1103/PhysRevLett.74.2002CrossRefGoogle ScholarPubMed
Levy, M., Blackburn, T., Ratan, N., Sadler, J., Ridgers, C.P., Kasim, M., Ceurvorst, L., Holloway, J., Baring, M.G., Bell, A.R., et al. 2019 QED-driven laser absorption. arXiv:1609.00389v2 [physics.plasm-ph].Google Scholar
Lezhnin, K., Sasorov, P., Korn, G. & Bulanov, S. 2018 High power gamma flare generation in multi-petawatt laser interaction with tailored targets. Phys. Plasmas 25, 123105.10.1063/1.5062849CrossRefGoogle Scholar
Macchi, A., Borghesi, M. & Passoni, M. 2013 Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 85, 751–793.10.1103/RevModPhys.85.751CrossRefGoogle Scholar
Max, C., Arons, J. & Langdon, A. 1974 Self-modulation and self-focusing of electromagnetic waves in plasmas. Phys. Rev. Lett. 33, 209–212.10.1103/PhysRevLett.33.209CrossRefGoogle Scholar
McKenna, P., Carroll, D., Lundh, O., Nürnberg, F., Markey, K., Bandyopadhyay, S., Batani, D., Evans, R.G., Jafer, R., Kar, S., et al. 2008 Effects of front surface plasma expansion on proton acceleration in ultraintense laser irradiation of foil targets. Laser Particle Beams 26 (4), 591–596.10.1017/S0263034608000657CrossRefGoogle Scholar
Mourou, G., Tajima, T. & Bulanov, S. 2006 Optics in the relativistic regime. Rev. Mod. Phys. 78, 309.10.1103/RevModPhys.78.309CrossRefGoogle Scholar
Najmudin, Z., Krushelnick, K., Tatarakis, M., Clark, E.L., Danson, C.N., Malka, V., Neely, D., Santala, M.I.K. & Dangor, A.E. 2003 The effect of high intensity laser propagation instabilities on channel formation in underdense plasmas. Phys. Plasmas 10, 438.10.1063/1.1534585CrossRefGoogle Scholar
Nakamura, T., Koga, J., Esirkepov, T.Z. , Kando, M., Korn, G. & Bulanov, S.V. 2012 High-power ${\gamma }$-ray flash generation in ultraintense laser-plasma interactions. Phys. Rev. Lett. 108, 195001.10.1103/PhysRevLett.108.195001CrossRefGoogle ScholarPubMed
Nerush, E.N., Kostyukov, I.Y., Fedotov, A.M., Narozhny, N.B., Elkina, N.V. & Ruhl, H. 2011 Laser field absorption in self-generated electron-positron pair plasma. Phys. Rev. Lett. 106, 035001.10.1103/PhysRevLett.106.035001CrossRefGoogle ScholarPubMed
Palaniyappan, S., Hegelich, B.M., Wu, H., Jung, D., Gautier, D., Yin, L., Albright, B., Johnson, R., Shimada, T., Letzring, S., et al. 2012 Dynamics of relativistic transparency and optical shuttering in expanding overdense plasmas. Nat. Phys. 8, 763–769.10.1038/nphys2390CrossRefGoogle Scholar
Peebles, J., Wei, M., Arefiev, A., McGuffey, C., Stephens, R.B., Theobald, W., Haberberger, D., Jarrott, L.C., Link, A., Chen, H., et al. 2017 Investigation of laser pulse length and pre-plasma scale length impact on hot electron generation on omega-ep. New J. Phys. 19, 023008.10.1088/1367-2630/aa5a21CrossRefGoogle Scholar
Piazza, A.D., Muller, C., Hatsagortsyan, K. & Keitel, C.H. 2012 Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 84, 1177.10.1103/RevModPhys.84.1177CrossRefGoogle Scholar
Polz, J., Robinson, A., Kalinin, A., Becker, G.A., Costa Fraga, R.A., Hellwing, M., Hornung, M., Keppler, S., Kessler, A., Klöpfel, D., et al. 2019 Efficient laser-driven proton acceleration from a cryogenic solid hydrogen target. Sci. Rep. 9, 16534.10.1038/s41598-019-52919-7CrossRefGoogle ScholarPubMed
Powell, H., King, M., Gray, R., MacLellan, D.A., Gonzalez-Izquierdo, B., Stockhausen, L.C., Hicks, G., Dover, N.P., Rusby, D.R., Carroll, D.C., et al. 2015 Proton acceleration enhanced by a plasma jet in expanding foils undergoing relativistic transparency. New J. Phys. 17, 103033.10.1088/1367-2630/17/10/103033CrossRefGoogle Scholar
Qiao, B., Kar, S., Geissler, M., Gibbon, P., Zeph, M. & Borghesi, M. 2012 Dominance of radiation pressure in ion acceleration with linearly polarized pulses at intensities of $10^{21}\ \mathrm {W}\ \mathrm {cm}^{-2}$. Phys. Rev. Lett. 108, 115002.10.1103/PhysRevLett.108.115002CrossRefGoogle Scholar
Ridgers, C., Brady, C., Duclous, R., Kirk, J.G., Bennett, K., Arber, T.D., Robinson, A.P.L. & Bell, A.R. 2012 Dense electron-positron plasmas and ultraintense ${\gamma }$ rays from laser-irradiated solids. Phys. Rev. Lett. 108, 165006.10.1103/PhysRevLett.108.165006CrossRefGoogle ScholarPubMed
Ridgers, C., Kirk, J., Duclous, R., Blackburn, T.G., Brady, C.S., Blackburn, K., Arber, T.D. & Bell, A.R. 2014 Modelling gamma-ray photon emission and pair production in high-intensity laser–matter interactions. J. Comput. Phys. 260, 273–285.10.1016/j.jcp.2013.12.007CrossRefGoogle Scholar
Robinson, A., Zepf, M., Kar, S., Evans, R.G. & Bellei, C. 2008 Radiation pressure acceleration of thin foils with circularly polarized laser pulses. New J. Phys. 10, 01302.10.1088/1367-2630/10/1/013021CrossRefGoogle Scholar
Sadighi-Bonabi, R., Yazdani, E., Cang, Y. & Hora, H. 2010 Dielectric magnifying of plasma blocks by nonlinear force acceleration with delayed electron heating. Phys. Plasmas 17, 113108.10.1063/1.3497009CrossRefGoogle Scholar
Sahai, A., Tsung, F., Tableman, A., Mori, W.B. & Katsouleas, T.C. 2013 Relativistically induced transparency acceleration of light ions by an ultrashort laser pulse interacting with a heavy-ion-plasma density gradient. Phys. Rev. E 88, 043105.10.1103/PhysRevE.88.043105CrossRefGoogle ScholarPubMed
Santala, M., Zeph, M., Watts, I., Beg, F.N., Clark, E., Tatarakis, M., Krushelnick, K., Dangor, A.E., McCanny, T., Spencer, I., et al. 2000 Effect of the plasma density scale length on the direction of fast electrons in relativistic laser-solid interactions. Phys. Rev. Lett 84, 1459–1462.10.1103/PhysRevLett.84.1459CrossRefGoogle ScholarPubMed
Savin, A., Ross, A., Aboushelbaya, R., Mayr, M.W., Spiers, B., Wang, R.H.-W. & Norreys, P.A. 2019 Energy absorption in the laser-qed regime. Sci. Rep. 9, 8956.10.1038/s41598-019-45536-xCrossRefGoogle ScholarPubMed
Savin, A., Ross, A., Serzans, M., Trines, R.M.G.M., Ceurvorst, L., Ratan, N., Spiers, B., Bingham, R., Robinson, A.P.L. & Norreys, P.A. 2017 Attosecond-scale absorption at extreme intensities. Phys. Plasmas 24, 113103.10.1063/1.4989798CrossRefGoogle Scholar
Schwinger, J. 1951 On gauge invariance and vacuum polarization. Phys. Rev. 82, 664.10.1103/PhysRev.82.664CrossRefGoogle Scholar
Shen, B., Li, Y., Yu, M.Y. & Cary, J. 2007 Bubble regime for ion acceleration in a laser-driven plasma. Phys. Rev. E 76, 055402.10.1103/PhysRevE.76.055402CrossRefGoogle Scholar
Silva, L., Marti, M., Davies, J., Fonseca, R.A., Ren, C., Tsung, F.S. & Mori, W.B. 2004 Proton shock acceleration in laser-plasma interactions. Phys. Rev. Lett. 92, 015002.10.1103/PhysRevLett.92.015002CrossRefGoogle ScholarPubMed
Sokolov, I., Naumova, N.M. & Nees, J. 2011 Numerical modeling of radiation-dominated and quantum-electrodynamically strong regimes of laser-plasma interaction. Phys. Plasmas 18, 093109.10.1063/1.3638138CrossRefGoogle Scholar
Sokolov, I., Nees, J.A., Yanovsky, V., Naumova, N.M. & Mourou, G.A. 2010 Emission and its back-reaction accompanying electron motion in relativistically strong and qed-strong pulsed laser fields. Phys. Rev. E 81, 036412.10.1103/PhysRevE.81.036412CrossRefGoogle ScholarPubMed
Sorbo, D.D., Blackman, D., Capdessus, R., Small, K., Slade-Lowther, C., Luo, W., Duff, M.J., Robinson, A.P.L., McKenna, P., Sheng, Z.-M., et al. 2018 Efficient ion acceleration and dense electron–positron plasma creation in ultra-high intensity laser-solid interactions. New J. Phys. 20, 033014.10.1088/1367-2630/aaae61CrossRefGoogle Scholar
Steinke, S., van Tilborg, J., Benedetti, C., Geddes, C.G.R., Schroeder, C.B., Daniels, J., Swanson, K.K., Gonsalves, A.J., Nakamura, K., Matlis, N.H., et al. 2016 Multi stage coupling of independent laser-plasma accelerators. Nature 530, 190–193.10.1038/nature16525CrossRefGoogle Scholar
Tajima, T. & Dawson, J. 1979 Laser electron accelerator. Phys. Rev. Lett. 43 (4), 267–270.10.1103/PhysRevLett.43.267CrossRefGoogle Scholar
Tamburini, M., Pegoraro, F., Piazza, A.D., Keitel, C.H. & Macchi, A. 2010 Radiation reaction effects on radiation pressure acceleration. New J. Phys. 12, 123005.10.1088/1367-2630/12/12/123005CrossRefGoogle Scholar
Vshivkov, V., Naumova, N., Pegoraro, F. & Bulanov, S. 1998 Nonlinear electrodynamics of the interaction of ultra-intense laser pulses with a thin foil. Phys. Plasmas 5, 2727.10.1063/1.872961CrossRefGoogle Scholar
Wang, W.-M., Gibbon, P., Sheng, M., Li, Y.-T. & Zhang, J. 2017 Laser opacity in underdense preplasma of solid targets due to quantum electrodynamics effects. Phys. Rev. E 96, 013201.10.1103/PhysRevE.96.013201CrossRefGoogle ScholarPubMed
Wilks, S., Kruer, W., Tabak, M. & Langdon, A.B. 1992 Absorption of ultra-intense laser pulses. Phys. Rev. Lett. 69, 1383.10.1103/PhysRevLett.69.1383CrossRefGoogle ScholarPubMed
Wilks, S., Langdon, A., Cowan, T., Roth, M., Singh, M., Hatchett, S., Key, M.H., Pennington, D., MacKinnon, A. & Snavely, R.A. 2001 Ion acceleration by superintense laser-plasma interaction. Phys. Plasmas 8, 542.10.1063/1.1333697CrossRefGoogle Scholar
Xu, Y., Wang, J., Hora, H., Qi, X., Xing, Y., Yang, L. & Zhu, W. 2018 Plasma block acceleration based upon the interaction between double targets and an ultra-intense linearly polarized laser pulse. Phys. Plasmas 25, 043102.10.1063/1.5024032CrossRefGoogle Scholar
Yazdani, E., Sadighi-Bonabi, R., Afarideh, H., Yazdanpanah, J. & Hora, H. 2014 Enhanced laser ion acceleration with a multi-layer foam target assembly. Laser Particle Beams 32, 509–515.10.1017/S0263034614000342CrossRefGoogle Scholar
Yin, L., Albright, B., Hegelich, B., Bowers, K.J., Flippo, K.A., Kwan, T.J.T. & Fernández, J.C. 2007 Monoenergetic and Gev ion acceleration from the laser breakout afterburner using ultrathin targets. Phys. Plasmas 14, 056706.10.1063/1.2436857CrossRefGoogle Scholar
Zhang, P., Ridgers, C. & Thomas, A. 2015 The effect of nonlinear quantum electrodynamics on relativistic transparency and laser absorption in ultra-relativistic plasmas. New J. Phys. 17, 043051.10.1088/1367-2630/17/4/043051CrossRefGoogle Scholar
Zhang, X., Shen, B., Ji, L., Wang, F., Wen, M., Wang, W., Xu, J. & Yu, Y. 2010 Ultrahigh energy proton generation in sequential radiation pressure and bubble regime. Phys. Plasmas 17, 123102.Google Scholar
Figure 0

Figure 1. (a) Electron and (b) proton number densities for $5\ \mathrm {\mu }\textrm {m}$ scale length at several time steps, including QED effects.

Figure 1

Figure 2. (a) Electron and (b) proton average kinetic energies for $5\ \mathrm {\mu }\textrm {m}$ scale length at several time steps, without QED effects.

Figure 2

Figure 3. (a) Electron and (b) proton average kinetic energies for $5 \ \mathrm {\mu }\textrm {m}$ scale length at several time steps, including QED effects.

Figure 3

Figure 4. Longitudinal laser electric field ($E_x$) and proton number density for no QED, QED and only RR cases at different simulation time steps for $L = 5\ \mathrm {\mu }\textrm {m}$ scale length.

Figure 4

Figure 5. Proton phase space ($P_x-x$) distributions at different scale lengths for the cases of without (a) and with (b) the effects of QED and RR-only (c). Colourbar shows the weight of protons in arbitrary units.

Figure 5

Figure 6. Electron phase space ($P_x-x$) distributions at different scale lengths for the cases of without (a) and with (b) the effects of QED and RR-only (c). Colourbar shows the weight of electrons in arbitrary units.

Figure 6

Figure 7. Electron (a–c) and proton (d–f) energy spectra for the cases of without (a,d) and with (b,e) the effects of QED and RR-only (c,f) for the $L = 5\ \mathrm {\mu }\textrm {m}$ scale length case at different time steps.

Figure 7

Figure 8. Electron (a–c) and proton (d–f) energy spectra for the cases of without (a,d) and with (b,e) the effects of QED and RR-only (c,f) for different scale lengths varying from 0 to $7\ \mathrm {\mu }\textrm {m}$ at the end of the simulation time.

Figure 8

Figure 9. Radiation reaction effects on single electron dynamics are shown for classical plasma without RR effect (red line), for classical RR (blue line) and QED and for quantum corrected RR effect (black line).

Figure 9

Figure 10. Laser energy $E_L$ and plasma number density without QED, with QED and only RR cases at different simulation time steps for $L = 5\ \mathrm {\mu }\textrm {m}$ scale length.

Figure 10

Figure 11. The $E_y$ laser electric field for $5\ \mathrm {\mu }\textrm {m}$ scale length at several time steps (a) without QED and (b) with QED cases.

Figure 11

Figure 12. Photon energy spectra with QED (a) and RR (b) effects for several plasma scale lengths.

Figure 12

Figure 13. Positron energy spectra for (a) several different time steps when $L = 3\ \mathrm {\mu }\textrm {m}$ and (b) for several plasma scale lengths at the end of the simulation ($t = 500\ \textrm {fs}$).

Figure 13

Figure 14. The conversion efficiency of intense laser pulse into energetic particles via absorption for no QED (a), QED (b) and RR (c) cases at different scale lengths.

Figure 14

Figure 15. Total laser absorption by the plasma and by the particles inside the plasma as a function of plasma scale length for the cases with no QED (a), QED (b) and RR (c) at different scale lengths.

Figure 15

Figure 16. Calculated electron temperature $T_e$ as a function of plasma scale length with ($\square$, blue) and without ($\circ$, red) QED cases.

Figure 16

Figure 17. Electron (a–c) and proton (d–f) average energy for the cases without (a–d) and with (b–e) the effects of QED and RR-only (c–f) as a function of time for several scale lengths.

Figure 17

Figure 18. Average photon energy as a function of time with QED (a) and RR-only(b) effects for several plasma scale lengths.

Figure 18

Figure 19. Average positron energy as a function of time for several scale lengths.

Figure 19

Figure 20. Proton angular distributions at different scale lengths for the cases of without (a) and with (b) the effects of QED and RR-only (c). Colourbar shows the weight of protons in arbitrary units.