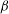1 Introduction
Space is an interesting and fascinating laboratory of nonlinear structures wherein solitary waves in plasmas are a fertile area of research. The dust grains in space plasmas can have opposite polarity – large grains are negatively charged and small grains are positively charged. The new time scales associated with the slower dust component (larger) leads to an extremely low-frequency dust wave mode called dust acoustic waves (DAW). The presence of dust charged particles is found to drastically change the properties of plasma waves. The investigation of electrostatic solitary waves in dusty plasma is an interesting recent area of research.
It is well known that in the presence of dust particles with negative charge and of micrometre or sub-micrometre size that the plasma current could change the characteristics of plasma waves in space due to of field emission. In many astrophysical environments, such as in the interstellar medium, in asteroid zones, in cometary tails (Chow, Mendis & Rosenberg Reference Chow, Mendis and Rosenberg1993; Mendis & Rosenberg Reference Mendis and Rosenberg1994), in planetary rings (Shukla & Silin Reference Shukla and Silin1992), in the Earth’s magnetosphere (Vette Reference Vette1970; Tokar & Gary Reference Tokar and Gary1984) and in the neighbourhood of stars (Verheest Reference Verheest2000; Shukla & Mamun Reference Shukla and Mamun2002) dusty plasmas are abundantly found. The interpretation of low-frequency noise enhancement observed by the Vego and Goitto space probes in the dusty region of Haley’s Comet is an interesting application. The Cassini plasma spectrometer instrument over the main A and B rings of Saturn reflects many properties of dust grains (dust density, temperature, particle size and charge). In interstellar clouds in space, much information about dusty plasmas is also found (Mendis Reference Mendis2005).
Dust acoustic (DA) waves propagating linearly as a normal mode and nonlinearly as supersonic solitons of either positive or negative electrostatic potential with inertial charged dusts and Boltzmann distributed electrons and ions in dusty plasmas have been investigated by Rao, Shukla & Yu (Reference Rao, Shukla and Yu1990). Mamun, Cairns & D’Angelo (Reference Mamun, Cairns and D’Angelo1996) have reported the existence of large-amplitude rarefactive, as well as compressive, solitons in their study of nonlinear dust acoustic waves in unmagnetized dusty plasmas with the effects of vortex-like and non-thermal ion distributions. In the magnetized three component dusty plasma Mamun (Reference Mamun1998) has briefly discussed the effects of an external magnetic field, trapped ions and free electrons in the propagation of dust acoustic solitary waves. In a similar approach, with sufficient non-thermality in the ions, following Cairns distribution (Cairns et al. Reference Cairns, Mamun, Bingham, Dendy, Boström, Nairns and Shukla1995) and sufficient negative charges on the dusts along with electrons, Verheest & Pillay (Reference Verheest and Pillay2008a) have shown the existence of both positive and negative solitary structures in some part of parameter space. Besides taking some non-thermal parameters in the non-thermal distribution of ions as variables, dust DA solitary waves are studied (Pakzad Reference Pakzad2009) in dusty plasmas with the help of the pseudo-potential method. Through the Zakharov–Kuznetsov (ZK) equation, dust acoustic solitary waves in obliquely propagating magnetized dusty plasmas with mobile negatively charged dust, two-temperature Maxwellian ions and non-inertial electrons have also been studied by Masud, Asaduzzaman & Mamun (Reference Masud, Asaduzzaman and Mamun2012). The existence of rarefactive solitons in magnetized non-thermal dusty electronegative plasmas (Kundu et al. Reference Kundu, Masud, Ashraf and Mamun2013) have been investigated in which width is shown to decrease with an increase of 
$\bar{B}_{o}$, whereas amplitude is shown to remain unaffected. The stability of low-frequency dust acoustic waves in collisional dusty plasmas of planetary rings (in the vicinity of the main Saturn rings) is considered by Yaroshenko, Verheest & Morfill (Reference Yaroshenko, Verheest and Morfill2007) with the effects of magnetized electrons, ions and neutral drag forces where dust particles are considered unmagnetized. Dust ion acoustic solitary waves and instability in multi-component magnetized dusty plasmas consisting of negative and positive ions, Boltzmann distributed hot electrons and immobile negative and positive dust charges have been studied theoretically by Haider et al. (Reference Haider, Ferdous, Duha and Mamun2014) through the ZK equation.
The relativistic and quantum effects are now being incorporated into the study of solitary waves in multi-component plasmas. Enumerable papers have already been published in the last four decades with various compositions covering many directions. Very recently, Kalita & Deka (Reference Kalita and Deka2013) have studied ion acoustic (IA) solitons in weakly relativistic plasmas based on initial streaming speeds characterizing relativistic compressive solitons in the lower limit of the speed of light (
$c$). The role of unidirected relativistic electrons with inertia in the formation of weakly relativistic ion acoustic solitons in magnetized plasmas showing the existence of subsonic and supersonic compressive solitons has also been focused on by Kalita & Choudhury (Reference Kalita and Choudhury2013). The effects of relativistic electron temperature on parametric instabilities for intense laser propagation in under-dense plasmas form the most recent investigation of a group of authors (Zhao et al. Reference Zhao, Zheng, Chen, Yu, Weng, Ren, Liu and Sheng2014) in which the concept of stimulated Raman scattering and Brilliouin scattering are considered. Different kinds of streaming instabilities of low-frequency waves due to relative motion of the plasma components are dealt with in the dusty plasma modes of Saturn’s rings. Theoretically, Rosenberg (Reference Rosenberg1993) has discussed excitation of dust acoustic wave modes by ions and electrons streaming through the dust grains. Ion and electron streaming are essentially required in instability studies for relativistic plasma waves also. The plausible relativistic effects (with streaming) of the small particles – electrons and ions are usually not considered in space plasmas where dust charges may be present. In an unmagnetized plasma, relativistic ions and Boltzmann electrons (with passive relativistic effects) are considered in the formation of solitary waves (Liu et al. Reference Liu, Wang, Li, Xiang, Yang and Liu2010, Reference Liu, Wang, Wang, Yang, Liu and Li2013). Initially, in presence of stationary dust, dust ion acoustic (DIA) solitary waves in fully relativistic dusty plasmas have been investigated by Choi et al. (Reference Choi, Lee, Kim and Lee2009) where the pseudo-potential method is considered with a numerical treatment. But ultimately they have taken 
$\partial /\partial t=0$ even though the enthalpy concept is introduced. Ironically, this fully relativistic consideration is interpreted by Verheest & Heillberg (Reference Verheest and Heillberg2009) as ‘completely erroneous and contravenes generic rules for pseudo potential treatments’. Very recently, DIA solitary waves in plasmas with weak relativistic effects in the electrons and ions have been investigated by Kalita & Das (Reference Kalita and Das2014). In this investigation, compressive DIA solitons of the same amplitude are established to exist at some critical dust charge 
$Z_{dc}$ for a critical temperature ratio 
${\it\alpha}_{c}$ (electron-to-ion temperature) of the dusty plasma. Dust acoustic waves with Cairns-like distributed ions and Boltzmann electrons without relativistic effects are also studied (Asgari, Muniandy & Wong Reference Asgari, Muniandy and Wong2013) in dusty plasmas. Hence until now, the investigation of dust acoustic waves with relativistic effects is not thorough. On the other hand, quantum effects have been incorporated in some situations of dusty plasmas.
In quantum hydrodynamical models, DA solitary waves have been studied by Ali & Shukla (Reference Ali and Shukla2006) using the Korteweg–de-Vries (KdV) equation. Further, Misra & Chowdhury (Reference Misra and Chowdhury2006) have employed the nonlinear Schrodinger equation in three species plasmas with quantum effects so as to suppress the instability. The existence of both compressive and rarefactive double layers has been shown by Moslem et al. (Reference Moslem, Shukla, Ali and Schlickeiser2007) in plasmas but with positively charged dust particles only. Very recently, the authors Kalita & Kalita (Reference Kalita and Kalita2015) have established DIA compressive and rarefactive, supersonic and subsonic solitons of interesting character in plasmas with negatively charged dust, cold ions and inertialess quantum effected electrons. A new technique was employed to derive the ‘energy integral’ through a differential equation to predict a range of the new quantum parameter 
$C_{2}$.
Besides, many laboratory experiments are performed to establish DIA waves and shock waves, inserting dust grains in the plasma, however these references are beyond the scope of the manuscript.
Moreover, Verheest & Pillay (Reference Verheest and Pillay2008a,Reference Verheest and Pillayb) have considered dust acoustic waves taking into account 
${\it\tau}=T_{i}/T_{e}$ (
$=$ temperature of ions/temperature of electrons) 
$=$ 1, i.e. 
$T_{i}=T_{e}$, to show negative solitary waves with Cairns distributed ions and electrons using different normalization techniques. This present model works in a dusty plasma where the ion temperature is comparable to (or eventually greater than, for the relativistic increase in mass of the electrons and coalescence of the number of negative charges) that of the electrons in the plasma which can be easily observed from the normalization scale factors with 
$T_{i}$ (similar to Verheest & Pillay Reference Verheest and Pillay2008a) of the non-thermal or energetic dominant ions. The existence of non-thermal or energetic ions (subjected to high temperature) follows a Cairns distribution.
We know that the fascinating space laboratory consists of non-thermal ions through the ‘Nozomi satellite’ (Futaana et al. Reference Futaana, Machida, Saito, Matsuoka and Hayakawa2001), and electrons (Cairns et al. Reference Cairns, Mamun, Bingham, Dendy, Boström, Nairns and Shukla1995) following a family of distributions such as the Cairns distribution and the Kappa distribution which are non-Maxwellian. The dust acoustic wave mode in the presence of massive dust particles in space plasmas consists of an extremely low-frequency wave. A behavioural study of the properties of these waves can be readily undertaken by space probes due to their low speeds. This is helpful to identify the character of the dust, an ingredient of any space body from which they are discharged. For complete determination of phase space (position, velocity out of any form) mapping of dust particles in the plasmas surrounding space bodies such as the Moon or Mars through ‘Spectrometer’ and ‘Imager’ have been investigated in space missions similar to ASPERA (Automatic Space Plasma Experiment with a Rotating Analyzer) on the ‘Phobos Satellite’ (Lundin et al. Reference Lundin, Zakharov, Pellinen, Borg, Hultqvist, Pissarenko, Dubinin, Barabash, Liede and Koskinen1989).
In this paper, we have investigated DA solitary waves with negatively charged mobile dust, Cairns distributed ions and weak relativistic electrons in the plasma. The paper is organized as follows – ‘Introduction’ in § 1, ‘Dynamics of the motion’ in § 2, ‘Derivation of KdV equation’ in § 3, ‘ Solitary wave solution’ in § 4, ‘Discussion’ in § 5 and at the end ‘References’ are included.
2 Dynamics of the motion
The equations of motion governing the state of this plasma model are as follows:
For negatively charged dust,
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial n_{d}}{\partial t}+\frac{\partial }{\partial x}(n_{d}v_{d})=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial v_{d}}{\partial t}+v_{d}\frac{\partial v_{d}}{\partial x}=\frac{\partial {\it\phi}}{\partial x}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{i}=(1+{\it\beta}{\it\phi}+{\it\beta}{\it\phi}^{2})\exp (-{\it\phi}),\quad \text{where }{\it\beta}=\frac{4{\it\alpha}}{3{\it\alpha}+1}. & & \displaystyle\end{eqnarray}$$For the electrons
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial t}({\it\gamma}_{e}n_{e})+\frac{\partial }{\partial x}({\it\gamma}_{e}n_{e}v_{e})=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial t}({\it\gamma}_{e}v_{e})+v_{e}\frac{\partial }{\partial x}({\it\gamma}_{e}v_{e})=\frac{1}{Q}\left(\frac{\partial {\it\phi}}{\partial x}-\frac{{\it\tau}}{{\it\gamma}_{e}n_{e}}\frac{\partial }{\partial x}({\it\gamma}_{e}n_{e})\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{where }Q=\frac{m_{e}}{m_{d}},\,{\it\gamma}_{e}=\left(1-\frac{v_{e}^{2}}{c^{2}}\right)^{-(1/2)},\,{\it\tau}=\frac{T_{e}}{T_{i}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial ^{2}{\it\phi}}{\partial x^{2}}=({\it\gamma}_{e}n_{e}+z_{d}n_{d}-n_{i}),\end{eqnarray}$$ where we consider the system of equations (2.1)–(2.6) in non-dimensional form by normalizing the densities by the equilibrium ion density 
$n_{io}$, velocities by the dust acoustic speed 
$C_{d}=(z_{d}kT_{i}/m_{d})^{1/2}$, distances by the Debye length 
${\it\lambda}_{Di}=(z_{d}kT_{i}/4{\rm\pi}n_{io}e^{2})^{1/2}$, electrostatic potential 
${\it\phi}$ by 
$z_{d}kT_{i}/e$ and time by the 
${\it\lambda}_{Di}/C_{d}$ following the procedure of Verheest & Pillay (Reference Verheest and Pillay2008a).
3 Derivation of Korteweg–de-Vries equation
In deriving the KdV equation, we introduce a new slow stretched coordinate system
$$\begin{eqnarray}{\it\eta}={\it\varepsilon}^{1/2}(x-Mt),\quad {\it\tau}={\it\varepsilon}^{3/2}t,\end{eqnarray}$$ where 
$M$ is the phase velocity of the dust acoustic wave in 
$(x,t)$ space and 
${\it\varepsilon}$ is a small dimensionless expansion parameter. We expand the flow variables asymptotically about the equilibrium state in terms of this parameter as follows:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle n_{d}=n_{do}+{\it\varepsilon}n_{d1}+{\it\varepsilon}^{2}n_{d2}+\cdots \\ \displaystyle n_{e}=n_{eo}+{\it\varepsilon}n_{e1}+{\it\varepsilon}^{2}n_{e2}+\cdots \\ \displaystyle n_{i}=1+{\it\varepsilon}n_{i1}+{\it\varepsilon}^{2}n_{i2}+\cdots \\ \displaystyle v_{d}=v_{do}+{\it\varepsilon}v_{d1}+{\it\varepsilon}^{2}v_{d2}+\cdots \\ \displaystyle v_{e}=v_{eo}+{\it\varepsilon}v_{e1}+{\it\varepsilon}^{2}v_{e2}+\cdots \\ \displaystyle {\it\phi}={\it\varepsilon}{\it\phi}_{1}+{\it\varepsilon}^{2}{\it\phi}_{2}+\cdots \,.\end{array}\right\}\end{eqnarray}$$ With the use of the transformations (2.1) and the expansions (3.4) in the normalized set (2.1)–(2.6) subject to the boundary condition 
$v_{d1}=0$, 
$v_{e1}=0$ and 
${\it\phi}_{1}=0$ as 
$|{\it\eta}|\rightarrow \infty$, we obtain from 
${\it\varepsilon}$ order equations, the following quantities:
$$\begin{eqnarray}\displaystyle & \displaystyle n_{d1}=-\frac{n_{do}}{(M-v_{do})^{2}}{\it\phi}_{1} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle n_{i1}=(1-{\it\beta}){\it\phi}_{1} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle n_{e1}=\frac{n_{eo}(c^{2}A-Mv_{eo})}{Bc^{2}[{\it\tau}-AQ(M-v_{eo})^{2}]}{\it\phi}_{1} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle v_{d1}=-\frac{{\it\phi}_{1}}{(M-v_{do})} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle v_{e1}=\frac{(M-v_{eo}){\it\phi}_{1}}{{\it\tau}-AQ(M-v_{eo})^{2}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle n_{eo}+z_{d}n_{do}-1=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Bn_{e1}+\frac{n_{eo}v_{eo}}{c^{2}}v_{e1}+z_{d}n_{d1}-n_{i1}=0, & \displaystyle\end{eqnarray}$$
$A=(1+(3v_{eo}^{2}/2c^{2}))$, 
$B=(1+(v_{eo}^{2}/2c^{2}))$. Using the values of 
$n_{e1}$, 
$n_{d1}$ and 
$n_{i1}$ in (3.9), we obtain the phase velocity equation as
$$\begin{eqnarray}\frac{n_{eo}B}{{\it\tau}-AQ(M-v_{eo})^{2}}-\frac{z_{d}n_{do}}{(M-v_{do})^{2}}-({\it\beta}-1)=0.\end{eqnarray}$$ The expression for the phase velocity 
$M$ of the wave depends on electron–dust mass density, electron–dust mass ratio 
$Q$, speed of light 
$c$, number of dust charges 
$z_{d}$, compositional parameter 
${\it\beta}$ and the relativistic factors 
$A,B$ with initial streaming 
$v_{eo}$.
Again from the 
${\it\varepsilon}^{2}$-order equations obtained from (2.1)–(2.6), with the use of the first-order quantities, we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial n_{d2}}{\partial {\it\eta}}=-\frac{2n_{do}}{(M-v_{do})^{3}}\frac{\partial {\it\phi}_{1}}{\partial {\it\tau}}+\frac{3n_{do}}{(M-v_{do})^{4}}{\it\phi}_{1}\frac{\partial {\it\phi}_{1}}{\partial {\it\eta}}-\frac{n_{do}}{(M-v_{do})^{2}}\frac{\partial {\it\phi}_{2}}{\partial {\it\eta}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial n_{i2}}{\partial {\it\eta}}={\it\phi}_{1}\frac{\partial {\it\phi}_{1}}{\partial {\it\eta}}+({\it\beta}-1)\frac{\partial {\it\phi}_{2}}{\partial {\it\eta}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial n_{e2}}{\partial {\it\eta}} & = & \displaystyle -\frac{n_{eo}[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}]}{Bc^{2}[{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}\frac{\partial {\it\phi}_{1}}{\partial {\it\tau}}-\frac{n_{eo}AQ(c^{2}A-Mv_{eo})(M-v_{eo})}{Bc^{2}[{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}\frac{\partial {\it\phi}_{1}}{\partial {\it\tau}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2n_{eo}(c^{2}A-Mv_{eo})^{2}(M-v_{eo})[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}]}{B^{3}c^{6}[{\it\tau}-AQ(M-v_{eo})^{2}]^{3}}{\it\phi}_{1}\frac{\partial {\it\phi}_{1}}{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n_{eo}(M-3v_{eo})(M-v_{eo})^{2}[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}]}{B^{2}c^{4}[{\it\tau}-AQ(M-v_{eo})^{2}]^{3}}{\it\phi}_{1}\frac{\partial {\it\phi}_{1}}{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{n_{eo}(c^{2}A-Mv_{eo})(M-v_{eo})^{2}[{\it\tau}-3QBv_{eo}(M-v_{eo})]}{B^{2}c^{4}[{\it\tau}-AQ(M-v_{eo})^{2}]^{3}}{\it\phi}_{1}\frac{\partial {\it\phi}_{1}}{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n_{eo}(c^{2}A-Mv_{eo})}{Bc^{2}[{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}{\it\phi}_{1}\frac{\partial {\it\phi}_{1}}{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2n_{eo}v_{eo}{\it\tau}(c^{2}A-Mv_{eo})^{2}(M-v_{eo})}{B^{3}c^{6}[{\it\tau}-AQ(M-v_{eo})^{2}]^{3}}{\it\phi}_{1}\frac{\partial {\it\phi}_{1}}{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n_{eo}(c^{2}A-Mv_{eo})}{Bc^{2}[{\it\tau}-AQ(M-v_{eo})^{2}]}\frac{\partial {\it\phi}_{2}}{\partial {\it\eta}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial ^{2}{\it\phi}_{1}}{\partial {\it\eta}^{2}} & = & \displaystyle Bn_{e2}+\frac{v_{eo}}{c^{2}}n_{e1}v_{e1}+\frac{n_{eo}v_{eo}}{c^{2}}v_{e2}+\frac{n_{eo}}{2c^{2}}v_{e1}^{2}+z_{d}n_{d2}-n_{i2}\nonumber\\ \displaystyle \Rightarrow \frac{\partial ^{3}{\it\phi}_{1}}{\partial {\it\eta}^{3}} & = & \displaystyle B\frac{\partial n_{e2}}{\partial {\it\eta}}+\frac{v_{eo}}{c^{2}}\frac{\partial }{\partial {\it\eta}}(n_{e1}v_{e1})+\frac{n_{eo}v_{eo}}{c^{2}}\frac{\partial }{\partial {\it\eta}}(v_{e2})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n_{eo}}{2c^{2}}\frac{\partial }{\partial {\it\eta}}(v_{e1}^{2})+z_{d}\frac{\partial n_{d2}}{\partial {\it\eta}}-\frac{\partial n_{i2}}{\partial {\it\eta}}.\end{eqnarray}$$ Putting the values of 
$\partial n_{e2}/\partial {\it\eta},\partial n_{d2}/\partial {\it\eta},\partial n_{i2}/\partial {\it\eta},n_{e1},v_{e1}$ and 
$v_{e2}$ from the above equations and with the use of relations (3.14) and (3.10), we obtain the KdV equation as
$$\begin{eqnarray}\frac{\partial {\it\phi}_{1}}{\partial {\it\tau}}+p{\it\phi}_{1}\frac{\partial {\it\phi}_{1}}{\partial {\it\eta}}+q\frac{\partial ^{3}{\it\phi}_{1}}{\partial {\it\eta}^{3}}=0,\end{eqnarray}$$ where 
$p=X/Y$ and 
$q=1/Y$, with
$$\begin{eqnarray}\displaystyle X & = & \displaystyle 1-\frac{3z_{d}n_{do}}{(M-v_{do})^{4}}+\frac{2n_{eo}QA(M-v_{eo})^{2}(c^{2}A-Mv_{eo})(c^{2}A-Mv_{eo})}{Bc^{4}[{\it\tau}-AQ(M-v_{eo})^{2}]^{3}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{n_{eo}QA(M-3v_{eo})(M-v_{eo})^{3}}{c^{2}[{\it\tau}-AQ(M-v_{eo})^{2}]^{3}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n_{eo}QA(M-v_{eo})^{3}(c^{2}A-Mv_{eo})[{\it\tau}-3QBv_{eo}(M-v_{eo})]}{c^{2}[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}][{\it\tau}-AQ(M-v_{eo})^{2}]^{3}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n_{eo}QAB(M-v_{eo})(c^{2}A-Mv_{eo})}{[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}][{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2n_{eo}QAv_{eo}{\it\tau}(M-v_{eo})^{2}(c^{2}A-Mv_{eo})^{2}}{Bc^{4}[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}][{\it\tau}-AQ(M-v_{eo})^{2}]^{3}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{n_{eo}v_{eo}(M-v_{eo})^{2}[{\it\tau}-3QBv_{eo}(M-v_{eo})]}{c^{2}[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}][{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n_{eo}Bv_{eo}}{[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}][{\it\tau}-AQ(M-v_{eo})^{2}]}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2n_{eo}v_{eo}^{2}(c^{2}A-Mv_{eo})(M-v_{eo})}{Bc^{4}[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}][{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2n_{eo}v_{eo}(c^{2}A-Mv_{eo})(M-v_{eo})}{Bc^{4}[{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}-\frac{n_{eo}(M-v_{eo})^{2}}{c^{2}[{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y & = & \displaystyle \frac{n_{eo}QAB(M-v_{eo})}{[{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}+\frac{n_{eo}Q^{2}A^{2}B(M-v_{eo})^{2}(c^{2}A-Mv_{eo})}{[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}][{\it\tau}-AQ(M-v_{eo})^{2}]^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{QABn_{eo}v_{eo}(M-v_{eo})}{[QABc^{2}(M-v_{eo})-v_{eo}{\it\tau}][{\it\tau}-AQ(M-v_{eo})^{2}]}+\frac{2z_{d}n_{do}}{(M-v_{do})^{3}}.\end{eqnarray}$$4 Solitary wave solution
Using the transformation 
${\it\chi}={\it\eta}-V{\it\tau}$, the KdV equation (3.15) can be simplified to give the solitary wave solution as 
${\it\phi}_{1}=(3V/p)\sec h^{2}({\it\chi}/{\it\Delta})$, where 
$V$ is the velocity with which the solitary waves travel to the right. Thus, the wave amplitude of the soliton is given by 
${\it\phi}_{o}=3V/p$ and the corresponding width by 
${\it\Delta}=2\sqrt{q/V}$.
5 Discussion
In this model of dusty plasmas, the existence of both compressive and rarefactive solitons have been established based on the relativistic effect, dust charge and the parameter 
${\it\beta}$ in terms of the non-thermal parameter 
${\it\alpha}$ involved in the Cairns-distributed ions. The relativistic consideration of the plasma appears to expand the range of 
${\it\beta}$ (in implicit form), otherwise the non-thermal parameter range of 
${\it\alpha}$ in 
${\it\beta}$. In graphical representation, we have investigated the cases for 
${\it\tau}=1$.
The increase in density of the electrons due to relativistic effects appears to serve as a booster to the growth of amplitude of compressive DA solitons up to a certain 
${\it\beta}$ (figure 1, 
$n_{eo}=0.45$, 0.5) in its lower existence regime for 
$v_{eo}=2.5$, 
$v_{do}=0.7$, 
$c=250$, 
$Q=0.81\times 10^{-4}$ and 
$Z_{d}=15$. Computation work also reflects this kind of booster growth (concave) in amplitude even for 
$n_{eo}=0.4$ when 
${\it\beta}<0.1$. But weak relativistic effects which do not cause much of a density increase (figure 2, 
$n_{eo}=0.08$, 0.07, 0.06) admit a continuous convex decrease in amplitudes of compressive solitons similar to those of figure 1 after some critical value of 
${\it\beta}$ for the whole range of 
${\it\beta}$ in this case. Finally, the soliton tends to disappear in both cases for the upper range of 
${\it\beta}$. In plasmas with small initial electron density, comparatively high-amplitude compressive solitons (figure 2) are observed to exist for small 
${\it\beta}$ which are characterized by the non-thermal parameter 
${\it\alpha}$. The relativistic effect for small 
$c$ (normalized) solely due to the rest energy 
$m_{o}c^{2}$ appears to contribute in the plasma waves which start with high 
${\it\alpha}$ to increase 
${\it\beta}$ so that the convex growth of solitons ceases to exist.
Figure 1. Amplitudes of compressive relativistic solitons versus 
${\it\beta}$ for fixed values of 
$v_{eo}=2.5$, 
$v_{do}=0.7$, 
$c=250$, 
$Q=0.81\times 10^{-4}$ and 
$Z_{d}=15$.
Figure 2. Amplitudes of compressive relativistic solitons versus 
${\it\beta}$ for fixed values of 
$v_{eo}=2.5$, 
$v_{do}=0.7$, 
$c=250$, 
$Q=0.81\times 10^{-4}$ and 
$Z_{d}=15$.
Very small-amplitude relativistic solitons are seen to exist in the smaller range of 
$Z_{d}$, compressive for 
$1<Z_{d}<3.5$ and rarefactive for 
$3.5<Z_{d}<5$ (figure 3) in plasmas with a small initial density of electrons. Comparison of figures 2 and 3 reveals that the decrease in the number of negative charges 
$Z_{d}$ of the dust dampens the soliton amplitudes. Otherwise, the relativistic effects of electrons (yielding high density) supplemented by the increase in number of negative dust charges 
$Z_{d}=15$ (figure 1) become instrumental in yielding relatively high-amplitude solitons.
Figure 3. Amplitudes of compressive and rarefactive relativistic solitons versus 
$Z_{d}$ for fixed values of 
$v_{eo}=2.5$, 
$v_{do}=0.7$, 
$c=250$, 
$Q=0.81\times 10^{-4}$ and 
${\it\beta}=0.3$.
The concave amplitude growth of compressive relativistic solitons are noticed to decay uniformly (figure 4) in the higher range of 
$Z_{d}$ for the same set of other fixed parameters 
$v_{eo}=2.5$, 
$v_{do}=0.7$, 
$Q=0.81\times 10^{-4}$, 
$c=250$ and 
${\it\beta}=0.3$. The increase of the number of dust charges 
$Z_{d}$ in the plasma, supplemented by the relativistic increase in initial electron density, force the soliton amplitudes to diminish uniformly throughout the range of 
$Z_{d}$ which approaches its higher regime (figure 4). The flux of negative charges to the dust particles, together with relativistic effects of the electrons, appear to balance the positive charges of the Cairns distributed massive ions for this nearly constant growth of amplitudes for higher 
$Z_{d}$.
Figure 4. Amplitudes of compressive relativistic solitons versus 
$Z_{d}$ for fixed values of 
$v_{eo}=2.5$, 
$v_{do}=0.7$, 
$c=250$, 
$Q=0.81\times 10^{-4}$ and 
${\it\beta}=0.3$.
The soliton profile representing smaller amplitude but bigger widths of positive potentials are reflected in figure 5 corresponding to a greater number of dust charges 
$Z_{d}=30$, 50, 70 at 
$v_{eo}=2.5$, 
$n_{eo}=0.45$ and with the other parameters as shown in the figure. Compressive relativistic solitons of gradually smaller amplitude are found, produced in this case with a proportional increase in 
$Z_{d}$.
Figure 5. Compressive soliton profiles with respect to space 
${\it\chi}$ with fixed values of 
$n_{eo}=0.45$, 
$v_{eo}=2.5$, 
$v_{do}=0.7$, 
$c=250$, 
$Q=0.81\times 10^{-4}$ and 
${\it\beta}=0.3$.
The potential depths of rarefactive relativistic solitons are seen to increase (figure 6) with 
$v_{eo}=2.25$, 3.25, 4.25 for fixed values of the other parameters as seen in figure 9. At small 
$Z_{d}=5$ an increase in the potential depths of the negative potential implies a decrease in soliton widths and an increase in amplitudes.
Figure 6. Rarefactive soliton profiles with respect to space 
${\it\chi}$ for electron streaming speeds 
$v_{eo}=2.25$, 
$v_{eo}=3.25$ and 
$v_{eo}=4.25$ with fixed values of 
$n_{eo}=0.45$, 
$Z_{d}=5$, 
$v_{do}=0.7$, 
$c=250$, 
$Q=0.81\times 10^{-4}$ and 
${\it\beta}=0.3$.
For the plasmas with small initial electron streaming 
$v_{eo}$, very-small-amplitude compressive solitons (figure 7) are generated which convexly decrease and vanish for some 
$v_{eo}$ due to the relativistic increase in electron density 
$n_{eo}=0.45$, and for all the three values of 
${\it\beta}=0.1$, 0.15, 0.2. However, the amplitudes are found to be higher for smaller 
${\it\beta}$, i.e. with the presence of a smaller number of non-thermal ions in the plasma.
Figure 7. Amplitudes of compressive relativistic solitons versus 
$v_{eo}$ for fixed values of 
$v_{do}=0.7$, 
$c=250$, 
$n_{eo}=0.45$, 
$Q=0.81\times 10^{-4}$ and 
$Z_{d}=15$.
On the contrary, an increase in the initial electron streaming 
$v_{eo}$ (
$3.5<v_{eo}<4.5$) causing little relativistic increase in density 
$n_{eo}=0.09$ and yields high-amplitude compressive solitons for higher 
${\it\beta}=0.2$ (figure 8) when the parameter 
${\it\beta}$ is within its normal range without being subjected to relativistic effects. The amplitudes of the compressive solitons grow to a maximum (for all three 
${\it\beta}$’s) for some critical 
$v_{eo}$ within the above range and come down ahead of its upper limit to admit small-amplitude relativistic solitons. The nonlinearity inherent in 
${\it\alpha}$ of 
${\it\beta}$ appears to diminish the value of 
${\it\beta}$, which causes a decrease in the amplitudes of the compressive relativistic solitons with an increase of 
$v_{eo}$ (figure 8). The relativistic streaming speed 
$v_{eo}$, we observe, is seen to play the vital role in the growth of soliton amplitudes, implicating initial changes of 
${\it\beta}$. We observe that there exists a critical value of 
$v_{eo}$ (mentioned above) for each 
${\it\beta}$ to yield the maximum amplitudes of compressive relativistic solitons.
Figure 8. Amplitudes of compressive relativistic solitons versus 
$v_{eo}$ for fixed values of 
$v_{do}=0.7$, 
$c=250$, 
$n_{eo}=0.09$, 
$Q=0.81\times 10^{-4}$ and 
$Z_{d}=15$.
Very high initial streaming of electrons 
$v_{eo}$ yielding relativistically high density 
$n_{eo}=0.45$ in the plasma appears to generate high-amplitude compressive solitons and low-amplitude rarefactive solitons for all the values of 
${\it\beta}=0.1$, 0.15, 0.2 and for fixed 
$Z_{d}=15$. A greater value of 
${\it\beta}$ is seen to produce small-amplitude solitons of both kinds (figure 9). This confirms the results of figure 7 except for the generation of very-high-amplitude compressive solitons against high electron streaming. For all 
${\it\beta}$, the amplitudes become maximum almost for the same 
$v_{eo}$ and subsequently decrease to yield rarefactive solitons of maximum amplitude for another common 
$v_{eo}$.
Figure 9. Amplitudes of compressive and rarefactive relativistic solitons versus 
$v_{eo}$ for fixed values of 
$v_{do}=0.7$, 
$c=250$, 
$n_{eo}=0.45$, 
$Q=0.81\times 10^{4}$ and 
$Z_{d}=15$.
An increase of 
$c$ may increase either the kinetic energy or the rest energy or both. Eventually, an increase in rest energy (
$m_{o}c^{2}$) due to 
$c$ is obvious, which is not based on the dynamical aspect. Otherwise, if it is to kinetically increase with 
$c$, then the temperature must increase, imbibing an implicit decrease/increase of the amplitude 
${\it\phi}_{o}$ (here) of compressive/rarefactive solitons (figure 10a,b) respectively with 
${\it\beta}$. However, the parameter 
${\it\beta}$ is related to the non-thermal parameter 
${\it\alpha}$. Evidently, the increase of 
${\it\beta}$ being independent of temperature becomes instrumental in increasing or decreasing both kinds of solitons. Hence, it is worthwhile to mention that the increase in 
${\it\beta}$ is solely due to the rest energy but not due to the kinetic energy in this relativistic plasma. We further observe that the complete linear growths of both the cases (figure 10a,b) for 
$c$ are due to this reason only. This is one of the most significant results of our investigation.
Figure 10. Amplitudes of compressive and rarefactive relativistic solitons versus 
$c$ for fixed values of 
$v_{do}=0.7$, 
$v_{eo}=2.5$, 
$n_{eo}=0.45$, 
$Q=0.81\times 10^{4}$, 
${\it\beta}=0.1$ (1), 0.15 (2), 0.2 (3), 
$Z_{d}=15$ and 
$Z_{d}=5$ respectively.
In our present case, many other behavioural changes are put forward for in-depth reflection of this investigation (figures 1–4, 9 and 10) which were not found by Asgari et al. (Reference Asgari, Muniandy and Wong2013). Ironically, our earlier paper Kalita & Das (Reference Kalita and Das2014) with pressure variations of non-isothermal ions was completely dependent on temperature and subjected to weak relativistic effects, instead of Cairns distributed ions in this case, where the non-thermal parameter 
${\it\beta}$ is independent of temperature. Further, the existence of both compressive and rarefactive solitons is shown with a disjoint critical range of 
$v_{eo}$ and that too in a much smaller range subject to higher values of 
$Z_{d}=300$. The existence of rarefactive solitons in the lower range of 
$v_{eo}<30$ (supported by small ion streaming 
$v_{io}=2$, 3, 4) and compressive solitons in the upper range 
$v_{eo}<50$ with a larger critical range (disjoint) was shown in the case of the earlier paper. Contrary to this, both rarefactive (in the upper range) and compressive (in the lower range) solitons are shown to exist in a continuous but higher range of 
$v_{eo}$ (
$70<v_{eo}<105$) in the present investigation. A similar result was reported to hold in a lower disjoint range of 
$v_{eo}$ but with a different growth pattern due to high 
$v_{io}=14{-}19$.
Higher values of 
$c$ (
$250\leqslant c\leqslant 350$) or rest energy (
$m_{o}c^{2}$) appear to produce compressive and rarefactive solitons of quite constant growth. However, in our earlier paper (Kalita & Das Reference Kalita and Das2014), KdV solitons of insignificant amplitude were observed and they were not found to exist for the higher range of 
$c>250$.
Acknowledgements
The author B.C.K. has acknowledged with gratitude the University Grants Commission (UGC), Government of India for sponsoring Professor-Emeritus Fellowship award to pursue this research. Besides, the authors are very much thankful to the referees for raising some fundamental queries for improvement of the standard of the manuscript.
