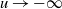1. Introduction
The Wiener-Hopf factorization for Lévy processes has become a very important tool due to its applications in several branches of applied probability, such as insurance mathematics, theory of branching processes, mathematical finance, and optimal control. For instance, when the market is modelled by a Lévy process, the positive Wiener–Hopf factor allows us to solve the optimal stopping problem corresponding to the pricing of a perpetual call option, while the negative Wiener–Hopf factor is used to solve the optimal stopping problem corresponding to the pricing of a perpetual put option. This negative Wiener–Hopf factor also arises in insurance mathematics in connection with scale functions appearing in fluctuation identities. Such identities allow us to obtain the joint distribution of the first passage time below a certain level and the position of the process at this time, which is the classical ruin problem.
For a one-dimensional Lévy process
![]() ${\mathcal{X}}=\{{\mathcal{X}}(t),t\geq0\}$
we denote
${\mathcal{X}}=\{{\mathcal{X}}(t),t\geq0\}$
we denote
![]() $S_t =\sup_{0\leq s\leq t}{\mathcal{X}}(s)$
and
$S_t =\sup_{0\leq s\leq t}{\mathcal{X}}(s)$
and
![]() $I_t =\inf_{0\leq s\leq t}{\mathcal{X}}(s)$
. The explicit distribution of
$I_t =\inf_{0\leq s\leq t}{\mathcal{X}}(s)$
. The explicit distribution of
![]() $S_t$
and
$S_t$
and
![]() $I_t$
in general is difficult to obtain but the following relation holds. Let
$I_t$
in general is difficult to obtain but the following relation holds. Let
![]() $e_q$
be an independent exponential random variable with parameter
$e_q$
be an independent exponential random variable with parameter
![]() $q>0$
. The positive and negative Wiener–Hopf factors of
$q>0$
. The positive and negative Wiener–Hopf factors of
![]() ${\mathcal{X}}$
are defined respectively as the random variables
${\mathcal{X}}$
are defined respectively as the random variables
![]() $S_{e_q} $
and
$S_{e_q} $
and
![]() $I_{e_q}$
and they satisfy the identity
$I_{e_q}$
and they satisfy the identity
where
![]() $\psi_{\mathcal{X}}(r)=-\log{\mathrm{E}}[ {\rm e}^{{\rm i} r {\mathcal{X}}(1)}]$
is the characteristic exponent of
$\psi_{\mathcal{X}}(r)=-\log{\mathrm{E}}[ {\rm e}^{{\rm i} r {\mathcal{X}}(1)}]$
is the characteristic exponent of
![]() ${\mathcal{X}}$
. Only a few results are known for the explicit distribution of both Wiener–Hopf factors for processes with positive and negative jumps; see, e.g., [Reference Asmussen, Avram and Pistorius1,Reference Borovkov3,Reference Feller6,Reference Kuznetsov9,Reference Kuznetsov10]. While the distribution of the positive Wiener–Hopf factor has been studied recently by several authors under some rather general conditions on the positive jumps (see, e.g., [Reference Kuznetsov9,Reference Kuznetsov and Peng11,Reference Lewis and Mordecki13] and the references therein), the distribution of the negative factor in these cases has not been obtained explicitly.
${\mathcal{X}}$
. Only a few results are known for the explicit distribution of both Wiener–Hopf factors for processes with positive and negative jumps; see, e.g., [Reference Asmussen, Avram and Pistorius1,Reference Borovkov3,Reference Feller6,Reference Kuznetsov9,Reference Kuznetsov10]. While the distribution of the positive Wiener–Hopf factor has been studied recently by several authors under some rather general conditions on the positive jumps (see, e.g., [Reference Kuznetsov9,Reference Kuznetsov and Peng11,Reference Lewis and Mordecki13] and the references therein), the distribution of the negative factor in these cases has not been obtained explicitly.
In this paper we consider Lévy processes
![]() ${\mathcal{X}}$
with two-sided jumps such that the positive jumps have a rational Laplace transform, and with general negative jumps. This class of Lévy processes has been studied recently in [Reference Lewis and Mordecki13], where the authors obtained the explicit distribution of the positive Wiener–Hopf factor as well as asymptotic results for the tail of
${\mathcal{X}}$
with two-sided jumps such that the positive jumps have a rational Laplace transform, and with general negative jumps. This class of Lévy processes has been studied recently in [Reference Lewis and Mordecki13], where the authors obtained the explicit distribution of the positive Wiener–Hopf factor as well as asymptotic results for the tail of
![]() $S _\infty$
. The particular case of Lévy processes with positive jumps which have phase-type distribution has been studied in [Reference Asmussen, Avram and Pistorius1], where the authors obtained the distributions of both Wiener–Hopf factors. The class of distributions having rational Laplace transforms is rich enough since it is dense in the class of nonnegative distributions. By inverting the Laplace transform of the random variable
$S _\infty$
. The particular case of Lévy processes with positive jumps which have phase-type distribution has been studied in [Reference Asmussen, Avram and Pistorius1], where the authors obtained the distributions of both Wiener–Hopf factors. The class of distributions having rational Laplace transforms is rich enough since it is dense in the class of nonnegative distributions. By inverting the Laplace transform of the random variable
![]() $-I_{e_q} $
we provide an explicit expression for the probability density of the negative Wiener–Hopf factor
$-I_{e_q} $
we provide an explicit expression for the probability density of the negative Wiener–Hopf factor
![]() $I_{e_q} $
in terms of given functions. Under additional regularity assumptions on the Lévy measure of
$I_{e_q} $
in terms of given functions. Under additional regularity assumptions on the Lévy measure of
![]() ${\mathcal{X}}$
we obtain asymptotic results as
${\mathcal{X}}$
we obtain asymptotic results as
![]() $u\to-\infty$
for the distribution function F(u) of the negative Wiener–Hopf factor
$u\to-\infty$
for the distribution function F(u) of the negative Wiener–Hopf factor
![]() $I_{e_q} $
. Our formula for the density of the negative Wiener–Hopf factor generalizes the corresponding result in [Reference Asmussen, Avram and Pistorius1].
$I_{e_q} $
. Our formula for the density of the negative Wiener–Hopf factor generalizes the corresponding result in [Reference Asmussen, Avram and Pistorius1].
The paper is organized as follows. In Section 2 we introduce basic concepts and notations and give some preliminary results. In Section 3 we obtain an expression for the Laplace transform of
![]() $-I_{e_q} $
, which we invert in order to get an explicit formula for its probability density. In Section 4 we derive asymptotic results for the distribution of the negative Wiener–Hopf factor, while some relevant examples are given in Section 5. In the final section we give the proof of the auxiliary Lemma 5.
$-I_{e_q} $
, which we invert in order to get an explicit formula for its probability density. In Section 4 we derive asymptotic results for the distribution of the negative Wiener–Hopf factor, while some relevant examples are given in Section 5. In the final section we give the proof of the auxiliary Lemma 5.
2. Preliminary results
We consider the class of two-sided jump Lévy processes
![]() ${\mathcal{X}}=\{{\mathcal{X}}(t),t\geq0 \}$
, where
${\mathcal{X}}=\{{\mathcal{X}}(t),t\geq0 \}$
, where
In the above expression,
![]() $c\geq0$
is a drift term,
$c\geq0$
is a drift term,
![]() $\mathcal{B}=\{\mathcal{B}(t),\ t\geq0\}$
is a standard Brownian motion with variance parameter 2,
$\mathcal{B}=\{\mathcal{B}(t),\ t\geq0\}$
is a standard Brownian motion with variance parameter 2,
![]() ${\mathcal{S}}=\{{\mathcal{S}}(t),\ t\geq0\}$
is a pure jump Lévy process having only positive jumps, and
${\mathcal{S}}=\{{\mathcal{S}}(t),\ t\geq0\}$
is a pure jump Lévy process having only positive jumps, and
![]() $\mathcal{Z}=\{\mathcal{Z}(t),\ t\geq0\}$
is a compound Poisson process with Lévy measure
$\mathcal{Z}=\{\mathcal{Z}(t),\ t\geq0\}$
is a compound Poisson process with Lévy measure
![]() $\lambda_1f_1(x)\,{\rm d}x$
, where
$\lambda_1f_1(x)\,{\rm d}x$
, where
![]() $\lambda_1>0$
is constant. The function
$\lambda_1>0$
is constant. The function
![]() $f_1$
is assumed to be a probability density with Laplace transform of the form
$f_1$
is assumed to be a probability density with Laplace transform of the form
where
![]() $N, n_i\in {\mathbb{N}}$
with
$N, n_i\in {\mathbb{N}}$
with
![]() $n_1+n_2+\cdots +n_N=m$
,
$n_1+n_2+\cdots +n_N=m$
,
![]() $0 < \alpha_1 < \alpha_2 < \cdots < \alpha_N$
are real numbers, and Q(r) is a polynomial of degree at most
$0 < \alpha_1 < \alpha_2 < \cdots < \alpha_N$
are real numbers, and Q(r) is a polynomial of degree at most
![]() $m-1$
. Let
$m-1$
. Let
![]() $\Psi_\mathcal{S}(r)=-\log {\mathrm{E}}[ {\rm e}^{-r {\mathcal{S}}(1)}]$
be the Laplace exponent of the process
$\Psi_\mathcal{S}(r)=-\log {\mathrm{E}}[ {\rm e}^{-r {\mathcal{S}}(1)}]$
be the Laplace exponent of the process
![]() ${\mathcal{S}}$
. It is known (see [Reference Sato15]) that
${\mathcal{S}}$
. It is known (see [Reference Sato15]) that
where h is a truncation function and
![]() $\nu_{\mathcal{S}}$
is the Lévy measure of
$\nu_{\mathcal{S}}$
is the Lévy measure of
![]() ${\mathcal{S}}$
, which satisfies
${\mathcal{S}}$
, which satisfies
We also set
![]() $\overline{\mathcal{V}}_{\mathcal{S}}(u)=\int_u^\infty\nu_{\mathcal{S}}({\rm d}x)$
. For
$\overline{\mathcal{V}}_{\mathcal{S}}(u)=\int_u^\infty\nu_{\mathcal{S}}({\rm d}x)$
. For
![]() ${\mathcal{X}}$
given in (2) we consider the function
${\mathcal{X}}$
given in (2) we consider the function
Note that, for
![]() $0\leq r < \alpha_1$
,
$0\leq r < \alpha_1$
,
![]() $\Psi_{\mathcal{X}}(r)=\log {\mathrm{E}}[ {\rm e}^{r{\mathcal{X}}(1)}]$
. When
$\Psi_{\mathcal{X}}(r)=\log {\mathrm{E}}[ {\rm e}^{r{\mathcal{X}}(1)}]$
. When
![]() ${\mathcal{S}}$
is a subordinator we replace
${\mathcal{S}}$
is a subordinator we replace
![]() $\Psi_{\mathcal{S}}(r)$
in the above expression by
$\Psi_{\mathcal{S}}(r)$
in the above expression by
![]() $G_{\mathcal{S}}(r)=\int^\infty_{0+}(1-{\rm e}^{-rx})\nu_{\mathcal{S}}({\rm d}x),$
and assume that the drift term c includes the constant
$G_{\mathcal{S}}(r)=\int^\infty_{0+}(1-{\rm e}^{-rx})\nu_{\mathcal{S}}({\rm d}x),$
and assume that the drift term c includes the constant
![]() $\int_{0+}^\infty x h(x)\nu_{\mathcal{S}}({\rm d}x)$
. In what follows we consider the sets
$\int_{0+}^\infty x h(x)\nu_{\mathcal{S}}({\rm d}x)$
. In what follows we consider the sets
![]() ${\mathbb{C}}_+=\{z\in{\mathbb{C}}\,:\, {\rm Re}(z)\geq0\}$
and
${\mathbb{C}}_+=\{z\in{\mathbb{C}}\,:\, {\rm Re}(z)\geq0\}$
and
![]() ${\mathbb{C}}_{++}=\{z\in{\mathbb{C}}\,:\,{\rm Re}(z) > 0\}$
. We consider the following cases.
${\mathbb{C}}_{++}=\{z\in{\mathbb{C}}\,:\,{\rm Re}(z) > 0\}$
. We consider the following cases.
Case A.
![]() $c=\gamma=0$
and
$c=\gamma=0$
and
![]() ${\mathcal{S}}$
is a driftless subordinator other than a compound Poisson process or
${\mathcal{S}}$
is a driftless subordinator other than a compound Poisson process or
![]() ${\mathcal{S}}$
is a compound Poisson process such that
${\mathcal{S}}$
is a compound Poisson process such that
![]() ${\mathrm{E}}[{\mathcal{X}}(1)]>0$
.
${\mathrm{E}}[{\mathcal{X}}(1)]>0$
.
Case B.
![]() $c > 0$
,
$c > 0$
,
![]() $\gamma=0$
, and
$\gamma=0$
, and
![]() ${\mathcal{S}}$
is a driftless subordinator.
${\mathcal{S}}$
is a driftless subordinator.
Case C. Any other case, except when
![]() $c=\gamma=0$
and
$c=\gamma=0$
and
![]() ${\mathcal{S}}$
is a compound Poisson process with
${\mathcal{S}}$
is a compound Poisson process with
![]() ${\mathrm{E}}[{\mathcal{X}}(1)]\leq 0$
. In this case we also assume that
${\mathrm{E}}[{\mathcal{X}}(1)]\leq 0$
. In this case we also assume that
![]() $\int_{0+}^\infty(x^2\wedge x)\nu_{\mathcal{S}}({\rm d}x)<\infty$
.
$\int_{0+}^\infty(x^2\wedge x)\nu_{\mathcal{S}}({\rm d}x)<\infty$
.
Remark 1. The assumption that
![]() $\int_{0+}^\infty(x^2\wedge x)\nu_{\mathcal{S}}({\rm d}x)<\infty$
is true, for instance, when
$\int_{0+}^\infty(x^2\wedge x)\nu_{\mathcal{S}}({\rm d}x)<\infty$
is true, for instance, when
![]() $\int_{0+}^\infty x\nu_{\mathcal{S}}({\rm d}x)<\infty$
.
$\int_{0+}^\infty x\nu_{\mathcal{S}}({\rm d}x)<\infty$
.
The following result from [Reference Lewis and Mordecki13] holds for the roots of the equation
![]() $ \Psi_{\mathcal{X}}(r)-q=0$
, which we the call generalized Cramér–Lundberg equation:
$ \Psi_{\mathcal{X}}(r)-q=0$
, which we the call generalized Cramér–Lundberg equation:
Lemma 1. Let
![]() $q\geq0$
and assume
$q\geq0$
and assume
![]() ${\mathrm{E}}[{\mathcal{X}}(1)]>0$
when
${\mathrm{E}}[{\mathcal{X}}(1)]>0$
when
![]() $q=0$
. Then:
$q=0$
. Then:
(a) In case A, the equation
![]() $ \Psi_{\mathcal{X}}(r)-q=0$
has m roots in
$ \Psi_{\mathcal{X}}(r)-q=0$
has m roots in
![]() ${\mathbb{C}}_{++}$
.
${\mathbb{C}}_{++}$
.
(b) In cases B and C, the equation
![]() $ \Psi_{\mathcal{X}}(r)-q=0$
has
$ \Psi_{\mathcal{X}}(r)-q=0$
has
![]() $m+1$
roots in
$m+1$
roots in
![]() ${\mathbb{C}}_{++}$
.
${\mathbb{C}}_{++}$
.
In all the cases above, there is exactly one real root
![]() $\beta_1(q)$
in the interval
$\beta_1(q)$
in the interval
![]() $(0,\alpha_1)$
, and it satisfies
$(0,\alpha_1)$
, and it satisfies
![]() $\lim_{q\downarrow0}\beta_1(q)=0$
. When
$\lim_{q\downarrow0}\beta_1(q)=0$
. When
![]() $q=0$
,
$q=0$
,
![]() $\beta_1(0)=0$
is a simple root of
$\beta_1(0)=0$
is a simple root of
![]() $ \Psi_{\mathcal{X}}(r)=0$
in all cases A, B, and C.
$ \Psi_{\mathcal{X}}(r)=0$
in all cases A, B, and C.
Let us assume that the equation
![]() $ \Psi_{\mathcal{X}}(r)-q=0$
has R different roots in
$ \Psi_{\mathcal{X}}(r)-q=0$
has R different roots in
![]() ${\mathbb{C}}_{++}$
, denoted by
${\mathbb{C}}_{++}$
, denoted by
![]() $\beta_1(q),\dots,\beta_R(q)$
, with respectively multiplicities
$\beta_1(q),\dots,\beta_R(q)$
, with respectively multiplicities
![]() $k_1,k_2,\dots,k_R$
, where
$k_1,k_2,\dots,k_R$
, where
![]() $\sum_{j=1}^{R}k_j=m+1- \mathbf{1}_{\{\rm case\ A\}}$
, and
$\sum_{j=1}^{R}k_j=m+1- \mathbf{1}_{\{\rm case\ A\}}$
, and
![]() $\mathbf{1}_{\{\rm case\ A\}}=1$
in case A and
$\mathbf{1}_{\{\rm case\ A\}}=1$
in case A and
![]() $\mathbf{1}_{\{\rm case\ A\}}=0$
in the other cases. We let
$\mathbf{1}_{\{\rm case\ A\}}=0$
in the other cases. We let
![]() $\beta_1(q)$
be the real root such that
$\beta_1(q)$
be the real root such that
![]() $\beta_1(q)\in[0,\alpha_1)$
, hence
$\beta_1(q)\in[0,\alpha_1)$
, hence
![]() $k_1=1$
. The case when
$k_1=1$
. The case when
![]() $q=0$
is taken in the limiting sense. When
$q=0$
is taken in the limiting sense. When
![]() ${\mathrm{E}}[{\mathcal{X}}(1)]\leq 0$
, we have
${\mathrm{E}}[{\mathcal{X}}(1)]\leq 0$
, we have
![]() ${\mathrm{P}}[ I_\infty=-\infty]=1$
, hence we have the following condition:
${\mathrm{P}}[ I_\infty=-\infty]=1$
, hence we have the following condition:
Condition 2.1. For
![]() $q=0$
, we assume that
$q=0$
, we assume that
![]() ${\mathrm{E}}[{\mathcal{X}}(1)]>0$
.
${\mathrm{E}}[{\mathcal{X}}(1)]>0$
.
For
![]() $a=0,1,\dots,m+1$
, we define the linear operator
$a=0,1,\dots,m+1$
, we define the linear operator
![]() $\mathcal{T}_{s,a}$
by the expression
$\mathcal{T}_{s,a}$
by the expression
for all measurable, nonnegative functions f and complex numbers s such that the integral above exists and is finite. If
![]() $\nu$
is a measure such that
$\nu$
is a measure such that
![]() $\int_u^\infty(y-u)^a{\rm e}^{-s(y-u)}\nu({\rm d}y)$
exists, we define, for
$\int_u^\infty(y-u)^a{\rm e}^{-s(y-u)}\nu({\rm d}y)$
exists, we define, for
![]() $a=0,1,\dots,m+1$
,
$a=0,1,\dots,m+1$
,
and denote the Laplace transforms of these two operators by
![]() $\widehat{\mathcal{T}}_{s,a} f$
and
$\widehat{\mathcal{T}}_{s,a} f$
and
![]() $\widehat{\mathcal{T}}_{s,a} \nu$
. When
$\widehat{\mathcal{T}}_{s,a} \nu$
. When
![]() $a=0$
, we obtain the Dickson–Hipp operator
$a=0$
, we obtain the Dickson–Hipp operator
![]() $T_sf$
defined in [Reference Dickson and Hipp4] and write
$T_sf$
defined in [Reference Dickson and Hipp4] and write
![]() $\mathcal{T}_{s}f(u)=\int_u^\infty {\rm e}^{-s(y-u)}f(y)\,{\rm d} y$
, with the corresponding modification when f is replaced by a measure
$\mathcal{T}_{s}f(u)=\int_u^\infty {\rm e}^{-s(y-u)}f(y)\,{\rm d} y$
, with the corresponding modification when f is replaced by a measure
![]() $\nu$
. We shall use the following elementary properties and lemma:
$\nu$
. We shall use the following elementary properties and lemma:
Lemma 2. Let f be a function (or a measure) such that
![]() $\mathcal{T}_{s,k} f(u)$
exists for every
$\mathcal{T}_{s,k} f(u)$
exists for every
![]() $s\in{\mathbb{C}}_{++}$
,
$s\in{\mathbb{C}}_{++}$
,
![]() $k\in {\mathbb{N}}\cup\{0\}$
, and
$k\in {\mathbb{N}}\cup\{0\}$
, and
![]() $u > 0$
. For each
$u > 0$
. For each
![]() $r\in {\mathbb{C}}_+$
,
$r\in {\mathbb{C}}_+$
,
![]() $s\in{\mathbb{C}}_{++}$
, and
$s\in{\mathbb{C}}_{++}$
, and
![]() $k\in{\mathbb{N}}\cup\{0\}$
,
$k\in{\mathbb{N}}\cup\{0\}$
,
![]() $\frac{\partial^k}{\partial s^k}\widehat{T}_sf(r)=({-}1)^k\widehat{\mathcal{T}}_{s,k}f(r)$
holds.
$\frac{\partial^k}{\partial s^k}\widehat{T}_sf(r)=({-}1)^k\widehat{\mathcal{T}}_{s,k}f(r)$
holds.
The following result follows from Theorem 6.16 in [Reference Kyprianou12].
Lemma 3. Let
![]() $S_{e_q}$
be the positive Wiener–Hopf factor of a Lévy process, other than a compound Poisson process, and denote by
$S_{e_q}$
be the positive Wiener–Hopf factor of a Lévy process, other than a compound Poisson process, and denote by
![]() $\kappa$
the joint Laplace exponent for the bivariate subordinator representing the ascending ladder process
$\kappa$
the joint Laplace exponent for the bivariate subordinator representing the ascending ladder process
![]() $( {\mathbb{L}}^{-1},\mathbb{H})$
, and by
$( {\mathbb{L}}^{-1},\mathbb{H})$
, and by
![]() $\Lambda ({\rm d}x,{\rm d}y)$
its bivariate Lévy measure. Then there exist
$\Lambda ({\rm d}x,{\rm d}y)$
its bivariate Lévy measure. Then there exist
![]() $b\geq 0$
such that, for
$b\geq 0$
such that, for
![]() $r\geq0$
and
$r\geq0$
and
![]() $q > 0$
,
$q > 0$
,
and
Here,
![]() $e_{\kappa(q,0)}$
is an exponential random variable with mean
$e_{\kappa(q,0)}$
is an exponential random variable with mean
![]() $1/\kappa(q,0)$
, independent of the Lévy process. We also have
$1/\kappa(q,0)$
, independent of the Lévy process. We also have
where
![]() $\widehat{\kappa}$
is the joint Laplace exponent for the bivariate subordinator representing the descending ladder process
$\widehat{\kappa}$
is the joint Laplace exponent for the bivariate subordinator representing the descending ladder process
![]() $( {\mathbb{L}}^{-1},\mathbb{\widehat{H}})$
.
$( {\mathbb{L}}^{-1},\mathbb{\widehat{H}})$
.
In order to simplify our notation we define the following constants:
 \begin{equation}
E(j,a,q)=\binom{k_j-1}{a}\frac{({-}1)^{1-k_j+a}}{(k_j-1)!}\frac{\partial^{k_j-1-a}}{\partial s^{k_j-1-a}}\Bigg[\frac{\prod_{l=1}^N(\alpha_l-s)^{n_l}(\beta_j(q)-s)^{k_j}}{\prod_{l=1}^R(\beta_l(q)-s)^{k_l}}\Bigg]_{s=\beta_j(q)},
\end{equation}
\begin{equation}
E(j,a,q)=\binom{k_j-1}{a}\frac{({-}1)^{1-k_j+a}}{(k_j-1)!}\frac{\partial^{k_j-1-a}}{\partial s^{k_j-1-a}}\Bigg[\frac{\prod_{l=1}^N(\alpha_l-s)^{n_l}(\beta_j(q)-s)^{k_j}}{\prod_{l=1}^R(\beta_l(q)-s)^{k_l}}\Bigg]_{s=\beta_j(q)},
\end{equation}
 \begin{equation}
E_*(j,a,q)=\binom{k_j-1}{a}\frac{({-}1)^{1-k_j+a}}{(k_j-1)!}\frac{\partial^{k_j-1-a}}{\partial s^{k_j-1-a}}\Bigg[\frac{\prod_{l=1}^N(\alpha_l-s)^{n_l}(\beta_j(q)-s)^{k_j}}{\prod_{l=1}^R(\beta_l(q)-s)^{k_l}}s\Bigg]_{s=\beta_j(q)},
\end{equation}
\begin{equation}
E_*(j,a,q)=\binom{k_j-1}{a}\frac{({-}1)^{1-k_j+a}}{(k_j-1)!}\frac{\partial^{k_j-1-a}}{\partial s^{k_j-1-a}}\Bigg[\frac{\prod_{l=1}^N(\alpha_l-s)^{n_l}(\beta_j(q)-s)^{k_j}}{\prod_{l=1}^R(\beta_l(q)-s)^{k_l}}s\Bigg]_{s=\beta_j(q)},
\end{equation}
for each
![]() $j=1,2,\dots,R$
. The constants E(j,0,q) and E(j,a,q) for
$j=1,2,\dots,R$
. The constants E(j,0,q) and E(j,a,q) for
![]() $a>0$
correspond, respectively, to those given in expressions (2.4) and (2.5) in [Reference Lewis and Mordecki13]. For
$a>0$
correspond, respectively, to those given in expressions (2.4) and (2.5) in [Reference Lewis and Mordecki13]. For
![]() $q\ge0$
we define the functions
$q\ge0$
we define the functions
 \begin{align*}
\ell_q(u)= \sum_{j=1}^R\sum_{a=0}^{k_j-1}E(j,a,q)\mathcal{T}_{\beta_j(q),a}\nu_{\mathcal{S}}(u),
\qquad {\mathcal{L}}_q(u)= \sum_{j=1}^R\sum_{a=0}^{k_j-1}E_*(j,a,q)\mathcal{T}_{\beta_j(q),a}\overline{\mathcal{V}}_{\mathcal{S}}(u),
\end{align*}
\begin{align*}
\ell_q(u)= \sum_{j=1}^R\sum_{a=0}^{k_j-1}E(j,a,q)\mathcal{T}_{\beta_j(q),a}\nu_{\mathcal{S}}(u),
\qquad {\mathcal{L}}_q(u)= \sum_{j=1}^R\sum_{a=0}^{k_j-1}E_*(j,a,q)\mathcal{T}_{\beta_j(q),a}\overline{\mathcal{V}}_{\mathcal{S}}(u),
\end{align*}
and the measure
 \begin{equation}
\chi_{q,{\mathcal{S}}}({\rm d}x )=\left\{\!\!
\begin{array}{llll}
\nu_{\mathcal{S}}({\rm d}x)+\ell_q(x)\,{\rm d} x&\mbox{in case A},\\[3pt]
&\\
\ell_q(x)\,{\rm d} x&\mbox{in case B},\\[3pt]
&\\
\big[\overline{\mathcal{V}}_{\mathcal{S}}(x)-{\mathcal{L}}_q(x)\big] \,{\rm d} x&\mbox{in case C}.
\end{array}
\right.
\end{equation}
\begin{equation}
\chi_{q,{\mathcal{S}}}({\rm d}x )=\left\{\!\!
\begin{array}{llll}
\nu_{\mathcal{S}}({\rm d}x)+\ell_q(x)\,{\rm d} x&\mbox{in case A},\\[3pt]
&\\
\ell_q(x)\,{\rm d} x&\mbox{in case B},\\[3pt]
&\\
\big[\overline{\mathcal{V}}_{\mathcal{S}}(x)-{\mathcal{L}}_q(x)\big] \,{\rm d} x&\mbox{in case C}.
\end{array}
\right.
\end{equation}
3. Main results
In this section we obtain an explicit expression for the probability density of the negative Wiener–Hopf factor
![]() $I _{e_q}$
of the process
$I _{e_q}$
of the process
![]() ${\mathcal{X}}$
defined in (2). The results presented for
${\mathcal{X}}$
defined in (2). The results presented for
![]() $q=0$
are all under the assumption that Condition 2.1 holds.
$q=0$
are all under the assumption that Condition 2.1 holds.
For
![]() $a>0$
let
$a>0$
let
![]() ${\mathcal{E}}_a(x)$
denote the exponential density
${\mathcal{E}}_a(x)$
denote the exponential density
![]() ${\mathcal{E}}_a(x)=a {\rm e}^{-ax}$
,
${\mathcal{E}}_a(x)=a {\rm e}^{-ax}$
,
![]() $ x>0$
, and define, for
$ x>0$
, and define, for
![]() $q\ge0$
, the function
$q\ge0$
, the function
![]() $\widehat{W}_q$
by
$\widehat{W}_q$
by
where
![]() $\kappa$
is given in Lemma 3. By Theorem 2.2 in [Reference Lewis and Mordecki13], we know that
$\kappa$
is given in Lemma 3. By Theorem 2.2 in [Reference Lewis and Mordecki13], we know that
 \begin{equation}
\kappa(q,r)=\frac{\prod_{j=1}^R(\beta_j(q)+r)^{k_j}}{\prod_{l=1}^N(\alpha_l+r)^{n_l}},
\end{equation}
\begin{equation}
\kappa(q,r)=\frac{\prod_{j=1}^R(\beta_j(q)+r)^{k_j}}{\prod_{l=1}^N(\alpha_l+r)^{n_l}},
\end{equation}
so
![]() $\kappa(q,0)=\frac{\prod_{j=1}^R\beta_j^{k_j}(q)}{\prod_{l=1}^N\alpha_l^{n_l}(q)}$
. Since
$\kappa(q,0)=\frac{\prod_{j=1}^R\beta_j^{k_j}(q)}{\prod_{l=1}^N\alpha_l^{n_l}(q)}$
. Since
![]() $\beta_1(0)=0$
, it follows that
$\beta_1(0)=0$
, it follows that
![]() $\kappa(0,0)=0$
. Hence, since from L’Hôpital’s rule
$\kappa(0,0)=0$
. Hence, since from L’Hôpital’s rule
![]() $\lim_{\beta_1(q) \to 0}{ \frac{\Psi_{{\mathcal{X}}}(\beta_{1}(q))}{\beta_{1}(q))}}={\mathrm{E}}({\mathcal{X}}(1)),$
we obtain
$\lim_{\beta_1(q) \to 0}{ \frac{\Psi_{{\mathcal{X}}}(\beta_{1}(q))}{\beta_{1}(q))}}={\mathrm{E}}({\mathcal{X}}(1)),$
we obtain
 \begin{equation}
\lim_{q\downarrow0}\frac{q}{\kappa(q,0)}=\lim_{q\downarrow0}\frac{q}{\beta_1(q)}\frac{\prod_{l=1}^N\alpha_l^{n_l}}{\prod_{j=2}^R\beta_j^{k_j}(q)}={\mathrm{E}}[{\mathcal{X}}(1)]\frac{\prod_{l=1}^N\alpha_l^{n_l}}{\prod_{j=2}^R\beta_j^{k_j}(0)}.
\end{equation}
\begin{equation}
\lim_{q\downarrow0}\frac{q}{\kappa(q,0)}=\lim_{q\downarrow0}\frac{q}{\beta_1(q)}\frac{\prod_{l=1}^N\alpha_l^{n_l}}{\prod_{j=2}^R\beta_j^{k_j}(q)}={\mathrm{E}}[{\mathcal{X}}(1)]\frac{\prod_{l=1}^N\alpha_l^{n_l}}{\prod_{j=2}^R\beta_j^{k_j}(0)}.
\end{equation}
We define, for
![]() $q>0$
,
$q>0$
,
![]() $a(q)=q/\kappa(q,0)$
and
$a(q)=q/\kappa(q,0)$
and
![]() $a(0)=\lim_{q\downarrow0}a(q)$
. Hence, we have the following result.
$a(0)=\lim_{q\downarrow0}a(q)$
. Hence, we have the following result.
Lemma 4. The Laplace transforms of
![]() $-I _{e_q}$
for
$-I _{e_q}$
for
![]() $q > 0$
and
$q > 0$
and
![]() $-I_\infty $
satisfy the following equalities for
$-I_\infty $
satisfy the following equalities for
![]() $r\geq0$
:
$r\geq0$
:
Hence, for
![]() $q\geq0$
,
$q\geq0$
,
![]() $a(q) W_q$
is the density of
$a(q) W_q$
is the density of
![]() $-I_{e_q} $
.
$-I_{e_q} $
.
Proof. Using (1), Lemma 3, and the relation
![]() $\psi_{\mathcal{X}}(s)=-\Psi_{\mathcal{X}}({\rm i} s)$
, we get
$\psi_{\mathcal{X}}(s)=-\Psi_{\mathcal{X}}({\rm i} s)$
, we get
The function on the right-hand side can be analytically extended to the negative part of the imaginary axis. Hence the result follows taking
![]() $s=-{\rm i} r$
for
$s=-{\rm i} r$
for
![]() $r\geq0$
. The case for
$r\geq0$
. The case for
![]() $q=0$
follows by taking limits when
$q=0$
follows by taking limits when
![]() $q\downarrow0$
.
$q\downarrow0$
.
In the following result we invert
![]() $a(q)\widehat{W}_q$
.
$a(q)\widehat{W}_q$
.
Theorem 1. (a) The function
![]() $\widehat{W}_q$
satisfies the equalities
$\widehat{W}_q$
satisfies the equalities
 \begin{equation}
a(q) \widehat{ W}_q(r)=\left\{
\begin{array}{ll}
\frac{\widehat{{\mathcal{E}}}_{a(q)}(r)}{1-(1-\widehat{{\mathcal{E}}}_{a(q)}(r))(1-\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r))} &\text{ in cases A and C with }\gamma=0,\\[9pt]
\frac{\frac{a(q)}{c}}{1-\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(r)} &\text{ in case B},\\[9pt]
\frac{\widehat{{\mathcal{E}}}_{a(q)\gamma^{-2}}(r)}{1+\gamma^{-2}(1-\widehat{{\mathcal{E}}}_{a(q)\gamma^{-2}}(r))\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)} &\text{ in case C with } \gamma>0.
\end{array}\right.
\end{equation}
\begin{equation}
a(q) \widehat{ W}_q(r)=\left\{
\begin{array}{ll}
\frac{\widehat{{\mathcal{E}}}_{a(q)}(r)}{1-(1-\widehat{{\mathcal{E}}}_{a(q)}(r))(1-\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r))} &\text{ in cases A and C with }\gamma=0,\\[9pt]
\frac{\frac{a(q)}{c}}{1-\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(r)} &\text{ in case B},\\[9pt]
\frac{\widehat{{\mathcal{E}}}_{a(q)\gamma^{-2}}(r)}{1+\gamma^{-2}(1-\widehat{{\mathcal{E}}}_{a(q)\gamma^{-2}}(r))\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)} &\text{ in case C with } \gamma>0.
\end{array}\right.
\end{equation}
(b) For
![]() $q\geq0$
and
$q\geq0$
and
![]() $u\ge0$
the negative Wiener–Hopf factor
$u\ge0$
the negative Wiener–Hopf factor
![]() $I_{e_q}$
has a generalized density function given by:
$I_{e_q}$
has a generalized density function given by:
 \begin{align}
&a(q) W_q(u)\nonumber \\
&=\left\{
\begin{array}{ll}
{\mathcal{E}}_{a(q)}*\sum_{n=0}^\infty\sum_{k=0}^n\binom{n}{k}({-}1)^k\big({\overline{\chi}}_{q,{\mathcal{S}}}+{\mathcal{E}}_{a(q)}-{\mathcal{E}}_{a(q)}*{\overline{\chi}}_{q,{\mathcal{S}}}\big)^{*k}(u) & \text{in cases A, C}\\[5pt]
& \text{with }\gamma=0,\\[5pt]
&\\
\frac{a(q)}{c}\delta_0(u)+\frac{a(q)}{c}\sum_{n=1}^\infty\big(\frac{1}{c}\big)^n\chi_{q,{\mathcal{S}}}^{*n}(u)&\text{in case B},\\[5pt]
&\\
{\mathcal{E}}_{a(q)\gamma^{-2}}*\sum_{n=0}^\infty\Big({-}\frac{1}{\gamma^2}\Big)^n\big({\overline{\chi}}_{q,{\mathcal{S}}}-{\mathcal{E}}_{a(q)\gamma^{-2}}*{\overline{\chi}}_{q,{\mathcal{S}}}\big)^{*n}(u)&\text{in case C}\nonumber
\\
& \text{with }\gamma>0,
\end{array}\right.
\end{align}
\begin{align}
&a(q) W_q(u)\nonumber \\
&=\left\{
\begin{array}{ll}
{\mathcal{E}}_{a(q)}*\sum_{n=0}^\infty\sum_{k=0}^n\binom{n}{k}({-}1)^k\big({\overline{\chi}}_{q,{\mathcal{S}}}+{\mathcal{E}}_{a(q)}-{\mathcal{E}}_{a(q)}*{\overline{\chi}}_{q,{\mathcal{S}}}\big)^{*k}(u) & \text{in cases A, C}\\[5pt]
& \text{with }\gamma=0,\\[5pt]
&\\
\frac{a(q)}{c}\delta_0(u)+\frac{a(q)}{c}\sum_{n=1}^\infty\big(\frac{1}{c}\big)^n\chi_{q,{\mathcal{S}}}^{*n}(u)&\text{in case B},\\[5pt]
&\\
{\mathcal{E}}_{a(q)\gamma^{-2}}*\sum_{n=0}^\infty\Big({-}\frac{1}{\gamma^2}\Big)^n\big({\overline{\chi}}_{q,{\mathcal{S}}}-{\mathcal{E}}_{a(q)\gamma^{-2}}*{\overline{\chi}}_{q,{\mathcal{S}}}\big)^{*n}(u)&\text{in case C}\nonumber
\\
& \text{with }\gamma>0,
\end{array}\right.
\end{align}
where
![]() $\delta_0$
is Dirac’s delta function.
$\delta_0$
is Dirac’s delta function.
In order to prove Theorem 1 we need the following lemma. Its proof is technical and lengthy and is deferred to Section 6.
Lemma 5. For
![]() $q\geq0$
we have
$q\geq0$
we have
 \begin{equation}
[ q- \Psi_{\mathcal{X}}(r)]( \kappa(q,-r))^{-1}=\left\{
\begin{array}{ll}
a(q)+G_\mathcal{S}(r)+\widehat{\ell}_q(0)-\widehat{\ell}_q(r) &\text{in case A},\\[5pt]
a(q)+\widehat{\ell}_q(0)-\widehat{\ell}_q(r) &\text{in case B},\\[5pt]
a(q) +\gamma^2 r-\frac{\Psi_{\mathcal{S}}(r)}{r}-\big[\widehat{{\mathcal{L}}}_q(0)-\widehat{{\mathcal{L}}}_q(r)\big] &\text{in case C}.
\end{array}\right.
\end{equation}
\begin{equation}
[ q- \Psi_{\mathcal{X}}(r)]( \kappa(q,-r))^{-1}=\left\{
\begin{array}{ll}
a(q)+G_\mathcal{S}(r)+\widehat{\ell}_q(0)-\widehat{\ell}_q(r) &\text{in case A},\\[5pt]
a(q)+\widehat{\ell}_q(0)-\widehat{\ell}_q(r) &\text{in case B},\\[5pt]
a(q) +\gamma^2 r-\frac{\Psi_{\mathcal{S}}(r)}{r}-\big[\widehat{{\mathcal{L}}}_q(0)-\widehat{{\mathcal{L}}}_q(r)\big] &\text{in case C}.
\end{array}\right.
\end{equation}
Proof of Theorem 1. Clearly, part (b) follows by inverting (11). To prove (11) we assume
![]() $q>0$
. The case
$q>0$
. The case
![]() $q=0$
follows by letting
$q=0$
follows by letting
![]() $q\downarrow0$
. From (10), (7), (8), (12), and the definition of a(q) we obtain
$q\downarrow0$
. From (10), (7), (8), (12), and the definition of a(q) we obtain
 \begin{eqnarray}\nonumber
{\mathrm{E}}\big[ {\rm e}^{-r [-I _{e_q}]}\big]\ =\ a(q) \widehat{ W}_q(r)
&=&\frac{a(q)}{a(q)+\int_{0+}^\infty(1-{\rm e}^{-rx})\chi_{q,{\mathcal{S}}}({\rm d}x )} \\
& =& \frac{q}{q+\int_{0+}^\infty(1-{\rm e}^{-rx})\kappa(q,0)\chi_{q,{\mathcal{S}}}({\rm d}x )}.
\end{eqnarray}
\begin{eqnarray}\nonumber
{\mathrm{E}}\big[ {\rm e}^{-r [-I _{e_q}]}\big]\ =\ a(q) \widehat{ W}_q(r)
&=&\frac{a(q)}{a(q)+\int_{0+}^\infty(1-{\rm e}^{-rx})\chi_{q,{\mathcal{S}}}({\rm d}x )} \\
& =& \frac{q}{q+\int_{0+}^\infty(1-{\rm e}^{-rx})\kappa(q,0)\chi_{q,{\mathcal{S}}}({\rm d}x )}.
\end{eqnarray}
To obtain (11) in case A, we use
and apply Fubini’s theorem to
![]() $\int_{0+}^\infty(1-{\rm e}^{-rx})\chi_{q,{\mathcal{S}}}({\rm d}x )$
. This yields
$\int_{0+}^\infty(1-{\rm e}^{-rx})\chi_{q,{\mathcal{S}}}({\rm d}x )$
. This yields
 \begin{eqnarray*}
a(q) \widehat{ W}_q(r)&=&\frac{a(q)}{a(q)+\int_{0+}^\infty(1-{\rm e}^{-rx})\chi_{q,{\mathcal{S}}}({\rm d}x )}
=\frac{a(q)}{a(q)+r\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)}\\
& = &\frac{\widehat{{\mathcal{E}}}_{a(q)}(r)}{1-\big(1-\widehat{{\mathcal{E}}}_{a(q)}(r)\big)\big(1-\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)\big)}.\nonumber
\end{eqnarray*}
\begin{eqnarray*}
a(q) \widehat{ W}_q(r)&=&\frac{a(q)}{a(q)+\int_{0+}^\infty(1-{\rm e}^{-rx})\chi_{q,{\mathcal{S}}}({\rm d}x )}
=\frac{a(q)}{a(q)+r\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)}\\
& = &\frac{\widehat{{\mathcal{E}}}_{a(q)}(r)}{1-\big(1-\widehat{{\mathcal{E}}}_{a(q)}(r)\big)\big(1-\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)\big)}.\nonumber
\end{eqnarray*}
Hence, (11) follows in this case. In case B, by (8) and (12) we have
 \begin{align}
a(q)\widehat{W}_q(r)&=\frac{a(q)}{a(q)+\widehat{\ell}_q(0)-\widehat{\ell}_q(r)} =\frac{\frac{a(q)}{a(q)+\widehat{\ell}_q(0)}}{1-\frac{1}{a(q)+\widehat{\ell}_q(0)}\widehat{\ell}_q(r)}.
\end{align}
\begin{align}
a(q)\widehat{W}_q(r)&=\frac{a(q)}{a(q)+\widehat{\ell}_q(0)-\widehat{\ell}_q(r)} =\frac{\frac{a(q)}{a(q)+\widehat{\ell}_q(0)}}{1-\frac{1}{a(q)+\widehat{\ell}_q(0)}\widehat{\ell}_q(r)}.
\end{align}
Due to (43) we have
![]() $a(q)+\widehat{\ell}_q(0)=c$
, and from (7) it follows that
$a(q)+\widehat{\ell}_q(0)=c$
, and from (7) it follows that
![]() $\widehat{\ell}_q(r)=\widehat{\chi}_{q,{\mathcal{S}}}(r)$
. Substituting these two equalities into (15) and using (10) gives (11).
$\widehat{\ell}_q(r)=\widehat{\chi}_{q,{\mathcal{S}}}(r)$
. Substituting these two equalities into (15) and using (10) gives (11).
We now deal with case C. Using (8) and (12), we obtain
Now we apply Fubini’s theorem to
![]() $\Psi_{\mathcal{S}}(r)/r$
to obtain, for
$\Psi_{\mathcal{S}}(r)/r$
to obtain, for
![]() $\gamma>0$
,
$\gamma>0$
,
 \begin{align}
a(q)\widehat{W}_q(r)
&=\frac{\frac{a(q)\gamma^{-2}}{a(q)\gamma^{-2}+r}}{1+\gamma^{-2}\frac{r}{a(q)\gamma^{-2}+r}\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)}
=\frac{\widehat{{\mathcal{E}}}_{a(q)\gamma^{-2}(r)}}{1+\gamma^{-2}\big(1-\widehat{{\mathcal{E}}}_{a(q)\gamma^{-2}(r)}\big)\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)},\nonumber
\end{align}
\begin{align}
a(q)\widehat{W}_q(r)
&=\frac{\frac{a(q)\gamma^{-2}}{a(q)\gamma^{-2}+r}}{1+\gamma^{-2}\frac{r}{a(q)\gamma^{-2}+r}\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)}
=\frac{\widehat{{\mathcal{E}}}_{a(q)\gamma^{-2}(r)}}{1+\gamma^{-2}\big(1-\widehat{{\mathcal{E}}}_{a(q)\gamma^{-2}(r)}\big)\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)},\nonumber
\end{align}
where we have used (14) with a(q) replaced by
![]() $a(q)\gamma^{-2}$
. When
$a(q)\gamma^{-2}$
. When
![]() $\gamma=0$
we have
$\gamma=0$
we have
 \begin{align}
a(q)\widehat{W}_q(r)
&=\frac{\frac{a(q)}{a(q)+r}}{1+\frac{r}{a(q)+r}\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)}
=\frac{\widehat{{\mathcal{E}}}_{a(q)(r)}}{1+\big(1-\widehat{{\mathcal{E}}}_{a(q)(r)}\big)\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)},\nonumber
\end{align}
\begin{align}
a(q)\widehat{W}_q(r)
&=\frac{\frac{a(q)}{a(q)+r}}{1+\frac{r}{a(q)+r}\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)}
=\frac{\widehat{{\mathcal{E}}}_{a(q)(r)}}{1+\big(1-\widehat{{\mathcal{E}}}_{a(q)(r)}\big)\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)},\nonumber
\end{align}
and we obtain (11) using (10).
Lemma 6. For all
![]() $q\ge0$
the measure
$q\ge0$
the measure
![]() $\kappa (q,0) \chi_{q,{\mathcal{S}}}$
is the Lévy measure of
$\kappa (q,0) \chi_{q,{\mathcal{S}}}$
is the Lévy measure of
![]() $-I_{e_q}$
.
$-I_{e_q}$
.
Proof. The nonnegative random variable
![]() $-I_{e_q} $
is infinitely divisible, with Laplace transform
$-I_{e_q} $
is infinitely divisible, with Laplace transform
where the measure
is the Lévy measure of
![]() $-I_{e_q}$
(see, e.g., Lemma 6.17 in [Reference Kyprianou12]). On the other hand, from the formula for Frullani’s integral, we have, for
$-I_{e_q}$
(see, e.g., Lemma 6.17 in [Reference Kyprianou12]). On the other hand, from the formula for Frullani’s integral, we have, for
![]() $\alpha,\beta>0$
and
$\alpha,\beta>0$
and
![]() $z\leq 0$
,
$z\leq 0$
,
Let
![]() $\mathcal{N}_q$
denote the subordinator with Lévy measure
$\mathcal{N}_q$
denote the subordinator with Lévy measure
![]() $\kappa(q,0)\chi_{q,{\mathcal{S}}}$
, and denote its Laplace exponent by
$\kappa(q,0)\chi_{q,{\mathcal{S}}}$
, and denote its Laplace exponent by
![]() $\Psi_q$
. From (13) we have
$\Psi_q$
. From (13) we have
![]() ${\mathrm{E}}\big[ {\rm e}^{-r({-}I_{e_q} )}\big]=
\frac{q}{q+\Psi_q(r)}$
, and hence, using (18) with
${\mathrm{E}}\big[ {\rm e}^{-r({-}I_{e_q} )}\big]=
\frac{q}{q+\Psi_q(r)}$
, and hence, using (18) with
![]() $\alpha=q$
,
$\alpha=q$
,
![]() $\beta=1$
, and
$\beta=1$
, and
![]() $z=-\Psi_q(r)$
, we obtain
$z=-\Psi_q(r)$
, we obtain
Since
![]() $1-{\rm e}^{-t\Psi_q(r)}=\int_0^\infty (1-{\rm e}^{-rx})\ {\mathrm{P}}[ \mathcal{N}_q(t)\in {\rm d}x]$
, by setting
$1-{\rm e}^{-t\Psi_q(r)}=\int_0^\infty (1-{\rm e}^{-rx})\ {\mathrm{P}}[ \mathcal{N}_q(t)\in {\rm d}x]$
, by setting
and using Fubini’s theorem in (19) it follows that
Now, from (16) we deduce that
Using (20) and (17) we obtain the result.
Remark 2. Since
![]() $-I_{e_q}=\widehat{H}(e_{\widehat{\kappa}(q,0)})$
in distribution [Reference Kyprianou12, Theorem 6.16], it follows that the measure
$-I_{e_q}=\widehat{H}(e_{\widehat{\kappa}(q,0)})$
in distribution [Reference Kyprianou12, Theorem 6.16], it follows that the measure
![]() $\kappa (q,0) \chi_{q,{\mathcal{S}}}$
is also the Lévy measure of the descending ladder-height process
$\kappa (q,0) \chi_{q,{\mathcal{S}}}$
is also the Lévy measure of the descending ladder-height process
![]() $\widehat{H}$
corresponding to
$\widehat{H}$
corresponding to
![]() ${\mathcal{X}}(t)$
, killed at the uniform rate
${\mathcal{X}}(t)$
, killed at the uniform rate
![]() $\widehat{\kappa}(q,0)$
.
$\widehat{\kappa}(q,0)$
.
4. Asymptotic behavior of the negative Wiener–Hopf factor
For
![]() $u>0$
we denote
$u>0$
we denote
![]() $F_{I_{e_q} }({-}u)={\mathrm{P}}[ I_{e_q} <-u]$
. We obtain asymptotic expressions for
$F_{I_{e_q} }({-}u)={\mathrm{P}}[ I_{e_q} <-u]$
. We obtain asymptotic expressions for
![]() $F_{I_{e_q} }({-}u)$
when
$F_{I_{e_q} }({-}u)$
when
![]() $u\to\infty$
. For this, we use the following technical result.
$u\to\infty$
. For this, we use the following technical result.
Lemma 7. The equality
 \begin{align}
r\widehat{F}_{I_{e_q}}(r)
&=\frac{\sum_{j=1}^{m+2}A_j'r^j+\Psi_{\mathcal{S}}(r)\prod_{l=1}^N\alpha_l^{n_l}+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r)-\widehat{\kappa}(q,0)\sum_{j=1}^{m+1}B_jr^j}{q\prod_{l=1}^N\alpha_l^{n_l}+\sum_{j=1}^{m+2}A_j'r^j+\Psi_{\mathcal{S}}(r)\prod_{l=1}^N\alpha_l^{n_l}+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r)}
\end{align}
\begin{align}
r\widehat{F}_{I_{e_q}}(r)
&=\frac{\sum_{j=1}^{m+2}A_j'r^j+\Psi_{\mathcal{S}}(r)\prod_{l=1}^N\alpha_l^{n_l}+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r)-\widehat{\kappa}(q,0)\sum_{j=1}^{m+1}B_jr^j}{q\prod_{l=1}^N\alpha_l^{n_l}+\sum_{j=1}^{m+2}A_j'r^j+\Psi_{\mathcal{S}}(r)\prod_{l=1}^N\alpha_l^{n_l}+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r)}
\end{align}
holds for some constants
![]() $A_j$
,
$A_j$
,
![]() $j=1,\dots,m$
,
$j=1,\dots,m$
,
![]() $B_k$
,
$B_k$
,
![]() $k=1,\dots,m+1$
, and
$k=1,\dots,m+1$
, and
![]() $A_l'$
,
$A_l'$
,
![]() $l=1,\dots,m+2$
.
$l=1,\dots,m+2$
.
Proof. Using that
![]() $r\widehat{F}_{I_{e_q}}(r)=1-\widehat{f}_{-I_{e_q}}(r)$
, where
$r\widehat{F}_{I_{e_q}}(r)=1-\widehat{f}_{-I_{e_q}}(r)$
, where
![]() $\widehat{f}_{-I_{e_q}}(r)$
denotes the Laplace transform of the density of
$\widehat{f}_{-I_{e_q}}(r)$
denotes the Laplace transform of the density of
![]() $-I_{e_q}$
, we obtain, as in (5),
$-I_{e_q}$
, we obtain, as in (5),
On the other hand, from (6) and (9) it follows that
 \begin{equation}
\widehat{\kappa}(q,r)=\prod_{l=1}^N(\alpha_l-r)^{n_l}\frac{q-\Psi_{\mathcal{X}}(r)}{\prod_{j=1}^R(\beta_j(q)-r)^{k_j}}.
\end{equation}
\begin{equation}
\widehat{\kappa}(q,r)=\prod_{l=1}^N(\alpha_l-r)^{n_l}\frac{q-\Psi_{\mathcal{X}}(r)}{\prod_{j=1}^R(\beta_j(q)-r)^{k_j}}.
\end{equation}
Since
and
can be written as the quotient of some polynomial
![]() $\mathcal{P}_1$
with degree m and
$\mathcal{P}_1$
with degree m and
![]() $\prod_{j=1}^N(\alpha_j-r)^{n_j}$
, which is also a polynomial of degree m, we have
$\prod_{j=1}^N(\alpha_j-r)^{n_j}$
, which is also a polynomial of degree m, we have
Since
![]() $\frac{Q(0)}{\prod_{j=1}^N\alpha_j^{n_j}}=1$
, we obtain that
$\frac{Q(0)}{\prod_{j=1}^N\alpha_j^{n_j}}=1$
, we obtain that
![]() $\mathcal{P}_1$
is a polynomial with constant term 0. Using
$\mathcal{P}_1$
is a polynomial with constant term 0. Using
![]() $\prod_{j=1}^N(\alpha_j-r)^{n_j}=\sum_{j=0}^mA_j r^j$
, it follows that
$\prod_{j=1}^N(\alpha_j-r)^{n_j}=\sum_{j=0}^mA_j r^j$
, it follows that
 \begin{align}
\prod_{j=1}^N(\alpha_j-r)^{n_j}(q-\Psi_{\mathcal{X}}(r))&=qA_0+q\sum_{j=1}^mA_j r^j-c\sum_{j=0}^mA_j r^{j+1}-\gamma^2\sum_{j=0}^mA_j r^{j+2}\nonumber\\
& \quad -\mathcal{P}_1(r)+A_0\Psi_{\mathcal{S}}(r)+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r)\nonumber\\
&=qA_0+\sum_{j=1}^{m+2}A_j'r^j+A_0\Psi_{\mathcal{S}}(r)+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r).
\end{align}
\begin{align}
\prod_{j=1}^N(\alpha_j-r)^{n_j}(q-\Psi_{\mathcal{X}}(r))&=qA_0+q\sum_{j=1}^mA_j r^j-c\sum_{j=0}^mA_j r^{j+1}-\gamma^2\sum_{j=0}^mA_j r^{j+2}\nonumber\\
& \quad -\mathcal{P}_1(r)+A_0\Psi_{\mathcal{S}}(r)+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r)\nonumber\\
&=qA_0+\sum_{j=1}^{m+2}A_j'r^j+A_0\Psi_{\mathcal{S}}(r)+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r).
\end{align}
Evaluating
![]() $\prod_{j=1}^N(\alpha_j-r)^{n_j}$
at
$\prod_{j=1}^N(\alpha_j-r)^{n_j}$
at
![]() $r=0$
we obtain
$r=0$
we obtain
![]() $A_0=\prod_{l=1}^N\alpha_l^{n_l}$
. Moreover, setting
$A_0=\prod_{l=1}^N\alpha_l^{n_l}$
. Moreover, setting
![]() $r=0$
in (24) gives
$r=0$
in (24) gives
 \begin{equation}
q\prod_{l=1}^N\alpha_l^{n_l}=\widehat{\kappa}(q,0)\prod_{j=1}^R\beta_j^{k_j}(q).
\end{equation}
\begin{equation}
q\prod_{l=1}^N\alpha_l^{n_l}=\widehat{\kappa}(q,0)\prod_{j=1}^R\beta_j^{k_j}(q).
\end{equation}
Hence, using that
![]() $\prod_{j=1}^R(\beta_j(q)-r)^{k_j}$
can be expressed as
$\prod_{j=1}^R(\beta_j(q)-r)^{k_j}$
can be expressed as
![]() $\sum_{j=0}^{m+1}B_jr^j$
, and substituting (26) and (25) into (23), (22) follows.
$\sum_{j=0}^{m+1}B_jr^j$
, and substituting (26) and (25) into (23), (22) follows.
In what follows we write
![]() $f\approx c g$
for any two nonnegative functions f and g on
$f\approx c g$
for any two nonnegative functions f and g on
![]() $[0,\infty)$
such that
$[0,\infty)$
such that
![]() $\lim_{u\to\infty}\frac{f(u)}{g(u)}=c$
, with
$\lim_{u\to\infty}\frac{f(u)}{g(u)}=c$
, with
![]() $c\neq 0$
. Now we can derive the first asymptotic expression for
$c\neq 0$
. Now we can derive the first asymptotic expression for
![]() $F_{I_{e_q} }$
.
$F_{I_{e_q} }$
.
Proposition 1. If
![]() $r^{-\xi}\Psi_{\mathcal{S}}(r)\to D$
as
$r^{-\xi}\Psi_{\mathcal{S}}(r)\to D$
as
![]() $r\downarrow 0$
for some
$r\downarrow 0$
for some
![]() $\xi\in(0,1)$
and some positive constant D, then
$\xi\in(0,1)$
and some positive constant D, then
Proof. Due to Theorem 4 in [6, p. 446], we only need to prove that
From (22), we have
 \begin{multline*}
r^{-\xi+1}\widehat{F}_{I_{e_q} }(r) = \\
\frac{\sum_{j=1}^{m+2}A_j'r^{j-\xi}+r^{-\xi}\Psi_{\mathcal{S}}(r)\prod_{l=1}^N\xi_l^{n_l}+\sum_{j=1}^mA_j r^{j-\xi}\Psi_{\mathcal{S}}(r)-\widehat{\kappa}(q,0)\sum_{j=1}^{m+1}B_jr^{j-\xi}}{q\prod_{l=1}^N\xi_l^{n_l}+\sum_{j=1}^{m+2}A_j'r^j+\Psi_{\mathcal{S}}(r)\prod_{l=1}^N\xi_l^{n_l}+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r)}.
\end{multline*}
\begin{multline*}
r^{-\xi+1}\widehat{F}_{I_{e_q} }(r) = \\
\frac{\sum_{j=1}^{m+2}A_j'r^{j-\xi}+r^{-\xi}\Psi_{\mathcal{S}}(r)\prod_{l=1}^N\xi_l^{n_l}+\sum_{j=1}^mA_j r^{j-\xi}\Psi_{\mathcal{S}}(r)-\widehat{\kappa}(q,0)\sum_{j=1}^{m+1}B_jr^{j-\xi}}{q\prod_{l=1}^N\xi_l^{n_l}+\sum_{j=1}^{m+2}A_j'r^j+\Psi_{\mathcal{S}}(r)\prod_{l=1}^N\xi_l^{n_l}+\sum_{j=1}^mA_j r^j\Psi_{\mathcal{S}}(r)}.
\end{multline*}
Since none of the polynomial terms in the numerator have a constant term and
![]() $\xi\in(0,1)$
, we have
$\xi\in(0,1)$
, we have
![]() ${j-\xi}>0$
; hence, letting
${j-\xi}>0$
; hence, letting
![]() $r\downarrow0$
and using the hypothesis on
$r\downarrow0$
and using the hypothesis on
![]() $r^{-\xi}\Psi_{\mathcal{S}}(r)$
, we obtain (27).
$r^{-\xi}\Psi_{\mathcal{S}}(r)$
, we obtain (27).
Let us denote by
![]() ${\overline{\chi}}_{q,{\mathcal{S}}}$
the tail of the Lévy measure
${\overline{\chi}}_{q,{\mathcal{S}}}$
the tail of the Lévy measure
![]() $\chi_{q,{\mathcal{S}}}$
.
$\chi_{q,{\mathcal{S}}}$
.
Proposition 2. In case B, if
![]() $1-\frac{{\overline{\chi}}_{q,{\mathcal{S}}}(u)}{\widehat{\chi}_{q,{\mathcal{S}}}(0)}$
is a subexponential distribution, then
$1-\frac{{\overline{\chi}}_{q,{\mathcal{S}}}(u)}{\widehat{\chi}_{q,{\mathcal{S}}}(0)}$
is a subexponential distribution, then
![]() $F_{I_{e_q} }({-}u)\approx q^{-1}\kappa(q,0){\overline{\chi}}_{q,{\mathcal{S}}}(u)$
.
$F_{I_{e_q} }({-}u)\approx q^{-1}\kappa(q,0){\overline{\chi}}_{q,{\mathcal{S}}}(u)$
.
Proof. First, we note that from (43) we get
![]() $c=a(q)+\widehat{\ell}_q(0)$
, hence
$c=a(q)+\widehat{\ell}_q(0)$
, hence
![]() $a(q)=c-\widehat{\chi}_{q,{\mathcal{S}}}(0)$
, and
$a(q)=c-\widehat{\chi}_{q,{\mathcal{S}}}(0)$
, and
 \begin{align}
\widehat{F}_{I_{e_q} }(r)
&=\frac{1}{r}\bigg(\frac{\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(0)-\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(r)}{1-\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(r)}\bigg)
=\frac{\frac{1}{c}\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)}{1-\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(r)},\nonumber
\end{align}
\begin{align}
\widehat{F}_{I_{e_q} }(r)
&=\frac{1}{r}\bigg(\frac{\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(0)-\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(r)}{1-\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(r)}\bigg)
=\frac{\frac{1}{c}\widehat{{\overline{\chi}}}_{q,{\mathcal{S}}}(r)}{1-\frac{1}{c}\widehat{\chi}_{q,{\mathcal{S}}}(r)},\nonumber
\end{align}
where in the last equality we have used that
![]() $\widehat{\overline{F}}(r)=r^{-1}(1-\widehat{f}(r))$
for a probability density f with tail
$\widehat{\overline{F}}(r)=r^{-1}(1-\widehat{f}(r))$
for a probability density f with tail
![]() $\overline{F}$
. It follows that
$\overline{F}$
. It follows that
Now we set
![]() $p=\frac{\widehat{\chi}_{q,{\mathcal{S}}}(0)}{a(q)+\widehat{\chi}_{q,{\mathcal{S}}}(0)}$
. Then
$p=\frac{\widehat{\chi}_{q,{\mathcal{S}}}(0)}{a(q)+\widehat{\chi}_{q,{\mathcal{S}}}(0)}$
. Then
![]() $p\in(0,1)$
, and from (43) it follows that
$p\in(0,1)$
, and from (43) it follows that
![]() $p=\frac{\widehat{\chi}_{q,{\mathcal{S}}}(0)}{c}$
. Using (28) we get
$p=\frac{\widehat{\chi}_{q,{\mathcal{S}}}(0)}{c}$
. Using (28) we get
Let us define the probability distribution
and denote its density by h. Since
![]() ${\overline{\chi}}_{q,{\mathcal{S}}}(u)/\widehat{\chi}_{q,{\mathcal{S}}}(0)$
is the tail of a proper distribution, due to Corollary 3 in [Reference Embrechts, Goldie and Veraverbeke5] and the assumption that
${\overline{\chi}}_{q,{\mathcal{S}}}(u)/\widehat{\chi}_{q,{\mathcal{S}}}(0)$
is the tail of a proper distribution, due to Corollary 3 in [Reference Embrechts, Goldie and Veraverbeke5] and the assumption that
![]() $1-{\overline{\chi}}_{q,{\mathcal{S}}}/\widehat{\chi}_{q,{\mathcal{S}}}(0)$
is subexponential, we obtain
$1-{\overline{\chi}}_{q,{\mathcal{S}}}/\widehat{\chi}_{q,{\mathcal{S}}}(0)$
is subexponential, we obtain
and hence H is a subexponential distribution. From Lemma 2.5.2 in [Reference Rolski, Schmidli, Schmidt and Teugels14] and (29), we have
 \begin{align}
\lim_{u\to\infty}\frac{F_{I_{e_q} }({-}u)}{{\overline{\chi}}_{q,{\mathcal{S}}}(u)/\widehat{\chi}_{q,{\mathcal{S}}}(0)}&=\lim_{u\to\infty}\frac{\frac{p}{1-p}\frac{{\overline{\chi}}_{q,{\mathcal{S}}}}{\widehat{\chi}_{q,{\mathcal{S}}}(0)}*h(u)}{{\overline{\chi}}_{q,{\mathcal{S}}}(u)/\widehat{\chi}_{q,{\mathcal{S}}}(0)}
=\frac{p}{1-p}=\widehat{\chi}_{q,{\mathcal{S}}}(0)q^{-1}\kappa(q,0),\nonumber
\end{align}
\begin{align}
\lim_{u\to\infty}\frac{F_{I_{e_q} }({-}u)}{{\overline{\chi}}_{q,{\mathcal{S}}}(u)/\widehat{\chi}_{q,{\mathcal{S}}}(0)}&=\lim_{u\to\infty}\frac{\frac{p}{1-p}\frac{{\overline{\chi}}_{q,{\mathcal{S}}}}{\widehat{\chi}_{q,{\mathcal{S}}}(0)}*h(u)}{{\overline{\chi}}_{q,{\mathcal{S}}}(u)/\widehat{\chi}_{q,{\mathcal{S}}}(0)}
=\frac{p}{1-p}=\widehat{\chi}_{q,{\mathcal{S}}}(0)q^{-1}\kappa(q,0),\nonumber
\end{align}
which implies the result.
Let us define
We recall that a probability distribution F is a subexponential distribution if
![]() $\overline{F^{*2}}(x)\approx 2\overline{F}(x)$
as
$\overline{F^{*2}}(x)\approx 2\overline{F}(x)$
as
![]() $x\to\infty$
.
$x\to\infty$
.
Proposition 3. Suppose that
![]() $\Pi$
is a subexponential distribution and set
$\Pi$
is a subexponential distribution and set
where
![]() $\nu_q$
is the Lévy measure of
$\nu_q$
is the Lévy measure of
![]() $-I_{e_q}$
. Then the random variable
$-I_{e_q}$
. Then the random variable
![]() $-I_{e_q} $
has a subexponential distribution, and
$-I_{e_q} $
has a subexponential distribution, and
Proof. The assertion that
![]() $-I_{e_q} $
has a subexponential distribution and that (30) holds follow from (21) and [5, Theorem 1].
$-I_{e_q} $
has a subexponential distribution and that (30) holds follow from (21) and [5, Theorem 1].
5. Examples
In this section we apply the results from the previous section to several particular examples in which we obtain simple asymptotic expressions for the negative Wiener–Hopf factor
![]() $F_{I_{e_q} }$
. For simplicity, in cases A and C we will assume that the roots of
$F_{I_{e_q} }$
. For simplicity, in cases A and C we will assume that the roots of
![]() $\Psi_{\mathcal{X}}(r)-q=0$
in
$\Psi_{\mathcal{X}}(r)-q=0$
in
![]() ${\mathbb{C}}_{++}$
are all different. This assumption holds, for example, when the density
${\mathbb{C}}_{++}$
are all different. This assumption holds, for example, when the density
![]() $f_1$
is a convex combination of exponential densities.
$f_1$
is a convex combination of exponential densities.
Example 1. (Case A.) We take
![]() $\Psi_{\mathcal{S}}(r)=r^\xi$
, for
$\Psi_{\mathcal{S}}(r)=r^\xi$
, for
![]() $\xi \in(0,1)$
; hence,
$\xi \in(0,1)$
; hence,
![]() ${\mathcal{S}}$
is a
${\mathcal{S}}$
is a
![]() $\xi$
-stable subordinator and the assumptions on Proposition 1 hold. Hence,
$\xi$
-stable subordinator and the assumptions on Proposition 1 hold. Hence,
Example 2. (Case B.) First, let us suppose that
![]() $G_{\mathcal{S}}(r)=\lambda_2\widehat{f}_2(r)-\lambda_2$
, i.e.
$G_{\mathcal{S}}(r)=\lambda_2\widehat{f}_2(r)-\lambda_2$
, i.e.
![]() ${\mathcal{S}}$
is a compound Poisson process with Lévy measure
${\mathcal{S}}$
is a compound Poisson process with Lévy measure
![]() $\lambda_2f_2(x)$
,
$\lambda_2f_2(x)$
,
![]() $\lambda_2 > 0$
. In this case the resulting Lévy risk process is the classical two-sided jump risk process. Therefore,
$\lambda_2 > 0$
. In this case the resulting Lévy risk process is the classical two-sided jump risk process. Therefore,
 \begin{equation}
\chi_{q,{\mathcal{S}}}(u)=\lambda_2\sum_{j=1}^R\sum_{a=0}^{k_j-1}E(j,a,q)
\int_u^\infty(y-u)^a {\rm e}^{-\beta_j(q)(y-u)}f_2(y)\,{\rm d} y.
\end{equation}
\begin{equation}
\chi_{q,{\mathcal{S}}}(u)=\lambda_2\sum_{j=1}^R\sum_{a=0}^{k_j-1}E(j,a,q)
\int_u^\infty(y-u)^a {\rm e}^{-\beta_j(q)(y-u)}f_2(y)\,{\rm d} y.
\end{equation}
When
![]() $k_j=1$
for all
$k_j=1$
for all
![]() $j=1,2,\dots,R$
, and
$j=1,2,\dots,R$
, and
![]() $f_2$
is a mixture of exponential densities, the above expression can be easily calculated. Let us consider the particular case when
$f_2$
is a mixture of exponential densities, the above expression can be easily calculated. Let us consider the particular case when
![]() $f_1(x)= q{\rm e}^{-qx}$
,
$f_1(x)= q{\rm e}^{-qx}$
,
![]() $x>0$
,
$x>0$
,
![]() $\lambda_2=1$
, and
$\lambda_2=1$
, and
![]() $f_2(x)=p{\rm e}^{-px}$
,
$f_2(x)=p{\rm e}^{-px}$
,
![]() $x>0$
. In this case the generalized Lundberg equation
$x>0$
. In this case the generalized Lundberg equation
![]() $\Psi_{\mathcal{X}}(r)-q=0$
has two real roots
$\Psi_{\mathcal{X}}(r)-q=0$
has two real roots
![]() $\beta_1(q)$
and
$\beta_1(q)$
and
![]() $\beta_2(q)$
such that
$\beta_2(q)$
such that
![]() $0<\beta_1(q)<q<\beta_2(q)$
. Hence,
$0<\beta_1(q)<q<\beta_2(q)$
. Hence,
which means that the associated subordinator
![]() $\mathcal{N}_{2,q}$
is a compound Poisson process with intensity
$\mathcal{N}_{2,q}$
is a compound Poisson process with intensity
![]() $C_q$
and jump sizes with density
$C_q$
and jump sizes with density
![]() $f_2$
. In this case we obtain an explicit expression for
$f_2$
. In this case we obtain an explicit expression for
![]() $F_{I_{e_q}}$
and its Laplace transform:
$F_{I_{e_q}}$
and its Laplace transform:
 \begin{equation}\label{CP}
\widehat{F}_{I_{e_q} }(r)=\frac{\frac{C_q p}{c}}{\frac{p(c-C_q)}{c}+r}\quad\mbox{and}\quad
F_{I_{e_q} }({-}x)=\frac{C_q p}{c}{\rm e}^{-p(c-C_q) x}.
\end{equation}
\begin{equation}\label{CP}
\widehat{F}_{I_{e_q} }(r)=\frac{\frac{C_q p}{c}}{\frac{p(c-C_q)}{c}+r}\quad\mbox{and}\quad
F_{I_{e_q} }({-}x)=\frac{C_q p}{c}{\rm e}^{-p(c-C_q) x}.
\end{equation}
Second, let us suppose that
This corresponds to a classical two-sided jump risk process with claims given by a Burr distribution with parameters
![]() $\xi$
,
$\xi$
,
![]() $\theta$
, and c. Then
$\theta$
, and c. Then
 \begin{equation}
\chi_{q,{\mathcal{S}}}(u)=\lambda_2\sum_{j=1}^{m+1}E(j,0,q)\int_u^\infty {\rm e}^{-\beta_j(q)(y-u)} \frac{\xi\theta^\xi}{(\theta+y)^{1+\xi}}\,{\rm d} y,
\end{equation}
\begin{equation}
\chi_{q,{\mathcal{S}}}(u)=\lambda_2\sum_{j=1}^{m+1}E(j,0,q)\int_u^\infty {\rm e}^{-\beta_j(q)(y-u)} \frac{\xi\theta^\xi}{(\theta+y)^{1+\xi}}\,{\rm d} y,
\end{equation}
and by applying L’Hôpital’s rule twice we get
 \begin{eqnarray*}
\lim_{u\to\infty}\frac{{\overline{\chi}}_{q,{\mathcal{S}}}(u)}{\big(\frac{\theta}{\theta+u^c}
\big)^{\xi}}&=&\lambda_2\sum_{j=1}^{m+1}E(j,0,q)\lim_{u\to\infty}
\frac{\int_u^\infty {\rm e}^{\beta_j(q)x}\int_x^\infty
{\rm e}^{-\beta_j(q)y} \frac{\xi\theta^\xi}{(\theta+y^c)^{1+\xi}}\,{\rm d} y}{\big(\frac{\theta}
{\theta+u^c}\big)^{\xi}}\\
&=&\lambda_2\sum_{j=1}^{m+1}E(j,0,q)\frac{1}{\beta_j(q)}.\nonumber
\end{eqnarray*}
\begin{eqnarray*}
\lim_{u\to\infty}\frac{{\overline{\chi}}_{q,{\mathcal{S}}}(u)}{\big(\frac{\theta}{\theta+u^c}
\big)^{\xi}}&=&\lambda_2\sum_{j=1}^{m+1}E(j,0,q)\lim_{u\to\infty}
\frac{\int_u^\infty {\rm e}^{\beta_j(q)x}\int_x^\infty
{\rm e}^{-\beta_j(q)y} \frac{\xi\theta^\xi}{(\theta+y^c)^{1+\xi}}\,{\rm d} y}{\big(\frac{\theta}
{\theta+u^c}\big)^{\xi}}\\
&=&\lambda_2\sum_{j=1}^{m+1}E(j,0,q)\frac{1}{\beta_j(q)}.\nonumber
\end{eqnarray*}
Using the second equality in [Reference Kolkovska and Martn-González7, Lemma 5.2], it follows that
 \begin{equation}
\lim_{u\to\infty}\frac{{\overline{\chi}}_{q,{\mathcal{S}}}(u)}
{\big(\frac{\theta}{\theta+u^c}\big)^{\xi}}=\lambda_2{\prod_{i=1}^N\alpha_i^{n_i}\bigg(\prod_{j=1}^{m+1}\beta_j(q)\bigg)^{-1}}=
\frac{\lambda_2a(q)}{q},
\end{equation}
\begin{equation}
\lim_{u\to\infty}\frac{{\overline{\chi}}_{q,{\mathcal{S}}}(u)}
{\big(\frac{\theta}{\theta+u^c}\big)^{\xi}}=\lambda_2{\prod_{i=1}^N\alpha_i^{n_i}\bigg(\prod_{j=1}^{m+1}\beta_j(q)\bigg)^{-1}}=
\frac{\lambda_2a(q)}{q},
\end{equation}
which implies that
![]() $1-\frac{{\overline{\chi}}_{q,{\mathcal{S}}}(u)}{\widehat{\chi}_{q,{\mathcal{S}}}(0)}$
is a subexponential distribution. Therefore, due to Proposition 2 we obtain
$1-\frac{{\overline{\chi}}_{q,{\mathcal{S}}}(u)}{\widehat{\chi}_{q,{\mathcal{S}}}(0)}$
is a subexponential distribution. Therefore, due to Proposition 2 we obtain
Example 3. (Case C.) Let us suppose that
![]() ${\mathcal{S}}$
is a spectrally positive
${\mathcal{S}}$
is a spectrally positive
![]() $\xi$
-stable process, with
$\xi$
-stable process, with
![]() ${\mathrm{E}}[{\mathcal{S}}(1)]=0$
and
${\mathrm{E}}[{\mathcal{S}}(1)]=0$
and
![]() $\xi \in (1,2)$
. In this case,
$\xi \in (1,2)$
. In this case,
![]() $-\Psi_{\mathcal{S}}(r)=r^\xi$
and
$-\Psi_{\mathcal{S}}(r)=r^\xi$
and
 \begin{equation}
\chi_{q,{\mathcal{S}}}(x)=\frac{1}{\xi} \bigg( x^{-\xi}-\sum_{j=1}^{m+1}\beta_j(q)E(j,0,q)\int_x^\infty {\rm e}^{-\beta_j(q)(y-x)}y^{-\xi}\,{\rm d} y\bigg),
\end{equation}
\begin{equation}
\chi_{q,{\mathcal{S}}}(x)=\frac{1}{\xi} \bigg( x^{-\xi}-\sum_{j=1}^{m+1}\beta_j(q)E(j,0,q)\int_x^\infty {\rm e}^{-\beta_j(q)(y-x)}y^{-\xi}\,{\rm d} y\bigg),
\end{equation}
where we have used that
![]() $E_*(j,0,q)=\beta_j(q)E(j,0,q)$
. Notice that the function
$E_*(j,0,q)=\beta_j(q)E(j,0,q)$
. Notice that the function
![]() $\mathcal{L}_{\xi}(x)=\sum_{j=1}^{m+1}\beta_j(q)E(j,0,q)\int_x^\infty {\rm e}^{-\beta_j(q)(y-x)}y^{-\xi}\,{\rm d} y$
coincides with the function
$\mathcal{L}_{\xi}(x)=\sum_{j=1}^{m+1}\beta_j(q)E(j,0,q)\int_x^\infty {\rm e}^{-\beta_j(q)(y-x)}y^{-\xi}\,{\rm d} y$
coincides with the function
![]() $F_\xi$
defined in [Reference Kolkovska and Martn-González8]; hence, from Proposition 1 in the aforementioned work we obtain
$F_\xi$
defined in [Reference Kolkovska and Martn-González8]; hence, from Proposition 1 in the aforementioned work we obtain
 \begin{equation}
\int_x^\infty\mathcal{L}_{\xi}(y)\,{\rm d} y\approx \bigg(1-{\prod_{i=1}^N\alpha_i^{n_i}\bigg(\prod_{j=1}^{m+1}\beta_j(q)\bigg)^{-1}}\bigg)\frac{x^{1-\xi}}{\Gamma(2-\xi)}\quad\mbox{as}\ x\to\infty.
\end{equation}
\begin{equation}
\int_x^\infty\mathcal{L}_{\xi}(y)\,{\rm d} y\approx \bigg(1-{\prod_{i=1}^N\alpha_i^{n_i}\bigg(\prod_{j=1}^{m+1}\beta_j(q)\bigg)^{-1}}\bigg)\frac{x^{1-\xi}}{\Gamma(2-\xi)}\quad\mbox{as}\ x\to\infty.
\end{equation}
Since
![]() ${\prod_{i=1}^N\alpha_i^{n_i}\big(\prod_{j=1}^{m+1}\beta_j(q)\big)^{-1}}=\frac{a(q)}{q}$
, it follows that
${\prod_{i=1}^N\alpha_i^{n_i}\big(\prod_{j=1}^{m+1}\beta_j(q)\big)^{-1}}=\frac{a(q)}{q}$
, it follows that
![]() ${\overline{\chi}}_{q,{\mathcal{S}}}(x)\approx C_{\xi} \frac{x^{1-\xi}}{\Gamma(2-\xi)}$
as
${\overline{\chi}}_{q,{\mathcal{S}}}(x)\approx C_{\xi} \frac{x^{1-\xi}}{\Gamma(2-\xi)}$
as
![]() $x\to\infty,$
where
$x\to\infty,$
where
![]() $C_{\xi}=\frac{1}{\xi}\big(\frac{\Gamma(2-\xi)}{\xi-1}-1+\frac{a(q)}{q}\big)$
. Therefore, from Proposition 4 we obtain
$C_{\xi}=\frac{1}{\xi}\big(\frac{\Gamma(2-\xi)}{\xi-1}-1+\frac{a(q)}{q}\big)$
. Therefore, from Proposition 4 we obtain
![]() $F_{I_{e_q} }({-}u)\approx\frac{C_{\xi}}{a(q)\Gamma(2-\xi)}u^{1-{\xi}}$
as
$F_{I_{e_q} }({-}u)\approx\frac{C_{\xi}}{a(q)\Gamma(2-\xi)}u^{1-{\xi}}$
as
![]() $u\to\infty$
.
$u\to\infty$
.
6. Proof of Lemma 5
This section is devoted to the proof of Lemma 5. It requires some preliminary results which we state first. Let
![]() $x_1, x_2,\dots,x_k$
be different complex numbers. For
$x_1, x_2,\dots,x_k$
be different complex numbers. For
![]() $m\in \{1,2,\ldots\}$
let us denote
$m\in \{1,2,\ldots\}$
let us denote
![]() $(x_i)_{m}= \underbrace{x_i,x_i,\dots,x_i}_{m \ \text{times}},$
$(x_i)_{m}= \underbrace{x_i,x_i,\dots,x_i}_{m \ \text{times}},$
![]() $i=1,\ldots,k$
. The following result follows from standard tools in interpolation theory.
$i=1,\ldots,k$
. The following result follows from standard tools in interpolation theory.
Lemma 8. Let
![]() $f\,:\,{\mathbb{C}}\to{\mathbb{C}}$
be an analytic function and define
$f\,:\,{\mathbb{C}}\to{\mathbb{C}}$
be an analytic function and define
![]() $g\,:\,{\mathbb{C}}^m\to{\mathbb{C}}$
by
$g\,:\,{\mathbb{C}}^m\to{\mathbb{C}}$
by
 \begin{equation}
g[x_1,\dots,x_m]=({-}1)^{m-1}\sum_{j=1}^m\frac{f(x_j)}{\prod_{l\neq j}(x_l-x_j)},
\end{equation}
\begin{equation}
g[x_1,\dots,x_m]=({-}1)^{m-1}\sum_{j=1}^m\frac{f(x_j)}{\prod_{l\neq j}(x_l-x_j)},
\end{equation}
where
![]() $x_i \neq x_j$
for
$x_i \neq x_j$
for
![]() $i \neq j$
. Let
$i \neq j$
. Let
![]() $n_1$
,
$n_1$
,
![]() $n_2,\ldots,n_k$
be given natural numbers, and
$n_2,\ldots,n_k$
be given natural numbers, and
![]() $m=\sum_{j=1}^kn_j$
. Then the function g can be extended analytically for multiple points by the expression
$m=\sum_{j=1}^kn_j$
. Then the function g can be extended analytically for multiple points by the expression
 \begin{align}
g[ (x_1)_{n_1},\dots,(x_k)_{n_k}]&=({-}1)^{m-1}\sum_{j=1}^k\frac{({-}1)^{m-n_j}}{(n_j-1)!}\frac{\partial ^{n_j-1}}{\partial s^{n_j-1}}\bigg[\frac{f(s)(x_j-s)^{n_j}}{\prod_{l=1}^k(x_l-s)^{n_l}}\bigg]_{s=x_j}.\nonumber
\end{align}
\begin{align}
g[ (x_1)_{n_1},\dots,(x_k)_{n_k}]&=({-}1)^{m-1}\sum_{j=1}^k\frac{({-}1)^{m-n_j}}{(n_j-1)!}\frac{\partial ^{n_j-1}}{\partial s^{n_j-1}}\bigg[\frac{f(s)(x_j-s)^{n_j}}{\prod_{l=1}^k(x_l-s)^{n_l}}\bigg]_{s=x_j}.\nonumber
\end{align}
We also need the following two lemmas. The first one is a well-known formula in interpolation theory, while the second one is part of the proof of [7, Proposition 5.4].
Lemma 9. Let
![]() $m\ge1$
and let
$m\ge1$
and let
![]() $a_1,\ldots, a_m$
be given different numbers. Then
$a_1,\ldots, a_m$
be given different numbers. Then
 \begin{equation}
\sum_{j=1}^m\frac{(a_j-s)^k}{\prod_{l=1,l\neq j}^m(a_l-a_j)}=\left\{
\begin{array}{ll}
({-}1)^{m-1}&k=m-1,\\[3pt]
0&k=0,1,\dots,m-2,\\[3pt]
\frac{1}{\prod_{j=1}^m(a_j-s)}&k=-1.
\end{array}
\right.
\end{equation}
\begin{equation}
\sum_{j=1}^m\frac{(a_j-s)^k}{\prod_{l=1,l\neq j}^m(a_l-a_j)}=\left\{
\begin{array}{ll}
({-}1)^{m-1}&k=m-1,\\[3pt]
0&k=0,1,\dots,m-2,\\[3pt]
\frac{1}{\prod_{j=1}^m(a_j-s)}&k=-1.
\end{array}
\right.
\end{equation}
In what follows we set
![]() $P_1(r)=\prod_{j=1}^N(\alpha_j-r)^{n_j}$
.
$P_1(r)=\prod_{j=1}^N(\alpha_j-r)^{n_j}$
.
Lemma 10. Let
![]() $r,r_1,r_2,\dots,r_{m+1}$
be
$r,r_1,r_2,\dots,r_{m+1}$
be
![]() $m+2$
different complex numbers and define
$m+2$
different complex numbers and define
 \begin{equation}
J_0(r)=\lambda_1\sum_{j=1}^{m+1}P_1(r_j)\frac{1}{
\prod_{k=1,i\neq j}^{m+1}(r_k-r_j)}
\frac{\frac{Q({-}r)}{\prod_{l=1}^N(\alpha_l-r)^{n_l}}-\frac{Q({-}r_j)}{\prod_{l=1}^N(\alpha_l-r_j)^{n_l}}}
{r_j-r}.
\end{equation}
\begin{equation}
J_0(r)=\lambda_1\sum_{j=1}^{m+1}P_1(r_j)\frac{1}{
\prod_{k=1,i\neq j}^{m+1}(r_k-r_j)}
\frac{\frac{Q({-}r)}{\prod_{l=1}^N(\alpha_l-r)^{n_l}}-\frac{Q({-}r_j)}{\prod_{l=1}^N(\alpha_l-r_j)^{n_l}}}
{r_j-r}.
\end{equation}
Then
![]() $J_0(r)=0$
for all
$J_0(r)=0$
for all
![]() $r\in \mathbb{C}$
.
$r\in \mathbb{C}$
.
The following result is used in case C.
Lemma 11. Let
![]() $\nu_\mathcal{S}$
be the Lévy measure of a spectrally positive pure jump Lévy process such that
$\nu_\mathcal{S}$
be the Lévy measure of a spectrally positive pure jump Lévy process such that
Then
Moreover, for any
![]() $r_1,r_2\in{\mathbb{C}}_+$
such that
$r_1,r_2\in{\mathbb{C}}_+$
such that
![]() $r_1\neq r_2$
and
$r_1\neq r_2$
and
![]() $\Psi_\mathcal{S}$
exists, we have
$\Psi_\mathcal{S}$
exists, we have
Proof. From assumption (32) we can restrict to
![]() $h\equiv1$
, and by applying Fubini’s theorem we get (33). On the other hand, we have
$h\equiv1$
, and by applying Fubini’s theorem we get (33). On the other hand, we have
 \begin{align}
\frac{\Psi_\mathcal{S}(r_1)-\Psi_\mathcal{S}(r_2)}{r_2-r_1}
&=\frac{r_1\frac{\Psi_\mathcal{S}(r_1)}{r_1}-r_2\frac{\Psi_\mathcal{S}(r_2)}{r_2}}{r_2-r_1}=\frac{r_1-r_2}{r_2-r_1}\frac{\Psi_\mathcal{S}(r_1)}{r_1}+r_2\frac{\frac{\Psi_\mathcal{S}(r_1)}{r_1}-\frac{\Psi_\mathcal{S}(r_2)}{r_2}}{r_2-r_1}\nonumber \\
&=r_2\frac{\frac{\Psi_\mathcal{S}(r_1)}{r_1}-\frac{\Psi_\mathcal{S}(r_2)}{r_2}}{r_2-r_1}-\frac{\Psi_\mathcal{S}(r_1)}{r_1}.
\end{align}
\begin{align}
\frac{\Psi_\mathcal{S}(r_1)-\Psi_\mathcal{S}(r_2)}{r_2-r_1}
&=\frac{r_1\frac{\Psi_\mathcal{S}(r_1)}{r_1}-r_2\frac{\Psi_\mathcal{S}(r_2)}{r_2}}{r_2-r_1}=\frac{r_1-r_2}{r_2-r_1}\frac{\Psi_\mathcal{S}(r_1)}{r_1}+r_2\frac{\frac{\Psi_\mathcal{S}(r_1)}{r_1}-\frac{\Psi_\mathcal{S}(r_2)}{r_2}}{r_2-r_1}\nonumber \\
&=r_2\frac{\frac{\Psi_\mathcal{S}(r_1)}{r_1}-\frac{\Psi_\mathcal{S}(r_2)}{r_2}}{r_2-r_1}-\frac{\Psi_\mathcal{S}(r_1)}{r_1}.
\end{align}
Similarly,
and
 \begin{align*}
\frac{\Psi_\mathcal{S}(r_1)}{r_1}-\frac{\Psi_\mathcal{S}(r_2)}{r_2}&=\int_{0+}^\infty\Big[\frac{1-{\rm e}^{-r_1x}-r_1x}{r_1}-\frac{1-{\rm e}^{-r_2x}-r_2x}{r_2}\Big]\nu_\mathcal{S}({\rm d}x)\nonumber\\
&=\int _{0+}^\infty\int _0^x \big[ {\rm e}^{-r_1y}-1-( {\rm e}^{-r_2y}-1)\big] \,{\rm d} y\nu_\mathcal{S}({\rm d}x)\\ &=\int _{0+}^\infty\int _y^\infty \nu_\mathcal{S}({\rm d}x)\big[ {\rm e}^{-r_1y}-{\rm e}^{-r_2y}\big] \,{\rm d} y\nonumber\\
&=\widehat{\overline{\mathcal{V}}}_\mathcal{S}(r_1)-\widehat{\overline{\mathcal{V}}}_\mathcal{S}(r_2),\nonumber
\end{align*}
\begin{align*}
\frac{\Psi_\mathcal{S}(r_1)}{r_1}-\frac{\Psi_\mathcal{S}(r_2)}{r_2}&=\int_{0+}^\infty\Big[\frac{1-{\rm e}^{-r_1x}-r_1x}{r_1}-\frac{1-{\rm e}^{-r_2x}-r_2x}{r_2}\Big]\nu_\mathcal{S}({\rm d}x)\nonumber\\
&=\int _{0+}^\infty\int _0^x \big[ {\rm e}^{-r_1y}-1-( {\rm e}^{-r_2y}-1)\big] \,{\rm d} y\nu_\mathcal{S}({\rm d}x)\\ &=\int _{0+}^\infty\int _y^\infty \nu_\mathcal{S}({\rm d}x)\big[ {\rm e}^{-r_1y}-{\rm e}^{-r_2y}\big] \,{\rm d} y\nonumber\\
&=\widehat{\overline{\mathcal{V}}}_\mathcal{S}(r_1)-\widehat{\overline{\mathcal{V}}}_\mathcal{S}(r_2),\nonumber
\end{align*}
where the third equality follows from Fubini’s theorem. Substituting the last equality in (35) and (36), and using (4), we obtain the result.
Now we are ready to prove Lemma 5.
Proof of Lemma 5. We deal only with the case
![]() $q > 0$
. The case
$q > 0$
. The case
![]() $q=0$
follows by taking limits when
$q=0$
follows by taking limits when
![]() $q\downarrow0$
and that the limit
$q\downarrow0$
and that the limit
![]() $\lim_{q\downarrow0}\beta_j(q)$
exists and
$\lim_{q\downarrow0}\beta_j(q)$
exists and
![]() $ \lim_{q\downarrow0}\frac{q}{\beta_1(q)}={\mathrm{E}}[{\mathcal{X}}(1)]$
.
$ \lim_{q\downarrow0}\frac{q}{\beta_1(q)}={\mathrm{E}}[{\mathcal{X}}(1)]$
.
The proof of the lemma is simpler when the roots
![]() $\beta_j(q)$
of the generalized Lundberg equation are simple. In the case of multiple roots we will approximate the Lundberg equation by a Lundberg equation depending on parameter
$\beta_j(q)$
of the generalized Lundberg equation are simple. In the case of multiple roots we will approximate the Lundberg equation by a Lundberg equation depending on parameter
![]() $\epsilon$
which has simple roots, and such that when
$\epsilon$
which has simple roots, and such that when
![]() $\epsilon \to 0$
the roots of the approximating Lundberg equation approximate the multiple roots of the given equation. At the end of the proof we take
$\epsilon \to 0$
the roots of the approximating Lundberg equation approximate the multiple roots of the given equation. At the end of the proof we take
![]() $\epsilon \to 0$
to obtain Lemma 5 in the case of multiple roots
$\epsilon \to 0$
to obtain Lemma 5 in the case of multiple roots
![]() $\beta_j(q)$
. First, we obtain the result for case C. Recall that
$\beta_j(q)$
. First, we obtain the result for case C. Recall that
![]() $\beta_j(q)$
are the roots of the generalized Lundberg function of
$\beta_j(q)$
are the roots of the generalized Lundberg function of
![]() ${\mathcal{X}}$
. Let
${\mathcal{X}}$
. Let
![]() $\varepsilon\in( 0,E)$
, where
$\varepsilon\in( 0,E)$
, where
and define the complex numbers
 \begin{equation}
\begin{array}{l}
\begin{gathered}
\beta_1(q)^*=\beta_1(q),
\beta_2(q)^*=\beta_2(q) + \frac{1}{m+1}\varepsilon,
\dots, \beta_{k_1}(q)^*=\beta_1(q)+\frac{k_1-1}{m+1}\varepsilon,\\ $\,$ \\
\beta_{k_1+1}(q)^*=\beta_2(q),\dots, \beta_{k_1+k_2}(q)^*=\beta_2(q)+\frac{k_1+k_2-1}{m+1}\varepsilon,\\
\beta_{k_1+\dots+k_{R-1}+1}(q)^*=\beta_R(q),\dots, \beta_{m+1}(q)^*=\beta_R(q)+\frac{\sum_jk_j-1}{m+1}\varepsilon,
\end{gathered}
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}
\begin{gathered}
\beta_1(q)^*=\beta_1(q),
\beta_2(q)^*=\beta_2(q) + \frac{1}{m+1}\varepsilon,
\dots, \beta_{k_1}(q)^*=\beta_1(q)+\frac{k_1-1}{m+1}\varepsilon,\\ $\,$ \\
\beta_{k_1+1}(q)^*=\beta_2(q),\dots, \beta_{k_1+k_2}(q)^*=\beta_2(q)+\frac{k_1+k_2-1}{m+1}\varepsilon,\\
\beta_{k_1+\dots+k_{R-1}+1}(q)^*=\beta_R(q),\dots, \beta_{m+1}(q)^*=\beta_R(q)+\frac{\sum_jk_j-1}{m+1}\varepsilon,
\end{gathered}
\end{array}
\end{equation}
where we have omitted the dependence on
![]() $\varepsilon$
for simplicity.
$\varepsilon$
for simplicity.
It follows that
![]() $\lim_{\varepsilon\rightarrow 0}\beta_{l_j+a_j}(q)^*=\beta_j(q)$
,
$\lim_{\varepsilon\rightarrow 0}\beta_{l_j+a_j}(q)^*=\beta_j(q)$
,
![]() $j=1,2,\dots,R$
, for
$j=1,2,\dots,R$
, for
![]() $l_1=0,l_2=k_1,\dots,l_R=k_{R-1}$
, and
$l_1=0,l_2=k_1,\dots,l_R=k_{R-1}$
, and
![]() $a_j=1,2,\dots,k_j$
. This gives
$a_j=1,2,\dots,k_j$
. This gives
![]() $m+1$
different numbers
$m+1$
different numbers
![]() $\beta_1^*,\dots,\beta_{m+1}^*$
such that, as
$\beta_1^*,\dots,\beta_{m+1}^*$
such that, as
![]() $\varepsilon\downarrow0$
, the first
$\varepsilon\downarrow0$
, the first
![]() $k_1$
numbers converge to
$k_1$
numbers converge to
![]() $\beta_1(q)$
, the next
$\beta_1(q)$
, the next
![]() $k_2$
numbers converge to
$k_2$
numbers converge to
![]() $\beta_2(q)$
, and so on. From the definition of
$\beta_2(q)$
, and so on. From the definition of
![]() $\Psi_{\mathcal{X}}$
,
$\Psi_{\mathcal{X}}$
,
 \begin{multline*}
\Psi_{\mathcal{X}}[ \beta_j(q)^* ]-q = \\
-\Psi_\mathcal{S}[ \beta_j(q)^* ]+\lambda_1\frac{Q({-}\beta_j(q)^*)}{\prod_{l=1}^N( \alpha_l-\beta_j(q)^*)^{n_l}} +c\beta_j(q)^* +\gamma^2[\beta_j(q)^* ]^2-q-\lambda_1. \nonumber
\end{multline*}
\begin{multline*}
\Psi_{\mathcal{X}}[ \beta_j(q)^* ]-q = \\
-\Psi_\mathcal{S}[ \beta_j(q)^* ]+\lambda_1\frac{Q({-}\beta_j(q)^*)}{\prod_{l=1}^N( \alpha_l-\beta_j(q)^*)^{n_l}} +c\beta_j(q)^* +\gamma^2[\beta_j(q)^* ]^2-q-\lambda_1. \nonumber
\end{multline*}
Therefore, for each
![]() $j=1,2,\dots,m+1$
we obtain
$j=1,2,\dots,m+1$
we obtain
 \begin{align*}
\lambda_1+q &= -\Psi_\mathcal{S}[ \beta_j(q)^* ]+\lambda_1\frac{Q({-}\beta_j(q)^*)}{\prod_{l=1}^N( \alpha_l-\beta_j(q)^*)^{n_l}}+c\beta_j(q)^*\\
& \quad +\gamma^2[\beta_j(q)^* ]^2-( \Psi_{\mathcal{X}}[ \beta_j(q)^* ]-q),\nonumber
\end{align*}
\begin{align*}
\lambda_1+q &= -\Psi_\mathcal{S}[ \beta_j(q)^* ]+\lambda_1\frac{Q({-}\beta_j(q)^*)}{\prod_{l=1}^N( \alpha_l-\beta_j(q)^*)^{n_l}}+c\beta_j(q)^*\\
& \quad +\gamma^2[\beta_j(q)^* ]^2-( \Psi_{\mathcal{X}}[ \beta_j(q)^* ]-q),\nonumber
\end{align*}
which yields
 \begin{align}\nonumber
\Psi_{\mathcal{X}}(r)-q&=-\Psi_\mathcal{S}(r)+\lambda_1\frac{Q({-}r)}{\prod_{l=1}^N( \alpha_l-r)^{n_l}}+cr+\gamma^2 r^2+ \Psi_\mathcal{S}[ \beta_j(q)^* ] \nonumber \\[3pt]
&\quad-\lambda_1\frac{Q({-}\beta_j(q)^*)}{\prod_{l=1}^N( \alpha_l-\beta_j(q)^*)^{n_l}}\nonumber \\[3pt]
&\quad-c\beta_j(q)^* -\gamma^2[\beta_j(q)^* ]^2+ \Psi_{\mathcal{X}}[ \beta_j(q)^* ]-q.
\end{align}
\begin{align}\nonumber
\Psi_{\mathcal{X}}(r)-q&=-\Psi_\mathcal{S}(r)+\lambda_1\frac{Q({-}r)}{\prod_{l=1}^N( \alpha_l-r)^{n_l}}+cr+\gamma^2 r^2+ \Psi_\mathcal{S}[ \beta_j(q)^* ] \nonumber \\[3pt]
&\quad-\lambda_1\frac{Q({-}\beta_j(q)^*)}{\prod_{l=1}^N( \alpha_l-\beta_j(q)^*)^{n_l}}\nonumber \\[3pt]
&\quad-c\beta_j(q)^* -\gamma^2[\beta_j(q)^* ]^2+ \Psi_{\mathcal{X}}[ \beta_j(q)^* ]-q.
\end{align}
Since
![]() $P_1$
is a polynomial with degree m, using Lagrange interpolation we obtain the equivalent representation
$P_1$
is a polynomial with degree m, using Lagrange interpolation we obtain the equivalent representation
 \begin{equation}
P_1(r)=\sum_{l=1}^{m+1}\frac{\prod_{j=1}^N[ \alpha_j-\beta_l(q)^* ]^{n_j}}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\prod_{j\neq l}[\beta_j(q)^* -r].
\end{equation}
\begin{equation}
P_1(r)=\sum_{l=1}^{m+1}\frac{\prod_{j=1}^N[ \alpha_j-\beta_l(q)^* ]^{n_j}}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\prod_{j\neq l}[\beta_j(q)^* -r].
\end{equation}
This and (38) give
 \[\begin{array}{*{20}{c}}
{\left[ {{\Psi _{\cal X}}(r) - q} \right]{P_1}(r)} \hfill & = \hfill \\
{} \hfill & { = \sum\limits_{l = 1}^{m + 1} {\frac{{{P_1}\left[ {{\beta _l}{{(q)}^*}} \right]}}{{\prod\limits_{j \ne l} {\left[ {{\beta _j}{{(q)}^*} - {\beta _l}{{(q)}^*}} \right]} }}} \prod\limits_{j \ne l} {\left[ {{\beta _j}{{(q)}^*} - r} \right]} \left\{ { - ({\beta _l}{{(q)}^*} - r)\frac{{{\Psi _{\cal S}}(r) - {\Psi _{\cal S}}({\beta _l}{{(q)}^*})}}{{{\beta _l}{{(q)}^*} - r}}} \right.} \hfill \\
{} \hfill & { + \left. {\smallint ({\beta _l}{{(q)}^*} - r)\left( {{\lambda _1}J_0^* - c - {\gamma ^2}({\beta _l}{{(q)}^*} + r)} \right) + {\Psi _{\cal X}}({\beta _l}{{(q)}^*}) - q} \right\}} \hfill \\
{} \hfill & { = \prod\limits_{j = 1}^{m + 1} {\left[ {{\beta _j}{{(q)}^*} - r} \right]} \sum\limits_{l = 1}^{m + 1} {\frac{{{P_1}\left[ {{\beta _l}{{(q)}^*}} \right]}}{{\prod\limits_{j \ne l} {\left[ {{\beta _j}{{(q)}^*} - {\beta _l}{{(q)}^*}} \right]} }}} \left\{ { - \frac{{{\Psi _{\cal S}}(r) - {\Psi _{\cal S}}({\beta _l}{{(q)}^*})}}{{{\beta _l}{{(q)}^*} - r}}} \right.} \hfill \\
{} \hfill & {\left. { + {\lambda _1}J_0^* - c - {\gamma ^2}({\beta _l}{{(q)}^*} + r) + \frac{{{\Psi _{\cal X}}({\beta _l}{{(q)}^*}) - q}}{{{\beta _l}{{(q)}^*} - r}}} \right\},} \hfill \\
\end{array}\]
\[\begin{array}{*{20}{c}}
{\left[ {{\Psi _{\cal X}}(r) - q} \right]{P_1}(r)} \hfill & = \hfill \\
{} \hfill & { = \sum\limits_{l = 1}^{m + 1} {\frac{{{P_1}\left[ {{\beta _l}{{(q)}^*}} \right]}}{{\prod\limits_{j \ne l} {\left[ {{\beta _j}{{(q)}^*} - {\beta _l}{{(q)}^*}} \right]} }}} \prod\limits_{j \ne l} {\left[ {{\beta _j}{{(q)}^*} - r} \right]} \left\{ { - ({\beta _l}{{(q)}^*} - r)\frac{{{\Psi _{\cal S}}(r) - {\Psi _{\cal S}}({\beta _l}{{(q)}^*})}}{{{\beta _l}{{(q)}^*} - r}}} \right.} \hfill \\
{} \hfill & { + \left. {\smallint ({\beta _l}{{(q)}^*} - r)\left( {{\lambda _1}J_0^* - c - {\gamma ^2}({\beta _l}{{(q)}^*} + r)} \right) + {\Psi _{\cal X}}({\beta _l}{{(q)}^*}) - q} \right\}} \hfill \\
{} \hfill & { = \prod\limits_{j = 1}^{m + 1} {\left[ {{\beta _j}{{(q)}^*} - r} \right]} \sum\limits_{l = 1}^{m + 1} {\frac{{{P_1}\left[ {{\beta _l}{{(q)}^*}} \right]}}{{\prod\limits_{j \ne l} {\left[ {{\beta _j}{{(q)}^*} - {\beta _l}{{(q)}^*}} \right]} }}} \left\{ { - \frac{{{\Psi _{\cal S}}(r) - {\Psi _{\cal S}}({\beta _l}{{(q)}^*})}}{{{\beta _l}{{(q)}^*} - r}}} \right.} \hfill \\
{} \hfill & {\left. { + {\lambda _1}J_0^* - c - {\gamma ^2}({\beta _l}{{(q)}^*} + r) + \frac{{{\Psi _{\cal X}}({\beta _l}{{(q)}^*}) - q}}{{{\beta _l}{{(q)}^*} - r}}} \right\},} \hfill \\
\end{array}\]
where
 \begin{equation}
J_0^*=\frac{\frac{Q({-}r)}{\prod_{j=1}^N(\alpha_j-r)^{n_j}}-\frac{Q({-}\beta_l(q)^*)}{\prod_{j=1}^N(\alpha_j-\beta_l(q)^*)^{n_j}}}{\beta_l(q)^* -r}.
\end{equation}
\begin{equation}
J_0^*=\frac{\frac{Q({-}r)}{\prod_{j=1}^N(\alpha_j-r)^{n_j}}-\frac{Q({-}\beta_l(q)^*)}{\prod_{j=1}^N(\alpha_j-\beta_l(q)^*)^{n_j}}}{\beta_l(q)^* -r}.
\end{equation}
Equation (31) and Lemma 10 imply, respectively:
Substituting these two equalities in (39), using the first equality in (34) in order to calculate
![]() $\frac{\Psi_\mathcal{S}(r)-\Psi_\mathcal{S}(\beta_j(q)^* )}{\beta_j(q)^* -r}$
, and dividing by
$\frac{\Psi_\mathcal{S}(r)-\Psi_\mathcal{S}(\beta_j(q)^* )}{\beta_j(q)^* -r}$
, and dividing by
![]() $\prod_{j=1}^{m+1}[\beta_j(q)^* -r]$
, we obtain
$\prod_{j=1}^{m+1}[\beta_j(q)^* -r]$
, we obtain
 \begin{align}\nonumber
& [ \Psi_{\mathcal{X}}(r)-q] \frac{P_1(r)}{\prod_{j=1}^{m+1}[\beta_j(q)^* -r]} \\ \nonumber
&=\sum_{l=1}^{m+1}\frac{P_1[\beta_l(q)^* ]}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\\ \nonumber &\quad\times\bigg\{{-}\beta_l(q)^* \widehat{T}_{\beta_l(q)^* }\overline{\mathcal{V}}_\mathcal{S}(r)+\frac{\Psi_\mathcal{S}(r)}{r}-c
-\gamma^2[ r+\beta_l(q)^* ]
+\frac{ \Psi_{\mathcal{X}}[\beta_l(q)^* ]-q}{\beta_j(q)^* -r}\bigg\}\nonumber \\ \nonumber
&=\frac{\Psi_\mathcal{S}(r)}{r}-c-\gamma^2r\\ &-
\sum_{l=1}^{m+1}\frac{P_1[\beta_l(q)^* ]}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\bigg\{\beta_l(q)^* \widehat{T}_{\beta_l(q)^* }\overline{\mathcal{V}}_\mathcal{S}(r)+\gamma^2\beta_l(q)^*
-\frac{ \Psi_{\mathcal{X}}[\beta_l(q)^* ]-q}{\beta_j(q)^* -r} \bigg\},
\end{align}
\begin{align}\nonumber
& [ \Psi_{\mathcal{X}}(r)-q] \frac{P_1(r)}{\prod_{j=1}^{m+1}[\beta_j(q)^* -r]} \\ \nonumber
&=\sum_{l=1}^{m+1}\frac{P_1[\beta_l(q)^* ]}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\\ \nonumber &\quad\times\bigg\{{-}\beta_l(q)^* \widehat{T}_{\beta_l(q)^* }\overline{\mathcal{V}}_\mathcal{S}(r)+\frac{\Psi_\mathcal{S}(r)}{r}-c
-\gamma^2[ r+\beta_l(q)^* ]
+\frac{ \Psi_{\mathcal{X}}[\beta_l(q)^* ]-q}{\beta_j(q)^* -r}\bigg\}\nonumber \\ \nonumber
&=\frac{\Psi_\mathcal{S}(r)}{r}-c-\gamma^2r\\ &-
\sum_{l=1}^{m+1}\frac{P_1[\beta_l(q)^* ]}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\bigg\{\beta_l(q)^* \widehat{T}_{\beta_l(q)^* }\overline{\mathcal{V}}_\mathcal{S}(r)+\gamma^2\beta_l(q)^*
-\frac{ \Psi_{\mathcal{X}}[\beta_l(q)^* ]-q}{\beta_j(q)^* -r} \bigg\},
\end{align}
where the last equality follows from (40). Using Lemma 3 and [13, Theorem 2.2] we obtain
Now we let
![]() $\varepsilon\downarrow0$
on both sides of (41) and apply Lemma 8. This yields:
$\varepsilon\downarrow0$
on both sides of (41) and apply Lemma 8. This yields:
 \begin{align*}
&[ \Psi_{\mathcal{X}}(r)-q] (\kappa(q,-r))^{-1}\nonumber \\
&=\frac{\Psi_\mathcal{S}(r)}{r}-c-\gamma^2r\\
&\quad-\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_l-1}}\times \bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}} s\widehat{T}_s\overline{\mathcal{V}}_\mathcal{S}(r)\bigg]_{s=\beta_l(q)}\nonumber \\
&\quad-\gamma^2\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_j-1}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}} s\bigg]_{s=\beta_l(q)}\nonumber \\
&\quad+\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_l-1}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}}\frac{ \Psi_{\mathcal{X}}(s)-q}{s-r}\bigg]_{s=\beta_l(q)}.\nonumber
\end{align*}
\begin{align*}
&[ \Psi_{\mathcal{X}}(r)-q] (\kappa(q,-r))^{-1}\nonumber \\
&=\frac{\Psi_\mathcal{S}(r)}{r}-c-\gamma^2r\\
&\quad-\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_l-1}}\times \bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}} s\widehat{T}_s\overline{\mathcal{V}}_\mathcal{S}(r)\bigg]_{s=\beta_l(q)}\nonumber \\
&\quad-\gamma^2\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_j-1}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}} s\bigg]_{s=\beta_l(q)}\nonumber \\
&\quad+\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_l-1}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}}\frac{ \Psi_{\mathcal{X}}(s)-q}{s-r}\bigg]_{s=\beta_l(q)}.\nonumber
\end{align*}
Since, for
![]() $j=1,2,\dots,R$
,
$j=1,2,\dots,R$
,
![]() $\beta_j(q)$
are roots of
$\beta_j(q)$
are roots of
![]() $ \Psi_{\mathcal{X}}(s)-q=0$
in
$ \Psi_{\mathcal{X}}(s)-q=0$
in
![]() ${\mathbb{C}}_{++}$
with respective multiplicities
${\mathbb{C}}_{++}$
with respective multiplicities
![]() $k_j,$
it follows from the Leibniz rule that
$k_j,$
it follows from the Leibniz rule that
 \begin{equation}
\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_l-1}}\bigg[\frac{P_1(s)(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}}\frac{ \Psi_{\mathcal{X}}(s)-q}{s-r}\bigg]_{s=\beta_l(q)}=0.
\end{equation}
\begin{equation}
\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_l-1}}\bigg[\frac{P_1(s)(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}}\frac{ \Psi_{\mathcal{X}}(s)-q}{s-r}\bigg]_{s=\beta_l(q)}=0.
\end{equation}
Hence, substituting this in the equality above and setting
 \begin{equation}
D_q=\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_j-1}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}} s\bigg]_{s=\beta_l(q)},
\end{equation}
\begin{equation}
D_q=\sum_{l=1}^R\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1}}{\partial s^{k_j-1}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}} s\bigg]_{s=\beta_l(q)},
\end{equation}
we obtain:
 \[\begin{array}{l}
[q - {\Psi _{\cal X}}(r)]{(\kappa (q, - r))^{ - 1}} \\
= c + {\gamma ^2}{D_q} + {\gamma ^2}r - \frac{{{\Psi _{\cal S}}(r)}}{r} \\
+ \sum\limits_{l = 1}^R {\frac{{{{( - 1)}^{1 - {k_l}}}}}{{({k_l} - 1)!}}} \frac{{{\partial ^{{k_l} - 1}}}}{{\partial {s^{{k_l} - 1}}}}{[\frac{{\prod\limits_{j = 1}^N {{{({\alpha _j} - s)}^{{n_j}}}} {{({\beta _l}(q) - s)}^{{k_l}}}}}{{\prod\limits_{j = 1}^R {{{({\beta _j}(q) - s)}^{{k_j}}}} }}s{{\hat T}_s}{\overline {\cal V} _{\cal S}}(r)]_{s = {\beta _l}(q)}}. \\
\end{array}\]
\[\begin{array}{l}
[q - {\Psi _{\cal X}}(r)]{(\kappa (q, - r))^{ - 1}} \\
= c + {\gamma ^2}{D_q} + {\gamma ^2}r - \frac{{{\Psi _{\cal S}}(r)}}{r} \\
+ \sum\limits_{l = 1}^R {\frac{{{{( - 1)}^{1 - {k_l}}}}}{{({k_l} - 1)!}}} \frac{{{\partial ^{{k_l} - 1}}}}{{\partial {s^{{k_l} - 1}}}}{[\frac{{\prod\limits_{j = 1}^N {{{({\alpha _j} - s)}^{{n_j}}}} {{({\beta _l}(q) - s)}^{{k_l}}}}}{{\prod\limits_{j = 1}^R {{{({\beta _j}(q) - s)}^{{k_j}}}} }}s{{\hat T}_s}{\overline {\cal V} _{\cal S}}(r)]_{s = {\beta _l}(q)}}. \\
\end{array}\]
Using the Leibniz rule and Lemma 2 we get
 \begin{align*}
&\sum_{l=1}^R\sum_{a=0}^{k_l-1}\binom{k_l-1}{a}\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1-a}}{\partial s^{k_l-1-a}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}}s\bigg]_{s=\beta_l(q)}\\
&\qquad\times \frac{\partial^a}{\partial s^a} \big[\widehat{T}_s\overline{\mathcal{V}}_\mathcal{S}(r)\big]_{s=\beta_l(q)}\nonumber \\
&=\sum_{l=1}^R\sum_{a=0}^{k_l-1}E_*(l,a,q)\widehat{\mathcal{T}}_{\beta_l(q),a}\overline{\mathcal{V}}_\mathcal{S}(r)=\sum_{l=1}^R\sum_{a=0}^{k_l-1}E_*(l,a,q)\widehat{\mathcal{T}}_{\beta_l(q),a}\overline{\mathcal{V}}_\mathcal{S}(r)
=\widehat{{\mathcal{L}}}_q(r);\nonumber
\end{align*}
\begin{align*}
&\sum_{l=1}^R\sum_{a=0}^{k_l-1}\binom{k_l-1}{a}\frac{({-}1)^{1-k_l}}{(k_l-1)!}\frac{\partial^{k_l-1-a}}{\partial s^{k_l-1-a}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}}s\bigg]_{s=\beta_l(q)}\\
&\qquad\times \frac{\partial^a}{\partial s^a} \big[\widehat{T}_s\overline{\mathcal{V}}_\mathcal{S}(r)\big]_{s=\beta_l(q)}\nonumber \\
&=\sum_{l=1}^R\sum_{a=0}^{k_l-1}E_*(l,a,q)\widehat{\mathcal{T}}_{\beta_l(q),a}\overline{\mathcal{V}}_\mathcal{S}(r)=\sum_{l=1}^R\sum_{a=0}^{k_l-1}E_*(l,a,q)\widehat{\mathcal{T}}_{\beta_l(q),a}\overline{\mathcal{V}}_\mathcal{S}(r)
=\widehat{{\mathcal{L}}}_q(r);\nonumber
\end{align*}
hence, from (42) we obtain
Since by L’Hôpital’s rule
![]() $\lim_{r\downarrow0}\frac{\Psi_\mathcal{S}(r)}{r}=0$
, it follows that
$\lim_{r\downarrow0}\frac{\Psi_\mathcal{S}(r)}{r}=0$
, it follows that
![]() $a(q)=c+\gamma^2D_q+\widehat{{\mathcal{L}}}_q(0)$
. Hence,
$a(q)=c+\gamma^2D_q+\widehat{{\mathcal{L}}}_q(0)$
. Hence,
 \begin{align}
[ q- \Psi_{\mathcal{X}}(r)](\kappa(q,-r))^{-1}
&=a(q)-\widehat{{\mathcal{L}}}_q(0)+\gamma^2r-\frac{\Psi_\mathcal{S}(r)}{r}+\widehat{{\mathcal{L}}}_q(r)&\nonumber \\
&=a(q)+\gamma^2r-\frac{\Psi_\mathcal{S}(r)}{r}-\big( \widehat{{\mathcal{L}}}_q(0)-\widehat{{\mathcal{L}}}_q(r)\big),\nonumber
\end{align}
\begin{align}
[ q- \Psi_{\mathcal{X}}(r)](\kappa(q,-r))^{-1}
&=a(q)-\widehat{{\mathcal{L}}}_q(0)+\gamma^2r-\frac{\Psi_\mathcal{S}(r)}{r}+\widehat{{\mathcal{L}}}_q(r)&\nonumber \\
&=a(q)+\gamma^2r-\frac{\Psi_\mathcal{S}(r)}{r}-\big( \widehat{{\mathcal{L}}}_q(0)-\widehat{{\mathcal{L}}}_q(r)\big),\nonumber
\end{align}
and we obtain the result for case C.
To obtain the result for case B, we use the same notation as above for the
![]() $m+1$
roots of the generalized Lundberg equation, and use (39) with
$m+1$
roots of the generalized Lundberg equation, and use (39) with
![]() $\Psi_{\mathcal{S}}(r)$
replaced by
$\Psi_{\mathcal{S}}(r)$
replaced by
![]() $G_{\mathcal{S}}(r)$
and setting
$G_{\mathcal{S}}(r)$
and setting
![]() $\gamma=0$
. This gives:
$\gamma=0$
. This gives:
 \begin{align}
{[ \Psi_{\mathcal{X}}(r)-q] P_1(r)} \\
&=\prod_{j=1}^{m+1}[\beta_j(q)^* -r]\sum_{l=1}^{m+1}\frac{P_1[\beta_l(q)^* ]}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\\ &\quad\times\left\{{-}\frac{G_{\mathcal{S}}(r)-G_{\mathcal{S}}(\beta_l(q)^* )}{\beta_l(q)^* -r}+\lambda_1 J_0^*-c+\frac{ \Psi_{\mathcal{X}}(\beta_l(q)^* )-q}{\beta_l(q)^* -r}\right\}\nonumber \\
&=-c+\prod_{j=1}^{m+1}[\beta_j(q)^* -r]\sum_{l=1}^{m+1}\frac{P_1[\beta_l(q)^* ]}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\left\{\widehat{T}_{\beta_l(q)^* }\nu_{\mathcal{S}}(r)+\frac{ \Psi_{\mathcal{X}}(\beta_l(q)^* )-q}{\beta_l(q)^* -r}\right\},\nonumber
\end{align}
\begin{align}
{[ \Psi_{\mathcal{X}}(r)-q] P_1(r)} \\
&=\prod_{j=1}^{m+1}[\beta_j(q)^* -r]\sum_{l=1}^{m+1}\frac{P_1[\beta_l(q)^* ]}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\\ &\quad\times\left\{{-}\frac{G_{\mathcal{S}}(r)-G_{\mathcal{S}}(\beta_l(q)^* )}{\beta_l(q)^* -r}+\lambda_1 J_0^*-c+\frac{ \Psi_{\mathcal{X}}(\beta_l(q)^* )-q}{\beta_l(q)^* -r}\right\}\nonumber \\
&=-c+\prod_{j=1}^{m+1}[\beta_j(q)^* -r]\sum_{l=1}^{m+1}\frac{P_1[\beta_l(q)^* ]}{\prod_{j\neq l}[\beta_j(q)^* -\beta_l(q)^* ]}\left\{\widehat{T}_{\beta_l(q)^* }\nu_{\mathcal{S}}(r)+\frac{ \Psi_{\mathcal{X}}(\beta_l(q)^* )-q}{\beta_l(q)^* -r}\right\},\nonumber
\end{align}
where in the second equality we used (40) and the fact that
![]() $\frac{G_\mathcal{S}(r)-G_\mathcal{S}(s)}{s-r}=-\widehat{T}_s\nu_\mathcal{S}(r),$
which follows from the second equality in (4). Proceeding as in case C, we obtain
$\frac{G_\mathcal{S}(r)-G_\mathcal{S}(s)}{s-r}=-\widehat{T}_s\nu_\mathcal{S}(r),$
which follows from the second equality in (4). Proceeding as in case C, we obtain
 \begin{align*}
&[ q- \Psi_{\mathcal{X}}(r)] (\kappa(q,-r))^{-1}\nonumber\\
&=c-\sum_{l=1}^R\sum_{a=0}^{k_l-1}\binom{k_l-1}{a}\frac{({-}1)^{1-k_l+a}}{(k_l-1)!}\frac{\partial^{k_l-1-a}}{\partial s^{k_l-1-a}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}}\bigg]_{s=\beta_l(q)}\\ &\quad\times \widehat{\mathcal{T}}_{\beta_l(q),a}\nu_{\mathcal{S}}(r)\nonumber \\
&=c-\widehat{\ell}_q(r).
\end{align*}
\begin{align*}
&[ q- \Psi_{\mathcal{X}}(r)] (\kappa(q,-r))^{-1}\nonumber\\
&=c-\sum_{l=1}^R\sum_{a=0}^{k_l-1}\binom{k_l-1}{a}\frac{({-}1)^{1-k_l+a}}{(k_l-1)!}\frac{\partial^{k_l-1-a}}{\partial s^{k_l-1-a}}\bigg[\frac{\prod_{j=1}^N(\alpha_j-s)^{n_j}(\beta_l(q)-s)^{k_l}}{\prod_{j=1}^R(\beta_j(q)-s)^{k_j}}\bigg]_{s=\beta_l(q)}\\ &\quad\times \widehat{\mathcal{T}}_{\beta_l(q),a}\nu_{\mathcal{S}}(r)\nonumber \\
&=c-\widehat{\ell}_q(r).
\end{align*}
Now we set
![]() $r=0$
in the above equality to obtain
$r=0$
in the above equality to obtain
This gives the result for case B.
In case A we have
![]() $\Psi_{{\mathcal{X}}}(r)=\lambda_1(\widehat{f}_1({-}r)-1)-G_\mathcal{S}(r)$
. For now we assume that
$\Psi_{{\mathcal{X}}}(r)=\lambda_1(\widehat{f}_1({-}r)-1)-G_\mathcal{S}(r)$
. For now we assume that
![]() ${\mathcal{S}}$
is not a compound Poisson process. In this case we know from Lemma 1 that the equation
${\mathcal{S}}$
is not a compound Poisson process. In this case we know from Lemma 1 that the equation
![]() $\Psi_{{\mathcal{X}}}(r)-q=0$
has only m roots in
$\Psi_{{\mathcal{X}}}(r)-q=0$
has only m roots in
![]() ${\mathbb{C}}_{++}$
, denoted as before, and that they have respective multiplicities
${\mathbb{C}}_{++}$
, denoted as before, and that they have respective multiplicities
![]() $k_1\equiv1,k_2,\dots,k_R$
, where
$k_1\equiv1,k_2,\dots,k_R$
, where
![]() $\sum_{j=1}^R k_j=m$
. Now we consider the numbers
$\sum_{j=1}^R k_j=m$
. Now we consider the numbers
![]() $\beta_1^*(q),\dots,\beta_m(q)^*$
as defined in (37) with
$\beta_1^*(q),\dots,\beta_m(q)^*$
as defined in (37) with
![]() $\beta_{m+1}(q)^*$
replaced by
$\beta_{m+1}(q)^*$
replaced by
![]() $\beta_\infty(n)=\sqrt{n}$
. We also take
$\beta_\infty(n)=\sqrt{n}$
. We also take
![]() $c_n=\frac{1}{n}$
. In this case, the function
$c_n=\frac{1}{n}$
. In this case, the function
![]() $\Psi_{\mathcal{X}}(r)+c_nr$
is the generalized Lundberg function of some Lévy process of the form (2) with
$\Psi_{\mathcal{X}}(r)+c_nr$
is the generalized Lundberg function of some Lévy process of the form (2) with
![]() $\gamma=0$
and drift term
$\gamma=0$
and drift term
![]() $c_n$
. Hence we can use (39) with
$c_n$
. Hence we can use (39) with
![]() $\gamma=0$
,
$\gamma=0$
,
![]() $G_{\mathcal{S}}$
instead of
$G_{\mathcal{S}}$
instead of
![]() $\Psi_{\mathcal{S}}$
, and
$\Psi_{\mathcal{S}}$
, and
![]() $c_n$
instead of c. This gives
$c_n$
instead of c. This gives
 \begin{align*}
&[ \Psi_{\mathcal{X}}(r)+c_nr-q] P_1(r)\nonumber \\
&=(\beta_\infty(n)-r)\prod_{k=1}^m[\rho^*_{k,q}-r]\sum_{l=1}^m\frac{P_1[\beta_l(q)^*]}{(\beta_\infty(n)-\beta_l(q)^*)\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}
\\ &\quad\times \bigg\{{-}\frac{G_{\mathcal{S}}(r)-G_{\mathcal{S}}(\beta_l(q)^*)}
{\beta_l(q)^*-r}\nonumber \\
&\quad+\lambda_1 \frac{\frac{Q({-}r)}{\prod_{a=1}^N(\alpha_a-r)^{n_a}}-
\frac{Q({-}\beta_l(q)^*)}
{\prod_{a=1}^N(\alpha_a-\beta_l(q)^*)^{n_a}}}{\beta_l(q)^*-r}
-c_n+\frac{\Psi_{\mathcal{X}}(\beta_l(q)^*)-q}{\beta_l(q)^*-r}
\bigg\}\nonumber \\
&\quad+(\beta_\infty(n)-r)\prod_{k=1}^m[\rho^*_{k,q}-r]\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}\bigg\{{-}\frac{G_{\mathcal{S}}(r)-G_{\mathcal{S}}(\beta_\infty(n))}{\beta_l(q)^*-r}\nonumber \\
&\quad+\lambda_1 \frac{\frac{Q({-}r)}{\prod_{a=1}^N(\alpha_a-r)^{n_a}}-\frac{Q({-}\beta_\infty(n))}{\prod_{a=1}^N(\alpha_a-\beta_\infty(n))^{n_a}}}{\beta_\infty(n)-r}
-c_n+\frac{\Psi_{\mathcal{X}}(\beta_\infty(n))-q}{\beta_\infty(n)-r}
\bigg\}.\nonumber
\end{align*}
\begin{align*}
&[ \Psi_{\mathcal{X}}(r)+c_nr-q] P_1(r)\nonumber \\
&=(\beta_\infty(n)-r)\prod_{k=1}^m[\rho^*_{k,q}-r]\sum_{l=1}^m\frac{P_1[\beta_l(q)^*]}{(\beta_\infty(n)-\beta_l(q)^*)\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}
\\ &\quad\times \bigg\{{-}\frac{G_{\mathcal{S}}(r)-G_{\mathcal{S}}(\beta_l(q)^*)}
{\beta_l(q)^*-r}\nonumber \\
&\quad+\lambda_1 \frac{\frac{Q({-}r)}{\prod_{a=1}^N(\alpha_a-r)^{n_a}}-
\frac{Q({-}\beta_l(q)^*)}
{\prod_{a=1}^N(\alpha_a-\beta_l(q)^*)^{n_a}}}{\beta_l(q)^*-r}
-c_n+\frac{\Psi_{\mathcal{X}}(\beta_l(q)^*)-q}{\beta_l(q)^*-r}
\bigg\}\nonumber \\
&\quad+(\beta_\infty(n)-r)\prod_{k=1}^m[\rho^*_{k,q}-r]\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}\bigg\{{-}\frac{G_{\mathcal{S}}(r)-G_{\mathcal{S}}(\beta_\infty(n))}{\beta_l(q)^*-r}\nonumber \\
&\quad+\lambda_1 \frac{\frac{Q({-}r)}{\prod_{a=1}^N(\alpha_a-r)^{n_a}}-\frac{Q({-}\beta_\infty(n))}{\prod_{a=1}^N(\alpha_a-\beta_\infty(n))^{n_a}}}{\beta_\infty(n)-r}
-c_n+\frac{\Psi_{\mathcal{X}}(\beta_\infty(n))-q}{\beta_\infty(n)-r}
\bigg\}.\nonumber
\end{align*}
Again, proceeding as in case C it follows that
 \begin{align}
&[ \Psi_{\mathcal{X}}(r)+c_nr-q] \frac{P_1(r)}{\prod_{j=1}^m[\beta_j(q)^*-r]} \nonumber \\
& = -c_n(\beta_\infty(n)-r)\nonumber \\
&\quad+\sum_{l=1}^m\frac{\beta_\infty(n)-r}{\beta_\infty(n)-\beta_l(q)^*}\frac{P_1[\beta_l(q)^*]}{\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}\Bigg\{\widehat{T}_{\beta_l(q)^*}\nu_\mathcal{S}(r)+\frac{\Psi_{\mathcal{X}}[\beta_l(q)^*]-q}{\beta_l(q)^*-r}\Bigg\}\nonumber \\
&\quad+\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}\big\{(\beta_\infty(n)-r)\widehat{T}_{\beta_\infty(n)}\nu_\mathcal{S}(r)+( \Psi_{\mathcal{X}}[\beta_\infty(n)]-q)\big\}\nonumber\\
&=-c_n(\beta_\infty(n)-r)+\sum_{l=1}^m\frac{\beta_\infty(n)-r}{\beta_\infty(n)-\beta_l(q)^*}\frac{P_1[\beta_l(q)^*]}{\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}\bigg\{\widehat{T}_{\beta_l(q)^*}\nu_\mathcal{S}(r)
\nonumber \\
&\quad+\frac{\Psi_{\mathcal{X}}[\beta_l(q)^*]-q}{\beta_l(q)^*-r}\bigg\}
+\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}\bigg\{{-}G_\mathcal{S}(r)+G_\mathcal{S}(\beta_\infty(n))
\nonumber \\
&\quad+( \Psi_{\mathcal{X}}[\beta_\infty(n)]-q)\bigg\},\nonumber
\end{align}
\begin{align}
&[ \Psi_{\mathcal{X}}(r)+c_nr-q] \frac{P_1(r)}{\prod_{j=1}^m[\beta_j(q)^*-r]} \nonumber \\
& = -c_n(\beta_\infty(n)-r)\nonumber \\
&\quad+\sum_{l=1}^m\frac{\beta_\infty(n)-r}{\beta_\infty(n)-\beta_l(q)^*}\frac{P_1[\beta_l(q)^*]}{\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}\Bigg\{\widehat{T}_{\beta_l(q)^*}\nu_\mathcal{S}(r)+\frac{\Psi_{\mathcal{X}}[\beta_l(q)^*]-q}{\beta_l(q)^*-r}\Bigg\}\nonumber \\
&\quad+\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}\big\{(\beta_\infty(n)-r)\widehat{T}_{\beta_\infty(n)}\nu_\mathcal{S}(r)+( \Psi_{\mathcal{X}}[\beta_\infty(n)]-q)\big\}\nonumber\\
&=-c_n(\beta_\infty(n)-r)+\sum_{l=1}^m\frac{\beta_\infty(n)-r}{\beta_\infty(n)-\beta_l(q)^*}\frac{P_1[\beta_l(q)^*]}{\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}\bigg\{\widehat{T}_{\beta_l(q)^*}\nu_\mathcal{S}(r)
\nonumber \\
&\quad+\frac{\Psi_{\mathcal{X}}[\beta_l(q)^*]-q}{\beta_l(q)^*-r}\bigg\}
+\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}\bigg\{{-}G_\mathcal{S}(r)+G_\mathcal{S}(\beta_\infty(n))
\nonumber \\
&\quad+( \Psi_{\mathcal{X}}[\beta_\infty(n)]-q)\bigg\},\nonumber
\end{align}
where in the second equality we have used that
Now we substitute
in the above equality and rearrange terms to obtain
 \begin{align}
&[ \Psi_{\mathcal{X}}(r)+c_nr-q] \frac{P_1(r)}{\prod_{j=1}^m[\beta_j(q)^*-r]}\nonumber \\
&=-c_n(\beta_\infty(n)-r)+\sum_{l=1}^m\frac{\beta_\infty(n)-r}{\beta_\infty(n)-\beta_l(q)^*}\frac{P_1[\beta_l(q)^*]}{\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}\bigg\{\widehat{T}_{\beta_l(q)^*}\nu_\mathcal{S}(r) \nonumber \\
&\quad+\frac{\Psi_{\mathcal{X}}[\beta_l(q)^*]-q}{\beta_l(q)^*-r}\bigg\}-\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}G_\mathcal{S}(r)\nonumber \\
&\quad+\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}\bigg\{c_n\beta_\infty(n)+\lambda_1\frac{Q({-}\beta_\infty(n))}{\prod_{a=1}^N(\alpha_a-\beta_\infty(n))^{n_a}}-(\lambda_1+q)\bigg\} .
\end{align}
\begin{align}
&[ \Psi_{\mathcal{X}}(r)+c_nr-q] \frac{P_1(r)}{\prod_{j=1}^m[\beta_j(q)^*-r]}\nonumber \\
&=-c_n(\beta_\infty(n)-r)+\sum_{l=1}^m\frac{\beta_\infty(n)-r}{\beta_\infty(n)-\beta_l(q)^*}\frac{P_1[\beta_l(q)^*]}{\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}\bigg\{\widehat{T}_{\beta_l(q)^*}\nu_\mathcal{S}(r) \nonumber \\
&\quad+\frac{\Psi_{\mathcal{X}}[\beta_l(q)^*]-q}{\beta_l(q)^*-r}\bigg\}-\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}G_\mathcal{S}(r)\nonumber \\
&\quad+\frac{P_1[\beta_\infty(n)]}{\prod_{j=1}^m[\beta_j(q)^*-\beta_\infty(n)]}\bigg\{c_n\beta_\infty(n)+\lambda_1\frac{Q({-}\beta_\infty(n))}{\prod_{a=1}^N(\alpha_a-\beta_\infty(n))^{n_a}}-(\lambda_1+q)\bigg\} .
\end{align}
Since both polynomials
![]() $P_1(r)=\prod_{j=1}^N(\alpha_j-r)^{n_j}$
and
$P_1(r)=\prod_{j=1}^N(\alpha_j-r)^{n_j}$
and
![]() $\prod_{j=1}^m(\beta_j(q)^*-r)$
have degree m, and since Q(r) given in (3) is a polynomial of degree at most
$\prod_{j=1}^m(\beta_j(q)^*-r)$
have degree m, and since Q(r) given in (3) is a polynomial of degree at most
![]() $m-1$
, it follows that for any fixed r and s such that
$m-1$
, it follows that for any fixed r and s such that
![]() $r\neq \beta_\infty(n)$
and
$r\neq \beta_\infty(n)$
and
![]() $s\neq \beta_\infty(n)$
,
$s\neq \beta_\infty(n)$
,
and
Hence, letting
![]() $n\rightarrow\infty$
on both sides of (44) we get
$n\rightarrow\infty$
on both sides of (44) we get
 \begin{align}
&[ q-\Psi_{\mathcal{X}}(r)]\frac{\prod_{j=1}^N(\alpha_j-r)^{n_j}}{\prod_{j=1}^m(\beta_j(q)^*-r)}\nonumber \\
&=-\sum_{l=1}^m\frac{P_1[\beta_l(q)^*]}{\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}\bigg\{\widehat{T}_{\beta_l(q)^*}\nu_\mathcal{S}(r)+\frac{\Psi_{\mathcal{X}}[\beta_l(q)^*]-q}{\beta_l(q)^*-r}\bigg\}+G_\mathcal{S}(r)+\lambda_1+q.\nonumber
\end{align}
\begin{align}
&[ q-\Psi_{\mathcal{X}}(r)]\frac{\prod_{j=1}^N(\alpha_j-r)^{n_j}}{\prod_{j=1}^m(\beta_j(q)^*-r)}\nonumber \\
&=-\sum_{l=1}^m\frac{P_1[\beta_l(q)^*]}{\prod_{j\neq l}[\beta_j(q)^*-\beta_l(q)^*]}\bigg\{\widehat{T}_{\beta_l(q)^*}\nu_\mathcal{S}(r)+\frac{\Psi_{\mathcal{X}}[\beta_l(q)^*]-q}{\beta_l(q)^*-r}\bigg\}+G_\mathcal{S}(r)+\lambda_1+q.\nonumber
\end{align}
The remaining part of the proof is similar to cases B and C using Lemma 3.
The case when
![]() ${\mathcal{S}}$
is a compound Poisson process with
${\mathcal{S}}$
is a compound Poisson process with
![]() ${\mathrm{E}}[ {\mathcal{S}}(1)]>0$
is obtained from case B as follows.
${\mathrm{E}}[ {\mathcal{S}}(1)]>0$
is obtained from case B as follows.
When
![]() $c=0$
we have
$c=0$
we have
![]() $\Psi_{\mathcal{X}}'(r)\big|_{r=0+}=\lambda_1\mu_1-\lambda_2\mu_2$
, and hence
$\Psi_{\mathcal{X}}'(r)\big|_{r=0+}=\lambda_1\mu_1-\lambda_2\mu_2$
, and hence
![]() $\psi_{\mathcal{X}}(r)-q=0$
has m roots under the assumption that
$\psi_{\mathcal{X}}(r)-q=0$
has m roots under the assumption that
![]() $\lambda_1\mu_1-\lambda_2\mu_2>0$
.
$\lambda_1\mu_1-\lambda_2\mu_2>0$
.
If
![]() ${\mathcal{X}}_c$
denotes the process
${\mathcal{X}}_c$
denotes the process
![]() ${\mathcal{X}}$
with drift
${\mathcal{X}}$
with drift
![]() $c>0$
when
$c>0$
when
![]() ${\mathcal{S}}$
is a subordinator and
${\mathcal{S}}$
is a subordinator and
![]() ${\mathcal{X}}$
denotes the same process with
${\mathcal{X}}$
denotes the same process with
![]() $c=0$
then we have
$c=0$
then we have
![]() $\psi_{{\mathcal{X}}_c}(r)\to\psi_{\mathcal{X}}(r)$
for all
$\psi_{{\mathcal{X}}_c}(r)\to\psi_{\mathcal{X}}(r)$
for all
![]() $r>0$
when
$r>0$
when
![]() $c\downarrow0$
.
$c\downarrow0$
.
This implies that the roots of
![]() $\psi_{{\mathcal{X}}_c}(r)-q$
must converge to those of
$\psi_{{\mathcal{X}}_c}(r)-q$
must converge to those of
![]() $\psi_{{\mathcal{X}}}(r)-q$
, but since the latter function has only m roots, one of the roots of
$\psi_{{\mathcal{X}}}(r)-q$
, but since the latter function has only m roots, one of the roots of
![]() $\psi_{{\mathcal{X}}_c}(r)-q$
(say
$\psi_{{\mathcal{X}}_c}(r)-q$
(say
![]() $\beta_{m+1}(q)$
) must converge to infinity when
$\beta_{m+1}(q)$
) must converge to infinity when
![]() $c\downarrow0$
. Hence the result is obtained by the same procedure as before, replacing
$c\downarrow0$
. Hence the result is obtained by the same procedure as before, replacing
![]() $c_n$
by c and
$c_n$
by c and
![]() $\beta_\infty(n)$
by
$\beta_\infty(n)$
by
![]() $\beta_{m+1}(q)$
.
$\beta_{m+1}(q)$
.
Acknowledgements
The authors are grateful to the two anonymous referees for their careful reading of the paper and for many useful suggestions which greatly improved the presentation of the results. The first-named author appreciates partial support from CONACyT Grant No. 257867.