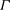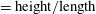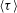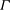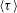1. Introduction
Turbulent Rayleigh–Bénard (RB) convection in a fluid heated from below and cooled from above has been a subject of longstanding interest and has many applications in science and engineering (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012; Xia Reference Xia2013). A salient feature of turbulent RB convection is a large-scale circulation (LSC) superimposed on the turbulent background. The LSC in three-dimensional (3D) cylindrical cells of aspect ratio around one has a quasi-2D single-roll structure with a finite width of approximately half the cell diameter (Xi, Zhou & Xia Reference Xi, Zhou and Xia2006). Driven by the small-scale turbulent fluctuations, the vertical circulating plane of the LSC has an incessant azimuthal meandering in this particular geometry (Cioni, Ciliberto & Sommeria Reference Cioni, Ciliberto and Sommeria1997; Brown, Nikolaenko & Ahlers Reference Brown, Nikolaenko and Ahlers2005; Sun, Xi & Xia Reference Sun, Xi and Xia2005; Xi et al. Reference Xi, Zhou and Xia2006). In addition, the LSC sometimes stops and restarts in a different direction, termed cessation. When the new direction is opposite to the one before cessation, this event is called reversal (Cioni et al. Reference Cioni, Ciliberto and Sommeria1997; Brown et al. Reference Brown, Nikolaenko and Ahlers2005; Tsuji et al. Reference Tsuji, Mizuno, Mashiko and Sano2005; Xi et al. Reference Xi, Zhou and Xia2006; Xi & Xia Reference Xi and Xia2007), which has also been observed in the magnetic polarity of the Earth (Glatzmaier et al. Reference Glatzmaier, Coe, Hongre and Roberts1999) and in the wind direction in the Earth’s atmosphere (van Doorn et al. Reference van Doorn, Dhruva, Sreenivasan and Cassella2000).
The observed reversal phenomenon of the LSC has prompted several models based on either stochastic differential equations (Sreenivasan, Bershadskii & Niemela Reference Sreenivasan, Bershadskii and Niemela2002; Benzi Reference Benzi2005) or deterministic ones (Araujo, Grossmann & Lohse Reference Araujo, Grossmann and Lohse2005). All of these 2D models are able to produce switchings between two bistable states. However, as they are not derived from the equations of motion, it is not possible for them to make quantitative comparisons between model predictions and experimentally measured quantities. Motivated by this, Brown & Ahlers (Reference Brown and Ahlers2007, Reference Brown and Ahlers2008) proposed a deterministic model consisting of two coupled stochastic ordinary differential equations that were able to produce some of the important features of the LSC in 3D RB convection, such as cessations and the azimuthal meandering. Later, Assaf, Angheluta & Goldenfeld (Reference Assaf, Angheluta and Goldenfeld2011) improved the model by including the diffusion effect in the equation.
A common feature in all of the previous models is the assumption, either explicitly or implicitly, that the cessations (and reversals) of the LSC are largely independent of its azimuthal orientational dynamics. An intuitive expectation would be that if one confines the LSC into a 2D or quasi-2D convection cell, the geometry will limit the azimuthal position of the LSC plane, and with the removal of the complicated 3D dynamics, some essential features of the reversal dynamics may be revealed. Motivated by this, Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010) made a combined experimental and numerical study of LSC reversals in the 2D/quasi-2D system, which covered a wide region of the
![]() $Ra{-}Pr$
phase space (
$Ra{-}Pr$
phase space (
![]() $Ra$
: Rayleigh number;
$Ra$
: Rayleigh number;
![]() $Pr$
: Prandtl number. Their exact definitions can be found in § 2). Their study revealed the key role played by the corner rolls in triggering reversal events and found an important difference between the 2D/quasi-2D and the 3D geometries, i.e. the mean time between successive reversals has a strong
$Pr$
: Prandtl number. Their exact definitions can be found in § 2). Their study revealed the key role played by the corner rolls in triggering reversal events and found an important difference between the 2D/quasi-2D and the 3D geometries, i.e. the mean time between successive reversals has a strong
![]() $Ra$
dependence in the former and is essentially
$Ra$
dependence in the former and is essentially
![]() $Ra$
-independent in the latter (Brown & Ahlers Reference Brown and Ahlers2006; Xi & Xia Reference Xi and Xia2007). The importance of the corner rolls was also found later by a number of numerical and experimental studies in the 2D/quasi-2D system (Chandra & Verma Reference Chandra and Verma2011, Reference Chandra and Verma2013; Vasilev & Frick Reference Vasilev and Frick2011; Yanagisawa et al.
Reference Yanagisawa, Yamagishi, Hamano, Tasaka and Takeda2011; Wagner & Shishkina Reference Wagner and Shishkina2013). As the dynamics of flow reversals appears to have quite different dimensional dependence, the question then is whether flow reversals in the RB system in the 2D and 3D cases can be described by a unified framework. A related question would be how to quantify the role played by the corner rolls.
$Ra$
-independent in the latter (Brown & Ahlers Reference Brown and Ahlers2006; Xi & Xia Reference Xi and Xia2007). The importance of the corner rolls was also found later by a number of numerical and experimental studies in the 2D/quasi-2D system (Chandra & Verma Reference Chandra and Verma2011, Reference Chandra and Verma2013; Vasilev & Frick Reference Vasilev and Frick2011; Yanagisawa et al.
Reference Yanagisawa, Yamagishi, Hamano, Tasaka and Takeda2011; Wagner & Shishkina Reference Wagner and Shishkina2013). As the dynamics of flow reversals appears to have quite different dimensional dependence, the question then is whether flow reversals in the RB system in the 2D and 3D cases can be described by a unified framework. A related question would be how to quantify the role played by the corner rolls.
In this paper, we report an experimental study of flow reversals in a quasi-2D geometry. We use the aspect ratio
![]() ${\it\Gamma}$
(
${\it\Gamma}$
(
![]() $=\text{height}/\text{length}$
of the vertical plane in a rectangular box) as a tuning parameter for the weight of the corner rolls relative to that of the LSC. It should be noted that in Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010) it was already found that
$=\text{height}/\text{length}$
of the vertical plane in a rectangular box) as a tuning parameter for the weight of the corner rolls relative to that of the LSC. It should be noted that in Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010) it was already found that
![]() ${\it\Gamma}$
has a strong effect on the flow dynamics, but no quantitative and systematic study on the effect of
${\it\Gamma}$
has a strong effect on the flow dynamics, but no quantitative and systematic study on the effect of
![]() ${\it\Gamma}$
was made. The remainder of the paper is organized as follows. In § 2, we give a brief discussion of the experimental methods and the algorithm used to extract the reversal events. In § 3, we present the statistics of the time intervals between successive reversals and its dependence on the Rayleigh number and aspect ratio. We explain our experimental observations by extending the model of Brown & Ahlers (Reference Brown and Ahlers2007, Reference Brown and Ahlers2008) to include the effects of corner rolls and thermal diffusion through thermal plumes. Our model not only accurately reproduces the experimental findings, but may also be used to bridge the differences between 2D and 3D systems.
${\it\Gamma}$
was made. The remainder of the paper is organized as follows. In § 2, we give a brief discussion of the experimental methods and the algorithm used to extract the reversal events. In § 3, we present the statistics of the time intervals between successive reversals and its dependence on the Rayleigh number and aspect ratio. We explain our experimental observations by extending the model of Brown & Ahlers (Reference Brown and Ahlers2007, Reference Brown and Ahlers2008) to include the effects of corner rolls and thermal diffusion through thermal plumes. Our model not only accurately reproduces the experimental findings, but may also be used to bridge the differences between 2D and 3D systems.
2. Methods
It is known that the reversal dynamics is very sensitive to the aspect ratio
![]() ${\it\Gamma}$
in 3D (Xi & Xia Reference Xi and Xia2007) and in 2D/quasi-2D (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). In this study we use
${\it\Gamma}$
in 3D (Xi & Xia Reference Xi and Xia2007) and in 2D/quasi-2D (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). In this study we use
![]() ${\it\Gamma}$
as a parameter to perturb the stability of the LSC and also test our proposed model. Six convection cells are used, which are vertical rectangular boxes with top and bottom copper plates and plexiglas sidewalls (Xia, Sun & Zhou Reference Xia, Sun and Zhou2003). They have the same horizontal cross-section of 126.0
${\it\Gamma}$
as a parameter to perturb the stability of the LSC and also test our proposed model. Six convection cells are used, which are vertical rectangular boxes with top and bottom copper plates and plexiglas sidewalls (Xia, Sun & Zhou Reference Xia, Sun and Zhou2003). They have the same horizontal cross-section of 126.0
![]() $(L)\times 38.0\,(W)\,(\text{mm}^{2})$
, but have heights
$(L)\times 38.0\,(W)\,(\text{mm}^{2})$
, but have heights
![]() $H$
(mm) of 150.0, 140.8, 131.4, 126.3, 121.0 and 114.6. The corresponding aspect ratios
$H$
(mm) of 150.0, 140.8, 131.4, 126.3, 121.0 and 114.6. The corresponding aspect ratios
![]() ${\it\Gamma}=H/L$
are thus 0.84, 0.89, 0.96, 1.00, 1.04 and 1.10. All experiments are conducted at the same Prandtl numbers
${\it\Gamma}=H/L$
are thus 0.84, 0.89, 0.96, 1.00, 1.04 and 1.10. All experiments are conducted at the same Prandtl numbers
![]() $Pr\,(={\it\nu}/{\it\kappa})=5.7$
, with the Rayleigh number
$Pr\,(={\it\nu}/{\it\kappa})=5.7$
, with the Rayleigh number
![]() $Ra\,(={\it\alpha}g{\rm\Delta}TH^{3}/{\it\nu}{\it\kappa})$
spanning from
$Ra\,(={\it\alpha}g{\rm\Delta}TH^{3}/{\it\nu}{\it\kappa})$
spanning from
![]() $10^{8}$
to
$10^{8}$
to
![]() $2\times 10^{9}$
. Here,
$2\times 10^{9}$
. Here,
![]() ${\rm\Delta}T$
is the temperature difference across the fluid layer,
${\rm\Delta}T$
is the temperature difference across the fluid layer,
![]() $g$
is the gravitational acceleration, and
$g$
is the gravitational acceleration, and
![]() ${\it\alpha}$
,
${\it\alpha}$
,
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() ${\it\kappa}$
are the thermal expansion coefficient, kinematic viscosity and thermal diffusivity of water respectively. With the rectangular geometry, the large-scale flow is expected to be largely confined in the vertical
${\it\kappa}$
are the thermal expansion coefficient, kinematic viscosity and thermal diffusivity of water respectively. With the rectangular geometry, the large-scale flow is expected to be largely confined in the vertical
![]() $LH$
plane (Xia et al.
Reference Xia, Sun and Zhou2003). During a reversal process, the hot rising and cold falling plumes will switch their positions, causing the temperature change in the left and right sides of the plate. This allows us to use their contrast
$LH$
plane (Xia et al.
Reference Xia, Sun and Zhou2003). During a reversal process, the hot rising and cold falling plumes will switch their positions, causing the temperature change in the left and right sides of the plate. This allows us to use their contrast
![]() ${\it\Delta}_{bot}=T_{bot,right}-T_{bot,left}$
as a measure of reversals of the LSC (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010), where
${\it\Delta}_{bot}=T_{bot,right}-T_{bot,left}$
as a measure of reversals of the LSC (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010), where
![]() $T_{bot,right}$
and
$T_{bot,right}$
and
![]() $T_{bot,left}$
are the temperatures measured by the thermistors embedded inside the bottom plate:
$T_{bot,left}$
are the temperatures measured by the thermistors embedded inside the bottom plate:
![]() ${\sim}2$
mm away from the fluid–copper interface,
${\sim}2$
mm away from the fluid–copper interface,
![]() $W/2$
from the long edges and
$W/2$
from the long edges and
![]() $L/4$
away from its right and left edges respectively. The typical value of the ratio
$L/4$
away from its right and left edges respectively. The typical value of the ratio
![]() ${\it\Delta}_{bot}/{\rm\Delta}T$
is approximately
${\it\Delta}_{bot}/{\rm\Delta}T$
is approximately
![]() $0.05$
.
$0.05$
.
3. Results and discussion
Figure 1 shows typical time series of
![]() ${\it\Delta}_{bot}$
for four values of
${\it\Delta}_{bot}$
for four values of
![]() $Ra$
ranging from
$Ra$
ranging from
![]() $4.27\times 10^{8}$
to
$4.27\times 10^{8}$
to
![]() $2.38\times 10^{9}$
in the
$2.38\times 10^{9}$
in the
![]() ${\it\Gamma}=0.89$
cell. In the plot,
${\it\Gamma}=0.89$
cell. In the plot,
![]() ${\it\Delta}_{bot}$
is normalized by the standard deviation
${\it\Delta}_{bot}$
is normalized by the standard deviation
![]() ${\it\sigma}$
of
${\it\sigma}$
of
![]() ${\it\Delta}_{bot}$
for either flow direction and the time
${\it\Delta}_{bot}$
for either flow direction and the time
![]() $t$
is normalized by the LSC turnover time
$t$
is normalized by the LSC turnover time
![]() $t_{E}=(2H+2L)/U$
, where
$t_{E}=(2H+2L)/U$
, where
![]() $U$
is the typical velocity of the LSC measured at
$U$
is the typical velocity of the LSC measured at
![]() ${\sim}H/10$
from the sidewalls and plates in a similar set-up using laser Doppler velocimetry (Xia, Zhou & Sun Reference Xia, Zhou and Sun2005). It is seen that there are several events with abrupt changes of temperature for all four examples shown here, and the frequency of reversal seems to increase with decreasing Rayleigh number. To quantitatively discuss the reversal frequency, we define the start (
${\sim}H/10$
from the sidewalls and plates in a similar set-up using laser Doppler velocimetry (Xia, Zhou & Sun Reference Xia, Zhou and Sun2005). It is seen that there are several events with abrupt changes of temperature for all four examples shown here, and the frequency of reversal seems to increase with decreasing Rayleigh number. To quantitatively discuss the reversal frequency, we define the start (
![]() $t_{s}$
) and end (
$t_{s}$
) and end (
![]() $t_{e}$
) times of one reversal event as the respective time instant when
$t_{e}$
) times of one reversal event as the respective time instant when
![]() ${\it\Delta}_{bot}$
departs from one state and reaches the other one. Three reversals determined in this way are marked by the red circles (
${\it\Delta}_{bot}$
departs from one state and reaches the other one. Three reversals determined in this way are marked by the red circles (
![]() $t_{s}$
) and blue triangles (
$t_{s}$
) and blue triangles (
![]() $t_{e}$
) in figure 1(a). We further define the time interval between two successive reversals
$t_{e}$
) in figure 1(a). We further define the time interval between two successive reversals
![]() $n$
and
$n$
and
![]() $n+1$
as
$n+1$
as
![]() ${\it\tau}=t_{s}(n+1)-t_{e}(n)$
, using the criterion that after each reversal the flow must persist in the new direction for at least one LSC turnover time
${\it\tau}=t_{s}(n+1)-t_{e}(n)$
, using the criterion that after each reversal the flow must persist in the new direction for at least one LSC turnover time
![]() $t_{E}$
. The bistable behaviour of the LSC can also be seen from the probability density function (PDF) of
$t_{E}$
. The bistable behaviour of the LSC can also be seen from the probability density function (PDF) of
![]() ${\it\Delta}_{bot}/{\it\sigma}$
shown in figure 2. The
${\it\Delta}_{bot}/{\it\sigma}$
shown in figure 2. The
![]() $Ra$
dependence of the normalized mean time interval between successive reversals
$Ra$
dependence of the normalized mean time interval between successive reversals
![]() $\langle {\it\tau}\rangle /t_{E}$
for different values of
$\langle {\it\tau}\rangle /t_{E}$
for different values of
![]() ${\it\Gamma}$
is shown in figure 3. It is seen that there is a strong
${\it\Gamma}$
is shown in figure 3. It is seen that there is a strong
![]() $Ra$
dependence of the mean time interval for all values of
$Ra$
dependence of the mean time interval for all values of
![]() ${\it\Gamma}$
, and the dependence, surprisingly, cannot be explained by a simple power-law relationship. Moreover, unlike the aspect ratio dependence of the Reynolds number (Lam et al.
Reference Lam, Shang, Zhou and Xia2002), there is no simple function of
${\it\Gamma}$
, and the dependence, surprisingly, cannot be explained by a simple power-law relationship. Moreover, unlike the aspect ratio dependence of the Reynolds number (Lam et al.
Reference Lam, Shang, Zhou and Xia2002), there is no simple function of
![]() ${\it\Gamma}$
that can collapse all curves.
${\it\Gamma}$
that can collapse all curves.

Figure 1. Time series of the normalized bottom plate temperature difference
![]() ${\it\Delta}_{bot}/{\it\sigma}$
for four Rayleigh numbers, (a)
${\it\Delta}_{bot}/{\it\sigma}$
for four Rayleigh numbers, (a)
![]() $2.38\times 10^{9}$
, (b)
$2.38\times 10^{9}$
, (b)
![]() $1.02\times 10^{9}$
, (c)
$1.02\times 10^{9}$
, (c)
![]() $6.55\times 10^{8}$
, (d)
$6.55\times 10^{8}$
, (d)
![]() $4.27\times 10^{8}$
, in
$4.27\times 10^{8}$
, in
![]() ${\it\Gamma}=0.89$
. The red circles and blue triangles in (a) are respectively reversal start points and end points determined by using the criterion described in the text.
${\it\Gamma}=0.89$
. The red circles and blue triangles in (a) are respectively reversal start points and end points determined by using the criterion described in the text.

Figure 2. The PDF of the normalized LSC amplitude
![]() ${\it\Delta}_{bot}/{\it\sigma}$
(
${\it\Delta}_{bot}/{\it\sigma}$
(
![]() $Ra=2.38\times 10^{9}$
,
$Ra=2.38\times 10^{9}$
,
![]() ${\it\Gamma}=0.89$
). The solid line is the fitting result using the sum of two independent Gaussian functions. The two dashed lines show the most probable states corresponding to the two circulation directions of the LSC.
${\it\Gamma}=0.89$
). The solid line is the fitting result using the sum of two independent Gaussian functions. The two dashed lines show the most probable states corresponding to the two circulation directions of the LSC.

Figure 3. The Rayleigh number dependence of the normalized mean time interval between two successive reversals
![]() $\langle {\it\tau}\rangle$
. From left to right, the symbols represent
$\langle {\it\tau}\rangle$
. From left to right, the symbols represent
![]() ${\it\Gamma}=1.10$
(black left-pointing triangle), 1.04 (blue triangle), 1.00 (two independent measurements, yellow right-pointing triangles and green squares), 1.00 (green circles, simulation data from Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010)), 0.96 (red down-pointing triangle), 0.89 (magenta crosses), 0.84 (cyan diamonds). See the text for the explanation of the solid lines.
${\it\Gamma}=1.10$
(black left-pointing triangle), 1.04 (blue triangle), 1.00 (two independent measurements, yellow right-pointing triangles and green squares), 1.00 (green circles, simulation data from Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010)), 0.96 (red down-pointing triangle), 0.89 (magenta crosses), 0.84 (cyan diamonds). See the text for the explanation of the solid lines.
The stochastic model proposed by Brown and Ahlers can explain the experimental results well in a three-dimensional cylindrical cell (Brown & Ahlers Reference Brown and Ahlers2007, Reference Brown and Ahlers2008). The model is motivated from the physically relevant terms in the Navier–Stokes equation for the Rayleigh–Bénard convection (Brown & Ahlers Reference Brown and Ahlers2008). This model predicts a skewed PDF of the LSC amplitude that favours a small LSC amplitude (Brown & Ahlers Reference Brown and Ahlers2008), which is very different from the Gaussian distribution of
![]() ${\it\Delta}_{bot}$
for the quasi-2D case as shown in figure 2. This is another feature that differentiates 3D from 2D/quasi-2D cases, apart from that of the mean time between successive reversals (or reversal frequency). We now extend the Brown–Ahlers model to explain the reversal behaviour of the LSC in quasi-2D geometry. Following the same procedure as that in Brown & Ahlers (Reference Brown and Ahlers2007) and using
${\it\Delta}_{bot}$
for the quasi-2D case as shown in figure 2. This is another feature that differentiates 3D from 2D/quasi-2D cases, apart from that of the mean time between successive reversals (or reversal frequency). We now extend the Brown–Ahlers model to explain the reversal behaviour of the LSC in quasi-2D geometry. Following the same procedure as that in Brown & Ahlers (Reference Brown and Ahlers2007) and using
![]() ${\it\delta}$
, the absolute value of
${\it\delta}$
, the absolute value of
![]() ${\it\Delta}_{bot}$
, for the LSC strength, we derived the Langevin equation for the 2D geometry and found it to be
${\it\Delta}_{bot}$
, for the LSC strength, we derived the Langevin equation for the 2D geometry and found it to be
where
![]() ${\it\tau}_{{\it\delta}}=H^{2}/(108{\it\nu}Re^{1/2})$
and
${\it\tau}_{{\it\delta}}=H^{2}/(108{\it\nu}Re^{1/2})$
and
![]() ${\it\delta}_{0}=216Re^{3/2}{\it\nu}^{2}/({\it\alpha}gH^{3})$
. We also note that (3.1) is the same as that in Brown & Ahlers (Reference Brown and Ahlers2007) for the azimuthal temperature amplitude which was assumed to be instantaneously proportional to the LSC flow strength. However, the coefficients in
${\it\delta}_{0}=216Re^{3/2}{\it\nu}^{2}/({\it\alpha}gH^{3})$
. We also note that (3.1) is the same as that in Brown & Ahlers (Reference Brown and Ahlers2007) for the azimuthal temperature amplitude which was assumed to be instantaneously proportional to the LSC flow strength. However, the coefficients in
![]() ${\it\tau}_{{\it\delta}}$
and
${\it\tau}_{{\it\delta}}$
and
![]() ${\it\delta}_{0}$
are slightly different from the 3D case due to the different geometries. Since
${\it\delta}_{0}$
are slightly different from the 3D case due to the different geometries. Since
![]() ${\it\delta}=|{\it\Delta}_{bot}|$
, the equation is invariant to the change of the flow directions, namely the sign of
${\it\delta}=|{\it\Delta}_{bot}|$
, the equation is invariant to the change of the flow directions, namely the sign of
![]() ${\it\Delta}_{bot}$
(see (3.4) below on how to map
${\it\Delta}_{bot}$
(see (3.4) below on how to map
![]() ${\it\delta}(t)$
back to the measured quantity
${\it\delta}(t)$
back to the measured quantity
![]() ${\it\Delta}_{bot}(t)$
).
${\it\Delta}_{bot}(t)$
).
The first two terms on the right-hand side represent respectively the buoyancy force and the viscous drag from the boundary layer. The stochastic driving term
![]() $f_{{\it\delta}}$
models the small-scale turbulent fluctuations and is assumed to be Gaussian distributed noise with zero mean. Equation (3.1) is motivated from the Navier–Stokes equation, which is only one of two governing equations for Rayleigh–Bénard convection. The other one is the heat transport equation
$f_{{\it\delta}}$
models the small-scale turbulent fluctuations and is assumed to be Gaussian distributed noise with zero mean. Equation (3.1) is motivated from the Navier–Stokes equation, which is only one of two governing equations for Rayleigh–Bénard convection. The other one is the heat transport equation
![]() ${\dot{T}}=-\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}T+{\it\kappa}{\rm\nabla}^{2}T$
. In the quasi-2D system, the main LSC is diagonally oriented in the cell and the two small diagonally opposing corner rolls are occupied by the counter-rotating rolls (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). Roughly speaking, the temperature difference across, and the velocity of, the corner rolls are of the same order as those of the main LSC roll. However, the corner rolls constantly damp the LSC because of their opposite flow directions. This may be modelled using the advective term in the heat transport equation, i.e.
${\dot{T}}=-\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}T+{\it\kappa}{\rm\nabla}^{2}T$
. In the quasi-2D system, the main LSC is diagonally oriented in the cell and the two small diagonally opposing corner rolls are occupied by the counter-rotating rolls (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). Roughly speaking, the temperature difference across, and the velocity of, the corner rolls are of the same order as those of the main LSC roll. However, the corner rolls constantly damp the LSC because of their opposite flow directions. This may be modelled using the advective term in the heat transport equation, i.e.
![]() $-\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}T\sim -{\it\nu}Re{\it\delta}/H^{2}$
. This term is proportional to
$-\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}T\sim -{\it\nu}Re{\it\delta}/H^{2}$
. This term is proportional to
![]() ${\it\delta}$
, similar to the buoyancy term that describes the driving force of the LSC. This is because the corner rolls are also fed from buoyancy force through plume detachments from the boundary layers (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). In the above, we have taken the size and velocity of the corners to be constant and have lumped their fluctuations into the stochastic term because their variations are affected by similar turbulent fluctuations. It should be noted that, due to the inertia of the growing corner roll, the stochastic term
${\it\delta}$
, similar to the buoyancy term that describes the driving force of the LSC. This is because the corner rolls are also fed from buoyancy force through plume detachments from the boundary layers (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). In the above, we have taken the size and velocity of the corners to be constant and have lumped their fluctuations into the stochastic term because their variations are affected by similar turbulent fluctuations. It should be noted that, due to the inertia of the growing corner roll, the stochastic term
![]() $f_{{\it\delta}}(t)$
in our case could be a coloured noise instead of a white noise for a 3D system. This effect would make the system favour the reversal when
$f_{{\it\delta}}(t)$
in our case could be a coloured noise instead of a white noise for a 3D system. This effect would make the system favour the reversal when
![]() ${\it\delta}$
is close to zero. However, detailed examination of these arguments is beyond the scope of this paper and should be tested in the future.
${\it\delta}$
is close to zero. However, detailed examination of these arguments is beyond the scope of this paper and should be tested in the future.
The other term in the heat equation is thermal diffusion, which has been assumed to contribute mostly in the thermal boundary layers (Brown & Ahlers Reference Brown and Ahlers2008; Assaf et al.
Reference Assaf, Angheluta and Goldenfeld2011). As the LSC is the self-organized flow of thermal plumes (Kadanoff Reference Kadanoff2001; Xi, Lam & Xia Reference Xi, Lam and Xia2004), it is important to include thermal diffusion of plumes when considering the LSC dynamics. Thermal plumes may be viewed as consisting of a cap with a sharp temperature gradient over a distance close to the thermal boundary layer thickness. Therefore the thermal diffusion of plumes is of the order of
![]() ${\it\kappa}{\rm\nabla}^{2}T\approx {\it\kappa}({\rm\Delta}T/2)/{\it\lambda}_{{\it\theta}}^{2}$
, where
${\it\kappa}{\rm\nabla}^{2}T\approx {\it\kappa}({\rm\Delta}T/2)/{\it\lambda}_{{\it\theta}}^{2}$
, where
![]() ${\it\lambda}_{{\it\theta}}$
is the thermal boundary layer thickness
${\it\lambda}_{{\it\theta}}$
is the thermal boundary layer thickness
![]() ${\it\lambda}_{{\it\theta}}=H/(2Nu)$
. This term contributes in the fractional volume
${\it\lambda}_{{\it\theta}}=H/(2Nu)$
. This term contributes in the fractional volume
![]() $V_{pl}/V$
, with
$V_{pl}/V$
, with
![]() $V_{pl}$
and
$V_{pl}$
and
![]() $V$
the volume of thermal plumes and that of the system respectively. The thickness of the thermal plumes is proportional to the thermal boundary layer thickness, so
$V$
the volume of thermal plumes and that of the system respectively. The thickness of the thermal plumes is proportional to the thermal boundary layer thickness, so
![]() $V_{pl}/V=c^{\prime }f_{pl}{\it\lambda}_{{\it\theta}}/H\times N_{pl}$
, where
$V_{pl}/V=c^{\prime }f_{pl}{\it\lambda}_{{\it\theta}}/H\times N_{pl}$
, where
![]() $N_{pl}$
is the total number of thermal plumes,
$N_{pl}$
is the total number of thermal plumes,
![]() $f_{pl}$
is the surface area ratio between the plumes and the plate, and
$f_{pl}$
is the surface area ratio between the plumes and the plate, and
![]() $c^{\prime }$
is a constant. It has been found experimentally that
$c^{\prime }$
is a constant. It has been found experimentally that
![]() $N_{pl}$
is related to
$N_{pl}$
is related to
![]() $Nu$
, i.e.
$Nu$
, i.e.
![]() $N_{pl}\sim Nu$
, and
$N_{pl}\sim Nu$
, and
![]() $f_{pl}\sim Ra^{0.23}$
(Zhou & Xia Reference Zhou and Xia2010). The experiment by Zhou & Xia (Reference Zhou and Xia2010) was conducted in three cells with different aspect ratios, and it was found that there is a positive relation between
$f_{pl}\sim Ra^{0.23}$
(Zhou & Xia Reference Zhou and Xia2010). The experiment by Zhou & Xia (Reference Zhou and Xia2010) was conducted in three cells with different aspect ratios, and it was found that there is a positive relation between
![]() $N_{pl}$
and
$N_{pl}$
and
![]() ${\it\Gamma}$
, but the exact relation is not known due to the limited choices of aspect ratio. Here, for simplicity, we assume that there is a power-law relation
${\it\Gamma}$
, but the exact relation is not known due to the limited choices of aspect ratio. Here, for simplicity, we assume that there is a power-law relation
![]() $N_{pl}\sim Nu{\it\Gamma}^{{\it\alpha}}$
with
$N_{pl}\sim Nu{\it\Gamma}^{{\it\alpha}}$
with
![]() ${\it\alpha}>0$
. With the two extra terms from the heat transport equation added to (3.1), we have
${\it\alpha}>0$
. With the two extra terms from the heat transport equation added to (3.1), we have
where
![]() $V_{c}({\it\Gamma})$
and
$V_{c}({\it\Gamma})$
and
![]() $C$
are two prefactors that represent the geometrical coefficients from volume averaging, and
$C$
are two prefactors that represent the geometrical coefficients from volume averaging, and
![]() $C$
also contains the prefactor
$C$
also contains the prefactor
![]() $c^{\prime }$
in the plume volume ratio
$c^{\prime }$
in the plume volume ratio
![]() $V_{pl}/V$
. The equation represents a generic model that should apply to both 2D and 3D cases. We remark, however, that in addition to the corner roll term, the thermal diffusion term in the present model represents thermal diffusion in the bulk rather than in the boundary layers as in the previous 3D models (Brown & Ahlers Reference Brown and Ahlers2008; Assaf et al.
Reference Assaf, Angheluta and Goldenfeld2011), as thermal diffusion is bulk-dominated after volume averaging (He, Tong & Xia Reference He, Tong and Xia2007).
$V_{pl}/V$
. The equation represents a generic model that should apply to both 2D and 3D cases. We remark, however, that in addition to the corner roll term, the thermal diffusion term in the present model represents thermal diffusion in the bulk rather than in the boundary layers as in the previous 3D models (Brown & Ahlers Reference Brown and Ahlers2008; Assaf et al.
Reference Assaf, Angheluta and Goldenfeld2011), as thermal diffusion is bulk-dominated after volume averaging (He, Tong & Xia Reference He, Tong and Xia2007).
We next simplify the model for the 2D case. The factor
![]() $V_{c}({\it\Gamma})$
controls the contribution of the corner roll relative to that of the LSC main roll and in principle depends on the aspect ratio. We set it as a constant for now as a first-order approximation, but will later make higher-order corrections using experimentally determined potential parameters. Based on experimental observations, we set the volume ratio between the corner roll and the main LSC roll to be
$V_{c}({\it\Gamma})$
controls the contribution of the corner roll relative to that of the LSC main roll and in principle depends on the aspect ratio. We set it as a constant for now as a first-order approximation, but will later make higher-order corrections using experimentally determined potential parameters. Based on experimental observations, we set the volume ratio between the corner roll and the main LSC roll to be
![]() $0.1$
. As the geometrical coefficient for the main LSC roll is 108 in the first term
$0.1$
. As the geometrical coefficient for the main LSC roll is 108 in the first term
![]() ${\it\delta}/{\it\tau}_{{\it\delta}}$
, this gives
${\it\delta}/{\it\tau}_{{\it\delta}}$
, this gives
![]() $V_{c}\approx 10.8$
. For a median value of
$V_{c}\approx 10.8$
. For a median value of
![]() $Ra$
in our parameter range,
$Ra$
in our parameter range,
![]() ${\it\delta}=0.1$
K and
${\it\delta}=0.1$
K and
![]() $Re=5000$
, the damping force from the corner roll is thus
$Re=5000$
, the damping force from the corner roll is thus
![]() $10.8{\it\nu}Re{\it\delta}/H^{2}=0.28$
, which is much larger than the damping from the viscous boundary layer
$10.8{\it\nu}Re{\it\delta}/H^{2}=0.28$
, which is much larger than the damping from the viscous boundary layer
![]() $\sqrt{54{\it\alpha}g}Re^{-1/4}{\it\delta}^{3/2}/H^{1/2}=4\times 10^{-3}$
. This quantitative result is consistent with the previous observation that the growth of the corner roll is the main force that damps the LSC and leads to reversals (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). Therefore the equation becomes a linear differential equation,
$\sqrt{54{\it\alpha}g}Re^{-1/4}{\it\delta}^{3/2}/H^{1/2}=4\times 10^{-3}$
. This quantitative result is consistent with the previous observation that the growth of the corner roll is the main force that damps the LSC and leads to reversals (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). Therefore the equation becomes a linear differential equation,
where
![]() $A=-1/{\it\tau}_{{\it\delta}}+10.8{\it\nu}Re/H^{2}$
and
$A=-1/{\it\tau}_{{\it\delta}}+10.8{\it\nu}Re/H^{2}$
and
![]() $B=C{\it\kappa}{\rm\Delta}TNu^{2}Ra^{0.23}{\it\Gamma}^{{\it\alpha}}/H^{2}$
. To obtain the measurable quantity
$B=C{\it\kappa}{\rm\Delta}TNu^{2}Ra^{0.23}{\it\Gamma}^{{\it\alpha}}/H^{2}$
. To obtain the measurable quantity
![]() ${\it\Delta}_{bot}$
, we recall that
${\it\Delta}_{bot}$
, we recall that
![]() ${\it\delta}=|{\it\Delta}_{bot}|$
, thus
${\it\delta}=|{\it\Delta}_{bot}|$
, thus
![]() ${\it\Delta}_{bot}$
can be numerically solved from
${\it\Delta}_{bot}$
can be numerically solved from
In contrast to
![]() ${\it\delta}(t)$
, the quantity in the square brackets could become negative. When it does, it would switch the sign of
${\it\delta}(t)$
, the quantity in the square brackets could become negative. When it does, it would switch the sign of
![]() ${\it\Delta}_{bot}$
, leading to a possible reversal event. Equations (3.3) and (3.4) combined together state that the motion of
${\it\Delta}_{bot}$
, leading to a possible reversal event. Equations (3.3) and (3.4) combined together state that the motion of
![]() ${\it\Delta}_{bot}$
may be described by diffusion in two symmetrical harmonic potential wells driven by a stochastic force.
${\it\Delta}_{bot}$
may be described by diffusion in two symmetrical harmonic potential wells driven by a stochastic force.
As
![]() $f_{{\it\delta}}(t)$
is a Gaussian distributed noise with zero mean, the diffusivity
$f_{{\it\delta}}(t)$
is a Gaussian distributed noise with zero mean, the diffusivity
![]() $D_{{\it\delta}}$
is used to describe the diffusion and can be determined from the experimental data. From the measured time series through
$D_{{\it\delta}}$
is used to describe the diffusion and can be determined from the experimental data. From the measured time series through
![]() $\langle [{\it\delta}(t+\text{d}t)-{\it\delta}(t)]^{2}\rangle =D_{{\it\delta}}\,\text{d}t$
, we find that the non-dimensionalized diffusivity for different aspect ratios collapses onto one single power-law relation:
$\langle [{\it\delta}(t+\text{d}t)-{\it\delta}(t)]^{2}\rangle =D_{{\it\delta}}\,\text{d}t$
, we find that the non-dimensionalized diffusivity for different aspect ratios collapses onto one single power-law relation:
![]() $D_{{\it\delta}}(H^{2}/{\rm\Delta}T^{2}{\it\nu})\sim Ra^{0.43}$
. Comparing with
$D_{{\it\delta}}(H^{2}/{\rm\Delta}T^{2}{\it\nu})\sim Ra^{0.43}$
. Comparing with
![]() ${\sim}Ra^{-0.04}$
in the 3D case (Brown & Ahlers Reference Brown and Ahlers2008), the
${\sim}Ra^{-0.04}$
in the 3D case (Brown & Ahlers Reference Brown and Ahlers2008), the
![]() $Ra$
dependence of diffusivity in the quasi-2D case is much stronger.
$Ra$
dependence of diffusivity in the quasi-2D case is much stronger.

Figure 4. Comparison between experimental results and model predictions. The solid lines in both panels represent a linear relationship between the
![]() $x$
and
$x$
and
![]() $y$
axes, and all symbols are the same as in figure 3. (a) The separation
$y$
axes, and all symbols are the same as in figure 3. (a) The separation
![]() $d/2$
between the two peaks in
$d/2$
between the two peaks in
![]() $p({\it\delta})$
versus the prediction from the model,
$p({\it\delta})$
versus the prediction from the model,
![]() $B/A$
. (b) The variance
$B/A$
. (b) The variance
![]() ${\it\sigma}$
of
${\it\sigma}$
of
![]() ${\it\delta}$
for each flow direction of the LSC versus the model prediction
${\it\delta}$
for each flow direction of the LSC versus the model prediction
![]() $\sqrt{D_{{\it\delta}}/A}$
.
$\sqrt{D_{{\it\delta}}/A}$
.
The probability distribution
![]() $p({\it\delta})$
of the amplitude
$p({\it\delta})$
of the amplitude
![]() ${\it\delta}$
can be calculated from the steady-state solution of the Fokker–Planck equation corresponding to (3.3), which is
${\it\delta}$
can be calculated from the steady-state solution of the Fokker–Planck equation corresponding to (3.3), which is
![]() $p({\it\delta})\sim \exp (-2V_{{\it\delta}}/D_{{\it\delta}})$
with the parabolic potential well
$p({\it\delta})\sim \exp (-2V_{{\it\delta}}/D_{{\it\delta}})$
with the parabolic potential well
![]() $V_{{\it\delta}}=A{\it\delta}^{2}/2-B{\it\delta}$
(Gardiner Reference Gardiner2004). Therefore
$V_{{\it\delta}}=A{\it\delta}^{2}/2-B{\it\delta}$
(Gardiner Reference Gardiner2004). Therefore
![]() $p({\it\delta})$
is a Gaussian function with variance
$p({\it\delta})$
is a Gaussian function with variance
![]() ${\it\sigma}^{2}=D_{{\it\delta}}/A$
and peak position at
${\it\sigma}^{2}=D_{{\it\delta}}/A$
and peak position at
![]() $B/A$
. In figure 2 the experimentally measured
$B/A$
. In figure 2 the experimentally measured
![]() $p({\it\delta})$
for each circulation state of the LSC is independently fitted with a Gaussian function, from which we obtain the variance
$p({\it\delta})$
for each circulation state of the LSC is independently fitted with a Gaussian function, from which we obtain the variance
![]() ${\it\sigma}$
and the peak position for each flow direction. It is found that
${\it\sigma}$
and the peak position for each flow direction. It is found that
![]() ${\it\sigma}$
is almost the same for the two peaks, but due to measurement uncertainties and imperfections in the experimental apparatus, the two peak positions in figure 2 are not exactly symmetric about zero. Therefore we use the separation
${\it\sigma}$
is almost the same for the two peaks, but due to measurement uncertainties and imperfections in the experimental apparatus, the two peak positions in figure 2 are not exactly symmetric about zero. Therefore we use the separation
![]() $d$
between the two peaks, which is roughly twice the peak position for each individual flow direction, for comparison with the model predicted position
$d$
between the two peaks, which is roughly twice the peak position for each individual flow direction, for comparison with the model predicted position
![]() $B/A$
. In both figures 4(a) and (b) the
$B/A$
. In both figures 4(a) and (b) the
![]() $y$
axes are experimental results from the measured PDF and the
$y$
axes are experimental results from the measured PDF and the
![]() $x$
axes are the corresponding model predictions. The solid line shows a linear relation between the
$x$
axes are the corresponding model predictions. The solid line shows a linear relation between the
![]() $x$
and
$x$
and
![]() $y$
axes, which corresponds to the case that the model and experiments agree with each other. It is seen that nearly all symbols collapse with this solid line, indicating that our model captures the essential physics of the reversal process in a quasi-2D system. It should be noted that the exponent
$y$
axes, which corresponds to the case that the model and experiments agree with each other. It is seen that nearly all symbols collapse with this solid line, indicating that our model captures the essential physics of the reversal process in a quasi-2D system. It should be noted that the exponent
![]() ${\it\alpha}$
in the constant term
${\it\alpha}$
in the constant term
![]() $B=C{\it\kappa}{\rm\Delta}TNu^{2}Ra^{0.23}{\it\Gamma}^{{\it\alpha}}/H^{2}$
is not known in the model and it is determined here by minimizing experimental data scatter around the solid line in figure 4(a). This gives
$B=C{\it\kappa}{\rm\Delta}TNu^{2}Ra^{0.23}{\it\Gamma}^{{\it\alpha}}/H^{2}$
is not known in the model and it is determined here by minimizing experimental data scatter around the solid line in figure 4(a). This gives
![]() ${\it\alpha}=4$
. The coefficient
${\it\alpha}=4$
. The coefficient
![]() $C$
is set to be one in figure 4(a), as its value is not important in demonstrating the linear relationship between
$C$
is set to be one in figure 4(a), as its value is not important in demonstrating the linear relationship between
![]() $d$
and
$d$
and
![]() $B/A$
.
$B/A$
.
Having calculated the complete
![]() $p({\it\delta})$
, we can now extract the time interval between two successive reversals using the backward Fokker–Planck equation (Gardiner Reference Gardiner2004), i.e.
$p({\it\delta})$
, we can now extract the time interval between two successive reversals using the backward Fokker–Planck equation (Gardiner Reference Gardiner2004), i.e.
where
![]() $C_{p}/t_{E}=\sqrt{2{\rm\pi}D_{{\it\delta}}/A}/Bt_{E}=2\sqrt{2{\rm\pi}}{\it\sigma}^{3}/dD_{{\it\delta}}t_{E}$
. In our parameter range,
$C_{p}/t_{E}=\sqrt{2{\rm\pi}D_{{\it\delta}}/A}/Bt_{E}=2\sqrt{2{\rm\pi}}{\it\sigma}^{3}/dD_{{\it\delta}}t_{E}$
. In our parameter range,
![]() $C_{p}/t_{E}$
is almost a constant, but the model prediction will be smaller than the experimental result because of the unsymmetrical PDF shown in figure 2. From figure 4 we see that there are small variations in the slope among different data sets. This is caused by setting
$C_{p}/t_{E}$
is almost a constant, but the model prediction will be smaller than the experimental result because of the unsymmetrical PDF shown in figure 2. From figure 4 we see that there are small variations in the slope among different data sets. This is caused by setting
![]() $V_{c}({\it\Gamma})$
as a constant, since the two terms that make up the parameter
$V_{c}({\it\Gamma})$
as a constant, since the two terms that make up the parameter
![]() $A$
both have power-law dependences on
$A$
both have power-law dependences on
![]() $Ra$
and thus give rise to a composite power law with an effective exponent. This effective exponent in fact varies over a small range, depending on the value of
$Ra$
and thus give rise to a composite power law with an effective exponent. This effective exponent in fact varies over a small range, depending on the value of
![]() $V_{c}({\it\Gamma})$
(and hence
$V_{c}({\it\Gamma})$
(and hence
![]() ${\it\Gamma}$
). Figure 4 shows that, to a first-order approximation, ignoring this variation works well for the purpose of testing the model prediction for the PDF
${\it\Gamma}$
). Figure 4 shows that, to a first-order approximation, ignoring this variation works well for the purpose of testing the model prediction for the PDF
![]() $p({\it\delta})$
. However, for
$p({\it\delta})$
. However, for
![]() $\langle {\it\tau}\rangle$
this will not be the case, as it has an exponential dependence on the harmonic potential. To make a high-order correction, we can fit a power law to the measured
$\langle {\it\tau}\rangle$
this will not be the case, as it has an exponential dependence on the harmonic potential. To make a high-order correction, we can fit a power law to the measured
![]() $d$
and
$d$
and
![]() ${\it\sigma}$
for each aspect ratio separately and then from them obtain the parameters
${\it\sigma}$
for each aspect ratio separately and then from them obtain the parameters
![]() $A$
(and
$A$
(and
![]() $B$
) for the corresponding
$B$
) for the corresponding
![]() ${\it\Gamma}$
. Operationally, we simply substitute
${\it\Gamma}$
. Operationally, we simply substitute
![]() $A$
and
$A$
and
![]() $B$
in the model potential with
$B$
in the model potential with
![]() $d$
and
$d$
and
![]() ${\it\sigma}$
. The results are shown as the solid lines in figure 3. Here,
${\it\sigma}$
. The results are shown as the solid lines in figure 3. Here,
![]() $C_{p}/t_{E}$
is chosen by shifting the solid lines vertically to match the symbols. It is seen that our model can describe the highly nonlinear and non-power-law dependence of
$C_{p}/t_{E}$
is chosen by shifting the solid lines vertically to match the symbols. It is seen that our model can describe the highly nonlinear and non-power-law dependence of
![]() $\langle {\it\tau}\rangle$
on
$\langle {\it\tau}\rangle$
on
![]() $Ra$
well, which again is an indication that our model correctly captures the essential features of the reversal dynamics in quasi-2D convection. It should be noted that the
$Ra$
well, which again is an indication that our model correctly captures the essential features of the reversal dynamics in quasi-2D convection. It should be noted that the
![]() $Ra$
dependence of
$Ra$
dependence of
![]() $\langle {\it\tau}\rangle$
predicted by the model is stretched exponential, which is the strongest
$\langle {\it\tau}\rangle$
predicted by the model is stretched exponential, which is the strongest
![]() $Ra$
dependence that has ever been observed. This will lead to extremely fast growth of
$Ra$
dependence that has ever been observed. This will lead to extremely fast growth of
![]() $\langle {\it\tau}\rangle$
as
$\langle {\it\tau}\rangle$
as
![]() $Ra$
increases and explains why it is difficult to observe any reversals in the quasi-2D system when
$Ra$
increases and explains why it is difficult to observe any reversals in the quasi-2D system when
![]() $Ra$
becomes large (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010).
$Ra$
becomes large (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010).
Finally, we comment on the relationship between the quasi-2D and 3D systems. It is known that corner rolls exist also in 3D systems (Sun et al.
Reference Sun, Xi and Xia2005). However, unlike the quasi-2D case, the corner rolls in 3D are not confined in the LSC plane. This means that, when fed with energy, the corner rolls do not need to grow in diameter, at the expense of shrinking the main LSC roll; rather, they can move or grow outside the LSC plane. Thus, the more generic corner roll term in (3.2) should be
![]() $-{\it\nu}V_{c}Re{\it\delta}/H^{2}\times (\hat{\boldsymbol{u}}_{c}\boldsymbol{\cdot }\hat{\boldsymbol{u}})$
, where the two unit vectors
$-{\it\nu}V_{c}Re{\it\delta}/H^{2}\times (\hat{\boldsymbol{u}}_{c}\boldsymbol{\cdot }\hat{\boldsymbol{u}})$
, where the two unit vectors
![]() $\hat{\boldsymbol{u}}_{c}$
and
$\hat{\boldsymbol{u}}_{c}$
and
![]() $\hat{\boldsymbol{u}}$
denote the directions of the velocities of the corner roll and the LSC. The extra term
$\hat{\boldsymbol{u}}$
denote the directions of the velocities of the corner roll and the LSC. The extra term
![]() $(\hat{\boldsymbol{u}}_{c}\boldsymbol{\cdot }\hat{\boldsymbol{u}})$
represents the projection of the corner roll contribution to the LSC plane. This term goes to one for a quasi-2D system. In a 3D system, previous models without consideration of the corner rolls work well for experimental results (Brown & Ahlers Reference Brown and Ahlers2008; Assaf et al.
Reference Assaf, Angheluta and Goldenfeld2011), which suggests that the corner roll effect in 3D is negligibly small compared with the viscous damping. This may suggest that the corner roll effect in a 3D system is most likely to influence motions perpendicular to the main LSC plane. For instance, its growth pushes the LSC plane to rotate in the azimuthal direction and could be the origin of the azimuthal oscillation (Cioni et al.
Reference Cioni, Ciliberto and Sommeria1997; Brown et al.
Reference Brown, Nikolaenko and Ahlers2005; Sun et al.
Reference Sun, Xi and Xia2005; Xi et al.
Reference Xi, Zhou and Xia2006).
$(\hat{\boldsymbol{u}}_{c}\boldsymbol{\cdot }\hat{\boldsymbol{u}})$
represents the projection of the corner roll contribution to the LSC plane. This term goes to one for a quasi-2D system. In a 3D system, previous models without consideration of the corner rolls work well for experimental results (Brown & Ahlers Reference Brown and Ahlers2008; Assaf et al.
Reference Assaf, Angheluta and Goldenfeld2011), which suggests that the corner roll effect in 3D is negligibly small compared with the viscous damping. This may suggest that the corner roll effect in a 3D system is most likely to influence motions perpendicular to the main LSC plane. For instance, its growth pushes the LSC plane to rotate in the azimuthal direction and could be the origin of the azimuthal oscillation (Cioni et al.
Reference Cioni, Ciliberto and Sommeria1997; Brown et al.
Reference Brown, Nikolaenko and Ahlers2005; Sun et al.
Reference Sun, Xi and Xia2005; Xi et al.
Reference Xi, Zhou and Xia2006).
Acknowledgements
We thank E. Brown for helpful discussions and the Hong Kong Research Grants Council (RGC) for support under grant nos CUHK 403712 and 404513.