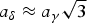II. EXPERIMENTAL

The thermal behaviour of a K₄P₂O₇ sample from Sigma–Aldrich was followed by temperature resolved powder diffractometry (TXRD) (Siemens D5000 θ/θ diffractometer equipped with an Elphyse position-sensitive detector and a HTK10 Anton Paar temperature attachment). The sample was dusted on a platinum foil serving as heating source in a chamber pumped under vacuum, then filled with dried helium. A light He flow was maintained during the experiment. The time interval between successive powder patterns was 2880 s, including a measuring time of 2580 s; the temperature was increased by steps of 10 °C starting from 30 to 700 °C. CuKα radiation was used; measurements were from 9° to 139° in 0.03°2θ steps. A contour scale plot is shown in Figure 1. The starting material contained traces of the hydrated phase which retransformed readily at 50 °C into the δ-K₄P₂O₇ anhydrous phase. The expected δ → γ transition occurs at ~280 °C; however, the event announced at 486 °C for the γ → β transition (Znamierowska, Reference Znamierowska1978) remains undetected up to 700 °C, confirming the similar non-observation (by thermal analysis and powder TXRD by 100 °C steps, no indexing) by Sandström (Reference Sandström2006). Another TXRD was performed in the range 30–300–30 °C in steps of 5 °C in the 260–300–260 °C range and 10 °C elsewhere, establishing the reversibility of the transition which, under these conditions, appears to be close to 275 °C, also showing pre-transitional effects (accelerated cell parameter and intensities changes) occurring in the 230–270 °C range. Events in the 220–250 °C range during fast (3 °C/min) neutron thermodiffractomy experiments (instrument D20, ILL, Grenoble) confirmed the possibility of another phase transition close to 270 °C by Shekhtman et al. (Reference Shekhtman, Smirnov and Burmakin2000), but these data were of no help in indexing attempts (see the neutron contour plots in supplementary material available at http://journals.cambridge.org/pdj)). Given the difficulties in solving the δ-K₄P₂O₇ crystal structure from such conventional laboratory or neutron data (due to the large cell dimensions), a synchrotron pattern was recorded at ESRF (Grenoble) on the ID31 instrument (Fitch, Reference Fitch2004), λ = 0.399 90 Å from a sample loaded in a (0.9 mm) capillary as trihydrate, dried and fired at 500 °C, then sealed in the oven.

Figure 1. TXRD contour plot (CuKα).

III. INDEXING, STRUCTURE DETERMINATIONS AND RIETVELD REFINEMENTS

A. γ-K₄P₂O₇ at 300 and 600 °C from conventional X-ray data

The γ-form being simpler than the one at room temperature, it was first indexed easily in a hexagonal cell by various software, including McMaille (Le Bail, Reference Le Bail2004). The FoMs (Figures of Merit) for the pattern selected at 300 °C were M ₂₀ = 54.6 (de Wolf, Reference de Wolf1968), F ₂₀ = 54.5 (0.0111, 33) (Smith and Snyder, Reference Smith and Snyder1979) and McM ₂₀ = 165.5 (Le Bail, Reference Le Bail, Clearfield, Reibenspies and Bhuvanesh2008). The cell volume suggested Z = 2. Using Le Bail fitting (Le Bail, Reference Le Bail2005) for evaluating the reliability of the indexing and for intensity extraction, the P6₃/mmc space group was the most probable. The structure solution was carried out in direct space using the ESPOIR software (Le Bail, Reference Le Bail2001), moving in the cell (by a Monte Carlo process) various numbers of K, P, and O atoms. This led to the best solution with R = 14% on the first 120 hkl extracted at low diffraction angles. Refinements were undertaken by Rietveld (Reference Rietveld1969) FULLPROF software (Rodriguez-Carvajal, Reference Rodriguez-Carvajal1993). Patterns in the 280–700 °C range could be fitted continuously with the structural model of the γ-form. No clear-cut event was observed on the cell parameters or atomic coordinates as a function of temperature. This confirms the same non-observation of the β/γ phase transition at 486 °C by Sandström (Reference Sandström2006). This transition thermal effect was described by Znamierowska (Reference Znamierowska1978) appearing only “as a result of prolonged heating of powdered melts at 500 °C and is rather weak.” The Rietveld fits for the λ-form at 300 °C and at 600 °C (much above the expected β/γ transition at 486 °C) are shown in Figures 2 and 3. The 115–139°2θ range was excluded from the refinement, being essentially dominated by two peaks from the Pt holder. The Rietveld refinement details, the atomic coordinates, selected geometric parameters, and X-ray diffraction data are shown in Tables I–IV, respectively.

Figure 2. Rietveld plot for γ-K₄P₂O₇ at 300 °C (CuKα). The second phase corresponds to the Pt holder.

Figure 3. Rietveld plot for K₄P₂O₇ at 600 °C (CuKα). The second phase corresponds to the Pt holder.

Table I. Experimental and Rietveld refinement details for the γ-K₄P₂O₇ form at 300 and 600 °C.

Table II. Fractional atomic coordinates and isotropic displacement parameters (Ų) for the γ-K₄P₂O₇ form at 300 °C (first line) and 600 °C (second line if different value) in the P6₃/mmc space group; BV is the bond-valence calculated according to Brese and O'Keefe (Reference Brese and O'Keefe1991).

Table III. Selected interatomic distances (Å) for the γ-K₄P₂O₇ form at 300 °C (first line) and 600 °C (second line).

Table IV. X-ray diffraction data for the γ-K₄P₂O₇ form at 300 °C (CuK α1). Observed values from EVA software (Bruker).

B. δ-K₄P₂O₇ from synchrotron data

The room-temperature phase could not be indexed from low-resolution TXRD data. A large hexagonal cell could be deduced from new conventional data (CuKα) from a Rigaku Miniflex diffractometer (an oven-dried sample was transferred to the standard flat-plate holder and stored in a heat-sealed plastic bag ‘immediately’), but the structure solution was not obtained until synchrotron data (ESRF – Grenoble, instrument ID31, λ = 0.399 90 Å) were recorded. Various indexing software including McMaille, yielded a hexagonal supercell with $a_\delta = a_\gamma \sqrt{3}$ and c _δ = 3 c _γ, leading to Z = 18 (M ₂₀ = 84.3, F ₂₀ = 749 (0.0005, 43) and McM ₂₀ = 181.4). Since the only systematic extinction corresponds to 00l, l = 6n, the space group is either P6₁22, P6₅22, P6₁ or P6₅. Incomplete starting models were obtained either by the direct method approach using SHELXS (Sheldrick, Reference Sheldrick2008) or in direct space by using ESPOIR (Le Bail, Reference Le Bail2001). However, given the clear relation between both phases, refinements were attempted by starting directly from the γ-K₄P₂O₇ structure expanded, using the CRYSCON software (Dowty, Reference Dowty2006), to fit in all possible space groups for the supercell, and using restraints forcing the existence of the P₂O₇ groups. A best fit was clearly obtained in the P6₁ space group. Anisotropic line broadening was detected and treated phenomenologically by separating the peaks into three categories, 00l, hk0, and the others, obtaining a decrease from R _P = 12.8% and R _WP = 13.7% to R _P = 9.25% and R _WP = 8.71%. The hk0 lines present the smallest full width at half maximum (0.0055–0.0680°) in the whole °2θ range (2–31°) and the 00l lines present the largest ones (0.0191–0.0924°); other lines show FWHMs between 0.0083° and 0.0805°. The Rietveld fit is in Figure 4, the Rietveld refinement details, the atomic coordinates, selected geometric parameters, and X-ray diffraction data are shown in Tables V–VIII, respectively.

Figure 4. Rietveld plot for δ-K₄P₂O₇ (synchrotron powder pattern on instrument ID31, ESRF) at room temperature (λ = 0.399 90 Å).

Table V. Experimental and Rietveld refinement details for the δ-K₄P₂O₇ form at room temperature.

Table VI. Fractional atomic coordinates and isotropic displacement parameters (Ų) for the δ-K₄P₂O₇ form in the P6₁ space group (all atoms in general Wyckoff position 6a); Δγ is the amplitude of the displacement (Å) of the atoms after joining their sites in the γ-form at 300 °C; BV is the bond-valence calculated according to Brese and O'Keefe (Reference Brese and O'Keefe1991).

*Fixed origin along the z-axis.

Table VII. Selected interatomic distances (Å) for the δ-K₄P₂O₇ form.

Table VIII. X-ray diffraction data for the δ-K₄P₂O₇ form (λ = 0.399 90 Å). Observed values from EVA software (Bruker).

IV. STRUCTURES DESCRIPTIONS AND DISCUSSION

The γ-form (Figure 5) looks like an idealized view of the structure of Na₄P₂O₇, which, though orthorhombic (space group P2₁2₁2₁), is pseudo-hexagonal with $a \sim b \sqrt{3}$ and with a similar c parameter (Leung and Calvo, Reference Leung and Calvo1972). The distorted 6-fold coordinations of two of the four independent Na sites disposed in chains of cations along the c-axis in Na₄P₂O₇ become K3 and K2 alternating octahedra and trigonal prisms (TPs) sharing faces (Figure 6). The two other Na sites in the tetrasodium pyrophosphate in 5-fold coordination become K1 in a strange 9-fold coordination with a hexagonal face as a basis of the polyhedron and a triangle from a PO₄ tetrahedron face at the top. Two such polyhedra have their hexagonal face building an empty hexagonal prism of oxygen atoms (Figure 7). The pyrophosphate group is in an eclipsed conformation. Two potassium-rare-earth silicates K₃RESi₂O₇ (RE = Lu, Sc) adopt a similar structure as γ-K₄P₂O₇, same space group and very close cell parameters, the rare-earth replacing the K3 atom in octahedral coordination (Vidican et al., Reference Vidican, Smith and zur Loye2003; Napper et al., Reference Napper, Layland, Smith and zur Loye2004). For the γ-form, the P–O distances were not constrained, resulting in values reasonably close to the standard ones (Table III), though the bond valence calculated values (Table II) are far too large for K3 (1.54 instead of 1) in 6-fold coordination and too small for K1 (0.66). This, and the fact that the P–O distances are slightly shorter at 600 °C than at 300 °C, gives another proof that the accuracy from powder data cannot beat that from a single crystal. For the δ-form, in spite of the synchrotron data quality, strong divergences occurred with the expected values so that the P–O distances were restrained to be close to those in the CaK₂P₂O₇ crystal structure (Sandström et al., Reference Sandström, Fischer and Boström2003), with the P–O bond involved in the P–O–P at 1.634 Å and the others at 1.514 Å. The δ-form projections along the c-axis (Figure 8) and along the [110]-direction (Figure 9) evidence helicoïdal (6₁) modulation of the pyrophosphate groups and of the K⁺ cations, with considerable moves (though always less than 1 Å, see the amplitude Δγ of the displacement for each atom Table VI) if compared with the γ-form (Figure 5). However, such displacements are larger than those occurring at the phase transition, since the intensities and positions of the diffraction peaks of the δ-form continuously evolve closer to those of the γ-form in the range 20–260 °C. Unfortunately, a refinement at 260° from the conventional X-ray laboratory data is even more unstable than from the synchrotron data at room temperature and the atomic coordinates would be too uncertain. The coordinations of the K atoms (with upper limitation to K–O = 3.5 Å) are no longer as symmetrical as they were in the γ-form. We examine first those K1, K2, K5, K6, K7, and K8 atoms which will become the K1 type in the γ-form (coordination 6 + 3). In no case does the hexagonal plane of six oxygen atoms exist at room temperature; it transforms each time into a distorted plane of 5 oxygen atoms. Moreover, the PO₄ tetrahedron face providing three oxygen atoms is sometimes displaced so as to share with either an edge or a corner, and a supplementary oxygen atom may contribute to potassium coordination on the other side of the pentagonal face. According to this description, the K1O₇ polyhedron coordination is 5 + 2, close to be a monocapped TP; K2O₈ has a 1 + 5 + 2 coordination; K5O₈, K7O₈, and K8O₈ have lost one oxygen atom of the hexagonal plane but still share a face with a PO₄ tetrahedron, leading to the 5 + 3 coordination; K6O₇ can be described as a 1 + 5 + 1 pentagonal bipyramid. For those K3, K9, and K10 atoms of the δ-form, forming the K2O₆ TP in the γ-form, K3O₈ is a highly distorted bicapped TP; K9O₉ looks like a very distorted tricapped TP, the main distortion coming from face sharing with a PO₄ tetrahedron; K10O₆ is a TP. For those K4, K11, and K12 atoms of the δ-form, forming the K3O₆ octahedra in the γ-form, K4O₆ and K12O₆ are both octahedra and K11O₇ is a monocapped TP. Two of the three different [P₂O₇]⁴⁻ groups are staggered (average torsion angles O–P1···4–O = 60° and O–P2···P3–O = 67°), the third is eclipsed (O–P5···P6–O = 11°). This complex ordering at room temperature is probably not free from stacking faults along the c-axis, as suggested by the anisotropic line broadening and the fact that the 00l lines are the broadest. This broadening, intrinsic to the sample, considerably decreases the resolution and explains the difficulties in refining all coordinates without distance restraints in the [P₂O₇]⁴⁻ groups, despite the use of instrumental high-resolution synchrotron powder data. Finally, the bond valence calculations (Table VI) look better than for the γ-form, though K10, in a TP, presents a large bond valence (1.45 instead of 1). The very similar bond valence values for the six P atoms (4.82 ± 0.02 instead of five) is the consequence of the distance restraint on the PO₄ tetrahedra.

Figure 5. Projection along the c-axis of the structure of γ-K₄P₂O₇ at 300 °C showing the eclipsed pyrophosphate groups, and columns of potassium atoms K2 and K3.

Figure 6. View of the structure of γ-K₄P₂O₇ at 300 °C showing the columns of potassium atoms K2 and K3 alternating K3O₆ octahedra and K2O₆ TPs sharing faces along the c-axis.

Figure 7. K1O₉ polyhedra in γ-K₄P₂O₇ at 300 °C opposing their hexagonal faces.

Figure 8. Projection along the c-axis of the structure of δ-K₄P₂O₇.

Figure 9. Projection along the [110]-direction of the structure of δ-K₄P₂O₇.