Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-06T15:58:47.602Z Has data issue: false hasContentIssue false
  • English
  • Français

One-dimensional model of the electrostatic ion acceleration in the ultraintense laser–solid interaction

Published online by Cambridge University Press:  01 June 2004

M. PASSONI  and
M. LONTANO
M. PASSONI
Affiliation:
Dipartimento di Ingegneria Nucleare, Politecnico di Milano, Milan, Italy Istituto di Fisica del Plasma, Consiglio Nazionale delle Ricerche, Milan, Italy
M. LONTANO
Affiliation:
Istituto di Fisica del Plasma, Consiglio Nazionale delle Ricerche, Milan, Italy
Rights & Permissions [Opens in a new window]

Abstract

Effective ion acceleration of picosecond-duration well-collimated bunches in the strong relativistic interaction of a short laser pulse with a thin solid target has been experimentally demonstrated. In this work, with reference to the sharp rear solid–vacuum interface, where ion energization takes place, the one-dimensional Poisson–Boltzmann equation is analytically solved on a finite spatial interval whose extension is determined by requiring electron energy conservation, resulting in the consistent spatial distributions of the hot electrons created by the laser and of the corresponding electrostatic potential. Then, the equation of motions for an ensemble of test ions, initially distributed in a thin layer of the rear target surface, with different initial conditions, is solved and the energy spectrum corresponding to a given initial ion distribution is determined.

Keywords

Fast ignitionHadrontherapyLaser based ion accelerationLaser-plasma interactionRelativistic electrons
Type
Research Article
Information
Laser and Particle Beams , Volume 22 , Issue 2 , June 2004 , pp. 163 - 169
Copyright
© 2004 Cambridge University Press

1. INTRODUCTION

One of the most promising applications of the rapidly growing technological achievements of high-power lasers is their ability in producing well-collimated, picosecond-duration bunches of energetic ions, in particular protons (with energies of the order of several tens of megaelectron volts), as a consequence of the interaction with thin solid targets. The development of compact sources of multimegaelectron volt/nucleon ions would provide a spinoff for several fields, as diagnostic tools in high-density plasmas (Borghesi et al., 2002), in the implementation of the proton-based fast ignitor scheme (Roth et al., 2001), in materials science (Gemmel, 1974; Boody et al., 1996), in accelerator science (Haseroth & Hill, 1996), in medical physics (applications to PET [Nemoto et al., 2001; Santala et al., 2001] and hadrontherapy [Bulanov & Khoroshkov, 2002; Fourkal et al., 2002]).

The process of laser-driven ion acceleration has been investigated by several experimental teams under very different physical conditions. The introduction of the paper by Badziak et al. (2003) contains an exhaustive and updated description of the state of the art of the experiments. The most striking results have been obtained by the Lawrence Livermore National Laboratory group (Hatchett et al., 2000; Snavely et al., 2000). The Nova laser (intensity up to

, energy

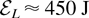
, wavelength λ = 1 μm, pulse duration τp ≈ 0.5 ps, focal spot ≈ 8–9 μm) has produced a picosecond bunch of ≈3 × 1013 protons, with energies >40 MeV, up to a maximum energy of 58 MeV, during the interaction with a 100-μm-thick CH target. Highly effective laser-driven acceleration has been also observed for ions heavier than protons (Pb [Clark et al., 2000a; Krushelnick et al., 2000], C, and F [Hegelich et al., 2002]), with final energies of the order of several megaelectron volts/nucleon.

According to the present understanding, a principal role in the ion acceleration process is played by a relativistically hot electron component, which is produced in the earliest phase of the laser–solid interaction (Hatchett et al., 2000; Wilks et al., 2001). The relativistically strong laser pulse impinging on the front surface of the target delivers its electromagnetic energy and momentum to electrons that are accelerated up to an energy of the order of the laser ponderomotive potential. The efficiency ηe of the energy conversion process from the laser to the fast electrons has been inferred to be as high as 50% (Hatchett et al., 2000), even if a more typical and reasonable value should be of the order of 20%–30%. After crossing the target, the relativistic electrons distribute themselves at the rear surface–vacuum interface, typically over few “hot” Debye lengths, λe,hot, which for nhot = 3 × 1019 cm−3 and Thot = 6 MeV, is λe,hot ≈ 3 μm. The resulting quasistationary electric field is of the order of 2 MV/μm, which can accelerate protons up to ≈40 MeV over a distance of ≈20 μm, in agreement with the experimental observations (Hatchett et al., 2000; Snavely et al., 2000). However, these are only order-of-magnitude estimates, which are not sufficient if the detailed characteristics of the energetic ion spectra (the presence of low- and/or high-energy cutoffs and the dependence on the ion energy) are to be modeled.

We have formulated a one-dimensional model for the determination of the quasistatic hot electron spatial distribution by solving the Poisson–Boltzmann equation for hot electrons at the sharp solid–vacuum interface, over a finite spatial interval. Then, the equation of motion of a test ion, initially located on the rear surface of the target, with a small spread both in its spatial position and in its energy, has been analytically solved for several initial conditions. The energy spectrum of test ions, accelerated by the space charge, has been calculated. Comparisons between the model predictions and the experimental observations and scalings of laser parameters to future medical applications have been carried out.

The article is organized as follows: in Section 2 the physical model is discussed and the analytical solutions are given. The results are presented in Section 3. Section 4 is devoted to concluding remarks.

2. THE MODEL

Let us consider a one-dimensional slab along the coordinate x, extending from x = 0 (the unperturbed position of the solid–vacuum interface at the rear side of the target) up to x = h (the farther limit of the electron cloud, which will be determined later on), and assume that for 0 ≤ x ≤ h, the fast electron density follows the Boltzmann distribution

where φ(x) is the electrostatic potential, neh is the value of the hot electron density where φ = 0, e is the modulus of the electron charge, and T is the constant temperature of the electrons produced by the laser pulse.

It is worth mentioning that experimental measurements (True et al., 1981; Wickens et al., 1978) and three-dimensional numerical simulations (Pukhov, 2001) suggest that more complicated electron distribution functions are produced. A typical situation is represented by the creation of two electron populations, where the “hotter” species is driven directly by the laser, and the “colder” one represents the backgrounds electrons, which are subject to resistive heating (Davies, 2002). In this analysis we consider a one-temperature electron population, only; the two temperature case has been recently investigated elsewhere (Passoni et al., 2004).

By assuming that, over the electron time scale, the ion distribution remains localized for x ≤ 0 (immobile ions), the Poisson–Boltzmann equation in the “vacuum” region, x ≥ 0, reads

Notice that the right-hand side of Eq. (1) does not vanish for x → +∞, unless φ (x = +∞) = −∞, which is not physically acceptable because any positive charge at x = 0 would be accelerated indefinitely in such a potential distribution (Crow et al., 1975; Mora, 2003). It is therefore necessary to introduce an upper boundary, h, to the integration range, which we choose on the basis of electron energy conservation: that is, the kinetic energy acquired by a test electron from the laser pulse should be equal to the work done from the electron to cover the distance h in the presence of the spatial distribution of the other fast electrons (Tikhonchuk, 2002). The resulting expression reads

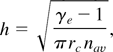
where rc = e2/mc2 is the classical electron radius, γe is the relativistic factor of the test electron, nav = Ne /V the average density of the hot electrons, Ne the total number of fast electrons produced by the laser, and V = πRe2L the volume they occupy. Finally, Re and L are the radius and the longitudinal extension of the region where the hot electrons are emitted, respectively (Hatchett et al., 2000).

Equation (2), together with Eq. (1), is then solved with boundary conditions (1) φ(x = h) = 0, and (2) φ′(x = h) = 0. Condition 1 implies that the “unperturbed” density neh is found at x = h. For x > h, ne(x) = 0, that is, the electron distribution has a discontinuity at x = h. However, due to condition 2, the corresponding electric field profile is continuous, being zero at x = h. The solution of Eq. (1) gives the electrostatic potential

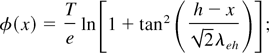
accordingly, we obtain the analytical expressions of the electron density

and of the electric field

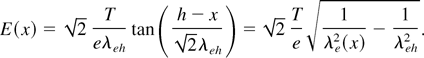
In the above equations, the “local” electron Debye length λe(x) = [T/4πe2ne(x)]1/2 has been defined, and also λeh ≡ λe(h).

We can now use our model equations of the self-consistent electrostatic potential and electric field, Eqs. (4) and (5), to find the maximum energy (at x = h) gained by an ion, with constant charge state Z, initially at rest in x = 0:

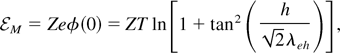
which can be compared with the values of the maximum ion energies observed in the experiments.

Moreover, we can solve the relevant equation of motion for an ensemble of ions initially at rest, but uniformly distributed in a thin layer (of width Δ << s, s being the target thickness) placed at x = 0, and, accordingly, derive their energy spectrum at x = h. It reads

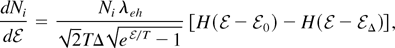
where the energy of the ions starting at x = 0 and at x = Δ are

, respectively, and Ni is the total number of accelerated ions. As it is evident from Eq. (8), a lower and an upper cutoff in the ion energy spectra appear, as a consequence of the finite extension width of the proton emitting layer.

Finally, the closure of our model is achieved by relating the physical quantities to the parameters of the target and of the laser pulse.

To this aim, we first express the temperature T in terms of the laser intensity

(Lefebvre & Bonneaud, 1997; Wilks et al., 1992),

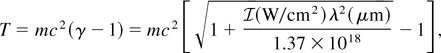
where γ is the relativistic factor of an electron in the laser field and λ is the vacuum wavelength of the laser. Then, the total number of fast electrons Ne is obtained from the energy balance

, where 〈e〉 is the mean electron energy in a relativistic Maxwellian distribution, ηe the laser energy conversion efficiency and

is the total energy of the laser pulse. Re is estimated as Re = (f/2) + s tan ϑ, taking into account the experimentally observed divergence of the electron beam, where f is the laser focal spot and ϑ is the electron beam aperture semi-angle (Snavely et al., 2000). We also assume L = s. By imposing the normalization condition, that is, the integral of the electron density over the occupied volume πRe2h must be equal to Ne, we obtain an implicit relation

which gives the last quantity we need, neh.

3. THE RESULTS

The one-dimensional model discussed in Section 2 can be used to calculate (1) the quasistatic electron distribution of a given temperature at a sharp solid–vacuum interface, (2) the maximum energy achievable by a test ion in the calculated electron distribution and the relevant energy spectrum for specific experimental conditions.

As for point 1, in Figure 1 the electrostatic potential (a) from Eq. (4), the electron density (b) from Eq. (5), and the electric field (c) from Eq. (6), are displayed as functions of the x-coordinate. The parameter values used to obtain the plots are relevant to the experiment described by Clark et al. (2000b): laser energy

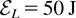
, peak laser intensity

, target thickness s = 125 μm, efficiency ηe = 0.2, aperture semi-angle ϑ = 25°. By inspection of Figure 1 it turns out that the spatial profiles present very steep gradients, especially close to the rear target surface; in particular, the values assumed by the accelerating electric field around x = 0 are quite large and, correspondingly, the electrostatic potential decreases by 50% in the first 2 μm. Therefore, estimates of the maximum ion energies based on “average” values of such quantities can give unrealistic results.

The electrostatic potential (a), the electron density (b), and the electric field (c) are plotted as functions of x for , s = 125 μm, ηe = 0.2, and ϑ = 25° (Clark et al., 2000b).

Going to point 2, let us consider the two experiments described by Hatchett et al. (2000) and by Clark et al. (2000b). The parameters characterizing the laser–target interaction in the two experimental configurations have been already reported in this text, in the introduction for the Nova laser, and commenting on Figure 1 for the Vulcan laser, respectively. Let us first consider the maximum proton energy predicted by our model (see Eq. (7)). Figure 2 shows the (solid) lines of constant maximum proton energy

in the plane laser intensity–laser energy

, for ηe = 20% and ϑ = 25°. The two considered experiments are indicated by means of two filled circles. The experimental values are

(Hatchett et al., 2000) and

(Clark et al., 2000b), respectively, which are quite in agreement with the predictions of our model. The dashed curves represent the loci of the points at constant total electron number in the cloud. We see that in the case of the Vulcan experiment, the number of expected hot electrons, ≈1013, is much larger than the number of observed accelerated protons, ≈1012 (Clark et al., 2000b). This is one of the conditions for the one-dimensional model to be valid. In the Nova case, for CH targets, the ratio of the two numbers is ≈4 × 1013 against ≤3 × 1013 (Hatchett et al., 2000), which makes the assumption marginally valid. However, it should be noted that on one side 3 × 1013 is the total number of accelerated protons, integrated over all energies, whereas the ions with energy larger than 20 MeV can be estimated lower by an order of magnitude (Snavely et al., 2000); on the other side, when Au targets have been used, five times less protons have been observed (Snavely et al., 2000).

The (solid) lines at constant maximum proton energy (in megaelectron volts), and the (dashed) lines at fixed total electron number are shown in the plane laser energy versus laser intensity. The “positions” of the two experiments considered in the text (Clark et al., 2000b; Hatchett et al., 2000) are marked by the two filled circles.

In Figure 3, the energy spectrum given by Eq. (8) for the parameters of the experiment described by Hatchett et al. (2000) is shown with the solid line. It is limited between

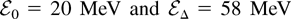
. The dots represent the experimental points. The calculation assumes that the proton-emitting layer on the rear surface of the target has a thickness of 2 μm and a radius of 5 μm. It corresponds to a total proton number of Ni ≈ 1.5 × 1012, at least an order of magnitude less than the number of electrons forming the electron cloud.

The energy spectrum (solid line) of the accelerated protons (Z = 1), given by Eq. (8), for the parameters of Hatchett et al. (2000), is displayed. It is assumed that the proton-emitting layer on the rear surface of the target has a thickness of 2 μm and a radius of 5 μm, corresponding to a proton number of Ni ≈ 1.5 × 1012. The dots correspond to the experimental data (Snavely et al., 2000).

These results support the rear side proton acceleration mechanism, that is, they show that the maximum energy gained by a positive charge in the hot electron cloud, starting from the rear surface of the solid target, is similar to what is observed. However, it should be noticed that for a more correct energy balance, the energy that goes into the target ionization should be properly considered (Tikhonchuk, 2002).

Let us use our model to make predictions on the experimental regimes, which will become feasible hopefully in a not far future. For example, it has been proposed to use a double-layer geometry (Bulanov et al., 2002; Esirkepov et al., 2002) to produce well-collimated proton bunches in the energy range of

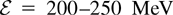
for the proton therapy. In Figure 4 the plane

, as in Figure 2, is shown, with the lines of constant maximum energy in the suitable energy range, that is, for more powerful and more energetic lasers. Here, Ni = 3 × 1012, s = 100 μm, ηe = 30%, and ϑ = 25° have been considered. The two filled circles corresponds to two possible experimental realizations of a proton bunch characterized by a narrow spectral distribution

, centered around 250 MeV, displayed in Figure 5. The broader spectrum (solid line) refers to a laser energy of

and an intensity of

. The narrower spectrum (dashed line) refers to

. Both sets of values satisfy the needs for proton therapy as it is presently conceived (Arduini et al., 1996; Bulanov & Khoroshkov, 2002; Fourkal et al., 2002).

The (solid) lines at constant maximum proton energy (in megaelectron volts), and the (dashed) lines at fixed total electron number are shown in the plane laser energy versus laser intensity. The following parameters have been chosen: s = 100 μm, ηe = 0.3, and ϑ = 25°. The two filled circles correspond to two possible implementations of a proton bunch in the energy range of 250 MeV, and with an energy spread of (see Fig. 5).

The proton energy spectra, given by Eq. (8), for two different sets of parameters are displayed. The broader spectrum (solid line) refers to a laser energy of 1 kJ and intensity of 1.2 × 1022 W/cm2. The narrower spectrum refers to . In both cases, s = 100 μm, ηe = 0.3, and ϑ = 25°.

4. CONCLUDING REMARKS

The one-dimensional electrostatic model formulated in this article, although following previous similar investigations (Crow et al., 1975; Mora, 2003), tackles the problem of the analytical solution of the Poisson–Boltzmann equation on a finite domain by introducing, on physical ground, an upper limit of integration, which is expressed in terms of known or measurable physical parameters (Tikhonchuk, 2002). The existence of a limited interval on which the fast electrons are distributed in the stationary state causes an ion, initially at rest, to gain a finite amount of energy in the corresponding potential distribution. In addition, the knowledge of the actual spatial profile of the physical quantities shows that, close to the ion source (x = 0), large values of the electric field are produced. It means that, with reference to the case of Figure 1, within the first couple of microns, the ion gains half of the energy it will have after crossing the full electron cloud (h ≈ 19 μm). As a consequence, we can state that the model of rear side acceleration, when the actual spatial inhomogeneity of the self-consistent electric field is taken into account, is able to explain the maximum energies observed in the experiments.

The spatial distributions of the electric field and of the electron density are determined self-consistently and they turn out to depend on several external parameters, which are assigned according to what is observed in the experiments. The model is relativistically correct, and then applicable to the regimes of interaction of petawatt lasers. Once the spatial profile of the electrostatic field has been determined, the energy spectrum of an initially distributed (in space and in energy) ensemble of ions can also be consistently determined.

We wish to notice that the problem of the divergence of the potential at infinity, which corresponds to vanishing charge density and field, is well known (Crow et al., 1975; Mora, 2003) and, to our understanding is quite general and independent of the number of dimensions of the space where the physical system is located. Indeed, once the Boltzmann distribution is assumed, in order to have a zero charge density at infinity the potential must go to minus infinity. This is strictly related to the finite number of electrons that we try to distribute over a infinite spatial interval. For its similarity with the case of the gravitational field, see the discussion by Landau & Lifshitz (1968).

Therefore, independently of the dimensionality of the system, one should introduce a cutoff in the spatial extension of the electron cloud, or in the electron velocity distribution (Khishimoto et al., 1983), or alternatively in the time interval over which the assumed stationarity of the system is valid (the possibility that the hot electron temperature decreases due to their coupling with cold electrons has been considered by Hatchett et al., 2000). Obviously, these three possibilities are related to each other. Our choice was to introduce a space limitation on physical ground.

The applicability of the one-dimensional model is, however, limited due to a number of conditions that the physical system should satisfy. So that the ion motion during the acceleration process can be assumed to be one dimensional, the electron cloud should be considered spatially uniform in the plane normal to the ion motion. A way to impose this condition is to require that h/2Re < 1. The violation of this condition can be taken as an indication of the need of retaining three-dimensional effects. The regimes described in Figure 2 well satisfy this request, whereas at much larger laser intensities the model can become only marginally applicable: for a given final ion energy, “low” intensity and high energies should be preferred to high intensities and “low” energies, in order to have a one-dimensional accelerating electrostatic field.

In addition, we have neglected the possible insurgence of self-generated magnetic fields, which could affect the trajectory of the accelerated protons. However, experimentally the role of the induced magnetic field is not yet well established. Indeed, although in several experiments (Clark et al., 2000b; Krushelnick et al., 2000; Murakami et al., 2001) the proton emission from the target manifests a ringlike structure, which is considered a signature of the presence of an azimuthal magnetic field, the observations of protons at the highest energies (Hatchett et al., 2000; Snavely et al., 2000) are characterized by well-focused particle bunches without an annular distribution.

Our model is stationary. The electron cloud is assumed neither to evolve during the acceleration process, nor to be affected by the ions flowing through it. The latter condition requires that the number of the ions that are accelerated be smaller that that of the hot electrons, Ni < Ne.

Concerning the electron energy distribution, we have limited our analysis to a one-temperature electron population, although there is experimental and computational evidence that a two- (True et al., 1981; Wickens et al., 1978) or even three-temperature (Pukhov, 2001) electron population is produced during the laser–target interaction. The discussion of the two electron temperature case can be found in Passoni et al. (2004)

Moreover, we have assumed that the electron temperature is also not evolving with time, although it is expected that the energy of the hot electrons will decay in time due to their expansion and to collisional and radiative losses. Therefore, a better characterization of the ion acceleration process would incorporate the temporal evolution of the electron temperature, which could compete with the effect of a finite acceleration length in the determination of the maximum energy gain. Work in these directions is under way (Bychenkov, personal communication).

Finally, the resulting ion energy spectrum will inevitably be affected by several spurious mechanisms, which are expected to broaden the lower energy cutoff.

ACKNOWLEDGMENTS

The authors thank S.V. Bulanov and V.I. Tikhonchuk for discussions on several aspects of the laser–target interaction and of the ion acceleration problems. Part of this work has been carried out in the frame of the INTAS Project 01-0233.

References

REFERENCES

Arduini, G., Cambria, R., Canzi, C., Gerardi, F., Gottschalk, B., Leone, R., Sangaletti, L. & Silari, M. (1996). Physical specifications of clinical proton beams from a synchrotron. Med. Phys. 23, 939–951.Google Scholar
Badziak, J., Woryna, e., Parys, P., Platonov, K.Y., Jablonski, S., Ryc, L., Vankov, A.B. & Wolowski, J. (2003). Generation of energetic protons from this foil targets irradiated by a high-intensity ultrashort laser pulse. Nucl. Instr. Methods In Physics Res. A 498, 503–516.Google Scholar
Boody, F.P., Hoepfl, R., Hora, H. & Kelly, J.C. (1996). Laser-driven ion source for reduced-cost implantation of metal ions for strong reduction of dry friction and increased durability. Laser Part. Beams 14, 443–448.Google Scholar
Borghesi, M., Campbell, D.H., Schiavi, A., Haines, M.G., Willi, O., Mackinnon, A.J., Patel, P., Gizzi, L.A., Galimberti, M., Clarke, R.J., Pegoraro, F., Ruhl, H. & Bulanov, S.V. (2002). Electric field detection in laser-plasma interaction experiments via the proton imaging technique. Phys. Plasmas 9, 2214–2220.Google Scholar
Bulanov, S.V. & Khoroshkov, V.S. (2002). Feasibility of using laser ion accelerators in proton therapy. Plasma Phys. Rep. 28, 453–456.Google Scholar
Bulanov, S.V., Esirkepov, T.Zh., Kamenets, F.F., Kato, Y., Kuznetsov, A.V., Nishihara, K., Pegoraro, F., Tajima, T. & Khoroshkov, V.S. (2002). Generation of high-quality charged particle beams during the acceleration of ions by high-power laser radiation. Plasma Phys. Rep. 28, 975–991.Google Scholar
Clark, E.L., Kurshelnick, K., Zepf, M., Beg, F.N., Tatarakis, M., Machacek, A., Santala, M.I.K., Watts, I., Norreys, P.A. & Dangor, A.E. (2000a). Energetic heavy-ion and proton generation from ultraintense laser-plasma interactions with solids. Phys. Rev. Lett. 85, 1654–1657.Google Scholar
Clark, E.L., Krushelnick, K., Davirs, J.R., Zepf, M., Tatarakis, M., Beg, F.N., Machacek, A., Norreys, P.A., Santala, M.I.K., Watts, I. & Dangor, A.E. (2000b). Measurements of energetic proton transport through magnetized plasma from intense laser interactions with solids. Phys. Rev. Lett. 84, 670–673.Google Scholar
Crow, J.E., Auer, P.L. & Allen, J.E. (1975). The expansion of a plasma into a vacuum. J. Plasma Phys. 14, 65–76.Google Scholar
Davies, J.R. (2002). Proton acceleration by fast electrons in laser-solid interactions. Laser Part. Beams 20, 243–253.Google Scholar
Esirkepov, T.Zh., Bulanov, S.V., Nishihara, K., Tajima, T., Pegoraro, F., Khoroshkov, V.S., Mima, K., Daido, H., Kato, Y., Kitagawa, Y., Nagai, K. & Sakabe, S. (2002). Proposed double-layer target for the generation of high-quality laser-accelerated ion beams. Phys. Rev. Lett. 89, 175003.Google Scholar
Fourkal, E., Shahine, B., Ding, M., Li., J., Tajima, T. & Ma, C. (2002). Particle in cell simulation of laser accelerated proton beams for radiation therapy. Med. Phys. 29, 2788–2798.Google Scholar
Gemmel, D.S. (1974). Channeling and related effects in the motion of charged particles through crystals. Rev. Mod. Phys. 46, 129–227.Google Scholar
Haseroth, H. & Hill, C.E. (1996). Multicharged ion sources for pulsed accelerators. Rev. Sci. Instr. 67, 945–949.Google Scholar
Hatchett, S.P., Brown, C.G., Cowan, T.E., Henry, E.A., Johnson, J.S., Key, M.H., Koch, J.A., Langdon, A.B., Lasinski, B.F., Lee, R.W., Mackinnon, A.J., Pennington, D.M., Perry, M.D., Phillips, T.W., Roth, M., Sangster, T.C., Singh, M.S., Snavely, R.A., Stoyer, M.A., Wilks, S.C. & Yasuike, K. (2000). Electron, photon, and ion beams from the relativistic interaction of Petawatt laser pulses with solid targets. Phys. Plasmas 7, 2076–2082.Google Scholar
Hegelich, M., Karsch, S., Pretzler, G., Habs, D., Witte, K., Guenther, W., Allen, M., Blazevic, A., Fuchs, J., Gauthier, J.C., Geissel, M., Audebert, P., Cowan, T. & Roth, M. (2002). MeV ion jets from short-pulse-laser interaction with this foils. Phys. Rev. Lett. 89, 085002.Google Scholar
Khishimoto, Y., Mima, K., Watanabe, T. & Nishikawa, K. (1983). Analysis of fast-ion velocity distributions in laser plasmas with a truncated Maxwellian velocity distribution of hot electrons. Phys. Fluids 26, 2308–2315.Google Scholar
Krushelnick, K., Clark, E.L., Zepf, M., Davies, J.R., Beg, F.N., Machacek, A., Santala, M.I.K., Tatarakis, M., Watts, I., Norreys, P.A. & Dangor, A.E. (2000). Energetic proton production from relativistic laser interaction with high density plasmas. Phys. Plasmas 7, 2055–2061.Google Scholar
Landau, L.D. & Lifshitz, E.M. (1968). Statistical Physics, 2nd ed. Oxford: Pergamon.
Lefebvre, E. & Bonneaud, G. (1997). Nonlinear electron heating in ultrahigh-intensity-laser-plasma interaction. Phys. Rev. E 55, 1011–1014.Google Scholar
Mora, P. (2003). Plasma expansion into a vacuum. Phys. Rev. Lett. 90, 185002.Google Scholar
Murakami, Y., Kitagawa, Y., Sentoku, Y., Mori, M., Kodama, R., Tanaka, K.A., Mima, K. & Yamanaka, T. (2001). Observation of proton rear emission and possible gigagauss scale magnetic fields from ultra-intense laser illuminated plastic target. Phys. Plasmas 8, 4138–4143.Google Scholar
Nemoto, K., Maksimchuk, A., Banerjee, S., Flippo, K., Mourou, G., Umstadter, D. & Bychenkov, V.Y. (2001). Laser-triggered ion acceleration and table top isotope production. Appl. Phys. Lett. 78, 595–597.Google Scholar
Passoni, M., Tikhonchuk, V.T., Lontano, M. & Bichenkov, V.Yu. (2004). Charge separation effects in solid targets and ion acceleration with a two temperature electron distribution. Phys. Rev. E 69, 026411.Google Scholar
Pukhov, A. (2001). Three-dimensional simulations of ion acceleration from a foil irradiated by a short-pulse laser. Phys Rev. Lett. 86, 3562–3565.Google Scholar
Roth, M., Cowan, T.E., Key, M.H., Hatchett, S.P., Brown, C., Fountain, W., Johnson, J., Pennington, D.M., Snavely, R.A., Wilks, S.C., Yasuike, K., Ruhl, H., Pegoraro, F., Bulanov, S.V., Campbell, E.M., Perry, M.D. & Powell, H. (2001). Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 86, 436–439.Google Scholar
Santala, M.I.K., Zepf, M., Beg, F.N., Clark, E.L., Dangor, A.E., Krushelnick, K., Tatarakis, M., Watts, I., Ledingham, K.W.D., McCanny, T., Spencer, I., Machacek, A.C., Allott, R., Clarke, R.J. & Norreys, P.A. (2001). Production of radioactive nuclides by energetic protons generated from intense laser-plasma interactions. Appl. Phys. Lett. 78, 19–21.Google Scholar
Snavely, R.A., Key, M.H., Hatchett, S.P., Cowan, T.E., Roth, M., Phillips, T.W., Stoyer, M.A., Henry, E.A., Sangster, T.C., Singh, M.S., Wilks, S.C., Mackinnon, A., Offenberger, A., Pennington, D.M., Yasuike, K., Langdon, A.B., Lasinski, B.F., Johnson, J., Perry, M.D. & Campbell, E.M. (2000). Intense high-energy proton beams from petawatt-laser irradiation of solids. Phys. Rev. Lett. 85, 2945–2948.Google Scholar
Tikhonchuk, V.T. (2002). Interaction of a beam of fast electrons with solids. Phys. Plasmas 9, 1416–1421.Google Scholar
True, M.A., Albritton, J.R. & Williams, E.A. (1981). Fast ion production by suprathermal electrons in laser fusion plasma. Phy. Fluids 24, 1885–1893.Google Scholar
Wickens, L.M., Allen, J.E. & Rumsby, P.T. (1978). Ion emission from laser-produced plasma with two electron temperatures. Phys. Rev. Lett. 41, 243–246.Google Scholar
Wilks, S.C., Kruer, W.L., Tabak, M. & Langdon, A.B. (1992). Absorption of ultra-intense laser-pulses. Phys. Rev. Lett. 69, 1383–1386.Google Scholar
Wilks, S.C., Langdon, A.B., Cowan, T.E., Roth, M., Singh, M., Hatchett, S., Key, M.H., Pennington, D., Mackinnon, A. & Snavely, R.A. (2001). Energetic proton generation in ultra-intense laser-solid interactions. Phys. Plasmas 8, 542–549.Google Scholar
Figure 0

The electrostatic potential (a), the electron density (b), and the electric field (c) are plotted as functions of x for , s = 125 μm, ηe = 0.2, and ϑ = 25° (Clark et al., 2000b).

Figure 1

The (solid) lines at constant maximum proton energy (in megaelectron volts), and the (dashed) lines at fixed total electron number are shown in the plane laser energy versus laser intensity. The “positions” of the two experiments considered in the text (Clark et al., 2000b; Hatchett et al., 2000) are marked by the two filled circles.

Figure 2

The energy spectrum (solid line) of the accelerated protons (Z = 1), given by Eq. (8), for the parameters of Hatchett et al. (2000), is displayed. It is assumed that the proton-emitting layer on the rear surface of the target has a thickness of 2 μm and a radius of 5 μm, corresponding to a proton number of Ni ≈ 1.5 × 1012. The dots correspond to the experimental data (Snavely et al., 2000).

Figure 3

The (solid) lines at constant maximum proton energy (in megaelectron volts), and the (dashed) lines at fixed total electron number are shown in the plane laser energy versus laser intensity. The following parameters have been chosen: s = 100 μm, ηe = 0.3, and ϑ = 25°. The two filled circles correspond to two possible implementations of a proton bunch in the energy range of 250 MeV, and with an energy spread of (see Fig. 5).

Figure 4

The proton energy spectra, given by Eq. (8), for two different sets of parameters are displayed. The broader spectrum (solid line) refers to a laser energy of 1 kJ and intensity of 1.2 × 1022 W/cm2. The narrower spectrum refers to . In both cases, s = 100 μm, ηe = 0.3, and ϑ = 25°.