1. INTRODUCTION
Production of fusion energy by burning mixtures of light hydrogen (1H) and the Boron-11 isotope (11B) is of interest because the entire reaction does not produce neutrons (Weaver et al., Reference Weaver, Zimmerman and Wood1973; Nuckolls, Reference Nuckolls, Schwarz and Hora1974; Miley, Reference Miley1976; Ray et al., Reference Ray and Hora1976; Hora, Reference Hora1977). Historically, it was the first reaction to discover the tremendous anomaly of nuclear fusion reactions (Cockroft & Walton, Reference Cockroft and Walton1932) at very much lower energy than known by then in nuclear physics. Initially, it was necessary—and this is valid for all larger nuclei—that reactions between nuclei occur only if their distances for collisions are in the range of femtometers (or Fermi, Fm), where the collision energy to overcome the Coulomb repulsion has to be above MeV per nucleon.
When Cockroft and Walton (Reference Cockroft and Walton1932) developed their accelerator for smashing nuclei together; they were keen enough to try whether the energy of nuclei for producing reactions could be much lower than many MeVs. They discovered that only 150 keV were sufficient for protons to react with boron nuclei. Oliphant and Rutherford (Reference Oliphant and Rutherford1933) used intense 100 keV gas discharges to measure the exact detail of the H-11B reaction producing 8.9 MeV energy into three equal alpha particles (helium, 4He). This result of the anomalously low collision energy for fusion was then even more drastic when verifying the reaction of deuterons (D) only, where the super heavy hydrogen isotope tritium (T) was discovered (Oliphant et al., Reference Oliphant, Harteck and Rutherford1934), which reaction with D happened at smashing energies of 10 keV or even less. In these cases, the nuclei reacted at distances about hundred times of their radii and not within the usual fm distance of the nuclear radii only (Hora, Reference Hora2004).
Realizing this significant anomaly of more than 100 times lower fusion energy, laser driven fusion energy was from the beginning focusing on the H-11B reaction apart from the main interest in the DT reaction (Weaver et al., Reference Weaver, Zimmerman and Wood1973; Hora, Reference Hora1977). It is remarkable that the very precisely measured cross sections of these fusion reactions for the mentioned very large distances could be reproduced by a physical theory only recently (Li et al., Reference Li, Tian, Mei and Li2000, Reference Li, Liu, Chen, Wei and Hora2004). It was evident from the very beginning that, the H-11B reaction is much more difficult than the DT reaction (Nuckolls, Reference Nuckolls, Schwarz and Hora1974, p. 103), though the interest for energy production was very interesting because less radioactivity was produced (only by secondary reactions of the alpha particles with boron (see Weaver et al., Reference Weaver, Zimmerman and Wood1973)) per generated energy than from burning coal due to the 2 ppm content of uranium in all coal.
The difficulty for laser driven fusion from radially irradiated fuel pellets of H-11B consists in the need of very high ignition temperatures and extremely high compression. After the reheat in the fusion pellets by alpha particles was resulting in a much lower stopping length based on the collective effect (Gabor, Reference Gabor1933, Reference Gabor1952) in contrast to the binary collisions of the Bethe-Bloch theory (Stepanek, Reference Stepanek, Schwarz, Hora, Lubin and Yaacobi1981), the volume ignition (Hora & Ray, Reference Hora and Ray1978) for inertial confinement fusion (ICF) resulted in interesting gains for DT and offered an access to treat H-11B (Ray et al., Reference Ray and Hora1976; Hora, Reference Hora1977). In due course, it was elaborated (Pieruschka et al., Reference Pieruschka, Cicchitelli, Khoda-Bakhsh, Kuhn, Miley and Hora1992; Stening et al., Reference Stening, Kasotakis, Khoda-Bakhsh, Pieruschka, Kuhn, Miley, Hora, Hora and Miley1992; Khoda-Bakhsh, Reference Khoda-Bakhsh1993) that the self-heating by alpha particles can reduce the ignition temperature from about 200 keV down to 23 keV, however, needing compression in the range of 100,000-times the solid state and needing laser energies above 10 MJ in the compressed plasma. The retrograde behavior of the reaction was clarified (Scheffel et al., Reference Scheffel, Stening, Hora, Höpfl, Martinez-Val, Eliezer, Kasotakis, Piera and Sarris1997) explaining why compression much above 2 × 105 times the solid state is not helpful. Questions about the stopping length are still under discussion but may lead to some gradual modification only. It should be mentioned that the reaction of 3He-3He arrives at similar results as H-11B burning (Khoda-Bakhsh et al., Reference Khoda-Bakhsh, Soltanian and Amniat-Talab2008). This reaction is of importance for the present discussion of the climatic catastrophe (Hora, Reference Hora2007a) where the harvesting of the huge amounts of 3He from the surface of the moon may be of interest. One load of a space shuttle could produce fusion energy equal to all energy used in the USA within half a year (Kulcinski, Reference Kulcinski2007).
2. DIFFICULTIES AT SPHERICAL COMPRESSION
Nevertheless, the consideration of problems with the equation of state (Lomonosov, Reference Lomonosov2007; Eliezer et al., Reference Eliezer, Murakami and Martinez-Val2007), with the pressure ionization and polarization shift (Ebeling et al., Reference Ebeling, Meister, Sandig and Kraeft1979; Hora & Henry, Reference Hora and Henry1983), with electron pressure (Meister et al., Reference Meister, Staude and Pregla1999), or with dissociation problems (Bunker et al., Reference Bunker, Nagel, Redmer and Roepke1997) arrived at critical results for the spherical pellet H-11B reaction by volume ignition for ICF. It was concluded by Eliezer et al. (Reference Eliezer, Murakami and Martinez-Val2007) “that the desired clean fusion reaction p + B(11) → 3α is not suitable for a magnetic confinement or inertial confinement (at any density) reactor.” Apart from clarification of more details of this analysis (Malekynia et al., Reference Malekynia, Hora, Ghoranneviss and Miley2009, Fig. 2), there may a basically different and alternatively simplified way for the H-11B reaction, if instead of the laser ignition of spherical fuel pellets, the plane geometry block ignition (Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikova, Kraska, Laska, Parys, Perina, Pfeifer and Rohlena2002, Reference Hora, Malekynia, Ghoranneviss, Miley and He2008; Hora, Reference Hora2003, Reference Hora2007a, Reference Hora2007b; Miley et al., Reference Miley, Hora, Cang, Osman, Badziak, Wolowski, Sheng, Zhang, Zhang and He2008) is considered. This is based on the generalization of the results of Chu (Reference Chu1972) by inclusion of later discovered phenomena as the inhibition factor for reduction of thermal conduction (Ghoranneviss et al., Reference Ghoranneviss, Malekynia, Hora, Miley and He2008) or of collective effects (Hora et al., Reference Hora, Malekynia, Ghoranneviss, Miley and He2008) as elaborated for the case of DT. This paper presents the first results derived for the case of H-11B.
3. LASER NONLINEAR FORCE DRIVEN BLOCK IGNITION
A very anomalous phenomenon was measured if the laser beams were of very high quality leading to an alternative concept for fast ignition (Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikova, Kraska, Laska, Parys, Perina, Pfeifer and Rohlena2002, Reference Hora, Malekynia, Ghoranneviss, Miley and He2008; Hora, Reference Hora2003). This concept of block ignition comes from the analysis of preceding laser interaction experiments. Usual results from experiments with TW-PW laser pulses of ps duration for interaction with plasmas were diversified with many new phenomena. Laser intensities above 1019 W/cm2 result in various relativistic effects producing beams of intense accelerated electron jets with energies up to several 100 MeV, highly charged ions with energies in the GeV range, and gamma bursts with subsequent nuclear reactions and pair production. Another anomalous observation is the generation of intense electron jets at oblique incidence on targets. Later, it was found that the suppression of laser prepulses avoids relativistic self-focusing and, as a result, leads to plasma block formation and acceleration of highly directed plane plasma layers from the target surface. These experimental observations have been explained theoretically (Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikova, Kraska, Laska, Parys, Perina, Pfeifer and Rohlena2002).
Block ignition relies on the generation of space-charge neutral plasma blocks (plasma “bunches”) by preventing self-focusing of the laser beam such that it remains uniformly distributed over a broad area of the target surface. Physically, this requires strong suppression of laser prepulses, i.e., a very high contrast ratio (ratio of the main pulse intensity to prepulse intensity). This has to be higher than 107 for times less than a dozens of ps before arrival of the main pulse. The resulting plasma blocks have high momentum and are directed back toward the incoming laser beam. Momentum conservation causes an imploding block of plasma toward the inner portion of the target fuel and is considered to produce a thermonuclear reaction wave (Chu, Reference Chu1972).
The mechanism for creating these high velocity quasi-neutral plasma blocks is based on skin-layer acceleration by nonlinear forces (SLANF) (see also Hora, Reference Hora2009; Malekynia et al., Reference Malekynia, Hora, Ghoranneviss and Miley2009; Yazdani et al., Reference Yazdani, Cang, Sadighi-Bonabi, Hora and Osman2009). This effect was first observed experimentally although long expected theoretically (Hora, Reference Hora1981, Section 10.5), before the very clean ultra-intense TW-ps laser pulses were available. Since the acceleration of the ions is electrodynamic, and not thermokinetic, by the nonlinear force, the observed blocks (pistons) are highly directed and have a comparably low temperature (Badziak et al., Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005, Reference Badziak, Glowacz, Hora, Jablonski and Wolowski2006) for the proton fast ignition (Roth et al., Reference Roth, Brambrink, Audebert, Blazevic, Clarke, Cobble, Cobble, Habs, Hegelich, Karsch, Ledingham, Neely, Ruhl, Schlegel and Schreiber2005; Hoffmann et al., Reference Hoffmann, Blazevic, Ni, Rosemej, Roth, Tahir, Tauschwitz, Udrea, Varentsov, Weyrich and Maron2005). The DT ion beam current density in the space charge neutral block with
exceeds the threshold value j* for a fusion reaction wave in solid DT.
However, another necessary condition was that the energy flux density E* of the irradiation had to be larger than the threshold E*0
following the hydrodynamic analysis by Chu (Reference Chu1972) for ignition of solid DT. Though this value is exceedingly high, this is not too far out for the experimental conditions achieved in experiments (Badziak et al., Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005), or for next generation PW-ps laser pulses.
4. CHU-THRESHOLD FOR HYDROGEN-BORON(11)
The possibility that PW-ps laser pulses may generate plasma blocks of quasi-neutral current density above 1011 A/cm2 (Hora, Reference Hora2003; Badziak et al., Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005) for igniting DT fuel at solid state density or some higher compression, led to the reconsideration of the conditions of the derivations of Chu (Reference Chu1972). A further motivation was given by the results of Nuckolls et al. (Reference Nuckolls and Wood2002) that PW-ps laser pulses should produce 5 MeV electron beams of such intensity, that large volumes of only 12-times solid state density DT could be ignited, where laser pulses of 10 kJ may produce 100 MJ fusion energy. The block ignition would then be the analogue process with the ion beams in the block generated by SLANF mechanisms instead of using electron beams.
One point of improvement of the Chu (Reference Chu1972) results was to include the later discovered inhibition factor F* for reduction of thermal conductivity (Ghoranneviss et al., Reference Ghoranneviss, Malekynia, Hora, Miley and He2008). We studied first the generation of a thermonuclear reaction wave in H-11B under the same conditions as Chu (Reference Chu1972) used for DT. The hydrodynamic code was established under the same conditions as by Chu (Reference Chu1972) for DT and checked by comparison with these results, similar to the tests reported earlier (Ghoranneviss et al., Reference Ghoranneviss, Malekynia, Hora, Miley and He2008).
Using the H-11B fusion cross-sections, the hydrodynamic calculation results in the time dependence of the plasma temperature are shown in Figure 1. This is in analogy to Figure 2 of Chu (Reference Chu1972) for DT. The parameter of the curves is the energy flux density E*. What is important is to find the value of E*0 of the ignition threshold. This is identified by such a curve where the plasma temperature T merges in a constant value of time t. This value is found to be
at an ignition temperature T of the plasma of
These results seem to be very remarkably modest compared with the values of DT according to Chu (Reference Chu1972) with the threshold of 4 × 108 J/cm2 and the ignition temperature of 7.25 keV (Ghoranneviss et al., Reference Ghoranneviss, Malekynia, Hora, Miley and He2008). In view of the exorbitant difference between DT and H-11B for volume ignition at spherical pellet compression, it is really surprising, how much easier the ignition of H-11B works for a thermonuclear reaction wave.

Fig. 1. In analogy to Figure 2 of Chu (Reference Chu1972) for DT with his same detailed hydrodynamic presumptions, the plasma temperature T for hydrogen-boron(11) as function of the time t for a given parameter of the input energy flux density E*.
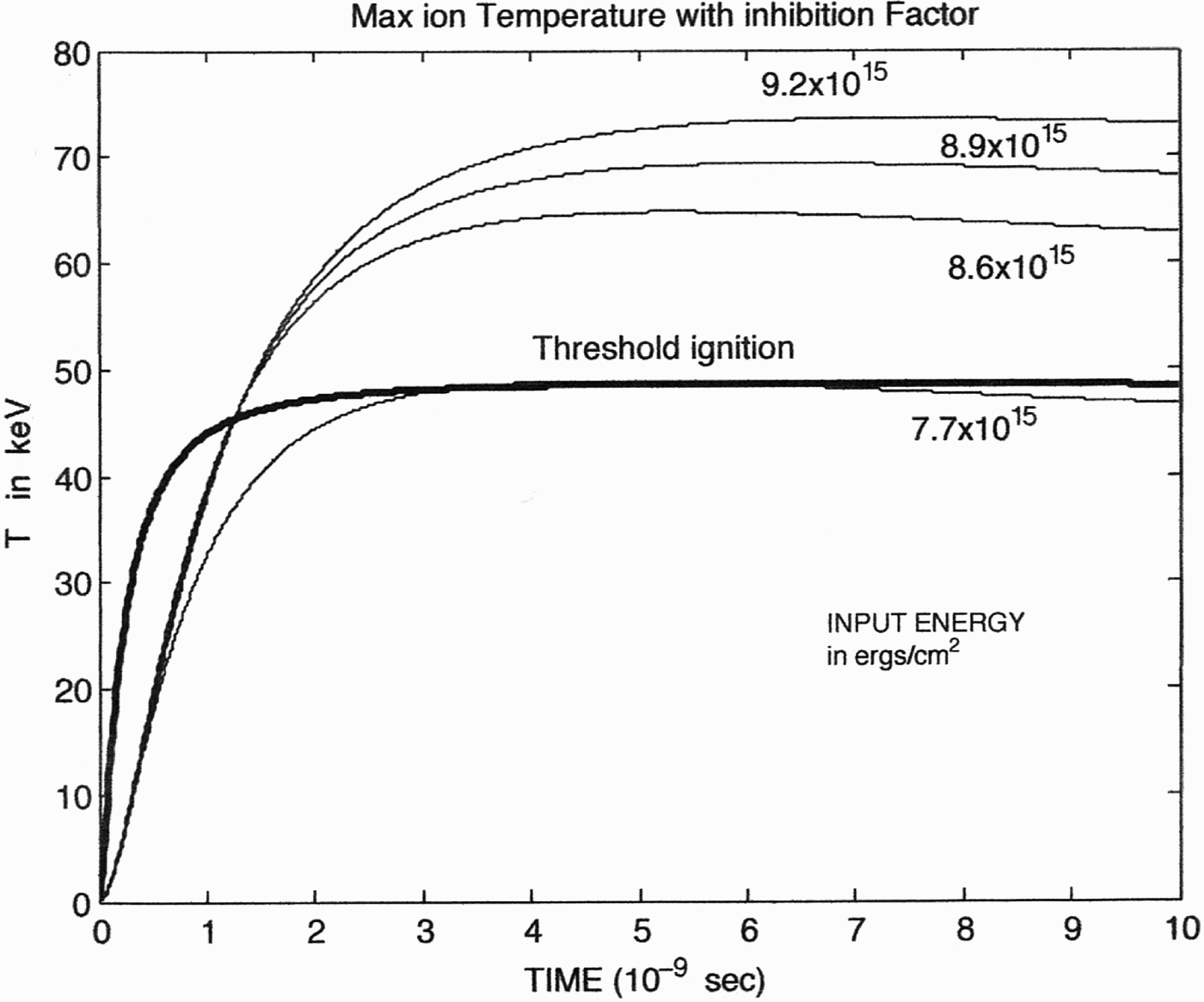
Fig. 2. Same as Figure 1 but with adding the inhibition factor into the calculations of Section 5.
The ignition temperature for block ignition of H-11B can be achieved without problem in the interaction front by the igniting ions of the plasma block, because the uniform energy of the block is not thermal but has a rather precise value determined by the nonlinear (ponderomotive) force acceleration. All these results are in favor for the block ignition of H-11B as envisaged initially for a fusion power reactor (Hora, Reference Hora2002), though the conditions for generating the blocks are still within one order of magnitude more difficult to achieve than for DT, but may not be too far out of reach. The four times more difficult ignition conditions for H-11B in comparison with DT are definitely not a so exorbitant problem as it was shown for the spherical pellet ignition.
5. INCLUSION OF INHIBITION FACTOR FOR THERMAL CONDUCTION
The modification of the initial conditions of Chu (Reference Chu1972) was due to effects which were not known at that time. One question is the use of the stopping length of the alpha particles in the plasma where there is to be decided between the binary collision model of Bethe and of Bloch and the collective model of Gabor (Reference Gabor1933, Reference Gabor1952) as elaborated by Stepanek (Reference Stepanek, Schwarz, Hora, Lubin and Yaacobi1981) following Ray and Hora. (Reference Ray and Hora1976). While these questions are still under discussion for the DT case (Hora et al., Reference Hora, Malekynia, Ghoranneviss, Miley and He2008), we are first focusing on the problem of the inhibition factor F*, that means on the reduction of the thermal conductivity, as treated in details before for the DT case (Ghoranneviss et al., Reference Ghoranneviss, Malekynia, Hora, Miley and He2008; see also Hora, Reference Hora2009).
The reduction of the thermal conduction between hot and cold plasma is based on experimental evidence. Some authors found a value of 30 or 100 for the inhibition factor of deuterium. One model to explain a factor F* = 67 was based on the fact that an electric double layer between the hot and the cold plasma is working only through the ions of the layer depleted from electrons. This was a straight-forward explanation (Fig. 1 of Ghoranneviss et al., Reference Ghoranneviss, Malekynia, Hora, Miley and He2008). After the inhibition was measured, a lot of more or less transparent theories were developed. One of these models is that of Tan and Gu (Reference Tan and Gu1985) where the alternative explanation by the double layers is well acknowledged.
Including the inhibition factor F* = 116 for DT into the hydrodynamic computation as a new condition compared with those of Chu (Reference Chu1972), we obtain the results shown in Figure 2. The curve with the time independent plasma temperature for large times was reached again at the temperature of 48 keV as in the case without inhibition (given by the line “Threshold ignition” in Fig. 2). But due to the lower thermal conduction, the threshold energy flux density E* occurs at a lower value of 7.7 × 108 J/cm2 compared with Eq. (3).
Figure 3 shows the same results as presented in Figure 2, only more detailed for early times. This shows again a retrograde behavior of the temperature dependence on time in a similar way as this was observed before for DT (Ghoranneviss et al., Reference Ghoranneviss, Malekynia, Hora, Miley and He2008) and discussed there.

Fig. 3. Same as Figure 2 but with more details for the first three nanoseconds of the computations.
6. CONCLUSIONS
The here reported results about plasma block ignition of H-11B with PW-ps laser pulses are of crucial importance for fusion energy production (Hora, Reference Hora2003, 2007) as well as for propulsion of space crafts (Miley et al., Reference Miley, Hora, Cang, Osman, Badziak, Wolowski, Sheng, Zhang, Zhang and He2008). Laser driven fusion by spherical compression (Scheffel et al., Reference Scheffel, Stening, Hora, Höpfl, Martinez-Val, Eliezer, Kasotakis, Piera and Sarris1997; Eliezer et al., Reference Eliezer, Murakami and Martinez-Val2007) needs exorbitant compression densities (100,000 times the solid state) and driver energies (above several 107 J) while our new result of laser driven block ignition of uncompressed H-11B is only about one order of magnitude more difficult than the deuterium tritium (DT) fusion.
The spherical laser compression scheme is close to confirming the demonstration of exothermal fusion energy with megajoule lasers (Moses et al., Reference Moses, Miller and Kauffman2006; Bigot, Reference Bigot2006) as a single interaction scheme (Miley et al., Reference Miley, Hora, Osman, Evans and Toups2005) where only a cost reduction for lasers is needed. This is different from a new scheme which was opened for fast ignition (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994) based on the alternative of particle block ignition (Nuckolls & Wood, Reference Nuckolls and Wood2002; Hora, Reference Hora2003) of uncompressed fuel. This alternative with electron beam ignition (Nuckolls & Wood, Reference Nuckolls and Wood2002) or with plasma blocks (Hora, Reference Hora2002, Reference Hora2003) along with the proton fast ignition (Roth et al., Reference Roth, Brambrink, Audebert, Blazevic, Clarke, Cobble, Cobble, Habs, Hegelich, Karsch, Ledingham, Neely, Ruhl, Schlegel and Schreiber2005; Ter-Avetisian et al., Reference Ter-Avetisyan, Schnürer, Polster, Nickles and Sanders2008) using PW-ps laser pulses is very much less explored than the well matured and established (Moses et al., Reference Moses, Miller and Kauffman2006; Bigot, Reference Bigot2006) spherical laser fusion scheme for a DT laser fusion power station; but the here first presented result for the simplified ignition of H-11B may be encouraging for considering to explore this alternative option for a possibly very low cost energy production (Hora, 2007; Hora et al., 2007). The advantage for space application (Miley et al., Reference Miley, Hora, Cang, Osman, Badziak, Wolowski, Sheng, Zhang, Zhang and He2008) is based on the fact that the reaction products are only mono-energetic alpha particles to be directed by magnetic fields for propulsion.
It has to be acknowledged that the spherical laser ignition of H-11B resulted in a reduction of the ignition temperature of uncompressed fuel from much more than 100 keV (Hora, Reference Hora1975, Reference Hora1977; Miley, Reference Miley1976; Ray et al., Reference Ray, Hora, Schwarz and Hora1977) to 23 keV (Scheffel et al., Reference Scheffel, Stening, Hora, Höpfl, Martinez-Val, Eliezer, Kasotakis, Piera and Sarris1997), but it is remarkable that our result of Figure 2 with block ignition of uncompressed H-11B arrived at an ignition temperature of 48 keV only.





