Introduction
It is now known that our Galaxy, the Milky Way harbours a quite number of habitable planets around their host stars. Any forms of life could appear under the conditions which might be similar to Earth's. One of the most important questions about the extraterrestrial life is whether or not there are any civilizations which might have advanced technologies as we know of ours or more progressive, referring to the concept of extraterrestrial intelligence (ETI). All research for ETI is indeed those concerning extraterrestrial technologies, including engineering masterpieces or electromagnetic radiation that would not come from natural sources (Tarter, Reference Tarter2001). By the Kardashev scale, which classifies civilizations in their ability to consume energy, such extraterrestrial structures would indicate the civilizations above Type-I.
The Kardashev scale (Kardashev, Reference Kardashev1964) defines the level of civilizations in the Universe as numerical values of energy consumption rates, 4 × 1019erg s−1 for Type-I, 4 × 1033erg s−1 for Type-II and 4 × 1044erg s−1 for Type-III. Extension of that scale is also described in other hypothetical types, which may have harnessing technologies far beyond what human beings could ever imagine within basic science and engineering (Benjamin, Reference Benjamin2016; Meinzer and Cloney, Reference Meinzer and Cloney2018). It is estimated that the human race is around Type-I and beyond that required energy consumption rates could begin to exceed a planetary civilization. An important objective in energy consumption of an ETI's civilization above Type-I is to meet the energy requirement for a communication mechanism so that its signals could be detected by other supposedly existing civilizations. An enlightening study of Chennamangalam et al. (Reference Chennamangalam, Siemion, Lorimer and Werthimer2015) has proposed that if an ETI whose technology has just achieved ability to dispatch interstellar spacecrafts decides to announce its very presence to the Galaxy, they could have a beacon more powerful than their entire energy consumption rate through a compact object class called pulsars. It is also emphasized that the engineering of pulsar domain becomes important if the cost of accessing nearby ones is lower than in the corresponding beacon luminosity level.
Pulsars are neutron stars which are the most compact objects without event horizons and have such extreme environments (Lattimer and Prakash, Reference Lattimer and Prakash2007). Their magnetic fields are driven by their rotation or accretion power and they emit coherent electromagnetic radiation at radio frequency from their magnetic axes (Ghosh, Reference Ghosh2007). Pulsars are known as stable radio sources although the measured flux density, which is one of the main observables of radio emission varies due to diffractive and refractive scintillation effects, usually caused by interstellar electron density variation (Maron et al., Reference Maron, Kijaj, Kramer and Wielebinski2000). Another class of neutron stars are magnetars which are powered by the decay of their very powerful magnetic fields accounted for by magnetohydrodynamic events. There are no compelling arguments on why most of the magnetars cannot be radio emitters (Lazarus et al., Reference Lazarus, Kaspi, Champion, Hessels and Dib2012; Szary et al., Reference Szary, Melikidze and Gil2015) but they vary from pulsars in that they have more lethal characteristics for engineering in their own domain.
An ETI's needs to utilize pulsars for galactic scale broadcasting instead of their own beacons could be investigated by comparing their beacon's required transmitter power with pulsar luminosities. The relation between isotropically transmitted and received powers is given by
$$P_{\rm t} = P_{\rm r}\displaystyle{{4{\rm \pi} R_{\rm d}^2} \over {A_{\rm r}}}$$where P t and P r are transmitted and received powers, respectively, R d is the detection range and A r is the collecting area of receiver. The reason why the transmitter is isotropic is because the entire celestial sphere must be scanned to reach to all solar systems. In addition, P r is proportional to the detection threshold parameter m, noise temperature T and signal bandwidth b as P r = mkTb, where k is the Boltzmann constant (Drake et al., Reference Drake, Wolfe and Seeger1984). Using the assumptions of Kardashev (Reference Kardashev1964) with m = 100 and technical specification of Five-hundred-meter Aperture Spherical radio Telescope (FAST) with A r ≈ 1.96 × 109 cm2, T < 7K (Dunning et al., Reference Dunning, Bowen, Castillo, Chung, Doherty, George, Hayman, Jeganathan, Kanoniuk, Mackay, Reilly, Roush, Severs, Smart, Shaw, Smith, Tzioumis and Venables2017), the power needed to send an isotropic 1 GHz signal likely to be received by FAST from 1 kpc is in the order of 1030 erg s−1. Even with a narrow solid angle of transmission (with apex angle of 2°), the needed power will be roughly 1025 erg s−1, besides probability to encounter any solar system is very low. Similar results apply for the Arecibo radio telescope (Chennamangalam et al., Reference Chennamangalam, Siemion, Lorimer and Werthimer2015). Since the transmitter power has to be proportional to the energy consumption rate, civilization should be remarkably more advanced than Type-I, around the lower limit of Type-II. On the other hand, radio luminosities of pulsars could be calculated as follows:
$$L = {\rm \Omega} R_{\rm d}^2 \int_{\,f_1}^{\,f_2} {S_{{\rm peak}}(\,f){\rm d}f} $$where Ω = 4πsin 2(ρ/2) is solid angle of the radio beam in terms of half apex angle ρ and S peak(f) = Smean(f)/δ the peak flux density in terms of pulse duty cycle δ (Lorimer and Kramer, Reference Lorimer and Kramer2005). Using some averages for pulsars from the observed results in Henry and Paik (Reference Henry and Paik1969), Kijak and Gil (Reference Kijak and Gil1997) as δ ≈ 0.05 and ρ ≈ 6°, for a 1400 MHz flux density of 1 mJy from 1 kpc range, luminosity would be in the order of 1026 erg s−1. Higher values of flux densities (Lorimer et al., Reference Lorimer, Yates, Lyne and Gould1995) may carry the luminosity up to high levels. Also one of the most important benefits here is that the solid angle direction of the pulsars’ radio emission is not fixed and would sweep a large region of space due to the inclination between rotational and magnetic axes. If it is mentioned what is the relation between pulsar's luminosity and its rotational period which is also the period of sweeping, it is necessary to know that where the pulsar's radio energy comes from. Since the total energy is to be conserved, radio energy originates from the loss of the rotational kinetic energy of pulsar with any non-accreting pulsar gradually slowing down. The kinetic energy of a rotating pulsar is 2π2IP −2, where I is the moment of inertia and P is the period. Then the luminosity is
$$L = -4{\rm \pi} ^2IP^{-3}\dot{P}\;. $$By rearranging the above equation in terms of the rate of change of the period and assuming that pulsars are spherical objects, the equation becomes
$$\dot{P} = -\displaystyle{5 \over {8{\rm \pi} ^2}}\displaystyle{{LP^3} \over {mr^2}}\;, $$where m is the mass and r is the radius of the pulsar. For instance, 
$\dot{P}$ value of the Crab pulsar is approximately 13 μs per year, which shows us the slow-down in the spin periods of the pulsars is a long term process, maintaining the luminosity levels for a long time even for a Crab-type supernova remnant (Weiler and Panagia, Reference Weiler and Panagia1978). Thus, the sweeping might not be counted as an obstacle to use of pulsars for the broadcasting. One can say that the radio luminosity addresses more regions of the space at a sweeping conical angle than at a certain conical angle with the rotation of the pulsars. The lighthouse phenomena of beam sweeping may act as a directed broadcast network until given communications are provided.
The purpose of this study is to investigate how many solar systems could be reached in a portion of our galactic habitable zone (GHZ) which can be scanned by such broadcast networks of pulsars which some ETI between Types-I and II would establish and to examine the suitability of modulators in a pulsar's domain. Section ‘Sweeping by different inclination geometries’ covers sweeping areas and volumes of pulsar radio beams with respect to different inclination angles (α, the one between rotation and magnetic axes), Section ‘Structure of the broadcast network’ discusses structure of the broadcast network and the number of solar systems with habitable planets in the beam range and Section ‘Modulator structures around pulsars’ discusses a simple analysis of how signal modulators around pulsars with different α could be engineered safely. The paper concludes with discussion and conclusions.
Sweeping by different inclination geometries
The rotation and magnetic axes are known to be placed randomly on the neutron star as in their natural formation. Inclination angles of observed pulsars have a wide range of distribution (Rookyard et al., Reference Rookyard, Weltevrede and Johnston2002). The rotation of pulsars’ magnetic axes implies that the conical shape radio emission, also known as the emission cone, rotates. Thus, different sweeping areas (Fig. 1(a)–(c)) and volumes can be calculated for several different cases. Furthermore, since beams are emitted only in the region to be swept, it is geometries not the rotation period which are important. In this case, time dependency for sweeping is not taken into account.
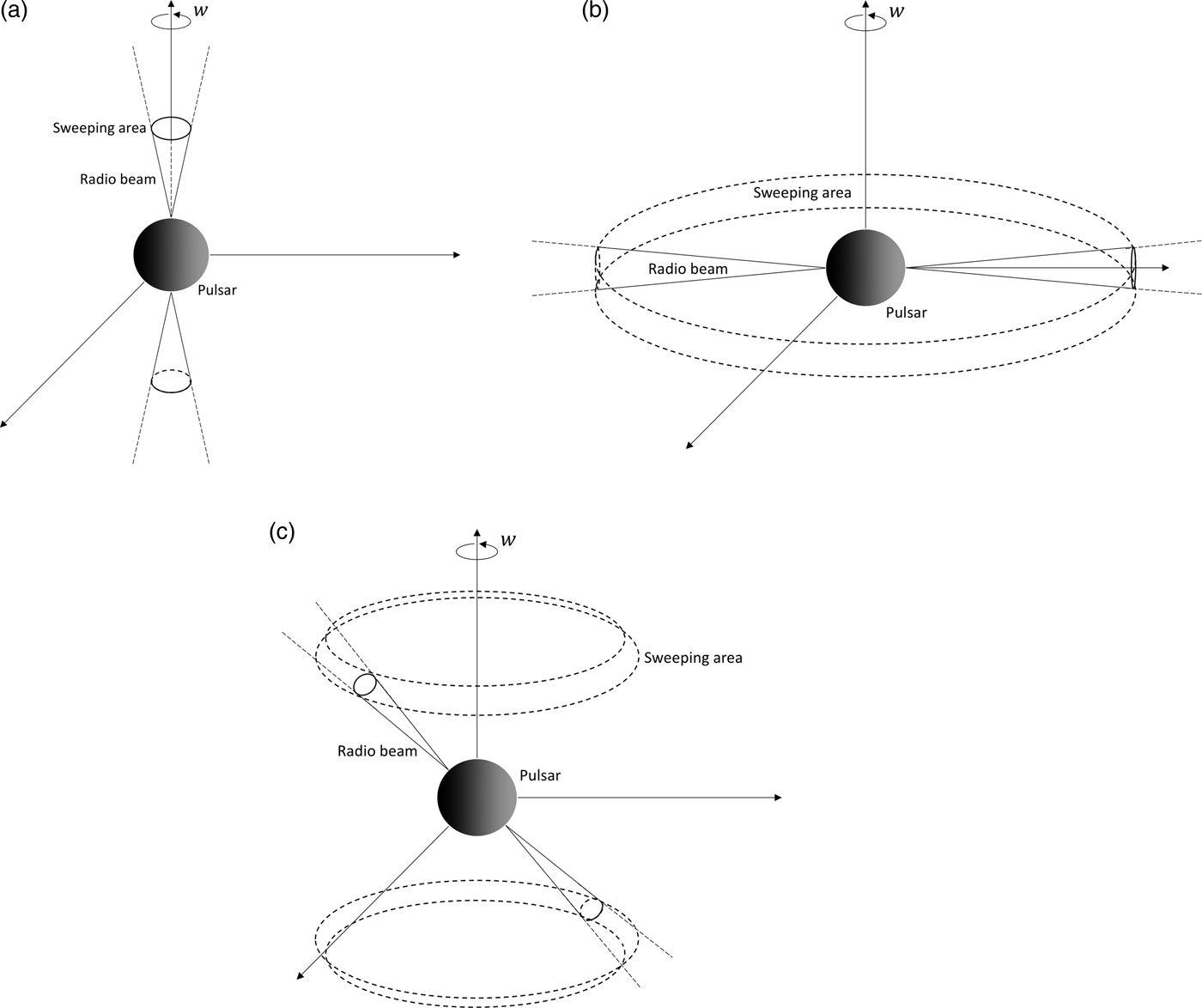
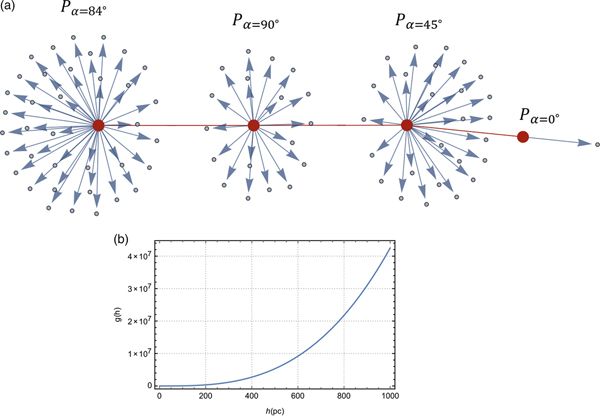
Fig. 1. Schemes of pulsars (a) with an inclination angle α = 0°, sweeping circular areas departing in the opposite directions, (b) α = 90° and sweeping area, a cylindrical surface and (c) ρ < α ≤ 90° − ρ, the area constituting frustums in the opposite directions as well. Note that the parabolic cambers of the ends of the emission cones are neglected for simplicity.
Beam sweeping areas illustrate how much area the beams could scan in a 2D sky map at a certain distance from pulsar and one can also examine how many solar systems would be reached in various ranges by sweeping volumes, in both of which all different consequences depend on the inclination angle. Cases of the inclination angle can be simply considered α = 0°, α = 90° and 0° < α < 90°. However, for the interval of 0° < α < ρ the area and volume can be assumed again as a circle and cone only with large values due to the enlarged beam radii from the precession. A similar situation occurs for 90° − ρ < α < 90°. In those intervals, half apex angles of the emission cones become α + ρ for 0° < α < ρ and (90° − α) + ρ for 90° − ρ < α < 90°, respectively. Additionally, if α = ρ, sweeping area becomes the surface area of a cone and volume turns out to be two oppositely oriented cones. Considering all these conditions, there are six areal and volumetric cases due to α. For some geometric derivations, a longitudinal section of inclined pulsar beam and required lengths are shown in Fig. 2.
Fig. 2. Longitudinal section and significant dimensions of a pulsar beam at a given time. h is the beam's altitude.
Sweeping areas are given as follows:
$$\left. {\matrix{ {{\rm \alpha} = 0{\rm^\circ}} \cr {0{\rm^\circ} \lt {\rm \alpha} \lt {\rm \rho}} \cr}} \right\}\Rightarrow \; A = 2{\rm \pi} h^2\tan ^2{\rm \rho}, $$
$${\rm \alpha} = {\rm \rho} \Rightarrow A = 8{\rm \pi} h^2\sin {\rm \rho} \tan {\rm \rho}, $$
$${\rm \rho} \lt {\rm \alpha} \le 90{\rm ^\circ} \Rightarrow A = 8{\rm \pi} h^2\sin {\rm \alpha} \tan {\rm \rho}, $$
$$\left. {\matrix{ {{\rm \alpha} = 90{\rm^\circ}} \cr {90{\rm^\circ} -{\rm \rho} \lt {\rm \alpha} \lt 90{\rm^\circ}} \cr}} \right\}\Rightarrow A = 4{\rm \pi} h^2\tan {\rm \rho}. $$Sweeping volumes are thus:
$$\left. {\matrix{ {{\rm \alpha} = 0{\rm^\circ}} \cr {0{\rm^\circ} \lt {\rm \alpha} \lt {\rm \rho}} \cr}} \right\}\Rightarrow \; V = \displaystyle{2 \over 3}{\rm \pi} h^3\tan ^2{\rm \rho}, $$
$${\rm \alpha} = {\rm \rho} \Rightarrow V = \displaystyle{4 \over 3}{\rm \pi} h^3\left[ {\displaystyle{{1-\cos (2{\rm \rho} )} \over {\cos {\rm \rho}}}} \right],$$
$$\left. {\matrix{ {{\rm \alpha} = 90{\rm^\circ}} \cr {90{\rm^\circ} -{\rm \rho} \lt {\rm \alpha} \lt 90{\rm^\circ}} \cr}} \right\}\Rightarrow V = \displaystyle{4 \over 3}{\rm \pi} h^3\tan {\rm \rho}, $$
$$\eqalign{& {\rm \rho} \lt {\rm \alpha} \le 90{\rm ^\circ} -{\rm \rho} \Rightarrow V \cr & \quad = \displaystyle{2 \over 3}{\rm \pi} \lsqb {y_1\lpar {R_1^2 -R_3^2} \rpar + y_2\lpar {R_1^2 -R_3^2 + R_1R_2-R_2R_3} \rpar } \rsqb } $$where R 1 = (h/cosρ)sin (α + ρ), R 2 = (h/cosρ)sin (α − ρ), R 3 = (h/cosρ)cos (α + ρ)tan (α − ρ), y 1 = (h/cosρ)cos (α + ρ) and y 2 = 2hsinαtanρ. Note that in 0° < α < ρ, ρ becomes α + ρ and in 90° − ρ < α < 90°, ρ becomes (90° − α) + ρ. If the radio beam travelled for 1 pc and ρ = 6°, sweeping areas and volumes with respect to α are shown in Fig. 3(a) and (b).
Fig. 3. (a) Graph of pulsar beam sweeping area and (b) sweeping volume versus inclination angle. The maximum values corresponds to α = 84°. Then the 90° − ρ < α < 90° region begins and the area so does the volume decreases until α = 90°. The behavioural resemblance between sweeping areas and volumes is caused by the fact that the former determines the latter in a certain beam altitude.
Structure of the broadcast network
Polar cap model of pulsar beams indicates the symmetry of emission cones which correspond to the outer emitting region of any pulsar (Tauris and Manchester, Reference Tauris and Manchester1997). In some cases, beams can asymmetrically be deflected or bent in the rotational direction of pulsar by some retardation effects of magnetosphere (Cordes, Reference Cordes1978; Gangadhara and Gupta, Reference Gangadhara and Gupta2001), which is not the circumstance applying for most of the pulsars hence the current study only deals with usual emission geometries. To receive such a radio emission, line of sight must be within the beaming angle thus the emission cone. Therefore, each pulsar beam's sweeping volume consists of numerous edges which conveys radio waves to every solar system in their path. In network terminology, every pulsar that ETI can control is a root node and every solar system inside the beam is a leaf node of the broadcast network, which can be accepted in a topology similar to a directed star graph. A star graph is a tree network of n nodes with one root node having degree of n − 1 and other n − 1 leaf nodes with degree 1. In some systems, root nodes are like hubs making the star graph directed. Consequently, roots have an out-degree of n − 1 and leaves have an in-degree of 1. Broadcast network model shows that the pulsars are the root nodes and solar systems inside their beams are leaves. Thus, sweeping volume of pulsar beams determines the out-degree and increase in the out-degree of broadcast network due to the beam altitude means the same thing as the growth of the network. If any ETI is capable of controlling more than one pulsar, every network of individual pulsars would be root nodes of a broadcast meta-network which can also increase the number of other solar systems in range.
How many solar systems a pulsar beam may cover or how many edges such a beam may have depends on the stellar density of different galactic regions, which could be assumed as 1 star pc−3 for disc (thick-thin average), 102 stars pc−3 for bulge and 103 stars pc−3 for core (Kennicutt and Evans, Reference Kennicutt and Evans2012). Galactic halo is excluded from this approach since fewer lone stars with deficiency of metallicity and globular clusters are not suitable places to detect terrestrial planets harbouring intelligent or even primitive life (Gonzalez et al., Reference Gonzalez, Brownlee and Ward2001). For an inclined pulsar beam with ρ = 6°, α = 45° and h = 1 kpc (Fig. 4), total V becomes roughly 0.6 kpc3 from equation (12). Then the maximum number of possible edges will be 6 × 108 for disc, 6 × 1011 for bulge and 6 × 1012 for core. However, galactic bulge and core are places very rich in metallicity. If a solar system has an overdose metallicity, the planets to be formed are very heavy which could easily annihilate Earth-like planets, if they ever exist. Moreover, those regions have intense supernova frequency, preventing many terrestrial planets from supporting life. A GHZ, an annular region between 7 and 9 kpc from the centre of Milky Way is proposed by Lineweaver et al. (Reference Lineweaver, Fenner and Gibson2004).
Fig. 4. Representation of sweeping volume of a pulsar beam with ρ = 6°, α = 45° $α = 45° and h = 1 kpc. Pulsar is in the origin and the total volume, also a composite of numerous edges is the oppositely oriented internal regions between the two outer and inner cones.
The exact fraction of stars in GHZ which are solar systems with terrestrial planets in their stars’ own habitable zones is currently unknown since the search techniques are still sufficient to discover such celestial bodies with certain characteristics. Besides, solar-type stars (K-G-F-type) can be examined thanks to their known convenience for intelligent life. Solar-type stars constitute a group of roughly 
$10\% $ in the stellar population of Milky Way (Soderblom and King, Reference Soderblom and King1998) and Petigura et al. (Reference Petigura, Howard and Marcy2013) estimated that a fraction such as 
$22\% $ of them have Earth-like planets in their habitable zones. The present work considers that habitable planet distribution is homogeneous and the out-degree is the number of Earth-like planets in their solar-type star's habitable zones, according to which increase in their out-degrees (k out) with respect to beam altitude (up to 1 kpc) is shown in Fig. 5 supposing that a pulsar of α = 0°, α = 90° and the pulsar in Fig. 4 (as 0° < α < 90°) are located on the GHZ. It follows from the graphs’ data and the volume equations in section ‘Sweeping by different inclination geometries’ that the out-degrees of networks are proportional to h 3, in which case k out,α(h) = ξαh 3 with a coefficient ξα = 0.022V α changing with inclination angle.
Fig. 5. Growth of three different pulsars’ (ρ = 6° and α = 0°, α = 45°, α = 90°) broadcast networks with respect to beam altitude up to 1 kpc.
As seen from the results even under the control of a single pulsar, especially α ≠ 0° cases, a large number of solar systems with Earth-like planets could be reached. Each of these planets in the vicinity might have a sufficiently complex and developed life to analyse modulated radio signals sent therefrom. In case of more than one pulsar, even more such planets can be reached, which could be modelled in general form with simplifications. First, all of the controlled pulsars can be considered to be close to each other for a few pc or closer. Second, it can be considered that the beams do not overlap or would overlap in a very minute portion. Then the growth (increase in the total out-degree) of the overall network is given below:
$$g(h) = \sum\nolimits_{\rm \alpha} {N_{\rm \alpha} {\rm \xi} _{\rm \alpha} h^3} $$where N α is the number of pulsars of the same inclination angle. Now broadcast networks of each pulsar turn out to be a broadcast meta-network from star graph to a decentralized topology which is shown as an example in Fig. 6(a). The meta-network does not have any single point of control and must have a decentralized topology by design such as in the e-mail network. Every pulsar and their modulators can operate their own search. If a modulator goes offline so do the benefits of pulsar, others may still work and send signals. Each pulsar–modulator system is a one way mail server as an analogy. In case that each pulsar–modulator system operates, network growth would increase drastically (Fig. 6(b)), reaching to 4.25 × 107 habitable planets even in 1 kpc.
Fig. 6. (a) A meta-network example of four controlled pulsars which are large central nodes. Edges between pulsars are undirected, showing that they belong to the same civilization. When the rightmost one, 
$P_{{\rm \alpha} = 0{\rm ^\circ}} $ has an edge, 
$P_{{\rm \alpha} = 45{\rm ^\circ}} $ would have 27, 
$P_{{\rm \alpha} = 90{\rm ^\circ}} $, 19 and 
$P_{{\rm \alpha} = 84{\rm ^\circ}} $, 38 edges, which would continue in the above proportionality as the network growths. Note that the beams do not overlap. (b) Growth of the meta-network.
Modulator structures around pulsars
In order to search for the galaxy with pulsars’ broadcast networks, an ETI must firstly invent a technology of modulators around pulsars. Although such technologies have yet to be progressed by mankind, we could simply assume several mechanisms around pulsars with each having pros and cons. All the modulator geometries have in common in that they have to be farther from the radio emission altitude (r em) in order to catch and modulate radio beams emitted by pulsars. Magnetic field lines of a pulsar is closed in a region called the light cylinder and it is generally accepted that the r em lies within 
$10\% $ of the light cylinder radius which comes from equating the linear sweeping speed of the beam to the speed of light (c), thus R LC = cP/2π (Kijak and Gil, Reference Kijak and Gil2003) where P is the rotation period, from which it can be seen that the modulator would be contained in the pulsar's magnetosphere. Interaction of the modulator with the particles and field lines of the magnetosphere could cause serious problems. However, there are solutions likely to be considered such as some modulator particles’ injection into magnetosphere. Chennamangalam et al. (Reference Chennamangalam, Siemion, Lorimer and Werthimer2015) proposed that the modulating mechanism could be based on confined plasma or electro-optics.
One of the modulator geometries is a satellite which follows the pulsar beam synchronously. It seems to be suitable for pulsars whose magnetic axes are perpendicular to rotation axes but for a pulsar with α = 90°, P = 1 s and 
$M = 1.4M_\odot $ orbital radius 
$r = (1.4GM_\odot )^{1/3}(1/2{\rm \pi })^{2/3}$ is smaller than R LC/10, creating the possibility to miss the emission. The orbital speed of satellite will also be approximately 
$3.5\% $ of c. Thus, the satellite concerned cannot be considered for relatively fast rotating pulsars. Osmanov (Reference Osmanov2016) suggested structures like Dyson rings (Dyson, Reference Dyson1960) could be proper for such pulsars for a continuous beam tracking and modulation. A ring-like structure can be constructed at r em and does not have to move at a certain speed to stay in orbit. In the α ≠ 90° case, gravitational attraction between a pulsar and a wide ring of mass is as follows:
$$F = \displaystyle{{2GM_{{\rm pulsar}}m_{{\rm ring}}d} \over {r_{{\rm out}}^2}} \lpar {1-\cos {\rm \theta}_{r_{{\rm out}}}} \rpar $$where r out is the outer radius of the ring and d is the axial distance. For pulsars as in Fig. 1(c), two ring modulators can track the oppositely directed beams sweeping a cone. Calculations for an α = 45° pulsar indicates that the F would be in the order of 1023 dyn for each ring, which is quite large and requires a lot of booster power to stay in balance. Although the required power could be obtained from the pulsar, where its luminosity is greatly likely to be far enough to create 1023 dyn of force for each ring at a distance of R LC/10, gravitationally non-symmetric geometries would have high perturbations in the modulator with respect to gravitationally symmetric geometries and cause a substantial amount of sweeping area of the emission cone to be missed in such a way not to make a complete signal modulation during the oscillation or high perturbations would remove the ring modulator completely from the balance. All of this and additionally the possible effects of magnetosphere on the boosters make this kind of architecture inefficient for 0° < α < 90°. For such pulsars, a Dyson sphere which tends to be a scaffold around a pulsar may be constructed with a radius greater than r em by paying close attention to the effects of gravity and magnetosphere.
If the stabilities of such megastructures were examined, important principle is the spherical symmetry with the application of Gauss's Law, addressing that any field is effectively zero within that sphere. Naturally, the gravitational field inside the Dyson sphere (0° < α < 90°) would not be zero in the presence of a pulsar but the contribution from the sphere could be zero if the matter is perfectly distributed. However, although the gravitational perfect symmetry was satisfied, location of the pulsar would still not be irrelevant to the system's stability due to its vast amount of radiative energy. In case of any asymmetric shifting in the Dyson sphere–pulsar system, the part of the inner surface of the sphere which is closer to the pulsar will experience higher radiation pressure than the opposite side. Subsequently a restoring force will appear, leading the megastructure to oscillate. Small oscillations resulting from small restoring force increase the stability of the system. For any stellar Dyson sphere, mathematical derivations of the oscillation period and lifespan of the system are made by Osmanov and Berezhiani (Reference Osmanov and Berezhiani2018). Since oscillations would be much more challenging in Dyson spheres around pulsars, an advanced civilization should focus its attention on the centrality of the system which should be almost central. This is obviously the ideal case which could only be available if the related civilization minimizes the system perturbations to the lowest limits by some counter-pressure or attitude correction techniques. When the oscillations are in an acceptable level, and if the entire sphere is the modulator itself, there would not be a distortion in the signal modulation.
Unlike Dyson spheres, a ring structure is dynamically unstable to transverse (in-plane) displacements because the gravitational attraction of the near-side is greater than that of the far-side (Mcinnes, Reference Mcinnes2003). A small disturbance such as the inhomogeneities in the magnetosphere or debris strikes would grow gradually and the ring would lose its centricity until it runs into its host pulsar and be destroyed. By forming an active stabilization system against the in-plane perturbations, the required power gained from the pulsar's luminosity is sent to the boosters along the edges. However, small perturbations in this phenomenon would cause the ring to oscillate axially (out-of-plane) around its equilibrium position. Now the ring is stable against axial displacements after which it would smoothly oscillate around the pulsar. Even in the α = 0° or 90°, the ring could lose an areal fraction of the emission cone, preventing a complete modulation. Consequently, axial boosters fuelled by pulsar's luminosity and increasing the surface area of the ring larger than the sweeping area could be thought to prevent distortion of the signal modulation.
One briefly infers that a Dyson ring seems to be suitable for α = 0° and 90° and a Dyson sphere for all inclination angles. Such megastructures, if their deliberately signals have not reached us yet, could be searched under certain circumstances (Dyson, Reference Dyson1960; Osmanov, Reference Osmanov2018).
In addition to the modulator geometries, modulation feasibility is of great importance. First, the amplitude modulation (AM) may be considered. AM can be based on pulse nulling which toggles between 0 (radio waves cannot pass) and 1 (direct pass). Nulling through prime numbers or particular number sequences can be used by advanced civilizations to prevent an ordinary nulling from not being disguised as if nulling glitch of pulsars. Here the modulator would need to absorb or scatter the entire radiation of pulsar. Second, the frequency modulation can be taken into account as an increase in the data rate. A modulating signal may be used whose frequency is much larger than the period of the pulsar but less than the carrier frequency (Chennamangalam et al., Reference Chennamangalam, Siemion, Lorimer and Werthimer2015).
Besides those modulation assumptions, the major factor to determine the feasibility is the lifetime of the modulator system which primarily depends on restraining several factors stemming from pulsar's energetics. Pressure of radio beam radiation and those of particles following the magnetic field lines of the pulsar must be evaded by a counter-pressure mechanism or attitude correction of the modulator. Effects of the surrounding environment of the pulsar which contains destructive debris would be precluded by strengthening the structure of modulators. Also radiation-induced heating would cause any modulator mechanism to melt and evaporate. Constructions of such modulators should therefore be able to overcome heating.
Discussion
In the topological structure of broadcast networks, pulsars are central nodes and planets that may have civilizations are leaf nodes. Edges are inside the radio beams and their number is determined by the sweeping geometries and stellar densities. Sweeping volumes show that a small though significant amount of their celestial sphere may be covered if an ETI controls several pulsars for broadcasting. Example of four pulsars in Fig. 6 shows us a total sweeping volume of 0.4 kpc3 which is approximately 
$1\% $ of the volume of entire celestial sphere at 1 kpc beam altitude. We can thus figure out how many possible planets the sphere contains in that it scans 4.25 × 107 planets, even in 1% of its volume.
It is due to their stability and slow spin down rate that the lighthouse structure of ETI controlled pulsars are suitable for a galactic search of other civilizations (Beskin et al., Reference Beskin, Galishnikova, Novoselov, Philippov and Rashkovetskyi2017). Some other strong radio sources like quasars, types of active galactic nucleus are definitely out of this concept (Mathur et al., Reference Mathur, Kuraszkiewicz and Czerny2001). Moreover, there are magnetars considered a small part of the life of the pulsars could not be engineered for modulation. When the spin, temperature and magnetic field of a neutron star have a perfect threshold, it forms a dynamo to amplify the magnetic field at least by a factor of 103, becoming a magnetar. So much magnetic field even messes with the individual electrons in atoms to finally cause anything to be torn apart. On the other hand, accreting pulsars in binary systems can transform into magnetars (Tong, Reference Tong2015) and accretion discs also make the domain unbuildable.
In addition to how much space the pulsars could sweep or to construction of modulators, it is also of importance that the sent signals could be solved by the intelligent life on the target planet. Radio signals of pulsars are affected by interstellar medium (ISM). A receiver civilization needs to decouple the ISM effects from the beam. Controlled pulsars are likely to be located in the galactic disc which contains the GHZ and their detection is affected by the dispersion and scattering effects and background radio emissions (Xu et al., Reference Xu, Wang, Han and Hu2011). The receiver civilization is supposed to choose suitable observation conditions which could minimize such influences and have a better detection fraction.
For an example from our planet Earth, the pulsars discovered so far are a fairly small fraction of all the pulsars in the Galaxy, one reason for which is that sweeping beams do not intersect with our line of sight and the other is that we may not have sorted out the ETI message from the received signal. According to the catalogue data (Hobbs et al., Reference Hobbs, Manchester, Teoh and Hobbs2004), no ETI-created signals were detected on thousands of pulsars observed from Earth. One may assume that we have no neighbour between Types-I and II in our Galaxy. However, number of data is too small yet and it does not mean that this situation would not happen if more pulsars are believed to be found in the future.
Conclusion
Now that we human beings return to the natural energy sources of our planet, extraterrestrial civilizations between Types-I and II would do so in an astronomical scale, supposing they exist. Some of these sources could also be used for signal transmission in astronomical scales and thus radio pulsars appear to be the best candidates. Unless an extraterrestrial civilization is over-powered like Type-II and more, it would probably use them for the announcement of their existence. As also mentioned in this paper, only signal modulation could be created without changing the natural states of the pulsars like beam directions or inclination angles whereas it could be targeted to the desired galactic region by changing the directions of the radio beams via modulators at a higher engineering level.
Even with the signal modulations in the natural orientation of pulsars, a large number of Earth-like planets could be reached in habitable zone of the Milky Way. The number of nodes in a broadcast network established with pulsars is very high, which is already considered the number of Earth-like planets in their solar-type star's habitable zones (Petigura et al., Reference Petigura, Howard and Marcy2013). This is clearly a lower limit which does not include the moons of gas giants or planets smaller than the Earth. Such places may also be habitable for complex life. And there are planets around M-dwarf stars which are the most common type of stars in the galaxy. Accordingly, any civilizations are expected to have reached us by now. In future, addition of both topological and dynamical models to the broadcast networks would provide us with more insight into the well-known question whether we have been in a galaxy teeming with ETIs at least as advanced as us, or not.
Acknowledgements
The author would like to thank the anonymous referee for valuable comments and suggestions.
Author ORCIDs
Emir Haliki 0000-0002-5462-6522
