1. Context and objectives

A great deal of farming across the world takes place in mountainous areas that are ecologically fragile. It is also in these areas that the question of the availability of arable land is the most serious and the problem of soil erosion the most acute because of the instability of slopes which do not allow the soil cover to evolve. The problem with soil erosion is multifaceted. First and foremost is the potential negative impact of on-site soil erosion on agricultural yield. Soil is the most essential input in agriculture while eroded land suffers from depletion of nutrients such as nitrogen, phosphorus and potassium, organic and moisture content of the soil, and reduction in cultivable soil depth. The result is an inevitable decline in soil fertility (Mbaga-Semgalawe and Folmer, Reference Mbaga-Semgalawe and Folmer2000). Soil erosion also results in significant negative externalities such as sedimentation in the river bed, water pollution, and a reduction in the water-carrying capacity of the soil which could, in turn, cause silting in dams and water channels and affect local flora and fauna. The impact on the hydrological cycle is another as erosion increases the quantity of water runoff in the rainy season and reduces it during the dry season (Somanathan, Reference Somanathan1991; Mbaga-Semgalawe and Folmer, Reference Mbaga-Semgalawe and Folmer2000). The resultant degradation in land reduces crop yield forcing farmers, in turn, to intensify their contribution to deforestation (Lopez, Reference Lopez, Gardner and Rausser2002).

Adoption of proper soil and water conservation measures undoubtedly limits soil erosion and reduces top soil loss. Among farm-level measures widely adopted worldwide are terracing, stone walls, revegetation, agro-forestry, crop mixture, fallow practices, land drainage systems and crop residue management (Stocking and Murnaghan, Reference Stocking and Murnaghan2001). Soil conservation is today universally regarded as a sustainable agricultural practice as it minimizes soil disturbance ( Teklewold et al., Reference Teklewold, Kassie and Shiferaw2013). Among its recognized benefits are regulating services such as carbon sequestration (Lal, Reference Lal2004), preservation of the nutrient cycle (Adimassu et al., Reference Adimassu, Mekonnen, Yirga and Kessler2014), contributions to the maintenance of the hydrological cycle (Hueso-González et al., Reference Hueso-González, Ruiz-Sinoga, Martínez-Murillo and Lavee2015), supporting services such as improvement in soil fertility (Mwango et al., Reference Mwango, Msanya, Mtakwa, Kimaro, Deckers and Poesen2016), biodiversity conservation (Chirwa et al., Reference Chirwa, Akinnifesi, Sileshi, Syampungani, Kalaba and Ajayi2008) and provisioning services such as food (Thierfelder et al., Reference Thierfelder, Matemba-Mutasa and Rusinamhodzi2015), wood (Kuntashula and Mungatana, Reference Kuntashula and Mungatana2015) and water (Pattanayak and Kramer, Reference Pattanayak and Kramer2001) for area residents. Nevertheless, there are barriers to the adoption of conservation measures by farmers, principal among them being poverty, the risks associated with agriculture production, the high discount rate, government policy, the low benefit-cost ratio of soil conservation, and credit constraints (Stocking and Murnaghan, Reference Stocking and Murnaghan2001; Antle and Diagana, Reference Antle and Diagana2003; Bouma et al., Reference Bouma, van Soest and Bulte2007).

Quantifying the regulating and supporting services provided by soil conservation measures is methodologically challenging and/or potentially expensive. For instance, carbon sequestration, flood protection services and biodiversity conservation are public goods for which a market is absent.Footnote ¹ Measuring soil fertility and soil nutrients across randomly selected plots is also costly. But provisioning services such as crops and wood have a market and can be valued using market prices, which makes them relatively easy to compare between adopters and non-adopters of conservation measures (Ma and Swinton, Reference Ma and Swinton2011).

The present study seeks to estimate the impacts of farm-level adoption of vegetative soil conservation measures (afforestation and/or bamboo planting) on farm profit and its constituents, revenue and cost.Footnote ² Our objective is to provide causal estimates of the impact – in particular, the average impact – farm-level vegetative soil conservation measures on adopters or the average treatment effect on the treated (ATT) (Heckman and Vytlacil, Reference Heckman, Vytlacil, Heckman and Leamer2007). We assess the impacts of vegetative soil conservation only on agricultural outcomes, ignoring other by-products of soil conservation such as fuel and fodder as outcome variables in order to maintain uniformity in the comparison of outcomes between adopters and non-adopters.

A large body of literature has estimated the benefits of soil conservation vis-à-vis crop production utilizing methods such as the cost-benefit method (Lutz et al., Reference Lutz, Pagiola and Reiche1994; Bizoza and de Graaff, Reference Bizoza and de Graaff2012); estimation of the damage function (Walker and Young, Reference Walker and Young1986; Shiferaw and Holden, Reference Shiferaw and Holden2001); hedonic price of the land (Gardner and Barrows, Reference Gardner and Barrows1985; King and Sinden, Reference King and Sinden1988); and the production function approach (Pattanayak and Mercer, Reference Pattanayak and Mercer1998; Bravo-Ureta et al., Reference Bravo‐Ureta, Solis, Cocchi and Quiroga2006). While the studies cited have been able to provide the welfare measure of soil conservation to the farmer, all of them, with the exception of Pattanayak and Mercer (Reference Pattanayak and Mercer1998), have failed to consider the problem of the missing counterfactual. But finding the appropriate counterfactual to compare the outcomes of technology adoption remains a major challenge as failure to do so would provide a biased estimate of the adoption of soil conservation measures (Godtland et al., Reference Godtland, Sadoulet, Janvry, Murgai and Ortiz2004).

The ideal evaluation of soil conservation measures is only possible when the assignment of soil conservation measures involves an ex-ante experimental design. But a randomized control experiment to evaluate outcomes emanating from soil conservation is costly. A few studies have evaluated the impact of on-farm soil conservation on farm outcome using quasi-experimental methods (such as propensity score matching (PSM)) where farmers self-select themselves into the categories of adopter and non-adopter. Considering the confounding factors that would affect both the adoption decision of farmers and agricultural outcome, quasi-experimental methods control these confounding factors in the impact evaluation.Footnote ³ Among studies using the PSM method to control the confounding characteristics in impact evaluation are those by Faltermeier and Abdulai (Reference Faltemeier and Abdulai2009) and Kuntashula and Mungatana (Reference Kuntashula and Mungatana2015). The former, which estimated the causal impact of the adoption and intensification of water conservation practices on farm output, demand for input, and net returns in Ghana, found that while the adoption of bund technology increased input demand, it did not affect the household's output or net returns. The latter, which evaluated the impact of on-farm adoption of agroforestry on the consumption of fuel wood from public land in Ghana, found that the adoption of the agroforestry measure significantly reduced fuel-wood collection from public land.

We use PSM methodology to measure the impact of adoption of vegetative soil conservation practices (afforestation and/or bamboo planting) on farmer profit, revenue and variable cost. In identifying the causal impact, the maintained assumption is that the farm-level adoption decision is based on observable household, farm-level and village characteristics. Once these covariates are accounted for, the assumption is that the adoption decision is independent of potential outcomes – in this case, farmer profit, revenue and cost. PSM accounts for the observed covariates that might simultaneously determine adoption and farm outcomes. However, it does not account for the non-observed characteristics that might also simultaneously govern on-farm adoption, farmer profit, revenue and cost. We see this as one of the major limitations of PSM.

The PSM methodology matches adopters with non-adopters based on their propensity score. The propensity score is defined as the probability of adoption conditional on observed covariates (Caliendo and Kopeinig, Reference Caliendo and Kopeinig2008). Therefore, to estimate the propensity score we need to identify the key determinants of the decision to adopt soil conservation, since a farmer's decision to adopt soil conservation measures is influenced by a variety of socioeconomic factors of the farm household and farm characteristics.

In the literature on agricultural technology adoption, some studies have introduced neighborhood aspects. They attempt to capture the role of interaction with neighbors (strategic substitutability or strategic complementarity) on the decisions to adopt a given technology by using techniques of spatial econometrics. In this technique, the interaction is based on a measure of proximity that is typically geographical in nature. Studies on technology adoption in agriculture such as Colney (Reference Colney1999), Holloway et al. (Reference Holloway, Lapar and Lucila2007), Wang et al. (Reference Wang, Iglesias and Wooldridge2013) and Läpple and Kelly (Reference Läpple and Kelley2015) have used the spatial dependence models.

In analyzing the adoption of soil conservation practices, the use of the spatial dependence framework is logical for many reasons. Firstly, soil conservation in one farm can assist or constrain it in adjacent farms. The assumption is that households located near each other exhibit similar behavior; the closer the household, the more similar the behavior (Holloway et al., Reference Holloway, Lapar and Lucila2007).Footnote ⁴ Factors such as inter-farm information flow, neighborhood competition or cooperation, and geographical clustering of innovators could induce similar adoption behavior in farmers (Abdulai and Huffman, Reference Abdulai and Huffman2005). Secondly, agricultural productivity also depends on various localized factors, such as soil type and quality, ambient and soil moisture, ecosystem services, topography of land, and distance from the nearest stream (Colney, Reference Colney1999). Similarity in these factors may lead to similarity in farming and conservation practices (Pattanayak and Burty, Reference Pattanayak and Burty2005). These variables are often not measured, resulting in dependence in residuals. Thus, it is important to examine how spatial factors contribute indirectly to the observed adoption of soil conservation practices (Holloway et al., Reference Holloway, Lapar and Lucila2007).

The literature evaluating natural resource conservation cited above assumes that the adoption of conservation measures by one farmer does not affect the outcome of another farmer. This assumption is known as the Stable-Unit-Treatment-Value-Assumption (SUTVA). However, as noted above, soil conservation can potentially be an instance where this assumption is not feasible. Therefore, it is important to model the interdependence of the farmers' decisions as, otherwise, the estimated coefficients of the determinants of soil conservation practice can be biased, resulting in an inaccurate propensity score. One way to address this is to directly model the interdependence of farmers with regard to their adoption decisions (Imbens and Wooldridge, Reference Imbens and Wooldridge2009). We model the interdependence in the adoption of soil conservation by using spatial econometrics, which helps us to identify the magnitude of the (spatial) interdependence as well as the optimum area of the (spatial) neighborhood. The present study adds to the literature on evaluating natural resource conservation by highlighting potential biases in ATT that may result from ignoring spatial interdependence.

We first use a standard binary probit model to derive propensity scores. After matching, we compare the expected values of farm profit, revenue and cost between adopters and non-adopters to estimate the impact of adoption of plot-level vegetative soil conservation measures. In order to consider spatial correlation, we consider a model of spatial dependence in outcome (the spatial lag model), following Anselin (Reference Anselin2002) and LeSage and Pace (Reference LeSage and Pace2009).

We use survey data from the Darjeeling district of the Teesta River Basin of the Eastern Himalayan region. The findings suggest strong evidence of a positive neighborhood impact on the farmer's decision to invest in afforestation and/or bamboo planting. We also find that the spatial lag probit model best describes our data as it performs better than a non-spatial/ordinary probit model. Further analysis indicates that some specific on-farm soil conservation measures do affect revenue and cost positively but not farm profit.

2. Study area

3. Sampling, data and description of variables

3.2 Data and descriptive statistics

3.2.1 Adoption

As described in section 2, farmers resort to different types of soil conservation measures. An exhaustive list of possible combinations of soil conservation measures is given in online appendix table A1, which indicates that farmers practice multiple measures on their plot although there was not much variation in the adoption of some measures (either none or all). Only a few used stone terracing (less than 4 per cent); the low adoption rate is driven not only by the high initial cost but also the frequent maintenance and monitoring costs (see online appendix A for details). On the other hand, terracing was the most commonly used conservation measure due both to its lower initial cost as well as shorter gestation period in comparison with many of the other measures.Footnote ¹¹ The major difference among the sample farmers lies mainly in terms of integration of structural (stone wall) and vegetative measures (afforestation and bamboo planting). While some farmers have integrated these two types of measures, some have not. We derive the distribution of adoption measures of sample farmers from online appendix table A1 which is reported in table 1.

Table 1. Distribution of sample farmers by number of adoption measures

Source: Based on a primary survey carried out in Darjeeling district, West Bengal, India in the year 2013.

Table 1 shows 100 per cent of the farmers reporting the adoption of terracing as a soil conservation measure. Therefore, we consider terracing as ‘baseline level conservation' for the purposes of our study.Footnote ¹² Table 1 also shows that 27 per cent of the farmers have adopted the measures terracing and stone wall along with either afforestation or bamboo planting (category c) while 22 per cent of the sample farmers opted for terracing, stone wall, bamboo planting and afforestation simultaneously. We define the 49 per cent of farmers in categories c and d as adopters. As such, farmers who integrate the structural (terracing and stone wall) and vegetative measure(s) (either afforestation or bamboo planting or both) are categorized as adopters (or treated farmers).Footnote ^13, Footnote ¹⁴ The farmers concerned have been practicing these measures for more than 10 years. We expect the synergistic impact of structural and vegetative measures to likely have a higher yield effect than the impact of structural measure(s) alone (see also section 2.2).

3.2.2 Explanatory variables

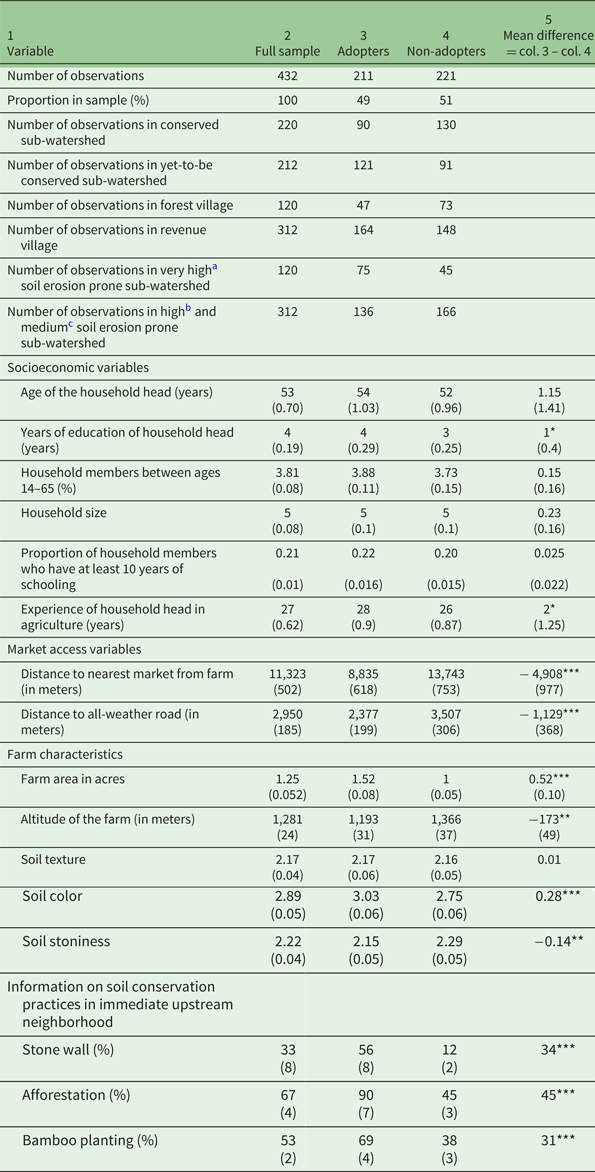
Adoption of soil conservation practices depends on a number of factors such as the socioeconomic characteristics of the farmer/farming households, farm characteristics, measures of market access, and information on soil conservation in the immediate upstream neighborhood. We present the description and summary statistics of the above variables in table 2.

Table 2. Summary statistics and two sample t-test of the variables used in the analysis

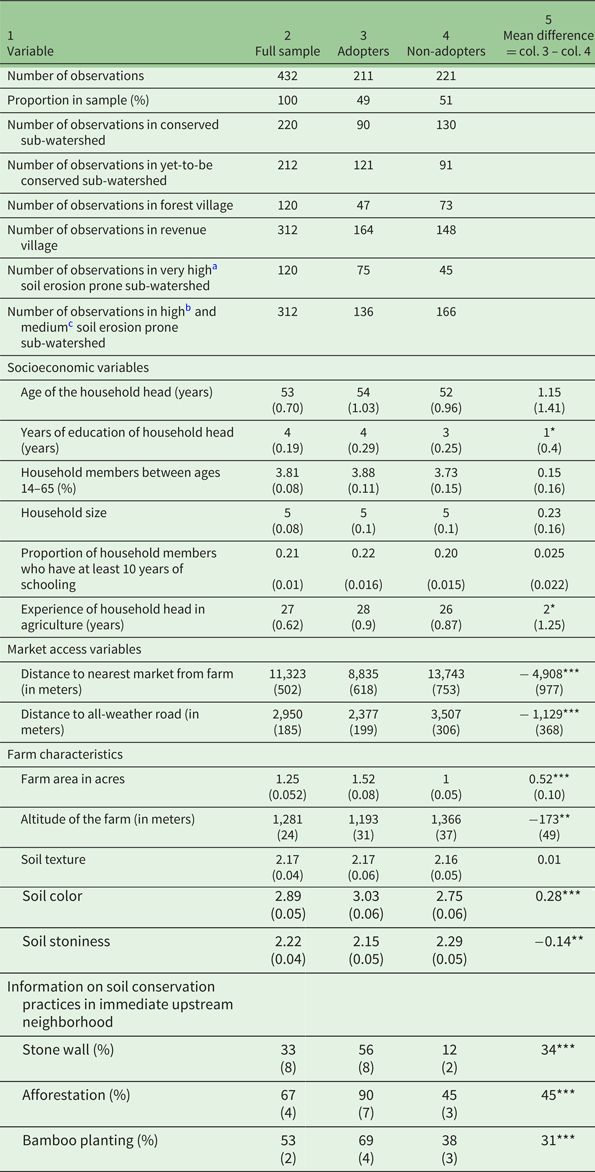
^a Sediment yield index (SYI) is 1,450 and above,

^b SYI is 1,350 − 1,449,

^c SYI is 1,250– 1,349. SYI is calculated as the weighted arithmetic mean of the products of the erosion intensity weightage value and delivery ratio over the entire area of the hydrologic unit by using suitable empirical equation (Soil and Land Use Survey of India, 1992).

Notes: Standard error in parentheses. ***, ** and * denote significance at 1, 5 and 10% respectively. Adopter: Farmer who adopted terracing, stone wall, afforestation and/or bamboo planting; Non-adopter: Farmer who adopted terracing and stone wall. In conserved sub-watersheds, the State Forest Department of West Bengal has implemented soil conservation measures in the forest area. In yet-to-be conserved sub-watersheds, there are no government initiatives for soil conservation. Information on soil conservation practices in immediate upstream neighborhood elicited information on the percentage of adoption of stone wall, afforestation and bamboo planting from the nine nearest upstream farms. Soil texture, soil color and soil stoniness have been reported by the respondent according to a hedonic scale. Scale of soil texture: sandy/coarse – 1, loamy/medium coarse – 2, clay – 3, silt – 4. Scale of soil color: grey – 1, reddish – 2, brown – 3, black – 4. Scale of soil stoniness: high stoniness – 1, medium stoniness – 2, low stoniness – 3, non-stony – 4.

Sources: A primary survey carried out in Darjeeling district, West Bengal, India, in the year 2013; Kalimpong Soil Conservation Division (2010); Kurseong Soil Conservation Division (2011).

Most of the variables we used were drawn from the studies of Mbaga-Semgalawe and Folmer (Reference Mbaga-Semgalawe and Folmer2000),  Teklewold et al. (Reference Teklewold, Kassie and Shiferaw2013), Läpple and Kelly (Reference Läpple and Kelley2015) and Wossen et al. (Reference Wossen, Berger and Di Falco2015). We assume that all these explanatory variables are non-constant exogenous variables. They were used to study the factors that influence a farmer's decision to adopt soil erosion prevention measures. Some variables, such as government support to farmers for soil conservation, extension services to farmers, membership in farmers' organizations, and accessibility of credit from the formal credit market could not be included due to similarity in answers leading to lack of variability among the respondents. For instance, all the respondents reported that extension services were not available for farmers in the surveyed area. They also reported that they never accessed credit from the formal credit market.

For each respondent farmer, we also elicited information on the soil conservation practices adopted on the nine nearest upstream farms (Läpple and Kelly, Reference Läpple and Kelley2015) as soil conservation activity in the immediate upstream neighborhood may have significant complementary or substitution effects on the conservation decisions of downstream farmers (Battaglini et al., Reference Battaglini, Nunnari and Palfrey2012).

In addition, we use three dummy variables to capture sub-watershed characteristics that may impact the soil conservation decision. The first dummy captures government-led sub-watershed soil conservation under TRVP (conserved sub-watershed dummy). Under TRVP, the government agency develops infrastructure in the upstream forest areas of certain sub-watersheds (see section 2 for details of conservation under TRVP). Farmers' decisions to adopt on-farm conservation practices may depend on the distribution of benefits of government-led soil conservation in the upstream neighborhood forest (Feder and Slade, Reference Feder and Slade1985). The same conservation practices could also influence farm outcomes in the downstream of the same sub-watershed through provision of soil conservation services (Pattanayak and Kramer, Reference Pattanayak and Kramer2001). Consequently, TRVP conservation status could serve as a potential confounding factor. This makes it necessary to factor in the government-led sub-watershed conservation status as one of the determinants of soil conservation practices. The second dummy captures whether the sub-watershed belongs to the very high erosion-prone category or not. The third dummy relates to whether the village is a forest village or not, as many villages are situated in or near forest areas. The lack of exclusive property rights over land in such villages may become a disincentive for farmers to invest in soil conservation. We regard these sub-watershed characteristics as exogenous variables as with other explanatory variables.

Table 2 suggests that there are significant differences between adopters and non-adopters in several covariates. Though we will not go into a lengthy discussion, it is important to note that these differences in covariates provide support for controlling for confounding factors in order to assess the causal impact of on-farm soil conservation measures. As mentioned in section 3.1, approximately 5 per cent of our observations had to be dropped in the second round because the farmers could not be located.

3.2.3 Outcome variables

Table 3 compares differences by season in the three outcome variables (profit, revenue and variable cost per acre). It shows that adopters bear a significantly higher cost than non-adopters in the winter season though we do not see any significant difference in the other outcome variables for the winter crop. On the other hand, in the monsoon season, the mean difference is positively significant with regard to total revenue per acre (at the 1 per cent level of significance), and variable cost (at the 5 per cent level of significance). In addition, we also observe significant differences in these agricultural outcomes when we combine winter and monsoon crops. We report on the construction of these variables in online appendix B.

Table 3. Summary statistics of outcome variables, adopters and non-adopters

Notes: Standard error in parentheses. *** and ** denote significance at 1 and 5% respectively.

Adopters: Farmers who adopted terracing, stone wall, afforestation and/or bamboo planting; Non-adopters: Farmers who adopted terracing and stone wall. NA: Not applicable. INR: Indian Rupee. US$1 = INR 59 (approx.) in 2013 Historical Chart of U.S. Dollar to Indian Rupee (https://www.poundsterlinglive.com/bank-of-england-spot/historical-spot-exchange-rates/usd/USD-to-INR-2013, 3 April, 2019).

Source: Based on a primary survey carried out in the Darjeeling district, West Bengal, India, in the year 2013.

4. Conceptual framework

A fundamental problem in causal inference is that it is impossible to observe the outcome and its counterfactuals on the same farmer (Holland, Reference Holland1986). One solution would be to use a randomized control trial in which soil conservation measures are assigned randomly, although this can rarely be implemented practically. For this reason, we relied on a PSM methodology to deal with the problem of the missing counterfactual. This section discusses the problem of selection bias in studying the causal impact of soil conservation measures and how PSM can be used to overcome it.

D _i = 1 if farmer i is an adopter of vegetative soil conservation measure(s)

D _i = 0 if farmer i is a non-adopter of vegetative soil conservation measure(s)

To estimate ATT, we need to determine the outcome of the counterfactual state, which is to observe the counterfactual outcome of the adopter of the soil conservation measure in a non-adoption state. Thus,

(1)\begin{equation} ATT = E[\pi (1){\rm \vert} D = 1]-\; E[\pi (0){\rm \vert} D = 1] \end{equation}

where π is the outcome variable, i.e., farm profit and its components, namely, revenue and variable cost. Although the outcome for the adopter in the non-adoption state, that is, $E[\pi (0){\rm \vert} D = 1]$, cannot be observed, it is possible to estimate the difference:

(2)\begin{equation} E[\pi (1){\rm \vert} D = 1]-\; E[\pi (0){\rm \vert} D = 0].\end{equation}

This is the difference in expected farm outcomes between adopters and non-adopters of vegetative conservation practices. However, this is a biased estimate of the impact of adoption since it is more than likely that the outcomes of adopters and non-adopters would have been different even in the absence of any soil conservation measures (Duflo et al., Reference Duflo, Glennerster and Kremer2007). For instance, determinants of vegetative soil conservation measures and outcome variables have many factors in common (as mentioned in section 3.2.2). In general, outcomes on farms with soil conservation measures do not represent the outcomes on farms without soil conservation measures, due to the non-random or voluntary nature of adoption (Godtland et al., Reference Godtland, Sadoulet, Janvry, Murgai and Ortiz2004; Caliendo and Kopeinig, Reference Caliendo and Kopeinig2008).

The matching approach is one possible way to overcome selection bias. It assumes that the adoption decision is based on observables and that once these are accounted for, it is possible to construct, for each adopter of soil conservation measures, a comparable group of non-adopters who have similar observable characteristics. The matching techniques impose three assumptions. The first is the assumption of unconfoundedness or conditional independence. That is, given a set of observable Z, the farm outcomes are independent of the adoption of soil conservation measures.

We assume that these covariates are all exogenous. If so, the conditional independence can be written as follows:

Assumption 1. Conditional independence: $\pi (0),\; \pi (1)\mathop \coprod \nolimits^ D\; \vert \; Z$ (Caliendo and Kopeinig, Reference Caliendo and Kopeinig2008).

The second assumption is common support, which is written as follows:

Assumption 2. Common support: 0 <P(D = 1|Z) <1 (Caliendo and Kopeinig, Reference Caliendo and Kopeinig2008).

In other words, the probability of adoption lies between 0 and 1 for both adopters and non-adopters of vegetative conservation practices. The common support assumption ensures that the farmer, with the same observable covariates, can be both adopter and non-adopter with a positive probability.

Assumption 3. SUTVA (see section 1 for definition): according to this, a farmer's adoption of soil conservation measures does not depend on another farmer's adoption. (We consider interdependence of soil conservation measures within a specified neighborhood in section 5.)

One implication of these assumptions is that no unobservable factors influence adoption and farm profit (and its components) simultaneously (Caliendo and Kopeinig, Reference Caliendo and Kopeinig2008). If these assumptions are met, the PSM technique can be used to match adopters and non-adopters and create counterfactuals. The ATT is given by:

(3)\begin{equation} {\rm ATT}({\rm PSM}) = E[\Pi(1)\left \vert {D = 1,P(Z)]-E[\Pi(0)\vert {D = 0,P(Z)]} } \right.,\end{equation}

where P(Z) = P(D = 1 | Z) is the propensity score, which is the conditional probability for a farmer to adopt soil conservation measures given his observed covariates Z. Therefore, ATT (PSM) is the mean difference in farm outcomes (profit, revenue and variable cost) over common support between adopters and non-adopters.

5. Estimation method

In order to show interdependence in the adoption decision of farmers, we adapt the empirical specification provided by Anselin (Reference Anselin2002),

(4)\begin{equation} e^* = ( {I-\rho W} ) ^{-1}Z\beta + \varepsilon, \end{equation}

where e* is a vector of unobserved latent effort in soil conservation by our representative farmer i. The unobserved effort of the neighborhood farmer $e_{-i}^*$ influences $e_i^*$. We include Z, which is a (n X k + 1) matrix of the other observed explanatory variables (as defined in section 3.2.2). β is (k + 1 X 1) a vector of parameters and ε = (I − ρW)⁻¹u with $E(u) = 0,\; E(uu^/) = \sigma _u^2 I_n$. W is a (n X n) spatial weight matrix. ρ is the spatial autoregressive parameter (scalar), which is additional to any standard latent variable model. The specification (4) is known as the spatial lag model or spatial autocorrelation model (Anselin, Reference Anselin2002).

Following Anselin (Reference Anselin2002) and LeSage and Pace (Reference LeSage and Pace2009), we use a discrete variablee _i to define whether a farmer adopts soil conservation measures or not. In this case, it can be shown that

(5)\begin{equation} \Pr (e_i = 1) = {\rm Pr}[\varepsilon _i \lt h_i(X,W,\beta, \rho )], \end{equation}

where h _i is the multivariate normal density function, following the assumption of normality of u. The non-zero values in the i ^th row of W govern the array of interaction with neighborhood farmers. This interaction affects the probability of adoption of farmer i. Thus, the above specification (5) violates SUTVA.

Instead of dependency on the adoption decision, there can be dependency on unobserved factors. If we further assume that these unobserved factors are not correlated with the exogenous variables, then equation (4) can be modified as a model that is going to exhibit spatial dependency on the error term, which is termed the spatial error model. The model that incorporates spatial dependence in both outcome as well as errors is known as the general spatial autocorrelation model. In addition, the general spatial autocorrelation model also allows non-zero covariance between exogenous and unmeasured factors (LeSage and Pace, Reference LeSage and Pace2009). Analogous to equation (5), it is possible to observe violation of SUTVA due to spatial dependency on unobserved factors (spatial error model) and spatial dependency in both outcome as well as errors (general spatial autocorrelation model).Footnote ¹⁵

The study estimates the probability of adoption in relation to non-adoption by using the probit model. We estimate the propensity score using the variables which are mentioned in table 2. Estimation of a spatial lag model must account for the fact that the covariance structures make the marginal distribution of ε_i heteroscedastic (Anselin, Reference Anselin2002). In addition, ε_i is not independent and identically distributed due to spatial correlation. Consequently, the likelihood function involves multidimensional integration, which is computationally intensive (Wang et al., Reference Wang, Iglesias and Wooldridge2013). This study uses the Bayesian method in conjunction with the Markov chain Monte Carlo (MCMC) method to estimate the spatial probit model, following LeSage and Pace (Reference LeSage and Pace2009).

Our spatial analysis is built on 2,500 MCMC draws (with the first 500 draws excluded to account for burn-in) and 250 passes. We separately conduct another run with 5,000 MCMC draws (with the first 1,000 draws excluded to account for burn-in) and 500 passes and find that both runs produce almost similar estimates and inferences. Therefore, there are unlikely to be any problems with the convergence with 2,500 MCMC draws. The present study uses the Epanechnikov Kernel matching, as it uses information from all observations, thus providing for lower variance (Caliendo and Kopeinig, Reference Caliendo and Kopeinig2008).

6. Econometric results

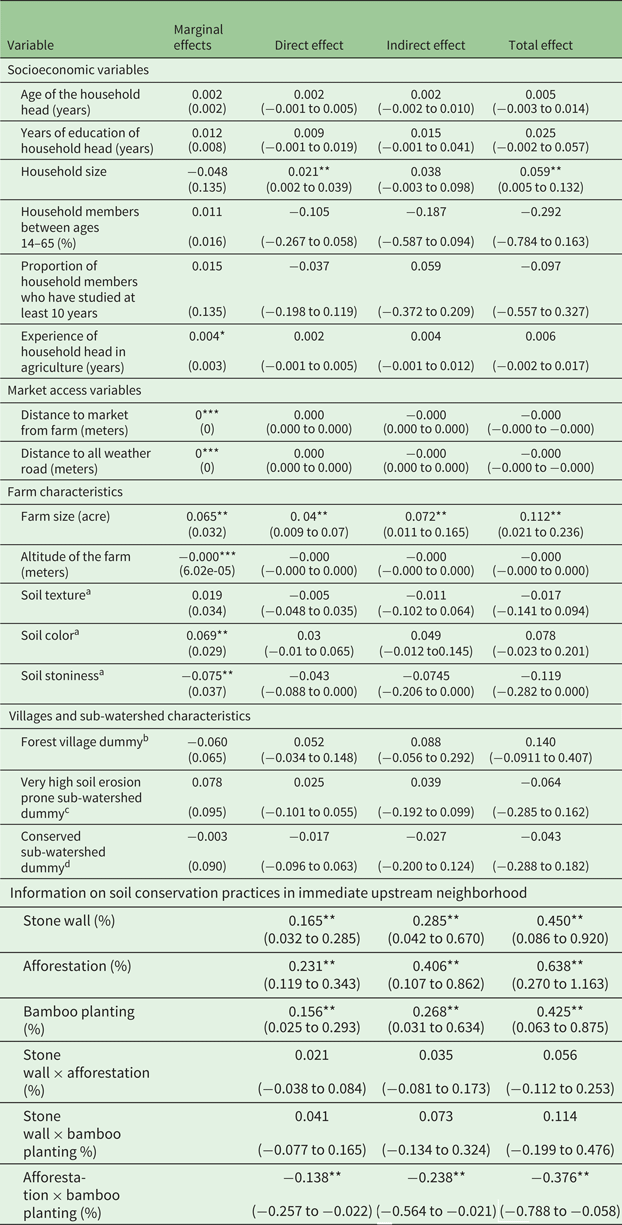
We present the marginal effects from the binary probit model of the propensity score of adoption in the second column of table 4.

Table 4. Non-spatial (ordinary) probit analysis results (marginal effects) and spatial lag effects of factors influencing adoption of soil conservation practices with neighborhood up to three kilometers

Notes: Heteroscedasticity-consistent robust standard error in parentheses in column 2. 95% confidence intervals in parentheses in columns 3, 4 and 5. ***, ** and * denote significance at 1, 5 and 10% respectively.

Adopter: Farmer who adopted terracing, stone wall, afforestation and/or bamboo planting; Non-adopter: Farmer who adopted terracing and stone wall. Number of adopters: 211, number of non-adopters: 221. Information on soil conservation practices in immediate upstream neighborhood elicited information on the percentage of adoption of stone wall, afforestation and bamboo planting from the nine nearest upstream farms.

^a has been reported by the respondent according to a hedonic scale. Scale of soil texture: sandy/coarse – 1, loamy/medium coarse – 2, clay – 3, silt – 4. Scale of soil color: grey – 1, reddish – 2, brown – 3, black – 4. Scale of soil stoniness: high stoniness – 1, medium stoniness – 2, low stoniness – 3, non-stony – 4.

^bInhabitants do not enjoy exclusive property rights (Maharashtra Forest Department, n.d.).

^cSediment yield index (SYI) is 1,450 and above. SYI is calculated as weighted arithmetic mean of the products of the erosion intensity weightage value and delivery ratio over the entire area of the hydrologic unit by using a suitable empirical equation (Soil and Land Use Survey of India, available at slusi.dacnet.nic.in/rrs.pdf).

^d The State Forest Department of West Bengal has implemented soil conservation measures in the forest area of the sub-watershed.

Sources: A primary survey carried out in Darjeeling district, West Bengal, India, in the year 2013; Kalimpong Soil Conservation Division (2010); Kurseong Soil Conservation Division (2011).

The PSM results from the binary probit model serve as a benchmark for the PSM results from the spatial probit model. The second column of table 4 suggests that the experience of the household head in agriculture, farm size, soil color, soil texture and soil stoniness have significant marginal effects. However, the presence of any sort of spatial pattern in the adoption decision, or error, or both adoption decision and error, may provide a biased marginal effect of the explanatory variables. We estimate three sets of spatial models – spatial lag model, spatial error model and general spatial autocorrelation model – for a range of specifications of the spatial weighting matrix, including the inverse distance spatial weight matrix (with a neighborhood cut-off 1 km, 3 km, 5 km, …, 15 km) and the contiguity matrix (with a neighborhood cut-off within village, nearest 1 village, …, nearest 5 villages). Though we will not go into a detailed discussion here, we wish to underline that the spatial lag model best fits our data compared to other spatial models (see the discussion in online appendix D for details).Footnote ¹⁶ The model choice was motivated by the fact that, once we allow for spatial dependence in outcome and error, the spatial dependence in error is no longer significant.Footnote ¹⁷ In addition, an inverse weight matrix up to the neighborhood cut-off of three km has the highest posterior probability among the competing spatial lag models. The value of the spatial is ρ = 0.6 and it is statistically significant at the 1 per cent level of significance (see online appendix D, table A2). This justifies the use of the spatial lag probit model rather than the non-spatial probit model and suggests that farmers within the specified neighborhood (within the 3 km radius) are spatially dependent.

6.2 Comparing adopters with non-adopters

We present the distribution of propensity scores estimated by the ordinary probit model and the spatial lag probit in online appendix figure A2. These figures suggest that there is a substantial region of common support over which matching can be undertaken.

For the PSM estimates to be valid, the characteristics of adopters and non-adopters need to balance after matching. We use the two-sample t-test for difference in means to evaluate if this is indeed the case. Online appendix table A4 reports the post-matching two-sample t-tests (the absolute p-value of mean difference) for all the variables (except for dummy and interaction variables). As is evident from the comparison of columns 2 and 3 of online appendix table A4, post-matching eliminates, by and large, the differences for market access and socioeconomic and farm characteristics variables when the propensity score is estimated by the spatial lag probit. However, there are still differences in some covariates. In online appendix table A5, we also compare the pre- and post-matching mean percentage bias between the two propensity score estimation methods (i.e., ordinary probit and spatial lag probit). On the basis of these percentage biases, we can conclude that the kernel matching procedure based on the spatial lag probit is better able to reduce the bias (or balance the covariates) between adopters and non-adopters than the ordinary probit.

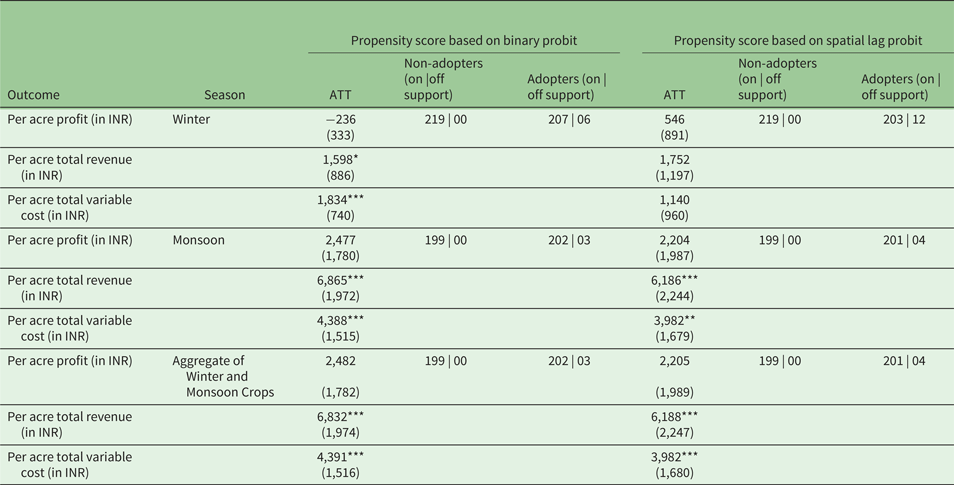
Table 5 reports the results of the causal effect of adoption on various outcomes. We report the ATT conditional on the binary probit as well as the binary spatial lag probit propensity score. A comparison between columns 3 and 6 indicates that in a couple of cases (i.e., per acre total revenue and cost in the winter season), the PSM based on ordinary probit tends to overestimate the ATT. However, the number of matched adopters and non-adopters is roughly the same. Nevertheless, a difference is observed in ATT. This is because the kernel matching method puts a higher weight on adopters who are close (in terms of the propensity score) to the non-adopters and a lower weight on distant adopters (Caliendo and Kopeinig, Reference Caliendo and Kopeinig2008). The same observation is likely to have a very different propensity score in two different methods of estimating the propensity score. This difference is driven by a spatial correlation and it has a huge implication for the identification of the impacts on agricultural outcomes. For instance, ATT on per acre total revenue based on the binary probit PSM is significant in the winter season. On the contrary, the same ATT is insignificant when we use the other method to estimate the propensity score. Nevertheless, ATT based on the spatial lag probit is reliable since the assumption of SUTVA is violated.

Table 5. Impact of adoption of vegetative measures on farm profit, revenue and variable cost: comparing adopters with non-adopters

Notes: Standard error in parentheses. ***, ** and * denote significance at 1, 5 and 10% respectively. ATT is based on equation (4).

Adopter: Farmer who adopted terracing, stone wall, afforestation and/or bamboo planting. Non-adopter: Farmer who adopted terracing and stone wall. INR: Indian Rupee. US$1 = INR59 (approx.) in U.S. Dollar to Indian Rupee Spot Exchange Rates for 2013 from the Bank of England (2019).

Source: Based on a primary survey carried out in the Darjeeling district, West Bengal, India, in the year 2013.

We find that ATT is statistically significant for per acre total revenue (with an estimated impact of INR6,865 per acre) and per acre variable cost (with an estimated impact of INR4,388 per acre) during the monsoon season at the 1 per cent level of significance. During the winter season, on the other hand, the ATT is insignificant for all the outcome variables. The seasonal difference in the outcome variable may be due to the uneven distribution of rainfall (see section 2.1). This could be because, in the monsoon season, farmers face surplus water while they face dry conditions in the winter months, which means that the dry conditions of the winter season necessitate intensive soil and water conservation from the farmer (Bhutia, Reference Bhutia2014). The on-farm opportunity cost of these vegetative measures is quite high since a portion of farmland has to be taken off from farming for the purpose. In addition, the gestation period for the vegetative measures is higher than for the other measures and can vary between three to seven years. These factors can also be seen as barriers for investment in certain types of soil conservation. Furthermore, the seasonal aggregation also reveals that ATT is statistically significant for per acre total revenue and per acre total variable cost.

The results suggest that vegetative soil conservation measures lead to a significant increase in yield for adopters. Although the higher yield comes with higher costs, the impact on farm revenues is positive in the rainy season. The variable cost component consists largely of labor costs (see online appendix B for details). Hence, the positive and significant ATT of the total variable cost per acre during the monsoon season may be suggestive of complementarity between labor demand and on-farm soil conservation (Pattanayak and Burty, Reference Pattanayak and Burty2005). Overall, these estimates of impact suggest that the simultaneous adoption of terracing, stone wall, afforestation and (or) bamboo planting leads to higher revenues but with higher costs attached.

7. Conclusions and policy implications

This study estimated the impact of the adoption of soil conservation measures (afforestation and/or planting of bamboo) using a survey of farmers in the Teesta Valley, where the problem of soil erosion is severe. To estimate the causal impact of the adoption of afforestation and/or planting of bamboo, we created a counterfactual comparison group using matching techniques, assuming that it is possible to capture the factors that influence the farmers' decision to adopt afforestation and/or planting of bamboo on their farms.

One of the crucial assumptions for identifying the causal impact is ‘the absence of interaction among the farmers in adoption decisions’, i.e., SUTVA. However, neighborhood effects are crucial in the adoption decision, given that soil conservation is location-specific, where ‘location’ extends beyond an individual farm. We modelled this interaction explicitly estimating the propensity score with a spatial lag probit model which outperforms an ordinary probit model.

We find that farmers located in close proximity exhibit similar adoption behavior and that adoption of soil conservation measures (stone wall, afforestation and/or planting of bamboo) is spatially interdependent. Therefore, the assumption of SUTVA is violated. Consequently, we find the propensity score estimated by the spatial lag probit to balance the observed covariates better than the propensity score estimated by the ordinary probit. In addition, PSM based on the spatial lag probit is also able to reduce bias in the estimated ATT. Results from the PSM methodology suggest no difference in per acre profits between the winter and monsoon seasons. Although revenues from adoption are higher, they also come with higher variable costs so that there is no difference in profits.

The adoption of multiple soil conservation measures may be an essential precondition for farming in an ecologically fragile ecosystem like the Himalayas. However, the results of our study suggest that insufficient financial gain from adoption of afforestation and/or planting of bamboo to farmers in the Teesta River valley may halt their efforts at soil conservation as it acts as a disincentive given the high expenses associated with it. Though the maintenance cost of afforestation is lower than that for structural measures, it takes a major portion of land out of farm production for years, thus incurring a huge opportunity cost for the farmer.

Government investment in sub-watersheds to reduce top soil loss also does not have any impact on private adoption of stone wall, afforestation and/or planting of bamboo on farms. Nevertheless, the significance of the spatial parameter in our study suggests neighbors' influence as an avenue for influencing farmers to adopt soil conservation measures by government and other developing agencies. It may be useful to invest in geographically-intensive information dissemination programmes to promote sustainable agricultural practices. In addition, alternative incentive mechanisms to encourage afforestation (e.g., an incentive design like a contract between farmers and the government (or a private agency) to sequester carbon through afforestation) could be adopted, especially, if such contracts carry a monetary incentive which would encourage farmers to participate.

This study is not without its limitations. One major limitation is that the study is based on a partial equilibrium analysis of adoption decisions among farmers and considers impacts only at the farm level. However, as noted above, the impacts of such actions by the government and the individual farmer are bound to extend beyond the river basin, carrying general equilibrium implications for the supply of farm products and prices in the local economy. An analysis of these effects is merited in future work. The second limitation relates to the need to track these farmers over time and to construct a panel data set. It would assist in understanding the timing of adoption decisions in general and of specific measures in particular. Given that adoption decisions are undertaken gradually over time, understanding the dynamics of adoption and their implications is possible only through a panel study. Thirdly, this study has used a narrow definition of the neighborhood, defined in terms of physical proximity, i.e., spatial distance. However, ‘neighborhood’ can also be defined in terms of socioeconomic, cultural and kinship ties. The role played by strategic interactions, defined in these terms, in determining adoption could be considered in future research. There can also be significant differences between a farmer who uses stone wall and afforestation and/or planting of bamboo in a small share of the plot versus one who uses one of these measures more intensively, another difference warranting future research. Lastly, it is also important to note that perhaps structural conservation measures improve profitability – but we cannot capture this in our study design.