Introduction
It has been realized that the particle velocity distribution function can deviate from the Maxwellian behavior in space and laboratory plasma. In recent years, the field of non-extensive statistics (or Tsallis statistics) has been extensively considered for describing non-Maxwellian plasmas. Tsallis statistics proposed non-extensive entropy for non-equilibrium systems, which possess long-range interactions such as plasmas and gravitational systems (Renyi, Reference Renyi1955; Tsallis, Reference Tsallis1988). It is formulated by a non-extensive parameter q, which is a measure of the non-extensivity. For q > 1 and q < 1, q-distribution contains subthermal and superthermal particles, respectively. The Boltzmann–Gibbs (B–G) entropy is recovered in the limit q → 1 (Tsallis, Reference Tsallis2002). A large variety of applications have been introduced, for example, DNA molecules for q < 1 (Moreira et al., Reference Moreira, Albuquerque, da Silva and Galvao2008), real earthquakes for q > 1 (Caruso et al., Reference Caruso, Pluchino, Latora, Vinciguerra and Rapisarda2007) and non-linear diffusion for different values of q (Plastino & Plastino, Reference Plastino and Plastino1995). The q-distribution in non-extensive statistics has been used to investigate the waves and instability phenomena in the plasmas, such as ion-acoustic solitary waves (Tribeche et al., Reference Tribeche, Amour and Shukla2012), dust-acoustic rogue waves (Moslem et al., Reference Moslem, Sabry, El-Labany and Shukla2011) and dust ion-acoustic instability (Dai et al., Reference Dai, Chen and Li2013). Since plasmas have been studied out of equilibrium, B–G statistics might be insufficient for describing and analyzing these investigations.
Among the many plasma instabilities, the Weibel instability is one of the most fundamental instabilities that were introduced by Weibel (Reference Weibel1959). This instability, which occurs in electron beams (Ghorbanalilu et al., Reference Ghorbanalilu, Abdollahzadeh and Ebrahimnazhad Rahbari2014a, Reference Ghorbanalilu, Sadeghzadeh, Ghaderi and Niknamb), electromagnetic radiation (Bendib et al., Reference Bendib, Bendib and Sid1997), and temperature anisotropy (Schaefer-Rolffs et al., Reference Schaefer-Rolffs, Lerche and Schlickeiser2006), is a very efficient mechanism for generating magnetic field. The free-energy stored in an anisotropic particle distribution in velocity space produces an exponential magnetic field growing as time increases. The behavior of electron beam during the Weibel instability is investigated analytically (Siemon et al., Reference Siemon, Khudik and Shvets2011). The produced magnetic field via Weibel instability can be estimated in relativistic shocks (Ghorbanalilu & Sadegzadeh, Reference Ghorbanalilu and Sadegzadeh2017). Moreover, the Weibel instability has been investigated in the optical breakdown of a dilute neutral gas (Ghorbanalilu, Reference Ghorbanalilu2013) and microwave gas discharge (Shokri & Ghorbanalilu, Reference Shokri and Ghorbanalilu2004). Therefore, much attention has been paid to analytical analysis (Bendib et al., Reference Bendib, Bendib, Bendib, Bendib, Sid and Bendib1998; Basu, Reference Basu2002; Bret, Reference Bret2006) and or simulations (Morse & Nielson, Reference Morse and Nielson1971; Stockem et al., Reference Stockem, Dieckmann and Schlickeiser2010; Kuri et al., Reference Kuri, Das and Patel2017) of the Weibel instability.
It is well known that the particle-in-cell (PIC) is one of the most used numerical methods to simulate real plasma behavior. The first PIC models have been introduced by Buneman (Reference Buneman1959) and Dawson (Reference Dawson1962), which did not use mesh for calculation of fields. Then, first mesh models in one (Burger Reference Burger1965) and two dimensions (Hockney & Eastwood, Reference Hockney and Eastwood1988) were developed. In PIC method, the distribution function is discretized into a set of superparticle, while the electromagnetic fields are calculated on the grid. According to the simulation results, we can track the particles’ motion in phase space. Thus, it is of interest to investigate plasma instabilities (Seough et al., Reference Seough, Yoon and Hwang2015a, Reference Seough, Yoon, Hwang and Nariyukib; Rajawat & Sengupta, Reference Rajawat and Sengupta2016), laser–plasma interaction (Pukhov & Meyer-ter-vehn, Reference Pukhov and Meyer-ter-vehn1999; Pommier & Lefebvre, Reference Pommier and Lefebvre2004; Benedetti et al., Reference Benedetti, Londrillo, Petrillo, Serafini, Sgattoni, Tomassini and Turchetti2009; Wu et al., Reference Wu, Zhou, He and Zhu2009; Drouin et al., Reference Drouin, Gremillet, Adam and Heron2010) and waves in plasma (Mishchenko et al., Reference Mishchenko, Hatzky and Konies2008; Qi et al., Reference Qi, Xu, Duan, Zhang and Yang2014).
The Weibel instability driven by temperature anisotropy has been widely examined in different simulations in the context of B–G statistics (Morse & Nielson, Reference Morse and Nielson1971; Okada et al., Reference Okada, Sajiki and Satou1999; Stockem et al., Reference Stockem, Dieckmann and Schlickeiser2010). The thermal velocity of the bi-Maxwellian distribution is larger along one axis than another. This anisotropy can induce strong micro-currents along the hot direction and their magnetic repulsion separates the electron movements in opposite directions. The electrons with low thermal energy are unable to do anything against the structure formation. Therefore, a net current and electromagnetic fields develop. The magnetic energy density can reach in extreme cases up to 1/12 of the total energy density (Lemons et al., Reference Lemons, Winske and Gary1979) and exceeds by far the electric one.
In the course of the present paper, we examine the Weibel instability driven by electrons temperature anisotropy in the context of non-extensive statistics in the relativistic regime. The examination is based on the two-dimensional (2D) PIC simulation. We discuss the Weibel instability for electrons in a homogenous, collisionless plasma and assume the ions as neutralizing background, which is equivalent to an infinitely large ion mass (m i → ∞).
The paper is organized in the following fashion. In the next section, we introduce a new two dimension anisotropic distribution function in the context of non-extensive statistics. Furthermore, we explain the Weibel instability based on the linear theory for an isotropic non-extensive plasma. In the section ‘The simulation method and results’, we present the simulation method and discuss the numerical results. Finally, in the section ‘Summary and discussion’, the summary and conclusion are given.
The linear analysis
In the first step, we describe the initial conditions to investigate the Weibel instability. We suppose a homogeneous, collisionless plasma without the initial magnetic and electric fields. According to the fact that ions are much more massive than electrons, we can consider ions as an immobile background. Initially, electrons have an anisotropic distribution function in velocity space and are distributed in the x–y plane uniformly. The non-extensive anisotropic distribution function is widely introduced in one and three dimensions previously (Silva et al., Reference Silva, Plastino and Lima1998). Here, we would like to introduce a new form in two dimensions, which will be used in our simulation in the next section. Similar to the one and three dimensions, we obtain the 2D anisotropic non-extensive electron distribution function as below:
$$f_{\rm q} (v_x, v_y ) = \displaystyle{q \over {{\rm \pi} v_{{\rm th}x} v_{{\rm th}y}}} \left[ {1 - (q - 1)\left(\displaystyle{{v_x^2} \over {v_{{\rm th}x}^2}} + \displaystyle{{v_y^2} \over {v_{{\rm th}y}^2}} \right)} \right]^{\displaystyle{1 \over {q - 1}}},$$
where 
$v_{{\rm th}x} = \sqrt {(2k_{\rm B} T_x )/m_{\rm e}} $ and 
$v_{{\rm th}y} = \sqrt {(2k_{\rm B} T_y )/m_{\rm e}} $ are the electron thermal velocities in the x- and y-directions, respectively. We know, if parameter q differs from unity, the entropy becomes non-extensive with the Boltzmann factor generated by a power of law. The structures q < 1 and q > 1 are called subextensive and superextensive, respectively. In other words, |q − 1| quantifies the lack of extensivity of the system. The distribution function has a thermal cutoff on the maximum value allowed for the velocity of electrons for q > 1. Therefore, electrons with superthermal velocity are omitted by this cutoff. This means that an increase of non-extensivity degree q decreases the thermal spreading. In contrast, there are a number of electrons with superthermal velocity for q < 1 in the tail of distribution function.
The analytical investigation on the Weibel instability with q-non-extensive electrons and immobile ions in collisionless and homogenous plasma revealed that the instability growth rate depends on a non-extensive parameter. It has been shown that the instability growth rate enhanced as the non-extensive parameter of electron increased. The investigation was performed using the electron distribution function similar to Eq. (1) in three dimensions. The analytical discussion is valid in linear regime and unable to describe the non-linear evolution of the Weibel instability in non-extensive statistic mechanics (Qiu & Liu, Reference Qiu and Liu2013).
The simulation method and results
To begin the simulation, we obtain the dimensionless forms of Maxwell and Lorentz equations:
$$\eqalign{\vec \nabla \times \vec E = & - \displaystyle{{\partial \vec B} \over {\partial t}}, \cr \vec \nabla \times \vec B = & \displaystyle{{\partial \vec E} \over {\partial t}} + \vec J, \cr \vec \nabla. \vec E = & {\rm \rho}, \cr \vec \nabla. \vec B = & 0, \cr \displaystyle{{d\vec x} \over {dt}} = & \vec v, \cr \displaystyle{{d{\rm \gamma} \vec v} \over {dt}} = & \vec E + (\vec v \times \vec B).}$$
where γ is the relativistic factor, and 
$\vec E$ and 
$\vec B$ are normalized to ωpm ec/e and ωpm e/e, respectively. In addition, the position 
$\vec x$, simulation time t and velocity 
$\vec v$ are given in units of λD (the Debye length), 
${\rm \omega} _{\rm p}^{ - 1} $ (the electron plasma frequency), and c(the light speed), respectively. According to these normalized units, the current density 
$\vec J$ is normalized to n 0 ec where n 0 is the density of background neutralizing heavy ions.
Our PIC simulation started with uniform distribution of electrons in position space and non-extensive velocity distribution Eq. (1). Next, the Maxwell equations were solved by the Yee scheme on a grid. Following that, the electric and magnetic fields were interpolated from the grid to the electron position. After that, the electron equations of motion were calculated by the Boris scheme in the relativistic regime. The current and charge density on the grid points were obtained by interpolating from the electron's position on the grid. After all, because of microscopic inconsistencies between current and charge density due to use of the mesh and weights, the Poisson equation was fulfilled (Birdsall & Langdon, Reference Birdsall and Langdon1985).
It should be noted that the initial velocity distribution function (1), which is used to generate the velocity of particles, is related to the non-extensive parameter q. Therefore, the non-extensive parameter q plays an important role to set the initial condition for the velocity of particles. According to this fact that the initial conditions definitely affect results, so we can expect different results for different values of q.
The simulation was performed in the simulation box L xωp/c = L yωp/c = 15 × 15 with periodic boundary condition in both directions. The number of grid points was N x = N y = 256 × 256. The number of superparticles was chosen N p = 106 that consists of many physical particles. Therefore, the number of superparticles per cell is N = 15. We choose the reference value for plasma frequency (8.9 × 109 s−1) means that the plasma density is around to 1018 m−2, a value achieved easily in laser–plasma interaction.
The time step was given by 
${\rm \Delta} t = 0.001{\rm \omega} _{\rm p}^{ - 1}. $ The initial thermal velocities were v thy/c = 0.05 and v thx = 5v thy. This corresponds to a temperature anisotropy A = (v thx/v thy)2 − 1 = 24.
In Figures 1–3, phase plots (xω p/c, v x/c) and (yω p/c, v y/c) of distribution of simulation particles and spatial variations of generated magnetic fields are displayed for different values of q at corresponding saturation times, respectively. Note that just the z-component of the magnetic field is generated in the present simulation. As is known, increasing of non-extensivity degree q decreases the thermal spreading (Ghorbanalilu et al., Reference Ghorbanalilu, Abdollahzadeh and Ebrahimnazhad Rahbari2014a, Reference Ghorbanalilu, Sadeghzadeh, Ghaderi and Niknamb). Since the electrons initial temperature in the x-direction is sufficiently more than the y-direction, we expect the energy transition between two directions by the passage of time. This transition accompanies by reduction of initial temperature anisotropy and generation of the magnetic field. The figures show that the Weibel instability evolution can be affected by non-extensive parameter q as well as temperature anisotropy A. we observe strong localized magnetic fields for structure q = 0.5 compared with q = 1 and q = 5. It seems that the strong localized magnetic field arises from superenergetic electrons on the tail of distribution function.
Fig. 1. (color online) (a) f(x, v x), (b) f(y, v y), and (c) eB z/ωpm e for q = 0.5 at ωpt ≈ 14.
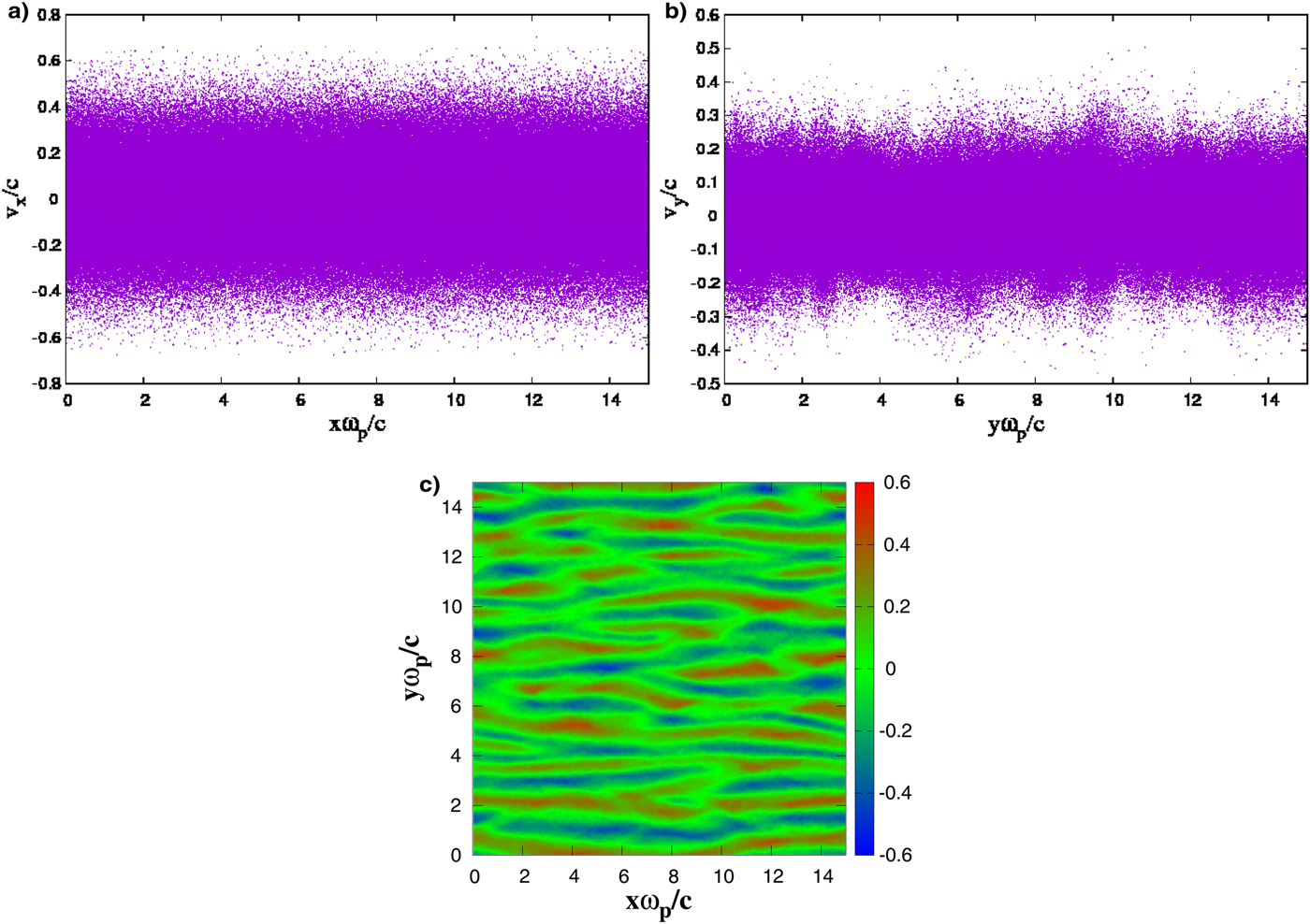
Fig. 2. (color online) (a) f(x, v x), (b) f(y, v y), and (c) eB z/ωpm e for q = 1 at ωpt ≈ 19.
Fig. 3. (color online) (a) f(x, v x), (b) f(y, v y), and (c) eB z/ωpm e for q = 5 at ωpt ≈ 39.
In Figure 4, we plotted the ratio of produced magnetic field energy to the initial kinetic energy of particles for structures q = 0.5, 1, 5 as a function of ωpt. We should be noted that the initial kinetic energy are not the same for each of the system. As we mentioned, the thermal spreading decreases by increasing the parameter q. Therefore, the corresponding initial kinetic energy for q = 0.5 is larger than q = 1 and 5. Therefore, the ratio of generated magnetic field energy to the initial kinetic energy is small compare with structures q = 1 and 5 in spite of the produced magnetic field is very strong for structure q = 0.5. Actually, we obtained that the efficiency of magnetic field generation increases by increasing the parameter q. The figure shows that a small fraction of initial energy is transferred into the magnetic perturbation for each of the systems. We find that the structure with q = 0.5 was saturated before other structures during the time around 
$t = 14{\rm \omega} _{\rm p}^{ - 1} $. The structures q = 1 and 5 were in the next step with saturation times 
$t = 19{\rm \omega} _{\rm p}^{ - 1} $ and 
$t = 39{\rm \omega} _{\rm p}^{ - 1} $, respectively. In the linear regime (t <t satu) the instability experiences exponential growth and saturates, then instability enters the non-linear regime (t >t satu). The non-linear evolution involves the transition phase (t satu <t <t qstat, where t qstat is quasi-stationary time). For t >t satu the magnetic field energy is transferred to the long wavelength part of the spectrum, and the quasi-stationary regime (t >t qstat) is characterized by sufficient reduction in temperature anisotropy. We find from the Figure 4 that the peak magnetic energy is smaller for structure q = 0.5 compared with q = 1 and q = 5, while the generated localized magnetic field is stronger for structure q = 0.5. While the linear stage for structure q = 0.5 with superthermal electrons develops very fast, the fraction of initial electron energy, which is transferred to magnetic perturbation is smaller compared to structures q = 1 and 5.
Fig. 4. (color online) The ratio of magnetic energy to the initial electrons kinetic energy for q = 0.5(red), 1(blue), and 5(green) as a function of ωpt.
The movie displays the time evolution of initial electron velocity distribution function Eq. (1) for two different structures with non-extensive parameters q = 0.5 and 5. The counter in the top of the screen counts in 10ωpt units. We observe the fast reduction in temperature anisotropy between the time steps 70 and 140 for structure q = 0.5, which is in good agreement with Figure 4. We find that near the saturation time (time step = 140) the electron distribution function is weakly anisotropic, while the structure q = 5 still conserves its anisotropic form. As time goes on, near the time step 170 a dramatic reduction in temperature anisotropy starts for structure q = 5 and at time step 390 the distribution function reduces to a weakly anisotropic form. The movie clearly shows that the quasi-stationary time is perceptibly greater for structure q = 5.
For a better understanding of instability evolution, we plotted Figure 5, which clearly confirms the energy conservation. As we mentioned, during instability evolution, two processes will happen simultaneously: attaining the temperature isotropy and the magnetic field production. The orange and black solid lines depict the ratio of particles kinetic energy variation to initial kinetic energy in the y- and x-directions as a function of ωpt, respectively. Furthermore, the blue and red lines demonstrate the variation of the ratio of kinetic energy and space averaged magnetic field energy to the initial kinetic energy in terms of ωpt, respectively. In other words, the blue and red lines show the produced electromagnetic and magnetic energy variations, respectively. We assume the x to be hot axes; therefore as time goes on, the corresponding energy reduces in x and increases in the y-direction, respectively. As the figure shows the magnetic field is produced during the energy trading between the two axes. We see that just a small fraction of initial energy can be converted to magnetic perturbation. The figure shows for structures q = 0.5 and 1 the thermalization established in time around 
$t = 120{\rm \omega} _{\rm p}^{ - 1} $ and 
$t = 130{\rm \omega} _{\rm p}^{ - 1} $, respectively. However, as illustrated in Figure (5c), the structure q = 5 needs more time to stabilize. The comparison between red and blue lines confirms the electromagnetic energy is accumulated mainly in the magnetic field perturbations (E 2/B 2 ≤ 10−2), which is expected.
Fig. 5. (color online) 
$(W_{Kx}^n - W_{Kx}^0 )/W_K^0 $ (black), 
$(W_{Ky}^n - W_{Ky}^0 )/W_K^0 $ (orange), 
$(W_K^n - W_K^0 )/W_K^0 $ (blue), and 
$W_B^n /W_K^0 $ (red) as a function of ωpt. (a) q = 0.5, (b) q = 1, and (c) q = 5.
Summary and discussion
To conclude, we have examined the thermal anisotropy-driven Weibel instability in the context of non-extensive plasma. We have limited our investigation to initially unmagnetized homogeneous and collisionless plasma in the relativistic regime with immobile neutralizing ions. We have performed the 2D PIC simulation for electrons freely moving in the x–y plane and the waves that grow due to the Weibel instability are planar with a wave vector in the x–y plane. We introduced a new 2D non-extensive anisotropic electron distribution function. As expected, a minor part of the initial kinetic energy of electrons is transferred into the magnetic perturbations and the z-component of the magnetic field exponentially grows in the linear regime. At the end of linear regime the instability is saturated and then instability enters the non-linear regime. We observed that for plasmas with the same temperature anisotropy, the saturation time increased by increasing the non-extensive parameter q. This means that for a plasma with superthermal electrons the strong magnetic field can be produced in short time compared with the plasma with the same temperature anisotropy and no more energetic electrons. The simulation results show that the fraction of initial electrons energy, which is transferred into the magnetic perturbations is increased by non-extensive parameter q. It is shown that plasmas with the large q-parameter (q > 1) are thermalized very slowly compared with the plasmas with small q-parameter (q < 1). The results in this paper are in good agreement with simulation for the anisotropic Maxwellian plasmas.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S0263034617000842
