1. INTRODUCTION
The excitation of lower hybrid wave is a widely discussed mechanism of interaction between plasma species in ionospheric and magnetospheric plasmas. Lower hybrid waves are electrostatic waves with wave vectors nearly perpendicular to the magnetic field, and involve oscillations of both the ions and electrons. If the wave electric field is nearly perpendicular to the magnetic field, then the electron response time is greatly increased. The lower hybrid resonance occurs only when the ion response time is less than or comparable to the electron response time, i.e., 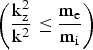 $\left({\displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }} \leq \displaystyle{{{\rm m}_{\rm e} } \over {{\rm m}_{\rm i} }}} \right)$. Lower hybrid wave at the same frequency can satisfy the resonance conditions for interacting with unmagnetized ions and magnetized electrons. Thus, lower hybrid wave may transfer energy from the perpendicular motion of ions to the parallel motion of electrons or vice versa, either accelerating the electrons or heating the ions. Such a redistribution of energy occurs in many regions of the heliosphere, including in the outer heliosheath where pick-up ions form a ring beam distribution (Cairns & Zank, Reference Cairns and Zank2002), and near magnetic reconnection sites where bulk ions flow across B and electrons accelerated along B are observed (Cairns, Reference Cairns2001), such as occur in the Earth's magnetotail and possibly in the solar corona. These waves play an important role in space and laboratory plasmas due to their ability to interact with electrons propagating along the magnetic field and with ions in the transverse plane.
$\left({\displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }} \leq \displaystyle{{{\rm m}_{\rm e} } \over {{\rm m}_{\rm i} }}} \right)$. Lower hybrid wave at the same frequency can satisfy the resonance conditions for interacting with unmagnetized ions and magnetized electrons. Thus, lower hybrid wave may transfer energy from the perpendicular motion of ions to the parallel motion of electrons or vice versa, either accelerating the electrons or heating the ions. Such a redistribution of energy occurs in many regions of the heliosphere, including in the outer heliosheath where pick-up ions form a ring beam distribution (Cairns & Zank, Reference Cairns and Zank2002), and near magnetic reconnection sites where bulk ions flow across B and electrons accelerated along B are observed (Cairns, Reference Cairns2001), such as occur in the Earth's magnetotail and possibly in the solar corona. These waves play an important role in space and laboratory plasmas due to their ability to interact with electrons propagating along the magnetic field and with ions in the transverse plane.
Recently, there has been a great deal of interest in studying lower hybrid waves. Various mechanisms for lower hybrid wave excitation have been studied so far theoretically as well as experimentally, for example, by electron beam (Papadopoulos & Palmadesso, Reference Papadopoulos and Palmadesso1976; Shoucri & Gagne, Reference Shoucri and Gagne1978; Gupta & Sharma, Reference Gupta and Sharma2004), by modulated electron beam (Sharma et al., Reference Sharma, Srivastava, Sugawa and Tripathi1998; Allen et al., Reference Allen, Owens, Seiler, Yamada, Ikezi and Porkolab1978), by laser (Sajal & Tripathi, Reference Sajal and Tripathi2008; Purohit et al., Reference Purohit, Chauhan and Sharma2008), by a slow-wave structure (Bellan & Porkolab, Reference Bellan and Porkolab1975), by gyrating (Seiler et al., Reference Seiler, Yamada and Ikezi1976; Sharma & Tripathi, Reference Sharma and Tripathi1988) or axial ion beam (Chang, Reference Chang1975), etc. Papadopoulos and Palmadesso (Reference Papadopoulos and Palmadesso1976) have demonstrated that lower hybrid waves can be generated by an energetic electron beam streaming through plasma along the magnetic field. Shoucri and Gagne (Reference Shoucri and Gagne1978) have studied the excitation of quasi-static lower hybrid Eigen modes by a small density electron beam in finite geometry plasmas. Gupta and Sharma (Reference Gupta and Sharma2004) have studied the nonlinear coupling of a large amplitude Trivelpiece Gould mode with the electron beam mode in a magnetized beam-plasma system. Sharma et al. (Reference Sharma, Srivastava, Sugawa and Tripathi1998) have studied the excitation of lower hybrid waves by a density modulated electron beam in a plasma cylinder. Allen et al. (Reference Allen, Owens, Seiler, Yamada, Ikezi and Porkolab1978) have experimentally investigated the parametric excitation of lower hybrid waves. Sajal and Tripathi (Reference Sajal and Tripathi2008) have observed that a lower hybrid wave having frequency less than the plasma frequency can be driven to large amplitude by a laser propagating through a magnetic plasma channel. Purohit et al. (Reference Purohit, Chauhan and Sharma2008) have studied the excitation of an upper hybrid wave by a high power laser beam in plasma. Bellan and Porkolab (Reference Bellan and Porkolab1975) have reported the excitation of lower hybrid waves by a multiple ring slow wave structure in magnetized plasma. Seiler et al. (Reference Seiler, Yamada and Ikezi1976) have reported experimental results on the excitation of lower hybrid instability by a spiraling ion beam in a linear Princeton Q-1 device. In this case, the frequency measurement shows that the instability occurs at just above the cyclotron harmonics, probably as a coupling of the beam cyclotron mode with the lower hybrid mode supported by the plasma. Sharma and Tripathi (Reference Sharma and Tripathi1988) have developed a nonlocal theory of the excitation of lower hybrid waves by a gyrating ion beam in a magnetized plasma cylinder. Chang (Reference Chang1975) has observed experimentally that a perpendicular ion beam drives lower hybrid mode with unmagnetized beam and target ions in nonisothermal radio frequency discharge plasma. In this case, Chang (Reference Chang1975) noted that because of this lower hybrid instability, part of the ion-beam energy will be consumed to heat the electrons. Moreover, the instability had a maximum growth rate when the phase velocity of the wave along the magnetic field was comparable to the electron thermal velocity. Recently, Kumar and Tripathi (Reference Kumar and Tripathi2012) have studied the excitation of ion Bernstein and ion cyclotron waves by a gyrating ion beam in a plasma column. Sharma et al. (Reference Sharma, Sharma, Jain and Gahlot2013) have studied the excitation of lower hybrid waves by a gyrating beam in negative ion plasma.
In the present paper, we study the excitation of lower hybrid waves by an ion beam propagating at right angles to the external static magnetic field in plasma. An ion beam drives electrostatic lower hybrid wave to instability via Cerenkov interaction. In Section 2, we carry out the instability analysis. The plasma and beam responses are obtained using fluid treatment. The growth rate of the instability is obtained using first-order perturbation theory. Results and discussions are given in Section 3 and conclusions are given in Section 4.
2. INSTABILITY ANALYSIS
Consider plasma with equilibrium electron and ion densities being given as n eo and n io, respectively, immersed in a static magnetic field Bs in the z-direction. The charge, mass, and temperature of the electrons and ions are denoted by (-e, m e, T e) and (e, m i, T i), respectively. We consider a low frequency electrostatic wave, such as a lower hybrid mode, propagating nearly perpendicular to the external magnetic field with propagation vector k lying in the x-z plane. An ion beam is considered propagating along x-axis perpendicular to the magnetic field with density n bo and equilibrium beam velocity v bo![]() $\hat {\rm x}$. The quasi-neutrality condition at equilibrium is given by en io + en bo = en eo. The equilibrium is perturbed by an electrostatic perturbation with potential
$\hat {\rm x}$. The quasi-neutrality condition at equilibrium is given by en io + en bo = en eo. The equilibrium is perturbed by an electrostatic perturbation with potential
The response of plasma electrons to the perturbation is governed by the equations of motion and continuity, which on linearization yield velocity and density perturbations
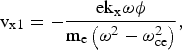 $${\rm v}_{{\rm x1}}=- \displaystyle{{{\rm ek}_{\rm x} {\rm {\rm \omega} {\rm \phi} }} \over {{\rm m}_{\rm e} \left({{\rm {\rm \omega} }^2 - {\rm {\rm \omega} }_{{\rm ce}}^2 } \right)}}\comma \;$$
$${\rm v}_{{\rm x1}}=- \displaystyle{{{\rm ek}_{\rm x} {\rm {\rm \omega} {\rm \phi} }} \over {{\rm m}_{\rm e} \left({{\rm {\rm \omega} }^2 - {\rm {\rm \omega} }_{{\rm ce}}^2 } \right)}}\comma \;$$ $${\rm v}_{{\rm y1}} = - \displaystyle{{{\rm ek}_{\rm x} {\rm {\rm \phi} {\rm \omega} }_{{\rm ce}}^{} } \over {{\rm im}_{\rm e} \left({{\rm {\rm \omega} }^2 - {\rm {\rm \omega} }_{{\rm ce}}^2 } \right)}}\comma \;$$
$${\rm v}_{{\rm y1}} = - \displaystyle{{{\rm ek}_{\rm x} {\rm {\rm \phi} {\rm \omega} }_{{\rm ce}}^{} } \over {{\rm im}_{\rm e} \left({{\rm {\rm \omega} }^2 - {\rm {\rm \omega} }_{{\rm ce}}^2 } \right)}}\comma \;$$and
where ![]() ${\rm {\rm \omega} }_{\rm ce} \left(= \displaystyle{{\rm eB}_{\rm s} } \over {{\rm m}_{\rm e} {\rm c}} \right)$ is the electron cyclotron frequency and subscript 1 refers to perturbed quantities.
${\rm {\rm \omega} }_{\rm ce} \left(= \displaystyle{{\rm eB}_{\rm s} } \over {{\rm m}_{\rm e} {\rm c}} \right)$ is the electron cyclotron frequency and subscript 1 refers to perturbed quantities.
The response of the plasma ions can be obtained from Eq. (5) by replacing –e, m e, ωce by e, m i, ωci, respectively
 $${\rm n}_{{\rm i1}}=\displaystyle{{{\rm n}_{{\rm io}} {\rm e{\rm \phi} }} \over {{\rm m}_{\rm i} }}\left[{\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm {\rm \omega} }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 }}+\displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm {\rm \omega} }^2 }}} \right].$$
$${\rm n}_{{\rm i1}}=\displaystyle{{{\rm n}_{{\rm io}} {\rm e{\rm \phi} }} \over {{\rm m}_{\rm i} }}\left[{\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm {\rm \omega} }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 }}+\displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm {\rm \omega} }^2 }}} \right].$$The response of beam ions to the perturbation is governed by the equation of motion
On linearization, Eq. (7) yields the perturbed beam velocities
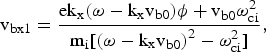 $${\rm v}_{{\rm bx1}} = \displaystyle{{{\rm ek}_{\rm x} {\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar {\rm \phi}+v}_{{\rm b0}} {\rm {\rm \omega} }_{{\rm ci}}^2 } \over {{\rm m}_{\rm i} {\rm \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }}\comma \;$$
$${\rm v}_{{\rm bx1}} = \displaystyle{{{\rm ek}_{\rm x} {\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar {\rm \phi}+v}_{{\rm b0}} {\rm {\rm \omega} }_{{\rm ci}}^2 } \over {{\rm m}_{\rm i} {\rm \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }}\comma \;$$ $$\eqalign{{\rm v}_{{\rm by1}}&=\displaystyle{{{\rm v}_{{\rm b0}} {\rm {\rm \omega} }_{{\rm ci}}^{} } \over {{\rm i\lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }}}+\displaystyle{{{\rm ek}_{\rm x} {\rm {\rm \phi} {\rm \omega} }_{{\rm ci}}^{} } \over {{\rm im}_{\rm i} {\rm \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }} \cr & \quad +\displaystyle{{{\rm v}_{{\rm b0}} {\rm {\rm \omega} }_{{\rm ci}}^3 } \over {{\rm i\lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }}\comma \; }$$
$$\eqalign{{\rm v}_{{\rm by1}}&=\displaystyle{{{\rm v}_{{\rm b0}} {\rm {\rm \omega} }_{{\rm ci}}^{} } \over {{\rm i\lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }}}+\displaystyle{{{\rm ek}_{\rm x} {\rm {\rm \phi} {\rm \omega} }_{{\rm ci}}^{} } \over {{\rm im}_{\rm i} {\rm \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }} \cr & \quad +\displaystyle{{{\rm v}_{{\rm b0}} {\rm {\rm \omega} }_{{\rm ci}}^3 } \over {{\rm i\lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }}\comma \; }$$and
Substituting the perturbed velocities given by Eqs. (8), (9), and (10) in the equation of continuity
we obtain the perturbed beam density as
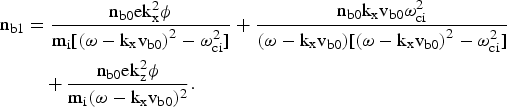 $$\eqalign{{\rm n}_{{\rm b1}}&=\displaystyle{{{\rm n}_{{\rm b0}} {\rm ek}_{\rm x}^2 {\rm {\rm \phi} }} \over {{\rm m}_{\rm i} {\rm \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }}+\displaystyle{{{\rm n}_{{\rm b0}} {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm {\rm \omega} }_{{\rm ci}}^2 } \over {{\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }} \cr & \quad +\displaystyle{{{\rm n}_{{\rm b0}} {\rm ek}_{\rm z}^2 {\rm {\rm \phi} }} \over {{\rm m}_{\rm i} {\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2 }}.}$$
$$\eqalign{{\rm n}_{{\rm b1}}&=\displaystyle{{{\rm n}_{{\rm b0}} {\rm ek}_{\rm x}^2 {\rm {\rm \phi} }} \over {{\rm m}_{\rm i} {\rm \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }}+\displaystyle{{{\rm n}_{{\rm b0}} {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm {\rm \omega} }_{{\rm ci}}^2 } \over {{\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar \lsqb \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} {\rm \rpar }^2 - {\rm {\rm \omega} }_{{\rm ci}}^2 \rsqb }} \cr & \quad +\displaystyle{{{\rm n}_{{\rm b0}} {\rm ek}_{\rm z}^2 {\rm {\rm \phi} }} \over {{\rm m}_{\rm i} {\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2 }}.}$$Using Eqs. (5), (6), and (12) in the Poisson's equation
we obtain
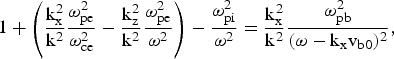 $$1{\bf } + \left({\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm {\rm \omega} }_{{\rm pe}}^2 } \over {{\rm {\rm \omega} }_{{\rm ce}}^2 }} - \displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm {\rm \omega} }_{{\rm pe}}^2 } \over {{\rm {\rm \omega} }^2 }}} \right)- \displaystyle{{{\rm {\rm \omega} }_{{\rm pi}}^2 } \over {{\rm {\rm \omega} }^2 }}=\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 } \over {{\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2 }}\comma \;$$
$$1{\bf } + \left({\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm {\rm \omega} }_{{\rm pe}}^2 } \over {{\rm {\rm \omega} }_{{\rm ce}}^2 }} - \displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm {\rm \omega} }_{{\rm pe}}^2 } \over {{\rm {\rm \omega} }^2 }}} \right)- \displaystyle{{{\rm {\rm \omega} }_{{\rm pi}}^2 } \over {{\rm {\rm \omega} }^2 }}=\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 } \over {{\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2 }}\comma \;$$
where 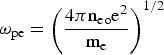 ${\rm {\rm \omega} }_{{\rm pe}} = \left({\displaystyle{{4{\rm {\rm \pi} n}_{{\rm eo }} {\rm e}^2 } \over {{\rm m}_{\rm e} }}} \right)^{{1 / 2}} $,
${\rm {\rm \omega} }_{{\rm pe}} = \left({\displaystyle{{4{\rm {\rm \pi} n}_{{\rm eo }} {\rm e}^2 } \over {{\rm m}_{\rm e} }}} \right)^{{1 / 2}} $, 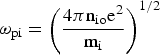 ${\rm {\rm \omega} }_{{\rm pi}} =\left({\displaystyle{{4{\rm {\rm \pi} n}_{{\rm io }} {\rm e}^2 } \over {{\rm m}_{\rm i} }}} \right)^{{1 / 2}}$ are the electron and ion plasma frequencies, respectively, and we have taken ωci≪ω≪ωce and kz≪k for beam ions.
${\rm {\rm \omega} }_{{\rm pi}} =\left({\displaystyle{{4{\rm {\rm \pi} n}_{{\rm io }} {\rm e}^2 } \over {{\rm m}_{\rm i} }}} \right)^{{1 / 2}}$ are the electron and ion plasma frequencies, respectively, and we have taken ωci≪ω≪ωce and kz≪k for beam ions.
Eq. (14) can be rewritten as
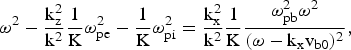 $${\rm {\rm \omega} }^{\rm 2} - \displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }}\displaystyle{{\rm 1} \over {\rm K}}{\rm {\rm \omega} }_{{\rm pe}}^2 - \displaystyle{{\rm 1} \over {\rm K}}{\rm {\rm \omega} }_{{\rm pi}}^2 = \displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{1 \over {\rm K}}\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 {\rm {\rm \omega} }^2 } \over {{\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2 }}\comma \;$$
$${\rm {\rm \omega} }^{\rm 2} - \displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }}\displaystyle{{\rm 1} \over {\rm K}}{\rm {\rm \omega} }_{{\rm pe}}^2 - \displaystyle{{\rm 1} \over {\rm K}}{\rm {\rm \omega} }_{{\rm pi}}^2 = \displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{1 \over {\rm K}}\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 {\rm {\rm \omega} }^2 } \over {{\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2 }}\comma \;$$where
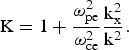 $${\rm K} = 1{\bf } + \displaystyle{{{\rm {\rm \omega} }_{{\rm pe}}^2 } \over {{\rm {\rm \omega} }_{{\rm ce}}^2 }}\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}.$$
$${\rm K} = 1{\bf } + \displaystyle{{{\rm {\rm \omega} }_{{\rm pe}}^2 } \over {{\rm {\rm \omega} }_{{\rm ce}}^2 }}\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}.$$From Eq. (15), we obtain the dispersion relation as
 $$\left({{\rm {\rm \omega} }^{\rm 2} - {\rm {\rm \alpha} }^{\rm 2} } \right)= \displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{1 \over {\rm K}}\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 {\rm {\rm \omega} }^2 } \over {{\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2 }}.$$
$$\left({{\rm {\rm \omega} }^{\rm 2} - {\rm {\rm \alpha} }^{\rm 2} } \right)= \displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{1 \over {\rm K}}\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 {\rm {\rm \omega} }^2 } \over {{\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2 }}.$$In the limit of vanishing beam density Eq. (16) yields
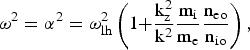 $${\rm {\rm \omega} }^{\rm 2} = {\rm {\rm \alpha} }^{\rm 2}={\rm {\rm \omega} }_{{\rm lh}}^2 \left({{\rm 1+}\displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm m}_{\rm i} } \over {{\rm m}_{\rm e} }}\displaystyle{{{\rm n}_{{\rm eo}} } \over {{\rm n}_{{\rm io}} }}} \right)\comma \;$$
$${\rm {\rm \omega} }^{\rm 2} = {\rm {\rm \alpha} }^{\rm 2}={\rm {\rm \omega} }_{{\rm lh}}^2 \left({{\rm 1+}\displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm m}_{\rm i} } \over {{\rm m}_{\rm e} }}\displaystyle{{{\rm n}_{{\rm eo}} } \over {{\rm n}_{{\rm io}} }}} \right)\comma \;$$where
 $${\rm {\rm \omega} }_{{\rm lh}}^2={{{\rm {\rm \omega} }_{{\rm pi}}^2 } {\left({1{\rm+}\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm {\rm \omega} }_{{\rm pe}}^2 } \over {{\rm {\rm \omega} }_{{\rm ce}}^2 }}} \right)}}.$$
$${\rm {\rm \omega} }_{{\rm lh}}^2={{{\rm {\rm \omega} }_{{\rm pi}}^2 } {\left({1{\rm+}\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm {\rm \omega} }_{{\rm pe}}^2 } \over {{\rm {\rm \omega} }_{{\rm ce}}^2 }}} \right)}}.$$For a plasma with n eo = n io, Eq. (17) yields
 $${\rm {\rm \alpha} }^{\rm 2} = {\rm {\rm \omega} }_{{\rm lh}}^2 \left({1{\rm+}\displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm m}_{\rm i} } \over {{\rm m}_{\rm e} }}} \right).$$
$${\rm {\rm \alpha} }^{\rm 2} = {\rm {\rm \omega} }_{{\rm lh}}^2 \left({1{\rm+}\displaystyle{{{\rm k}_{\rm z}^2 } \over {{\rm k}^2 }}\displaystyle{{{\rm m}_{\rm i} } \over {{\rm m}_{\rm e} }}} \right).$$This result is the same as given by Papadopoulous and Palmadesso (Reference Papadopoulos and Palmadesso1976).
In Cerenkov interaction, (ω – kx vbo) ≈ 0 and under the resonance condition ω ≈ kx vbo. Rewriting Eq. (16), we obtain
or
 $${\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2= - \displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{1 \over {\rm K}}\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 } \over {\left({{{{\rm {\rm \alpha} }^{\rm 2} } / {{\rm {\rm \omega} }^{\rm 2} }} - {\rm 1}} \right)}}.$$
$${\rm \lpar {\rm \omega} } - {\rm k}_{\rm x} {\rm v}_{{\rm b0}} \rpar ^2= - \displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}\displaystyle{1 \over {\rm K}}\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 } \over {\left({{{{\rm {\rm \alpha} }^{\rm 2} } / {{\rm {\rm \omega} }^{\rm 2} }} - {\rm 1}} \right)}}.$$Assuming perturbed quantity ω = kx vb0 + δ, where δ = δr + iγ we obtain the following expression for the instability growth rate γ (which is the imaginary part of the unstable frequency)
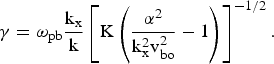 $${\rm {\rm \gamma}} = {\rm {\rm \omega} }_{\rm pb} \displaystyle{{\rm k}_{\rm x} \over {\rm k}}\left[{\rm K}\left(\displaystyle{{\rm {\rm \alpha} }^{\rm 2} \over {{\rm k}_{\rm x}^2 {\rm v}_{\rm bo}^2 }} - 1 \right)\right]^{- 1/ 2}.$$
$${\rm {\rm \gamma}} = {\rm {\rm \omega} }_{\rm pb} \displaystyle{{\rm k}_{\rm x} \over {\rm k}}\left[{\rm K}\left(\displaystyle{{\rm {\rm \alpha} }^{\rm 2} \over {{\rm k}_{\rm x}^2 {\rm v}_{\rm bo}^2 }} - 1 \right)\right]^{- 1/ 2}.$$From Eq. (19), we find that the growth rate is maximum when ω = kx vbo, i.e., when the beam mode intersects with the lower hybrid mode. To obtain the maximum growth rate, we assume the perturbed quantities in Eq. (16)
where δ is the small frequency mismatch.
The maximum growth rate of the unstable mode is obtained as
 $${\rm {\rm \gamma} }_{\max } = {\rm Im} \ {\rm \delta} = \displaystyle{{\sqrt 3 } \over 2}\left[{\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 } \over {\rm K}}\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}{\rm {\rm \alpha} }} \right]^{1/3}.$$
$${\rm {\rm \gamma} }_{\max } = {\rm Im} \ {\rm \delta} = \displaystyle{{\sqrt 3 } \over 2}\left[{\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 } \over {\rm K}}\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}{\rm {\rm \alpha} }} \right]^{1/3}.$$The real part of the frequency of unstable wave scales as the square root of the beam energy and in terms of beam voltage V b is given by
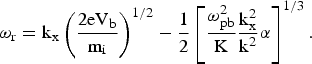 $${\rm {\rm \omega} }_{\rm r} = {\rm k}_{\rm x} \left({\displaystyle{{2{\rm eV}_{\rm b} } \over {{\rm m}_{\rm i} }}} \right)^{1/2} - \displaystyle{1 \over 2}\left[{\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 } \over {\rm K}}\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}{\rm {\rm \alpha} }} \right]^{1/3}.$$
$${\rm {\rm \omega} }_{\rm r} = {\rm k}_{\rm x} \left({\displaystyle{{2{\rm eV}_{\rm b} } \over {{\rm m}_{\rm i} }}} \right)^{1/2} - \displaystyle{1 \over 2}\left[{\displaystyle{{{\rm {\rm \omega} }_{{\rm pb}}^2 } \over {\rm K}}\displaystyle{{{\rm k}_{\rm x}^2 } \over {{\rm k}^2 }}{\rm {\rm \alpha} }} \right]^{1/3}.$$3. RESULTS AND DISCUSSIONS
We have used the experimental parameters of lower hybrid beam plasma instability for our numerical calculations which are as follows: ion plasma density n io = 109cm−3, guide magnetic field BS = 320 G, mass of ion m i = 39 × 1836m e (Potassium-plasma), temperature of electron T e = 3 eV and temperature of ion T i = 0.2 eV.
We have plotted the dispersion curves of lower hybrid waves in Figure 1, where the normalized frequency ω/ωpi taken from Eq. (17) is plotted as a function of normalized wave number kx/k. We have also plotted in Figure 1, the beam mode for beam velocity = 2.7 × 106 cm/s. The velocity of the beam mode is chosen in such a way so that it intersects with the lower hybrid mode where kx ≈ k or kz≪k, a condition necessary for the existence of lower hybrid waves. It is observed that the wave frequency decreases with an increase in the value of kx/k. The unstable wave number decreases and the unstable frequency increases with an increase in beam velocity, similar to the results of Idehara and Tomita (Reference Idehara and Tomita1986).

Fig. 1. (Color online) Dispersion curve of lower hybrid wave over a magnetized plasma and beam mode.
We have also plotted the dispersion curves of lower hybrid waves for different plasma parameters in Figure 2. It can be seen from the figure that the frequency decreases with the normalized wave number and therefore the beam velocity required for the excitation of lower hybrid wave decreases with an increase in the electron plasma density. However, a decrease in the electron plasma density from quasi-neutral condition does not alter the frequency too much. It is also found that an increase in the magnetic field increases the frequency and hence the beam velocity required for excitation increases with an increase in magnetic fields.

Fig. 2. (Color online) Dispersion curves of lower hybrid wave for (1) neo = 0.001 × nio, (2) neo = 0.1 × nio, (3) neo = nio, (4) neo = 10 × nio and (5) neo = 1000 × nio.
In Figure 3, we have plotted the normalized frequency ω/ωpi taken from Eq. (17) as a function of ![]() $\left( \left({\rm k}_{\rm z} / {\rm k} \right)\sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)$ for the same parameters used for plotting Figure 1, so that we can compare our theoretical results quantitatively with the experimental observations of Chang (Reference Chang1975) on lower-hybrid instability.
$\left( \left({\rm k}_{\rm z} / {\rm k} \right)\sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)$ for the same parameters used for plotting Figure 1, so that we can compare our theoretical results quantitatively with the experimental observations of Chang (Reference Chang1975) on lower-hybrid instability.

Fig. 3. (Color online) Dispersion curve of lower hybrid wave over magnetized plasma: ω/ωpi vs. 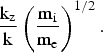 $\displaystyle{{\rm k}_{\rm z} \over {\rm k}} \left({\displaystyle{{{\rm m}_{\rm i} } \over {{\rm m}_{\rm e} }}} \right)^{1/2}.$
$\displaystyle{{\rm k}_{\rm z} \over {\rm k}} \left({\displaystyle{{{\rm m}_{\rm i} } \over {{\rm m}_{\rm e} }}} \right)^{1/2}.$
Figure 4 shows the plots of growth rate γ versus ![]() $\left(\left({\rm k}_{\rm z} / {\rm k} \right) \sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)$ for different values of beam velocities using Eq. (19). From Eq. (19), we find that the maximum growth rate occurs when the phase velocity ω/kx is comparable to the ion beam velocity, as is observed in Figure 4. This is in good agreement with Figures 1 and 3, where the beam mode intersects with the lower hybrid wave mode to make it unstable. The point of intersection between the beam mode and the lower hybrid mode corresponds to ω/ωpi = 0.573 and kx/k = 0.999978, which gives the value of ω/kz= 2.9 × 108 cm/s. This value of ω/kz is comparable to the electron thermal velocity vte = (2Te/me)1/2 ≈ 1.03 × 108 cm/s. We find that the maximum growth rate occurs when ω/kz ≈ vte in agreement with previous investigations (Chang, Reference Chang1975).
$\left(\left({\rm k}_{\rm z} / {\rm k} \right) \sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)$ for different values of beam velocities using Eq. (19). From Eq. (19), we find that the maximum growth rate occurs when the phase velocity ω/kx is comparable to the ion beam velocity, as is observed in Figure 4. This is in good agreement with Figures 1 and 3, where the beam mode intersects with the lower hybrid wave mode to make it unstable. The point of intersection between the beam mode and the lower hybrid mode corresponds to ω/ωpi = 0.573 and kx/k = 0.999978, which gives the value of ω/kz= 2.9 × 108 cm/s. This value of ω/kz is comparable to the electron thermal velocity vte = (2Te/me)1/2 ≈ 1.03 × 108 cm/s. We find that the maximum growth rate occurs when ω/kz ≈ vte in agreement with previous investigations (Chang, Reference Chang1975).

Fig. 4. (Color online) Growth rate γ of the unstable mode as a function of 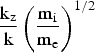 $\displaystyle{{{\rm k}_{\rm z} } \over {\rm k}}\left({\displaystyle{{{\rm m}_{\rm i} } \over {{\rm m}_{\rm e} }}} \right)^{1/2} $ for different ion beam velocities.
$\displaystyle{{{\rm k}_{\rm z} } \over {\rm k}}\left({\displaystyle{{{\rm m}_{\rm i} } \over {{\rm m}_{\rm e} }}} \right)^{1/2} $ for different ion beam velocities.
Since the growth rate is maximum when the parallel-wave phase velocity of the lower hybrid wave is approximately of the order of the electron thermal velocity, we expect efficient energy transport from the perpendicular ion beam to the bulk of the electrons via Landau damping, accelerating the electrons or heating them. The emission caused by this energetic electron component could explain the observed X-ray spectra (Bingham et al., Reference Bingham, Dawson and Shapiro2002). The spectrum of instability is quite broad, extending from the region ![]() $\left(\left({\rm k}_{\rm z} / {\rm k} \right)\sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)\simeq0.3$ to 1.2, and damps out after this value. It can be seen from Figure 4 that the beam modes with velocities 2.65 × 106 cm/s [cf. Fig. 4(1)] and 2.68 ×106 cm/s [cf. Fig. 4(2)] do not show any growth rate. As the velocity increases from 2.69 × 106 cm/s [cf. Fig. 4(3)] to 2.70 × 106 cm/s [cf. Fig. 4(5)], the maximum value of the growth rate increases from 8.6 × 107 rad/s to 13.7 × 107 rad/s. The growth rate is maximum for
$\left(\left({\rm k}_{\rm z} / {\rm k} \right)\sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)\simeq0.3$ to 1.2, and damps out after this value. It can be seen from Figure 4 that the beam modes with velocities 2.65 × 106 cm/s [cf. Fig. 4(1)] and 2.68 ×106 cm/s [cf. Fig. 4(2)] do not show any growth rate. As the velocity increases from 2.69 × 106 cm/s [cf. Fig. 4(3)] to 2.70 × 106 cm/s [cf. Fig. 4(5)], the maximum value of the growth rate increases from 8.6 × 107 rad/s to 13.7 × 107 rad/s. The growth rate is maximum for ![]() $\left(\left({\rm k}_{\rm z} / {\rm k} \right)\sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)\simeq0.84$, which gives kx/k = 0.999974 and which corresponds to the point of intersection of beam mode and lower hybrid mode (cf. Fig. 1). For any further increase in the beam velocity, the beam does not interact with the plasma mode in the lower hybrid range. A similar explanation goes for beam velocities less than or equal to 2.68 × 106 cm/s. These results are similar to the experimental results of Chang (Reference Chang1975), where the maximum growth rate has been observed for
$\left(\left({\rm k}_{\rm z} / {\rm k} \right)\sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)\simeq0.84$, which gives kx/k = 0.999974 and which corresponds to the point of intersection of beam mode and lower hybrid mode (cf. Fig. 1). For any further increase in the beam velocity, the beam does not interact with the plasma mode in the lower hybrid range. A similar explanation goes for beam velocities less than or equal to 2.68 × 106 cm/s. These results are similar to the experimental results of Chang (Reference Chang1975), where the maximum growth rate has been observed for ![]() $\left(\left({\rm k}_{\rm z} / {\rm k} \right)\sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)\simeq1.5$ and ω/kz = 108 cm/s.
$\left(\left({\rm k}_{\rm z} / {\rm k} \right)\sqrt {{\rm m}_{\rm i} / {\rm m}_{\rm e}} \right)\simeq1.5$ and ω/kz = 108 cm/s.
It is found that the beam velocities required for the excitation of lower hybrid wave using an ion beam are comparatively 10 to 100 times lower than the beam velocities required for excitation using an electron beam. Allen et al. (Reference Allen, Owens, Seiler, Yamada, Ikezi and Porkolab1978) have biased the beam-ionizer plate at 12 V in their experiment on parametric excitation of electrostatic lower-hybrid and ion-cyclotron modes by modulated electron-beam, giving a beam velocity of 2.05 × 108 cm/s. Papadopoulos and Palmadesso (Reference Papadopoulos and Palmadesso1976) have considered electron beam velocity of 3 × 109 cm/s. Idehara and Tomita (Reference Idehara and Tomita1986) have considered beam velocities ranging from 2.4 × 106 cm/s to 3.3 × 106 cm/s in an ion beam-plasma system and a test wave was found to become unstable near the lower-hybrid frequency in this velocity range. The velocity range observed in this article for the growth of lower hybrid wave also lies in this range.
This lower hybrid instability may also be relevant to the enhanced backscatter from the Space Shuttle exhaust as given in Bernhardt et al. (Reference Bernhardt, Ganguli, Kelley and Swartz1995). Assuming an oxygen plasma with density of O+ ions in the plume of order of 2 × 105cm−3 and magnetic field BS = 0.35 G, we have ωpi/ωci = 702 and with ωpe/ωce = 4.1 (for neo = nio), we have a lower hybrid frequency of about 3.5 × 104 rad/s. The corresponding beam velocity for maximum growth rate is 3.4 × 103 cm/s.
It is interesting to notice that the maximum growth rate increases with an increase in perpendicular ion beam velocity but it decreases as the parallel electron beam velocity increases (Papadopoulos & Palmadesso, Reference Papadopoulos and Palmadesso1976). It is because the maximum growth rate is directly proportional to the unstable wave frequency in both the cases and the unstable frequency decreases with an increase in parallel electron velocity but increases with an increase in perpendicular ion beam velocity.
We have plotted in Figure 5, the maximum growth rate of the lower hybrid wave instability as a function of beam density. The maximum growth rate of the unstable mode increases with the beam density and scales as the one-third power of the beam density.

Fig. 5. (Color online) Maximum growth rate γmax of the unstable mode as a function of nbo.
4. CONCLUSION
An ion beam in the presence of an external static magnetic field efficiently excites a lower hybrid wave in plasma. The electrostatic lower hybrid waves were driven to instability via Cerenkov interaction. As the beam velocity was increased, an increase in the most unstable frequency of lower hybrid mode was observed. It was found that the instability had the maximum growth rate when the perpendicular phase velocity of the lower hybrid mode was comparable to the velocity of beam, and parallel phase velocity was comparable to electron thermal velocity. The maximum growth rate increases with an increase in the velocity of the beam. The maximum growth rate [cf. Eq. (20)] is independent of the dissipative mechanisms in the plasma. For a collisionless plasma, it can be mode conversion into a short wavelength mode, as in the present article, the lower hybrid mode with frequency ωlh is converted to a high frequency mode with frequency α [cf. Eq. (17)]. Our results are reasonably in line with the experimental observations of Chang (Reference Chang1975).



