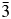I. INTRODUCTION
Double-perovskite transition-metal oxides (TMO), with a general formula A 2BB'O6, have attracted increasing attention in recent years. These perovskites possess interesting structural and transport properties (e.g., magnetic, optical, and electrical) and exhibit a variety of exotic properties, including colossal magnetoresistance, high-temperature superconductivity, half-metallicity (differentiated conducting response of the spin-up and spin-down electrons), leading to possible applications in spintronic devices. As these materials are stable at high temperature, and a number of these materials show reasonably high values of power factors P [P = S 2⋅σ, where S is the Seebeck coefficient and σ is the electrical conductivity (Tritt, Reference Tritt1996)]; therefore, in recent years, they are also potential candidates for energy conversion applications.
In general, perovskites are distinguished by their ability to simultaneously accommodate a wide range of species on both the 12-fold coordinated A cation site and sixfold B cation sites. A mismatch between ionic sizes and radii for cations sharing the same crystallographic sites provides a driving force for the ordering of these structures. Complex perovskite oxides result from the ordering of B and B′ cations in the octahedral sites of the primitive perovskite. Common examples of ordered arrangements for the B cations correspond to the general stoichiometries A 2BB'O6 and A 3B 2B'O9, which have been studied extensively (Viola et al., Reference Viola, Martínez-Lope, Alonso, Martínez, De Paoli, Pagola, Pedregosa, Fernández-Díaz and Carbonio2003; Manoun et al., Reference Manoun, Ezzahi, Benmokhtar, Bihc, Tamraoui, Haloui, Mirinioui, Addakiri, Igartua and Lazor2013). Cobalt tungstate, with a general formula A 2CoWO6 (A = Ba, Sr, and Ca) are among the largely studied double perovskites. The crystal field effect on the effective magnetic moment of these A 2CoWO6 phases has been investigated by Lòpez et al. (Reference Lòpez, Saleta, Curiale and Sānchez2012).
The double-perovskite Sr2CoWO6 was first studied in the 1960s (Blasse, Reference Blasse1965; Galasso, Reference Galasso1969), and it was reported to be an antiferromagnet with T N = 22 K (Blasse, Reference Blasse1965). The structure of SrCoWO6 was described as having tetragonal distortion and it assumes a random distribution of Co and W atoms in the I4/m space group (Kupriyanov and Fesenko, Reference Kupriyanov and Fesenko1962; Viola et al., Reference Viola, Martínez-Lope, Alonso, Martínez, De Paoli, Pagola, Pedregosa, Fernández-Díaz and Carbonio2003) with a = 5.58277(1) Å and c = 7.97740(1) Å. The double-perovskite Ba2CoWO6, on the other hand, is cubic, space group 
$Fm \bar{3} m$ (No. 225), with the lattice parameter, a = 8.103 Å (Cox et al., Reference Cox, Shirane and Frazer1967). It would be instructional to study the solid solution series of (BaxSr1–x)2CoWO6, to confirm where phase transition takes place across the series (Fresia et al., Reference Fresia, Katz and Ward1959; Gateshki et al., Reference Gateshki, Igartua and Hernandez-Bocanegra2003; Zhao et al., Reference Zhao, Yue, Gui and Li2005; Manoun et al., Reference Manoun, Ezzahi, Benmokhtar, Bihc, Tamraoui, Haloui, Mirinioui, Addakiri, Igartua and Lazor2013), and to compute the electronic properties including the bandgap value of the selected solid solution member.
There are two main goals in the current study. First, the structures of (BaxSr1–x)2CoWO6 (x = 0.1, 0.2, 0.3, 0.5, 0.7, and 0.9) compounds are investigated for the effects of ionic size difference between Ba2+ and Sr2+ on their structure. We will also use density functional theory (DFT) to compute the electronic structure and the bandgap of the two end members and the intermediate member of this series (x = 0, 0.5, and 1). Additionally, the reference X-ray diffraction (XRD) patterns for (BaxSr1–x)2CoWO6 (x = 0.2 and 0.7) are measured to make them available as references through submission to the Powder Diffraction File (PDF, 2019).
II. EXPERIMENTAL
A. Materials synthesis
The (BaxSr1–x)2CoWO6 (x = 0.1–0.9) samples were prepared from stoichiometric amounts of SrCO3, BaCO3, Co3O4, and WO3 using solid-state high-temperature techniques. The starting materials were mixed, pelletized, and heat-treated in air at 800 °C for 12 h and at 1000 °C for 12 h, with intermediate re-grindings, and finally at 1300 °C for 24 h. During each heat treatment, the samples were furnace cooled. The heat-treatment process was repeated until no further changes were detected in the powder XRD patterns.
B. Estimation of composition using X-ray fluorescence
The composition estimation of a sample of nominal (Ba0.2Sr0.8)2CoWO6 was performed on a Bruker M4 Tornado micro X-ray fluorescence instrument. (The purpose of identifying the equipment in this article is to specify the experimental procedure. Such an identification does not imply recommendation or endorsement by the National Institute of Standards and Technology.) An Rh X-ray source, set to 50 kV and 300 μA, with a 20 μm monocapillary was used for excitation (S.N. 2001495). A Bruker XFlash 450 μm thick, Silicon Drift Detector (S.N. 11881_0239) was used for data collection for the scans. Each spectrum used a minimum peak sum of over 100 000 X-ray counts per analyzed element, reducing counting statistics as a source of uncertainty below all other contributions. Analyses were performed using Bruker Quantify version 1.6.0.286 with a standard Spectrum Elements method and calibrated for our instrument (S.N. 6099). For statistical sampling, 26 independent, 120 s live time measurements were performed, and the variance of the composition derived from these measurements was used for error analysis.
C. X-ray Rietveld refinements and powder reference patterns
The (BaxSr1–x)2CoWO6 (x = 0.1, 0.2, 0.3, 0.5, 0.7, and 0.9) samples were mounted as acetone slurries on a zero-background single-crystal Si sample holder. The X-ray powder patterns of the former samples were measured on a Bruker “stock” D2 Phaser diffractometer with 141 mm radius, Cu tube, 0.6 mm divergence slit, 2.5° Soller slits, a LynxEye position-sensitive detector, with a Ni filter. The CuKα 1/2 wavelengths were 1.5405929/1.544451 Å. (Operation condition: 30 kV, 10 mA, 5–130° 2θ in 0.0202144° steps, 0.5 s step−1).
The Rietveld refinement technique (Rietveld, Reference Rietveld1969) with software suite GSAS (Larson and von Dreele, Reference Larson and von Dreele2004) was used to determine the structure. Reference patterns were obtained with a Rietveld pattern decomposition technique. Using this technique, the reported peak positions were derived from the extracted integrated intensities, and positions were calculated from the lattice parameters. When peaks are not resolved at the resolution function, the intensities are summed, and an intensity-weighted d-spacing is reported.
D. Bond valence sum calculations
The bond valence sum (BVS) values for the Ba, Sr, Co, and W sites in (BaxSr1–x)2CoWO6 were calculated using the Brown–Altermatt empirical expression (Brown and Altermatt, Reference Brown and Altermatt1985; Brese and O'Keeffe, Reference Brese and O'Keeffe1991). The BVS of an atom i is defined as the sum of the bond valences vij of all the bonds from atoms i to atoms j. The most commonly adopted empirical expression for the bond valence vij as a function of the interatomic distance dij is vij = exp[(R 0 – dij)/B]. The parameter, B, is commonly taken to be a “universal” constant equal to 0.37 Å. The values for the reference distance R 0 for Ba2+–O, Sr2+–O, W6+–O, Co2+–O are 2.29, 2.118, 1.921, and 1.692, respectively (Brown and Altermatt, Reference Brown and Altermatt1985; Brese and O'Keeffe, Reference Brese and O'Keeffe1991). If more than one atom type occupies the same site, the resulting BVS is the weighted sum of each site occupancy.
E. Bandgap calculations
We used the linearized augmented planewave (LAPW) method for the computation of the electronic structure within DFT. The calculations were performed using the ELK package (2018). The generalized gradient approximations (GGA) of Perdew, Burke, and Ernzerhof were used for the correlation and exchange potentials (Perdew et al., Reference Perdew, Burke and Ernzerhof1996). The atomic radii are 2.5 a.u. for Ba, 2.24 a.u. for Sr, 2.01 a.u. for Co, 1.82 a.u. for W, and 1.57 a.u. for O, respectively. The RK max parameter is set to be 7. Self-interaction correction for d electrons are introduced by an on-site Coulomb and exchange interactions, namely the Hubbard and exchange parameter U and J, with U = 0.329 and J = 0.061 Ry for Co and U = 0.193 and J = 0.035 Ry for W (Solovyev et al., Reference Solovyev, Dederichs and Anisimov1994). The energy convergence criteria are 10−5 Ry and the charge convergence criteria are 10−3.
III. RESULTS AND DISCUSSION
The atomic ratio for Ba/Co, Sr/Co, and W/Co for the nominal (Ba0.2Sr0.8)2CoWO6 sample were calculated using the X-ray fluorescence technique, with the Co concentration normalized to 1. The results show that the ratio of concentration for Sr/Co = 1.75 ± 0.30 (XRD value of 1.6) and W/Co [0.99 ± 0.17] (XRD value of 1) agree with 95% confidence (K = 1 confidence interval) and that the ratio of the concentration of Ba/Co = 0.317 ± 0.054 (XRD value of 0.4) agrees with 68% confidence (K = 2 confidence interval). Note that the uncertainties stated within the brackets represent 1 sigma (s) estimates.
The results of Rietveld refinement for the (BaxSr1–x)2CoWO6 (x = 0.1–0.9) series are shown in Table I and Figures 1 and 2. Table I gives various refinement statistical agreement factors, whereas in Figures 1 and 2, the observed (crosses), calculated (solid line), and difference XRD patterns (bottom) for (BaxSr1–x)2CoWO6 (x = 0.7 and 0.2) are illustrated; the difference pattern is plotted at the same scale. The row of tick marks indicates the calculated peak positions. In these figures, the small peak in the 2θ (°) around 28° region is the Kβ peak of the 110 reflection. Its presence does not interfere with the refinement. Table II lists the lattice parameters, while atomic coordinates and displacement parameters are shown in Table III. The bond distances and BVS values are summarized in Table IV.
Figure 1. Observed (crosses), calculated (solid line), and difference XRD patterns (bottom) for (Ba0.7Sr0.3)2CoWO6 by a Rietveld analysis technique. The difference pattern is plotted at the same scale as the other calculated peak positions. The small peak in the 2θ (°) around 28° region is the Kβ peak of the 110 reflection. Its presence does not interfere with the refinement.
Figure 2. Observed (crosses), calculated (solid line), and difference XRD patterns (bottom) for (Ba0.2Sr0.8)2CoWO6 by a Rietveld analysis technique. The difference pattern is plotted at the same scale as the other calculated peak positions.
TABLE I. Rietveld refinement residuals for (BaxSr1−x)2CoWO6 (x = 0.1, 0.2, 0.3, 0.5, 0.7, and 0.9).
For x = 0.1 and 0.2, the structure is tetragonal I4/m, and for x = 0.3–0.9, the structure is cubic Fm 
$\bar{3}$m (No. 225).
TABLE II. Cell parameters for (BaxSr1−x)2CoWO6 (x = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9).
For x = 0.1 and 0.2, the structure is tetragonal I4/m, and for x = 0.3–1.0, the structure is cubic Fm 
$\bar{3}$m (No. 225), Z = 4. For comparison purpose (with the same Z value per unit cell), the unit-cell volumes for the tetragonal compounds are doubled.
TABLE III. Atomic coordinates and displacement parameters for compounds for (BaxSr1−x)2CoWO6 (x = 0.1, 0.2, 0.3, 0.5, 0.7, and 0.9).
For x = 0.1 and 0.2, the structure is tetragonal I4/m, and for x = 0.3–0.9, the structure is cubic Fm 
$\bar{3}$m (No. 225).
TABLE IV. Bond distances and BVS values for (BaxSr1−x)2CoWO6 [x = 0.1 (T), 0.2 (T), 0.3 (C), 0.5 (C), 0.7 (C), and 0.9 (C)].
The ideal BVS values are 2.0 for Ba1 site, 6.0 for the W site, and 2.0 for the Co site, respectively. The values for the reference distance R 0 for Ba2+–O, Sr2+–O, Co2+–O, and W6+–O are 2.29, 2.118, 1.692, and 1.921, respectively (Brown and Altermatt, Reference Brown and Altermatt1985; Brese and O'Keeffe, Reference Brese and O'Keeffe1991).
The (BaxSr1−x)2CO6 solid solution series is confirmed to be double perovskite, having two types of structures across the series. When Sr concentration is rich (x = 0.1 and 0.2), the structure is of Sr2CoWO6 type, tetragonal I4/m (No. 87) (a = 5.60481(6) and 5.62305(11) Å and c = 7.97989(12) and 7.9847(2) Å, respectively). These unit-cell parameters are related to a 0 (ideal cubic perovskite, a 0 ≈ 3.95 Å) as a ≈ b ≈ 
$\surd 2$a 0, c ≈ 2a 0. When x > 0.2, the structure was found to be cubic Fm 
$\bar{3}$m (No. 225) (from x = 0.3–0.9, a increases from 7.98399(13) to 8.08871(10) Å, respectively). These cubic unit-cell parameters are related to a 0 as a ≈ 2a 0. In both type of structures, there is an apparent disorder in the Ba and Sr sites, in contrast to the ordering of CoO6 and WO6 octahedra. Figure 3 illustrates changes in the unit-cell volumes, V, in the (BaxSr1−x)2CoWO6 series (x = 0.1–0.9) as a function of x. V increases slightly (5.76%) across the entire solid solution series [from 500.360(14) to 529.22(2) Å3].
Figure 3. Compositional dependence of the unit-cell volume, V, for (BaxSr1−x)2CoWO6. For comparison purpose (with the same Z value per unit cell), the unit-cell volumes for the tetragonal compounds are doubled. A monotonic increase of V is observed as a function of x.
Figures 4–6 illustrate the tetragonal structure of (BaxSr1−x)2CoWO6 viewing along the a-axis, ab-diagonal, and c-axis, respectively. The structure is built from corner-sharing WO6 and CoO6 octahedra just like the rock salt structure. In the tetragonal structure, it is obvious that there is a rotational mismatch of the distorted WO6 and CoO6 octahedra while viewing along the c-axis. This series of compounds exhibit the characteristics of the distorted double-perovskite structure, with the rotational mismatch angles of 13.776° counter-clockwise for CoO6 octahedra, 12.143° clockwise for WO6 octahedra in x = 0.1 compounds, and the rotational mismatch angles of 7.44° counter-clockwise for CoO6 octahedra, 6.999° clockwise for WO6 octahedra in x = 0.2 compounds. One also observes the distorted tetragonal channels that are tilted with respect to the a-axis. Ba atoms were found inside the channels. From Figures 4–6, it is seen that WO6 and CoO6 octahedra alternate with each other along the ab-diagonal or c-axis. Viewing along the [001] direction of the pseudo-cubic cell, the alternating CoO6 and WO6 octahedra were found to tilt in an antiphase fashion. Agreeing with Viola et al. (Reference Viola, Martínez-Lope, Alonso, Martínez, De Paoli, Pagola, Pedregosa, Fernández-Díaz and Carbonio2003), this tilting corresponds to the a 0a 0c − Glazer's notation (Reference Glazer1972) derived by Woodward (Reference Woodward1997) for the 1:1 ordering of double perovskites (consistent with the space group I4/m). The distorted nature of the WO6 and CoO6 octahedra are also revealed in the bond distances of W–O and Co–O, while the bond angles of O–W–O and O–Co–O are either 90° or 180°. For example, the W–O distances range from 1.89740(3) to 1.94858(6) Å in WO6 and from 2.15949(2) to 2.04377(6) Å in CoO6. In Figure 7, the structure of cubic (BaxSr1−x)2CoWO6 is shown. Similar to the tetragonal structure, one finds alternate arrangement of the WO6 and CoO6 octahedra along all three-axis.
Figure 4. Tetragonal structure of (Ba0.2Sr0.8)2CoWO6 viewed along the a-axis.
Figure 5. Tetragonal structure of (Ba0.2Sr0.8)2CoWO6 along the ab-diagonal.
Figure 6. Tetragonal structure of (Ba0.2Sr0.8)2CoWO6 viewed along the c-diagonal.
Figure 7. Cubic structure of (Ba0.7Sr0.3)2CoWO6 viewed along the a-axis.
The Ba/Sr atoms were found to be inside the channels, occupying a 12 oxygen coordination site. The average Ba/Sr–O bond distances range from 2.51589(3) to 2.86128(5) Å. The BVS values of the (Ba, Sr) site are, in general, greater than the ideal value of 2.0. It is interesting that in the tetragonal case, the BVS value decreases from 2.368 to 2.170, but the opposite trend exists in the cubic case, increases from 2.095 to 2.467 when x increases from 0.3 to 0.9, respectively. All these values are greater than the ideal value of 2.0, indicating over-bonding situation, or the cage size is too small.
The BVS values for the sixfold coordinated W site in both the tetragonal and cubic cases have deviated from the ideal value of 6.0. In both cases, as the concentration of Ba increases, the BVS value decreases (from 6.287 to 5.624 Å in the tetragonal case and from 6.267 to 5.857 Å in the cubic case), indicating a change from over-bonding to slightly under-bonding situation. For the sixfold Co sites, although no specific trend is observed, all BVS values are slightly deviate from the ideal value of 2.0.
A. Bandgap calculations
Table V gives the DFT calculated lattice constants and bandgap values (spin-up) using GGA and GGA + U methods. Results of DFT calculations show that after considering Coulomb exchange (U = 0.392 and J = 0.061 Ry for Co and U = 0.193 and J = 0.035 Ry for W), the bandgaps increased about 0.5–0.7 eV (Figures 8–11). The calculated bandgap values are 2.71, 2.57, 2.52, and 2.42 eV for Sr2CoWO6 [Figure 8(b)], cubic SrBaCoWO6 [Figure 9(b)], tetragonal SrBaCoWO6 [Figure 10(b)], and Ba2CoWO6 [Figure 11(b)], respectively. From the results of the density of states (DOS) calculations, the state density of Sr2CoWO6 (x = 0.0) near the Fermi energy level is shown to be both zero in the spin-up and spin-down bands, which is a pattern of a typical semiconductor [Figure 8(b)]. The spin-up band of Ba2CoWO6 (x = 1.0) [Figure 11(b)] is zero near the Fermi energy level, while the state density of the spin-down band has a peak through the Fermi energy level, showing typical half metallicity [Figure 11(b)]. In other words, a half-metal is any substance that acts as a conductor to electrons of one spin orientation, but as an insulator or semiconductor to those of the opposite orientation. When BaSrCoWO6 (x = 0.5) was calculated using the cubic structure model it is half-metallic [Figure 9(b)], while using the tetragonal structure model BaSrCoWO6 (x = 0.5) is a semiconductor [Figure 10(b)]. The total energy of the tetragonal structure is higher than that of the cubic structure when there is no Hubbard potential added to the d-electrons, but it changes to a lower energy value when the Hubbard potential is added, which illustrates that the Hubbard potential influences the stability of a structure and a reasonable U and J values should be used to match the experiments. It also seems to show that the Hubbard potential should have been included in the calculations from the beginning of the structure optimization process. The result of U and J addition is somewhat different from that of XRD. XRD gave better Rietveld refinement results for the cubic structure but calculation with the addition of Hubbard potential (U = 0.392 and J = 0.061 Ry for Co and U = 0.193 and J = 0.035 Ry for W) showed the tetragonal structure to be more stable. The DFT calculations used an ordered Ba and Sr model in the tetragonal case; however, we did not observe any satellite peaks related to the ordered feature in the XRD diffraction pattern, indicating a disordered structure. Lastly, in all cases, the state density near the Fermi energy level is almost completely contributed by the Co atom from its projection, and the magnetic moments of these compounds also almost come entirely from the Co atoms (Table VI).
Figure 8. Bandgap calculations using DFT for Sr2CoWO6, (a) bandgap E g using GGA and (b) using GGA + U. The partial DOS contribution from W and Co are shown.
Figure 9. Bandgap calculations using DFT for (SrBa)CoWO6 using a cubic model, (a) bandgap E g using GGA and (b) using GGA + U. The partial DOS contribution from W and Co are shown.
Figure 10. Bandgap calculations using DFT for (SrBa)CoWO6 using a tetragonal model, (a) bandgap E g using GGA and (b) using GGA + U. The partial DOS contribution from W and Co are shown.
Figure 11. Bandgap calculations using DFT for Ba2CoWO6, (a) bandgap E g using GGA and (b) using GGA + U. The partial DOS contribution from W and Co are shown.
TABLE V. DFT calculated lattice constants and bandgap values (spin-up) using GGA and GGA + U methods.
TABLE VI. Magnetic moment (μ B) of the (BaxSr1−x)2CoWO6 compounds. The interstitial presents the moment of interstitial electrons between atomic spheres.
B. Reference XRD pattern
Examples of reference patterns, namely the tetragonal (Ba0.2Sr0.8)2CoWO6 and the cubic (Ba0.7Sr0.3)2CoWO6, are given in Tables VII and VIII, respectively. In these patterns, the symbols “M” refers to peaks containing contributions from two reflections. The particular peak that has the strongest intensity in the entire pattern is assigned an intensity of 999 and other lines are scaled relative to this value. In general, the d-spacing values are calculated values from refined lattice parameters. The intensity values reported are integrated intensities (rather than peak heights) based on the corresponding profile parameters, as reported in Table I. For resolved overlapped peaks, intensity-weighted calculated d-spacing, along with the observed integrated intensity and the hkl indices of both peaks (for “M”) are used. For peaks that are not resolved at the instrumental resolution, the intensity-weighted average d-spacing and the summed integrated intensity value are used. In the case of a cluster, unconstrained profile fits often reveal the presence of multiple peaks, even when they are closer than the instrumental resolution. In this situation, both d-spacing and intensity values are reported independently. The (BaxSr1−x)2CoWO6 (x = 0.1, 0.2, 0.3, 0.5, 0.7, and 0.9) patterns have been submitted for inclusion in the PDF.
TABLE VII. X-ray powder pattern for (Ba0.2Sr0.8)2CoWO6, tetragonal I4/m (No. 74) (a = 5.62305(11) Å, c = 7.9847(2) Å, V = 252.466(13) Å3, and Z = 2).
The symbols “M” refers to peaks containing contributions from two reflections. The particular peak that has the strongest intensity in the entire pattern is assigned an intensity of 999 and other lines are scaled relative to this value. The d-spacing values are calculated values from refined lattice parameters, and “I” represents integrated intensity values.
TABLE VIII. X-ray powder pattern for (Ba0.7Sr0.3)2CoWO6, cubic Fm 
$\bar{3}$m (No. 225) (Z = 4, a = 8.02004(11) Å, and V = 515.86(2) Å3).
The symbols “M” refers to peaks containing contributions from two reflections. The particular peak that has the strongest intensity in the entire pattern is assigned an intensity of 999 and other lines are scaled relative to this value. The d-spacing values are calculated values from refined lattice parameters, and “I” represents integrated intensity values.
IV. SUMMARY
Crystal structures and reference patterns of the (BaxSr1−x)2CoWO6 (x = 0.1, 0.2, 0.3, 0.5, 0.7, and 0.9) series of compounds have been determined and submitted to the PDF. (BaxSr1−x)2CoWO6 adopts a double-perovskite structure. From x = 0–0.2, the structure is tetragonal with space group I4/m, whereas when x ≥ 0.3 the structure is cubic with a space group of Fm 
$\bar{3}$m. The alternating CoO6 and WO6 octahedra were found to tilt in an antiphase fashion, corresponding to the a 0a 0c − Glazer's notation for the 1:1 ordering of double perovskites, consistent with the space group I4/m. All Ba sites have 12-fold coordination environment and all the ordered W and Co sites are sixfold (octahedral) coordinated. The BVS values for the Ba sites are all greater than the ideal value of 2.0 in both the tetragonal and cubic cases, indicating over-bonding situation, or compressive coordination environment. DFT calculations concluded that with the addition of Hubbard potential on d-electrons the solid solution formation increases the bandgap width as compared to the end members, namely bandgap values of 2.43, 2.69, and 2.36 eV for Sr2CoWO6, SrBaCoWO6, and Ba2CoWO6, respectively. Furthermore, while Sr2CoWO6 is a semiconductor, SrBaCoWO6 and Ba2CoWO6 are half-metals.
SUPPLEMENTARY MATERIAL
The supplementary material for this article can be found at https://doi.org10.1017/S0885715620000342.
ACKNOWLEDGEMENT
ICDD is acknowledged for the Grants-in-Aid assistance for the project. Grant No. 0903, Grant holder James A. Kaduk.
