INTRODUCTION
Increasing the rate of inflation causes nominal interest rates to increase. In response, agents attempt to substitute away from non-interest-bearing monetary assets, which causes the price level to increase and real monetary asset stocks to decline. This idea underlies a long line of research on the welfare cost of inflation. Lucas (2000) estimates the welfare cost of inflation in a general-equilibrium money-in-the-utility-function model, where money is non-interest-bearing. In that model, steady-state consumption is invariant to inflation and the real stock of money is inversely related to the rate of inflation in steady state. The welfare cost of inflation is expressed as the percentage increase in steady-state consumption needed to offset the utility loss caused by inflation.1
Lucas (2000) finds that the estimated welfare cost of inflation is approximately the area under the inverse money demand function, which establishes the connection to the classic literature going back to Bailey (1956). This connection is also present in the shopping-time approach developed by Lucas (2000, Sect. 5). See Simonsen and Cysne (2001) for an upper bound on the difference between the classic and the general equilibrium estimates.
Gillman (
1993), Dotsey and Ireland (
1996), Marquis (
1999), Bali (
2000), Simonsen and Cysne (
2001), and Cysne (
2003) investigate the welfare cost of inflation in alternative models.
2 Simonsen and Cysne (2001) extend a shopping-time-model to include both currency and interest-bearing deposits. They derive upper and lower bounds for the welfare cost of inflation, assuming that the bank spread on demand deposits is constant. Cysne (2003) extends these results to the case in which the spreads on different deposits are allowed to vary with inflation. Simonsen and Cysne (2001) do not calibrate the model or provide estimates of the welfare costs of inflation. Marquis (1999) calibrates a general equilibrium model of the Japanese economy and highlights the significance of financial intermediation in lowering the welfare costs of inflation.
Lucas (2000) estimates the welfare cost of inflation, assuming that all assets in M1 are non-interest-bearing. He finds that estimated demand functions for simple sum M1 perform poorly in the 1990's and suggests that M1 is too narrow for this period. To resolve the problem, Lucas suggests using Divisia indexes to measure the flow of monetary services, following Barnett (1978, 1980). The user cost of an interest-bearing monetary asset is the discounted spread between the rate of return on an alternative asset and the own rate on the asset. The growth rate of a Divisia quantity index is a weighted average of the growth rates of the components, where the weights are the expenditure shares of the components.
The purpose of this paper is to incorporate interest-bearing monetary assets into the money-in-the-utility-function model and to derive estimates of the welfare cost of inflation that can be compared to estimates from similar models containing only non-interest-bearing money. In our model, households derive utility from consumer goods, real currency stocks, and financial services. Goods and financial services are each produced by profit-maximizing firms. We equate financial services with an aggregate of interest-bearing monetary assets (deposits), and we assume that monetary assets are weakly separable from consumer goods. We assume that all deposits are interest bearing and we calibrate the model using Divisia indexes at the M1 and MZM levels of aggregation. Divisia indexes for the United States usually have been based on the assumption that some or all demand deposits in M1 earn implicit interest.3
Barnett and Spindt (1982), Farr and Johnson (1985), and Thornton and Yue (1992) assumed that household demand deposits were non-interest-bearing, but assumed that business-demand deposits earned a fully competitive implicit interest derived by Klein (1974). Thornton and Yue (1992) indicate that business-demand deposits were approximately two-thirds of the total in 1990. Anderson et al. (1997) assume that all demand deposits earn an implicit return based on Startz (1979). It is responsive to market rates, but is not fully competitive.
In addition, M1 includes interest-bearing checkable deposits, which expanded throughout the 1980's. MZM includes all components of M2, except for small-denomination time deposits.
We find that the welfare cost of inflation is substantially lower in models with interest-bearing deposits than in models that assume all monetary assets are non-interest-bearing. This property results from several key assumptions: demand deposits are assumed to earn implicit interest, production is constant returns to scale, and banks do not hold reserves. If some demand deposits do not earn implicit interest or if the implicit interest rate is not fully competitive, then we would obtain higher welfare cost estimates. If production in the financial sector is not constant returns to scale or, if banks hold reserves, then the user costs of interest-bearing deposits could be affected by inflation. We provide an empirical analysis of the relationship between user costs of deposits and inflation in OECD countries that did not experience high inflation. We find some evidence for a small positive impact of inflation on the user cost of deposits. This consideration, which could be even more important for high-inflation countries that are not considered in our analysis, would lead to higher estimated welfare costs of inflation. Thus, we interpret our results as being conservative estimates of the welfare cost of inflation for low-to moderate-inflation countries, which can be compared and contrasted with higher estimates in the literature.
Our results are consistent with other recent research. Cysne (2003) shows that under some assumptions a Divisia monetary services index provides a reasonable approximation of the welfare cost of inflation in a shopping-time-model. He also derives sufficient conditions under which the welfare cost measure is very close to the area under the inverse demand for the monetary base. Thus, he argues that welfare cost estimates based on the assumption that M1 is entirely non-interest-bearing will be overstated by a factor of three, which is the monetary base multiplier for M1 in the United States. Bali (2000) finds that ignoring the distinction between currency and deposits in M1 leads to overstatement of the welfare cost of inflation by a factor of three in an empirical study. We compare our welfare cost estimates derived from Divisia M1 and MZM to estimates derived from the monetary base, which is equivalent to the currency stock in our model. We find that the estimates derived from the monetary base are similar to one type of estimate from our model.
We calculate welfare cost estimates using the steady state of the model. Because our model incorporates capital, we can also use it to analyze the transition path. Fischer (1979) and Asako (1983) showed that inflation could affect the rate of convergence to steady state in money-in-the-utility-function models. We use a simplified version of our model to determine the importance of such an effect. We find that changes in inflation can increase or decrease the rate of convergence, depending on the coefficient of relative risk aversion. The effect is found to be weak, however, implying that steady-state welfare costs are of primary interest.
In Section 2, we describe the model; in Section 3, we calibrate the model and estimate the welfare cost of inflation; in Section 4, we determine the impact of inflation on the rate of convergence; in Section 5, we provide empirical evidence on the relationship between the user cost of deposits and inflation; in Section 6, we discuss directions for further research; and in Section 7, we conclude.
MONEY-IN-THE-UTILITY-FUNCTION MODEL
The model consists of three agents: a utility maximizing household, and two profit maximizing firms.
Utility Maximizing Household
The household maximizes lifetime utility as a function of goods, c, real currency, m, and financial services, d. Real currency is m=M/p, where p is the price of goods and M is the nominal stock of currency. The household maximizes lifetime utility
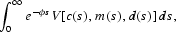
subject to flow budget constraints of the form
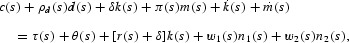
where ρd(s) is the relative price of financial services; k(s) is capital stock; δ is the rate of depreciation;
is the rate of inflation; τ(s) is the real value of a transfer of currency; r(s)+δ is the real user cost of capital; ni(s) is labor supplied to sector i=1, 2; wi(s) is the real wage in sector i; and θ(s) is real dividend income from both sectors.
The household rents capital to the two sectors at real rental price r(s)+δ. Capital rented to each sector is denoted by ki(s), so that k1(s)+k2(s)=k(s). It also inelasticly supplies one unit of labor, which is divided between both sectors so that n1+n2=1. Total labor income is ω(s)=w1(s)n1(s)+w2(s)n2(s). Interior solutions require that wages in both sectors be equal. If they are not, then all labor is supplied to the high-wage sector. In either case, ω(s)=max{w1(s), w2(s)}.
Let a=k+m and substitute it into the budget constraint to get the following:
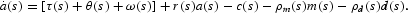
The real user cost of currency, ρm(s), equals r(s)+π(s). The decision is equivalent to one in which d is the real stock of a deposit that earns nominal interest rate id(s). In this case, a=k+m+d and the real user cost of deposits, ρd(s), equals r(s)+π(s)−id(s).
Assuming V is differentiable and quasi concave and assuming an interior solution, optimality implies the following conditions:
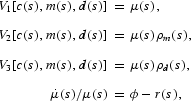
where μ is the costate variable for the current-value Hamiltonian. We also impose the transversality condition,
.
Goods Producers
The goods producer hires labor, n1(s), and rents capital, k1(s). We assume that the production function, y=f(n1, k1), is concave, homogenous of degree one in labor and capital, and satisfies Inada conditions. The firm maximizes instantaneous profits:
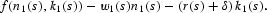
The necessary conditions for optimality are as follows:
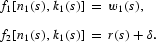
The resource constraint derived from this sector is
.
Financial Services Producers
The financial firm hires labor, n2(s), and rents capital, k2(s), to produce financial services. We assume labor and capital are transformed into financial services by a production function, d=h(n2, k2).
4 See King and Plosser (1984) and Barnett (1987) for interpretations.
The production function is assumed to be concave, to be homogeneous of degree one in capital and labor, and to satisfy Inada conditions. The financial firm maximizes instantaneous profits: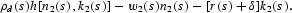
The necessary conditions for optimality are as follows:
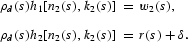
The instantaneous profits from both sectors are paid to the household as dividend income, θ(s).
Steady State
We assume there is no growth in population or productivity for simplicity. We also assume that τ(s)=σm(s), where
is constant. The growth rate of the real stock of currency is
. These equations and the optimality conditions imply the following steady-state conditions (denoted by an asterisk):
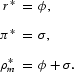
If n*1 and n*2 are nonzero, then wages in the two sectors must be equal. Profit maximization and wage equalization yield the steady-state conditions
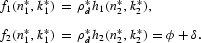
The resource constraints yield the steady-state conditions
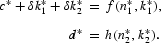
Linear homogeneity of the production functions in capital and labor implies that we can rewrite the conditions in terms of the capital-labor ratios, z*i=k*i/n*i. Dividend income is zero because of constant returns to scale. We also eliminate n*1 using the condition n*1+n*2=1. The resulting steady-state conditions are as follows:
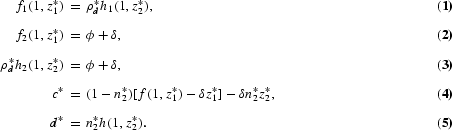
The household optimality conditions evaluated in steady state are as follows:
Equations (1)–(8) determine the steady-state values of z*1, z*2, ρ*d, c*, m*, μ*, n*2.
The capital-labor ratios and the relative price of financial services do not depend on inflation in steady state because z*1, z*2, and ρ*d are determined by (1)–(3), which do not contain σ. We can differentiate the other equations, (4)–(8), with respect σ to produce a system of equations. The solution to this system can be used to determine the impact of inflation on the other steady-state variables. The impact can be summarized in terms of ∂m*/∂σ and ∂n*2/∂σ. It is not possible to determine the signs of these partial derivatives, however, without additional assumptions.
In the next section, we make assumptions that imply ∂m*/∂σ<0. Optimization implies that the marginal rate of substitution between financial services and goods, V3/V1, equals the relative price, ρd. If m* adjusts in response to a change in σ, then this marginal rate of substitution will change in steady state. This causes c* and d* to adjust, because ρ*d is invariant to inflation. The adjustment in c* and d* must be in opposite directions because labor supply is inelastic in the model. The signs of ∂c*/∂σ and ∂d*/∂σ cannot be determined, however, without additional assumptions. The sign of ∂n*2/∂σ is positive if labor is reallocated toward the financial sector in response to higher inflation and negative if it is reallocated toward the goods-producing sector.
WELFARE COST OF INFLATION
Lucas (2000) expresses the welfare cost of inflation as the proportion by which steady-state consumption would have to increase to offset the utility loss caused by increasing the rate of inflation from a benchmark rate. In our model, the welfare cost function, λ(σ, σB), is defined implicitly from the following equation:
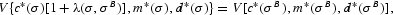
where c*, m*, and d* are functions of σ. Welfare costs are computed relative to a benchmark inflation rate, σB. To calibrate the model, we interpret d as an aggregate of interest-bearing monetary assets and ρd as the corresponding dual price aggregate. We refer to d as deposits for the remainder of the paper.
Functional Forms
We assume that currency and deposits are homogeneously weakly separable from consumer goods. The utility function has the form V(c, m, d)=U[c, g(m, d)], where g is linearly homogeneous.
5 See Barnett (1980, 1987), Barnett and Serletis (2000), or Anderson et al. (1997) for more discussion of monetary aggregation theory.
Weak separability and linear homogeneity imply that
g(
m,
d) evaluated at the optimum is a monetary quantity aggregate. We assume that the subutility function is CES:
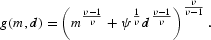
The dual price aggregate is the unit expenditure function, which has the form
Under these assumptions, the household can be viewed as making a two-stage decision. In the first stage, the household maximizes lifetime utility,
subject to flow budget constraints of the form
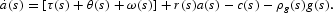
The solution to the first stage produces optimal values of the monetary aggregate. In the second stage, the household minimizes expenditure on m and d, subject to the constraint that g(m, d) equals the optimal value of the monetary aggregate determined from the first stage.
The function U determines the relationship between consumption and the monetary aggregate. Following Lucas (2000), we assume that U has the form
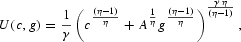
where γ<1. Under this assumption, the optimal control solution implies
Finally, we assume that production in both sectors is constant returns to scale and Cobb-Douglas:
Calibration
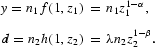
The steady-state values z*1, z*2, ρ*d, c*, m*, d* for these functional forms are as follows:
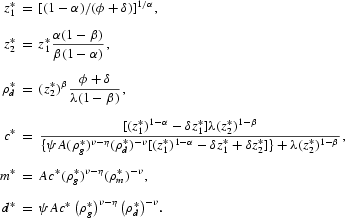
The steady state does not depend on γ. We set ϕ=0.0545, which is determined from an annual discount factor in Cooley and Prescott (1995). Labor's share of income is set to the same value in both sectors: α=β=0.6. We set the depreciation rate equal to δ=0.079, which determines the ratio of investment to capital stock in steady state.6
The ratio of annual investment to capital stock produced by the model in Cooley and Prescott (1995) is 0.076. We treat this value as the annual depreciation rate and convert it to continuous time. The assumption that α=β implies that the depreciation rate does not affect the welfare cost estimates presented in this section.
We obtained data for stocks and user costs of U.S. monetary assets from the Federal Reserve Bank of St. Louis. Anderson et al. (1997) describe the data set. We computed Divisia quantity indexes and dual price indexes for all components of M1 and MZM except currency for 1959–2000 using these data.
7 We add traveler's checks to currency. Let (d1, …, dn) be a vector of n interest-bearing monetary assets and ρd1, …, ρdn be the corresponding vector of user costs. The assumption that d is an aggregate of these interest-bearing assets is equivalent to assuming the utility function has the form V(c, m, d1, …, dn)=U{c, g[m, d(d1, …, dn)]}, where d is a linearly homogeneous subutility function.
These indexes include demand deposits and OCD for M1 and, in addition, savings deposits, MMDA, and noninstitutional money market mutual funds for MZM. We use these indexes along with currency and its user cost to estimate a linearly homogeneous CES demand system. The expenditure share for currency is as follows:
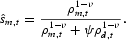
In the demand-system estimation, we assume that the observed share is generated by
, where ut=ρut−1+εt and εt is a zero-mean i.i.d. normal process. We assume a distribution for the initial point, u1, that ensures stationarity [see Pollack and Wales (1992)]. We set ψ and ν equal to their maximum likelihood estimates.
8 In the estimation, we substitute ν=1/(1−b) and impose |ρ|<0.99, b<0.95, and ψ>0. We also estimated the demand system using a generalized first-difference method that does not impose stationarity, which produced similar estimates of the elasticity of substitution for both M1 and MZM.
Divisia monetary services indexes (MSI) for the United States at the M1 and MZM levels of aggregation are available from the Federal Reserve Bank of St. Louis. We measure consumption as the nondurable and service components of PCE. Let Ratio denote the natural logarithm of the nominal MSI quantity index divided by nominal consumption. Let Dual denote the natural logarithm of the real MSI price index. We calibrate η using two methods. First, we calibrate it by regressing Ratio against a constant and Dual. The residuals of the regression are highly serially correlated and the regression equations overpredict Ratio for both Divisia M1 and MZM throughout the 1990's, which is similar to the results in Lucas (2000) for simple-sum M1. Second, we calibrate it by computing the long-run derivative (LRD) of Ratio with respect to Dual, using the formulas of Fischer and Seater (1993). We assume that both series are I(1) in the LRD calculations.9
We set the lag length of the regressions used to calculate the LRD by minimizing AIC for 1–12 quarterly lags.
The steady-state expenditure share of the monetary aggregate, s*g, is determined from (9) as follows:
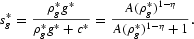
The inflation rate, σ, used to compute the steady-state user cost of currency is the average annual rate of inflation in the United States from 1959 to 2000 converted to continuous time, σ=0.0411.
10 The rate of inflation is calculated from a price index for the nondurable and service components of PCE.
We set
A so that
s*
g equals the average expenditure share for the MSI relative to total expenditure on consumption and MSI, during 1959–2000. The average shares are 0.0178 for M1 and 0.0336 for MZM, which are calculated using the nondurable and service components of PCE.
The steady-state share of currency within the monetary portfolio, s*m, is given by the following equation:
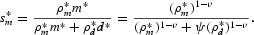
We set λ so that s*m equals the average expenditure share of currency relative to total MSI expenditure for our data during 1959–2000. The average shares are 0.38 for M1 and 0.20 for MZM.
11 This is equivalent to choosing units for d and ρd. The deposit aggregate used in the demand system estimation is an index number, which can be scaled arbitrarily. The value of λ is chosen so that the scaling of deposits in the model is consistent with the data.
The values of the calibrated parameters that depend on the level of monetary aggregation are reported in the notes to
Tables 1 and
2.
We also calibrated the model under the assumption that all money is non-interest-bearing, by restricting ψ=0. Under this restriction, n*1=1, d*=0, c*=(z*1)1−α−δz*1, and the steady-state relationship between money and consumption is as follows:
Steady-state consumption is invariant to the rate of inflation in the restricted model, in contrast to the model with interest-bearing deposits. The reason is that all money is assumed to be currency, which is not produced using labor and capital. The parameters α, ϕ, δ,and η are calibrated as described previously. We set A using the expenditure share of either currency or the simple-sum monetary aggregates as described below.
Model with Interest-Bearing Deposits
We calculated welfare costs numerically for zero to 20% inflation, using zero as the benchmark.12
This assumes banks are able to offer interest-bearing deposits in a steady state with no inflation.
We report various welfare cost estimates for inflation rates between 1% and 5%, 10%, 15%, and 20% in Tables
1 and
2. The estimates for the M1 level of aggregation are in
Table 1A (regression estimate of η) and Table
1B (LRD estimate of η). The corresponding estimates for the MZM level of aggregation are presented in
Tables 2A and
2B.
Changing the rate of inflation has two effects in our model. Higher inflation causes the steady-state price of money, ρ*g, to increase. The money demand function implies that g*/c* decreases in response, causing utility to decline holding c* constant. The higher the value of η, the more g*/c* decreases in response to higher inflation.
Steady-state consumption, c*, is also affected by inflation. Using our functional forms, the sign of ∂c*/∂σ is the same as the sign of η−ν, where ν is the elasticity of substitution between currency and deposits. If ν is zero, then an increase in σ causes both m* and d* to decrease. Labor is reallocated from the financial sector to the goods-producing sector, implying that consumption increases in steady state. The negative effect of σ on d* diminishes as the elasticity of substitution increases. If ν>η, then the effects on c* and d* are reversed.
In each table, Cost 1 is the welfare cost of inflation as a percentage of steady-state consumption, λ(σ, σB) multiplied by 100. This welfare cost measure accounts for the effects of inflation on both c* and g*/c*. The estimates do not differ much across level of aggregation. If we estimate the price elasticity of money demand by LRD, then the welfare cost of increasing steady-state inflation from 0% to 20% is equivalent to 0.192% of steady-state consumption for M1 and 0.177% for MZM. The welfare cost estimates are approximately doubled in both cases if we estimate the price elasticity of money demand by regression.
Lucas (2000) proves that the welfare cost of inflation is approximately equal to the area under the inverse money demand function if steady-state consumption is invariant to inflation. The argument in Lucas (2000) applied to our model produces the welfare cost expression
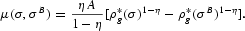
In each table, Cost 2 is μ(σ, σB) multiplied by 100. The difference between the two welfare cost expressions is approximately the percentage change in steady-state consumption from the benchmark
Cost 2 is higher than Cost 1 in our calibrations, which is due to the fact that ν is less than η, implying that ∂c*/∂σ<0.
If we estimate the price elasticity of money demand by LRD, then Cost 2 for 20% inflation is 0.341% for M1 and 0.208% for MZM. In the case of MZM, the elasticity of substitution, ν, is close to η, implying that Cost 1 and Cost 2 are very similar. The difference between Cost 1 and 2 is more substantial if the price elasticity of money demand is estimated by regression. In this case, the welfare cost estimates are similar for M1 and MZM, with the cost of 20% inflation being 0.735% for M1 and 0.782% for MZM. Cost 2 is higher for the regression-based estimates than for the LRD-based estimates, because the demand functions for M1 and MZM are more price elastic when estimated by regression.
Restricted Model
Cost 3 and Cost 4 are welfare cost estimates for the restricted models, which contain only non-interest-bearing money. In the restricted models, d*=0 implying that g*=m* and ρ*g=ρ*m. The steady-state expenditure share of money in the restricted model can, therefore, be determined from (10) as follows:
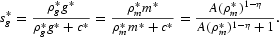
Cost 3 is calibrated by setting A so that s*g equals the average expenditure share of currency relative to total expenditure on currency and consumption, during 1959–2000. The average share is 0.0067 for our data. Cost 4 is calibrated by setting A so that the expenditure share equals 0.0245 for M1 and 0.0569 for MZM. These are the average expenditure shares for the simple-sum aggregates, which are computed under the assumption that all components of the aggregates are non-interest-bearing.
Cost 4 is similar to the welfare cost estimates for the United States presented by Lucas (2000). The main difference is that Lucas calculated the expenditure share of simple-sum M1 relative to GDP, whereas we calculate expenditure shares relative to consumption.13
There are several other minor differences. Lucas assumes an interest rate of 3% under zero inflation and he incorporates population and productivity growth into the model.
Costs 3 and 4 can both be directly compared to Cost 2 because steady-state consumption does not depend on the rate of inflation in the restricted model. The welfare cost of inflation is, therefore, approximately equal to the area under the inverse money demand function.
14 Thus, λ(σ, σB) and μ(σ, σB) are numerically very close for the restricted models. We report λ(σ, σB) in the tables.
Cost 3 is very similar to Cost 2, corroborating similar findings for a shopping-time model in Cysne (2003). The relationship between the two welfare cost estimates can be explained in terms of aggregation theory. Cost 3 treats the real currency stock as a monetary quantity aggregate and it treats the user cost of currency as its dual price aggregate. If subutility is Leontief, g(m, d)=min{m, μd}, then μd=m at the optimum. Consequently, the quantity aggregate is m and the dual price aggregate is ρLg=ρm+ρd/μ. Cost 2 differs from Cost 3 because the elasticity of substitution between currency and deposits is assumed to be positive and it is based on the dual price aggregate. Figure 1 displays graphs of Costs 1–3 in the four cases. In the figure, Cost 2 is a solid curve and Costs 1 and 3 are both dashed. Cost 1 is the lowest of the three in all four cases.
Welfare cost functions, Costs 1–3. Note: Cost 2 is a solid curve and Cost 1 is lower dashed curve.
Cost 4 is substantially higher than Costs 1–3. Cost 4 assumes that all monetary assets are non-interest-bearing, whereas Costs 1 and 2 assume all deposits are interest-bearing and Cost 3 eliminates deposits from the model. The welfare cost of 20% inflation is 2.5% in Table 1A for Cost 4. The assumption that MZM is entirely non-interest-bearing is not reasonable and results in very high estimates in Table 2A. The ratio of Cost 4 to Cost 3 is approximately the average of the ratio of the simple-sum aggregate to currency during our sample period. These results corroborate similar findings in the literature. Cysne (2003) argues on theoretical grounds that welfare cost estimates for M1 (using an estimate comparable to Cost 4) would overstate the true welfare cost of inflation by a factor of approximately three, which is the monetary base multiplier for M1. Bali (2000) presents comparable empirical estimates. The interpretation of our results is the same, but we do not incorporate reserves in the model. Thus, currency and monetary base are equivalent in our model. The ratio of Cost 4 to Cost 3 is much higher for MZM than for M1 because the average ratio of simple-sum MZM to currency is much higher.
INFLATION AND TRANSITION DYNAMICS
The steady-state capital stock is invariant to inflation in our model, but capital accumulation can be affected by inflation on the transition path. Fischer (1979) showed that increasing the rate of inflation in a Sidrauski model could lead to an increase in the rate of capital accumulation along the transition path using a particular utility function for consumption and non-interest-bearing money. Asako (1983) showed that the opposite could occur for some values of the coefficient of relative risk aversion using a different utility function. We consider the same issue in a simplified version of our model.
We simplify the model by assuming that the subutility function is Leontief: g(m, d)=min{m, μd}. Under this assumption, the monetary quantity aggregate is g=m and the dual price aggregate is ρgL=ρm+ρd/μ. The simplification allows us to eliminate deposits, using the optimality condition d=m/μ. We assume that the factor shares in the two sectors are equal. This along with wage equalization implies that the two capital-labor ratios are the same along the transition path. It also implies that the user cost of deposits is constant along the transition path and equals 1/λ. In all other respects, the model is the same as in Section 3. We eliminate n2 from the system using the production function for the financial sector and linearize around the steady state to produce the following system:
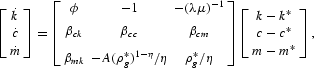
where
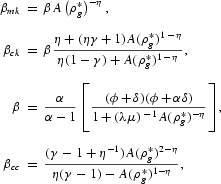
and
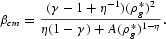
The steady-state price of money is ρ*g=ϕ+σ+(μλ)−1. The Jacobian has positive trace and negative determinant for all permissible parameter values, implying saddlepath stability. Let
be the unique negative eigenvalue.
If μ→∞ and η=1, then (in the limit) the equations are equivalent to those of Fischer (1979) under Cobb-Douglas production, which were derived from a model containing only non-interest-bearing money. Fischer proved that in this case
as long as γ≠0 (if γ=0, then
, meaning that the system converges to steady state more rapidly as the steady state rate of inflation increases. Similarly, if γ=0 in our model, then we obtain an explicit formula for
that does not contain σ.15
If γ=0, then
, where ξ=[α(ϕ+δ)(ϕ+αδ)]/(1−α).
We calculated the stable eigenvalue numerically to determine the quantitative effects of inflation on the rate of convergence to steady state. We varied inflation from 1% to 10% and we let γ take the following values: −9.0, −1.0, −0.1, 0.1, and 0.9. We calibrated the model based on M1. We set η=0.57 and λ=15.46 to match Table 1A. We set μ so that the steady-state expenditure share of currency within the monetary portfolio is 0.38. A is set so that the steady-state expenditure share of the monetary aggregate is 0.0178. The results are presented in Table 3A.
We also calculated the stable eigenvalue for the version of the model corresponding to Fischer (1979). The results for this model are presented in Table 3B.
The main determinant of the stable eigenvalue in both tables is γ. As γ moves from 0.9 to −9.0, the stable eigenvalue approaches zero from below. The results in Table 3A indicate that steady-state inflation can affect the stable eigenvalue in either direction, depending on the value of γ, but the effect is quantitatively weak. If γ>0, then higher inflation rates lead to higher absolute values of the stable eigenvalue,
. If γ<0, then the effect is reversed. For comparison with a similar theoretical result, see Asako (1983).
The results in Table 3B are consistent with Fischer's theoretical result. Higher inflation rates lead to higher absolute values of the stable eigenvalue,
, for all γ≠0. The effect on the stable eigenvalue is again weak, however.
We conclude that moderately high inflation rates do not seem to have quantitatively significant effects on the rate of convergence to steady state in either model.
EMPIRICAL ANALYSIS
Taking into consideration the fact that interest-bearing deposits are used for transaction purposes leads to lower estimates of the welfare cost of inflation in steady state than would have been obtained, had we assumed that all deposits are non-interest-bearing. In our model, the steady-state user cost of deposits is invariant to the rate of inflation. If the user cost of deposits is positively related to inflation, then the welfare cost of inflation will be higher than we have estimated. In this sense, our model provides a lower bound on the welfare cost, whereas a model that assumes all deposits are non-interest-bearing provides an upper bound.
In this section, we provide cross-country empirical results on the relationship between user costs of deposits and inflation. The framework of our theoretical model may not be reasonable for analyzing countries that have relatively undeveloped financial sectors. In addition, recent empirical research points out that high rates of inflation can negatively impact financial depth.16
While we think this statement is reasonable for many countries, there are some exceptions. For example, Brazil in the 1980's managed to develop a very sophisticated indexation of its financial assets, and inflation did not severely impact financial depth using conventional measures. More importantly, the opportunity cost of interest-bearing deposits was an increasing function of the rate of inflation. This is a case in which the results in our paper should be taken with caution.
Therefore, we consider only OECD countries that experienced low to moderately high levels of inflation.
Data Description
We obtained data for the annual percentage change of CPI (inf), the annual rate paid by commercial or similar banks on demand, time, and savings deposits (rdep), and the annual rate charged by banks on loans to prime customers (rlend) from the World Development Indicator database. We treat rlend as the benchmark rate and approximate the real user cost of deposits in discrete time as uc=(rlend−rdep)/(1+rlend), following Barnett (1978). The data are annual and span the period 1960–1999, with some missing observations. We eliminated Mexico, Poland, Turkey, and Iceland because they experienced sustained high rates of inflation during some parts of the sample period. We also eliminated the Czech Republic and the Slovak Republic because few observations were available, leaving us with an unbalanced panel of 24 countries for 1960–1999.
Empirical Results
We regressed rlend, rdep, and uc against inf with country and time-fixed effects, assuming i.i.d. residuals. The results are presented in Table 4A. In the table, β is the estimated regression coefficient on inf. The regression of rdep and rlend against inf indicate that β is positive and significant in both cases. The values of β also indicate that neither rate is fully responsive to inflation. In the regressions of uc against inf, we found that β was not significantly different from zero at the 10% level.
Figures 2 and 3 present scattergraphs of rlend and rdep, respectively, against inflation with the fixed effects removed from the interest rates. Figure 2 suggests that rlend might be more responsive to inf at lower inflation rates. To explore this possibility, we deleted all observations for which inf<10% and reran the regressions. These results are presented in Table 4B. These regressions produced higher estimates of β for the regression of rlend against inf, and the coefficient on rlend is higher than the one on rdep. This suggests that inflation has a positive effect on user costs, which is confirmed by the regression of uc against inf. The coefficient estimate for this regression, β=0.07, seems reasonable and is statistically significant at the 10% level.
Lending rate and inflation fixed effects removed.
Deposit rate and inflation fixed effects removed.
We conclude that neither lending nor deposit rates fully respond to changes in inflation in our sample. Our findings suggest that there could be a small positive effect of inflation on the user cost of deposits for some OECD countries.
FURTHER DIRECTIONS
In our model, deposits are interest bearing and the user cost of deposits is invariant to inflation in steady state. This implies that welfare costs of inflation are low and do not vary much across the level of monetary aggregation. The welfare cost of inflation will be higher, however, if inflation has a positive effect on the user cost of some types of deposits. We provided cross-country empirical evidence suggesting that this might be the case for some countries with low to moderately high inflation rates and the effect could potentially be stronger in high-inflation countries, which we did not consider in our analysis. A positive effect could be due to such factors as scale effects in financial production, regulation, and reserve holding. The model presented in this paper could be extended to account for these factors and to determine their impact on the estimated welfare cost of inflation. In this section, we briefly highlight two potential directions for further research.
The first direction involves demand deposits. Lucas (2000) calculated the welfare cost of inflation for the United States under the assumption that all checkable deposits in M1 are non-interest-bearing. We account for the interest-bearing assets in M1 and MZM, assuming that demand deposits earn implicit interest at competitive rates. Our model could be extended to treat demand deposits as a separate output of the financial sector. We could then evaluate the impact of alternative assumptions about demand deposits on the estimated welfare costs of inflation. The estimated welfare cost of inflation would be higher if demand deposits were not assumed to earn implicit interest, because the expenditure share of non-interest-bearing money would be greater than in our calibrations. Alternatively, we could assume that demand deposits earn implicit interest, but that the implicit return is not fully competitive. In this case, the user cost of demand deposits would be positively related to inflation, which would also lead to higher estimated welfare costs.17
The expenditure share on demand deposits in MZM has declined steadily over the past two decades from a decade average of 0.20 in the 1980's to an average of 0.12 in the 1990's, using Federal Reserve Bank of St. Louis data. This suggests that the issues raised by demand deposits are becoming less important over time. See note 3 for additional references regarding demand deposits and monetary aggregation.
A second direction involves reserve holding. If financial firms hold required reserves, then the profit function for the financial sector is
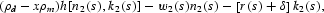
where x is the required reserve rate.
18 See Hancock (1985, 1986), Barnett (1987), and Fixler and Zieschang (1999) for models that incorporate multiple inputs, outputs, and reserves. The supply-side user cost, ρSd=(ρd−xρm), differs from the demand-side user cost, ρd, by an inflation tax. See Barnett et al. (1986) for results regarding this “price wedge.”
In our model, wages and user costs of capital are equalized across sectors, which would imply that (ρ*
d−
xρ*
m) will be invariant to inflation and, therefore, ∂ρ*
d/∂σ=
x. This implies that the steady-state user cost of deposits, ρ*
d, is not invariant to inflation, but it is less responsive to inflation than the user cost of currency. Thus, incorporating reserve requirements into the model would lead to somewhat higher welfare costs of inflation, but they would still be lower than in a model where all deposits are assumed to be non-interest-bearing. We could also incorporate excess reserves into the model by treating them as a factor of production in the financial sector [see Barnett (
1987)]. In this case, a change in inflation would have more complex effects on financial firms and it is difficult to predict, in general, how our conclusions about the welfare cost of inflation might be altered.
CONCLUSION
We generalize a money-in-the-utility-function model to include both currency and interest-bearing deposits that are produced by the financial sector. In the model, the steady-state user cost of interest-bearing deposits is invariant to inflation. We calibrate the model using Divisia indexes and calculate the welfare cost of inflation. We also calculate the welfare cost of inflation in restricted models that contain only non-interest-bearing money.
We produced a range of welfare cost estimates for the model with interest-bearing deposits at both the M1 and MZM levels of monetary aggregation for the United States. The highest estimate we obtained indicated that the welfare cost of increasing inflation from zero to 20% is equivalent to less than 0.8% of steady-state consumption. Lucas (2000) estimated the welfare cost of inflation for the United States assuming that M1 is entirely non-interest-bearing. We produced comparable estimates and found that the welfare cost of increasing inflation from zero to 20% is equivalent to 2.5% of steady-state consumption for the United States.
If our estimates are believed, then the welfare costs of inflation caused by its effects on money demand are not very significant. Feldstein (1996; pp. 5–6) states, “The interaction of inflation and tax rules also causes distortions in the mix of business investment, in corporate finance, and in the structure of individual portfolios. Higher inflation rates may also imply more volatile inflation.” If inflation imposes substantially higher welfare costs on the economy, it is likely to be through one of these alternative channels.
The welfare costs of inflation will be higher if either some deposits are non-interest-bearing or the user costs of some deposits are positively related to inflation, which could be the result of factors such as regulation, scale effects in financial production, and bank reserve holding. We interpret our results as being low welfare cost estimates produced under strong assumptions that can be compared and contrasted with higher welfare cost estimates produced under alternative assumptions.
We thank the Department of Economics at West Virginia University for comments in a seminar delivered there. We also thank an anonymous referee for comments that greatly improved this paper. All remaining errors are our responsibility.
