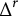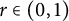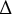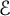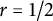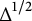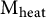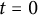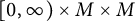1 Introduction
Let
![]() $\operatorname {\Delta }$
be a self-adjoint generalized Laplacian acting on the sections of a Hermitian vector bundle
$\operatorname {\Delta }$
be a self-adjoint generalized Laplacian acting on the sections of a Hermitian vector bundle
![]() $\mathcal {E}$
over an oriented, compact Riemannian manifold M of dimension n. Denote by
$\mathcal {E}$
over an oriented, compact Riemannian manifold M of dimension n. Denote by
![]() $p_t$
the heat kernel of
$p_t$
the heat kernel of
![]() $\operatorname {\Delta }$
, i.e., the Schwartz kernel of the operator
$\operatorname {\Delta }$
, i.e., the Schwartz kernel of the operator
![]() $e^{-t\operatorname {\Delta }}$
. It is known since Minakshisundaram–Pleijel [Reference Minakshisundaram and Pleijel21] that
$e^{-t\operatorname {\Delta }}$
. It is known since Minakshisundaram–Pleijel [Reference Minakshisundaram and Pleijel21] that
![]() $p_t(x,y)$
has an asymptotic expansion as
$p_t(x,y)$
has an asymptotic expansion as
![]() $t\searrow 0$
near the diagonal
$t\searrow 0$
near the diagonal
 $$ \begin{align} p_t(x,y) \stackrel{t \searrow 0}{\sim} t^{-n/2} e^{-\frac{d(x,y)^2}{4t}} \sum_{j=0}^{\infty} t^j \Psi_j (x,y), \end{align} $$
$$ \begin{align} p_t(x,y) \stackrel{t \searrow 0}{\sim} t^{-n/2} e^{-\frac{d(x,y)^2}{4t}} \sum_{j=0}^{\infty} t^j \Psi_j (x,y), \end{align} $$
where
![]() $d(x,y)$
is the geodesic distance between x and y, and the
$d(x,y)$
is the geodesic distance between x and y, and the
![]() $\Psi _j$
’s are recursively defined as solutions of certain ODE’s along geodesics (see, e.g., [Reference Berger, Gauduchon and Mazet4, Reference Berline, Getzler and Vergne5]). This asymptotic expansion applied to
$\Psi _j$
’s are recursively defined as solutions of certain ODE’s along geodesics (see, e.g., [Reference Berger, Gauduchon and Mazet4, Reference Berline, Getzler and Vergne5]). This asymptotic expansion applied to
![]() $\operatorname {D}^*\operatorname {D}$
, where
$\operatorname {D}^*\operatorname {D}$
, where
![]() $\operatorname {D}$
is a twisted Dirac operator, plays a leading role in the heat kernel proofs of the Atiyah–Singer index theorem (see [Reference Berline and Vergne6, Reference Bismut7, Reference Getzler12]).
$\operatorname {D}$
is a twisted Dirac operator, plays a leading role in the heat kernel proofs of the Atiyah–Singer index theorem (see [Reference Berline and Vergne6, Reference Bismut7, Reference Getzler12]).
Bär and Moroianu [Reference Bär and Moroianu2] studied the short-time asymptotic behavior of the heat kernel of
![]() $ \operatorname {\Delta }^{1/m}$
,
$ \operatorname {\Delta }^{1/m}$
,
![]() $m \in {\mathbb N}^*$
, for a strictly positive self-adjoint generalized Laplacian
$m \in {\mathbb N}^*$
, for a strictly positive self-adjoint generalized Laplacian
![]() $\operatorname {\Delta }$
. They give explicit asymptotic formulæ separately in the case when
$\operatorname {\Delta }$
. They give explicit asymptotic formulæ separately in the case when
![]() $t \searrow 0$
along the diagonal
$t \searrow 0$
along the diagonal
![]() $\operatorname {Diag} \subset M \times M$
, and when t goes to
$\operatorname {Diag} \subset M \times M$
, and when t goes to
![]() $0$
in a compact set away from the diagonal. The asymptotic behavior depends on the parity of the dimension n and of the root m. More precisely, logarithmic terms appear when n is odd and m is even. They use the Legendre duplication formula, and the more general Gauss multiplication formula for the
$0$
in a compact set away from the diagonal. The asymptotic behavior depends on the parity of the dimension n and of the root m. More precisely, logarithmic terms appear when n is odd and m is even. They use the Legendre duplication formula, and the more general Gauss multiplication formula for the
![]() $\Gamma $
function (see, e.g., [Reference Paris and Kaminski22]). Another crucial argument in [Reference Bär and Moroianu2] is to use integration by parts in order to show that the Schwartz kernel
$\Gamma $
function (see, e.g., [Reference Paris and Kaminski22]). Another crucial argument in [Reference Bär and Moroianu2] is to use integration by parts in order to show that the Schwartz kernel
![]() $q_{-s}$
of the pseudodifferential operator
$q_{-s}$
of the pseudodifferential operator
![]() $\operatorname {\Delta }^{-s}$
,
$\operatorname {\Delta }^{-s}$
,
![]() $s \in {\mathbb C}$
, defines a meromorphic function when restricted to the diagonal in
$s \in {\mathbb C}$
, defines a meromorphic function when restricted to the diagonal in
![]() $M \times M$
.
$M \times M$
.
1.1 Small-time heat asymptotic for real powers of
 $\operatorname {\Delta }$
$\operatorname {\Delta }$
The purpose of this paper is to study the short-time asymptotic of the Schwartz kernel
![]() $h_t$
of the operator
$h_t$
of the operator
![]() $e^{-t\operatorname {\Delta }^r}$
, where
$e^{-t\operatorname {\Delta }^r}$
, where
![]() $r \in (0,1)$
and
$r \in (0,1)$
and
![]() $\operatorname {\Delta }$
is a non-negative self-adjoint generalized Laplacian, like, for instance,
$\operatorname {\Delta }$
is a non-negative self-adjoint generalized Laplacian, like, for instance,
![]() $\operatorname {\Delta }=\operatorname {D}^*\operatorname {D}$
for a Dirac operator
$\operatorname {\Delta }=\operatorname {D}^*\operatorname {D}$
for a Dirac operator
![]() $\operatorname {D}$
. We give separate formulæ as t goes to
$\operatorname {D}$
. We give separate formulæ as t goes to
![]() $0$
in
$0$
in
![]() $[0, \infty ) \times \operatorname {Diag}$
, and when
$[0, \infty ) \times \operatorname {Diag}$
, and when
![]() $t \searrow 0$
in
$t \searrow 0$
in
![]() $[0,\infty ) \times K$
, where
$[0,\infty ) \times K$
, where
![]() $K \subset M \times M$
is a compact set disjoint from the diagonal. In Theorem 6.1, we obtain that
$K \subset M \times M$
is a compact set disjoint from the diagonal. In Theorem 6.1, we obtain that
![]() ${h_t}_{\vert [0,\infty ) \times K} \in t \cdot {\mathcal C}^{\infty } \left ( [0, \infty ) \times K \right )$
is a smooth function vanishing at least to order
${h_t}_{\vert [0,\infty ) \times K} \in t \cdot {\mathcal C}^{\infty } \left ( [0, \infty ) \times K \right )$
is a smooth function vanishing at least to order
![]() $1$
at
$1$
at
![]() $\{ t=0 \}$
. The asymptotic along the diagonal depends on the parity of n (like in [Reference Bär and Moroianu2]) and on the rationality of r. In Theorem 7.1, the most interesting case occurs when logarithmic terms appear. This happens only if n is odd,
$\{ t=0 \}$
. The asymptotic along the diagonal depends on the parity of n (like in [Reference Bär and Moroianu2]) and on the rationality of r. In Theorem 7.1, the most interesting case occurs when logarithmic terms appear. This happens only if n is odd,
![]() $r=\frac {\alpha }{\beta }$
is rational, and the denominator
$r=\frac {\alpha }{\beta }$
is rational, and the denominator
![]() $\beta $
is even. In that case,
$\beta $
is even. In that case,

Similar expansions are proved in Theorem 7.1 in all the other cases. Furthermore, we prove the non-triviality of the coefficients appearing in the diagonal asymptotics (Theorem 1.1), and also the non-locality of some of them (Theorem 1.3).
In the special case
![]() $r=1/2$
, Bär and Moroianu [Reference Bär and Moroianu2] described the small-time asymptotic behavior of
$r=1/2$
, Bär and Moroianu [Reference Bär and Moroianu2] described the small-time asymptotic behavior of
![]() $h_t$
on the diagonal and away from it separately. In Theorem 1.4, we give an uniform description of the transition between the on- and off-diagonal behavior by proving that the heat kernel of
$h_t$
on the diagonal and away from it separately. In Theorem 1.4, we give an uniform description of the transition between the on- and off-diagonal behavior by proving that the heat kernel of
![]() $\operatorname {\Delta }^{1/2}$
is a polyhomogeneous conormal section in
$\operatorname {\Delta }^{1/2}$
is a polyhomogeneous conormal section in
![]() $\mathcal {E} \boxtimes \mathcal {E}^* $
on the standard blow-up space
$\mathcal {E} \boxtimes \mathcal {E}^* $
on the standard blow-up space
![]() $[[0,\infty )\times M \times M, \{ t=0 \} \times \operatorname {Diag}]$
.
$[[0,\infty )\times M \times M, \{ t=0 \} \times \operatorname {Diag}]$
.
1.2 Comparison to previous results
Fahrenwaldt [Reference Fahrenwaldt11] studied the off-diagonal short-time asymptotics of the heat kernel of
![]() $e^{-t f(P)}$
, where
$e^{-t f(P)}$
, where
![]() $f: [0,\infty ) \longrightarrow [0,\infty )$
is a smooth function with certain properties, and P is a positive self-adjoint generalized Laplacian. The function
$f: [0,\infty ) \longrightarrow [0,\infty )$
is a smooth function with certain properties, and P is a positive self-adjoint generalized Laplacian. The function
![]() $f(x)=x^r$
,
$f(x)=x^r$
,
![]() $r \in (0,1)$
does not satisfy the third condition in [Reference Fahrenwaldt11, Hypothesis 3.3], which seems to be crucial for the arguments and statements in that paper, so the results of [Reference Fahrenwaldt11] do not seem to apply here.
$r \in (0,1)$
does not satisfy the third condition in [Reference Fahrenwaldt11, Hypothesis 3.3], which seems to be crucial for the arguments and statements in that paper, so the results of [Reference Fahrenwaldt11] do not seem to apply here.
Duistermaat and Guillemin [Reference Duistermaat and Guillemin10] give the asymptotic expansion of the heat kernel of
![]() $e^{-tP}$
, where P is a scalar positive elliptic self-adjoint pseudodifferential operator. The order of P in [Reference Duistermaat and Guillemin10] seems to be a positive integer. It is claimed in [Reference Agronovič1] that this asymptotic holds true in the context of fiber bundles. Furthermore, Grubb [Reference Grubb16, Theorem 4.2.2] studied the heat asymptotics for
$e^{-tP}$
, where P is a scalar positive elliptic self-adjoint pseudodifferential operator. The order of P in [Reference Duistermaat and Guillemin10] seems to be a positive integer. It is claimed in [Reference Agronovič1] that this asymptotic holds true in the context of fiber bundles. Furthermore, Grubb [Reference Grubb16, Theorem 4.2.2] studied the heat asymptotics for
![]() $e^{-tP}$
in the context of fiber bundles when the order of P is positive, not necessary an integer. In Theorem 7.1, we obtain the vanishing of some terms appearing in [Reference Grubb16, Corollary 4.2.7] in our particular case when
$e^{-tP}$
in the context of fiber bundles when the order of P is positive, not necessary an integer. In Theorem 7.1, we obtain the vanishing of some terms appearing in [Reference Grubb16, Corollary 4.2.7] in our particular case when
![]() $P=\operatorname {\Delta }^r$
is a real power of a self-adjoint non-negative generalized Laplacian
$P=\operatorname {\Delta }^r$
is a real power of a self-adjoint non-negative generalized Laplacian
![]() $\operatorname {\Delta }$
,
$\operatorname {\Delta }$
,
![]() $r \in (0,1)$
. We also show that the remaining terms do not vanish in general.
$r \in (0,1)$
. We also show that the remaining terms do not vanish in general.
Theorem 1.1 For each
![]() $r \in (0,1)$
, none of the coefficients in the small-time asymptotic expansion of
$r \in (0,1)$
, none of the coefficients in the small-time asymptotic expansion of
![]() $h_t$
appearing in Theorem 7.1 vanishes identically for every generalized Laplacian
$h_t$
appearing in Theorem 7.1 vanishes identically for every generalized Laplacian
![]() $\operatorname {\Delta }$
.
$\operatorname {\Delta }$
.
The logarithmic coefficients
![]() $B_l$
and the coefficients
$B_l$
and the coefficients
![]() $A_j$
for
$A_j$
for
![]() $j \notin {\mathbb Z}$
can be computed in terms of the heat coefficients for
$j \notin {\mathbb Z}$
can be computed in terms of the heat coefficients for
![]() $e^{-t\Delta }$
appearing in (1.1). It is well known that the heat coefficients of a generalized Laplacian are locally computable in terms of the curvature of the connection on
$e^{-t\Delta }$
appearing in (1.1). It is well known that the heat coefficients of a generalized Laplacian are locally computable in terms of the curvature of the connection on
![]() $\mathcal {E}$
, the Riemannian metric of M and their derivatives (see, e.g., [Reference Berline, Getzler and Vergne5]). This is no longer the case for the coefficients of positive integer powers of t from Theorem 7.1 as we shall see now.
$\mathcal {E}$
, the Riemannian metric of M and their derivatives (see, e.g., [Reference Berline, Getzler and Vergne5]). This is no longer the case for the coefficients of positive integer powers of t from Theorem 7.1 as we shall see now.
By applying Theorem 7.1 for
![]() $r \in (0,1)$
and a set of geometric data, namely a hermitic vector bundle
$r \in (0,1)$
and a set of geometric data, namely a hermitic vector bundle
![]() $\mathcal {E}$
over an oriented, compact Riemannian manifold
$\mathcal {E}$
over an oriented, compact Riemannian manifold
![]() $(M,g)$
, a metric connection
$(M,g)$
, a metric connection
![]() $\nabla $
and an endomorphism
$\nabla $
and an endomorphism
![]() $F \in \operatorname {End} \mathcal {E}$
,
$F \in \operatorname {End} \mathcal {E}$
,
![]() $F^*=F$
, we produce an endomorphism
$F^*=F$
, we produce an endomorphism
![]() $A_l \left ( M,g,\mathcal {E},h_{\mathcal {E}},\nabla ,F \right ) \in {\mathcal C}^{\infty } \left ( M, \operatorname {End} \mathcal {E} \right )$
for each index l appearing in (1.2).
$A_l \left ( M,g,\mathcal {E},h_{\mathcal {E}},\nabla ,F \right ) \in {\mathcal C}^{\infty } \left ( M, \operatorname {End} \mathcal {E} \right )$
for each index l appearing in (1.2).
Definition 1.1
-
(i) We say that a function A which associates to any set of geometric data
 $(M,g,\mathcal {E},h_{\mathcal {E}},\nabla , F)$
a section in
$(M,g,\mathcal {E},h_{\mathcal {E}},\nabla , F)$
a section in
 ${\mathcal C}^{\infty }(M,\operatorname {End} \mathcal {E})$
is locally computable if for any two sets of geometric data
${\mathcal C}^{\infty }(M,\operatorname {End} \mathcal {E})$
is locally computable if for any two sets of geometric data
 $(M,g,\mathcal {E},h_{\mathcal {E}},\nabla , F)$
,
$(M,g,\mathcal {E},h_{\mathcal {E}},\nabla , F)$
,
 $(M',g',\mathcal {E}',h_{\mathcal {E}'}, \nabla ', F')$
which agree on an open set (i.e., there exist an isometry
$(M',g',\mathcal {E}',h_{\mathcal {E}'}, \nabla ', F')$
which agree on an open set (i.e., there exist an isometry
 $\alpha : U \longrightarrow U'$
between two open sets
$\alpha : U \longrightarrow U'$
between two open sets
 $U \subset M$
,
$U \subset M$
,
 $U' \subset M'$
, and a metric isomorphism
$U' \subset M'$
, and a metric isomorphism
 $\beta : \mathcal {E}_{\vert _U} \longrightarrow \mathcal {E}^{\prime }_{\vert _{U'}}$
which preserves the connection and
$\beta : \mathcal {E}_{\vert _U} \longrightarrow \mathcal {E}^{\prime }_{\vert _{U'}}$
which preserves the connection and
 $\beta _x \circ F_x \circ \beta _{\alpha (x)}^{-1}=F^{\prime }_{\alpha (x)}$
), we have
$\beta _x \circ F_x \circ \beta _{\alpha (x)}^{-1}=F^{\prime }_{\alpha (x)}$
), we have  $$\begin{align*}\beta_x \circ A_x \circ \beta_{\alpha(x)}^{-1} = A_{\alpha(x)}, \end{align*}$$
$$\begin{align*}\beta_x \circ A_x \circ \beta_{\alpha(x)}^{-1} = A_{\alpha(x)}, \end{align*}$$
for any
 $x \in U$
.
$x \in U$
. -
(ii) A scalar function a defined on the set of all geometric data
 $(M,g,\mathcal {E},h_{\mathcal {E}},\nabla ,F)$
with values in
$(M,g,\mathcal {E},h_{\mathcal {E}},\nabla ,F)$
with values in
 ${\mathbb C}$
is called locally computable if there exists a locally computable function C as in (i) above such that
${\mathbb C}$
is called locally computable if there exists a locally computable function C as in (i) above such that
 $a=\int _M \operatorname {Tr} C \operatorname {dvol}_g$
for any
$a=\int _M \operatorname {Tr} C \operatorname {dvol}_g$
for any
 $\left ( M,g, \mathcal {E}, h_{\mathcal {E}}, \nabla , F \right )$
.
$\left ( M,g, \mathcal {E}, h_{\mathcal {E}}, \nabla , F \right )$
. -
(iii) A function A as in (i) is called cohomologically locally computable if there exists a locally computable function C as in (i) such that for any
 $\left ( M,g, \mathcal {E}, h_{\mathcal {E}}, \nabla , F \right )$
,
$\left ( M,g, \mathcal {E}, h_{\mathcal {E}}, \nabla , F \right )$
,  $$\begin{align*}\left[ \operatorname{Tr} A \operatorname{dvol}_g \right] = \left[ \operatorname{Tr} C \operatorname{dvol}_g \right] \in H^n_{dR} \left( M \right). \end{align*}$$
$$\begin{align*}\left[ \operatorname{Tr} A \operatorname{dvol}_g \right] = \left[ \operatorname{Tr} C \operatorname{dvol}_g \right] \in H^n_{dR} \left( M \right). \end{align*}$$
Remark 1.2
-
(i) If a function A is locally computable, then the integral
 ${a:=\int _{M} \operatorname {Tr} A \operatorname {dvol}_g}$
is locally computable.
${a:=\int _{M} \operatorname {Tr} A \operatorname {dvol}_g}$
is locally computable. -
(ii) A function A is cohomologically locally computable if and only if
 ${a:=\int _{M} \operatorname {Tr} A \operatorname {dvol}_g}$
is locally computable.
${a:=\int _{M} \operatorname {Tr} A \operatorname {dvol}_g}$
is locally computable.
Theorem 1.3 If r is irrational, the heat coefficients
![]() $A_j$
in Theorem 7.1 (and in particular in (
1.2
)) are not locally computable for integer
$A_j$
in Theorem 7.1 (and in particular in (
1.2
)) are not locally computable for integer
![]() $j \geq 1$
. If
$j \geq 1$
. If
![]() $r=\frac {\alpha }{\beta }$
is rational, then
$r=\frac {\alpha }{\beta }$
is rational, then
![]() $A_j$
are not locally computable for
$A_j$
are not locally computable for
![]() $j \in {\mathbb N} \setminus \{ l \beta : l \in {\mathbb N} \}$
. All the other coefficients can be written in terms of the heat coefficients of
$j \in {\mathbb N} \setminus \{ l \beta : l \in {\mathbb N} \}$
. All the other coefficients can be written in terms of the heat coefficients of
![]() $e^{-t\operatorname {\Delta }}$
, hence they are locally computable.
$e^{-t\operatorname {\Delta }}$
, hence they are locally computable.
Consider the asymptotic expansion in [Reference Duistermaat and Guillemin10, Corollary 2.2’] for a scalar admissible operator, i.e., an elliptic, self-adjoint, positive pseudodifferential operator P of positive integer order d:
 $$\begin{align*}e^{-tP} \stackrel{t \searrow 0}{\sim} \sum_{l=0}^{\infty} A_l(P) t^{(l-n)/d} + \sum_{k=1}^{\infty} B_k(P) t^k \log t. \end{align*}$$
$$\begin{align*}e^{-tP} \stackrel{t \searrow 0}{\sim} \sum_{l=0}^{\infty} A_l(P) t^{(l-n)/d} + \sum_{k=1}^{\infty} B_k(P) t^k \log t. \end{align*}$$
Gilkey and Grubb [Reference Gilkey and Grubb14, Theorem 1.4] proved that the coefficients
![]() $a_l(P)$
for
$a_l(P)$
for
![]() $l \geq 0$
and
$l \geq 0$
and
![]() $b_k(P)$
for
$b_k(P)$
for
![]() $k \geq 1$
from the corresponding small-time heat trace expansion
$k \geq 1$
from the corresponding small-time heat trace expansion
 $$ \begin{align} \operatorname{Tr} e^{-tP} \stackrel{t \searrow 0}{\sim} \sum_{l=0}^{\infty} a_l(P) t^{(l-n)/d} + \sum_{k=1}^{\infty} b_k(P) t^k \log t \end{align} $$
$$ \begin{align} \operatorname{Tr} e^{-tP} \stackrel{t \searrow 0}{\sim} \sum_{l=0}^{\infty} a_l(P) t^{(l-n)/d} + \sum_{k=1}^{\infty} b_k(P) t^k \log t \end{align} $$
are generically non-zero in the above class of admissible operators. In Theorem 1.1, we prove the same type of statement. However, in our case, the order of the operator
![]() $\Delta ^r$
is
$\Delta ^r$
is
![]() $2r$
; thus, it is integer only for
$2r$
; thus, it is integer only for
![]() $r = 1/2$
. Even in this case, the non-vanishing result in Theorem 1.1 is not a consequence of [Reference Gilkey and Grubb14, Theorem 1.4] since, in our case, we do not consider the whole class of admissible operators of fixed integer order d in the sense of Gilkey and Grubb [Reference Gilkey and Grubb14], but the smaller class of square roots of generalized Laplacians.
$r = 1/2$
. Even in this case, the non-vanishing result in Theorem 1.1 is not a consequence of [Reference Gilkey and Grubb14, Theorem 1.4] since, in our case, we do not consider the whole class of admissible operators of fixed integer order d in the sense of Gilkey and Grubb [Reference Gilkey and Grubb14], but the smaller class of square roots of generalized Laplacians.
Furthermore, in [Reference Gilkey and Grubb14, Theorem 1.7], it is proved that the coefficients
![]() $a_l(P)$
in (1.3) corresponding to
$a_l(P)$
in (1.3) corresponding to
![]() $t^{(l-n)/d}$
, for
$t^{(l-n)/d}$
, for
![]() $(l-n)/d \in {\mathbb N}$
, are not locally computable. Remark that the meaning of “locally computable” in [Reference Gilkey and Grubb14] is different from our Definition 1.1. More precisely, in the definition of Gilkey and Grubb, a locally computable function A has to be a smooth function in the jets of the homogeneous components of the total symbol of the operator. A locally computable coefficient in the sense of Gilkey and Grubb [Reference Gilkey and Grubb14] is clearly locally computable in the sense of Definition 1.1(ii).
$(l-n)/d \in {\mathbb N}$
, are not locally computable. Remark that the meaning of “locally computable” in [Reference Gilkey and Grubb14] is different from our Definition 1.1. More precisely, in the definition of Gilkey and Grubb, a locally computable function A has to be a smooth function in the jets of the homogeneous components of the total symbol of the operator. A locally computable coefficient in the sense of Gilkey and Grubb [Reference Gilkey and Grubb14] is clearly locally computable in the sense of Definition 1.1(ii).
For
![]() $r=1/2$
, Bär and Moroianu [Reference Bär and Moroianu2] remark that for odd
$r=1/2$
, Bär and Moroianu [Reference Bär and Moroianu2] remark that for odd
![]() $k=1,3,\ldots $
, the coefficients
$k=1,3,\ldots $
, the coefficients
![]() $A_k$
in (1.2) corresponding to
$A_k$
in (1.2) corresponding to
![]() $t^k$
appear to be non-local. In Section 9, we clarify this remark by proving that they are indeed non-local in the sense of Definition 1.1 (i) (Theorem 1.3). In fact, we prove that the
$t^k$
appear to be non-local. In Section 9, we clarify this remark by proving that they are indeed non-local in the sense of Definition 1.1 (i) (Theorem 1.3). In fact, we prove that the
![]() $A_k$
’s are not cohomologically local. By Remark 1.2 (ii), it also follows that the integrals
$A_k$
’s are not cohomologically local. By Remark 1.2 (ii), it also follows that the integrals
![]() $a_k:=\int _M \operatorname {Tr} A_k \operatorname {dvol}_g$
are not locally computable in the sense of Definition 1.1 (ii). Therefore, the
$a_k:=\int _M \operatorname {Tr} A_k \operatorname {dvol}_g$
are not locally computable in the sense of Definition 1.1 (ii). Therefore, the
![]() $a_k$
’s for odd k are also not locally computable in the sense of Gilkey and Grubb [Reference Gilkey and Grubb14].
$a_k$
’s for odd k are also not locally computable in the sense of Gilkey and Grubb [Reference Gilkey and Grubb14].
For
![]() $d=1$
, the non-local coefficients in the heat expansion (1.3) in [Reference Gilkey and Grubb14] are
$d=1$
, the non-local coefficients in the heat expansion (1.3) in [Reference Gilkey and Grubb14] are
![]() $a_{n+1}, a_{n+2},\ldots $
, whereas in our case corresponding to
$a_{n+1}, a_{n+2},\ldots $
, whereas in our case corresponding to
![]() $r=d/2=1/2$
, the non-local coefficients are
$r=d/2=1/2$
, the non-local coefficients are
![]() $a_1,a_3,\ldots $
. Despite some formal resemblances, it appears therefore that the results of the present paper are quite different from those of [Reference Gilkey and Grubb14].
$a_1,a_3,\ldots $
. Despite some formal resemblances, it appears therefore that the results of the present paper are quite different from those of [Reference Gilkey and Grubb14].
1.3 The heat kernel as a conormal section
Recall that a smooth function f on the interior of a manifold with corners is said to be polyhomogeneous conormal if for any boundary hypersurface given by a boundary defining function
![]() $\theta $
, f has an expansion with terms of the form
$\theta $
, f has an expansion with terms of the form
![]() $\theta ^k \log ^l \theta $
toward
$\theta ^k \log ^l \theta $
toward
![]() ${\{ \theta =0 \}}$
(only natural powers l are allowed). In [Reference Melrose19], Melrose introduced the heat space
${\{ \theta =0 \}}$
(only natural powers l are allowed). In [Reference Melrose19], Melrose introduced the heat space
![]() $M_H^2$
by performing a parabolic blow-up of the diagonal in
$M_H^2$
by performing a parabolic blow-up of the diagonal in
![]() $M \times M$
at time
$M \times M$
at time
![]() $t=0$
. The new space is a manifold with corners with boundary hypersurfaces given by the boundary defining functions
$t=0$
. The new space is a manifold with corners with boundary hypersurfaces given by the boundary defining functions
![]() $\rho $
and
$\rho $
and
![]() $\omega _0$
. Then the heat kernel
$\omega _0$
. Then the heat kernel
![]() $p_t$
has the form
$p_t$
has the form
![]() $\rho ^{-n} {\mathcal C}^{\infty }(M_H^2)$
, and it vanishes rapidly at
$\rho ^{-n} {\mathcal C}^{\infty }(M_H^2)$
, and it vanishes rapidly at
![]() $\{ \omega _0=0 \}$
(see [Reference Melrose19, Theorem 7.12]).
$\{ \omega _0=0 \}$
(see [Reference Melrose19, Theorem 7.12]).
In the special case
![]() $r=1/2$
, we are able to give a simultaneous formula for the asymptotic behavior of
$r=1/2$
, we are able to give a simultaneous formula for the asymptotic behavior of
![]() $h_t$
as t goes to zero both on the diagonal and away from it. We can understand better the heat operator
$h_t$
as t goes to zero both on the diagonal and away from it. We can understand better the heat operator
![]() $e^{-t \operatorname {\Delta }^{1/2}}$
on a homogeneous (rather than parabolic) blow-up heat space
$e^{-t \operatorname {\Delta }^{1/2}}$
on a homogeneous (rather than parabolic) blow-up heat space
![]() $\operatorname {M_{heat}}$
, the usual blow-up of
$\operatorname {M_{heat}}$
, the usual blow-up of
![]() $\{ 0 \} \times \operatorname {Diag}$
in
$\{ 0 \} \times \operatorname {Diag}$
in
![]() $[0,\infty ) \times M \,{\times}\, M$
. The new added face is called the front face and we denote it
$[0,\infty ) \times M \,{\times}\, M$
. The new added face is called the front face and we denote it
![]() $\operatorname {ff}$
, whereas the lift of the old boundary is the lateral boundary, denoted
$\operatorname {ff}$
, whereas the lift of the old boundary is the lateral boundary, denoted
![]() $\operatorname {lb}$
.
$\operatorname {lb}$
.
Theorem 1.4 If n is even, then the Schwartz kernel
![]() $h_t$
of the operator
$h_t$
of the operator
![]() $e^{-t\operatorname {\Delta }^{1/2}}$
belongs to
$e^{-t\operatorname {\Delta }^{1/2}}$
belongs to
![]() $ \rho ^{-n}\omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) $
, while if n is odd,
$ \rho ^{-n}\omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) $
, while if n is odd,
![]() $h_t \in \rho ^{-n} \omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) + \rho \log \rho \cdot \omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) $
.
$h_t \in \rho ^{-n} \omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) + \rho \log \rho \cdot \omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) $
.
Theorem 1.4 improves the results of [Reference Bär and Moroianu2] twofold. First, it holds true for non-negative generalized Laplacians. Second, while Bär–Moroianu describe the asymptotic behavior of
![]() $h_t$
on the diagonal and away from it separately, this theorem also gives a precise, uniform description of the transition between these two regions by showing that
$h_t$
on the diagonal and away from it separately, this theorem also gives a precise, uniform description of the transition between these two regions by showing that
![]() $h_t$
is a polyhomogeneous conormal section on
$h_t$
is a polyhomogeneous conormal section on
![]() $\operatorname {M_{heat}}$
with values in
$\operatorname {M_{heat}}$
with values in
![]() $\mathcal {E} \boxtimes \mathcal {E}^*$
.
$\mathcal {E} \boxtimes \mathcal {E}^*$
.
Note that throughout the paper, integral kernels act on sections by integration with respect to the fixed Riemannian density from M in the second variable, so
![]() $h_t$
does not contain a density factor. We feel that in the present context this exhibits more clearly the asymptotic behavior.
$h_t$
does not contain a density factor. We feel that in the present context this exhibits more clearly the asymptotic behavior.
Based on the study of the case
![]() $r=1/2$
and on the separate asymptotic expansions of the heat kernel
$r=1/2$
and on the separate asymptotic expansions of the heat kernel
![]() $h_t$
of
$h_t$
of
![]() $\operatorname {\Delta }^r$
,
$\operatorname {\Delta }^r$
,
![]() $r \in (0,1)$
as t goes to
$r \in (0,1)$
as t goes to
![]() $0$
given in Theorems 6.1 and 7.1, we can conjecture that the heat kernel
$0$
given in Theorems 6.1 and 7.1, we can conjecture that the heat kernel
![]() $h_t$
is a polyhomogeneous conormal function for all
$h_t$
is a polyhomogeneous conormal function for all
![]() $r \in (0,1)$
on a “transcendental” heat blow-up space
$r \in (0,1)$
on a “transcendental” heat blow-up space
![]() $M^r_{heat}$
depending on r. We leave this as a future project.
$M^r_{heat}$
depending on r. We leave this as a future project.
2 The heat kernel of a generalized Laplacian
Let
![]() $\mathcal {E}$
be a Hermitian vector bundle over a compact Riemannian manifold M of dimension n. Consider
$\mathcal {E}$
be a Hermitian vector bundle over a compact Riemannian manifold M of dimension n. Consider
![]() $\operatorname {\Delta }$
to be a generalized Laplacian, i.e., a second-order differential operator which satisfies
$\operatorname {\Delta }$
to be a generalized Laplacian, i.e., a second-order differential operator which satisfies
For example, if
![]() $\nabla $
is a connection on
$\nabla $
is a connection on
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $F \in \Gamma (\operatorname {End} \mathcal {E})$
,
$F \in \Gamma (\operatorname {End} \mathcal {E})$
,
![]() $F^*=F$
, then
$F^*=F$
, then
![]() $\nabla ^*\nabla +F$
is a symmetric generalized Laplacian on
$\nabla ^*\nabla +F$
is a symmetric generalized Laplacian on
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Suppose that
![]() $\operatorname {\Delta }$
is self-adjoint. Since M is compact, the spectrum of
$\operatorname {\Delta }$
is self-adjoint. Since M is compact, the spectrum of
![]() $\operatorname {\Delta }$
is discrete and
$\operatorname {\Delta }$
is discrete and
![]() $L^2(M,\mathcal {E})$
splits as an orthogonal Hilbert direct sum
$L^2(M,\mathcal {E})$
splits as an orthogonal Hilbert direct sum
 $$\begin{align*}L^2(M,\mathcal{E})=\bigoplus_{\lambda \in \operatorname{Spec} \operatorname{\Delta}}^{\perp} E_{\lambda}, \end{align*}$$
$$\begin{align*}L^2(M,\mathcal{E})=\bigoplus_{\lambda \in \operatorname{Spec} \operatorname{\Delta}}^{\perp} E_{\lambda}, \end{align*}$$
where
![]() $E_{\lambda }$
is the eigenspace corresponding to the eigenvalue
$E_{\lambda }$
is the eigenspace corresponding to the eigenvalue
![]() $\lambda $
of
$\lambda $
of
![]() $\operatorname {\Delta }$
. Moreover,
$\operatorname {\Delta }$
. Moreover,
![]() ${\dim E_{\lambda } < \infty }$
and by elliptic regularity, the eigensections are smooth (see, e.g., [Reference Bourguignon, Hijazi, Milhorat, Moroianu and Moroianu8]). Let
${\dim E_{\lambda } < \infty }$
and by elliptic regularity, the eigensections are smooth (see, e.g., [Reference Bourguignon, Hijazi, Milhorat, Moroianu and Moroianu8]). Let
![]() $e^{-t\operatorname {\Delta }}$
be the heat operator defined as
$e^{-t\operatorname {\Delta }}$
be the heat operator defined as
for any
![]() $\Phi \in E_{\lambda }$
,
$\Phi \in E_{\lambda }$
,
![]() $\lambda \in \operatorname {Spec} \operatorname {\Delta }$
.
$\lambda \in \operatorname {Spec} \operatorname {\Delta }$
.
Definition 2.1 The heat kernel of a self-adjoint elliptic pseudodifferential operator P acting on the sections of
![]() $\mathcal {E}$
is the Schwartz kernel of the operator
$\mathcal {E}$
is the Schwartz kernel of the operator
![]() $e^{-tP}$
.
$e^{-tP}$
.
If we denote by
![]() $\lbrace \Phi _j \rbrace $
an orthonormal Hilbert basis of
$\lbrace \Phi _j \rbrace $
an orthonormal Hilbert basis of
![]() $\operatorname {\Delta }$
-eigensections, then the heat kernel
$\operatorname {\Delta }$
-eigensections, then the heat kernel
![]() $p_t(x,y)$
satisfies
$p_t(x,y)$
satisfies
in
![]() ${\mathcal C}^{\infty } \left ( (0,\infty ) \times M \times M \right )$
.
${\mathcal C}^{\infty } \left ( (0,\infty ) \times M \times M \right )$
.
Recall that the
![]() $L^2$
-product of two sections
$L^2$
-product of two sections
![]() $s_1, s_2 \in \Gamma (\mathcal {E})$
is given by
$s_1, s_2 \in \Gamma (\mathcal {E})$
is given by
where g is the metric on M and
![]() $h_{\mathcal {E}}$
is the Hermitian product on
$h_{\mathcal {E}}$
is the Hermitian product on
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Let
![]() $y \in M$
be a fixed point. We work in geodesic normal coordinates defined by the exponential map
$y \in M$
be a fixed point. We work in geodesic normal coordinates defined by the exponential map
Since M is compact, there exists a global injectivity radius
![]() $\epsilon $
. For x close enough to y (
$\epsilon $
. For x close enough to y (
![]() $d(x,y) \leq \epsilon $
), take
$d(x,y) \leq \epsilon $
), take
![]() $\operatorname {x} \in T_yM$
the unique tangent vector of length smaller than
$\operatorname {x} \in T_yM$
the unique tangent vector of length smaller than
![]() $\epsilon $
such that
$\epsilon $
such that
![]() $x=\exp _y\operatorname {x}$
. Let
$x=\exp _y\operatorname {x}$
. Let
namely the pull-back of the volume form
![]() $dx$
on M through the exponential map
$dx$
on M through the exponential map
![]() $\exp _{y}$
is equal with
$\exp _{y}$
is equal with
![]() $\operatorname {j}(\operatorname {x})d\operatorname {x}$
. More precisely,
$\operatorname {j}(\operatorname {x})d\operatorname {x}$
. More precisely,
Denote by
![]() $\tau _{x}^{y}: \mathcal {E}_x \longrightarrow \mathcal {E}_y$
the parallel transport along the unique minimal geodesic
$\tau _{x}^{y}: \mathcal {E}_x \longrightarrow \mathcal {E}_y$
the parallel transport along the unique minimal geodesic
![]() $x_s=\exp _{y} (s\operatorname {x})$
, where
$x_s=\exp _{y} (s\operatorname {x})$
, where
![]() $s \in [0,1]$
, which connects the points x and y. The heat kernel
$s \in [0,1]$
, which connects the points x and y. The heat kernel
![]() $p_t(x,y)$
belongs to the space
$p_t(x,y)$
belongs to the space
![]() $ {\mathcal C}^{\infty } \left ( (0,\infty ) \times M \times M, \mathcal {E}_x \otimes \mathcal {E}_y^* \right )$
and
$ {\mathcal C}^{\infty } \left ( (0,\infty ) \times M \times M, \mathcal {E}_x \otimes \mathcal {E}_y^* \right )$
and
![]() $p_t(x,y)$
satisfies the heat equation
$p_t(x,y)$
satisfies the heat equation
Furthermore,
![]() $ \lim _{t\rightarrow 0} P_t s=s,$
in
$ \lim _{t\rightarrow 0} P_t s=s,$
in
![]() $\Vert \cdot \Vert _0$
, for any smooth section
$\Vert \cdot \Vert _0$
, for any smooth section
![]() $s \in \Gamma (M, \mathcal {E})$
, where
$s \in \Gamma (M, \mathcal {E})$
, where
where
![]() $dg(y)$
is the Riemannian density of the metric g. The next theorem is due to Minakshisundaram and Pleijel (see, for instance, [Reference Berger, Gauduchon and Mazet4, Reference Minakshisundaram and Pleijel21]).
$dg(y)$
is the Riemannian density of the metric g. The next theorem is due to Minakshisundaram and Pleijel (see, for instance, [Reference Berger, Gauduchon and Mazet4, Reference Minakshisundaram and Pleijel21]).
Theorem 2.1 The heat kernel
![]() $p_t$
has the following asymptotic expansion near the diagonal:
$p_t$
has the following asymptotic expansion near the diagonal:
where
![]() $\Psi _i: \mathcal {E}_y \longrightarrow \mathcal {E}_x $
are
$\Psi _i: \mathcal {E}_y \longrightarrow \mathcal {E}_x $
are
![]() ${\mathcal C}^{\infty }$
sections defined near the diagonal. Moreover, the
${\mathcal C}^{\infty }$
sections defined near the diagonal. Moreover, the
![]() $\Psi _i$
’s are given by the following explicit formulæ:
$\Psi _i$
’s are given by the following explicit formulæ:
 $$ \begin{align*} {}&\Psi_0(x,y)=\operatorname{j}^{-1/2}(\operatorname{x})\tau_{y}^{x}, \\ {}&\tau_{x}^y \Psi_i(x,y)=-\operatorname{j}^{-1/2}(\operatorname{x}) \int_{0}^{1}s^{i-1} \operatorname{j}^{-1/2}(x_s)\tau_{x_s}^{y} \operatorname{\Delta}_x \Psi_{i-1}(x_s,y)ds. \end{align*} $$
$$ \begin{align*} {}&\Psi_0(x,y)=\operatorname{j}^{-1/2}(\operatorname{x})\tau_{y}^{x}, \\ {}&\tau_{x}^y \Psi_i(x,y)=-\operatorname{j}^{-1/2}(\operatorname{x}) \int_{0}^{1}s^{i-1} \operatorname{j}^{-1/2}(x_s)\tau_{x_s}^{y} \operatorname{\Delta}_x \Psi_{i-1}(x_s,y)ds. \end{align*} $$
The asymptotic sum in Theorem 2.1 can be understood using truncation and bounds of derivatives as in [Reference Berline, Getzler and Vergne5]. We prefer the interpretation given in [Reference Melrose19], where the heat kernel
![]() $p_t$
is shown to belong to
$p_t$
is shown to belong to
![]() $\rho ^{-n} {\mathcal C}^{\infty }(M_H^2)$
on the parabolic blow-up space
$\rho ^{-n} {\mathcal C}^{\infty }(M_H^2)$
on the parabolic blow-up space
![]() $M_H^2$
and to vanish rapidly at the temporal boundary face
$M_H^2$
and to vanish rapidly at the temporal boundary face
![]() $\{ \omega _0 =0 \}$
(see Section 10).
$\{ \omega _0 =0 \}$
(see Section 10).
Example 2.2 Let
![]() $\mathbb {T}^n=\left ( S^1\right )^n={\mathbb R}^n/(2 \pi {\mathbb Z})^n$
be the n-dimensional torus with the standard product metric
$\mathbb {T}^n=\left ( S^1\right )^n={\mathbb R}^n/(2 \pi {\mathbb Z})^n$
be the n-dimensional torus with the standard product metric
![]() $g=d\theta _1^2 \otimes \cdots \otimes d\theta _n^2$
. Consider the trivial bundle
$g=d\theta _1^2 \otimes \cdots \otimes d\theta _n^2$
. Consider the trivial bundle
![]() $\mathcal {E}= \underline {{\mathbb C}}$
over
$\mathcal {E}= \underline {{\mathbb C}}$
over
![]() $\mathbb {T}^n$
with the standard metric
$\mathbb {T}^n$
with the standard metric
![]() $h_{\mathcal {E}}$
, the trivial connection
$h_{\mathcal {E}}$
, the trivial connection
![]() $\nabla =d$
, and the zero endomorphism F. Let
$\nabla =d$
, and the zero endomorphism F. Let
![]() $\operatorname {\Delta }_1$
be the Laplacian on
$\operatorname {\Delta }_1$
be the Laplacian on
![]() $\mathbb {T}^n$
given by the metric g. The eigenvalues of
$\mathbb {T}^n$
given by the metric g. The eigenvalues of
![]() $\operatorname {\Delta }_1$
are
$\operatorname {\Delta }_1$
are
![]() $\{k_1^2+\cdots +k_n^2: k_1,\ldots ,k_n \in {\mathbb Z} \}$
. Let
$\{k_1^2+\cdots +k_n^2: k_1,\ldots ,k_n \in {\mathbb Z} \}$
. Let
![]() $\varphi _l(\xi )=\frac {1}{\sqrt {2\pi }} e^{il\xi }$
be the standard orthonormal basis of eigenfunctions of each
$\varphi _l(\xi )=\frac {1}{\sqrt {2\pi }} e^{il\xi }$
be the standard orthonormal basis of eigenfunctions of each
![]() $\operatorname {\Delta }_{S^1}$
. Then, for
$\operatorname {\Delta }_{S^1}$
. Then, for
![]() $\theta =(\theta _1,\ldots ,\theta _n) \in \mathbb {T}^n$
, the heat kernel
$\theta =(\theta _1,\ldots ,\theta _n) \in \mathbb {T}^n$
, the heat kernel
![]() $p_t$
of
$p_t$
of
![]() $\operatorname {\Delta }_1$
is the following:
$\operatorname {\Delta }_1$
is the following:
Since
![]() $\varphi _l(\xi )\overline {\varphi _l(\xi )}=\frac {1}{2\pi }$
, for any
$\varphi _l(\xi )\overline {\varphi _l(\xi )}=\frac {1}{2\pi }$
, for any
![]() $\xi \in S^1$
, we get
$\xi \in S^1$
, we get
Remark that the Fourier transform of the function
![]() $f_t: {\mathbb R}^n \longrightarrow {\mathbb R}$
,
$f_t: {\mathbb R}^n \longrightarrow {\mathbb R}$
,
![]() $f_t(x)=e^{-t \vert x \vert ^2}$
is given by
$f_t(x)=e^{-t \vert x \vert ^2}$
is given by
Using the multidimensional Poisson formula (see, for instance, [Reference Bellman3]), we obtain that
 $$ \begin{align*} p_t(\theta,\theta)=\tfrac{1}{(2 \pi)^n} \sum_{k \in {\mathbb Z}^n} f_t(k)=\sum_{k \in {\mathbb Z}^n} \hat{f_t}(2 \pi k)=\tfrac{\pi^{n/2}}{(2 \pi )^n} t^{-n/2} + \tfrac{\pi^{n/2}}{(2 \pi )^n} t^{-n/2} \sum_{k \in {\mathbb Z}^n \setminus \{ 0 \}} e^{-\frac{\pi^2 \vert k \vert^2}{t}}. \end{align*} $$
$$ \begin{align*} p_t(\theta,\theta)=\tfrac{1}{(2 \pi)^n} \sum_{k \in {\mathbb Z}^n} f_t(k)=\sum_{k \in {\mathbb Z}^n} \hat{f_t}(2 \pi k)=\tfrac{\pi^{n/2}}{(2 \pi )^n} t^{-n/2} + \tfrac{\pi^{n/2}}{(2 \pi )^n} t^{-n/2} \sum_{k \in {\mathbb Z}^n \setminus \{ 0 \}} e^{-\frac{\pi^2 \vert k \vert^2}{t}}. \end{align*} $$
Since the last sum is of order
![]() ${\mathcal O} \left ( e^{-\frac {1}{t}} \right )$
as
${\mathcal O} \left ( e^{-\frac {1}{t}} \right )$
as
![]() $t \rightarrow 0$
, it follows that the first coefficient in the asymptotic expansion at small-time t of
$t \rightarrow 0$
, it follows that the first coefficient in the asymptotic expansion at small-time t of
![]() $p_t$
is
$p_t$
is
![]() $\tfrac {\pi ^{n/2}}{(2 \pi )^n}$
and all the others vanish.
$\tfrac {\pi ^{n/2}}{(2 \pi )^n}$
and all the others vanish.
From now on, suppose that
![]() $\operatorname {\Delta }$
is non-negative (i.e.,
$\operatorname {\Delta }$
is non-negative (i.e.,
![]() $h_{\mathcal {E}} \left ( \operatorname {\Delta } f, f \right ) \geq 0$
, for any
$h_{\mathcal {E}} \left ( \operatorname {\Delta } f, f \right ) \geq 0$
, for any
![]() $f \in {\mathcal C}^{\infty } (M,\mathcal {E})$
). For
$f \in {\mathcal C}^{\infty } (M,\mathcal {E})$
). For
![]() $s \in {\mathbb C}$
, we define the complex powers
$s \in {\mathbb C}$
, we define the complex powers
![]() $\operatorname {\Delta }^{-s} \in \Psi ^{-2s} \left ( M, \mathcal {E} \right )$
of
$\operatorname {\Delta }^{-s} \in \Psi ^{-2s} \left ( M, \mathcal {E} \right )$
of
![]() $\operatorname {\Delta }$
as
$\operatorname {\Delta }$
as
 $$\begin{align*}\operatorname{\Delta}^{-s} \Phi= \left\{ \begin{array}{ll} \lambda^{-s}\Phi, & \mbox{ if } \Phi \in E_{\lambda}, \ \lambda \neq 0, \\ 0, & \mbox{ if } \Phi \in \operatorname{Ker} \operatorname{\Delta}. \end{array} \right. \end{align*}$$
$$\begin{align*}\operatorname{\Delta}^{-s} \Phi= \left\{ \begin{array}{ll} \lambda^{-s}\Phi, & \mbox{ if } \Phi \in E_{\lambda}, \ \lambda \neq 0, \\ 0, & \mbox{ if } \Phi \in \operatorname{Ker} \operatorname{\Delta}. \end{array} \right. \end{align*}$$
Remark that
![]() $(\operatorname {\Delta }^s)_{s \in {\mathbb C}}$
is a holomorphic family of pseudodifferential operators. Let
$(\operatorname {\Delta }^s)_{s \in {\mathbb C}}$
is a holomorphic family of pseudodifferential operators. Let
![]() $r \in (0,1)$
. We denote by
$r \in (0,1)$
. We denote by
![]() $h_t$
the heat kernel of
$h_t$
the heat kernel of
![]() $\operatorname {\Delta }^r$
, namely the Schwartz kernel of the operator
$\operatorname {\Delta }^r$
, namely the Schwartz kernel of the operator
![]() $e^{-t\operatorname {\Delta }^r}$
. We have seen that
$e^{-t\operatorname {\Delta }^r}$
. We have seen that
 $$ \begin{align} p_t(x,x) \stackrel{t \searrow 0}{\sim} t^{-n/2} \sum_{j=0}^{\infty} t^{j}a_{j}(x,x), \end{align} $$
$$ \begin{align} p_t(x,x) \stackrel{t \searrow 0}{\sim} t^{-n/2} \sum_{j=0}^{\infty} t^{j}a_{j}(x,x), \end{align} $$
with smooth sections
![]() $a_j(x,x) \in \mathcal {E}_x \otimes \mathcal {E}_x^*$
.
$a_j(x,x) \in \mathcal {E}_x \otimes \mathcal {E}_x^*$
.
3 The link between the heat kernel and complex powers of the Laplacian
Proposition 1 (Mellin Formula)
With the notations above, for
![]() $\Re s>0$
, we have
$\Re s>0$
, we have
where
![]() $\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}$
is the orthogonal projection onto the kernel of
$\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}$
is the orthogonal projection onto the kernel of
![]() $\operatorname {\Delta }$
.
$\operatorname {\Delta }$
.
Proof It is straightforward to check that both sides coincide on eigensections
![]() $\Phi \in E_{\lambda }$
,
$\Phi \in E_{\lambda }$
,
![]() $\lambda \in \operatorname {Spec} \operatorname {\Delta }$
. Since
$\lambda \in \operatorname {Spec} \operatorname {\Delta }$
. Since
![]() $\lbrace \Phi _j \rbrace _{j}$
is a Hilbert basis, the result follows.
$\lbrace \Phi _j \rbrace _{j}$
is a Hilbert basis, the result follows.
We will write
![]() $\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
for the Schwartz kernel
$\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
for the Schwartz kernel
![]() $\sum _{k} \varphi _k(x) \otimes \varphi _k^*(y)$
, where
$\sum _{k} \varphi _k(x) \otimes \varphi _k^*(y)$
, where
![]() $\{ \varphi _k \}$
is an orthonormal basis in
$\{ \varphi _k \}$
is an orthonormal basis in
![]() $\operatorname {Ker} \operatorname {\Delta }$
. Denote by
$\operatorname {Ker} \operatorname {\Delta }$
. Denote by
![]() $q_{-s}$
the Schwartz kernel of the operator
$q_{-s}$
the Schwartz kernel of the operator
![]() $\operatorname {\Delta }^{-s}$
. Let us first study the poles and the zeros of
$\operatorname {\Delta }^{-s}$
. Let us first study the poles and the zeros of
![]() $q_{-s}$
away from the diagonal.
$q_{-s}$
away from the diagonal.
Proposition 2 Let K be a compact in
![]() $M \times M \setminus \operatorname {Diag}$
. Then, for
$M \times M \setminus \operatorname {Diag}$
. Then, for
![]() $(x,y)\in K $
, the function
$(x,y)\in K $
, the function
![]() $s \longmapsto {q_{-s}}_{\vert _K} \in {\mathcal C}^{\infty } \left ( K, \mathcal {E} \boxtimes \mathcal {E}^* \right ) $
is entire. Moreover,
$s \longmapsto {q_{-s}}_{\vert _K} \in {\mathcal C}^{\infty } \left ( K, \mathcal {E} \boxtimes \mathcal {E}^* \right ) $
is entire. Moreover,
![]() ${q_{-s}}_{\vert _K}$
vanishes at each negative integer s.
${q_{-s}}_{\vert _K}$
vanishes at each negative integer s.
Proof For
![]() $\Re s>0$
, let
$\Re s>0$
, let
![]() $f_{x,y}(s)= \int _{0}^{\infty } t^{s-1}\left ( p_t(x,y)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y) \right ) dt $
. Remark that
$f_{x,y}(s)= \int _{0}^{\infty } t^{s-1}\left ( p_t(x,y)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y) \right ) dt $
. Remark that
 $$ \begin{align*} f_{x,y}(s)&=\int_{0}^{\infty} t^{s-1}\left( p_t(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \right) dt \\&={} \int_{1}^{\infty} t^{s-1} \left( p_t(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \right) dt \\ &\quad+{} \int_{0}^{1} t^{s-1}p_t(x,y) dt - \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \cdot \int_{0}^{1} t^{s-1}dt. \end{align*} $$
$$ \begin{align*} f_{x,y}(s)&=\int_{0}^{\infty} t^{s-1}\left( p_t(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \right) dt \\&={} \int_{1}^{\infty} t^{s-1} \left( p_t(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \right) dt \\ &\quad+{} \int_{0}^{1} t^{s-1}p_t(x,y) dt - \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \cdot \int_{0}^{1} t^{s-1}dt. \end{align*} $$
Since
![]() $p_t(x,y)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
decays exponentially fast as t goes to
$p_t(x,y)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
decays exponentially fast as t goes to
![]() $\infty $
, the first integral is absolutely convergent in
$\infty $
, the first integral is absolutely convergent in
![]() $ C^k$
norms. The heat kernel
$ C^k$
norms. The heat kernel
![]() $p_t$
vanishes with all of its derivatives as
$p_t$
vanishes with all of its derivatives as
![]() $t \searrow 0$
in the compact K, thus the second integral is also absolutely convergent. The last integral term is well-defined for
$t \searrow 0$
in the compact K, thus the second integral is also absolutely convergent. The last integral term is well-defined for
![]() $\Re s>0$
, and it extends to a meromorphic function on
$\Re s>0$
, and it extends to a meromorphic function on
![]() ${\mathbb C}$
with a simple pole in
${\mathbb C}$
with a simple pole in
![]() $s=0$
. Therefore,
$s=0$
. Therefore,
![]() $s \mapsto f_{x,y}(s)$
extends to a meromorphic function on
$s \mapsto f_{x,y}(s)$
extends to a meromorphic function on
![]() ${\mathbb C}$
. By Proposition 1 and the identity theorem, the equality of meromorphic functions
${\mathbb C}$
. By Proposition 1 and the identity theorem, the equality of meromorphic functions
holds for any
![]() $s \in {\mathbb C}$
. In particular, we obtain
$s \in {\mathbb C}$
. In particular, we obtain
![]() $q_0(x,y)=- \operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
. Furthermore,
$q_0(x,y)=- \operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
. Furthermore,
![]() ${q_{-s}}_{\vert _{K}}$
is an entire function and vanishes in
${q_{-s}}_{\vert _{K}}$
is an entire function and vanishes in
![]() $s=-1,-2,\ldots $
.
$s=-1,-2,\ldots $
.
Remark 3.1 The fact that
![]() ${q_{-s}}_{\vert _K}$
vanishes for negative integers s also follows from the fact that then
${q_{-s}}_{\vert _K}$
vanishes for negative integers s also follows from the fact that then
![]() $\Delta ^{-s}$
is a differential operator.
$\Delta ^{-s}$
is a differential operator.
Now we check the behavior of
![]() $q_{-s}$
along the diagonal. It is no longer holomorphic there, and the coefficients
$q_{-s}$
along the diagonal. It is no longer holomorphic there, and the coefficients
![]() $a_j(x,x)$
from (2.1) appear as residues of
$a_j(x,x)$
from (2.1) appear as residues of
![]() $q_{-s}(x,x)$
.
$q_{-s}(x,x)$
.
Proposition 3 Let
![]() $x \in M$
. Then the function
$x \in M$
. Then the function
![]() $s \mapsto \Gamma (s)q_{-s}(x,x)$
has a meromorphic extension from the set
$s \mapsto \Gamma (s)q_{-s}(x,x)$
has a meromorphic extension from the set
![]() $\{s \in {\mathbb C} : \Re s> \frac {n}{2} \}$
to
$\{s \in {\mathbb C} : \Re s> \frac {n}{2} \}$
to
![]() ${\mathbb C}$
with simple poles in
${\mathbb C}$
with simple poles in
![]() $s \in \lbrace 0 \rbrace \cup \lbrace \frac {n}{2}-j : j \in {\mathbb N} \rbrace $
. The residue of
$s \in \lbrace 0 \rbrace \cup \lbrace \frac {n}{2}-j : j \in {\mathbb N} \rbrace $
. The residue of
![]() $\Gamma (s)q_{-s}(x,x)$
in
$\Gamma (s)q_{-s}(x,x)$
in
![]() $s=\frac {n}{2}-j$
,
$s=\frac {n}{2}-j$
,
![]() $j \neq \frac {n}{2}$
, is
$j \neq \frac {n}{2}$
, is
![]() $a_j(x,x)$
. If n is even, then the residue of
$a_j(x,x)$
. If n is even, then the residue of
![]() $\Gamma (s)q_{-s}(x,x)$
in
$\Gamma (s)q_{-s}(x,x)$
in
![]() $s=0$
is
$s=0$
is
![]() $a_{\frac {n}{2}}(x,x)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,x)$
. If n is odd, the residue in
$a_{\frac {n}{2}}(x,x)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,x)$
. If n is odd, the residue in
![]() $s=0$
is
$s=0$
is
![]() $-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,x)$
and the meromorphic extension of
$-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,x)$
and the meromorphic extension of
![]() $q_{-s}(x,x)$
vanishes at
$q_{-s}(x,x)$
vanishes at
![]() ${s \in \{ -1,-2,\ldots \}}$
.
${s \in \{ -1,-2,\ldots \}}$
.
Proof Consider the function
![]() $f_{x,x}(s)=\int _{0}^{\infty } t^{s-1}\left ( p_t(x,x)- \operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,x) \right ) dt$
for
$f_{x,x}(s)=\int _{0}^{\infty } t^{s-1}\left ( p_t(x,x)- \operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,x) \right ) dt$
for
![]() $\Re s> \frac {n}{2}$
. We have
$\Re s> \frac {n}{2}$
. We have
 $$ \begin{align*} f_{x,x}(s)&=\int_{0}^{\infty} t^{s-1}\left( p_t(x,x)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) \right) dt \\&={} \int_{1}^{\infty} t^{s-1} \left( p_t(x,x)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) \right) dt \\ &\quad+{} \int_{0}^{1} t^{s-1}p_t(x,x) dt - \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) \cdot \int_{0}^{1} t^{s-1}dt. \end{align*} $$
$$ \begin{align*} f_{x,x}(s)&=\int_{0}^{\infty} t^{s-1}\left( p_t(x,x)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) \right) dt \\&={} \int_{1}^{\infty} t^{s-1} \left( p_t(x,x)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) \right) dt \\ &\quad+{} \int_{0}^{1} t^{s-1}p_t(x,x) dt - \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) \cdot \int_{0}^{1} t^{s-1}dt. \end{align*} $$
The first integral is absolutely convergent, as seen in the proof of Proposition 2. The last integral term is meromorphic with a simple pole at
![]() $s=0$
with residue
$s=0$
with residue
![]() $-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,x)$
. Let us analyze the behavior of the second term
$-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,x)$
. Let us analyze the behavior of the second term
![]() $A_x(s)=\int _{0}^{1} t^{s-1}p_t(x,x)dt$
.
$A_x(s)=\int _{0}^{1} t^{s-1}p_t(x,x)dt$
.
Using (2.1), we have that for
![]() $N \geq 0$
,
$N \geq 0$
,
 $$\begin{align*}t^{n/2}p_t(x,x)=\sum_{j=0}^N t^j a_j(x,x)+R_{N+1}(t,x), \end{align*}$$
$$\begin{align*}t^{n/2}p_t(x,x)=\sum_{j=0}^N t^j a_j(x,x)+R_{N+1}(t,x), \end{align*}$$
where
![]() $R_{N+1}$
is of order
$R_{N+1}$
is of order
![]() ${\mathcal O} (t^{N+1})$
as
${\mathcal O} (t^{N+1})$
as
![]() $t \to 0$
. Furthermore, we obtain
$t \to 0$
. Furthermore, we obtain
 $$ \begin{align*} A_x(s)=\!\int_{0}^{1}\! t^{s-\frac{n}{2}-1} t^{\frac{n}{2}}p_t(x,x)dt=\!&\sum_{j=0}^N \int_{0}^{1}\! t^{s-\frac{n}{2}-1} t^j a_j(x,x)dt + \!\int_{0}^{1} \!t^{s-\frac{n}{2}-1} R_{N+1}(t,x)dt \\ =\!&\sum_{j=0}^N a_j(x,x) \frac{1}{s-\frac{n}{2}+j} + \int_{0}^{1} t^{s-\frac{n}{2}-1} R_{N+1}(t,x)dt. \end{align*} $$
$$ \begin{align*} A_x(s)=\!\int_{0}^{1}\! t^{s-\frac{n}{2}-1} t^{\frac{n}{2}}p_t(x,x)dt=\!&\sum_{j=0}^N \int_{0}^{1}\! t^{s-\frac{n}{2}-1} t^j a_j(x,x)dt + \!\int_{0}^{1} \!t^{s-\frac{n}{2}-1} R_{N+1}(t,x)dt \\ =\!&\sum_{j=0}^N a_j(x,x) \frac{1}{s-\frac{n}{2}+j} + \int_{0}^{1} t^{s-\frac{n}{2}-1} R_{N+1}(t,x)dt. \end{align*} $$
Thus
![]() $s \mapsto A_x(s)$
extends to a meromorphic function on
$s \mapsto A_x(s)$
extends to a meromorphic function on
![]() ${\mathbb C}$
with simple poles in
${\mathbb C}$
with simple poles in
![]() ${\{ \frac {n}{2}-j : \ j=\overline {0,N+1} \}}$
. Using again Proposition 1 and the identity theorem, we deduce the equality
${\{ \frac {n}{2}-j : \ j=\overline {0,N+1} \}}$
. Using again Proposition 1 and the identity theorem, we deduce the equality
for any
![]() $s \in {\mathbb C}$
. It follows that
$s \in {\mathbb C}$
. It follows that
![]() $\Gamma (s) q_{-s}(x,x)$
is meromorphic on
$\Gamma (s) q_{-s}(x,x)$
is meromorphic on
![]() ${\mathbb C}$
with simple poles in
${\mathbb C}$
with simple poles in
![]() $s \in \lbrace 0 \rbrace \cup \lbrace \frac {n}{2}-j : j \in {\mathbb N} \rbrace $
. Moreover, the residue of
$s \in \lbrace 0 \rbrace \cup \lbrace \frac {n}{2}-j : j \in {\mathbb N} \rbrace $
. Moreover, the residue of
![]() $\Gamma (s)q_{-s}(x,x)$
in a pole
$\Gamma (s)q_{-s}(x,x)$
in a pole
![]() $\frac {n}{2}-j$
is
$\frac {n}{2}-j$
is
![]() $a_j(x,x)$
, and the conclusion follows.
$a_j(x,x)$
, and the conclusion follows.
For
![]() $p\in {\mathbb C}$
and
$p\in {\mathbb C}$
and
![]() $\epsilon>0$
, let
$\epsilon>0$
, let
![]() $B_{\epsilon }(p)$
be the open disk centered in p of radius
$B_{\epsilon }(p)$
be the open disk centered in p of radius
![]() $\epsilon $
. We need the following technical result.
$\epsilon $
. We need the following technical result.
Proposition 4 Consider
![]() $\alpha < \beta $
, and let
$\alpha < \beta $
, and let
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $l \in {\mathbb N}$
.
$l \in {\mathbb N}$
.
-
• If K is a compact set disjoint from the diagonal, then the function
 $ s \longmapsto \Gamma (s){q_{-s}}_{\vert _K} $
is uniformly bounded in
$ s \longmapsto \Gamma (s){q_{-s}}_{\vert _K} $
is uniformly bounded in
 $\{ s \in {\mathbb C} : \alpha \leq \Re s \leq \beta \} \setminus B_{\epsilon }(0)$
in the
$\{ s \in {\mathbb C} : \alpha \leq \Re s \leq \beta \} \setminus B_{\epsilon }(0)$
in the
 ${\mathcal C}^{l}$
norm on K.
${\mathcal C}^{l}$
norm on K. -
• The function
 $ s \longmapsto \Gamma (s){q_{-s}}_{\vert _{\operatorname {Diag}}} $
defined on
$ s \longmapsto \Gamma (s){q_{-s}}_{\vert _{\operatorname {Diag}}} $
defined on
 $\{ s \in {\mathbb C}: \ \alpha \leq \Re s \leq \beta \}\setminus \bigcup _{j \in {\mathbb N} \cup \lbrace \frac {n}{2} \rbrace } B_{\epsilon }(\frac {n}{2}-j) \longrightarrow {\mathcal C}^l \left ( \operatorname {Diag}, \mathcal {E} \otimes \mathcal {E}^* \right )$
is uniformly bounded.
$\{ s \in {\mathbb C}: \ \alpha \leq \Re s \leq \beta \}\setminus \bigcup _{j \in {\mathbb N} \cup \lbrace \frac {n}{2} \rbrace } B_{\epsilon }(\frac {n}{2}-j) \longrightarrow {\mathcal C}^l \left ( \operatorname {Diag}, \mathcal {E} \otimes \mathcal {E}^* \right )$
is uniformly bounded.
Proof With the same argument as in the proof of Proposition 2, the restriction of the
![]() ${\mathcal C}^l$
norm on K of the function
${\mathcal C}^l$
norm on K of the function
![]() $s \mapsto f_{x,y}(s) $
is absolutely convergent in
$s \mapsto f_{x,y}(s) $
is absolutely convergent in
![]() $\{ s \in {\mathbb C} : \alpha \leq \Re s \leq \beta \} \setminus B_{\epsilon }(0)$
, hence it is uniformly bounded.
$\{ s \in {\mathbb C} : \alpha \leq \Re s \leq \beta \} \setminus B_{\epsilon }(0)$
, hence it is uniformly bounded.
As in the proof of Proposition 3, the
![]() ${\mathcal C}^l$
norm along
${\mathcal C}^l$
norm along
![]() $\operatorname {Diag}$
of
$\operatorname {Diag}$
of
![]() $s \longmapsto f_{x,x}(s)$
converges absolutely in
$s \longmapsto f_{x,x}(s)$
converges absolutely in
![]() $\{ s \in {\mathbb C}: \ \alpha \leq \Re s \leq \beta \}\setminus \bigcup _{j \in {\mathbb N} \cup \lbrace \frac {n}{2} \rbrace } B_{\epsilon }(\frac {n}{2}-j)$
, thus the conclusion follows.
$\{ s \in {\mathbb C}: \ \alpha \leq \Re s \leq \beta \}\setminus \bigcup _{j \in {\mathbb N} \cup \lbrace \frac {n}{2} \rbrace } B_{\epsilon }(\frac {n}{2}-j)$
, thus the conclusion follows.
4 The behavior of quotients of Gamma functions along vertical lines
A fundamental result used in [Reference Bär and Moroianu2] is the Legendre duplication formula
 $$\begin{align*}\frac{\Gamma(s)}{\Gamma \left( \frac{s}{2} \right) } = \tfrac{1}{\sqrt{2\pi}} 2^{s- \frac{1}{2}} \Gamma\left( \frac{s+1}{2} \right), \end{align*}$$
$$\begin{align*}\frac{\Gamma(s)}{\Gamma \left( \frac{s}{2} \right) } = \tfrac{1}{\sqrt{2\pi}} 2^{s- \frac{1}{2}} \Gamma\left( \frac{s+1}{2} \right), \end{align*}$$
together with the rapid decay of the Gamma function in vertical lines
![]() $\Re s = \tau $
(see, e.g., [Reference Paris and Kaminski22]). These results are replaced in our case by the following estimate.
$\Re s = \tau $
(see, e.g., [Reference Paris and Kaminski22]). These results are replaced in our case by the following estimate.
Proposition 5 The function
![]() $s \longmapsto \frac {\Gamma (s)}{\Gamma (rs)}$
decreases in vertical lines faster than
$s \longmapsto \frac {\Gamma (s)}{\Gamma (rs)}$
decreases in vertical lines faster than
![]() $\vert s \vert ^{-k}$
, for any
$\vert s \vert ^{-k}$
, for any
![]() $k \geq 0$
, uniformly in each strip
$k \geq 0$
, uniformly in each strip
![]() $\lbrace s \in {\mathbb C} : \alpha \leq \Re (s) \leq \beta \rbrace $
, for any
$\lbrace s \in {\mathbb C} : \alpha \leq \Re (s) \leq \beta \rbrace $
, for any
![]() $\alpha ,\beta \in {\mathbb R}$
.
$\alpha ,\beta \in {\mathbb R}$
.
Proof For
![]() $z \in {\mathbb C} \setminus {\mathbb R}_{-}$
, recall the Stirling formula (see, for instance, [Reference Whittaker and Watson23])
$z \in {\mathbb C} \setminus {\mathbb R}_{-}$
, recall the Stirling formula (see, for instance, [Reference Whittaker and Watson23])
where
![]() $\log $
is defined on its principal branch, and
$\log $
is defined on its principal branch, and
![]() $\Omega $
is an analytic function of z. For
$\Omega $
is an analytic function of z. For
![]() $|\arg z|<\pi $
and
$|\arg z|<\pi $
and
![]() $|z| \to \infty $
,
$|z| \to \infty $
,
![]() $\Omega $
can be written as
$\Omega $
can be written as
 $$\begin{align*}\Omega(z)=\sum_{j=1}^{N-1} \frac{B_{2j}}{2j(2j-1)z^{2j-1}}+R_N(z), \end{align*}$$
$$\begin{align*}\Omega(z)=\sum_{j=1}^{N-1} \frac{B_{2j}}{2j(2j-1)z^{2j-1}}+R_N(z), \end{align*}$$
where
![]() $B_{2j}$
are the Bernoulli numbers
$B_{2j}$
are the Bernoulli numbers
![]() $\left ( B_2=\frac {1}{6}, \ B_4=-\frac {1}{30}, \ B_6=\frac {1}{42}, \text {etc.} \right )$
. Moreover, the error term satisfies
$\left ( B_2=\frac {1}{6}, \ B_4=-\frac {1}{30}, \ B_6=\frac {1}{42}, \text {etc.} \right )$
. Moreover, the error term satisfies
 $$\begin{align*}|R_N(z)| \leq \frac{|B_{2N}|}{2N(2N-1)} \cdot \frac{\sec^{2N}(\frac{\arg z}{2})}{|z|^{2N-1}}; \end{align*}$$
$$\begin{align*}|R_N(z)| \leq \frac{|B_{2N}|}{2N(2N-1)} \cdot \frac{\sec^{2N}(\frac{\arg z}{2})}{|z|^{2N-1}}; \end{align*}$$
thus,
![]() $R_N(z)$
is of order
$R_N(z)$
is of order
![]() ${\mathcal O} \left ( |z|^{-2N+1} \right )$
as
${\mathcal O} \left ( |z|^{-2N+1} \right )$
as
![]() $|z| \to \infty $
(see, for instance, [Reference Paris and Kaminski22, equation (2.1.6)]). For
$|z| \to \infty $
(see, for instance, [Reference Paris and Kaminski22, equation (2.1.6)]). For
![]() $s \notin (-\infty ,0)$
, it follows that
$s \notin (-\infty ,0)$
, it follows that
 $$ \begin{align*} \frac{\Gamma(s)}{\Gamma(rs)}=s^{-s(r-1)}e^{s(r-1)}r^{\frac{1}{2}-rs}e^{\Omega(s)-\Omega(rs)}. \end{align*} $$
$$ \begin{align*} \frac{\Gamma(s)}{\Gamma(rs)}=s^{-s(r-1)}e^{s(r-1)}r^{\frac{1}{2}-rs}e^{\Omega(s)-\Omega(rs)}. \end{align*} $$
Let
![]() $s=a+ib$
,
$s=a+ib$
,
![]() $a \in {\mathbb R}$
fixed. As
$a \in {\mathbb R}$
fixed. As
![]() $|b| \to \infty $
, the difference
$|b| \to \infty $
, the difference
![]() $\vert \Omega (s)-\Omega (rs) \vert \to 0$
; thus,
$\vert \Omega (s)-\Omega (rs) \vert \to 0$
; thus,
![]() $\vert e^{\Omega (s)-\Omega (rs)} \vert \to 1$
. Note that
$\vert e^{\Omega (s)-\Omega (rs)} \vert \to 1$
. Note that
![]() $\vert r^{\frac {1}{2}-rs} \vert = \vert r^{\frac {1}{2}-ra} \vert $
and
$\vert r^{\frac {1}{2}-rs} \vert = \vert r^{\frac {1}{2}-ra} \vert $
and
![]() $\vert e^{(r-1)s} \vert = e^{(r-1)a}$
, so these terms are bounded. We show in Lemma 4.1 that for any
$\vert e^{(r-1)s} \vert = e^{(r-1)a}$
, so these terms are bounded. We show in Lemma 4.1 that for any
![]() $k \geq 0$
,
$k \geq 0$
,
![]() $\vert s \vert ^{k} \vert s^s \vert $
goes to
$\vert s \vert ^{k} \vert s^s \vert $
goes to
![]() $0$
as
$0$
as
![]() $\Re s =a$
is fixed and
$\Re s =a$
is fixed and
![]() $\vert \operatorname {Im} s \vert $
tends to
$\vert \operatorname {Im} s \vert $
tends to
![]() $\infty $
. It follows that the quotient
$\infty $
. It follows that the quotient
![]() $\frac {\Gamma (s)}{\Gamma (rs)}$
indeed decreases in vertical lines faster than
$\frac {\Gamma (s)}{\Gamma (rs)}$
indeed decreases in vertical lines faster than
![]() $\vert s \vert ^{-k}$
, for any
$\vert s \vert ^{-k}$
, for any
![]() $k \geq 0$
, uniformly in vertical strips.
$k \geq 0$
, uniformly in vertical strips.
Lemma 4.1 Let
![]() $k \geq 0$
. If
$k \geq 0$
. If
![]() $a \in {\mathbb R}$
is fixed and
$a \in {\mathbb R}$
is fixed and
![]() $\vert b \vert \to \infty $
, then
$\vert b \vert \to \infty $
, then
![]() $\vert (a+ib)^{k+a+ib} \vert $
tends to zero.
$\vert (a+ib)^{k+a+ib} \vert $
tends to zero.
Proof Let
![]() $s=a+ib \notin (-\infty ,0)$
and set
$s=a+ib \notin (-\infty ,0)$
and set
![]() $\log (a+ib)=x+iy$
. Then
$\log (a+ib)=x+iy$
. Then
![]() $x=\log \sqrt {a^2+b^2}$
,
$x=\log \sqrt {a^2+b^2}$
,
![]() $y=\arg s \in (-\pi ,\pi )$
; hence,
$y=\arg s \in (-\pi ,\pi )$
; hence,
Since
![]() $b=\tan \arg s \cdot a$
, the exponent is equal to
$b=\tan \arg s \cdot a$
, the exponent is equal to
 $$ \begin{align} &(k+a)\log \sqrt{a^2+b^2}-b \arg s \\&\quad= (k+a) \log a +\frac{k+a}{2} \log \left( 1+\tan^2 \arg s \right) -a \tan \arg s \cdot \arg s. \nonumber\end{align} $$
$$ \begin{align} &(k+a)\log \sqrt{a^2+b^2}-b \arg s \\&\quad= (k+a) \log a +\frac{k+a}{2} \log \left( 1+\tan^2 \arg s \right) -a \tan \arg s \cdot \arg s. \nonumber\end{align} $$
If
![]() $a>0$
, then
$a>0$
, then
![]() $\arg s\nearrow \frac {\pi }{2}$
or
$\arg s\nearrow \frac {\pi }{2}$
or
![]() $ \arg s \searrow -\frac {\pi }{2}$
, and in both cases
$ \arg s \searrow -\frac {\pi }{2}$
, and in both cases
![]() $t:=\tan \arg s$
tends to
$t:=\tan \arg s$
tends to
![]() $\infty $
. The exponent (4.1) behaves as the function
$\infty $
. The exponent (4.1) behaves as the function
![]() $t \longmapsto \log (1+t^2)-t$
; therefore, as
$t \longmapsto \log (1+t^2)-t$
; therefore, as
![]() $t \to \infty $
, the exponent goes to
$t \to \infty $
, the exponent goes to
![]() $-\infty $
and the statement of the claim follows.
$-\infty $
and the statement of the claim follows.
If
![]() $a<0$
, then
$a<0$
, then
![]() $\arg s \searrow \frac {\pi }{2}$
or
$\arg s \searrow \frac {\pi }{2}$
or
![]() $\arg s \nearrow -\frac {\pi }{2}$
. In the first case when
$\arg s \nearrow -\frac {\pi }{2}$
. In the first case when
![]() $\arg s \searrow \frac {\pi }{2}$
, it follows that
$\arg s \searrow \frac {\pi }{2}$
, it follows that
![]() $ t = \tan \arg s \to -\infty $
. The exponent (4.1) behaves as
$ t = \tan \arg s \to -\infty $
. The exponent (4.1) behaves as
![]() $ \pm \log (1+t^2)+t $
; hence, the conclusion follows. While if
$ \pm \log (1+t^2)+t $
; hence, the conclusion follows. While if
![]() $\arg s \nearrow -\frac {\pi }{2}$
, then
$\arg s \nearrow -\frac {\pi }{2}$
, then
![]() $t \to \infty $
, and the exponent (4.1) behaves as
$t \to \infty $
, and the exponent (4.1) behaves as
![]() $ \pm \log (1+t^2)-t $
; thus, the exponent tends again to
$ \pm \log (1+t^2)-t $
; thus, the exponent tends again to
![]() $-\infty $
. Therefore,
$-\infty $
. Therefore,
![]() $\vert s^{k+s} \vert $
goes to zero, which ends the proof.
$\vert s^{k+s} \vert $
goes to zero, which ends the proof.
5 Link between the complex powers of
 $\operatorname {\Delta }$
and the heat kernel of
$\operatorname {\Delta }$
and the heat kernel of
 $\operatorname {\Delta }^r$
$\operatorname {\Delta }^r$
Proposition 6 (Inverse Mellin Formula)
For
![]() $\Re \tau>0$
, the operators
$\Re \tau>0$
, the operators
![]() $e^{-t\operatorname {\Delta }^r}$
and
$e^{-t\operatorname {\Delta }^r}$
and
![]() $\operatorname {\Delta }^{-s}$
are related by the following formula:
$\operatorname {\Delta }^{-s}$
are related by the following formula:
Proof The equality holds on each eigensection
![]() $\Phi _j$
corresponding to an eigenvalue
$\Phi _j$
corresponding to an eigenvalue
![]() $\lambda _j \in \operatorname {Spec} \operatorname {\Delta }$
. Since
$\lambda _j \in \operatorname {Spec} \operatorname {\Delta }$
. Since
![]() $\lbrace \Phi _j \rbrace _{j}$
is a Hilbert basis, the result follows.
$\lbrace \Phi _j \rbrace _{j}$
is a Hilbert basis, the result follows.
Set
![]() $\tau> \frac {n}{2r}$
. Then the Schwartz kernel
$\tau> \frac {n}{2r}$
. Then the Schwartz kernel
![]() $q_{-rs}$
of
$q_{-rs}$
of
![]() $\operatorname {\Delta }^{-rs}$
is continuous and by the inverse Mellin formula, we get an identity which relates the Schwartz kernels
$\operatorname {\Delta }^{-rs}$
is continuous and by the inverse Mellin formula, we get an identity which relates the Schwartz kernels
![]() $h_t$
and
$h_t$
and
![]() $q_{-rs}$
:
$q_{-rs}$
:
 $$ \begin{align*} h_t(x,y)- \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) ={}& \tfrac{1}{2 \pi i} \int_{\Re s=\tau} t^{-s}\Gamma(s) q_{-rs}(x,y) ds \\ ={}&\tfrac{1}{2 \pi i} \int_{\Re s = \tau} t^{-s}\frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,y) ds. \end{align*} $$
$$ \begin{align*} h_t(x,y)- \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) ={}& \tfrac{1}{2 \pi i} \int_{\Re s=\tau} t^{-s}\Gamma(s) q_{-rs}(x,y) ds \\ ={}&\tfrac{1}{2 \pi i} \int_{\Re s = \tau} t^{-s}\frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,y) ds. \end{align*} $$
Now let
![]() $k>0$
. By changing
$k>0$
. By changing
![]() $\tau $
to
$\tau $
to
![]() $\tau + \epsilon $
(for a small
$\tau + \epsilon $
(for a small
![]() $\epsilon>0$
) if needed, we can assume that
$\epsilon>0$
) if needed, we can assume that
![]() $\tau -k \notin \lbrace \frac {n}{2}-j :j \in {\mathbb N} \rbrace \cup \{ 0 \}$
. Using Propositions 4 and 5, we can apply the residue formula and move the line of integration to the left:
$\tau -k \notin \lbrace \frac {n}{2}-j :j \in {\mathbb N} \rbrace \cup \{ 0 \}$
. Using Propositions 4 and 5, we can apply the residue formula and move the line of integration to the left:
 $$ \begin{align} \begin{aligned} h_t(x,y) ={}&\tfrac{1}{2 \pi i} \int_{\Re s = \tau -k} t^{-s}\frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,y) ds \\ {}& +\sum_{s \in -{\mathbb N} \cup \lbrace \frac{n-2j}{2r} : \ j \in {\mathbb N} \rbrace} \operatorname{Res}_{s} \left( t^{-s} \Gamma(s) q_{-rs}(x,y) \right) + \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} h_t(x,y) ={}&\tfrac{1}{2 \pi i} \int_{\Re s = \tau -k} t^{-s}\frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,y) ds \\ {}& +\sum_{s \in -{\mathbb N} \cup \lbrace \frac{n-2j}{2r} : \ j \in {\mathbb N} \rbrace} \operatorname{Res}_{s} \left( t^{-s} \Gamma(s) q_{-rs}(x,y) \right) + \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y). \end{aligned} \end{align} $$
Notice that
![]() $-{\mathbb N} \cup \lbrace \frac {n-2j}{2r} : \ j \in {\mathbb N} \rbrace $
is the set of all possible poles of
$-{\mathbb N} \cup \lbrace \frac {n-2j}{2r} : \ j \in {\mathbb N} \rbrace $
is the set of all possible poles of
![]() $s \mapsto \Gamma (s) q_{-rs}(x,y)$
, but some of them might actually be regular points. We will study the sum (5.1) in detail in Theorems 6.1 and 7.1.
$s \mapsto \Gamma (s) q_{-rs}(x,y)$
, but some of them might actually be regular points. We will study the sum (5.1) in detail in Theorems 6.1 and 7.1.
Let K be a compact set in
![]() $M \times M \setminus \operatorname {Diag}$
and
$M \times M \setminus \operatorname {Diag}$
and
![]() $l \in {\mathbb N}$
. Remark that the integral term in (5.1) is of order
$l \in {\mathbb N}$
. Remark that the integral term in (5.1) is of order
![]() ${\mathcal O} \left ( t^{k-\tau } \right )$
in
${\mathcal O} \left ( t^{k-\tau } \right )$
in
![]() ${\mathcal C}^l (K, \mathcal {E} \boxtimes \mathcal {E}^*)$
. Indeed,
${\mathcal C}^l (K, \mathcal {E} \boxtimes \mathcal {E}^*)$
. Indeed,
 $$ \begin{align*} \left\Vert \int_{\Re s = \tau-k} t^{-s}\Gamma(s){q_{-rs}}_{\vert_K} ds \right\Vert{}_l \leq t^{-\tau+k} \cdot \int_{ s = \tau-k+i u} \left\Vert \frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs) {q_{-rs}}_{\vert_K} \right\Vert{}_l du, \end{align*} $$
$$ \begin{align*} \left\Vert \int_{\Re s = \tau-k} t^{-s}\Gamma(s){q_{-rs}}_{\vert_K} ds \right\Vert{}_l \leq t^{-\tau+k} \cdot \int_{ s = \tau-k+i u} \left\Vert \frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs) {q_{-rs}}_{\vert_K} \right\Vert{}_l du, \end{align*} $$
and using again Propositions 4 and 5, the claim follows. Furthermore, when k goes to
![]() $\infty $
, we get
$\infty $
, we get
The meaning of the asymptotic sign in (5.2) is that if we set
![]() $h_t^N$
to be the right-hand side in (5.2) restricted to
$h_t^N$
to be the right-hand side in (5.2) restricted to
![]() $\alpha \leq N$
, then the difference
$\alpha \leq N$
, then the difference
![]() $\vert \partial _t^j \left ( {h_t}_{\vert _K}- h_t^N \right ) \vert $
is of order
$\vert \partial _t^j \left ( {h_t}_{\vert _K}- h_t^N \right ) \vert $
is of order
![]() ${\mathcal O} (t^{N+1-j})$
in
${\mathcal O} (t^{N+1-j})$
in
![]() ${\mathcal C}^l(K, \mathcal {E} \boxtimes \mathcal {E}^*)$
, for any
${\mathcal C}^l(K, \mathcal {E} \boxtimes \mathcal {E}^*)$
, for any
![]() $N,j \in {\mathbb N}$
.
$N,j \in {\mathbb N}$
.
Remark that using again Propositions 4 and 5, the integral term in (5.1) is of order
![]() ${\mathcal O} \left ( t^{k-\tau } \right )$
in
${\mathcal O} \left ( t^{k-\tau } \right )$
in
![]() ${\mathcal C}^l (\operatorname {Diag}, \mathcal {E} \otimes \mathcal {E}^*)$
. Therefore when k tends to
${\mathcal C}^l (\operatorname {Diag}, \mathcal {E} \otimes \mathcal {E}^*)$
. Therefore when k tends to
![]() $\infty $
, we obtain
$\infty $
, we obtain
 $$ \begin{align} {h_t}_{\vert_{\operatorname{Diag}}} \stackrel{t \searrow 0}{\sim} \sum_{\alpha \in \left( -{\mathbb N} \right) \cup \lbrace \frac{n-2j}{2r}: j \in {\mathbb N} \rbrace } t^{-\alpha} \cdot \operatorname{Res}_{s=\alpha} \left( \Gamma(s) {q_{-rs}}_{\vert_{\operatorname{Diag}}} \right) + t^0 \cdot {\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}}_{\vert_{\operatorname{Diag}}}, \end{align} $$
$$ \begin{align} {h_t}_{\vert_{\operatorname{Diag}}} \stackrel{t \searrow 0}{\sim} \sum_{\alpha \in \left( -{\mathbb N} \right) \cup \lbrace \frac{n-2j}{2r}: j \in {\mathbb N} \rbrace } t^{-\alpha} \cdot \operatorname{Res}_{s=\alpha} \left( \Gamma(s) {q_{-rs}}_{\vert_{\operatorname{Diag}}} \right) + t^0 \cdot {\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}}_{\vert_{\operatorname{Diag}}}, \end{align} $$
in the sense of the following:
Definition 5.1 Consider
![]() $l \in {\mathbb N}$
and let
$l \in {\mathbb N}$
and let
![]() $A,B \subset {\mathbb R}$
. We say that
$A,B \subset {\mathbb R}$
. We say that
![]() $ {h_t}_{\vert _{\operatorname {Diag}}} \stackrel {t \searrow 0}{\sim } \sum _{\alpha \in A} t^{\alpha } {c_{\alpha }} + \sum _{\beta \in B} t^{\beta } \log t \cdot c_{\beta } $
if for any
$ {h_t}_{\vert _{\operatorname {Diag}}} \stackrel {t \searrow 0}{\sim } \sum _{\alpha \in A} t^{\alpha } {c_{\alpha }} + \sum _{\beta \in B} t^{\beta } \log t \cdot c_{\beta } $
if for any
![]() $k,N \in {\mathbb N}$
, the difference
$k,N \in {\mathbb N}$
, the difference
 $$\begin{align*}\partial_t^j \left( {h_t}_{\vert_{\operatorname{Diag}}}- \sum_{\alpha \leq N} t^{\alpha} {c_{\alpha}} - \sum_{\beta \leq N} t^{\beta} \log t \cdot c_{\beta} \right) \end{align*}$$
$$\begin{align*}\partial_t^j \left( {h_t}_{\vert_{\operatorname{Diag}}}- \sum_{\alpha \leq N} t^{\alpha} {c_{\alpha}} - \sum_{\beta \leq N} t^{\beta} \log t \cdot c_{\beta} \right) \end{align*}$$
is of order
![]() ${\mathcal O} (t^{N+1-j} \log t)$
in
${\mathcal O} (t^{N+1-j} \log t)$
in
![]() ${\mathcal C}^l(\operatorname {Diag}, \mathcal {E} \otimes \mathcal {E}^*)$
.
${\mathcal C}^l(\operatorname {Diag}, \mathcal {E} \otimes \mathcal {E}^*)$
.
6 The asymptotic expansion of
 $h_t$
away from the diagonal
$h_t$
away from the diagonal
Theorem 6.1 The Schwartz kernel
![]() $h_t$
of the operator
$h_t$
of the operator
![]() $e^{-t\operatorname {\Delta }^r}$
is
$e^{-t\operatorname {\Delta }^r}$
is
![]() ${\mathcal C}^{\infty }$
on
${\mathcal C}^{\infty }$
on
![]() $[0,\infty )\times \left ( M \times M \setminus \operatorname {Diag} \right )$
. Furthermore, let
$[0,\infty )\times \left ( M \times M \setminus \operatorname {Diag} \right )$
. Furthermore, let
![]() $K \subset M \times M \setminus \operatorname {Diag}$
be a compact set. Then the Taylor series of
$K \subset M \times M \setminus \operatorname {Diag}$
be a compact set. Then the Taylor series of
![]() ${h_t}_{\vert _{K}}$
as
${h_t}_{\vert _{K}}$
as
![]() $t \searrow 0$
is the following:
$t \searrow 0$
is the following:
 $$\begin{align*}{h_t}_{\vert_K} \stackrel{t \searrow 0}{\sim} \sum_{j=1}^{\infty} t^{j} {q_{rj}}_{\vert_K} \frac{(-1)^j}{j!}. \end{align*}$$
$$\begin{align*}{h_t}_{\vert_K} \stackrel{t \searrow 0}{\sim} \sum_{j=1}^{\infty} t^{j} {q_{rj}}_{\vert_K} \frac{(-1)^j}{j!}. \end{align*}$$
Moreover, if
![]() $r=\frac {\alpha }{\beta }$
is rational with
$r=\frac {\alpha }{\beta }$
is rational with
![]() $\alpha ,\beta $
coprime, then the coefficient of
$\alpha ,\beta $
coprime, then the coefficient of
![]() $t^j$
vanishes for
$t^j$
vanishes for
![]() $j \in \beta {\mathbb N}^*$
.
$j \in \beta {\mathbb N}^*$
.
Proof Let
![]() $j \in {\mathbb N}$
. Using Propositions 4 and 5,
$j \in {\mathbb N}$
. Using Propositions 4 and 5,
![]() $(-s)(-s-1)\ldots (-s-j+1) t^{-s-j} \frac {\Gamma (s)}{\Gamma (rs) } \Gamma (rs){q_{-rs}}_{\vert _{K}} $
is
$(-s)(-s-1)\ldots (-s-j+1) t^{-s-j} \frac {\Gamma (s)}{\Gamma (rs) } \Gamma (rs){q_{-rs}}_{\vert _{K}} $
is
![]() $L^1$
integrable on
$L^1$
integrable on
![]() $ \Re s = \tau -k$
in
$ \Re s = \tau -k$
in
![]() ${\mathcal C}^l (K, \mathcal {E} \boxtimes \mathcal {E}^*)$
, for sufficiently large k and for any
${\mathcal C}^l (K, \mathcal {E} \boxtimes \mathcal {E}^*)$
, for sufficiently large k and for any
![]() $l \in {\mathbb N}$
. It follows that
$l \in {\mathbb N}$
. It follows that
![]() $h_t$
is
$h_t$
is
![]() ${\mathcal C}^{\infty }$
on
${\mathcal C}^{\infty }$
on
![]() $(0,\infty )\times \left ( M \times M \setminus \operatorname {Diag} \right )$
. By Proposition 2, the function
$(0,\infty )\times \left ( M \times M \setminus \operatorname {Diag} \right )$
. By Proposition 2, the function
![]() $s \mapsto q_{-rs}(x,y)$
is entire for any
$s \mapsto q_{-rs}(x,y)$
is entire for any
![]() $(x,y) \in K$
. Since
$(x,y) \in K$
. Since
![]() $\operatorname {Res}_{s=-j} \Gamma (s)= \frac {(-1)^j}{j!} $
, using (5.2) we get
$\operatorname {Res}_{s=-j} \Gamma (s)= \frac {(-1)^j}{j!} $
, using (5.2) we get
 $$\begin{align*}{h_t}_{\vert_K} \stackrel{t \searrow 0}{\sim} \sum_{j=0}^{\infty} t^{j} {q_{rj}}_{\vert_K} \frac{(-1)^j}{j!} +{\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}}_{\vert_K}.\end{align*}$$
$$\begin{align*}{h_t}_{\vert_K} \stackrel{t \searrow 0}{\sim} \sum_{j=0}^{\infty} t^{j} {q_{rj}}_{\vert_K} \frac{(-1)^j}{j!} +{\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}}_{\vert_K}.\end{align*}$$
We obtained in the proof of Proposition 2 that
![]() ${q_0}_{\vert _K}=-{\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}}_{\vert _K}$
; thus,
${q_0}_{\vert _K}=-{\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}}_{\vert _K}$
; thus,
 $$\begin{align*}{h_t}_{\vert_K} \stackrel{t \searrow 0}{\sim} \sum_{j=1}^{\infty} t^{j} {q_{rj}}_{\vert_K} \frac{(-1)^j}{j!}, \end{align*}$$
$$\begin{align*}{h_t}_{\vert_K} \stackrel{t \searrow 0}{\sim} \sum_{j=1}^{\infty} t^{j} {q_{rj}}_{\vert_K} \frac{(-1)^j}{j!}, \end{align*}$$
and therefore
![]() $h_{t_{\vert _K}}$
is
$h_{t_{\vert _K}}$
is
![]() ${\mathcal C}^{\infty }$
also at
${\mathcal C}^{\infty }$
also at
![]() $t=0$
, and vanishes at order
$t=0$
, and vanishes at order
![]() $1$
. Moreover, using again Proposition 2, if
$1$
. Moreover, using again Proposition 2, if
![]() $r=\frac {\alpha }{\beta }$
is rational and j is a non-zero multiple of
$r=\frac {\alpha }{\beta }$
is rational and j is a non-zero multiple of
![]() $\beta $
, then
$\beta $
, then
![]() $q{_{rj}}_{\vert _K} \equiv 0$
and the conclusion follows.
$q{_{rj}}_{\vert _K} \equiv 0$
and the conclusion follows.
7 The asymptotic expansion of
 $h_t$
along the diagonal
$h_t$
along the diagonal
To obtain the coefficients in the asymptotic of
![]() $h_t$
along the diagonal as
$h_t$
along the diagonal as
![]() $t\searrow 0$
, we need to compute the residues from (5.3). Some of them are related to the heat coefficients
$t\searrow 0$
, we need to compute the residues from (5.3). Some of them are related to the heat coefficients
![]() $a_j$
’s of
$a_j$
’s of
![]() $p_t$
due to Proposition 3. We will distinguish three cases. If n is even,
$p_t$
due to Proposition 3. We will distinguish three cases. If n is even,
![]() $\Gamma (s)q_{-rs}(x)$
has simple poles in
$\Gamma (s)q_{-rs}(x)$
has simple poles in
![]() $\lbrace \frac {n}{2r},\frac {n-2}{2r},\ldots ,\frac {2}{2r} \rbrace \cup \lbrace 0,-1,\ldots \rbrace $
and the residues will give rise to real powers of t. If n is odd and either r is irrational or r is rational with odd denominator,
$\lbrace \frac {n}{2r},\frac {n-2}{2r},\ldots ,\frac {2}{2r} \rbrace \cup \lbrace 0,-1,\ldots \rbrace $
and the residues will give rise to real powers of t. If n is odd and either r is irrational or r is rational with odd denominator,
![]() $\Gamma (s)q_{-rs}(x)$
has simple poles in
$\Gamma (s)q_{-rs}(x)$
has simple poles in
![]() $\lbrace 0,-1,\ldots \rbrace \cup \lbrace \frac {n-2j}{2r} : j=0,1,\ldots \rbrace $
. Otherwise, if n is odd and r is rational with even denominator, then there exist some double poles which give rise to logarithmic terms in the asymptotic expansion of
$\lbrace 0,-1,\ldots \rbrace \cup \lbrace \frac {n-2j}{2r} : j=0,1,\ldots \rbrace $
. Otherwise, if n is odd and r is rational with even denominator, then there exist some double poles which give rise to logarithmic terms in the asymptotic expansion of
![]() $h_t$
.
$h_t$
.
Theorem 7.1 Let
![]() $a_j(x,x)$
be the coefficients in (
2.1
) of the heat kernel
$a_j(x,x)$
be the coefficients in (
2.1
) of the heat kernel
![]() $p_t$
of the non-negative self-adjoint generalized Laplacian
$p_t$
of the non-negative self-adjoint generalized Laplacian
![]() $\operatorname {\Delta }$
. The asymptotic expansion of the Schwartz kernel
$\operatorname {\Delta }$
. The asymptotic expansion of the Schwartz kernel
![]() $h_t$
of the operator
$h_t$
of the operator
![]() $e^{-t\operatorname {\Delta }^r}$
,
$e^{-t\operatorname {\Delta }^r}$
,
![]() $r \in (0,1)$
along the diagonal when
$r \in (0,1)$
along the diagonal when
![]() $t\searrow 0$
is the following:
$t\searrow 0$
is the following:
-
(1) If n is even, then
 $$\begin{align*}{h_t}_{\vert_{\operatorname{Diag}}} \stackrel{t \searrow 0}{\sim} \sum_{j=0}^{n/2-1} t^{- \frac{n-2j}{2r}} \cdot A_{-\frac{n-2j}{2r}} + a_{n/2} + \sum_{j=1}^{\infty} t^j \cdot A_j. \end{align*}$$
$$\begin{align*}{h_t}_{\vert_{\operatorname{Diag}}} \stackrel{t \searrow 0}{\sim} \sum_{j=0}^{n/2-1} t^{- \frac{n-2j}{2r}} \cdot A_{-\frac{n-2j}{2r}} + a_{n/2} + \sum_{j=1}^{\infty} t^j \cdot A_j. \end{align*}$$
If
 $r=\frac {\alpha }{\beta }$
is rational, for
$r=\frac {\alpha }{\beta }$
is rational, for
 $j=l \beta $
,
$j=l \beta $
,
 $ l \in {\mathbb N}^*$
, we obtain that
$ l \in {\mathbb N}^*$
, we obtain that
 $q_{rj}(x,x)=(-1)^j \cdot j! \cdot a_{\frac {n}{2}+l \alpha }(x,x)$
, and the coefficient of
$q_{rj}(x,x)=(-1)^j \cdot j! \cdot a_{\frac {n}{2}+l \alpha }(x,x)$
, and the coefficient of
 $t^{l \beta }$
can be described more precisely as
$t^{l \beta }$
can be described more precisely as  $$\begin{align*}A_{l \beta}=a_{\frac{n}{2}+l \alpha}. \end{align*}$$
$$\begin{align*}A_{l \beta}=a_{\frac{n}{2}+l \alpha}. \end{align*}$$
-
(2) If n is odd and either
 $r \in {\mathbb R} \setminus {\mathbb Q}$
or the denominator of r is odd, then
$r \in {\mathbb R} \setminus {\mathbb Q}$
or the denominator of r is odd, then  $$\begin{align*}{h_t}_{\vert_{\operatorname{Diag}}} \stackrel{t \searrow 0}{\sim} \sum_{j=0}^{(n-1)/2} t^{- \frac{n-2j}{2r}} \cdot A_{-\frac{n-2j}{2r}} + \sum_{j=1}^{\infty} t^j \cdot A_j + \sum_{j=1}^{\infty} t^{\frac{2j+1}{2r}} \cdot A_{\frac{2j+1}{2r}}. \end{align*}$$
$$\begin{align*}{h_t}_{\vert_{\operatorname{Diag}}} \stackrel{t \searrow 0}{\sim} \sum_{j=0}^{(n-1)/2} t^{- \frac{n-2j}{2r}} \cdot A_{-\frac{n-2j}{2r}} + \sum_{j=1}^{\infty} t^j \cdot A_j + \sum_{j=1}^{\infty} t^{\frac{2j+1}{2r}} \cdot A_{\frac{2j+1}{2r}}. \end{align*}$$
Moreover, if
 $r=\frac {\alpha }{\beta }$
is rational and
$r=\frac {\alpha }{\beta }$
is rational and
 $\beta $
is odd, then
$\beta $
is odd, then
 $ A_{l \beta } \equiv 0$
for any
$ A_{l \beta } \equiv 0$
for any
 $l \in {\mathbb N}^*$
.
$l \in {\mathbb N}^*$
. -
(3) If n is odd,
 $r=\frac {\alpha }{\beta }$
is rational and its denominator
$r=\frac {\alpha }{\beta }$
is rational and its denominator
 $\beta $
is even, then
$\beta $
is even, then 
In all these cases, the coefficients are
 $$ \begin{align*} {}&A_{-\frac{n-2j}{2r}}(x)= \frac{\Gamma \left( \frac{n-2j}{2r} \right)} {\Gamma \left( \frac{n-2j}{2} \right)} \cdot \frac{1}{r} \cdot a_j(x,x), && A_{j}(x)=\frac{(-1)^j}{j!} \cdot q_{rj}(x,x), \\ {}&A_{\frac{2j+1}{2r}}(x)=\frac{\Gamma \left( - \frac{2j+1}{2r} \right)} {\Gamma \left( - \frac{2j+1}{2} \right)} \cdot \frac{1}{r} \cdot a_{\frac{n+2j+1}{2}}(x,x), && B_{l\frac{\beta}{2}}(x)=\frac{(-1)^{l\frac{\beta}{2}}}{r \left( l\frac{\beta}{2} \right) ! \Gamma \left( - l\frac{\beta}{2} \cdot r \right)} \cdot a_{\frac{n+l \alpha}{2}}(x,x), \end{align*} $$
$$ \begin{align*} {}&A_{-\frac{n-2j}{2r}}(x)= \frac{\Gamma \left( \frac{n-2j}{2r} \right)} {\Gamma \left( \frac{n-2j}{2} \right)} \cdot \frac{1}{r} \cdot a_j(x,x), && A_{j}(x)=\frac{(-1)^j}{j!} \cdot q_{rj}(x,x), \\ {}&A_{\frac{2j+1}{2r}}(x)=\frac{\Gamma \left( - \frac{2j+1}{2r} \right)} {\Gamma \left( - \frac{2j+1}{2} \right)} \cdot \frac{1}{r} \cdot a_{\frac{n+2j+1}{2}}(x,x), && B_{l\frac{\beta}{2}}(x)=\frac{(-1)^{l\frac{\beta}{2}}}{r \left( l\frac{\beta}{2} \right) ! \Gamma \left( - l\frac{\beta}{2} \cdot r \right)} \cdot a_{\frac{n+l \alpha}{2}}(x,x), \end{align*} $$
 $$\begin{align*}A_{l \frac{\beta}{2}}(x)= \frac{(-1)^{l \frac{\beta}{2}}}{(l \frac{\beta}{2})! \Gamma(-rl \frac{\beta}{2})} \cdot \operatorname{FP}_{s=-l \frac{\beta}{2}} \left( \Gamma(rs)q_{-rs}(x,x) \kern-1pt\right) + \operatorname{FP}_{s=-l \frac{\beta}{2}} \!\left(\kern-1pt \frac{\Gamma(s)}{\Gamma(rs)} \kern-1pt\right) \cdot \frac{a_{\frac{n+l\alpha}{2}(x,x)}}{r}. \end{align*}$$
$$\begin{align*}A_{l \frac{\beta}{2}}(x)= \frac{(-1)^{l \frac{\beta}{2}}}{(l \frac{\beta}{2})! \Gamma(-rl \frac{\beta}{2})} \cdot \operatorname{FP}_{s=-l \frac{\beta}{2}} \left( \Gamma(rs)q_{-rs}(x,x) \kern-1pt\right) + \operatorname{FP}_{s=-l \frac{\beta}{2}} \!\left(\kern-1pt \frac{\Gamma(s)}{\Gamma(rs)} \kern-1pt\right) \cdot \frac{a_{\frac{n+l\alpha}{2}(x,x)}}{r}. \end{align*}$$
7.1 The case when n is even
For
![]() $j \in \{0,1,\ldots ,n/2-1 \}$
, we have
$j \in \{0,1,\ldots ,n/2-1 \}$
, we have
 $$ \begin{align} \operatorname{Res}_{s=\frac{n-2j}{2r}} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \Gamma(rs)q_{-rs}(x,x) \right) =t^{-\frac{n-2j}{2r}} \cdot \frac{\Gamma(\frac{n-2j}{2r})}{\Gamma(\frac{n-2j}{2})} \cdot \frac{a_j(x,x)}{r}. \end{align} $$
$$ \begin{align} \operatorname{Res}_{s=\frac{n-2j}{2r}} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \Gamma(rs)q_{-rs}(x,x) \right) =t^{-\frac{n-2j}{2r}} \cdot \frac{\Gamma(\frac{n-2j}{2r})}{\Gamma(\frac{n-2j}{2})} \cdot \frac{a_j(x,x)}{r}. \end{align} $$
The residue in
![]() $s=0$
is given by
$s=0$
is given by
 $$ \begin{align*} \operatorname{Res}_{s=0} \left( t^{-s} \Gamma(s) q_{-rs}(x,x) \right) ={}& \operatorname{Res}_{s=0} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \Gamma(rs)q_{-rs}(x,x) \right) \\ ={}& r \cdot \frac{1}{r} \kern-1.2pt\left(\kern-1pt a_{\frac{n}{2}}(x,x) \kern1pt{-}\kern1pt \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) \kern-1pt\right)\kern1.2pt{=}\kern1.2pt a_{\frac{n}{2}}(x,x)\kern1pt{-}\kern1pt\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x), \end{align*} $$
$$ \begin{align*} \operatorname{Res}_{s=0} \left( t^{-s} \Gamma(s) q_{-rs}(x,x) \right) ={}& \operatorname{Res}_{s=0} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \Gamma(rs)q_{-rs}(x,x) \right) \\ ={}& r \cdot \frac{1}{r} \kern-1.2pt\left(\kern-1pt a_{\frac{n}{2}}(x,x) \kern1pt{-}\kern1pt \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) \kern-1pt\right)\kern1.2pt{=}\kern1.2pt a_{\frac{n}{2}}(x,x)\kern1pt{-}\kern1pt\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x), \end{align*} $$
thus the coefficient of
![]() $t^0$
in the asymptotic expansion (5.3) is
$t^0$
in the asymptotic expansion (5.3) is
![]() $a_{\frac {n}{2}}(x,x)$
.
$a_{\frac {n}{2}}(x,x)$
.
7.1.1 The case when n is even and r is irrational
Let
![]() $j \in {\mathbb N}^*$
. Then
$j \in {\mathbb N}^*$
. Then
 $$ \begin{align} \operatorname{Res}_{s=-j} \left( t^{-s} \Gamma(s) q_{-rs}(x,x) \right) = t^j \frac{(-1)^j}{j!} \cdot q_{rj}(x,x). \end{align} $$
$$ \begin{align} \operatorname{Res}_{s=-j} \left( t^{-s} \Gamma(s) q_{-rs}(x,x) \right) = t^j \frac{(-1)^j}{j!} \cdot q_{rj}(x,x). \end{align} $$
Therefore, in this case, the asymptotic expansion of
![]() $h_t$
is the following:
$h_t$
is the following:
 $$\begin{align*}h_t(x,x) \stackrel{t \searrow 0}{\sim} \sum_{j=0}^{n/2-1} t^{-\frac{n-2j}{2r}} \frac{\Gamma \left( \frac{n-2j}{2r} \right)}{\Gamma \left( \frac{n-2j}{2} \right)} \frac{a_j(x,x)}{r} + a_{\frac{n}{2}}(x,x) + \sum_{j=1}^{\infty} t^j \frac{(-1)^j}{j!} q_{rj}(x,x). \end{align*}$$
$$\begin{align*}h_t(x,x) \stackrel{t \searrow 0}{\sim} \sum_{j=0}^{n/2-1} t^{-\frac{n-2j}{2r}} \frac{\Gamma \left( \frac{n-2j}{2r} \right)}{\Gamma \left( \frac{n-2j}{2} \right)} \frac{a_j(x,x)}{r} + a_{\frac{n}{2}}(x,x) + \sum_{j=1}^{\infty} t^j \frac{(-1)^j}{j!} q_{rj}(x,x). \end{align*}$$
7.1.2 The case when n is even and
 $r=\frac {\alpha }{\beta }$
is rational with
$r=\frac {\alpha }{\beta }$
is rational with
 $(\alpha ,\beta )=1$
$(\alpha ,\beta )=1$
Some of the coefficients
![]() $q_{rj}(x,x)$
from (7.2) can be expressed in terms of the
$q_{rj}(x,x)$
from (7.2) can be expressed in terms of the
![]() $a_{k}$
’s from (2.1). Remark that
$a_{k}$
’s from (2.1). Remark that
![]() $\frac {\Gamma (s)}{\Gamma (rs)}$
has simple poles in
$\frac {\Gamma (s)}{\Gamma (rs)}$
has simple poles in
![]() $\{-1,-2,\ldots \} \setminus \{ \frac {-1}{r}, \frac {-2}{r},\ldots \}$
. For
$\{-1,-2,\ldots \} \setminus \{ \frac {-1}{r}, \frac {-2}{r},\ldots \}$
. For
![]() $j \in {\mathbb N}^*$
,
$j \in {\mathbb N}^*$
,
![]() $s:=-\frac {j}{r} \in \{-1,-2,\ldots \}$
if and only if j is a multiple of
$s:=-\frac {j}{r} \in \{-1,-2,\ldots \}$
if and only if j is a multiple of
![]() $\alpha $
, which is equivalent to
$\alpha $
, which is equivalent to
![]() $s=\frac {-l\alpha }{r}=-l\beta $
for some
$s=\frac {-l\alpha }{r}=-l\beta $
for some
![]() $l \in {\mathbb N}^*$
. In this case, we obtain
$l \in {\mathbb N}^*$
. In this case, we obtain
 $$ \begin{align*} \operatorname{Res}_{s=-l\beta} \left( t^{-s} \Gamma(s) q_{-rs}(x,x) \right) ={}& \operatorname{Res}_{s=-l\beta} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \Gamma(rs)q_{-rs}(x,x) \right) \\ ={}& t^{l\beta} r \cdot \frac{1}{r} a_{\frac{n}{2}+l\alpha}(x,x)=t^{l\beta} a_{\frac{n}{2}+l \alpha}(x,x). \end{align*} $$
$$ \begin{align*} \operatorname{Res}_{s=-l\beta} \left( t^{-s} \Gamma(s) q_{-rs}(x,x) \right) ={}& \operatorname{Res}_{s=-l\beta} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \Gamma(rs)q_{-rs}(x,x) \right) \\ ={}& t^{l\beta} r \cdot \frac{1}{r} a_{\frac{n}{2}+l\alpha}(x,x)=t^{l\beta} a_{\frac{n}{2}+l \alpha}(x,x). \end{align*} $$
Hence, for rational
![]() $r=\frac {\alpha }{\beta }$
, if
$r=\frac {\alpha }{\beta }$
, if
![]() $j=l\beta $
,
$j=l\beta $
,
![]() $l \in {\mathbb N}^*$
, we conclude that
$l \in {\mathbb N}^*$
, we conclude that
and
![]() $h_t(x,x)$
has the following asymptotic expansion as
$h_t(x,x)$
has the following asymptotic expansion as
![]() $t \searrow 0$
:
$t \searrow 0$
:

7.2 The case when n is odd
For
![]() $j \in \lbrace 0,1,\ldots ,(n-1)/2 \rbrace $
, the coefficient of
$j \in \lbrace 0,1,\ldots ,(n-1)/2 \rbrace $
, the coefficient of
![]() $t^{-\frac {n-2j}{2r}}$
is computed as in (7.1). Furthermore, in
$t^{-\frac {n-2j}{2r}}$
is computed as in (7.1). Furthermore, in
![]() $s=0$
,
$s=0$
,
 $$ \begin{align*} \operatorname{Res}_{s=0} \left( t^{-s} \Gamma(s) q_{-rs}(x,x) \right) ={}& \operatorname{Res}_{s=0} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,x) \right) \\ ={}& r \cdot \frac{-1}{r} \cdot \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) =-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x); \end{align*} $$
$$ \begin{align*} \operatorname{Res}_{s=0} \left( t^{-s} \Gamma(s) q_{-rs}(x,x) \right) ={}& \operatorname{Res}_{s=0} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,x) \right) \\ ={}& r \cdot \frac{-1}{r} \cdot \operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x) =-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,x); \end{align*} $$
hence, there is no free term in the asymptotic expansion of
![]() $h_t$
as t goes to zero.
$h_t$
as t goes to zero.
Now we have to compute the residues of the function
![]() $t^{-s} \Gamma (s) q_{-rs}(x,x)$
in
$t^{-s} \Gamma (s) q_{-rs}(x,x)$
in
![]() ${s \in \{ -1,-2,\ldots \}}$
and
${s \in \{ -1,-2,\ldots \}}$
and
![]() $ s \in \{ \frac {-1}{2r}, \frac {-3}{2r},\ldots \}$
.
$ s \in \{ \frac {-1}{2r}, \frac {-3}{2r},\ldots \}$
.
7.2.1 The case when n is odd and r is irrational
Then these sets are disjoint; thus, all poles of the function
![]() $\Gamma (s) q_{-rs}(x)$
are simple. For
$\Gamma (s) q_{-rs}(x)$
are simple. For
![]() $j \in {\mathbb N}^*$
, the coefficient of
$j \in {\mathbb N}^*$
, the coefficient of
![]() $t^j$
is obtained as in (7.2). Furthermore, for
$t^j$
is obtained as in (7.2). Furthermore, for
![]() $j \in {\mathbb N}$
, we get
$j \in {\mathbb N}$
, we get
 $$ \begin{align} \operatorname{Res}_{s=-\frac{2j+1}{2r}} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,x) \right) =t^{\frac{2j+1}{2r}} \cdot \frac{\Gamma(-\frac{2j+1}{2r})}{\Gamma(-\frac{2j+1}{r})} \cdot \frac{a_{\frac{n+2j+1}{2}}(x,x)}{r}. \end{align} $$
$$ \begin{align} \operatorname{Res}_{s=-\frac{2j+1}{2r}} \left( t^{-s} \frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,x) \right) =t^{\frac{2j+1}{2r}} \cdot \frac{\Gamma(-\frac{2j+1}{2r})}{\Gamma(-\frac{2j+1}{r})} \cdot \frac{a_{\frac{n+2j+1}{2}}(x,x)}{r}. \end{align} $$
Therefore, the small-time asymptotic expansion of
![]() $h_t$
is the following:
$h_t$
is the following:
 $$ \begin{align*} h_t(x,x) \stackrel{t \searrow 0}{\sim}{}& \sum_{j=0}^{n/2-1} t^{-\frac{n-2j}{2r}} \cdot \frac{\Gamma \left( \frac{n-2j}{2r} \right)}{\Gamma \left( \frac{n-2j}{2} \right)} \cdot \frac{a_j(x,x)}{r} + \sum_{j=1}^{\infty} t^j \cdot \frac{(-1)^j}{j!} q_{rj}(x,x) \\ +{}& \sum_{j=0}^{\infty} t^{\frac{2j+1}{2r}} \cdot \frac{\Gamma \left( -\frac{2j+1}{2r} \right)}{\Gamma \left( - \frac{2j+1}{2} \right)} \cdot \frac{a_{\frac{n+2j+1}{2}}(x,x)}{r}. \end{align*} $$
$$ \begin{align*} h_t(x,x) \stackrel{t \searrow 0}{\sim}{}& \sum_{j=0}^{n/2-1} t^{-\frac{n-2j}{2r}} \cdot \frac{\Gamma \left( \frac{n-2j}{2r} \right)}{\Gamma \left( \frac{n-2j}{2} \right)} \cdot \frac{a_j(x,x)}{r} + \sum_{j=1}^{\infty} t^j \cdot \frac{(-1)^j}{j!} q_{rj}(x,x) \\ +{}& \sum_{j=0}^{\infty} t^{\frac{2j+1}{2r}} \cdot \frac{\Gamma \left( -\frac{2j+1}{2r} \right)}{\Gamma \left( - \frac{2j+1}{2} \right)} \cdot \frac{a_{\frac{n+2j+1}{2}}(x,x)}{r}. \end{align*} $$
7.2.2 The case when n is odd and
 $r=\frac {\alpha }{\beta }$
is rational
$r=\frac {\alpha }{\beta }$
is rational
Consider the sets
Remark that A is the set of negative poles of
![]() $s \longmapsto t^{-s}\Gamma (s)q_{-rs}(x,x)$
, and
$s \longmapsto t^{-s}\Gamma (s)q_{-rs}(x,x)$
, and
![]() $A \setminus C$
is the set of poles of the function
$A \setminus C$
is the set of poles of the function
![]() $s \longmapsto \frac {\Gamma (s)}{\Gamma (rs)}$
. Clearly B and C are disjoint. Moreover,
$s \longmapsto \frac {\Gamma (s)}{\Gamma (rs)}$
. Clearly B and C are disjoint. Moreover,
![]() $A \cap C=\{ -l\beta : \ l \in {\mathbb N}^* \}$
. Furthermore, if
$A \cap C=\{ -l\beta : \ l \in {\mathbb N}^* \}$
. Furthermore, if
![]() $\beta $
is odd, then
$\beta $
is odd, then
![]() $A\cap B=\emptyset $
, and otherwise if
$A\cap B=\emptyset $
, and otherwise if
![]() $\beta $
is even, then
$\beta $
is even, then
![]() $A\cap B=\{-l\frac {\beta }{2}: \ l \in 2 {\mathbb N}+1 \}$
. Such an
$A\cap B=\{-l\frac {\beta }{2}: \ l \in 2 {\mathbb N}+1 \}$
. Such an
![]() $s=-\frac {2j+1}{2r}=l\frac {\beta }{2} \in A \cap B$
is a double pole for
$s=-\frac {2j+1}{2r}=l\frac {\beta }{2} \in A \cap B$
is a double pole for
![]() $\Gamma (s)q_{rs}(x)$
.
$\Gamma (s)q_{rs}(x)$
.
7.2.3 Suppose that
 $\beta $
is odd
$\beta $
is odd
Then A and B are disjoint. Thus, for
![]() $s=-\frac {2j+1}{2r} \in B$
,
$s=-\frac {2j+1}{2r} \in B$
,
![]() $j \in {\mathbb N}$
, the residue of
$j \in {\mathbb N}$
, the residue of
![]() $t^{-s}\Gamma (s)q_{rs}(x,x)$
is the one computed in (7.4).
$t^{-s}\Gamma (s)q_{rs}(x,x)$
is the one computed in (7.4).
For
![]() $s=-j \in A\setminus C$
(which means that
$s=-j \in A\setminus C$
(which means that
![]() $j \in {\mathbb N}^*$
,
$j \in {\mathbb N}^*$
,
![]() $\beta \nmid j$
), the residue of
$\beta \nmid j$
), the residue of
![]() $t^{-s}\Gamma (s)q_{-rs}(x,x)$
in s is the one computed in (7.2).
$t^{-s}\Gamma (s)q_{-rs}(x,x)$
in s is the one computed in (7.2).
If
![]() $s=-l\beta =-\frac {l\alpha }{r} \in A\cap C$
for some
$s=-l\beta =-\frac {l\alpha }{r} \in A\cap C$
for some
![]() $l \in {\mathbb N}^*$
, then
$l \in {\mathbb N}^*$
, then
![]() $\Gamma (s)$
has a simple pole in s and by Proposition 3, (the meromorphic extension of)
$\Gamma (s)$
has a simple pole in s and by Proposition 3, (the meromorphic extension of)
![]() $q_{-rs}(x,x)$
vanishes at
$q_{-rs}(x,x)$
vanishes at
![]() $s=-l\beta $
. Hence, the product
$s=-l\beta $
. Hence, the product
![]() $t^{-s}\Gamma (s)q_{-rs}(x,x)$
is holomorphic in
$t^{-s}\Gamma (s)q_{-rs}(x,x)$
is holomorphic in
![]() $s=-l\beta $
and
$s=-l\beta $
and
![]() $t^{l\beta }$
,
$t^{l\beta }$
,
![]() $l \in {\mathbb N}^*$
, does not appear in the asymptotic expansion.
$l \in {\mathbb N}^*$
, does not appear in the asymptotic expansion.
Therefore, if
![]() $r=\frac {\alpha }{\beta }$
is rational and
$r=\frac {\alpha }{\beta }$
is rational and
![]() $\beta $
is odd, we obtain
$\beta $
is odd, we obtain

7.2.4 Assume now that
 $\beta $
is even
$\beta $
is even
For
![]() $s=-\frac {2j+1}{2r}\in B \setminus A$
(
$s=-\frac {2j+1}{2r}\in B \setminus A$
(
![]() $j \in {\mathbb N} $
with
$j \in {\mathbb N} $
with
![]() $\alpha \nmid 2j+1$
), the residue is computed as in (7.4). For
$\alpha \nmid 2j+1$
), the residue is computed as in (7.4). For
![]() $s=-j \in A\setminus \left ( B\cup C \right )$
(namely
$s=-j \in A\setminus \left ( B\cup C \right )$
(namely
![]() $j \in {\mathbb N}^*$
,
$j \in {\mathbb N}^*$
,
![]() $\frac {\beta }{2} \nmid j$
), the residue is computed as in (7.2).
$\frac {\beta }{2} \nmid j$
), the residue is computed as in (7.2).
For
![]() $s \in C \cap A$
(namely
$s \in C \cap A$
(namely
![]() $s=-l\beta $
,
$s=-l\beta $
,
![]() $l \in {\mathbb N}^*$
), the residue is again
$l \in {\mathbb N}^*$
), the residue is again
![]() $0$
. Indeed,
$0$
. Indeed,
![]() $\Gamma (s)$
has a simple pole in
$\Gamma (s)$
has a simple pole in
![]() $-l\beta $
and by Proposition 3, (the meromorphic extension of)
$-l\beta $
and by Proposition 3, (the meromorphic extension of)
![]() $q_{-rs}(x,x)$
vanishes in
$q_{-rs}(x,x)$
vanishes in
![]() $-l\beta $
, thus
$-l\beta $
, thus
![]() $t^{l\beta }$
does not appear in the asymptotic expansion of
$t^{l\beta }$
does not appear in the asymptotic expansion of
![]() $h_t$
.
$h_t$
.
Finally, if
![]() $s=-\frac {l\alpha }{2r}=-l\frac {\beta }{2} \in A \cap B$
,
$s=-\frac {l\alpha }{2r}=-l\frac {\beta }{2} \in A \cap B$
,
![]() $l \in 2 {\mathbb N} +1$
, then s is a double pole for
$l \in 2 {\mathbb N} +1$
, then s is a double pole for
![]() $\Gamma (s)q_{-rs}(x,x)$
. We write the Laurent expansions of the functions
$\Gamma (s)q_{-rs}(x,x)$
. We write the Laurent expansions of the functions
![]() $t^{-s}$
,
$t^{-s}$
,
![]() $\frac {\Gamma (s)}{\Gamma (rs)}$
, and
$\frac {\Gamma (s)}{\Gamma (rs)}$
, and
![]() $\Gamma (rs)q_{-rs}(x,x),$
respectively, in
$\Gamma (rs)q_{-rs}(x,x),$
respectively, in
![]() $s=-\frac {l\alpha }{2r}=-l\frac {\beta }{2}=:-k$
:
$s=-\frac {l\alpha }{2r}=-l\frac {\beta }{2}=:-k$
:
 $$ \begin{align*} {}&t^{-s}=t^k-t^k \log t + {\mathcal O} (s+k)^2, \\ {}&\frac{\Gamma(s)}{\Gamma(rs)}=\frac{(-1)^k}{k! \cdot \Gamma(-kr)} (s+k)^{-1}+\cdots, \\ {}&\Gamma(rs)(q_{-rs}(x,x))=\frac{1}{r}a_{\frac{n+l\alpha}{2}}(x,x) (s+k)^{-1}+\cdots. \end{align*} $$
$$ \begin{align*} {}&t^{-s}=t^k-t^k \log t + {\mathcal O} (s+k)^2, \\ {}&\frac{\Gamma(s)}{\Gamma(rs)}=\frac{(-1)^k}{k! \cdot \Gamma(-kr)} (s+k)^{-1}+\cdots, \\ {}&\Gamma(rs)(q_{-rs}(x,x))=\frac{1}{r}a_{\frac{n+l\alpha}{2}}(x,x) (s+k)^{-1}+\cdots. \end{align*} $$
Thus, we finally obtain that
 $$ \begin{align*} \operatorname{Res}_{s=-k}\left( t^{-s} \cdot \frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,x)\right)={}& t^k \cdot \frac{(-1)^k}{k! \Gamma(-kr)} \cdot \operatorname{FP}_{s=-k} \left( \Gamma(rs)q_{-rs}(x,x) \right) \\ {}&+ t^k \operatorname{FP}_{s=-k} \left(\frac{\Gamma(s)}{\Gamma(rs)} \right) \cdot\frac{a_{\frac{n+l\alpha}{2}(x,x)}}{r} \\ {}&+t^k \log t \cdot \frac{(-1)^k}{k! \Gamma(-kr)} \frac{a_{\frac{n+l\alpha}{2}(x,x)}}{r}. \end{align*} $$
$$ \begin{align*} \operatorname{Res}_{s=-k}\left( t^{-s} \cdot \frac{\Gamma(s)}{\Gamma(rs)} \cdot \Gamma(rs)q_{-rs}(x,x)\right)={}& t^k \cdot \frac{(-1)^k}{k! \Gamma(-kr)} \cdot \operatorname{FP}_{s=-k} \left( \Gamma(rs)q_{-rs}(x,x) \right) \\ {}&+ t^k \operatorname{FP}_{s=-k} \left(\frac{\Gamma(s)}{\Gamma(rs)} \right) \cdot\frac{a_{\frac{n+l\alpha}{2}(x,x)}}{r} \\ {}&+t^k \log t \cdot \frac{(-1)^k}{k! \Gamma(-kr)} \frac{a_{\frac{n+l\alpha}{2}(x,x)}}{r}. \end{align*} $$
8 Non-triviality of the coefficients
Let us prove Theorem 1.1. Recall the definition of the zeta function of a non-negative self-adjoint generalized Laplacian
![]() $\Delta $
:
$\Delta $
:
 $$\begin{align*}\zeta_{\Delta}(s):=\sum_{\lambda \in \operatorname{Spec} \Delta \setminus \{ 0 \}} \lambda^{-s}=\int_{M} q_{-s}(x,x)dg(x). \end{align*}$$
$$\begin{align*}\zeta_{\Delta}(s):=\sum_{\lambda \in \operatorname{Spec} \Delta \setminus \{ 0 \}} \lambda^{-s}=\int_{M} q_{-s}(x,x)dg(x). \end{align*}$$
This series is absolutely convergent for
![]() $\Re s> \frac {n}{2}$
and extends meromorphically to
$\Re s> \frac {n}{2}$
and extends meromorphically to
![]() ${\mathbb C} $
with possible simple poles in the set
${\mathbb C} $
with possible simple poles in the set
(see, for instance, [Reference Gilkey13]).
Consider the trivial bundle
![]() ${\mathbb C}$
over a compact Riemannian manifold M. As in [Reference Loya, Moroianu and Ponge17], let
${\mathbb C}$
over a compact Riemannian manifold M. As in [Reference Loya, Moroianu and Ponge17], let
![]() $\left ( \operatorname {\Delta } + \xi \right )_{\xi> 0}$
be a family of generalized Laplacians indexed by
$\left ( \operatorname {\Delta } + \xi \right )_{\xi> 0}$
be a family of generalized Laplacians indexed by
![]() $\xi>0$
, and denote by
$\xi>0$
, and denote by
![]() $ q_{-s}^{\xi } $
the Schwartz kernels of the operators
$ q_{-s}^{\xi } $
the Schwartz kernels of the operators
![]() $(\operatorname {\Delta }+\xi )^{-s}$
. Note that for
$(\operatorname {\Delta }+\xi )^{-s}$
. Note that for
![]() $\Re s> \frac {n}{2}$
,
$\Re s> \frac {n}{2}$
,
 $$ \begin{align} \int_M q_{-s}^{\xi} (x,x) dx = \operatorname{Tr} \left( \operatorname{\Delta} +\xi \right)^{-s}=\zeta_{\operatorname{\Delta}+\xi}(s) = \sum_{\lambda_j \in \operatorname{Spec} \operatorname{\Delta}} \left( \lambda_j +\xi \right)^{-s}. \end{align} $$
$$ \begin{align} \int_M q_{-s}^{\xi} (x,x) dx = \operatorname{Tr} \left( \operatorname{\Delta} +\xi \right)^{-s}=\zeta_{\operatorname{\Delta}+\xi}(s) = \sum_{\lambda_j \in \operatorname{Spec} \operatorname{\Delta}} \left( \lambda_j +\xi \right)^{-s}. \end{align} $$
Since for
![]() $\Re s> \frac {n}{2}$
the sum is absolutely convergent, we obtain
$\Re s> \frac {n}{2}$
the sum is absolutely convergent, we obtain
 $$\begin{align*}\frac{d}{d\xi} \zeta_{\operatorname{\Delta}+\xi} (s) =-s \cdot \sum_{\lambda_j \in \operatorname{Spec} \operatorname{\Delta}} \left( \lambda_j +\xi \right)^{-s-1}= -s\cdot \zeta_{ \operatorname{\Delta} +\xi}( s+1). \end{align*}$$
$$\begin{align*}\frac{d}{d\xi} \zeta_{\operatorname{\Delta}+\xi} (s) =-s \cdot \sum_{\lambda_j \in \operatorname{Spec} \operatorname{\Delta}} \left( \lambda_j +\xi \right)^{-s-1}= -s\cdot \zeta_{ \operatorname{\Delta} +\xi}( s+1). \end{align*}$$
By induction, it follows that for
![]() $\Re s> \frac {n}{2}$
,
$\Re s> \frac {n}{2}$
,
Using the identity theorem, (8.2) holds true on
![]() ${\mathbb C}$
as an equality of meromorphic functions. Consider
${\mathbb C}$
as an equality of meromorphic functions. Consider
![]() $s \in {\mathbb R} \setminus (-{\mathbb N})$
and
$s \in {\mathbb R} \setminus (-{\mathbb N})$
and
![]() $k \in {\mathbb N}$
large enough such that
$k \in {\mathbb N}$
large enough such that
![]() $s+k> \frac {n}{2}$
. Since
$s+k> \frac {n}{2}$
. Since
![]() $\zeta _{\operatorname {\Delta }+\xi }(s+k)$
is a convergent sum of strictly positive numbers, the right-hand side is non-zero. Thus, for any fixed
$\zeta _{\operatorname {\Delta }+\xi }(s+k)$
is a convergent sum of strictly positive numbers, the right-hand side is non-zero. Thus, for any fixed
![]() $s \in {\mathbb R} \setminus (- {\mathbb N}) $
, on any open set
$s \in {\mathbb R} \setminus (- {\mathbb N}) $
, on any open set
![]() $U \subset (0, \infty )$
, the function
$U \subset (0, \infty )$
, the function
![]() $\xi \longmapsto \zeta _{\operatorname {\Delta }+\xi }(s)$
is not identically zero on U, and by (8.1),
$\xi \longmapsto \zeta _{\operatorname {\Delta }+\xi }(s)$
is not identically zero on U, and by (8.1),
![]() $q_{-s}^{\xi }(x,x)$
cannot be constant zero on M. Hence, for
$q_{-s}^{\xi }(x,x)$
cannot be constant zero on M. Hence, for
![]() $s=-rj \notin - {\mathbb N}$
, there exist
$s=-rj \notin - {\mathbb N}$
, there exist
![]() $\xi _0 \in (0, \infty )$
and
$\xi _0 \in (0, \infty )$
and
![]() $x_0 \in M$
such that the coefficient
$x_0 \in M$
such that the coefficient
![]() $q_{rj}^{\xi _0}(x_0,x_0)$
of the asymptotic expansion of the Schwartz kernel
$q_{rj}^{\xi _0}(x_0,x_0)$
of the asymptotic expansion of the Schwartz kernel
![]() $h_t$
of
$h_t$
of
![]() $e^{-t (\operatorname {\Delta }+\xi _0)^r}$
is non-zero.
$e^{-t (\operatorname {\Delta }+\xi _0)^r}$
is non-zero.
Now suppose that
![]() $rj \in {\mathbb N}$
. Then
$rj \in {\mathbb N}$
. Then
![]() $r=\frac {\alpha }{\beta }$
is rational and j is a multiple of
$r=\frac {\alpha }{\beta }$
is rational and j is a multiple of
![]() $\beta $
,
$\beta $
,
![]() $j:=l\beta $
. If n is odd, we already proved in Theorem 7.1 that
$j:=l\beta $
. If n is odd, we already proved in Theorem 7.1 that
![]() $t^{l\beta }$
does not appear in the asymptotic expansion of
$t^{l\beta }$
does not appear in the asymptotic expansion of
![]() $h_t$
as
$h_t$
as
![]() $t \searrow 0$
. Furthermore, if n is even, by (7.3),
$t \searrow 0$
. Furthermore, if n is even, by (7.3),
![]() $q_{rj}(x,x)$
is a non-zero multiple of the coefficient
$q_{rj}(x,x)$
is a non-zero multiple of the coefficient
![]() $a_{\frac {n}{2}+l\alpha }(x,x)$
in the asymptotic expansion (2.1) of the heat kernel
$a_{\frac {n}{2}+l\alpha }(x,x)$
in the asymptotic expansion (2.1) of the heat kernel
![]() $p_t$
. It is well known that the heat coefficients in (2.1) are non-trivial (see, for instance, [Reference Gilkey13]). It follows that all coefficients obtained in Theorem 7.1 indeed appear in the asymptotic expansion, proving Theorem 1.1.
$p_t$
. It is well known that the heat coefficients in (2.1) are non-trivial (see, for instance, [Reference Gilkey13]). It follows that all coefficients obtained in Theorem 7.1 indeed appear in the asymptotic expansion, proving Theorem 1.1.
9 Non-locality of the coefficients
 $A_j(x)$
in the asymptotic expansions
$A_j(x)$
in the asymptotic expansions
Let us prove Theorem 1.3. We give an example of an n-dimensional manifold and a Laplacian for which the coefficients
![]() $A_{j}(x)=\frac {(-1)^j}{j!} q_{rj(x,x)}$
,
$A_{j}(x)=\frac {(-1)^j}{j!} q_{rj(x,x)}$
,
![]() $j \in {\mathbb N}^*$
,
$j \in {\mathbb N}^*$
,
![]() $rj \notin {\mathbb N}$
appearing in Theorem 7.1 are not locally computable in the sense of Definition 1.1 (i). Let
$rj \notin {\mathbb N}$
appearing in Theorem 7.1 are not locally computable in the sense of Definition 1.1 (i). Let
![]() ${\mathbb {T}^n={\mathbb R}^n / \left ( 2\pi {\mathbb Z} \right )^n}$
be the n-dimensional torus from Example 2.2. Let
${\mathbb {T}^n={\mathbb R}^n / \left ( 2\pi {\mathbb Z} \right )^n}$
be the n-dimensional torus from Example 2.2. Let
![]() $\operatorname {\Delta }_g$
be the Laplacian on
$\operatorname {\Delta }_g$
be the Laplacian on
![]() $\mathbb {T}^n$
given by the metric
$\mathbb {T}^n$
given by the metric
![]() $g=d\theta _1^2 +\cdots + d\theta _n^2$
.
$g=d\theta _1^2 +\cdots + d\theta _n^2$
.
Remark that the eigenvalues of
![]() $\operatorname {\Delta }_g$
are
$\operatorname {\Delta }_g$
are
![]() $\{ k_1^2 +\cdots +k_n^2 : k_1,\ldots ,k_n \in {\mathbb Z} \}$
. Let
$\{ k_1^2 +\cdots +k_n^2 : k_1,\ldots ,k_n \in {\mathbb Z} \}$
. Let
![]() $ {\varphi _l(t)= \frac {1}{\sqrt {2\pi }} e^{il t} }$
be the standard orthonormal basis of eigenfunctions of each
$ {\varphi _l(t)= \frac {1}{\sqrt {2\pi }} e^{il t} }$
be the standard orthonormal basis of eigenfunctions of each
![]() $\operatorname {\Delta }_{S^1}$
. Then, for
$\operatorname {\Delta }_{S^1}$
. Then, for
![]() $\Re s> \frac {n}{2}$
and
$\Re s> \frac {n}{2}$
and
![]() $\theta =(\theta _1,\ldots ,\theta _n) \in \mathbb {T}^n$
, the Schwartz kernel of
$\theta =(\theta _1,\ldots ,\theta _n) \in \mathbb {T}^n$
, the Schwartz kernel of
![]() $\operatorname {\Delta }_g^{-s}$
is given by
$\operatorname {\Delta }_g^{-s}$
is given by
Consider the n-dimensional zeta function
where
![]() $R_n(k)$
is the number of representations of k as a sum of n squares. Since
$R_n(k)$
is the number of representations of k as a sum of n squares. Since
![]() $\varphi _{l}(t) \overline {\varphi _{l}(t)} =\frac {1}{2\pi }$
for any
$\varphi _{l}(t) \overline {\varphi _{l}(t)} =\frac {1}{2\pi }$
for any
![]() $t \in S^1$
, it follows that
$t \in S^1$
, it follows that
for any
![]() $\Re s> \frac {n}{2}$
, and clearly
$\Re s> \frac {n}{2}$
, and clearly
![]() $q_{-s}^{\operatorname {\Delta }_g}$
is independent of
$q_{-s}^{\operatorname {\Delta }_g}$
is independent of
![]() $\theta $
.
$\theta $
.
Now let us change the metric locally on each component
![]() $S^1$
. Let U be an open interval in
$S^1$
. Let U be an open interval in
![]() $S^1$
, and
$S^1$
, and
![]() $\psi :S^1 \longrightarrow [0,\infty )$
a smooth function with
$\psi :S^1 \longrightarrow [0,\infty )$
a smooth function with
![]() $\operatorname {supp} \psi \subset U$
. Consider the new metric
$\operatorname {supp} \psi \subset U$
. Consider the new metric
![]() $\left ( 1+\psi (\theta ) \right ) d\theta ^2$
on each
$\left ( 1+\psi (\theta ) \right ) d\theta ^2$
on each
![]() $S^1$
. Then there exist
$S^1$
. Then there exist
![]() $p>0$
and an isometry
$p>0$
and an isometry
![]() $\Phi : \left ( S^1, \left ( 1+\psi (\theta ) \right ) d\theta ^2 \right ) \longrightarrow \left ( S^1, p^2 d\theta ^2 \right )$
. Remark that the Laplacian on
$\Phi : \left ( S^1, \left ( 1+\psi (\theta ) \right ) d\theta ^2 \right ) \longrightarrow \left ( S^1, p^2 d\theta ^2 \right )$
. Remark that the Laplacian on
![]() $S^1$
given by the metric
$S^1$
given by the metric
![]() $p^2 d \theta ^2$
corresponds under this isometry to
$p^2 d \theta ^2$
corresponds under this isometry to
![]() $p^{-2}$
times the Laplacian for the metric
$p^{-2}$
times the Laplacian for the metric
![]() $d\theta ^2$
. Let
$d\theta ^2$
. Let
 $$ \begin{align*} \tilde{g}= \sum_{j=1}^n \left( 1+ \psi(\theta_j) \right) d\theta_j^2 && g_p=\sum_{j=1}^n p^2 d\theta_j^2=p^2g. \end{align*} $$
$$ \begin{align*} \tilde{g}= \sum_{j=1}^n \left( 1+ \psi(\theta_j) \right) d\theta_j^2 && g_p=\sum_{j=1}^n p^2 d\theta_j^2=p^2g. \end{align*} $$
Then clearly
![]() $\Phi \times \cdots \times \Phi : (\mathbb {T}^n, \tilde {g}) \longmapsto (\mathbb {T}^n, g_p) $
is an isometry, and let
$\Phi \times \cdots \times \Phi : (\mathbb {T}^n, \tilde {g}) \longmapsto (\mathbb {T}^n, g_p) $
is an isometry, and let
![]() $\tilde {\Delta }$
,
$\tilde {\Delta }$
,
![]() $\Delta _{p }$
be the corresponding Laplacians on
$\Delta _{p }$
be the corresponding Laplacians on
![]() $\mathbb {T}^n$
. Denote by
$\mathbb {T}^n$
. Denote by
![]() $q_{-s}^{\tilde {\Delta }}$
and
$q_{-s}^{\tilde {\Delta }}$
and
![]() $q_{-s}^{\Delta _{p }}$
the Schwartz kernels of the complex powers
$q_{-s}^{\Delta _{p }}$
the Schwartz kernels of the complex powers
![]() $ \tilde {\Delta } ^{-s}$
and
$ \tilde {\Delta } ^{-s}$
and
![]() $\Delta _{p }^{-s}$
. We have for
$\Delta _{p }^{-s}$
. We have for
![]() $\Re s>\frac {n}{2}$
,
$\Re s>\frac {n}{2}$
,
 $$ \begin{align} q_{-s}^{\operatorname{\Delta}_{p }} \left( \theta, \theta \right) = \frac{1}{(2 \pi p)^n} \sum_{k=(k_1,\ldots,k_n) \in {\mathbb Z}^n \setminus \{ 0 \}} \left( p^{-2}k_1^2 +\cdots+p^{-2}k_n^2 \right)^{-s} = \frac{p^{2s}}{(2 \pi p)^n} \zeta_n(s). \end{align} $$
$$ \begin{align} q_{-s}^{\operatorname{\Delta}_{p }} \left( \theta, \theta \right) = \frac{1}{(2 \pi p)^n} \sum_{k=(k_1,\ldots,k_n) \in {\mathbb Z}^n \setminus \{ 0 \}} \left( p^{-2}k_1^2 +\cdots+p^{-2}k_n^2 \right)^{-s} = \frac{p^{2s}}{(2 \pi p)^n} \zeta_n(s). \end{align} $$
Remark that
and both of them are independent of
![]() $\theta $
. By (9.2), for
$\theta $
. By (9.2), for
![]() $\Re s>\frac {n}{2}$
, we obtain
$\Re s>\frac {n}{2}$
, we obtain
 $$ \begin{align} q_{-s}^{\tilde{\operatorname{\Delta}}} \left( \theta,\theta \right) = \frac{p^{2s-n}}{(2 \pi )^n} \zeta_n(s). \end{align} $$
$$ \begin{align} q_{-s}^{\tilde{\operatorname{\Delta}}} \left( \theta,\theta \right) = \frac{p^{2s-n}}{(2 \pi )^n} \zeta_n(s). \end{align} $$
Now we prove that
![]() $\zeta _n(s)$
has a meromorphic extension on
$\zeta _n(s)$
has a meromorphic extension on
![]() ${\mathbb C}$
with so-called trivial zeros at
${\mathbb C}$
with so-called trivial zeros at
![]() $s=-1,-2,\ldots $
. By Proposition 1, for
$s=-1,-2,\ldots $
. By Proposition 1, for
![]() $\Re s> \frac {n}{2}$
, we have
$\Re s> \frac {n}{2}$
, we have
 $$\begin{align*}\zeta_n(s) \Gamma(s)=\int_{0}^{\infty} t^{s-1} \sum_{k=(k_1,\ldots,k_n) \in {\mathbb Z}^n \setminus \{ 0 \}} e^{-t(k_1^2+\cdots+k_n^2)} dt = \int_0^{\infty} t^{s-1} F(t) dt, \end{align*}$$
$$\begin{align*}\zeta_n(s) \Gamma(s)=\int_{0}^{\infty} t^{s-1} \sum_{k=(k_1,\ldots,k_n) \in {\mathbb Z}^n \setminus \{ 0 \}} e^{-t(k_1^2+\cdots+k_n^2)} dt = \int_0^{\infty} t^{s-1} F(t) dt, \end{align*}$$
where
![]() $F(t):= \sum _{k=(k_1,\ldots ,k_n) \in {\mathbb Z}^n \setminus \{ 0 \}} e^{-t(k_1^2+\cdots +k_n^2)}$
. Using the multidimensional Poisson formula (see, for instance, [Reference Bellman3]), it follows that
$F(t):= \sum _{k=(k_1,\ldots ,k_n) \in {\mathbb Z}^n \setminus \{ 0 \}} e^{-t(k_1^2+\cdots +k_n^2)}$
. Using the multidimensional Poisson formula (see, for instance, [Reference Bellman3]), it follows that
 $$\begin{align*}1+F(t)= \sum_{k \in {\mathbb Z}^n} f_t(k)=\sum_{k \in {\mathbb Z}^n} \hat{f_t}(2 \pi k)=\pi^{n/2} t^{-n/2} \left( 1 + F \left( \frac{\pi^2}{t} \right) \right), \end{align*}$$
$$\begin{align*}1+F(t)= \sum_{k \in {\mathbb Z}^n} f_t(k)=\sum_{k \in {\mathbb Z}^n} \hat{f_t}(2 \pi k)=\pi^{n/2} t^{-n/2} \left( 1 + F \left( \frac{\pi^2}{t} \right) \right), \end{align*}$$
and therefore
 $$\begin{align*}F(t)=-1+\pi^{n/2}t^{-n/2} + \pi^{n/2} t^{-n/2} F \left( \frac{\pi^2}{t} \right). \end{align*}$$
$$\begin{align*}F(t)=-1+\pi^{n/2}t^{-n/2} + \pi^{n/2} t^{-n/2} F \left( \frac{\pi^2}{t} \right). \end{align*}$$
Since
![]() $F(t)$
goes to
$F(t)$
goes to
![]() $0$
rapidly as
$0$
rapidly as
![]() $t \to \infty $
, the function
$t \to \infty $
, the function
![]() $A(s)= \int _{1}^{\infty } t^{s-1} F(\pi t)dt $
is entire. Remark that
$A(s)= \int _{1}^{\infty } t^{s-1} F(\pi t)dt $
is entire. Remark that
 $$ \begin{align*} \zeta_n(s) \Gamma(s)={}& \int_{0}^{\pi} t^{-s} F(t)dt + \int_{\pi}^{\infty} t^{s-1}F(t) dt \\ ={}& \pi^s \left( -\frac{1}{s} + \frac{1}{s-\frac{n}{2}} + A\left( \frac{n}{2}-s \right) + A(s)\right), \end{align*} $$
$$ \begin{align*} \zeta_n(s) \Gamma(s)={}& \int_{0}^{\pi} t^{-s} F(t)dt + \int_{\pi}^{\infty} t^{s-1}F(t) dt \\ ={}& \pi^s \left( -\frac{1}{s} + \frac{1}{s-\frac{n}{2}} + A\left( \frac{n}{2}-s \right) + A(s)\right), \end{align*} $$
so
Therefore,
![]() $\zeta _n$
extends meromorphically to
$\zeta _n$
extends meromorphically to
![]() ${\mathbb C}$
with a simple pole in
${\mathbb C}$
with a simple pole in
![]() $s=\frac {n}{2}$
and zeros at
$s=\frac {n}{2}$
and zeros at
![]() $s=-1,-2,\ldots $
. Furthermore, since the RHS is invariant through the involution
$s=-1,-2,\ldots $
. Furthermore, since the RHS is invariant through the involution
![]() $s \mapsto \frac {n}{2}-s$
, it follows that
$s \mapsto \frac {n}{2}-s$
, it follows that
![]() $\zeta _n(s)$
does not have any other zeros for
$\zeta _n(s)$
does not have any other zeros for
![]() $s \in (-\infty ,0)$
. We obtain the well-known functional equation of the Epstein zeta function
$s \in (-\infty ,0)$
. We obtain the well-known functional equation of the Epstein zeta function
(see, for instance, [Reference Chandrasekharan and Narasimhan9, equation (63)]). Remark that for
![]() $r \in (0,1)$
and
$r \in (0,1)$
and
![]() $j \in {\mathbb N}^*$
with
$j \in {\mathbb N}^*$
with
![]() $rj \notin {\mathbb N}$
,
$rj \notin {\mathbb N}$
,
![]() $\zeta _n (-rj )$
is not zero.
$\zeta _n (-rj )$
is not zero.
Using the identity theorem, it follows that (9.1) and (9.3) hold true as an equality of meromorphic functions on
![]() ${\mathbb C}$
, and furthermore, we get
${\mathbb C}$
, and furthermore, we get
for
![]() $rj \notin {\mathbb N}$
. Since we modified the metric locally in
$rj \notin {\mathbb N}$
. Since we modified the metric locally in
![]() $U^n \subset \mathbb {T}^n$
and the corresponding kernel
$U^n \subset \mathbb {T}^n$
and the corresponding kernel
![]() $q_{rj}^{\tilde {\operatorname {\Delta }}}$
changed its behavior globally, it follows that it is not locally computable in the sense of Definition 1.1 (i).
$q_{rj}^{\tilde {\operatorname {\Delta }}}$
changed its behavior globally, it follows that it is not locally computable in the sense of Definition 1.1 (i).
Furthermore, let us see that the heat coefficients
![]() $A_j(x)=\frac {(-1)^j}{j!} q_{rj}(x,x)$
for
$A_j(x)=\frac {(-1)^j}{j!} q_{rj}(x,x)$
for
![]() $j={\mathbb N}^*$
,
$j={\mathbb N}^*$
,
![]() $rj \notin {\mathbb N}$
are not cohomologically local in the sense of Definition 1.1 (iii). We argue by contradiction. Let j be fixed. Suppose that there exists a function C, locally computable in the sense of Definition 1.1 (i), such that
$rj \notin {\mathbb N}$
are not cohomologically local in the sense of Definition 1.1 (iii). We argue by contradiction. Let j be fixed. Suppose that there exists a function C, locally computable in the sense of Definition 1.1 (i), such that
Using (9.1) and (9.3), it follows that
Remark that in the case of the trivial bundle with the trivial connection over a locally homogeneous Riemannian manifold
![]() $(M,h)$
(i.e., such that every two points have isometric neighborhoods), the function
$(M,h)$
(i.e., such that every two points have isometric neighborhoods), the function
![]() $C(M,h) \in {\mathcal C}^{\infty }(M)$
is constant on M. This follows directly from Definition 1.1 (i). Therefore,
$C(M,h) \in {\mathcal C}^{\infty }(M)$
is constant on M. This follows directly from Definition 1.1 (i). Therefore,
![]() $C(g)$
,
$C(g)$
,
![]() $C(\tilde {g}),$
and
$C(\tilde {g}),$
and
![]() $C(g_p)$
are constant functions.
$C(g_p)$
are constant functions.
Since
![]() $(\mathbb {T}^n , \tilde {g})$
is (globally) isometric to
$(\mathbb {T}^n , \tilde {g})$
is (globally) isometric to
![]() $(\mathbb {T}^n , g_p)$
, it follows that
$(\mathbb {T}^n , g_p)$
, it follows that
![]() $C(\tilde {g})=C(g_p)$
. Furthermore, since
$C(\tilde {g})=C(g_p)$
. Furthermore, since
![]() $(\mathbb {T}^n , g_p)$
is locally isometric to
$(\mathbb {T}^n , g_p)$
is locally isometric to
![]() $(\mathbb {T}^n , g)$
and
$(\mathbb {T}^n , g)$
and
![]() $C(g_p)$
,
$C(g_p)$
,
![]() $C(g)$
are constant functions, it also follows that they are equal:
$C(g)$
are constant functions, it also follows that they are equal:
![]() $C(g_p)=C(g)$
. Hence we conclude that
$C(g_p)=C(g)$
. Hence we conclude that
![]() $C(\tilde {g})=C(g_p)=C(g)=:C$
, for some
$C(\tilde {g})=C(g_p)=C(g)=:C$
, for some
![]() $C \in {\mathbb C}$
, and thus we have
$C \in {\mathbb C}$
, and thus we have
Since
![]() $g_p=p^2 g$
, we obtain that
$g_p=p^2 g$
, we obtain that
and then using (9.5)–(9.7), we get
But, we proved above that
![]() $\zeta _n (-rj)$
does not vanish for
$\zeta _n (-rj)$
does not vanish for
![]() $rj \notin {\mathbb N}$
. We obtain a contradiction because
$rj \notin {\mathbb N}$
. We obtain a contradiction because
![]() $p^{-2rj} \neq 1$
for
$p^{-2rj} \neq 1$
for
![]() $r \in (0,1)$
,
$r \in (0,1)$
,
![]() $j=1,2,\ldots $
.
$j=1,2,\ldots $
.
10 Interpretation of
 $h_t$
on the heat space for
$h_t$
on the heat space for
 $r=1/2$
$r=1/2$
In Theorems 6.1 and 7.1, we studied the asymptotic behavior of the heat kernel
![]() $h_t$
of
$h_t$
of
![]() ${ \operatorname {\Delta }^r}$
,
${ \operatorname {\Delta }^r}$
,
![]() $r \in (0,1)$
for small-time t in two distinct cases: when we approach
$r \in (0,1)$
for small-time t in two distinct cases: when we approach
![]() $t=0$
along the diagonal in
$t=0$
along the diagonal in
![]() $M \times M$
, and when we approach a compact set away from the diagonal. We now give a simultaneous asymptotic expansion formula for both cases when
$M \times M$
, and when we approach a compact set away from the diagonal. We now give a simultaneous asymptotic expansion formula for both cases when
![]() $r=\frac {1}{2}$
. Furthermore, in order to understand the asymptotic behavior as t goes to zero in any direction (not just the case when t goes to
$r=\frac {1}{2}$
. Furthermore, in order to understand the asymptotic behavior as t goes to zero in any direction (not just the case when t goes to
![]() $0$
in the vertical one),we will pull-back the formula on a certain linear heat space
$0$
in the vertical one),we will pull-back the formula on a certain linear heat space
![]() $\operatorname {M_{heat}}$
.
$\operatorname {M_{heat}}$
.
In [Reference Melrose19], Melrose used his blow-up techniques to give a conceptual interpretation for the asymptotic of the heat kernel
![]() $p_t$
. Recall that the heat space
$p_t$
. Recall that the heat space
![]() $M_H^2$
is obtained by performing a parabolic blow-up of
$M_H^2$
is obtained by performing a parabolic blow-up of
![]() $ \{ t=0 \} \times \operatorname {Diag} $
in
$ \{ t=0 \} \times \operatorname {Diag} $
in
![]() $[0,\infty ) \times M \times M$
. The heat space
$[0,\infty ) \times M \times M$
. The heat space
![]() $M_H^2$
is a manifold with corners with boundary hypersurfaces given by the boundary defining functions
$M_H^2$
is a manifold with corners with boundary hypersurfaces given by the boundary defining functions
![]() $\rho $
and
$\rho $
and
![]() $\omega _0$
. The heat kernel
$\omega _0$
. The heat kernel
![]() $p_t$
belongs to
$p_t$
belongs to
![]() $\rho ^{-n} {\mathcal C}^{\infty }(M_H^2)$
, and vanishes rapidly at the boundary hypersurface
$\rho ^{-n} {\mathcal C}^{\infty }(M_H^2)$
, and vanishes rapidly at the boundary hypersurface
![]() $\{ \omega _0=0 \}$
(see [Reference Melrose19, Theorem 7.12]).
$\{ \omega _0=0 \}$
(see [Reference Melrose19, Theorem 7.12]).
In order to study the Schwartz kernel
![]() $h_t$
of
$h_t$
of
![]() $e^{-t \operatorname {\Delta }^{1/2}}$
, we introduce the linear heat space
$e^{-t \operatorname {\Delta }^{1/2}}$
, we introduce the linear heat space
![]() $\operatorname {M_{heat}}$
, which is just the standard blow-up of
$\operatorname {M_{heat}}$
, which is just the standard blow-up of
![]() $\{ 0 \} \times \operatorname {Diag}$
in
$\{ 0 \} \times \operatorname {Diag}$
in
![]() $[0,\infty ) \times M \times M$
(see [Reference Melrose and Mazzeo20] for details regarding the blow-up of a submanifold). Let
$[0,\infty ) \times M \times M$
(see [Reference Melrose and Mazzeo20] for details regarding the blow-up of a submanifold). Let
![]() $\operatorname {ff}$
be the front face, i.e., the newly added face, and denote by
$\operatorname {ff}$
be the front face, i.e., the newly added face, and denote by
![]() $\operatorname {lb}$
the lateral boundary which is the lift of the old boundary
$\operatorname {lb}$
the lateral boundary which is the lift of the old boundary
![]() $\{ 0 \} \times M \times M$
. The blow down map is given locally by
$\{ 0 \} \times M \times M$
. The blow down map is given locally by
where
Proof of Theorem 1.4
We want to show that
![]() $h_t \in \rho ^{-n} \omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) + \rho \log \rho \cdot \omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) $
, and in fact, the second (logarithmic) term does not occur when n is even. First, we deduce the unified formula for
$h_t \in \rho ^{-n} \omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) + \rho \log \rho \cdot \omega _0 \cdot {\mathcal C}^{\infty } (\operatorname {M_{heat}}) $
, and in fact, the second (logarithmic) term does not occur when n is even. First, we deduce the unified formula for
![]() $h_t$
as
$h_t$
as
![]() $t \searrow 0$
both on the diagonal and away from it. By Mellin formula 1 and inverse Mellin formula 6, for
$t \searrow 0$
both on the diagonal and away from it. By Mellin formula 1 and inverse Mellin formula 6, for
![]() $\tau>n$
, we get
$\tau>n$
, we get
 $$ \begin{align*} h_t(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y)={}& \tfrac{1}{2\pi i} \int_{\Re s=\tau} t^{-s} \frac{\Gamma(s)}{\Gamma \left( \frac{s}{2} \right)} \Gamma \left(\frac{s}{2} \right)q_{-s/2}(x,y)ds \\ ={}& \tfrac{1}{2\pi i} \int_{\Re s = \tau} t^{-s} \frac{\Gamma(s)}{\Gamma \left( \frac{s}{2} \right)} \int_{0}^{\infty} T^{\tfrac{s}{2}-1} \left( p_T(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \right) dT ds. \end{align*} $$
$$ \begin{align*} h_t(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y)={}& \tfrac{1}{2\pi i} \int_{\Re s=\tau} t^{-s} \frac{\Gamma(s)}{\Gamma \left( \frac{s}{2} \right)} \Gamma \left(\frac{s}{2} \right)q_{-s/2}(x,y)ds \\ ={}& \tfrac{1}{2\pi i} \int_{\Re s = \tau} t^{-s} \frac{\Gamma(s)}{\Gamma \left( \frac{s}{2} \right)} \int_{0}^{\infty} T^{\tfrac{s}{2}-1} \left( p_T(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \right) dT ds. \end{align*} $$
We use the Legendre duplication formula as in [Reference Bär and Moroianu2] (see, for instance, [Reference Paris and Kaminski22]):
 $$\begin{align*}\frac{\Gamma(s)}{\Gamma\left( \frac{s}{2} \right) } = \frac{1}{\sqrt{2\pi}} 2^{s-\tfrac{1}{2}} \Gamma \left( \frac{s+1}{2} \right), \end{align*}$$
$$\begin{align*}\frac{\Gamma(s)}{\Gamma\left( \frac{s}{2} \right) } = \frac{1}{\sqrt{2\pi}} 2^{s-\tfrac{1}{2}} \Gamma \left( \frac{s+1}{2} \right), \end{align*}$$
obtaining that
![]() $h_t(x,y)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
is equal to
$h_t(x,y)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
is equal to
 $$ \begin{align*} \tfrac{1}{\sqrt{4 \pi}} \tfrac{1}{2\pi i} \int_{\Re s = \tau} \int_{0}^{\infty} \left( \frac{2 \sqrt{T}}{t} \right)^s \Gamma \left( \frac{s+1}{2} \right) \left( p_T(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \right) dT ds. \end{align*} $$
$$ \begin{align*} \tfrac{1}{\sqrt{4 \pi}} \tfrac{1}{2\pi i} \int_{\Re s = \tau} \int_{0}^{\infty} \left( \frac{2 \sqrt{T}}{t} \right)^s \Gamma \left( \frac{s+1}{2} \right) \left( p_T(x,y)-\operatorname{P}_{\operatorname{Ker} \operatorname{\Delta}}(x,y) \right) dT ds. \end{align*} $$
Set
![]() $X:=\tfrac {2\sqrt {T}}{t}$
. Using Propositions 4, 5, and Fubini, we first compute the integral in s. Changing the variable
$X:=\tfrac {2\sqrt {T}}{t}$
. Using Propositions 4, 5, and Fubini, we first compute the integral in s. Changing the variable
![]() $S=\frac {s+1}{2}$
and applying the residue theorem, we get
$S=\frac {s+1}{2}$
and applying the residue theorem, we get
 $$ \begin{align*} \tfrac{1}{2\pi i} \int_{\Re s = \tau} X^s \Gamma \left( \frac{s+1}{2} \right) ds={}& \tfrac{2}{2\pi i} \int_{\Re S = \frac{\tau+1}{2}} X^{2S-1} \Gamma(S) dS = 2 \sum_{k=0}^{\infty} \frac{(-1)^k}{k!} X^{-2k-1} \\ ={}& 2 X^{-1}e^{-X^{-2}}=\frac{t}{\sqrt{T}}e^{-\frac{t^2}{4T}}. \end{align*} $$
$$ \begin{align*} \tfrac{1}{2\pi i} \int_{\Re s = \tau} X^s \Gamma \left( \frac{s+1}{2} \right) ds={}& \tfrac{2}{2\pi i} \int_{\Re S = \frac{\tau+1}{2}} X^{2S-1} \Gamma(S) dS = 2 \sum_{k=0}^{\infty} \frac{(-1)^k}{k!} X^{-2k-1} \\ ={}& 2 X^{-1}e^{-X^{-2}}=\frac{t}{\sqrt{T}}e^{-\frac{t^2}{4T}}. \end{align*} $$
Thus, we obtain
Since
![]() $p_T(x,y)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
decays exponentially as T goes to infinity, it follows that the integral from
$p_T(x,y)-\operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
decays exponentially as T goes to infinity, it follows that the integral from
![]() $1$
to
$1$
to
![]() $\infty $
in the right-hand side of equation (10.1) is of the form
$\infty $
in the right-hand side of equation (10.1) is of the form
![]() $t \cdot {\mathcal C}^{\infty }_{t,x,y} \left ( [0,\infty ) \times M^2 \right )$
. Furthermore, by the change of variable
$t \cdot {\mathcal C}^{\infty }_{t,x,y} \left ( [0,\infty ) \times M^2 \right )$
. Furthermore, by the change of variable
![]() $u=\tfrac {t}{2\sqrt {T}}$
, we have
$u=\tfrac {t}{2\sqrt {T}}$
, we have
Since
![]() $ \int _{t/2}^{\infty } e^{-u^2}du$
tends to
$ \int _{t/2}^{\infty } e^{-u^2}du$
tends to
![]() $\frac {\sqrt {\pi }}{2}$
as
$\frac {\sqrt {\pi }}{2}$
as
![]() $t \searrow 0$
, the term
$t \searrow 0$
, the term
![]() $-\tfrac {t}{2\sqrt {\pi }}\int _{0}^{1} T^{-3/2}e^{-\frac {t^2}{4T}} dT \operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
will cancel in the limit as
$-\tfrac {t}{2\sqrt {\pi }}\int _{0}^{1} T^{-3/2}e^{-\frac {t^2}{4T}} dT \operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
will cancel in the limit as
![]() $t \to 0$
with
$t \to 0$
with
![]() $- \operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
from the left-hand side of (10.1).
$- \operatorname {P}_{\operatorname {Ker} \operatorname {\Delta }}(x,y)$
from the left-hand side of (10.1).
Let us study the remaining integral term
![]() $\tfrac {t}{2\sqrt {\pi }} \int _{0}^{1} T^{-3/2}e^{-\frac {t^2}{4T}} p_T(x,y)dT$
. By Theorem 2.1,
$\tfrac {t}{2\sqrt {\pi }} \int _{0}^{1} T^{-3/2}e^{-\frac {t^2}{4T}} p_T(x,y)dT$
. By Theorem 2.1,
 $$ \begin{align*} p_T(x,y)=T^{-n/2} e^{-\frac{d(x,y)^2}{4T}} \sum_{j=0}^N T^j a_j(x,y) + R_{N+1}(T,x,y), \end{align*} $$
$$ \begin{align*} p_T(x,y)=T^{-n/2} e^{-\frac{d(x,y)^2}{4T}} \sum_{j=0}^N T^j a_j(x,y) + R_{N+1}(T,x,y), \end{align*} $$
where the remainder
![]() $R_{N+1}(T,x,y)$
is of order
$R_{N+1}(T,x,y)$
is of order
![]() ${\mathcal O} (T^{N+1})$
; therefore,
${\mathcal O} (T^{N+1})$
; therefore,
 $$ \begin{align*} \tfrac{t}{2\sqrt{\pi}} \int_{0}^{1} T^{-3/2}e^{-\frac{t^2}{4T}} p_T(x,y)dT={}& \tfrac{t}{2\sqrt{\pi}} \int_{0}^{1} T^{-3/2}e^{-\frac{t^2}{4T}} R_{N+1}(T,x,y) dT \\ +{}& \tfrac{t}{2\sqrt{\pi}} \!\int_{0}^{1} \!T^{-3/2}e^{-\frac{t^2}{4T}} T^{-n/2}e^{-\frac{d(x,y)^2}{4T}} \sum_{j=0}^{N} T^j a_{j}(x,y) dT. \end{align*} $$
$$ \begin{align*} \tfrac{t}{2\sqrt{\pi}} \int_{0}^{1} T^{-3/2}e^{-\frac{t^2}{4T}} p_T(x,y)dT={}& \tfrac{t}{2\sqrt{\pi}} \int_{0}^{1} T^{-3/2}e^{-\frac{t^2}{4T}} R_{N+1}(T,x,y) dT \\ +{}& \tfrac{t}{2\sqrt{\pi}} \!\int_{0}^{1} \!T^{-3/2}e^{-\frac{t^2}{4T}} T^{-n/2}e^{-\frac{d(x,y)^2}{4T}} \sum_{j=0}^{N} T^j a_{j}(x,y) dT. \end{align*} $$
Since
![]() $R_{N+1}(T,x,y)$
is of order
$R_{N+1}(T,x,y)$
is of order
![]() ${\mathcal O} (T^{N+1})$
, the first integral is again of type
${\mathcal O} (T^{N+1})$
, the first integral is again of type
![]() $ t \cdot {\mathcal C}^{\infty }_{t,x,y} $
. By changing the variable
$ t \cdot {\mathcal C}^{\infty }_{t,x,y} $
. By changing the variable
![]() $u=\tfrac {t^2+d(x,y)^2}{4T}$
in the second integral, we get
$u=\tfrac {t^2+d(x,y)^2}{4T}$
in the second integral, we get
 $$ \begin{align*} {}&\tfrac{t}{2\sqrt{\pi}} \sum_{j=0}^N a_{j}(x,y) \int_{0}^{1} T^{-\frac{n+3}{2} +j}e^{-\frac{t^2+d(x,y)^2}{4T}} dT \\ ={}& \tfrac{t}{2 \sqrt{\pi}} \sum_{j=0}^N a_j(x,y) \left( \frac{t^2+d(x,y)^2}{4} \right)^{-\frac{n+1}{2}+j} \int_{\frac{t^2+d(x,y)^2}{4}}^{\infty} u^{\frac{n+1}{2}-j-1} e^{-u}du \\ ={}& \tfrac{t}{2 \sqrt{\pi}} \sum_{j=0}^N a_j(x,y) \Gamma \left( \frac{n+1}{2}-j, \frac{t^2+d(x,y)^2}{4} \right) \left( \frac{t^2+d(x,y)^2}{4} \right)^{-\frac{n+1}{2}+j}, \end{align*} $$
$$ \begin{align*} {}&\tfrac{t}{2\sqrt{\pi}} \sum_{j=0}^N a_{j}(x,y) \int_{0}^{1} T^{-\frac{n+3}{2} +j}e^{-\frac{t^2+d(x,y)^2}{4T}} dT \\ ={}& \tfrac{t}{2 \sqrt{\pi}} \sum_{j=0}^N a_j(x,y) \left( \frac{t^2+d(x,y)^2}{4} \right)^{-\frac{n+1}{2}+j} \int_{\frac{t^2+d(x,y)^2}{4}}^{\infty} u^{\frac{n+1}{2}-j-1} e^{-u}du \\ ={}& \tfrac{t}{2 \sqrt{\pi}} \sum_{j=0}^N a_j(x,y) \Gamma \left( \frac{n+1}{2}-j, \frac{t^2+d(x,y)^2}{4} \right) \left( \frac{t^2+d(x,y)^2}{4} \right)^{-\frac{n+1}{2}+j}, \end{align*} $$
where
![]() $\Gamma (z,\xi ):=\int _{\xi }^{\infty } u^{z-1}e^{-u}du$
is the upper incomplete Gamma function. We conclude that
$\Gamma (z,\xi ):=\int _{\xi }^{\infty } u^{z-1}e^{-u}du$
is the upper incomplete Gamma function. We conclude that
![]() $h_t(x,y)$
is equal to
$h_t(x,y)$
is equal to
 $$ \begin{align} t \cdot {\mathcal C}^{\infty}_{t,x,y} + \tfrac{t}{2 \sqrt{\pi}} \sum_{j=0}^N a_j(x,y) \Gamma \left( \frac{n+1}{2}-j, \frac{t^2+d(x,y)^2}{4} \right) \left( \frac{t^2+d(x,y)^2}{4} \right)^{-\frac{n+1}{2}+j}. \end{align} $$
$$ \begin{align} t \cdot {\mathcal C}^{\infty}_{t,x,y} + \tfrac{t}{2 \sqrt{\pi}} \sum_{j=0}^N a_j(x,y) \Gamma \left( \frac{n+1}{2}-j, \frac{t^2+d(x,y)^2}{4} \right) \left( \frac{t^2+d(x,y)^2}{4} \right)^{-\frac{n+1}{2}+j}. \end{align} $$
10.1 The case when n is even
If
![]() $z>0$
, then one can easily check that
$z>0$
, then one can easily check that
![]() $\Gamma (z,\xi ) \in \xi ^z {\mathcal C}^{\infty }_{\xi }[0,\epsilon ) + \Gamma (z)$
, for some
$\Gamma (z,\xi ) \in \xi ^z {\mathcal C}^{\infty }_{\xi }[0,\epsilon ) + \Gamma (z)$
, for some
![]() $\epsilon>0$
. Furthermore, for
$\epsilon>0$
. Furthermore, for
![]() $z \in (-\infty ,0] \setminus \lbrace 0,-1,-2,\ldots \rbrace $
,
$z \in (-\infty ,0] \setminus \lbrace 0,-1,-2,\ldots \rbrace $
,
 $$ \begin{align*} \Gamma(z,\xi)={}&-\frac{1}{z}\xi^ze^{-\xi}+\frac{1}{z} \Gamma(z+1,\xi) \\ ={}&\xi^z e^{-\xi} \sum_{k=0}^{a-1} \frac{-1}{z(z+1)\ldots(z+k)} \xi^k + \frac{1}{z(z+1)\ldots(z+a)} \Gamma(z+a,\xi) \\ ={}& \xi^z {\mathcal C}^{\infty}_{\xi}[0, \epsilon) + \frac{1}{z(z+1)\ldots(z+a-1)} \Gamma(z+a,\xi), \end{align*} $$
$$ \begin{align*} \Gamma(z,\xi)={}&-\frac{1}{z}\xi^ze^{-\xi}+\frac{1}{z} \Gamma(z+1,\xi) \\ ={}&\xi^z e^{-\xi} \sum_{k=0}^{a-1} \frac{-1}{z(z+1)\ldots(z+k)} \xi^k + \frac{1}{z(z+1)\ldots(z+a)} \Gamma(z+a,\xi) \\ ={}& \xi^z {\mathcal C}^{\infty}_{\xi}[0, \epsilon) + \frac{1}{z(z+1)\ldots(z+a-1)} \Gamma(z+a,\xi), \end{align*} $$
where a is a positive integer such that
![]() $z+a>0$
. Thus, for a non-integer
$z+a>0$
. Thus, for a non-integer
![]() $z<0$
, we have
$z<0$
, we have
We want to interpret equation (10.2) on the heat space
![]() $\operatorname {M_{heat}}$
; thus, we pull back (10.2) through
$\operatorname {M_{heat}}$
; thus, we pull back (10.2) through
![]() $\beta _H$
:
$\beta _H$
:
 $$ \begin{align*} \beta_H^*h={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \tfrac{1}{2 \sqrt \pi} \rho \omega_0 \sum_{j=0}^{N} \left( \tfrac{\rho^2}{4} \right)^{-\frac{n+1}{2}+j} \beta_H^*a_j(x,y) \Gamma\left( \frac{n+1}{2}-j , \frac{\rho^2}{4} \right) \\ ={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \tfrac{1}{2 \sqrt{\pi}} \rho^{-n}\omega_0 \sum_{j=0}^{n/2} \rho^{2j} 2^{n+1-2j} \beta_H^*a_j(x,y) \Gamma \left( \frac{n+1}{2}-j \right) \\ {}&+ \tfrac{1}{2 \sqrt{\pi}} \rho \omega_0 \sum_{j=0}^{n/2} \beta_H^* a_j(x,y) {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) + \tfrac{1}{2 \sqrt{\pi}} \rho\omega_0 \sum_{j=n/2 +1}^{N} \beta_H^* a_j(x,y) {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) \\ {}&+\tfrac{1}{2 \sqrt{\pi}} \rho^{-n}\omega_0 \sum_{j=n/2+1}^{N} \rho^{2j} 2^{n+1-2j} \beta_H^*a_j(x,y) \frac{2^{-n/2+j}}{\left( n+1-2j \right) \left( n+3-2j \right)\ldots(-1)} \Gamma \left( \frac{1}{2} \right). \end{align*} $$
$$ \begin{align*} \beta_H^*h={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \tfrac{1}{2 \sqrt \pi} \rho \omega_0 \sum_{j=0}^{N} \left( \tfrac{\rho^2}{4} \right)^{-\frac{n+1}{2}+j} \beta_H^*a_j(x,y) \Gamma\left( \frac{n+1}{2}-j , \frac{\rho^2}{4} \right) \\ ={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \tfrac{1}{2 \sqrt{\pi}} \rho^{-n}\omega_0 \sum_{j=0}^{n/2} \rho^{2j} 2^{n+1-2j} \beta_H^*a_j(x,y) \Gamma \left( \frac{n+1}{2}-j \right) \\ {}&+ \tfrac{1}{2 \sqrt{\pi}} \rho \omega_0 \sum_{j=0}^{n/2} \beta_H^* a_j(x,y) {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) + \tfrac{1}{2 \sqrt{\pi}} \rho\omega_0 \sum_{j=n/2 +1}^{N} \beta_H^* a_j(x,y) {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) \\ {}&+\tfrac{1}{2 \sqrt{\pi}} \rho^{-n}\omega_0 \sum_{j=n/2+1}^{N} \rho^{2j} 2^{n+1-2j} \beta_H^*a_j(x,y) \frac{2^{-n/2+j}}{\left( n+1-2j \right) \left( n+3-2j \right)\ldots(-1)} \Gamma \left( \frac{1}{2} \right). \end{align*} $$
Since
![]() $\Gamma \left ( \frac {n+1}{2} -j \right ) = \frac {\sqrt {\pi } (n-2j-1)!!}{2^{n/2-j}} $
for
$\Gamma \left ( \frac {n+1}{2} -j \right ) = \frac {\sqrt {\pi } (n-2j-1)!!}{2^{n/2-j}} $
for
![]() $j \in \{0,1,\ldots ,n/2 \}$
, it follows that
$j \in \{0,1,\ldots ,n/2 \}$
, it follows that
 $$ \begin{align} \begin{aligned} \beta_H^* h={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \omega_0 \rho {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) + \rho^{-n} \omega_0 \sum_{j=0}^{n/2} \rho^{2j} 2^{n/2-j} (n-2j-1)!! \beta_H^* a_j(x,y) \\ {}&+ \rho^{-n}\omega_0 \sum_{j=n/2+1}^{N} \rho^{2j} \frac{ (-1)^{j-n/2} 2^{n/2-j} }{(2j-n-1)!!} \beta_H^*a_j(x,y). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \beta_H^* h={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \omega_0 \rho {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) + \rho^{-n} \omega_0 \sum_{j=0}^{n/2} \rho^{2j} 2^{n/2-j} (n-2j-1)!! \beta_H^* a_j(x,y) \\ {}&+ \rho^{-n}\omega_0 \sum_{j=n/2+1}^{N} \rho^{2j} \frac{ (-1)^{j-n/2} 2^{n/2-j} }{(2j-n-1)!!} \beta_H^*a_j(x,y). \end{aligned} \end{align} $$
The case
![]() $\rho \neq 0$
and
$\rho \neq 0$
and
![]() $\omega _0 \to 0$
corresponds to
$\omega _0 \to 0$
corresponds to
![]() $x \neq y$
and
$x \neq y$
and
![]() $t \searrow 0$
before the pull-back. We obtain that
$t \searrow 0$
before the pull-back. We obtain that
![]() $\beta _H^*h$
is in
$\beta _H^*h$
is in
![]() ${\mathcal C}^{\infty }(\operatorname {M_{heat}})$
and it vanishes at first order on
${\mathcal C}^{\infty }(\operatorname {M_{heat}})$
and it vanishes at first order on
![]() $\operatorname {lb}$
, which is compatible with Theorem 6.1.
$\operatorname {lb}$
, which is compatible with Theorem 6.1.
If
![]() $\rho \to 0$
and
$\rho \to 0$
and
![]() $\omega _0=1$
, which corresponds to
$\omega _0=1$
, which corresponds to
![]() $x=y$
and
$x=y$
and
![]() $t \searrow 0$
, then
$t \searrow 0$
, then
![]() $\beta _H^*h= \rho ^{-n}\omega _0 \sum _{j=0}^{N} \rho ^{2j} A_{j}(x)$
, where we denoted by
$\beta _H^*h= \rho ^{-n}\omega _0 \sum _{j=0}^{N} \rho ^{2j} A_{j}(x)$
, where we denoted by
![]() $A_j(x)$
the coefficients appearing in (10.3). Again, this result is compatible with Theorem 7.1, and moreover, the coefficients are precisely the ones from [Reference Bär and Moroianu2, Theorem 3.1].
$A_j(x)$
the coefficients appearing in (10.3). Again, this result is compatible with Theorem 7.1, and moreover, the coefficients are precisely the ones from [Reference Bär and Moroianu2, Theorem 3.1].
Remark that formula (10.3) is stronger than Theorems 6.1 and 7.1. If both
![]() $\rho $
and
$\rho $
and
![]() $\omega _0$
tend to
$\omega _0$
tend to
![]() $0$
(with different speeds), it describes the behavior of
$0$
(with different speeds), it describes the behavior of
![]() $h_t$
as t goes to zero from any positive direction (not only the vertical one).
$h_t$
as t goes to zero from any positive direction (not only the vertical one).
10.2 The case when n is odd
Remark that for small
![]() $\xi $
, we have
$\xi $
, we have
 $$ \begin{align*} \Gamma(0,\xi)={}&\int_{\xi}^{\infty} t^{-1}e^{-t} dt = \int_{\xi}^{1} \frac{e^{-t}-1}{t} dt +\int_{\xi}^{1} t^{-1} dt + \int_{1}^{\infty}t^{-1}e^{-t}dt \\ ={}&- \log \xi + {\mathcal C}^{\infty}_{\xi}[0,\epsilon). \end{align*} $$
$$ \begin{align*} \Gamma(0,\xi)={}&\int_{\xi}^{\infty} t^{-1}e^{-t} dt = \int_{\xi}^{1} \frac{e^{-t}-1}{t} dt +\int_{\xi}^{1} t^{-1} dt + \int_{1}^{\infty}t^{-1}e^{-t}dt \\ ={}&- \log \xi + {\mathcal C}^{\infty}_{\xi}[0,\epsilon). \end{align*} $$
Furthermore, if p is a negative integer, inductively we obtain
 $$ \begin{align*} \Gamma(-p,\xi)={}& \frac{e^{-\xi}\xi^{-p}}{p!} \sum_{k=0}^{p-1} (-1)^k (p-k-1)! \xi^k + \frac{(-1)^p}{p!} \Gamma(0,\xi) \\ ={}& \xi^{-p} {\mathcal C}^{\infty}_{\xi}[0,\epsilon)-\frac{(-1)^p}{p!} \log \xi +{\mathcal C}^{\infty}_{\xi}[0,\epsilon). \end{align*} $$
$$ \begin{align*} \Gamma(-p,\xi)={}& \frac{e^{-\xi}\xi^{-p}}{p!} \sum_{k=0}^{p-1} (-1)^k (p-k-1)! \xi^k + \frac{(-1)^p}{p!} \Gamma(0,\xi) \\ ={}& \xi^{-p} {\mathcal C}^{\infty}_{\xi}[0,\epsilon)-\frac{(-1)^p}{p!} \log \xi +{\mathcal C}^{\infty}_{\xi}[0,\epsilon). \end{align*} $$
We pull-back equation (10.2) on the heat space
![]() $\operatorname {M_{heat}}$
:
$\operatorname {M_{heat}}$
:
 $$ \begin{align*} \beta_H^*h={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \tfrac{1}{2 \sqrt \pi} \rho \omega_0 \sum_{j=0}^{N} \left( \tfrac{\rho^2}{4} \right)^{-\frac{n+1}{2}+j} \beta_H^*a_j(x,y) \Gamma\left( \frac{n+1}{2}-j , \frac{\rho^2}{4} \right) \\ ={}& \rho \omega_0 \beta_H^*a_j(x,y) + \tfrac{1}{2\sqrt{\pi}} \rho \omega_0 \sum_{l=0}^{(n-1)/2} \beta_H^* a_j(x,y) {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) \\ {}&+\frac{1}{\sqrt{\pi}} \rho^{-n}\omega_0 \sum_{j=0}^{(n-1)/2} \rho^{2j} \beta_H^*a_j(x,y) 2^{n-2j} \Gamma \left( \frac{n+1}{2}-j \right) \\ {}&+ \frac{2}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \log \rho \beta_H^{*} a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}+1}}{\left( j-\frac{n+1}{2} \right)!} \\ {}&+ \frac{2}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \beta_H^{*} a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}}}{\left( j-\frac{n+1}{2} \right)!} \log 2 \\ {}&+\tfrac{1}{2\sqrt{\pi}} \rho \omega_0 \sum_{j=(n+1)/2}^{N} \beta_H^*a_j(x.y) {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) \\ {}&+ \tfrac{1}{ \sqrt{\pi}} \rho^{-n}\omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \beta_H^*a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}}}{\left( j-\frac{n+1}{2} \right)!} {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon). \end{align*} $$
$$ \begin{align*} \beta_H^*h={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \tfrac{1}{2 \sqrt \pi} \rho \omega_0 \sum_{j=0}^{N} \left( \tfrac{\rho^2}{4} \right)^{-\frac{n+1}{2}+j} \beta_H^*a_j(x,y) \Gamma\left( \frac{n+1}{2}-j , \frac{\rho^2}{4} \right) \\ ={}& \rho \omega_0 \beta_H^*a_j(x,y) + \tfrac{1}{2\sqrt{\pi}} \rho \omega_0 \sum_{l=0}^{(n-1)/2} \beta_H^* a_j(x,y) {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) \\ {}&+\frac{1}{\sqrt{\pi}} \rho^{-n}\omega_0 \sum_{j=0}^{(n-1)/2} \rho^{2j} \beta_H^*a_j(x,y) 2^{n-2j} \Gamma \left( \frac{n+1}{2}-j \right) \\ {}&+ \frac{2}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \log \rho \beta_H^{*} a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}+1}}{\left( j-\frac{n+1}{2} \right)!} \\ {}&+ \frac{2}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \beta_H^{*} a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}}}{\left( j-\frac{n+1}{2} \right)!} \log 2 \\ {}&+\tfrac{1}{2\sqrt{\pi}} \rho \omega_0 \sum_{j=(n+1)/2}^{N} \beta_H^*a_j(x.y) {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) \\ {}&+ \tfrac{1}{ \sqrt{\pi}} \rho^{-n}\omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \beta_H^*a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}}}{\left( j-\frac{n+1}{2} \right)!} {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon). \end{align*} $$
Therefore, we obtain
 $$ \begin{align} \begin{aligned} \beta_H^* h={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \omega_0 \rho {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) + \omega_0 \rho^{-n} {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) \\ {}&+ \frac{1}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=0}^{(n-1)/2} \rho^{2j} \beta_H^*a_j(x,y) 2^{n-2j} \left( \frac{n+1}{2}-j \right) ! \\ {}&+ \frac{2}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \log \rho \beta_H^{*} a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}+1}}{\left( j-\frac{n+1}{2} \right)!} \\ {}&+ \frac{2}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \beta_H^{*} a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}}}{\left( j-\frac{n+1}{2} \right)!} \log 2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \beta_H^* h={}& \rho \omega_0 \beta_H^* {\mathcal C}^{\infty}_{t,x,y} + \omega_0 \rho {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) + \omega_0 \rho^{-n} {\mathcal C}^{\infty}_{\rho^2}[0,\epsilon) \\ {}&+ \frac{1}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=0}^{(n-1)/2} \rho^{2j} \beta_H^*a_j(x,y) 2^{n-2j} \left( \frac{n+1}{2}-j \right) ! \\ {}&+ \frac{2}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \log \rho \beta_H^{*} a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}+1}}{\left( j-\frac{n+1}{2} \right)!} \\ {}&+ \frac{2}{\sqrt{\pi}} \rho^{-n} \omega_0 \sum_{j=(n+1)/2}^{N} \rho^{2j} \beta_H^{*} a_j(x,y) 2^{n-2j} \frac{(-1)^{j-\frac{n+1}{2}}}{\left( j-\frac{n+1}{2} \right)!} \log 2. \end{aligned} \end{align} $$
If
![]() $\rho \neq 0$
and
$\rho \neq 0$
and
![]() $\omega _0 \to 0$
(corresponding to
$\omega _0 \to 0$
(corresponding to
![]() $x \neq y$
and
$x \neq y$
and
![]() $t \searrow 0$
before the pull-back on
$t \searrow 0$
before the pull-back on
![]() $\operatorname {M_{heat}}$
), we obtain that
$\operatorname {M_{heat}}$
), we obtain that
![]() $\beta _H^* h \in {\mathcal C}^{\infty }(M_{heat})$
and it vanishes at order
$\beta _H^* h \in {\mathcal C}^{\infty }(M_{heat})$
and it vanishes at order
![]() $1$
at
$1$
at
![]() $\operatorname {lb}$
, which is compatible with the result of Theorem 6.1.
$\operatorname {lb}$
, which is compatible with the result of Theorem 6.1.
In the case
![]() $\rho \to 0$
and
$\rho \to 0$
and
![]() $\omega _0=1$
which corresponds to
$\omega _0=1$
which corresponds to
![]() $x=y$
and
$x=y$
and
![]() $t \searrow 0$
, we obtain
$t \searrow 0$
, we obtain
![]() $\beta _H^* h= \rho ^{-n}{\mathcal C}^{\infty }_{\rho ^2} + \rho ^{-n}\sum _{j=0}^N \rho ^{2j} A_j(x) + \rho ^{-n} \sum _{j=(n+1)/2}^N \rho ^{2j} \log \rho B_j(x)$
, where we denoted by
$\beta _H^* h= \rho ^{-n}{\mathcal C}^{\infty }_{\rho ^2} + \rho ^{-n}\sum _{j=0}^N \rho ^{2j} A_j(x) + \rho ^{-n} \sum _{j=(n+1)/2}^N \rho ^{2j} \log \rho B_j(x)$
, where we denoted by
![]() $A_j$
and
$A_j$
and
![]() $B_j$
the coefficients appearing in (10.4). This result is compatible with Theorem 7.1 and again, we find some of the coefficients appearing in [Reference Bär and Moroianu2, Theorem 3.1].
$B_j$
the coefficients appearing in (10.4). This result is compatible with Theorem 7.1 and again, we find some of the coefficients appearing in [Reference Bär and Moroianu2, Theorem 3.1].
11 The heat kernel as a polyhomogeneous conormal section
Let us recall the notions of index family and polyhomogeneous conormal functions on a manifold with corners with two boundary hypersurfaces. (For an accessible introduction, see [Reference Grieser, Gil, Grieser and Lesch15], and for full details of the theory, see [Reference Melrose18].) A discrete subset
![]() $F \in {\mathbb C} \times {\mathbb N} $
is called an index set if the following conditions are satisfied:
$F \in {\mathbb C} \times {\mathbb N} $
is called an index set if the following conditions are satisfied:
-
1) For any
 $N \in {\mathbb R}$
, the set
$N \in {\mathbb R}$
, the set
 $F \cap \{ (z,p): \Re z < N \} $
is finite.
$F \cap \{ (z,p): \Re z < N \} $
is finite. -
2) If
 $p> p_0$
and
$p> p_0$
and
 $(z,p) \in F$
, then
$(z,p) \in F$
, then
 $(z, p_0) \in F$
.
$(z, p_0) \in F$
.
If X is a manifold with corners with two boundary hypersurfaces
![]() $B_1$
and
$B_1$
and
![]() $B_2$
given by the boundary defining functions x and y, a smooth function f on
$B_2$
given by the boundary defining functions x and y, a smooth function f on
![]() is said to be polyhomogeneous conormal with index sets E and F, respectively, if in a small neighborhood
is said to be polyhomogeneous conormal with index sets E and F, respectively, if in a small neighborhood
![]() $[0,\epsilon ) \times B_1$
, f has the asymptotic expansion
$[0,\epsilon ) \times B_1$
, f has the asymptotic expansion
where
![]() $a_{z,p}$
are smooth coefficients on
$a_{z,p}$
are smooth coefficients on
![]() $B_2$
, and for each
$B_2$
, and for each
![]() $a_{z,p}$
there exists a sequence of real numbers
$a_{z,p}$
there exists a sequence of real numbers
![]() $b_{w,q}$
, such that
$b_{w,q}$
, such that
One can prove that f is a polyhomogeneous conormal function on X with index sets
![]() $F_p= \{ (k,0) : k \in {\mathbb Z}, k \geq -p \}$
and
$F_p= \{ (k,0) : k \in {\mathbb Z}, k \geq -p \}$
and
![]() $F_0=\{ (n,0) : n \in {\mathbb N} \}$
if and only if
$F_0=\{ (n,0) : n \in {\mathbb N} \}$
if and only if
![]() $f \in y^{-p} {\mathcal C}^{\infty }(X)$
. Furthermore, f is a polyhomogeneous conormal function on X with index sets
$f \in y^{-p} {\mathcal C}^{\infty }(X)$
. Furthermore, f is a polyhomogeneous conormal function on X with index sets
![]() $F'=\{ (n,1) : n \in {\mathbb N}^* \}$
and
$F'=\{ (n,1) : n \in {\mathbb N}^* \}$
and
![]() $F_0$
if and only if
$F_0$
if and only if
![]() $f \in {\mathcal C}^{\infty }(X)+ \log y \cdot {\mathcal C}^{\infty }(X)$
. Therefore, we can restate Theorem 1.4 as follows:
$f \in {\mathcal C}^{\infty }(X)+ \log y \cdot {\mathcal C}^{\infty }(X)$
. Therefore, we can restate Theorem 1.4 as follows:
Theorem 11.1 For
![]() $r=\frac {1}{2}$
, the heat kernel
$r=\frac {1}{2}$
, the heat kernel
![]() $h_t$
of the operator
$h_t$
of the operator
![]() $e^{-t \operatorname {\Delta }^{1/2}}$
is a polyhomogeneous conormal section on the linear heat space
$e^{-t \operatorname {\Delta }^{1/2}}$
is a polyhomogeneous conormal section on the linear heat space
![]() $\operatorname {M_{heat}}$
with values in
$\operatorname {M_{heat}}$
with values in
![]() $\mathcal {E} \boxtimes \mathcal {E}^*$
. The index set for the lateral boundary is
$\mathcal {E} \boxtimes \mathcal {E}^*$
. The index set for the lateral boundary is
If n is even, the index set of the front face is
whereas for n odd, the index set toward
![]() $\operatorname {ff}$
is given by
$\operatorname {ff}$
is given by
It seems reasonable to expect that the Schwartz kernel
![]() $h_t$
of the operator
$h_t$
of the operator
![]() $e^{-t\operatorname {\Delta }^r}$
for
$e^{-t\operatorname {\Delta }^r}$
for
![]() $r \in (0,1)$
can be lifted to a polyhomogeneous conormal section in a certain “transcendental” heat space
$r \in (0,1)$
can be lifted to a polyhomogeneous conormal section in a certain “transcendental” heat space
![]() $M^r_{Heat}$
depending on r with values in
$M^r_{Heat}$
depending on r with values in
![]() $\mathcal {E} \boxtimes \mathcal {E}^*$
. However, already in the case
$\mathcal {E} \boxtimes \mathcal {E}^*$
. However, already in the case
![]() $r=1/3,$
our method leads to complicated computations involving Bessel modified functions. We therefore leave this investigation open for a future project.
$r=1/3,$
our method leads to complicated computations involving Bessel modified functions. We therefore leave this investigation open for a future project.
Acknowledgment
I am grateful to my advisor Sergiu Moroianu for many enlightening discussions and for a careful reading of the paper. I would like to thank the anonymous referee for helpful suggestions and remarks leading to the improvement of the presentation.