One of the most fruitful results from Minkowski’s geometric viewpoint on number theory is his so-called first fundamental theorem. It provides an optimal upper bound for the volume of a $0$ -symmetric convex body whose only interior lattice point is the origin. Minkowski also obtained a discrete analog by proving optimal upper bounds on the number of lattice points in the boundary of such convex bodies. Whereas the volume inequality has been generalized to any number of interior lattice points already by van der Corput in the 1930s, a corresponding result for the discrete case remained to be proven. Our main contribution is a corresponding optimal relation between the number of boundary and interior lattice points of a $0$ -symmetric convex body. The proof relies on a congruence argument and a difference set estimate from additive combinatorics.

We continue our study of intermediate sums over polyhedra, interpolating between integrals and discrete sums, which were introduced by Barvinok [Computing the Ehrhart quasi-polynomial of a rational simplex. Math. Comp. 75 (2006), 1449–1466]. By well-known decompositions, it is sufficient to consider the case of affine cones $s+\mathfrak{c}$ , where $s$ is an arbitrary real vertex and $\mathfrak{c}$ is a rational polyhedral cone. For a given rational subspace  $L$ , we define the intermediate generating functions $S^{L}(s+\mathfrak{c})(\unicode[STIX]{x1D709})$ by integrating an exponential function over all lattice slices of the affine cone  $s+\mathfrak{c}$ parallel to the subspace  $L$ and summing up the integrals. We expose the bidegree structure in parameters $s$ and $\unicode[STIX]{x1D709}$ , which was implicitly used in the algorithms in our papers [Computation of the highest coefficients of weighted Ehrhart quasi-polynomials of rational polyhedra. Found. Comput. Math.12 (2012), 435–469] and [Intermediate sums on polyhedra: computation and real Ehrhart theory. Mathematika59 (2013), 1–22]. The bidegree structure is key to a new proof for the Baldoni–Berline–Vergne approximation theorem for discrete generating functions [Local Euler–Maclaurin expansion of Barvinok valuations and Ehrhart coefficients of rational polytopes. Contemp. Math.452 (2008), 15–33], using the Fourier analysis with respect to the parameter  $s$ and a continuity argument. Our study also enables a forthcoming paper, in which we study intermediate sums over multi-parameter families of polytopes.

Based on a construction method introduced by Bourgain and Delbaen, we give a general definition of a Bourgain–Delbaen space and prove that every infinite-dimensional separable ${\mathcal{L}}_{\infty }$ -space is isomorphic to such a space. Furthermore, we provide an example of a ${\mathcal{L}}_{\infty }$ and asymptotic $c_{0}$ space not containing $c_{0}$ .

We consider an elliptic self-adjoint first-order differential operator $L$ acting on pairs (2-columns) of complex-valued half-densities over a connected compact three-dimensional manifold without boundary. The principal symbol of the operator $L$ is assumed to be trace-free and the subprincipal symbol is assumed to be zero. Given a positive scalar weight function, we study the weighted eigenvalue problem for the operator $L$ . The corresponding counting function (number of eigenvalues between zero and a positive $\unicode[STIX]{x1D706}$ ) is known to admit, under appropriate assumptions on periodic trajectories, a two-term asymptotic expansion as $\unicode[STIX]{x1D706}\rightarrow +\infty$ and we have recently derived an explicit formula for the second asymptotic coefficient. The purpose of this paper is to establish the geometric meaning of the second asymptotic coefficient. To this end, we identify the geometric objects encoded within our eigenvalue problem—metric, non-vanishing spinor field and topological charge—and express our asymptotic coefficients in terms of these geometric objects. We prove that the second asymptotic coefficient of the counting function has the geometric meaning of the massless Dirac action.

We prove a family of sharp bilinear space–time estimates for the half-wave propagator $\text{e}^{\text{i}t\sqrt{-\unicode[STIX]{x1D6E5}}}$ . As a consequence, for radially symmetric initial data, we establish sharp estimates of this kind for a range of exponents beyond the classical range.

We show that if a collection of lines in a vector space over a finite field has “dimension” at least $2(d-1)+\unicode[STIX]{x1D6FD}$ , then its union has “dimension” at least $d+\unicode[STIX]{x1D6FD}$ . This is the sharp estimate of its type when no structural assumptions are placed on the collection of lines. We also consider some refinements and extensions of the main result, including estimates for unions of $k$ -planes.

In this paper we study the Duffin–Schaeffer conjecture, which claims that $\unicode[STIX]{x1D706}(\bigcap _{m=1}^{\infty }\bigcup _{n=m}^{\infty }{\mathcal{E}}_{n})=1$ if and only if $\sum _{n=1}^{\infty }\unicode[STIX]{x1D706}({\mathcal{E}}_{n})=\infty$ , where $\unicode[STIX]{x1D706}$ denotes the Lebesgue measure on $\mathbb{R}/\mathbb{Z}$ ,

$$\begin{eqnarray}{\mathcal{E}}_{n}={\mathcal{E}}_{n}(\unicode[STIX]{x1D713})=\mathop{\bigcup }_{\substack{ m=1 \\ (m,n)=1}}^{n}\bigg(\frac{m-\unicode[STIX]{x1D713}(n)}{n},\frac{m+\unicode[STIX]{x1D713}(n)}{n}\bigg),\end{eqnarray}$$

$\unicode[STIX]{x1D713}$

$\bigcap _{m=1}^{\infty }\bigcup _{n=m}^{\infty }{\mathcal{E}}_{n}$

$\bigcup _{n=1}^{\infty }{\mathcal{E}}_{n}$

$C>0$

$$\begin{eqnarray}\unicode[STIX]{x1D706}\bigg(\mathop{\bigcup }_{n=1}^{\infty }{\mathcal{E}}_{n}\bigg)\geqslant C\min \bigg\{\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D706}({\mathcal{E}}_{n}),1\bigg\}.\end{eqnarray}$$

$p$

For a half-integral weight modular form $f=\sum _{n=1}^{\infty }a_{f}(n)n^{(k-1)/2}q^{n}$ of weight $k=\ell +1/2$ on $\unicode[STIX]{x1D6E4}_{0}(4)$ such that $a_{f}(n)$ ( $n\in \mathbb{N}$ ) are real, we prove for a fixed suitable natural number $r$ that $a_{f}(n)$ changes sign infinitely often as $n$ varies over numbers having at most $r$ prime factors, assuming the analog of the Ramanujan conjecture for Fourier coefficients of half-integral weight forms.

We relate Catalan numbers and Catalan determinants to random matrix integrals and to moments of spin representations of odd orthogonal groups.

We prove that the log-Brunn–Minkowski inequality (log-BMI) for the Lebesgue measure in dimension $n$ would imply the log-BMI and, therefore, theB-conjecture for any even log-concave measure in dimension $n$ . As a consequence, we prove the log-BMI and the B-conjecture for any even log-concave measure in the plane. 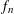Moreover, we prove that the log-BMI reduces to the following: for each dimension $n$ , there is a density $f_{n}$ , which satisfies an integrability assumption, so that the log-BMI holds for parallelepipeds with parallel facets, for the density 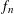$f_{n}$ . As a byproduct of our methods, we study possible log-concavity of the function 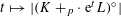$t\mapsto |(K+_{p}\cdot ~\text{e}^{t}L)^{\circ }|$ , where 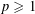$p\geqslant 1$ and $K$ , 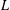$L$ are symmetric convex bodies, which we are able to prove in some instances and, as a further application, we confirm the variance conjecture in a special class of convex bodies. Finally, we establish a non-trivial dual form of the log-BMI.

We give non-trivial bounds for the bilinear sums

$$\begin{eqnarray}\mathop{\sum }_{u=1}^{U}\mathop{\sum }_{v=1}^{V}\unicode[STIX]{x1D6FC}_{u}\unicode[STIX]{x1D6FD}_{v}\,\mathbf{e}_{p}(u/f(v)),\end{eqnarray}$$

$\,\mathbf{e}_{p}(z)$

$\mathbb{F}_{p}$

$p$

$U$

$V$

$f\in \mathbb{F}_{p}[X]$

$\{\unicode[STIX]{x1D6FC}_{u}\}$

$\{\unicode[STIX]{x1D6FD}_{v}\}$

$f(X)=aX+b$

$\mathbb{F}_{p}$

In this paper, we study how small a box contains at least two points from a modular hyperbola $xy\equiv c\;(\text{mod}\;p)$ . There are two such points in a square of side length $p^{1/4+\unicode[STIX]{x1D716}}$ . Furthermore, it turns out that either there are two such points in a square of side length $p^{1/6+\unicode[STIX]{x1D716}}$ or the least quadratic non-residue is less than $p^{1/(6\sqrt{e})+\unicode[STIX]{x1D716}}$ .

We establish lower bounds for (i) the numbers of positive and negative terms and (ii) the number of sign changes in the sequence of Fourier coefficients at squarefree integers of a half-integral weight modular Hecke eigenform.

Let $\unicode[STIX]{x1D6FD}>1$ be a real number and define the $\unicode[STIX]{x1D6FD}$ -transformation on $[0,1]$ by $T_{\unicode[STIX]{x1D6FD}}:x\mapsto \unicode[STIX]{x1D6FD}x\,\text{mod}\,1$ . Further, define

$$\begin{eqnarray}W_{y}(T_{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6F9}):=\{x\in [0,1]:|T_{\unicode[STIX]{x1D6FD}}^{n}x-y|<\unicode[STIX]{x1D6F9}(n)\text{ for infinitely many }n\}\end{eqnarray}$$

$$\begin{eqnarray}W(T_{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6F9}):=\{(x,y)\in [0,1]^{2}:|T_{\unicode[STIX]{x1D6FD}}^{n}x-y|<\unicode[STIX]{x1D6F9}(n)\text{ for infinitely many }n\},\end{eqnarray}$$

$\unicode[STIX]{x1D6F9}:\mathbb{N}\rightarrow \mathbb{R}_{{>}0}$

$\unicode[STIX]{x1D6F9}(n)\rightarrow 0$

$n\rightarrow \infty$

We study the average value of the divisor function $\unicode[STIX]{x1D70F}(n)$ for $n\leqslant x$ with $n\equiv a~\text{mod}~q$ . The divisor function is known to be evenly distributed over arithmetic progressions for all $q$ that are a little smaller than $x^{2/3}$ . We show how to go past this barrier when $q=p^{k}$ for odd primes $p$ and any fixed integer $k\geqslant 7$ .

We prove that among all flag triangulations of manifolds of odd dimension $2r-1$ , with a sufficient number of vertices, the unique maximizer of the entries of the $f$ -, $h$ -, $g$ - and $\unicode[STIX]{x1D6FE}$ -vector is the balanced join of $r$ cycles. Our proof uses methods from extremal graph theory.

We study ultrasymmetric spaces in the case in which the fundamental function belongs to a limiting class of quasiconcave functions. In the process, we study limiting cases of $J$ interpolation spaces and establish new $J$ – $K$ identities as well as a reiteration theorem for these limiting interpolation methods.

In a $d$ -dimensional convex body $K$ random points $X_{0},\ldots ,X_{d}$ are chosen. Their convex hull is a random simplex. The expected volume of a random simplex is monotone under set inclusion if $K\subset L$ implies that the expected volume of a random simplex in $K$ is smaller than the expected volume of a random simplex in $L$ . Continuing work of Rademacher [On the monotonicity of the expected volume of a random simplex. Mathematika58 (2012), 77–91], it is shown that moments of the volume of random simplices are, in general, not monotone under set inclusion.