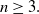1. Introduction
A gradient Ricci soliton is a Riemannian manifold
![]() $\Sigma$
satisfying
$\Sigma$
satisfying
where Ric denotes the Ricci tensor,
![]() $f\;:\;\Sigma\rightarrow\mathbb{R}$
is a smooth function, and
$f\;:\;\Sigma\rightarrow\mathbb{R}$
is a smooth function, and
![]() $\lambda\in\mathbb{R}.$
A Ricci soliton is called expanding, steady or shrinking if, respectively,
$\lambda\in\mathbb{R}.$
A Ricci soliton is called expanding, steady or shrinking if, respectively,
![]() $\lambda \lt 0, $
$\lambda \lt 0, $
![]() $\lambda = 0$
or
$\lambda = 0$
or
![]() $ \lambda \gt 0.$
Ricci flow was introduced by Hamilton in his seminal work [Reference Hamilton6] to study closed three manifolds with positive Ricci curvature. Ricci solitons generate self-similar solutions to the Ricci flow and often arise as singularity models of the flow; therefore, it is important to study and classify them in order to understand the geometry of singularities.
$ \lambda \gt 0.$
Ricci flow was introduced by Hamilton in his seminal work [Reference Hamilton6] to study closed three manifolds with positive Ricci curvature. Ricci solitons generate self-similar solutions to the Ricci flow and often arise as singularity models of the flow; therefore, it is important to study and classify them in order to understand the geometry of singularities.
A standard example of expanding Ricci soliton is given by
![]() $(\mathbb{R}^{n},g_0, -\frac{|x|^{2}}{4}),$
where
$(\mathbb{R}^{n},g_0, -\frac{|x|^{2}}{4}),$
where
![]() $g_0$
is the Euclidean metric. In fact, note that
$g_0$
is the Euclidean metric. In fact, note that
![]() $Ric+\nabla^{2}f=-\frac{1}{2}.$
We recall that an expanding Ricci soliton is related to the limit solution of Type III singularities of the Ricci flow, see [Reference Lott7]. Besides, the characterization of expanding Ricci soliton has attracted the attention of many researchers, see for instance [Reference Catino2, Reference Chan3, Reference Ma8–Reference Schulze and Simon11].
$Ric+\nabla^{2}f=-\frac{1}{2}.$
We recall that an expanding Ricci soliton is related to the limit solution of Type III singularities of the Ricci flow, see [Reference Lott7]. Besides, the characterization of expanding Ricci soliton has attracted the attention of many researchers, see for instance [Reference Catino2, Reference Chan3, Reference Ma8–Reference Schulze and Simon11].
In the steady case, Hamilton [Reference Hamilton6] discovered the first example of a complete noncompact steady soliton on
![]() $\mathbb{R}^{2}$
called the cigar soliton, where the metric is given by
$\mathbb{R}^{2}$
called the cigar soliton, where the metric is given by
![]() $ds^{2}=\frac{dx^{2}+dy^{2}}{1+x^{2}+y^{2}}$
with potential function
$ds^{2}=\frac{dx^{2}+dy^{2}}{1+x^{2}+y^{2}}$
with potential function
![]() $f(x,y)=-\log\!(1+x^{2}+y^{2}),$
$f(x,y)=-\log\!(1+x^{2}+y^{2}),$
![]() $(x,y)\in\mathbb{R}^{2}$
. The cigar has positive Gaussian curvature
$(x,y)\in\mathbb{R}^{2}$
. The cigar has positive Gaussian curvature
![]() $R = 4e^{f}$
and linear volume growth, and it is asymptotic to a cylinder of finite circumference at infinity. In the three-dimensional case, the known examples are given by quotients of
$R = 4e^{f}$
and linear volume growth, and it is asymptotic to a cylinder of finite circumference at infinity. In the three-dimensional case, the known examples are given by quotients of
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
![]() $\mathbb{R}\times\Sigma^{2}$
, where
$\mathbb{R}\times\Sigma^{2}$
, where
![]() $\Sigma^{2}$
is the cigar soliton, and the rotationally symmetric one constructed by Bryant [Reference Bryant1].
$\Sigma^{2}$
is the cigar soliton, and the rotationally symmetric one constructed by Bryant [Reference Bryant1].
We say that
![]() $\Sigma$
is a generalized cigar soliton, if
$\Sigma$
is a generalized cigar soliton, if
![]() $\Sigma$
is isometric to
$\Sigma$
is isometric to
![]() $M\times\mathbb{R}^{n-2},$
where M is the cigar soliton. Recently, Deruelle [Reference Deruelle5] obtained the following rigidity result to generalized cigar soliton
$M\times\mathbb{R}^{n-2},$
where M is the cigar soliton. Recently, Deruelle [Reference Deruelle5] obtained the following rigidity result to generalized cigar soliton
Theorem 1.
Let
![]() $\Sigma$
be a complete nonflat noncompact steady gradient Ricci soliton of dimension
$\Sigma$
be a complete nonflat noncompact steady gradient Ricci soliton of dimension
![]() $n\geq 3$
such that the sectional curvature is nonnegative and
$n\geq 3$
such that the sectional curvature is nonnegative and
![]() $R\in L^{1}(\Sigma).$
Then the universal covering of
$R\in L^{1}(\Sigma).$
Then the universal covering of
![]() $\Sigma$
is isometric to
$\Sigma$
is isometric to
![]() $M\times\mathbb{R}^{n-2}$
, where M is the cigar soliton.
$M\times\mathbb{R}^{n-2}$
, where M is the cigar soliton.
In [Reference Catino2], Catino et al. obtained a suitable Bochner-type formula for the tensor
![]() $\left(Ric-\frac{R}{2}\right)e^{-f}$
, where R is the scalar curvature, to guarantee that the condition
$\left(Ric-\frac{R}{2}\right)e^{-f}$
, where R is the scalar curvature, to guarantee that the condition
![]() $R\in L^{1}(\Sigma)$
in the above theorem can be relaxed to
$R\in L^{1}(\Sigma)$
in the above theorem can be relaxed to
![]() $\liminf_{r\rightarrow\infty}\frac{1}{r}\int_{B_r(0)}R=0.$
Besides, using a similar strategy they were able to prove the following rigidity result addressed to expanding Ricci solitons
$\liminf_{r\rightarrow\infty}\frac{1}{r}\int_{B_r(0)}R=0.$
Besides, using a similar strategy they were able to prove the following rigidity result addressed to expanding Ricci solitons
Theorem 2.
Let
![]() $\Sigma$
be a complete noncompact expanding gradient Ricci soliton of dimension
$\Sigma$
be a complete noncompact expanding gradient Ricci soliton of dimension
![]() $n\geq 3$
such that the sectional curvature is nonnegative. If
$n\geq 3$
such that the sectional curvature is nonnegative. If
![]() $R\in L^1(\Sigma)$
, then
$R\in L^1(\Sigma)$
, then
![]() $\Sigma$
is isometric to a quotient of the Gaussian soliton
$\Sigma$
is isometric to a quotient of the Gaussian soliton
![]() $\mathbb{R}^{n}.$
$\mathbb{R}^{n}.$
In this paper, motivated by Deruelle [Reference Deruelle5] and Catino et al. [Reference Catino2], we obtain rigidity results for steady and expanding Ricci solitons under an assumption that the scalar curvature lies in
![]() $L^{p}(\Sigma)$
, with respect to a suitable volume element. We point out that our rigidity results are obtained from a different approach. Now, we can state our first result.
$L^{p}(\Sigma)$
, with respect to a suitable volume element. We point out that our rigidity results are obtained from a different approach. Now, we can state our first result.
Theorem 3.
Let
![]() $\Sigma$
be a complete noncompact steady gradient Ricci soliton of dimension
$\Sigma$
be a complete noncompact steady gradient Ricci soliton of dimension
![]() $n\geq 3$
such that the sectional curvature is nonnegative. If
$n\geq 3$
such that the sectional curvature is nonnegative. If
![]() $Re^{-f}\in L^{p}_{-f}(\Sigma)$
,
$Re^{-f}\in L^{p}_{-f}(\Sigma)$
,
![]() $p>1$
, then
$p>1$
, then
![]() $\Sigma$
is either isometric to a quotient of
$\Sigma$
is either isometric to a quotient of
![]() $\mathbb{R}^{n}$
or
$\mathbb{R}^{n}$
or
![]() $M\times\mathbb{R}^{n-2}$
, where M is the cigar soliton.
$M\times\mathbb{R}^{n-2}$
, where M is the cigar soliton.
We recall that, from [Reference Chen4], a complete three-dimensional noncompact steady gradient Ricci soliton has nonnegative scalar curvature. Thus, we conclude that
Corollary 1.
Let
![]() $\Sigma$
be a complete three-dimensional noncompact steady gradient Ricci soliton. If
$\Sigma$
be a complete three-dimensional noncompact steady gradient Ricci soliton. If
![]() $Re^{-f}\in L^{p}_{-f}(\Sigma)$
,
$Re^{-f}\in L^{p}_{-f}(\Sigma)$
,
![]() $p>1$
, then
$p>1$
, then
![]() $\Sigma$
is either isometric to a quotient of
$\Sigma$
is either isometric to a quotient of
![]() $\mathbb{R}^{3}$
or
$\mathbb{R}^{3}$
or
![]() $M\times\mathbb{R}$
, where M is the cigar soliton.
$M\times\mathbb{R}$
, where M is the cigar soliton.
Analogously, we can apply the same ideas of Theorem 3 to guarantee a rigidity result addressed to complete noncompact expanding gradient Ricci soliton as follows.
Theorem 4.
Let
![]() $\Sigma$
be a complete noncompact expanding gradient Ricci soliton of dimension
$\Sigma$
be a complete noncompact expanding gradient Ricci soliton of dimension
![]() $n\geq 3$
such that the sectional curvature is nonnegative. If
$n\geq 3$
such that the sectional curvature is nonnegative. If
![]() $Re^{-f}\in L^{p}_{-f}(\Sigma)$
,
$Re^{-f}\in L^{p}_{-f}(\Sigma)$
,
![]() $p>1$
, then
$p>1$
, then
![]() $\Sigma$
is isometric to a quotient of the Gaussian soliton
$\Sigma$
is isometric to a quotient of the Gaussian soliton
![]() $\mathbb{R}^{n}.$
$\mathbb{R}^{n}.$
2. Proof of the theorems
Let
![]() $\psi$
be a smooth function on
$\psi$
be a smooth function on
![]() $\Sigma$
, let us define the weighted Laplacian on
$\Sigma$
, let us define the weighted Laplacian on
![]() $\Sigma^n$
by
$\Sigma^n$
by
for all
![]() $\varphi\in C^{\infty}(\Sigma^n)$
, where
$\varphi\in C^{\infty}(\Sigma^n)$
, where
![]() $\langle,\rangle$
denotes the Riemannian metric on
$\langle,\rangle$
denotes the Riemannian metric on
![]() $\Sigma.$
$\Sigma.$
In what follows, we denote the space of Lebesgue integrable functions on
![]() $\Sigma^n$
by
$\Sigma^n$
by
where
![]() $d\Sigma$
stands for the volume element induced by the metric of
$d\Sigma$
stands for the volume element induced by the metric of
![]() $\Sigma^n$
. Furthermore, given a smooth function
$\Sigma^n$
. Furthermore, given a smooth function
![]() $\psi\;:\;\Sigma\rightarrow\mathbb{R}$
, we denote by
$\psi\;:\;\Sigma\rightarrow\mathbb{R}$
, we denote by
![]() $L^1_{\psi}(\Sigma^n)$
the set of Lebesgue integrable functions on
$L^1_{\psi}(\Sigma^n)$
the set of Lebesgue integrable functions on
![]() $\Sigma^n$
with respect to the modified volume element
$\Sigma^n$
with respect to the modified volume element
Given an oriented Riemannian manifold
![]() $\Sigma^n$
and
$\Sigma^n$
and
![]() $p>1$
, we can consider the following space of integrable functions
$p>1$
, we can consider the following space of integrable functions
From a straightforward adaptation of [Reference Yau12, Theorem 3], we obtain the following criterion of integrability.
Lemma 1.
Let
![]() $\Sigma^n$
be an n-dimensional complete oriented Riemannian manifold. If
$\Sigma^n$
be an n-dimensional complete oriented Riemannian manifold. If
![]() $\varphi\in C^\infty(\Sigma^n)$
is a nonnegative
$\varphi\in C^\infty(\Sigma^n)$
is a nonnegative
![]() $\psi$
-subharmonic function on
$\psi$
-subharmonic function on
![]() $\Sigma^n$
and
$\Sigma^n$
and
![]() $\varphi\in L^p_{\psi}(\Sigma^n)$
, for some
$\varphi\in L^p_{\psi}(\Sigma^n)$
, for some
![]() $p>1$
, then
$p>1$
, then
![]() $\varphi$
is constant.
$\varphi$
is constant.
Now, we can prove our main result.
Proof of Theorem 3. Let
![]() $k\in\mathbb{R}$
be a constant. Thus, a straightforward calculation shows that
$k\in\mathbb{R}$
be a constant. Thus, a straightforward calculation shows that
Since
![]() $\Sigma$
is a steady gradient Ricci soliton, from Lemma
$\Sigma$
is a steady gradient Ricci soliton, from Lemma
![]() $2.3$
of [Reference Petersen and Wylie10], we have
$2.3$
of [Reference Petersen and Wylie10], we have
Note that
Plugging (2.3) and (2.2) into (2.1) and taking the trace of the steady soliton equation, we conclude that:
Finally, from the definition of weighted Laplacian, we get that
Choosing
![]() $k=-1$
, we conclude that
$k=-1$
, we conclude that
Since the sectional curvature of
![]() $\Sigma$
is nonnegative, we get that
$\Sigma$
is nonnegative, we get that
![]() $-2|Ric|^{2}+R^{2}\geq 0.$
In fact, given
$-2|Ric|^{2}+R^{2}\geq 0.$
In fact, given
![]() $\lambda_k$
,
$\lambda_k$
,
![]() $k=1,2,...,n$
, the eigenvalue of the Ricci tensor, it is not hard to see that
$k=1,2,...,n$
, the eigenvalue of the Ricci tensor, it is not hard to see that
![]() $\sum_{i\neq j}\lambda_i>\lambda_j$
and, therefore,
$\sum_{i\neq j}\lambda_i>\lambda_j$
and, therefore,
![]() $R\geq 2\lambda_j.$
Thus,
$R\geq 2\lambda_j.$
Thus,
From above inequality, we conclude that
On the other hand, since
![]() $Re^{-f}$
is a nonnegative function and
$Re^{-f}$
is a nonnegative function and
![]() $Re^{-f}\in L^{p}_{-f}(\Sigma)$
, from Lemma 1, we conclude that
$Re^{-f}\in L^{p}_{-f}(\Sigma)$
, from Lemma 1, we conclude that
![]() $Re^{-f}$
is a constant. If R is constant zero, from [Reference Deruelle5],
$Re^{-f}$
is a constant. If R is constant zero, from [Reference Deruelle5],
![]() $\Sigma$
is isometric to a quotient of
$\Sigma$
is isometric to a quotient of
![]() $\mathbb{R}^{n}.$
If
$\mathbb{R}^{n}.$
If
![]() $Re^{-f}=c,$
where c is a nonzero constant, we get that
$Re^{-f}=c,$
where c is a nonzero constant, we get that
![]() $\Sigma$
has finite
$\Sigma$
has finite
![]() $-f$
-volume and, therefore,
$-f$
-volume and, therefore,
![]() $R\in L^{1}(\Sigma).$
From [Reference Deruelle5], we conclude the desired result.
$R\in L^{1}(\Sigma).$
From [Reference Deruelle5], we conclude the desired result.
We recall that a complete three-dimensional steady gradient Ricci soliton has nonnegative sectional curvature. Thus, as a consequence of anterior result, we get that
Corollary 2.
Let
![]() $\Sigma$
be a complete three-dimensional noncompact steady gradient Ricci soliton. If
$\Sigma$
be a complete three-dimensional noncompact steady gradient Ricci soliton. If
![]() $Re^{-f}\in L^{p}_{-f}(\Sigma)$
,
$Re^{-f}\in L^{p}_{-f}(\Sigma)$
,
![]() $p>1$
, then
$p>1$
, then
![]() $\Sigma$
is either isometric to a quotient of
$\Sigma$
is either isometric to a quotient of
![]() $\mathbb{R}^{3}$
or
$\mathbb{R}^{3}$
or
![]() $M\times\mathbb{R}$
, where M is the cigar soliton.
$M\times\mathbb{R}$
, where M is the cigar soliton.
Now, we are able to prove our rigidity result, in the expanding case, as follows.
Proof of Theorem 4. In fact, since we are supposing that
![]() $Ric+\nabla^{2}f=\lambda g,$
from Lemma 2.3, [Reference Petersen and Wylie10], we conclude that
$Ric+\nabla^{2}f=\lambda g,$
from Lemma 2.3, [Reference Petersen and Wylie10], we conclude that
Thus, following the same steps of the anterior result, we conclude from (2.1) and above equation that
Again, choosing
![]() $k=-1$
, we conclude that
$k=-1$
, we conclude that
Since the sectional curvature is nonnegative, reasoning like the anterior result, we get that
![]() $-2|Ric|^{2}+R^{2}\geq 0.$
Taking into account that
$-2|Ric|^{2}+R^{2}\geq 0.$
Taking into account that
![]() $\lambda \lt 0,$
we get that
$\lambda \lt 0,$
we get that
Finally, from Lemma 1, we get that
![]() $Re^{-f}$
is a constant and, therefore, from (2.4) we guarantee that
$Re^{-f}$
is a constant and, therefore, from (2.4) we guarantee that
![]() $R=0.$
Since
$R=0.$
Since
![]() $\Sigma$
has nonnegative sectional curvature, we conclude that
$\Sigma$
has nonnegative sectional curvature, we conclude that
![]() $\Sigma$
has sectional curvature equals to zero. Thus, we conclude that
$\Sigma$
has sectional curvature equals to zero. Thus, we conclude that
![]() $\Sigma$
must be a quotient of the Gaussian soliton
$\Sigma$
must be a quotient of the Gaussian soliton
![]() $\mathbb{R}^n.$
$\mathbb{R}^n.$
Acknowledgments
The author is partially supported by Paraíba State Research Foundation (FAPESQ), Brazil, grant 3025/2021 and CNPq, Brazil, grant 306524/2022-8, respectively.
Data availability
Data sharing not applicable to this article as no data sets were generated or analyzed during the current study.