2. C-BAND TRANSFER RANGING MODEL

The time signals modulated by the pseudo code with the same carrier frequency are simultaneously dispatched to the satellite from all stations. Receivers at the stations receive the signals from all stations via the satellite transponder. There are several modes, including “receiving the own station-disseminated signals mode”, “receiving the master station-disseminated signals mode” and “receiving all station-disseminated signals mode” (Li et al., Reference Li, Yang, Ai, Si, Qiao and Feng2009; Cheng et al., Reference Cheng, Li, Yang, Wu, Lei and Feng2012). Usually, the observation of “receiving the own station-disseminated signals mode” are used to achieve POD of GEO satellite.

For the mode of receiving the own station-disseminated signals, the instantaneous observations can be expressed as (t,ρ). These can be defined as

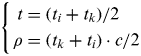(1)$$\left\{ \eqalign{t & = (t_i + t_k )/2 \cr \rho & = (t_k + t_i ) \cdot c/2} \right.$$

Where,

t

is the instantaneous observation time.

ρ

is the pseudo-range between station and satellite.

t _i

is the moment that the signal is dispatched from station.

t _k

is the moment that the signal is received at the own station from satellite transponder.

c

is the light velocity, with unit of m/s.

If the position and velocity vector of the satellite in J2000 Inertial Coordinate System at time of t are expressed as $\vec r$ and $\dot{\vec r}$ , the two vector would change to $\vec r_b $ and $\dot {\vec r_b} $ in Earth-Fixed Coordinate System, after precession transformation, nutation transformation, Greenwich sidereal time angle and polar motion transformation.

The station vector is always given at epoch 00:00 1 January 2000 in International Terrestrial Reference Frame (ITRF) 2000, then the station vector at instantaneous moment t should take the plate movement into consideration. In addition, the solid tides, ocean loading tides and Earth rotation also change station coordinates.

Since all CAPS stations are located in China, the Eurasian plate should be used (http://www.iers.org/nn_11216/IERS/EN/Publications/TechnicalNotes/tn21.html). The station coordinate change caused by solid tides can be calculated by applying the Wahr model (Li, Reference Li1995; Wahr, Reference Wahr1981). While the station coordinate change caused by ocean loading tides can be corrected by applying the Schwiderski (Reference Schwiderski1980) model and Green function (Li Reference Li1995; Melbourne et al., Reference Melbourne, Anderle, Fessiel, King, McCarthy, Smith, Tapley and Vicente1983), with the change caused by Earth rotation referring to International Earth Rotation and Reference System Service (IERS) 1996.

If the station vector at instantaneous moment t in ITRF2000 is expressed as $\vec R_p $ after consideration of plate movement, tidal function and Earth rotation, then the geometrical distance at instantaneous moment t can be expressed as Equation (2):

(2)$$\rho _c = \left| {\vec r_b - \vec R_p} \right|$$

Taking the errors in propagation of C-B and transfer ranging method into consideration, the ranging corrections can be expressed as

(3)$$\Delta \rho = \Delta \rho _{OFC} + \Delta \rho _{DEL} + \Delta \rho _{TRO} + \Delta \rho _{ION} + \Delta \rho _{RLA} + \Delta \rho _{OFF} + \Delta \rho _{TRA} + \Delta \rho _{NOI} $$

Where,

∆ρ _OFC

is the centre correction of station antenna phase centre.

∆ρ _DEL

is the time delay in station instrument. For CAPS, the first 10 minutes in every hour are used to measure this time delay. In data pre-processing, this time delay can be eliminated from ranging observation.

∆ρ _TRO

is the time delay in tropospheric propagation. This time delay can be corrected by applying the Saastamoinen Reference Saastamonien1973 model (Saastamonien, Reference Saastamonien1973) and the Niell model (Niell, Reference Niell1996), which can be used in calculating the delay in zenith and observation direction respectively.

∆ρ _ION

is the time delay in ionospheric propagation. This time delay can be corrected by calculating the mean of the up-link and down-link ionospheric delays. The two delays should be calculated respectively, since the up-link carrier frequency is about 6 GHz, with the down-link frequency being 4 GHz (Kong et al., Reference Kong, Yang, Sun, Li and Chen2012).

∆ρ _RLA

is the time delay due to general relativistic effect. This time delay can be corrected by applying the Shapiro Reference Shapiro1964 model (Shapiro, Reference Shapiro1964).

∆ρ _OFF

is the centre correction of satellite transponder antenna phase centre. It is the satellite transponder but not the satellite centre of mass that receives the C-Band signal arriving at the satellite. This centre correction can be corrected by transforming the transponder antenna phase centre in Satellite-Fixed Coordinates to Topocentric Terrestrial Coordinates. Before satellite transmission, the transponder antenna phase centre vector in the system can be measured.

∆ρ _TRA

is the transponder delay. Though it can be measured before satellite transmission, there is still some uncertainty. Therefore, the transponder delay is always treated as a parameter to be solved.

∆ρ _NOI

is the random noise in ranging. It and the model construction errors are always treated as the system error.

From the above ranging model analysis, the C-Band transfer ranging equation can be obtained from Equations (2) and (3).

(4)$$\eqalign{\rho& = \rho _c + \Delta \rho \cr & = \rho _c + \Delta \rho _{OFC} + \Delta \rho _{DEL} + \Delta \rho _{TRO} + \Delta \rho _{ION} + \Delta \rho _{RLA} + \Delta \rho _{OFF} + \Delta \rho _{TRA} + \Delta \rho _{NOI}}$$

3. EXPERIMENTAL TEST

In order to evaluate the POD precision of a GEO satellite using the C-Band transfer ranging method, 2010-001A satellite was measured at the Changchun, Linton and Kashi stations of CAPS. Meanwhile, for the first time, SLR has also been used to measure the same satellite at both domestic and foreign sites such as the Changchun site, the Shanghai site and the Yarragadee site, with SLR site numbers 7237, 7821 and 7090 respectively.

The kinetic batch processing method has been applied to POD of C-Band transfer pseudo-range observation. For a GEO satellite, the dynamical perturbation models are (1) gravitational attractions of the non-spherical Earth (Earth gravity model JGM3, truncated to 10th degree and order), (2) three-body gravitational attractions of the Sun and Moon, (3) relativistic perturbation, (4) gravitational attractions of solid-Earth tides and oceanic tides, (5) radiation pressure of the Sun, (6) earthshine radiation pressure, (7) perturbation of Earth's rotational deformation and (8) empirical radial-transverse-normal accelerations (Tapley et al., Reference Tapley, Shutz and Born2004). The reference systems are (1) the mean equator (x–y plane) and mean spring equinox (the direction of the x-axis) at J2000·0, (2) ITRF2000 for the coordinates of the stations, and (3) the planetary ephemeris DE403/LE403 (Song et al., Reference Song, Mao and Jia2012). The adopted astronomical constants, reference system, dynamical and measurement models are referred to IERS 1996.

The residual RMS of each station in POD are analysed including orbit difference over overlaps of adjacent orbit arcs. In addition, the orbit of GEO satellite has been evaluated by SLR data by both domestic and foreign SLR sites for the first time.

3.1. Residuals RMS in POD of GEO Satellite

The orbit determination slip arc has been chosen as 1·5 days, shifting about one day every time. And the strategy for POD is as follows. The sets of parameters, including six sets for satellite orbit parameters, six sets for solar radiation coefficient, six sets for experimental acceleration, and six sets for transponder delay, are estimated. Moreover, the sum of bias of each station is restricted to zero.

The residual RMS calculation of station i can be completed using Equation (5).

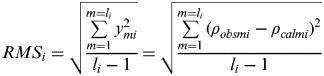(5)$$RMS_i = \sqrt {\displaystyle{{\sum\limits_{m = 1}^{m = l_i} {y_{mi} ^2}} \over {l_i - 1}}} = \sqrt {\displaystyle{{\sum\limits_{m = 1}^{m = l_i} {(\rho _{obsmi} - \rho _{calmi} )^2}} \over {l_i - 1}}} $$

Where, m is from 1 to l _i, with l _i being the number of observation of station i.

y _mi is the residual of the m item of station i. ρ _obsmi is the observation range of the m item of station i. ρ _calmi is the calculated range of the m item of station i.

The residuals RMS of all stations can be calculated using Equation (6).

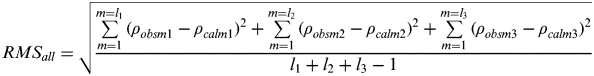(6)$$RMS_{all} = \sqrt {\displaystyle{{\sum\limits_{m = 1}^{m = l_1} {(\rho _{obsm1} - \rho _{calm1} )^2} + \sum\limits_{m = 1}^{m = l_2} {(\rho _{obsm2} - \rho _{calm2} )^2} + \sum\limits_{m = 1}^{m = l_3} {(\rho _{obsm3} - \rho _{calm3} )^2}} \over {l_1 + l_2 + l_3 - 1}}} $$

Where, l ₁, l₂ and l ₃ are the observation number of station Changchun, Linton and Kashi respectively.

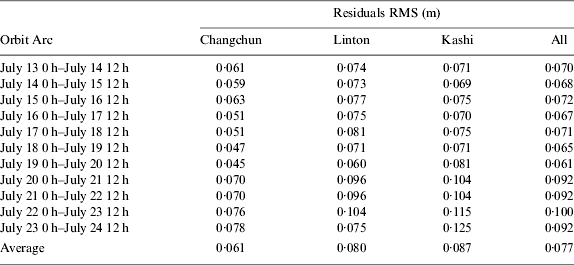
Table 1 shows the residuals RMS of Changchun, Linton and Kashi stations of CAPS from 13 to 24 July 2012. Figure 1 gives the residuals of the first three orbit arcs.

Figure 1. Residuals of stations in CAPS of orbit arc from 13 July to noon of 16 July 2012.

Table 1. Residual RMS of stations in CAPS for different orbit arcs.

From Table 1, the average of residual RMS of POD using C-Band observation is about 0·077 m. Therefore, the satellite orbit determined can reflect the C-Band observation very well.

The Kashi station antenna angle of observing 2010-001A satellite is not high. Moreover, the observation data is not consecutive for Linton and Changchun stations on some days, as Figure 1 shows. All would affect the residuals of these three stations.

3.2. Orbit difference in overlap of adjacent arcs

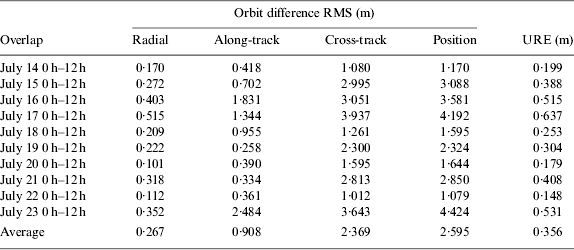
The POD precision can be estimated by the orbit overlaps of adjacent arcs. Each two adjacent arcs have an orbit overlap of half a day. The orbit difference in radial, along-track and cross-track direction, with User Range Error (URE) (Zhou et al., Reference Zhou, Hu and Wu2010) are both analysed. Table 2 gives the orbit difference RMS in radial, along-track, cross-track direction and URE in overlaps of two adjacent arcs. Figure 3 shows the orbit difference of the first three overlaps.

Table 2. Orbit difference RMS and URE in overlaps of adjacent arcs.

From Table 2 and Figure 2, the orbit difference RMS is better than 0·3 m for radial direction, 0·908 m for along-track direction and 2·369 m for cross-track direction. The average position RMS is about 2·595 m, with URE being 0·356 m.

Figure 2. Orbit difference in overlaps at 14 July to noon of 16 July 2012.

3.3. Evaluation of POD using SLR data

Domestic and foreign SLR sites observed the same GEO satellite simultaneously with CAPS in July 2012. The line-of-sight residuals of SLR sites can be obtained from the orbit determined using C-Band transfer data and SLR data. Table 3 depicts the SLR data volume and residuals RMS of the SLR sites. The residuals of SLR sites on 13 July 2012 are shown in Figure 3.

Figure 3. Residuals of SLR site 7237 and 7090 on 13 July 2012.

Table 3. SLR data volume and residual RMS analysis in July 2012.

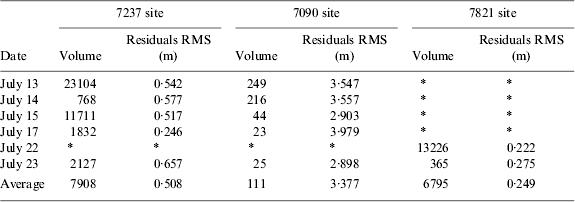
The average of residual RMS of 7237 site is about 0·508 m. Meanwhile, the value for 7821 site is about 0·249 m. RMSs for both domestic SLR sites are better than 1 m. Therefore, the orbit determined using C-Band transfer observation can satisfy users' need in the Chinese area.

However, the average of residual RMS for the foreign SLR site 7090 is about 3·4 m, which is about 3 m larger than that for the domestic SLR sites. This may be caused by the distribution of the CAPS stations. Since all of the CAPS stations are located in China, the orbit determined using C-Band transfer observation would lean to the northern hemisphere.

From the residual RMS analysis, the distribution of CAPS stations affects POD precision. The orbit determined using CAPS observations lean to the northern hemisphere, which makes residual RMS for domestic SLR sites less than those for the SLR site in Australia.