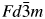I. INTRODUCTION
In the past few decades, Laves phases with AB 2 compositions have been employed in many important and attractive applications, such as superconducting materials, giant magnetostrictive materials, hydrogen storage materials, and high-temperature structural materials, owing to their excellent physical and chemical properties (Strnat and Strnat, Reference Strnat and Strnat1991; Szytula and Leciejewicz, Reference Szytula and Leciejewicz1994; Tao et al., Reference Tao, Ouyang, Liu, Zeng, Feng, Du and Jin2008). For instance, binary rare-earth Laves phase NdAl2 (Gschneidner and Calderwood, Reference Gschneidner and Calderwood1989) that crystallizes in the cubic MgCu2-type structure C15 phase has been reported. The crystal and magnetic properties of NdAl2 have been investigated by Nereson et al. (Reference Nereson, Olsen and Arnold1966) using neutron diffraction and susceptibility measurements. The results showed Curie–Weiss behavior in the paramagnetic region and the compound was basically ferromagnetic below Curie temperatures. Another Laves phase compound NdCo2 has been investigated by Xiao et al. (Reference Xiao, Huang, Ouyang, Lynn, Liang and Rao2006). The compound was investigated using the Rietveld refinement technique based on high-resolution neutron powder diffraction data. Detailed information pertaining to the crystal and magnetic structures of NdCo2 at different temperatures was reported. Furthermore, a study showed that adding a third group member, such as B, Al, or Ga, to an R–T (R = rare-earth, T = transition element) alloy and adjusting its chemical composition can significantly improve the magnetic properties of the material (Weitzer et al., Reference Weitzer, Hiebl and Rogl1989). Therefore, R–Co–Al ternary intermetallic compounds and their remarkable physical properties have attracted the attention of many researchers.
To our best knowledge, the ternary compounds Nd4CoAl, Nd2Co6Al19, and Nd13Co14−xAl4+x have been reported and their crystal structures have been investigated by Riani et al. (Reference Riani, Freccero, Sufryd, Arrighi and Cacciamani2020). Moreover, several other ternary compounds have already been reported in the literature. For example, Nd6Co2Al was synthesized by Stegemann and Janka (Reference Stegemann and Janka2018). Its unit-cell parameters were refined via powder X-ray diffraction (XRD) experiments. NdCo2Al8 was studied by He et al. (Reference He, Zhong, Liu, Zhang and Zeng2009) using the Rietveld refinement method to determine its crystal structure parameters. The Nd2Co2Al structure was investigated by Pani et al. (Reference Pani, Merlo and Fornasini2002) via single-crystal and powder XRD. The structure and magnetic properties of Nd7Co6Al7 were investigated by Yarmolyuk et al. (Reference Yarmolyuk, Zarechnyuk, Aksel'Rud, Rykhal and Rozhdestvenskaya1986) and Canepa et al. (Reference Canepa, Manfrinetti, Palenzona, Cirafifici, Merlo and Cimberle2000). They stated that this compound undergoes a ferromagnetic transition at 15.5 K. NdCoAl4 and Nd2Co3Al9 were refined by Tougait and Noël (Reference Tougait and Noël2006) based on single-crystal XRD data. Their magnetic susceptibility measurements revealed an antiferroelectric ordering at low temperatures.
In our investigation of the title compound in the R–Co–Al system, Al3CoNd2 was synthesized in an argon-filled nonconsumable arc furnace and subjected to vacuum thermal annealing at 923 K for 4 weeks. In this study, we report our experimental results of the synthesis and Rietveld refinement results of the crystal structure and magnetic properties of Al3CoNd2.
II. EXPERIMENTAL
A sample of the ternary compound Al3CoNd2 was prepared by melting high-purity metals of Al, Co, and Nd in an arc furnace under an argon atmosphere (Liang et al., Reference Liang, Zeng, Liu and He2013). All the raw materials were flaky, and the purity of all the elements was 99.99%. The cooled buttons were flipped and remelted three times to achieve homogeneity. The mass loss after arc melting was less than 0.5 wt.%. After melting, the sample was thermally treated for 4 weeks at 973 K in an evacuated quartz tube. The sample was ground in an agate mortar and pestle to particle sizes of no greater than 20 μm. The powder XRD patterns for the Al3CoNd2 compound were collected at room temperature using a powder X-ray diffractometer (Smart Lab (9), Rigaku Corporation). The 300-mm radius diffractometer was equipped with CuKα radiation (λ = 1.54060 Å) and a graphite monochrometer. The operating voltage and current were 40 kV and 150 mA. The 2θ scan range was from 10° to 100° with a step size of 0.02° and a count time of 2 s per step. Finally, 50 wt.% Al3CoNd2 and 50 wt.% corundum were prepared to determine the reference intensity ratio (RIR) value (Walter and Schreiner, Reference Walter and Schreiner1995).
A powder sample of 18.5 mg was used for magnetic measurements. The magnetic susceptibility of the Al3CoNd2 compound was measured on a Quantum Design SQUID physical property measurement system (PPMS-9#VSM) in the temperature range of 2–450 K under an applied field of 50 Oe. Moreover, the field-dependent data of the saturation magnetic moment and magnetic hysteresis loop for the compound were measured at 2, 5, 10, 150, and 300 K under applied fields of up to 6.5 T.
III. RESULTS AND DISCUSSION
A. Structural refinement results and discussion
The Al3CoNd2 compound was verified via powder XRD analysis using the program JADE 6.0 (Materials Data Inc., 2002). The powder XRD patterns for the Al3CoNd2 compound were successfully indexed based on the cubic lattice. The reflection conditions, reflection intensities, and calculated lattice parameters proved that the compound is isostructural with Al2Nd and crystallizes in the MgCu2-type structure (cubic Laves C15 phase) with a space group of 
$Fd\bar{3}m$ (No. 227). The atomic positions of the elements were selected as a starting model for the Rietveld refinement using the DBWS9807a program (Young et al., Reference Young, Larson and Paiva-Santos2000). The pseudo-Voigt function was used to simulate the peak shapes. The lattice parameters were obtained using JADE 6.0. During the refinement process, the DMPLOT program (Marciniak and Diduszko, Reference Marciniak and Diduszko1997) was used to record the refinement results. Figure 1 shows the observed, calculated data, and residuals of the powder XRD patterns of Al3CoNd2. Details of the refinement are summarized in Table I. After the refinement of 23 parameters, including the sample shift, scale factor, lattice constants, full width at half maximum, preferred orientation, thermal parameters, occupancy, and background parameters, the residual factors converged to R p = 0.1024 and R wp = 0.1287. Table II summarizes the final results for the atomic coordinates, occupancy, and thermal parameters. Al and Co atoms occupy the same positions, and their occupancies are 0.74 and 0.26, respectively. The uncertainty for the occupancies is 0.05. Table III lists the selected interatomic distances for the Al3CoNd2 compound. The interatomic distances of Nd–Nd, M–Nd, and M–M atoms are all close to the sum of their metallic radii (r Nd = 0.181 nm, r Co = 0.135 nm, and r Al = 0.143 nm). Figure 2(a) shows the Al3CoNd2 structure, indicating that the number of atoms per unit cell is 24 and the formula units per unit cell, Z = 4. The coordination environments of M and Nd are presented in Figures 2(b) and 2(c), respectively. Where M is the atomic position of 16c. Each M atom is surrounded by 6 Nd and M. Each Nd atom is surrounded by 4 Nd and 12 M.
Figure 1. X-ray powder diffraction patterns for Al3CoNd2. “+” symbols represent observed patterns, the solid line represents the calculated patterns, “|” symbols represent the possible positions of Bragg reflections, and the bottom curve represents the difference between the observed and calculated patterns.
Figure 2. Structure and coordination environments of Al3CoNd2. (a) Al3CoNd2 structure, (b) M atom (74% Al and 26% Co), and (c) Nd atom.
TABLE I. Rietveld refinement data of Al3CoNd2.
$R_{\rm P} = {{\sum {\vert {Y_i( {\rm obs}) -Y_i( {\rm calc}) } \vert } } \over {\sum {Y_i( {\rm obs}) } }}, \quad R_{{\rm WP}} = \left\{{{{\sum {\omega_i{[ {Y_i( {\rm obs}) -Y_i( {\rm calc}) } ] }^2} } \over {\sum {\omega_i{[ {Y_i( {\rm obs}) } ] }^2} }}} \right\}^{1/2}.$
TABLE II. Atomic coordinates, occupancy, and thermal parameters for Al3CoNd2.
TABLE III. Interatomic distances in the crystal structure of Al3CoNd2.
M = 74%Al + 26%Co.
B. Reference intensity ratio
To quantitatively analyze the phase in the future, the RIR value of Al3CoNd2 was calculated using the I/I c method (Snyder, Reference Snyder1992). I/I c is defined as the ratio of the intensity of the strongest line of an analyte to the corundum (113) line when the analyte is mixed at 50:50 by weight with corundum. Therefore, the powder XRD patterns for a mixture comprising 50 wt.% Al3CoNd2 and 50 wt.% corundum were measured, as shown in Figure 3. However, the main peak for the compound at 2θ = 38.018° overlaps another Al2O3 peak. Therefore, the Rietveld refined structure parameters were used to calculate the RIR value (Chung, Reference Chung1974; Hubbard and Snyder, Reference Hubbard and Snyder1988), which is 3.03 based on the simulated structure data. This value is slightly smaller than the value obtained after adding Al2O3 powder, i.e., 3.23.
Figure 3. Low 2θ portions of the powder XRD pattern of 50 wt.% Al3CoNd2 and 50 wt.% corundum.
C. Magnetic properties
The temperature dependence of the magnetic susceptibility measured in an applied field of 50 Oe is plotted in Figure 4. The associated field-cooled/zero field-cooled (FC/ZFC) was observed at 280 K. Furthermore, the Curie temperature T c identified as the minima in the first derivative of the χ–T curves is 302.5 K (Zeng et al., Reference Zeng, Qin, Qin and Zhang2007). Figure 5 shows the reciprocal of the magnetic susceptibilities as a function of the temperature for the compound. In the temperature range of 385–450 K, the linearity of the curve indicates agreement with the Curie–Weiss law:
$$1/\chi = ( T-\theta _{\rm p}) /C$$where χ is the magnetic susceptibility, C is the Curie constant, and T is the temperature. The paramagnetic Curie temperature of θ p = 379.9 K was obtained by extrapolating the linear 1/χ. The effective magnetic moment of μ eff = 6.57 μ B per Nd3+ was calculated using the following formula (Koch and Strydom, Reference Koch and Strydom2008):
$$\mu _{{\rm eff}} = \sqrt {\displaystyle{{3\kappa _{\rm B}\chi ( { T}-\theta _{\rm p}) } \over {N_{\rm A}\mu _0}}} $$where N A is the Avogadro number, k B is the Boltzmann constant, μ B is the Bohr magneton, and μ 0 is the permeability of vacuum. The effective magnetic moment value is larger than the theoretical effective magnetic moment of μ eff = 3.62 μ B per Nd3+, obtained using the following formula (Taylor and Darby, Reference Taylor and Darby1972; Lu et al., Reference Lu, Zeng and Shih2011):
$$\mu _{{\rm eff}} = g\sqrt {J( J + 1) } \mu _{\rm B}$$where J is the angular momentum quantum number and g is the Lander factor. This indicates that both rare-earth elements and cobalt ions contribute to the paramagnetic moment.
Figure 4. Temperature dependence of the magnetic susceptibility for Al3CoNd2.
Figure 5. Reciprocal of the magnetic susceptibilities (x −1) of the Al3CoNd2 compound. The red solid line represents the fit to the experimental data based on the Curie–Weiss law and circles represent the reciprocal of the magnetic susceptibilities.
To further explore the magnetism of the compound, magnetization measurements were performed at various temperatures. Figure 6 shows the isothermal magnetization curves (M–H) measured under the applied field of 0–6.5 T and at 2, 5, 10, 150, and 300 K. Full saturation is not achieved at the applied field of up to 6.5 T. Therefore, the empirical formula (Dai and Qian, Reference Dai and Qian2017) is used
$$M_H = M_S\left({1-\displaystyle{\alpha \over H}} \right)$$where M H is the corresponding magnetization under the applied field of H and α is a constant, to plot several curves for determining the saturation magnetization M S (Figure 7) and extrapolating the linear part of the curve to the plot (1/H) = 0; consequently, the M S value was obtained. Obviously, the maximum saturation magnetic moment at 2 K is 0.89 μ B/f.u. and this value decreases with an increase in temperature. Figure 8 shows the magnetic hysteresis loop curves of the compound at various temperatures. Weak ferromagnetism is observed at 300 K and a hysteresis with a remnant magnetization M r of 0.27 μ B/f.u. and a coercive field H c of 0.17 T is seen, which continues to enlarge as the temperature is reduced. At 2 K, M r of 0.57 μ B/f.u. and H c of 0.73 T. Compared with the magnetic hysteresis loop at 2 K, Al3CoNd2 is a softer ferromagnet at a higher temperature. This implies that the compound is a ferromagnet below the Curie temperature T c.
Figure 6. Isothermal magnetization curves (M–H) measured at various temperatures for the Al3CoNd2 compound.
Figure 7. Isothermal magnetization curves (M − (1/H)) measured at various temperatures for the Al3CoNd2 compound.
Figure 8. Magnetic hysteresis loop curves for the Al3CoNd2 compound at various temperatures.
IV. CONCLUSION
In summary, the crystal structure of the Al3CoNd2 compound was determined by the powder XRD technique and structural refinement was performed using the Rietveld method. The compound is isostructural with Al2Nd and crystallizes in the MgCu2-type structure (cubic Laves C15 phase), with a space group of 
$Fd\bar{3}m$ (No. 227), a lattice parameter of a = 7.8424(2) Ǻ, and a unit-cell volume of V = 482.33 Å3. The residual factors converge to R p = 0.1024 and R wp = 0.1287. The RIR value obtained experimentally is 3.03. The magnetic susceptibility curves follow the Curie–Weiss law in the temperature range of 385–450 K and the paramagnetic Curie temperature of θ p = 379.9 K. The saturation magnetic moment and magnetic hysteresis loop for the compound were measured at various temperatures. The results show that the saturation magnetic moment value decreased with an increase in temperature and the compound is a ferromagnet below the Curie temperature T c.
V. DEPOSITED DATA
CIF and/or RAW data files were deposited with ICDD. You may request this data from ICDD at info@icdd.com.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the support from the National Natural Science Foundation of China (No. 51861001), the Guangxi Natural Science Foundation (No. 2018GXNSFAA138133 and 2016GXNSFDA380024), and the International Centre for Diffraction Data (No. 16-03).
