1. INTRODUCTION
The acceleration of energetic ions by interaction of intense short laser pulse with solid thin foil target is an area of great interest (Macchi et al., Reference Macchi, Sgattoni, Sinigardi, Borghesi and Passoni2013) and importance having potential applications such as, producing high-energy-density matter (Patel, Reference Patel2003; Borghesi, Reference Borghesi2004), radio graphing transient processes (Borghesi et al., Reference Borghesi, Campbell, Schiavi, Haines and Willi2002), tumor therapy (Bulanov et al., Reference Bulanov, Esirkepov, Khoroshkov, Kuznetsov and Pegoraro2002; Fourkal et al., Reference Fourkal, Velchev, Fan, Luo and Maet2007), generating isotopes in positron emission tomography (Spencer et al., Reference Spencer, Ledingham, Singhal, Mccanny, Mckenna, Clark, Krushelnick, Zepf, Beg, Tatarakis, Dangor, Norreys, Clarke, Allott and Ross2001), material modification (Trtica et al., Reference Trtica, Batani, Redaelli, Limpouch, Kmetik, Ciganovic, Stasic, Gakovic and MOMCILOVIC2013; Ahmad et al., Reference Ahmad, Rafique, Tahir and Malik2014; Akram et al., Reference Akram, Bashir, Hayat, Mahmood, Ahmad and Khaleeq-U-rahaman2014), X-ray generation (Kumar et al., Reference Kumar, Singh and Verma2014), and fast ignition of fusion cores (Temporal et al., Reference Temporal, Ramis, Honrubia and Atzeni2009; Roth, Reference Roth2001). Ion beams with energies up to several tens of MeV has been obtained in experiments and mechanism is generally attributed to target normal sheath acceleration (TNSA) (Clark, Reference Clark2000; Psikal et al., Reference Psikal, Tikhonchuk, Limpouch, Andreev and Brantov2008; Bin, Reference Bin2009; Macchi et al., Reference Macchi, Veghini and Pegoraro2009; Brady & Arber, Reference Brady and Arber2011). However, these beams have low particle density and high-energy spread. Several schemes for enhanced interaction of ultrashort laser pulses with plasmas are being pursued worldwide to understand the physics of the process and its effects on the ion acceleration mechanisms (Lee et al., Reference Lee, Pae, Suk and Hahn2004; Bagchi et al., Reference Bagchi, Kiran and Bhuyan2008; Shoucri et al., Reference Shoucri, Afeyan and Lefort2008; Andreev et al., Reference Andreev, Platonov and Kawata2009; Regam, Reference Regam2011; Jablonski et al., Reference Jablonski, Badziak and Raczka2014).
Recent theories and simulation studies have focused on the use of circularly polarized (CP) laser pulses to accelerate high-density ion bunches at the front surface of thin foils (Macchi et al., Reference Macchi, Cattani, Liseykina and Cornolti2005; Hegelich et al., Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernandez2006; Chen et al., Reference Chen, Pukhov, Sheng and Yan2008; Eliasson et al., Reference Eliasson, Liu, Shao, Sagdeev and Shukla2009; Robinson et al., Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009; Yan et al., Reference Yan, Chen, Sheng and Chen2009; Tripathi et al., Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009; Kim et al., Reference Kim, Pae, Kim, Kim, Sung, Lee, Yu, Choi, Lee, Nam, Nickles, Jeong and Lee2013). For CP pulses, the ponderomotive force has no oscillating component; hence, electrons are steadily pushed forward inducing a charge separation field which can accelerate ions. The absence of hot electrons circulating through the target suppresses rapid foil decompression and allows radiation pressure acceleration (RPA) to dominate at more moderate intensities. Yan et al. (Reference Yan, Chen, Sheng and Chen2009) in simulations and Tripathi et al. (Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009) theoretically, presented a novel scheme for producing mono energetic protons, in hundreds of MeV range, with a specific foil thickness, equal to the distance of maximum charge separation at which the space charge force on electrons is balanced by the ponderomotive force. Nearly all the electrons of the foil are swept by ponderomotive force and piled up at the rear surface of the foil. Ions are detached from the surface by the combined repulsive electric force and the laser ponderomotive force, into vacuum to form a moving double layer, trapping the ions in the sheath of width/ω p, the skin depth. Qiao et al. (Reference Qiao, Zepf, Borghesi and Geissler2009) suggested that the acceleration process is composed of two connected stages: Relativistic “hole boring” (Gibbon, Reference Gibbon2005; Macchi et al., Reference Macchi, Cattani, Liseykina and Cornolti2005) and “light sail” (Robinson et al., Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009) RPA. They found that the stability of acceleration process depends critically on a smooth transition between two stages. Jain et al. (Reference Jain, Maheshwari, Jaiman and Malav2013) have numerically studied the interaction of ultrashort pulses with relativistic mirrors and conjectured the generation of intense X rays and γ rays. Many studies in the TNSA regime have reported that target curvatures can affect the hot electron generation in laser–solid interactions (Clark, Reference Clark2000; Psikal et al., Reference Psikal, Tikhonchuk, Limpouch, Andreev and Brantov2008; Bin, Reference Bin2009). Psikal et al. (Reference Psikal, Tikhonchuk, Limpouch, Andreev and Brantov2008) found that the proton energy can be increased using a cylindrical target in TNSA. The increase is attributed to an enhancement of light absorption by the curved front surface of the target. Curvature can also affect the hot electron transport inside the target. Bin (Reference Bin2009) studied the effect of front-surface curvature on TNSA protons using two-dimensional (2D) particle-in-cell (PIC) simulations, and found that the highest energy protons were from the concave target. Furthermore in the RPA regime, when solid thin foil of sub-micron thickness is irradiated by Gaussian laser pulses, the foil gets curved due to non-uniform laser intensity in transverse dimension. PIC simulations results indicate that Rayleigh–Taylor or Weibel-like transverse instabilities grows as foil changes shape (Silva et al., Reference Silva, Fonseca, Tonge, Mori and Dawson2002; Pegoraro & Bulanov, Reference Pegoraro and Bulanov2007; Robinson et al., Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009; Palmer et al., Reference Palmer, Schreiber, Nagel, Dover, Bellei, Beg, Bott, Clarke, Dangor, Hassan, Hilz, Jung, Kneip, Mangles, Lancaster, Rehman, Robinson, Spindloe, Szerypo, Tatarakis, Yeung, Zepf and Najmudin2012). These factors increase the energy spread and limit the higher energy gain. Sentoku et al. (Reference Sentoku, Mima, Ruhl, Toyama, Kodama and Cowan2004) have performed 3D PIC simulations to study short pulse interaction with conical targets and conjectured efficient energy transfer to the target electrons.
In this paper, we restudy the ion acceleration scheme in the RPA regime by considering concave and convex curvatures in thin foil targets. Comparisons are made with the flat foil target proposed in the earlier studies (Qiao et al., Reference Qiao, Zepf, Borghesi and Geissler2009; Tripathi et al., Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009; Yan et al., Reference Yan, Chen, Sheng and Chen2009). Concave and convex foil targets have radius of curvature of the order of laser spot size. The growth of transverse instabilities, during changing shape phase, is least in the concave target; this results in highest peak energy and least energy spread. In Section 2, we develop a theoretical estimate for the variation in the curvature of the foil with different spot size of the pulse. In Section 3, the results of the corresponding PIC simulations are presented. In Section 4, the numerical and simulation results are analyzed and discussed.
2. THEORETICAL ANALYSIS
Let us consider a curved foil of uniform thickness (l) given by the equation
$$z(t)\, = \,z_0 (t) + \displaystyle{{x^2} \over {2R(t)}}, $$where R(t) is the radius of curvature as a function of time, z 0(t) is the location of the center of axis at t = 0 (cf. Fig. 1). Defining G≡1/R, Eq. (1) can be rewritten as
$$z(t) = z_0 (t) + G(t)\displaystyle{{x^2} \over 2}. $$
Fig. 1. The Gaussian laser pulse with spot size (r 0) impinges on the convex foil with radius of curvature (R 0). Laser makes an angle θ with length element ds.
The laser intensity profile impinged on the foil from left is
$$I = I_0 \; e^{ - x^2 /r_0^2}, $$where r 0 is the laser spot size. The force exerted by the laser on a segment of the foil of length ds is given by
$$\displaystyle{{2I} \over c}\cos ^2 {\rm \theta} \,ds, $$where θ is the angle laser makes with the normal to the segment, and
$$\cos ^2 {\rm \theta} = [1 + (dz/dx)^2 ]^{ - 1} \; \approx 1 - x^2 /R^2. $$The equation of motion of the foil segment ds (in the x–z plane) and γ the width unity can be written as
$$m_i \; n_0 \; l\displaystyle{{d^2 z} \over {dt^2}} = \displaystyle{{2I} \over c}\cos ^2 {\rm \theta}, $$where m i is the mass of ions.
$$\displaystyle{{d^2 z} \over {dt^2}} = g_0 e^{ - x^2 /r_0^2} \; \cos ^2 {\rm \theta}, $$
where 
$g_0 \equiv (2\; I_0 )/(c\; m_i \; n_0 \; l)$. Using Eq. (5), the above equation can be expressed as
$$\displaystyle{{d^2 z} \over {dt^2}} = g_0 \; \left( {1 - \displaystyle{{x^2} \over {r_0^2}} \;} \right)\left( {1 - \displaystyle{{x^2} \over {R^2}} \;} \right), $$Using Eq. (2) and equating different powers of x on both sides one gets
$$\displaystyle{{d^2 G} \over {dt^2 \;}} = - 2\; g_0 \left[ {\displaystyle{1 \over {r_0^2}} + G^2} \right], $$
$$\displaystyle{{d^2 z_0} \over {dt^2}} = g_0 \;, $$and
$$z_0 = g_0 t^2 /2. $$ By replacing 
${\rm \partial}^2 /{\rm \partial} t^2 \; $ by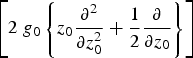 
$\left[ {2\; g_0 \left\{ z_0 \displaystyle{{\rm \partial} ^2 \over {\rm \partial} z_0^2} + \displaystyle{1 \over 2}\displaystyle{{\rm \partial} \over {\rm \partial} z_0} \right\}} \right]$ and defining the radius of curvature as 
${\rm \Psi} ( \equiv r_0 G)$ and the normalized distance of propagation of the center of the foil as 
${\rm \xi} ( \equiv z_0 /r_0 )$, one can rewrite Eq. (9) as
$${\rm \xi} \displaystyle{{{{\rm \partial}} ^2 {\rm \Psi}} \over {{{\rm \partial}} {\rm \xi} ^2 \;}} + \displaystyle{1 \over 2}\displaystyle{{{{\rm \partial}} {\rm \Psi}} \over {{{\rm \partial}} \; {\rm \xi}}} = - 2 - {\rm \Psi} ^2. $$3. PIC SIMULATION
We carried out 2D simulations using fully relativistic PIC code VORPAL (Nieter & Cary, Reference Nieter and Cary2004). A high-power CP Gaussian laser pulse strikes a thin foil of the highly overdense plasma. Required laser intensity and optimum target thickness for stable and sustained acceleration in the RPA regime, are calculated according to the schemes described in recent studies (Qiao et al., Reference Qiao, Zepf, Borghesi and Geissler2009; Tripathi et al., Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009). Laser intensity required to produce relativistic ions in the hole-boring stage is [Eq. (3). of Qiao et al. (Reference Qiao, Zepf, Borghesi and Geissler2009)].
$$\displaystyle{{I_0} \over {m_i n_i c^3}} \approx \displaystyle{1 \over 4}. $$ For protons (m i/m e = 1836), the intensity is 
$I_0 {\rm \gtrsim} (n_0 /n_{\rm e} \, ) \times 10^{20} $
$\times \, (1\,{\rm \mu m}/\lambda )^2 \; \; {\rm W}\,{\rm cm}^{ - 2}, $ where n 0 is the initial foil density, λ is the laser wavelength in microns, 
$n_{\rm c} = m_{\rm e} \; \; \omega ^2 /4\pi e^2 $ is the critical density with e and m e the electron charge and mass, respectively and ω is the laser frequency. Such intensities are large enough to achieve a smooth transition between “hole boring” and “light sail” stages. Target thickness required to prevent blow out of all electrons in foil by laser ponderomotive force, is estimated by condition that maximum charge separation field 
$E_{\parallel, {\rm max}} = 4\; \pi \; e\; n_0 \; l_0 $ should be larger than the ponderomotive force (v × B L). This gives the condition [Eq. (4). of Qiao et al. (Reference Qiao, Zepf, Borghesi and Geissler2009)]
$$\displaystyle{{l_0} \over \lambda} \,{\gt \sim}\, \displaystyle{1 \over {2\pi}} \; \sqrt {\displaystyle{{n_{\rm c} m_i} \over {n_i m_e}}} \; \; \sqrt {\displaystyle{I \over {m_i n_i c^3}}} {\rm \;} {\rm.} $$
Choosing l = l 0 and n i = n 0, the foil thickness should satisfy 
$l_0 \,{\gt \sim}\,3.41\; \sqrt {n_{\rm c} /n_0} \; \lambda $.
In our simulations, a CP laser pulse, Gaussian in space and time, having peak intensity 6.3 × 1022 W cm−2, wavelength 1 μm, spot size 16 μm (full width at half maximum) and duration 250 fs, is launched from the left boundary. Laser strikes an overdense plasma foil normally. The total simulation box is 60 × 50 μm2 having 6000 × 5000 cells in the (z, x) plane. Each cell is filled with 100 macroparticles per species. The foil plasma consists of two species: Electrons and protons, both having equal density n = n e = n i = 100 n c, where n c = 1.1 × 1021 cm3 is the critical density. Thickness of foil is 0.35 μm [from Eq. (14)]. Radius of curvature of concave and convex foil targets is 50 μm. The boundary conditions are absorbing for both electromagnetic waves and macro particles.
4. RESULTS AND DISCUSSION
We start with the flat target case, Figure 2 plots ion density n i/n c at (a) 10, (b) 44, (c) 60, (d) 74, (e) 90, (f) 160, and (g) 230 fs. Figure 2a shows the foil target of 100 n c density and 0.35 μm thickness just before the laser pulse strikes the target. Figure 2b corresponds to hole-boring stage, two layers starts to appear: Highly dense green layer on the back side of the target and lower density protons left as red layer. The flat foil changes shape due to non-uniform laser push in the transverse direction and the resulting curved foil is shown in Figure 2c. Transverse bunching of protons grows as the change in the shape of foil continues in Fig. 2d. The foil attains its maximum curvature and looks like a concave foil in Figure 2e. As the foil is moving with relativistic velocity, and the growth rate of transverse instabilities depends inversely on the relativistic factor, the foil stays intact and continues to work as a relativistic plasma mirror for laser. Figure 2g shows the foil at the end of simulation, having peak density of accelerated bunch at 52 n c. The curvature of the foil within the laser spot size has not changed from Figure 2e to 2g, but the thickness has increased, suggesting a slight increase in the energy spread of the accelerated bunch.
Fig. 2. Ion density n i/n c in flat target case at (a) 10, (b) 44, (c) 60, (d) 74, (e) 90, (f) 160, and (g) 230 fs.
Ion density n i/n c in the convex target case is plotted in Figure 3 at (a) 10, (b) 44, (c) 66, (d) 110, (e) 160, and (f) 230 fs. Convex foil of 50 μm radius of the curvature, before laser irradiation is shown in Figure 3a. After the hole-boring stage two layers start to appear in Fig. 3b. Shape-changing phase of the foil due to Gaussian laser pulse is shown in Figure 3c, where the transverse bunching of protons has also appeared. The foil attains its final shape and looks like a concave foil in Figure 3d. After this stage, the foil is accelerated by the laser pulse and the final foil shape at the end of simulation is shown in Figure 3g. Density of the accelerated bunch is 45 n c. In initial stages of the acceleration process, the geometrical effect in the convex target slightly enhances the number of protons in the detached foil. This happens because protons come out in the normal direction from the convex foil after the hole-boring stage and gets focused. This effect can be observed in the proton phase space plot in the (z, x) plane in Figure 4 at (a) 10, (b) 44, and (c) 60 fs. The focusing of protons ejected normally from the foil during the formation of detached layer is shown in Figure 4b and 4c. This results in more number of protons in the detached foil, but energy spread is higher. It happens due to comparatively longer shape change phase in convex targets as compared with the flat target case.
Fig. 3. Ion density n i/n c in convex target case at (a) 10, (b) 44, (c) 66, (d) 110, (e) 160, and (f) 230 fs. Target radius of the curvature is 50 μm.
Fig. 4. Ion phase space in the (z, x) plane at (a) 10, (b) 44, and (c) 66 fs, for the convex target case.
Ion density n i/n c in the concave target case at (a) 10, (b) 28, (c) 38, (d) 55, (e) 110, (f) 160, and (g) 230 fs. Target radius of the curvature is 50 μm. Figure 5b and 5c shows compressed foil in the hole-boring stage. Transverse bunching is lowest in Figure 5d as foil is not changing its shape. This becomes possible because the radius of curvature of the foil is chosen after simulating the flat target case, and the estimated radius of curvature of the final curved foil in Figure 2e is 50 μm. Figure 5e–5g shows the detached foil as it is further accelerated to higher energies. Increment in foil thickness is very small and peak density of accelerated bunch is 60 n c, the highest among all the three targets considered. The growth of transverse instabilities in initial stages is lowest due to the absence of the shape change phase. Geometrical effects responsible for slightly more number of protons in the case of convex target are reversed and the total amount of accelerated charge is the lowest. The benefits of concave target become more clear from the energy spectra of protons plotted in Figure 6 for all the three target cases. Due to more stability in the concave case, accelerated proton beam has a peak energy around 3.2 GeV as compared with the peak energies of flat and convex targets found to be around 3.0 and 2.8 GeV, respectively. Total accelerated charge and energy spread are highest in convex followed by flat and concave targets.
Fig. 5. Ion density n i/n c in concave target case at (a) 10, (b) 28, (c) 38, (d) 55, (e) 110, (f) 160, and (g) 230 fs. Target radius of curvature is 50 μm.
Fig. 6. Energy spectra of ions in region of z > 20 μm and 10 μm<x > 40 μm at t = 230 fs for all the three target cases.
Equation (12) is numerically evaluated for the characteristic parameters described in the simulation section and results are plotted in Figure 7. For laser of spot size 50 μm and equal radius of curvature of the convex foil, it is observed to reverse the curvature after propagating to ~40 μm (Fig. 7c). For short spot sizes 25 and 10 μm of the pulse, the foil becomes flattened after traversing the normalized distance ~0.35 and ~0.50 r 0, respectively (Fig. 7a and 7b).
Fig. 7. The normalized variation in the curvature of the foil as the center of the foil propagates with respect to the normalized distance. The initial radius of curvature to the laser spot size ratio is 0.2, 0.5, and 1.0 in plot (A), (B), and (C), respectively.
In conclusion, the curvature in target affects the energy spread, peak energy, and amount of charge accelerated in the RPA regime. During the shape-changing phase of the acceleration process, target shapes modifies the growth of transverse instabilities, geometrical effects responsible for stability, and the total amount of charge accelerated in ion acceleration process. If the radius of curvature of concave target is chosen such that no change in shape occurs during the laser irradiation then acceleration process becomes much more stable leading to less energy spread and higher peak energy. The ratio of pulse spot size to the radius of curvature is a crucial parameter for obtaining the optimized change in foil curvature as it accelerates. The conjecture is validated by the numerical estimates and simulation results. One may envisage other types of target structuring such as rippling or non-uniformity based on the above model for efficient ion acceleration schemes.
ACKNOWLEDGEMENTS
The work was carried out under the financial support from DST, Govt. of India.
