Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T07:46:39.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Shock pressure induced by 0.44 μm laser radiation on aluminum targets

Published online by Cambridge University Press:  25 March 2004

D. BATANI ,
H. STABILE ,
A. RAVASIO ,
T. DESAI ,
G. LUCCHINI ,
F. STRATI ,
J. ULLSCHMIED ,
E. KROUSKY ,
J. SKALA  and
B. KRALIKOVA
...Show all authors
D. BATANI
Affiliation:
Dipartimento di Fisica “G. Occhialini,” Università degli Studi di Milano Bicocca and INFM, Milano, Italy
H. STABILE
Affiliation:
Dipartimento di Fisica “G. Occhialini,” Università degli Studi di Milano Bicocca and INFM, Milano, Italy
A. RAVASIO
Affiliation:
Dipartimento di Fisica “G. Occhialini,” Università degli Studi di Milano Bicocca and INFM, Milano, Italy
T. DESAI
Affiliation:
Dipartimento di Fisica “G. Occhialini,” Università degli Studi di Milano Bicocca and INFM, Milano, Italy
G. LUCCHINI
Affiliation:
Dipartimento di Fisica “G. Occhialini,” Università degli Studi di Milano Bicocca and INFM, Milano, Italy
F. STRATI
Affiliation:
Dipartimento di Fisica “G. Occhialini,” Università degli Studi di Milano Bicocca and INFM, Milano, Italy
J. ULLSCHMIED
Affiliation:
Prague Asterix Laser Research Centre, Prague, Czech Republic
E. KROUSKY
Affiliation:
Prague Asterix Laser Research Centre, Prague, Czech Republic
J. SKALA
Affiliation:
Prague Asterix Laser Research Centre, Prague, Czech Republic
B. KRALIKOVA
Affiliation:
Prague Asterix Laser Research Centre, Prague, Czech Republic
M. PFEIFER
Affiliation:
Prague Asterix Laser Research Centre, Prague, Czech Republic
C. KADLEC
Affiliation:
Prague Asterix Laser Research Centre, Prague, Czech Republic
T. MOCEK
Affiliation:
Prague Asterix Laser Research Centre, Prague, Czech Republic
A. PRÄG
Affiliation:
Prague Asterix Laser Research Centre, Prague, Czech Republic
H. NISHIMURA
Affiliation:
Institute of Laser Engineering (ILE), Osaka University, Osaka, Japan
Y. OCHI
Affiliation:
Institute of Laser Engineering (ILE), Osaka University, Osaka, Japan
A. KILPIO
Affiliation:
General Physics Institute, Russian Academy of Sciences, Moscow, Russia
E. SHASHKOV
Affiliation:
General Physics Institute, Russian Academy of Sciences, Moscow, Russia
I. STUCHEBRUKHOV
Affiliation:
General Physics Institute, Russian Academy of Sciences, Moscow, Russia
V. VOVCHENKO
Affiliation:
General Physics Institute, Russian Academy of Sciences, Moscow, Russia
I. KRASUYK
Affiliation:
General Physics Institute, Russian Academy of Sciences, Moscow, Russia
Rights & Permissions [Opens in a new window]

Abstract

Shock pressure generated in aluminum targets due to the interaction of 0.44 μm (3 ω of iodine laser) laser radiation has been studied. The laser intensity profile was smoothed using phase zone plates. Aluminum step targets were irradiated at an intensity I ≈ 1014 W/cm2. Shock velocity in the aluminum target was estimated by detecting the shock luminosity from the target rear using a streak camera to infer the shock pressure. Experimental results show a good agreement with the theoretical model based on the delocalized laser absorption approximation. In the present report, we explicitly discuss the importance of target thickness on the shock pressure scaling.

Keywords

Rear target luminosityShock pressureShort laser wavelength interactionStreak images
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 4 , October 2003 , pp. 481 - 487
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

The topic of high pressure generation induced by intense laser radiation has been a subject of interest for more than 2 decades due to its potential applications in high pressure physics, laboratory astrophysical plasmas, equation of state (EOS) of materials, and so forth. This subject has been well studied theoretically and experimentally (Kidder, 1974; Ripin et al., 1980; Max et al., 1982; Grun et al., 1981; Nishimura et al., 1981; Pant et al., 1984; Shirsat et al., 1989; Lindl, 1995). Scaling of ablation parameters (like ablation pressure, mass ablation rate, and plasma velocity) at various laser intensities using radiation at different wavelengths like 1.06 μm or its harmonics up to the 4th order (Nishimura et al., 1981; Key et al., 1983; Meyer & Thiell, 1984; Pant et al., 1984) have been reported. In the past, several experimental techniques have been used to measure the mass ablation rate and the pressure. These include the measurement of ablation parameters like the mass ablation rate, the plasma expansion velocity, the momentum of the ablating plasma (Decoste et al., 1979; Grun et al., 1981), the ablation thickness using time resolved X-ray spectroscopy (Goldsack et al., 1982), the recoil momentum measurement (Arad et al., 1979), layered target burn through measurements (Nishimura et al., 1981), time resolved X-ray radiography (Key et al., 1983), ballistic pendula (Meyer & Thiell, 1984), shock velocity measurements (Veeser & Solem, 1978; Trainer et al., 1979), Faraday cups (Pelah, 1976; Gupta et al., 1987), the target terminal velocity using a rear side cone calorimeter (Eidmann et al., 1984; Godwal et al., 1989), a time-resolved streak record of visible emission from the rear surface of the impact foil (Obenschain et al., 1981) and so forth.

Various theoretical models have been discussed to estimate the shock pressure and some of them are mentioned below.

According to a recent review (Lindl, 1995), shock pressure can be estimated when laser radiation deposits its energy at the critical density (ne ≈ nc) as

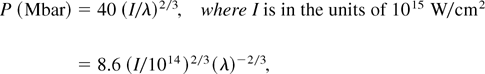
where λ is in microns. The model reported by Fabbro (Fabbro et al., 1985) calculates the pressure for the laser absorption at the critical density (ne ≈ nc) as

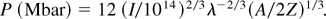
When the laser absorption is delocalized (ne < nc), pressure can be evaluated by the equation given by Mora (1982) and Fabbro (1982):

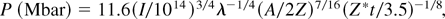
where t is the time in nanoseconds and Z* is the ionization degree of the material. The dependence on time is due to the fact that when laser radiation is absorbed below the critical density layer, the separation between absorption region (ne < nc) and ablation surface (ne = ns, solid density) increases, resulting in the decrease of ablation efficiency. Such a decrease in time of ablation pressure, even for a constant laser irradiation, was first described by Caruso and Gratton (1968) and later by Mora (1982). The difference between delocalized absorption models and localized (at critical density) models has been already discussed by Meyer and Thiell (1984).

Scaling laws of ablation parameters have been derived based on the laser absorption region either at the critical density layer (ne ≈ nc) or below (ne< nc). However, in the present case we restrict our discussion to the shock pressures only.

Although the above equations were well accepted, two important issues which had drawn the attention of the earlier researchers include the following:

1. The presence of hot spots, which gives rise to nonuniform intensity distribution within the focal spot area.

2. In many cases, laser intensity was increased by decreasing the laser focal spot. Such small spots were sensitive to edge effects associated with energy flow through the focal spot periphery. This gave rise to a well-known phenomenon of lateral energy transport (Ripin et al., 1980).

Even when large enough focal spots were used, the laser intensity profile was not optically smoothed.

Therefore, a careful study raises an ambiguity in the quality and magnitude of the shock pressures reported earlier in the literature. However, the progress in laser technology and in laser smoothing techniques has allowed the realization of much cleaner experiments in recent times. The measured ablation rate was therefore dominated by the “drilling effect” connected to such hot spots, that is, again by two-dimensional (2D) effects connected to the short-scale inhomogeneities.

With the development of techniques like random phase plates (RPP) and phase zone plates (PZP) to attain laser uniformity on the target surface, to a great extent, the hot spots were eliminated, although not completely. The first optical smoothing technique, RPP was introduced in the 1980s (Kato et al., 1984). The use of PZP also allowed us to get a flat-top intensity profiles directly comparable with one-dimensional (1D) models. In this context, recently interesting results have also been obtained with the partial coherent light technique, PCL, adopted at Institute of Laser Engineering (ILE) (Sakaiya et al., 2002). First results on pressure generation at 0.53 μm using PZP were obtained by Koenig et al. (1995). In the present work, we report the pressure scaling at I ≈ 1014 W/cm2 induced in an aluminum target using 0.44-μm radiation. We have adopted a large spot to irradiate the target in combination with PZP. This configuration minimizes the nonuniformity in the irradiation area and the large laser spot of ≈400 μm overcomes the effects of lateral energy transport.

Besides the above mentioned issues another important factor is the following:

3. There is still some incertitude concerning the scaling of ablation processes versus laser intensity at short laser wavelengths. For instance, measurements at 0.351 μm performed by Key et al. (1983) did show a scaling ≈I0.3, very different from what was predicted by various theoretical models (usually ≈I0.7). Indeed such experimental results were affected by 2D and drilling effects, which could burn through thicker foil in the ablated plasma (Lebo et al., 1999).

To our knowledge, data for short wavelength (0.44 μm) laser ablation on aluminum targets in the range 1013 to 1014 W/cm2 have not been reported. This is important because shorter laser wavelengths (third and fourth harmonics of Nd, as well as other wavelengths produced by gas lasers) have the advantage of giving a higher ablation rate and pressure, and are thereby envisaged as future drivers for the inertial confinement fusion direct drive experiment (Koenig et al., 1992; Lindl, 1995).

Therefore, we believe, despite all the extensive work reported so far, there are still some good reasons to study the process of laser ablation at short wavelengths in combination with optical smoothing techniques.

Our present experiment aimed to address to the issues described in items 1–3 and was performed at the Prague Asterix Laser (PALS) laboratory using laser irradiation at λ = 0.44 μm. The high laser energy per shot (up to a maximum of 400 J) allowed us to obtain laser intensities exceeding 2 × 1014 W/cm2 using relatively large focal spots (diameter 400 μm) and avoiding 2D effects. Our results show a scaling of ablation pressure versus laser intensity that is quite close to the theoretical prediction and gives some evidence for the mechanism of delocalized laser absorption.

In the present experiment, we detect the shock luminosity from the target rear using a streak camera, taking advantage of the recent advancement in the generation of high quality shocks (Batani et al., 2003) and in the measurements of shock velocities using stepped targets (Koenig et al., 1995). The ablation pressure is therefore estimated by measuring the shock velocity. As compared to other methods, this is a quite direct measurement of ablation pressure. Also it is less prone to 2D effects because we measure the shock velocity in the central region of the focal spot where shock dynamics is practically 1D, thanks to the use of PZPs.

2. EXPERIMENT

Schematics of the experimental setup are shown in Figure 1 and experiments were performed using the PALS. Details of the system are described by Jungwirth et al. (2001). In the present experiment, the laser chain was operated to deliver ∼120 J energy in 450 ps (FWHM) at 0.44 μm wavelength. Laser radiation was focused using an f/2 lens of focal length f = 60 cm that was placed behind the entrance window of the interaction chamber (of 1 m diameter). A blue filter in front of the entrance window was used to cut any residual ω and 2ω light. The diagnostics used to detect the shock breakout from the target rear face consisted of a pair of lenses imaging the rear face onto the slit of a streak camera (Hamamatsu C7700 with S-1 photocathode). The first one was a complex f/2 objective, with a focal length f = 100 mm, producing a parallel beam between the two lenses. A protection tube was used to shield the diagnostic light path from scattered laser light. A red filter RG60 was used before the streak camera to cut out any 3 ω light. The second lens had f = 98 cm, giving a total optical magnification M = 9.8. The spatial resolution, measured on the CCD placed after the streak camera by imaging a suitable grid (90 μm pitch), was 2.6 μm/pixel. The CCD had a 512 × 512 pixel and 16 bits dynamic range. The obtained temporal resolution was 3.22 ps/pixel.

Experimental setup in PALS.

Stepped targets were fabricated by General Atomics, USA, by structuring the required dimensions from the bulk aluminum. The Al base was ≈8 μm, and the step thickness was ≈8.5 μm. Al was chosen as its behavior at high pressure is rather well known, making it a typical reference material for laser-driven shock wave experiments.

The laser intensity on target is obtained by measuring shot by shot the laser energy (through a calibrated reflection from the entrance window of the interaction chamber) and includes the typical losses (about 20%) due to the use of PZPs. Also it is calculated taking into account the flat-top intensity profile, that is, it corresponds to the effective intensity in the central region of the focal spot. As for the time dependence, the x-axis in Figure 4 reports the time-averaged intensity over the laser pulse (FWHM) duration.

3. PZP AND FLAT SHOCK GENERATION

PZP is an optical smoothing technique (Stevenson et al., 1994; Batani et al., 2002) that allows a flat-top intensity distribution to be produced. Phased zone plates are a bidimensional array of Fresnel lenses etched on a glass slab. These are disposed so as to randomly introduce phase differences of 0 or π on the wave front of the laser. This breaks the spatial coherence of the laser beam and produces a smooth intensity profile. Because, for technical reason, it was not possible to produce a PZP with the full size of the laser beam, we designed a smaller PZP to be placed at f/2 from the target. The design of this plate had Fresnel lenses of 1 cm diameter, which implies that 225 Fresnel lenses are covered by the laser beam. The characteristics of our optical system (PZP + focusing lens) was such that we could produce a total focal spot of 400 μm FWHM with a ∼200-μm-wide flat region at the center, corresponding to a laser intensity up to 2 × 1014 W/cm2.

4. SHOCK PRESSURE RESULTS

Figure 2 shows the streak camera image of the shock luminosity from the rear surface of the flat aluminum target. Shock luminosity from the rear surface of the stepped target is shown in Figure 3. The time interval between the shock luminosity from the rear of the base and the step corresponds to the shock transit time (Δt) in the step thickness. Thus the shock velocity D was calculated as d/Δt where d is the step thickness. From such a shock velocity we determine the shock pressure using the Hugoniot data for Al obtained from the Sesame tables (T4 Group, 1983). Such a shock pressure coincides with the pressure produced by the laser beam on the irradiation side, that is, the ablation pressure.

Shock breakout image obtained from a flat aluminum target using a PZP recorded with the streak camera. Dimension of the image are 1.69 ns × 1300 μm. Time is along the vertical axis.

Shock breakout image obtained from a stepped aluminum target for laser energy EL = 108 J. The dimensions of the images are 1.69 ns × 1300 μm. Time is along the vertical axis. The time between the shock luminosity from rear of base and step is Δt = 267 ps, giving a shock velocity D = 31.84 μm/ns.

Experimental results (dots) with the scaling law corresponding to absorption at the critical density, Eq. (2, continuous line), and to delocalized absorption, Eq. (3, dotted line).

Figure 4 represents the shock pressure versus laser intensity on the target surface. We also show two theoretical curves obtained using Eqs. (2) and (3) for localized and delocalized absorption, respectively. It is clearly seen that the experimental results are closer to Eq. (3) described for delocalized absorption. The typical errors were calculated by taking into account the error on the target thickness (including surface roughness), the streak camera resolution, as determined by the streak temporal window (we used 1.69 ns) and the slit size (115 μm), and the typical errors made in reading experimental data. The error on shock velocity D was then propagated to calculate the error on P. We finally observe that errors are typically ±20 % on shock pressure.

5. DISCUSSION

From Figure 4, it is seen that our experimental results can be better explained by using Eq. (3), has dependence on time (t) and assumes laser absorption at a density ne < nc than the critical density approximation, which has dependence on time (t). For the interpolation of experimental data with Mora's law the quantity, time (t) described in the Eq. (3) needs a careful modification. Indeed, in the case of delocalized absorption, the shock pressure (and shock velocity) decrease with time. Hence, weaker shocks produced at lower laser intensities will travel more slowly in the targets and will break out at later times; thereby they will have more time to slow down. The shock velocity (and thereby the shock pressure) is measured at shock breakout, but the shock breakout time is different for low and high laser intensity for a given target thickness. The shock breakout time is the time t to be inserted in Eq. (3).

To take this effect into account, we write that

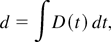
where d is the target thickness, D is shock velocity, and the time integral goes from 0 to the shock breakout time at the target rear. The relation between the shock velocity D and the shock pressure P is given by Zeldovich & Raizer (1967) as

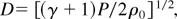
where γ is the adiabatic constant of the material and ρ0 is the unperturbed target density. Eqs. (4) and (5) allow the shock breakout time to be determined, and by inserting it into Eq. (3), we finally get an equation that is formally independent of time, but dependent on target thickness, that is,

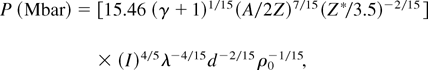
where I is in the units of 1014 W/cm2 and λ and d are in microns.

From the general Eq. (6), as a specific case, we consider aluminum, which was our experimental target A = 27, Z = 13 = Z*, γ = 1.65 and ρ0 = 2.7 g/cc and we get

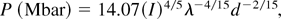
where I is in the units of 1014 W/cm2, λ and d are in microns, and the constant has been calculated for A = 27 and Z = Z* = 13 (however, the dependence on the ionization degree Z* is practically negligible). Here we have simplified the calculation by calculating the shock breakout time for an “average” target thickness d = (dbase + dstep)/2. This approximation may be done because the time exponent in Eq. (3) is very small (t−1/8), which means that the shock decreases quite slowly with time.

Because target thickness is an important factor in the measurement of shock velocity, it is necessary to consider the limitation of the target thickness. The optimization of target thickness is discussed for a trapezoidal laser pulse with an approximation that temporal pulse is Gaussian in nature (Batani et al., 2003). For a steady-state shock, minimum thickness dmin ≥ DtR /2 where tR is the rise time of the laser pulse. After the termination of the laser pulse, a rarefaction wave generates and propagates at a speed higher than the shock wave. This eventually weakens the shock. Therefore the shock wave has to emerge before the rarefaction wave reaches the target rear surface; otherwise the shock wave will not be steady. Therefore, the maximum target thickness should be dmax < 4Cs tL /(4Cs − D), where Cs is velocity of the unloading wave ≈ sound speed, and tL is the time at which intensity starts to decrease in the laser pulse (Batani et al., 2003). This characterizes the required target thickness.

For a steady-state shock, the minimum base target thickness should be 5–8 μm and maximum thickness (base + step) of 16–24 μm for a shock pressure applied on the target that is in the range of 15–33 Mbars. In the present experiment, the choice of the target thickness was based on the above calculation.

To corroborate our results on the applicability of delocalized laser absorption, we calculate the plasma density at the laser absorption layer under our experimental conditions λ = 0.44 μm, t = 450 ps. For a short wavelength laser radiation, density scale length (Max et al., 1982) L = CS t where CS is coronal sound speed = [ZkT/mi]1/2 and t is pulse duration. For our situation, the estimated plasma temperature T = 900 eV, CS ∼2 × 107 cm/s, and L ∼ 90 μm. In the case of short wavelength lasers, absorption is predominantly by inverse bremstrahlung and it takes place at n0 = 2nc(c/νc L)1/2 where νc is the collision frequency at critical density (Mora, 1982). In our case, n0 ∼ 3 × 1021 /cc. Assuming the plasma density fall is exponential. We observe about 50% of the laser absorption is at a distance of ∼ 40 μm from the critical density layer.

As discussed above, our experimental results are more closely reproduced for noncritical absorption approximation. This concerns not only the absolute values of pressures but also the trend versus laser intensity. From this point of view, substituting the factor 12 with the factor 8.6, that is, using Eq. (1) instead of Eq. (2), may probably be considered as a tentative fitting of the theoretical scaling obtained for absorption at the critical surface with existing experimental data.

6. CONCLUSIONS

In summary, the laser-induced shock pressures at 0.44 μm have been measured in planar aluminum targets at an irradiance up to 2 × 1014 W/cm2. By adopting relatively large focal spots and a smoothed laser beam, the lateral energy transport and the “drilling effect” have been avoided. The measured scaling shows a fair agreement with available analytical models based on delocalized laser absorption. These data can also be of interest for an experimental database of ablation pressure scaling for further study on equation-of-state (EOS) experiments, as laser-driven shock waves have recently become a useful tool in high pressure physics and, in particular, for the realization of EOS experiments.

ACKNOWLEDGMENTS

The present work was performed at the PALS Laboratory under the E.U. contract HPRI-CT-1999-00053 (PALS), Transnational Access to Major Research Infrastructures (ARI) of the Improving Human Potential (IHP) programme of the 5th FP. We also thank M. Moret, M. Tomasini, C. Olivotto, J. Kaae, and S. Alba for their help in target production or characterization. Finally, we thank Colin Danson and Dave Pepler, Rutherford Appleton Laboratory, UK, for having produced the PZPs used in the experiment at PALS, and Michel Koenig and Alessandra Benuzzi, LULI, for useful discussions.

References

REFERENCES

Arad, B., Eliezer, S., Gazit, Y., Loebenstein, H.M., Zigler, A., Zmora, H. & Zweigenbaum, S. (1979). Burn-through of thin aluminum foils by laser-driven ablation. J. Appl. Phys. 50, 6617–6821.Google Scholar
Batani, D., Bleu, C. & Lower, Th. (2002). Modelistic, simulation and application of phase plates. Eur. Phys. J. D 19, 231–238.Google Scholar
Batani, D., Löwer, Th., Strati, F., Hall, T., Benuzzi, A. & Koenig, M. (2003). Production of high quality shocks for Equation of State Experiments. Eur. Phys. J. D 23, 99–107.Google Scholar
Caruso, A. & Gratton, R. (1968). Some properties of the plasmas produced by irradiating light solids by laser pulses. Plasma Phys. 10, 867–877.Google Scholar
Decoste, R., Bodner, S.E., Ripin, B.H., McLean, E.A., Obenschain, S.P. & Armstrong, C.M. (1979). Ablative Acceleration of Laser-Irradiated Thin-Foil Targets. Phys. Rev. Lett. 42, 1673–1677.Google Scholar
Eidmann, K., Amiranoff, F., Fedosejevs, R., Maaswinkel, A.G.M., Petsch, R., Sigel, R., Spindler, G., Yung-lu, Teng, Tsakiris, G. & Witkowski, S. (1984). Interaction of 1.3-μm laser radiation with thin foil targets. Phys. Rev. A 30, 2568–2589.Google Scholar
Fabbro, R. (1982). Etude de L'influence de la longuer D'onde laser sur les processus de conduction thermique et D'ablation dans les plasmas crees par laser. Ph.D. thesis, Paris, France: University of Paris.
Fabbro, R., Max, C. & Fabre, E. (1985). Planar laser-driven ablation: Effect of inhibited electron thermal conduction. Phys. Fluids 28, 1463–1481.Google Scholar
Godwal, B.K., Shirsat, T.S. & Pant, H.C. (1989). Laser-induced ablation pressure in thin gold foils. J. Appl. Phys. 65, 4608–4611.Google Scholar
Goldsack, T.J., Kilkenny, J.D., MacGowan, B.J., Veats, S.A., Cunningham, P.F., Lewis, C.L.S., Key, M.H., Rumsby, P.T. & Toner, W.T. (1982). The variation of mass ablation rate with laser wavelength and target geometry. Op. Comm. 42, 55–59.Google Scholar
Grun, J., Decoste, R., Ripin, B.H. & Gardner, J. (1981). Characteristics of ablation plasma from planar, laser-driven targets. Appl. Phys. Lett. 39, 545–547.Google Scholar
Gupta, P.D., Tsui, Y.Y., Popil, R., Fedosejevs, R. & Offenberger, A.A. (1987). Ablation parameters in KrF laser/plasma interaction: An experimental study. Phys. Fluids 30, 179–185.Google Scholar
Jungwirth, K., Cejnarova, A., Juba, L., Kralikova, B., Krasa, J., Krousky, E., Krupickova, P., Laska, L., Masek, K., Mocek, T., Pfeifer, M., Präg, A., Renner, O., Rohlena, K., Rus, B., Skala, J., Straka, P. & Ullschmied, J. (2001). The Prague Astrix Laser System. Phys. Plasmas 8, 2495–2501.Google Scholar
Kato, Y., Mima, K., Miyanaga, N., Arinaga, S., Kitagawa, Y., Nakatsuka, M. & Yamanaka, C. (1984). Random phasing of high-power lasers for uniform target acceleration and plasma-instability suppression. Phys. Rev. Lett. 53, 1057–1060.Google Scholar
Key, M.H., Toner, W.T., Goldsack, T.J., Kilkenny, J.D., Veats, S.A., Cunningham, P.F. & Lewis, C.L.S. (1983). A study of ablation by laser irradiation of plane targets at wavelengths 1.05, 0.53, and 0.35 μm. Phys. Fluids 26, 2011–2026.Google Scholar
Kidder, R.E. (1974). Inertial fusion energy. Nucl. Fus. 14, 797.Google Scholar
Koenig, M., Fabre, E., Malka, V., Michard, A., Hammerling, P., Batani, D., Boudenne, J.M., Garconnet, J.P. & Fews, P. (1992). Recent results on implosions directly driven at I = 0.26 I¼m laser wavelength. Laser Part. Beams 10, 573–583.Google Scholar
Koenig, M., Faral, B., Boudenne, J.M., Batani, D., Benuzzi, A., Bossi, S., Remond, C., Perrine, J.P., Temporal, M. & Atzeni, S. (1995). Relative consistency of equations of state by laser driven shock waves. Phys. Rev. Lett. 74, 2260–2263.Google Scholar
Lebo, I.G., Mikhailov, Yu.A., Tishkin, V.F. & Zvorykin, V.D. (1999). Analysis and 2D numerical modeling of burn through of metallic foil experiments using power KrF and Nd lasers. Laser Part. Beams 17, 753–758.Google Scholar
Lindl, J. (1995). Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain. Phys. Plasmas 2, 3933–4024.Google Scholar
Max, C.E., McKee, C.F. & Mead, W.C. (1982). A model for laser driven ablative implosions. Phys. Fluids 23, 1620–1645.Google Scholar
Meyer, B. & Thiell, G. (1984). Experimental scaling laws for ablation parameters in plane target-laser interaction with 1.06 μm and 0.35 μm laser wavelengths. Phys. Fluids 27, 302–311.Google Scholar
Mora, P. (1982). Theoretical model of absorption of laser light by a plasma. Phys. Fluids 25, 1051–1056.Google Scholar
Nishimura, H., Azechi, H., Yamada, K., Tamura, A., Inada, Y., Matsuoka, F., Hamada, M., Suzuki, Y., Nakai, S. & Yamanaka, C. (1981). Experimental study of wavelength dependences of laser-plasma coupling, transport, and ablation processes. Phys. Rev. A 23, 2011–2019.Google Scholar
Obenschain, S.P., Grun, J., Ripin, B.H. & McLean, E.A. (1981). Uniformity of laser-driven, ablatively accelerated targets. Phys. Rev. Lett. 46, 1402–1405.Google Scholar
Pant, H.C., Sharma, S. & Shirsat, T.S. (1984). Effect of lateral energy transport on ion expansion energy scaling in laser produced plasma. J. Appl. Phys. 55, 697–704.Google Scholar
Pelah, I. (1976). Diagnosis of laser produced plasma with charge collectors. Phys. Lett. A 59, 348–352.Google Scholar
Ripin, B.H., Decoste, R., Obenschain, S.P., Bodner, S.E., McLean, E.A., Young, F.C., Whitlock, R.R., Armstrong, C.M., Grun, J., Stamper, J.A., Gold, S.H., Nagel, D.J., Lehmberg, R.H. & McMahon, J.M. (1980). Laser-plasma interaction and ablative acceleration of thin foils at 1012–1015 W/cm2. Phys. Fluids 23, 1012–1030.Google Scholar
Sakaiya, T., Azechi, H., Matsuoka, M., Izumi, N., Nakai, M., Shigemori, K., Shiraga, H., Sunahara, A., Takabe, H. & Yamanaka, T. (2002). Ablative Rayleigh-Taylor instability at short wavelenghts observed with moiré interferometry. Phys. Rev. Lett. 88, 145003.Google Scholar
Shirsat, T.S., Sharma, S. & Pant, H.C. (1986). Calorimetric study of laser irradiated thin foil targets. Pramana, Ind. J. Phys. 27, 701–710.Google Scholar
Shirsat, T.S., Parab, H.D. & Pant, H.C. (1989). Effect of target atomic number on laser induced ablation pressure scaling. Laser Part. Beams 7, 795–799.Google Scholar
SESAME Report on the Los Alamos equation-of-state library. (1983). Report No. LALP-83-4 (T4 Group LANL, Los Alamos).
Stevenson, R.M., Norman, M.J., Bett, T.H., Pepler, D.A., Danson, C.N. & Ross, I.N. (1994). Binary-phase zone plate arrays for the generation of uniform focal profiles. Optics Letters 19, 363–369.Google Scholar
Trainor, R.J., Shaner, J.W., Auerbach, J.M. & Holmes, N. C. (1979). Ultrahigh-pressure laser-driven shock-wave experiments in aluminum. Phys. Rev. Lett. 42, 1154–1157.Google Scholar
Veeser, L.R., & Solem, J.C. (1978). Studies of laser-driven shock waves in aluminum. Phys. Rev. Lett. 40, 1391–1394.Google Scholar
Zeldovich, Ya.B. & Raizer, Yu.P. (1967). Physics of shock waves and high temperature hydrodynamic phenomena. New York: Academic Press.
Figure 0

Experimental setup in PALS.

Figure 1

Shock breakout image obtained from a flat aluminum target using a PZP recorded with the streak camera. Dimension of the image are 1.69 ns × 1300 μm. Time is along the vertical axis.

Figure 2

Shock breakout image obtained from a stepped aluminum target for laser energy EL = 108 J. The dimensions of the images are 1.69 ns × 1300 μm. Time is along the vertical axis. The time between the shock luminosity from rear of base and step is Δt = 267 ps, giving a shock velocity D = 31.84 μm/ns.

Figure 3

Experimental results (dots) with the scaling law corresponding to absorption at the critical density, Eq. (2, continuous line), and to delocalized absorption, Eq. (3, dotted line).