1. INTRODUCTION
X-ray sources are useful for the analysis of materials and X-ray examination of the human body. A conventional X-ray device is an X-ray tube, which consists of a filament and a tungsten target. Kmetec et al. (Reference Kmetec, Gordon, Macklin, Lemoff, Brown and Harris1992) succeeded in producing hard X-rays by a new method employing a short-pulse high-power laser, and a target (Kmetec et al., Reference Kmetec, Gordon, Macklin, Lemoff, Brown and Harris1992). When such a laser is focused on a target, the laser-irradiated region of the target becomes a plasma. Then, electrons inside the plasma are heated by laser-plasma interactions (Kruer, Reference Kruer2003; Brunel, Reference Brunel1987). Bremsstrahlung and characteristic X-rays are emitted as a result of the interaction of the electrons and the target. The most important feature of these X-rays is their short pulse duration. X-rays with picosecond duration can be obtained by controlling the pulse duration of the laser (Dorchies et al., Reference Dorchies, Blasco, Bonte, Caillaud, Fourment and Peyrusse2008).
A solid target is often used as the laser-plasma X-ray source because high-flux X-rays can be easily obtained. A problem with using a solid target is that debris from the solid adheres to the focusing mirror, causing its reflectivity to decrease. In serious cases, the mirror is damaged as a result of the debris absorbing the laser energy. Instead of a solid target, a cluster target can also be employed. Since the atomic density of a cluster is almost equal to that of a solid target, a high X-ray photon number is anticipated. Moreover, using a cluster target reduces the risk of debris formation.
Clusters of rare gases have been investigated for X-ray generation. In particular, krypton (Kr) and xenon (Xe) clusters are attractive because the X-ray energies of Kr and Xe K-shells are high (11 keV for the Kr K-shell and 30 keV for the Xe K-shell). Although the generation of argon (Ar) K-shell and Xe L-shell X-rays, for which the energy is less than 5 keV, has been extensively investigated (McPherson et al., Reference McPherson, Thompson, Borisov, Boyer and Rhodes1994; Ditmire et al., Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996), there have been few reports on the experimental result of Kr K-shell X-ray generation (Issac et al., Reference Issac, Vieux, Ersfeld, Brunetti, Jamison, Gallacher, Clark and Jaroszynski2004; Kugland et al., Reference Kugland, Neumayer, Doppner, Chung, Constantin, Girard, Glenzer, Kemp and Niemann2008; Zhang et al., Reference Zhang, Chen, Yuan, Yan, Wang, Liu, Shen, Faenov, Pikuz, Skobelev, Gasilov, Boldarev, Mao, Li, Dong, Lu, Ma, Wang, Sheng and Zhang2011) and only one report on the experimental result of Xe K-shell X-ray generation by our group (Hayashi et al., Reference Hayashi, Pirozhkov, Kando, Fukuda, Faenov, Kawase, Pikuz, Nakamura, Kiriyama, Okada and Bulanov2011). On the assumption that plasma electrons have energies corresponding to ponderomotive potential, the threshold laser intensity of Kr K-shell X-rays is estimated to be 2.0 × 1017 W/cm2. However, the experimental generation of Kr K-shell X-rays at 2.0 × 1016 W/cm2 was reported (Issac et al., Reference Issac, Vieux, Ersfeld, Brunetti, Jamison, Gallacher, Clark and Jaroszynski2004). A laser-cluster interaction model: the nanoplasmas model proposed by Ditmire et al. (Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996), could not explain the experimental result of Kr K-shell X-ray generation (Issac et al., Reference Issac, Vieux, Ersfeld, Brunetti, Jamison, Gallacher, Clark and Jaroszynski2004). Little is known about the production of the Kr and Xe K-shell X-rays and their mechanisms.
In the above-mentioned report on Xe K-shell X-ray generation, a special three-staged nozzle was utilized for Xe cluster formation. This nozzle has a complicated structure wherein the inner diameter of the nozzle expands from 0.5 to 0.7 mm in the first stage, from 0.7 to 0.8 mm in the second stage, and up to 2 mm in the third stage (Boldarev et al., Reference Boldarev, Gasilov, Faenov, Fukuda and Yamakawa2006). The high Xe K-shell X-ray photon number of approximately 3 × 107 was reported when using this nozzle (Hayashi et al., Reference Hayashi, Pirozhkov, Kando, Fukuda, Faenov, Kawase, Pikuz, Nakamura, Kiriyama, Okada and Bulanov2011). Recently, a laser scattering method has been used to determine the size of Xe clusters produced by this nozzle (S. Jinno, private communication). From the measurement, we found that the size distribution of the Xe clusters was broad up to a huge size of 100 nm order. To increase the X-ray photon number, it is important to find the optimum cluster size for the X-ray emission. However, the nozzle is unsuitable for understanding Xe K-shell X-ray photon number dependence on the radius of Xe clusters.
As atomic density increases, the collision frequency of K-shell electrons and plasma electrons becomes higher. K-shell X-rays are emitted by K-shell recombination when the K-shell electrons are excited (ionized) by the collision of the hot electrons, the energies of which exceed the excitation energy (ionization potential) of the K-shell. Hence, the rate of K-shell X-ray emission is determined by atomic density and the number of hot electrons exceeding the excitation energy or ionization potential. If the penetration length of a laser has no limitation, larger clusters make it possible to produce a higher K-shell X-ray photon number by laser-cluster interaction. However, in a high density state such as a cluster or a solid, the penetration length of a laser has an upper limitation length called the skin depth. This means that the number of hot electrons is restricted by the skin depth. It is important to study K-shell X-ray photon number dependence on cluster size.
In our study, a conical nozzle was used for Xe K-shell X-ray production instead of the three-staged nozzle. This nozzle is advantageous for obtaining information on clusters because an empirical formula for cluster size is applicable. With this nozzle, we investigated Xe K-shell X-ray photon number dependence on cluster size.
Iodine is doped as the angiographic contrast agent; and the iodine absorption efficiency of Xe Kα X-rays is significantly different from that of Xe Kβ X-rays. From this reason, Xe K-shell X-ray sources will be expected to be utilized for angiography, which is a medical imaging technique used to visualize blood vessels and organs in the body.
2. EXPERIMENTAL SETUP AND METHOD
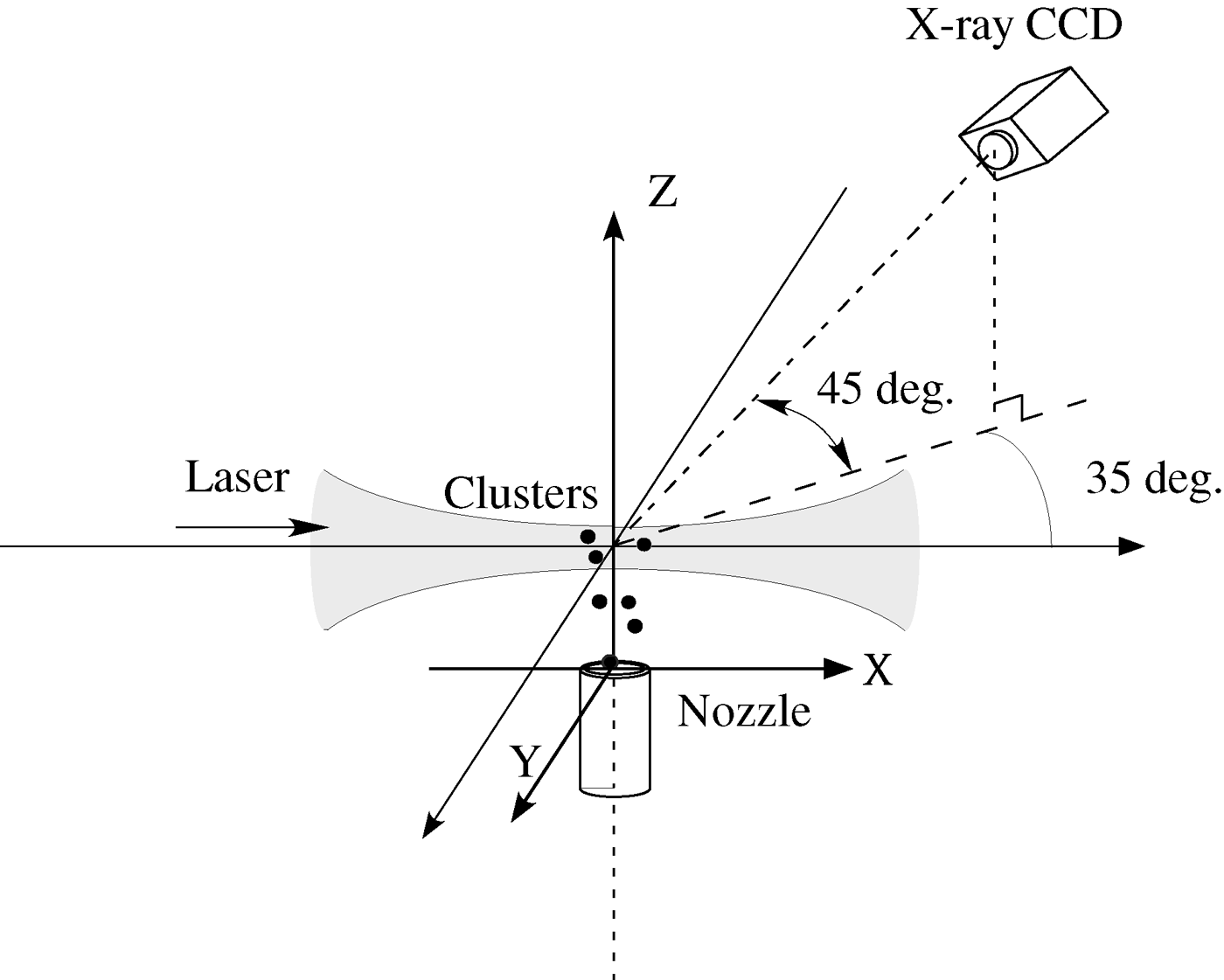
The experiment was carried out using the short-pulse high-power J-KAREN laser of Japan Atomic Energy Agency (JAEA), which emits 25 TW pulses of 40 fs duration. The use of a double chirped-pulse amplifier (CPA) with an optical parametric chirped-pulse preamplifier, a main amplifier, and a saturable absorber results in extremely high temporal contrast exceeding 1010 on sub-nanosecond time scales before the main pulse (Kiriyama et al., Reference Kiriyama, Mori, Nakai, Shimomura, Sasao, Tanoue, Kanazawa, Wakai, Sasao, Okada, Daito, Suzuki, Kondo, Kondo, Sugiyama, Bolton, Yokoyama, Daido, Kawanishi, Kimura and Tajima2010). The wavelength of the laser is 800 nm. Figure 1 shows a schematic setup of the experiment. The laser passed through a laser beamline and was guided to an experimental chamber, where it was focused on a Xe cluster target using an F/9 off-axis parabolic mirror. The beamline and chamber were kept under a vacuum condition using vacuum pumps. The best focal diameter (4 · σ) defined by the four-sigma method [ISO, 2005] was 35 µm × 36 µm.
Fig. 1. Experimental setup.
A conical nozzle was utilized to produce the Xe cluster target. The throat diameter of the nozzle was 0.5 mm and the output diameter was 1 mm. The Xe gas was supplied by a gas cylinder outside the experimental chamber and the backing pressure was controlled by a gas regulator. The Xe clusters were prepared by the adiabatic expansion of the Xe gas flowing inside the nozzle. The peak laser intensity on the cluster was changing the X position of the nozzle as shown in the figure. Y and Z positions of the nozzle were fixed to Y = 0 mm and Z = 1.5 mm.
The X-rays were measured with a PI-LCX400 hard X-ray charge-coupled device (CCD) manufactured by Princeton Instruments. According to the datasheet, the CCD has a quantum efficiency of about 1.5% for Xe K-shell X-rays with an energy of approximately 30 keV. The energy resolution of the CCD for 30 keV X-rays is about 0.32 keV (Hayashi et al., Reference Hayashi, Pirozhkov, Kando, Fukuda, Faenov, Kawase, Pikuz, Nakamura, Kiriyama, Okada and Bulanov2011). The CCD can be treated as a multielement detector since it contains 5.2 × 105 silicon elements. Therefore, the CCD can be utilized in the single-photon counting mode (Issac et al., Reference Issac, Vieux, Ersfeld, Brunetti, Jamison, Gallacher, Clark and Jaroszynski2004). A 200 µm aluminum filter was set in front of the CCD. The filter removes not only the scattered laser light but also low-energy X-rays (≤10 keV), which is important for the single-photon counting mode. The CCD was oriented at an angle of 35° from the laser propagation direction in the horizontal plane (xy plane) and 45° from the vertical axis. The distance from the CCD to the point of laser-cluster interaction was about 0.9 m and the solid angle of the CCD was 2.65 × 10−4 sr.
3. ESTIMATION OF CLUSTER RADIUS
In this section, we discuss a formula for estimating the cluster radius. Hagena carefully measured cluster radii using several types of nozzle and found an empirical equation for estimating the cluster radius involving the Hagena parameter Γ* (Hagena, Reference Hagena1992):
$$\overline N=33 \cdot \left({\Gamma^{\ast} \over 1000}\right)^{2.35} \quad \lpar 10^3\lt \Gamma ^ {\ast} \lt 10^4 \rpar \comma \;$$
$$\Gamma^{\ast} ={5554 \cdot P \over T_0 ^{2.29}} \cdot \left({0.74 \cdot \Phi \over \tan{\rm \alpha} } \right)^{0.85}\comma \;$$
where 
$\overline N $ is the average number of atoms comprising a cluster, P is the backing pressure in mbar, T 0 is the initial gas temperature in K, Φ is the throat diameter of the nozzle in μm, and α is the half-angle of the region of gas expansion. The mean cluster radius R cl is calculated by the equation 
$R_{cl}=R_{ws} \cdot \mathop {\overline N }\nolimits^{1/3}$ for Wigner-Seitz radius R ws, which is 0.273 nm [Krainov & Smirnov, Reference Krainov and Smirnov2002] for Xe gas.
Eqs. (1) and (2) can be used when the parameter Γ* is smaller than 104. For Γ* ≥ 104, the cluster radii can be measured by an electron diffraction approach, and the following relation between 
$\overline N $ and the slightly corrected parameter Γc* (Danylchenko et al., Reference Danylchenko, Kovalenko and Samovarov2008) has been obtained:
$$\overline N=\exp [{-} 12.83+3.51 \times \lpar \ln {\Gamma }_c^ {\ast} \rpar ^{0.8}] \; \comma \;$$
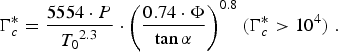$${\Gamma }_c^ {\ast} =\displaystyle{{5554 \cdot P} \over {\mathop {T_0 }\nolimits^{2.3} }} \cdot \mathop {\left({\displaystyle{{0.74 \cdot \Phi } \over {\tan{\rm \alpha} }}} \right)}\nolimits^{0.8} \, \lpar {\Gamma }_c^ {\ast} \gt 10^4 \rpar \;.$$When the Xe gas and clusters can be treated as a compressible fluid, the Mach number M is estimated by
$$\displaystyle{A \over {A^ {\ast} }}=\displaystyle{1 \over M}\mathop {\left[{\displaystyle{{2+\lpar {\rm \gamma} - 1\rpar \cdot M^2 } \over {{\rm \gamma}+1}}} \right]}\nolimits^{{\textstyle{{{\rm \gamma}+1} \over {2\lpar {\rm \gamma} - 1\rpar }}}} \; \comma \;$$where A is the output area of the nozzle, A* is the throat area of the nozzle, and γ is the specific heat ratio of the gas.
On the basis of fluid dynamics (Semushin & Malka, Reference Semushin and Malka2001), the angle α is obtained from the expression
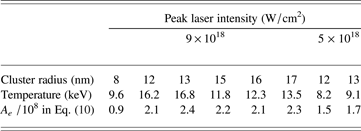
$$\sin{\rm \alpha}={1 \over M}.$$From these formulas, it is possible to estimate the cluster radius. In our experiment, Φ = 500 µm and T 0 = 297 K. The ratio of the output area to the throat area of the nozzle, A/A*, is 4, and we assume that the flow of the Xe clusters is supersonic. Cluster radii estimated from Eqs. (3)–(6) are shown in Table 1. The cluster radius is larger than 10 nm for pressures exceeding 2 × 104 mbar.
Table 1. Xe cluster size produced by conical nozzle
4. RESULTS AND DISCUSSION
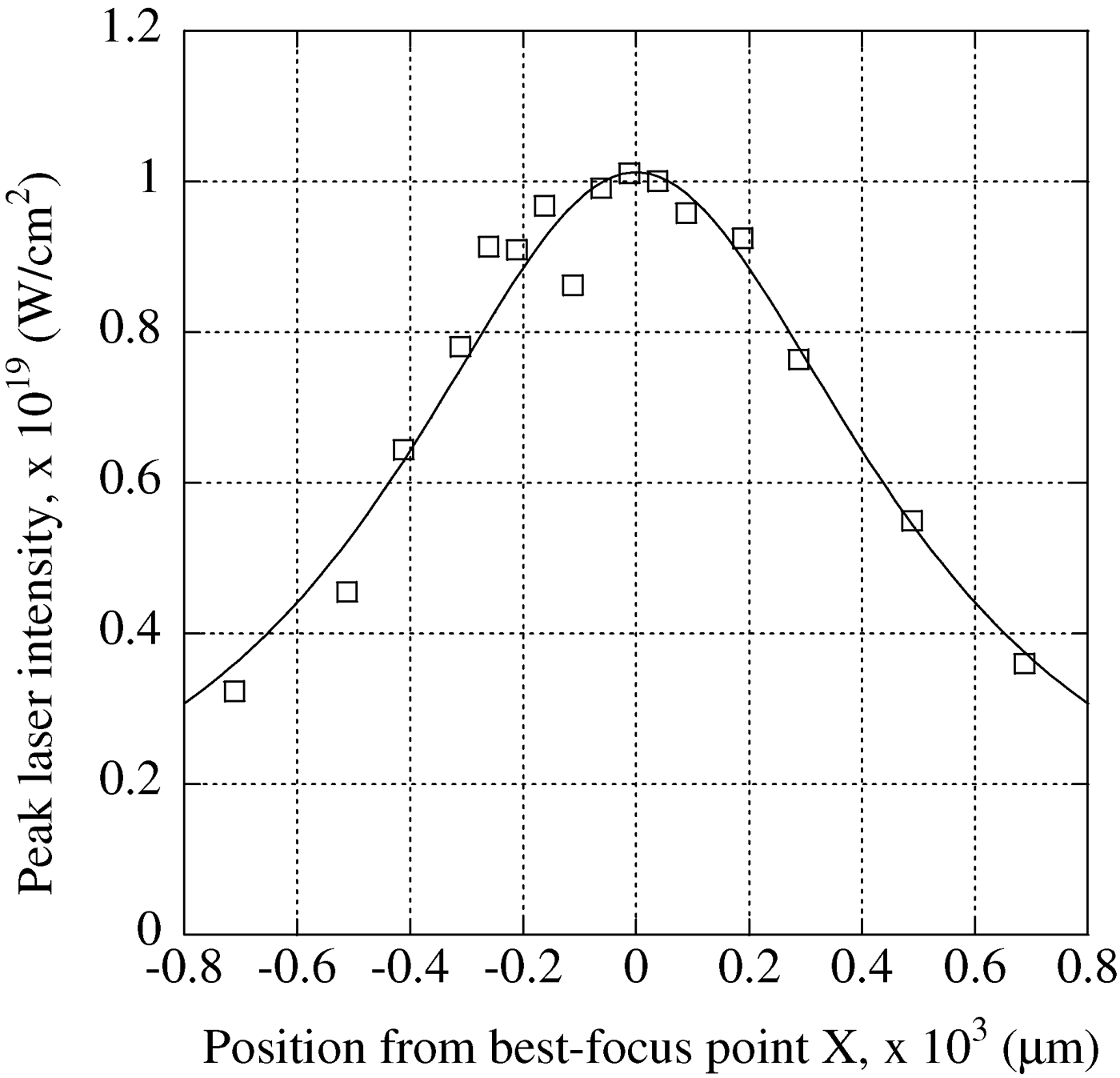
We first placed the nozzle 250 µm from the best-focus point in the laser propagation direction. Figure 2 shows the relationship between the peak laser intensity I and the position X from the best-focus point in μm. The peak laser intensity is estimated from the measured laser beam profile, laser energy, and laser pulse duration. Usually, the peak laser intensity I is found by (ISO, 2005)
$$I=\displaystyle{{2 \cdot P} \over {{\rm \pi} \cdot \Delta t}} \cdot \mathop {\left[{w^2+M^2 \times \mathop {\left({\displaystyle{{{\rm \lambda} \cdot X} \over {{\rm \pi} \cdot w}}} \right)}\nolimits^2 } \right]}\nolimits^{ - 1} \; \comma \;$$where P is the laser energy, Δt is the FWHM pulse duration of the laser, w is a value corresponding to the focal spot size, λ is the laser wavelength, and M 2 is the beam quality factor.
Fig. 2. Peak laser intensity dependence on position from best-focus point. Squares: data; solid line: fitted curve.
By fitting Eq. (7) to the measured results in Figure 2, the peak laser intensity at 250 µm from the best-focus point is found to be 9 × 1018 W/cm2. The experiment was carried out at a Xe gas backing pressure of 1.1 × 104–4 × 104 mbar. The cluster radius was found to be 8–17 nm, as shown in Table 1.
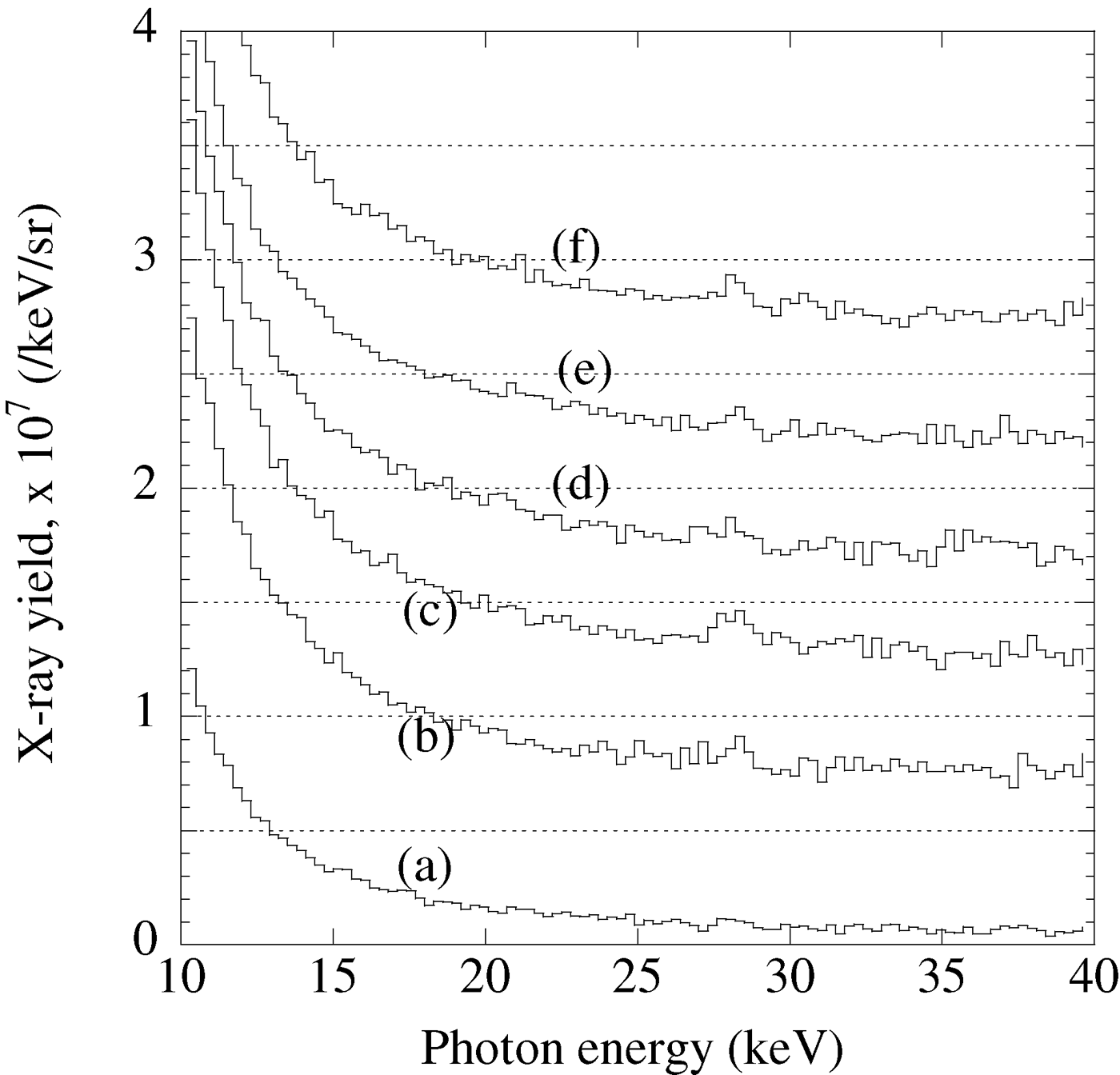
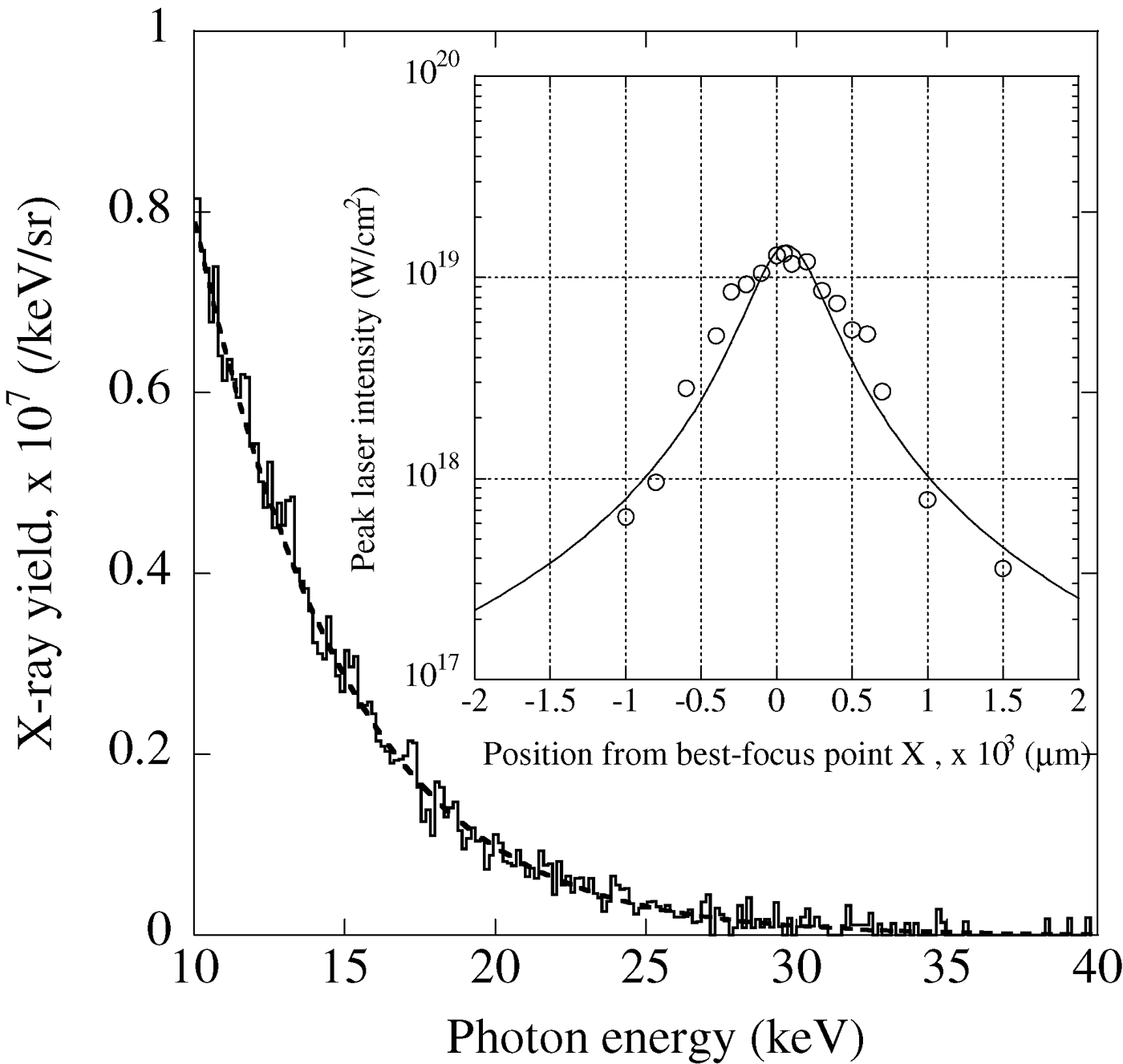
X-ray energy spectra averaged over 25 laser shots are shown in Figure 3. X-ray photon numbers at the source point are calculated by using the transmittance of the aluminum filter and the quantum efficiency of the CCD.
Fig. 3. Energy spectra for cluster radii R Cl at peak laser intensity of 9 × 1018 W/cm2. (a) R Cl = 8 nm; (b) R Cl =12 nm; (c) R Cl =13 nm; (d) R Cl = 15 nm; (e) R Cl = 16 nm; (f) R Cl = 17 nm.
A peak with an energy of approximately 28.5 keV can be observed. We attribute this peak to the Xe K-shell X-ray, which is generated from the Xe K-shell upon excitation and ionization by the laser plasma electrons. The peak energy is slightly lower than the real energy of the Xe Kα X-ray. Since a lower energy X-ray source (Fe55: 5.9 keV) was utilized for the energy calibration of the CCD, the peak energy was slightly underestimated. The broad energy spectrum from 10 to 40 keV is due to the bremsstrahlung X-ray.
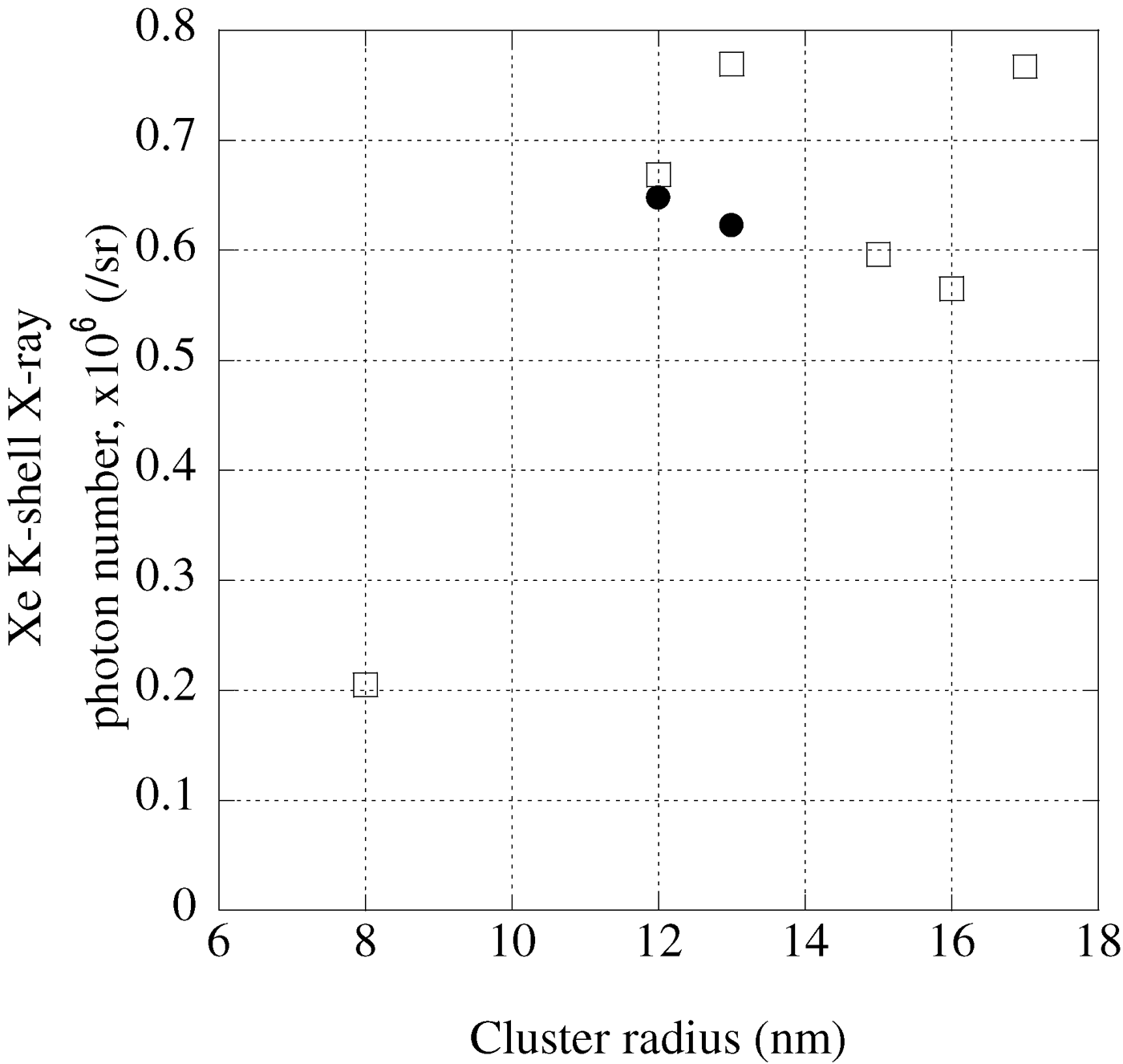
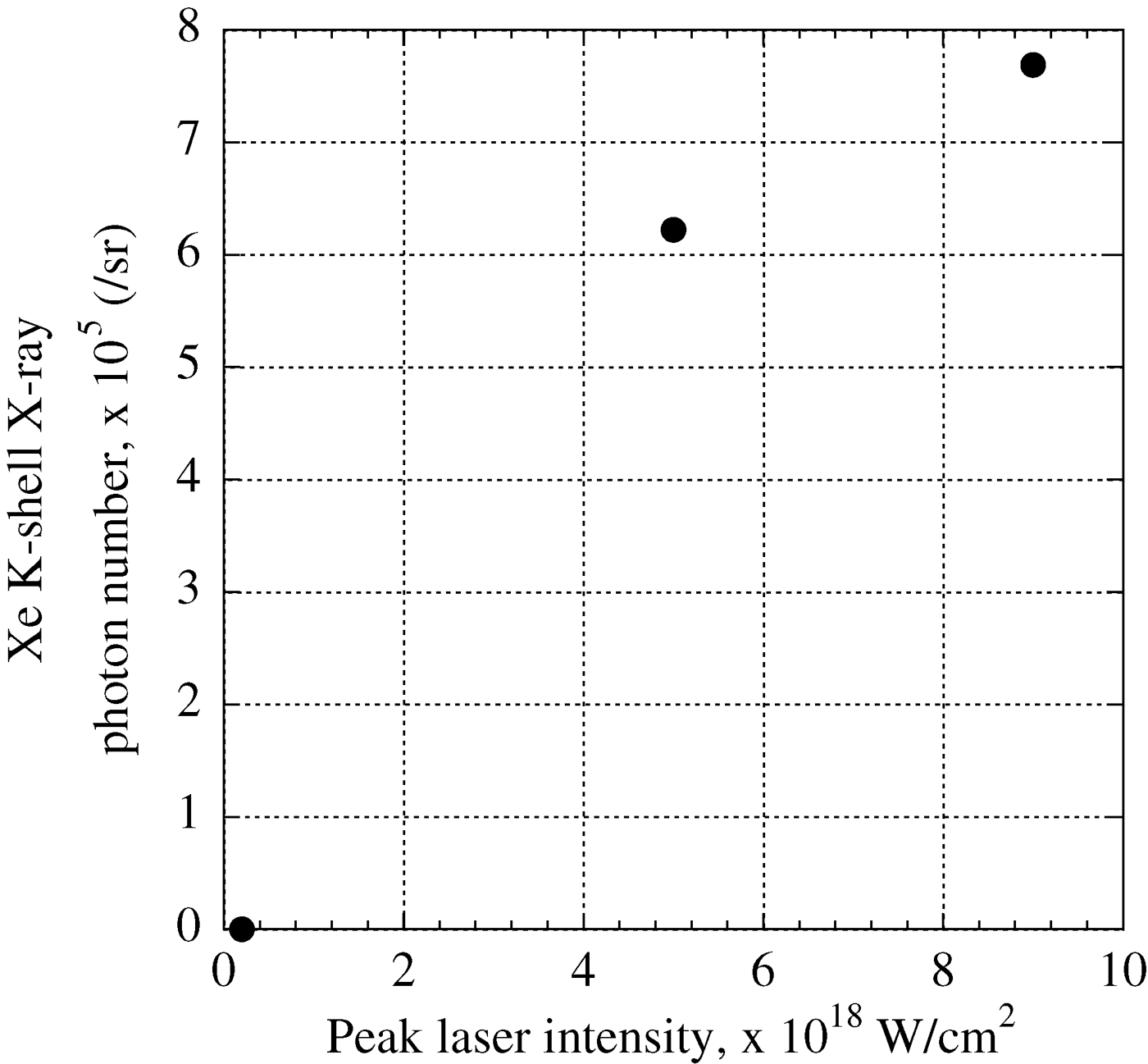
The Xe K-shell X-ray photon number is calculated by subtracting the background counts from the integrated counts from 28.2 keV to 28.8 keV and is summarized in Figure 4. As the cluster radius increases from 8 to 12 nm, the Xe K-shell X-ray photon number increases from 2 × 105 to 6.7 × 105 photons/sr. Then, the photon number becomes saturated at around 7 × 105 photons/sr, when the cluster radius increases from 12 to 17 nm.
Fig. 4. Xe K-shell X-ray photon numbers and cluster radii. Squares: 9 × 1018 W/cm2; closed circles: 5 × 1018 W/cm2.
A similar cluster radius dependence was found for Ar K-shell X-ray generation simulated by Deiss (Reference Deiss2009). Laser-cluster interaction was simulated with a mean-field classical transport approach. The Ar K-shell X-ray photon number increases sharply with increasing cluster radius, and saturates at the radius of 10 nm order. Then the photon number gradually decreases upon further increase of the radius.
We consider that skin depth is one of the reasons for the above-described behavior. The skin depth δ is the distance that the laser can penetrate into the overdense plasma and is estimated (Milosavljevic & Nakar, Reference Milosavljevic and Naker2006)
$${\rm \delta}=\displaystyle{{c\sqrt {\rm \gamma} } \over {{\rm \omega} _p }}=5.31 \times 10^5 \sqrt {\displaystyle{{\rm \gamma} \over {n_e [{\rm cm}^{ - 3}] }}} \quad [{\rm cm}] \comma \;$$
$${\rm \gamma}=\sqrt {1+3.613 \times 10^{ - 19} I [{\rm W}/{\rm cm}^2] {\rm \lambda} ^2 [{\rm \mu} {\rm m}^2] }\comma \;$$where c is the light speed, ωp is the plasma frequency, n e is the electron density in cm−3, γ is the Lorentz factor, I is the peak laser intensity, and λ is laser wavelength. When the electron density n e of 3.5 × 1023 cm−3 is assumed in our experiment, the skin depth is estimated as 12 nm. Therefore, the energy absorption rate of the cluster increases with increasing radius up to the skin depth of 12 nm.
When K-shell electrons are excited or ionized, K-shell X-rays are emitted by the recombination of the K-shell. Excitation or ionization of K-shell electrons occurs when the electron energy is higher than the K-shell excitation energy or ionization potential. The ionization potential and excitation energy of the Xe K-shell are 40 and 35 keV, respectively. For this reason, electrons with energy exceeding 35 keV are required for Xe K-shell X-ray generation. The distribution function of the bremsstrahlung X-ray spectrum f is known to be related to electron temperature T e (McCall, Reference McCall1982; Issac et al., Reference Issac, Vieux, Ersfeld, Brunetti, Jamison, Gallacher, Clark and Jaroszynski2004):
$$\,f\lpar E\rpar =\displaystyle{{A_e } \over {\mathop {T_e }\nolimits^{1.5} }} \cdot \sqrt E \cdot \exp\lpar {-} E/T_e \rpar \; \comma \;$$where E is the photon energy, A e is the factor depending on the X-ray photon number, and T e is the electron temperature.
By fitting Eq. (10) to the bremsstrahlung X-ray spectra, high electron temperatures T e of 11.8–16.2 keV and A e of (2.1–2.4) × 108 are obtained for cluster radii of 12–17 nm (see Table 2). At the cluster radius of 8 nm, T e and A e are reduced to 9.6 keV and 0.9 × 108, respectively. The lower X-ray photon number at the cluster radius of 8 nm is due to the decrement of A e and T e.
Table 2. Parameters of X-ray energy spectrum under each condition
When the nozzle position was moved 500 µm from the position of best-focus in the laser propagation direction, the peak laser intensity on the target was 5 × 1018 W/cm2 (see Fig. 2). Figure 5 shows energy spectra averaged over 25 laser shots for the cluster radii of 12 and 13 nm. The energy spectra are similar to each other, and the peak of the Xe K-shell X-ray is observed in both cases. The high electron temperatures and values of A e are 8.2 keV and 1.5 × 108, and 9.1 keV and 1.7 × 108 for the cluster radii of 12 and 13 nm, respectively. These temperatures are slightly lower than that at a peak laser intensity of 9 × 1018 W/cm2. The Xe K-shell X-ray photon number is 6.5 × 105 photons/sr for the cluster radius of 12 nm and 6.2 × 105 photons/sr for the radius of 13 nm (see Fig. 4).
Fig. 5. Energy spectra at peak laser intensity of 5 × 1018 W/cm2.
To confirm the dependence of the Xe K-shell X-ray photon number on the peak laser intensity, the cluster nozzle was moved 2 mm from the best-focus point. Figure 6a indicates the peak laser intensity at the position from the best-focus point in this measurement. From the fitted curve in Figure 6a, the peak laser intensity is found to be 2 × 1017 W/cm2. The average energy spectrum of 50 laser shots for cluster radius of 13 nm is shown in Figure 6b. The X-ray photon number decreases sharply with increasing photon energy. The electron temperature T e is clearly lower than those in the cases of Figures 3 and 5, and T e of 4.1 keV is obtained. Almost no photons are measured around the energy of 30 keV, and no peak of the Xe K-shell X-ray is observed. Since the electron temperature is too low, most of the plasma electrons do not have sufficient energies to excite the Xe K-shell electrons.
Fig. 6. (a) Peak laser intensity dependence on position from best-focus point. Circles: measured value; solid line: fitted curve. (b) Energy spectrum at peak laser intensity of 2 × 1017 W/cm2 for cluster radius of 13 nm (solid line) and fitted curve (broken line).
It is also interesting to discuss the Xe K-shell X-ray photon number dependence on peak laser intensity. Figure 7 indicates the dependence for the Xe cluster radius of 13 nm. When the peak laser intensity is reduced from 9 × 1018 to 5 × 1018 W/cm2, the photon number shows slight change. However, when the laser intensity is reduced to 2 × 1017 W/cm2, the X-ray photon number decreases to the background noise level of the CCD. From the figure, it was found that the threshold laser intensity of the Xe K-shell X-ray generation exists between 2 × 1017 and 5 × 1018 W/cm2.
Fig. 7. Dependence of Xe K-shell X-ray photon number on peak laser intensity for cluster radius of 13 nm.
In order to generate a high K-shell X-ray photon number, it is important to understand the mechanism of K-shell X-ray generation. In this part, we discuss the mechanism of K-shell X-ray generation. Issac et al. (Reference Issac, Vieux, Ersfeld, Brunetti, Jamison, Gallacher, Clark and Jaroszynski2004) simulated the Kr K-shell X-ray generation using the nanoplasmas model. In the model, it is assumed that plasma electrons inside clusters are heated by inverse bremsstrahlung (Ditmire et al., Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996). However, they have reported that the model explains only the production of electrons with a temperature of 2 keV, which is too low for Kr K-shell X-ray generation.
Another interpretation is that the high energy electrons production is due to the electron oscillation energy by the laser: ponderomotive potential U p. Hence, we assume that plasmas electrons have energies equal to the ponderomotive potential U p. U p is given as 9.3 × 10−14I·λ2 in eV by using the laser intensity I in W/cm2 and laser wavelength λ in μm. The results can be seen in Table 3. Threshold laser intensities for K-shell X-ray generation are estimated under the condition that the energy of plasma electrons U p is equal to the binding energy I e. Two experimental results are also shown in the table. One experimental result indicates that the laser intensity of 2.9 × 1015 W/cm2 is a threshold for Ar K-shell X-ray production with a 56 fs laser pulse width (Prigent et al., Reference Prigent, Deiss, Lamour, Rozet, Vernhet and Burgdorfer2008). The other result describes that the Kr K-shell X-ray is observed at the intensity of 2 × 1016 W/cm2 (Issac et al., Reference Issac, Vieux, Ersfeld, Brunetti, Jamison, Gallacher, Clark and Jaroszynski2004). The laser intensities measured in the experiments are less than one-tenth of the intensities assumed from the binding energy I e (see Table 3). This inconsistency suggests that different mechanisms are essential in X-ray generation.
Table 3. Threshold laser intensity of K-shell X-ray generation
The threshold laser intensity for Ar K-shell X-ray generation was simulated by a mean-field classical transport approach by Deiss and coworkers (Deiss, Reference Deiss2009; Prigent et al., Reference Prigent, Deiss, Lamour, Rozet, Vernhet and Burgdorfer2008), who found that an optimum cluster radius was of 10 nm order for Ar K-shell X-ray generation. The threshold intensity of 2 × 1015 W/cm2 was obtained by the simulation, and it is close to the 2.9 × 1015 W/cm2 observed experimentally, as shown in Table 3. Unfortunately, Kr and Xe K-shell X-ray generation were not simulated by this approach. We anticipate that this approach will clarify the mechanism of Kr and Xe K-shell K-shell X-ray generation by laser-cluster interaction.
5. CONCLUSION
Although the cluster size is one of the key parameters in Xe K-shell X-ray generation, its effect had not been previously investigated. The optimal cluster size for Xe K-shell X-ray generation was investigated by focusing 25 TW, 40 fs laser pulses onto Xe clusters produced by a supersonic conical nozzle. The cluster size was controlled by adjusting the backing pressure of the nozzle. We found that the Xe K-shell X-ray photon number increases with increasing cluster radius from 8 to 12 nm, and then saturates at cluster radii between 12 and 17 nm. This result is similar to the result obtained by Deiss (Reference Deiss2009) that an Ar cluster radius on the order of 10 nm is optimum for Ar K-shell X-ray generation.
The laser intensity dependence of the Xe K-shell X-ray photon number was also studied, and it was found that the threshold laser intensity of the Xe K-shell X-ray generation exists between 2 × 1017 and 5 × 1018 W/cm2.
In the near future, Xe K-shell X-ray sources are expected to be utilized for angiography, which is a medical imaging technique used to visualize blood vessels and organs in the body. Conventionally, iodine is doped as the angiographic contrast agent; and the energy of the iodine K-shell absorption edge is slightly higher than the energy of Xe Kα X-rays and slightly lower than that of Xe Kβ X-rays. The iodine absorption efficiency of Xe Kα X-rays is significantly different from that of Xe Kβ X-rays. Therefore, we believe that this difference in the iodine absorption efficiency of these X-rays makes them suitable for application to angiography.
ACKNOWLEDGMENTS
We thank Professors K. Yamada, Y. Masumoto, Y. Tokura, and K. Shiraishi at the University of Tsukuba, and M. Mori at JAEA for help and many useful discussions. We also thank T. Shimomura, Y. Nakai, M. Tanoue, M. Okamoto, S. Kanazawa, and S. Kondo at JAEA for operation of the J-KAREN laser.
