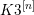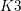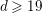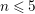1 Introduction
The aim of this note is to provide a classification of non-symplectic involutions on irreducible holomorphic symplectic (IHS) manifolds of 
$K3^{[n]}$-type, thus generalizing to all even dimensions the classification which is already known for 
$n=1$ by a foundational work of Nikulin [Reference Nikulin33] on K3 surfaces and for 
$n=2$ by the work of Beauville [Reference Beauville5] and of Boissière, the first author, and Sarti [Reference Boissière, Camere and Sarti6]. The core of the classification result contained in this work comes from Joumaah’s Ph.D thesis [Reference Joumaah22], but he kindly decided to let us publish by ourselves. On the other hand, the proof of one of the main results in [Reference Joumaah22] is not entirely correct, so in this paper, we prove a revised statement (Proposition 2.8) in order to obtain the correct classification of non-symplectic involutions on manifolds of 
$K3^{[n]}$-type.
In the first two authors’ work [Reference Camere and Cattaneo11], the interested reader can find the analogue classification for non-symplectic automorphisms of odd prime order. Although the lattice-theoretical techniques used here are similar and rely on Nikulin’s work [Reference Nikulin31], the prime 
$p=2$ is somewhat different from the other primes because for 
$n\geqslant 2$, it always divides 
$2(n-1)$, which is the discriminant of 
$L_{n}:=U^{\oplus 3}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$, that is, the second integral cohomology group of any manifold of 
$K3^{[n]}$-type equipped with the Beauville–Bogomolov–Fujiki quadratic form.
Concerning involutions, in [Reference Cattaneo13], the second author computed the automorphism group of the Hilbert scheme of 
$n$ points over a generic projective 
$K3$ surface, showing that this group (if not trivial) is generated by exactly one nonnatural and non-symplectic involution (for 
$n=2$, this had already been proved by Boissière, the third author, Nieper-Wisskirchen, and Sarti [Reference Boissière, Cattaneo, Nieper-Wisskirchen and Sarti8]). The present paper also provides an extension of these results, as we allow the pair consisting of a Hilbert scheme and its involution to be deformed.
1.1 IHS manifolds and automorphisms
We recall that an IHS manifold is a compact complex Kähler manifold 
$X$ which is simply connected and such that 
$H^{2,0}(X)$ is generated by the class of a single holomorphic symplectic (i.e. everywhere nondegenerate) 
$2$-form. Basic examples of IHS manifolds are provided by 
$K3$ surfaces and, in dimension 
$2n$, by the Hilbert scheme of zero-dimensional subschemes of length 
$n$ of a 
$K3$ surface. As small deformations of IHS manifolds are still IHS, we can then produce new examples: we say that an IHS manifold is of 
$K3^{[n]}$-type if it is deformation equivalent to the Hilbert scheme of 
$n$ points on a 
$K3$ surface. Even though, in this paper, we focus mainly on the case of manifolds of 
$K3^{[n]}$-type, some of the results of Section 2.1 hold also for other deformation classes of IHS manifolds. We say that an IHS manifold is of Kummer type if it is deformation equivalent to a generalized Kummer manifold (see [Reference Beauville4, Section 7] for the definition), while it is of 
$\text{OG}10$-type if it is deformation equivalent to the 
$10$-dimensional IHS manifold constructed by O’Grady in [Reference O’Grady34].
The deformation theory of IHS manifolds is sufficiently well understood. For any manifold 
$X$ of 
$K3^{[n]}$-type, a marking is a lattice isometry 
$\unicode[STIX]{x1D702}:H^{2}(X,\mathbb{Z})\longrightarrow L_{n}$, where we recall that 
$H^{2}(X,\mathbb{Z})$ is a lattice by means of the Beauville–Bogomolov–Fujiki quadratic form (see [Reference Beauville4, Section 8]). Then, there exists a well-defined compact complex moduli space which parametrizes marked IHS manifolds of 
$K3^{[n]}$-type. A fundamental result, due to the work by Huybrechts, Markman, and Verbitsky, is the global Torelli theorem [Reference Verbitsky40, Corollary 1.20], which describes the fibers of the period map associated with this moduli space.
The use of markings allows us to transfer most of the questions about automorphisms to a purely algebraic setting, involving lattices and their properties. However, we need to determine which of the isometries of the abstract lattice 
$L_{n}$ correspond, via the marking, to automorphisms of the IHS manifold. To this end, we will make use of Markman’s version of the Torelli theorem [Reference Markman25, Theorem 1.3].
1.2 Structure of the paper and main results
Our study of involutions on manifolds of 
$K3^{[n]}$-type will be conducted in two steps. In Section 2, we study the problem only from a lattice-theoretical point of view: our aim is to classify the possible discriminant groups of pairs 
$T,S\subset L_{n}$ consisting of the invariant lattice 
$T$ and the coinvariant lattice 
$S$ of a non-symplectic involution. We provide this classification in Proposition 2.8, fixing the inaccuracies of [Reference Joumaah22]. An important ingredient of our proof is the fact that either the invariant or the coinvariant lattice is 
$2$-elementary (Corollary 2.4): we prove this in a more general setting, for involutions of IHS manifolds which act as 
$\pm \operatorname{id}$ on the discriminant group of the second cohomology lattice, and we remark that this holds for all involutions of manifolds of 
$K3^{[n]}$-type, Kummer type, or OG
$10$-type.
In Section 3, by using the global Torelli theorem, we prove that the conditions determined in Section 2 on the abstract lattices 
$T,S$ are also sufficient to obtain a marked manifold of 
$K3^{[n]}$-type with a non-symplectic involution, having 
$T$ and 
$S$ as invariant and coinvariant lattice, respectively.
Theorem. [Theorem 3.3] Let 
$\unicode[STIX]{x1D70C}\in O(L_{n})$ be an involution whose invariant lattice 
$T$ is hyperbolic. Assume also that the action of 
$\unicode[STIX]{x1D70C}$ on 
$A_{L}$ is either 
$\operatorname{id}$ or 
$-\text{id}$. Then there exists a marked manifold 
$(X,\unicode[STIX]{x1D702})$ of 
$K3^{[n]}$-type with a non-symplectic involution 
$i\in \operatorname{Aut}(X)$ such that 
$\unicode[STIX]{x1D702}\circ i^{\ast }=\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D702}$.
In Section 4, we focus on the cases where the invariant lattice has small rank, that is, 
$\operatorname{rk}(T)=1$ or 
$2$. For 
$2\leqslant n\leqslant 5$, we explicitly classify the isometry classes of the pairs of lattices 
$T,S$ (Propositions 4.3, 4.5, and 4.6). Non-symplectic involutions of manifolds of 
$K3^{[n]}$-type having invariant lattice of small rank are particularly interesting since they deform in families of large dimensions. For each possible action on cohomology 
$\unicode[STIX]{x1D70C}\in O(L_{n})$ in our classification, we study the corresponding moduli space 
${\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}$ of 
$(\unicode[STIX]{x1D70C},T)$-polarized manifolds of 
$K3^{[n]}$-type with a non-symplectic involution.
Theorem. [Theorem 4.12] Let 
$(X,\unicode[STIX]{x1D702})$ be a marked manifold of 
$K3^{[n]}$-type for 
$2\leqslant n\leqslant 5$, and let 
$i\in \operatorname{Aut}(X)$ be a non-symplectic involution such that the pair 
$(X,i)$ deforms in a family of dimension 
$d\geqslant 19$ (i.e. 
$rk(T)\leqslant 2$). Then 
$(X,\unicode[STIX]{x1D702})$ belongs to the closure (as a complex space) of one of the following moduli spaces:
$n=2$:- ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a}}$ or ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$
- $n=3$:
- ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a}}$, ${\mathcal{M}}_{\langle 4\rangle ,\unicode[STIX]{x1D70C}}$ or ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$
- $n=4$:
- ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a}}$, ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{b}}$ or ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$
- $n=5$:
- ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a}}$, ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$ or ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{2}}$
where 
$\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}_{a},\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2}$ are defined in Section 4.2.
All these moduli spaces are irreducible with the exception of 
${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{2}}$ for 
$n=5$, which has three distinct irreducible components.
Finally, in Section 5, we use moduli spaces of twisted sheaves on 
$K3$ surfaces to describe the generic element in the maximal moduli spaces 
${\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}$ of dimension 
$19$ (Propositions 5.1 and 5.3), and we show that in one case, the involution is induced by a non-symplectic involution of the underlying 
$K3$ surface. Finding an explicit description of the automorphism in the other families is still an open problem.
1.3 Notations and conventions
Throughout the paper, all the varieties will be defined over the field 
$\mathbb{C}$ of complex numbers.
A lattice is a free abelian group 
$M$ equipped with a symmetric nondegenerate bilinear form 
$(\cdot ,\cdot ):M\times M\rightarrow \mathbb{Z}$. Its discriminant group 
$A_{M}$ is defined as 
$A_{M}=M^{\vee }/M$, where 
$M^{\vee }=\operatorname{Hom}_{\mathbb{Z}}(M,\mathbb{Z})$ is the dual lattice of 
$M$. The length of the lattice 
$M$ is defined as the minimal number of generators of 
$A_{M}$ and it is smaller or equal than 
$\operatorname{rk}(M)$. We say that a lattice 
$M$ is hyperbolic if its signature is 
$(1,r)$ for some 
$r\geqslant 0$ (in particular, positive definite lattices of rank one are also considered to be hyperbolic, for the purposes of this work).
A lattice 
$M$ is even if 
$(m,m)\in 2\mathbb{Z}$ for all 
$m\in M$. For an even lattice 
$M$, if 
$A_{M}$ is cyclic of order 
$m$, we write 
$A_{M}\cong \frac{\mathbb{Z}}{m\mathbb{Z}}(\unicode[STIX]{x1D6FC})$ if the finite quadratic form 
$q_{M}:A_{M}\rightarrow \mathbb{Q}/2\mathbb{Z}$ (induced by the quadratic form on 
$M$) takes value 
$\unicode[STIX]{x1D6FC}$ on a generator of 
$A_{M}$. We will denote by 
$u_{2}:(\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus 2}\rightarrow \mathbb{Q}/2\mathbb{Z}$ the finite quadratic form associated with the finite bilinear form 
$\Big(\!\begin{smallmatrix}0 & \frac{1}{2}\\ \frac{1}{2} & 0\end{smallmatrix}\!\Big)$.
For any positive integer 
$n\geqslant 2$, we define
$$\begin{eqnarray}L_{n}:=U^{\oplus 3}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle ,\end{eqnarray}$$ where 
$U$ is the hyperbolic plane, 
$E_{8}$ is the unique unimodular lattice of signature 
$(0,8)$, and for any integer 
$t\neq 0$, we denote by 
$\langle t\rangle$ the lattice generated by an element 
$\unicode[STIX]{x1D6FF}$ with 
$(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF})=t$.
For a pair of lattices 
$M$, 
$N$, there may be several nonisometric embeddings of 
$M$ into 
$N$. When we say that 
$M$ is embedded in 
$N$, writing 
$M\subset N$, we always mean that an embedding 
$j:M{\hookrightarrow}N$ has been fixed. We will consider two such embeddings 
$j,j^{\prime }$ as being isomorphic if there exist isometries 
$\unicode[STIX]{x1D713}\in O(M)$ and 
$\unicode[STIX]{x1D711}\in O(N)$ such that 
$j\circ \unicode[STIX]{x1D713}=\unicode[STIX]{x1D711}\circ j^{\prime }$. The images 
$j(M)$, 
$j^{\prime }(M)$ inside 
$N$ are also called isomorphic sublattices following [Reference Nikulin31, Section 1.5].
2 Involutions of the lattice $L_{n}$
2.1 Invariant and coinvariant lattices
Let 
$(X,i)$ be a pair consisting of an IHS manifold 
$X$ of 
$K3^{[n]}$-type and an involution 
$i\in \operatorname{Aut}(X)$. The lattice 
$H^{2}(X,\mathbb{Z})$ is isometric to 
$L_{n}=U^{\oplus 3}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$, as we already recalled, and 
$i^{\ast }\in \operatorname{Mon}^{2}(X)$, which is the subgroup of monodromy operators inside 
$O(H^{2}(X,\mathbb{Z}))$. We now fix 
$n\geqslant 2$ and we write 
$L:=L_{n}$ for the sake of simplicity.
We have a primitive embedding 
$L{\hookrightarrow}M$ where 
$M:=U^{\oplus 4}\oplus E_{8}^{\oplus 2}$ is the Mukai lattice, unimodular of rank 
$24$. Observe that, if we call 
$\unicode[STIX]{x1D6FF}$ a generator of 
$\langle -2(n-1)\rangle$ in 
$L$, then 
$A_{L}$ is generated by 
$\frac{1}{2(n-1)}\unicode[STIX]{x1D6FF}$, that is,
$$\begin{eqnarray}A_{L}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(-\frac{1}{2(n-1)}\biggr).\end{eqnarray}$$ We denote by 
$L^{\bot }$ the orthogonal complement of 
$L$ inside 
$M$, whose discriminant group is
$$\begin{eqnarray}A_{L^{\bot }}\cong \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(\frac{1}{2(n-1)}\biggr).\end{eqnarray}$$ Since 
$L^{\bot }\subset M$ has rank one, we deduce that 
$L^{\bot }\cong \langle 2(n-1)\rangle$.
After choosing a marking (i.e. an isometry) 
$\unicode[STIX]{x1D702}:H^{2}(X,\mathbb{Z})\rightarrow L$, we can consider the action 
$i^{\ast }\in O(L)$. By [Reference Markman25, Lemma 9.2], 
$i^{\ast }$ satisfies the following properties: it has spin norm equal to 
$1$ (equivalently, it is orientation preserving) and it acts either as 
$\operatorname{id}$ or as 
$-\text{id}$ on the discriminant group 
$A_{L}$. This means that one between 
$i^{\ast }$ and 
$-i^{\ast }$ belongs to 
$\widetilde{O}(L)$, where for any lattice 
$\unicode[STIX]{x1D6EC}$, the stable orthogonal group 
$\widetilde{O}(\unicode[STIX]{x1D6EC})$ is the subgroup of 
$O(\unicode[STIX]{x1D6EC})$ consisting of isometries that induce the identity on the discriminant group 
$A_{\unicode[STIX]{x1D6EC}}$.
The invariant lattice of the involution 
$i\in \operatorname{Aut}(X)$ is the sublattice 
$H^{2}(X,\mathbb{Z})^{i^{\ast }}\subset H^{2}(X,\mathbb{Z})$ of elements that are fixed by 
$i^{\ast }$. Its orthogonal complement in 
$H^{2}(X,\mathbb{Z})$ is called the coinvariant lattice. Both these sublattices are primitive; if the involution 
$i$ is non-symplectic, then 
$H^{2}(X,\mathbb{Z})^{i^{\ast }}$ is hyperbolic (possibly positive definite of rank one), while the coinvariant lattice has signature 
$(2,\ast )$ (see, for instance, [Reference Boissière, Nieper-Wißkirchen and Sarti9, Section 5]).
Proposition 2.1. Let 
$\unicode[STIX]{x1D6EC}$ be an even lattice and 
$\unicode[STIX]{x1D70C}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$ be an involution. Then
$\unicode[STIX]{x1D6EC}^{-\unicode[STIX]{x1D70C}}=(\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}})^{\bot }$ is 
$2$-elementary.
Proof. If 
$x\in \unicode[STIX]{x1D6EC}^{-\unicode[STIX]{x1D70C}}$, then for any 
$y\in \unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}$, we have 
$(x,y)=(\unicode[STIX]{x1D70C}(x),\unicode[STIX]{x1D70C}(y))=-(x,y)$; hence, 
$\unicode[STIX]{x1D6EC}^{-\unicode[STIX]{x1D70C}}\subset (\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}})^{\bot }$. Vice versa, if 
$x\in (\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}})^{\bot }$, then 
$x+\unicode[STIX]{x1D70C}(x)$ is orthogonal to any element inside the finite-index sublattice 
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}\oplus (\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}})^{\bot }\subset \unicode[STIX]{x1D6EC}$; hence, 
$\unicode[STIX]{x1D70C}(x)=-x$ since the quadratic form on 
$\unicode[STIX]{x1D6EC}$ is nondegenerate. Note that 
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}=\ker (\unicode[STIX]{x1D70C}-\operatorname{id})$ and 
$(\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}})^{\bot }=\ker (\unicode[STIX]{x1D70C}+\operatorname{id})$ are primitive sublattices of 
$\unicode[STIX]{x1D6EC}$, as kernels of module homomorphisms.
By [Reference Nikulin31, Theorem 1.1.2], there exists a primitive embedding 
$\unicode[STIX]{x1D6EC}{\hookrightarrow}V$, for some even unimodular lattice 
$V$, and by [Reference Gritsenko, Hulek and Sankaran18, Lemma 7.1], we can extend 
$\unicode[STIX]{x1D70C}$ to an isometry 
$\unicode[STIX]{x1D70F}\in \widetilde{O}(V)$ such that:
(1)
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}\subset V^{\unicode[STIX]{x1D70F}}$;(2)
$\unicode[STIX]{x1D6EC}^{-\unicode[STIX]{x1D70C}}\subset V^{-\unicode[STIX]{x1D70F}}$;(3)
$\unicode[STIX]{x1D6EC}^{\bot }\subset V^{\unicode[STIX]{x1D70F}}$.
As a consequence, 
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}\oplus \unicode[STIX]{x1D6EC}^{\bot }\subset V^{\unicode[STIX]{x1D70F}}$ is a finite-index sublattice and moreover, inside the lattice 
$V$:
$$\begin{eqnarray}V^{-\unicode[STIX]{x1D70F}}=(V^{\unicode[STIX]{x1D70F}})^{\bot }\subset (\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}\oplus \unicode[STIX]{x1D6EC}^{\bot })^{\bot }=(\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}})^{\bot }\cap \unicode[STIX]{x1D6EC}\subset \unicode[STIX]{x1D6EC}.\end{eqnarray}$$ Hence, 
$\unicode[STIX]{x1D6EC}^{-\unicode[STIX]{x1D70C}}=V^{-\unicode[STIX]{x1D70F}}$. The invariant and coinvariant lattices of an involution of an even unimodular lattice are 
$2$-elementary by [Reference Gritsenko, Hulek and Sankaran16, Lemma 3.5]: this concludes the proof.◻
With the same notation used above, we remark the following facts.
(1) The lattice
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}$ is primitively embedded in $V^{\unicode[STIX]{x1D70F}}$.(2) The lattice
$\unicode[STIX]{x1D6EC}^{\bot }$ is primitively embedded in $V^{\unicode[STIX]{x1D70F}}$.(3) The lattices
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}$ and $\unicode[STIX]{x1D6EC}^{\bot }$ are the orthogonal complement of each other in $V^{\unicode[STIX]{x1D70F}}$.
(1) As
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}\subset \unicode[STIX]{x1D6EC}$ and $\unicode[STIX]{x1D6EC}\subset V$ are primitive, we deduce that $\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}\subset V$ is primitive. The claim follows then from the inclusion $\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}\subset V^{\unicode[STIX]{x1D70F}}$.(2) This follows from the fact that
$\unicode[STIX]{x1D6EC}^{\bot }\subset V$ is primitive and $\unicode[STIX]{x1D6EC}^{\bot }\subset V^{\unicode[STIX]{x1D70F}}\subset V$.(3) Since
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}}$ and $\unicode[STIX]{x1D6EC}^{\bot }$ are orthogonal in $V$, we deduce that $\unicode[STIX]{x1D6EC}^{\bot }\subset (\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}})^{\bot _{V^{\unicode[STIX]{x1D70F}}}}$. Moreover, both $\unicode[STIX]{x1D6EC}^{\bot }$ and $(\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D70C}})^{\bot _{V^{\unicode[STIX]{x1D70F}}}}$ are primitive sublattices of $V^{\unicode[STIX]{x1D70F}}$: since they have the same rank, they must coincide. ◻
Proposition 2.1 gives as corollaries some results already observed in the literature about involutions of IHS manifolds, such as [Reference Mongardi, Tari and Wandel30, Sections 3.1, 3.2] about involutions of generalized Kummer manifolds and [Reference Mongardi29, Corollary 5.1] about symplectic involutions of manifolds of 
$K3^{[n]}$-type. We also obtain some new, to our knowledge, corollaries.
Corollary 2.3. Let 
$X$ be any IHS manifold such that the lattice 
$H^{2}(X,\mathbb{Z})$ is even and let 
$i\in \operatorname{Aut}(X)$ be an involution. Then:
(1) if
$i^{\ast }$ acts as $\operatorname{id}$ on the discriminant group of $H^{2}(X,\mathbb{Z})$, the sublattice $H^{2}(X,\mathbb{Z})^{-i^{\ast }}$ is $2$-elementary;(2) if
$i^{\ast }$ acts as $-\text{id}$ on the discriminant group of $H^{2}(X,\mathbb{Z})$, the sublattice $H^{2}(X,\mathbb{Z})^{i^{\ast }}$ is $2$-elementary.
Proof. If 
$i^{\ast }\in \widetilde{O}(H^{2}(X,\mathbb{Z}))$, the result is Proposition 2.1. If 
$i^{\ast }$ acts as 
$-\text{id}$ on the discriminant group of 
$H^{2}(X,\mathbb{Z})$, then 
$-i^{\ast }\in \widetilde{O}(H^{2}(X,\mathbb{Z}))$, and again, we use Proposition 2.1.◻
Corollary 2.4. Let 
$X$ be an IHS manifold of 
$K3^{[n]}$-type, of Kummer type or of 
$\text{OG}10$-type, and let 
$i\in \operatorname{Aut}(X)$ be an involution. Then one of the following holds:
(1)
$i^{\ast }$ acts as $\operatorname{id}$ on the discriminant group of $H^{2}(X,\mathbb{Z})$ and $H^{2}(X,\mathbb{Z})^{-i^{\ast }}$ is $2$-elementary;(2)
$i^{\ast }$ acts as $-\text{id}$ on the discriminant group of $H^{2}(X,\mathbb{Z})$ and $H^{2}(X,\mathbb{Z})^{i^{\ast }}$ is $2$-elementary.
Proof. As we already stated at the beginning of the section, if 
$X$ is of 
$K3^{[n]}$-type, then the action of 
$i^{\ast }$ on 
$A_{H^{2}(X,\mathbb{Z})}$ is either 
$\operatorname{id}$ or 
$-\text{id}$ by [Reference Markman25, Lemma 9.2]. The same holds for manifolds of Kummer type (whose second cohomology lattice is even) by [Reference Mongardi28, Theorem 4.3]. The Beauville–Bogomolov–Fujiki quadratic form for manifolds of 
$\text{OG}10$-type was computed in [Reference Rapagnetta37, Theorem 3.0.11]: the second cohomology lattice is even, with discriminant group 
$\frac{\mathbb{Z}}{3\mathbb{Z}}(-\frac{2}{3})$. As a consequence, 
$i^{\ast }$ can only induce 
$\operatorname{id}$ or 
$-\text{id}$ on the discriminant group. The statement then follows from Corollary 2.3.◻
As in [Reference Mongardi26, Definition 2.3], we give the following definition.
Definition 2.5. An automorphism 
$f$ of a manifold 
$X$ of 
$K3^{[n]}$-type is natural if there exists a 
$K3$ surface 
$\unicode[STIX]{x1D6F4}$ and 
$\unicode[STIX]{x1D711}\in \operatorname{Aut}(\unicode[STIX]{x1D6F4})$ such that 
$(X,f)$ is deformation equivalent to 
$(\unicode[STIX]{x1D6F4}^{[n]},\unicode[STIX]{x1D711}^{[n]})$.
Lemma 2.6. Let 
$X$ be a manifold of 
$K3^{[n]}$-type and 
$i\in \operatorname{Aut}(X)$ be a natural involution. Then 
$i^{\ast }\in \widetilde{O}(H^{2}(X,\mathbb{Z}))$.
Proof. As shown in [Reference Boissière, Camere and Sarti6, Section 4], the isometry class of the invariant lattice of an involution is deformation invariant. For the pair 
$(\unicode[STIX]{x1D6F4}^{[n]},\unicode[STIX]{x1D711}^{[n]})$, the action of the natural involution on the exceptional divisor of the Hilbert–Chow morphism 
$\unicode[STIX]{x1D6F4}^{[n]}\rightarrow \unicode[STIX]{x1D6F4}^{(n)}$ is trivial by [Reference Boissière and Sarti10, Theorm 1]. Let 
$\unicode[STIX]{x1D6FF}\in H^{2}(\unicode[STIX]{x1D6F4}^{[n]},\mathbb{Z})$ be the class whose double is the exceptional divisor. From 
$i^{\ast }(2\unicode[STIX]{x1D6FF})=2\unicode[STIX]{x1D6FF}$, we get that the image of 
$L+\frac{1}{2(n-1)}\unicode[STIX]{x1D6FF}\in A_{L}$ by the map induced by 
$i^{\ast }$ on the discriminant group is 
$L+\frac{1}{2(n-1)}\unicode[STIX]{x1D6FF}$; hence, 
$i^{\ast }$ acts as the identity on 
$A_{L}$.◻
Corollary 2.7. Let 
$X$ be a manifold of 
$K3^{[n]}$-type and 
$i\in \operatorname{Aut}(X)$ be a natural involution. Then the coinvariant lattice 
$H^{2}(X,\mathbb{Z})^{-i^{\ast }}$ is 
$2$-elementary.
2.2 Discriminant groups
We explain in this section the inaccuracies in the proof of [Reference Joumaah22, Proposition 5.1.1] and provide the necessary corrections. Adopting our notation, which differs from the one used by Joumaah in [Reference Joumaah22], let 
$X$ be a manifold of 
$K3^{[n]}$-type with a non-symplectic involution 
$i\in \operatorname{Aut}(X)$. Let 
$T=L^{i^{\ast }}$, 
$S=L^{-i^{\ast }}$ be, respectively, the invariant and coinvariant lattices of the involution. The aim of [Reference Joumaah22, Proposition 5.1.1] is to classify the discriminant groups 
$A_{T},A_{S}$. In order to do so, Joumaah considers the isotropic subgroup 
$H_{L}\subset A_{T}\oplus A_{S}$, which is isomorphic to 
$\frac{L}{T\oplus S}\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{a}$ for some 
$a\geqslant 0$, and its projections 
$H_{T}:=p_{T}(H_{L})\subset A_{T}$, 
$H_{S}:=p_{S}(H_{L})\subset A_{S}$. In particular, 
$H_{L}\cong H_{T}\cong H_{S}$ as groups, 
$\frac{H_{L}^{\bot }}{H_{L}}\cong A_{L}$ and 
$\unicode[STIX]{x1D6FE}:=p_{S}\circ p_{T}^{-1}:H_{T}\rightarrow H_{S}$ is an anti-isometry.
The following proposition provides the complete classification for the discriminant groups 
$A_{T}$, 
$A_{S}$. We refer to [Reference Camere and Cattaneo11, Proposition 3.2] for the analogous classification in the case of automorphisms of odd prime order.
Proposition 2.8. Let 
$X$ be a manifold of 
$K3^{[n]}$-type, for 
$n\geqslant 2$, and let 
$l\geqslant 1$ and 
$m$ odd such that 
$2(n-1)=2^{l}m$. Let 
${\mathcal{G}}\subset \operatorname{Aut}(X)$ be a group of order 
$2$ acting non-symplectically on 
$X$, and let 
$a\in \mathbb{Z}_{{\geqslant}0}$ be such that 
$\frac{L}{T\oplus S}\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{a}$. Then one of the following cases holds:
(i)
$A_{T}\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus a}\oplus \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}$, $A_{S}\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus a}$ or vice versa;(ii)
$a\geqslant 1$, $A_{T}\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus a-1}\oplus \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}$, $A_{S}\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus a+1}$ or vice versa;(iii)
$l=1$, $a=0$, $A_{T}\cong \frac{\mathbb{Z}}{m\mathbb{Z}}$, $A_{S}\cong \frac{\mathbb{Z}}{2\mathbb{Z}}$ or vice versa.
Proof. Let 
$i$ be the non-symplectic involution generating the group 
${\mathcal{G}}$ and let 
$\unicode[STIX]{x1D70E}\in \{\pm i^{\ast }\}$ be the isometry such that 
$\unicode[STIX]{x1D70E}\in \widetilde{O}(L)$. Let 
$T,S$ be the invariant and coinvariant lattices of 
$i^{\ast }$. If 
$\unicode[STIX]{x1D70E}=i^{\ast }$, then 
$T=L^{\unicode[STIX]{x1D70E}}$, 
$S=L^{-\unicode[STIX]{x1D70E}}$; if 
$\unicode[STIX]{x1D70E}=-i^{\ast }$, then 
$T=L^{-\unicode[STIX]{x1D70E}}$, 
$S=L^{\unicode[STIX]{x1D70E}}$.
As we showed in Corollary 2.4, the lattice 
$L^{-\unicode[STIX]{x1D70E}}$ is 
$2$-elementary; therefore, 
$A_{L^{-\unicode[STIX]{x1D70E}}}$ coincides with its Sylow 
$2$-subgroup (it actually coincides with its 
$2$-torsion part). Moreover, 
$A_{L^{\unicode[STIX]{x1D70E}}}=(A_{L^{\unicode[STIX]{x1D70E}}})_{2}\oplus \frac{\mathbb{Z}}{m\mathbb{Z}}$, where 
$(A_{L^{\unicode[STIX]{x1D70E}}})_{2}$ denotes the Sylow 
$2$-subgroup of 
$A_{L^{\unicode[STIX]{x1D70E}}}$ (see [Reference Joumaah22, Proposition 5.1.1]). Using the notation introduced at the beginning of the section, there exist subgroups 
$H_{L^{\unicode[STIX]{x1D70E}}}\subset (A_{L^{\unicode[STIX]{x1D70E}}})_{2}$ and 
$H_{L^{-\unicode[STIX]{x1D70E}}}\subset A_{L^{-\unicode[STIX]{x1D70E}}}$ isomorphic to 
$\frac{L}{L^{\unicode[STIX]{x1D70E}}\oplus L^{-\unicode[STIX]{x1D70E}}}\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{a}$. The case 
$l=1$ was correctly discussed by Joumaah in his proof: the only possibilities are 
$A_{L^{\unicode[STIX]{x1D70E}}}=H_{L^{\unicode[STIX]{x1D70E}}}\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}\oplus \frac{\mathbb{Z}}{m\mathbb{Z}}$, 
$A_{L^{-\unicode[STIX]{x1D70E}}}=H_{L^{-\unicode[STIX]{x1D70E}}}$ (i.e. case (i) of the statement) or 
$A_{L^{\unicode[STIX]{x1D70E}}}=H_{L^{\unicode[STIX]{x1D70E}}}\oplus \frac{\mathbb{Z}}{m\mathbb{Z}}$, 
$A_{L^{-\unicode[STIX]{x1D70E}}}=H_{L^{-\unicode[STIX]{x1D70E}}}\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}$ (case (ii) if 
$a\geqslant 1$ or case (iii) if 
$a=0$).
If 
$l\geqslant 2$, we define 
$G:=(A_{L^{\unicode[STIX]{x1D70E}}})_{2}\oplus A_{L^{-\unicode[STIX]{x1D70E}}}$ and let 
$G_{2}\subset G$ be the subgroup of elements of order 
$2$ in 
$G$. Joumaah showed that 
$[G:G_{2}]=2^{l-1}$, which implies 
$G\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{2a}\oplus \frac{\mathbb{Z}}{2^{l}\mathbb{Z}}$. As a consequence, we obtain two possible structures (not just one, as stated in [Reference Joumaah22, Proposition 5.1.1]; see below for details) for the summands 
$(A_{L^{\unicode[STIX]{x1D70E}}})_{2}$ and 
$A_{L^{-\unicode[STIX]{x1D70E}}}$ of 
$G$, recalling that 
$L^{-\unicode[STIX]{x1D70E}}$ is 
$2$-elementary and that both 
$(A_{L^{\unicode[STIX]{x1D70E}}})_{2}$, 
$A_{L^{-\unicode[STIX]{x1D70E}}}$ contain a subgroup isomorphic to 
$(\frac{\mathbb{Z}}{2\mathbb{Z}})^{a}$:
∙
$(A_{L^{\unicode[STIX]{x1D70E}}})_{2}=(\frac{\mathbb{Z}}{2\mathbb{Z}})^{a}\oplus \frac{\mathbb{Z}}{2^{l}\mathbb{Z}},A_{L^{-\unicode[STIX]{x1D70E}}}=(\frac{\mathbb{Z}}{2\mathbb{Z}})^{a}$ (case (i));∙
$a\geqslant 1$, $(A_{L^{\unicode[STIX]{x1D70E}}})_{2}=(\frac{\mathbb{Z}}{2\mathbb{Z}})^{a-1}\oplus \frac{\mathbb{Z}}{2^{l}\mathbb{Z}},A_{L^{-\unicode[STIX]{x1D70E}}}=(\frac{\mathbb{Z}}{2\mathbb{Z}})^{a+1}$ (case (ii)). ◻
Remark 2.9. Assume that 
$i^{\ast }\in \widetilde{O}(L)$ so that 
$\unicode[STIX]{x1D70E}=i^{\ast }$. If 
$l>1$, Joumaah correctly highlighted in his proof that the index 
$[G:G_{2}]$ needs to be 
$2^{l-1}$ and, therefore, 
$G\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{2a}\oplus \frac{\mathbb{Z}}{2^{l}\mathbb{Z}}$. However, contrary to what he stated, this does not necessarily imply that 
$G=H_{T}\oplus H_{S}\oplus \frac{\mathbb{Z}}{2^{l}\mathbb{Z}}$, from which he inferred 
$A_{T}\cong H_{T}\oplus A_{L},A_{S}=H_{S}$ as the only possibility for the discriminant groups. Indeed, in the next paragraph, we will show that it is possible to find manifolds of 
$K3^{[3]}$-type admitting non-symplectic involutions whose invariant and coinvariant lattices are in contrast with [Reference Joumaah22, Proposition 5.1.1].
For 
$n=3$, we have 
$2(n-1)=4$, meaning 
$l=2$, 
$m=1$. The authors of [Reference Iliev, Kapustka, Kapustka and Ranestad21] describe a
$20$-dimensional family of manifolds of 
$K3^{[3]}$-type, called double EPW cubes, with polarization of degree four and divisibility two (see [Reference Iliev, Kapustka, Kapustka and Ranestad21, Proposition 5.3]), whose members are always endowed with a non-symplectic involution 
$i$. As a consequence, the invariant lattice of 
$i$ is 
$T\cong \langle 4\rangle$ and the coinvariant lattice is 
$S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2\rangle ^{\oplus 2}$. In particular, the discriminant groups are
$$\begin{eqnarray}A_{T}=\langle t\rangle \cong \frac{\mathbb{Z}}{4\mathbb{Z}}\biggl(\frac{1}{4}\biggr),\qquad A_{S}=\langle s_{1},s_{2}\rangle \cong \frac{\mathbb{Z}}{2\mathbb{Z}}\biggl(-\frac{1}{2}\biggr)\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}\biggl(-\frac{1}{2}\biggr).\end{eqnarray}$$ In this case, 
$G=A_{T}\oplus A_{S}$ since 
$m=1$. Moreover,
$$\begin{eqnarray}16=|A_{T}\oplus A_{S}|=[L:T\oplus S]^{2}|A_{L}|=2^{2a}\cdot 4;\end{eqnarray}$$ therefore, 
$a=1$. Looking at the discriminant quadratic forms on 
$A_{T}$ and 
$A_{S}$, the only possible choice for the subgroups of order two 
$H_{T}\subset A_{T}$ and 
$H_{S}\subset A_{S}$, with 
$H_{T}\cong H_{S}(-1)$, is the following:
$$\begin{eqnarray}H_{T}=\langle 2t\rangle \subset A_{T},\qquad H_{S}=\langle s_{1}+s_{2}\rangle \subset A_{S},\end{eqnarray}$$ which implies 
$H_{L}=\langle 2t+s_{1}+s_{2}\rangle \subset A_{T}\oplus A_{S}$. One can check that 
$H_{L}^{\bot }=\langle 2t+s_{1}+s_{2},t+s_{1}\rangle$; hence, the quotient 
$\frac{H_{L}^{\bot }}{H_{L}}$ is generated by the equivalence class of 
$t+s_{1}$ and is isomorphic to 
$A_{L}=\frac{\mathbb{Z}}{4\mathbb{Z}}(-\frac{1}{4})$.
This is therefore a case where 
$l=2>1$ and 
$[G:G_{2}]=2=2^{l-1}$. However, it is not possible to write the group 
$G=A_{T}\oplus A_{S}$ as 
$G=H_{T}\oplus H_{S}\oplus \frac{\mathbb{Z}}{2^{l}\mathbb{Z}}$ and it is not true that 
$A_{T}\cong H_{T}\oplus A_{L}$, 
$A_{S}=H_{S}$.
Remark 2.10. In the case of manifolds of 
$K3^{[2]}$-type, it was proved in [Reference Boissière, Camere and Sarti6, Lemma 8.1] (extending results from [Reference Boissière, Nieper-Wißkirchen and Sarti9, Section 6]) that the discriminant groups can only be 
$A_{S}\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus a}$, 
$A_{T}\cong (\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus a+1}$ or vice versa. This is coherent with the classification of Proposition 2.8 (if 
$n=2$, we have 
$2(n-1)=2$; hence, 
$l=m=1$).
3 Existence of automorphisms
In this section, we show that the lattice-theoretical conditions of Corollary 2.4 are actually sufficient to give rise to a geometric realization. First, we prove that every 
$2$-elementary sublattice of 
$L=L_{n}$ is the invariant (or coinvariant) lattice of some involution of 
$L$ and finally that we can generically lift this abstract involution to an involution of a manifold of 
$K3^{[n]}$-type.
Proposition 3.1. Let 
$S$ be an even 
$2$-elementary lattice, primitively embedded into an even lattice 
$\unicode[STIX]{x1D6EC}$. Then 
$\operatorname{id}_{S^{\bot }}\oplus (-\text{id}_{S})$ (resp. 
$(-\text{id}_{S^{\bot }})\oplus \operatorname{id}_{S}$) extends to an isometry 
$\unicode[STIX]{x1D719}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$ (resp. 
$-\unicode[STIX]{x1D719}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$).
Proof. By [Reference Nikulin31, Theorem 1.1.2], we can primitively embed 
$\unicode[STIX]{x1D6EC}$ into an even unimodular lattice 
$V$ of high enough rank. We fix such a primitive embedding and consider the orthogonal complements 
$\unicode[STIX]{x1D6EC}^{\bot _{V}}$ and 
$S^{\bot _{V}}$ of 
$\unicode[STIX]{x1D6EC}$ and 
$S$ inside 
$V$. Obviously, 
$V$ is an overlattice of 
$S\oplus S^{\bot _{V}}$. We want to show that 
$\unicode[STIX]{x1D6FC}:=\operatorname{id}_{S^{\bot _{V}}}\oplus (-\text{id}_{S})$ extends to 
$V$. A completely analogous proof will show that also 
$(-\text{id}_{S^{\bot _{V}}})\oplus \operatorname{id}_{S}$ extends, as in the statement. Let 
$H_{V}=V/(S\oplus S^{\bot _{V}})$ be the isotropy subgroup of 
$A_{S}\oplus A_{S^{\bot _{V}}}$ corresponding to the overlattice 
$V$ and let 
$p_{S}$, 
$p_{S^{\bot _{V}}}$ be the two projections to 
$A_{S}$ and 
$A_{S^{\bot _{V}}}$:
Since 
$V$ is unimodular, we have 
$H_{S^{\bot _{V}}}=A_{S^{\bot _{V}}}$ and 
$H_{S}=A_{S}$. As before, let 
$\unicode[STIX]{x1D6FE}:A_{S^{\bot _{V}}}\longrightarrow A_{S}$ be the anti-isometry given by 
$p_{S}\circ (p_{S^{\bot _{V}}})^{-1}$. By [Reference Nikulin31, Proposition 1.5.1], the existence of an extension of 
$\unicode[STIX]{x1D6FC}$ to 
$V$ is equivalent to the commutativity of the diagram
where, for any lattice 
$N$ and 
$\unicode[STIX]{x1D707}\in O(N)$, we denote by 
$\overline{\unicode[STIX]{x1D707}}$ the isometry of finite quadratic forms induced by 
$\unicode[STIX]{x1D707}$ on the discriminant group 
$A_{N}$. The diagram is commutative because 
$-\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}$ since 
$S$ is 
$2$-elementary; hence, we get the extension 
$\widetilde{\unicode[STIX]{x1D6FC}}\in O(V)$ of 
$\unicode[STIX]{x1D6FC}$ to 
$V$.
As 
$S^{\bot _{\unicode[STIX]{x1D6EC}}}\oplus \unicode[STIX]{x1D6EC}^{\bot _{V}}\subset S^{\bot _{V}}$, we deduce that 
$\unicode[STIX]{x1D6EC}^{\bot _{V}}$ is invariant for the action of 
$\widetilde{\unicode[STIX]{x1D6FC}}$. Let 
$\unicode[STIX]{x1D719}$ be the restriction 
$\widetilde{\unicode[STIX]{x1D6FC}}|_{\unicode[STIX]{x1D6EC}}$. Since 
$\unicode[STIX]{x1D719}\oplus \operatorname{id}_{\unicode[STIX]{x1D6EC}^{\bot _{V}}}$ extends to 
$\widetilde{\unicode[STIX]{x1D6FC}}\in O(V)$, we have a commutative diagram
where 
$\unicode[STIX]{x1D6FD}:=p_{\unicode[STIX]{x1D6EC}^{\bot _{V}}}\circ (p_{\unicode[STIX]{x1D6EC}})^{-1}$. Hence, 
$\overline{\unicode[STIX]{x1D719}}=\operatorname{id}_{A_{\unicode[STIX]{x1D6EC}}}$, that is, 
$\unicode[STIX]{x1D719}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$.◻
Remark 3.2. This is in some sense a converse of [Reference Gritsenko, Hulek and Sankaran16, Lemma 3.5]. See also [Reference Dolgachev15, Proposition 1.5.1].
We come now to the second part of the section. First, we recall some results on lattice-polarized manifolds of 
$K3^{[n]}$-type.
Let 
$T$ be a hyperbolic lattice which admits a primitive embedding 
$j:T{\hookrightarrow}L$. We identify 
$T$ with the sublattice 
$j(T)\subset L$ and we denote by 
$S$ its orthogonal complement in 
$L$. Following [Reference Joumaah22, Section 4.1], we say that 
$T$ is admissible if it is the invariant lattice of a monodromy operator 
$\unicode[STIX]{x1D70C}\in \operatorname{Mon}^{2}(L)$ of order two. In particular, 
$T$ and 
$S$ are as in Corollary 2.4; therefore, one of them is 
$2$-elementary. This implies, by Proposition 3.1, that 
$\unicode[STIX]{x1D70C}$ is the unique extension of 
$\operatorname{id}_{T}\oplus (-\text{id}_{S})$ to 
$L$.
Let 
$X$ be a manifold of 
$K3^{[n]}$-type and 
$i\in \operatorname{Aut}(X)$ be a non-symplectic involution acting on it. In [Reference Joumaah22, Section 4.2], the pair 
$(X,i)$ is called of type 
$T$ if it admits a 
$(\unicode[STIX]{x1D70C},T)$-polarization, that is, a marking 
$\unicode[STIX]{x1D702}:H^{2}(X,\mathbb{Z})\rightarrow L$ such that 
$\unicode[STIX]{x1D702}\circ i^{\ast }=\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D702}$. If 
$(X,i)$ and 
$(X^{\prime },i^{\prime })$ are two pairs of type 
$T$, they are said to be isomorphic if there exists an isomorphism
$f:X\rightarrow X^{\prime }$ such that 
$i^{\prime }=f\circ i\circ f^{-1}$. The monodromy operators 
$f^{\ast }\in \operatorname{Mon}^{2}(L)$ induced by these isomorphisms of pairs are the isometries contained in
$$\begin{eqnarray}\operatorname{Mon}^{2}(L,T):=\{g\in \operatorname{Mon}^{2}(L)\mid g\circ \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}\circ g\}=\{g\in \operatorname{Mon}^{2}(L)\mid g(T)=T\}.\end{eqnarray}$$ In particular, for any 
$g\in \operatorname{Mon}^{2}(L,T)$, we have that 
$g|_{T}\in O(T)$ and 
$g|_{S}\in O(S)$. We can then define the following subgroups:
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{T}:=\{g|_{T}\mid g\in \operatorname{Mon}^{2}(L,T)\}\subset O(T),\qquad \unicode[STIX]{x1D6E4}_{S}:=\{g|_{S}\mid g\in \operatorname{Mon}^{2}(L,T)\}\subset O(S).\end{eqnarray}$$ Note that local deformations of a pair 
$(X,i)$ of type 
$T$ are parametrized by 
$H^{1,1}(X)^{i^{\ast }}$ (more details on this are provided in [Reference Beauville5, Theorem 2] and [Reference Boissière, Camere and Sarti6, Section 4]).
Inside the moduli space 
${\mathcal{M}}_{L}$ of marked IHS manifolds of 
$K3^{[n]}$-type, let 
${\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}$ be the subspace of 
$(\unicode[STIX]{x1D70C},T)$-polarized marked manifolds 
$(X,\unicode[STIX]{x1D702})\in {\mathcal{M}}_{L}$. Since the symplectic form 
$\unicode[STIX]{x1D714}_{X}$ generating 
$H^{2,0}(X)$ is orthogonal to the Néron–Severi group (which contains 
$T$), for any 
$(X,\unicode[STIX]{x1D702})\in {\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}$ the period point 
$\unicode[STIX]{x1D702}(H^{2,0}(X))$ belongs to
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{S}:=\{\unicode[STIX]{x1D705}\in \mathbb{P}(S\otimes \mathbb{C})\mid (\unicode[STIX]{x1D705},\unicode[STIX]{x1D705})=0,(\unicode[STIX]{x1D705},\overline{\unicode[STIX]{x1D705}})>0\}.\end{eqnarray}$$ Moreover, in [Reference Joumaah22], the author computes the image inside 
$\unicode[STIX]{x1D6FA}_{S}$ of the period map restricted to 
${\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}$. Given any 
$(X,\unicode[STIX]{x1D702})\in {\mathcal{M}}_{L}$, a wall divisor on 
$X$ is a primitive divisor 
$D\in \operatorname{NS}(X)$ such that 
$q(D)<0$ and such that 
$g(D^{\bot })\cap {\mathcal{B}}{\mathcal{K}}_{X}=\emptyset$ for any Hodge isometry 
$g\in \operatorname{Mon}^{2}(X)$ (see [Reference Mongardi27, Definition 1.2]), where 
${\mathcal{B}}{\mathcal{K}}_{X}$ denotes the birational Kähler cone of 
$X$. One can then consider, for any sublattice 
$S\subset L$, the set 
$\unicode[STIX]{x1D6E5}(S)$ of 
$\unicode[STIX]{x1D6FF}\in S$ for which there exists 
$(X,\unicode[STIX]{x1D702})\in {\mathcal{M}}_{L}$ such that 
$\unicode[STIX]{x1D702}^{-1}(\unicode[STIX]{x1D6FF})\in \operatorname{NS}(X)$ is a wall divisor on 
$X$. By [Reference Joumaah22, Proposition 4.6.7], the period map restricts to a holomorphic surjective morphism
$$\begin{eqnarray}{\mathcal{P}}:{\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}\longrightarrow \unicode[STIX]{x1D6FA}_{S}^{0}:=\unicode[STIX]{x1D6FA}_{S}\setminus \mathop{\bigcup }_{\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}(S)}(\unicode[STIX]{x1D6FF}^{\bot }\cap \unicode[STIX]{x1D6FA}_{S}).\end{eqnarray}$$ This restriction is equivariant with respect to the action of 
$\operatorname{Mon}^{2}(L,T)$; hence, we also obtain a surjection
$$\begin{eqnarray}{\mathcal{P}}:{\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}/\operatorname{Mon}^{2}(L,T)\longrightarrow \unicode[STIX]{x1D6FA}_{S}^{0}/\unicode[STIX]{x1D6E4}_{S}.\end{eqnarray}$$Theorem 3.3. Let 
$\unicode[STIX]{x1D70C}\in O(L)$ be an involution whose invariant lattice 
$T$ is hyperbolic. Assume also that the action of 
$\unicode[STIX]{x1D70C}$ on 
$A_{L}$ is either 
$\operatorname{id}$ or 
$-\text{id}$. Then there exists a marked manifold 
$(X,\unicode[STIX]{x1D702})$ of 
$K3^{[n]}$-type with a non-symplectic involution 
$i\in \operatorname{Aut}(X)$ such that
$\unicode[STIX]{x1D702}\circ i^{\ast }=\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D702}$.
Proof. Assume first that 
$\operatorname{rk}(T)\leqslant 20$ so that the period domain has positive dimension. Let 
$S\subset L$ be the coinvariant lattice of 
$\unicode[STIX]{x1D70C}$, that is, the orthogonal complement of 
$T$. By [Reference Boissière, Camere and Sarti6, Proposition 5.3], a very general point 
$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{S}^{0}$ is the image under the period map of an ample 
$T$-polarized marked manifold of 
$K3^{[n]}$-type 
$(X,\unicode[STIX]{x1D702})$ with 
$\operatorname{NS}(X)=\unicode[STIX]{x1D702}^{-1}(T)$. If 
$\operatorname{rk}(T)=21$, then any point in 
$\unicode[STIX]{x1D6FA}_{S}^{0}=\unicode[STIX]{x1D6FA}_{S}$ is the period point of an ample 
$T$-polarized marked manifold of 
$K3^{[n]}$-type 
$(X,\unicode[STIX]{x1D702})$ with 
$\operatorname{NS}(X)=\unicode[STIX]{x1D702}^{-1}(T)$. We can then consider 
$\unicode[STIX]{x1D6FC}:=\unicode[STIX]{x1D702}^{-1}\circ \unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D702}\in O(H^{2}(X,\mathbb{Z}))$, which is an involution, and we observe the following:
(1)
$\unicode[STIX]{x1D6FC}$ induces a Hodge isometry on $H^{2}(X,\mathbb{C})$ since the period point $\unicode[STIX]{x1D702}(H^{2,0}(X))$ is invariant for the action of $\unicode[STIX]{x1D70C}$ on $\unicode[STIX]{x1D6FA}_{S}$;(2)
$\unicode[STIX]{x1D6FC}$ is effective because the equality $\operatorname{NS}(X)=\unicode[STIX]{x1D702}^{-1}(T)=\unicode[STIX]{x1D702}^{-1}(L^{\unicode[STIX]{x1D70C}})$ implies that there is an $\unicode[STIX]{x1D6FC}$-fixed Kähler (even ample) class on $X$;(3)
$\unicode[STIX]{x1D6FC}$ is orientation preserving by [Reference Boissière, Cattaneo, Markushevich and Sarti7, Remark 2.2];(4) the action of
$\unicode[STIX]{x1D6FC}$ on $A_{H^{2}(X,\mathbb{Z})}$ is $\operatorname{id}$ or $-\text{id}$.
Hence, 
$\unicode[STIX]{x1D6FC}$ is a monodromy operator by [Reference Markman25, Lemma 9.2] and, by [Reference Markman25, Theorem 1.3], there exists 
$i\in \operatorname{Aut}(X)$ such that 
$i^{\ast }=\unicode[STIX]{x1D6FC}$. Since the map 
$\operatorname{Aut}(X)\longrightarrow O(H^{2}(X,\mathbb{Z}))$, sending an automorphism to its action on 
$H^{2}(X,\mathbb{Z})$, is injective for manifolds of 
$K3^{[n]}$-type (see [Reference Beauville3, Proposition 10] and [Reference Mongardi26, Lemma 1.2]), the automorphism 
$i$ is both unique and an involution. It is then straightforward to check that 
$\unicode[STIX]{x1D702}\circ i^{\ast }=\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D702}$ and that 
$i$ is non-symplectic.◻
Remark 3.4. There exists at least one case with 
$\operatorname{rk}(T)=21$ for each 
$n\geqslant 2$: the natural non-symplectic involution induced on 
$\unicode[STIX]{x1D6F4}^{[n]}$ where 
$\unicode[STIX]{x1D6F4}$ is the 
$K3$ surface described in [Reference Nikulin32].
4 Geography for IHS manifolds of small dimension
The aim of this section is to understand which families of large dimension can be expected to exist as a consequence of the results of the previous section. We first classify the admissible invariant lattices of ranks one and two, respectively, for any 
$n$ and for 
$n\leqslant 5$, and then we describe the geography of these cases for manifolds of 
$K3^{[n]}$-type when 
$n\leqslant 5$.
4.1 Invariant sublattices of rank one and two
Let 
$T,S$ be the invariant and coinvariant lattices of a non-symplectic involution of a manifold of 
$K3^{[n]}$-type. As we saw in Corollary 2.4, either 
$S$ or 
$T$ is 
$2$-elementary, depending on the action of the involution on the discriminant group of 
$L$ (which is 
$\operatorname{id}$ or 
$-\text{id}$, respectively). Assume that 
$S$ is 
$2$-elementary and consider it embedded in the Mukai lattice 
$M$ (the case where 
$T$ is 
$2$-elementary is similar). Starting from the signature of 
$S^{\bot _{M}}$, we can use [Reference Dolgachev15, Theorem 1.5.2] to deduce the possible isometry classes for 
$S^{\bot _{M}}$. As observed in Lemma 2.2, we have that 
$T$ is the orthogonal complement in 
$S^{\bot _{M}}$ of 
$L^{\bot }$: since we know the latter lattice explicitly (see (1)), we can use [Reference Nikulin31, Proposition 1.15.1] to classify all primitive embeddings 
$L^{\bot }{\hookrightarrow}S^{\bot _{M}}$ and to compute, in each case, the discriminant group 
$A_{T}$. By [Reference Nikulin31, Proposition 1.15.1], if 
$J$ is the orthogonal complement of a primitive element of square 
$2(n-1)$ inside an even lattice 
$\unicode[STIX]{x1D6EC}$, the discriminant quadratic form 
$q_{J}:A_{J}\rightarrow \mathbb{Q}/2\mathbb{Z}$ can be expressed as follows. There exists an isometry of finite quadratic forms 
$\unicode[STIX]{x1D6FE}:H_{\langle 2(n-1)\rangle }\rightarrow H_{\unicode[STIX]{x1D6EC}}$ between two isomorphic subgroups 
$H_{\langle 2(n-1)\rangle }\subset A_{\langle 2(n-1)\rangle }$, 
$H_{\unicode[STIX]{x1D6EC}}\subset A_{\unicode[STIX]{x1D6EC}}$ such that, if 
$\unicode[STIX]{x1D6E4}\subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$ is the (isotropic) graph of 
$\unicode[STIX]{x1D6FE}$, then 
$\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}\cong A_{J}$ (as groups) and 
$q_{J}$ is isomorphic to the finite quadratic form induced on the quotient 
$\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}$ by the restriction of 
$-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}}$ to 
$\unicode[STIX]{x1D6E4}^{\bot }$. With a slight abuse of notation, we will write 
$q_{J}=(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}$. The following lemma classifies the discriminant quadratic forms of the orthogonal complements of primitive elements of square 
$2(n-1)$ inside certain lattices 
$\unicode[STIX]{x1D6EC}$ which we will need in this section.
Lemma 4.1. Let 
$e$ be a generator of 
$A_{\langle 2(n-1)\rangle }=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(\frac{1}{2(n-1)})$ such that 
$q(e)=\frac{1}{2(n-1)}$. Let 
$\unicode[STIX]{x1D6EC}$ be an even lattice such that 
$A_{\unicode[STIX]{x1D6EC}}$ is as in the first column of Table 1, and let 
$j:\langle 2(n-1)\rangle {\hookrightarrow}\unicode[STIX]{x1D6EC}$ be a primitive embedding. Then, up to isometries of 
$\unicode[STIX]{x1D6EC}$, we have only the possibilities listed in Table 1 for the quadratic form 
$q_{J}=(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}$ on 
$A_{J}$. Moreover, in all cases, the isomorphism 
$\unicode[STIX]{x1D6FE}:H_{\langle 2(n-1)\rangle }\rightarrow H_{\unicode[STIX]{x1D6EC}}$ is unique.
Table 1. List of the discriminant quadratic forms from Lemma 4.1.
Remark 4.2. In Lemma 4.1, we list only the possible discriminant quadratic forms 
$q_{J}$, but we do not discuss whether they are realized by some lattice. We will use this lemma in Sections 4.1.1 and 4.1.2, where the problem of describing explicitly the lattices 
$J$ realizing such discriminant quadratic forms is addressed.
Proof. The proof is based on Nikulin’s result [Reference Nikulin31, Proposition 1.15.1], which is used as we recalled above.
For any 
$A_{\unicode[STIX]{x1D6EC}}$ listed in Table 1 and for any 
$n\geqslant 2$, one can choose the pair of trivial subgroups 
$H_{\langle 2(n-1)\rangle }=0$, 
$H_{\unicode[STIX]{x1D6EC}}=0$. With this choice, one obtains 
$\unicode[STIX]{x1D6E4}=0$ and 
$\unicode[STIX]{x1D6E4}^{\bot }=A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$, which implies
$$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(-\frac{1}{2(n-1)}\biggr)\oplus q_{\unicode[STIX]{x1D6EC}}.\end{eqnarray}$$ We now discuss possible nontrivial pairs 
$(H_{\langle 2(n-1)\rangle },H_{\unicode[STIX]{x1D6EC}})$ for nonunimodular 
$\unicode[STIX]{x1D6EC}$ in Table 1. Any subgroup of 
$A_{\langle 2(n-1)\rangle }$ is cyclic and, for all the considered lattices 
$\unicode[STIX]{x1D6EC}$, there are only nontrivial cyclic subgroups of order two. Hence, necessarily in all the cases below, we choose 
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$ since it is the only subgroup of order two inside 
$A_{\langle 2(n-1)\rangle }$.
(1) If
$A_{\unicode[STIX]{x1D6EC}}=\langle t\rangle \cong \frac{\mathbb{Z}}{2\mathbb{Z}}(\frac{1}{2})$, $H_{\langle 2(n-1)\rangle }$ is isometric to $H_{\unicode[STIX]{x1D6EC}}=A_{\unicode[STIX]{x1D6EC}}=\langle t\rangle$ if and only if $n\equiv 2\;\text{mod}\;4$ since $q_{\langle 2(n-1)\rangle }((n-1)e)=\frac{n-1}{2}\in \mathbb{Q}/2\mathbb{Z}$. The graph of the (only) isometry $\unicode[STIX]{x1D6FE}:H_{\langle 2(n-1)\rangle }\rightarrow H_{\unicode[STIX]{x1D6EC}}$, $(n-1)e\mapsto t$ is $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$. We compute $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t\rangle$; therefore, (recalling that $n$ is even) we have $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t]\rangle =\langle [2e]\rangle \cong \frac{\mathbb{Z}}{(n-1)\mathbb{Z}}$ and $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{(n-1)\mathbb{Z}}\biggl(-\frac{2}{n-1}\biggr).\end{eqnarray}$$(2) The case
$A_{\unicode[STIX]{x1D6EC}}=\langle t\rangle \cong \frac{\mathbb{Z}}{2\mathbb{Z}}(-\frac{1}{2})$ is similar to ($1$): $H_{\langle 2(n-1)\rangle }$ is isometric to $H_{\unicode[STIX]{x1D6EC}}=A_{\unicode[STIX]{x1D6EC}}=\langle t\rangle$ if and only if $n\equiv 0\;\text{mod}\;4$. In this case, the isometry $\unicode[STIX]{x1D6FE}:H_{\langle 2(n-1)\rangle }\rightarrow H_{\unicode[STIX]{x1D6EC}}$ has again graph $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$; we compute $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t\rangle$, $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t]\rangle =\langle [2e]\rangle \cong \frac{\mathbb{Z}}{(n-1)\mathbb{Z}}$, and $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{(n-1)\mathbb{Z}}\biggl(-\frac{2}{n-1}\biggr).\end{eqnarray}$$(3) When
$A_{\unicode[STIX]{x1D6EC}}=\langle t_{1},t_{2}\rangle \cong \frac{\mathbb{Z}}{2\mathbb{Z}}(\frac{1}{2})\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}(-\frac{1}{2})$, then $A_{\unicode[STIX]{x1D6EC}}$ has three cyclic subgroups $\langle t_{1}\rangle$, $\langle t_{2}\rangle$ and $\langle t_{1}+t_{2}\rangle$.(a)
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$, $H_{\unicode[STIX]{x1D6EC}}=\langle t_{i}\rangle$ for $i=1,2$, isometric only if $n\equiv 2i\;\text{mod}\;4$. Then $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t_{i}\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$ and we compute $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t_{i},t_{j}\rangle$, where $j\in \{1,2\},j\neq i$. Since $n$ is even, we conclude $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t_{i}],[t_{j}]\rangle =\langle [e+t_{1}+t_{2}]\rangle \cong \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}$ and $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(-\frac{1}{2(n-1)}\biggr).\end{eqnarray}$$(b)
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$, $H_{\unicode[STIX]{x1D6EC}}=\langle t_{1}+t_{2}\rangle$, isometric only if $n\equiv 1\;\text{mod}\;4$. The graph is $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t_{1}+t_{2}\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$ and $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t_{1},t_{1}+t_{2}\rangle$. Then $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t_{1}],[t_{1}+t_{2}]\rangle =\langle [e+t_{1}]\rangle \cong \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}$, since $n$ is odd, and $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(\frac{n-2}{2(n-1)}\biggr).\end{eqnarray}$$
(4) Assume
$A_{\unicode[STIX]{x1D6EC}}=A_{U(2)}=\langle t_{1},t_{2}\rangle \cong \Big((\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus 2},\Big(\begin{smallmatrix}0 & \frac{1}{2}\\ \frac{1}{2} & 0\end{smallmatrix}\Big)\!\Big)$. As in ($3$), the only nontrivial choices for the pair $(H_{\langle 2(n-1)\rangle },H_{\unicode[STIX]{x1D6EC}})$ are the following:(a)
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$, $H_{\unicode[STIX]{x1D6EC}}=\langle t_{i}\rangle$ for $i=1,2$, isometric only if $n\equiv 1\;\text{mod}\;4$. Then $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t_{i}\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$ and $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t_{j},t_{i}\rangle$, where $j\in \{1,2\},j\neq i$. Since $n$ is odd, we have $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t_{j}],[t_{i}]\rangle =\langle [e+t_{j}]\rangle \cong \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}$ and $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(-\frac{1}{2(n-1)}\biggr).\end{eqnarray}$$(b)
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$, $H_{\unicode[STIX]{x1D6EC}}=\langle t_{1}+t_{2}\rangle$. The two subgroups are isometric only if $n\equiv 3\;\text{mod}\;4$ and we have $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t_{1}+t_{2}\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$. We compute $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t_{1},t_{1}+t_{2}\rangle$ and $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t_{1}],[t_{1}+t_{2}]\rangle =\langle [e+t_{1}]\rangle \cong \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}$ since $n$ is odd; therefore, also in this case, $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(-\frac{1}{2(n-1)}\biggr).\end{eqnarray}$$
(5) Assume
$A_{\unicode[STIX]{x1D6EC}}=\langle t_{1},t_{2},t_{3}\rangle \cong \biggl((\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus 3},\biggl(\!\begin{smallmatrix}0 & \frac{1}{2} & 0\\ \frac{1}{2} & 0 & 0\\ 0 & 0 & \frac{1}{2}\end{smallmatrix}\biggr)\biggr)$.(a)
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$, $H_{\unicode[STIX]{x1D6EC}}=\langle t_{3}\rangle$, isometric only if $n\equiv 2\;\text{mod}\;4$. The graph is $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t_{3}\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$ and $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t_{3},t_{1},t_{2}\rangle$. We have $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t_{3}],[t_{1}],[t_{2}]\rangle =\langle [2e],[t_{1}],[t_{2}]\rangle \cong \frac{\mathbb{Z}}{(n-1)\mathbb{Z}}\oplus (\frac{\mathbb{Z}}{2\mathbb{Z}})^{\oplus 2}$, since $n$ is even, and $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{(n-1)\mathbb{Z}}\biggl(-\frac{2}{n-1}\biggr)\oplus u_{2}.\end{eqnarray}$$(b)
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$, $H_{\unicode[STIX]{x1D6EC}}=\langle t_{i}\rangle$ for $i=1,2$, isometric only if $n\equiv 1\;\text{mod}\;4$. Then $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t_{i}\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$ and $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t_{j},t_{i},t_{3}\rangle$, where $j\in \{1,2\},j\neq i$. Since $n$ is odd, we have $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t_{j}],[t_{i}],[t_{3}]\rangle =\langle [e+t_{j}],[t_{3}]\rangle \cong \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}$ and $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(-\frac{1}{2(n-1)}\biggr)\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}\biggl(\frac{1}{2}\biggr).\end{eqnarray}$$(c)
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$, $H_{\unicode[STIX]{x1D6EC}}=\langle t_{1}+t_{2}\rangle$, isometric only if $n\equiv 3\;\text{mod}\;4$. We have $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t_{1}+t_{2}\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$ and $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t_{1},t_{1}+t_{2},t_{3}\rangle$. Since $n$ is odd, we conclude $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t_{1}],[t_{1}+t_{2}],[t_{3}]\rangle =\langle [e+t_{1}],[t_{3}]\rangle \cong \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}$ with $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(-\frac{1}{2(n-1)}\biggr)\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}\biggl(\frac{1}{2}\biggr).\end{eqnarray}$$(d)
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$, $H_{\unicode[STIX]{x1D6EC}}=\langle t_{i}+t_{3}\rangle$ for $i=1,2$. The two subgroups are isometric only if $n\equiv 2\;\text{mod}\;4$. Then $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t_{i}+t_{3}\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$ and $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t_{j},t_{i},t_{j}+t_{3}\rangle$, where $j\in \{1,2\},j\neq i$. Since $n$ is even, we have $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t_{j}],[t_{i}],[t_{j}+t_{3}]\rangle =\langle [e+t_{j}],[t_{j}+t_{3}]\rangle \cong \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}$ and $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(-\frac{1}{2(n-1)}\biggr)\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}\biggl(\frac{1}{2}\biggr).\end{eqnarray}$$(e)
$H_{\langle 2(n-1)\rangle }=\langle (n-1)e\rangle$, $H_{\unicode[STIX]{x1D6EC}}=\langle t_{1}+t_{2}+t_{3}\rangle$, isometric only if $n\equiv 0\;\text{mod}\;4$. We have $\unicode[STIX]{x1D6E4}=\langle (n-1)e+t_{1}+t_{2}+t_{3}\rangle \subset A_{\langle 2(n-1)\rangle }(-1)\oplus A_{\unicode[STIX]{x1D6EC}}$ and $\unicode[STIX]{x1D6E4}^{\bot }=\langle e+t_{1},t_{1}+t_{2},t_{1}+t_{3}\rangle$. Since $n$ is even, we conclude $\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}=\langle [e+t_{1}],[t_{1}+t_{2}],[t_{1}+t_{3}]\rangle =\langle [e+t_{1}],[t_{1}+t_{3}]\rangle \cong \frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}$ with $$\begin{eqnarray}(-q_{\langle 2(n-1)\rangle }\oplus q_{\unicode[STIX]{x1D6EC}})|_{\unicode[STIX]{x1D6E4}^{\bot }/\unicode[STIX]{x1D6E4}}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}\biggl(-\frac{1}{2(n-1)}\biggr)\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}\biggl(\frac{1}{2}\biggr).\end{eqnarray}$$
In all cases, the isometry 
$\unicode[STIX]{x1D6FE}:H_{\langle 2(n-1)\rangle }\rightarrow H_{\unicode[STIX]{x1D6EC}}$ is unique since the two subgroups are either trivial or isomorphic to 
$\mathbb{Z}/2\mathbb{Z}$.◻
4.1.1 Invariant sublattice of rank one
In this section, we prove the following proposition, which describes the pairs 
$T$ and 
$S$ that can occur when 
$\operatorname{rk}(T)=1$.
Proposition 4.3. Let 
$X$ be a manifold of 
$K3^{[n]}$-type for some 
$n\geqslant 2$, and let 
$i\in \operatorname{Aut}(X)$ be a non-symplectic involution. If the invariant lattice 
$T\subset H^{2}(X,\mathbb{Z})$ has rank one, then one of the following holds:
(1) if
$i^{\ast }$ acts as $\operatorname{id}$ on $A_{H^{2}(X,\mathbb{Z})}$, then $-1$ is a quadratic residue modulo $n-1$ and $$\begin{eqnarray}T\cong \langle 2(n-1)\rangle ,\qquad S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2\rangle \oplus \langle -2\rangle ;\end{eqnarray}$$(2) if
$i^{\ast }$ acts as $-\text{id}$ on $A_{H^{2}(X,\mathbb{Z})}$, then $T\cong \langle 2\rangle$ and(a) either
$S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle \oplus \langle -2\rangle$(b) or
$n\equiv 0\;\text{mod}\;4$ and $$\begin{eqnarray}S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \left(\begin{array}{@{}cc@{}}-2 & -1\\ -1 & \displaystyle -\frac{n}{2}\end{array}\right).\end{eqnarray}$$
Proof. This result generalizes [Reference Cattaneo13, Proposition 5.1], which holds for nonnatural involutions of Hilbert schemes of points on a generic projective 
$K3$ surface.
We deal first with the case where 
$T,S$ are the invariant and coinvariant lattices of an involution 
$i$ such that 
$\overline{i^{\ast }}=\operatorname{id}_{A_{L}}$. This means that 
$S$ is 
$2$-elementary and that 
$T\oplus L^{\bot }\subset S^{\bot _{M}}$. Since both 
$T$ and 
$L^{\bot }$ have signature 
$(1,0)$, we deduce that 
$S^{\bot _{M}}$ has signature 
$(2,0)$. By [Reference Conway and Sloane14, Table 15.1], there is only one possible choice for 
$S^{\bot _{M}}$, which embeds primitively in 
$M$ in a unique way by [Reference Nikulin31, Theorem 1.1.2]: this is enough to claim that there is only one possible choice for 
$S$, up to isometries, which explicitly is
$$\begin{eqnarray}S=U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2\rangle \oplus \langle -2\rangle ,\qquad S^{\bot _{M}}=\langle 2\rangle \oplus \langle 2\rangle .\end{eqnarray}$$ We then need to look at how 
$L^{\bot }\cong \langle 2(n-1)\rangle$ embeds primitively in 
$S^{\bot _{M}}$. A pair 
$(x,y)$ gives the coordinates of a primitive vector in 
$S^{\bot _{M}}=\langle 2\rangle \oplus \langle 2\rangle$ of square 
$2(n-1)$ if and only if 
$\gcd (x,y)=1$ and 
$x^{2}+y^{2}=n-1$. The orthogonal complement of 
$L^{\bot }$ in 
$S^{\bot _{M}}$, which is 
$T$, is then a lattice isometric to 
$\langle 2(n-1)\rangle$, generated by 
$(-y,x)$. Note that there exist two coprime integers 
$x,y$ such that 
$x^{2}+y^{2}=n-1$ if and only if 
$-1$ is a quadratic residue modulo 
$n-1$.
We now consider the case where 
$\overline{i^{\ast }}=-\text{id}_{A_{L}}$. We have that 
$T$ is 
$2$-elementary of signature 
$(1,0)$; hence, 
$T\cong \langle 2\rangle$. It follows that 
$T$ embeds in a unique way (up to isometries) in the Mukai lattice, with orthogonal complement
$$\begin{eqnarray}T^{\bot _{M}}\cong U^{\oplus 3}\oplus E_{8}^{\oplus 2}\oplus \langle -2\rangle .\end{eqnarray}$$ By Lemma 4.1, there are two distinct discriminant quadratic forms for the orthogonal complement of 
$L^{\bot }$ in 
$T^{\bot _{M}}$, that is, for 
$S$.
(a)
$q_{S}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(-\frac{1}{2(n-1)})\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}(-\frac{1}{2})$.By [Reference Nikulin31, Corollary 1.13.3], up to isometries, there exists only one lattice of signature
$(2,20)$ and with this discriminant quadratic form, which is $$\begin{eqnarray}S=U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle \oplus \langle -2\rangle .\end{eqnarray}$$(b)
$n\equiv 0\;\text{mod}\;4$ and $q_{S}=\frac{\mathbb{Z}}{(n-1)\mathbb{Z}}(-\frac{2}{n-1})$.By the same argument as above, there exists only one isometry class of lattices in this genus. A representative, which can be computed by applying [Reference Gritsenko, Hulek and Sankaran17, Proposition 3.6], is
$$\begin{eqnarray}\hspace{128.39996pt}S=U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \left(\begin{array}{@{}cc@{}}-2 & -1\\ -1 & \displaystyle -\frac{n}{2}\end{array}\right).\hspace{102.0pt}\square\end{eqnarray}$$
Remark 4.4. The three cases of Proposition 4.3 can be distinguished also by looking at the generator 
$t\in H^{2}(X,\mathbb{Z})$ of the invariant lattice 
$T$. In fact, by [Reference Gritsenko, Hulek and Sankaran17, Proposition 3.6], we have the following:
∙ in case (1),
$t$ has square $2(n-1)$ and divisibility $n-1$;∙ in case (2a),
$t$ has square $2$ and divisibility $1$;∙ in case (2b),
$t$ has square $2$ and divisibility $2$.
We point out that, by the global Torelli theorem for IHS manifolds, the existence of a primitive ample 
$t\in \text{NS}(X)$ with one of these three combinations of square and divisibility is sufficient to prove the existence of a non-symplectic involution on 
$X$, whose invariant lattice is 
$T=\langle t\rangle$ (see [Reference Cattaneo13, Proposition 5.3]).
4.1.2 Invariant sublattice of rank two
The aim of this section is to study the cases where 
$\operatorname{rk}(T)=2$. In particular, we describe the discriminant groups of the invariant and coinvariant lattices in complete generality, but we address the problem of their realization and uniqueness only for 
$n\leqslant 5$.
Assume that 
$\operatorname{rk}(T)=2$ so that the signature of 
$T$ is 
$(1,1)$. We first consider the case where the induced action on 
$A_{L}$ is the identity; hence, 
$S$ is a 
$2$-elementary lattice of signature 
$(2,19)$ and 
$S^{\bot _{M}}$ is 
$2$-elementary of signature 
$(2,1)$. It follows from [Reference Nikulin31, Theorem 1.1.2] that 
$S^{\bot _{M}}$ has a unique embedding in the Mukai lattice, up to isometries. By [Reference Dolgachev15, Theorem 1.5.2], we have then two possibilities:
$$\begin{eqnarray}S^{\bot _{M}}=U\oplus \langle 2\rangle \qquad \text{or}\qquad S^{\bot _{M}}=U(2)\oplus \langle 2\rangle .\end{eqnarray}$$ The invariant lattice 
$T$ is realized as the orthogonal complement of a primitive element of square 
$2(n-1)$ inside 
$S^{\bot _{M}}$.
∙ Case
$S^{\bot _{M}}=U\oplus \langle 2\rangle$. By Lemma 4.1, we have two possibilities.(1)
$q_{T}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(-\frac{1}{2(n-1)})\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}(\frac{1}{2})$.A realization for this lattice
$T$ is given by $T=\langle -2(n-1)\rangle \oplus \langle 2\rangle$; if $n\leqslant 5$, this is the only isometry class in the genus by the classification of indefinite binary forms [Reference Conway and Sloane14, Chapter 15, Table 15.2a].(2)
$n\equiv 2\;\text{mod}\;4$ and $q_{T}=\frac{\mathbb{Z}}{(n-1)\mathbb{Z}}(-\frac{2}{n-1})$.A lattice
$T$ with this discriminant quadratic form and signature $(1,1)$ is the following: For$$\begin{eqnarray}T=\left(\begin{array}{@{}cc@{}}2 & -1\\ -1 & \frac{2-n}{2}\end{array}\right).\end{eqnarray}$$$n=2$, this lattice is unimodular, isometric to $U$, and therefore unique in its genus.
∙ Case
$S^{\bot _{M}}=U(2)\oplus \langle 2\rangle$. By Lemma 4.1, we have the following possibilities:(1)
$q_{T}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(-\frac{1}{2(n-1)})\oplus u_{2}\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}(\frac{1}{2})$.This quadratic form cannot be realized by a lattice of signature
$(1,1)$ since its length is $4$.(2)
$n\equiv 2\;\text{mod}\;4$ and $q_{T}=\frac{\mathbb{Z}}{(n-1)\mathbb{Z}}(-\frac{2}{n-1})\oplus u_{2}$.For
$n=2$, the quadratic form is $2$-elementary, and, therefore, there is a unique lattice in the genus up to isometries, namely $U(2)$ (see [Reference Dolgachev15, Theorem 1.5.2]).(3)
$q_{T}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(-\frac{1}{2(n-1)})\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}(\frac{1}{2})$.A realization for this lattice is given by
$T=\langle -2(n-1)\rangle \oplus \langle 2\rangle$; if $n\leqslant 5$, this is the only isometry class in the genus by the classification of indefinite binary forms [Reference Conway and Sloane14, Chapter 15, Table 15.2a].
For 
$n\leqslant 5$, we summarize these results as follows.
Proposition 4.5. Let 
$X$ be a manifold of 
$K3^{[n]}$-type for 
$2\leqslant n\leqslant 5$, and let 
$i\in \operatorname{Aut}(X)$ be a non-symplectic involution. If the invariant lattice 
$T\subset H^{2}(X,\mathbb{Z})$ has rank two and 
$i^{\ast }$ acts as 
$\operatorname{id}$ on 
$A_{H^{2}(X,\mathbb{Z})}$, then one of the following holds:
(1)
$T\cong \langle 2\rangle \oplus \langle -2(n-1)\rangle$ and $S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2\rangle$;(2)
$T\cong \langle 2\rangle \oplus \langle -2(n-1)\rangle$ and $S\cong U\oplus U(2)\oplus E_{8}^{\oplus 2}\oplus \langle -2\rangle$;(3)
$n=2$, $T\cong U$, and $S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2\rangle$;(4)
$n=2$, $T\cong U(2)$, and $S\cong U\oplus U(2)\oplus E_{8}^{\oplus 2}\oplus \langle -2\rangle$.
We assume now that the action of the involution on the discriminant group is 
$-\text{id}$. In this case, 
$T$ is 
$2$-elementary of signature 
$(1,1)$, so 
$T^{\bot _{M}}$ is also 
$2$-elementary and its signature is 
$(3,19)$. This implies that 
$S$ (which is the orthogonal complement of a primitive element of square 
$2(n-1)$ inside 
$T^{\bot _{M}}$) has signature 
$(2,19)$. By [Reference Dolgachev15, Theorem 1.5.2], there exist three 
$2$-elementary lattices of signature 
$(1,1)$, namely 
$U$, 
$U(2)$, and 
$\langle 2\rangle \oplus \langle -2\rangle$. Every such lattice, by [Reference Nikulin31, Theorem 1.1.2], embeds in the Mukai lattice in a unique way (up to isometries); hence, the orthogonal complement is uniquely determined too. We analyze the three cases separately: in each of them, there is only one isometry class in the genus of 
$S$ by [Reference Nikulin31, Corollary 1.13.3].
∙ Case
$T=U$. We have $T^{\bot _{M}}\cong U^{\oplus 3}\oplus E_{8}^{\oplus 2}$, which is unimodular. By Lemma 4.1, the only possible orthogonal complement of $\langle 2(n-1)\rangle$ inside $T^{\bot _{M}}$ is $$\begin{eqnarray}S=U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle .\end{eqnarray}$$∙ Case
$T=U(2)$. Here $T^{\bot _{M}}\cong U^{\oplus 2}\oplus U(2)\oplus E_{8}^{\oplus 2}$. By Lemma 4.1, we have the following possible quadratic forms on $A_{S}$:(1)
$q_{S}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(-\frac{1}{2(n-1)})\oplus u_{2}$.The only isometry class in the genus is
$$\begin{eqnarray}S=U\oplus U(2)\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle .\end{eqnarray}$$(2)
$n\equiv 1\;\text{mod}\;2$ and $q_{S}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(-\frac{1}{2(n-1)})$.The only isometry class in the genus is
$$\begin{eqnarray}S=U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle .\end{eqnarray}$$
∙ Case
$T=\langle 2\rangle \oplus \langle -2\rangle$. We have $T^{\bot _{M}}=U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle 2\rangle \oplus \langle -2\rangle$. By Lemma 4.1, there are three possibilities.(1)
$q_{S}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(-\frac{1}{2(n-1)})\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}(\frac{1}{2})\oplus \frac{\mathbb{Z}}{2\mathbb{Z}}(-\frac{1}{2})$.The only isometry class in the genus is
$$\begin{eqnarray}S=U\oplus E_{8}^{\oplus 2}\oplus \langle 2\rangle \oplus \langle -2\rangle \oplus \langle -2(n-1)\rangle .\end{eqnarray}$$(2)
$n\equiv 0\;\text{mod}\;2$ and $q_{S}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(-\frac{1}{2(n-1)})$.The only isometry class in the genus is
$$\begin{eqnarray}S=U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle .\end{eqnarray}$$(3)
$n\equiv 1\;\text{mod}\;4$ and $q_{S}=\frac{\mathbb{Z}}{2(n-1)\mathbb{Z}}(\frac{n-2}{2(n-1)})$.For
$n=5$, a representative of the unique isometry class in this genus is $$\begin{eqnarray}S=U\oplus E_{8}^{\oplus 2}\oplus \left(\begin{array}{@{}ccc@{}}-2 & 1 & 0\\ 1 & -2 & 1\\ 0 & 1 & 2\end{array}\right).\end{eqnarray}$$
The next proposition summarizes all possible pairs of lattices 
$T,S$ corresponding to involutions whose action on the discriminant group 
$A_{L}$ is 
$-\text{id}$, for 
$n\leqslant 5$.
Proposition 4.6. Let 
$X$ be a manifold of 
$K3^{[n]}$-type for 
$2\leqslant n\leqslant 5$, and let 
$i\in \operatorname{Aut}(X)$ be a non-symplectic involution. If the invariant lattice 
$T\subset H^{2}(X,\mathbb{Z})$ has rank two and 
$i^{\ast }$ acts as 
$-\text{id}$ on 
$A_{H^{2}(X,\mathbb{Z})}$, then one of the following holds:
(1)
$T\cong U$ and $S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$;(2)
$T\cong U(2)$ and $S\cong U\oplus U(2)\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$;(3)
$T\cong \langle 2\rangle \oplus \langle -2\rangle$ and $S\cong U\oplus E_{8}^{\oplus 2}\oplus \langle 2\rangle \oplus \langle -2\rangle \oplus \langle -2(n-1)\rangle$;(4)
$n\in \{3,5\}$, $T\cong U(2)$, and $S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$;(5)
$n\in \{2,4\}$, $T\cong \langle 2\rangle \oplus \langle -2\rangle$, and $S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$;(6)
$n=5$, $T\cong \langle 2\rangle \oplus \langle -2\rangle$, and $S\cong U\oplus E_{8}^{\oplus 2}\oplus \Big(\!\begin{smallmatrix}-2 & 1 & 0\\ 1 & -2 & 1\\ 0 & 1 & 2\end{smallmatrix}\!\Big)$.
Remark 4.7. For 
$n=2$, the isometries 
$\operatorname{id}$ and 
$-\text{id}$ of 
$A_{L}\cong \mathbb{Z}/2\mathbb{Z}$ coincide; hence, Propositions 4.5 and 4.6 give the same classification (to check this, recall that 
$U(2)\oplus \langle -2\rangle \cong \langle 2\rangle \oplus \langle -2\rangle \oplus \langle -2\rangle$ by [Reference Dolgachev15, Theorem 1.5.2]).
4.2 Deformation types for families of large dimension
The lattice computations of Sections 4.1.1 and 4.1.2 allow us to determine all moduli spaces 
${\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}$, for 
$T$ an admissible invariant sublattice of rank one or two inside 
$L$ (recall the definitions from Section 3), for IHS manifolds of 
$K3^{[n]}$-type of dimension 
$2n\leqslant 10$. By construction, the moduli spaces 
${\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}$ arise as subspaces of the complex space 
${\mathcal{M}}_{L}$, which parametrizes marked IHS manifolds of 
$K3^{[n]}$-type. The following fact was remarked in [Reference Artebani, Sarti and Taki1, Theorem 9.5] for 
$K3$ surfaces, and it can be easily generalized to manifolds of 
$K3^{[n]}$-type.
Lemma 4.8. Let 
$T^{\prime },T^{\prime \prime }\subset L$ be the invariant lattices of two monodromy operators 
$\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D70C}^{\prime \prime }\in \operatorname{Mon}^{2}(L)$, respectively, and let 
$S^{\prime }=(T^{\prime })^{\bot },S^{\prime \prime }=(T^{\prime \prime })^{\bot }$ be their orthogonal complements in 
$L$. The moduli space 
${\mathcal{M}}_{T^{\prime },\unicode[STIX]{x1D70C}^{\prime }}$ is in the closure (as a complex space) of 
${\mathcal{M}}_{T^{\prime \prime },\unicode[STIX]{x1D70C}^{\prime \prime }}$ if and only if 
$S^{\prime }\subset S^{\prime \prime }\subset L$ and 
$(\unicode[STIX]{x1D70C}^{\prime \prime })|_{S^{\prime }}=(\unicode[STIX]{x1D70C}^{\prime })|_{S^{\prime }}$.
Remark 4.9. In our setting, we can slightly improve the result of Lemma 4.8. In fact, as observed in Section 3, the orthogonal sublattices 
$T,S\subset L$ determine the involution 
$\unicode[STIX]{x1D70C}\in \operatorname{Mon}^{2}(L)$ as the unique extension of 
$\operatorname{id}_{T}\oplus (-\text{id}_{S})$ to 
$L$. So, if we assume that 
$S^{\prime }\subset S^{\prime \prime }$, then
$$\begin{eqnarray}(\unicode[STIX]{x1D70C}^{\prime \prime })|_{S^{\prime }}=(-\text{id}_{S^{\prime \prime }})|_{S^{\prime }}=-\text{id}_{S^{\prime }}=(\unicode[STIX]{x1D70C}^{\prime })|_{S^{\prime }}.\end{eqnarray}$$ In the case of involutions, we can then say that 
${\mathcal{M}}_{T^{\prime },\unicode[STIX]{x1D70C}^{\prime }}$ is in the closure of 
${\mathcal{M}}_{T^{\prime \prime },\unicode[STIX]{x1D70C}^{\prime \prime }}$ if and only if 
$S^{\prime }\subset S^{\prime \prime }\subset L$, as embedded sublattices.
In this sense, the moduli spaces 
${\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}$ of maximal dimension (where maximality is with respect to this notion) correspond to minimal (with respect to inclusion) admissible sublattices 
$T\subset L$. This is the reason why, in the previous section, we investigated in detail admissible invariant lattices of low rank. Any of these admissible lattices 
$T$ will give rise to at least one (but there could be more a priori, depending on the number of connected components of the moduli space) projective family of dimension 
$21-\operatorname{rk}(T)$, whose generic member has a non-symplectic involution with invariant lattice 
$T$. We are now interested in computing the number of irreducible components for some of these moduli spaces.
We adopt the notation of [Reference Joumaah22, Chapter 4]. Let 
$T\subset L$ be an admissible sublattice, that is, the (hyperbolic) invariant lattice of an involution 
$\unicode[STIX]{x1D70C}\in \operatorname{Mon}^{2}(L)$, and let 
${\mathcal{C}}_{T}$ be one of the two connected components of the cone 
$\{x\in T\otimes \mathbb{R}\mid (x,x)>0\}$. The Kähler-type chambers of 
$T$ are the connected components of
$$\begin{eqnarray}{\mathcal{C}}_{T}\setminus \mathop{\bigcup }_{\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}(T)}\unicode[STIX]{x1D6FF}^{\bot }\end{eqnarray}$$ where 
$\unicode[STIX]{x1D6E5}(T)$ is the set of wall divisors in 
$T$. As before, let 
$\unicode[STIX]{x1D6E4}_{T}$ be the image of the restriction map 
$\operatorname{Mon}^{2}(L,T)\rightarrow O(T)$: the subgroup 
$\unicode[STIX]{x1D6E4}_{T}\subset O(T)$ has finite index and it conjugates invariant wall divisors; therefore, it also acts on the set 
$\text{KT}(T)$ of Kähler-type chambers of 
$T$ (see [Reference Joumaah22, Section 4.7]). In [Reference Joumaah22, Theorem 4.8.11], Joumaah proved that the quotient 
$\text{KT}(T)/\unicode[STIX]{x1D6E4}_{T}$ is in one-to-one correspondence with the set of distinct deformation types of marked manifolds 
$(X,\unicode[STIX]{x1D702})\in {\mathcal{M}}_{T,\unicode[STIX]{x1D70C}}$.
Proposition 4.10. Let 
$T\cong U(2)$ be a primitive sublattice of 
$L=U^{\oplus 3}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$ with orthogonal complement 
$S\cong U\oplus U(2)\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$. Let 
$\unicode[STIX]{x1D70C}_{1}\in \operatorname{Mon}^{2}(L)$ be the involution which extends 
$\operatorname{id}_{T}\oplus (-\text{id}_{S})$. Then, for any 
$n\geqslant 2$, there is a single deformation type of marked manifolds of 
$K3^{[n]}$-type 
$(X,\unicode[STIX]{x1D702})\in {\mathcal{M}}_{T,\unicode[STIX]{x1D70C}_{1}}$.
Proof. As we recalled above, the number of deformation types of 
$(\unicode[STIX]{x1D70C}_{1},T)$-polarized marked manifolds of 
$K3^{[n]}$-type is equal to the number of orbits of Kähler-type chambers of 
$T$ with respect to the action of the subgroup 
$\unicode[STIX]{x1D6E4}_{T}\subset O(T)$. Let 
$T\cong U(2)$ be as in the statement and let 
${\mathcal{B}}=\{f_{1},f_{2}\}$ be a basis of 
$T$ such that 
$f_{1}^{2}=f_{2}^{2}=0$ and 
$f_{1}f_{2}=2$; an element 
$\unicode[STIX]{x1D6FF}\in T$ with coordinates 
$(a,b)$ with respect to 
${\mathcal{B}}$ has square 
$4ab$ and divisibility in 
$L$ equal to 
$\gcd (a,b)$. In particular, the divisibility can only be one, if 
$\unicode[STIX]{x1D6FF}$ is primitive. However, a direct computation using [Reference Bayer and Macrì2, Theorem 12.1] shows that, if 
$\unicode[STIX]{x1D6FF}$ is a wall divisor with 
$\operatorname{div}(\unicode[STIX]{x1D6FF})=1$, then 
$\unicode[STIX]{x1D6FF}^{2}=-2$ (see [Reference Mongardi27, Remark 2.5]). We conclude that there are no wall divisors 
$\unicode[STIX]{x1D6FF}\in T$ since 
$T\cong U(2)$ contains no elements of square 
$-2$.◻
As we showed in Section 4.1.2, when 
$n$ is odd, there is a second way to embed the lattice 
$U(2)$ in 
$L$, which is not isometric to the one studied in Proposition 4.10.
Proposition 4.11. For 
$n$ odd, let 
$T\cong U(2)$ be a primitive sublattice of 
$L=U^{\oplus 3}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$ with orthogonal complement 
$S\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$. Let 
$\unicode[STIX]{x1D70C}_{2}\in \operatorname{Mon}^{2}(L)$ be the involution which extends 
$\operatorname{id}_{T}\oplus (-\text{id}_{S})$. Then, if 
$n=5$, there are three distinct deformation types of marked manifolds 
$(X,\unicode[STIX]{x1D702})\in {\mathcal{M}}_{T,\unicode[STIX]{x1D70C}_{2}}$.
Proof. As in the proof of Proposition 4.10, we need to study the Kähler-type chambers of 
$T$ and therefore determine whether the lattice contains any wall divisors. Up to isometries, the embedding 
$U(2){\hookrightarrow}L$ in the statement can be realized as follows. Let 
$t=\frac{n-1}{2}\in \mathbb{N}$ and consider the map
$$\begin{eqnarray}j:U(2){\hookrightarrow}L=U^{\oplus 3}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle ,\qquad (a,b)\mapsto 2ae_{1}+(at+b)e_{2}+ag,\end{eqnarray}$$ where 
$\{e_{1},e_{2}\}$ is a basis for one of the summands 
$U$ of 
$L$ and 
$g$ is a generator of 
$\langle -2(n-1)\rangle$. We then have 
$j(U(2))^{\bot }\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$, as required. Let 
${\mathcal{B}}=\{f_{1},f_{2}\}$ be a basis of 
$T=j(U(2))$ as in the proof of the previous proposition. If 
$n=5$ (i.e. 
$t=2$), one can show that the divisibility in 
$L$ of 
$af_{1}+bf_{2}\in T$ is 
$\gcd (2a,b)$; hence, it can only be one or two if the element is primitive. We compute explicitly all possible pairs 
$(\unicode[STIX]{x1D6FF}^{2},\operatorname{div}(\unicode[STIX]{x1D6FF}))$ for wall divisors 
$\unicode[STIX]{x1D6FF}\in L_{5}=U^{\oplus 3}\oplus E_{8}^{\oplus 2}\oplus \langle -8\rangle$. This is an application of [Reference Bayer and Macrì2, Theorem 12.1] and [Reference Mongardi27, Theorem 1.3], which gives the following results:
Since for any 
$\unicode[STIX]{x1D6FF}\in T$, we have 
$\unicode[STIX]{x1D6FF}^{2}\in 4\mathbb{Z}$, the only pairs 
$(\unicode[STIX]{x1D6FF}^{2},\operatorname{div}(\unicode[STIX]{x1D6FF}))$ for wall divisors 
$\unicode[STIX]{x1D6FF}\in T$ are 
$(\unicode[STIX]{x1D6FF}^{2},\operatorname{div}(\unicode[STIX]{x1D6FF}))=(-8,2),(-16,2)$. Each of the two admissible pairs 
$(\unicode[STIX]{x1D6FF}^{2},\operatorname{div}(\unicode[STIX]{x1D6FF}))$ yields a single wall divisor 
$\unicode[STIX]{x1D6FF}\in T$, whose orthogonal complement 
$\unicode[STIX]{x1D6FF}^{\bot }$ intersects the positive cone of 
$T$ in its interior. We therefore have two (distinct) walls, which cut out three Kähler-type chambers in 
${\mathcal{C}}_{T}$. These three chambers correspond to three distinct orbits with respect to the action of the group 
$\unicode[STIX]{x1D6E4}_{T}$ on 
$\text{KT}(T)$. This is due to the fact that an isometry 
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{T}$ permutes the walls of the chambers, which, in our case, are generated by primitive vectors having all different squares.◻
By Proposition 4.3(2a), for any 
$n$, there is always at least one 
$(\unicode[STIX]{x1D70C},T)$-polarization with 
$T\cong \langle 2\rangle$, which we will denote by 
$(\unicode[STIX]{x1D70C}_{a},\langle 2\rangle )$ in what follows; in this case, the orthogonal complement is 
$S=U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle \oplus \langle -2\rangle$. We will also denote by 
$(\unicode[STIX]{x1D70C}_{b},\langle 2\rangle )$ the 
$(\unicode[STIX]{x1D70C},T)$-polarization corresponding to the embedding of 
$T$ given in Proposition 4.3(2b) for 
$n\equiv 0\;\text{mod}\;4$. We will then consider, respectively, for all 
$n\geqslant 2$ and for all positive 
$n\equiv 0\;\text{mod}\;4$, the nonempty moduli spaces 
${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a}}$ and 
${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{b}}$. Furthermore, again by Proposition 4.3, for 
$n\geqslant 3$, there is at most one 
$(\unicode[STIX]{x1D70C},T)$-polarization with 
$T\cong \langle 2(n-1)\rangle$: we denote by 
${\mathcal{M}}_{\langle 2(n-1)\rangle ,\unicode[STIX]{x1D70C}}$ the corresponding moduli space, which is nonempty if and only if 
$-1$ is a quadratic residue modulo 
$n-1$. Finally, for 
$T\cong U(2)$, we have the two polarizations 
$(\unicode[STIX]{x1D70C}_{1},U(2))$, 
$(\unicode[STIX]{x1D70C}_{2},U(2))$ which we studied in Propositions 4.10 and 4.11, respectively.
Theorem 4.12. Let 
$(X,\unicode[STIX]{x1D702})$ be a marked manifold of 
$K3^{[n]}$-type for 
$2\leqslant n\leqslant 5$, and let 
$i\in \operatorname{Aut}(X)$ be a non-symplectic involution such that the pair 
$(X,i)$ deforms in a family of dimension 
$d\geqslant 19$ (i.e. 
$rk(T)\leqslant 2$). Then 
$(X,\unicode[STIX]{x1D702})$ belongs to the closure (as a complex space) of one of the following moduli spaces:
- $n=2$:
- ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a}}$ or ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$;
- $n=3$:
- ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a}}$, ${\mathcal{M}}_{\langle 4\rangle ,\unicode[STIX]{x1D70C}}$, or ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$;
- $n=4$:
- ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a}}$, ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{b}}$, or ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$;
- $n=5$:
- ${\mathcal{M}}_{\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a}}$, ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$, or ${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{2}}$.
All these moduli spaces are irreducible with the exception of 
${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{2}}$ for 
$n=5$, which has three distinct irreducible components.
Proof. Since 
$(X,i)$ deforms in a family of dimension at least 
$19$, it is a pair of type 
$T$ for some admissible lattice 
$T$ with 
$\operatorname{rk}(T)\leqslant 2$. The analogous statement for period domains is an easy consequence of Lemma 4.8 and of Propositions 4.3, 4.5, and 4.6. Moreover, the period map is generically injective when restricted to manifolds polarized with a lattice of rank one, and the same is true in the case of 
$U(2)$ by Proposition 4.10 and by [Reference Joumaah22, Corollary 4.9.6], with the exception of 
$n=5$ and 
${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{2}}$ as explained in Proposition 4.11.◻
5 Examples
Even when we limit ourselves to 
$n\leqslant 5$, we observe that we lack the description of most of the projective families listed in Theorem 4.12. Indeed, while for 
$n=2$, both families have been described in [Reference Boissière, Cattaneo, Markushevich and Sarti7, Reference O’Grady35], and in [Reference Iliev, Kapustka, Kapustka and Ranestad20], for 
$n\geqslant 3$, the family of 
$(\langle 2\rangle ,\unicode[STIX]{x1D70C}_{a})$-polarized manifolds of 
$K3^{[n]}$-type is still unknown. In fact, when 
$n\geqslant 3$, the only two explicit examples which have been found are for 
$n=3$, 
$T\cong \langle 4\rangle$ (see [Reference Iliev, Kapustka, Kapustka and Ranestad21] and Section 2.2) and 
$n=4$, 
$T\cong \langle 2\rangle$ with polarization 
$\unicode[STIX]{x1D70C}_{b}$ (involution of the Lehn–Lehn–Sorger–van Straten eightfold; see, for instance, [Reference Lahoz, Lehn, Macrì and Stellari23]), in addition to the involutions of Hilbert schemes of points on generic projective 
$K3$ surfaces whose existence has been proved by the second author in [Reference Cattaneo13].
We conclude by observing that all families of dimension 
$19$ can, in fact, be realized as families of moduli spaces of stable twisted sheaves on a 
$K3$ surface. We briefly recall the construction and the properties of these moduli spaces.
Let 
$\unicode[STIX]{x1D6F4}$ be a 
$K3$ surface. By [Reference van Geemen39, Section 2], a Brauer class 
$\unicode[STIX]{x1D6FC}\in H^{2}(\unicode[STIX]{x1D6F4},{\mathcal{O}}_{\unicode[STIX]{x1D6F4}}^{\ast })_{\text{tor}}$ of order 
$2$ corresponds to a surjective homomorphism 
$\unicode[STIX]{x1D6FC}:\operatorname{Tr}(\unicode[STIX]{x1D6F4})\rightarrow \mathbb{Z}/2\mathbb{Z}$, where 
$\operatorname{Tr}(\unicode[STIX]{x1D6F4})=\operatorname{NS}(\unicode[STIX]{x1D6F4})^{\bot }\subset H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Z})$ is the transcendental lattice of the surface. A 
$B$-field lift of 
$\unicode[STIX]{x1D6FC}$ is a class 
$B\in H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Q})$ (which can be determined via the exponential sequence) such that 
$2B\in H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Z})$ and 
$\unicode[STIX]{x1D6FC}(v)=(2B,v)$ for all 
$v\in \operatorname{Tr}(\unicode[STIX]{x1D6F4})$ (see [Reference Huybrechts and Stellari19, Section 3]). Note that 
$B$ is defined only up to an element in 
$H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Z})+\frac{1}{2}\operatorname{NS}(\unicode[STIX]{x1D6F4})$.
The full cohomology 
$H^{\ast }(\unicode[STIX]{x1D6F4},\mathbb{Z})=H^{0}(\unicode[STIX]{x1D6F4},\mathbb{Z})\oplus H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Z})\oplus H^{4}(\unicode[STIX]{x1D6F4},\mathbb{Z})$, endowed with the pairing 
$(r,H,s)\cdot (r^{\prime },H^{\prime },s^{\prime })=H\cdot H^{\prime }-rs^{\prime }-r^{\prime }s$, is a lattice isometric to the Mukai lattice 
$M=U^{\oplus 4}\oplus E_{8}^{\oplus 2}$. A Mukai vector 
$v=(r,H,s)$ is said to be positive if 
$H\in \operatorname{Pic}(\unicode[STIX]{x1D6F4})$ and either 
$r>0$ or 
$r=0$ and 
$H\neq 0$ effective or 
$r=H=0$ and 
$s>0$. If 
$v=(r,H,s)\in H^{\ast }(\unicode[STIX]{x1D6F4},\mathbb{Z})$ is positive, and 
$B$ is a 
$B$-field lift of 
$\unicode[STIX]{x1D6FC}$, we define the twisted Mukai vector 
$v_{B}:=(r,H+rB,s+B\cdot H+r\frac{B^{2}}{2})$. If 
$v_{B}$ is primitive and positive, let 
$D$ be a 
$v_{B}$-generic polarization of 
$\unicode[STIX]{x1D6F4}$ so that every Gieseker 
$D$-semistable sheaf of Mukai vector 
$v_{B}$ is 
$D$-stable (see, for instance, [Reference Perego and Rapagnetta36, Section 2.1] for more details on 
$v$-generic polarizations and results on their existence). Then the coarse moduli space 
$M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})$ of 
$\unicode[STIX]{x1D6FC}$-twisted 
$D$-stable sheaves with Mukai vector 
$v_{B}$ is a projective IHS manifold of 
$K3^{[n]}$-type, with 
$n=\frac{v_{B}^{2}}{2}+1$. Moreover, the image of the canonical embedding 
$H^{2}(M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC}),\mathbb{Z}){\hookrightarrow}M$, which we recalled at the beginning of Section 2.1, is the subspace 
$v_{B}^{\bot }\subset M$ (see [Reference Yoshioka41, Section 3]). For the sake of readability, we do not specify the ample divisor 
$D$ in the notation for 
$M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})$, even though the construction depends on it: we will always assume that a choice of a 
$v_{B}$-generic polarization has been made. The transcendental lattice of 
$M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})$ is isomorphic to 
$\ker (\unicode[STIX]{x1D6FC})\subset \operatorname{Tr}(\unicode[STIX]{x1D6F4})$, which is a sublattice of index 
$2$ if 
$\unicode[STIX]{x1D6FC}$ is not trivial. In turn, 
$\operatorname{Pic}(M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC}))\cong v_{B}^{\bot }\cap \operatorname{Pic}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})$ inside 
$H^{\ast }(\unicode[STIX]{x1D6F4},\mathbb{Z})$, where 
$\operatorname{Pic}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})$ is the sublattice generated by 
$\operatorname{Pic}(\unicode[STIX]{x1D6F4})$ and by the vectors 
$(0,0,1),(2,2B,0)$ (see [Reference Yoshioka41, Section 3] and [Reference Macrì and Stellari24, Lemma 3.1]).
Proposition 5.1. For 
$n\geqslant 2$, let 
$(X,\unicode[STIX]{x1D702})$ be a generic element in the moduli space 
${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$ of Proposition 4.10 such that 
$\unicode[STIX]{x1D702}(\operatorname{Pic}(X))\cong U(2)$. Then, the manifold 
$X$ is isomorphic to a moduli space of twisted sheaves on a generic projective 
$\langle 2(n-1)\rangle$-polarized 
$K3$ surface.
Proof. Let 
$\unicode[STIX]{x1D6F4}$ be a generic projective 
$K3$ surface of degree 
$2(n-1)$, that is, 
$\operatorname{Pic}(\unicode[STIX]{x1D6F4})=\mathbb{Z}L$ with 
$L={\mathcal{O}}_{\unicode[STIX]{x1D6F4}}(H)$ for an effective, ample divisor 
$H$ such that 
$H^{2}=2(n-1)$. Let 
$\{e_{1},e_{2}\}$ generate one of the summands 
$U$ in 
$\operatorname{Tr}(\unicode[STIX]{x1D6F4})\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle$ and consider the Brauer class of order two:
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:\operatorname{Tr}(\unicode[STIX]{x1D6F4})\rightarrow \mathbb{Z}/2\mathbb{Z},\qquad v\mapsto (e_{1},v).\end{eqnarray}$$ Clearly, 
$B=\frac{e_{1}}{2}\in H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Q})$ is a 
$B$-field lift of 
$\unicode[STIX]{x1D6FC}$ such that 
$B^{2}=0$ and 
$B\cdot H=0$ since 
$2B\in \operatorname{Tr}(\unicode[STIX]{x1D6F4})$. Consider the primitive positive Mukai vector 
$v=(0,H,0)$: then
$$\begin{eqnarray}v_{B}=(0,H,B\cdot H)=v\end{eqnarray}$$ and the moduli space 
$M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})$ is a manifold of 
$K3^{[n]}$-type with
$$\begin{eqnarray}\operatorname{Tr}(M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC}))\cong \ker (\unicode[STIX]{x1D6FC})\cong U\oplus U(2)\oplus E_{8}^{\oplus 2}\oplus \langle -2(n-1)\rangle .\end{eqnarray}$$ Moreover, 
$\operatorname{Pic}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})=\langle (0,H,0),(0,0,1),(2,2B,0)\rangle \cong \langle 2(n-1)\rangle \oplus U(2)$; thus,
$$\begin{eqnarray}\operatorname{Pic}(M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC}))\cong v_{B}^{\bot }\cap \operatorname{Pic}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})=\langle (0,0,1),(2,e_{1},0)\rangle \cong U(2).\end{eqnarray}$$ Hence, the moduli space 
$Y=M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})$ constructed above has 
$\operatorname{Pic}(Y)\cong T$, 
$\operatorname{Tr}(Y)\cong S$ for the lattices 
$T,S$ of Proposition 4.10. By the same proposition, we know that the moduli space 
${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$ is irreducible. For 
$(X,\unicode[STIX]{x1D702})\in {\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$ generic, we also have 
$\operatorname{Pic}(X)\cong T$ and 
$\operatorname{Tr}(X)\cong S$ (via the marking 
$\unicode[STIX]{x1D702}$). Hence, the statement follows from the generic injectivity of the period map for 
$U(2)$-polarized manifolds of 
$K3^{[n]}$-type (see [Reference Joumaah22, Corollary 4.9.6]).◻
Remark 5.2. Even though we can realize the generic element of 
${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{1}}$ as a marked moduli space of stable twisted sheaves on a smooth 
$K3$ surface 
$\unicode[STIX]{x1D6F4}$ as in the previous proposition, if 
$n\geqslant 3$, we cannot realize the corresponding involution 
$i$ as a twisted induced involution on 
$Y$ (in the sense of [Reference Camere, Kapustka, Kapustka and Mongardi12]) since the group of automorphisms of the 
$K3$ surface 
$\unicode[STIX]{x1D6F4}$ is trivial (see [Reference Saint-Donat38, Section 5]). As a consequence, the problem of finding an explicit description of such a non-symplectic involution remains open.
Proposition 5.3. For 
$n=5$, let 
${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{2}}$ be the moduli space from Proposition 4.11. There exists an irreducible component 
${\mathcal{M}}^{0}\subset {\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{2}}$ such that, for the generic element 
$(X,\unicode[STIX]{x1D702})\in {\mathcal{M}}^{0}$ with 
$\unicode[STIX]{x1D702}(\operatorname{Pic}(X))\cong U(2)$, the manifold 
$X$ is isomorphic to a moduli space 
$Y$ of twisted sheaves on a generic projective 
$\langle 2\rangle$-polarized 
$K3$ surface. Moreover, the non-symplectic involution 
$i\in \operatorname{Aut}(X)$ such that 
$\unicode[STIX]{x1D702}\circ i^{\ast }=\unicode[STIX]{x1D70C}_{2}\circ \unicode[STIX]{x1D702}$ is realized by a twisted induced automorphism on 
$Y$.
Proof. Let 
$\unicode[STIX]{x1D6F4}$ be a generic double cover of 
$\mathbb{P}^{2}$ branched along a smooth sextic curve such that 
$\operatorname{Pic}(\unicode[STIX]{x1D6F4})\cong \langle 2\rangle$ and 
$\operatorname{Tr}(\unicode[STIX]{x1D6F4})\cong U^{\oplus 2}\oplus E_{8}^{\oplus 2}\oplus \langle -2\rangle$. If we denote by 
$g$ the generator of the summand 
$\langle -2\rangle$ inside 
$\operatorname{Tr}(\unicode[STIX]{x1D6F4})$, then the (nonprimitive) index two sublattice 
$U^{\oplus 2}E_{8}^{\oplus 2}\oplus \langle 2g\rangle \subset \operatorname{Tr}(\unicode[STIX]{x1D6F4})$ is isometric to 
$S=U^{\oplus 2}\oplus E_{8}^{\oplus }\oplus \langle -8\rangle$. Let 
$\unicode[STIX]{x1D6FC}$ be the following Brauer class of order two:
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:\operatorname{Tr}(\unicode[STIX]{x1D6F4})\rightarrow \mathbb{Z}/2\mathbb{Z},\qquad \unicode[STIX]{x1D706}+mg\mapsto m,\end{eqnarray}$$ where 
$\unicode[STIX]{x1D706}\in U^{\oplus 2}\oplus E_{8}^{\oplus 2}$ and 
$m\in \mathbb{Z}$. Clearly, 
$\ker (\unicode[STIX]{x1D6FC})=U^{\oplus 2}E_{8}^{\oplus 2}\oplus \langle 2g\rangle \cong S$. Let 
$\{e_{1},e_{2}\}$ generate a summand 
$U$ inside 
$H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Z})\cong U^{\oplus 3}\oplus E_{8}^{\oplus 2}$. We can assume that 
$e_{1}+e_{2}$ is the generator of 
$\operatorname{Pic}(\unicode[STIX]{x1D6F4})$ and, therefore, 
$g=e_{1}-e_{2}$. Note that the rational class 
$B=\frac{e_{2}}{2}\in H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Q})$ is a 
$B$-field lift for 
$\unicode[STIX]{x1D6FC}$ since 
$\unicode[STIX]{x1D6FC}(x)=(e_{2},x)\in \mathbb{Z}/2\mathbb{Z}$ for all 
$x\in \operatorname{Tr}(\unicode[STIX]{x1D6F4})$. Consider the (nonprimitive) positive Mukai vector 
$v=(0,2(e_{1}+e_{2}),0)\in H^{\ast }(\unicode[STIX]{x1D6F4},\mathbb{Z})$. When twisting 
$v$ with respect to the 
$B$-field lift 
$B$, we obtain 
$v_{B}=(0,2(e_{1}+e_{2}),1)$, which is now primitive of square 
$8$. Hence, the moduli space 
$M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})$ is a manifold of 
$K3^{[5]}$-type with transcendental lattice isomorphic to 
$S$. Moreover,
$$\begin{eqnarray}\operatorname{Pic}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})=\langle (0,e_{1}+e_{2},0),(0,0,1),(2,e_{2},0)\rangle ;\end{eqnarray}$$thus,
$$\begin{eqnarray}\operatorname{Pic}(M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC}))\cong v_{B}^{\bot }\cap \operatorname{Pic}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})=\langle (0,0,1),(2,e_{2},0)\rangle \cong U(2).\end{eqnarray}$$ Since 
$\unicode[STIX]{x1D6F4}$ is a generic double cover of the plane, it is equipped with a non-symplectic involution 
$\unicode[STIX]{x1D704}$, which acts as 
$\operatorname{id}$ on 
$H^{0}(\unicode[STIX]{x1D6F4},\mathbb{Z})\oplus \operatorname{Pic}(\unicode[STIX]{x1D6F4})\oplus H^{4}(\unicode[STIX]{x1D6F4},\mathbb{Z})$ and as 
$-\text{id}$ on 
$\operatorname{Tr}(\unicode[STIX]{x1D6F4})$. This implies that both the Brauer class 
$\unicode[STIX]{x1D6FC}:\operatorname{Tr}(\unicode[STIX]{x1D6F4})\rightarrow \mathbb{Z}/2\mathbb{Z}$ and the twisted Mukai vector 
$v_{B}=(0,2(e_{1}+e_{2}),1)$ are 
$\unicode[STIX]{x1D704}$-invariant. Then, by [Reference Camere, Kapustka, Kapustka and Mongardi12, Section 3], the moduli space 
$Y=M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC})$ comes with a (non-symplectic) induced involution 
$\widetilde{\unicode[STIX]{x1D704}}$. In particular, the invariant lattice of 
$\widetilde{\unicode[STIX]{x1D704}}$ is the whole 
$\operatorname{Pic}(M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC}))$ since 
$\unicode[STIX]{x1D704}$ acts trivially on 
$\langle (0,0,1),(2,e_{2},0)\rangle$ by [Reference Camere, Kapustka, Kapustka and Mongardi12, Remark 2.4] (the two classes 
$(2,e_{2},0)$ and 
$(2,\unicode[STIX]{x1D704}^{\ast }(e_{2}),0)=(2,e_{1},0)$ coincide in 
$H^{2}(M_{v_{B}}(\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FC}),\mathbb{Z})$). As in Proposition 5.1, the statement follows from the generic injectivity of the period map after recalling that 
${\mathcal{M}}_{U(2),\unicode[STIX]{x1D70C}_{2}}$ has three irreducible components by Proposition 4.11.◻
Acknowledgments
Chiara Camere and Alberto Cattaneo are grateful to Max Planck Institute for Mathematics in Bonn for its hospitality and financial support. Alberto Cattaneo was also supported by Università degli Studi di Roma Tor Vergata as a member of the project “Families of curves: their moduli and their related varieties” (Codice Unico Progetto: E81
$|$18000100005, in the framework of Mission Sustainability 2017 – Tor Vergata University of Rome, PI: Prof. Flaminio Flamini). Andrea Cattaneo was supported by the LABEX MILYON (ANR-10-LABX-0070) of Université de Lyon, within the program “Investissements d’Avenir” (ANR-11-IDEX- 0007) operated by the French National Research Agency (ANR) and is member of GNSAGA of INdAM. The authors are grateful to Alessandra Sarti and Bert van Geemen for reading the paper and for their suggestions as well as to Giovanni Mongardi for useful remarks. They also want to thank the referee for his/her careful work and comments on a first version of this paper.
