Two-dimensional PIC simulation of atomic clusters in intense laser fields

F. GRESCHIK; H.-J. KULL

doi:10.1017/S026303460422208X

Two-dimensional PIC simulation of atomic clusters in intense laser fields

Published online by Cambridge University Press: 01 June 2004

F. GRESCHIK and

H.-J. KULL

Show author details

F. GRESCHIK: Affiliation:
Institut für Theoretische Physik A, Rheinisch-Westfälische Technische Hochschule Aachen, Germany
H.-J. KULL: Affiliation:
Institut für Theoretische Physik A, Rheinisch-Westfälische Technische Hochschule Aachen, Germany

Article contents

Abstract
1. INTRODUCTION
2. THERMAL EQUILIBRIUM
3. PIC SIMULATION
4. CONCLUSIONS
ACKNOWLEDGMENTS
References

Rights & Permissions

Abstract

Collective absorption of intense laser pulses by atomic clusters is studied by PIC simulations. The cluster is modeled in two-dimensional calculations as a cylindrical plasma column with a diameter of D = 6.4 nm and an initial electron density of ne0 = 1023 cm−3. The frequency and intensity dependence of absorption is discussed. It is found that nonresonant absorption by electron emission increases as a power law with the laser intensity. The absorbed energy per electron reaches a maximum of about Wmax = mωp2D2 (ωp: plasma frequency, m: electron mass) at the intensity where ionization saturates.

Keywords

Atomic clusters Intense laser fields Laser light absorption in plasmas Particle-in-cell method Plasma simulation

Type: Research Article
Information: Laser and Particle Beams , Volume 22 , Issue 2 , June 2004 , pp. 137 - 145

DOI: https://doi.org/10.1017/S026303460422208X [Opens in a new window]
Copyright: © 2004 Cambridge University Press

1. INTRODUCTION

In the past years the interaction of intense laser pulses with atomic clusters has received special attention. The specific absorption properties of atomic clusters (Ditmire et al., 1997a) provide an efficient transfer of energy from the laser pulse to electrons and ions (Shao et al., 1996; Ditmire et al., 1997b, 1999). Subsequent collision processes can triggger further atomic and nuclear reactions. Hard X rays from inner-shell transitions (McPherson et al., 1994; Ditmire et al., 1995) and high neutron yields from fusion reactions in DT clusters (Ditmire et al., 1999) have been observed. A survey of recent developments in this field has been presented by Posthumus (2001).

The effective heating of large atomic clusters has been attributed partly to collisional absorption and partly to resonance absorption. A plasma model of heating has been developed including ionization rates, collision rates and hydrodynamic motion (Ditmire et al., 1996). Particle simulations of small clusters have also been reported (Ditmire, 1998). In the present work, we wish to study collective absorption of a nano-plasma in the framework of particle-in-cell (PIC) simulations. This approach does not include atomic ionization and collisions but it can more fully account for collective absorption including resonance absorption and absorption by electron emission into vacuum (Brunel, 1987). We have performed various simulations in one, two, and three dimensions assuming plane, cylindrical, and spherical cluster geometries. Here we will present results for a cylindrical plasma column that we have obtained by relativistic electromagnetic PIC simulations in two dimensions. This work is an extension of a previous one-dimensional electrostatic analysis of a thin plasma layer (Greschik et al., 2000). Recently we have also accomplished calculations of three-dimensional spherical plasmas that represent the actual geometry of clusters. These results will be presented in detail elsewhere.

One of the major differences between atoms and clusters in strong fields is a quite different intensity dependence. A single-electron atom has a relatively sharp optical field ionization threshold. In contrast, for atomic clusters there is a considerable intensity range from the threshold intensity for ionization of single atoms up to the saturation intensity for the ionization of the whole cluster. In this work we have studied the ionization degree and the absorbed energy of clusters in the complete range of laser intensities. It is found that the number of free electrons increases approximately linearly with the laser field and the absorbed energy follows a simple power law up to a maximum energy where collective absorption saturates. However, the intensity scaling of the absorbed energy depends on the geometry and it therefore cannot be predicted by previous one-dimensional capacitor models (Brunel, 1987; Bonnaud et al., 1991; Greschik et al., 2000).

2. THERMAL EQUILIBRIUM

We first describe the equilibrium state that is reached after the electrons of a cylindrical plasma have been heated up to temperature T. We assume that the electrons reach equilibrium while the ions are still cold and uniformly distributed within a cylinder. This idealized equilibrium model can give some insight into the role of the Debye length in a finite size plasma, the magnitude of the surface electric field and into the maximum energy that can be absorbed by the cluster.

The electrostatic potential φ produced by the electron density n_e and the ion density n_i is determined by solving Poisson's equation

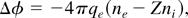
with

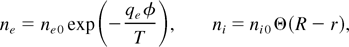
respectively. Here R denotes the radius of the ion density and Z the ion charge state. Looking for cylindrically symmetric solutions of (1) yields

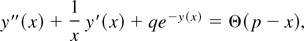
with the dimensionless variables

and the Debye length of the electrons

The differential equation (3) has to be supplemented by appropriate boundary conditions. Here it will be assumed that there is no charge singularity at the origin and that the total charge of the plasma is zero:

respectively. These conditions can be expressed by the boundary conditions

for the electric field y′(x). In the absence of a charge singularity, the potential remains finite at the origin and y(0) = 0 can be chosen without loss of generality. This choice defines the constant n_e0 in Eq. (2) to be the electron density on the axis.

The boundary conditions can only be met for a specific value of the parameter q, which determines the central density n_e0. We have numerically integrated the differential equation with the starting values y(0) = 0 and y′(0) = 0 at the center. The parameter q then was adjusted to achieve convergence at infinity. The results are presented in Figure 1. The typical behavior of these solutions depends on the ratio p = R/λ_D of the radius of the column over the Debye length of the electrons. For p >> 1 the column is neutralized in the center and the electric field is localized near the surface, reaching a maximum value close to T/|q_e|λ_D. When the cluster radius is reduced to the order of the Debye length, screening of the positive charge is no longer effective and the field approaches the field produced by the ions. For p < 2 the electrons are no longer bound by the ions and no equilibrium exists. This may be seen by noting that the number of electrons has to remain finite according to charge neutrality. The unscreened ion potential outside of the column is given by

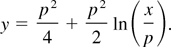
Because the actual potential will be less attractive, a necessary requirement for an equilibrium to exist is that the electron number given by the unscreened potential (4) remains finite:

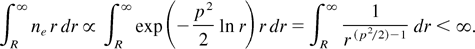
This integral will only converge if p²/2 − 1 > 1 or p > 2. In accordance with this criterium we could not find convergence of the numerical solution for the case p = 1.

Thermal equilibrium of a cylindrical plasma column of radius R. a–c: If the radius is much larger than the Debye length λD the electrons neutralize the interior of the column. The surface field is determined by eEλD ≈ T. d: If R < 2λD the ion field Ei can no longer be screened by electrons and no bound equilibrium exists.

As the cluster is heated, its Debye length increases. The maximum temperature of a bound equilibrium state, corresponding to the condition p = 2, is given by

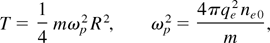
where ω_p denotes the plasma frequency and m_e the electron mass. Above this temperature, the electrons will be basically free and absorption can be expected to saturate in the collisionless limit. The following calculations indicate that the maximum absorbed energy per particle shows the same scaling, being of the order of mω_p²D², where D = 2R is the diameter of the column.

3. PIC SIMULATION

To gain a better understanding of collective absorption in clusters, we have performed PIC simulations for a plasma column in an intense laser field. It is assumed that the atoms of the cluster are ionized nearly instantaneously and homogeneously to some charge state Z. The initial densities of electrons and ions are taken as n_e0 = Zn_i0 = 10²³ cm⁻³, respectively, within a cylinder of radius R = 3.2 nm. Neglecting the ionization energy in comparison with the ponderomotive potential of the laser field, the particles are distributed at rest and the motion of the electrons is calculated in the mean-field approximation by the PIC method. The ions are treated as immobile. The present simulations focus on the collective dynamics of free electrons neglecting atomic processes as well as collisions.

The magnetic field of the incident laser pulse is oriented along the cylinder axis. The motion of the electrons takes place in a plane perpendicular to the cylinder axis. It is treated by relativistic electromagnetic 2d2v PIC simulations based on the methods of Birdsall and Langdon (1991). We use 16–64 particles per cell and 128–2048 cells per coordinate. The laser pulse is modeled as a sin²-pulse with eight cycles in most calculations. We have varied the frequency of the laser between ω = (0.05–1.3)ω_p to distinguish between nonresonant absorption of an overdense plasma and resonant absorption near the plasma frequency. The intensity has been varied in the range 10¹³–10¹⁹ W/cm², which starts at the threshold intensity for electron emission and extends up to the saturation intensity for complete ionization of the cluster. Some of the results are summarized in the following sections.

Nonresonant absorption at low frequencies and high intensities is mainly determined by electrons emitted from the cluster. Within the cluster the electrons are in a quasistatic equilibrium between the external laser field and the electrostatic restoring force of the ions. Far from the cluster, electrons are oscillating in the the laser field. Crossing of the surface of the cluster introduces some phase shift with respect to the quiver motion of free electrons that is responsible for energy gain. As a measure of the number of electrons emitted from the cluster we define an ionization degree of the cluster in the following manner. At the end of the laser pulse the fraction of electrons exterior to the ion cylinder is determined as a function of time and averaged over one further light period in the absence of the field. After the pulse, the number of emitted electrons varies only slightly due to electrons leaving or entering the cylinder and its average is a rather well-defined quantity in simulations. However it is noted that this definition is different from the experimentally accessible charge states of single ions or the theoretical ionization degree of atoms in thermal equilibrium.

3.1. Threshold intensity

First, we will discuss the plasma response at the intensity I = 10¹⁴ W/cm², which is close to the typical threshold intensities for tunneling ionization (Görlinger et al., 2000):

The intensity I_at denotes the intensity that corresponds to a field strength of one atomic unit. In the present simulations, atomic ionization is not included, but the binding potential due to the positive charge of the total cluster leads to a more gradual increase in the number of emitted electrons. At an intensity of I = 10¹⁴ W/cm² a typical fraction of a few percent of the electrons has been emitted.

In Figure 2, one can recognize the evolution of the charge density for two different laser pulses. The first pulse has a frequency ω = 0.1ω_p and a pulse duration of 8 periods. The second pulse has a frequency ω = ω_p and a pulse duration of 64 periods. For comparison, the resonance frequency of a cylindrical plasma column is given by

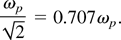
In the first case the quiver amplitudes of the electrons are much larger and one can recognize the acceleration of electrons emitted into vacuum. These electrons are first removed from a surface layer while the interior region remains neutral. Later, the interior of the cluster is also heated. In the second case, the quiver amplitudes on the vacuum side are reduced. The density distribution shows a more spherically symmetric shape with small superimposed dipole oscillations.

Charge density excitations below (ω = 0.1ωp) and above (ω = 1.0ωp) the resonance frequency of a cylindrical cluster at an intensity of 1014 W/cm2. D0: cylinder diameter, T0: laser period.

The frequency dependence of the absorbed energy is shown in Figure 3. In varying the frequency, the pulse duration, and therefore also the pulse energy, was kept constant. The absorbed energy is defined by the difference between the total energies per particle before and after the laser pulse. It is expressed in units of mω_p²D². The figure shows a clear resonance peak at the resonance frequency (7) of a cylindrical plasma column. The figure also shows the ionization degree as defined above, which has a similar resonance behavior. For nonresonant excitation only a few percent of the electrons leave the cluster.

Absorbed energy Wabs and fraction of emitted electrons g as a function of the laser frequency for I = 1014 W/cm2. The maximum corresponds to the resonance of a cylindrical plasma column at the frequency given by Eq. (7).

3.2. Saturation intensity

With increasing intensity, the fraction of emitted electrons plays a more dominant role until all electrons are removed from the cluster at the saturation intensity. We have plotted corresponding results for an intensity of I = 10¹⁷ W/cm², which is somewhat below the saturation intensity. Looking at the charge density distribution in Figure 4, one can no longer see major differences between excitations below and above the resonance frequency. In both cases more than 50% of the electrons have been emitted into vacuum in the final stage.

Charge density for nonresonant (ω = 0.1ωp) and resonant (ω = 1.0ωp) excitation of a cylindrical cluster at 1017 W/cm2. D0: cylinder diameter, T0: laser period.

The absorbed energy has also a different frequency dependence as can be seen in Figure 5. The resonance maximum is somewhat shifted to lower frequencies and its width is strongly broadened. This effect is to be expected because electrons that oscillate across the cluster surface experience a reduced restoring force on the vacuum side. On the average, this reduction will lead to lower oscillation frequencies. It can further be seen that absorption now increases towards lower frequencies. Nonresonant absorption at low frequencies can even be larger than resonance absorption. This nonresonant absorption is attributed to electrons emitted into vacuum. These electrons gain energies of the order of the quiver energy in the laser field. The quiver velocity v = qE/mω increases with decreasing frequency. The fraction of emitted electrons shows a smooth variation in the frequency range considered.

Absorbed energy Wabs and fraction of emitted electrons g as a function of the laser frequency for I = 1017 W/cm2. In addition to a broad resonance peak one observes significant absorption at low frequencies due to electrons that are emitted and subsequently accelerated by the laser field. The quiver energy of these electrons increases with decreasing frequency.

It is also interesting to note that the charge density patterns indicate the presence of harmonics of the laser frequency. These can most easily be recognized in Figure 4 for the smaller frequency ω = 0.1ω_p, being well separated from the plasma resonance. After one period of the laser, the density shows three wave trains excited by the third harmonic. Actually, the dipole spectrum shows maxima at the fundamental, at the third harmonic, and at the column resonance (Fig. 6).

Power spectrum of the x- and y-components of the dipole moment for ω = 0.1ωp (left) and ω = ωp (right) at I = 1017 W/cm2. There are peaks at the laser frequency and at the plasma resonance frequency. For ω = 0.1ωp one can observe in addition odd harmonics in the y-component and even harmonics in the x-component.

3.3. Intensity scaling

For nonresonant absorption by electrons emitted into vacuum one expects a simple scaling of the absorbed energy with the laser intensity. The number of emitted electrons N_free is determined by the displacement ξ of the electrons in the cluster. Assuming a linear restoring force within the cluster, one has N ∝ ξ ∝ E. The energy W_free gained by each emitted electron may be assumed to be some fraction of the quiver energy that is proportional to E². Based on these assumptions, the absorbed energy will scale with the laser intensity I ∝ E² as

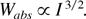
This scaling law was originally proposed by Brunel (1987).

In the framework of the present PIC simulations of a cylindrical plasma column, we have studied the intensity scaling of nonresonant absorption. For these calculations an 8-cycle sin²-pulse with a frequency of ω = 0.1ω_p has been used. The results are presented in Figure 7. In an intensity range between 10¹⁴ and 10¹⁸ W/cm² the absorbed energy obeys to a good approximation a power law

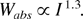
The exponent is larger than 1, corresponding to linear optics, but it is also somewhat smaller than the value 1.5 of Eq. (8). We note that this scaling law is not very sensitive to variations of the frequency between 0.1ω_p and 0.07ω_p or to variations of the particle numbers between 12,868 and 3,217. Differences between these cases can only be observed for intensities below 10¹⁴ W/cm².

Absorbed energy Wabs per particle as a function of the laser intensity. Solid squares indicate the data for the frequency ω = 0.1ωp. For the intensity range 1014 < I < 1018 W/cm2 absorption is dominated by electron emission and a scaling ∝ I1.3 can be found. The absorption of bound electrons at smaller intensities shows a scaling ∝ I but its magnitude depends on the details of the model (frequency, number of simulation particles J).

The discrepancy between the observed scaling (9) and the estimate (8) has the following origin. The fraction of emitted electrons as a function of the laser intensity is shown in Figure 8. One can recognize a gradual increase of the ionization degree around 10¹⁴ W/cm² up to the saturation around 10¹⁸ W/cm². In the intermediate intensity regime the fraction of emitted electrons increases roughly linearly with the laser field, as indicated by the solid line. The scaling N_free ∝ E therefore is satisfied to a reasonable approximation. The average energy per particle in units of the ponderomotive potential

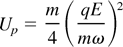
is represented in Figure 9. The total energy increases up to a maximum around 10¹⁸ W/cm². The partition of the total energy into kinetic and potential energies is also shown. It indicates that the potential energy also makes a significant contribution. Finally, one can see the average kinetic energy of the emitted electrons. These energies rise up to a broad plateau of about 0.5U_p but then decrease again toward higher intensities. The absorption efficiency of emitted electrons obviously decreases as one approaches the saturation intensity and the kinetic energy of the emitted electrons is no longer a constant fraction of the ponderomotive potential.

Ionization degree, defined as the fraction of emitted electrons, as a function of the laser intensity. One can recognize a gradual increase at around 1014 W/cm2 and saturation at about 1018 W/cm2. For intermediate intensities the number of emitted particles increases approximately linearly with the electric field .

Energies per particle in units of the ponderomotive potential Up = m(qE)2/(2mω)2 as a function of the laser intensity.

4. CONCLUSIONS

The interaction of atomic clusters with intense laser pulses has been modeled by 2d2v-PIC simulations. The code treats the interaction fully electromagnetic and relativistic but at present it is limited to two dimensions. In this framework, collective absorption of a cylindrical plasma column has been analyzed. It is found that resonance absorption occurs near the resonance frequency of the cylindrical plasma column at moderate laser intensities. At higher intensities the resonance is strongly broadened and in addition there is significant nonresonant absorption by electrons emitted into vacuum. Above the ionization threshold, the fraction of emitted electrons scales roughly linearly with the electric field. The absorption efficiency of free electrons, defined as the fraction of ponderomotive energy gained by these electrons, shows a more complicated behavior and decreases strongly towards the saturation intensity. As a result the intensity scaling of nonresonant absorption is different from the one-dimensional case. The maximum energy absorbed per particle by a single cluster with diameter D and plasma frequency ω_p is about W_max = mω_p²D². This energy is gained when the intensity reaches or exceeds the saturation intensity.

Presently our calculations are extended to three-dimensional spherical clusters. For this purpose it is found advantageous to use particle simulations with a regularized Coulomb interaction at small distances. This method avoids large numerical grids in PIC simulations and proves sufficient to deal with the long-range collective interaction. It is found that the intensity scaling in the three-dimensional case is further reduced.

Another extension of the present model concerns the inclusion of ion motion. As the cluster expands, its density varies from overcritical to undercritical. At the critical density strong resonance absorption can be observed. The particle simulations with ion motion indicate that the plasma resonance can actually be reached after about 35 laser periods for an intensity of 10¹⁴ W/cm². These and other results of the spherical system will be treated in a forthcoming paper.

ACKNOWLEDGMENTS

The authors are grateful to B.U. Felderhof, R. Schmitz, and P. Mulser for discussions.

References

REFERENCES

Birdsall, C.K. & Langdon, A.B. (1991). Plasma Physics via Computer Simulation. Bristol and Philadelphia: IOP Publishing.

Bonnaud, G., Gibbon, P., Kindel, J. & Williams, E. (1991). Laser interaction with a sharp-edged overdense plasma. Laser and Particle Beams 9, 339–354.Google Scholar

Brunel, F. (1987). Not-so-resonant, resonant absorption. Phys. Rev. Lett. 59, 52–55.Google Scholar

Ditmire, T. (1998). Simulation of exploding clusters ionized by high-density femtosecond laser pulses. Phys. Rev. A 57, R4094–R4097.Google Scholar

Ditmire, T., Donnelly, T., Falcone, R.W. & Perry, M.D. (1995). Strong X-ray emission from high-temperature plasmas produced by intense irradiation of clusters. Phys. Rev. Lett. 75, 3122–3125.Google Scholar

Ditmire, T., Donnelly, T., Rubenchik, A.M., Falcone, R.W. & Perry, M.D. (1996). Interaction of intense laser pulses with atomic clusters. Phys. Rev. A 53, 3379–3402.Google Scholar

Ditmire, T., Smith, R.A., Tisch, J.W.G. & Hutchinson, M.H.R. (1997a). High intensity laser absorption by gases of atomic clusters. Phys. Rev. Lett. 78, 3121–3124.Google Scholar

Ditmire, T., Springate, E., Tisch, J.W.G., Shao, Y.L., Mason, M.G., Hay, N., Marangos, J.P. & Hutchinson, M.H.R. (1997b). High-energy ions produced in explosions of superheated atomic clusters. Nature (London) 386, 54–56.Google Scholar

Ditmire, T., Zweiback, J., Yanovsky, V.P., Cowan, T.E., Hays, G. & Wharton, K.B. (1999). Nuclear fusion from explosions of femtosecond laser-heated deuterium clusters. Nature 398, 489–492.Google Scholar

Görlinger, J., Plagne, L. & Hull, H.-J. (2000). Above-barrier ionization and quantum interference in strong laser fields. Appl. Phys. B 71, 331–336.Google Scholar

Greschik, F., Dimou, L. & Hull, H.-J. (2000). Electrostatic model of laser pulse absorption by thin foils. Laser and Particle Beams 18, 367–373.Google Scholar

McPherson, A., Thompson, B.D., Borisov, A.B., Boyer, K. & Rhodes, C. (1994). Multiphoton-induced X-ray emission at 4–5 keV from Xe atoms with multiple core vacancies. Nature (London) 370, 631–634.Google Scholar

Posthumus, J. (2001). Molecules and clusters in intense fields. The Edinburgh Building, Cambridge CB2 2RU, UK: Cambridge University Press.

Shao, Y.L., Ditmire, T., Tisch, J.W.G., Springate, E., Marangos, J.P. & Hutchinson, M.H.R. (1996). Multi-keV electron generation in the interaction of intense laser pulses with Xe clusters. Phys. Rev. Lett. 77, 3343–3346.Google Scholar

Charge density excitations below (ω = 0.1ωp) and above (ω = 1.0ωp) the resonance frequency of a cylindrical cluster at an intensity of 1014 W/cm2. D0: cylinder diameter, T0: laser period.

Charge density for nonresonant (ω = 0.1ωp) and resonant (ω = 1.0ωp) excitation of a cylindrical cluster at 1017 W/cm2. D0: cylinder diameter, T0: laser period.