3.1 Basic framework

Instead of assuming that human beings are selfish and they ‘cooperate’ only when ‘cooperation’ is a derivative of selfish behaviour,Footnote ⁸ as most economics models do, I shall here assume that the cooperative instinct is innately human. Just as self-interest creates drive and ambition, so can these other social concerns. But, more importantly, it is these other social characteristics – mainly the cooperative instinct – that provide the glue to hold society together and prepare the ground for markets to function efficiently (Granovetter Reference Granovetter1985; Elster Reference Elster1989; Arrow Reference Arrow, Aoki and Hayami1998; Nee and Ingram Reference Nee, Ingram, Brinton and Nee1998; Platteau Reference Platteau2000; Basu Reference Basu2000; Francois Reference Francois2002). Turning this argument around, we could claim that economies can fail when the cooperative instinct breaks down. Traditional economics, rooted in methodological individualism, tends to make little room for our innate cooperative spirit and so is handicapped in commenting on its breakdown.

Digressing momentarily, I would like to point out that whether we view the present paper as breaking away from methodological individualism or not depends on how narrow a view we take of methodological individualism. The step taken here may be best thought of as a partial breakaway. If, for instance, we went further and assumed that the altruism that one individual feels for others and the intensity of it depends on how society as a whole behaves and on societal outcomes, then it would be impossible to fully describe an individual's preference without describing the behaviour of the whole group and we would clearly have moved away from the purest form of methodological individualism (Basu Reference Basu, Blume and Durlauf2008). As Pettit (Reference Pettit1993: 117) puts it, ‘the question is whether the whole is something more than a sum of the parts or [. . .] whether the parts are transformed through belonging to the whole’. I am arguing that, in an important sense, the answer to this last question is yes.Footnote ⁹

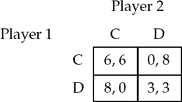
There are many different kinds of games that can be used to understand the connection between trust, altruism and identity – for instance, the Trust Game, the Ultimatum Game and the Traveller's Dilemma (Basu Reference Basu2000; Bowles Reference Bowles2004; Heinrich et al. Reference Heinrich, Boyd, Bowles, Camerer, Fehr and Gintis2004). But let me here use what is, arguably, the most familiar game in the social sciences – the Prisoner's Dilemma. Moreover, the Prisoner's Dilemma has been used very elegantly by Sen (Reference Sen and Korner1974) to motivate the dilemma individuals face between their selfish wants and innate value judgements. The game is illustrated below in Table 1.

Table 1. The Prisoner's Dilemma.

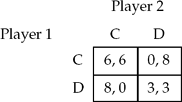
Though its mathematical structure is standard, it will be played differently than in most textbooks. Hence, it needs some explanation. What is illustrated above are the dollar payoffs and I shall take it (purely for expositional ease) that each number represents an index of each person's overall well-being, for instance, units of utility or ‘utils’. It is convenient to assume that utils match one-on-one with dollars. So in this game player 1 can choose between C and D and likewise for player 2. It is a useful mnemonic to think of C as ‘cooperative behaviour’ and D as ‘defection’. If player 1 chooses C and 2 chooses D – something that can equivalently be described as ‘if players 1 and 2 choose (C,D)’ – then 1 earns $0 and 2 earns $8. If they choose (D,C), they earn 8 and 0 dollars, respectively, or (8,0), in brief. And so on. This entire information is summarized in Table 1.

The standard analysis of the game goes as follows. Note that no matter what the other player does, it is better for a player to choose D. Hence, the outcome will be (D,D) – both players will choose defection – and so they will earn $3 each. It is an unfortunate outcome since they could have earned $6 each if both chose C, the cooperative strategy.

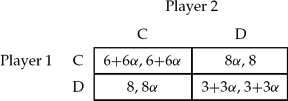
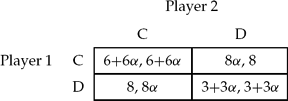
In reality, people do not just maximize their own dollar incomes or even their own utilities. People typically have fellow feeling, altruism, and sense of fairness. To keep the analysis as simple as possible, I shall allow for one kind of other-regardingness in the formal analysis, which will be referred to as altruism.Footnote ¹⁰ This will be captured by assuming as if $1 (or, what is the same in this paper, 1 util) earned by the other player is valued by this player as equal to α dollars of his own, where 0 ≤ α ≤ 1. Later I shall allow the possibility of α varying depending on who the other player is. Thus, α may be 1 for kin, ½ for kith, and 0 for an alien; and so on. But let us, for now, treat this as fixed. Hence, now if player 1 plays C and 2 plays C, player 1's behaviour is predicted by treating her (effective) payoff as 6 + 6α. So the game that the players actually play is described below.

It is possible to argue that the altruism that I feel for another person depends on the altruism he or she is expected to feel for me or how nice she is to me (Rabin Reference Rabin1993; Levine Reference Levine1998; Gintis et al. Reference Gintis, Bowles, Boyd and Fehr2003). Bringing in such interdependent altruism parameters would also allow us to talk about trust and other kinds of social behaviour. But I leave such complexities out of the present paper. Taking a rather novel route, Sen (Reference Sen and Korner1974) argued that our morals may be viewed as a meta-ordering, that is, an ordering over the orderings of all the possible outcomes of the Prisoner's Dilemma. It is interesting to see that, using α = 1, amounts to creating a moral ideal ordering over the four outcomes of the game; and setting α = 0, amounts to capturing the selfishly best (or least morally-tainted) ordering. So there is an implicit meta-binary relation suggested by the approach taken here.Footnote ¹¹

Two important clarifications are worth placing on record. First, one question that may arise in the reader's mind is about the meaning of selfishness. It appears at first sight that, once the α is treated as a part of a person's preference, she can, then on, be thought of being perfectly selfish, since it is her preference to give a weight of α to others’ income. So, it seems arguable that, given her preference, she is just as selfish as a person who values only his own dollars.Footnote ¹² The problem with this line of argument is that it reduces selfishness to a tautology; selfishness then becomes impervious to criticism.Footnote ¹³ To counter this, what has to be kept in mind is that, contrary to what many economists claim, it is not a tautological definition of selfishness that economists end up using. Economists would not have been able to derive any testable proposition if they did so. Because all behaviour would then be compatible with selfishness, the selfishness assumption would not be able to predict any behaviour.

Hence, the way I view α here is not as an innate part of a person's utility but simply as a guide to a person's behaviour. Indeed, it may not be a part of our preference; it could be simply that we behave as if we valued other people's dollars by that amount. A player's welfare or level of utility is throughout measured by the utils shown in Table 1. To prevent ambiguity, the reader may think of this as reflecting the person's economic well-being or welfare. What is being argued, in that case, is that people do not play to maximize their economic well-being but a hybrid of that and social and moral values, captured by α.

Consider a person who gives $1000 to a charity. It would be reasonable to say that he preferred to give this money (that would be pretty normal use of English). But would we say that he is better off by giving the $1000 to the charity? Many mainstream economists would say yes, but I would contest this and argue that the person is worse off, in terms of most reasonable interpretations of well-being (and, if we restrict attention to economic well-being, this is even more obvious) but that he, nevertheless, prefers to make that little sacrifice for a good cause.Footnote ¹⁴ Otherwise, ‘making a sacrifice’ would have to be deleted from our lexicons. This divergence between the index of individual well-being and what guides individual behaviour needs some getting used to since it is alien to traditional choice theory. Fortunately, there is a small literature in game theory that inclines towards this: see Weibull (Reference Weibull and Huck2004) and Battigalli and Dufwenberg (Reference Battigalli and Dufwenberg2005).Footnote ¹⁵

Another way to get to the same conclusion is by a slightly unusual use of the familiar mathematical method of ‘proof by contradiction’. Here we do not really reach a contradiction but an unacceptable conclusion. Assume that a person's choice always exactly reflects his or her utility or welfare. Economists often try to prevent excessive government intervention by arguing that, if an exchange or trade enhances the utilities of the buyer and the seller, and has no negative fall-out on a third party, then there is no moral justification for stopping the trade or exchange (this is the Paretian argument).Footnote ¹⁶ Suppose now a politician bans the sale of houses. The standard argument that economists use against such an ill-conceived intervention is to point out that if an adult wants to sell his house and another adult wants to buy it, it is reasonable to expect that they will be better off by this, and since this is no one else's concern, this is a Pareto improvement; and so government should not ban it. But note that the politician can turn around and argue that since she is choosing to stop the sale, and choice reflects utility, the sale is no longer a Pareto improvement.

So, by this argument, no government intervention can ever be stopped on the ground that the intervention impedes a Pareto improvement, because the mere fact of the politician choosing to stop a transaction makes the transaction a non-Pareto-improvement. This somewhat absurd conclusion arises from the supposition that choice always reflects the chooser's welfare. Indeed it seems entirely plausible to me that a politician's policy choice is not something that should be equated with the politician's own utility.

To sum up, there are three indicators associated with each person – the dollars earned by her, the utility she gets and what I call her ‘effective payoff’.Footnote ¹⁷ In this paper I treat the first two as the same – they are at times called ‘material payoffs’ in the literature (see Sethi and Somanathan Reference Sethi and Somanathan2001). This is an innocuous assumption, made for expositional convenience. However, I treat the third as distinct from the other two. This is a significant assumption – one that is crucial to this paper. Hence, what is being assumed is that the effective payoff numbers are guides to human behaviour. People behave as if they are maximizers of those numbers. Their well-being however is related to but distinct from those numbers. The well-being numbers are given in Table 1 and the effective payoffs shown in Table 2 are the numbers we get by making the α-based corrections to them. In a paper trying to develop criteria for moral decisions, Dietrich (Reference Dietrich2006) draws a useful distinction between (among other things) welfarism and preferencism. Using his language, moral evaluation based on Table 1 amounts to welfarism, whereas that based on Table 2 is preferencism. It must be evident that this paper is making a case for welfarism.Footnote ¹⁸

Table 2. The Behavioural Payoffs.

Second, while formally what I am modelling is altruism rather than trust, it is reasonable to think of the model as an idiom for trust or other indicators of a person's sense of society. As will be evident soon (from Figure 1 below), a person's likelihood of cooperation depends on her expectation that the other person will cooperate. Hence, we could think of the player's decision as follows. If she trusts that the other person will cooperate, then she will be more inclined to cooperate. Hence, the analysis that follows, while explicitly that of altruism, could also be thought of as a model of mutual trust.

Figure 1. The Zone of Cooperation.

We could similarly, introduce stigma into the model by assuming that there is some stigma attached to being selfish and playing D. Of course, the person who chooses D need not be selfish but could be playing this in anticipation of the other player choosing D. But one of the functions of stigmatization, as pointed out by Gans (Reference Gans1972), is to scapegoat individuals in order to maintain certain norms of behaviour. Further, in a more sophisticated and realistic model we may wish to allow for the fact that the α I attach to the other player's utility would generally depend on how she achieved it. I may attach a higher α to her income if she achieves it through (C,C), than if she achieves it through (C,D). But I shall here stay away from such complications.

Let me conclude this sub-section with a digression to address a question of language that arises here and later. It was argued above that, when people are asked to play the Prisoner's Dilemma game as described in Table 1, they often play it differently from what standard analysis suggests. It is possible to argue, however, that it is not as if people play the Prisoner's Dilemma game differently from what textbooks suggest, but that when they play the game in Table 1, they are not playing the Prisoner's Dilemma at all but a mentally re-interpreted ‘new’ game, that is described in Table 2. In that case, instead of saying that people play the Prisoner's Dilemma in a non-standard way, we would have to say that they end up playing another game in a standard way. As soon as we differentiate between what denotes a person's utility and what represents a person's behaviour, this dilemma becomes unavoidable, since what the players are playing may be the Prisoner's Dilemma when we look at the utilities but quite another game when we look at the behavioural payoffs. This is the same problem that Weibull (Reference Weibull and Huck2004) confronts and standard analysis does not have to contend with this problem because it assumes that players interpret games literally and utilities and behavioural payoffs are always identical.Footnote ¹⁹

Given these alternative conventions of language, I prefer to say that when two players play the game in Table 1 they are playing the Prisoner's Dilemma. More generally, the name of the game will be determined by the utilities and not the behavioural payoffs. This has the advantage that the name of the game does not depend on the mental processes of the players. It is just how they play the game that changes (with how they mentally interpret the game). This nomenclature has the added advantage of not rendering the claim of Nash equilibrium play into an unfalsifiable proposition.

3.2 Homogeneous society

Suppose we have a society with n individuals and players are randomly matched with each other and made to play the Prisoner's Dilemma. Note that a society in which players manage to cooperate a lot will become richer and better off over time. And if we append to this simple model a larger economy so that people can save a part of their income (over and above what they need to consume) and earn interest on that, then a society that manages to reach the outcome (C,C) often could become many times more prosperous than a society that always reaches the outcome (D,D). If, for instance, 3 is subsistence consumption, then the latter society will, presumably, have no savings, whereas the former will not only earn more, but save and become even richer in the long run.

Keeping in mind that the cooperative spirit, captured here by the altruism parameter, is natural to human beings, I want to locate conditions under which cooperation will occur and conditions where it will collapse into individualism and totally self-seeking behaviour.

Let us begin by considering the case where a player is uncertain about how her opponent will play. Suppose λ is the probability that the other player will play cooperatively, that is, choose C. Then, if this player plays C, her expected (effective) payoff, denoted by u(C), will be given by:

And, if she chooses D, her expected payoff, u(D), is given as follows.

These are easily derived from Table 2. Hence, she will choose C if and only if u(C) ≥ u(D), or

(1)

Strictly speaking, if u(C) = u(D), she is indifferent between C and D. In order to keep the language of discourse simple, I am using a harmless tie-breaking assumption here, namely, that, when a person is indifferent between cooperation and defection, she chooses cooperation.

Equation 1 can be used to draw a line in an (α, λ)-space which marks the zone where a player will choose to play cooperatively. In Figure 1, the line AB is the graph of (1), with the inequality sign replaced by an equality. Hence, if, for some α, the λ happens to be on or above the line AB, then a player will choose to play C. In other words, if a player's altruism parameter, α, and her expectation that the other player will cooperate, captured by λ, are such that (α, λ) lies on or above the line AB, then and only then will she choose to cooperate.

This does not as yet tell us how this society will behave. This is because, while the society's altruism parameter may be exogenously given,Footnote ²⁰ λ cannot be exogenous. Each individual's decision on how to play the game determines what fraction of society will play C and this determines what λ will be. Hence, we have to derive the value of λ.

This is easily done. If α is to the left of A, that is, α < 1/3, then no matter what the value of λ, a person will choose D. If everybody does this, λ will in fact be 0. Likewise consider the case where α is to the right of B, that is α > 3/5. Then, no matter what value λ takes, each player will choose C. Hence λ will be 1.

Finally, consider the case where . Let me use λ(α) to denote the point on the line AB. That is, λ(α) ≡ (3 − 5α)/(1 + α). If λ > λ(α), then a player confronting this λ will choose C. Since all players are identical, all will choose C under such circumstances; hence λ = 1. If, on the other hand, λ < λ(α), by a similar reasoning λ will be 0. In other words, we have multiple equilibria. This will lead to threshold effects and tipping behaviour, as in Granovetter and Soong (Reference Granovetter and Soong1983) and Schelling (Reference Schelling and Pascal1972), whereby behaviour can swing over from one extreme to another once it goes over a critical line. Finally, if λ = λ(α), then each player is indifferent between C and D. Hence, it is, in principle, possible to have λn players play C and (1 − λ)n players play D. Hence, λ = λ(α) is also an equilibrium, albeit a precarious one.

Gathering the above derivations together, we have the following possible societal equilibria. If α < 1/3, λ = 0. If α > 3/5, λ = 1. If 1/3 ≤ α ≤ 3/5, then λ = 0 or 1 or λ(α). This information is summed by the correspondence illustrated by the thickened line in Figure 1, denoted by FAB0.

If we ignore the points on AB, which depict unstable equilibria (a slight perturbation will have society spiralling away to one of the two other equilibria), then we see that if altruism is very high (α > 3/5) cooperation will be automatic. If altruism is very low (α < 1/3), there can be no cooperation. But with intermediate altruism there are multiple equilibria. The same society can behave totally cooperatively or totally non-cooperatively. By seeing one society behaving cooperatively and getting richer and another that is anarchistic, selfish and poor we cannot conclude that there are innate differences between the people of these societies. It could simply be the case of both behaviours being self-sustaining in equilibrium; and so two ex ante-identical societies could exhibit very different kinds of outcomes.

Some useful policy wisdom emerges from the above model. What we have modelled here as altruism is part of the general idea of other-regardingness and the social spirit. There are situations in life – for instance, in starting a business – where we have to take the risk of vulnerability for the business to work. This is akin to playing C in the Prisoner's Dilemma. If your business partner (player 2) is cooperative (chooses C) you both do well, but if he betrays you, you will do badly (get 0). Hence, what this model shows is that altruism and other-regardingness are critical ingredients for a society to do well and prosper. In the present model we have treated α as exogenous. But we know at an intuitive level that people (especially children) can be taught or inspired to be more altruistic, trustworthy and generally other-regarding. Now, one person being more altruistic (having high α) would not help that person economically. In fact, he would be vulnerable to being cheated. But, if at a societal level all individuals were more altruistic, for instance, with α going from less than 1/3 to over 1/3, then there would be the possibility of greater cooperation and, if α went above 3/5, cooperation would occur for sure, with all the attendant economic benefits of higher income and higher utility, as shown in Table 1.

Hence, greater altruism among a people is like a public good. How exactly a government or an educational institute can create and nurture a more altruistic society we do not fully understand, but, at the same time, we do know that these traits change and can be changed. People can be taught not to litter the streets. Societies can cultivate habits of charity. Corporations can become environment conscious. Even if we do not as yet understand how these things happen, it is important to recognize that (a) unselfishness, altruism and trustworthiness are traits that are innately present in human beings and so can, potentially, be modified and nurtured, and (b) such traits are valuable for economic development and efficiency.

3.3 Heterogeneous society

All this time I have dealt with a society where all individuals have the same level of altruism. But some of the more interesting and complex issues arise when we recognize that the ‘cooperative spirit’, while innate, can vary across individuals.

What we are interested in understanding is what generates greater cooperative behaviour among citizens. The degree of altruism, α, is an instrument towards this. In a homogeneous society, our aim would be to raise α if we wished to make cooperation more likely. But in a heterogeneous society the relation between the distribution of altruism and the possibility of cooperation can be complex. Interestingly, a tiny change in α can cause huge changes in behaviour. For instance, the addition of a small number of selfish individuals in a society can, like adding culture to milk, transform the character of the entire society, in this case to a non-cooperating one. Hence, the cooperative outcome can be a fragile equilibrium.

To understand this, let us suppose that person i has an altruism parameter of α_i. If we number individuals from the most selfish (person 1) to the least selfish (person n) – and clearly there is no loss of generality in this – then we have:

(2)

An individual's altruism parameter is not visible. It will be assumed throughout that n is large; and that, when a player faces an opponent, she assumes that his altruism parameter is α₁ with probability 1/n, α₂ with probability 1/n and so on.

Consider first a case where all n persons have altruism parameters in the interval [1/3, 3/5]. It is then easy to see that everybody playing C is an equilibrium and everybody playing D is another equilibrium. This is obvious. Since each person's α lies between 1/3 and 3/5 each person will choose C if he expects everybody else to choose C; and each person will choose D if he expects everybody to choose D.

What is interesting is that the introduction of one person can cause a breakdown in the cooperative equilibrium. Indeed, the introduction of one low-α (or high-selfishness) person can ensure that society will have a unique equilibrium, where nobody cooperates.

The algebra of this kind of result is rooted in the idea of ‘global games’ and Bayes–Nash equilibria; in different contexts a similar reasoning has been used – see, for instance, Baliga and Sjostrom (Reference Baliga and Sjostrom2004). The intuition is straightforward. Assume that the first t persons (i.e. persons 1 to t) prefer D over C. Now consider the (t + 1)^th person's decision problem. We know from (1), he will prefer D if

Now, since the first t persons prefer D, the probability that a randomly chosen person will play D must be greater than or equal to t/n. Hence, the λ (probability that the other player will play C) that player t + 1 faces is less than or equal to .

Hence, (continuing with the assumption that players 1 to t play D), player t + 1 will certainly play D if

This may be rewritten as

(3)

This is the crucial equation that can be used to show how a small injection of selfish individuals into society can cause a total breakdown in cooperation.

Here is an example. Let us start with a society of 9 individuals ranging from person 2 to person 10. So, as of now, mysteriously, there is no one called person 1. For person t in this society let α_t be equal to (t + 19)/60. Hence,

As we have already seen, since in this society all α's lie between 1/3 and 3/5, this society can be in an equilibrium where everybody cooperates at all times.

Let another person now join this society whose altruism parameter is 19/60. Call him person 1. That is, α₁ = 19/60.

So now we have a 10-person society. It is easy to verify that, for every t, going from 1 to 9, (3) holds. Let us, for instance, check this for t = 5. Since n = 10, the left-hand side of (3) is 25/55. Clearly this exceeds α₆ = 25/60.

Next note that α₁ < 1/3. Hence, player 1 will certainly choose D. Now, since all players, 2 to 10, (that is, t + 1 = 2,. . ., 10), satisfy (3), we know that every player will strictly prefer D. Hence, this society of 10 persons has a unique equilibrium, where nobody cooperates. Though everybody's altruism parameter is unchanged, the injection of one habitual non-cooperator results in a total breakdown of cooperation. In words, the addition of a new person who is innately non-cooperative, vitiates the atmosphere for those individuals in society who were close to the borderline – that is, they needed a lot of assurance that they will not be let down before they decided to play C. These individuals now switch to playing D. This means that for the rest of society the probability of encountering a D player rises. Hence, those on the next borderline switch their choice; and so on.

It should be obvious and can be demonstrated formally with a little additional algebra that if, instead of the addition of a non-cooperative person, one existing citizen had a change of preference whereby he or she became habitually non-cooperative, this could have the same cascading effect. One person's change of preference can cause a change in the behaviour of all other persons in society, despite their preferences remaining unaltered.

This result is akin to what I have in a different context described (Basu Reference Basu2005) as the ‘malignancy of identity’ whereby what may be a dormant marker of identity with no consequence on behaviour can, with a little egging on, acquire malignancy, leading to conflict between the races and different religious groups. This alerts us to the very real risk of how the injection of a small dose of new social norms or individuals carrying those different norms can create a cascading effect of change and breakdown. This must be happening nowadays with the global movement of people. And this must have happened in the heyday of colonialism, when the colonial masters arrived in new lands prepared to cooperate among themselves but not with the indigenous people. Radical writing in developing countries often talks about how the harmony of these economically backward societies, which nevertheless may have had a high moral code of behaviour among themselves, got disrupted by the colonial invasions. There may be an element of exaggeration and false nostalgia, and a tendency to glorify the distant past in this, but that huge disruptions in behaviour codes and social norms can happen is clear enough, as the above theoretical construction illustrates. Just as we now recognize that the injection of new viruses in a society can spell havoc, so can the injection of new norms. It is also conceivable that ‘good norms’ carried into a society by newcomers can spread through the entire society. These are subjects that will need to be studied much more fully in the future. What the above model does is to provide a few basic building blocks for such a venture.

3.4 Alcoves of altruism

Thus far, it was assumed that the altruism person i feels, she feels for everybody in her society. But, as the last discussion in the above sub-section alerts us and the examples in section 2 highlight, this need not be so. People do have different ethics and altruism for in-groups and out-groups. There are many societies fractured along lines of race, gender, religion, country of origin, language identities and caste and people often show extra trust and have an altruism premium for those with whom they share some common identity (see Glaeser et al. Reference Glaeser, Laibson, Scheinkman and Soutter2000; Luttmer Reference Luttmer2001).Footnote ²¹

With this recognition comes the possibility of many complexities. The simplest case is where in-group trust partitions the society into different alcoves, within each of which there is trust and altruism, but these do not extend to across groups. But there can occur situations where i treats j as belonging to i's in-group, unaware that this feeling is not reciprocated. Cooperation in a nation or a group can break down when there are these cross-cutting allegiances. If a nation tries to create fellow feeling and a sense of commitment among its citizens, but a subset of citizens have allegiance to a group identity which is different from that of common citizenship, then cooperation can break down.

Moreover, in the previous sub-sections altruism was always good. But in a society that is fractured, with altruism confined to in-groups, these traits can become instruments of group oppression – where one group oppresses another, building up greater power in the oppressing group than it would have managed if the members of the group tried to carry out the oppression atomistically.

These are directions that will take a lot of time and research effort to pursue. What I will do here is to take some short, tentative steps to illustrate the scope of research that opens up once we allow altruism to be limited to those with whom a player shares a common group identity. Where this sense of identity comes from, whether it is malleable or permanent and whether it can be contained from malignancy are large topics on which much has been writtenFootnote ²² and much more remains to be written. I shall here treat these as primitives by simply assuming that, when playing such games, people make use of some pre-existing sense of in-group allegiance to decide how they will classify their opponents and how they will play against them.

Let me return to the assumption where α is a constant and work with the more interesting case, where . It is not as if I am assuming that everybody feels altruism vis-à-vis everybody, but simply that, when i feels altruism towards j, it is always at a constant altruism parameter of α. We could, in principle, allow the α's to differ but that would complicate the algebra unnecessarily.

To fix the idea of non-symmetric identities, let N = {1,. . ., n} be the set of all people and for each iɛN, let G(i) be the set of people with whom i believes that she shares identity. The presumption is that i's altruism extends only to members of G(i). In the above section, we assumed G(i) = N, for all iɛN. That is, everyone shared the same identity, which in other words means that there was no sense of group identity of any consequence. What is now being claimed is that need not always be true.

Define C ≡ {X ⊂ N| there exists iɛN, such that X = G(i)}. In words, C is the collection of all subsets of N, which have the property that, for each subset, there is some person who considers the subset to be exactly equal to the set of people with whom he or she identifies.

If C happens to be a partition of N, then the analysis will be virtually the same as in the above sections. Within each element of the partition, the game is played exactly as described above. If we suppose people feel altruism only for their own group members, then we could do the same analysis as in sub-section 3.2, but simply think of each group as a society. The analysis then is trivial. When people play across groups they are selfish, that is, they choose D. But within each group there could be cooperation or defection as in Section 3.2. So we could, for instance, have an equilibrium, where group A cooperates and progresses economically, whereas group B is a fractious community living in poverty.

The interesting variations occur when C is not a partition. Suppose society consists of two groups. Let a fraction γ of the population belong to group A (A can be race, caste or the fact of belonging to the same fraternity) and (1 − γ) belong to group B. Hence, γn is the population of A and (1 − γ)n is the population of B. In the formal language developed above, C = {A, N}, where {A, B} is a partition of N.

So the people of group B think of A and B as a common identity, that is, their identity is a general national identity, whereas those in group A share an in-group identity with members of A. It could be that members of group A recognize each other because, for instance, they belong to a secret society, whereas to members in B everybody looks the same. So members of B feel altruism for all individuals in this society and cannot tell who belongs to A and who belongs to B. But members of A can tell a member of A from a non-member, and they have cultivated altruism α only towards their own group members.

Now when a type-B meets another player, the probability that the other player will cooperate is, at most, (1 − γ). Hence, using the same calculation that went behind equation (1) we can see that a type-B will cooperate only if

(4)

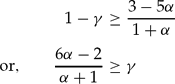
Assume, for instance, that α = 2/5. Then (4) gives us the condition γ ≤ 2/7. Let us suppose this is true and all type Bs cooperate. Type As, on the other hand, cooperate only with their own types.

Hence in this equilibrium type As earn an expected dollar income of 6 γ + 8(1 − γ) every time they play the Prisoner's Dilemma. This is because whenever they meet a type A (probability γ) they earn $6 and, when they meet type B (the trusting type whom they let down), they earn $8.

On the other hand, the expected income of type B is 6(1 − γ). Hence, type As earn more than Bs. But not just that, type As, by forming this in-group collusive block, earn more than they would have earned if they cooperated with all. The latter would give them a per-game income of $6.

There is a Machiavellian lesson tucked away in this algebra. Consider the case where α = 2/5 and γ>2/7. We know from (4) that type Bs will now not cooperate. It is however in the interest of type As to get them to play cooperatively, because that way they can be better ‘exploited’. One way of restoring the ‘exploitative equilibrium’ is for type As to decide, collusively, not to play D against type Bs always, but to occasionally play C. This will enable them to delude the masses into believing that they all share one common identity and play collusively at all times. It is in fact arguable that some of the most successful exploitations of the masses rely, wittingly or unwittingly, on strategies of this kind.

One question that may arise in the reader's mind is about the general applicability of these results, since all the derivations are being done here with the example of the Prisoner's Dilemma and that too for a certain class of payoffs. This would indeed have been cause for concern if I were trying to establish general results – about what will always be true in society. Instead, the aim here is to illustrate how society can exhibit certain kinds of behaviour that were treated as not possible in our textbook models. We have just shown how some groups can use their innate traits of (in-group) altruism to control or even exploit other groups. It is not being claimed that this will always happen but simply that it can happen under plausible conditions. Hence, the illustration of this argument with a game that is accepted as a good model for some social situations suffices for the present context. Of course, testing the frontiers of its generalization would be an interesting exercise for the future.

3.5 Focal identity

The discussion of in-group trust draws attention to another difficulty that could arise with identity-based collusive behaviour. As we have already seen, even if people want to trust others and cooperate, one problem could arise from there being no ‘focal identity’ in the society. In Subsections 3.2 and 3.3 we had assumed that an entire nation shares a common identity and they are bound by a common altruism towards all (though in 3.3 one person's extent of altruism could be different from another's). In 3.4 we saw cases where there could be conflicting identities and this could lead to a subset of society playing cooperatively.

One variant of this problem can lead to a total failure of cooperation in society. It is of course well-recognized that we have multiple identities and this can often (in fact, I believe, more often than not) help hold societies together (Dahrendorf Reference Dahrendorf1959; Sen Reference Sen2005). But this can also lead to a failure of cooperation. To see this, suppose people in a country resolve to be cooperative among those with whom he or she share their primary identity. But if this society lacks a focal identity or has overlapping identities instead of partitioned identities, cooperation may fail to occur in equilibrium.

To see this, suppose in a nation there are two races, 1 and 2, two religions, 1 and 2, and two language groups, 1 and 2. Using notation in an obvious way, we can describe a person as (1,2,1) or (2,2,1) and so on, where (1,2,1) means a person of race 1, religion 2 and language 1. Let me use A to denote the set of all people of type (1,2,1), B to denote all of type (1,1,2) and C to denote (2,1,1). Assume of the population is of type A, of type B and of type C.

Let us now assume that all As think that race is the primary identity (that is, they try to be cooperative with all and only those who share their race), all Bs think that religion is the primary identity and all Cs think that one's mother-tongue is the primary identity. In this society, each person will find that at least of the times they will have the other player choose defect.

Hence, we can see that if α is less than , the right-hand term in (1) is greater than . Since in this society λ is below , by (1) we know that no one will play cooperatively. Thus, even if every player has , no cooperation will occur in this society. The reason for this is the lack of a focal identity.

This has the policy implication that if a government or some collectivity wants to encourage cooperative behaviour in the country or among its members, it must try to create a focal identity among its citizens. Conversely, various repressed groups that fail to rise collectively against their oppressors probably do so for the reason that they do not have a focal identity among themselves. This is an equally useful result for a tyrant or malevolent government trying to prevent some group or nation from acting cooperatively within itself. The aim of the tyrant must be to destroy the group's ability to form a focal identity. Through a deliberate policy of splintering the group's identity into various overlapping and conflicting identities it can keep the group under control and keep at bay the possibility of group rebellion. If you can break up a large group into a partition of smaller groups, that can be useful in foiling rebellion. But if you can destroy the large group's focal identity by nurturing overlapping identities you can do even more damage to the large group. This is the reason why analyses of this kind can be both useful and dangerous.